Геометрические формы и геометрические фигуры: Основные геометрические фигуры 🟢🟨🔺 и их названия

Геометрические фигуры в нашей жизни

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Попова В.К. 1

---

1МОЙ гимназия № 16 “Интерес”

Мирошниченко Н.Р. 1

---

1МОУ гимназия 16 “Интерес”

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

ВЕДЕНИЕ

Вглядываясь в окружающий нас мир, каждый замечал как много фигур вокруг. Люди давно заинтересовались их разнообразием, строением и свойствами. Всем известна фраза: «Все естественное (природное) – красиво». В этой фразе содержится глубокий смысл. Я заметила, что окружающие нас предметы тоже похожи на геометрические фигуры. Меня заинтересовал вопрос о том, как взаимосвязаны между собой природные объекты и геометрические фигуры.

Так возникла идея создать исследование «В мире геометрических фигур».

Цель проекта: исследование и выделение основных геометрических фигур, поиск их в природных объектах, определение их роли в жизни человека.

Гипотеза: основные геометрические формы, окружающие человека, берут своё начало в природе.

Задачи проекта:

Изучить литературу по данному вопросу.

Завести дневник – таблицу: предмет – фигуры.

Проанализировать и сравнить предметы в окружающем пространстве на наличиегеометрических фигур.

Провести анкетирование среди учащихся начальных и старших классов.

С помощью свойств геометрических фигур научиться видеть красоту обычных вещей, смотреть и видеть, думать и делать выводы.

Теоретическая значимость работы

Теоретическая значимость моей работы заключается в том, что результаты изучения и обобщения знаний об основных геометрических фигура помогут мне в дальнейшем применять их при изучении математики (геометрии)в старших классах.

Практическая значимость работы

Моя работа имеет практическую значимость, потому что материалы могут быть использованы для подготовки к урокам, как наглядный материал.

Глава I. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

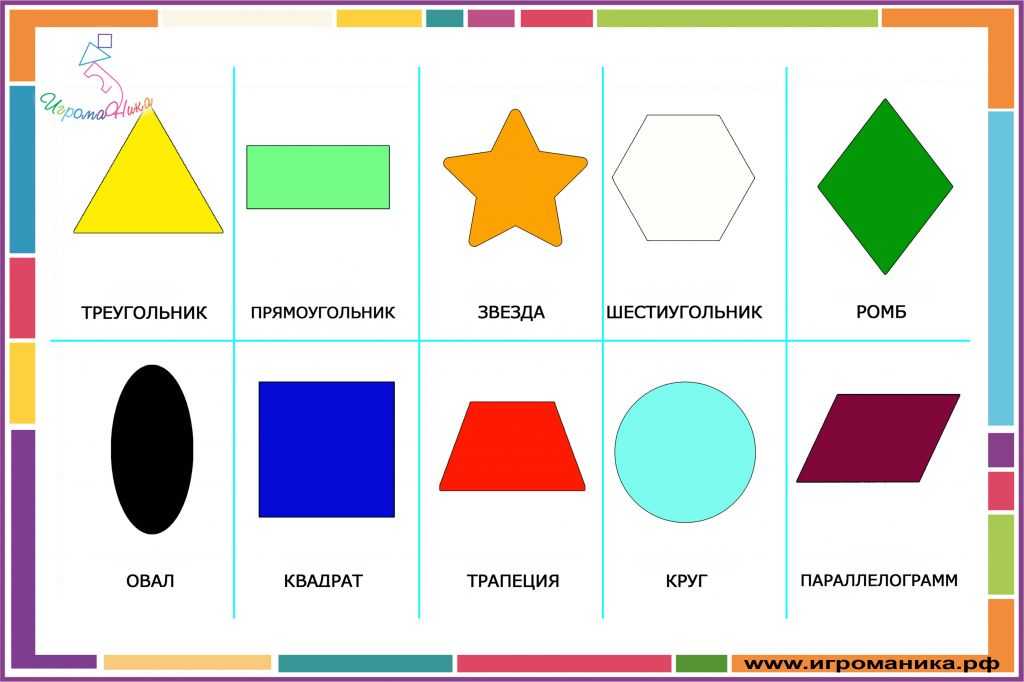
ОСНОВНЫЕ ГЕОМЕТРИЧЕСКИ ФИГУРЫ

Точка — мельчайшая геометрическая фигура, являющаяся основой других фигур во всяком изображении либо чертеже.

Прямая — это геометрическая фигура, обладающая определёнными свойствами. Через любые две точки можно провести прямую, и притом только одну.

Прямоугольник – четырёхугольник, у которого все углы прямые.

Квадрат – равносторонний прямоугольник.

Круг – часть плоскости ограниченная окружностью.

Окружность – граница круга.

Трапеция – четырехугольник, у которого две стороны параллельны, а две другие нет.

Параллелограмм, четырехугольник у которого противоположные стороны попарно параллельны.

Ромб, параллелограмм у которого все стороны равны.

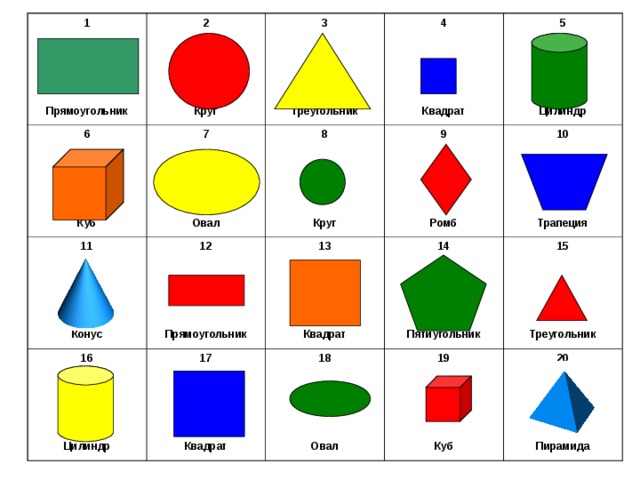
Параллелепипед – геометрическая фигура, у которой 6 граней и каждая из них прямоугольник.

Призма – латинская форма греческого слова «присма» – опиленная (имелось в виду опиленное бревно.

Конус – геометрическое тело, образованное вращением прямоугольного треугольника. Конус – тело, ограниченное конической поверхностью, точкой и кругом.

Цилиндр – это объемная геометрическая фигура, состоящая из двух оснований в виде кругов и одной боковой поверхности в виде прямоугольникаиз его сторон. Означает «валик», «каток».

Пирамида – многогранник, основание которого представляет собой многоугольник, аостальные грани — треугольники с общей вершиной.

Это название пошло от египетских пирамид.

Шар – часть пространства ограниченного сферой.

Разнообразие формы и цвета

Нам подарила родная планета.

А геометрия – это наука о форме предмета.

1.2. ГЕОМЕТРИЧЕСКИЕ ФОРМЫ В ОКРУЖАЮЩЕМ МИРЕ

Каждый из нас замечал, как много фигур существует вокруг нас. Стоит посмотреть вокруг, и мы увидим, что многие предметы имеют форму, похожую на уже знакомые нам геометрические фигуры. Оказывается их очень много.Ученые придерживаются мнения о том, что все, что создается человеком, создается на основе наблюдений за окружающей человека природой. Значит и геометрические фигуры нужно искать в природе.

        В самой природе очень много замечательных геометрических форм. Необыкновенно красивы и разнообразны многоугольники, созданные природой.

Кристаллы горного хрусталя напоминают отточенный карандаш.

Кристалл соли имеет форму куба.

А снежинки – это одна из самых красивых геометрических фигур многоугольники.

Обычная горошина, капельки росы – имеют форму шара.

Фигуры, созданные природой, не только красивы, их форма целесообразна, то есть наиболее удобна. А человеку только остаётся учиться у природы – самого гениального изобретателя.

1.3.ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ  У ЖИВОТНЫХ

Животные, конечно, же, геометрию не изучали, но природа наделила их талантом строить себе дома в форме геометрических тел. Многие птицы строят гнёзда в форме полушара. Необыкновенно красивы и разнообразны многоугольники, созданные природой. Соты пчёл имеют форму шестиугольника. Морские звезды имеют форму пятиугольника. Обычный одуванчик, капельки росы – принимают форму шара.

Внимательно наблюдая за полетом птиц и  формой крыла, человек создал летательные аппараты, за семенами одуванчика – парашют, за формой рыб – подводные лодки. Животные, конечно не ученые, но плотина бобра – это уникальное техническое сооружение с точной геометрией форм и математическими расчетами физических нагрузок.

1.3.ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ  В БЫТУ

В нашей жизни мы часто встречаем геометрические тела и фигуры. Из них состоят все предметы, которые нас окружают, начиная с тарелки с которой едим и заканчивая телевизионной тарелкой, которая передает программы со всего мира. Стены, пол и потолок являются прямоугольниками. Многие вещи напоминают окружность, например, обруч, кольцо, тарелка. Арбуз, глобус, мячи – похожи на геометрический шар. Предметов, имеющих форму цилиндра и конуса в окружающем нас мире очень много: трубы, кастрюли, бочки, стаканы, консервные банки.

II. ПРАКТИЧЕСКАЯ ЧАСТЬ

2.1. ЭКСПЕРИМЕНТ. ПРИРОДНЫЕ ТВОРЕНИЯ ВВИДЕ ГЕОМЕТРИЧЕСКИХ ФИГУР

Я провела небольшой эксперимент с целью выяснить, какие геометрические фигуры чаще всего воспринимают в окружающем мире обучающееся разного возраста, как обучение геометрии развивает воображение, наблюдательность и креативное мышление.

 

ПРИЛОЖЕНИЕ 1.

Дорисовать  геометрические фигурки так, чтобы получились объекты, встречающиеся в природе.

ПРИЛОЖЕНИЕ 2.

По фотографиям природных объектов увидеть геометрические фигуры и начертить их прямо на картинке.

Результаты:

Анализируя результаты выполненной работы своих одноклассников и обучающихся старших классов, я обнаружила, что обучающиеся младших классов плохо различают объемные и плоские фигуры, видят объекты, изображённые на пейзажах, как плоские, испытывают затруднения в определении объема предметов. Например – кактус – это круг, а не шар.  Конечно, мы ещё маленькие и нам ещё предстоит знакомство с геометрическими фигурами на уроках математики, окружающего мира, изобразительного искусства.

У детей старших классов более развито воображение, пространственное и образное мышление.Знание геометрических форм старшими школьниками позволяет воспринимать и структурировать окружающий мир, даёт базовые знания для изучения более сложных наук.

2.1. ИНТЕРЕСНЫЙ СПОСОБ ИСПОЛЬЗОВАНИЯ ГЕОМЕТРИЧЕСКИХ ФИГУР

Дети всегда много рисуют. Оказывается, наши рисунки могут очень многое о нас рассказать. Так пришла идея: с помощью геометрических фигур попытаться исследовать себя. Конечно, тестов мы не создавали, а попросили помощи у нашего школьного психолога Беззубовой Елены Вячеславовны. Она порекомендовал мне один из тестов «Рисунок человечка с помощью геометрических фигур».

Целью теста является определение индивидуальных типологических характеристик человека на основе соотношения геометрических фигур в рисунке, а также графических особенностей его выполнения (приложение 3).

Инструкция:  нарисуйте человечка из десяти геометрических фигур — треугольника, круга и квадрата.  Фигуры можно увеличивать или уменьшать в размере, накладывать друг на друга. Важно, чтобы они все использовались в рисунке, то есть нельзя нарисовать человечка из 10 квадратов, 10 треугольников или 10 кругов.

Обработка данных: подсчитайте, сколько у вас получилось треугольников, кругов и квадратов в рисунке  человечка, и запишите это количество трёхзначным числом, например: треугольников — 3, кругов – 2, квадратов  — 5. Получается число:  325 . Таким  образом, мы получаем трехзначное число, которое обозначает «формулу рисунка».

На основании различий в предпочтениях геометрических фигур при выполнении рисунков человечков образуется восемь основных типов (или групп)  и 63 подтипа.

Теперь выберите, к какой группе относится полученное число:

1. Тип  «Руководитель»: 901, 910, 802, 811, 820, 703, 712, 721, 604, 613, 622, 631, 640

2. Тип «Ответственный исполнитель»: 505, 514, 523, 532, 541, 550 

3. Тип  «Тревожно-мнительный»: 406, 415, 424, 433, 442, 451, 460

4. Тип «Ученый»: 307, 316, 325, 334, 343, 352, 361, 370

5. Тип «Интуитивный»: 208, 217, 226, 235, 244, 253, 262, 271, 280

6. Тип  «Изобретатель, конструктор»: 109, 118, 127, 136, 145, 019, 028, 037, 046

7. Тип  «эмотивный»: 550, 451, 460, 352, 361, 370, 253, 262, 271, 280,154, 163, 172, 181, 190, 055, 064, 073, 082, 091

8. Тип  «противоположный эмотивному»:   901, 802, 703, 604, 505, 406, 307, 208, 109  

ЗАКЛЮЧЕНИЕ

Данная работа посвящена изучению геометрических фигур в окружающем пространстве.

Подводя итог работы, я считаю, что источником изучения геометрических фигур является природа. Сколько она таит в себе загадок и тайн, люди веками изучают ее, но до конца так и не изучили. Человеку остается только учиться у природы – самого гениального изобретателя. Невозможно представить современную жизнь без геометрических фигур, они вокруг нас, мы живем среди них, они нам нужны.

Эксперименты еще раз подтвердили, что именно окружающая человека природа подсказала людям основные геометрические фигуры. И у каждой фигуры есть длина, ширина, высота, площадь и объем Природа подсказывает нам, самые правильные варианты их применения, так как наблюдаемые людьми природные творения не просто красивы, но и детально продуманы. Человеку есть откуда черпать свои идеи, главное научиться внимательно, наблюдать за ней и анализировать причинно – следственную связь.

Закончив своё исследование, я узнала, что  все, что нас окружает, имеет геометрическую форму: микроволновая печь, глобус, шкатулка и многое другое.

Геометрия встречается во многих профессиях, без которых человечество не смогло обойтись. Например, перед тем как построить жилое здание, люди проектируют будущую постройку на чертежах в уменьшенном масштабе. Этим занимается архитектор. Тот, кто руководит общестроительными работами и осуществляет контроль за качеством называется инженером-строителем. Конструктор разрабатывает элементы, части технологических конструкций. Для того чтобы стать конструктором, необходимо сначала выучить множество наук, среди которых присутствует геометрия. С помощью модельера наши вещи становятся более удобными, стильными и качественными. Его задача изготавливать новые модели одежды, определять общее конструктивное решение, придумывать различные дополнения. Психолог с помощью психогеометрии  быстро и точно нарисует психологический портрет испытуемого, узнает, какие черты его характера являются главными, а какие – второстепенными, а также поможет понять, с кем человеку сложнее всего взаимодействовать.

Результаты моего исследования показали, что прогресс и множество современных технологий были бы невозможны без применения знаний по геометрии.

Проведя исследование путём анкетирования детей младших и старших классов, мы выяснили, что у детей старших классов более развито воображение, пространственное и образное мышление. Обучающиеся младших классов испытывают затруднения в определении формы предметов.

Презентация может использоваться на уроках и внеклассных занятиях учащимся классов для введения в раздел математики – геометрии, чтобы вызвать интерес к предмету и помочь ученикам увидеть связь геометрии с окружающим миром.

Знание геометрических фигур, умение видеть их в природных объектах позволяет воспринимать и структурировать окружающий мир, даёт базовые знания для изучения более сложных наук. Сам процесс занятий геометрией имеет большое развивающее значение.

В ходе своей исследовательской работы я достигла поставленных целей, подтвердила свою гипотезу.

ПРИЛОЖЕНИЕ 1

Класс …………

ДОРИСУЙ ФИГУРЫ ТАК, ЧТОБЫ ПОЛУЧИЛИСЬ ОБЪЕКТЫ, КОТОРЫЕ ВСТРЕЧАЮТСЯ В ПРИРОДЕ

–

ПРИЛОЖЕНИЕ 2

Класс …………

КАКИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НАПОМИНАЮТ ДАННЫЕ ОБЪЕКТЫ ПРИРОДЫ

ПРИЛОЖЕНИЕ 3

Тест «Рисунок человека с помощью геометрических фигур»

Инструкция:  нарисуйте человечка из десяти геометрических фигур — треугольника, круга и квадрата.  Фигуры можно увеличивать или уменьшать в размере, накладывать друг на друга. Важно, чтобы они все использовались в рисунке, то есть нельзя нарисовать человечка из 10 квадратов, 10 треугольников или 10 кругов.

Обработка данных: подсчитайте, сколько у вас получилось треугольников, кругов и квадратов в рисунке  человечка, и запишите это количество трёхзначным числом, например: треугольников — 3, кругов – 2, квадратов  — 5. Получается число:  325 . Таким  образом, мы получаем трехзначное число, которое обозначает «формулу рисунка».

На основании различий в предпочтениях геометрических фигур при выполнении рисунков человечков образуется восемь основных типов (или групп)  и 63 подтипа.

Ключ к тесту «Рисунок человечка из геометрических фигур»

Тип 1 – «Руководитель» (901, 910, 802, 811, 820, 703, 712, 721, 604, 613, 622, 631, 640). 

Если вы относитесь к этому типу, то вам свойственны хорошие организаторские и ораторские способности. Вы умеете ставить цели и добиваться их, причем иногда, не взирая ни на здоровье, ни на условия. Люди этого типа хорошие рассказчики и преподаватели.

Ваша воля и энергия нескончаемы. Вы способны заставить себя трудиться долго и устойчиво, имеете твердость и настойчивость, выдержку и самообладание, что делает вас центром внимания. Вы умеете влиять на других людей, убеждать их и вести за собой. Поэтому вполне вероятно, что вы руководитель.

Тип 2— «Ответственный исполнитель» (505, 514, 523, 532, 541, 550). 

Этот тип схож с типом «руководитель», однако важные решения он принимает не так быстро. Но это и к лучшему — так решения получаются обдуманней. Эти люди хорошие профессионалы, нередко управляющие организаций. Они устойчивы и постоянны, экономны и бережливы, интеллектуально развиты. Нередко являются трудоголиками, доводя себя до изнеможения, не сохраняя свое здоровье. Поэтому они подвержены болезням нервного происхождения.
Однако понимание других людей и чувственная сфера у них развиты слабо. Из-за повышенных требований к себе могут работать, не замечая усталости, подрывая здоровье. Поэтому «ответственным исполнителям» необходимо тщательно следить за соблюдением режима труда и отдыха.

Тип 3 — «Тревожно-мнительный» (переживательный, сомневающийся)  (406, 415, 424, 433, 442, 451, 460).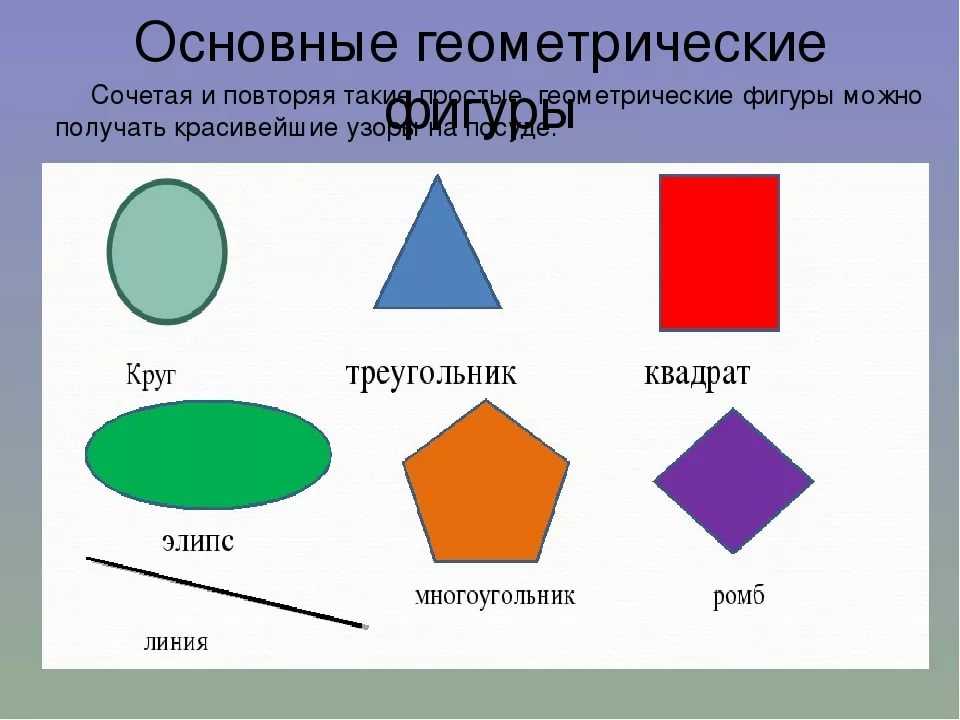

Если вы принадлежите к тревожно-мнительному типу, то вы человек творческий, имеющий разные способности. Однако нуждаетесь в постоянном подбадривании, так как часто сомневаетесь в себе, не верите в свои силы.
Эти люди любят фантазировать. Поэтому искусство для них является неотъемлемой частью жизни. Они наблюдательны, восприимчивы, имеют развитое воображение.
415 — данный подтип людей имеет поэтическую одаренность, способность к стихосложению.
424 — эти люди все делают очень тщательно.

Тип 4 — «Ученый» (307, 316, 325, 334, 343, 352, 361, 370). 

Это люди с развитым логическим мышлением. Нередко они имеют на все свою точку зрения и даже свою теорию. Практически все, происходящее в их жизни, они подвергают анализу, пытаясь из всего выстроить логическую цепочку. Это хорошие ученые, вдумчивые политики, успешные бизнесмены.
Нередко «ученые» желают поделиться своим опытом, обобщая его в книгах или диссертациях. Но они могут обладать и хорошими артистическими способностями, играть на сцене.
325 — природный подтип, любящий биологию, ботанику или медицину. Может с удовольствием выращивать растения и с любовью ухаживать за животными.

ПРИЛОЖЕНИЕ 4. ДНЕВНИК НАБЛЮДЕНИЙ

Предметы		Геометрическая фигура
Холодильник		Прямоугольный параллелепипед
Плита		Прямоугольный параллелепипед
Микроволновая печь		Прямоугольный параллелепипед
Кастрюля
Тарелка
Кровать		Прямоугольный параллелепипед
Шкаф		Прямоугольный параллелепипед
Банка сгущенки		цилиндр
колбаса		цилиндр
дом		Прямоугольный параллелепипед
Электрические провода		Параллельные прямые
ведро		Усеченный конус
капуста		шар
теплица
Сыр		Круг, круговой сектор

Используемая литература

1. Атанасян П.М., Бутузов М.В., Кадомцев А.В., Киселёва А.И.. “Геометрия 7-9” Просвещение 2001

2. Депман И.Я., Виленкин Н.Я. “За страницами учебника математики” Дрофа 2003

3. Дорохов А.А., Михайлов М.М., Куценко Г.М., Назаров А.А. “Что такое? Кто такой?” Дрофа 2005

4. Дорохов А.А., Михайлов М.М., Куценко Г.М., Назаров А.А. “Что такое? Кто такой?” Дрофа 2005

5. Погорелов М.И. “Геометрия 7-11” Просвещение 2001

6. Математический энциклопедический словарь. Гл.ред. Ю.В. Прохоров;Сов. Энциклопедия,1988

7.Энциклопедический словарь юного натуралиста/Сост. А.Г. рогожкин-1981

8. Занимательная геометрия/ К.И. Шевелёв-М.:Ювента,2009

Просмотров работы: 1238

Геометрические фигуры вокруг нас ☛ Helpstudent24.ru

Содержание

Куда бы мы ни посмотрели, везде нас окружают геометрические фигуры. Круг, квадрат, прямоугольник, треугольник, перечислять можно до бесконечности.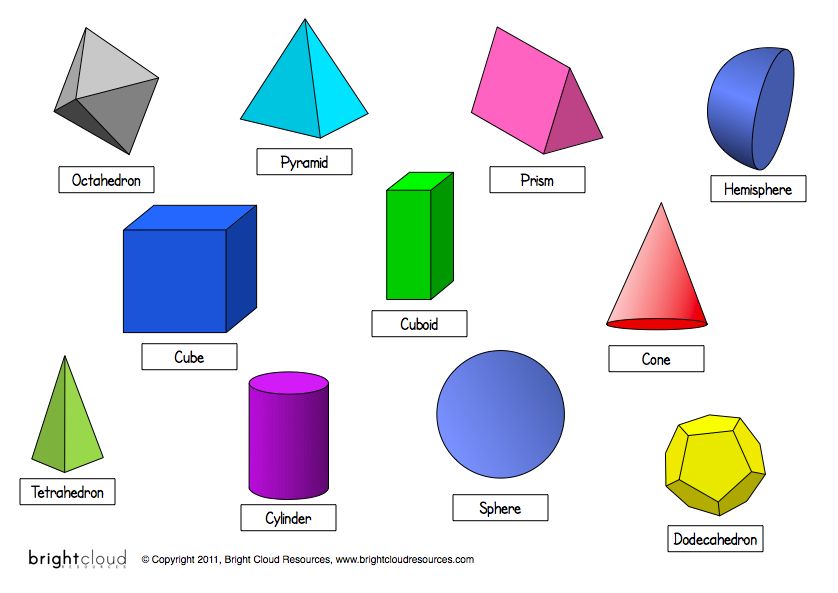 Это происходит потому, что все вещи в нашем мире – это и есть фигуры. Они могут быть разных размеров и разной формы, но все эти объекты называются одним словосочетанием – геометрические фигуры.

Ещё в древности люди создали такую науку, как геометрия. Основоположником данного направления стал Евклид. Именно этот учёный считается отцом математической науки. А ее родиной считается Греция. Постепенно все вещи стали принимать известные всем современникам названия: круг, ромб, квадрат и т.д.
В повседневной современной жизни нас повсюду окружает геометрия.

Геометрия в домашней обстановке

Если внимательно осмотреться, можно увидеть геометрию и в домашней обстановке. Например, картины и телевизор на стене имеют форму прямоугольника. А часы могут быть круглыми, овальными, квадратными и прямоугольными.

Когда человек садится за стол, он опять же может наблюдать в окружающей обстановке геометрию. Тарелка, на которой лежит еда, имеет форму овала. Стакан, в котором налита вода или другой напиток, имеет форму круга. Даже сам стол представляет собой геометрическую фигуру: прямоугольник, квадрат, овал или круг.

Наша пища и геометрические фигуры

Не стоит удивляться, но наша еда тоже напоминает геометрию. Торты, печенья, конфеты, или любая другая пища напоминают форму квадрата, прямоугольника или другой фигуры. Яблоко, помидор или апельсин похожи на круг. Они имеют шарообразную форму, а, например, огурец – овал.

Геометрия на улице. Гуляя по улице, можно увидеть светофор, который собрал в себе не одну, а сразу несколько фигур: круг и прямоугольник, а его ножка – это цилиндр. Крыши домов напоминают нам треугольник, ворота – прямоугольник или квадрат, точно также как и окна. Проезжающие мимо машины, полностью состоят из геометрических фигур. Колёса имеют форму окружности, а стекла состоят из прямоугольника с овальными краями.

Геометрические фигуры среди школьных предметов. Школьные предметы также могут напомнить нам шар, прямоугольник, квадрат, цилиндр. Карта географическая карта в классе, учебник на столе, классный журнал, доска на стене, глобус – все это геометрия, даже ручка в школьном пенале имеет свою геометрическую форму. Она представляет собой цилиндр.

Геометрия в праздничных украшениях. Все люди любят праздники, а украшения в эти дни – очень важные предметы, праздничные атрибуты. Они тоже имеют свою постоянную геометрическую форму. Например, новогодняя ёлка напоминает нам треугольник, а если посмотреть на неё сверху – вниз, то это будет конус. На день рождения мы кушаем торт. Чаще всего, он выполнен в форме круга. Подарки мы привыкли упаковывать в коробки, которые напоминают нам прямоугольный параллелепипед или куб.
Таким образом, окружающие предметы имеют свою геометрическую форму. А геометрия – наука, изучающая свойства различных геометрических фигур.

Другие статьи:

• Психотипы личности: разновидности и проявления
• Личность и семья
• Формирование и реализация кредитной политики банка
• Банковская система как связующее звено финансового рынка
• Кем был Андре Вейль?

геометрических фигур с примерами – Smartick

Сегодня вы узнаете о геометрических фигурах .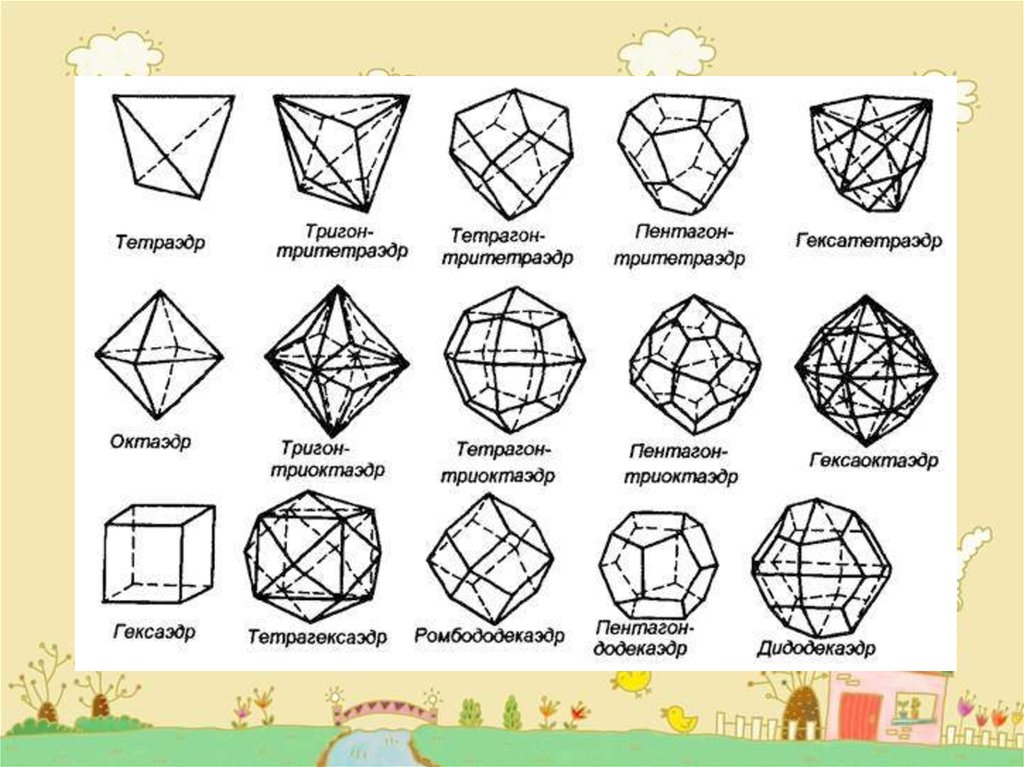 Мы научим вас характеристикам основных геометрических фигур, а чтобы помочь вам лучше понять, объясним на примерах.

Что такое геометрические фигуры?

Древние греки определяли прямые и изогнутые линии, глядя на окружающую среду. Думаете, они остановились на этом? Конечно, нет! Это потому, что прямые линии являются основой для нахождения некоторых фигур, которые мы часто встречаем в реальном мире: геометрические фигуры.

Под геометрическими фигурами понимаются плоские поверхности, ограниченные линиями, которые могут быть изогнутыми или прямыми. Чтобы помочь вам лучше понять, мы собираемся объяснить на примере.

Начнем с простого: две прямые линии .

Можно ли составить фигуру из двух прямых?

Ну конечно можно! При этом мы не называем эту фигуру геометрической фигурой. Для этого он должен быть закрыт. Это означает, что если мы поместим шарик внутрь фигуры, он не сможет убежать. На сделанном нами рисунке мяч мог улететь!

Если вы попытаетесь переместить две прямые линии, то увидите, что замкнуть их невозможно.

Трехсторонние геометрические фигуры: треугольники

Теперь попробуем три прямые линии .

Вот и все! Теперь мы можем создать фигуру, которая не позволит мячу убежать.

Каждая из использованных нами линий, которые теперь составляют часть фигуры, называется сторонами фигуры . У этой фигуры три стороны, и мы называем ее треугольником. Когда мы говорим «треугольник», мы можем иметь в виду либо форму трех линий, либо пространство, которое они заключают.

Можете ли вы назвать места, где мы можем найти вокруг себя треугольники? Я нашел кое-что в Smartick! Посмотрим, узнаете ли вы их.

Классификация треугольников

Существуют различные способы классификации треугольников в соответствии с их сторонами и углами.

В соответствии с их углами

• Прямоугольный треугольник : имеет прямой угол, другими словами, он измеряет 90º.
• Остроугольный треугольник : имеет три острых угла и имеет размеры менее 90º.
• Тупоугольный треугольник : имеет тупой угол и имеет размеры более 90º.

По сторонам

1. Равносторонний : имеет 3 равные стороны.
2. Равнобедренный : две стороны равны, а другая нет.
3. Scalene : все стороны имеют разную длину.

4-сторонние геометрические фигуры: четырехугольники

Теперь попробуем четыре прямые линии .

Например, мы могли бы расположить их так:

Мы называем эти фигуры четырехугольниками . Есть несколько особых четырехугольников, стороны которых параллельны две на две; другими словами, две стороны, которые параллельны друг другу, а затем две другие, которые также параллельны. Кроме того, параллельные стороны также равны. Как мы могли сделать эту форму? Берем две стороны и располагаем их так, чтобы они были параллельны:

Как расположить две другие стороны так, чтобы они тоже были параллельны? Вот и все!

Когда линии параллельны и правильны, у нас есть три возможности.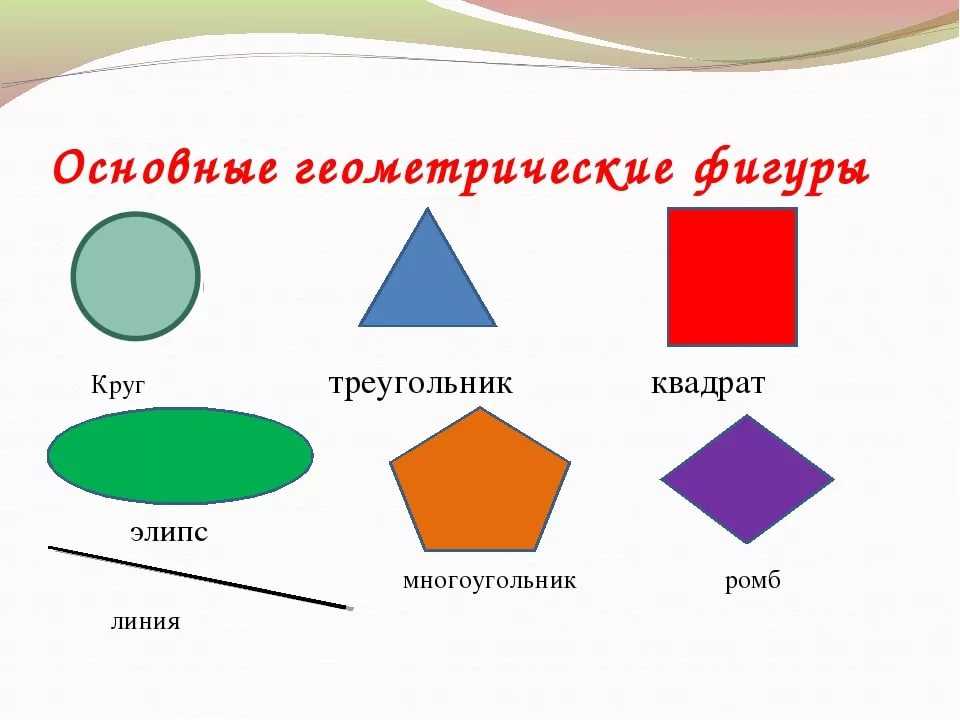

Ромб

Если четыре стороны равны, получается ромб.

Прямоугольник

Если четыре угла на фигуре прямые, то они образуют прямоугольник .

Квадрат

Если оба предыдущих пункта верны, то у нас есть квадрат с равными сторонами и четырьмя прямыми углами.

Видео для ознакомления с классификацией четырехугольников

Четырехугольники — геометрические фигуры с квадратными сторонами. Эти многоугольники подразделяются на параллелограммы и непараллелограммы. Для лучшего понимания предлагаю вам посмотреть следующее видео от Smartick, метод обучения математике для детей от 4 до 14 лет.

Это интерактивный учебник, преобразованный в видео, но если вы хотите решить его самостоятельно, зарегистрируйтесь в Smartick бесплатно и получите доступ ко всем нашим интерактивным учебникам.

 

Правильные геометрические фигуры с числом сторон более 4

Мы можем продолжить сложение всех равных линий, которые мы хотим создать, чтобы создать различные геометрические фигуры с разными сторонами.

Пятиугольник

Имеет 5 равных сторон.

Шестиугольник

Имеет 6 равных сторон.

Мы можем найти их в сотах!

Откуда пчелы умеют создавать такие идеальные геометрические формы?

Обзор геометрических фигур с примерами из реальной жизни

Даже не осознавая этого, геометрические фигуры стали частью нашей жизни в большей степени, чем мы думаем. Посмотрите внимательно на следующее изображение и посмотрите, сколько геометрических фигур вы сможете найти.

Мы рассмотрим некоторые из них.

Окружность

Окружность — это геометрическая фигура, построенная путем построения кривой, которая всегда находится на одном и том же расстоянии от точки, которую мы называем центр . Линия, ограничивающая круг, называется окружностью .

Мы получаем круг, когда мы делаем кривую, которая сохраняет свое расстояние от определенной точки. Например, с помощью циркуля мы выбираем точку с помощью стрелки, а затем, держа ее открытой, обводим карандашом окружность. Вы можете найти круги вокруг себя, например, на колесах автомобиля или теннисном мяче.

Треугольник

Треугольник — это многоугольник, полученный в результате соединения трех точек прямыми линиями. Точки пересечения — это вершины, а отрезки — стороны.

В данном случае в школе Смартика мы нашли равнобедренный треугольник. У равнобедренных треугольников две стороны одинаковой длины и одна разной длины.

Квадрат

Квадрат представляет собой четырехсторонний многоугольник, все стороны которого равны, а четыре угла равны 90 градусов каждый.

Прямоугольник

Прямоугольник представляет собой фигуру, состоящую из 4 прямых линий, называемых сторонами. Характеристики прямоугольников заключаются в том, что их противоположные стороны параллельны, а их 4 угла равны 9.0º.

Трапеция

Трапеция представляет собой четырехсторонний многоугольник, ни одна из сторон которого не параллельна другой. Трапеции могут быть симметричными или асимметричными, в зависимости от их характеристик.

В данном случае воздушный змей представляет собой симметричную трапецию . Это трапеции, у которых две пары равных сторон, причем одна из этих пар сторон меньше другой.

Восьмиугольник

Восьмиугольник — восьмиугольник. Правильный восьмиугольник — это многоугольник, у которого восемь равных сторон и восемь равных углов. Сумма внутренних углов восьмиугольника всегда равна 1080º.

Мы нашли много геометрических фигур!!! Мы уверены, что вы найдете гораздо больше в своем окружении.

Если вы хотите, вы можете продолжить изучать математику в начальной школе, адаптированную к вашему уровню, присоединившись к Smartick!

Подробнее:

• Автор
• Последние сообщения

Smartick

Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.

Последние сообщения Smartick (посмотреть все)

3D геометрические фигуры (видео и практические вопросы)

TranscriptPractice

Привет, ребята! Добро пожаловать в это видео Mometrix о трехмерной идентификации геометрических фигур .

Сначала мы рассмотрим, что такое 3D-форма, а затем рассмотрим различные свойства 3D-фигуры.

Давайте сделаем быстрый обзор. Одномерная фигура имеет длину. 2D имеет только длину и ширину.

Итак, что такое трехмерная фигура? Ну, 3D означает трехмерность; эти три разных измерения: длина, ширина и глубина (или высота) для многогранника, а также основание, радиус и высота для изогнутой трехмерной формы. Многогранник — это трехмерная фигура со всеми плоскими гранями. Изогнутая трехмерная форма будет похожа на сферу , конус или цилиндр. В этом видео мы сосредоточимся на многогранниках.

Длина относится к измерению чего-либо от одного конца сегмента до другого.

Ширина относится к измерению чего-либо от одной стороны сегмента до другой стороны.

Глубина (или высота) относится к расстоянию от верха сегмента до низа.

Теперь поговорим о свойствах трехмерной формы. Трехмерные многогранники имеют грани, ребра и вершины.

Грань относится к поверхности трехмерной формы. У куба 6 граней.

Край относится к месту соединения двух граней. У куба двенадцать ребер.

Вершина (или вершины, когда вы имеете в виду более одной) – это углы или места, где ребра сходятся. Куб имеет 8 вершин.

Понимание трехмерных форм и их свойств очень важно и поможет вам сделать гораздо больше, например вычислить объем .

Я надеюсь, что это видео о трехмерной идентификации геометрических фигур было полезным. Если вам понравилось, не забудьте поставить нам палец вверх и подписаться на наш канал для дальнейших видео.

Увидимся в следующий раз!

Вопрос №1:

 
Какое из следующих свойств не является свойством трехмерной формы?

Количество вершин

Количество углов

Количество граней

Количество граней

Показать Ответ

Ответ:

вершины. Помните, что количество граней описывает, сколько сторон у фигуры. Количество ребер представляет собой количество мест, где встречаются две грани (например, угол). Количество вершин описывает, сколько мест на фигуре являются точками, где соприкасаются углы граней.

Скрыть ответ

Вопрос № 2:

 
Сколько граней у ромба, показанного ниже?

8 граней

9 граней

10 граней

11 граней

Показать ответ

Ответ:

У ромба 9 граней; один на самом верху, затем четыре вокруг него в верхней части ромба и еще четыре составляют основание.

Скрыть ответ

Вопрос №3:

 
Сколько ребер у квадратной пирамиды, показанной ниже?

5 ребер

6 ребер

7 ребер

8 ребер

Показать Ответ

Ответ:

Квадратные пирамиды имеют 8 ребер; четыре из них очерчивают квадратное основание, а остальные четыре указывают на вершину и встречаются наверху.

Скрыть ответ

Вопрос № 4:

 
Обратите внимание на следующее изображение треугольной призмы. Сколько у него вершин?

Показать Ответ

Ответ:

Треугольные призмы имеют шесть вершин, точек, где ребра сходятся. По три расположены на каждом конце, в точках треугольников, образующих любой конец призмы.

Скрыть ответ

Вопрос №5:

У Шона есть восьмигранный кубик для игры, в которую он играет со своими друзьями. Сколько ребер у кубика?

8 ребер

10 ребер

12 ребер

14 ребер

Показать Ответ

Ответ:

Восьмигранный кубик имеет форму того, что мы называем октаэдром, который имеет двенадцать ребер.