Геометрические фигуры с: Картинки названия геометрических фигур (100 фото) • Прикольные картинки и позитив
Виды геометрических фигур / Бери и делай
Множество точек дает линию, а из нескольких соединенных между собой линий можно получить различные геометрические фигуры на плоскости и в пространстве. Таким образом, произвольное множество точек позволяет нам создавать геометрическую фигуру. Это может быть квадрат или куб, круг или шар, а также более сложные и неоднозначные фигуры, например икосаэдр, который может быть представлен двумя разными формами.
«Бери и Делай» предлагает узнать, чем отличаются разные виды геометрических фигур.
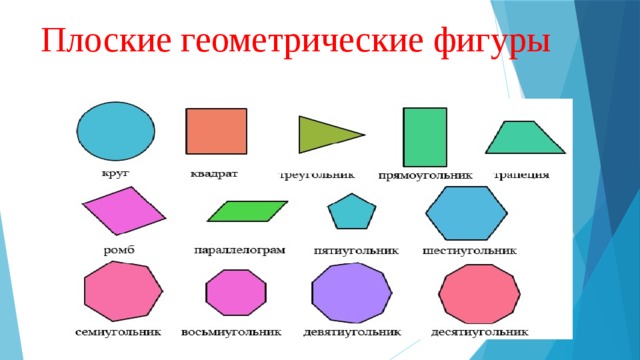
Плоские геометрические фигуры
Плоская геометрическая фигура располагается в двумерном пространстве, где объекты характеризуются только длиной и шириной. Различают следующие фигуры:
- Круг — это фигура, у которой нет углов и в которой все точки по окружности находятся на равном расстоянии от центра.
- Овал — это фигура, похожая на яйцо. У нее также нет углов.
- Квадрат — это фигура, у которой 4 равные стороны и 4 прямых угла.

- Прямоугольник — это фигура, похожая на квадрат: у нее 4 стороны и они пересекаются под прямым углом. В отличие от квадрата, у прямоугольника только противолежащие стороны равны. Если с помощью отрезка соединить любой угол с противоположным, получится диагональ. И у квадрата, и у прямоугольника диагонали равны.
- Ромб — это фигура, у которой 4 равные стороны, но пересекаются они не под прямыми углами. У ромба противоположные углы ромба равны. Ромб, так же как квадрат и прямоугольник, является четырехугольником.
- Треугольник — это фигура, у которой 3 угла и 3 стороны. Точки, в которых пересекаются стороны треугольника, принято называть его вершинами.
Виды треугольников в зависимости от размера углов:
🔷 остроугольный — все углы острые (каждый равен менее 90°)
🔷 тупоугольный — один угол является тупым (равным более 90°)
🔷 прямоугольный — один угол является прямым (равным 90°)
Различают также виды треугольников по соотношению их сторон:
🔶 равносторонний имеет 3 равные стороны
🔶 равнобедренный — 2 равные стороны
🔶 разносторонний — 3 разные стороны
Выше мы рассмотрели основные геометрические фигуры на плоскости.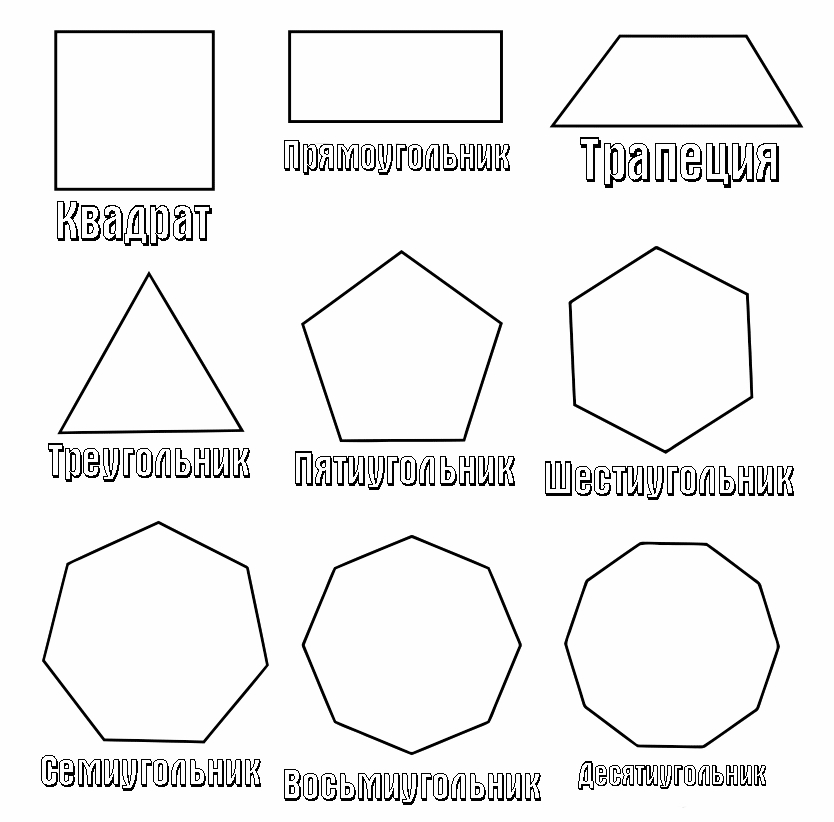 Но существует множество других, например:
Но существует множество других, например:
- Трапеция — это четырехугольник, у которого как минимум 2 стороны параллельны. Таким образом, квадрат, ромб и прямоугольник можно рассматривать как частные случаи трапеции.
- Параллелограмм — четырехугольник, у которого противолежащие стороны попарно параллельны. Так, прямоугольник, квадрат и ромб считаются частными случаями параллелограмма.
- Пентагон — фигура, представляющая собой правильный многоугольник с 5 сторонами. У пентагона все стороны и углы равны.
- Гексагон — это правильный многоугольник, у которого 6 равных сторон, а углы образуют 6 равносторонних треугольников.
- Крест — это фигура, которая состоит из 2 пересекающихся линий или прямоугольников.
- Звезда — плоский невыпуклый многоугольник, по форме напоминающий звезду. Звезда может быть трехконечной, четырехконечной, пятиконечной (как на картинке выше) и так далее.

Геометрическая фигура может быть выпуклой, если ей целиком принадлежат все точки отрезка, соединяющего любые ее две точки. Круг, шар, овал и треугольник являются выпуклыми фигурами. А четырехугольники могут быть как выпуклыми, так и невыпуклыми. К примеру, на картинке выше изображена одна и та же фигура — дельтоид. Это четырехугольник, стороны которого можно сгруппировать в две пары равных смежных сторон. Слева — дельтоид выпуклый, а справа — невыпуклый.
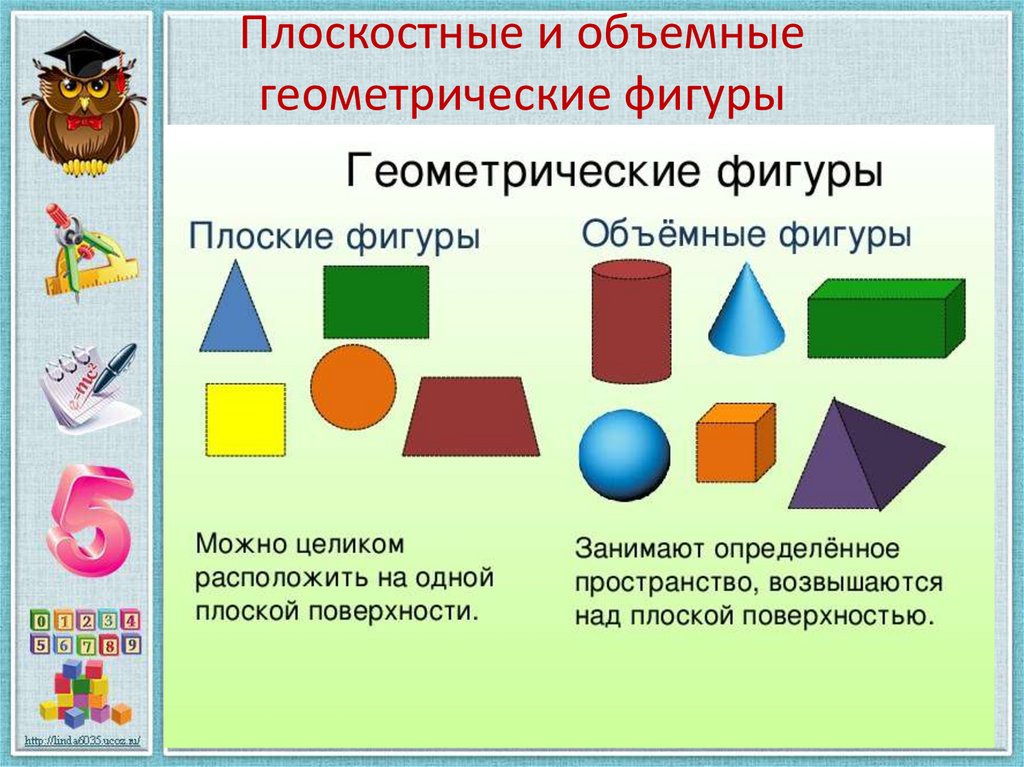
Пространственные геометрические фигуры
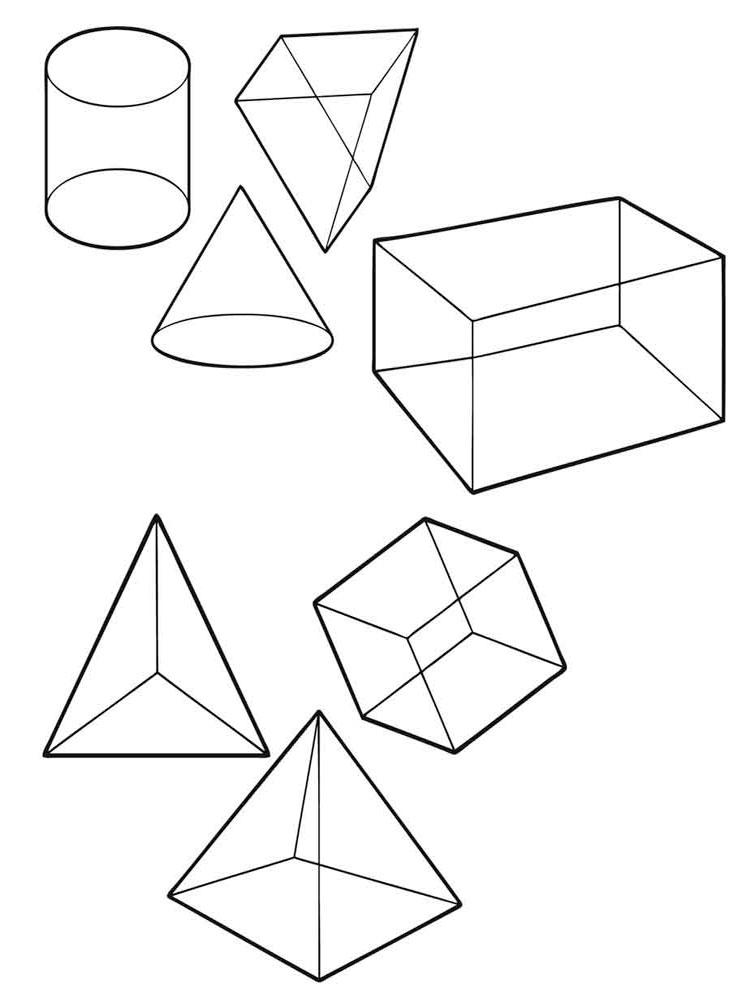
Если фигура располагается в трехмерном пространстве, где объекты характеризуются длиной, шириной и высотой, а также имеют глубину или толщину, ее называют пространственной. Чаще всего различают следующие пространственные фигуры:
- Шар можно назвать аналогом круга в пространстве. Все точки, располагающиеся на поверхности шара, находятся на равном расстоянии от его центра.
- Конус образован множеством лучей, которые соединяют все точки некоторой плоской кривой с единой точкой пространства (вершиной конуса).
 Конусы различаются между собой: например, если основанием конуса является круг, то это может быть прямой круговой конус.
Конусы различаются между собой: например, если основанием конуса является круг, то это может быть прямой круговой конус. - Цилиндр по своей форме напоминает валик. В его основании находятся круги, а между ними — часть цилиндрической поверхности.
- Куб — это многогранная фигура, каждая грань которой представляет собой квадрат. При этом у него 6 граней, 12 ребер и 8 вершин. Куб также можно назвать правильным гексаэдром, или шестигранником.
- Пирамида — это многогранник, у которого в основании находится многоугольник, а грани представлены треугольниками, имеющими общую вершину.
- Призма — это многогранник, 2 грани которого являются равными многоугольниками, располагающимися в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. На картинке выше частный пример — шестиугольная призма. У нее 8 граней, 18 ребер и 12 вершин.
Если выпуклый многогранник состоит из одинаковых правильных многоугольников и обладает пространственной симметрией, то его называют правильным многогранником, или платоновым телом. В трехмерном пространстве различают 5 таких правильных многогранников. Название каждого из них происходит от греческого наименования количества его граней:
В трехмерном пространстве различают 5 таких правильных многогранников. Название каждого из них происходит от греческого наименования количества его граней:
- Тетраэдр, или треугольная пирамида. У этого многогранника гранями являются 4 треугольника.
- Гексаэдр, или куб.
- Октаэдр — многогранник, чьими гранями являются 8 равносторонних треугольников. Если разрезать октаэдр пополам, можно получить две одинаковые пирамиды.
- Додекаэдр — многогранник, у которого 12 граней и все они правильные пятиугольники.
- Икосаэдр — многогранник, гранями которого являются 20 правильных треугольников.
При этом правильный икосаэдр может быть как выпуклым, так и невыпуклым. Но термин «правильный икосаэдр» чаще относится к выпуклому виду, а невыпуклая форма называется большим икосаэдром.
геометрические фигуры для детей
- Главная
- Геометрические фигуры для детей
Задания для детей “Учим геометрические фигуры” позволят малышам в непринужденной и легкой форме запомнить простейшие геометрические фигуры. В первой задаче ребенку необходимо соединить указанные в таблицах две части деталей и нарисовать получившиеся фигуры в пустых рамочках, а во втором – назвать фигуры, из которых состоят картинки и раскрасить их.
В первой задаче ребенку необходимо соединить указанные в таблицах две части деталей и нарисовать получившиеся фигуры в пустых рамочках, а во втором – назвать фигуры, из которых состоят картинки и раскрасить их.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Эти задания помогут ребятам изучить и запомнить простейшие геометрические фигуры в игровой и непринужденной форме. В данных заданиях ребенку нужно будет раскрасить картинки, собранные из различных фигур, предложенными цветами; разместить фигурки на этажах дома в разном порядке; нарисовать увеличивающиеся и уменьшающиеся фигуры по образцу.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Плоские геометрические фигуры для детей – это задания, которые будут интересны детям, изучающим геометрические фигуры. В первом задании ребенку необходимо раскрасить предложенные фигуры таким образом, чтобы одна находилась либо под, либо над другой, как указано в задаче, а во втором – обвести фигуры по пунктирным линиям и дорисовать их.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Геометрические фигуры для малышей “Найди в картинках” безусловно привлекут внимание малыша своими яркими картинками. Проследите за тем, чтобы в этих картинках ребенок нашел как можно больше знакомых ему геометрических фигур. Как правило, подобные занятия дети выполняют более охотно, а материал запоминается ими намного быстрее.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Геометрические фигуры “Раскраска для детей” отлично развивают внимание ребенка и помогут ему запомнить основные геометрические фигуры, знание которых в дальнейшем очень пригодятся ему в изучении геометрии. К тому же задания дают возможность малышу повторить математические знаки и усвоить счет до 10-ти.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Геометрические фигуры для детей – Картинки с заданиями – станут для вас хорошим помощником в дошкольном обучении ребенка. Малыш научится различать геометрические фигуры и решать с их помощью простейшие математические примеры.
Малыш научится различать геометрические фигуры и решать с их помощью простейшие математические примеры.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Геометрические фигуры и их названия лучше изучать с ребенком, имея под рукой различные образцы нужных вам фигур. Например: мячики, кубики и т. д., чтобы малышу было более понятно, что представляют собой объемные геометрические фигуры; либо фигуры, вырезанные из бумаги – объясняя на примере, какие бывают плоские геометрические фигуры.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Задания развивающие “Раскрась геометрические фигуры” развивают в ребенке умение выделять среди множества различных объектов геометрические фигуры.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Упражнение “Найди фигуры на картинке” – это задание, в котором ребенок должен найти на картинке круги, треугольники и прямоугольники (квадраты в том числе). Искать геометрические фигуры нужно очень внимательно – ведь их не так-то просто найти на форме и узорах животных.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Занятие на развитие логического мышления – Свойства геометрических фигур “Форма, цвет, размер” предназначена для освоения понятий, касающихся главных свойств геометрических фигур – цвета, формы и размера. В процессе занятия ребенок учится различать свойства фигур, изображенных на рисунке. Цель занятия: развитие логического мышления. Материал: распечатанный бланк методики, цветные карандаши.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Упражнение на логическое мышление “Найди формы геометрических фигур на картинках” – это довольно популярное задания для изучения геометрических фигур. Ребенок здесь должен разглядеть в каждой фигуре-картинке несколько геометрических фигур и выделить их на распечатанном бланке.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Упражнение на развитие логического мышления “Сложи из геометрических фигур нужные формы” – это интересное занятие, которое по свое сути напоминает собирание картинки из пазлов. Только здесь ребенку нужно сложить из одинаковых геометрических фигур определенную форму.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Здесь представлена математика – Задания по геометрии “Наложение фигур” – это примеры на сложение. Только складывать здесь нужно не цифры, а геометрические фигуры, накладывая одну на другую. Бланки с заданиями нужно распечатывать на цветном принтере.
Бланки с заданиями нужно распечатывать на цветном принтере.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Ребенку последовательно предлагается внимательно рассмотреть каждый бланк и определить, согласно какому признаку фигуры разбиты на группы. Мы рекомендуем вам регулярно проводить подобные занятия с ребенком. Для этого можно использовать настоящие предметы (например, пуговицы разной формы, цвета, размера, с разным количеством дырочек и т.п.), которые различаются между собой по одному или нескольким признакам.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Упражнение на развитие логического мышления – Геометрические фигуры карандашом “Обведи по точкам” -одно из самых интересных занятий, которое любят выполнять дети.Здесь малышам нужно по заданному примеру нарисовать фигуру, используя точки на бумаге.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Ребенку предлагается внимательно рассмотреть распечатанный Бланк №1 методики.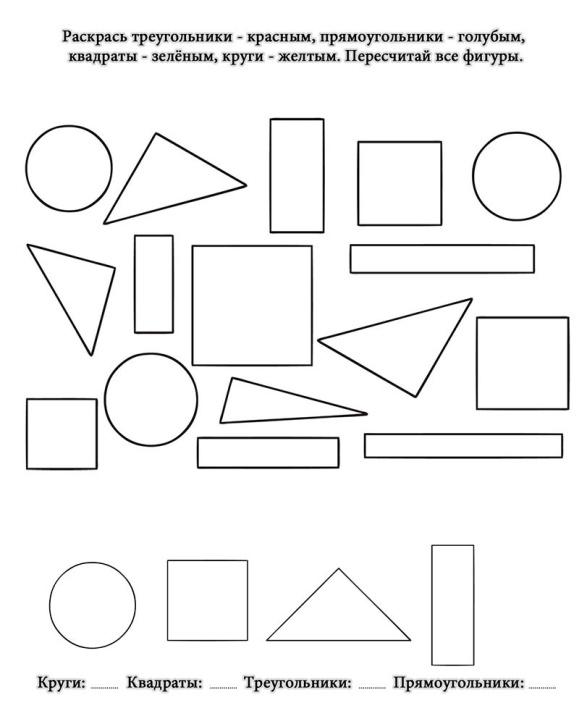 На нем слева изображена объемная фигура, напоминающая по форме дом с аркой. Стрелками отмечен вид фигуры спереди (1), сбоку (2) и сверху (3). Справа помещена таблица, состоящая из 3 столбцов и 4 строчек. Первый столбец – это варианты возможных видов фигуры спереди.
На нем слева изображена объемная фигура, напоминающая по форме дом с аркой. Стрелками отмечен вид фигуры спереди (1), сбоку (2) и сверху (3). Справа помещена таблица, состоящая из 3 столбцов и 4 строчек. Первый столбец – это варианты возможных видов фигуры спереди.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Развивающие задания для 1 класса “Геометрическая фабрика” – это задание на развитие логического мышления ребенка, в котором ему предстоит стать работником волшебной фабрики по обработке геометрических фигур, в процессе которой фигуры меняют свои свойства: цвет, форму, размер.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Упражнение “Дорисуй испорченную фигуру” – одно из тех развивающих занятий, в которых нужно дорисовать недостающие элементы. Здесь ребенку нужно дорисовать геометрические фигуры, которые немного испортились.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Упражнение “Найди геометрические фигуры” – это задание, которое очень важно выполнять детям, начинающим изучать основные математическо-геометрические понятия.
Опубликовано в Математика для детей 4, 5, 6, 7 лет – распечатай и занимайся
Презентация «Геометрические фигуры в пространстве» (20 слайдов)
Слайд 1
Обирина Людмила Ивановна
Преподаватель КГБОУ СПО «НПК»
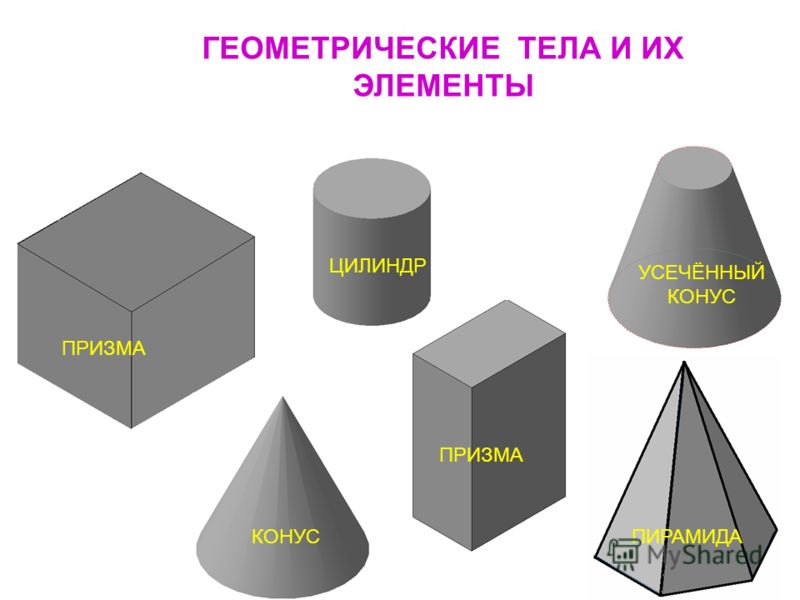
Геометрические фигуры в пространстве
Норильск, 2015
Слайд 2
В стереометрии изучают фигуры в пространстве, называемые телами.
Слайд 3
Поверхность многогранника состоит из конечного числа многоугольников, которые называются гранями многогранника.
Стороны граней называются ребрами, а вершины – вершинами многогранника.
Отрезок, соединяющий две вершины, не лежащие в одной грани многогранника, называется его диагональю.
Многогранником называется тело, ограниченное конечным числом плоскостей.
Слайд 4
Многогранник
выпуклый невыпуклый
Многогранник называется выпуклым, если он лежит по одну сторону от каждой из плоскостей, его ограничивающих.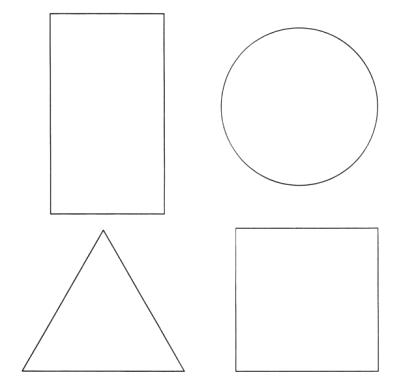
Слайд 5
Призма – это многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а все ребра вне этих граней параллельны между собой.
Грани, отличные от оснований, называются боковыми гранями, а их ребра называются боковыми ребрами.
Все боковые ребра равны и параллельны.
Все боковые грани призмы являются параллелограммами.
В основаниях призмы лежат равные многоугольники.
Слайд 6
Призма
прямая наклонная
Слайд 7
Параллелепипед – призма, у которой основания параллелограммы.
У параллелепипеда все грани –параллелограммы.
У параллелепипеда противолежащие грани параллельны и равны.
Все диагонали параллелепипеда пересекаются в одной точке.
Слайд 8
Пирамида – это многогранник, одна грань которого многоугольник, а остальные грани – треугольники с общей вершиной.
Грани, отличные от основания, называются боковыми.
Общая вершина боковых граней называется вершиной пирамиды. Ребра, соединяющие вершину пирамиды с вершинами основания называются боковыми.
Ребра, соединяющие вершину пирамиды с вершинами основания называются боковыми.
E
Слайд 9
Многогранник, все грани которого правильные и равные многоугольники, называется правильным.
Углы при вершинах правильного многогранника равны.
Тела Платона
Существует пять типов правильных многогранников.
Впервые их описал древнегреческий философов Платон (IV в до н.э).
Слайд 10
Тетраэдр – правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками.
ЧИСЛО ГРАНЕЙ – 4
ЧИСЛО РЁБЕР – 6
ЧИСЛО ВЕРШИН – 4
сумма плоских углов при каждой вершине 180°
Слайд 11
Октаэдр – правильный восьмигранник. Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины.
число граней – 8
число рёбер – 12
число вершин – 6
сумма плоских углов при каждой вершине 240°
Слайд 12
Икосаэдр –
Икосаэдр – состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины.
число граней – 20
число рёбер – 30
число вершин – 12
сумма плоских углов при каждой вершине 300°
Слайд 13
Гексаэдр – правильный шестигранник. Это куб состоящий из шести равных квадратов, соединенных по три около каждой вершины.
число граней – 6
число рёбер – 12
число вершин – 8
сумма плоских углов при каждой вершине 270°
Слайд 14
Додекаэдр – правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины.
число граней – 12
число рёбер – 30
число вершин – 20
сумма плоских углов при каждой вершине равна 324°
Слайд 15
Если соединить отрезками центры соседних граней правильного многоугольника, то эти отрезки станут ребрами другого правильного многогранника:
у куба – октаэдр, у октаэдра – куб;
у икосаэдра – додекаэдр, у додекаэдра – икосаэдр;
у тетраэдра – снова тетраэдр.
Т. е. каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.
е. каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.
Закон взаимности
Слайд 16
Знаменитый математик Леонард Эйлер получил формулу:
В + Г – Р = 2,
которая связывает
число вершин /В/, граней /Г/ и рёбер /Р/
любого многогранника.
Переменные в формуле не связаны ни с расстоянием, ни с углами.
Слайд 17
Тела вращения
Слайд 18
Цилиндром называется тело, которое состоит из двух кругов, не лежащих в одной плоскости, и всех отрезков, соединяющих соответствующие точки этих кругов.
Круги называются основаниями, а отрезки – образующими цилиндра.
Основания цилиндра равны.
Образующие цилиндра параллельны и равны.
Радиусом цилиндра называется радиус его основания.
Слайд 19
Конусом называется тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга, – вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.
Слайд 20
Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки.
Данная точка называется центром шара, а данное расстояние радиусом шара.
Граница шара называется шаровой поверхностью, или сферой.
O
игры, задания, шаблоны для скачивания
Звукоподражания, цвета и геометрические фигуры – одни из первых навыков, которые осваивает годовасик. К трём годам он уже не только говорит «котёнок – мяу», но и может многое рассказать о питомце из семейства кошачьих. В познаниях геометрических фигур ребёнок за два года тоже значительно продвигается – от наименования простых плоских фигур до их рисования и конструирования из кубиков. Но все эти навыки нужно постепенно развивать. Узнавать базовые геометрические формы интереснее и эффективнее в игровой форме. Давайте рассмотрим несколько проверенных игр для детей 1-3 лет.
Аудио-версия статьи “ИЗУЧАЕМ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ С ДЕТЬМИ 1-3 ЛЕТ” Тег audio не поддерживается вашим браузером. Скачать. ИЗУЧАЕМ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ С ДЕТЬМИ 1-3 ЛЕТ
Содержание
Учим геометрические фигуры с малышом в 1-2 года
Игры с геометрическими фигурами для детей 1-2 лет
- Посмотри вокруг
- Плакат на стене
- Сортер
- Сортировка предметов
Учим геометрические фигуры с ребенком в 2-3 года
Игры с геометрическими фигурами для детей 2-3 лет
- Игрушка-вкладыш
- Рисование с трафаретами
- Игры с иллюстрациями
- Найди лишнее
- Разложи правильно
- Сортировка
- Конструктор
- Игра «Домик для фигурок»
- Поиск сокровища
- Геометрическое лото
Скачать раскраски для детей
Аппликация из геометрических фигур для малышей
Для детей 1-3 лет при изучении новой информации очень важна последовательность и постепенность. Восприятие квадратиков и кружков помогает малышу задействовать логическое мышление, совершенствовать своё пространственное восприятие и определять форму предметов в повседневной жизни. Начните с простых игр и постепенно усложняйте их, улучшая математические способности малыша.
Восприятие квадратиков и кружков помогает малышу задействовать логическое мышление, совершенствовать своё пространственное восприятие и определять форму предметов в повседневной жизни. Начните с простых игр и постепенно усложняйте их, улучшая математические способности малыша.
Мы сделали подборку, ориентируясь на возраст детей и их усреднённые возможности. Но вам нужно, в первую очередь, смотреть не на возраст, а на умения вашего ребёнка. Начинайте с самых простых игр и постепенно переходите к более сложным задачам.
Учим геометрические фигуры с малышом в 1-2 года
В этот период стоит обучать ребёнка только самым базовым различиям, вряд ли он сразу поймёт, чем отличаются между собой круг и овал.
Поэтому начать стоит с таких фигуры, как квадрат, треугольник и круг. А после того, как малыш освоит эту базовую троицу, можно переходить к более сложным формам.
Игры с геометрическими фигурами для детей 1-2 лет
Посмотри вокруг
Самый доступный способ изучения фигур – смотреть по сторонам и отмечать, какую форму имеет тот или иной предмет. Например, вы раскладываете с ребёнком тарелки на стол и говорите: «Тарелки круглые, эта форма называется круг». Берёте на ночь книжку и отмечаете: «А вот книжка квадратная, эта форма – квадрат» и так далее.
Например, вы раскладываете с ребёнком тарелки на стол и говорите: «Тарелки круглые, эта форма называется круг». Берёте на ночь книжку и отмечаете: «А вот книжка квадратная, эта форма – квадрат» и так далее.
Со временем вы сами сможете спрашивать у ребёнка, какой формы тот или иной предмет дома, на улице. Посоревнуйтесь на прогулке, кто заметит больше круглых предметов, например, солнце, круглая лужа, дупло в дереве.
Плакат на стене
Распечатайте на листах А4 геометрические фигуры. Плакаты можно развесить в детской комнате на уровне глаз ребёнка.
В течение дня просите малыша показать, где та или иная геометрическая фигура.
Также можно распечатать небольшие карточки с геометрическими фигурами по этой ссылке. А в течение дня искать предметы похожие на квадрат, круг, прямоугольник или треугольник.
Постепенно малыш начнёт без труда различать основные геометрические фигуры.
Сортер
В продаже представлены самые различные сортеры – пластмассовые и деревянные, небольшие и с огромным набором фигур. Для начала лучше подобрать игрушку со скромным количеством основных фигурок.
Для начала лучше подобрать игрушку со скромным количеством основных фигурок.
Но если у вас уже есть сортер, может быть, преподнесённый ребёнку в качестве подарка, в котором много крестов, сердечек и полумесяцев, для малыша одного года жизни лучше временно убрать большую часть фигурок. Добавлять их можно по мере взросления, тем самым усложняя игру.
Приблизительно в год ребёнок начинает понимать, что фигурка легко проходит сквозь одно отверстие, но совсем не помещается в другое. Поэтому его начинает интересовать сортер. Поначалу игра будет очень долгой, малыш неумело подбирает фигурки и медленно их вращает, не всегда замечая закономерности. С практикой ребёнок начнёт быстрее взрослых сопоставлять фигурку и отверстие под неё.
Ваша задача – во время игры постоянно проговаривать названия геометрических фигур. «Вот это – круг. Круг не подходит сюда. Давай посмотрим, куда подходит круг?».
Сортировка предметов
Эта игра работает по принципу поиска общего. Ребёнку нужно присоединить фигуру к уже набранному количеству таких же форм. Мои ребята, и Миша, и Лёша, проявили интерес к сортировке ближе к полутора годам.
Мои ребята, и Миша, и Лёша, проявили интерес к сортировке ближе к полутора годам.
Причём сортировать детали можно не только по форме. Когда мы освоили складывание треугольника к треугольникам, начали придумывать другие основания для сортировки, например, по цвету или по размеру. Чтобы было интереснее, я внесла игровой формат, подключив мягкие игрушки. Задание сразу становилось игровым, я просила: «Дай собачке все кружки, потому что она больше всего любит играть с кружками». Так у каждой нашей игрушки появились любимые геометрические фигуры.
Чтобы играть сразу с двумя детьми, пришлось немного усложнить задание. Так младшего, Лёшу, я просила дать брату все квадраты. А Миша, получив все квадраты, раскладывал их от меньшего к большему или придумывал свою систему сортировки. Вообще, можно добавлять элемент сортировки в самые разные игры и занятия, даже бытовые.
Учим геометрические фигуры с ребенком в 2-3 года
К двум годам можно увеличить количество изучаемых фигур, добавив звезду, трапецию, ромб, овал.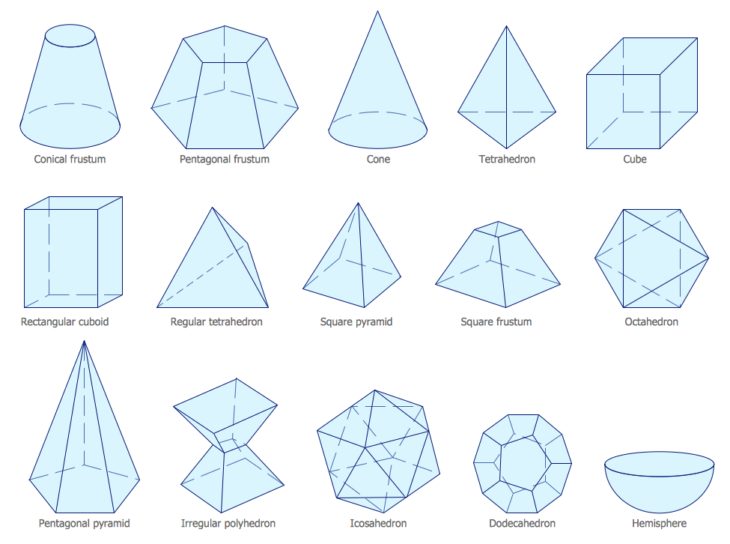 За этот год можно будет освоить понятие объёма и основные фигуры, например, кубик, шар, может быть, конус.
За этот год можно будет освоить понятие объёма и основные фигуры, например, кубик, шар, может быть, конус.
Предыдущие игры можно оставить, немного усложнив их правила. А также стоит добавить другие развлечения из списка ниже.
Игры с геометрическими фигурами для детей 2-3 лет
Ближе к трём годам начинает развиваться наглядно-образное мышление, в то время как ранее намного важнее было предметное восприятие. Если в 1-2 года малышу нужно было всё потрогать, подержать в руках, он буквально «думал руками», то к трём годам он уже начинает больше интересоваться картинками, образами. Поэтому, начиная с 2-3 лет, можно чаще привлекать карточки и другие дополнительные материалы.
Игрушка-вкладыш
Эта логическая игрушка предназначена для несложных манипуляций – достать, а затем вложить обратно предмет в подходящую ячейку.
Рамка-вкладыш может быть сделана из деревянных или пластиковых деталей.
Небольшая игрушка включает отдельно стоящие геометрические фигуры.
Но есть и более сложные рамки, в которых нужно как в «Тетрисе» уложить все фигурки друг к другу так, чтобы заполнить всё пространство.
Рисование с трафаретами
Сперва можно научить ребёнка закрашивать полностью трафарет, например, гуашью, а потом показать, как нужно обводить фигуру по контуру. Трафареты могут быть разные – со внутренней стороной или со внешними гранями.
Можно купить пластиковые карточки, использовать специальную линейку для рисования или смастерить трафареты самостоятельно. С Мишей у нас были самодельные трафареты из плотного картона, а уже с Лёшей я купила более долговечные пластиковые карточки. Фигуры могут быть разного размера, хотя для начала лучше взять 3-4 базовые формы.
Игры с иллюстрациями
По сути это тот же поиск предметов, только не в окружающем пространстве, а на картинке. Это здорово тренирует внимание и наблюдательность. А главное, играть можно с любой детской книжкой, например, во время вечернего чтения перед сном.
Задача у малыша простая – найти все предметы квадратной, треугольной или круглой формы на картинке. Если в обычных книжках слишком мало геометрических форм, можно найти специальные картинки.
Найди лишнее
Развивать логическое мышление можно с помощью игры «Найди лишнее». Малышу нужно будет из предложенного ряда фигурок выбрать ту, которая не подходит.
Для начала можно воспользоваться вырезанными геометрическими фигурами, положив 3 квадрата и один треугольник. Предложите ребёнку выбрать лишнюю фигуру.
Затем, когда он уже понял, как работать с такого рода заданиями, усложните игру. Разложите карточки с изображениями квадратных и треугольных предметов, опять предложите убрать лишнюю картинку.
Обязательно поинтересуйтесь, почему он выбрал именно эту карточку.
Помните, что детская логика не всегда работает в том же направлении, что и у вас, обычно взгляд ребёнка шире. Так малыш может взять другое обоснование для исключения предмета, например, цвет или действующие лица на картинке, поэтому нужно подбирать изображения, выполненные в одном ключе. Кстати, вы можете скачать карточки у нас. Чтобы сделать логические ряды, нужно будет распечатать этот шаблон в нескольких экземплярах.
Кстати, вы можете скачать карточки у нас. Чтобы сделать логические ряды, нужно будет распечатать этот шаблон в нескольких экземплярах.
Разложи правильно
Ребёнку нужно будет отсортировать карточки с картинками по фигуркам, которые на них изображены.
Для начала возьмите две геометрические фигуры, для каждой из них по 3-4 карточки. Предложите малышу разложить карточки на две стопки.
Когда ребёнок справится с задачей, увеличьте количество фигур и, соответственно, карточек.
Ничего страшного, если малыш будет ошибаться, подскажите ему, как правильно выполнить задание. Через время он будет без труда справляться самостоятельно.
Сортировка
Нарежьте из цветного картона разноцветные геометрические фигуры разных размеров. Теперь предложите ребёнку разложить их по кучкам, например, в одну сторону маленькие синие квадраты, а в другую – крупные зелёные треугольники.
Вместе с изучением геометрических фигур вы сможете подтянуть знание цветов и закрепить понятия больше/меньше.
Конструктор
Чтобы выйти из плоскости на изучение объёмных фигур, можно просто поиграть в конструктор или кубики. Занимаясь строительством, обращайтесь к ребёнку, называя фигуры.
Например: «Подай мне, пожалуйста, зелёный кубик», «Давай сюда поставим красную арку?» или «А где у нас лежат круглые колёса?». Конструирование помогает изучить геометрические формы, развить логическое мышление и фантазию.
Игра «Домик для фигурок»
Когда ребёнок уже познакомился с основными фигурами, можно поиграть с ним в игру на соотношение предметов с изображением. Для этого распечатайте карточки и вырежьте фигуры. Ребёнку нужно будет складывать разноцветные фигурки в заранее подготовленные места на карточках – в их домики.
Можно заполнять поля обычными геометрическими фигурами, а можно – предметами квадратной, круглой или треугольной формы. Карточки для игры с малышом можно скачать по ссылке.
Назад
Далее
Поиск сокровища
В эту игру можно начинать играть с 2-2,5 лет. Причём заниматься можно как с одним ребёнком, так и с несколькими детьми, тогда будет добавлен соревновательный момент. Если вы занимаетесь дома, то подберите объёмные геометрические фигурки, например, из сортера или из конструктора.
Причём заниматься можно как с одним ребёнком, так и с несколькими детьми, тогда будет добавлен соревновательный момент. Если вы занимаетесь дома, то подберите объёмные геометрические фигурки, например, из сортера или из конструктора.
Положите их в глубокую миску и засыпьте любой крупой. Предложите малышам раскапывать крупу и искать сокровища. Когда ребёнок находит фигурку, чтобы её забрать, он обязательно должен назвать её. А если на улице тепло, и вы выходите на детскую площадку, можно повторить эту игру в песочнице, тогда закапывать формы нужно прямо в песок. А ребёнка стоит оснастить лопаткой.
Геометрическое лото
Распечатайте карточки с нарисованными геометрическими фигурами в двух экземплярах. Один листок оставьте целым – это будет игровое поле. Другой разрежьте, вырезав все фигурки. Пусть малыш разложит все фигуры на карточке, помещая их в отведённые поля. Когда он освоит эту процедуру, можно поиграть в лото, доставая по одной фигурке и называя её. Например, вы говорите «квадрат», а ребёнок должен достать квадратик и положить его на место.
Скачать карточки для геометрического лото можно здесь. Кстати, первое время лучше раскрашивать фигуры неяркими цветами, чтобы они не отвлекали малыша от основной задачи. А со временем можно заменить разноцветные геометрические фигуры на картинки.
Скачать раскраски для детей
Геометрические фигуры имеют простые для раскрашивания контуры – прямые линии, чёткие углы, поэтому их часто используют в качестве первых раскрасок. Орудуя фломастерами или красками, ребёнок хорошо запоминает геометрические фигуры, особенно, если родители дают их названия. Делать это можно ненавязчиво, в таком духе: «А теперь давай раскрасим красным цветом этот маленький квадратик» или «Какого цвета ты хочешь сделать треугольник?».
Назад
Далее
Вы можете выбрать свои раскраски с геометрическими формами или скачать готовую подборку у нас.
Аппликация из геометрических фигур для малышей
Аппликации – несложный вид творчества, который развивает образное мышление, воображение, а также мелкую моторику рук. Это полезное занятие становится достаточно интересно детям ближе к двум годам, когда ребёнок без проблем обращается с клеем-карандашом. Причём на первых порах интерес вызывает не столько составление картин, сколько сам процесс приклеивания. Поэтому нет нужды брать сложные фигуры и картинки, вырежьте из цветной бумаги разные геометрические формы и просто приклеивайте их к холсту, так ребёнок быстро и прочно их запомнит.
Это полезное занятие становится достаточно интересно детям ближе к двум годам, когда ребёнок без проблем обращается с клеем-карандашом. Причём на первых порах интерес вызывает не столько составление картин, сколько сам процесс приклеивания. Поэтому нет нужды брать сложные фигуры и картинки, вырежьте из цветной бумаги разные геометрические формы и просто приклеивайте их к холсту, так ребёнок быстро и прочно их запомнит.
Когда этап хаотичного приклеивания фигур пройден, можно определять конкретные места и просить ребёнка поместить деталь именно сюда. С этого момента можно уже подключать воображение и составлять несложные композиции из геометрических фигур – цветы, домики, деревья, лодку-парусник, паровозик и т.д. Вы можете создавать картинки самостоятельно или воспользоваться нашими шаблонами для скачивания.
Назад
Далее
Ещё в продаже есть разнообразные книжки для творчества, они включают всё необходимое для аппликаций, нужно только вырезать деталь и приклеить в обозначенное место.
Среди обучающих пособий отдельно стоит отметить книжку «Цвет и форма» из серии «Школа Семи Гномов» для детей 1-2 лет. С ней в игровом формате можно выучить геометрические фигуры, приклеивая детали к картинкам.
А если вы не хотите возиться с клеем, можно использовать книжки с наклейками. Мне очень понравились книжки с наклейками от МОЗАИКА kids «Собери картинку». Яркие картинки нужно завершить, приклеив наклейку в отведённое место.
С использованием развивающих игр ребёнок намного быстрее запомнит названия геометрических фигур, научится сравнивать их, определяя, какая из них больше, а какая меньше. Игры с формами развивают пространственное мышление и логику, они направлены на формирование математического склада ума, хотя иногда задействуют и воображение, фантазию. Используйте развивающие занятия для изучения форм с детьми 1-3 лет, и не забывайте усложнять игры, добавлять знания об объёмных фигурах в более взрослом возрасте. Это мягко и постепенно подготавливает ваших детей к школе.
Геометрические фигуры как коммуникационные средства. Раздел “Маркетинговые коммуникации”
Опубликовано в журнале “Маркетинг в России и за рубежом” №5 год – 2014
Шкляр Т.Л.,
к. э. н., старший преподаватель кафедры маркетинга и коммерции
Московского государственного университета экономики,
статистики и информатики
АкаемоваА.В.,
к. ист. н., доцент кафедры маркетинга Киевского университета
управления и предпринимательства
В статье рассмотрено использование геометрических фигур в качестве коммуникативных средств. На экономических и политических примерах продемонстрировано воздействие символов на психологию потребителя. Предложено посмотреть, как влияют сущность и роль геометрических символов на покупателя и избирателя.
Ключевым моментом коммуникаций в маркетинге, экономике, политике является то, что коммуникации носят намеренный характер и рождаются для получения необходимой реакции со стороны получателя. Для этого создается реклама, пишутся статьи, плакаты и многое другое. В обоих вариантах создается бренд, который впоследствии продвигают.
Пробиться сквозь информационный шум к своему потребителю можно за счет использования «правильного» символа (знака, логотипа, эмблемы). Издревле человечество наделяет безграничной силой различные знаки, которые могут принести пользу, но также и нанести вред. Авторы предлагают рассмотреть особенности восприятия символов в маркетинговых коммуникациях как в экономике, так и в политике.
Символ (от греч. symbolon – признак) означает опознавательный знак для членов определенной группы людей, тайного сообщества; условный код, который обозначает или напоминает любое понятие; образ, воплощающий определенную идею [4, c. 487]. Семиотика исследует символы и знаки. Как наука она начала зарождаться в конце ХІХ – начале ХХ столетия. Ее основателями принято считать американского философа, логика и математика Чарльза Сандерса Пирса и швейцарского лингвиста Фердинанда де Соссюра.
487]. Семиотика исследует символы и знаки. Как наука она начала зарождаться в конце ХІХ – начале ХХ столетия. Ее основателями принято считать американского философа, логика и математика Чарльза Сандерса Пирса и швейцарского лингвиста Фердинанда де Соссюра.
Со времени основания науки семиотики полученные с ее помощью знания приобрели практическое приложение в таких отраслях, как лингвистика, история, философия, экономика, политология. С ее помощью можно найти верное значение тех или иных символов, ускорить процесс коммуникации и улучшить его качество, приблизить определенные идеи к целевой аудитории. С помощью знаков и символов осуществляется целеустремленная коммуникация с целевыми группами, ускоряется передача сообщений. Разнообразные эмблемы являются неотъемлемой составляющей экономических маркетинговых стратегий и политической рекламы, в частности они помогают более эффективно влиять на мнения и поведение субъектов коммуникации, что особенно важно сегодня.
Грамотно разработанный логотип донесет информацию потребителю о производителе, а также обеспечит узнаваемость продукта или политической партии.
Логотип – это определенный символ, который обозначает ту или иную компанию и представляет ее на рынке. Очень часто при создании логотипа или знака в качестве основы выбираются простейшие геометрические фигуры, такие как круг, прямоугольник, квадрат, звезда, ромб и т.д. [6]. Выбирая для базы своего логотипа определенную фигуру, вы получаете геометрический «код», который впоследствии будет влиять на организацию, выпускаемую продукцию или на политическую партию.
Геометрические фигуры непосредственно связаны с ценностями архетипичными символами, которые им приписывают в соответствующей социокультурной среде [2, с. 122]. Под архетипом понимаются универсальные образы и символы, которые содержатся в коллективном бессознательном. Благодаря архетипам у индивидуумов возникают определенные чувства и мысли относительно объекта, знака, события.
Визуальная семиотика оказывается эффективнее, чем лингвистическая или цветовая, поэтому стоит обратить внимание на известное высказывание: «увидеть собственными глазами». Преимуществами визуальной семиотики можно считать то, что она не нуждается в знании иностранных языков, на нее не нужно тратить дополнительные усилия, ее анализ происходит достаточно быстро.
Преимуществами визуальной семиотики можно считать то, что она не нуждается в знании иностранных языков, на нее не нужно тратить дополнительные усилия, ее анализ происходит достаточно быстро.
Рассмотрим несколько фигур в отдельности.
Круг, без сомнения, самая универсальная из всех геометрических фигур, символ цельности, полноты и ограниченности, вечности и бесконечности, единства и совокупности, постоянства и цикличности. Эта древняя символика круга раскрывается во многих выражениях великорусского языка: совокупность знакомых определяет «круг общения»; единство интересов цементирует «круг единомышленников»; безвыходную ограниченность в замкнутой цельности бытия иллюстрирует «замкнутый круг», а вечность и цикличность времени отмечает «круглый год», поскольку «все возвращается на круги своя».
Совершенная фигура в мифологии может олицетворять многие космические объекты: золотой круг (диск) представляет Солнце, серебряный – Луну, звездный – бездонный космос, голубой или синий – небо, отделяющий от хаоса упорядоченную Вселенную.
В мифологии круг – одна из основных форм структурирования пространства. Многие народы, такие как казахи, индейцы, чукчи, ненцы и др., строят жилища круглой формы: Бог построил шалаш вокруг шеста. Круг создает сакральную преграду, охраняющую человека и его мир от реальной или потенциальной опасности.
Магический круг защищает от ведьм посредством магического «закрытия» охраняемого объекта, делает его невидимым для «нечистых сил», создает границу, которую не может пересечь зло. Магический круг – универсальный оберег, хорошо подходящий для защиты от всего, что входит в сферу зла и смерти.
В современной эмблематике используются тысячи всевозможных знаков и символов, важной составной частью которых является круг. Условно их можно разделить на три группы:
1. Символические изображения, вписанные в круг (рис. 1 и 2).
Внутри круга изображена сирена-русалка: предполагалось, что эта сирена так же соблазнительна, как и кофе Starbucks.
2. Буквенные знаки, обведенные кругом (рис. 3 и 4).
3. Цифровые знаки, помещенные в круг (рис. 5).
Овал своей формой символизирует инволюцию и эволюцию, ассоциируется с динамикой, напором, стремлением вперед и инновационностью (рис. 6 и 7).
Квадрат – универсальная равносторонняя геометрическая фигура, символ стабильности и постоянства, равновесия и пропорциональности, защиты и ограничения. В Индии, Китае, Монголии и других странах Востока квадрат рассматривался как эмблема Земли и материального мира вообще в противоположность кругу, воплотившему в себе божественную, небесную и духовную сферу.
Квадрат в мифологии выступает как основная модель структурирования мира и является символом четырех в пространственном (четыре стороны света), в элементарном (четыре стихии), во временном (четыре времени года, стадии человеческой жизни и эпохи человечества) и в социальном (четыре основных класса) его аспекте.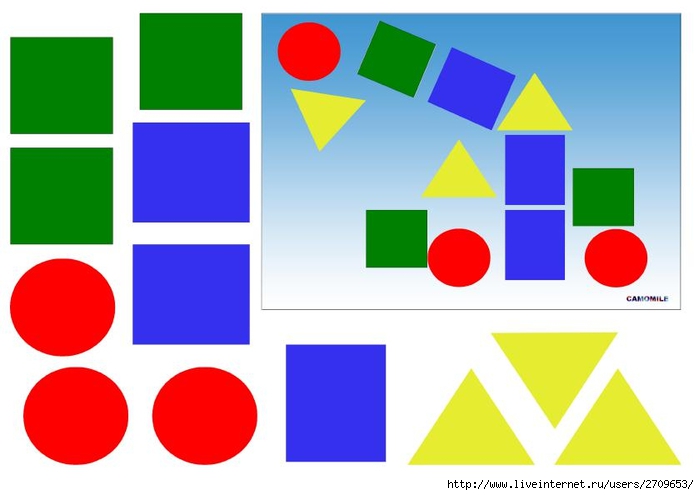 Все эти четверичные структуры задают основу порядка и стабильности мироздания (рис. 8 и 9). По этой причине связанные со сферой сакрального предметы, имеющие квадратную форму, могут рассматриваться в качестве символов мироздания (шахматная доска, бубны шаманов).
Все эти четверичные структуры задают основу порядка и стабильности мироздания (рис. 8 и 9). По этой причине связанные со сферой сакрального предметы, имеющие квадратную форму, могут рассматриваться в качестве символов мироздания (шахматная доска, бубны шаманов).
Обыгрывает форму коробки и форму деталей.
Прямоугольник всегда был и остается излюбленной для человека геометрической формой. Эта форма символизирует надежность и рациональность (рис. 10 и 11).
Треугольник является одной из первых геометрических фигур, которая стала использоваться в орнаментах древних народов. В Древнем Египте он был прямоугольным и являлся воплощением триады духовной воли, любви и высшего разума человека. Вертикальная сторона египетского треугольника составляла три единицы длины, основание – четыре, а гипотенуза – пять. Толковалась эта геометрическая фигура следующим образом: вертикальную сторону соотносили с мужским началом, основание – с женским, а гипотенуза символизировала плод их союза.
На Древнем Востоке почитали треугольник как символ природы всего сущего.
Примеры использования треугольника в настоящее время приводятся на рис. 12 и 13.
Ромб – мощь, сверхагрессия, смелость. Графический символ всесторонней активности. Сильный знак богатства и покровительства (рис. 14 и 15).
Mitsubishi в переводе означает «три бриллианта».
Звезда – закон, порядок, надежда. Символ престижа, энергии Солнца (рис. 16 и 17).
Гексагон – правильный шестиугольник, символ изобилия, красоты, гармонии, свободы, брака, любви, милости, удовольствий, мира, симметрий, символ числа 6, образ человека (две руки, две ноги, голова и туловище) (рис. 18). Данная геометрическая форма часто встречается в природе: пчелиные соты, строение некоторых сложных молекул и т. д.
д.
В заключение стоит отметить, что с помощью геометрических фигур осуществляется влияние на субъекты коммуникации. Поэтому в последнее время при создании логотипов данный аспект не остается без внимания. Исчерпывающее описание геометрической символики потребовало бы огромного объема текстового материала. Авторы данной статьи ограничились перечнем символических значений основных форм и описанием нескольких характерных примеров. Таким образом, можно смело утверждать, что относиться к использованию геометрических форм в логотипе несерьезно – нельзя. Символ может привлекать, а может отталкивать.
Он может как помочь, так и навредить. Прежде чем определиться, узнайте, какую информацию несет выбранный вами знак.
Используемые источники
1. Быкова Т.Н. Политическая символика: к проблеме определения и происхождения / Т.Н. Быкова // Вестник СевНТУ: сб. науч. тр. Вып. 91: Политология: – Севастополь: Изд-во СевНТУ, 2008.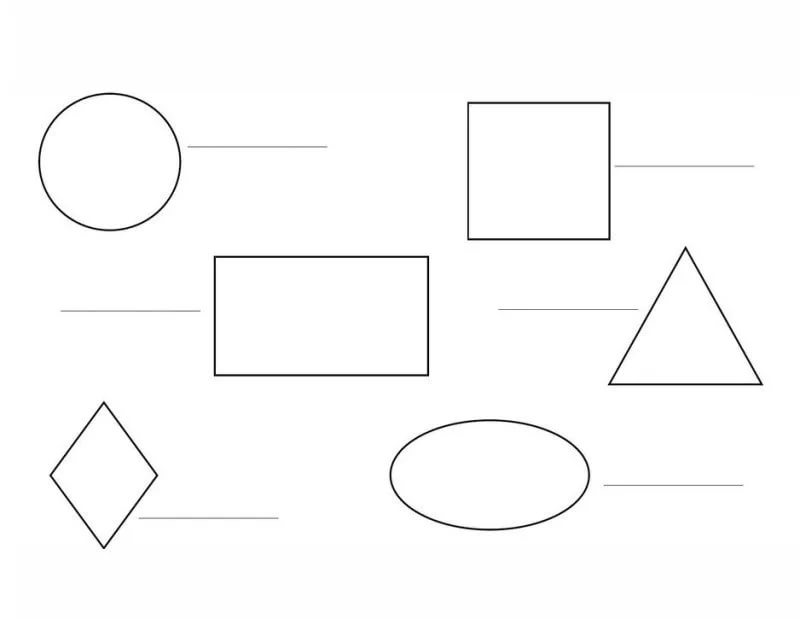 – С. 145–148.
– С. 145–148.
2. Егорова-Гантман Е.В. Политическая реклама / Е.В. Егорова-Гантман, К.В. Плешаков. – М.: Центр политического консультирования «Никколо М», 1999.
3. Лотман Ю.М. Символ в системе культуры: в 3 т. / Ю.М. Лотман. – Таллин: «Александра» Т. 1: Статьи по семиотике и топологии культуры. – 1992. – С. 191–197.
4. Холл Дж. Словарь сюжетов и символов в искусстве / Дж. Холл; пер. с англ. А.Е. Майкапара. – М.: КРОН-ПРЕСС, 1996.
5. Эко У. Отсутствующая структура. Введение в семиологию / У. Эко; пер. с англ. А.Г. Погоняйло, В.Г. Резник; под ред. М.Г. Ермакова. – СПб.: ТОО ТК «Метрополис», 1998.
6. Электронный ресурс. – Режим доступа: kurapov.name/lab/form_color_symbolism/
7. Электронный ресурс. – Режим доступа: phil-fak.uni-duesseldorf.de/fileadmin/Redaktion/Institute/Germanistik/AbteilungI/Busse/Texte/Busse-1993-03.pdf
Урок математики в 5-м классе “Геометрические фигуры”
- org/Person”> Тарасова Наталья Ивановна
Разделы: Математика
Данный урок позволяет учителю:
- Осуществлять мотивацию и стимулирование познавательной деятельности учащихся;
- Организовать самостоятельную работу школьников на различных уровнях – все, что дети могут усвоить самостоятельно или с дозированной помощью, должно быть отдано им.
- Обеспечить усвоение учебного материала каждым учеником в зоне его ближайшего развития на основе особенностей его субъективного опыта.
Цели изучения данного пункта:
- систематизировать знания учащихся о геометрических фигурах;
- повторить понятия: точка, прямая, отрезок, луч, угол, окружность, ломаная, многоугольник.
- познакомить с понятиями: поверхность, чертеж, круг, расстояние между точками.

План урока (для учащихся, если он работает самостоятельно по презентации урока
см. Приложение1).
- Изучение новый материал.
- Выполнение упражнения.
- Подведение итогов.
- Выполни дома.
- Закончи предложения.
Девиз урока. Легко учить, интересно учиться!
Ход урока.
- Работа с классом. (Или самостоятельная работа учащегося с самопроверкой)
Беседа.Геометрия и арифметика – важные части математики. В арифметике мы в основном занимаемся вычислениями, т. е. действиями с числами. Да и само название «арифметика» произошло от греческого слова «арифмос», что в переводе означает число. Разберем слово «геометрия» по частям: «гео» и «метрия». Какие известные слова начинаются со слова «гео»? ( География, геология, геодезия и др.)
Все эти науки изучают землю. Действительно, слово «гео» по-древнегречески означает «земля».
 А что означает слово «метрия»? Вспомним для чего нужен метр, и в каких случаях мы пользуемся метром. ( Для измерения). Следовательно, слово «геометрия», можно перевести как «землемерие». Бумагу в древности еще не изобрели, поэтому чертежи тогда часто выполняли на земле. Вы же будете чертить в тетрадях и на классной доске.
А что означает слово «метрия»? Вспомним для чего нужен метр, и в каких случаях мы пользуемся метром. ( Для измерения). Следовательно, слово «геометрия», можно перевести как «землемерие». Бумагу в древности еще не изобрели, поэтому чертежи тогда часто выполняли на земле. Вы же будете чертить в тетрадях и на классной доске.Поверхность классной доски и страницы тетради являются плоскими поверхностями или, как говорят в геометрии – плоскостями. Точнее говоря, они представляют собой только конечные части бесконечных плоскостей (вывести эти объекты на экран). О том что изучает геометрия, мы узнаем в ходе урока.
– Поверхности каких из следующих предметов: пол, потолок, занавеска, лепесток цветка, лист дерева, ручка – можно считать плоскими? (на экране).
– Приведите примеры своих плоских поверхностей.
В геометрии мы имеем дело с рисунками – чертежами, на которых изображаются геометрические фигуры.
- На экране появляются фигуры.
– По какому правилу фигуры объединили в группы?
(Плоские фигуры и объемные тела)– Назовите известные вам плоские фигуры
(квадрат, треугольник, круг, прямоугольник)На экране появляется фигура, дети называют ее, потом появляется слово – название фигуры.

– Назовите известные вам объемные тела.
(Куб, цилиндр, конус, пирамида, шар)Слово «фигура» в переводе с латинского языка означает «внешний вид», «образ». Назовите предметы, имеющие форму: шара, круга, квадрата, куба.
– С основными геометрическими фигурами вы уже знакомы. Это – (появляются на экране) точка, отрезок, луч, прямая, угол, треугольник, прямоугольник, многоугольник, окружность.
- Задание №94. На рисунке (на экране) изображены прямая, отрезок, луч, угол, треугольник, окружность, прямоугольник, окружность, прямоугольник, четырехугольник, пятиугольник, круг.
– Укажите каждую из этих фигур.
– Какие чертежные инструменты вам понадобятся для изображения таких фигур?
Все эти фигуры, кроме точки,
изображаются с помощью линий.Первое задание выполняется в парах. Сначала один из пары указывает на фигуру, а другой ее называет. А затем учащиеся меняются ролями.
- Задание №95.
 Выполняется самостоятельно.
Выполняется самостоятельно.1) Начертите отрезок АВ. Отметьте точки так, чтобы точка:
а) К не принадлежала отрезку АВ;
б) L принадлежала отрезку АВ;
в) N находилась между точками А и L;
г) М находилась на отрезке между точками N и L.2) Сколько отрезков образовалось на отрезке АВ?
ПРОВЕРКА – высветить на экран.
- Работа с текстом учебника.
Есть бесконечно много линий, которыми можно соединить точки А и В. (изобразить рис.10 стр.33 с помощью веревок, кнопок, магнитиков) Линия АМNВ называется ломаной, она состоит из трех звеньев – отрезков АМ, МN, NB. Представим себе, что все три наши линии являются нитями. Тогда и ломаную и AMNB, и кривую АВ можно распрямить, потянув, например, за конец В. А вот отрезок АВ не растянешь. Значит, он является самой короткой из всех линий, соединяющих точки А и В. Поэтому длину отрезка и считают расстоянием между точками А и В.
- Задание №96.
 Выполняется учениками на местах с последующим опросом. Ученики используют сигнальные карточки.
Выполняется учениками на местах с последующим опросом. Ученики используют сигнальные карточки.ПРАВИЛА чтения равенств и неравенств с отрезками.
В равенстве все, что стоит в левой части, читают в именительном падеже, а все, что стоит в правой части, читают в дательном падеже.НАПРИМЕР. АВ = 7см – длина отрезка АВ равна семи сантиметрам.
В неравенстве все, что стоит в левой части, читают в именительном падеже, а все, что стоит в правой части, читают в родительном падеже.
НАПРИМЕР. АB < CD – длина отрезка АВ меньше длины отрезка CD.
- Задание №99.
Точка К лежит между точками С и В, а точка N – между точками К и С. Сравните длины отрезков и результат запишите с помощью знаков неравенств:
1) СВ и NK; 2) СN и СК; 3) ВN и ВК; 4) СВ и СК.
ПРОВЕРКА:
1) СВ > NK; 2) СN < СК; 3) ВN > ВК; 4) СВ > СК.
- Задание №100. Выполняется устно.
Ученики могут рассуждать так: «Если точка лежит на отрезке АВ , то сумма расстояний от этой точки до концов отрезка должна быть равна длине отрезка АВ».
- Устная работа.
1) Прочитайте записи:
а) АВ = СD; д) РН = 5 м 6 дм;
б) ЕF < КL; е) NA = NL + LA;
в) МN > ОS; ж) XY = XE – EY;
г) RT = 3мм; з) DF = CD·5.2) Ответьте на вопросы.
– Какие точки принадлежат отрезку КL?
– Между какими точками расположена:
а) точка L? б) точка А?– Какая точка расположена между:
а) точками К и В?;
б) точками В и L?.– Найдите длину отрезка КL, если известно, что КД = 15см, ДВ = 9см, ВА = 21см, АL = 7см.
- Домашнее задание.
1) Тренировка в проведении отрезков с концами в заданных точках.
2) Задание №97.
3) Задание №4 – для сильных учащихся. Сделать вывод, что сумма расстояний от точки до концов отрезка равна длине отрезка, если точка принадлежит отрезку, и больше длины отрезка, если точка не принадлежит отрезку.

Итог урока. Закончить предложение. Я умею… Я могу… Я знаю…
(Приложение1)
Каковы примеры геометрических фигур в реальной жизни?
Геометрические фигуры повсюду. Куда бы вы ни посмотрели, почти все состоит из двухмерных (2D) и трехмерных (3D) геометрических фигур. Продолжайте читать, чтобы узнать о реальных примерах геометрических фигур, из которых состоит окружающий нас мир.
примеры геометрических фигур в дорожных знаках
Реклама
Примеры двухмерных геометрических фигур
Двумерные фигуры — это плоские фигуры, которые имеют ширину и высоту, но не имеют глубины. Круги, квадраты, треугольники и прямоугольники — это все типы двухмерных геометрических фигур. Ознакомьтесь со списком различных 2D-геометрических фигур, а также описанием и примерами их применения в повседневной жизни.
Имейте в виду, что все эти фигуры представляют собой плоские фигуры без глубины. Это означает, что вы можете сфотографировать эти предметы и определить их форму. То же самое не верно для трехмерных форм.
Примеры кругов
Круг — это круглая фигура с одинаковым радиусом от фиксированной точки в центре. Примеры кругов в реальной жизни:
- пироги с пиццей
- печенье
- колеса велосипеда
- циферблаты часов
- обеденные тарелки
Реклама
Квадрат Примеры
Четыре равных прямых стороны с четырьмя прямыми углами образуют квадрат. Некоторые реальные примеры квадратов:
- квадратные резиновые штампы
- квадратные плитки на полу
- квадратные бумажные салфетки
- шахматные доски
- клавиши виртуальной клавиатуры
треугольники с прямыми сторонами. Существует множество различных типов треугольников, в зависимости от их углов.
 Примеры треугольников в реальной жизни:
Примеры треугольников в реальной жизни: - ломтики пиццы
- бутерброд, разрезанный по диагонали
- чипсы из тортильи
- паруса на лодке
- дорожные знаки выхода
прямоугольник . Однако две стороны короче двух других сторон. Посмотрите на эти примеры реальных прямоугольников:
- обложки книг
- сотовые телефоны
- некоторые рамки для фотографий
- долларовых банкнот
- бутерброды с мороженым
Пятиугольник Примеры
Пятиугольники — фигуры с пятью сторонами одинаковой длины. Они менее распространены, чем четырехугольники, которые имеют четыре стороны, но все же встречаются в реальной жизни. Некоторые примеры пятиугольников:
- Здание Пентагона
- черные секции на футбольных мячах
- домашняя табличка в бейсболе
- знаки перехода
Шестиугольник Примеры
Если сложить одну сторону пятиугольника, получится шестиугольник. Шестиугольник имеет шесть прямых сторон одинаковой длины. Посмотрите на эти примеры шестиугольников из реальной жизни:
Шестиугольник имеет шесть прямых сторон одинаковой длины. Посмотрите на эти примеры шестиугольников из реальной жизни:
- кристаллы льда
- снежинки
- ячейки улья
- контур металлического ореха
- белые участки на футбольных мячах равной длины, сделать восьмиугольник. В реальной жизни они встречаются чаще, чем вы думаете. Некоторые примеры восьмиугольников:
- знаки остановки
- открытые зонты
- кольцо UFC
- покерные столы
реклама
Примеры трапеций
Трапеция — это всего лишь одна пара четырехгранных фигур с параллельными сторонами. Вы можете найти трапеции в следующих примерах:
- фермы на мостах
- некоторые стороны сумочки
- недоеденный кусок пиццы
- музыкальные цимбалы
реклама геометрические формы
- 80009
- баскетбольные мячи
- планеты
- апельсины
- шарики
- теннисные мячи
- шестигранные игральные кости
- кубики сахара
- квадратные строительные блоки
- кубики Rubix
- квадратные упаковочные коробки
- дорожные конусы
- вафельные рожки для мороженого
- шляпы для вечеринок
- рождественские елки
- воронки
- 90 круглое сечение. Некоторые реальные примеры цилиндров:
- картонная трубка для бумажных полотенец
- прямые трубки
- стаканы для питья
- тубы от гигиенической помады
- банки
примеры эллипсоида
эллипсоид представляет собой сферу, которая не является идеально круглой с двух сторон. Также известный как сфероид, эллипсоид создает эффект трехмерного овала. Некоторые примеры эллипсоидов:
- футбольные мячи
- яйца
- некоторые спутники Сатурна (Мимас, Энцелад, Тефия)
Примеры прямоугольной призмы
Прямоугольная призма представляет собой трехмерную фигуру, в которой одна пара противоположных сторон имеет одинаковую форму и соединена прямыми параллельными сторонами.
 У них четыре прямоугольные грани и две квадратные грани. Вы можете найти прямоугольные призмы в следующих примерах:
У них четыре прямоугольные грани и две квадратные грани. Вы можете найти прямоугольные призмы в следующих примерах:- палочки масла
- кирпичи
- камеры
- коробки для хлопьев
- прямоугольные упаковочные коробки
реклама
треугольная призма0015
Треугольные призмы такие же, как и прямоугольные, за исключением того, что их квадратные грани являются треугольниками, что делает их трехсторонними призмами. Примеры реальных треугольных призм включают:
- палатки
- дольки арбуза
- дольки сыра
- ломтики торта
Примеры пирамид
Плоская трехмерная фигура с одной стороной в точке есть пирамида. Они могут иметь любую форму с тремя или более сторонами в основании, включая треугольник (треугольная пирамида), квадрат (квадратная пирамида) и пятиугольник (пятиугольная пирамида). Примеры включают:
- Великая пирамида в Гизе
- крыша дома
- отдельно стоящие терки для сыра
- стеклянная пирамида Лурве
реклама
формы, которые строят29 наш мир 9000 и 3D формы.
 Базовое понимание геометрических фигур и того, где их можно найти в повседневной жизни, является отличным началом математического образования. Для получения дополнительной математической практики ознакомьтесь с этими основными математическими терминами, которые помогут вам начать работу. Вы также можете взглянуть на некоторые примеры одночленов и многочленов, если готовы перейти к алгебраическим понятиям.
Базовое понимание геометрических фигур и того, где их можно найти в повседневной жизни, является отличным началом математического образования. Для получения дополнительной математической практики ознакомьтесь с этими основными математическими терминами, которые помогут вам начать работу. Вы также можете взглянуть на некоторые примеры одночленов и многочленов, если готовы перейти к алгебраическим понятиям. Штатный писатель
Что такое геометрические фигуры? Определение, типы, свойства, факты
Геометрические фигуры Определение
Геометрические фигуры — это замкнутые фигуры, созданные с использованием точек, отрезков, окружностей и кривых. Такие формы можно увидеть повсюду вокруг нас.
Примерами геометрических фигур являются круг, прямоугольник, треугольник и т. д. Пицца круглая, а ее ломтики треугольные. Точно так же двери и окна являются примерами прямоугольников.
У правильной формы все стороны равны.
 Например, квадрат или правильный шестиугольник. Неправильные формы имеют стороны разной величины. Например, разносторонний треугольник.
Например, квадрат или правильный шестиугольник. Неправильные формы имеют стороны разной величины. Например, разносторонний треугольник.Некоторые из наиболее популярных фигур описаны ниже:
- Прямоугольник
Прямоугольник — это фигура, полученная в результате соединения четырех разных точек четырьмя разными линиями. В прямоугольнике противоположные стороны параллельны и равны по длине. Все углы в прямоугольнике прямые. Отличие прямоугольника от квадрата в том, что в прямоугольнике два параллельных отрезка длиннее двух других, а в квадрате все отрезки имеют одинаковую длину.
Примерами прямоугольных объектов являются экраны ноутбуков, экраны мобильных устройств и т. д.
- Квадрат
Квадрат — это четырехсторонняя геометрическая фигура, образованная путем соединения четырех отрезков прямой равной длины. Подобно прямоугольнику, отрезки, образующие квадрат, лежат под прямым углом друг к другу.
 Примерами квадратных объектов являются кубик Рубика, игральные кости, шахматные доски и т. д.
Примерами квадратных объектов являются кубик Рубика, игральные кости, шахматные доски и т. д.- Круг
Круг представляет собой геометрическую фигуру, состоящую из прямых линий. Можно считать, что окружность составлена из бесчисленных точек, расположенных на одинаковом расстоянии от центральной точки.
Примерами круглых объектов являются целые пиццы и колеса.
- Треугольник
Треугольник состоит из трех соединенных отрезков. Это сложная геометрическая фигура, поскольку она может иметь переменные углы и размеры.
Примерами треугольных объектов являются кусочки пиццы, начос, праздничные шапочки и т. д.
Примечательно, что название треугольника меняется в зависимости от его углов и размера сторон. Например, когда два отрезка треугольника образуют прямой угол, такой треугольник называется прямоугольным. Вот как это выглядит:
Любой треугольник с углами меньше 90 градусов называется остроугольным.
 Точно так же треугольник с одним углом больше 90 градусов называется тупоугольным треугольником. В равноугольном треугольнике все внутренние углы равны 60 градусов, а все стороны равны по длине. Обратитесь к диаграмме ниже, чтобы лучше понять.
Точно так же треугольник с одним углом больше 90 градусов называется тупоугольным треугольником. В равноугольном треугольнике все внутренние углы равны 60 градусов, а все стороны равны по длине. Обратитесь к диаграмме ниже, чтобы лучше понять.Применение геометрических фигур в реальной жизни
Геометрия — это изучение формы и пространства. Это помогает нам понять другие математические концепции, а также приложения в реальной жизни. Геометрию можно использовать для проектирования зданий, мостов, автомобилей и даже одежды. Принципы геометрии также используются в других разделах математики, таких как тригонометрия и исчисление.
Ниже приведены некоторые из реальных применений:
Квадраты: Квадраты можно найти в природе, например, кристаллы квадратной формы. Квадраты также используются в искусстве. Ярким примером является известная картина Пита Мондриана «Композиция с красным, синим и желтым».
Прямоугольники: Многие искусственные объекты, такие как телевизоры, книги и компьютерные мониторы, имеют прямоугольную форму.
 Есть много реальных примеров прямоугольников, таких как банкноты, сотовые телефоны и обложки книг.
Есть много реальных примеров прямоугольников, таких как банкноты, сотовые телефоны и обложки книг.Круги: Круги можно увидеть повсюду вокруг нас, от пиццы, которую мы едим, до циферблата часов.
Треугольники: Треугольники можно найти во многих местах. Большинство крыш имеют треугольную форму, называемую фронтонами. Треугольники могут помочь поддерживать такие конструкции, как мосты и здания. Есть даже некоторые чипы, которые имеют форму треугольников.
Овалы/эллипсы: Овал или эллипс представляет собой вытянутый круг (яйцевидной формы), длина которого больше ширины.
Примеры трехмерных фигур
Трехмерные фигуры представляют собой группу вершин, линии, соединяющие вершины, и грани, заключенные в эти линии. Они имеют длину, ширину и высоту и занимают некоторый объем. Для многих трехмерных фигур грани двумерны. Кроме того, некоторые фигуры в трех измерениях имеют криволинейные поверхности.
В трех измерениях основными фигурами являются:
- Кубик: Кубик Рубика, кубик сахара
- Конус: Конус для мороженого, пирамидка
- Кубовидный: Деревянная прямоугольная коробка, спичечный коробок
- Цилиндр: Рулон туалетной бумаги; банка газировки
- Сфера: Футбол, баскетбол
Решаемые примеры
Пример 1.
 Сколько сторон у десятиугольника?
Сколько сторон у десятиугольника? Решение : десятиугольник имеет десять сторон и десять вершин.
Пример 2: Как называется треугольник, у которого только две равные стороны?
Решение : Треугольник только с двумя равными сторонами называется равнобедренным треугольником.
Пример 3: конус имеет двумерную или трехмерную форму?
Решение : Конус представляет собой трехмерную фигуру.Практические задачи
Две равные стороны
Четыре равные стороны
Четыре неравные стороны
Ни одна из этих
Правильный ответ: Четыре равные стороны
Квадрат в геометрии — это плоская фигура, имеющая четыре равные стороны и четыре прямых угла.радиус
кривая
диаметр
хорда
Правильный ответ: радиус
Расстояние от центра круга до его внешней границы называется радиусом круга. Диаметр круга всегда вдвое больше его радиуса.
одномерная фигура
трехмерная фигура
двумерная фигура
Ничего из перечисленного
Правильный ответ: трехмерная фигура
Куб – трехмерная фигура. У него шесть граней, восемь вершин и двенадцать ребер. Каждая грань куба представляет собой квадрат, и все ребра имеют одинаковую длину. У куба шесть квадратных граней.открытая форма
неправильная форма
правильная форма
замкнутая кривая
Правильный ответ: правильная форма
Стороны равностороннего треугольника имеют одинаковую длину. Итак, равносторонний треугольник – это правильная фигура.Заключение
Геометрические фигуры являются частью нашей повседневной жизни. Учащимся они помогают заложить основу для более сложных понятий, таких как пространственные отношения.
Часто задаваемые вопросы
Основные геометрические фигуры?
Основными геометрическими формами являются круг, квадрат, прямоугольник, треугольник и т.
 д. Эти формы могут быть расположены в различных комбинациях.
д. Эти формы могут быть расположены в различных комбинациях.Как образуются геометрические фигуры?
Геометрические фигуры формируются с помощью линий, точек или кривых. Мы должны помнить, что эти формы должны соответствовать математическому определению. Если форму нельзя определить математически, она не является геометрической.
Какие примеры фигур не являются геометрическими?
В природе можно найти негеометрические формы. Например, галька, реки и т. д.
Как определить многоугольник?
Многоугольник — это фигура, состоящая из прямых линий без кривых. У него нет открытых сторон. «Многоугольник» — это широкий термин, обозначающий различные формы, такие как квадраты, треугольники и прямоугольники.
Список различных типов геометрических фигур с иллюстрациями
Мы сталкиваемся с различными типами объектов и материалов, в основе которых лежат определенные геометрические аспекты, которые делают их уникальными по-своему.
 Эта статья ScienceStruck предоставит вам подробную информацию о различных видах и названиях геометрических фигур, а также их значения и изображения.
Эта статья ScienceStruck предоставит вам подробную информацию о различных видах и названиях геометрических фигур, а также их значения и изображения.Краткий факт
Область геометрии и связанных с ней исследований форм и фигур, как сообщается, впервые возникла в цивилизации реки Инд и вавилонской цивилизации около 3000 г. до н.э. Некоторые сообщения предполагают, что у египтян была своя версия теоремы Пифагора еще до того, как Пифагор ее сформулировал.
Внешний вид или форма объекта или тела, которые остаются стабильными или постоянными при определенных нормальных условиях, называется геометрической формой этого объекта. Проще говоря, геометрические фигуры характеризуются как внешние ориентации рассматриваемых объектов. Поскольку параметры различаются, различаются и типы форм. Если формы двух объектов одинаковы или похожи, говорят, что они конгруэнтны друг другу. Можно сказать, что любое известное тело или материалистическая сущность во всей вселенной присутствует в форме геометрической формы.

В основном существует два типа геометрических фигур: двумерные (2D) и трехмерные (3D). Первый можно рисовать относительно осей X и Y, тогда как последний также включает ось Z. 2D-формы и фигуры в основном состоят из точек и соединительных линий, образующих форму. Они могут быть выпуклыми (обычный вид) или вогнутыми (неправильный вид). Во многих многоугольных 2D-фигурах выпуклые фигуры имеют углы менее 180 градусов, тогда как вогнутые формы имеют по крайней мере один угол больше 180 градусов. Трехмерные фигуры более сложны и состоят в основном из вершин, ребер, граней и т. д.
Следующие разделы помогут вам понять значение основных геометрических фигур вместе с их изображениями. Обратите внимание, что все упомянутые углы являются внутренними.
Различные типы геометрических фигур
Двухмерные (2D) фигуры
Треугольники
Это тип многоугольника, который состоит из трех сторон с тремя вершинами. Сумма углов треугольника равна 180 градусам в любом виде.
 Более подробную информацию см. в разделе ниже.
Более подробную информацию см. в разделе ниже.Равнобедренный треугольник
Две стороны имеют одинаковую длину, и два угла также равны. Линия симметрии присутствует.
Разносторонний треугольник
Длина всех сторон неодинакова, и все три угла имеют разные значения.
Равносторонний треугольник
Все три стороны и углы равны. Линия симметрии присутствует.
Прямоугольный треугольник
Один из углов равен 90 градусов. Линия симметрии может как присутствовать, так и отсутствовать.
Тупоугольный треугольник
Один из углов больше 90 градусов. Линия симметрии может как присутствовать, так и отсутствовать.
Остроугольный треугольник
Все углы острые (менее 90 градусов). Линия симметрии может как присутствовать, так и отсутствовать.
Четырехугольники
Эти многоугольники состоят из четырех сторон, а сумма углов равна 360 градусов в любом виде. Более подробную информацию см. в разделе ниже.

Прямоугольник
У них есть два набора противоположных сторон, которые равны, и все четыре угла равны 90 градусов. Присутствуют две линии симметрии.
Квадрат
Все четыре угла равны 90 градусов вместе с четырьмя равными сторонами. Этот многоугольник имеет четыре линии симметрии.
Параллелограмм
Они состоят из двух наборов противоположных прямых, равных и параллельных. Противоположные углы также равны относительно любой величины. Линия симметрии может присутствовать.
Ромб
Все четыре стороны равны и параллельны, но равны только противоположные углы. Присутствуют две линии симметрии. Он тесно связан с квадратом и параллелограммом.
Трапеция
Один набор противоположных прямых параллельен, а другой набор непараллелен. Линия симметрии может присутствовать. В Великобритании он называется трапецией.
Трапеция
Все четыре стороны неравны и непараллельны, линия симметрии отсутствует. В Великобритании это называется трапецией.
Воздушный змей
Два набора смежных сторон равны, и два противоположных угла также имеют равные значения. Линия симметрии присутствует.
Неправильный четырехугольник
Он имеет четыре неравные стороны и вогнутый вид, т. е. по крайней мере один угол больше 180 градусов.
Многоугольники
Фигуры, состоящие из трех и более сторон, называются многоугольниками. Углы таких геометрических фигур могут быть более 360 градусов. Ниже приведены как правильные, так и неправильные типы многоугольников.
Примечание : Хотя типы треугольников и четырехугольников включены в многоугольники, как они были описаны выше, они не перечислены в следующем разделе.
Пятиугольник
Состоит из пяти равных сторон, а сумма углов равна 540 градусов. Присутствуют пять линий симметрии.
Шестиугольник
Состоит из шести равных сторон, а сумма углов равна 720 градусов. Присутствуют шесть линий симметрии.

Семиугольник
Состоит из семи равных сторон, а сумма углов равна 900 градусов. Присутствуют семь линий симметрии.
Октагон
Состоит из восьми равных сторон, а сумма углов равна 1080 градусов. Присутствуют восемь линий симметрии.
Нонагон
Состоит из девяти равных сторон, а сумма углов равна 1260 градусов. Присутствуют девять линий симметрии.
Десятиугольник
Состоит из десяти равных сторон, а сумма углов равна 1440 градусов. Присутствуют десять линий симметрии.
Додекагон
Состоит из двенадцати равных сторон, а сумма углов равна 1800 градусов. Присутствуют двенадцать линий симметрии.
Неправильный многоугольник
Он может иметь четыре или более четырех неравных сторон, а внешний вид может быть вогнутым, т. е. по крайней мере один угол больше 180 градусов.
Изогнутые формы
Фигуры, состоящие из изогнутых линий и связанных точек, называются изогнутыми формами. Основные типы, включенные в эту категорию, описаны ниже:
Окружность
Состоящая только из одной изогнутой линии, эта форма не имеет какой-либо другой точки соединения или вершины.
 Расстояние от эпицентра до окружности одинаково во всех секторах.
Расстояние от эпицентра до окружности одинаково во всех секторах.Овал/эллипс
Похож на круг, но расстояние от центра до окружности постоянно меняется. Таким образом, эта форма имеет две оси: большую и малую, а также вытянутую форму.
Линза
Эта фигура похожа на эллипс, но состоит из двух отчетливых изогнутых линий, сходящихся на противоположных концах. В этом случае на их стыке присутствуют две точки.
Полумесяц
Эта форма характеризуется наличием двух изогнутых линий: одна выпуклая, а другая вогнутая. Они сходятся так же, как и у линзы, образуя своеобразную фигуру.
Арки
Эти фигуры состоят из изогнутой линии, пересекающейся с прямой в двух соседних точках. Первая линия может быть полностью изогнутой или может иметь форму двух параллельных линий, прежде чем соединиться с прямой линией.
Кольцо
Эта фигура характеризуется наличием двух концентрических круглых структур, каждая из которых отличается по размеру.
 В большинстве случаев внутренняя часть формы не закрыта. Эту фигуру также называют кольцевой структурой.
В большинстве случаев внутренняя часть формы не закрыта. Эту фигуру также называют кольцевой структурой.Сегмент окружности
В основном определяется как часть окружности, которая может состоять из части окружности вместе с хордой. Форма может быть полукругом или может быть фигурой с минимальной частью окружности. Оставшуюся часть также можно назвать сегментом.
Круговой сектор
В основном определяется как треугольная часть, отмеченная частью окружности и двумя прямыми линиями. Последние встречаются в общей точке, чаще всего в центре круга. Оставшуюся половину круга тоже можно назвать сектором.
Фигуры, описанные выше, являются основными, и помимо них существует множество других фигур в категории 2D-геометрии. Пройдя через эти формы, давайте взглянем на различные виды геометрических фигур, которые относятся к категории 3D.
Трехмерные (3D) фигуры
Куб/Шестигранник
Эта фигура имеет 12 ребер, 8 вершин и 6 граней.
 Все стороны равны по длине, а грани имеют квадратную форму.
Все стороны равны по длине, а грани имеют квадратную форму.Прямоугольная призма/кубовидная форма
Обладает теми же характеристиками, что и куб, в отношении количества сторон, граней и вершин, за исключением того, что грани имеют прямоугольную форму.
Цилиндр
Эта фигура не имеет вершин, но состоит из двух плоских граней (только в случае замкнутого цилиндра) и одной изогнутой грани. Два ребра также присутствуют.
Сфера
Эта геометрическая фигура не имеет ни ребер, ни вершин, и присутствует только одна изогнутая грань. Это наиболее равномерно изогнутая форма, включенная в категорию 3D.
Треугольная призма
Состоит из шести вершин, девяти ребер и пяти граней. Лица на обоих концах имеют треугольную форму, тогда как все остальные имеют прямоугольную форму.
Конус
Наряду с одной вершиной и одним ребром конусы имеют одну изогнутую грань и одну дополнительную плоскую грань (в закрытых конусах). Угол вершины может варьировать от острого до тупого.

Шестиугольная призма
Эта фигура, состоящая из двенадцати вершин, восемнадцати ребер и восьми граней, имеет два шестиугольника на противоположных концах. Остальные грани имеют прямоугольную или квадратную форму.
Пятиугольная призма
Эта фигура, состоящая из десяти вершин, пятнадцати ребер и семи граней, имеет два пятиугольника на противоположных концах. Остальные грани имеют прямоугольную или квадратную форму.
Квадратная пирамида
В этой форме основание состоит из квадрата, а остальные грани – треугольники. Всего у него 5 вершин, 8 ребер и 5 граней.
Треугольная пирамида
В этой форме основание и все грани – треугольники. Всего у него 4 вершины, 6 ребер и 4 грани. Базальный треугольник имеет другой размер по сравнению с гранями.
Шестиугольная пирамида
Эта форма состоит в основном из 7 вершин, 12 ребер и 7 граней. Его основание шестиугольной формы, а грани треугольные.
Параллелепипед
На этой фигуре все грани и основание имеют форму параллелограммов.
 Размеры граней могут отличаться, а могут быть одинаковыми.
Размеры граней могут отличаться, а могут быть одинаковыми.Тетраэдр
Он похож на треугольную пирамиду, за исключением того, что все грани и основание имеют одинаковый размер.
Октаэдр
Эта фигура состоит из восьми треугольников, образующих шесть вершин, восемь граней и двенадцать ребер. Треугольники могут быть как равносторонними, так и равнобедренными.
Додекаэдр
Они состоят из двенадцати пятиугольных граней, двадцати вершин и 30 ребер. Грани представляют собой пятиугольники одинакового размера.
Икосаэдр
Они характеризуются 30 ребрами, 20 гранями и 12 вершинами. Лица состоят из равносторонних треугольников.
Ромбический додекаэдр
Этот тип фигуры состоит из 12 ромбовидных граней, 14 вершин и 24 ребер.
Усеченный конус
Это конусообразная структура, но вместо вершины на одном конце присутствует круг.
Всестороннее знание геометрических форм и фигур очень важно, особенно если есть склонность к этой области математики.
 Кроме того, нужно научиться следовать различным математическим правилам, которые необходимы при рисовании геометрических фигур. Рисунки, описанные выше, вместе с примерами уравнений, несомненно, помогут вам разобраться в основах этой темы.
Кроме того, нужно научиться следовать различным математическим правилам, которые необходимы при рисовании геометрических фигур. Рисунки, описанные выше, вместе с примерами уравнений, несомненно, помогут вам разобраться в основах этой темы.Психология форм и их использование в дизайне
Успех любой стратегии визуального повествования или визуального маркетинга в основном зависит от того, что воспринимает аудитория. Сегодня я хочу вернуться к основам и поговорить о том, как все, что мы видим, может быть связано с простыми формами и как использование этих форм влияет на результат наших стратегий.
Все и вся, от элементов фотографии до определенной типографики, может быть проанализировано с точки зрения формы. Все детали наших презентаций, инфографики и визуальных стратегий рассказывают свою собственную историю. В наших силах соединить эти кусочки таким образом, чтобы творчески и эффективно рассказать нашу историю. Позвольте мне показать вам, как…
Вы можете просмотреть визуальную инфографику этого сообщения ниже или пропустить вперед, чтобы прочитать подробное объяснение различных типов фигур и их геометрических значений.

Создайте свою собственную удобную для чтения инфографику за считанные минуты с помощью этого инструмента перетаскивания. Попробуйте бесплатно
Сознательное сочетание форм и цветов
определенно будет использовать цвет. Сочетание определенных форм и цветов уже имеет определенный оттенок в нашем подсознании. Например, желтый круг обычно представляет собой солнце, а красный полукруг может представлять собой ломтик арбуза. Если вы не пытаетесь отправить прямое сообщение со своей композицией, 9Формы и цвета 0300 в основном являются аксессуарами
и должны рассматриваться как таковые. - Солнце
- Луна
- Земля
- Любая планета
- Мяч
- Апельсин
- Кольцо или лента
- Смайлик
- Кнопки
- Символ «играть»
- Символы «ускоренная перемотка вперед» и «назад»
- Пирамиды
- Горы
- Вымпелы
- Ломтики пиццы
- Здание Пентагона в США
- Черные фигуры на футбольном мяче
- Некоторые уличные знаки. Например: Детский/Школьный перекресток
- Символ дома или жилища
- Болты
- Напольная плитка
- Белые фигуры на футбольном мяче
- Секции улья
- Формы, образованные заборной проволокой
- Знаки остановки
- Зонты открытые
- Windows
- Плитка
- Свечи
- Наклейки с золотыми звездами
- Звезды на небе
- Призы и награды
- Звезды Голливудской Аллеи славы
- Кинозвезды
- Рождественская звезда
- Создайте подробную якорную диаграмму для каждой 2D-формы, которую вы обучаете. Нарисуйте фигуру, обозначьте ее и опишите, сколько сторон и углов у каждой из них.
- Разучите фигуру с помощью запоминающейся песни или стихотворения, чтобы помочь им запомнить, как она называется и ее части.
- Из цветных палочек от эскимо сформируйте двухмерные фигуры с прямыми сторонами. Оставьте их в центре, чтобы дети могли собрать их самостоятельно.
- Играйте и проявляйте творческий подход с танграмами. Посмотрите, какие рисунки могут сделать дети.
- Блоки-схемы — это также забавные, практические манипуляторы, которые побуждают детей к творчеству. Они являются идеальным дополнением к любой математической ванне!
- Достаньте геоборды и потренируйтесь формировать фигуры с помощью эластичных лент.
- Позвольте детям самостоятельно формировать фигуры с помощью Playdough.
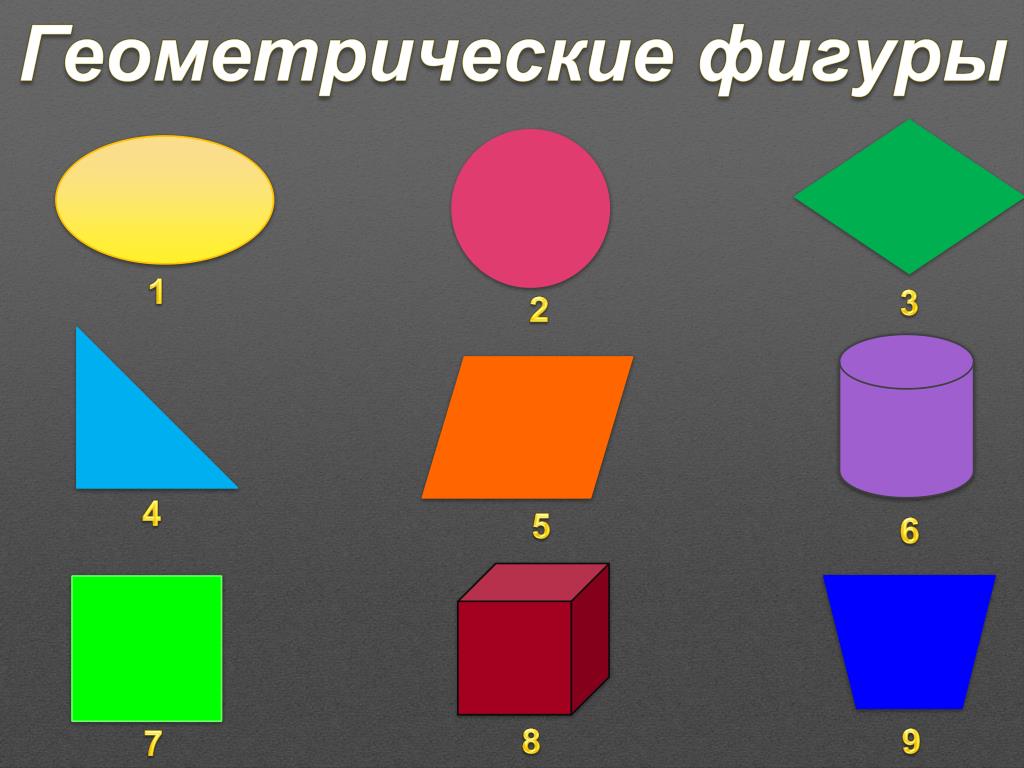
- Закрепите знания о формах с помощью увлекательных распечатываемых заданий, идеально подходящих для начальной школы!
- Потренируйтесь формировать фигуры с помощью различных инструментов, таких как маркеры или наклейки.
- Делайте простые поделки, используя фигуры, вырезанные из цветной бумаги. Пусть они изобретают форму, комбинируя части формы, чтобы сделать новые.
- Проверьте понимание с помощью небольших целенаправленных задач. Быстро проверьте распознавание фигур с помощью карточек.
- Рисуйте фигуры для практики, используя Boogie Board или другой инструмент для рисования и стирания. Умение рисовать базовые формы необходимо для того, чтобы позже приступить к более сложным вещам.
- Создайте подробную якорную диаграмму для каждой трехмерной формы, которую вы обучаете. Нарисуйте фигуру, обозначьте ее и опишите, сколько ребер, вершин и граней у каждой из них.
- Научите трехмерную форму с помощью запоминающейся песни или стихотворения, чтобы помочь им запомнить, как она называется и ее части.
- Создавайте 3D-фигуры с помощью маленьких шариков скрученной глины и зубочисток, чтобы скрепить все вместе.
- Позвольте детям слепить геометрические фигуры из пластилина.
- Играйте в игры, чтобы улучшить понимание и распознавание геометрических тел: формы Bump и Scoot — два интересных варианта.
- Проявите творческий подход к пеноблокам и постройте башню или другое сооружение.
- Детям нравятся магнитные детали, которые можно соединять в трехмерные объекты.
 Имейте их в наличии во время бесплатной игры или во время STEM.
Имейте их в наличии во время бесплатной игры или во время STEM. - Научите детей поэтапно рисовать объемную геометрическую фигуру. Они будут удивлены тем, насколько это просто!
- Просмотрите старые журналы, чтобы найти изображения различных трехмерных фигур. Добавьте изображения в якорную диаграмму класса.
- Головоломки, карточки с картинками и упражнения на сопоставление отлично подходят для запоминания форм и развития беглости речи.
- Создайте якорную диаграмму с примерами каждой формы в их мире. Пусть дети дают и рисуют предположения о том, как каждая фигура «выглядит…».
- Осмотрите класс и укажите на разные фигуры.
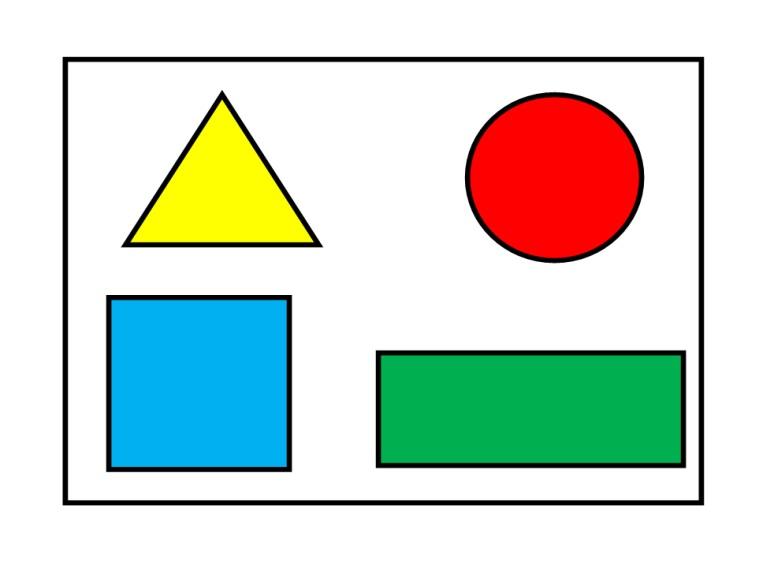
- Играйте в игры, в которых дети должны распознавать, какой объект имеет форму. Попробуйте эту игру в бинго!
- Отправляйтесь на поиски мусора снаружи и обратите внимание на увиденное.
- Сфотографируйте реальные примеры форм. Добавьте фотографии в карманную таблицу класса.
- Читайте книги о формах в реальном мире. «Форма вещей» — хорошая книга с множеством иллюстрированных примеров.
- Раздайте небольшие группы двухмерных или трехмерных фигур на пару учащихся. Попросите их по очереди сортировать фигуры и пусть другой человек попытается угадать их правило сортировки.
- Разложите фигуры стопкой перед классом. Попросите их отсортировать фигуры по типу или по определенному правилу.
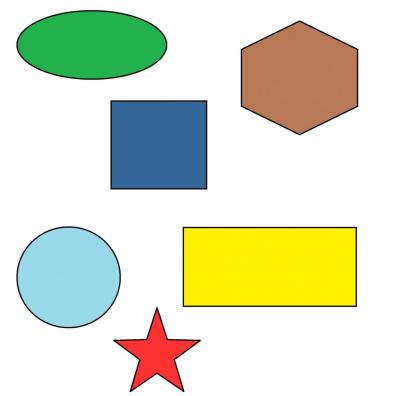
- Сортировка карточек с 2D- или 3D-изображениями по заданному атрибуту по классу или по центру
- Попросите детей найти симметричные предметы в классе и поделиться ими с классом.
- Выйдите на прогулку на природу и поищите симметричные вещи.
- Используйте блоки шаблонов для создания симметричных изображений. Получив половину изображения блока шаблона, создайте зеркальное отражение. Возьмите эти БЕСПЛАТНЫЕ карты симметрии блоков узоров ниже!
- Вместе с другом соберите конструкцию Lego, собрав одинаковые детали с обеих сторон.

- Постройте что-нибудь симметричное из небольших предметов, например блоков.
- Создайте произведение искусства, используя концепцию симметрии. Сложите лист бумаги и раскрасьте только с одной стороны. Сложите бумагу так, чтобы получились симметричные пятна краски.
- Треугольник
- Круг
- Полукруг
- Квадрат
- Прямоугольная форма
- Параллелограмм
- Ромб
- Трапеция
- Воздушный змей
- полигонов (правительство, шестиугольник, восьмиугольник, нонагон, десятиугольник и т. д.).
- Пицца и пироги
- Печенье
- Велосипедные шины
- Циферблаты
- Тарелки для ужина
- Квадратные резиновые штампы
- Черепица на полу
- Квадратные бумажные салфетки
- Шахматные доски
- Клавиши онлайн-клавиатуры
- Кусочки пиццы
- Нарезанный по диагонали сэндвич
- Чипсы из лепешек
- Лодка плывет
- Знак возврата информирует водителей о необходимости произвести
- Обложки книг глав
- Интеллектуальные устройства
- Рамки для изображений
- Долларовая банкнота
- Бутерброды с глазурью и лосьоном
- Структура Пентагона
- Футбольные мячи с черными секциями
- Бейсбольная тарелка
- Знаки перехода для движения по сайту
- Кристаллы льда
- Снег
- Ячейки улья
- Описание стальной гайки
- Белые секции на футбольных мячах
- Баскетбольные мячи
- Земли
- Апельсины
- Мрамор
- Теннисные сферы
- Шестигранный кубик
- Кубики сахара
- Квадратные строительные блоки
- Кубики Рубикса
- Квадратные упаковочные коробки
- Дорожные конусы
- Вафельные рожки для мороженого
- Головные уборы для мероприятий
- Рождественские елки
- Воронки
- Тубы из картона для бумажных полотенец
- Прямые трубопроводы
- Бокалы для питья
- Тубы для гигиенической помады
- Контейнеры
- футбольных мячей
- Яйца
- Несколько спутников Сатурна (Мимас, Энцелад, Тефия).
- Масляные палочки.
- Коробки с хлопьями.
- Прямоугольные упаковочные коробки.
- Уличные палатки.
- Дольки арбуза.
- Сырные дольки.
- Кусочки торта.
- Великая пирамида Гизы.
- Кровельная система дома.
- Отдельно стоящие терки для сыра.
- Стеклянная пирамида Лурв.
В отличие от двухмерных фигур, трехмерные фигуры имеют ширину, высоту и глубину. Примеры трехмерных фигур включают пирамиды, сферы и кубы.
 Взгляните на эти повседневные примеры трехмерных геометрических фигур.
Взгляните на эти повседневные примеры трехмерных геометрических фигур.Конечно, некоторые из этих форм взаимозаменяемы. Например, сумка не всегда может быть параллелограммом, поскольку, безусловно, возможны круглые сумки и другие типы. Этот список также не является исчерпывающим, так как существует множество других двухмерных и трехмерных геометрических фигур.
Реклама
Примеры сфер
Сферы – это круглые твердые фигуры. Как и у кругов, у них есть радиус в центре, который равноудален от каждой точки на сфере. Однако, в отличие от кругов, они имеют объем и глубину. Примеры реальных сфер:
Примеры кубов
Каждая из шести граней является квадратом куба. Когда они соединяются в форме трехмерного куба, также известного как квадратная призма, они создают глубину. Вот некоторые примеры кубов:
Примеры конусов
Конус имеет одно круглое основание.
 Конусы очень распространены в предметах повседневного обихода, в том числе:
Конусы очень распространены в предметах повседневного обихода, в том числе:цилиндры с параллельными сторонами и цилиндрическими фигурами
Использование фигур для создания чего-то еще
Вы также можете использовать фигуры как элементы большого изображения . Группа фиолетовых кругов, например, может быть объединена в гроздь винограда; белый прямоугольник и два белых треугольника могут составить конверт; из нескольких квадратов и прямоугольников можно сделать дом.
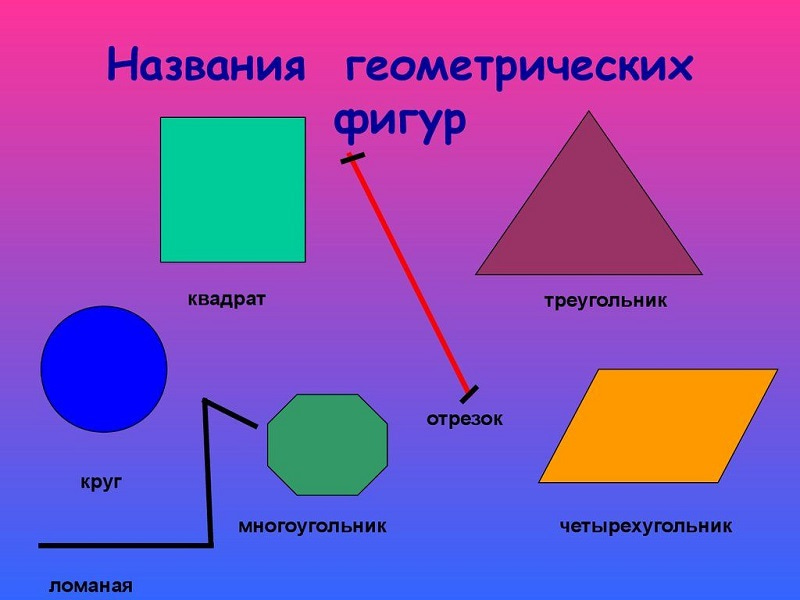 Все эти и многие другие возможности доступны для вас. Но вы должны думать о том, какова ваша конечная цель.
Все эти и многие другие возможности доступны для вас. Но вы должны думать о том, какова ваша конечная цель.Хотите создавать собственные фирменные значки? Или создавать свои собственные фоны? Вы хотите объединить свои фотографии в коллаж, который представляет что-то, например, форму рыбы? Формы — ваши лучшие союзники в подобных творениях. Все, что вам нужно сделать, это поиграть с ними, пока вы не получите композицию, которая вам нравится.
Использование фигур в качестве аксессуаров
В таких проектах, как презентации, инфографика и графика для социальных сетей, формы чаще используются в качестве аксессуаров или дополнений. Это не значит, что они менее важны — наоборот! В качестве аксессуаров они говорят больше сами по себе.
То, как мы размещаем наши аксессуары, может рассказать много разных историй. За формами стоит психология , о которой вы, возможно, даже не подозреваете. Есть эмоции и чувства, вызванные определенными формами, вдохновленные культурными условностями и формами, наблюдаемыми в природе.
 Мы не можем творить без форм. Даже бумага, на которой мы пишем или рисуем, имеет форму; наш экран форма!
Мы не можем творить без форм. Даже бумага, на которой мы пишем или рисуем, имеет форму; наш экран форма!Давайте углубимся в понимание форм и их (не очень) скрытых сообщений.
Геометрические, органические и абстрактные формы
Доступ к тысячам форм, значков и символов для использования в вашей графике. Попробуйте бесплатно
Все возможные формы делятся на три основные категории: геометрические, органические и абстрактные.
Геометрические
Геометрические фигуры — это те, о которых мы впервые узнаем в детстве. Это самые простые и наиболее распространенные формы из всех: квадраты, круги, треугольники и их производные, такие как прямоугольники, овалы и многоугольники. Большинство геометрических фигур симметричны и мгновенно узнаваемы, но они также передают молчаливые сообщения, о которых я расскажу позже в этом посте.
Органические
Органические формы представляют собой то, что мы знаем о природе и жизни вокруг нас.
 Наиболее распространенными органическими формами являются растения, такие как цветы и листья. Другой тип органических форм — это те, которые представляют собой формы, которые мы можем создать сами, например, брызги краски или акварельные капли. Эти формы в основном асимметричны, и их линии могут различаться.
Наиболее распространенными органическими формами являются растения, такие как цветы и листья. Другой тип органических форм — это те, которые представляют собой формы, которые мы можем создать сами, например, брызги краски или акварельные капли. Эти формы в основном асимметричны, и их линии могут различаться.Abstract
Абстрактные формы — это изображения реальных вещей, не являющиеся их точными представлениями. Значки, которые мы видим в веб-дизайне, наших телефонах и дорожных знаках, представляют собой абстрактные формы, которые мы привыкли видеть и легко распознаем. Отличным примером абстрактной формы является фигурка из палочек, изображающая человека. Символы также считаются абстрактными формами.
Квадраты и прямоугольники
Формы, с которыми мы чаще всего сталкиваемся в дизайне и в повседневной жизни, — это квадраты и прямоугольники как в горизонтальном, так и в вертикальном расположении. Уличные вывески, вывески магазинов, заголовки социальных сетей, заголовки блогов, визитки, листы бумаги — все это прямоугольники.

Знакомство с квадратами и прямоугольниками позволяет легко использовать их в качестве основы дизайна или рамки. Квадраты и прямоугольники заставляют нас чувствовать себя в безопасности и содержат . Они дают ощущение стабильности и уверенности, но также легко отходят на второй план, а чувства, которые они передают, в основном подсознательны.
Правило третей
Использование квадратов и прямоугольников в качестве основы композиции является хорошей практикой. Экспериментирование с масштабированием и соединением прямоугольников и квадратов может служить визуальным упражнением при разработке новой графики. Существует одна очень важная практика проектирования, называемая правилом третей . Все дело в том, как прямоугольники и линии контролируют баланс в любой композиции.
Правило третей лучше всего визуализировать в виде сетки. Лучшие веб-сайты проектируются и разрабатываются по сетке. Графические дизайнеры используют сетки для лучшей композиции.
 Архитекторы используют сетки для более качественных измерений. Из чего состоят сетки? Квадраты и прямоугольники (а иногда и треугольники, если вы хотите использовать более сложную сетку перспективы).
Архитекторы используют сетки для более качественных измерений. Из чего состоят сетки? Квадраты и прямоугольники (а иногда и треугольники, если вы хотите использовать более сложную сетку перспективы).Правило третей — это, по сути, сетка, которая разделяет пространство холста на девять равных частей. Идея заключается в том, что человеческий глаз имеет естественное направление, в котором он предпочитает двигаться от объекта к объекту. Наиболее важными областями являются точки пересечения , начиная с левого верхнего угла, а затем либо сразу справа, либо прямо вниз. Нижний правый угол — это точка пересечения, которая привлекает наименьшее внимание.
СВЯЗАННЫЕ: 12 принципов визуальной иерархии, которые должен знать каждый, кто не является дизайнером
Круги
В дизайне круги используются по-разному для разных целей. Например, в дизайне логотипов круги являются наиболее распространенной и широко распространенной формой или фоновым контуром логотипа.
 На веб-сайтах они в основном используются в качестве кнопок и небольших значков. Почему мы видим так много кругов, используемых в качестве вспомогательных фигур на веб-сайтах, в графике и даже в инфографике? Причина этого в том, что круги очень заметны и довольно сильны.
На веб-сайтах они в основном используются в качестве кнопок и небольших значков. Почему мы видим так много кругов, используемых в качестве вспомогательных фигур на веб-сайтах, в графике и даже в инфографике? Причина этого в том, что круги очень заметны и довольно сильны.Круги символизируют целостность , естественное чувство завершенности. Когда мы думаем о вещах в форме кругов в окружающем нас мире, мы можем назвать так много вещей.
Некоторые вещи, которые могут представлять кружки:
Примите во внимание силу круга и то, как он может повлиять на ваш дизайн. Круги могут представлять собой постоянное движение, такое как вращение или перекатывание. Контур круга может служить полосой или кольцом, представляющим цикл или продолжающееся действие. Круг может представлять собой отверстие, пробитое на странице.
 Круг с легким эффектом тени может выглядеть как наклейка или кнопка, «размещенная» поверх остального дизайна.
Круг с легким эффектом тени может выглядеть как наклейка или кнопка, «размещенная» поверх остального дизайна.Треугольники
Треугольники имеют два значения в зависимости от их положения. При направлении вверх они представляют стабильность и силу , при направлении вниз становятся неустойчивыми. Треугольник в первую очередь является мужской формой, но в перевернутом виде он также представляет женское воспроизводство. В духовности треугольники представляют союз тела, ума и духа.
В дизайне тонкие треугольники можно использовать вместо стрелок или указателей. Меньшие треугольники можно использовать в качестве фигур в коллаже со взаимосвязанной композицией или эффектом мозаики. Большие треугольники более заметны, поэтому вы должны принять во внимание их значение, прежде чем использовать их в больших размерах. Всегда лучше использовать треугольники, которые удобно сидят на основании или с острием, обращенным вправо, передавая сообщение о движении вперед.
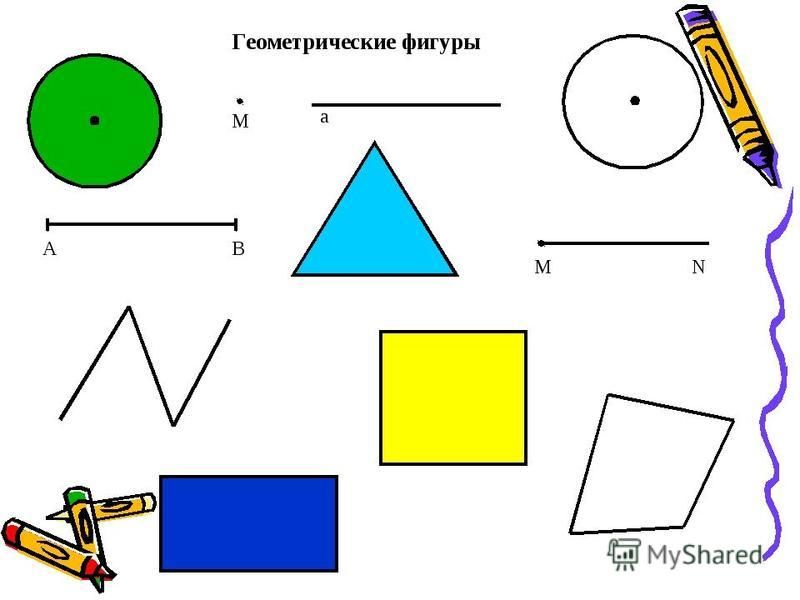
Создайте собственную графику для блога за считанные минуты с помощью этого инструмента перетаскивания. Попробуйте бесплатно
Треугольники, которые мы видим в повседневной жизни:
Треугольники также можно использовать для отказа от традиционного квадратного дизайна. Их можно комбинировать бесчисленным количеством способов для создания всевозможных динамических дизайнов, таких как показанный ниже.
Пятиугольники, шестиугольники и восьмиугольники
Пятиугольники, шестиугольники и восьмиугольники представляют собой геометрические фигуры с пятью, шестью и восемью сторонами соответственно. Это наиболее часто используемые многоугольники с более чем четырьмя сторонами. Конечно, их намного больше, но эти три являются наиболее универсальными для создания графики.

Давайте рассмотрим, что каждая из этих форм напоминает в нашей повседневной жизни, чтобы лучше понять, как их можно использовать в наших проектах.
Пентагоны
Шестигранники
Восьмиугольники
Самостоятельное использование многоугольников
Несколько простых способов использования любого из этих многоугольников – вставка текста внутрь них или вырезание изображений в виде фигур . Вы можете использовать эти методы в изображениях заголовков постов блога, булавках Pinterest, графике Instagram, миниатюрах YouTube или слайдах презентации.

Использование любого из этих многоугольников вместо обычного прямоугольника или квадрата придаст вашей графике вид, отличный от обычного. Понимание смысла каждой из этих фигур – это ключ к выбору наиболее подходящей для вашего бренда или сообщения. Используйте приведенный выше список, чтобы подумать о том, что эти формы напоминают вам, и подумайте, как это влияет на ваш дизайн.
Использование многоугольников в качестве взаимосвязанных фигур
Эти фигур также можно использовать в качестве кусочков головоломки для создания более крупной композиции и организации информации, например, в инфографике. С помощью шестиугольников вы можете создать композицию в стиле улья с аналогичными цветами. С помощью пятиугольников и восьмиугольников вы можете создать что-то похожее в горизонтальном, вертикальном и даже диагональном направлениях.
Пятиугольники, шестиугольники и восьмиугольники также могут быть разделены на более мелкие формы, такие как треугольники, для создания прогрессии с визуально круговым движением или визуализацией, подобной круговой диаграмме.

Природные фигуры
Естественные или органические формы представляют собой предметов и животных, встречающихся в мире природы , таких как листья, цветы, деревья или искусственные предметы, такие как брызги краски и капли чернил.
Вам обязательно следует использовать эти формы, если ваш дизайн связан с окружающей средой или экологией. Эти виды фигур также отлично подходят для графики о природе, такой как походы, кемпинг и тому подобное. Если ваш бизнес связан с цветами, вы можете выйти за рамки простого использования изображений настоящих цветов, используя естественные формы в качестве аксессуаров для своей графики.
Вы можете использовать естественные формы сами по себе или как часть более крупной композиции, например, как в примерах ниже. Но имейте в виду, что у таких форм есть четкое значение и послание — они вовсе не очень подсознательны.
Символы и значки
Символы и значки являются разновидностью абстрактных форм .
 Они могут представлять обычные вещи, а также могут нести высшую символику, религиозную, политическую или культурную. Символы и значки особенно полезны при создании графики, поскольку они быстро передают сообщения.
Они могут представлять обычные вещи, а также могут нести высшую символику, религиозную, политическую или культурную. Символы и значки особенно полезны при создании графики, поскольку они быстро передают сообщения.Разница между символами и фигурами заключается в том, что обычные формы могут использоваться в дизайне в большем количестве, в то время как слишком много символов может перегружать и создавать путаницу. Сведите использование символов к минимуму, а если вы их используете, выбирайте их с умом.
Иконки часто используются в инфографическом дизайне, чтобы свести к минимуму использование текста и привлечь внимание к определенным ключевым сообщениям. Но вам нужно тщательно выбирать иконки, чтобы оставаться на бренде. Убедитесь, что вы изменили цветовую схему своих значков в соответствии с вашим брендом и используете только один стиль значков в одной и той же инфографике.
СВЯЗАННЫЕ: Как выбрать и использовать значки в вашей инфографике
Звезды
Помимо геометрических фигур, звезды также могут считаться символами, поскольку они часто используются в религиозных изображениях и имеют различные коннотации.
 Звезды запоминаются и часто символизируют дурную славу и важность . Наши глаза всегда будут притягиваться к звезде (особенно если она желтая или золотая) раньше любой другой формы.
Звезды запоминаются и часто символизируют дурную славу и важность . Наши глаза всегда будут притягиваться к звезде (особенно если она желтая или золотая) раньше любой другой формы.Звезды отлично подходят для обозначения цен со скидкой, специальной информации о продукте или рекламной акции, скидках или бонусах. Желтые звезды могут напомнить нам о золотых звездах, которые мы получили, будучи студентами, а синие звезды напомнят о лентах за первое место. Используйте звезды соответственно, чтобы передать правильное сообщение.
Доступ к тысячам форм, символов и значков для использования в вашей графике. Попробуйте бесплатно
С чем у нас ассоциируются звезды?
Пятиконечные звезды острием вверх:
Стрелки
Стрелки бывают самых разных типов и стилей, каждая из которых имеет уникальную атмосферу.
 Жирные сплошные стрелки передают больше силы, чем тонкие или полые стрелки. Волнистые стрелки могут придать вашему дизайну игривый вид. Стрелки могут быть очень маленькими для использования в маркированных списках или достаточно большими для размещения внутри них текста. Концентрические стрелки в форме треугольника или круга могут использоваться для обозначения циклов и процессов. Международный символ вторичной переработки — треугольник из стрелок.
Жирные сплошные стрелки передают больше силы, чем тонкие или полые стрелки. Волнистые стрелки могут придать вашему дизайну игривый вид. Стрелки могут быть очень маленькими для использования в маркированных списках или достаточно большими для размещения внутри них текста. Концентрические стрелки в форме треугольника или круга могут использоваться для обозначения циклов и процессов. Международный символ вторичной переработки — треугольник из стрелок.Направление
Главной целью стрелки является передать направление . Использование стрелок может помочь вашему зрителю проследить путь информации от одной части вашего изображения к другой. Вы также можете использовать стрелки в графике «до и после» или другие виды преобразований. Как и в случае с иконками, лучше придерживаться бренда и использовать единый стиль стрелок во всем дизайне. Если вы используете нарисованные от руки стрелки в одной инфографике, не следует сочетать их с толстыми, блочными стрелками.

Формы и символы цифрового поколения
Смайлики
Использование смайликов в графике быстро становится тенденцией, которая, похоже, не скоро исчезнет. Если ваша клиентура состоит в основном из молодежи, вам следует рассмотреть возможность использования смайликов в своей графике. Миллениалы используют смайлики вместо слов. Почему бы не воспользоваться этим и не использовать в своих интересах?
Булавки-капли
Булавки-капли — это формы, которые мы узнали благодаря картам Google и другим приложениям для определения местоположения. Например, если у вас есть туристическая компания, вы можете использовать настраиваемые булавки в своей графике и картах. У Visme есть целый раздел булавок в библиотеке иконок!
Оставаться на бренде с помощью фигур
При использовании фигур для создания графики для нашей визуальной маркетинговой стратегии нам нужно помнить одну вещь: мы всегда должны оставаться на бренде. При создании руководства по визуальному стилю вы должны установить набор форм, которые должны использоваться для всей графики бренда.
 Старайтесь не использовать фигуры волей-неволей каждый раз, когда вы создаете новую графику.
Старайтесь не использовать фигуры волей-неволей каждый раз, когда вы создаете новую графику.Если ваши квадраты и прямоугольники всегда имеют закругленные углы, оставьте так. Если вы используете восьмиугольники для обрамления текста, всегда используйте восьмиугольники.
Подумайте о своих читателях, клиентах и последователях. Они лучше запомнят ваш бренд, если смогут сказать что-то вроде «тот бренд с крутым шестиугольником» или «тот бренд с концентрическими стрелками». Сохранение сознательной последовательности является ключом к тому, чтобы оставаться верным своей визуальной идентичности.
Your Turn
Бесплатные инструменты визуального контента, такие как Visme, поставляются с обширными библиотеками значков, которые включают все, от геометрических и естественных фигур до значков и символов. Вы также можете изменить цветовую схему своих фигур, чтобы было легче оставаться на бренде.
Вы можете пройти тест-драйв здесь и поделиться своими уникальными творениями со мной ниже.
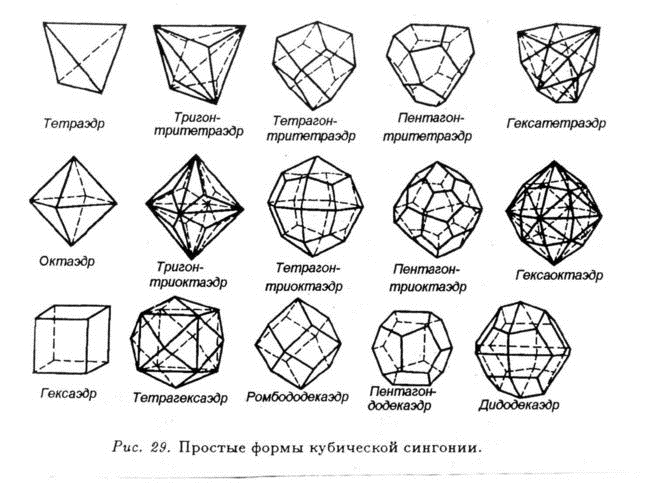 Удачного проектирования!
Удачного проектирования!Геометрия и фигуры для детей: увлекательные занятия —
Изучайте и стройте с помощью геометрии и форм для детей. Включено множество веселых математических заданий и БЕСПЛАТНОЕ задание по симметрии блоков узоров!
Вы искали Pinterest или гуглили, чтобы найти интересную, практическую геометрию и формы для детей? Вы ищете уроков и идей для занятий, которые помогут вам лучше понять формы и геометрию? Тогда вы попали по адресу!
Геометрия и фигуры для детей
Математические советы и стратегии, необходимые для преподавания геометрии в начальных классах, находятся прямо здесь. У вас будет все, что вам нужно, чтобы быстро внедрить множество геометрических заданий, игр и центров в свой класс или домой.
Занятия, книги, уроки по математике и другие полезные ресурсы ( , в том числе БЕСПЛАТНЫЙ ) охватывают множество понятий геометрии и идеально подходят для детского сада, первого и второго класса.
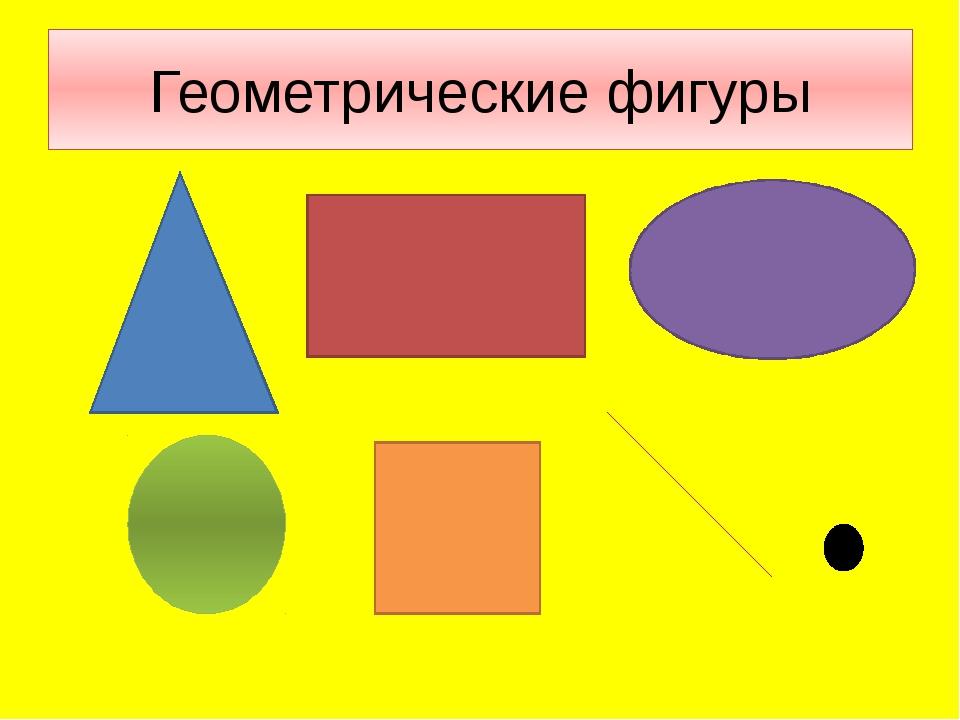 Кроме того, вы найдете ценные материалы по геометрии и советы по манипулированию, а также бесплатные подарки, которые вы можете получить уже сегодня! Этот пост наполнен огромным количеством полезной информации для вас во время вашего обучения.
Кроме того, вы найдете ценные материалы по геометрии и советы по манипулированию, а также бесплатные подарки, которые вы можете получить уже сегодня! Этот пост наполнен огромным количеством полезной информации для вас во время вашего обучения.Почему важно обучать детей геометрии и фигурам?
Детям нужно много возможностей, чтобы узнать о формах. Научиться определять и понимать, что представляют собой различные формы, а также их части, являются важными понятиями. Каждый день дети сталкиваются с формами в окружающей их среде. Они видят и взаимодействуют с ними повсюду ежедневно. Они должны уметь распознавать формы, озвучивать то, что видят, и понимать, почему они здесь.
Мы хотим, чтобы дети увидели форму и установили связь. Когда они смотрят на колесо автомобиля, мы хотим, чтобы они восприняли это изображение как круг, форму, которую они научились обозначать. В конце концов, мы хотим, чтобы дети научились различать формы и понимать формальные определения фигур.
 Когда они смотрят на хлопушку, мы хотим, чтобы они восприняли это изображение как квадрат, поскольку у него четыре равные стороны.
Когда они смотрят на хлопушку, мы хотим, чтобы они восприняли это изображение как квадрат, поскольку у него четыре равные стороны.По мере изучения каждой геометрической концепции дети переходят к следующему этапу понимания. Хорошее знание форм жизненно важно для дальнейшего изучения более сложных геометрических концепций.
Приведенные ниже упражнения помогут развить понимание форм. Используйте их так, как они описаны, или адаптируйте их к своим потребностям. Обсуждайте формы и поощряйте вопросы. Когда ребенок замечает фигуры в своем окружении, пусть они поделятся этим с классом! Находите время для веселых и увлекательных занятий по геометрии ежедневно в своем математическом центре и на бесплатных игровых площадках.
Геометрия и формы для занятий с детьми
Двухмерные фигуры
Первый этап в изучении геометрии – это умение идентифицировать, называть и описывать двухмерные фигуры. Говорите о формах всякий раз, когда вы их видите, и развешивайте плакаты с фигурами на стене, это полезно для детей! Имейте множество манипулятивных форм, доступных для изучения и «игры».

Упражнения
Трехмерные фигуры
Как и в случае с двумерными фигурами, важно уметь идентифицировать, называть и описывать трехмерные фигуры! Наш мир состоит из трехмерных форм, и нам нужно распознавать их, чтобы понимать вещи.
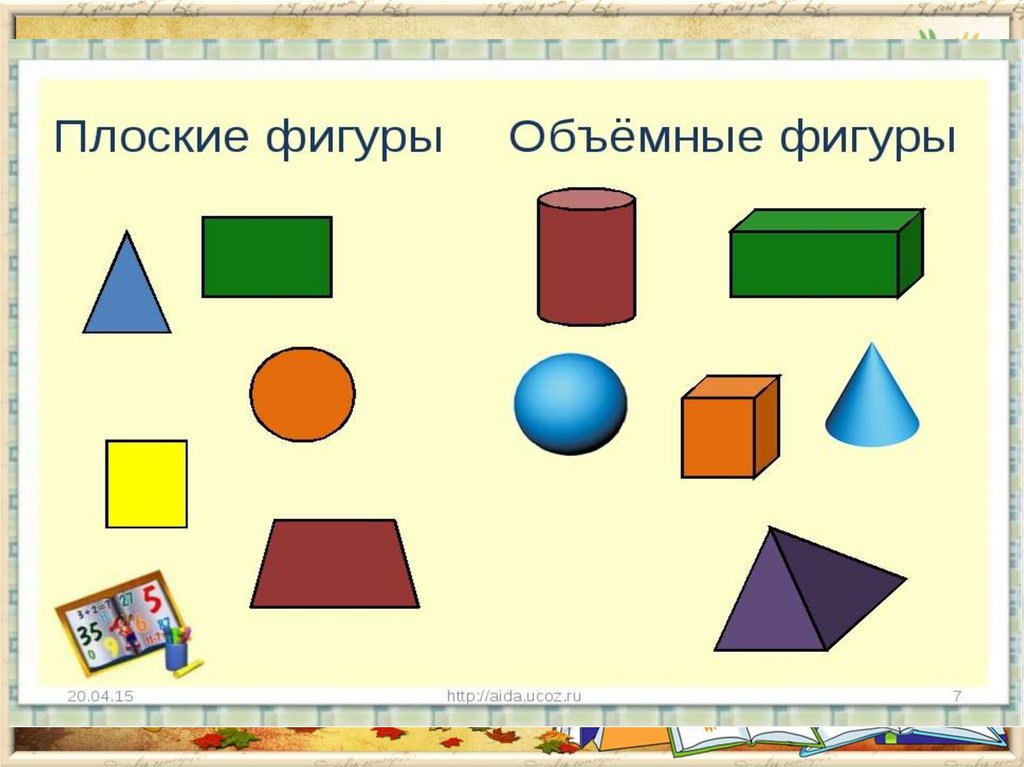 Удостоверьтесь, что у вас есть геометрические тела, которые можно держать и с которыми можно взаимодействовать, а также плакаты, на которые можно ссылаться.
Удостоверьтесь, что у вас есть геометрические тела, которые можно держать и с которыми можно взаимодействовать, а также плакаты, на которые можно ссылаться.Упражнения
Формы в окружающей среде
Основная цель обучения детей формам состоит в том, чтобы они могли видеть формы в окружающей среде и взаимодействовать с окружающей средой благодаря этому пониманию. Заставьте детей постоянно говорить о том, что они видят, и поощряйте их делиться.
Действия
Сравнение и сортировка фигур
Предоставьте детям возможность сравнивать разные фигуры друг с другом. После того, как будет достигнуто понимание частей фигур, научите детей сортировать фигуры по одному или двум признакам.
Упражнения
Симметрия
Расскажите детям младшего возраста об отражательной симметрии, которая является зеркальным отражением. Покажите детям, что если провести линию по центру изображения, обе стороны совпадут. Это называется линией симметрии. У одних фигур одна линия симметрии, у других больше. Познакомьте их также с симметрией, встречающейся в природе и окружающей их среде.
Деятельность
Ресурсы по геометрии и фигурам для K-2
Действия, представленные в этом посте, можно найти в следующих ресурсах.
Группа геометрии и форм для детского сада
Геометрия для первого класса, группа
Блок геометрии и дробей для второго класса
Бесплатные изображения симметрии блоков шаблонов
Распечатайте набор этих блоков, чтобы использовать их вместе с блоками шаблонов, чтобы создать простой математический центр. Детям понравится создавать симметричные узоры!
Получите БЕСПЛАТНЫЕ изображения симметрии блоков шаблонов для вашего математического центра, нажав на изображение ниже .
Книги по геометрии и фигурам
Вверх, вниз и вокруг Кэтрин Айес
Вперед, формы, вперед, Дениз Флеминг
Когда линия изгибается… форма начинается, Ронда Грин
Формы, формы, формы, Тана Хобан
Форма вещей, Дэйл Энн Доддс Прыжок Стюарт Дж. Мерфи
Мерфи
Если бы вы были многоугольником Марси Абофф
Если бы вы были четырехугольником Марси Абофф
Жадный треугольник Мэрилин Бернс
Приготовьтесь! Дэвид Адлер
Три поросенка, один волк, семь волшебных форм Грейс Маккароне
Форма Генри Плакроуза
Формы мыши Эллен Уолш
Форма за формой Сьюз Макдональд
Формы! от National Geographic Kids
Капитан-невидимка и космические формы Стюарта Дж. МерфиМатериалы по геометрии
Попробуйте комплексную программу Mindful Math
Узнайте о программе Mindful Math и о том, как она может изменить ваш математический блок в лучшую сторону! Эта всеобъемлющая учебная программа по математике доступна для детского сада, первого и второго класса.
Больше математических мероприятий для детей
Номер дневной деятельности
Добавление и вычитание до 20 действий для классной комнаты
Число. БЕСПЛАТНАЯ серия электронных писем Number Sense
Подпишитесь на серию электронных писем Building Number Sense, содержащую эффективные стратегии, обязательные задания и БЕСПЛАТНЫЕ ресурсы для создания распорядка в вашем классе.
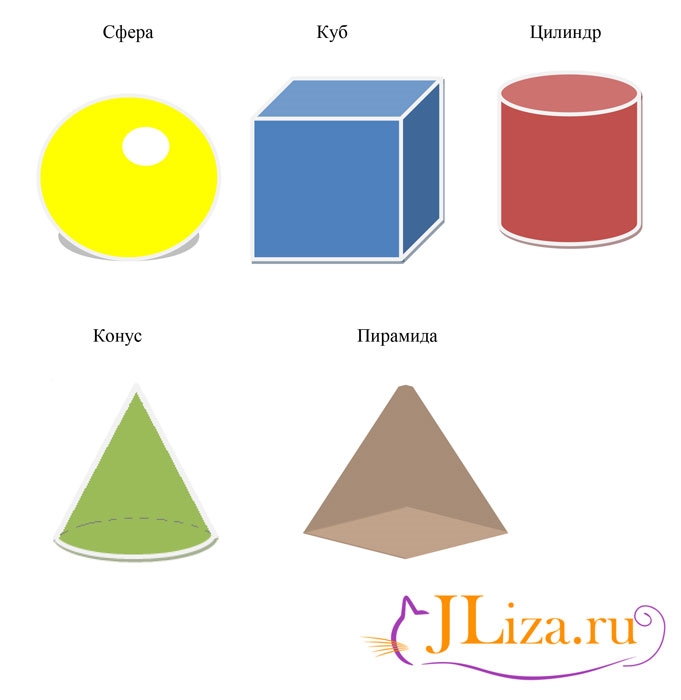 Все, что вам нужно, чтобы помочь детям развить их чувство числа и в то же время весело провести время!
Все, что вам нужно, чтобы помочь детям развить их чувство числа и в то же время весело провести время!Имя
Личный адрес электронной почты
Мы используем это поле для обнаружения спам-ботов. Если вы заполните это, вы будете отмечены как спамер.
Я хочу получить бесплатный курс по электронной почте.
Эта форма собирает информацию, которую я буду использовать для отправки еженедельных электронных писем со стратегиями, рекламными акциями и ресурсами. Отписаться в любое время. Работает на ConvertKitГеометрические фигуры: Объяснение типов фигур
Математические геометрические фигуры — это математические числа, которые представляют формы повседневных объектов. Геометрия форм — это исследование вещей с границами, углами и площадями поверхности. Рассматриваются как двумерные, так и трехмерные типы фигур.
Точно так же формы идентифицируются по их консистенции или однородности.
 Общая форма обычно сбалансирована, например, квадрат или круг. Асимметричные формы – это неровные формы. Их также называют естественными формами или формами произвольной формы. Деревья, например, имеют неправильную форму.
Общая форма обычно сбалансирована, например, квадрат или круг. Асимметричные формы – это неровные формы. Их также называют естественными формами или формами произвольной формы. Деревья, например, имеют неправильную форму.Двумерные формы в плоской геометрии — это плоские формы и замкнутые фигуры, такие как круги, квадраты, прямоугольные формы, ромбы и т. д. Многие из этих форм знакомы нам в повседневной жизни. Например, издания имеют прямоугольную форму. Очки имеют круглую форму. Конусы веб-трафика имеют конусообразную форму и т. д. В этом посте вы наверняка обнаружите различные геометрические формы и их значения.
Содержание
Может обозначать вещи геометрическими фигурами, которые являются геометрическими числами. Трехмерные формы иногда бывают двумерными, а иногда и двумерными. Двумерные числа лежат только на осях x и y, а трехмерные фигуры лежат на осях x, y и z. Это высота элемента по оси Z. В геометрии определяются различные формы. Мы уже обсуждали это во вступлении.
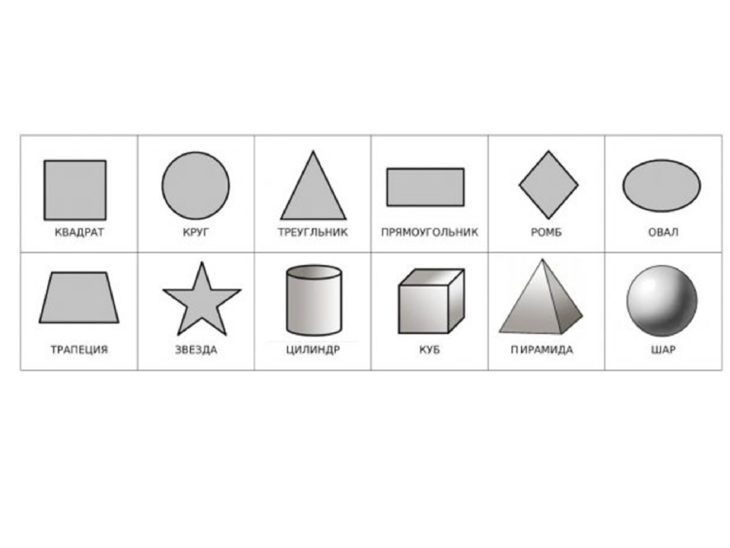
Эти фигуры можно нарисовать или развить, начав с линии, сектора линии или кривой. Мы можем создавать различные фигуры и формы, подготавливая эти линии разными способами, например, треугольную скульптуру, состоящую из связанных секций из 3 линий, правительство, состоящее из 5 линий, и многое другое. Однако не все числа являются итоговыми цифрами.
Геометрические типы фигур
Открытая геометрическая форма считается открытой, если у предмета или формы не соединены оба конца. Элементы или формы, соединенные с обоих концов, определяются как замкнутые геометрические фигуры. Есть два вида закрытых геометрических фигур:
Геометрические фигуры в 2 измерениях : Это двумерные фигуры только с осями x и y. Это плоские двухмерные каркасы. Примеры включают треугольники, квадраты, прямоугольники и так далее.
Трехмерные геометрические фигуры: Это трехмерные фигуры с осью x, y и z. Например, это могут быть игральные кости или кубоиды.

Мы должны начать с линии, кривой или сектора линии, чтобы привлечь эти числа. Таким образом, в зависимости от количества и настройки линий мы можем создавать различные формы и числа. Например, прямоугольная форма проявляется при подписке с четырехстрочными сегментами. При подписке с трехстрочными участками появляется треугольный и так далее.
Контрольный список двумерных геометрических типов фигур
Позвольте нам взглянуть на пять стандартных двумерных геометрических типов фигур.
Треугольный: Треугольник – замкнутая двумерная геометрическая фигура с тремя сторонами. Например, кусок пиццы.
Квадрат: Квадрат – это двухмерная геометрическая фигура с четырьмя равными сторонами.
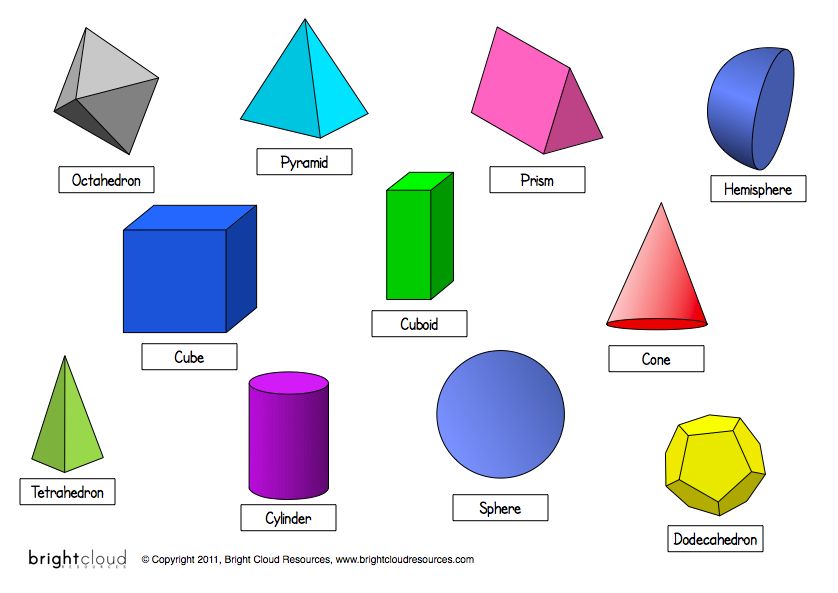 Например, формы шахматной доски, а также карромной доски.
Например, формы шахматной доски, а также карромной доски.Прямоугольная форма: Прямоугольная форма представляет собой четырехстороннюю двумерную геометрическую фигуру, противоположные стороны которой имеют одинаковый размер. Экраны компьютерной системы представляют собой экземпляры прямоугольников.
Овал: Овал похож на круг, но имеет вытянутую форму. В нем нет ни прямых линий, ни углов. Например, номер нет (0).
Список трехмерных геометрических типов фигур.
Давайте узнаем больше о шести стандартных трехмерных геометрических фигурах.
Кости: Кости представляют собой трехмерную геометрическую фигуру, состоящую из шести квадратов с равными сторонами. Примером могут служить кости людо и кости Рубика.
Прямоугольник: Прямоугольник представляет собой трехмерную геометрическую фигуру, состоящую из 6 прямоугольных фигур. В качестве примера включите книгу и коробку.

Цилиндр: Как геометрическая фигура, цилиндр имеет два одинаковых круглых плоских конца, прочных в трех измерениях — например, контейнер с прохладительными напитками или лапша для бассейна.
Мяч: Мяч представляет собой сплошную трехмерную геометрическую форму, напоминающую круг. Например, баскетбол, футбол и т. д.
Полушарие: Полушарие — это половина мяча, например тарелки для супа.
Конус: Конусы представляют собой геометрические трехмерные фигуры с плоским круглым основанием и закругленной вершиной, называемой вершиной, например шляпа клоуна из мороженого и конусы.
Примеры двухмерных геометрических фигур в повседневной жизни.
Двумерные фигуры — это номера уровней с шириной и высотой, но без глубины. Форма в форме прямоугольника, квадрата, треугольника или круга является типом двумерной геометрической формы. Ознакомьтесь со списком различных 2D-геометрических фигур, а также описаниями и примерами того, как их идентифицировать.
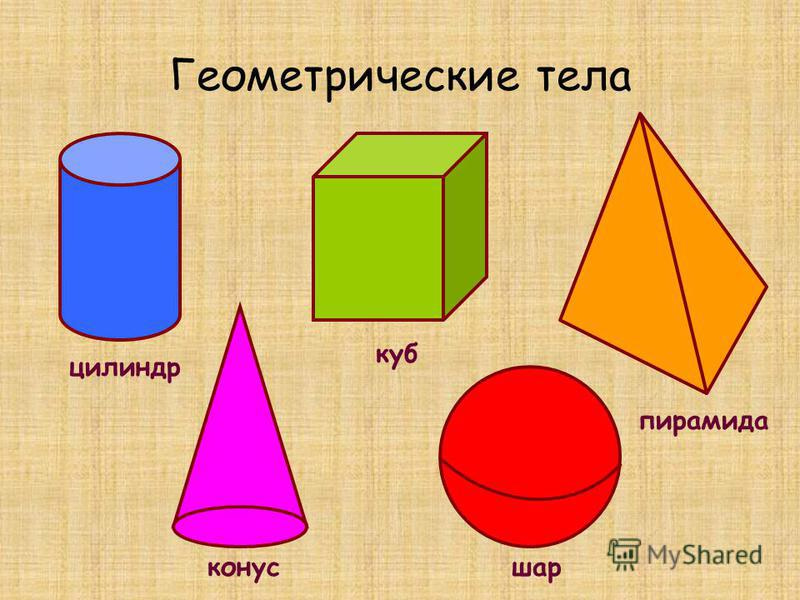
Это все плоские формы без глубины. Следовательно, вы все еще можете определить форму этих вещей с изображением. Это не точные трехмерные формы.
Примеры круглой формы
Это закругленная форма с тем же пролетом, что и коэффициент, установленный на объекте. Вот несколько примеров настоящих кругов:
Экземпляры квадрата
Четыре равные прямые стороны с четырьмя идеальными углами образуют квадрат. Некоторые реальные примеры квадратов:
Треугольные экземпляры
Треугольник — это трехстороннее число с прямыми сторонами. Существуют различные виды треугольников, в зависимости от их угла. Вот несколько реальных примеров треугольников:
Экземпляры прямоугольников
Прямоугольники имеют четыре прямые стороны с четырьмя идеальными углами, как и квадраты.
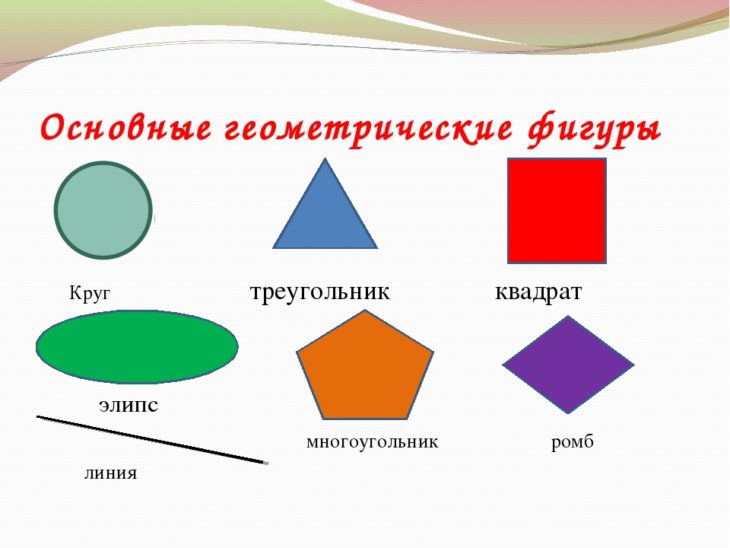 Однако две стороны намного короче других. Посмотрите на такие примеры:
Однако две стороны намного короче других. Посмотрите на такие примеры:Экземпляры Пентагона
Пятигранная фигура равной длины — это правительство. Четырехугольники имеют четыре стороны, а также встречаются гораздо чаще, чем восьмиугольники. Тем не менее, они все еще встречаются в природе. Примеры пятиугольников:
Экземпляры шестиугольников
Шестиугольники развиваются путем включения одной стороны в правительство. У них шесть прямых сторон одинакового размера. Взгляните на эти экземпляры:
Примеры трехмерных геометрических типов фигур
В отличие от двухмерных фигур трехмерная фигура имеет размер, размер и толщину.
 Формы в трех измерениях состоят из пирамид, кругов и рабочих мест. Взгляните на эти ежедневные трехмерные геометрические фигуры.
Формы в трех измерениях состоят из пирамид, кругов и рабочих мест. Взгляните на эти ежедневные трехмерные геометрические фигуры.Безусловно, многие из этих форм взаимозаменяемы. Есть круглые мешки и другие мешки, которые не обязательно являются параллелограммами. Есть также несколько различных двухмерных и трехмерных геометрических фигур, не входящих в этот список.
Круглые примеры
Шар — это круглое существенное число. Кроме того, каждая точка вокруг равноудалена от расстояния в центре. Они обладают количеством, но не глубиной, в отличие от кругов. Вот несколько примеров:
Экземпляры игральных костей
Все шесть граней игральных костей квадратные. Дополнительно называется квадратной призмой. Куб может включать в себя следующее:
Экземпляры конусов
Конус можно найти во многих повседневных вещах, таких как:
Экземпляры цилиндров
Цилиндры представляют собой трехмерные числа с одинаковыми сторонами, а также круглыми поперечными сечениями.
 Их можно найти в реальных обстоятельствах, подобных этим:
Их можно найти в реальных обстоятельствах, подобных этим:Экземпляры эллипсоида
Сфероид, также известный как эллипсоид, создает овальную форму в 3D. Экземпляры эллипсоидов состоят из:
Экземпляры призмы прямоугольной формы.
Прямоугольная призма — это абстрактный предмет, состоящий из двух противоположностей одного типа и соединенных одинаковыми прямыми сторонами. При копировании встречаются призмы прямоугольной формы.
Треугольная призма.
Треугольные призмы выглядят как прямоугольные призмы. Кроме того, их квадратные грани имеют треугольную форму, что делает их трехгранными призмами.
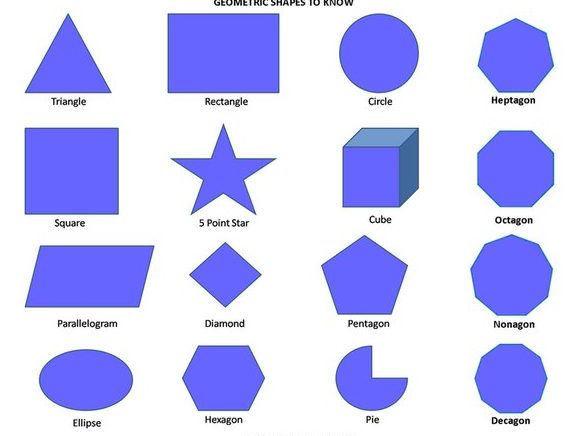 Реальные примеры треугольных призм включают.
Реальные примеры треугольных призм включают.Примеры пирамид.
Пирамида — это трехмерное число, стороны которого удовлетворяют множителю, а также одна сторона которого плоская. Возможна любая трехгранная форма, состоящая из треугольников (треугольные пирамиды), квадратов (квадратные пирамиды), а также правительств (пятиугольные пирамиды). Некоторые экземпляры есть.
Часто задаваемые вопросы.
Каковы примеры геометрических фигур?
Геометрические формы включают квадраты, прямоугольные формы, треугольники, круги, овалы, правительства и т. д.
Что такое геометрическая форма?
Математические фигуры — это геометрические фигуры. Они обычные, а также лучшие.
