Геометрические фигуры объемные все: Объёмные геометрические тела (фигуры) и их названия.

2 класс. Математика. Объемные тела. Элементы объемных тел – Объемные тела. Элементы объемных тел

Комментарии преподавателя

§1. Понятие «объемные тела»

В этом уроке познакомимся с понятием «объемные тела», а также изучим элементы объемных тел.

Треугольники, квадраты, ромбы, круги, окружности, кубы… Если посмотреть вокруг, то в привычных нам предметах и вещах можно увидеть геометрические фигуры и тела.

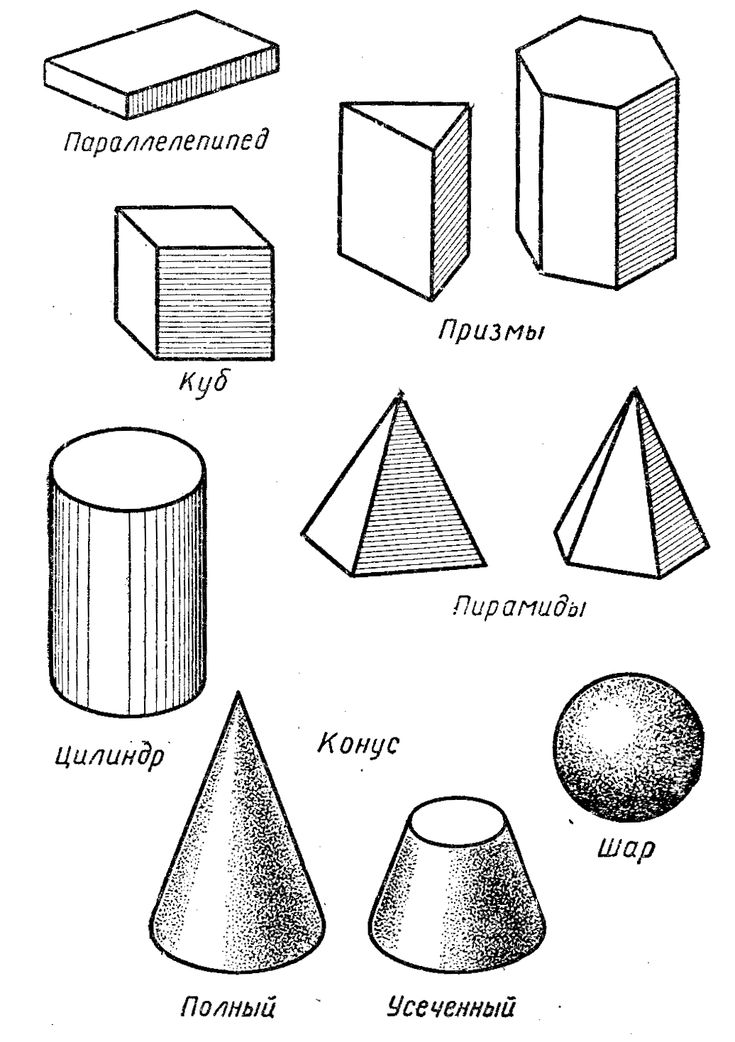
Рассмотрим геометрические фигуры, изображенные на рисунке, и попробуем назвать их.

Фигуры в верхнем ряду нам знакомы, и назвать их не составит труда: прямоугольник, квадрат, круг, треугольник, параллелограмм, овал. Все эти фигуры плоские.

Посмотрим внимательно на фигуры нижнего ряда, там расположены следующие фигуры: куб, параллелепипед, пирамида, цилиндр, шар. Все эти фигуры объемные.

С объемными фигурами мы часто сталкиваемся в обычной жизни.

На какие объемные геометрические фигуры похожи разные предметы?

Автобус формой похож на параллелепипед;

Мячик имеет форму шара;

Свеча – это цилиндр;

            

Египетская пирамида – пирамида;

Детские кубики – куб.

§2. Отличие геометрических фигур от плоских

Интересно, а в чем отличие объемных геометрических фигур от плоских?

Чтобы ответить на этот вопрос, рассмотрим следующие пары: квадрат и куб, треугольник и пирамида.

Рассмотрим первую пару: квадрат и куб.

Квадрат – это плоская геометрическая фигура, у которой 4 одинаковые стороны и 4 угла. У квадрата мы можем измерить длину и ширину.

Куб – это объемная фигура.

Если мы развернем куб, то увидим, что он состоит из 6 квадратов.

Значит, квадрат – это элемент куба, его сторона.

У куба мы можем измерить не только длину и ширину, но и высоту.

Рассмотрим вторую пару: треугольник и пирамида.

Треугольник – это плоская геометрическая фигура, у которой 3 стороны и 3 угла.

У треугольника мы можем измерить длины его сторон.

Пирамида – это объемная геометрическая фигура.

Если мы развернем пирамиду, то увидим, что она состоит из 4 треугольников и одного квадрата.

Значит, треугольники и квадрат – это элементы пирамиды, треугольники – это стороны пирамиды, а квадрат – ее основание.

У пирамиды мы можем измерить длину, ширину и высоту.

Проведем эксперимент.

На стол поставим объемные фигуры: куб, пирамиду и цилиндр.

С левой стороны включим настольную лампу.

Что заметим?

Объемные фигуры отбрасывают тень.

А теперь на стол положим плоские фигуры: квадрат, прямоугольник и треугольник. Включим лампу.

Что заметим на этот раз?

Плоские фигуры не отбрасывают тень, они полностью соприкасаются с поверхностью стола.

Сравнив пары фигур и проведя эксперимент, можем сделать вывод: объемные фигуры отбрасывают тень; у объемных фигур в отличие от плоских имеется три меры: длина, ширина и высота; плоские фигуры являются элементами объемных фигур.

§3. Краткие итоги урока

Подведем итоги урока:

1.  Все геометрические фигуры в математике можно разделить на две группы: плоские и объемные.

2.  Объемные геометрические фигуры – это фигуры, у которых можно измерить длину, ширину и высоту.

3.  Объемные фигуры на свету отбрасывают тень.

4.  Плоские фигуры являются элементами объемных фигур.

 

ИСТОЧНИКИ

http://znaika.ru/catalog/2-klass/matematika/Obemnye-tela.-Elementy-obemnykh-tel

https://vimeo.com/125124359

иллюстрации

http://www.clipartbest.com/bus-clip-art-pictures

http://www.gifmania.ru/Animated-Gifs-Sport/Animations-Futbol/Images-Soccer-Players/

http://netnotes.narod.ru/sbm/newyear/t16.html

http://www.liveinternet.ru/users/annazi/post267783885/

“Геометрические фигуры в природе”

В первом столетии до нашей эры еще Цицерон писал, что: «Изучение и наблюдение  природы  породило науку».

 

Каждый замечал как много фигур вокруг. Люди давно заинтересовались их разнообразием, строением и свойствами. Появилась наука геометрия, позволяющая изучать и измерять фигуры.

Мы, человеческие существа, рожденные на Земле, являемся детьми природы и, одновременно, ее частью.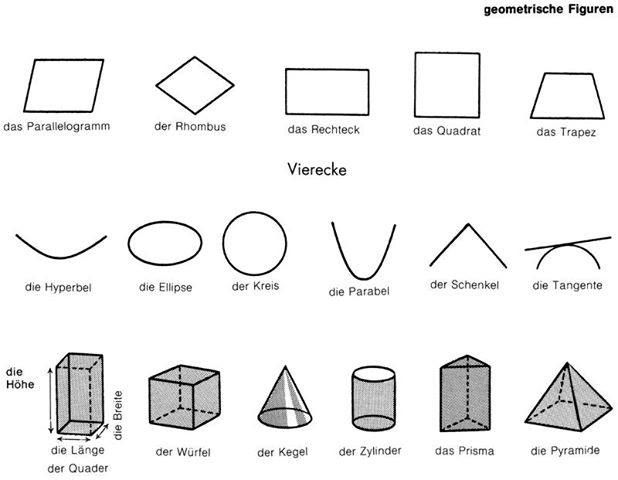 И то, какие формы порождает природа, мы естественно воспринимаем как свои, поэтому мы воспринимаем их как прекрасные.

В данной работе мы выдвигаем гипотезу, что геометрические фигуры окружающие современного человека берут свое начало в природе.

Геометрические фигуры в природе

Ученые придерживаются мнения о том, что все, что создается человеком, создается на основе наблюдений за окружающей человека природой. Значит и геометрические фигуры нужно искать в природе.

Теперь и прогулки по лесу были посвящены поиску геометрических фигур. Стволы деревьев – цилиндры, шляпка гриба – полушар, ель – конус. А на одном из деревьев висело сорочье гнездо – шар, свитый из веток.

 

Аналоги кубу и параллелепипеду нашлись в неживой природе. Например, кристаллы соли имеют форму куба.

Эксперименты еще раз подтвердили, что именно окружающая человека природа подсказала людям основные геометрические формы.

Фигуры, созданные природой, не только красивы, их форма целесообразна, то есть наиболее удобна. А человеку остается только учиться у природы – самого гениального изобретателя.

выводы:

1.    В ходе работы мы подтвердили гипотезу, что основные геометрические формы окружающие современного человека берут свое начало в природе.

2.    Геометрических фигур, которыми оперирует человек больше, чем встречается в природе.

 

 

Содержание

Введение

Глава I. Понятие о геометрических фигурах и телах , и обоснование выбора форм предметов в повседневной жизни человека.

1.    Плоские и объёмные геометрические фигуры

2.    Выбор геометрических форм человеком в повседневной жизни

Глава II. Наблюдение за использованием свойств и форм геометрических фигури тел в различных отраслях и их проявление в природе.

2.1. Геометрические фигуры в строительстве и архитектуре.

2.2. Геометрические фигуры в природе.

Глава III.

3.1.заключение

3.2.Список литературы

 

Абстракт

 

Цель- исследовать геометрические фигуры и тела , и уяснить их сущность, роль и место в повседневной жизни.

Для достижения данной цели необходимо было решить следущие задачи: изучить использование геометрических форм и линий вбыту; изучить отдельные творения, имеющие геометричекую форму;изучить использование геометрических фигур людьми и природой.

 

Объект исследования: геометрические фигуры и тела окружающие нас.

 

Гипотеза: исследование геометрических фигур и тел позволяет развивать не только математичекие и логические навыки, но оттачивает ассоциативное, пространственное и образное мышление учеников начальных классов.

 

Методы исследования: обзор литературы, повседневные наблюдения,самостоятельная исследовательская работа,формулирование выводов,оформление работы,сравнение,обобщение.

 

Новизна исследования заключается в наблюдении за проявлением ассоциативного и пространственного мышления школьников в процессе поиска геометрических фигур и тел вокруг себя,в том числе в быту.

Результаты проведённого исследования подтверждают , что следует уделять больше внимания изучению геометричеких фигур и тел школьниками начальног звена, так как наблюдения, проведённые в ходе исследования,показали заинтересованность и активность детей. Школьники начинают более широко и детально видеть не только окружающие предметы, но и в природных явлениях.

 

 

 

 

 

 

 

 

 

 

 

Геометрические фигуры в природе

 

Итальянский ученый Галилео Галилей был великим физиком и астрономом,  400 лет назад он сказал: “Книга природы написана на языке математики, ее герои — треугольники, круги  и другие геометрические фигуры”

 

Мы с первого класса на уроках математики стали знакомиться с различными геометрическими фигурами.

Каждый человек может заметить  как много фигур вокруг. Люди давно заинтересовались их разнообразием , строением и свойствами.

У меня возник вопрос: Почему все окружающие нас предметы имеют геометрическую форму?

Актуальность темы

Геометрия возникла очень давно, это одна из самых древних наук. Геометрия (греческое, от geо — земля и metrein — измерять) – такое название объясняется тем, что зарождение геометрии было связано с различными измерительными работами, которые приходилось выполнять при разметке земельных участков, проведении дорог, строительстве зданий и сооружений. В дальнейшем геометрия стала заниматься изучением геометрических фигур.

 

 

 

 

 

Школьный курс геометрии делится на :

 

 Планиметрия – это раздел геометрии, изучающий свойства фигур на плоскости .

Стереометрия – это раздел геометрии, который изучает свойства фигур в пространстве.

 

 

Я узнала, что геометрические фигуры бывают плоскими и объемными.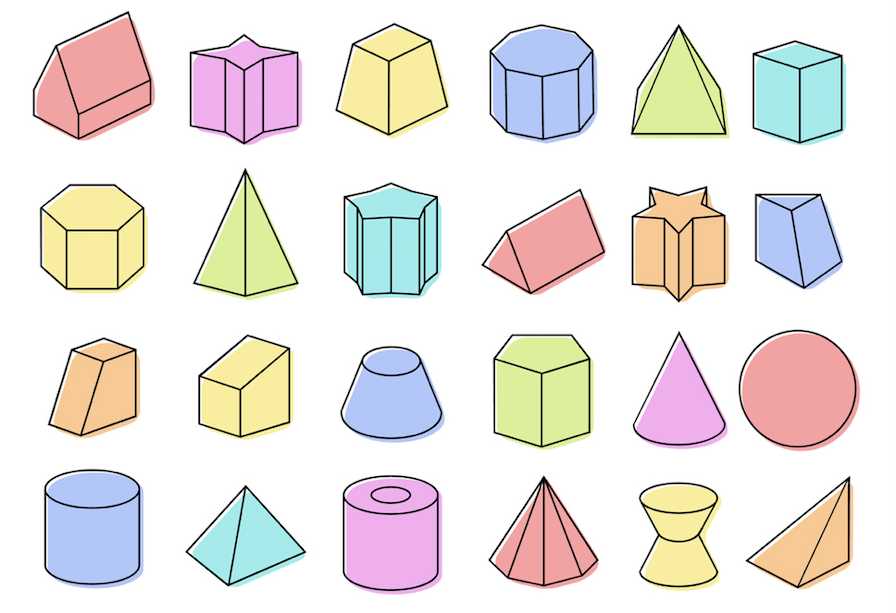

 

 

 

 

 

 

 

 

 

 

 

 

 

Цель:

·         Изучение геометрических фигур;

·         Исследование использования геометрических фигур людьми и природой;

·         Доказательство неразрывной связи геометрических фигур с природой.

Задачи:

·         Знакомство с основными геометрическими фигурами, которые изучаются в начальной школе;

·         Анализ взаимосвязи геометрических фигур с объектами природы.

Объект исследования:

·         Геометрические фигуры и тела, окружающие нас

Методы исследования:

·         Поиск информации из разных источников (специальная литература, интернет-ресурсы;

·         Обзор литературы, повседневные наблюдения, самостоятельная исследовательская работа;

Итог: Провести конкурс на лучшую творческую работу.

 

Плоские и объёмные геометрические фигуры

Наука гласит, что геометрия- это раздел математики , который изучает пространственные фигуры и формы.

 

 

 

1.    Крыша дома имеет треугольную форму, но этот треугольник повторяется со всех четырёх сторон ! А это уже объёмная геометрическая фигура,которая называется пирамидой. Она имеет такую форму,чтобы осадки ( дождь и снег) не задерживались на ней.

 

 

 

 

 

 

 

 

 

2.    Мячик похож на круг,но он весь выпуклый, а значит это уже шар, благодаря чем он легко катиться.

 

 

 

 

 

 

 

 

3.    Кубик-Рубик тоже нельзя назвать простом квадратом, так как он не плоский! Фигуру,которая состоит из 6 квадратных сторон (граней) называют кубом.

 

 

 

 

 

 

 

 

 

 

4.    Кирпич, из которого строят дома,имеет прямоугольные стороны,поэтому его называют параллелепипед.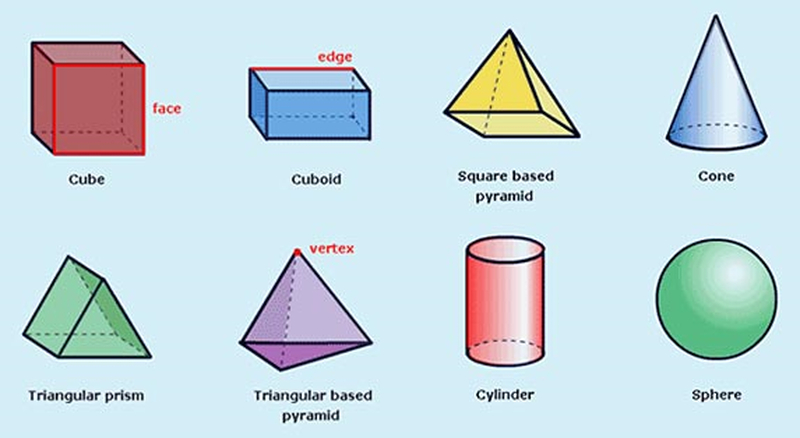 Параллелепипед одна из самых устойчивых фигур, поэтому её максимально используют в строительстве.

 

 

 

 

 

 

 

 

5.    Колеса автомобилей и велосипедов круглые,для того чтобы легко передвигаться.

 

 

 

 

 

 

 

 

 

 

Выбор геометрических форм человеком в повседневной жизни

Своё исследование применения геометрических фигур я начала со своего дома. Наблюдение показало, что:

– бокал имеет форму цилиндра;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

– комнаты,шкафы,тумба напоминают своей формой прямоугольник,но они объёмные и у них по шесть граней,соответственно они представляют собой параллелепипед;

 

 

– шахматная доска, поверхность журнального столика — это квадрат;

 

 

 

 

 

 

 

 

 

–        спортивный обруч,мамино кольцо напоминают окружность.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Наблюдение за использованием свойств и форм геометрических фигур тел в различных отраслях и их проявление в природе.

1.    Геометрические фигуры в строительстве и архитектуре.

Основание любого дома имеет вид прямоугольного параллелепипеда. Но люди,для того чтобы украсит жизнь и сделать мир вокруг красивее придумали науку- архитектуру. Архитекторы-это те же строители,но ещё они могут всё сделать красиво. Для этого они используют геометрические фигуры. Это кованные заборы и колонны,перила мостов и лестниц,арки, купола, и многое другое.

 

 

 

 

 

 

 

2. Геометрические фигуры в природе.

Все проведённые выше наблюдения геометрических фигур созданы руками человека. Но ведь замечательных геометрических форм можно встретить и в природе.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вечнозелёные и сезонные деревья имеют различную форму кроны. Ёлки имеют узкие макушки и широкие основания и напоминают треугольник. Это необходимо им, чтобы зимой снег сломал их,а скатывался с макушки вниз.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Как бы забавно не показалось, но даже животные подсознательно используют свойства геометрических фигур. Сохраняя тепло,на холоде они спят свернувшись в клубочек, поверхность тела уменьшается, и тепло лучше сохраняется. Мы понимаем,что животные,конечно же, геометрию не изучали, но природа наделила их талантом строить себе дома в форме геометрических тел.

 

 

Многие птицы –воробьи строят свои гнёзда в форме полушара.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Самые искусные геометры-пчёлы. Они строят соты из шестиугольников. В правильный шестиугольник поместится больше мёда, а зазоры между ячейками будут наименьшими!Разумная экономия усилий и строительных материалов. По этим же причинам северные народы строили круглые дома.

 

 

 

 

 

 

 

 

 

 

Заключение

 

В процессе проведения данного исследования мы видим сколько самых разнообразных геометрических фигур,тел и поверхности использует человек в своей деятельности –при строительстве зданий,сооружений,мостов,машин.

Вокруг нас находится большое количество предметов,имеющих форму геометрических фигур. Углы,отрезки и плоскости являются объектами искусственного происхождения и изготовлены человеком.

Природа же подсказывает нам, самые правильные варианты их применения,так как наблюдаемые людьми природные творения не просто красивы, но и детально продуманы. Человеку есть откуда черпать свои идеи,главное научиться внимательно наблюдать за ней и анализировать причинно-следственную связь.

Особенно интересным выводом стало то,что до начала работы над темой,очень мало задумывался о геометрии окружающего нас мира. Теперь не просто смотрю на форму окружающих предметов и творений, а уже задумываюсь и пытаюсь логически объяснить выбор формы каждого из них,нахожу им объяснения.

Геометрические фигуры играют очень важную роль в жизни человека, а знания их свойств может существенно её облегчить.

Математика действительно- Царица наук.

 

 

Список литературы

 

Математический энциклопедический словарь. Гл.ред. Ю.В. Прохоров;Сов. Энциклопедия,1988

Энциклопедический словарь юного натуралиста/Сост. А.Г. рогожкин-1981

Занимательная геометрия/ К. И. Шевелёв-М.:Ювента,2009

 

 

Природные творения в виде геометрических фигур:

Природные творения в виде геометрических фигур В самой природе очень много замечательных геометрических форм. Необыкновенно красивы и разнообразны многоугольники, созданные природой . Кристалл соли имеет форму куба. Кристаллы горного хрусталя напоминают отточенный с двух сторон карандаш. Алмазы чаще всего встречаются в виде октаэдра, иногда куба. Одна из самых изысканных геометрических фигур падает на нас с неба в виде снежинок . Шаровую форму принимают капельки росы, капли ртути из разбитого градусника, капли масла, оказавшиеся в толще воды… Отчего шар так популярен? Шар – единственное геометрическое тело, у которого наибольший объём заключен в наименьшую оболочку.

 

Использование геометрических форм животными:

Использование геометрических форм животными Принцип экономии хорошо «усвоили» животные. Сохраняя тепло, на холоде они спят свернувшись в клубочек, поверхность тела уменьшается, и тепло лучше сохраняется.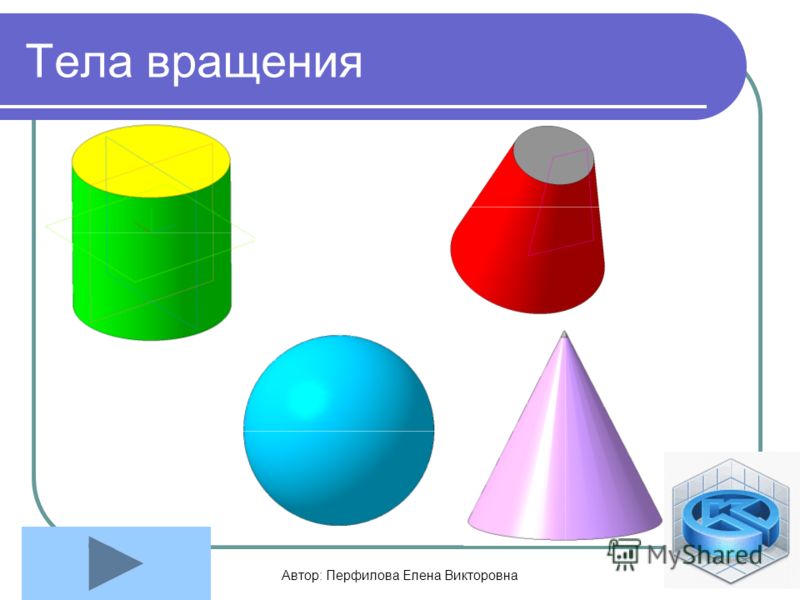 По этим же причинам северные народы строили круглые дома. Животные, конечно, же геометрию не изучали, но природа наделила их талантом строить себе дома в форме геометрических тел. Многие птицы – воробьи, крапивники, лирохвосты – строят свои гнёзда в форме полушара. самые искусные геометры – пчёлы. Они строят соты из шестиугольников. Любая ячейка в сотах окружена шестью другими ячейками. А основание, или донышко, ячейки представляет собой трехгранную пирамиду. Такая форма выбрана неспроста. В правильный шестиугольник поместится больше меда, а зазоры между ячейками будут наименьшими! Разумная экономия усилий и строительных материалов

 

Геометрия повсюду:

Геометрия повсюду Геометрия в нашей жизни на каждом шагу и играет очень большую роль. Она нужна не только для того, чтобы называть части строений или формы окружающего нас мира. С помощью геометрии мы можем решить многие задачи, ответить на многие вопросы . Мы убедились , сколько самых разнообразных геометрических линий и поверхностей использует человек в своей деятельности – при строительстве различных зданий, мостов, машин, в транспорте. Пользуются им не из простой любви к интересным геометрическим фигурам, а потому, что свойства этих геометрических линий и поверхностей позволяют с наибольшей простотой решать разнообразные технические задачи.

 

 

Содержание

Введение

Глава I. Понятие о геометрических фигурах и телах , и обоснование выбора форм предметов в повседневной жизни человека.

1.    Плоские и объёмные геометрические фигуры

2.    Выбор геометрических форм человеком в повседневной жизни

Глава II.Наблюдение за использованием свойств и форм геометрических фигури тел в различных отраслях и их проявление в природе.

2.1. Геометрические фигуры в строительстве и архитектуре.

2.2. Геометрические фигуры в природе.

Глава III.

3.1.заключение

3.2.Список литературы

Абстракт

 

Цель- исследовать геометрические фигуры и тела , и уяснить их сущность, роль и место в повседневной жизни. Для достижения данной цели необходимо было решить следущие задачи: изучить использование геометрических форм и линий вбыту; изучить отдельные творения, имеющие геометричекую форму;изучить использование геометрических фигур людьми и природой.

 

Объект исследования: геометрические фигуры и тела окружающие нас.

 

Гипотеза: исследование геометрических фигур и тел позволяет развивать не только математичекие и логические навыки, но оттачивает ассоциативное, пространственное и образное мышление учеников начальных классов.

 

Методы исследования: обзор литературы, повседневные наблюдения,самостоятельная исследовательская работа,формулирование выводов,оформление работы,сравнение,обобщение.

 

Новизна исследования заключается в наблюдении за проявлением ассоциативного и пространственного мышления школьников в процессе поиска геометрических фигур и тел вокруг себя,в том числе в быту.

Результаты проведённого исследования подтверждают , что следует уделять больше внимания изучению геометричеких фигур и тел школьниками начальног звена, так как наблюдения, проведённые в ходе исследования,показали заинтересованность и активность детей.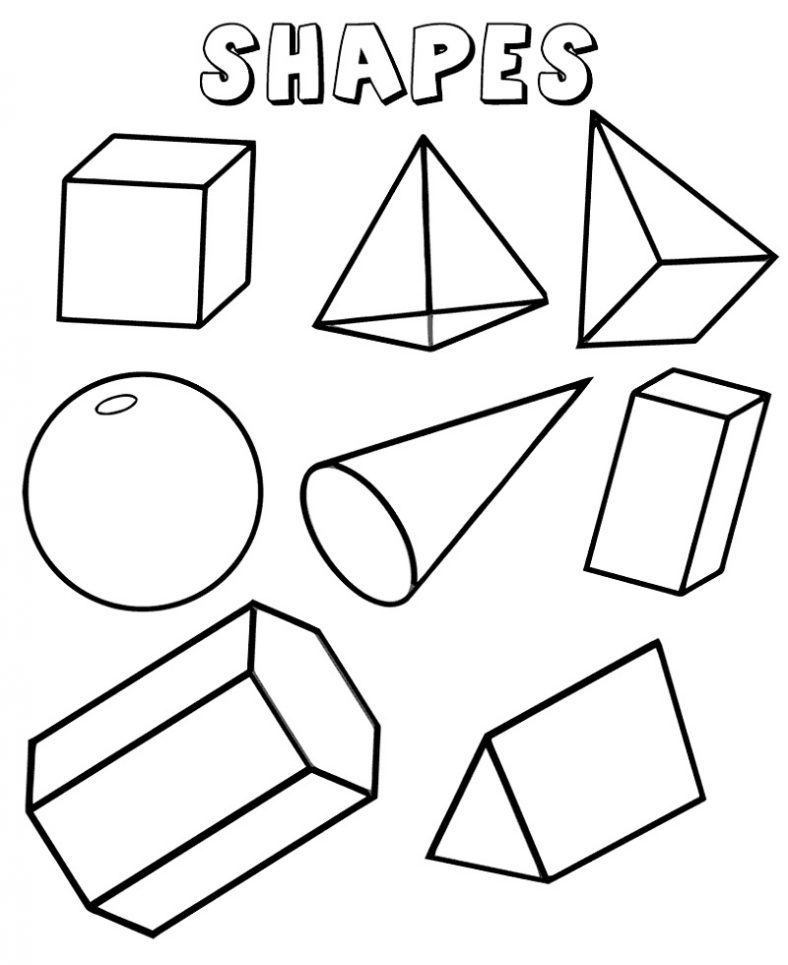 Школьники начинают более широко и детально видеть не только окружающие предметы, но и в природных явлениях.

 

Введение

 

Математику называют Царицей наук! Я с этим согласен. Мы с первого класса на уроках матматики стали знакомиться с различными геометрическими фигурами. Это меня очень увлекло. Я стал видеть в каждом предмете фигуры. Геометрические фигуры окружают каждого человека в повседневной жизни,но мы их не замечаем.

У меня зародились вопросы: почему все окружающие нас предметы имеют гелометрическую форму.

Каждый замечал как много фигур вокруг. Люди давно заинтересовались их разнообразием , строением и свойствами. ПОявилаь наука геометрия,позволяющая изучать и измерять фигуры.

В данной работе мы занялись исследованием геометрических фигур в быту, строительстве и в природе.

В исследовании мы выдвигаем гипотезу, что исследование геометричеких фигур и тел позволят развивать не только математические и логеческие навыки, но оттачивает ассоциативное, пространственное и образное мышление учеников начальбных классов.

 

Глава I. Понятие о геометрических фигурах и телах , и обоснование выбора форм предметов в повседневной жизни человека.

 

1.    Плоские и объёмные геометрические фигуры.

Наука гласит, что геометрия- это раздел математики , который изучает пространственные фигуры и формы.

Знакомясь с литературой , я узнал, что геометрические фигуры бывают плоскими и объёмными, а главное свойстваэ этих фигур определяет их использание в различных целях. Например:

1.    Крыша дома имеет треугольную форму, но этот треугольник повторяется со всех четырёх сторон ! А это уже объёмная геометрическая фигура,которая называется пирамидой. Она имеет таку форму,чтобы осадки ( дождь и снег) не задерживались на ней.

2.    Мячик похож а круг,но он весь выпуклый, а значит это уже шар, благодаря чем он легко катется.

3.    Кубик-Рубик тоже нельзя назвать простом квадратом, так как он не плоский! Фигуру,которая состоит из 6 квадратных сторон (граней) называют кубом.

4.    Кирпич, из которого сторят дома,имеет прямоугольные стороны,поэтому его называют параллелепипед.Параллелепипед одна из самых устойчивых фигур, поэтому её максимально используют в троительстве.

5.    Колеса автомобилей и велосипедов круглые,для того чтобы легко передвигаться.

 

2.    Выбор геометрических форм человеком в повседневной жизни.

Своё исследование применения геометрических фигур я начал со своего дома.Наблюдение показало, что:

– окна, двери,стены, пол и потолок имеют прямоугольную форму и не имеют объёма, значит, они являются прямгльниками;

– комнаты,шкафы,тумба напоминают своей формой прямоугольник,но они объёмные и у них по шесть граней,соотрветственно они представляют собой параллелепипед;

– посмотрим на плитку в ванной и кухне- это прямоугольники или квадраты;

– спортивный обруч,мамино кольцо напоминают окружность.

Заходя на кухню, можно так же повстречать много геометрических фигур. Это арбуз/шар,булка хлеба/параллелепипед, тарелка/круг,графин/цилиндр. Геометрия вокруг нас!

 

Глава II.Наблюдение за использованием свойств и форм геометрических фигури тел в различных отраслях и их проявление в природе.

 

1.    Геометрические фигуры в строительстве и архитектуре.

Основание любого дома имеет вид прямоугольного параллелепипеда. Но люди,для того чтобы украсит жизнь и сделать мир вокруг красивее придумали науку- архитектуру. Архитекторы-это теже строители,но ещё они могутвсё сделать красиво. Для этого они используют геометрические фигуры. Это кованные заборы и колонны,перила мостов и лестниц,арки, купола, и многое другое.

2. Геометрические фигуры в природе.

Все проведённые выше наблюдения геометрических фигур созданы руками челолвека. Но ведь замечательных геометрических форм можно встретить и в природе.Одна из самых изысканных геометрических фигур падает на нас с неба в виде снежинки.

Перейдём к исследованию растений и других природных явлений в огороде. Обычная горошина имеет форму шара.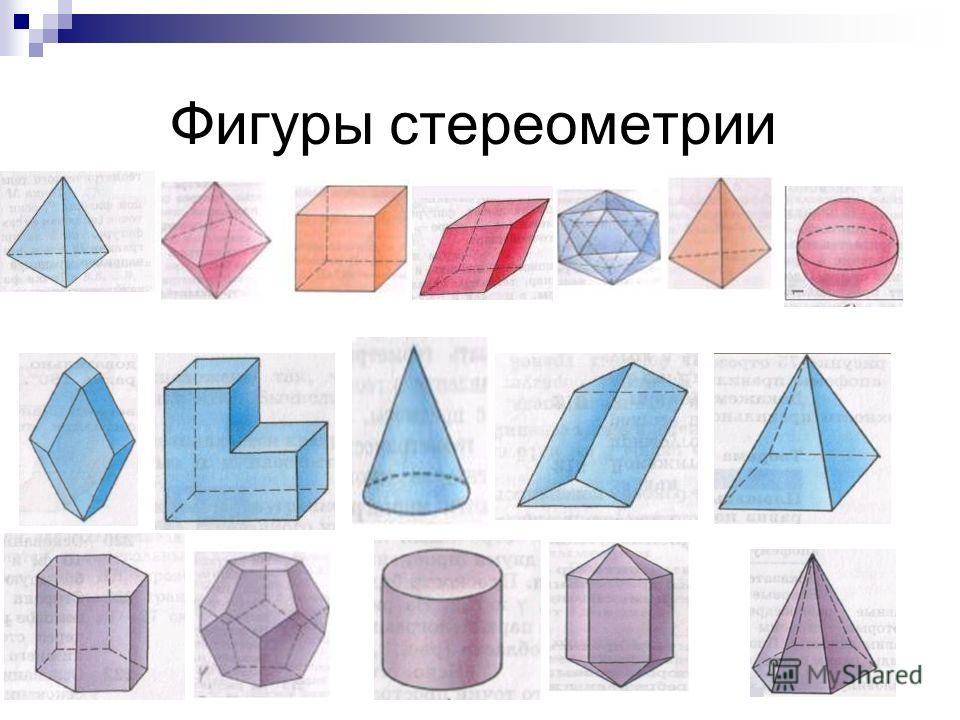

Вечнозелёные и сезонные деревья имеют различную форму кроны. Ёлки имеют узкие макушки и широкие основания и напоминают треугоник.Это необходимо им, чтобы зимой снегне сломал их,а скатывался с макушки вниз.

Как бы забавно не показалось, но даже животные подсознательно используют свойства геометрических фгур. Сохраняя тепло,на холоде они спят свернувшись в клубочек, поверхность тела уменьшается, и тепло лучше сохраняется. Мы понимаем,что животные,конечно же, геометрию не изучали, но природа наделила их талантом строить себе дома в форме геометрических тел. Многие птицы -воробьи,аркпивники-стрят свои гнёзда в форме полушара. Самые искуснеы геометры-пчёлы.Они строят соты из шестиугольников.В правильный шестиугольник поместится больше мёда, а зазоры между ячейками будут наименьшими!Разумная экономия усилий и строительных материалов. По этим же причинам северные народы строили крунлые дома.

 

Глава III.

1.    Заключение

 

В процессе проведения данного иследования мы види сколько самых разнообразных геометрических фигур,тел и поверхности использует человек в своей деятельности -при строительстве зданий,сооружений,мостов,машин.

Вокруг нас находится большое количество предметов,имеющих форму геометричесикх фигур. Углы,отрезки и плоскости являются объектами искусственного происхождения и изготовлены человеком.

Природа же подсказывает нам, самые правильные варианты их применения,так как наблюдаемые людьми природные творения не просто красивы, но и детально продуманы. Человеку есть откуда черпать свои идеи,главное научиться внимательно наблюдать за ней и анализировать причинно-следственную связь.

Особенно интересным выводом стало то,что до начала работы над темой,очень мало задумывался о геометрии окружажщего нас мира. Теперь не просто смотрю на форму окружающих предметов и творений, а уже задумываюсь и пытаюсь логически объяснить выбор формы каждого из них,нахожу им обюъяснения.

Геометрические фигуры играют очень важную роль в жизни человека, а знания их свойств может существенно её облегчить.

Математика действительно- Царица наук.

2.Список литературы

 

Математический энциклопедический словарь. Гл.ред. Ю.В. Прохоров;Сов. Энциклопедия,1988

Энциклопедический словарь юного натуралиста/Сост. А.Г. рогожкин-1981

Занимательная геометрия/ К.И. Шевелёв-М.:Ювента,2009

 

Как геометрия влияет на дизайн логотипа — Smashing Magazine

• Чтение за 20 мин. Дизайн, Графический дизайн
• Поделиться в Твиттере, LinkedIn

Об авторе

Мэгги Макнаб была признана инновационным коммуникатором в области дизайна и дизайнером логотипов на протяжении более трех десятилетий. Она написала две книги по теории дизайна,… Больше о Мэгги ↬

Галилей знал это. Каждая древняя культура, оставившая следы знаний в своем искусстве, знала это. Основные формы составляют фундаментальную геометрию Вселенной. Мы можем приписать себе многое, но люди не изобретали геометрические фигуры. Мы открыли их, наблюдая за природой. Понимание основных форм и их функций научило нас отмечают время и пространство различными способами , вдохновляя математику, технологии, язык и постоянно развивающуюся цивилизацию. Несколько простых форм использовались во все времена в искусстве всех культур: круг, пересекающиеся линии, треугольник, квадрат и спираль. Культурный антрополог Анхелес Арриен исследовал и задокументировал общие черты в формах культурного искусства на протяжении нескольких десятилетий и обнаружил устойчивые геометрические формы, присущие всему искусству. Она назвала их «пятью универсальными формами».

Галилей знал это. Каждая древняя культура, оставившая следы знаний в своем искусстве, знала это. Основные формы составляют фундаментальную геометрию Вселенной. Мы можем приписать себе многое, но люди не изобретали геометрические фигуры. Мы открыли их, наблюдая за природой. Понимание основных форм и их функций научило нас отмечать время и пространство различными способами, вдохновляя математику, технологии, язык и постоянно развивающуюся цивилизацию.

«Вселенная не может быть прочитана, пока мы не выучим язык, на котором она написана. Она написана по математике, а буквы — это треугольники, круги и другие геометрические фигуры, без которых по-человечески невозможно понять ни одно слово».

– Galileo Galilei

Несколько простых форм использовались во все времена в искусстве всех культур: круг, пересекающиеся линии, треугольник, квадрат и спираль. Культурный антрополог Анхелес Арриен исследовал и задокументировал общие черты в формах культурного искусства на протяжении нескольких десятилетий и обнаружил устойчивые геометрические формы, присущие всему искусству. Она назвала их «пятью универсальными формами».

Пять основных геометрических форм, используемых во всех культурных произведениях искусства, в порядке возрастания сложности. (Просмотреть увеличенную версию)

Еще после прыжка! Продолжить чтение ниже ↓

Каждая фундаментальная форма никогда не меняется в своей основной функции, потому что каждая из них объединяет цель с формой. Круг свободно катится, линии движутся и пересекаются, треугольник надежно сидит, но направлен от себя, четырехгранная форма неизбежно устойчива, а спираль закручивается с элегантной настойчивостью.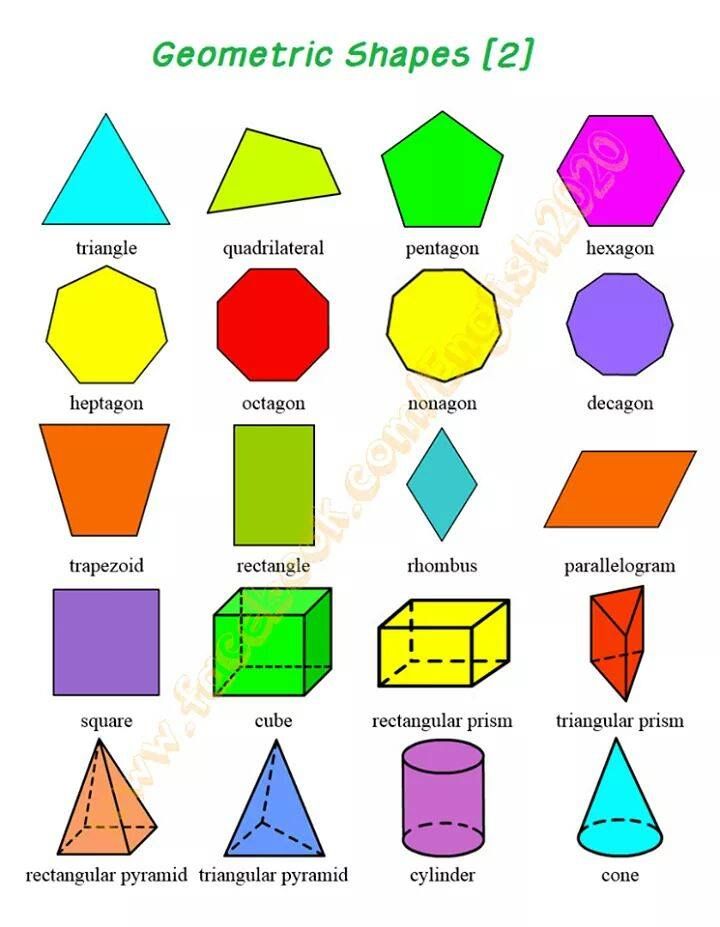 Не позволяйте простоте этих форм обмануть вас. Именно потому, что они настолько просты, они имеют возможность последовательного масштабирования и используются в качестве строительных блоков природы и созданного человеком мира. Они также обеспечивают последовательный обмен сообщениями для логотипа.

Дополнительная литература на SmashingMag:

• Эффективный дизайн логотипа, часть 1: символы, метафоры и интуиция
• Эффективный дизайн логотипа, часть 2: использование природных узоров в дизайне логотипа
• Эволюция логотипа
• Дизайн логотипа для отзывчивых Веб-сайты

В этой серии из трех статей рассматриваются основные творческие стратегии создания эффективных логотипов. Первая часть показывает, как использовать символы, метафоры и силу интуиции. Во второй части показано, как использовать природные узоры в дизайне логотипа. Последняя часть посвящена тому, как геометрия влияет на дизайн логотипа.

Немного геометрии (долгий путь)

Целью логотипа является общение с клиентом самым простым, но наиболее полным способом. Базовые формы самым непосредственным образом передают основные качества организации, и они используются в дизайне любого рода — графическом, экологическом, интерьерном, продуктовом и промышленном дизайне, а также архитектуре.

Чтобы понять связь между формой и функцией каждой геометрической формы, я расскажу о том, как она создается, как она подготавливает почву для следующей формы, как она проявляется в природе и искусственном мире, а также о ее видах. клиентов, для которых это было бы хорошо подходит. Формы начинаются просто, но усложняются по мере их развития, как и наш жизненный опыт с течением времени. Они также связаны с пространственными измерениями, которые мы переживаем в процессе жизни.

«Ни один опыт детства не укреплял меня так, как геометрия, в уверенности в своих собственных исследовательских способностях».

– Buckminster Fuller

Наши чувства отвечают за обработку невероятного количества информации каждый момент каждого дня. Лишь малая часть этой информации попадает в сознание, потому что мозг просто не может обработать бесконечный поток, генерируемый внешним миром. Из-за огромного его количества большая часть нашего опыта поглощается подсознательно.

Цифровые технологии всего за несколько десятилетий лишили многих тактильных ощущений. Но осязание было важной частью нашего понимания мира на протяжении всей нашей истории. Использование традиционных инструментов рисования удерживает нас в осязаемом мире. Итак, время от времени беритесь за дело, чтобы получить более полное представление о том, что вы создаете. Рисуйте, проводите время на природе без каких-либо планов и экспериментируйте с геометрией вручную, чтобы ваш дизайн был многогранным по смыслу, но элегантным в представлении. Точно так же, как геометрия дает фундаментальные истины о вселенной и о том, как она работает, помогая формировать наше понимание ее, понимание дизайнером того, как работают основные формы, может тонко и существенно усилить логотип, чтобы привести его в соответствие с его идеей.

Основные инструменты геометра: линейка и циркуль, выгравированные на масонском зале в Ланкастере, Великобритания.

Основные инструменты геометра так же просты, как и исходные формы, которые они создают. Циркуль, карандаш и линейка — единственные инструменты, которые вам нужны для создания ряда геометрических возможностей.

Мало того, что геометрические формы описывают определенные функции, которые не меняются при масштабировании от микро- до макроразмеров (например, содержание круглого яйца в сферической планете), прогрессивный порядок построения форм параллелен порядку мерного пространства. Нулевое, одно-, двух-, трех- и четырехмерное измерения также известны как степени свободы. Степени свободы выражают прогресс независимости от низших измерений к высшим, начиная с нулевого измерения, которое соответствует исходной геометрической форме круга.

Круг: нулевое измерение

Геометрия начинается с центральной точки компаса, источника всеобъемлющего круга. Простая точка также считается нулевым измерением. В физической терминологии нулевая точка относится к местоположению в пространстве и не более того; следовательно, у него нет свобод — или нулевая степень свободы. Начальная центральная точка компаса приводит к кругу, который, что интересно, имеет форму, достаточно независимую, чтобы непрерывно катиться или вращаться в физическом пространстве. У него нет тех же ограничений угловых форм, которые останавливаются углами (у которых тоже есть свое назначение).

Как основная форма геометрии, охватывающая окружность возникает из одной точки и является источником всех геометрических форм.

Круг известен как мать всех форм , потому что это архетипическая форма, из которой строится вся остальная геометрия. Это верно и в природе: жизнь начинается как абсолют в виде одноклеточного яйца или семени. Основной принцип круга — контейнер, который защищает, поддерживает и, в конечном счете, производит жизнь — позволяет ему масштабироваться от крошечных организмов, таких как клетки, до мегаразмеров нашей планеты, которая поддерживает огромное разнообразие форм жизни.

Яйцо на грани оплодотворения и одно из первых селфи Земли «Восход Земли», сделанное астронавтом Аполлона-8 Уильямом Андерсом в 1968 году. (Изображение предоставлено Себастьяном Каулитцки, НАСА). (Просмотреть большую версию)

В геометрии окружность начинается с одной точки, окруженной бесконечным числом точек, объединенных в окружность. Как оплодотворенная яйцеклетка содержит все необходимое для создания любой части живого организма, так и круг содержит в себе все возможности.

В логотипах шаблон круга подразумевает множество отдельных лиц или частей, составляющих единое целое. Круг эффективно представляет охватывающие группы, такие как коллективы, некоммерческие организации, глобальные организации и правительственные учреждения.

Примеры использования круглого шаблона в логотипах. Далласская опера, PBS™ и AgriCultura. (Дизайн: Dallas Opera/Woody Pirtle, AgriCultural/Maggie Macnab. Логотип PBS™ является зарегистрированным товарным знаком Службы общественного вещания. ) (Просмотреть увеличенную версию)

The Dallas Opera, PBS™ и AgriCultura являются примерами использования логотипы для передачи основной информации о клиенте. Буква «О» в логотипе Далласской оперы представляет собой одну из двух начальных букв их имени и представляет собой всеобъемлющий шаблон, который помогает «аранжировать» разнообразный коллектив музыкантов, составляющих всю организацию. Стиль дизайна также поддерживает клиента, ссылаясь на изящество и поток музыки. Круг, окружающий логотип PBS™, охватывает разнообразную демографическую группу (представленную несколькими повторяющимися головами) национальной общественной телерадиовещательной компании. А элементы руки/листа, представляющие сеть фермеров, составляющих некоммерческую организацию AgriCultura, включены в круговой шаблон для описания их единственной цели.

Линия: одно измерение

Так же, как яйцо должно сначала разделить, чтобы стать многоклеточным организмом, круг должен быть клонирован, чтобы создать следующую геометрическую форму. Поместив точку компаса на внешний край исходного круга и нарисовав второй круг того же диаметра, что и первый, оригинал будет дублирован. Это дает возможность соединить две центральные точки вместе и «вытолкнуть точку» в линию, превращая точку в одномерное пространство. Линия может двигаться только в одном направлении (вперед или назад) и, следовательно, имеет одну степень свободы. В одномерном пространстве мало что происходит, но оно имеет на одну степень свободы больше — или на один уровень независимости — больше, чем единственное положение в пространстве, которое занимает точка.

Начальное клеточное деление яйцеклетки, ведущее к новой жизни. (Изображение: Архив Ливерморской национальной лаборатории Лоуренса)

Два круга представляют собой еще одну ссылку на соединение линий в местах их пересечения. Вторая линия соединяет перекрывающиеся круги и пересекает первую линию, проведенную между центральными точками под углом 90°. Когда две противоположности вступают в контакт друг с другом, они устанавливают связь или отношения, что является важным фактором для некоторых клиентов.

Второй формой геометрии является линия или одномерное пространство, созданное путем соединения двух центральных точек. (Просмотреть увеличенную версию)

В логотипах элементы, пересекающиеся под прямым углом, представляют собой противоположностей, работающих вместе , как описывает визуальная конструкция. Сила символизма расширяет эту базовую концепцию для других целей, и эта конфигурация может быть полезна для представления слияния или сотрудничества между двумя основными, но разными целями.

Базовый шаблон из пересекающихся линий в логотипе Кардиологического госпиталя Нью-Мексико соответствует цели лечения пациентов, балансирующих между жизнью и смертью, и дополняет более конкретную визуальную коммуникацию дизайна.

Логотип Кардиологического госпиталя Нью-Мексико. (Дизайн: Мэгги Макнаб) (Просмотреть увеличенную версию)

Больницы (и большинство служб Красного Креста по всему миру) исторически использовали пересеченные линии в качестве общего значка.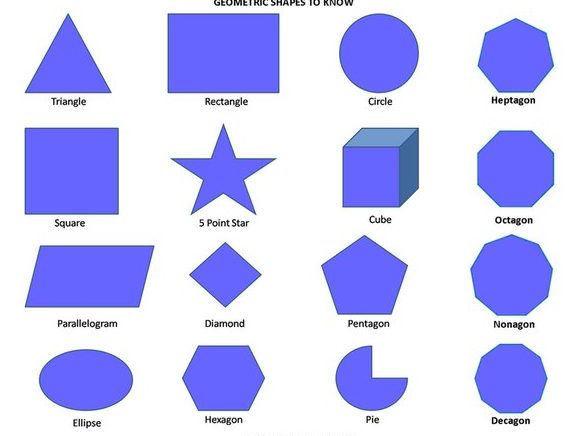 На символическом уровне больницы и службы экстренной помощи находятся на пересечении жизни (или рождения) и смерти. Я использовал Zia (символ, который Нью-Мексико использует для обозначения штата) и интегрировал сердце и руку, чтобы завершить эту концепцию логотипа для кардиологической больницы Нью-Мексико, чтобы отобразить основные критерии, которые клиент хотел, чтобы этот логотип передал Нью-Мексико, кардиологию. и ручной уход. Конкретные визуальные эффекты дают метафорическую информацию базовому шаблону дизайна (подробнее о метафорах в части 1, «Символы, метафоры и сила интуиции»).

Вы также можете передать идею взаимодополняющих противоположностей с помощью миндалевидного центра двух перекрывающихся «материнских» кругов. Эта форма, называемая mandorla или vesica piscis , является побочным продуктом геометрического процесса, который создает соединение точка-точка.

Разработка логотипа для шведской компании Broman Odell, производящей рыболовные снасти.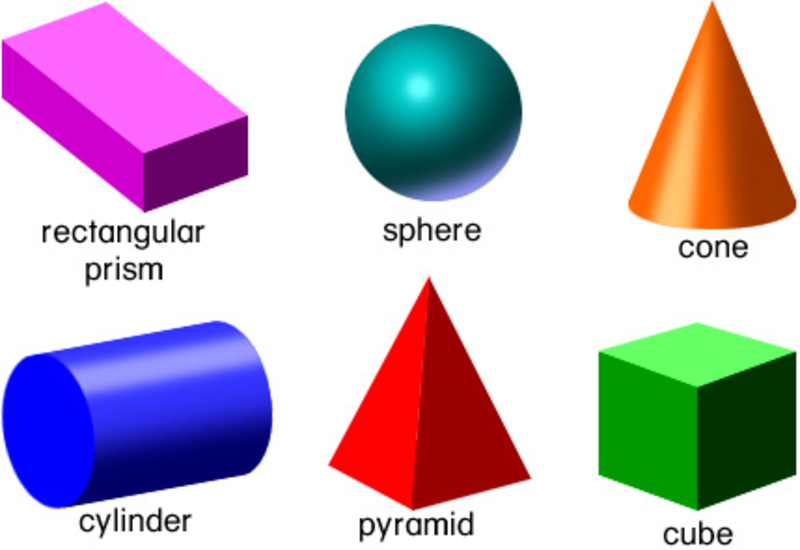 (Дизайн: Fredrik Lewander) (Просмотреть увеличенную версию)

Шведский дизайнер Фредрик Левандер использовал принципы формы мандорлы, чтобы представить Broman Odell, компанию по производству рыболовных снастей, которая объединяет давние знания двух владельцев бизнеса в области рыболовства и рыболовных снастей в один бизнес. Как показывает его процесс, он работал над многими вариантами, начиная с перекрытия начальных букв их имени. Расширив это первоначальное направление и используя простой набор концепций, он разработал элегантный логотип, который говорит все о том, кто они есть.

Треугольник: два измерения

После того, как точка вставлена ​​в линию, вы можете сделать следующий геометрический шаг, заключив три точки в двумерную треугольную плоскость. Две степени свободы — это намного больше, чем одна степень. Замкнутая плоскость допускает независимое движение осей x и y по всей ее поверхности, а не только движение вперед или назад по одномерной линии.

Третий шаг базовой геометрии заключает в себе три точки в виде треугольника или двумерного пространства, что обеспечивает свободу передвижения по всей плоскости.

Треугольник очень надежен, когда он установлен на основании или в сочетании с перевернутыми версиями самого себя в трансляционной симметрии, поэтому его часто используют в качестве структурной опоры при строительстве зданий или в качестве двумерного бордюра в художественных работах. Это форма геодезических куполов, мостовых ферм, арочных дверных проемов (треугольник с изгибом в верхней точке), а также треугольные скелетные леса человеческого таза, позволяющие ходить прямо.

Форма треугольника представляет собой надежную конструкционную ферму. (Просмотреть увеличенную версию)

Как форма, структура треугольника выстраивается из твердого основания в точку. С философской точки зрения оно основано на здесь и сейчас и указывает на нечто невидимое. Понятно, почему треугольник используется как стрела: он уводит взгляд от одного к другому. Из-за этих свойств треугольник часто используется для обозначения вдохновения или устремления за пределы текущего застоя. Вершина горы — это вдохновляющая метафора, как общий пример.

Символ переработки — это блестящее использование треугольника и треугольных стрелок для завершения сложной концепции в виде простого значка. (Изображение предоставлено Уиллом Смитом)

Переработка — это процесс, состоящий из трех частей: возникновение, существование, а затем обратное включение в смесь для другой будущей цели. Проще говоря, треугольник — это метафора рождения, жизни и смерти или начала, середины и конца. Символ рециркуляции выражает эту последовательность самым простым способом: в виде треугольных стрелок, которые заключают в себе три части треугольника.

Треугольник также является символом трансформации как посредника между одномерным и трехмерным пространством. Все слова, начинающиеся с префикса tri- (для трех частей, необходимых для достижения баланса средней точки) или trans- (по латыни «поперек») относятся к способности треугольника защищать пространство, так что могут произойти значительные изменения или движения.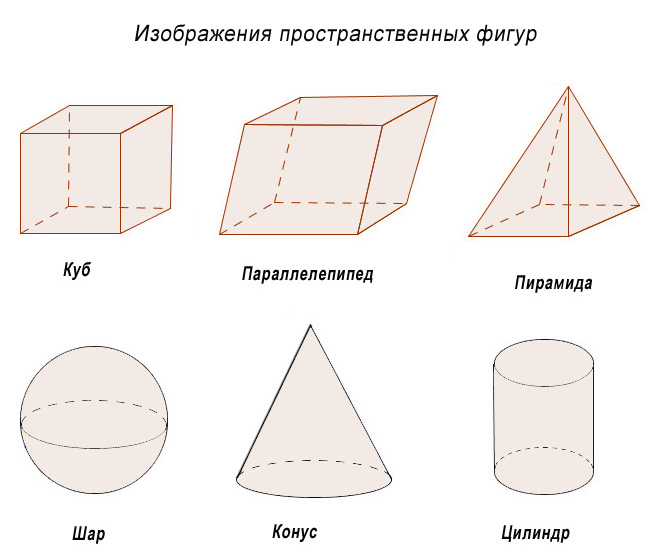 Метафорически жизнь начинается как нулевое измерение с одноклеточного яйца. Затем он делится, чтобы размножаться при зачатии (как метафора одного измерения) и развивается в многоклеточный эмбрион в безопасном треугольном пространстве таза (как метафора двух измерений). При созревании то, что когда-то было одноклеточным яйцом, появляется в жизнь полностью сформированным и бесконечно более сложным (как метафора трех измерений). Затем жизнь проживается во времени как метафорическая ссылка на четвертое измерение.

Каллиграфический рисунок девятнадцатого века японского мастера дзен Сэнгаи Гибона под названием «Вселенная» буквально переводится как «Круг, Треугольник, Квадрат». На картине показан вселенский процесс разделения, преобразования и становления целостности как символический процесс чтения справа налево в традиционном азиатском стиле.

Каллиграфический дизайн «Вселенная» буквально переводится как «Круг, Треугольник, Квадрат», читаемый справа налево. (Изображение: Художественный музей Идемицу, Токио)

Треугольник вызывает сильные ассоциации.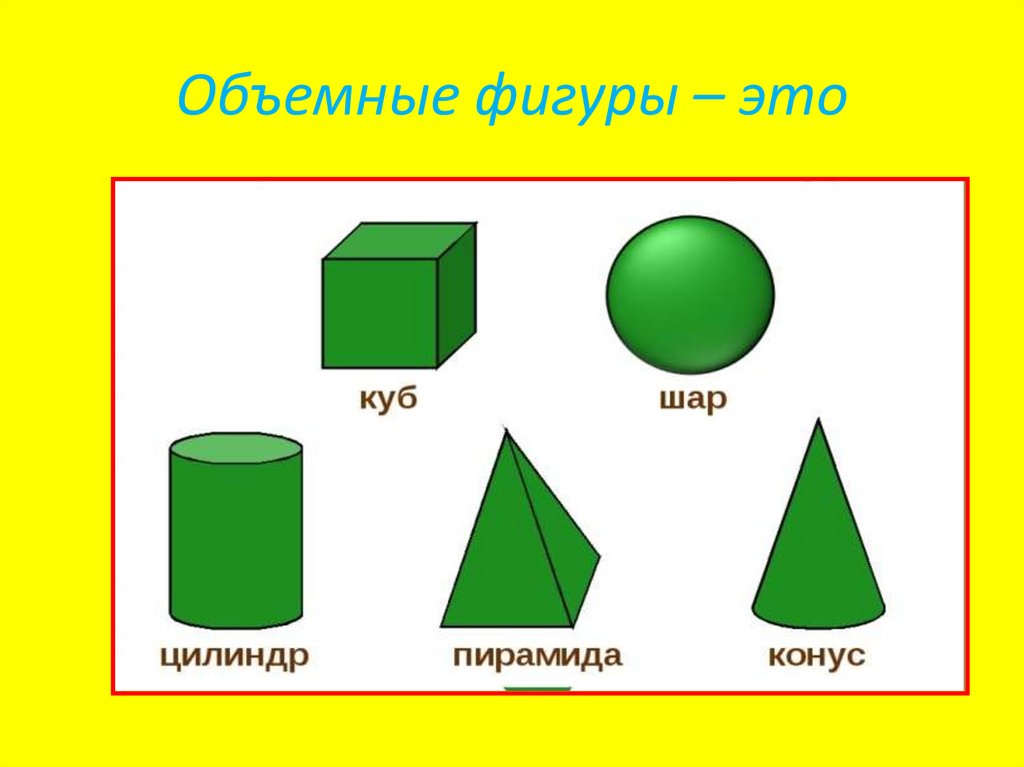 Включенный в логотип, он может символизировать «взгляд за пределы» или вдохновение, значительное изменение (транс формация ) или значительное перемещение (транс портация ). Обратите внимание, что многие производители автомобилей используют треугольник или три элемента для описания своей продукции.

Треугольник, сидящий на вершине недостроенной пирамиды на долларовой купюре, символизирует вдохновенную надежду на новую страну, безопасность и преобразование прошлого в лучшее будущее. Трехногий символ на логотипе Министерства транспорта отсылает к древнему трискелиону, символу вечного движения. Обратите внимание, что шаблон круга также используется здесь для обозначения организации, ответственной за массовое движение всей страны. Геометрические символы достаточно просты, чтобы их можно было использовать вместе, чтобы мгновенно усилить смысл логотипа.

Треугольник на долларовой купюре и логотип Министерства транспорта. (Изображение предоставлено Instamatic). (Просмотреть большую версию)

В дизайне логотипа для MuSE (многопользовательская синтетическая среда) я хотел представить цель клиента — интерпретировать необработанные компьютерные данные как полезные визуальные эффекты. Например, хирург должен использовать МРТ, чтобы успешно перемещаться по мозгу, чтобы удалить опухоль; программа также может тестировать различные модели запуска, чтобы убедиться, что ракета не будет запущена случайно в результате случайного события, такого как удар молнии.

Начальные наброски и окончательная работа над логотипом MuSE. (Дизайн: Мэгги Макнаб) (Просмотреть увеличенную версию)
Начальные наброски и окончательный вариант логотипа MuSE. (Дизайн: Мэгги Макнаб)

Мифические музы связывают образ с названием; треугольный шаблон соответствует цели компании по преобразованию числовых данных в нечто большее; а три части лица, обозначенные тенью, представляют качество контура или глубину, визуализируемую в двух измерениях.

Четырехсторонние фигуры: три измерения

Квадраты и прямоугольники, вероятно, наименее интересные из основных геометрических фигур, но они все же полезны.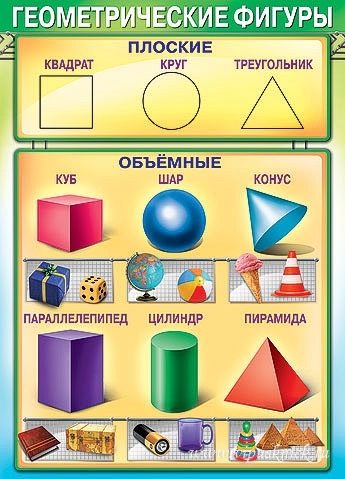 Добавление четвертой точки глубины создает тетраэдр (или пирамиду) с осью z, перенося его в трехмерную реальность. Мы используем сокращение четырехсторонней формы для описания четырех точек трехмерного пространства (или трех степеней свободы).

Четвертая точка придает треугольнику глубину (ось z), устойчивую форму в трехмерном пространстве. (Просмотреть увеличенную версию)

Все, что касается формы с четырьмя точками, говорит о стабильности. Хотя четырехсторонние формы не являются распространенной формой в природе, они создают надежные рукотворные структуры, такие как городские сетки, парки и центральные площади, здания, строительные материалы (кирпичи, саманы, потолочная и напольная плитка), окна, мониторы и произведения искусства в рамах. — даже бумажные деньги получают поддержку, чтобы еще больше обосновать свою ценность благодаря форме. (Драгоценные металлы, отчеканенные в монетах, являются историческим эталоном стоимости, который остается относительно постоянным, поскольку вес можно точно измерить. И наоборот, стоимость бумажных денег сильно колеблется, потому что они основаны на рынках, которыми можно умышленно манипулировать. Массовое печатание бумаги по всему миру валют во время экономического кризиса последних нескольких лет является примером этого.)

Четырехсторонняя фигура иллюстрирует мир как проявленный, плотный и реальный . Оно прямолинейно, укреплено и направлено вперед — слова, которые связывают этимологию числа четыре со стабильностью и осязаемостью. Эта форма простая и квадратная, и логотипы, в которых она используется, представляют клиента именно таким простым способом. Банки, адвокаты, страховые и бухгалтерские компании и, конечно же, подрядчики обычно используют этот шаблон, чтобы идентифицировать себя как стабильные учреждения или создатели надежных структур.

Логотип MediaDesk NM. (Дизайн: Мэгги Макнаб)

MediaDesk NM предоставляет некоммерческим организациям доступ к передовым услугам инфраструктуры связи, чтобы они могли использовать взаимные ресурсы, оставляя больше ресурсов для участия в жизни своих сообществ. Визуальные особенности были взяты из названия компании: media, desk и New Mexico. Столы четырехгранные, а форма штата Нью-Мексико квадратная. Эти качества были разбиты на более мелкие блоки в виде хвоста речевого пузыря, чтобы проиллюстрировать общение и средства массовой информации. Меньшие квадраты также метафорически представляют отдельные некоммерческие организации, которые способствуют общей стабильности некоммерческих организаций в Нью-Мексико.

Пятиконечная звезда и родственная ей форма, спираль: четыре степени свободы

Пять точек лежат в основе пятиугольников и пятиконечных звезд. Звезды ассоциируются с превосходством : на ум приходят пятизвездочные генералы, рестораны, отели и флаги, а также знаменитости, которые ярко горят над остальными как «звезды». Человеческое тело демонстрирует число пять в нескольких итерациях: у нас есть пять отростков, которые ответвляются от нашего туловища, пять пальцев на каждой руке для использования инструментов, пять пальцев на каждой ноге для перемещения в пространстве и пять основных чувств.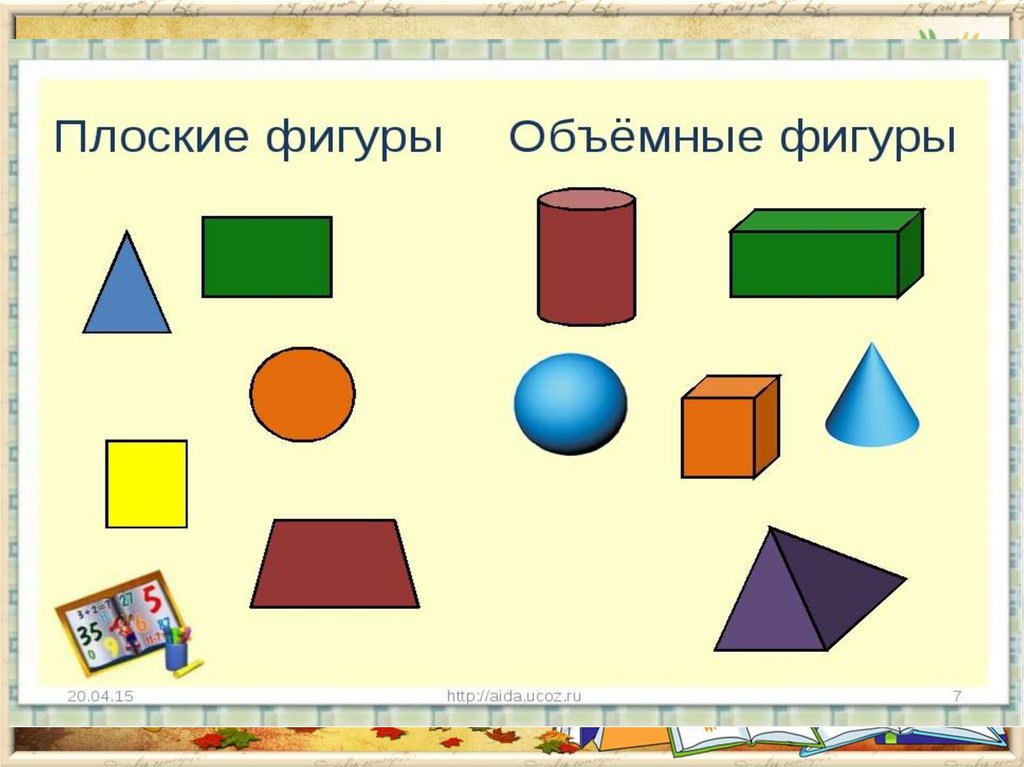 Число пять проникает в человеческую функциональность.

Классический Витрувианский человек Леонардо да Винчи.

Хотя я бы никогда не посоветовал вам есть что-то, о безопасности чего вы не знаете, если вы когда-нибудь столкнетесь с необходимостью получать пищу из природы, чтобы выжить (относительно говоря, это было нормой не так давно), держите Имейте в виду, что плоды, полученные из цветков с пятью лепестками (таких как абрикосы и груши) или спиралевидных цветущих растений (таких как роза, которая вырабатывает витамин С в плодах шиповника), обычно питательны для человеческого организма. Напротив, многие шестилепестковые цветковые растения являются ядовитыми или лекарственными (лекарство и яд — одно и то же в разных пропорциях).

Яблоки, вишни, персики, кабачки – все они имеют пятилепестковые цветки, которые производят питательные плоды для человеческого организма. (Изображение предоставлено: Rafal Ulicki, www.visuallanguage.com, CatbirdHill) (Просмотреть увеличенную версию)

Когда дело доходит до чего-то столь же важного, как наше тело и питание, которое его питает, неудивительно, что звезды представляют лучших из лучших.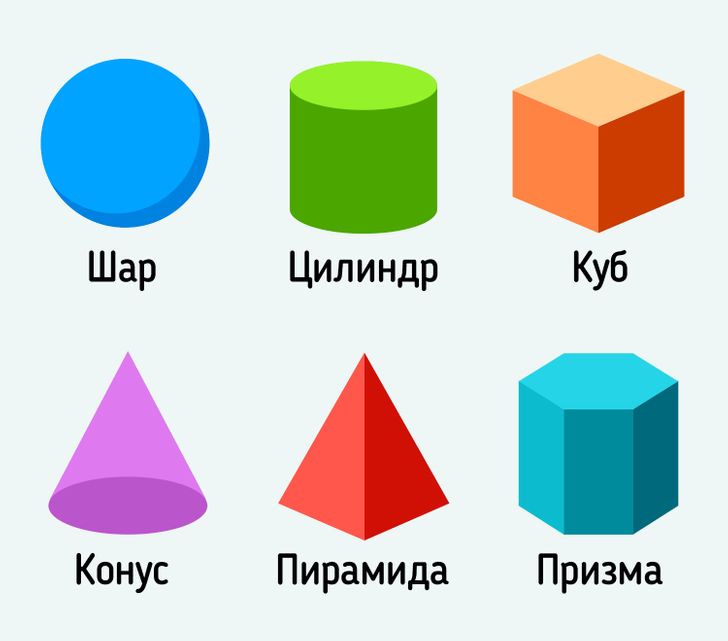 . Converse и Starbucks — два громких современных логотипа, в которых звезды используются в качестве элемента дизайна, чтобы передать свой статус самого лучшего. Звезды не являются одной из форм, широко используемых в произведениях искусства, но они тесно связаны со спиралью.

Звезды Любят Спирали И Спирали Любят Звезды

Звезду можно использовать в качестве шаблона для создания спирали, одной из универсальных форм. Множественные встроенные вращения треугольного рукава звезды можно масштабировать до все меньших и меньших размеров, а их контур проследить для создания спирали. Способность этой формы постоянно и бесконечно вращаться в меньшем или большем масштабе говорит о принципе регенерации.

Способность точек звезды бесконечно масштабироваться обеспечивает геометрический источник для построения спирали. Использование кривых вместо углов создает фи-спираль. (Просмотреть увеличенную версию)

Спираль — это визуальное представление циклического времени в пространстве, повторяющегося как последовательный, но новый цикл с каждым оборотом. Это четвертое измерение времени и пространства (см. анимацию построения фи в части 2, «Использование природных узоров в дизайне логотипов», для более интуитивного понимания этого явления).

Пятиконечная звезда и спираль тоже переплетены в природе. Вы можете увидеть эту связь в подсолнухе. С высоты птичьего полета пятиконечная звезда видна в последовательном росте листьев растения, а в профиль эти листья движутся по стеблю растения по спирали. Эти два аспекта работают вместе, чтобы обеспечить максимальный доступ солнечного света к растению из-за минимизации теней, а спиральный путь также направляет дождевую воду вдоль стебля, направляя ее непосредственно к корням, где она приносит наибольшую пользу.

Вид листьев в виде пятиконечной звезды с высоты птичьего полета показывает рисунок листьев, закрученных по спирали вокруг стебля растения в профиль. (Изображение предоставлено Андреем Соловьевым)

Клиенты, участвующие в творческих проектах и ​​потенциальных или футуристических видящих и мыслящих организациях (здесь снова фигурирует время), хорошо соответствуют принципам, выраженным этой формой.

«Лебединые песни» — некоммерческий коллектив музыкантов, исполняющих просьбы для умирающих, и я сразу понял, что скрипичный ключ может воплощать в себе форму лебедя. Осталось только нарисовать. Клиент выбрал подходящее название для своей организации, и я соединил качества лебедя с музыкальным символом, чтобы отразить их цель — исполнять музыкальные последние просьбы людям с неизлечимой болезнью.

Логотип Лебединых песен. (Изображение предоставлено Эриком Иссели, дизайн: Мэгги Макнаб) (Просмотреть увеличенную версию)

Помимо интеграции самых отличительных визуальных качеств организации, спиралевидная форма этого логотипа связана с символом бесконечности, метафорой бесконечного цикла существования, который возрождается. жизнь. Сообщение логотипа утешительно и позитивно для аудитории, и оно дополняет цель некоммерческой организации.

Заключение

Кто бы мог подумать, что простая геометрия имеет такую ​​глубину и актуальность? Он чрезвычайно эффективен при продуманном применении к логотипу. Хотя геометрические фигуры слишком широки, чтобы использовать их в качестве дизайна логотипа, их способность универсального общения может поддерживать общее сообщение, которое вы хотите передать своим дизайном. Добавьте к этому сочетание символов, метафор и соответствующих природных узоров, и ваш простой, но элегантно выполненный логотип будет говорите громко с вашей аудиторией мгновенно, плавно и незабываемо.

Геометрические фигуры для детей с четкостью и милыми иллюстрациями!

Вы пытаетесь научить своих детей геометрическим фигурам? Но вы не уверены в том, что такое 16 основных фигур в математике? и Как вы помогаете своим детям легко определять геометрические фигуры?
Здесь вы найдете наш список различных геометрических фигур в печатном листе по математике с очень симпатичными персонажами, определениями и предлагаемыми занятиями для ваших детей или учеников, чтобы они с удовольствием изучали их.
Существует изображение каждой формы, а также атрибуты этой формы.

Использование этих листов поможет вашим детям, ученикам:

1. Знать свойства различных форм;
2. Знать внутренние углы равностороннего многоугольника;
3. Определить список двумерных геометрических фигур, включая треугольники, четырехугольники и многоугольники

Список геометрических фигур — треугольники для учащихся

1. Равносторонний треугольник — неправильный треугольник
2. Квадрат – Неправильный четырехугольник
3. Пентагон – Неправильный пятиугольник

• Равносторонний треугольник
• Угол: 60°
• Внутренние углы в сумме дают 180°

Квадрат

• Угол: 90°
• Внутренние углы в сумме дают 360°

Пятиугольник

• Угол: 108°
• Внутренние углы в сумме дают 540°

| >>> Попробуйте обучающие игры с геометрическими фигурами для детей

Равносторонний треугольник

• Угол: 60°
• Внутренние углы в сумме дают 180°

Квадрат

• Угол: 90°
• Внутренние углы в сумме дают 360°

Пятиугольник

• Угол: 108°
• Внутренние углы в сумме дают 540°

| >>> Попробуйте бесплатно: Пазлы с фигурами для малышей

Шестиугольник

• Угол: 120°
• Внутренние углы в сумме составляют 720°

Семиугольник

• Угол: 128,6°
• Внутренние углы в сумме дают 900°

Октагон

• Угол: 135°
• Внутренние углы в сумме составляют 1080°

| >>> Попробуйте наши крутые математические игры для детей

Список геометрических фигур — четырехугольники

Список геометрических фигур — четырехугольники по математике для школьников. Четырехугольник – это многоугольник с четырьмя сторонами. Четырехугольник иногда называют четырехугольником или четырехугольником. Есть довольно много членов семейства четырехугольников.

Есть также некоторые члены, которые являются подмножеством других членов семьи! Смотрите ниже, если это вас смущает!

Квадраты имеют 4 равные стороны и 4 прямых угла.

Имеют 4 оси симметрии. Все квадраты принадлежат к семейству прямоугольников. Все квадраты относятся к семейству ромбов. Все квадраты также являются параллелограммами.

Прямоугольники имеют 4 стороны и 4 прямых угла.

Все они имеют 2 линии симметрии (4 линии, если они также являются квадратами!) Все прямоугольники принадлежат к семейству параллелограммов.

Ромбы  (ромбы) имеют 4 равные стороны.

Обе пары противоположных сторон параллельны. Все они имеют 2 линии симметрии (4 линии, если они квадратные!). Все ромбы принадлежат к семейству параллелограммов.