Геометрические фигуры и их названия 5 класс: Основные геометрические фигуры 🟢🟨🔺 и их названия
Геометрические тела и их изображения. | План-конспект урока по математике (5 класс):
Конспект урока по математике 5 класс
Автор: Шибанова Наталья Игоревна, учитель математики, ГБОУ Школа №268 Невского района Санкт-Петербурга
Описание материала: конспект урока по математике по теме «Геометрические тела и их изображение» для обучающихся 5 класса. Конспект урока геометрические тела и их изображение.
Тип урока: изучение нового материала.
УМК: Математика. 5 класс: учеб. для общеобразоват. организаций/ Г.В.Дорофеев, И.В.Шарыгин, С.Б.Суворова и др. – М.:Просвещение, 2016.
Цель урока:
- Познакомить обучающихся с разделами геометрии: планиметрия и стереометрия.
- Познакомить учащихся с понятием объемные тела.
- Сформулировать представление о многогранниках;
- Научить распознавать многогранники и их элементы по проекционному чертежу;
- Рассмотреть применение многогранников в различных сферах жизни.
Задачи урока:
- Формирование пространственных представлений учащихся;
- Развитие умения наблюдать, рассуждать по аналогии;
- Развитие интереса к предмету через использование информационных технологий.

Цели урока:
познакомить учащихся с геометрическими телами, научить распознавать на чертежах и рисунках эти фигуры, в окружающем мире — объекты, для которых эти фигуры являются моделями.
Планируемые результаты обучения:
Предметные:
- Оперировать на базовом уровне понятиями: фигура, точка, отрезок, прямая, луч, ломаная, угол, многоугольник, треугольник и четырехугольник, прямоугольник и квадрат, окружность и круг, прямоугольный параллелепипед, куб, шар. Изображать изучаемые фигуры от руки и с помощью линейки и циркуля.
Личностные:
- формирование познавательных интересов, интеллектуальных и творческих способностей обучающихся;
- самостоятельность в приобретении новых знаний и практических умений; креативность мышления, инициатива, находчивость, активность при решении математических задач;
- воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения.
Метапредметные:
Регулятивные УУД:
- определять необходимые действие(я) в соответствии с учебной и познавательной задачей и составлять алгоритм их выполнения;
- определять потенциальные затруднения при решении учебной и познавательной задачи и находить средства для их устранения; находить достаточные средства для выполнения учебных действий в изменяющейся ситуации и/или при отсутствии планируемого результата;
- анализировать и обосновывать применение соответствующего инструментария для выполнения учебной задачи.
Познавательные УУД:
|
|
Коммуникативные УУД:
|
|
- определять свои действия и действия партнера, которые способствовали или препятствовали продуктивной коммуникации
Ход урока
- Организационный момент.
Проверить готовность класса к уроку, настроить учащихся на деловой ритм.
– Ребята! Я рада вас видеть сегодня на уроке в хорошем настроении.
Посмотрите друг другу в глаза, улыбнитесь, глазками пожелайте товарищу хорошего рабочего настроения на уроке.
– Я вам желаю сегодня хорошей работы.
- Актуализация опорных знаний.
Ребята, отгадайте ребусы. СЛАЙД
Геометрия
Сторона
Фигура
Вершина
– Правильно.
– А как, вы, думаете, почему именно эти слова я зашифровала?
– Молодцы, мы начинаем изучать новую главу, в ней представлен геометрический материал.
– Ребята, посмотрите пожалуйста на слайд. Перед Вами геометрические фигуры , которые разделены на две группы. Ответьте на вопросы:
- По какому признаку мы разделили фигуры? (плоские и объемные или фигуры на плоскости и фигуры в пространстве)
- Какие фигуры мы уже рассматривали на уроках математики в этом учебном году и хорошо с ними знакомы? (многоугольники).
– Как вы думаете, ребята, о чём мы будем говорить сегодня на уроке? (о пространственных фигурах или геометрических телах)
3. Постановка целей и задач урока
Постановка целей и задач урока
Сегодня на уроке мы будем изучать «Геометрические тела». Все геометрические тела обладают неповторимым совершенством и красотой. Сегодня на уроке мы узнаем и увидим много интересного.
4. Первичное усвоение новых знаний.
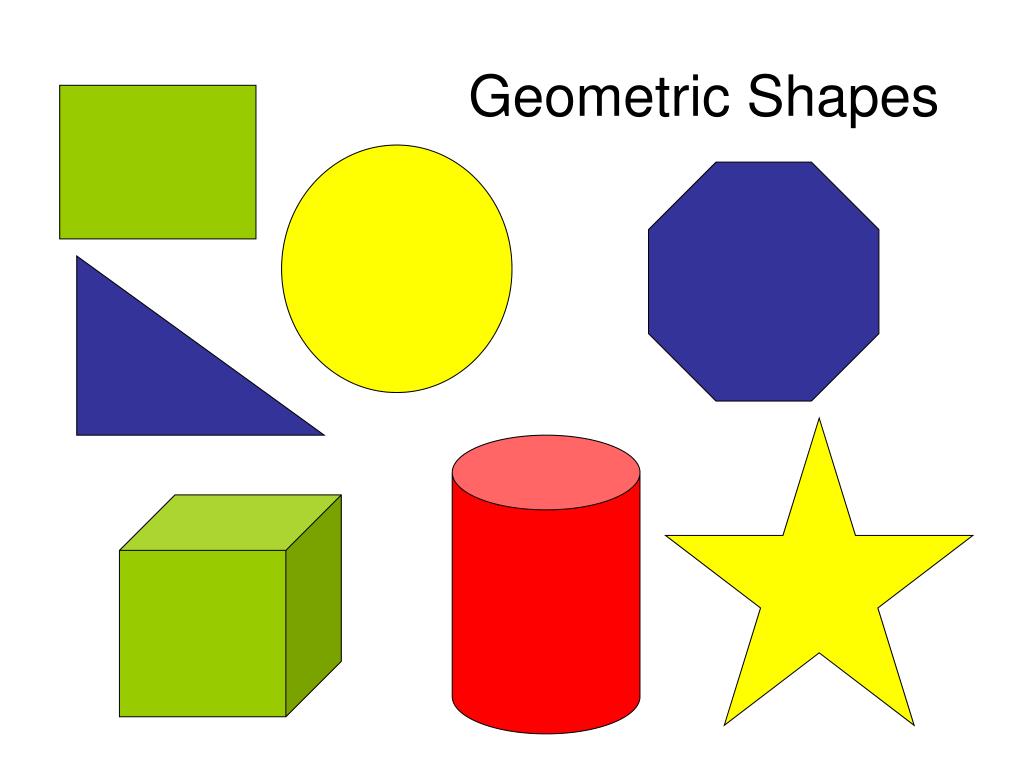
Нас окружает множество предметов, но математиков интересуют лишь форма предметов и их размеры, поэтому вместо предметов они рассматривают геометрические тела. Вы, конечно, знаете уже некоторые геометрические тела, как они называются? (изображение фигур – куб, цилиндр, шар, конус).
Сегодня мы с вами поговорим об объемных телах. СЛАЙД .
Для того чтобы больше узнать о геометрических телах мы воспользуемся учебником. Работать будете самостоятельно. Источником знаний у вас будет учебник,
а путеводителем для вас послужит рабочая карта урока.
Откройте учебники и прочитайте с. 232.
Обсуждаем кратко.
Физкультминутка
Вы, наверное, устали?
Ну, тогда все дружно встали.
Вверх ладошки! Хлоп! Хлоп!
По коленкам – шлёп, шлёп!
По плечам теперь похлопай!
Мы осанку исправляем
Спинки дружно прогибаем
Вправо, влево мы нагнулись,
До носочков дотянулись.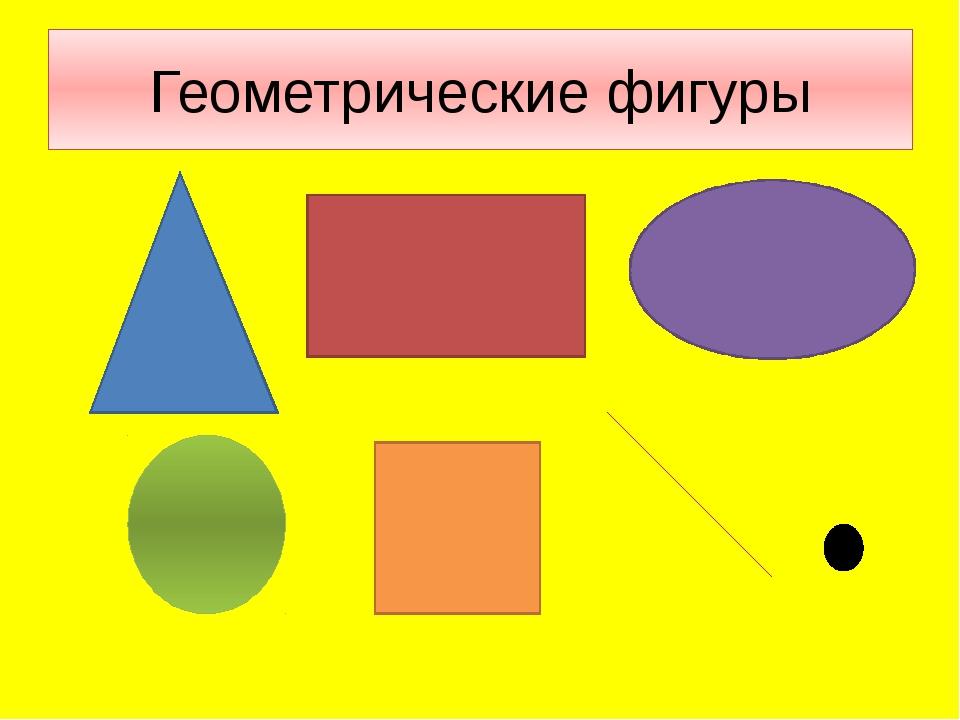
Плечи вверх, назад и вниз.
Улыбайся и садись!
Задание 1. Среди геометрических тел, изображенных на рисунке, выберите многогранники и запишите их номера:__________________
Задание 2. Подпишите названия выделенных элементов многогранника.
Взаимопроверка – доска
Итак, ребята, сделаем вывод.
Вершины – это точки.
Ребра – отрезки, соединяющие эти точки (вершины).
Грани – это многоугольники.
УСТНО. Возьмите модели квадрата и треугольника.
- Давайте посчитаем, чему равно количество вершин и сторон у многоугольника? (ОНИ МЕЖДУ СОБОЙ РАВНЫ)
- Возьмите модели куба и пирамиды. Чему равно число вершин и число граней у многогранника?
(ОНИ МЕЖДУ СОБОЙ МОГУТ БЫТЬ НЕРАВНЫМИ).
ВЫВОД: у многоугольника столько же вершин, сколько сторон, а у многогранника число вершин и число граней не обязательно одинаково.
5. Закрепление новых знаний и способов действий.
Ребята, давайте поупражняемся в подсчёте граней, рёбер, вершин многогранников. Обратить внимание, что
Обратить внимание, что
Вершины – это точки.
Ребра – отрезки, соединяющие эти точки (вершины).
Грани – это многоугольники.
Обсуждаем кратко и заполняем таблицу «Характеристика многогранников» рис. 10.2 учебника
Задание 3. Характеристика многогранников
№ фигуры | Число граней, и их форма | Число ребер | Число вершин | Число ребер в каждой вершине |
Взаимопроверка – доска
Тест на закрепление.
Продолжите уточняющие вопросы, запишите вывод в тетради. (Работаем с текстовыделителями)
- Правильно ли я понял, что все пространственные фигуры, с которыми мы познакомились на уроке называют (геометрическими телами).
- Правильно ли я понял, что геометрические тела делятся на две группы: (многогранники и тела вращения).
- Правильно ли я понял, что поверхность многогранника состоит из (многоугольников).
- Правильно ли я понял, что поверхность каждого геометрического тела разбивает пространство на (внутреннюю и внешнюю области).
- Правильно ли я понял, что поверхностью шара называется (сфера).
При наличии времени выполнить проверку. Ответы за доской.
6. Подведение итогов.
– Сегодня мы с вами на уроке познакомились с предметами, которые окружают нас в повседневной жизни.
– Назовите наиболее часто встречающиеся вам многогранники (куб, конус, шар, пирамида, цилиндр).
– В реальной жизни приведите примеры многогранников?
Где нам может пригодиться знание о геометрических телах?
Сегодня на уроке
Вы искали и творили,
Знания новые открыли,
Научились их применять,
Теперь задания легко вам выполнять!
– Большое спасибо всем за работу на уроке!
7. Рефлексия. Ассоциативный куст.
Рефлексия. Ассоциативный куст.
Выделить в каждом столбике нужное.
«Для меня сегодняшний урок…»
развернуть таблицу
Урок | Я на уроке | Итог урока |
Интересно | Работал | Понял материал |
Скучно | Отдыхал | Узнал больше, чем знал |
Безразлично | Помогал другим | Не понял |
развернуть таблицу
8. Домашнее задание.
№ 921, 927
Картины из геометрических фигур 5 класс презентация, доклад, проект
Картины из геометрических фигур
Выполняла:
ученица 5 «В» класса Осокина Мария
Руководитель:
Учитель математики Филиппова Т. Е.
Е.
Цели и задачи проекта
Цель:
Создать галерею картин из геометрических фигур
Выделить основные геометрические фигуры
Выполнить практическую работу из геометрических фигур
Содержание
Введение.
1. Основная часть работы.
1.1. Как возникла геометрия.
1.2. Происхождение геометрических фигур.
2. Практическая работа.
2.1. Сделать плоские поделки из геометрических фигур.
2.2. Сделать объёмные поделки из геометрических фигур.
Каждый замечал как много фигур вокруг. Люди давно заинтересовались их разнообразием, строением и свойствами. Мне тоже стало интересно как много геометрических фигур и что можно из них зделать.
Что изучает геометрия?
В геометрии изучаются формы, размеры, взаимное расположение предметов. Если взять во внимание только форму и размер предметов, мы приходим к понятию геометрической фигуры.
Если взять во внимание только форму и размер предметов, мы приходим к понятию геометрической фигуры.
Название «фигура» происходит от латинского слова figura, означающего «внешний вид» «образ». Почти все названия геометрических фигур греческого происхождения, как и само слово геометрия. Однако эти слова вошли в русский язык не непосредственно с греческого, а через латинский язык.
Квадрат
Термин образовался как буквальный перевод соответствующего греческого слова «квадратус» – «четырёхугольный».
КВАДРАТ – фигура с четырьмя сторонами.
Прямоугольник
Термин образован путём соединения двух слов: «прямой» и «угол».
ПРЯМОУГОЛЬНИК – это четырёхугольник, у которого все углы пямые.
Треугольник
Термин образован путём соединения двух слов: «три» и «угол». Слово «три» общеславянское. Индоевропейского характера.
Слово «три» общеславянское. Индоевропейского характера.
ТРЕУГОЛЬНИК – это многоугольник с тремя сторонами.
Круг
Общеславянское слово, имеющее соответствия в германских языках: в древнегерманском «кригер» – «кольцо», «круг», в греческом – «колесо», круг».
КРУГ – это множество всех точек плоскости, расстояние от каждой из которой до данной точки этой плоскости не больше данного расстояния.
Овал
Французское слово «оваль» – «овальный» произошло от латинского «овум» – «яйцо».
ОВАЛ – замкнутая выпуклая гладкая плоская кривая.
Ромб
Одни считают, что этот термин произошёл от греческого слова «ромбос», означающего «бубен», т.к. ромб похож на четырёхугольный бубен, другие – что от греческого слова «РОМБ», которое означает «вращающееся тело», «веретено», т. к. сечение в обмотанном веретене имеет форму ромба.
к. сечение в обмотанном веретене имеет форму ромба.
Трапеция
Греческое слово «трапедзион» переводится как «столик».
ТРАПЕЦИЯ – это выпуклый четырёхугольник, у которого две противоположные стороны параллельны, а две другие не параллельны.
Куб
Термин «КУБ» происходит от греческого слова в переводе означающего – «игральная кость». Она имела форму кубика, и название это перешлло на любое тело той же формы. Этот термин впервые встречался у пифагорейцев (четвёртого – шестого вв. до н.э.)
Параллелепипед
Термин образован путём соединения двух греческих слов: «параллелос» – «параллельный» и «эпитедос» – «плоскость».
ПАРАЛЛЕЛЕПИТЕД – призма, основанием которой является параллелограмм.
пирамида
ПИРАМИДА – от греческого слова «пюрамис», которым греки называли египетские пирамиды. А это слово происходит от древнеегипедского слова «пурама», которым эти пирамиды назвывали сами египтяне.
А это слово происходит от древнеегипедского слова «пурама», которым эти пирамиды назвывали сами египтяне.
Цилиндр
ЦИЛИНДР – от латинского «цилиндрус»
Объёмные геометрические фигуры
Фигуры
На плоскости в пространстве
Практическая работа
Чем же отличаются плоские фигуры от объёмных?
Плоские можно целиком расположить на одной плоской поверхности.
Объёмные фигуры занимают определённое пространство, возвышаются над плоской поверхностью.
Вывод:
Таким образом, я поняла что геометрические фигуры очень часто встречаются, и много что можно из них сделать.
Скачать презентацию
а | в | с | периметр | |
Прямоугольник | 3 см | 1 см 5 мм | Р = | |
Квадрат | 2 см | Р= | ||
Треугольник | 3 см | 3 см | 3 см | Р = | Плоские геометрические фигуры |
1. | 1. | |||
2. | 2. | |||
3. | 3. | 1куб | 2 куб | 3 куб |
Число граней | ||||
Число ребер | ||||
Число вершин | ||||
Форма граней куба | ||||
Цвет куба | ||||
Длина ребра куба |
Геометрические фигуры и их свойства с примерами и решением
Содержание:
Геометрия — наука о геометрических фигурах и их свойствах. Самая простая геометрическая фигура — точка. Каждая другая геометрическая фигура состоит из точек, то есть является некоторым множеством точек. Другие фигуры — прямая, плоскость. Их содержание раскрывают не определениями, а описывая их основные свойства. Фигуры, расположенные на одной плоскости, называют плоскими. Раздел геометрии, в котором изучаются фигуры на одной плоскости, называется планиметрией.
Раздел геометрии, в котором изучаются фигуры на одной плоскости, называется планиметрией.
Мы начинаем изучать планиметрию — раздел геометрии, в котором рассматриваются фигуры на плоскости. Из курса математики вы уже имеете представление о некоторых из них. Наша ближайшая цель — восстановить и дополнить эти начальные знания. Геометрические сведения мы будем излагать в определенной логической последовательности, чтобы они стали прочным фундаментом для дальнейшего изучения геометрии.
Основу любой науки составляют утверждения, которые принимаются как исходные и не требуют обоснования. В математике такие утверждения называют аксиомами. Аксиомы планиметрии, которые мы рассмотрим в этой главе, выражают основные свойства простейших геометрических фигур. На их основе с помощью логических рассуждений мы будем получать более сложные геометрические факты.
Планиметрия – от латинского “планум” и греческого “метрио” – измеряю.
Основные свойства расположения точек на прямой:
- Какой бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, ей не принадлежащие.

- Через любые две точки можно провести прямую, и только одну.
- Из трех точек прямой одна и только одна лежит между двумя другими.
Части прямой — отрезок и луч. Отрезок АВ — это часть прямой, содержащая точки А, В и все точки, лежащие между ними. Каждому отрезку соответствует его длина. Длина отрезка — расстояние между его концами. Расстояние и длину измеряют метрами, сантиметрами, миллиметрами, километрами, футами, дюймами и другими единичными отрезками.
Основные свойства измерения отрезков:
Каждый отрезок имеет определенную длину.
Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Часть плоскости, ограниченная двумя лучами с общим началом, называется углом. Углы бывают острые, прямые, тупые, развернутые и больше развернутого. Меры углов определяют в градусах, минутах, секундах, румбах и некоторых других единицах измерения.
Основные свойства измерения углов:
Каждый угол имеет определенную меру.
Мера угла равна сумме мер углов, на которые данный угол делится его внутренним лучом.
Биссектриса угла — внутренний луч, разбивающий данный угол на два равных угла.
Точки и прямыеГеометрия — это наука о геометрических фигурах и их свойствах. Самая простая геометрическая фигура — точка. Любая другая геометрическая фигура состоит из точек. Например, окружность — это фигура, состоящая из всех точек плоскости, равноудаленных от данной точки (рис. 1).
Отрезок также состоит из точек. Любое множество точек является геометрической фигурой. Часть геометрической фигуры или объединение нескольких фигур — тоже геометрическая фигура (рис. 2).
Одна из геометрических фигур — плоскость. Представление о части плоскости дает поверхность стола, потолка, пола. В геометрии плоскость считается неограниченной, идеально ровной и гладкой.
Фигуры, расположенные на одной плоскости, называют плоскими. Все вышеназванные геометрические фигуры — плоские. А куб, шар, прямоугольный параллелепипед — неплоские фигуры (рис. 3). Раздел геометрии, в котором изучаются фигуры на одной плоскости, называется планиметрией (латинское planum — плоскость).
Мы начинаем изучать планиметрию. Прежде всего рассмотрим, как могут быть расположены на плоскости точки и прямые.
Вы уже знаете, как с помощью линейки проводят прямые (рис. 4).
Прямая в геометрии — идеально ровная и бесконечная в обе стороны. Кик и любая другая фигура, прямая состоит из точек. Если точка А лежит на прямой а, говорят, что прямая а проходит через точку А. Записывают так: А е а. Если точка В не лежит на прямой а, пишут: (рис. 5).
Какой бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, ей не принадлежащие.
Через одну точку можно провести много прямых. На рисунке 6 вы видите прямые а и Ь, проходящие через точку Р.
Если прямой принадлежат точки А и В, говорят, что эта прямая проходит через точки А и В. Обозначают ее так: АВ.
Через любые две точки можно провести прямую, и только одну.
Можно ли провести прямую через три точки? Не всегда. Если точки А, B и C расположены, как показано на риcунке 7, через них прямую провести можно. А через точки А, В и D — нельзя. Говорят, что точки А, В и D Не лежат на одной прямой. Точки А, В, (- лежат на одной прямой, причем В — между А и С.
Простейшие геометрические фигуры и их свойства
Из трех точек прямой одна и только одна лежит между двумя другими.
Если точка В лежит между А и С, говорят, что точки А и С лежат по разные стороны от В, а точки А и В — по одну сторону от С.
Напечатанные выше жирным шрифтом три предложения со значком — это основные свойства расположения точек на прямой.
Любая точка А прямой делит эту прямую на две части (рис. 8). Каждую из частей прямой вместе с точкой А называют лучом, выходящим из точки А. Точку А называют началом луча. Если говорят «луч АВ», то имеют в виду, что начало луча находится в точке А (рис. 9).
Два луча, имеющие общее начало и дополняющие друг друга до прямой, называются дополнительными. На рисунке 10 вы видите луч ОК — дополнительный для луча ОР и луч ОР — дополнительный для ОК.
Геометрия — часть математики (рис. 11). Геометрическая наука богата содержанием и методами исследования. Она включает элементарную геометрию, высшую геометрию, неевклидовы геометрии, топологию и др. В школе изучают только элементарную геометрию.
Геометрия тесно связана со многими другими науками, прежде всего с физикой. Но физика занимается изучением материальных тел (имеющих массу, температуру, цвет и т. п.), а в геометрии абстрагируются от всего материального. Абстрагироваться — означает мысленно отвлечься от конкретных объектов, окружающих нас. Абстрагируясь от материальных вещей, мы в воображении создаем идеальные объекты по сходным свойствам. Конец иголки, натянутая струна — это материальные объекты. Они имеют определенную толщину, длину, массу. Абстрагируясь от таких физических свойств, человеческое воображение создало абстрактные геометрические понятия точка, прямая. В природе абстрактной прямой нет, но это понятие существует в человеческом воображении. И очень полезное понятие, поскольку все свойства прямой и ее частей, выявленные в геометрии, переносятся на миллионы и миллиарды всех натянутых струн, прямолинейных рельсов, труб, лент и т. п. Не существует в природе и плоскость без толщины, идеально ровная и гладкая, бесконечная в каждом ее направлении. Но для науки это идеальное понятие очень важно, поскольку свойства, установленные в геометрии для плоскости и ее частей, можно переносить на свойства миллиардов конкретных стен, оконных стекол и других предметов, имеющих плоские поверхности.
Абстрагируясь от материальных вещей, мы в воображении создаем идеальные объекты по сходным свойствам. Конец иголки, натянутая струна — это материальные объекты. Они имеют определенную толщину, длину, массу. Абстрагируясь от таких физических свойств, человеческое воображение создало абстрактные геометрические понятия точка, прямая. В природе абстрактной прямой нет, но это понятие существует в человеческом воображении. И очень полезное понятие, поскольку все свойства прямой и ее частей, выявленные в геометрии, переносятся на миллионы и миллиарды всех натянутых струн, прямолинейных рельсов, труб, лент и т. п. Не существует в природе и плоскость без толщины, идеально ровная и гладкая, бесконечная в каждом ее направлении. Но для науки это идеальное понятие очень важно, поскольку свойства, установленные в геометрии для плоскости и ее частей, можно переносить на свойства миллиардов конкретных стен, оконных стекол и других предметов, имеющих плоские поверхности.
На сколько частей могут разбивать плоскость три ее прямые?
Решение:
Если прямые расположены, как показано на рисунке 12, то они разбивают плоскость на 7 частей. Если они расположены, как показано на рисунке 13, то они разбивают плоскость на «4 или 6 частей.
Если они расположены, как показано на рисунке 13, то они разбивают плоскость на «4 или 6 частей.
Ответ. Три прямые разбивают плоскость, которой они принадлежат, на 4, 6 или 7 частей.
Дополнительное объяснение точки и прямой:
Основными геометрическими фигурами на плоскости являются точка и прямая. Плоскость можно представить как лист бумаги, точку — как след, оставленный иголкой на этом листе, а прямую — как тонкую натянутую нить. Точки обычно обозначают прописными латинскими буквами (А, В, С, D, …), а прямые — строчными латинскими буквами (а, b, с, d, …).
Ha рисунке 1 точки А и D лежат на прямой , а точки В и С не лежат на прямой . Можно это же сказать иначе: прямая проходит через точки
А и D, но не проходит через точки В и С .
Рис. 1
Прямая бесконечна и состоит из бесконечного множества точек. На рисунках мы изображаем лишь часть прямой.
Свойства точек и прямыхЧерез одну точку на плоскости можно провести бесконечно много прямых. Рассмотрим прямые и , проходящие через точку С (рис. 2). В этом случае говорят, что прямые
и пересекаются в точке С, а их общая точка С является точкой пересечения прямых и .
Рис. 2
Если на плоскости обозначены две точки [1]А и В, то через них можно провести прямую с (рис. 3). Отметим, что через точки А и B невозможно провести другую прямую, которая не совпадала бы с прямой с.
Это свойство называют аксиомой проведения прямой.
Рис. 3
[1] Здесь и далее, говоря «две точки» («две прямые», «три точки» и т. д.), мы будем считать, что эти точки (прямые) различны.
Аксиома проведения прямой
Через любые две точки можно провести прямую, и притом только одну.
Аксиома – от греческого «аксиос» – общепринятый, безоговорочный, не вызывающий сомнения
Из этого следует, что две прямые не могут иметь две или более общих точек: они либо имеют одну общую точку, либо не имеют общих точек вообще. Прямую, с выбранными на ней двумя точками, можно обозначать прописными буквами, которыми названы эти точки. Так, прямую на рисунке 3 можно назвать прямой АВ или прямой ВА.
Через три точки плоскости не всегда можно провести прямую. Так на рисунке 1 нельзя провести прямую через точки А, В, D.
На рисунке 4 точки А, В, С лежат на одной прямой, причем точка С лежит между точками А и В. Можно также сказать, что точки А и В лежат по разные стороны от точки С.
Можно также сказать, что точки А и В лежат по разные стороны от точки С.
Точки В и С лежат по одну сторону от точки А , а точки А и С лежат по одну сторону от точки В.
Аксиома расположения точек на прямой:
Из трех точек на прямой одна и только одна лежит между двумя другими.
ЛучЛюбая точка делит прямую на две части (рис. 5). Каждую из этих частей можно условно считать половиной прямой, поэтому образовавшиеся части прямой и получили название «полупрямые», или иначе — лучи
Рис. 5 Точка А делит прямую а на две полупрямые и
Лучом (или полупрямой) называется часть прямой, состоящая из всех Точек этой прямой, лежащих по одну сторону от некоторой данной на ней точки, а также самой этой точки. Данная точка называется начальной точкой (или началом) луча.
Данная точка называется начальной точкой (или началом) луча.
На рисунке 5 точка А — начальная точка двух лучей прямой . Лучи, как и прямые, можно обозначать строчными латинскими буквами или двумя точками: начальной (обязательно на первом месте!) и еще какои-нибудь точкой этого луча. Так, луч на рисунке 6 можно обозначить или ВС , но нельзя обозначить СВ.
Два различных луча одной прямой с общей начальной точкой называются дополнительными лучами.
На рисунке 5 и — дополнительные лучи. Они дополняют друг друга до прямой и имеют только одну общую точку — их начало.
Пример №2На прямой точка С лежит между точками А и В. Могут ли лучи АВ и АС быть дополнительными? Ответ обоснуйте.
Решение:
Пусть А, В и С — данные точки (рис. 7). Поскольку точка С лежит между точками А и В, то точки С и В лежат по одну сторону от точки А, значит, они принадлежат одному лучу с началом А. Этот луч можно назвать АВ или АС. Следовательно, данные лучи совпадают, поэтому они не являются дополнительными.
7). Поскольку точка С лежит между точками А и В, то точки С и В лежат по одну сторону от точки А, значит, они принадлежат одному лучу с началом А. Этот луч можно назвать АВ или АС. Следовательно, данные лучи совпадают, поэтому они не являются дополнительными.
Ответ: не могут.
Отрезки и их длиныДве точки прямой делят эту прямую на три части: два луча и отрезок.
Отрезком АВ называется та часть прямой, которая состоит из точек А а В и всех точек, лежащих между ними. Точки А и В называют концами отрезка АВ. Все другие точки этого отрезка — его внутренние точки.
На рисунке 19 изображен отрезок АВ.
Точки А и В — его концы, а любая точка, лежащая между А и В, — внутренняя точка отрезка АВ.
Два отрезка пересекаются, если они имеют только одну общую внутреннюю точку.
Чтобы измерять отрезки, нужно иметь единичный отрезок (единицу измерения).
Отрезок, показанный на рисунке 20, будем считать единичным. Его длина равна 1 см.
Если на отрезке АВ единичный отрезок откладывается ровно 3 раза, то это значит, что длина отрезка АВ равна 3 см (рис. 21). Если на отрезке ЕР единичный отрезок откладывается два раза с остатком, а в остатке десятая часть единичного отрезка — 7 раз, то длина отрезка ЕР равна 2,7 см. Записывают так: АВ = 3 см, ЕР = 2,7 см.
За единичный отрезок можно брать отрезки длиной 1 м, 1 км, I фут, 1 дюйм и т. д.
Каждый отрезок имеет определенную длину.
Два отрезка называются равными, если длины их равны. Из двух отрезков большим считается тот, длина которого больше.
В сантиметрах измеряют сравнительно небольшие отрезки. Большие отрезки измеряют в дециметрах, метрах, километрах; меньшие — в миллиметрах. Напомним, что
1 км = 1000 м, 1 м = 10 дм = 100 см = 1000 мм.
Длину отрезка называют также расстоянием между его концами. Если ХУ = 18 см, то это означает, что расстояние между точками X и У равно 18 см. Расстояние между X и У всегда равно расстоянию между У и X.
Если точка С отрезка АВ разбивает его на две части, длины которых равны, например 2 см и 1,2 см, то длина отрезка АВ равна 3,2 см (рис. 22).
Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Напечатанные выше жирным шрифтом два предложения со значком — это основные свойства измерения отрезков.
Серединой отрезка называется его внутренняя точка, разбивающая этот отрезок на две равные части.
Если точка С — середина отрезка АВ, то АС = СВ (рис. 23).
Если точка С не принадлежит отрезку АВ, то сумма длин отрезков АС и СВ больше длины АВ. Таким образом, для любых трех точек А, В и С всегда АВ + ВС > АС.
Измерять длины отрезков приходится многим специалистам. Чертежники измеряют их масштабными линейками, столяры — складными метрами, портные — клеенчатыми сантиметрами, строители — рулетками (рис. 24).
24).
Для любознательных:
Измерительные приборы обеспечивают ту или иную точность. Расстояние между городами обычно определяют с точностью до километра, между берегами реки — с точностью до метра, длину карандаша — с точностью до миллиметра, диаметр детали ручных часов — с точностью до десятой, а то и сотой части миллиметра. Разумеется, для измерений разных длин и расстояний используют соответствующие измерительные приборы: кроме уже названных, циркули, кронциркули, штангенциркули, дальномеры и др. С некоторыми из них вы познакомитесь позже. Единицы длины бывают разные. В англоязычных странах чаще всего используют следующие: фут, дюйм, миля. Подробнее о них — дальше.
На практике для различных расстояний существуют разные названия: длина, ширина, высота, глубина, дистанция, интервал (рис. 25).
Луч — часть прямой. Можно ли утверждать, что луч короче прямой?
Решение:
Прямая и луч не имеют длины, поэтому сравнивать и длины нет смысла.
Ответ. Нет.
Пример №4Точки К, Р и Т лежат на одной прямой. Найдите расстояние между Р и Т, если КР ~ 1,7 м, КТ = 4,8 м. Сколько решений имеет задача?
Решение:
Отметим точки К и Т так, что КТ = 4,8 м. Точка Р пр* мой КТ находится на расстоянии 1,7 м от К. Возможно два случая (рис. 26):
а) К лежит между PvlT: РТ = 1,7 м + 4,8 м = 6,5 м;
б) Р лежит между К и Т: РТ = 4,8 м – 1,7 м = 3,1 м.
Ответ. Задача имеет два решения: 6,5 м; 3,1 м.
Углы и их мерыДва луча, имеющих общее начало, разделяют плоскость на две части.
Часть плоскости, ограниченная двумя лучами с общим началом, называется углом.
Лучи, ограничивающие угол, называются сторонами, а их общее начало – вершиной уела (рис. 30, а). Такой угол называют углом А О В, или углом В О А, или углом О и записывают соответственно: , или или Все точки угла, не принадлежащие его сторонам, образуют внутреннюю область этого угла. Внутренняя область угла на рисунке 30, а закрашена. Иногда внутреннюю область угла обозначают дугой, иногда никак не обозначают, а только представляют себе. На рисунке 30, б, в вы видите углы с вершиной О и сторонами ОА и ОВ.
Внутренняя область угла на рисунке 30, а закрашена. Иногда внутреннюю область угла обозначают дугой, иногда никак не обозначают, а только представляют себе. На рисунке 30, б, в вы видите углы с вершиной О и сторонами ОА и ОВ.
Угол, стороны которого — дополнительные лучи, называют развернутым углом (рис. 31).
Чтобы измерять углы, необходимо иметь единицу измерения. Такой единицей принято считать угол в 1 градус (сокращенно: 1°).
В развернутом угле он вмещается 180 раз.
Представим полуокружность, разделенную на 18 равных дуг (рис. 32). Если из ее центра О через все точки деления и концы полуокружности провести лучи, они разделят развернутый угол на 18 углов по 10°. Один из таких углов (АОВ) делим на 10°. Мера угла АОС равна 1°.
Каждый угол имеет определенную меру.
Мера развернутого угла равна 180°.
Меру угла обозначают так же, как и угол. Например, если мера угла ABC равна 60 градусам, пишут: Очень маленькие углы измеряют в минутах и секундах.
Минутой называют часть градуса, а секундой — часть минуты.
Записывают так: 1° = 60′, 1′ = 60″.
Углы в тетради и на классной доске измеряют транспортиром (рис. 33), а на местности — астролябией (рис. 34), теодолитом (рис. 35) или другими угломерными приборами.
Два угла называются равными, если их меры равны.
Из двух углов большим считается тот, мера которого больше.
Угол называется прямым, если его мера равна 90°, острым — если он меньше прямого, тупым — если он больше прямого, но меньше развернутого (рис. 36).
Прямые углы на рисунках чаще обозначают не дугами, а квадратиками.
Углы больше развернутого (см. рис. 30, в) пока рассматривать не будем.
Луч, который исходит из вершины угла и лежит в его внутренней области,
называют внутренним лучом угла.
Внутренний луч делит данный угол на дна меньших угла. Например, внутренний луч ОК угла АОВ делит этот угол на углы АОК и КОВ (рис. 37). При этом Говорят, что угол АОВ равен сумме углов АОК и КОВ.
При этом Говорят, что угол АОВ равен сумме углов АОК и КОВ.
Мера угла равна сумме мер углов, на которые данный угол делится его внутренним лучом.
Два выделенных выше предложения со значком в — это основные свойства измерения углов.
Внутренний луч, который делит угол на два равных угла, называется биссектрисой этого угла. На рисунке 38 луч
ОС — биссектриса угла АОВ.
Для любознательных:
Углом часто называют также фигуру, составленную из двух лучей, имеющих общее начало, то есть углом называют и некую линию. Но разделить подобный угол на два или более равных углов нельзя. Таким образом, когда говорят о сложении, вычитании или делении углов, то угол рассматривают вместе с его внутренней областью. И хотя далее мы будем рассматривать в основном углы меньше развернутого, необходимо помнить, что бывают углы и больше развернутого, то есть больше 180°. Таким, например, является угол D четырехугольника ABCD (рис. 39).
Существуют и специальные транспортиры, которыми измеряют углы больше развернутого (рис. 40). Понятие угла часто используют также для характеристики поворотов. Например, велосипедное колесо можно повернуть на 100°, можно на 300°. А если колесо сделало полтора оборота? Считают, что оно повернулось на 360° и еще на 180°, всего — на 540°.
40). Понятие угла часто используют также для характеристики поворотов. Например, велосипедное колесо можно повернуть на 100°, можно на 300°. А если колесо сделало полтора оборота? Считают, что оно повернулось на 360° и еще на 180°, всего — на 540°.
Кроме градусов, минут и секунд, существуют и другие меры углов. Моряки измеряют углы в румбах. Румбом называют одну восьмую часть прямого угла, 1 румб = 11,25° (рис. 41). Научные работники чаще всего измеряют углы в радианах. Что это такое, вы узнаете в старших классах.
Найдите меру угла А О В, если лучи ОС и О К делят его на три равных угла и
Решение:
Угол СОК — третья часть угла АО В. Поэтому = 40° 3 = 120°.
Ответ. 120°.
Пример №6Найдите меры углов, образованных стрелками часов: в 3 часа; в 5 часов (рис. 42).
Решение:
На циферблате часов полуокружность соответствует 6 часам. Поэтому одному часу соответствует 1/6 часть развернутого угла, то есть 30°. Когда часы показывают 3 часа, угол между часовой и минутной стрелками равен 30° • 3 =
Поэтому одному часу соответствует 1/6 часть развернутого угла, то есть 30°. Когда часы показывают 3 часа, угол между часовой и минутной стрелками равен 30° • 3 =
= 90°. Когда часы показывают 5 часов, угол между стрелками равен 30° 5 = 150°.
Ответ. 90°; 150°.
Определение и его роль в геометрииВ пункте 1.3 описаны два понятия — «луч», которое известно вам из курса математики 5 класса, и новое понятие — «дополнительные лучи». Благодаря этим описаниям можно четко представить, какие именно фигуры рассматриваются. Данные нами описания являются определениями, указывающими на особенности описанной фигуры, которые отличают ее от других фигур.
Прочитаем еще раз определение дополнительных лучей. Если в нем пропустить лишь слова «одной прямой», то лучи MN и МК на рисунке 8, а придется считать дополнительными. Если же не уточнить, что дополнительные лучи должны иметь общее начало, то лучи АВ и CD на рисунке 8, б тоже следует назвать дополнительными. Таким образом, эти измененные определения не будут описывать тот объект, который мы имеем в виду.
Таким образом, эти измененные определения не будут описывать тот объект, который мы имеем в виду.
Рис. 8. К объяснению понятия «дополнительные лучи»:
а) лучи MN и МК не дополнительные;
б) лучи АВ и CD не дополнительные
Эти соображения свидетельствуют о том, как важно уделять внимание каждому слову в определении: только так можно по-настоящему понять геометрию.
Отрезок. Измерение и откладывание отрезковОпределение отрезкаЛюбой луч является частью прямой, «ограниченной» с одной стороны начальной точкой. Рассмотрим теперь отрезок — часть прямой, «ограниченную» точками с обеих сторон. Определение Отрезком называется часть прямой, состоящая из двух данных точек этой прямой (концов отрезка) и всех точек, лежащих между ними. Отрезок обозначают, записывая его концы в произвольном порядке. Так, отрезок на рисунке 10 можно назвать «отрезок АВ » или «отрезок ВА». Очевидно, что отрезок АВ является частью прямой АВ. При этом следует различать, идет ли речь о прямой АВ или об отрезке АВ.
Так, отрезок на рисунке 10 можно назвать «отрезок АВ » или «отрезок ВА». Очевидно, что отрезок АВ является частью прямой АВ. При этом следует различать, идет ли речь о прямой АВ или об отрезке АВ.
Если рассмотреть вместе с точками А и В некоторую другую точку прямой, то, в соответствии с аксиомой расположения точек на прямой, она либо лежит между точками А и В , то есть принадлежит отрезку АВ (на рисунке 11 такой точкой является ), либо не лежит между точками А и В , то есть не принадлежит отрезку АВ (на рисунке 11 такой точкой является ).
Равенство отрезков. Середина отрезкаОпределение:
Два отрезка называются: равными, если они совмещаются наложением.
Нанесем отрезок на прозрачную пленку и наложим erqm отрезок АВ так, чтобы точка А, совпала с точкой А и эти отрезки имели другие общие точки. Если точка В, совместится с точкой В (рис. 12), то отрезки АВ и равны (пишут так: ). Если же точки В и не совместятся, то меньшим из двух отрезков является тот, который составляет часть другого. На рисунке 13 точка В, совместилась с некоторой точкой отрезка АВ, отличной от точки В, поэтому отрезок больше отрезка . Кратко это обозначают так:
12), то отрезки АВ и равны (пишут так: ). Если же точки В и не совместятся, то меньшим из двух отрезков является тот, который составляет часть другого. На рисунке 13 точка В, совместилась с некоторой точкой отрезка АВ, отличной от точки В, поэтому отрезок больше отрезка . Кратко это обозначают так:
Определение:
Серединой отрезка называется точка отрезка, делящая его пополам (то есть на два равных отрезка).
На рисунке 14 отрезки DE и EF равны, то есть точка Е — середина отрезка DF. Обычно на рисунках равные отрезки обозначают одинаковым количеством черточек.
Измерение и откладывание отрезковВажным свойством отрезка является его длина. Она выражается положительным числом, которое может быть определено сравнением данного отрезка с отрезком, принятым за единицу измерения,— единичным отрезком. В качестве единичного отрезка можно выбрать отрезок любой длины. На практике выбирают единичные отрезки длиной 1 мм, 1 см, 1 м и др.
На практике выбирают единичные отрезки длиной 1 мм, 1 см, 1 м и др.
Например, на измерительной линейке, которой мы обычно пользуемся, маленькие деления задают единичные отрезки длиной 1 миллиметр, а большие — длиной 1 сантиметр (рис. 15).
Прикладывая линейку к данному отрезку, мы определяем, сколько единичных отрезков и их частей в нем содержится. Это число выражает длину отрезка. Число, выражающее длину отрезка, зависит от единицы измерения.
На рисунке 15 длина отрезка СЕ равна 70 мм, или 7 см, или 0,07 м и т. д. Длина отрезка CD равна 3 см, а отрезка DE — 4 см. Можно сказать, что отрезок СЕ состоит из двух частей — отрезков CD и DE . Точка D лежит между точками С и Е, а длина отрезка СЕ равна сумме длин отрезков CD и DE (пишут так: CD + DE = СЕ ).
Сформулируем аксиомы измерения и откладывания отрезков.
Аксиома измерения отрезков
Каждый отрезок имеет определенную длину, которая выражается положительным числом в заданных единицах измерения. Длина отрезка равна сумме длин частей, на которые отрезок делится любой его точкой.
Длина отрезка равна сумме длин частей, на которые отрезок делится любой его точкой.
Аксиома откладывания отрезков
Hа любом луче от его начальной точки можно отложить отрезок данной длины и только один.
Очевидно, что измерение отрезков состоит в последовательном наложении на данный отрезок определенного количества единичных отрезков. Поэтому равные отрезки имеют равные длины, а больший отрезок имеет большую длину. Верно и другое утверждение: если отрезки имеют равные длины, то они равны, а большим из двух отрезков является тот, который имеет большую длину. Таким образом, для сравнения отрезков можно сравнить их длины.
Длину отрезка АВ называют также расстоянием между точка ми А и В. Часто, говоря «отрезок AB », мы имеем в виду его длину.
Пример №7На луче АВ отмечена точка С, причем АВ = 12см, ВС – 7 см. Найдите длину отрезка АС
Решение:
Рассмотрим два случая расположения точки С на луче АВ.
- Точка С не лежит на: отрезке АВ (рис. 16, а). Тогда точка В лежит на отрезке АС По аксиоме измерения отрезков АС = АВ + ВС, то есть АС = 12 +7 =19 (см).
- Точка С лежит на отрезке АВ (рис. 16, 6). Тогда АВ = АС + ВС, то есть 12= АС + 7. Таким образом, АС = 12 – 7 = 5 (см).
Ответ: 19 см или 5 см.
Измерение, откладывание и определение углов
При изучении дополнительных лучей мы рассматривали случай, когда два луча имеют общую начальную точку. Рассмотрим теперь случай, когда два луча имеют общую начальную точку, но не обязательно являются полупрямыми одной прямой.
Определение:
Углом называется геометрическая фигура, которая состоит из двух лучей (сторон угла), исходящих из одной точки (вершины угла).
Для обозначения углов используют знак . На рисунке 17, а изображен угол с вершиной В, сторонами которого являются лучи и (или ВА и ВС ). Этот угол можно обозначить одним из следующих способов: . Если угол обозначают по вершине и двум точкам на сторонах, то вершину обязательно указывают на втором месте. Иногда углы обозначают греческими буквами (рис. 17, б), или числами (рис. 17, в).
Этот угол можно обозначить одним из следующих способов: . Если угол обозначают по вершине и двум точкам на сторонах, то вершину обязательно указывают на втором месте. Иногда углы обозначают греческими буквами (рис. 17, б), или числами (рис. 17, в).
Стороны угла делят плоскость на две части. Внутренней областью угла считается та из них, которая целиком содержит любой отрезок с концами на сторонах угла (на рисунке 17, а она заштрихована). Луч, который исходит из вершины угла и проходит в его внутренней области, делит данный угол на два угла. На рисунке 18 луч BD делит угол ABC на углы ABD и DBC .
Определение:
Развернутым углом называется угол, стороны которого являются дополнительными лучами.
На рисунке 19 изображен развернутый угол АОВ.
Прямая АВ делит плоскость на две части, каждую из которых можно считать внутренней областью развернутого угла АОВ . Договоримся ту из частей, которую мы рассматриваем как внутреннюю, обозначать дужкой.
Договоримся ту из частей, которую мы рассматриваем как внутреннюю, обозначать дужкой.
Определение:
Два угла называются равными, если они совмещаются наложением.
Биссектриса – от латинского «бис» — дважды и «секто» — рассекающая пополам.
На рисунке 20 изображены углы 1 и 2. Наложим угол 1 на угол 2 так, чтобы их вершины совпали, сторона первого угла совместилась со стороной второго, а внутренние области этих углов были расположены по одну сторону от прямой, содержащей совместившиеся стороны. Если другие стороны этих углов тоже совместятся, то углы 1 и 2 являются равными (пишут так: ).
Если же эти стороны не совместятся, то меньшим считается тот угол, сторона которого принадлежит внутренней области второго угла. На рисунке 21 угол 1 является частью угла 2, то есть он меньше угла 2 (пишут так: ).
Определение
Биссектрисой угла называется луч, который исходит из вершины угла и делит угол пополам (то есть на два равных угла).
На рисунке 22 углы DEK и KEF равны, поэтому луч ЕК — биссектриса угла DEF . Обычно на рисунках равные углы обозначают одинаковым количеством дужек.
Измерение и откладывание угловИзмерение углов имеет много общего с измерением отрезков. Величина отрезка количественно выражается мерой (длиной) отрезка, а величина угла — мерой угла. Мера угла выражается положительным числом, которое можно определить измерением, основанным на сравнении данного угла с углом, принятым за единицу измерения.
Обычно такой единицей является 1 гра дус (обозначается 1°) — угол, равный части развёрнутого угла. Градусная мера угла указывает, сколько углов величиной 1° и их частей содержится в данном угле. Для измерения углов обычно используют транспортир, деления которого задают меру угла в градусах (Рис. 23)
Градус – от латинского «градус» – шаг. По наблюдению вавилонян солнечный диск на дневном пути «делает 180 шагов».
Сформулируем аксиомы измерения и откладывания углов.
Аксиома измерения углов
Каждый угол имеет градусную меру. Которая выражается положительным числом. Развернутый угол равен 180°.
Если луч делит Данный угол на два угла, то градусная мера данного угла равна сумме градусных мер двух полученных углов;
Аксиома откладывания углов
От любого луча данной прямой можно отложить в заданную сторону от прямой угол с заданной градусной мерой, меньшей 180°, и только один.
Так, на рисунке 18 градусная мера угла ABC равна сумме градусных мер углов ABD и DBC (это утверждение можно записать в виде равенства: Часто, говоря «угол ABC >, мы имеем в виду градусную меру этого угла.
Биссектриса развернутого угла делит его на два угла, каждый из которых равен 90° (рис. 24). Такие углы называются прямыми. В отличие от других углов, обычно обозначаемых дужками, прямой угол обозначают знаком .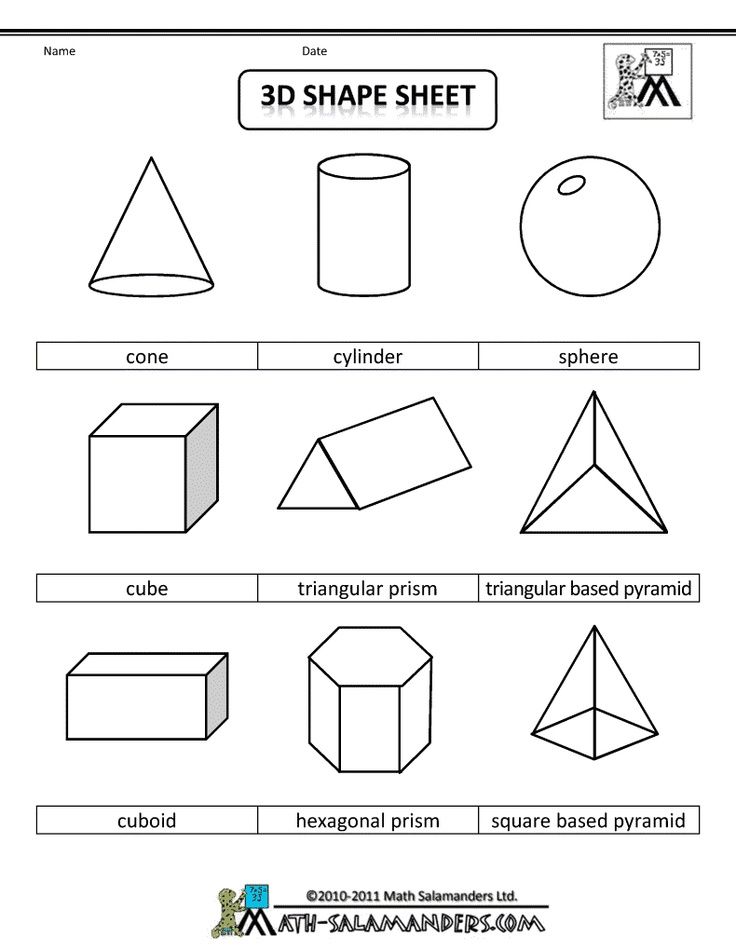
В 7 классе мы будем рассматривать углы, градусная мера которых не превышает 180°. Для более точных измерений используется 1 минута (обозначается ) – часть минуты.
Неразвернутые углы делятся на три вида (рис. 25):
- острые углы, меньше 90°;
- прямые углы, равны 90°;
- тупые углы, больше 90°, но меньше 180°.
На практике для построения углов используют транспортир. Для построения прямых углов используют угольник.
Измерение углов можно считать последовательным наложением на данный угол определенного (не обязательно целого) числа углов, равных 1°. Поэтому равные углы имеют равные градусные меры, а больший угол имеет большую градусную меру. Верно и другое утверждение: если углы имеют равные градусные меры, то они равны, а из двух углов большим является тот, который имеет большую градусную меру. Таким образом, для сравнения двух углов достаточно сравнить их градусные меры.
Луч b делит угол (aс), равный 120° на два угла, один, из которых втрое меньше угла (ас) .
Найдите эти углы.
Решение:
Пусть угол ( ab) втрое меньше угла (ас). Тогда Согласно аксиоме измерения углов, если луч b делит угол (ас) на два угла, то их сумма равна данному углу:
Тогда
Ответ:
Аналогия в геометрииИногда при решении задач о свойствах отрезков и углов применяются одни и те же методы и подходы. Это объясняется сходством некоторых свойств этих фигур. Такое сходство в науке называется аналогией.
Объясним суть аналогии на примере двух следующих задач.
Задача 1
На отрезке АВ, равном 20 см, отмечена точка С. Найдите расстояние между серединами отрезков АС и СВ.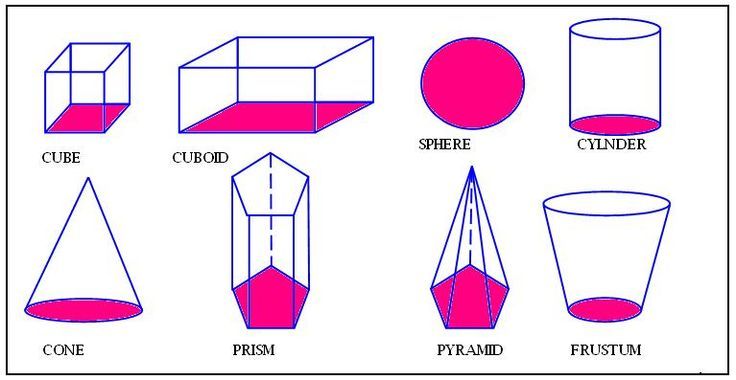
Задача 2
Луч С делит угол (аb), равный 140°, на два угла. Найдите угол между биссектрисами углов (ас) и (ab).
На первый взгляд, перед нами совершенно разные задачи, поскольку в одной речь идет об отрезках, а во второй — об углах. Однако в обеих задачах дано некоторое «целое», разделенное на части. Кроме того, понятия середины отрезка и биссектрисы угла связаны с делением целого пополам, и в обеих задачах нам необходимо найти сумму половин каждой из частей фигуры.
Решение 1
Пусть точка С принадлежит отрезку АВ, точки и — середины отрезков АС и СВ соответственно (рис. 26). Тогда
Найдем длину отрезка
Поскольку по условию задачи АВ = 20 см, имеем:
Ответ: 10 см
Решение 2
Пусть луч с делит угол (аb) на два угла, лучи и — биссектрисы углов (ас) и (cb) соответственно (рис. 27).
27).
Тогда
Найдем градусную меру угла
Поскольку по условию задачи имеем:
Ответ: 70°.
Как видим, в основе обоих решений лежит общая идея. Найдя ее при решении первой задачи, мы можем повторить основные этапы рассуждений применительно к условиям второй задачи, то есть решить ее аналогично.
Рассуждения по аналогии довольно часто применяются и в других науках. Например, биологи установили, что летучая мышь в полете испускает ультразвуковые колебания и, воспринимая колебания, отраженные от преграды, ориентируется по этим сигналам в темноте. По аналогичному принципу ученые создали радиолокатор, определяющий местонахождение объектов в любых погодных условиях. Но аналогия в науке не всегда дает желаемый результат: в течение многих веков человек старался взлететь в небо с помощью искусственных крыльев, аналогичных птичьим, но эти старания были напрасными. И только более основательные научные исследования привели к созданию дельтапланов, самолетов и других летательных аппаратов, с помощью которых человек поднялся в воздух. Выдающийся немецкий астроном и математик Иоганн Кеплер считал аналогии «своими верными учителями» и подчеркивал, что «аналогиями менее всего следует пренебрегать в геометрии». Однако при этом нужно учитывать, что аналогия, полезная как способ рассуждений, сама по себе не может служить доказательством каких-либо свойств геометрических фигур.
Выдающийся немецкий астроном и математик Иоганн Кеплер считал аналогии «своими верными учителями» и подчеркивал, что «аналогиями менее всего следует пренебрегать в геометрии». Однако при этом нужно учитывать, что аналогия, полезная как способ рассуждений, сама по себе не может служить доказательством каких-либо свойств геометрических фигур.
Известно, что если две прямые на плоскости имеют только одну общую точку, то они пересекаются. Рассмотрим теперь случай, когда две прямые не имеют общих точек.
Параллельный – от греческого слова «параляелос» — идущий рядом
Определение:
Две прямые на плоскости называются параллельными, если они не пересекаются.
Представление о параллельных прямых дают, например, железнодорожные рельсы или линейки нотного стана.
На рисунке 29 прямые и параллельны. Кратко это обозначают так: || . Такая запись читается: «Прямая параллельна прямой »
Итак, можно выделить два случая взаимного расположения прямых на плоскости: две прямые на плоскости или параллельны, или пересекаются.
Наряду с параллельностью прямых мы будем рассматривать также параллельность отрезков и лучей.
Определение:
Два отрезка называются параллельными, если они лежат на параллельных прямых.
Аналогично формулируются определения параллельности двух лучей, прямой и отрезка, луча и отрезка и т. п.
На рисунке 30 прямые АВ и CD параллельны, поэтому отрезки АВ и CD параллельны, лучи ВА и CD параллельны, отрезок АВ параллелен прямой CD и т. д.
На практике довольно часто приходится проводить прямую, параллельную данной,— например, делать разметку дороги или чертить поля в тетради. Всегда ли можно провести через данную точку прямую, параллельную данной? Сколько таких прямых проходит через точку, не лежащую на данной прямой? Ответ на эти вопросы дает аксиома параллельных прямых (аксиома Евклида).
Аксиома параллельных прямых (аксиома Евклида)
Через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной1.
Мы сформулировали лишь некоторые из аксиом планиметрии. Более полный перечень аксиом представлен в Приложении 1.
Теорема о двух прямых, параллельных третьей
На основе аксиом с помощью логических рассуждений (доказательств) мы будем получать новые геометрические факты. В математике утверждение, справедливость которого устанавливается путем доказательства, называется теоремой.
Доказывая теорему, используют определения, ак сиомы и теоремы, доказанные ранее.
Итак, сформулируем и докажем первую теоре му — теорему о параллельных прямых (рис. 31).
Теорема: (о двух прямых, параллельных третьей)
Две прямые, параллельные третьей, параллельны между собой.
‘ На самом деле имеет место такое утверждение: «Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну». Возможность провести такую прямую мы докажем в п. 14.3.
Возможность провести такую прямую мы докажем в п. 14.3.
Доказательство:
Пусть а, b и с — данные прямые, причем а || с, b || c. Докажем, что прямые а и b параллельны.
Предположим, что прямые а и b не параллельны. Тогда они должны пересекаться в некоторой точке С (рис. 32). Таким образом, через точку С проходят две прямые, параллельные прямой с. Но согласно аксиоме параллельных прямых через точку вне данной прямой может проходить не более одной прямой, параллельной данной. Следовательно, наше предположение о том, что прямые а и b могут пересекаться, неверно, то есть эти прямые параллельны. Теорема доказана.
Применим доказанную теорему для решения задачи.
Пример №9Если прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую прямую. Докажите.
Докажите.
Решение:
Пусть а || b, и прямая с пересекает прямую а (рис. 33). Докажем, что прямые b и с пересекаются. Предположим, что эти прямые не пересекаются. В таком случае b || с. Поскольку с || b и а || b, то по теореме о двух прямых, параллельных третьей, прямые а и с параллельны. Но это невозможно, так как по условию задачи прямые а и c пересекаются. Таким образом, предположение о том, что b || с, неверно. Значит, прямые b и с пересекаются, что и требовалось доказать.
Теорема – от греческого «теоремос» – рассматривать, обдумывать
Обратим внимание на рисунок 32, который использовался в ходе доказательства теоремы. Взаимное расположение прямых а, b, с на этом рисунке не соответствует формулировке теоремы, и это легко объяснить: ведь рисунок отражает предположение, впоследствии оказавшееся неверным. Вообще, рисункам в геометрических теоремах и задачах отводится особая роль — то, что на них изображено, следует из имеющихся у нас сведений, но не наоборот. Недоказанные свойства геометрических фигур, даже если они кажутся очевидными из рисунков, использовать нельзя. Рисунок в геометрии лишь отражает свойства и утверждения, выраженные словами, но сам по себе не является доказательством. К тому же рисунок может не охватывать всех возможных вариантов расположения элементов фигур, которые подразумеваются в задаче или теореме. Недаром геометрию называют «искусством правильно рассуждать на неправильных чертежах».
Недоказанные свойства геометрических фигур, даже если они кажутся очевидными из рисунков, использовать нельзя. Рисунок в геометрии лишь отражает свойства и утверждения, выраженные словами, но сам по себе не является доказательством. К тому же рисунок может не охватывать всех возможных вариантов расположения элементов фигур, которые подразумеваются в задаче или теореме. Недаром геометрию называют «искусством правильно рассуждать на неправильных чертежах».
В формулировке любой теоремы всегда можно четко выделить две части: то, что дано (условие), и то, что надо доказать (заключение). Переформулируем теорему о двух прямых, параллельных третьей, следующим образом: «Если две прямые параллельны третьей прямой, то эти прямые параллельны между собой». Нам известно, что две прямые параллельны третьей прямой — это условие теоремы. Требуется доказать, что эти прямые параллельны между собой — это заключение теоремы. Вообще говоря, выделить условие и заключение легче всего для утверждения, представленного в виде: «Если… (условие), то… (заключение)».
Вообще говоря, выделить условие и заключение легче всего для утверждения, представленного в виде: «Если… (условие), то… (заключение)».
Проанализируем доказательство теоремы о двух прямых, параллельных третьей. Сначала мы предположили, что прямые а и b не параллельны, то есть что заключение теоремы ошибочно. Затем, опираясь на известные свойства взаимного расположения прямых, установили, что через некоторую точку С проходят две прямые, параллельные с, то есть пришли к противоречию с аксиомой параллельных прямых. На основании этого противоречия мы сделали вывод о том, что наше предположение было неверным, а значит, верным является утверждение теоремы. Этот метод доказательства называется доказательством от противного, им мы воспользовались и в задаче, которую рассматривали после теоремы. Но этот метод не единственный: уже в следующем параграфе мы будем применять и другие методы доказательств.
Метод доказательства от противного иногда используется как в других науках, так и в повседневной жизни. Например, врач, чтобы убедиться, что пациент не болен гриппом, может рассуждать так: «Допустим, что у больного грипп; тогда у него должны быть характерные симптомы: повышение температуры, головная боль и т. п. Но этих симптомов нет, то есть предположение о гриппе неверно. Значит, пациент не болен гриппом».
Схема доказательства от противного| Утверждение: | Если А, то В |
| Доказательство: | |
1. Пусть A, но не B | Предполагаем, что условие теоремы выполняется, а заключение — нет |
| 2.Рассуждения | Проводим рассуждения, опираясь на аксиомы и ранее доказанные теоремы |
| 3.Противоречие | Получаем новое утверждение, противоречащее либо данному условию, либо одной из аксиом, либо ранее доказанной теореме |
4. Тогда B Тогда B | Убеждаемся, что наше предположение ошибочно, т. е. данное утверждение является верным |
В предыдущих параграфах мы рассматривали виды углов в зависимости от их градусной меры. Перейдем к изучению углов, имеющих общие элементы.
Пусть на прямой точка О лежит между точками А и В, а С — произвольная точка вне прямой АВ (рис. 35). Тогда углы АОС и СОВ имеют общую сторону, а стороны OA и ОВ данных углов являются дополнительными лучами.
Определение:
Два угла называются смежными, если они имеют общую сторону, а другие стороны этих углов являются дополнительными лучами.
Пропуск хотя бы одного условия в формулировании определения недопустим; это может привести к тому, что будет описан иной геометрический объект. Так, если стороны двух углов не являются дополнительными лучами, то даже при наличии общей стороны такие углы — не смежные (рис. 36). Не являются смежными и углы, которые не удовлетворяют первому условию определения, то есть не имеют общей стороны (рис. 37).
36). Не являются смежными и углы, которые не удовлетворяют первому условию определения, то есть не имеют общей стороны (рис. 37).
Теорема (о смежных углах)
Сумма смежных углов равна 180° .
Доказательство:
Пусть углы ( аb ) и (bс) — данные смежные углы (рис. 38). Тогда по определению смежных углов лучи а и с дополнительные, то есть угол (ас) развернутый, а его градусная мера равна 180°. Луч b делит угол (ас) на два угла, и по аксиоме измерения углов . Теорема доказана.
Сформулируем теперь несколько утверждений, которые легко обосновать с помощью доказанной теоремы.
1. Если два угла равны, то смежные с ними углы также равны.
Если два угла равны, то смежные с ними углы также равны.
Действительно, по теореме о смежных углах (рис.39). Если то то есть
2. Два угла, смежные с одним и тем же углом, равны.
На рисунке 40 углы 1 и 2, а также углы 1 и 3 являются смежными. Поскольку сумма смежных углов равна 180°, то
3. Угол, смежный с прямым углом, также прямой. Угол, смежный с тупым углом,— острый. Угол, смежный с острым углом,— тупой.
Эти утверждения вытекают из теоремы о смежных углах, поскольку 180°-90° = 90° (рис. 41), а если два неравных угла в сумме составляют 180°, то один из них больше 90° (то есть тупой), а второй — меньше 90° (то есть острый).
В математике утверждения, непосредственно вытекающие из теорем (или аксиом), называют следствиями. Обосновывая следствия 1—3, мы всякий раз упоминали теорему о смежных углах, причем делали это двумя способами: либо указывали ее название, либо пересказывали ее содержание. Такие обращения к известному утверждению с целью обоснования нового называют ссылками.
Такие обращения к известному утверждению с целью обоснования нового называют ссылками.
Решая геометрическую задачу или доказывая новую теорему, необходимо ссылаться на ранее изученные определения, аксиомы, теоремы и их следствия, а также на данные, содержащиеся в условии задачи или вытекающие из него. Например, при доказательстве теоремы о смежных углах мы ссылались на определения смежных углов, развернутого угла и аксиому измерения углов, а при доказательстве теоремы о двух прямых, параллельных третьей, — на аксиому параллельных прямых.
Пример №10Докажите, что если два смежных угла равны, то они прямые.
Решение:
Если — смежные углы, то (по теореме о смежных углах). Поскольку по условию задачи то каждый из этих углов равен то есть данные углы являются прямыми, что и требовалось доказать.
Вертикальные углы. Перпендикулярные прямые
Определение вертикальных углов
Рассмотрим еще один случай взаимного расположения углов с общими элементами. Вертикальный — от латинского «вертикалис» — вершинный
Вертикальный — от латинского «вертикалис» — вершинный
Определение:
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон второго. На рисунке 44 прямые АС и BD пересекаются в точке О. Стороны OD и OA угла AOD являются дополнительными лучами сторон ОВ и ОС угла ВОС , поэтому эти углы — вертикальные. Вертикальными являются также углы АОВ и DОС.
Таким образом, при пересечении двух прямых1 образуются две пары вертикальных углов. Наглядное представление о вертикальных углах дают, например, обычные ножницы.
Теорема о вертикальных углах. Угол между прямыми
Угол между прямымиОсновное свойство вертикальных углов выражает следующая теорема.
Теорема: (о вертикальных углах )
Вертикальные углы равны.
1 Здесь и далее, говоря об углах, образованных при пересечении двух прямых, мы будем иметь в виду неразвернутые углы.
Доказательство:
Пусть — вертикальные углы, образовавшиеся при пересечении прямых а и b (рис. 45). Рассмотрим угол 3, сторонами которого также являются полупрямые прямых a и b . Углы 1 и 2 смежные с углом 3 (по определению смежных углов), поэтому по следствию из теоремы о смежных углах . Теорема доказана.
Пример №11Сумма двух углов, образовавшихся при пересечении двух прямых, равна 100°. Найдите все образовавшиеся углы.
Решение:
По условию задачи при пересечении двух прямых образовались два угла, сумма которых составляет 100°. Эти углы могут быть или смежными, или вертикальными. Сумма смежных углов равна 180°, поэтому данные углы не могух быть смежными, значит, они вертикальные. Пусть (рис. 46). Так как вертикальные углы равны, то каждый из двух данных углов равен 100° : 2 = 50°. Таким образом, Поскольку углы 1 и 2 смежные, то (по теореме о смежных углах).
Эти углы могут быть или смежными, или вертикальными. Сумма смежных углов равна 180°, поэтому данные углы не могух быть смежными, значит, они вертикальные. Пусть (рис. 46). Так как вертикальные углы равны, то каждый из двух данных углов равен 100° : 2 = 50°. Таким образом, Поскольку углы 1 и 2 смежные, то (по теореме о смежных углах).
Поскольку углы 2 и 4 вертикальные, то (по теореме о вертикальных углах).
Ответ: 50°; 130°; 50°; 130°.
Определение:
Углом между двумя прямыми называется меньший из углов, образовавшихся при их пересечении.
На рисунке 47 две прямые при пересечении образуют два угла по 30° и два угла по 150°. Угол между данными прямыми по определению равен 30° (иначе говорят: прямые пересекаются под углом 30°).
Очевидно, что если при пересечении двух прямых образуются четыре равных угла, то все они равны 90°, то есть данные прямые пересекаются под прямым углом.
Перпендикулярные прямыеПерпендикулярный— от латинского слова «перпендикулярис» – отвесный.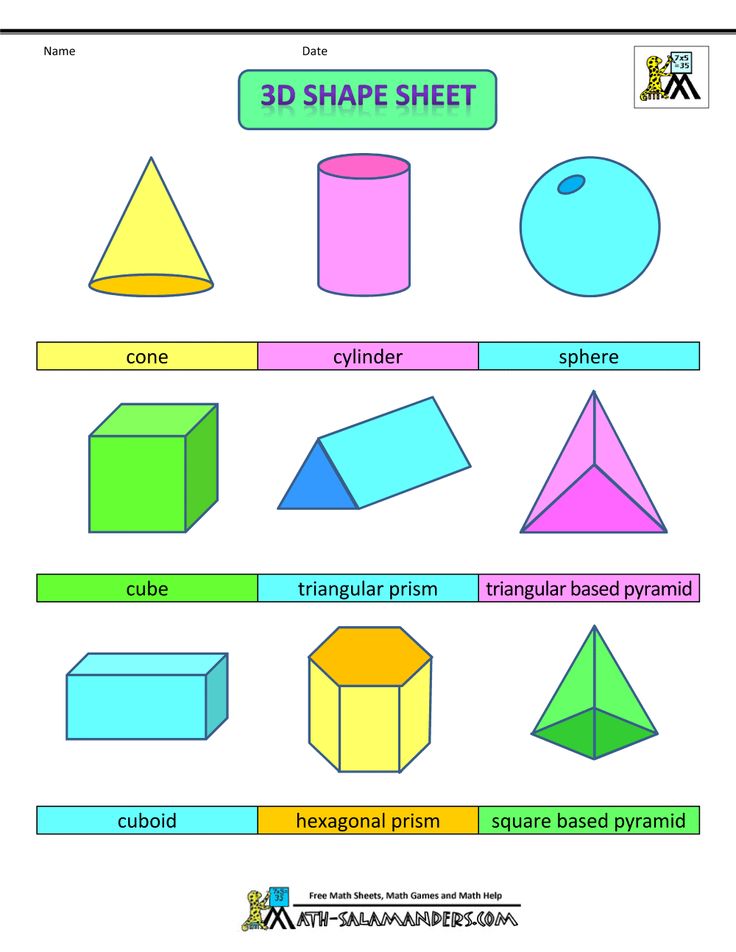
Определение:
Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
На рисунке 48 прямые а и b перпендикулярны. Кратко это обозначают так: .
Отрезки или лучи называются перпендикулярными, если они лежат на перпендикулярных прямых.
Докажем важное утверждение; связывающее понятия перпендикулярности и параллельности прямых.
Теорема (о двух прямых, перпендикулярных третьей) Две прямые, перпендикулярные третьей, параллельны.
Утверждение теоремы иллюстрирует рисунок 49. На этом рисунке
Доказательство:
Пусть даны прямые и , перпендикулярные прямой АВ. Докажем методом от противного, что
Предположим, что данные прямые не параллельны. Тогда они пересекаются в некоторой точке (рис. 50).
Перегнем рисунок по прямой АВ. Поскольку прямые углы 1 и 2 равны, то при перегибе луч совместится с лучом . Аналогично луч совместится с лучом . Поэтому точка в которой пересекаются данные прямые, должна совместиться с некоторой точкой , также лежащей на этих прямых. Таким образом, через точки и проходят две прямые и , что невозможно по аксиоме проведения прямой. Следовательно, наше предположение неверно, то есть прямые и параллельны. Теорема доказана.
Поскольку прямые углы 1 и 2 равны, то при перегибе луч совместится с лучом . Аналогично луч совместится с лучом . Поэтому точка в которой пересекаются данные прямые, должна совместиться с некоторой точкой , также лежащей на этих прямых. Таким образом, через точки и проходят две прямые и , что невозможно по аксиоме проведения прямой. Следовательно, наше предположение неверно, то есть прямые и параллельны. Теорема доказана.
Свойство, описанное в теореме, используется для построения параллельных прямых с помощью линейки и угольника (рис. 51). Дважды прикладывая угольник к линейке, можно провести две прямые, перпендикулярные краю линейки. По доказанной теореме такие прямые параллельны.
Историческая справкаДревнейшая наука геометрия как и математика в целом, зарождалась из потребностей практической деятельности. Везде, где жили и работали люди, необходимо было измерять, вычислять, размышлять.
Первые документальные свидетельства о геометрических знаниях дошли до нас из Древнего Египта.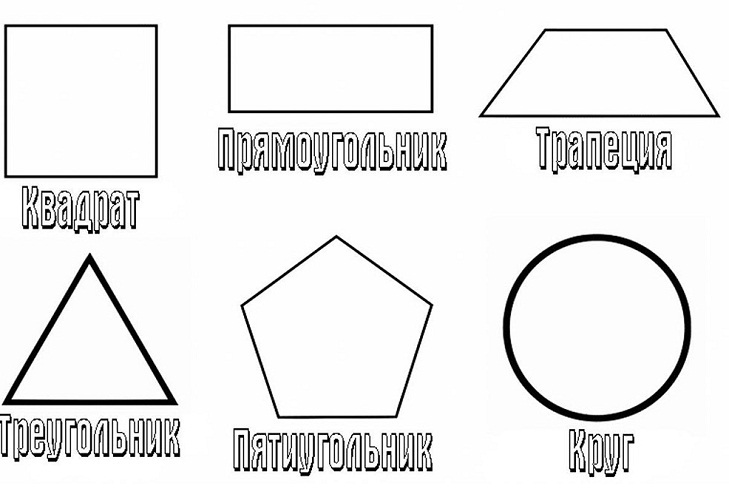 Каждый год воды Нила затапливали почти все прибрежные земли, поэтому египтянам приходилось вновь их размежевывать. Именно так в процессе работы устанавливались простейшие свойства геометрических фигур.
Каждый год воды Нила затапливали почти все прибрежные земли, поэтому египтянам приходилось вновь их размежевывать. Именно так в процессе работы устанавливались простейшие свойства геометрических фигур.
Становление геометрии. Становление геометрии как строгой науки связано с работами древнегреческих ученых: Фалеса (ориент. 625-547 гг. до н.э.), Пифагора (ориент. 570-500 гг. до н. э.), Евдокса (ориент. 408-355 гг. до н. э.). Одной из выдающихся фигур в истории геометрии по праву считается Евклид Александрийский (ориент. 330-275 гг. до н. э.). Его произведение «Начала» стало учебником, по которому изучали геометрию на протяжении почти двух тысяч лет. Евклид первым применил именно тот подход к изложению геометрии, которым мы пользуемся сейчас: сначала сформулировал основные определения и свойства простейших фигур (аксиомы), а затем, опираясь на них, доказал многие другие утверждения.
Возведенные за две-четыре тысячи лет до нашей эры, египетские пирамиды и сегодня поражают точностью метрических отношений; строители уже тогда знали немало геометрических положений и расчетов.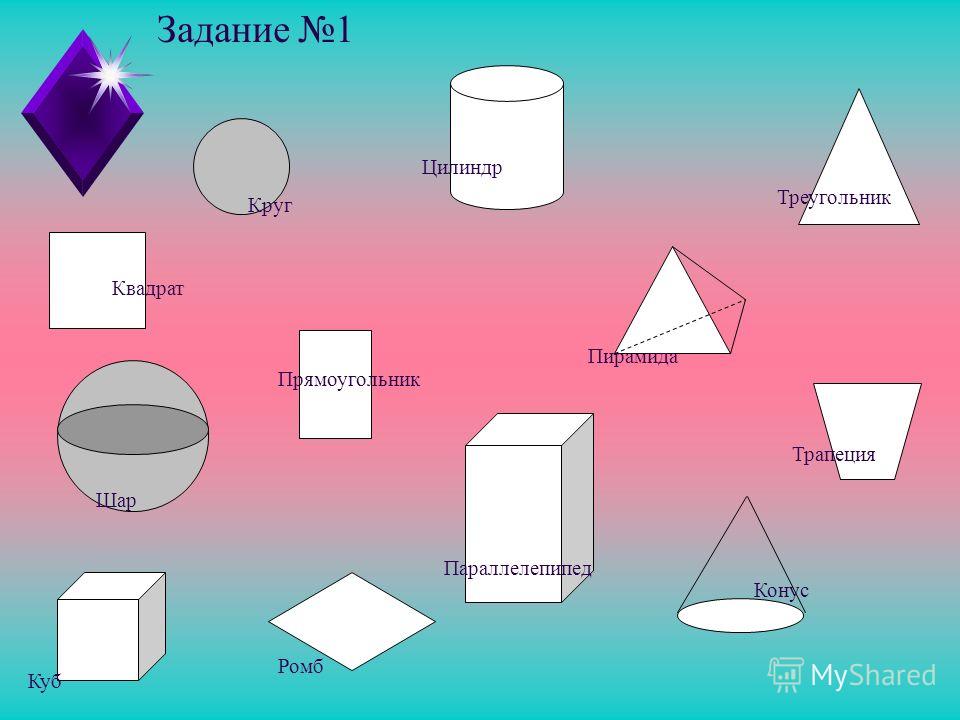
Профессор Харьковского университета Алексей Васильевич Погорелое (1919-2002) обогатил современную геометрию новейшими исследованиями и создал школьный учебник, по которому занимались несколько поколений учащихся.
Исследования и открытия ученых- геометров нашли применение во многих областях человеческой деятельности. Геометрия стала элементом общечеловеческой культуры – ведь без знания основ геометрии невозможно представить себе современного просвещенного человека.
Герметрия в Украине Интересные страницы истории развития геометрии, в частности ее преподавания в школе, связаны с Украиной. Именно здесь, в одной из харьковских гимназий, в конце XIX в. начинал свою деятельность известный русский педагог Андрей Петрович Киселев (1852-1940). по учебнику которого изучали геометрию нэ протяжении почти 60 лет.
Справочный материал по простейшим геометрическим фигурам1. Точки и прямые
- ✓ Основное свойство прямой.
 Через любые две точки можно провести прямую, и притом только одну.
Через любые две точки можно провести прямую, и притом только одну. - ✓ Две прямые, имеющие общую точку, называют пересекающимися.
- ✓ Любые две пересекающиеся прямые имеют только одну общую точку.
2. Отрезок и его длина
- ✓ Точки А и В прямой а (рис. 239) ограничивают часть прямой, которую вместе с точками А и В называют отрезком, а точки А и В — концами этого отрезка.
- ✓ Два отрезка называют равными, если их можно совместить наложением.
- ✓ Равные отрезки имеют равные длины, и наоборот, если длины отрезков равны, то равны и сами отрезки.
- ✓ Основное свойство длины отрезка. Если точка С является внутренней точкой отрезка АВ, то отрезок АВ равен сумме отрезков АС и СВ, то есть АВ = АС + СВ.
- ✓ Расстоянием между точками А и В называют длину отрезка АВ. Если точки А и В совпадают, то считают, что расстояние между ними равно нулю.
3. Луч. Угол
- ✓ Точка О прямой АВ (рис.
 240) разбивает прямую на две части, каждую из которых вместе с точкой О называют лучом или полупрямой. Точку О называют началом луча.
240) разбивает прямую на две части, каждую из которых вместе с точкой О называют лучом или полупрямой. Точку О называют началом луча. - ✓ Два луча, имеющих общее начало и лежащих на одной прямой, называют дополнительными.
- ✓ Два луча ОА и ОВ, имеющие общее начало (рис. 241), разбивают плоскость на две части, каждую из которых вместе с лучами ОА и ОВ называют углом. Лучи ОА и ОВ называют сторонами угла, а точку О — вершиной угла.
- ✓ Угол, сторонами которого являются дополнительные лучи, называют развернутым.
- ✓ Два угла называют равными, если их можно совместить наложением.
- ✓ Биссектрисой угла называют луч с началом в вершине угла, делящий этот угол на два равных угла.
4. Измерение углов
- ✓ Каждый угол имеет определенную величину (градусную меру).
- ✓ Угол, градусная мера которого равна 90°, называют прямым. Угол, градусная мера которого меньше 90°, называют острым. Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.
- ✓ Равные углы имеют равные величины, и наоборот, если величины углов равны, то равны и сами углы.
- ✓ Основное свойство величины угла. Если луч ОС делит угол АОВ на два угла АОС и СОВ (рис. 242), то
5. Смежные и вертикальные углы
- ✓ Два угла называют смежными, если у них одна сторона общая, а две другие являются дополнительными лучами.
- ✓ Сумма смежных углов равна 180°.
- ✓ Два угла называют вертикальными, если стороны одного угла являются дополнительными лучами сторон другого.
- ✓ Вертикальные углы равны.
6. Перпендикулярные прямые. Серединный перпендикуляр
- ✓ Две прямые называют перпендикулярными, если при их пересечении образовался прямой угол.
- ✓ Неперпендикулярные прямые при пересечении образуют пару равных острых углов и пару равных тупых углов. Величину острого угла называют углом между неперпендикулярными прямыми.
- ✓ Если прямые перпендикулярны, то считают, что угол между ними равен 90°.
- ✓ Два отрезка называют перпендикулярными, если они лежат на перпендикулярных прямых.
- ✓ На рисунке 243 изображены прямая а и перпендикулярный ей отрезок АВ, конец В которого принадлежит прямой а. В таком случае говорят, что из точки А на прямую а опущен перпендикуляр АВ. Точку В называют основанием перпендикуляра АВ.
- ✓ Длину перпендикуляра AB называют расстоянием от точки А до прямой а. Если точка А принадлежит прямой а, то считают, что расстояние от точки А до прямой а равно нулю.
- ✓Опустим из точки А на прямую а перпендикуляр АВ (рис. 244). Пусть X — произвольная точка прямой а, отличная от точки В. Отрезок АХ называют наклонной, проведенной из точки А к прямой а.
- ✓ Через данную точку проходит только одна прямая, перпендикулярная данной.
- ✓ Прямую, перпендикулярную отрезку и проходящую через его середину, называют серединным перпендикуляром отрезка.
- ✓ Каждая точка серединного перпендикуляра отрезка равноудалена от концов этого отрезка.
- ✓ Если точка равноудалена от концов отрезка, то она принадлежит серединному перпендикуляру этого отрезка.
Основными геометрическими фигурами на плоскости являются точка и прямая.
Отрезком называют часть прямой, которая состоит из всех точек этой прямой, которые лежат между двумя ее точками, вместе с этими точками. На рисунке 257: отрезок точки и – концы отрезка.
Точка делит прямую на две части (рис. 258). Каждую из полученных частей
вместе с точкой называют лучом, выходящим из точки Поэтому называют началом каждого из лучей.
• Два луча, имеющие общее начало и дополняющие друг друга до прямой, называют дополняющими.
Угол – это геометрическая фигура, состоящая из двух лучей, которые выходят из одной точки. Лучи называют сторонами угла, а их общее начало – вершиной угла. На рисунке 259: угол точка – его вершина; и – стороны угла. Записать этот угол можно так:
На рисунке 259: угол точка – его вершина; и – стороны угла. Записать этот угол можно так:
Биссектрисой угла называют луч, который выходит из вершины угла, проходит между его сторонами и делит его пополам.
Аксиомы планиметрии- I. Какова бы ни была прямая, существуют точки, принадлежащие ей, и точки, ей не принадлежащие.
- II. Через две точки можно провести прямую и к тому же только одну.
- III. Из трех точек на прямой одна и только одна лежит между двумя другими.
- IV. Каждый отрезок имеет определенную длину, большую нуля.
- V. Длина отрезка равна сумме длин частей, на которые он разбивается любой его внутренней точкой. (На рисунке 260
- VI. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°.
- VII. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами. (рис. 261).

Геометрические формы и их названия. Геометрические фигуры, или с чего начинается геометрия
Исторически понятие геометрической фигуры, так же как понятие натурального числа, было одним из исходных понятий математики. Как и натуральные числа, понятие геометрической фигуры образовалось с помощью абстракции отождествления, в основе которой лежит некоторое отношение эквивалентности. В данном случае таким отношением является «сходство», «подобие» предметов по их форме, с помощью которого множество предметов разбивается на классы эквивалентности так, что любые два предмета одного класса имеют одинаковую форму, а любые два предмета различных классов – различные формы. Абстрагируясь при этом от других свойств предметов (цвета, величины, материала, из …
которого они сделаны, назначения и т. д.), мы получаем самостоятельное понятие геометрической фигуры.
В математике поступают и так: класс подобных по форме предметов определяется любым принадлежащим ему предметом и называется формой.
В связи с рассмотрением отношения эквивалентности (глава IV, § 4) был приведен пример классификации блоков по их форме. Решая эту задачу, дети получают классы квадратных, круглых, треугольных и прямоугольных блоков, затем каждый из этих классов, так же как и отдельные их представители, называются соответственно квадратом, кругом, треугольником, прямоугольником. В основе выделения этих понятий лежит отношение эквивалентности
«иметь одинаковую форму».
В изучении геометрии, и в частности геометрических фигур,
различают несколько уровней мышления.
Первый, самый простейший уровень характеризуется тем, что геометрические фигуры рассматриваются как целые и различаются только по своей форме. Если показать дошкольнику круг, квадрат, прямоугольник и сообщить ему соответствующие названия, 1 то после некоторого времени он сможет безошибочно распознавать } эти фигуры исключительно по их форме (причем еще не аиалиаиро-ванной), не отличая квадрат от прямоугольника. На этом уровне квадрат противопоставляется прямоугольнику.
На этом уровне квадрат противопоставляется прямоугольнику.
На следующем, втором, уровне проводится анализ воспринимаемых форм, в результате которого выявляются их свойства. Геометрические фигуры выступают уже как носители своих свойств и распознаются по этим свойствам, свойства фигур логически еще не упорядочены, они устанавливаются эмпирическим путем. Сами фигуры также не упорядочены, так как они только описываются, но не определяются. Этот уровень мышления в области геометрии еще не включает структуру логического следования.
©писанные выше два уровня вполне доступны детям 4-6 лет, и это обстоятельство следует учитывать при составлении программ «Лучения и разработке методики.
Из чего состоит геометрическая фигура?
Всякая геометрическая фигура подразумевается состоящей из точек, т. е. всякая геометрическая фигура представляет собой множество точек, ъ том числе одну точку тоже принято считать
геометрической фигурой.
Поэтому операции над множествами и отношения между множествами, рассмотренные в главе Ш, можно переносить на геометрические фигуры как на множества точек.
Например, на рисунке 11 изображены всевозможные отношения, в которых могут находиться квадрат и круг:
/ – круг находится в квадрате;
Квадрат находится в круге;
Квадрат и круг пересекаются;
Квадрат и круг не пересекаются.
Предлагая детям располагать квадрат и круг всевозможными способами или нарисовать их и закрашивать общую часть (пересечение) определенным цветом, тем самым помогаем им выявить особенности каждого из отношений, изображенных на рисунке И:
а) все точки круга являются точками -квадрата;
Рис. 11.
б) все точки квадрата являются также точками круга;
в) квадрат и круг имеют общие и необщие точки;
г) у квадрата и круга нет общих точек.
На предматематическом уровне дети знакомятся с простейшими, но наиболее. распространенными геометрическими фигурами: различными линиями, формами блоков – квадратом, кругом, треугольником, а также пятиугольником, шестиугольником.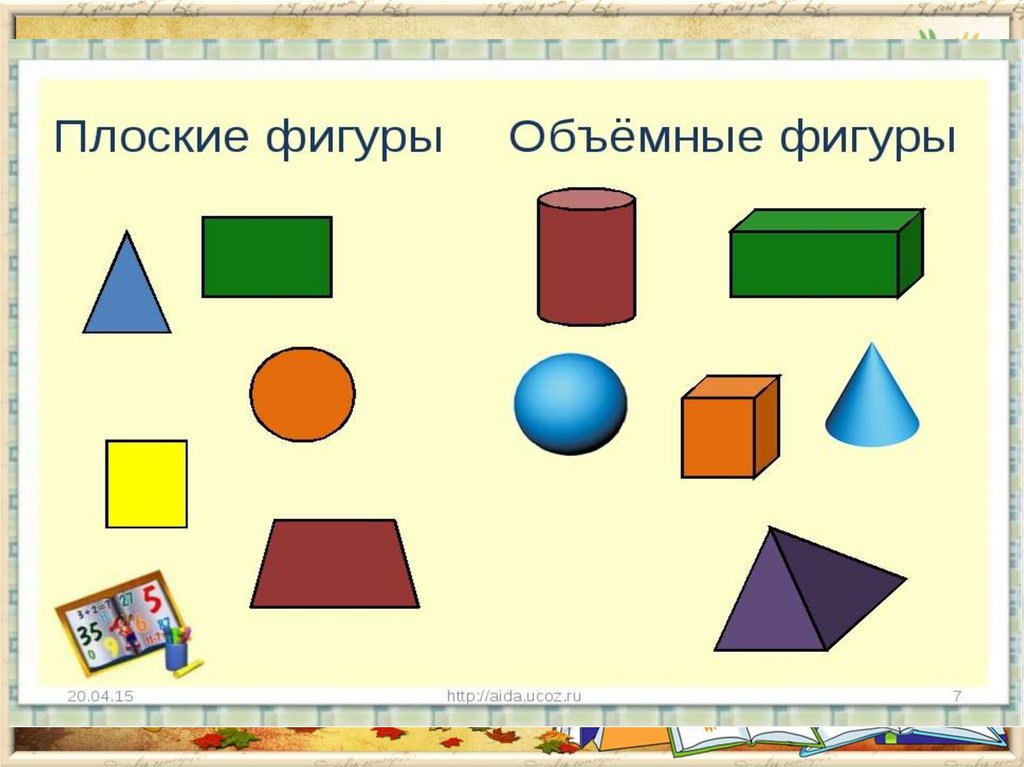 Строгих определений, разумеется, на этом уровне не дается.
Строгих определений, разумеется, на этом уровне не дается.
§ 2. Виды геометрических фигур
Все геометрические фигуры делятся на плоские и пространственные. Так, например, квадрат, круг – плоские фигуры; куб, шар – пространственные. Начнем с рассмотрения линий. Под линией будем иметь в виду плоскую линию -т- линию, все точки которой лежат на некоторой плоскости, а сама линия есть подмножество точек плоскости.
Очевидно, что такие разъяснения, как «длина без ширины» или «граница поверхности», не могут приниматься за точные определения, так как мы не знаем точный смысл терминов «длина», «ширина», «граница», «поверхность» и т. п. По существу в элементарной геометрии понятие линии считается интуитивно ясным и их изучение, сводится к рассмотрению различных примеров: прямая, ломаная, кривая, замкнутая линия, незамкнутая линия, отрезок и др.
Прямую линию, или просто прямую, можно выделить среди других линий с помощью ее характеристических свойств, т. е. таких свойств, которыми обладает только прямая и никакие другие линии.
На рисунке 12 между деревом и домом проложено несколько тропинок. На геометрическом языке это означает: через две точки D и С проходит несколько линий. Прямая выделяется среди них тем, что это – линия кратчайшего расстояния.
| Рис. 13. |
Еще одно характеристическое свойство прямой: через две точки D и С можно провести много различных линий, прямых – только одну, т. е. через две точки проходит одна и только одна
Линии бывают замкнутыми и незамкнутыми. Например, прямая – незамкнутая линия, окружность – замкнутая.
По отношению к прямой две точки могут находиться «по одну сторону» от нее или «по разные стороны». Например, дом и дерево могут находиться по одну сторону от речки и тогда можно дойти от дома до дерева или обратно, не проходя через мост. Если же они находятся по разным сторонам от реки, то дойти от дома до сада или обратно, не проходя через мост, нельзя.
На геометрическом языке эта ситуация описывается следую-
Sf; щим образом.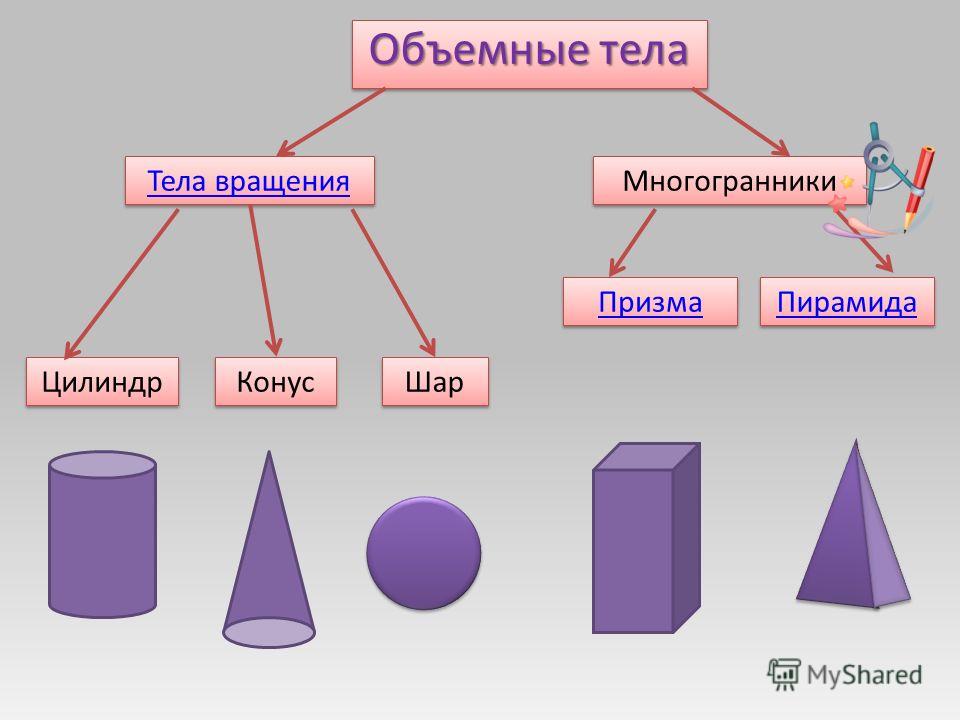 Две точки А к В находятся по одну сторону от
Две точки А к В находятся по одну сторону от
прямой /, если отрезок, соединяющий эти точки, не пересекает
прямую / (рис. 13).
Две точки Л и С (рис. 13) находятся по разные стороны от прямой /, если отрезок Л С, соединяющий эти точки, пересекает
прямую I.
По существу прямая I разбивает множество всех не принадлежащих ей точек плоскости на два класса (два подмножества), называемые п о л уплоскост я м и с границей /. Это разбиение порождается отношением эквивалентности, введенным в множество всех не принадлежащих / точек плоскости следующим образом: две точки находятся в этом отношении, если отрезок, соединяющий их, не пересекает прямую /, и не находятся в этом отношении, если этот отрезок пересекает прямую /.
Дети довольно рано усваивают, что означает «внутри» и «вне» некоторой замкнутой линии. Пример этого – детская игра в классы. Чтобы успешно переходить из класса в класс, нужно, прыгая и бросая биту, точно попадать внутрь определенного класса (квадрата).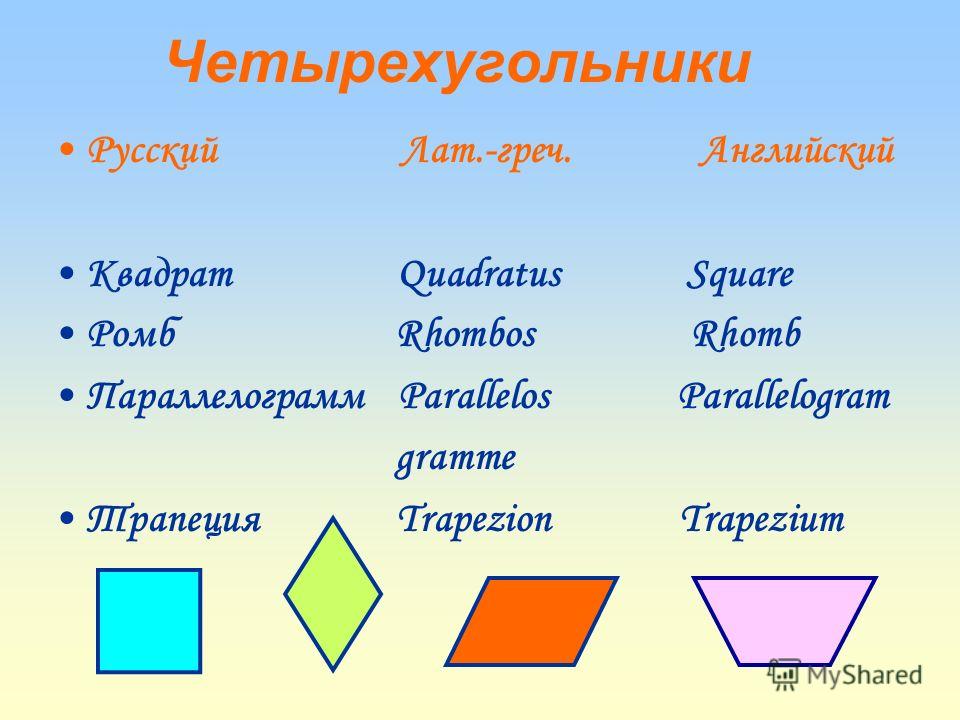 Первые представления о «внутри» и «вне» закрепляются в играх с обручами (глава III), когда дети встречаются со все усложняющимися ситуациями
Первые представления о «внутри» и «вне» закрепляются в играх с обручами (глава III), когда дети встречаются со все усложняющимися ситуациями
определение блоков внутри и вне одного обруча, внутри одного и вне другого обруча, внутри всех трех обручей, внутри двух обручей и вне третьего и т. п. Поэтому перед решением задач, связанных с- классификацией блоков, или фигур в играх с обручами необходимо выяснить, распознают ли дети внутреннюю и внешнюю области по отношению к каждому обручу.
Переведем теперь эти ситуации на язык геометрии. Интуитивно ясно, что всякая окружность разбивает множество всех не принадлежащих ей точек плоскости на две области (рис. 14). Если две точки Л и В или D и Е лежат в одной области, то отрезок, соединяющий их, не пересекает линии /; если две точки, например С и D, принадлежат различным областям, то соединяющий их отрезок пересекает линию / (в точке К)-
Одна из этих областей называется внутренней, другая – внешней.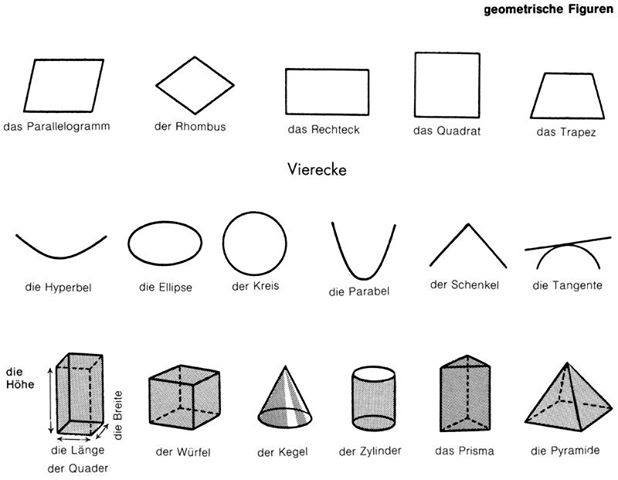 Каким же геометрическим свойством можно охарактеризовать внутреннюю или внешнюю область?
Каким же геометрическим свойством можно охарактеризовать внутреннюю или внешнюю область?
Область, которая интуитивно принимается за внешнюю, обладает следующим свойством: можно найти в этой области две точки, например D и Е, такие, что прямая, проходящая через них, целиком лежит в этой области. Вторая область, которая интуитивно принимается за внутреннюю, не обладает этим свойством или характеризуется свойством, представляющим собой отрицание характеристического свойства внешней области, т. е. нельзя найти в ней такие две точки, чтобы прямая, проходящая через них, лежала целиком в этой области (или, иначе, прямая, проходящая через любые две точки этой области, обязательно пересекает линию /).
Выше мы пользовались понятием «отрезок» и связывали его неизменно с двумя точками: «отрезок АВ», «отрезок, соединяющий точки Л и В» и т. п. Что же такое отрезок? Иногда говорят «часть прямой». Это можно понимать как подмножество точек прямой. Но какое это подмножество?
Иногда пользуются отношением «между», применимым к трем
Рис.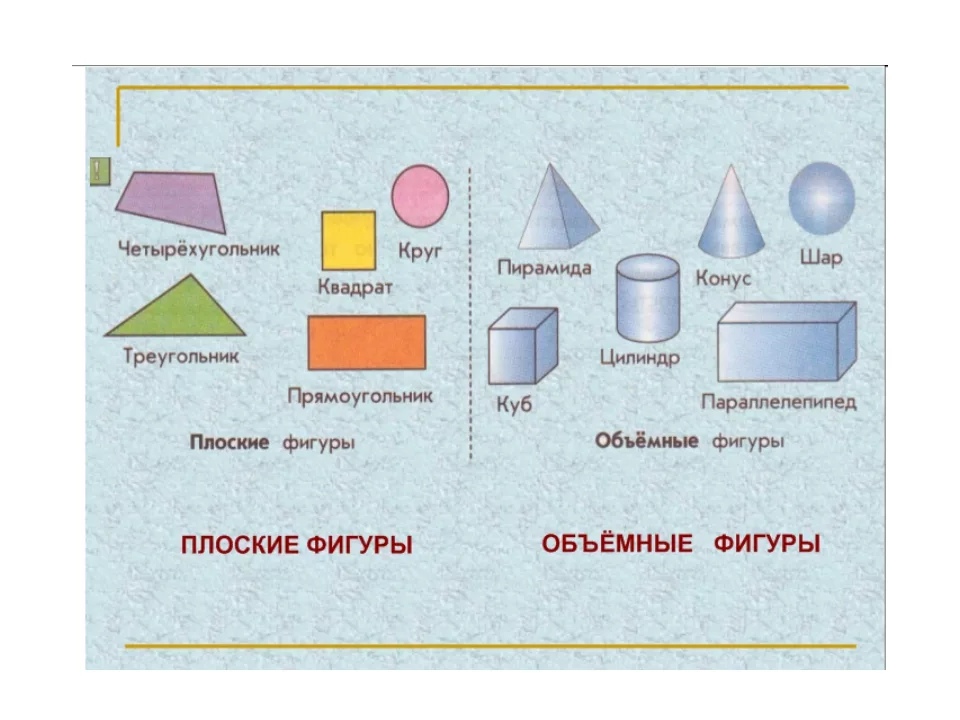 14. 14. |
точкам. Это отношение соответствует наглядному представлению о точке, лежащей на прямой между двумя другими точками: если точка С лежит между точками А и В, то нельзя «дойти» по прямой от Л к В, не пройдя через точку С. Эти наглядные представления подсказывают и некоторые свойства отношения «между»: если точка С лежит между А и В, то С лежит и между В и Л; из трех точек только одна лежит между двумя другими, т. е. если С лежит между Л и В, то уже А
не лежит между С и В, а также В не лежит между А и С.
Имеются две различные трактовки понятия отрезка {ш существу два различных понятия). По одной из них отрезку АВ принадлежат сами точки Л и В (концы отрезка) и все точки прямой АВ, лежащие между А и В. По другой трактовке точки А я В не считаются принадлежащими отрезку АВ, хотя по-прежнему называются его концами (т. е. концы отрезка не принадлежат
Мы будем придерживаться первой трактовки, дидактически
более целесообразной.
Так как через две точки Л и В проходит единственная прямая АВ, то эти две точки определяют и единственный отрезок с
концами Л и В.
Зная, что такое отрезок, можно уточнить и понятие ломаной
Если Ль Л2, Аъ, … ,
Многие люди ошибочно полагают, что впервые они встречают геометрические фигуры в средней школе. Там они изучают их названия, свойства и формулы. Но на самом деле с самого детства любой предмет, который видит ребенок, ощущает, чувствует его запах или взаимодействует с ним любым другим образом, представляет собой именно геометрическую фигуру. Кушетка, на которой лежит только что родившая женщина – прямоугольник, лампа, что дает акушерам свет – круглая фигура, форточки в окне – квадраты. Этот список можно продолжать бесконечно.
Геометрические фигуры, непосредственно как элемент науки, впервые встречается школьникам в средних классах. Можно даже сказать, что геометрия начинается именно с них. Однако, как уже говорилось выше, первые взаимодействия с ними происходят задолго до этого. Возьмем, к примеру, точку. Она представляет собой самую маленькую фигуру в геометрии. Кроме того, ее принято считать основой всех остальных (как атомы в химии). Все треугольники, квадраты и прочие фигуры на любом чертеже состоят из множества точек. Они обладают определенными свойствами, каждое из которых присуще только одной фигуре (ни одна другая не может быть ими наделена).
Возьмем, к примеру, точку. Она представляет собой самую маленькую фигуру в геометрии. Кроме того, ее принято считать основой всех остальных (как атомы в химии). Все треугольники, квадраты и прочие фигуры на любом чертеже состоят из множества точек. Они обладают определенными свойствами, каждое из которых присуще только одной фигуре (ни одна другая не может быть ими наделена).
Можно предположить, что все геометрические фигуры состоят непосредственно из линий, но чем является она? Это и есть множество точек, расположенных в ряд. Их можно продолжать бесконечно, поскольку прямая линия не заканчивается. Если же она ограничена с двух сторон, то ее принято называть отрезком. Если имеется только одно ограничение, то перед вами луч. Следовательно, все плоские фигуры в геометрии состоят из отрезков, так как составляющие имеют и конец, и начало. Стоит отметить, что прямая, которая была разделена точкой, является двумя лучами, направленными в противоположные друг другу стороны.
Не только из плоских элементов состоит геометрия, имеются также и объемные геометрические фигуры. К их изучению в школе приступают позже, ближе к окончанию учебы, но сталкивается с ними человек, опять же, гораздо раньше. К примеру, когда ребенок берет в руки кубик, то держит в ладонях куб. Или, если он смотрит на комод, то перед ним прямоугольный параллелепипед. Все объемные фигуры состоят из плоскостей (то есть, она является неопределенным первичным понятием, как и прямая). Тот же самый параллелепипед состоит из шести таких элементов. Наглядно ознакомиться с плоскостью можно, посмотрев на поверхность любого стола. Но это будет только ее часть, поскольку имеются ограничения. Непосредственно плоскость такая же бесконечная, как и прямая линия.
К их изучению в школе приступают позже, ближе к окончанию учебы, но сталкивается с ними человек, опять же, гораздо раньше. К примеру, когда ребенок берет в руки кубик, то держит в ладонях куб. Или, если он смотрит на комод, то перед ним прямоугольный параллелепипед. Все объемные фигуры состоят из плоскостей (то есть, она является неопределенным первичным понятием, как и прямая). Тот же самый параллелепипед состоит из шести таких элементов. Наглядно ознакомиться с плоскостью можно, посмотрев на поверхность любого стола. Но это будет только ее часть, поскольку имеются ограничения. Непосредственно плоскость такая же бесконечная, как и прямая линия.
Таким образом, нет сферы, где бы не встречались геометрические фигуры. Названия их различны, они определяют свойства и особенности. К примеру, формула не подойдет для прямоугольника или квадрата.
Желательно приобщать ребенка к геометрическим фигурам еще в дошкольном возрасте. Можно сделать их своими руками, а затем выкладывать ими различные рисунки на бумаге (если это плоские элементы).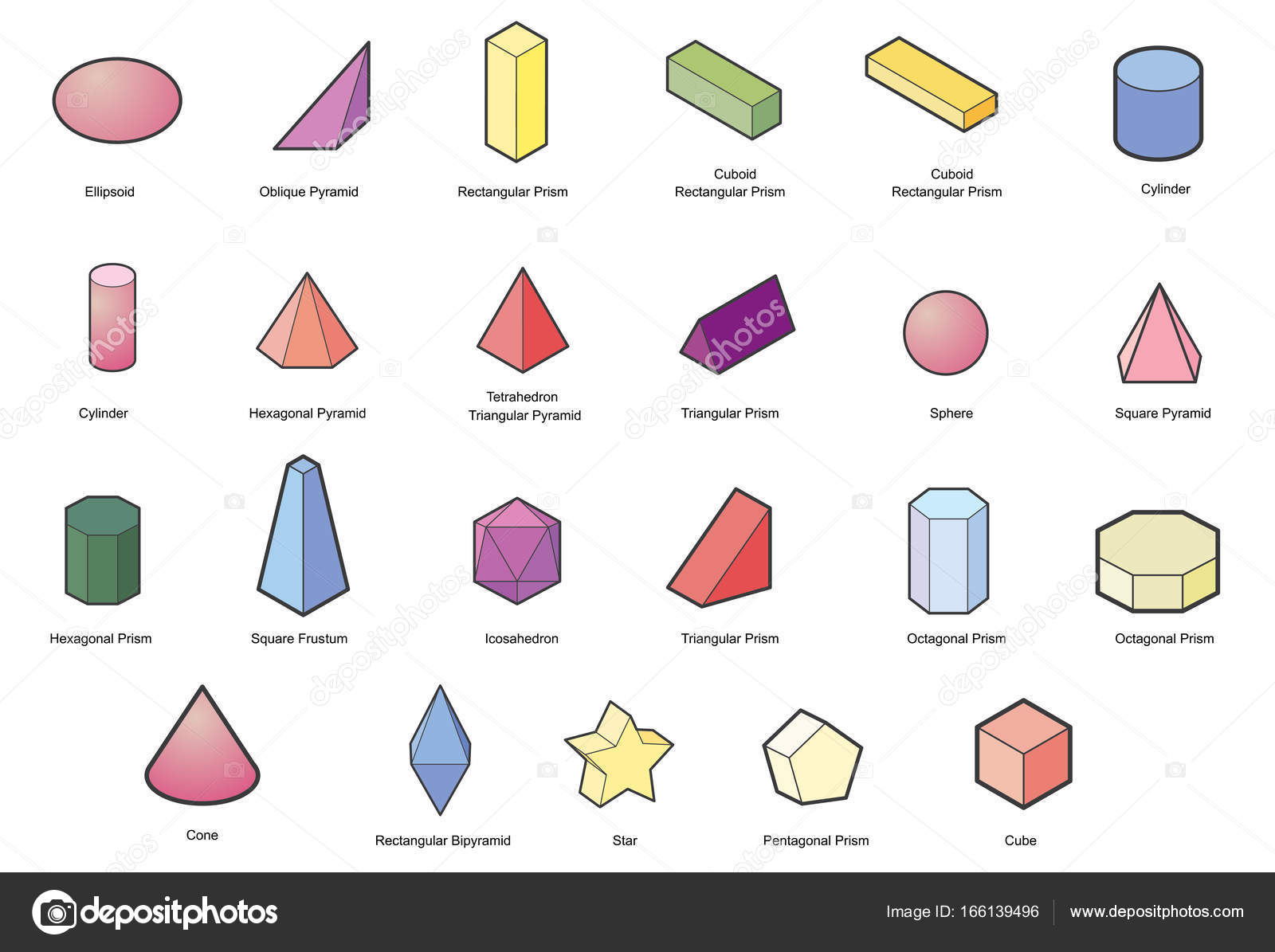 Однако не стоит отказываться и от объемных фигур. В интернете можно найти множество связанных с этим. Но нельзя откладывать знакомство с ними, ведь все, что мы видим – геометрические фигуры. Даже человек состоит из них!
Однако не стоит отказываться и от объемных фигур. В интернете можно найти множество связанных с этим. Но нельзя откладывать знакомство с ними, ведь все, что мы видим – геометрические фигуры. Даже человек состоит из них!
«Геометрические фигуры плоские и объёмные»
Цели урока :
1. Познавательная : создать условия для ознакомления с понятиями плоские и объёмные геометрические фигуры, расширить представление о видах объёмных фигур, научить определять вид фигуры, сравнивать фигуры.
2. Коммуникативная :создать условия для формирования умения работать в парах, группах; воспитание доброжелательного отношения друг к другу; воспитывать у учащихся взаимопомощь , взаимовыручку.
3. Регулятивная : создать условия для формирования планировать учебную задачу, выстраивать последовательность необходимых операций, корректировать свою деятельность.
4. Личностная : создать условия для развития вычислительных навыков, логического мышления, интереса к математике, формирования познавательных интересов, интеллектуальных способностей учащихся, самостоятельность в приобретении новых знаний и практических умений.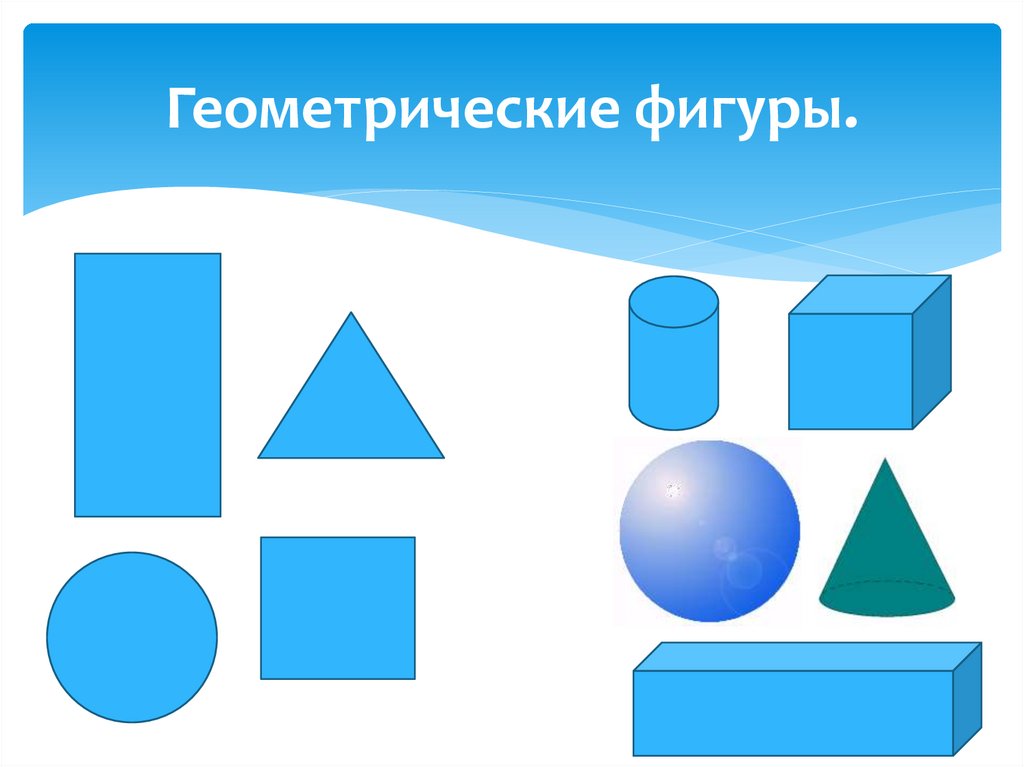
Планируемые результаты:
– личностные:
формирование познавательных интересов, интеллектуальных способностей учащихся; формирование ценностных отношений друг к другу;
самостоятельность в приобретении новых знаний и практических умений;
формирование умений воспринимать, перерабатывать полученную информацию, выделять основное содержание.
– метапредметные:
овладение навыками самостоятельного приобретения новых знаний;
развитие теоретического мышления на основе формирования умений устанавливать факты.
– предметные:
усвоить понятия плоские и объёмные фигуры, научиться сравнивать фигуры, находить плоские и объёмные фигуры в окружающей действительности, научиться работать с развёрткой.
УУД общенаучные :
поиск и выделение необходимой информации;
применение методов информационного поиска, осознанное и произвольное построение речевого высказывания в устной форме.
УУД личностные :
оценивать свои и чужие поступки;
проявление доверия, внимательности, доброжелательности,
умение работать в паре,
выражать положительное отношение к процессу познания.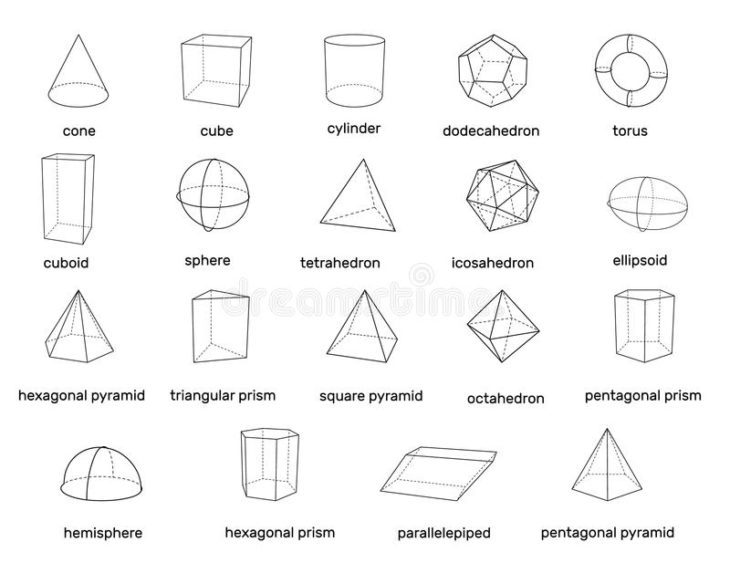
Оборудование : учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники-средства обратной связи, Толковый словарь.
Тип урока : изучение нового материала.
Методы : словесные, исследовательские, наглядные, практические.
Формы работы : фронтальная, групповая, парная, индивидуальная.
1. Организация начала урока.
Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!
2. Актуализация знаний.
1. Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!
Чтобы дойти до цели, надо прежде всего идти.
Перед вами высказывание, прочитайте.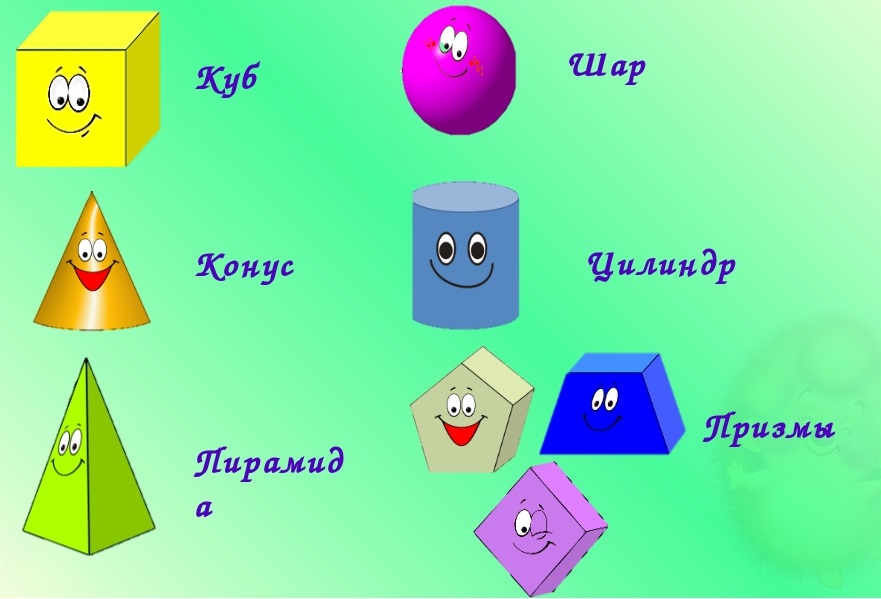 Что означает это высказывание?
Что означает это высказывание?
(Чтобы чего-то добиться, нужно что-то делать)
И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.
Начнем наш путь к достижению цели сегодняшнего урока.
3. Подготовительная работа.
Посмотрите на экран. Что вы видите? (Геометрические фигуры)
Назовите эти фигуры.
Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)
У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.
По какому признаку вы разделили эти фигуры?
· Плоские и объемные фигуры
· По основаниям объемных фигур
С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?
Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры. )
)
Чему мы должны научиться на уроке?
V. «Открытие» нового знания в практической исследовательской работе.
(Учитель показывает куб и квадрат.)
Чем они похожи?
Можно ли сказать, что это одно и тоже?
Чем же отличается куб от квадрата?
Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)
Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?
! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности?
(Плоской фигурой.)
Можно ли куб полностью (весь) прижать к парте? Проверим.
Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?
! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)
ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.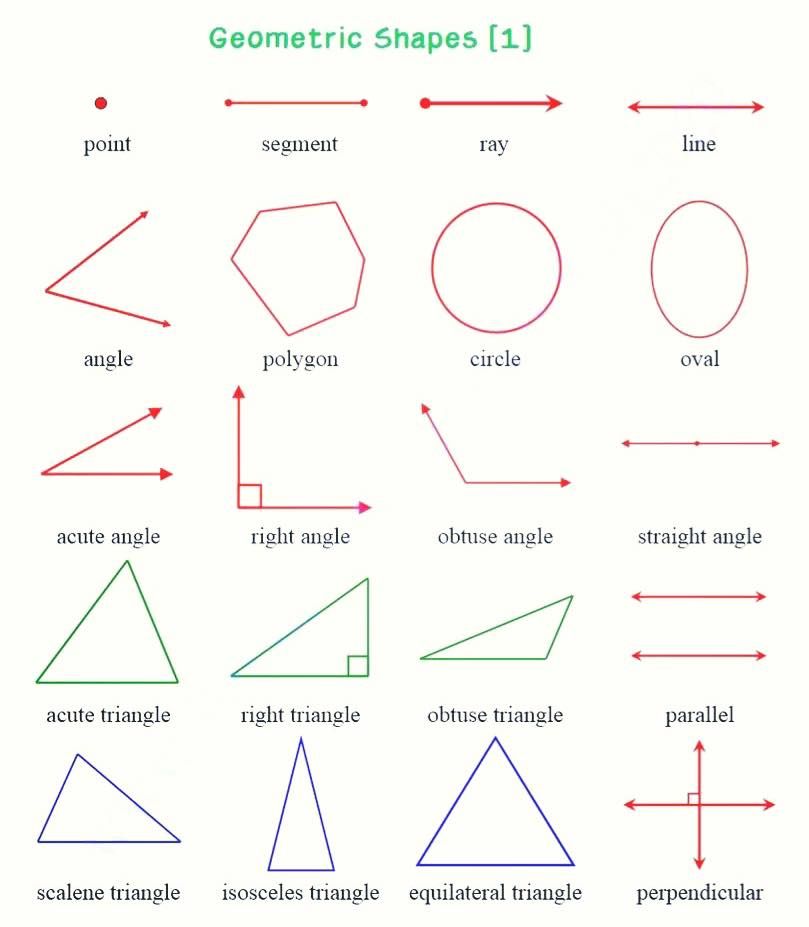 )
)
ПЛОСКИЕ ОБЪЁМНЫЕ
Можно целиком расположить Занимают определённое пространство,
на одной плоской поверхности. возвышаются над плоской поверхностью.
Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.
4.Открытие новых знаний.
1. Назовите фигуры, изображенные на рисунке.
Какую форму имеют основания этих фигур?
Какие еще формы можно увидеть на поверхности куба и призмы?
2. Фигуры и линии на поверхности объемных фигур имеют свои названия.
Предложите свои названия.
Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.
Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.
Работа с тетрадями: чтение нового материала
Соотнесение реальных объектов и объёмных тел.
А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.
Коробка – параллелепипед.
Яблоко – шар.
Пирамидка – пирамида.
Банка – цилиндр.
Горшок из-под цветка – конус.
Колпачок – конус.
Ваза – цилиндр.
Мяч – шар.
5. Физминутка.
6. 1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.
(Ученики «обхватывают» руками и гладят воображаемый шар.)
А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.
Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.
Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!
7. Групповая работа :
(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед. Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку. )
)
Группа 1. (Для изучения параллелепипеда)
Группа 2. (Для изучения пирамиды)
Группа 3. (Для изучения куба)
8. Решение кроссворда
9. Итог урока. Рефлексия деятельности.
Решение кроссворда в презентации
Что нового вы для себя сегодня открыли?
Все геометрические фигуры можно разделить на объёмные и плоские.
А я узнал названия объёмных фигур
Основные геометрические фигуры
Каждый из нас — и взрослый, и ребенок — замечал, как много геометрических фигур существует вокруг нас. Мы встречаемся с ними везде, во всех окружающих нас предметах. Где же встречаются геометрические фигуры в нашей жизни?
Где встречаются геометрические фигуры в нашей жизни?
Каждый из нас — и взрослый, и ребенок — замечал, как много геометрических фигур существует вокруг нас. Мы встречаемся с ними везде, во всех окружающих нас предметах.
Люди давно заинтересовались разнообразием геометрических фигур.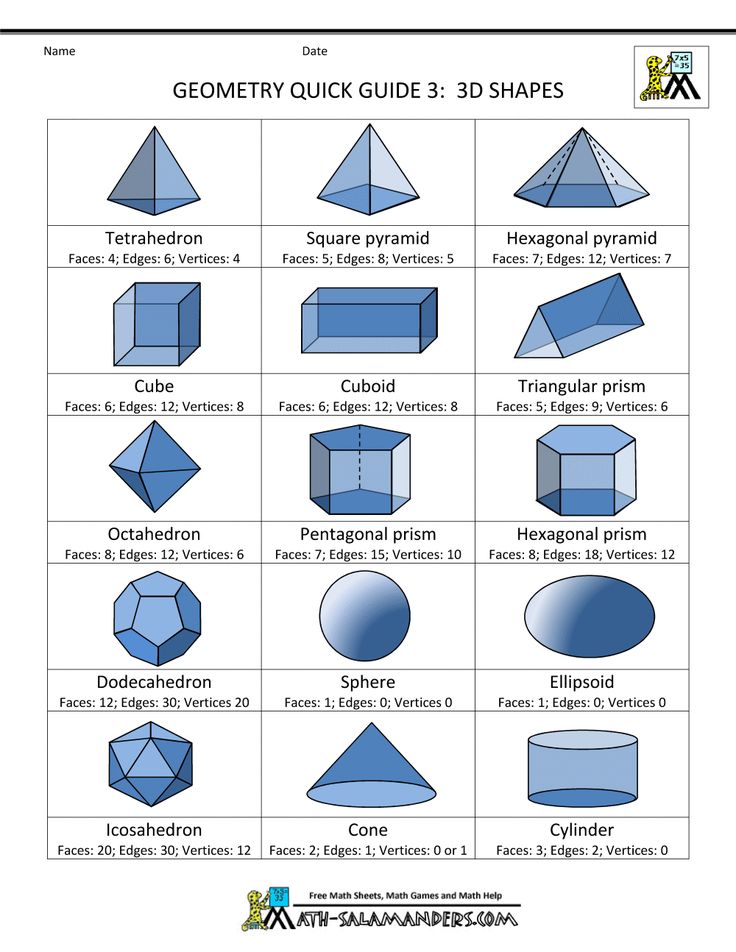 Ещё для первобытных людей важную роль играла форма окружавших их предметов. Овладевая миром, люди знакомились с простейшими геометрическими формами. Сначала они изготавливали орудия труда относительно правильной формы, потом научились их совершенствовать. Специальных названий для геометрических фигур тогда, конечно, не было. Их придумали значительно позже. Когда люди стали строить дома, им пришлось ещё глубже разбираться в особенностях разных фигур, чтобы понять, какую форму следует придавать стенам и крыше, какой формы должны быть брёвна или каменные глыбы. Сам того не зная, человек всё время занимался изучением фигур: женщины, изготавливая одежду, охотники — наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.
Ещё для первобытных людей важную роль играла форма окружавших их предметов. Овладевая миром, люди знакомились с простейшими геометрическими формами. Сначала они изготавливали орудия труда относительно правильной формы, потом научились их совершенствовать. Специальных названий для геометрических фигур тогда, конечно, не было. Их придумали значительно позже. Когда люди стали строить дома, им пришлось ещё глубже разбираться в особенностях разных фигур, чтобы понять, какую форму следует придавать стенам и крыше, какой формы должны быть брёвна или каменные глыбы. Сам того не зная, человек всё время занимался изучением фигур: женщины, изготавливая одежду, охотники — наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.
И в современном мире без этих знаний не прожить.
Где же встречаются геометрические фигуры в нашей жизни?
Возможно, кто-то считает, что различные линии фигуры «водятся» только в книгах учёных математиков. Однако, если посмотреть вокруг, становится понятно, что многие предметы имеют форму, похожую на основные геометрические фигуры. Просто мы не всегда это замечаем. Немало замечательных геометрических фигур встречается в окружающей нас природе. Поле имеет форму прямоугольника, река — кривой линии, озеро — круга, кристалл соли — форму куба, обычная горошинка, капелька росы — форму шара. Красивы и разнообразны многогранники — кристаллы горного хрусталя. Но и в привычной жизни основные геометрические фигуры тоже повсюду. Это здания, строения, транспорт, интерьер квартиры, даже посуда и предметы одежды. К примеру, женская юбка — это трапеция, тарелка — круг, дом — квадрат и треугольник, а в трубе — цилиндр.
Однако, если посмотреть вокруг, становится понятно, что многие предметы имеют форму, похожую на основные геометрические фигуры. Просто мы не всегда это замечаем. Немало замечательных геометрических фигур встречается в окружающей нас природе. Поле имеет форму прямоугольника, река — кривой линии, озеро — круга, кристалл соли — форму куба, обычная горошинка, капелька росы — форму шара. Красивы и разнообразны многогранники — кристаллы горного хрусталя. Но и в привычной жизни основные геометрические фигуры тоже повсюду. Это здания, строения, транспорт, интерьер квартиры, даже посуда и предметы одежды. К примеру, женская юбка — это трапеция, тарелка — круг, дом — квадрат и треугольник, а в трубе — цилиндр.
Знать все фигуры, их виды, названия и свойства очень важно. Систематизирует знания о геометрических фигурах и изучает их свойства математическая наука — геометрия. Наука эта очень важная, её применение просто бесценно во все времена и независимо от профессии. Без знаний геометрии не обходится ни рабочий, ни инженер, ни архитектор, ни художник.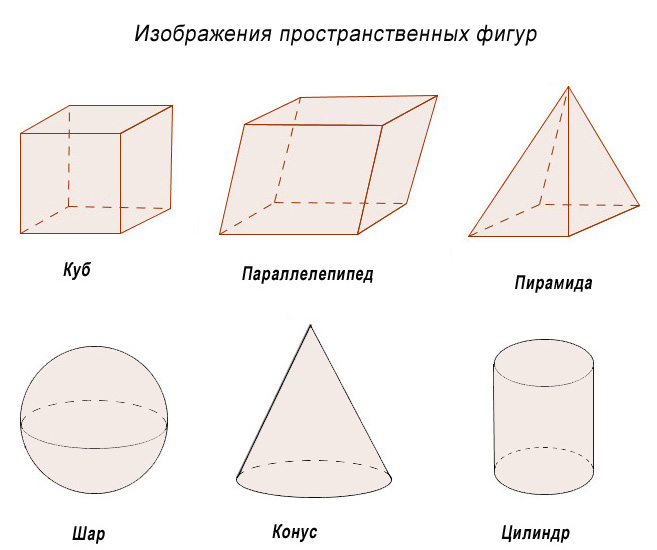 И очень важно начать осваивать эту науку в раннем возрасте.
И очень важно начать осваивать эту науку в раннем возрасте.
Прекрасным помощником ребёнку в этом станет образовательная платформа с умными тренажёрами iSmart. Основные виды геометрических фигур, их свойства, задачи на нахождение площади фигур и многое другое есть на платформе в разделе «Математика» https://www.ismart.org/zanyatiya/matematika. Тут собраны несколько тысяч заданий на освоение этих тем, не повторяющиеся при многократной отработке. Занимаясь на интерактивном онлайн-тренажёре iSmart.org, школьники начальных классов досконально разберутся в основах геометрии, это даст им хорошую базу по предмету для учёбы в средних и старших классах. Кроме того, интерактивные задания красочные, интересные, увлекательные.
Итак,
Простейшие виды фигур
Две основные фигуры — это точка и линия. Скопление точек и линий образует различные геометрические фигуры. Каждая из них индивидуальна, отличается своими параметрами, их формы очень разнообразны. Фигуры бывают простыми и сложными, плоскими и объёмными.
Точка
Точка — это самый минимальный, но в то же время самый главный объект в геометрии. Это самая малая геометрическая фигура, но именно она необходима для построения других фигур на плоскости и является основой для всех других фигур. Она не содержит таких свойств, как длина, высота, объём, площадь, не имеет измерительных особенностей и характеристик. Важно только то, где она расположена. Обозначается точка заглавной буквой латинского алфавита либо числом. Например, A, B, C или 1, 2, 3.
Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.
Самыми простейшими фигурами являются луч и отрезок.
- Луч — часть прямой, у которой есть начальная точка, но нет конца. Это продолжение в одну сторону.
- Отрезок — составная часть прямой, которая ограничена двумя точками. Он имеет начало и конец, поэтому измеряется. Длину отрезка можно определить, измерив расстояние между его концами.

Линия
Линия образуется из множества точек, последовательно расположенных друг за другом и соединённых между собой. Линии бывают замкнутыми и разомкнутыми, прямыми и кривыми, а также ломаными.
- Замкнутая — когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.
- Разомкнутая — когда начало и окончание линии не соединены.
- Прямая — непрерывная линия без изменений.
- Кривая — отличная от прямой линии.
- Ломаная — когда соединены отрезки не под углом 180 градусов.
Через одну точку можно провести бесконечное число линий, а через две — только одну прямую и множество кривых.
Основные геометрические фигуры
Соединённые между собой точки образуют линии, а соединённые между собой линии — основные геометрические фигуры на плоскости.
Геометрические фигуры бывают плоские или двухмерные (2D) и объёмные пространственные, или трёхмерные (3D).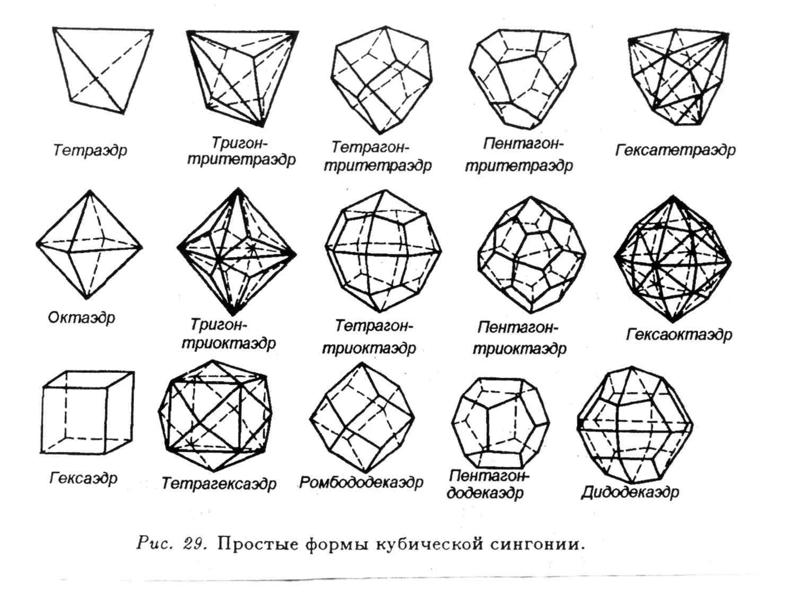 Они ограничены замкнутой поверхностью своей наружной границы.
Они ограничены замкнутой поверхностью своей наружной границы.
Если все точки фигуры находятся в одной плоскости, значит, она является плоской. Плоские фигуры, которые знают все: точка, квадрат, прямоугольник, треугольник, круг, полукруг, окружность, овал, ромб, трапеция.
А если у геометрической фигуры все точки не находятся в одной плоскости, то она объёмная. К ним относятся шар, конус, цилиндр, сфера, пирамида и др.
Разберём плоские фигуры.
Треугольник
Треугольник — это фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки называются вершинами, а отрезки — сторонами.
Есть три вида треугольников:
- Прямоугольный — когда один угол прямой, другие два меньше 90 градусов.
- Остроугольный — когда градус его углов больше 0, но меньше 90 градусов.
- Тупоугольный — когда один угол тупой, то есть больше 90 градусов, а два других — острые.

Треугольники имеют следующие свойства:
- в треугольнике напротив большего угла лежит большая сторона и наоборот;
- сумма углов треугольника всегда равна 180 градусам;
- все углы равностороннего треугольника равны 60 градусам;
- в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (но это изучается уже в старших классах).
Вершины треугольников обозначаются заглавными буквами латинского алфавита: A, B, C и др.
Примеры треугольников:
Окружность
Окружность — геометрическая фигура, образованная замкнутой кривой линией, все точки которой находятся на одинаковом от центра расстоянии.
Круг
Часть плоскости, находящаяся внутри окружности, называется кругом. То есть, окружность — это граница круга. А расстояние от центра окружности до любой точки на ней называется радиусом. Диаметр круга — это отрезок, который соединяет две точки на окружности и проходит через её центр.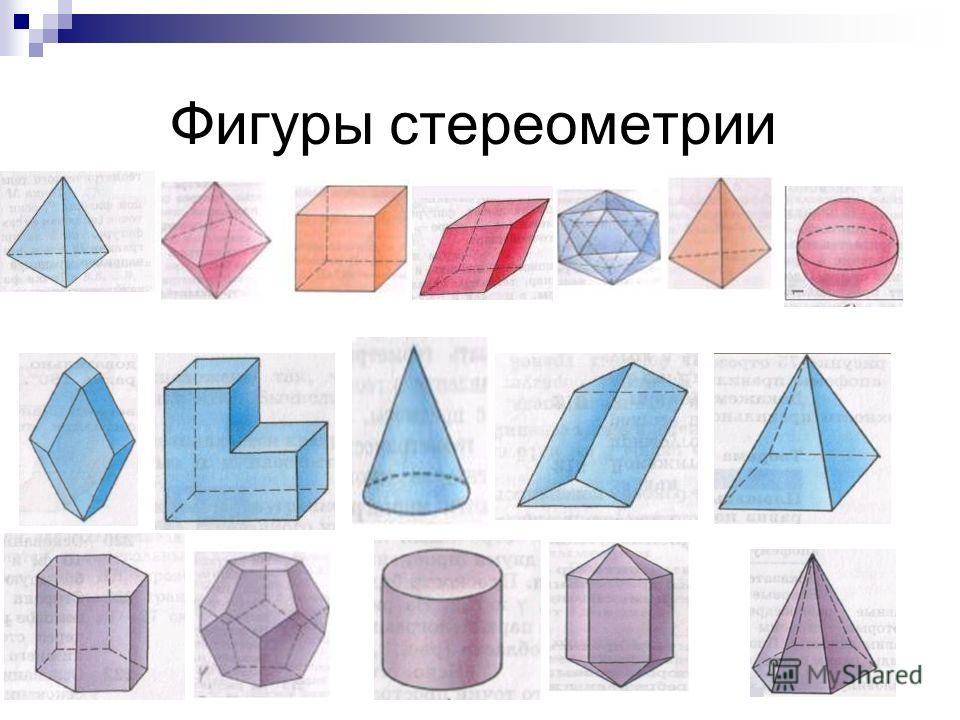 Диаметр круга равен двум его радиусам.
Диаметр круга равен двум его радиусам.
Прямоугольник
Прямоугольник — это фигура, состоящая из четырёх сторон и четырёх прямых углов, у которой:
- противоположные стороны равны между собой;
- диагонали равны и делятся в точке пересечения пополам;
- около прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагоналей.
Квадрат
Квадрат — это тот же прямоугольник, у которого:
- все стороны равны;
- все углы равны и составляют 90 градусов;
- диагонали равны и перпендикулярны;
- центры вписанной и описанной окружности совпадают и находятся в точке пересечения его диагоналей.
Трапеция
Четырёхугольник, у которого две стороны параллельны, а две — нет, называется трапецией. Если сумма длин оснований трапеции равна сумме длин боковых сторон, в неё можно вписать окружность.
Параллелограмм и ромб
Параллелограмм — четырёхугольник, противоположные стороны которого попарно параллельны.
Ромб — это параллелограмм с равными сторонами.
Параллелограмм имеет следующие свойства:
- противоположные стороны и углы равны;
- сумма двух любых соседних углов равна 180 градусам;
- диагонали пересекаются и точкой пересечения делятся пополам;
- каждая диагональ делит фигуру на два равных треугольника.
Основные величины и их формулы
Все геометрические фигуры имеют свои характеристики и собственную величину. Самыми распространёнными являются такие величины как площадь и периметр. Они используются в повседневной жизни, в строительстве и в других областях. Например, во время ремонта или нового строительства, количество необходимых материалов и объём работ не определить, не вычислив заранее площадь и периметр.
Периметр
Периметром называется замкнутая граница плоской геометрической фигуры, которая отделяет её внутреннюю область от внешней. Периметр есть у любой замкнутой геометрической фигуры:
Периметр есть у любой замкнутой геометрической фигуры:
На рисунке периметры выделены красной линией. Периметр окружности часто называют длиной.
Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.
Обозначается заглавной латинской P.
Площадь
Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой, то есть та часть плоскости, которая находится внутри периметра. Именно она даёт нам основную информацию о её размере. Любая плоская замкнутая геометрическая фигура имеет определённую площадь.
На рисунке площади фигур окрашены различными цветами.
Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм2, см2, м2, км2 и т. д. S (square) — знак площади.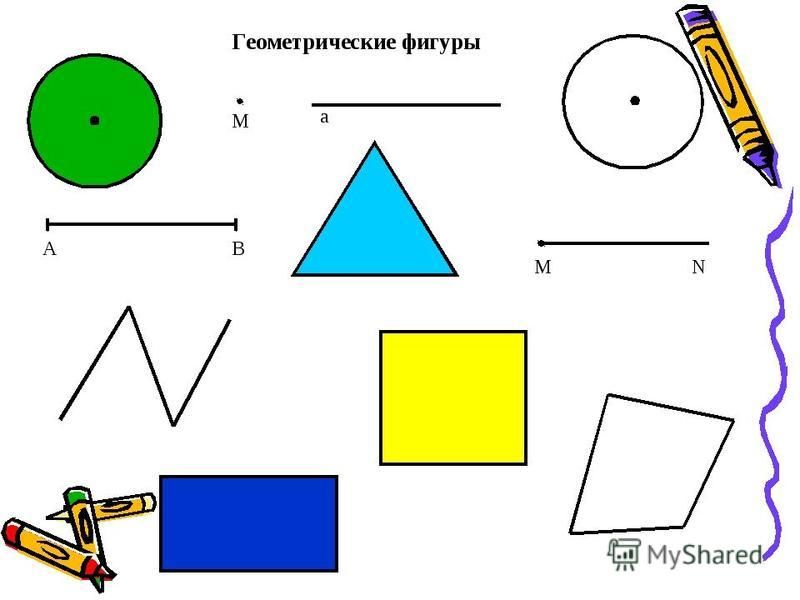
Вычисление периметра и площади
Периметр — это длина замкнутого контура геометрической фигуры. Можно, конечно, измерить линейкой длины всех сторон и сложить их. Но лучше
воспользоваться специальными формулами для вычисления периметра, это значительно упростит задачу.
- Квадрат: периметр = 4 * сторона.
- Треугольник: периметр = сторона 1 + сторона 2 + сторона 3.
- Неправильный многоугольник: периметр = сумме всех сторон многоугольника.
- Круг: длина окружности = 2 * π * радиус = π * диаметр (где π – это число пи (константа, примерно равная 3,14), радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности, диаметр – это длина отрезка, проходящего через центр окружности и соединяющего любые две точки, лежащие на этой окружности).
Для вычисления площади фигуры также потребуется соответствующая формула. К разным фигурам применяются разные формулы. Для вычисления площади стандартных геометрических фигур можно воспользоваться следующими формулами:
- Параллелограмм: площадь = основание * высота
- Квадрат: площадь = сторона 1 * сторона 2
- Треугольник: площадь = ½ * основание * высота
- Круг: площадь = π * радиус² (где радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности.
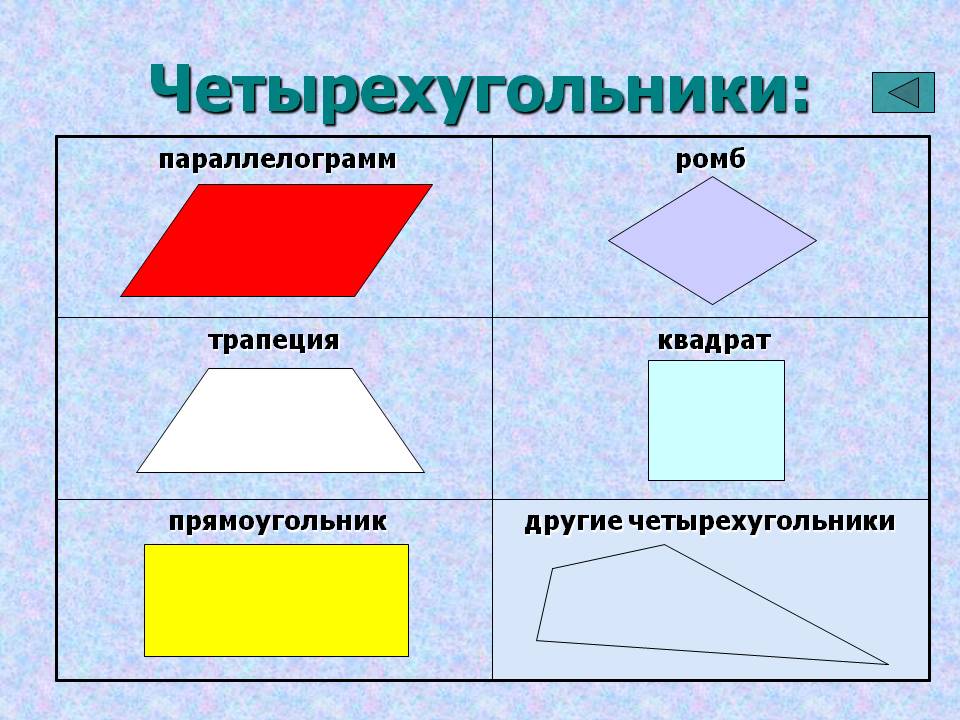 Квадрат радиуса – это значение радиуса, умноженное само на себя).
Квадрат радиуса – это значение радиуса, умноженное само на себя).
Итак, мы перечислили основные и самые распространённые геометрические фигуры и их свойства. Образовательная платформа с умными тренажёрами iSmart поможет вам познакомить своего ребёнка с этими и другими понятиями, погрузиться в мир математики и это будет не только нетрудно, но и очень увлекательно.
Здесь на тренажёре ваш ребёнок изучит основные геометрические фигуры, их виды, названия и свойства с помощью увлекательных заданий. Преимущества занятий на умных тренажёрах iSmart:
- интерактивные задания больше похожи на игру;
- их можно отрабатывать многократно и они не будут повторяться;
- система предлагает индивидуальный план обучения, сформированный на основе диагностики знаний;
- достаточно всего 20 минут занятий в день, чтобы в короткий срок увидеть прогресс в обучении.
Кроме того, занятия помогут вам освободить своё время, ведь ребёнок сможет заниматься самостоятельно, а родитель — получать отчёты и наблюдать за динамикой обучения. Метод обучения iSmart основан на последних научных практиках: микрообучение с поведенческим анализом.
Метод обучения iSmart основан на последних научных практиках: микрообучение с поведенческим анализом.
Образовательная платформа с умными тренажёрами iSmart предлагает программы подготовки по другим школьным предметам, пакеты заданий для подготовки к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.
Геометрические игры для первоклассников онлайн
Обзор: Элементарное обучение геометрии
Математическое мышление закладывается у детей задолго до того, как его учат в школе. Люди находят формы, рисунки и узоры привлекательными с самого детства. Это наблюдение подкрепляется, если давать детям игрушки, цветные картинки и фигуры. Младенцы очаровываются этими предметами еще до того, как они хватают их или манипулируют ими. Позже эти манипуляции дают им практические навыки для развития математических навыков. Эти объекты и конструкции составляют основу математической геометрии.
Основные математические стандарты геометрии включают понимание форм. Дети способны распознавать и ценить геометрические фигуры вокруг себя. Они развивают навыки решения геометрических задач и рассуждения. Они применяют геометрическое мышление в других областях математики. Например, они измеряют площадь и периметр прямоугольника. Они учатся применять формулу площади треугольника. Они также создают геометрические узоры.
Дети способны распознавать и ценить геометрические фигуры вокруг себя. Они развивают навыки решения геометрических задач и рассуждения. Они применяют геометрическое мышление в других областях математики. Например, они измеряют площадь и периметр прямоугольника. Они учатся применять формулу площади треугольника. Они также создают геометрические узоры.
Прогресс по геометрии с оценками
Детский сад: В детском саду дети учатся определять и описывать двух- и трехмерные фигуры. Они способны идентифицировать геометрические фигуры и названия независимо от их ориентации. Они анализируют и сравнивают формы разных размеров и атрибутов. Они также учатся составлять простые фигуры, чтобы формировать более крупные фигуры.
1 класс: В этом классе дети развивают навыки мышления с помощью форм и атрибутов. Они понимают определение основных геометрических фигур. Они анализируют формы по их определяющим атрибутам, таким как количество сторон. Они составляют двухмерные и трехмерные формы для создания более крупных составных фигур.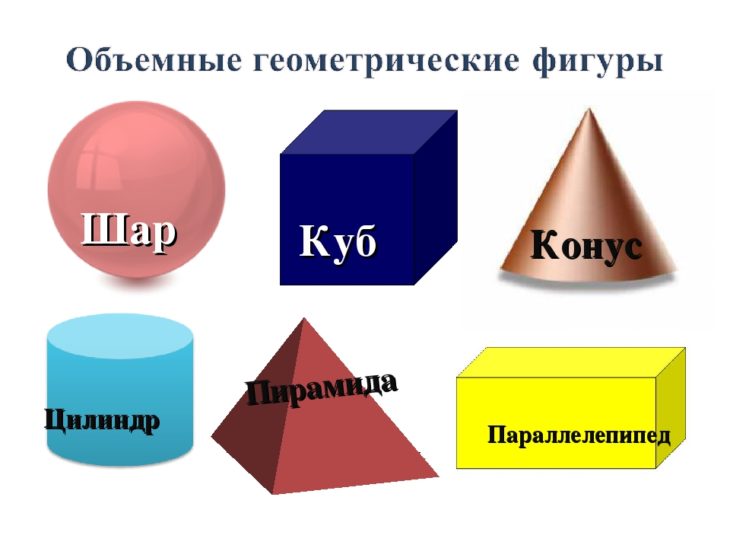 Они учатся делить прямоугольники и окружности на равные доли. Они изучают словарный запас, связанный с такими делениями, как четверти, четверти и половинки.
Они учатся делить прямоугольники и окружности на равные доли. Они изучают словарный запас, связанный с такими делениями, как четверти, четверти и половинки.
2 класс: Дети учатся определять и рисовать фигуры в соответствии с заданными признаками. Они учатся рисовать фигуры в соответствии с указанным количеством граней или углов геометрии. Они способны идентифицировать кубы, пятиугольники, шестиугольники, четырехугольники и треугольники. Они также учатся разбивать прямоугольник на квадраты одинакового размера. Затем они считают эти квадраты, чтобы определить размер прямоугольника. Дети учатся делить прямоугольники и круги на две-четыре равные части. Они описывают разделенные фигуры, используя такие слова, как половина, треть, третьи, половинки. Они понимают целое как четыре четверти, три трети и две половины.
3 класс: Дети понимают отношения между формами в соответствии с их атрибутами. Они узнают о более крупных формах категорий с общими атрибутами. Например, фигуры с четырьмя сторонами называются четырехугольниками. Они делят фигуры на равные части. Они учатся выражать площадь каждой части как единицу доли целого. Например, они делят фигуру на три равные части и описывают площадь каждой части как 1/3 площади целого.
Например, фигуры с четырьмя сторонами называются четырехугольниками. Они делят фигуры на равные части. Они учатся выражать площадь каждой части как единицу доли целого. Например, они делят фигуру на три равные части и описывают площадь каждой части как 1/3 площади целого.
4 класс: Дети узнают о точках, отрезках, прямых, лучах и типах углов. Дети определяют их в двухмерных фигурах. Они также узнают о параллельных и перпендикулярных линиях. Они классифицируют фигуры на основе параллельных или перпендикулярных линий. Они также классифицируют фигуры в соответствии с углами заданного размера. Кроме того, они узнают о различных треугольниках в геометрии. Дети также узнают о линии симметрии двухмерной фигуры. Они рисуют линии симметрии и определяют линейно-симметричные фигуры.
5 класс: Дети знакомятся с координатной геометрией. Они учатся отображать точки в системе координат, состоящей из перпендикулярных числовых линий, называемых осями. Они представляют математические задачи, изображая точки на геометрической плоскости.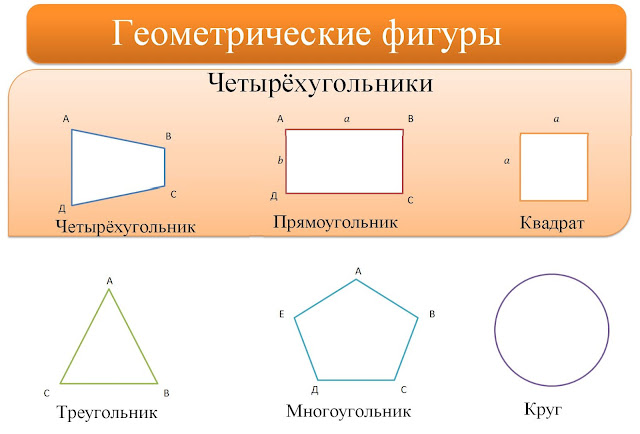 Они также учатся классифицировать простые геометрические фигуры по категориям и подкатегориям на основе геометрических свойств. Например, все квадраты и прямоугольники являются четырехугольниками. Все квадраты являются прямоугольниками. Они учатся классифицировать двумерные фигуры в иерархии.
Они также учатся классифицировать простые геометрические фигуры по категориям и подкатегориям на основе геометрических свойств. Например, все квадраты и прямоугольники являются четырехугольниками. Все квадраты являются прямоугольниками. Они учатся классифицировать двумерные фигуры в иерархии.
Обзор геометрии для 1 класса
В детском саду дети узнали о круге, квадрате, прямоугольнике, шестиугольнике и треугольнике. Они расширяют свой словарный запас, включая ромб и трапецию в 1 классе. Наряду со сферой, кубом и цилиндром, изученными в детском саду, дети узнают о прямоугольной призме и конусе.
- Определение фигур: В 1 классе дети учатся определять конкретные примеры двумерных и трехмерных фигур. Они способны идентифицировать формы любой формы и ориентации. Они связывают трехмерные геометрические фигуры с примерами из реальной жизни. Например, они связывают металлическую банку с цилиндром.
Дети узнают об атрибутах термина.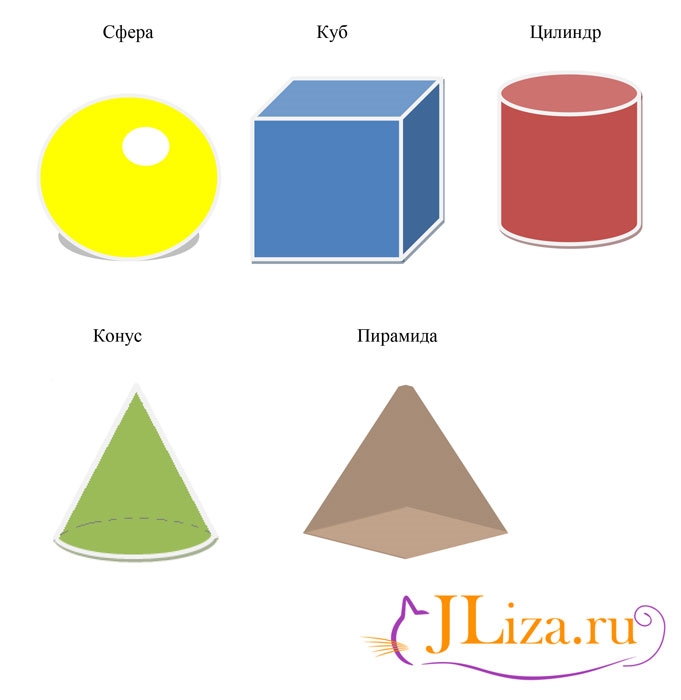 Они способны идентифицировать определяющие атрибуты формы. Этому понятию лучше всего обучают с помощью интерактивных занятий. Например, детей можно попросить составить из соломинок треугольник. Благодаря этому занятию они запомнят треугольник как трехстороннюю форму. Они описали бы треугольник как фигуру с тремя углами.
Они способны идентифицировать определяющие атрибуты формы. Этому понятию лучше всего обучают с помощью интерактивных занятий. Например, детей можно попросить составить из соломинок треугольник. Благодаря этому занятию они запомнят треугольник как трехстороннюю форму. Они описали бы треугольник как фигуру с тремя углами.
- Распознавание нетрадиционных форм: Дети применяют базовые знания геометрии, чтобы распознавать формы. Например, ребенку может показаться, что фигура внизу выглядит странно. Но так как это близкая трехсторонняя фигура, то признают ее треугольником.
Иногда дети неправильно определяют эти фигуры. Например, они заставляют думать, что следующие фигуры являются прямоугольниками.
- Описать фигуры: Дети учатся описывать геометрические свойства двухмерных фигур. На этом этапе они могут не полностью описать форму. Но постепенно у них развивается понимание геометрических терминов.
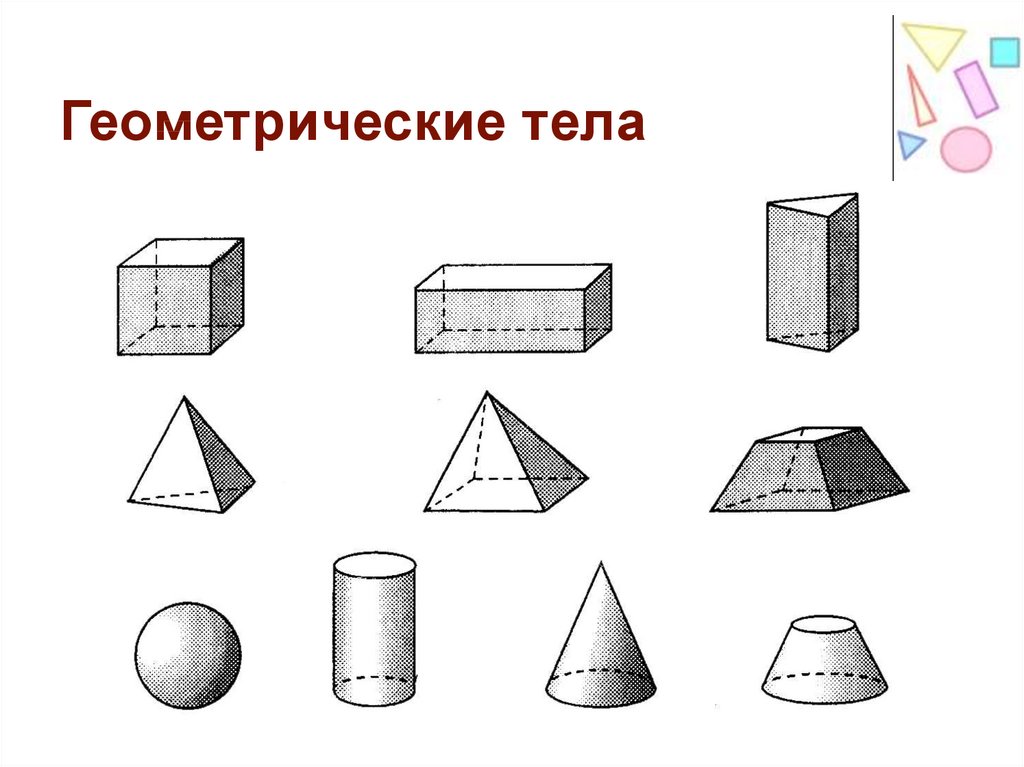 Они понимают такие термины, как грани, края и углы. Они способны описывать важные атрибуты форм. Например, они описывают «треугольник имеет три стороны».
Они понимают такие термины, как грани, края и углы. Они способны описывать важные атрибуты форм. Например, они описывают «треугольник имеет три стороны».
- Составление фигур: Дети используют свои знания об атрибутах фигур, чтобы составлять составные фигуры большего размера. Они делают составные формы, такие как трапеции, шестиугольники из треугольников, квадратов и прямоугольников. Дети узнают, что одну и ту же составную фигуру можно составить из разных фигур. Например, прямоугольник можно составить из нескольких квадратов. Шестиугольник можно создать из двух трапеций или шести треугольников.
- Разложить фигуры: Дети находят скрытые фигуры внутри большой составной фигуры. Они используют танграмы, чтобы исследовать способы формирования новых фигур из составных фигур. Они также определяют, что новая форма может быть сформирована из составной формы.
- Фигуры-перегородки: Дети узнают, что некоторые фигуры состоят из одинаковых и непересекающихся частей.
 Они учатся разбивать фигуры, такие как прямоугольник и круг, на части. Они идентифицируют эти разделы как половинки и четверти. Дети сортируют фигуры, которые можно разделить на равные части, и фигуры, которые нельзя разделить. Они изучают такие термины, как половина, четверть и четверть. Они также узнают о терминах четверть круга и полукруг, которые названы так из-за их размера.
Они учатся разбивать фигуры, такие как прямоугольник и круг, на части. Они идентифицируют эти разделы как половинки и четверти. Дети сортируют фигуры, которые можно разделить на равные части, и фигуры, которые нельзя разделить. Они изучают такие термины, как половина, четверть и четверть. Они также узнают о терминах четверть круга и полукруг, которые названы так из-за их размера.
Манипуляции для изучения геометрии в 1 классе
Геометрические понятия можно изучать несколькими способами. Геометрическое обучение можно проводить с помощью манипуляций, конкретных объектов, иллюстраций и диаграмм. Для эффективного понимания у детей должна быть возможность манипулировать твердыми моделями. Изучение геометрии не должно основываться только на картинках и диаграммах. Обучение должно поощрять детей представлять свои собственные математические идеи. Это можно сделать с помощью картинок и конкретных моделей.
Некоторые эффективные манипуляции, используемые для изучения геометрии в 1 классе:
- Геометрические тела: Детям легче изучать 2D-формы, чем 3D-геометрические фигуры.
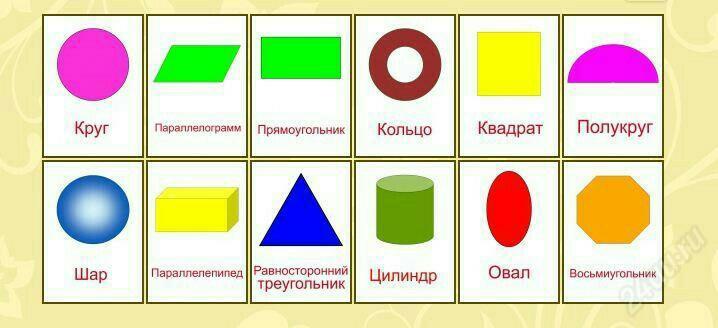 Одна из причин этого заключается в том, что имена трехмерных фигур реже используются в повседневной жизни. Другая причина заключается в том, что в большинстве занятий в классе трехмерные геометрические формы преподаются с помощью рисунков. К сожалению, многие дети не могут понять эти 3D-рисунки. Рисунок сферы выглядит как круг. Это затрудняет понимание разницы между сферой и кругом. Поэтому для обучения детей геометрическим фигурам в 3D отлично подходят геометрические тела.
Одна из причин этого заключается в том, что имена трехмерных фигур реже используются в повседневной жизни. Другая причина заключается в том, что в большинстве занятий в классе трехмерные геометрические формы преподаются с помощью рисунков. К сожалению, многие дети не могут понять эти 3D-рисунки. Рисунок сферы выглядит как круг. Это затрудняет понимание разницы между сферой и кругом. Поэтому для обучения детей геометрическим фигурам в 3D отлично подходят геометрические тела.
Дети могут трогать, держать и манипулировать этими предметами. Это дает им более четкое представление об атрибутах трехмерных геометрических фигур.
- Танграммы: Танграммы можно использовать для обучения детей пространственным отношениям. Это китайская головоломка, состоящая из 7 танов или фигур. Дети должны расположить эти фигуры, чтобы воссоздать заданную форму. Правило головоломки требует, чтобы все фигуры использовались без перекрытия. Игра с танграмами помогает детям улучшить пространственное понимание.
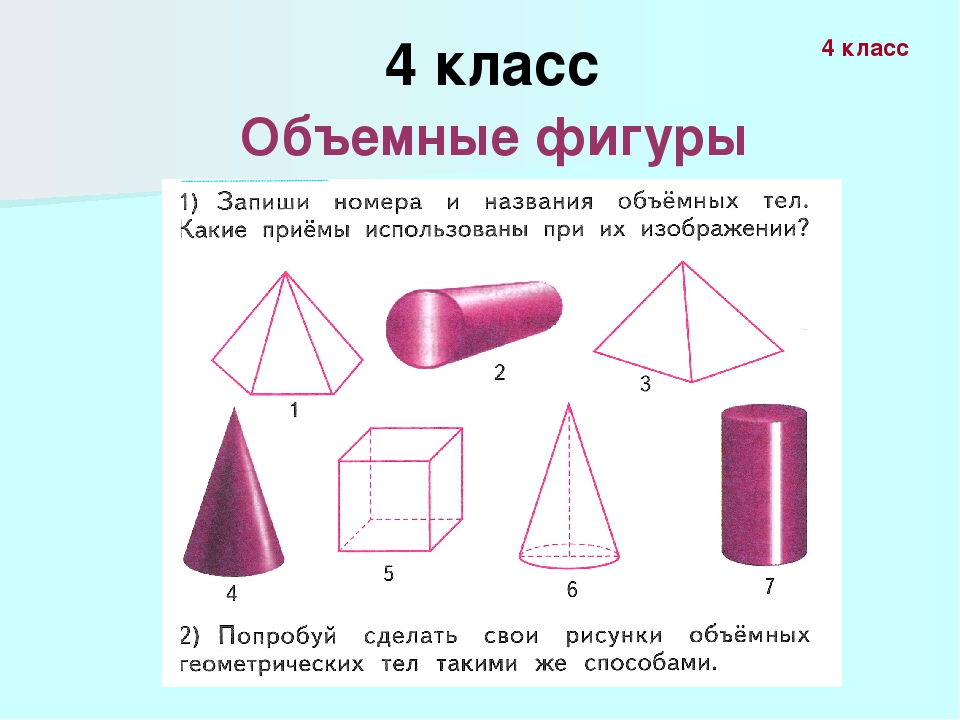 Они также узнают о навыках пространственного вращения и связанном с ним словарном запасе. Дети также учатся вычислять площади без изучения формул.
Они также узнают о навыках пространственного вращения и связанном с ним словарном запасе. Дети также учатся вычислять площади без изучения формул.
Попробуйте SplashLearn бесплатно
5.1 Треугольники, четырехугольники, окружности и другие | Геометрия фигур
В этой главе вы узнаете о различных видах 2D-фигур. Вы узнаете имена, данные разные формы. Вы также узнаете о различных свойствах, которые разные типы фигур имеют по отношению к своим сторонам и углам.
Треугольники, четырехугольники, окружности и др.
Решите, что есть что, и нарисуйте несколько фигур
Треугольник представляет собой замкнутую фигуру с тремя прямыми сторонами и тремя углами.
Четырехугольник имеет четыре прямые стороны и четыре угла.
Круг круглый, и край всегда находится на одинаковом расстоянии от центра.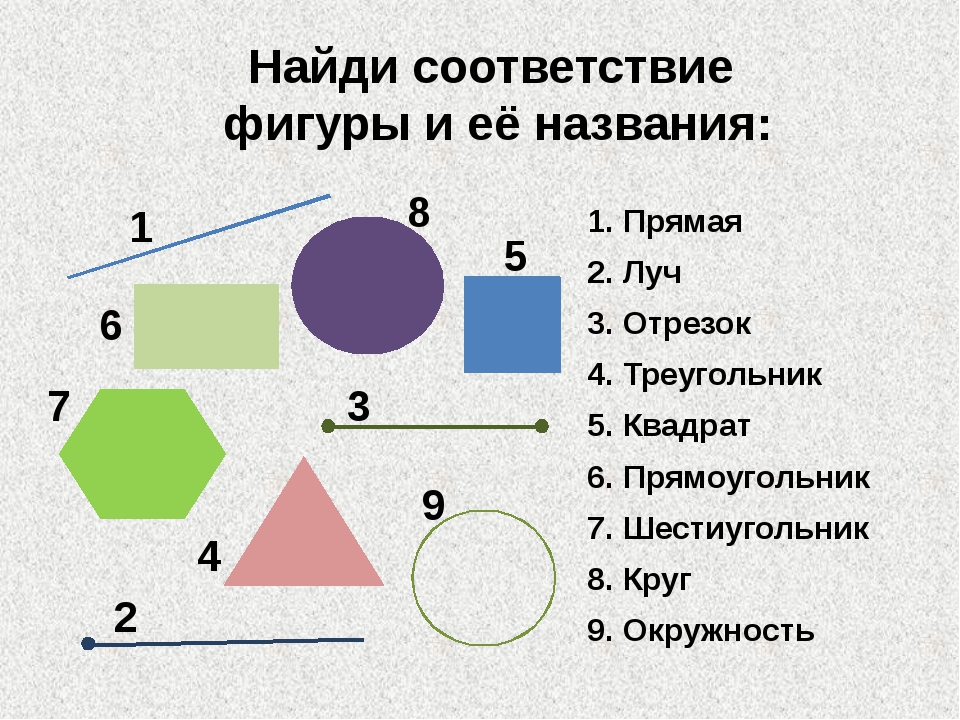
Какие фигуры на противоположной странице круги?
Какие фигуры на противоположной странице треугольники?
Какие фигуры на противоположной странице четырехугольники?
Используйте линейку, чтобы сделать следующее:
Сделать рисунок одного треугольника с тремя острыми углами и другого треугольника с одним тупой угол.
Начерти четырехугольник с двумя тупыми углами.
Можешь ли ты начертить треугольник с двумя тупыми углами?
Нарисуйте треугольник с одним прямым углом и треугольник без прямых углов.

Можешь ли ты нарисовать треугольник? с двумя прямыми углами?
Можешь нарисовать четырехугольник с четырьмя прямыми углами?
Эти четыре линии образуют четырехугольник АВСD.
Две красные стороны, ВС и AD, называются противоположными сторонами четырехугольника ABCD.
Какие две другие стороны ABCD также являются противоположными сторонами?
Линии DA и AB на рисунке в вопрос 7 называются смежных сторон . Они встречаются в точке, которая является одной из вершины (угловые точки) четырехугольника.
Назовите еще двоих смежные стороны в ABCD.
AB примыкает к DA в четырехугольнике ABCD.
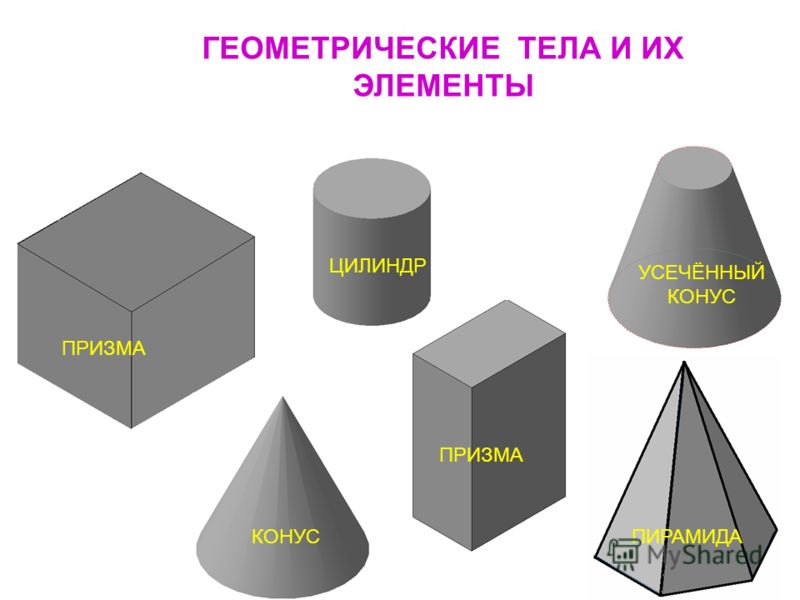 Какая другая сторона ABCD также примыкает к DA?
Какая другая сторона ABCD также примыкает к DA?
Уильям говорит:
“Каждая сторона четырехугольника имеет две смежные стороны.
Каждая сторона четырехугольника также имеет две противоположные стороны.”
Прав ли Уильям? Обоснуйте свой ответ.
Уильям также говорит:
“В треугольнике каждая сторона смежна со всеми остальными сторонами.”
Это правда? Обоснуйте свой ответ.
В каждом случае укажите, две стороны являются противоположными сторонами или смежными сторонами четырехугольника PQRS.
КП и ПС
КП и СР
PQ и RQ
PS и QR
SR и QR
w3.org/1999/xhtml”> Различные типы треугольников
Равнобедренные, равнобедренные, разносторонние и прямоугольные треугольники
Треугольник с двумя равными сторонами называется равнобедренным треугольником .
Треугольник с тремя равными сторонами называется равносторонний треугольник .
Треугольник с прямым углом называется прямоугольным треугольником .
Треугольник с тремя сторонами разной длины и без прямого угла называется разносторонним треугольником .
Измерьте каждый угол в каждом из равнобедренных треугольников , данных выше. Делать вы заметили что-нибудь особенное? Если вы не уверены, нарисуйте больше равнобедренных треугольников. в вашей тетради.
Измерьте углы и стороны следующие треугольники.
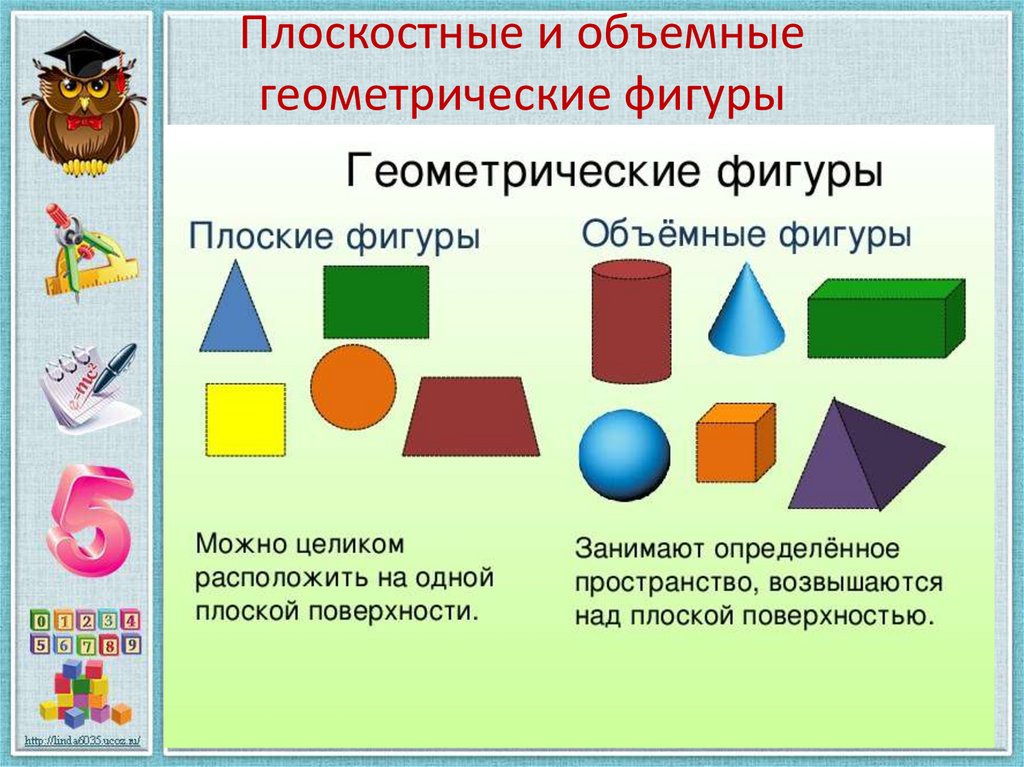 Что особенного в этих треугольниках? Другими словами, что
чем эти треугольники отличаются от других треугольников?
Что особенного в этих треугольниках? Другими словами, что
чем эти треугольники отличаются от других треугольников?Эти треугольники называются равносторонними треугольниками .
Измерьте каждый угол в каждом из следующих треугольников. Вы заметили что-то особенное в этих углах?
Определить самый длинный стороны в каждом из треугольников. Если вы не уверены, какой из них самый длинный сторону, измерьте стороны. Что вы заметили относительно самой длинной стороны в каждом из эти треугольники?
Эти треугольники называются прямоугольными треугольниками .
Сравнение и описание треугольников
w3.org/1999/xhtml”> Когда две или более сторон фигуры имеют одинаковую длину, мы показываем это короткими линиями на равных сторонах.
Используйте следующие треугольники, чтобы ответить на следующие вопросы:
Который у треугольника только две равные стороны?
Как называется этот тип треугольника?
В каком треугольнике есть все три стороны равны?
Как называется этот тип треугольника?
Какой треугольник имеет угол равен 90°?
Как называется этот тип треугольника?
Запишите тип каждого из следующих треугольников в пространстве при условии:
w3.org/1999/xhtml”> Нахождение неизвестных сторон в треугольниках
Назовите каждый тип треугольника ниже.
Используйте данную информацию для определить длину следующих сторон:
АБ:
до н.э.:
ЭФ:
Можете ли вы определить длины GH и HI? Поясните свой ответ.
Площадь в углу ул. \(\triangle\)JKL показывает, что это прямой угол. Назовите причину каждого вашего ответы ниже.
Это треугольник разносторонний, равнобедренный или равносторонний?
Назовите две стороны треугольника, которые равный.
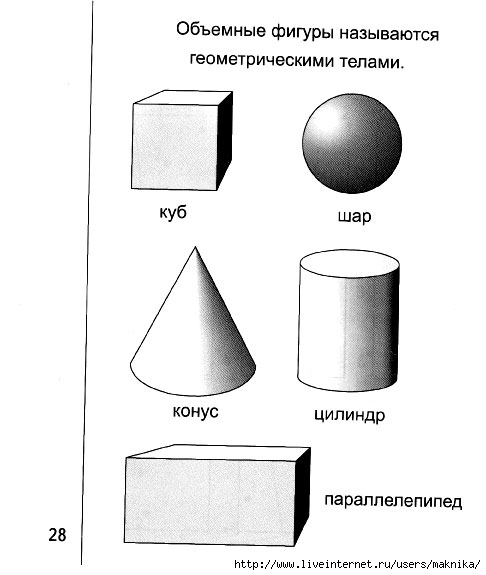
Какова длина JK?
Назовите два равных угла в этом треугольнике.
Какой размер \(\шляпа{J}\) и \(\шляпа{L}\) ?
Различные типы четырехугольников
Исследование четырехугольников
Двое на следующих страницах показаны различные группы четырехугольников.
В котором группы обе пары противоположных сторон параллельны?
В каких группах только некоторые смежные стороны равны?
В каких группах все четыре углы равны?
В каких группах находятся все стороны в каждом четырехугольнике равны?
В каких группах все четыре стороны равны?
В каких группах находится каждая сторона перпендикулярно примыкающим к ней сторонам?
В каких группах противоположны стороны равны?
В каких группах есть хотя бы один пара смежных сторон равны?
В каких группах есть хотя бы один пара противоположных сторон параллельна?
В каких группах находятся все углы прямые?
Цифры в группе 1 называются параллелограммов .

Что вы наблюдаете о противоположных сторонах параллелограмма?
Что вы заметили относительно углов параллелограммы?
Цифры в группе 2 называются воздушных змеев .
Что вы наблюдаете о боках воздушных змеев?
Что еще вы заметили в воздушных змеях?
Группа 1
Группа 2
Группа 3
Группа 4
Группа 5
Группа 6
Цифры в группа 3 называется ромб .
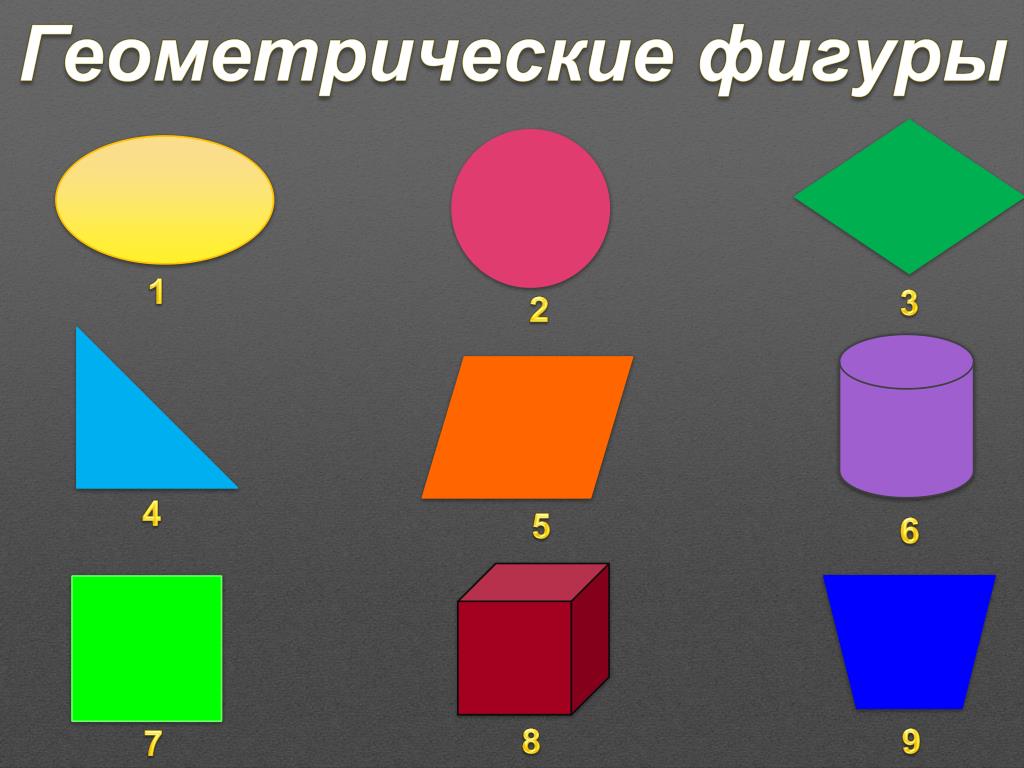
Что вы наблюдаете о сторонах ромба?
Что еще вы заметили в ромбах?
Примечание: один ромб ; два или более ромбов .
Цифры в группе 4 называются прямоугольники .
Что вы наблюдаете о противоположных сторонах прямоугольников?
Что вы заметили относительно углов прямоугольники?
Что вы наблюдаете на соседних сторонах прямоугольники?
Цифры в группе 5 называются трапеции . Что вы наблюдаете о противоположных сторонах трапеции?
Стрелки показывают, какие стороны параллельны друг другу.

Цифры в группе 6 называются квадратов .
Что вы наблюдаете о сторонах квадратов?
Что вы заметили относительно углов квадраты?
Сравнение и описание форм
Имя каждой формы в каждой группе.
Группа А
Группа Б
Каким способом(ами) одинаковы ли цифры в каждой группе?
Группа А:
Группа Б:
Каким образом одна из фигур в каждой группе отличаются от двух других цифр в группе?
Группа А:
Группа Б:
w3.org/1999/xhtml”> Нахождение неизвестных сторон четырехугольников
Используйте свои знания о сторонах и углах четырехугольников, чтобы ответить на следующие вопросы. Обоснуйте свои ответы.
Четырехугольник ABCD какого типа?
Назовите сторону, равную АВ.
Какова длина BC?
Какой тип четырехугольника EFGH?
Какова длина следующих сторон?
ЭФ:
Цвет:
Какой тип четырехугольника JKLM?
Какова длина JK?
Фигура PQRS — воздушный змей с PQ = 4 см и QR = 10 см.
 Завершите следующий чертеж:
Завершите следующий чертеж:маркировка вершин воздушного змея
показывает на чертеже, какие стороны равны
с указанием длины каждой стороны.
Круги
Поставьте точку в середине круга справа. Напишите букву М рядом с точкой. Если ваша точка находится в середине круга, она называется средней точкой или центром .
Проведите линии MA, MB и MC от M до красных точек A, B и C.
три красные точки находятся на окружности с серединой М.
Прямая линия, такая как AC, проведенная через окружности и проходящей через ее середину, называется диаметром круг.

Измерение MA, MB и MC.
Если MA, MB и MC равны по длине, вы правильно выбрали среднюю точку. Если они не равны, вы можете улучшить набросок круга и его частей.
Прямая линия от середины окружности до точка на окружности называется радиусом окружности.
Синяя линия, MA, представляет собой радиус . Любая прямая, идущая от центра к окружности, радиус.
Черная линия AB соединяет две точки окружности. Мы называем это аккордом круг.
В на следующих двух диаграммах цветные секции сегментов круг. Сегмент – это площадь между хордой и дугой.
В круге справа красная часть называется сектором круга. Как видите, сектор — это область между двумя радиусами и дугой.
w3.org/1999/xhtml”> Подобные и конгруэнтные формы
Три группы четырехугольников показаны на этой и следующей странице.
Чем каждая группа отличается от других групп, кроме цвета?
Группа А:
Группа Б:
Группа С:
Группа А
Группа Б
Группа С
Фигуры одинаковой формы, такие как синие фигуры на предыдущей странице, называются 9.0015 похожи друг на друга. Похожие фигуры могут отличаться по размеру, но всегда будут иметь одинаковую форму.
Пример похожих форм
Пример конгруэнтных форм
Фигуры одинаковой формы и размера, такие как красные фигуры на предыдущей странице, считаются на конгруэнтными на друг другу.
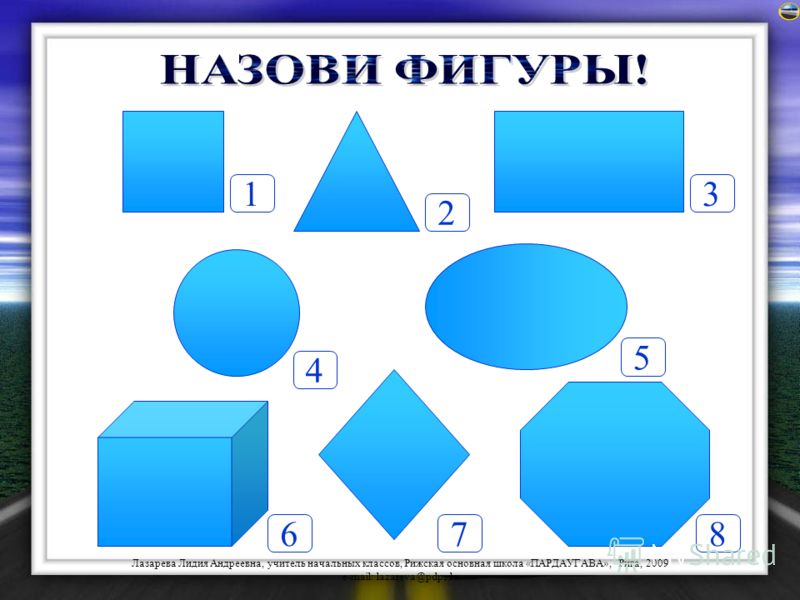 Эти фигуры всегда одного размера и формы.
Эти фигуры всегда одного размера и формы.Красные фигуры на предыдущей странице похожи друг на друга?
Посмотрите на группы D, E, F и G на этом страница и след. В каждом случае скажите, подобны ли фигуры и конгруэнтный, подобный, но не конгруэнтный, или ни похожий, ни конгруэнтный.
Группа Д:
Группа Е:
Группа F:
Группа G:
Группа D
Группа Е
Группа F
Группа G
Как называются 2D и 3D фигуры?
Мы объясняем, чем отличаются двухмерные и трехмерные фигуры, когда детей младшего школьного возраста учат называть их и сортировать фигуры в соответствии с их свойствами, а также когда они учатся идентифицировать и рисовать свои собственные сети трехмерных фигур.
или Зарегистрируйтесь, чтобы добавить к своим сохраненным ресурсам
На протяжении обучения в начальной школе дети будут изучать различные 2D (двумерные) и 3D (трехмерные) формы.
Первое, что им нужно усвоить, это разницу между 2D и 3D формами. Учителя часто говорят о том, что 2D-формы «плоские», а 3D-формы не . Ожидается, что дети смогут назвать эти фигуры, а также обсудить свойства этих фигур.
2D shapes| Circle | Square | ||
| Triangle | Rectangle | ||
| Pentagon | Hexagon | ||
| Octagon | Nonagon |
| Куб | Куб | ||
| Sphere | Square-based pyramid | ||
| Cylinder | Triangular prism | ||
| Pentagonal pyramid | Шестиугольная призма |
2D и 3D формы в KS1
In Year 1 , дети должны уметь распознавать и называть:
- 2D-фигуры, включая прямоугольники, квадраты, круги и треугольники
- 3D-фигуры, включая кубы, прямоугольные параллелепипеды, пирамиды и сферы
- сортировать, создавать и описывать распространенные 2D- и 3D-фигуры
В году 2 дети должны уметь:
- определять и описывать свойства 2D-фигур, включая симметрию и симметрию линий
- идентифицировать и описывать 3D-фигуры, включая количество ребер, вершин и граней
- идентифицировать 2D-формы на поверхности 3D-фигур
- сравнивать и сортировать распространенные 2D- и 3D-фигуры
- понимать, что прямой угол составляет четверть оборота, и знать, по часовой стрелке или против часовой стрелки
2D и 3D-фигуры в KS2
В 3-й год дети должны:
- рисовать 2D-фигуры и составлять 3D-фигуры
- определять прямые углы и знать, что два делают пол-оборота, три – три четверти оборота и четыре полный оборот
- определять горизонтальные и вертикальные линии и пары перпендикулярных и параллельных линий
В 4 классе дети должны:
- сравнивать четырехугольники и треугольники на основе их свойств и размеров
- определять острые и тупые углы и сравнивать и углов порядка
- определять линии симметрии в двумерных фигурах
В 5 классе дети должны:
- определять трехмерные фигуры из двумерных представлений
- оценивать и сравнивать острые, тупые и зеркальные углы
- рисовать заданные углы
- находить недостающие длины и углы прямоугольников
- различать правильные и неправильные многоугольники классифицировать 2D- и 3D-формы, говоря о параллельных и перпендикулярных ребрах и гранях
- рисовать 2D-фигуры, используя заданные размеры и углы
- распознавать, описывать и строить простые 3D-фигуры, включая создание сетей
- находить неизвестные углы в треугольниках, четырехугольниках и правильных многоугольниках
- иллюстрировать и называть части окружностей, включая радиус, диаметр и длину окружности, и знать, что диаметр в два раза больше радиуса
Равносторонний треугольник: Треугольник с 3 равными сторонами и 3 равными углами. 
Равнобедренный треугольник: Треугольник с 2 равными сторонами. Разносторонний треугольник: Треугольник с 3 неравными сторонами. Прямоугольный треугольник: Треугольник с прямым углом. Четырехугольник: Четырехсторонняя форма. Ромб: Четырехугольник, у которого обе пары или противоположные стороны параллельны и все стороны имеют одинаковую длину. (Отличается от квадрата тем, что углы НЕ 90˚). Трапеция: Четырехугольник с одной парой параллельных сторон. Параллелограмм: Четырехугольник, у которого обе пары противоположных сторон параллельны и обе пары имеют одинаковую длину. Воздушный змей : Четырехугольник с двумя парами сторон одинаковой длины. 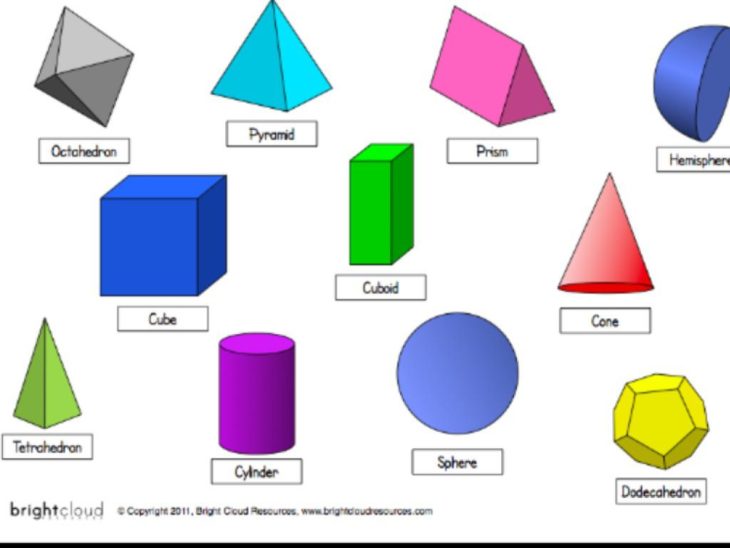 Одна пара диагонально противоположных сторон равна.
Одна пара диагонально противоположных сторон равна.Многоугольник : многоугольник – это двумерная фигура с прямыми сторонами. Больше похоже на это
Свойства 2D-фигур
Каковы свойства 2D- и 3D-фигур?
Свойства 3D -формы
Глоссарий первичного численности для родителей
2D Редакция формы
Учащийся 2D Shapes Lutorial
2 -й 2D SHADE
2?
Shape spy: ищите 3D-фигуры вокруг себя
Создание трехмерных фигур
Математика 4 класса | Формы и углы
Краткое содержание раздела
Модуль 8 в 4 классе знакомит учащихся с более абстрактными геометрическими понятиями точек, прямых, отрезков, лучей и углов. Учащиеся учатся измерять углы, а затем используют этот навык для классификации фигур на основе меры угла, геометрического свойства.
 Учащиеся также развивают понимание отражательной симметрии, определяя линейно-симметричные формы и рисуя их линии симметрии.
Учащиеся также развивают понимание отражательной симметрии, определяя линейно-симметричные формы и рисуя их линии симметрии.Этот модуль основан на большом количестве работ в предыдущих классах с распознаванием форм и классификацией (1.G.1, 2.G.1, 3.G.1). Чтобы отличить квадрат от ромба, учащиеся должны обратить внимание на угловую меру углов или вершин. Таким образом, этот модуль знакомит учащихся со словарным запасом, который позволит им говорить об измерении угла как атрибуте плоских фигур (как многоугольников, так и более абстрактных фигур, таких как наборы пересекающихся линий), а также о системе измерения, используемой для количественной оценки угла. точно измерить.
Модуль начинается с рисования учащимися точек, прямых, отрезков, лучей и углов и продолжается общей классификацией на основе углов, включая различие между прямыми, тупыми, острыми и прямыми углами, а также параллельными, перпендикулярными и пересекающимися углами. линии. Затем у учащихся формируется более точное представление об углах как о геометрических фигурах, которые можно измерить, и они учатся это делать.
 Студенты также учатся думать об углах не только как об объектах, но и как о действиях — они могут указывать на поворот или изменение направления. Учащиеся также видят, что углы являются аддитивными, как и другие геометрические меры, которые они изучали в предыдущих классах, такие как длина во 2 классе (2.MD.1—6) и площадь в 3 классе (3.MD.5—7). . Затем учащиеся используют свое углубленное понимание углов, чтобы классифицировать и рисовать треугольники в соответствии с их угловой мерой (прямой, тупой и острый), а также длиной стороны (равносторонний, равнобедренный и разносторонний) и четырехугольники в соответствии с параллельным и/или перпендикулярным. характер их сторон. Наконец, учащиеся исследуют линии симметрии, находят и рисуют их на фигурах.
Студенты также учатся думать об углах не только как об объектах, но и как о действиях — они могут указывать на поворот или изменение направления. Учащиеся также видят, что углы являются аддитивными, как и другие геометрические меры, которые они изучали в предыдущих классах, такие как длина во 2 классе (2.MD.1—6) и площадь в 3 классе (3.MD.5—7). . Затем учащиеся используют свое углубленное понимание углов, чтобы классифицировать и рисовать треугольники в соответствии с их угловой мерой (прямой, тупой и острый), а также длиной стороны (равносторонний, равнобедренный и разносторонний) и четырехугольники в соответствии с параллельным и/или перпендикулярным. характер их сторон. Наконец, учащиеся исследуют линии симметрии, находят и рисуют их на фигурах.Этот аппарат позволяет сосредоточиться на MP.2, MP.5 и MP.6. Например, когда учащимся «показывают два набора фигур и спрашивают, к какой из них принадлежит новая фигура», они рассуждают абстрактно и количественно (MP.2) (G Progression, стр.
 16). Студенты также учатся точно использовать новый инструмент, транспортир, обеспечивая правильное выравнивание вершины и основания и внимательно читая меру угла (MP.5, MP.6).
16). Студенты также учатся точно использовать новый инструмент, транспортир, обеспечивая правильное выравнивание вершины и основания и внимательно читая меру угла (MP.5, MP.6).Эта работа продолжает формализовать большую часть уже проделанной учащимися работы по пониманию геометрических фигур, которая будет формализована в ближайшие годы. Этот модуль готовит учащихся к иерархической классификации двумерных фигур в 5 классе (5.G.3, 5.G.4). Он также знакомит учащихся с рисованием геометрических фигур, которые они снова увидят в 7 классе (7.Г.1—3) и даже с геометрией средней школы и тригонометрическими аспектами алгебры II. Таким образом, хотя все стандарты, рассматриваемые в модуле, являются дополнительными кластерными стандартами, они закладывают важную основу для геометрической работы в ближайшие годы.
Темп: 20 учебных дней (18 уроков, 1 гибкий день, 1 контрольный день)
Fishtank Plus для математики
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
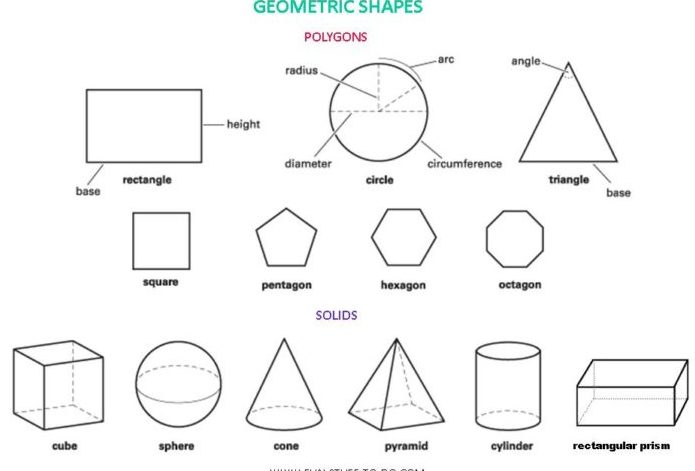
Узнать больше
Оценка
Следующие оценки сопровождают Раздел 8.
Предварительная часть
Предложите учащимся пройти предварительную оценку и самооценку перед началом модуля. Используйте Руководство по анализу предварительной оценки, чтобы определить пробелы в фундаментальном понимании и наметить план ускорения обучения на протяжении всего модуля.
Промежуточный модуль
Предложите учащимся выполнить оценку промежуточного модуля после урока 10.
Последующий модуль
Используйте приведенные ниже ресурсы для оценки усвоения учащимися содержания модуля и плана действий для будущих модулей.
Постмодальная оценка
Ключ к ответам после модульной оценки
Руководство по анализу послемодульной оценки
92F25A3F-8529-4314-9899-6EE68694E3D0Пост-юнит самооценка
Расширенный пакет оценивания
Используйте данные учащихся для управления планированием с помощью расширенного набора модульных оценок, помогающих оценить уровень владения учащимися базовыми навыками и понятиями, а также их прогресс в изучении содержания модуля.
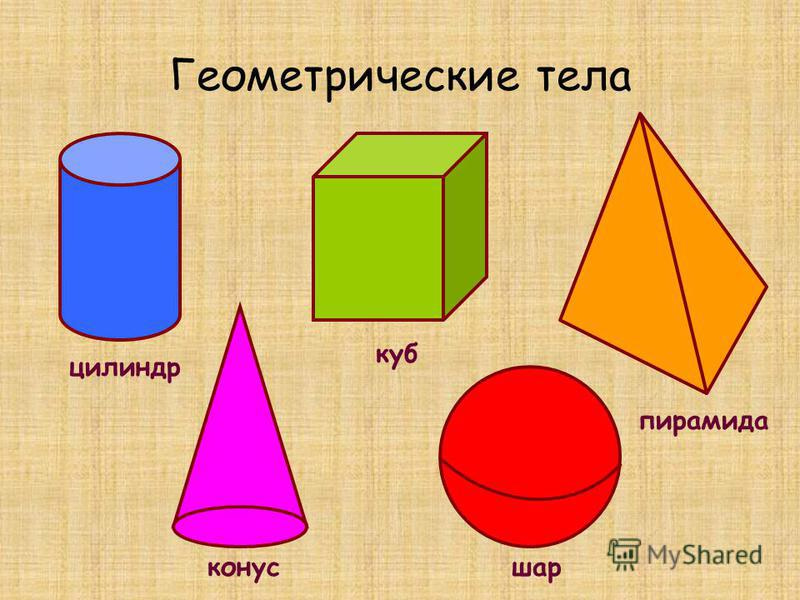
Скачать образец
Подготовка блока
Интеллектуальная подготовка
Рекомендации по подготовке к преподаванию данного модуля
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Интеллектуальная подготовка для всех модулей
- Прочтите и прокомментируйте разделы «Сводка модуля» и «Основные сведения» плана модуля.
- Выполните все целевые задачи и снабдите их комментариями с учетом «Сводки модуля» и «Основных сведений».
- Пройти итоговую оценку.
Основные понятия
Основные математические понятия, которые учащиеся поймут в этом модуле. Линии бесконечны по протяженности в одном измерении.
- Мера угла и длины независимы. То есть мера угла не зависит от длины сторон угла.
- Углы могут описывать как статические, так и динамические контексты. Например, угол можно использовать для описания меры разброса в вершине двумерной формы или для описания изменения направления.

- Как и другие геометрические измерения, которые учащиеся изучали в прошлом, такие как длина и площадь, угловая мера является аддитивной.
- Многоугольники можно описывать и классифицировать по их сторонам и углам.
- Некоторые фигуры могут отражаться через одну или несколько линий, проходящих через фигуру, так что фигура точно складывается сама на себя. Однако эта симметрия не является определяющим признаком формы.
Материалы
Материалы, иллюстрации и инструменты, которые потребуются преподавателям и учащимся для работы с данным модулем
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- Линейка (1 на учащегося)
- Чистый лист бумаги (всего 2 листа на учащегося)
- Шаблоны блоков (максимум 4 квадрата, 6 треугольников, 3 шестиугольника, 6 синих ромбов, 12 коричневых ромбов на учащегося или небольшую группу)
- Квадратная бумага (2 на учащегося)
- Шаблон: Треугольники (по 1 на учащегося или малую группу)
- Шаблон: Четырехугольники (по 1 на учащегося или малую группу)
- Ножницы (по 1 на учащегося)
- Шаблон: фигуры (по 1 на учащегося или небольшую группу)
- Шаблон: Углы (по 1 на учащегося или небольшую группу)
- Бумажные круги (всего 5 на учащегося).
 Бумажные круги в Уроке 7 должны быть разных размеров. Дополнительную информацию см. в разделе «Примечания к задаче 1 привязки к уроку 7».
Бумажные круги в Уроке 7 должны быть разных размеров. Дополнительную информацию см. в разделе «Примечания к задаче 1 привязки к уроку 7». - Круговой транспортир (1 на учащегося)
- Маркеры или мелки (по 1 на учащегося)
- Транспортир 180° (1 на учащегося)
Запас слов
Термины и обозначения, которые учащиеся изучают или используют на уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950острый угол
острый треугольник
смежные углы
угол $${\angle}$$
длина дуги
дуга
градус °
равносторонний треугольник AB}}$$
линия $${\overleftrightarrow{AB}}$$
линия симметрии, симметричная
тупоугольный треугольник
тупой угол
параллельный, ||
перпендикулярно $${\perp}$$
точка
транспортир
луч $${\overrightarrow{AB}}$$
прямоугольный треугольник
прямой угол
разносторонний треугольник
прямой угол
вершина
Чтобы увидеть весь словарный запас для Раздела 8, просмотрите наш глоссарий лексики для 4-го класса.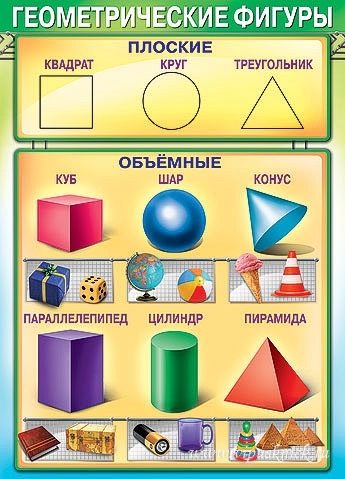
Модульная практика
Словесные задачи и упражнения на беглость речи
Получите доступ к ежедневным практикам со словесными задачами и нашим ориентированным на содержание упражнениям на беглость речи, созданным, чтобы помочь учащимся укрепить свои навыки применения и беглости речи.
Предварительный просмотр
Узнать больше
Карта урока
Тема A: Линии и углы
Определение и рисование точек, линий, отрезков, лучей и углов.
4.G.A.1 4.MD.C.5
Определите и нарисуйте прямые, тупые и острые углы.
4.G.A.1
Определите и нарисуйте перпендикулярные линии.
4.G.A.1
Определите и нарисуйте параллельные линии.
4.G.A.1
Тема B: Меры углов
Используйте итерацию с одной физической единицей для измерения эталонных углов.
4.MD.C.5 4.MD.C.6
Помните, что угол, который проходит через $${{1\over360}}$$ окружности, называется «угол в один градус» и может использоваться для измерения углов. Используйте самодельный транспортир для измерения контрольных углов.
Используйте самодельный транспортир для измерения контрольных углов.
4.MD.C.5 4.MD.C.6
Измерение углов меньше 180°. Различают измерение угла и измерение длины.
4.MD.C.5 4.MD.C.6
Измерение углов больше 180°.
4.MD.C.5 4.MD.C.6
Нарисуйте заданные размеры углов и проверьте их с помощью транспортира.
4.MD.C.5 4.MD.C.6
Определите и измерьте углы как повороты и распознайте их в различных контекстах.
4.MD.C.5 4.MD.C.6
Тема C: Меры смежных углов
Разложение углов с помощью блоков шаблонов.
4.MD.C.7
Решите задачи на измерение двух смежных углов.
4.MD.C.7
Решите задачи на измерение более чем двух смежных углов.
4.MD.C.7
Тема D: Формы и линии симметрии
Анализ и классификация треугольников на основе длины стороны, меры угла или того и другого.
4.G.A.1 4.G.A.2
Нарисуйте треугольники по заданным критериям.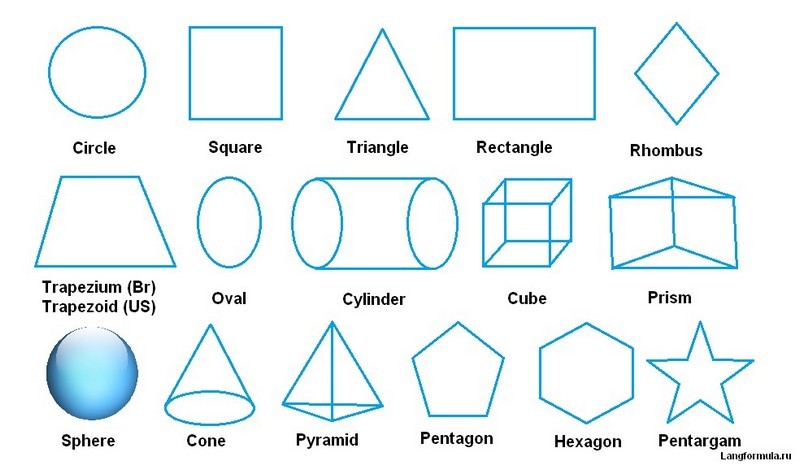
4.G.A.1 4.G.A.2
Анализ и классификация четырехугольников на основе параллельных и перпендикулярных прямых и наличия или отсутствия углов заданного размера.
4.G.A.1 4.G.A.2
Нарисуйте четырехугольники по заданным критериям.
4.G.A.1 4.G.A.2
Определите и нарисуйте линии симметрии в двухмерных фигурах.
4.G.A.3
Общие базовые стандарты
Ключ
Основной кластер
Вспомогательный кластер
Дополнительный кластер
Основные стандарты
Стандарты контента, описанные в этом модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Геометрия
4.Г.А.1 — Рисовать точки, прямые, отрезки, лучи, углы (прямые, острые, тупые), перпендикулярные и параллельные прямые. Определите их на двумерных фигурах.
4.Г.А.2 — Классифицировать двухмерные фигуры на основе наличия или отсутствия параллельных или перпендикулярных линий, а также наличия или отсутствия углов заданной величины.
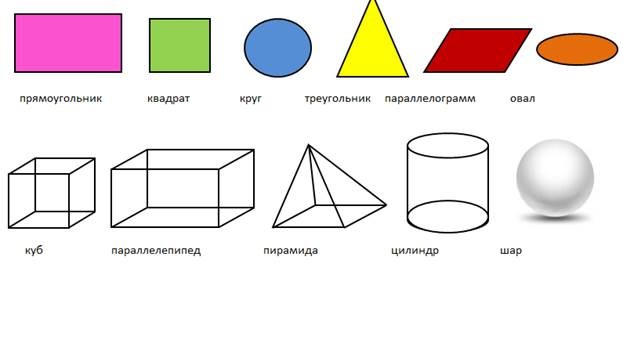 Распознавать прямоугольные треугольники как категорию и определять прямоугольные треугольники.
Распознавать прямоугольные треугольники как категорию и определять прямоугольные треугольники. 4.Г.А.3 – Распознавать линию симметрии двухмерной фигуры как линию, пересекающую фигуру, так что фигуру можно сложить по этой линии на соответствующие части. Определите линейно-симметричные фигуры и нарисуйте линии симметрии.
Измерения и данные
4.MD.C.5 – Распознавать углы как геометрические фигуры, которые образуются там, где два луча имеют общую конечную точку, и понимать принципы измерения углов:
4.MD.C.5.A – Угол измеряется относительно окружности с центром в общей конечной точке лучей, принимая во внимание долю дуги окружности между точками, где два луча пересекают окружность. Угол, который проходит через 1/360 окружности, называется «углом в один градус» и может использоваться для измерения углов.

4.MD.C.5.B – Говорят, что угол, который проходит через n одноградусных углов, имеет угловую меру n градусов.
4.MD.C.6 — Измерьте углы в целых числах градусов с помощью транспортира. Эскиз углов заданной меры.
4.MD.C.7 — Распознать угловую меру как аддитивную. Когда угол разлагается на непересекающиеся части, угловая мера целого равна сумме угловых мер частей. Решите задачи на сложение и вычитание, чтобы найти неизвестные углы на диаграмме в реальном мире, и математические задачи, например, используя уравнение с символом для неизвестной меры угла.
Основополагающие стандарты
Стандарты, рассмотренные в предыдущих разделах или классах, которые важны для текущего раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Геометрия
3.
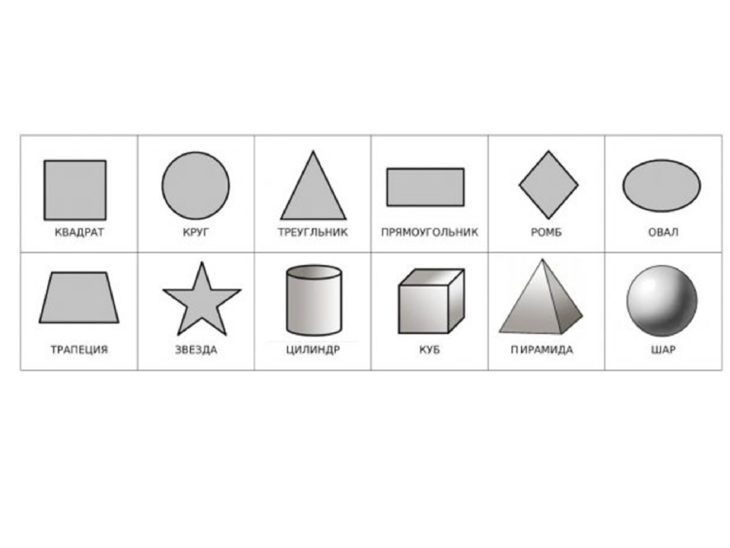 Г.А.1
Г.А.1
Операции и алгебраическое мышление
1.OA.D.8
Будущие стандарты
Стандарты будущих классов или разделов, которые связаны с содержанием данного раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Конгруэнтность
G.CO.A.1
Геометрия
5.RUS3
7.RUS5
Тригонометрические функции
F.TF.A.1
Стандарты математической практики
CCSS.MATH.PRACTICE.MP1 – Разбираться в проблемах и настойчиво решать их.
CCSS.MATH.PRACTICE.MP2 — Рассуждайте абстрактно и количественно.
CCSS.
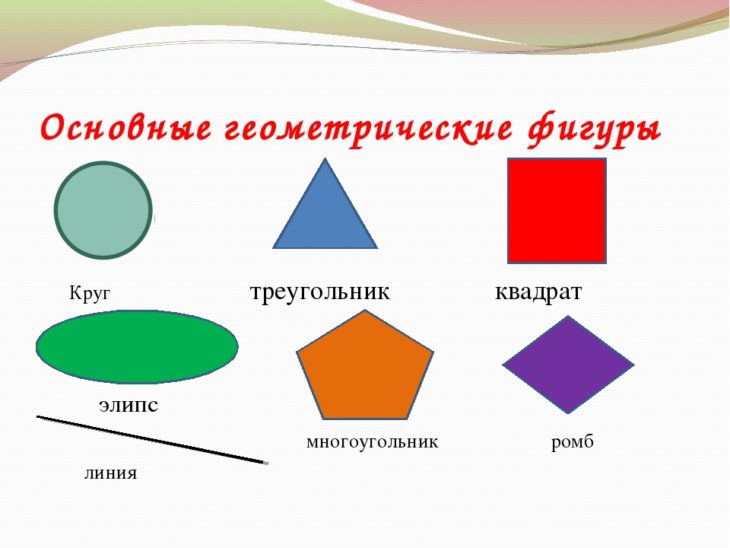 MATH.PRACTICE.MP3
— Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.
MATH.PRACTICE.MP3
— Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.CCSS.MATH.PRACTICE.MP4 — Модель с математикой.
CCSS.MATH.PRACTICE.MP5 — Стратегически используйте соответствующие инструменты.
CCSS.MATH.PRACTICE.MP6 — Следите за точностью.
CCSS.MATH.PRACTICE.MP7 — Ищите и используйте структуру.
CCSS.MATH.PRACTICE.MP8 — Ищите и выражайте закономерность в повторяющихся рассуждениях.
Единица 7
Преобразование единиц измерения
Геометрия и формы в 5-м классе (9–10 лет)
В 5-м классе ваш ребенок будет использовать острые, тупые и рефлекторные углы и будет рисовать и измерять углы в градусах. Они будут переводить и отражать формы, а также исследовать правильные и неправильные многоугольники.
Ключевые слова в этом разделе: 2D, 3D, ось и координата.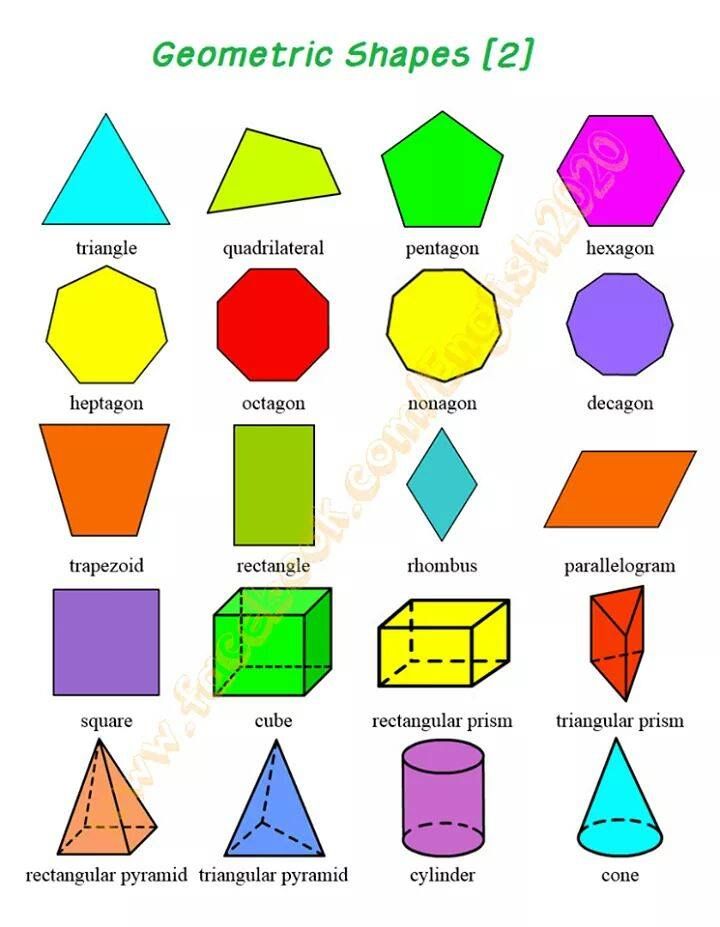
Ознакомьтесь с требованиями Национальной учебной программы к геометрии для 5-го класса (9–10 лет):
Определение трехмерных фигур
Ваш ребенок будет узнавать и называть трехмерные фигуры как в реальной жизни, так и на двухмерных изображениях и рисунках. .
Понимание острых, тупых и рефлекторных углов
Ваш ребенок будет знать, что угол — это мера того, насколько сильно что-то поворачивается, и что углы измеряются в градусах.
Они должны уметь оценивать и сравнивать острые (менее 90°), тупые (от 90° до 180°) и рефлекторные углы (от 180° до 360°).
Начертите и измерьте углы в градусах (°)
Ваш ребенок будет рисовать углы и измерять их в градусах (°) с помощью транспортира.
Определение углов на прямой линии и на поворотах
Ваш ребенок узнает, что сумма углов вокруг точки составляет 360°, а сумма углов на прямой линии составляет 180°.
Они будут знать, что один полный оборот составляет 360°, а пол-оборота — 180°. Они также научатся определять числа, кратные 9.0°, например 180°, 270°, 360°, 450° и так далее.
Используйте свойства прямоугольников, чтобы найти недостающие длины и углы.
Ваш ребенок будет знать свойства прямоугольников. Например, они будут знать, что все прямоугольники имеют прямые стороны, составляющие две пары параллельных линий, четыре угла и четыре прямых угла, и что сумма углов всех прямоугольников составляет 360°.
Они должны быть в состоянии использовать эти знания, чтобы найти недостающие длины и углы в прямоугольниках.
Различие между правильными и неправильными многоугольниками
Ваш ребенок будет знать, что правильный многоугольник — это двумерная фигура с равными углами и тремя или более прямыми сторонами одинаковой длины.
Они смогут отличить правильные многоугольники от неправильных. Они будут использовать такие языки, как обычные , нерегулярные, многоугольники, и неполигоны для их описания .
Они будут использовать такие языки, как обычные , нерегулярные, многоугольники, и неполигоны для их описания .
Отражение и преобразование форм
Ваш ребенок сможет показывать положение простых фигур на полной сетке координат, используя все четыре квадранта, используя положительные и отрицательные значения для x и y .
Ожидается, что они будут описывать и записывать положение фигуры с использованием полной координатной сетки после того, как фигура была перемещена или отражена.
Вы можете помочь своему ребенку сделать фигуру, нарисовав и вырезав копии сеток, чтобы проверить их ответы.
3. Сделайте коврик для транспортира
Ваш ребенок должен будет нарисовать заданные углы и измерить их в градусах с помощью транспортира.
Вы можете помочь своему ребенку научиться правильно пользоваться транспортиром, сделав «коврик для транспортира».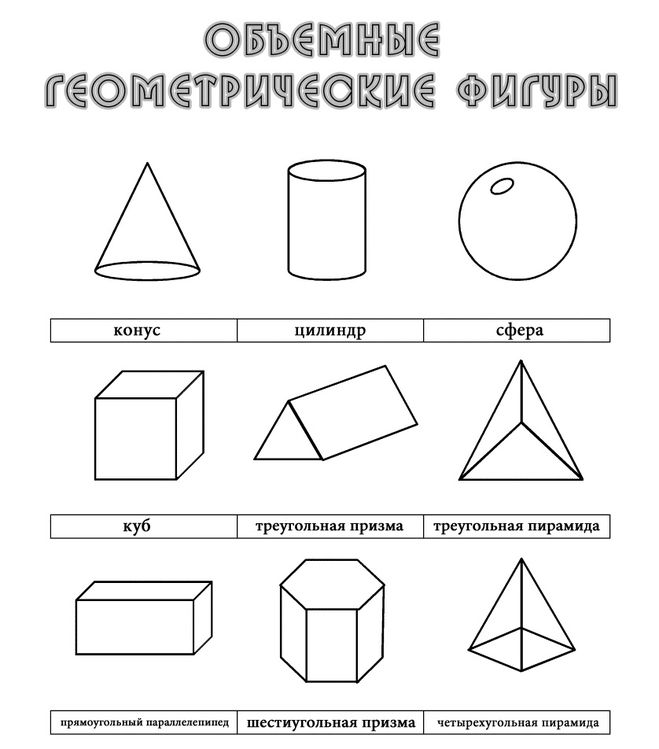 Используйте угол листа бумаги, чтобы создать коврик под углом 90 градусов в форме четверти круга. Отметьте линию для каждых 10°. В качестве альтернативы создайте коврик на 180 градусов в форме полукруга. Отметьте линию для каждых 10°. Это поможет им привыкнуть к тому, как выглядят различные приращения градусов.
Используйте угол листа бумаги, чтобы создать коврик под углом 90 градусов в форме четверти круга. Отметьте линию для каждых 10°. В качестве альтернативы создайте коврик на 180 градусов в форме полукруга. Отметьте линию для каждых 10°. Это поможет им привыкнуть к тому, как выглядят различные приращения градусов.
4. Найдите углы в своем имени
Ваш ребенок может написать свое имя (или даже инициалы) прямыми линиями, а затем измерить углы в своем имени. Какие буквы имеют наибольшее количество углов? Какие буквы имеют самые большие углы?
5. Играть в Battleships
Координаты — это числа, которые определяют положение точки на карте, сетке или графике. Координаты записываются с помощью квадратных скобок, где два числа разделяются запятой, например: (1,2). Первое число в координате говорит нам, где находится точка на x -ось (или горизонтальная ось ). Второе число говорит нам, где находится точка на оси y (или на вертикальной оси ).
Вы можете помочь своему ребенку учиться, читая и нанося координаты. В приведенном ниже примере координата точки на графике будет (5,6), где 5 — значение по оси x , а 6 — значение по оси y :
Линкоры дают вашему ребенку возможность использовать координаты. Поощряйте вашего ребенка создавать свои собственные сетки боевых кораблей и играть с вами или братом или сестрой. Это даст им возможность нарисовать пару осей с одинаковыми масштабами и метками, а также потренироваться в нахождении и описании координат.
6. Игра «Форма координат»
Ваш ребенок будет использовать координаты во всех четырех квадрантах в школе, включая использование отрицательных чисел. Используйте для ребенка бумагу со стороной 1 см в квадрате, чтобы нарисовать сетку из четырех квадрантов, например:
Ваш ребенок должен будет уметь описывать и записывать положение простых фигур, используя все четыре квадранта. Они будут использовать положительные и отрицательные значения для x и y и будут отображать точки на сетке для рисования заданного многоугольника.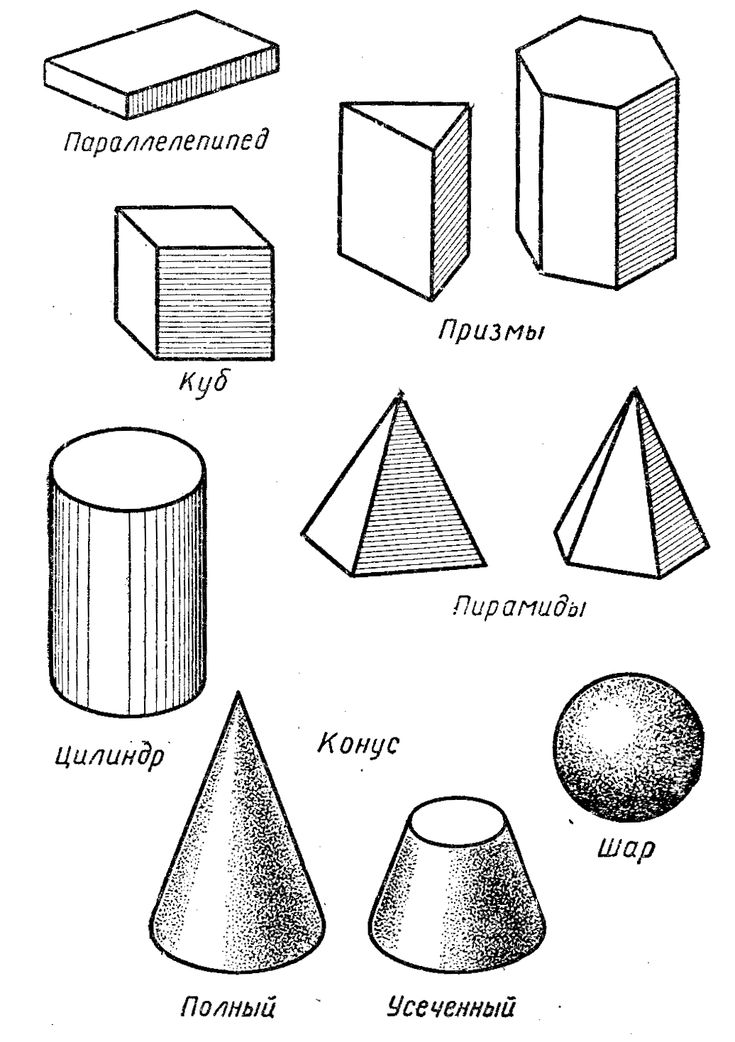
Придумайте фигуру, охватывающую четыре квадранта, и дайте ребенку ее координаты, чтобы он мог ее нарисовать. Вы можете попробовать, используя эти координаты:
А = (2,4)
Б = (5,3)
С = (-2,1)
Д = (-4,4)
Е = (-6,-3)
Ф = (-2,-4)
Г = (2,-3)
Н = (5,-2)
Тогда узнайте, смогут ли они сделать то же самое для вас!
Что такое трехмерные фигуры? Объяснение для родителей и учителей начальной школы
Трехмерные фигуры в начальной школе преподаются уже в 1 классе, когда дети знакомятся с прямоугольными параллелепипедами, пирамидами и конусами. Вот как помочь детям в KS1 и KS2 понять, что такое 3D-фигуры, как идентифицировать и распознавать определенные 3D-фигуры, а также как мы сравниваем и сопоставляем 3D-фигуры, используя список свойств.
Что такое трехмерные фигуры?
Трехмерные фигуры — это фигуры с тремя измерениями, такими как ширина, высота и глубина.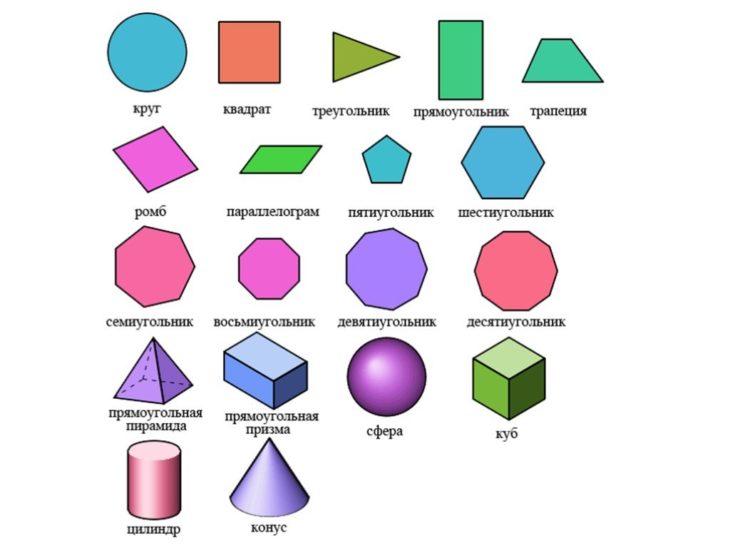 Примером трехмерной формы является призма или сфера. 3D-формы многомерны и их можно физически удерживать.
Примером трехмерной формы является призма или сфера. 3D-формы многомерны и их можно физически удерживать.
Что означает 3D
3D в трехмерных формах означает 3-мерный. Обычно мы говорим об измерениях как об измерениях в направлении. Примеры размеров включают длину, ширину или ширину, глубину и высоту.
Рабочий лист 3D-фигуры для 3-го класса
Загрузите этот БЕСПЛАТНЫЙ рабочий лист по распознаванию 3D-фигур по геометрии для учащихся 3-го класса из нашей коллекции независимых обзоров.
Пример трехмерных фигур
Примеры трехмерных фигур окружают нас все время. Почти все, что мы видим и с чем взаимодействуем в повседневной жизни, имеет трехмерную форму, от кубиков Lego до подсолнухов. Однако в начальной программе детям нужно знать только названия и понимать свойства наиболее распространенных трехмерных фигур. Это контрастирует с 2D-формами, где дети должны знать как о правильных, так и о неправильных формах.
Какие трехмерные фигуры будут изучать дети?
В начальной школе ваш ребенок познакомится со следующими основными геометрическими фигурами: сферами, конусами, призмами и пирамидами. Стоит знать, что геометрически призмы включают в себя более твердые формы, чем вы обычно думаете о призмах. Например, знаете ли вы, что и куб, и прямоугольный параллелепипед с квадратным основанием и прямыми сторонами на самом деле считаются призмами.
Каковы свойства трехмерных фигур?
Свойства трехмерных фигур — это их грани, ребра и вершины, которые имеют определенное значение в контексте уроков математики в начальной школе.
Что такое лицо ?Грань — это плоская поверхность трехмерного объекта. Например, призма с квадратным основанием имеет 5 граней. Сфера имеет 1 криволинейную поверхность, но не имеет грани.
Что такое ребро?
Ребро — это место, где встречаются два сегмента линии или грани. Цилиндр имеет 2 ребра.
Что такое вершины?
Вершины — это места, где встречаются две линии или ребра; в математике мы называем углы трехмерных фигур вершинами. Единственное число вершин на самом деле является вершиной, что может немного сбивать с толку. У конуса одна вершина, а у куба 4 вершины.
Единственное число вершин на самом деле является вершиной, что может немного сбивать с толку. У конуса одна вершина, а у куба 4 вершины.
3D shapes names
These are the 3D shapes names:
- Sphere
- Hemisphere
- Cone
- Tetrahedron or Triangular-based pyramid
- Cylinder
- Triangular prism
- Шестиугольная призма
- Пятиугольная призма
- Куб
- Прямоугольник
Свойства трехмерных фигур
Помимо названий, дети должны знать свойства трехмерных фигур, как указано ниже и в таблице для печати.
- Сфера имеет 1 изогнутую поверхность.
- Полусфера имеет 1 грань, 1 изогнутую поверхность и 1 ребро.
- Конус имеет 1 грань, 1 кривую поверхность, 1 ребро и 1 вершину.
- Тетраэдр или пирамида с треугольным основанием имеет 4 грани, 6 ребер и 4 вершины.
- Пирамида с квадратным основанием имеет 5 граней, 8 ребер и 5 вершин.

- Цилиндр имеет 2 грани, 1 изогнутую поверхность и 2 ребра.
Призмы
- Треугольная призма имеет 5 граней, 9ребра и 6 вершин.
- Куб имеет 6 граней, 12 ребер и 8 вершин.
- Кубоид имеет 6 граней, 12 ребер и 8 вершин.
- Пятиугольная призма имеет 7 граней, 15 ребер и 10 вершин.
- Шестиугольная призма имеет 8 граней, 18 ребер и 12 вершин.
Подробнее: 2D-и 3D-фигуры: Свойства фигур
Когда мой ребенок узнает о 3D-фигурах в начальной школе?
Геометрия преподается в каждой годичной группе в KS1 и KS2. Вот чему Национальная учебная программа предполагает преподавание двухмерных и трехмерных форм с разбивкой по годам:
3D-фигуры в 1-м классе
Учащиеся 1-го класса должны уметь:
- Распознавать и называть распространенные 2-D и 3-D фигуры, включая: 2-D фигуры [например, прямоугольники (включая квадраты), круги и треугольники]; Трехмерные формы [например, прямоугольные параллелепипеды (включая кубы), пирамиды и сферы].

- Неофициальное руководство: учащиеся обращаются с обычными двухмерными и трехмерными формами, бегло называя эти и связанные с ними предметы повседневного обихода. Они распознают эти формы в разных ориентациях и размерах и знают, что прямоугольники, треугольники, кубоиды и пирамиды не всегда похожи друг на друга.
Трехмерные фигуры для 2-го класса
Учащиеся 2-го класса должны уметь:
- Идентифицировать и описывать свойства двухмерных фигур, включая количество сторон и симметрию линий по вертикали.
- Определение и описание свойств трехмерных фигур, включая количество ребер, вершин и граней.
- Идентификация двумерных фигур на поверхности трехмерных фигур, [например, круг на цилиндре и треугольник на пирамиде].
- Сравнивайте и сортируйте распространенные двухмерные и трехмерные формы и предметы быта.
- Неофициальное руководство: учащиеся обращаются и называют самые разнообразные двухмерные и трехмерные фигуры, включая четырехугольники и многоугольники, прямоугольные параллелепипеды, призмы и конусы, и определяют свойства каждой формы (например, количество стороны, количество граней).
 Ученики идентифицируют, сравнивают и сортируют фигуры на основе их свойств и точно используют словарный запас, например стороны, ребра, вершины и грани.
Ученики идентифицируют, сравнивают и сортируют фигуры на основе их свойств и точно используют словарный запас, например стороны, ребра, вершины и грани.
Трехмерные фигуры в 3 классе
Учащиеся 3 класса должны уметь:
- Рисовать двухмерные фигуры и создавать трехмерные фигуры с использованием материалов для моделирования, а также распознавать трехмерные фигуры в различных ориентациях и описывать их.
- Необязательное руководство: На этом этапе знания учащихся о свойствах форм распространяются на симметричные и несимметричные многоугольники и многогранники. Учащиеся расширяют свое использование свойств фигур. Они должны быть в состоянии описать свойства 2-D и 3-D форм, используя точный язык, включая длину линий и острых и тупых углов для больших или меньших, чем прямой угол.
Трехмерные фигуры в 4 классе
Учащиеся 4 класса должны уметь:
- Определять линии симметрии в двухмерных фигурах, представленных в разных ориентациях.
- Дополнительное руководство: учащиеся продолжают классифицировать фигуры, используя геометрические свойства, распространяясь на классификацию различных треугольников (например, равнобедренный, равносторонний, разносторонний) и четырехугольников (например, параллелограмм, ромб, трапеция).
Трехмерные фигуры в 5 классе
Учащиеся 5 класса должны уметь:
- Идентифицировать трехмерные фигуры, включая кубы и другие прямоугольные параллелепипеды, из двухмерных представлений и различать правильные и неправильные многоугольники на основе рассуждений о равенстве сторон и углов.
Учащиеся 6 класса должны уметь:
- Рисовать двухмерные фигуры, используя заданные размеры и углы, а также распознавать, описывать и строить простые трехмерные фигуры, включая создание сетей.
Как трехмерные фигуры связаны с другими областями математики?
При работе с дробями детям часто приходится заштриховывать часть фигуры. Им придется связать свое понимание периметра, площади и объема с трехмерными формами.
Им придется связать свое понимание периметра, площади и объема с трехмерными формами.
1. Сколько вершин в кубе?
(ответ: 8)
2. Сколько квадратов составляют сетку куба?
(ответ: 6)
3. Заполните таблицу.
(Ответ: пирамида с треугольным основанием, 4 грани, 6 ребер / сфера, 0 граней, 0 ребер / треугольная призма, 5 граней, 9 ребер) Рабочий лист «3D-фигуры» Хотите знать, как объяснить своим детям другие ключевые слова по математике? Ознакомьтесь с нашим начальным математическим словарем для детей . Почему бы не просмотреть другие наши блоги, посвященные трехмерным фигурам: Индивидуальные онлайн-уроки по математике, которым доверяют школы и учителя
Каждую неделю репетиторы-специалисты по математике Third Space Learning проводят еженедельные индивидуальные онлайн-уроки и математические вмешательства для тысяч учащихся начальной школы.

 1
1 Определите номер рис. в соответствии с его описанием.
Определите номер рис. в соответствии с его описанием. Посмотри на рис. и определи, какие предложения верные. Около верных предложений поставь знак +.
Посмотри на рис. и определи, какие предложения верные. Около верных предложений поставь знак +.

 Дополните, используя слова в скобках:
Дополните, используя слова в скобках: .”
.” Определите вид получившихся треугольников._______________________________________________________________________________________________________________________________
Определите вид получившихся треугольников._______________________________________________________________________________________________________________________________
 16
16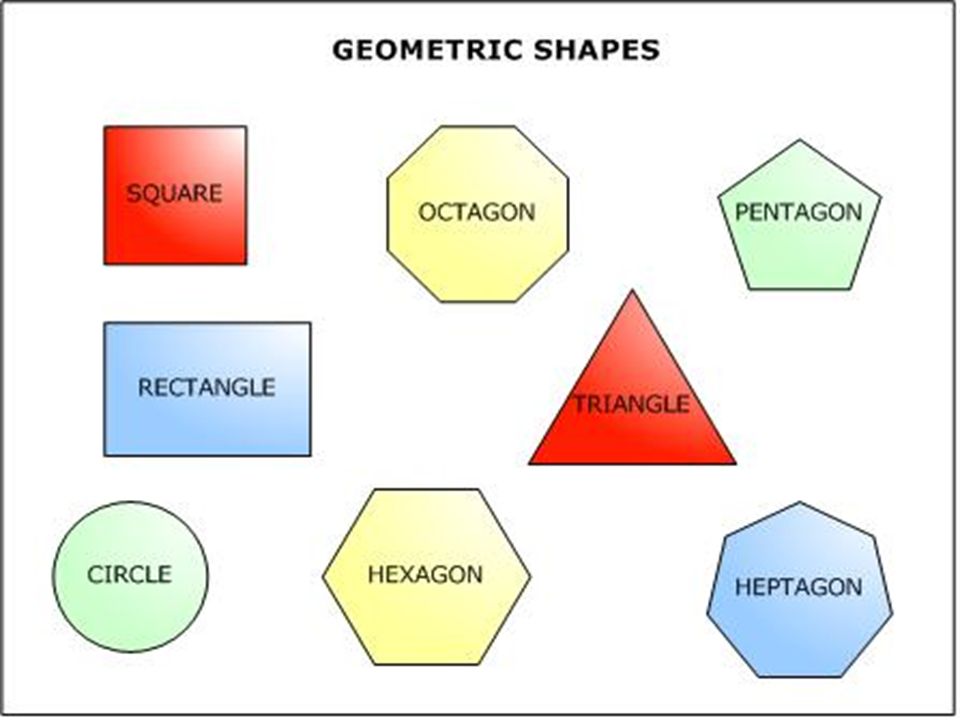
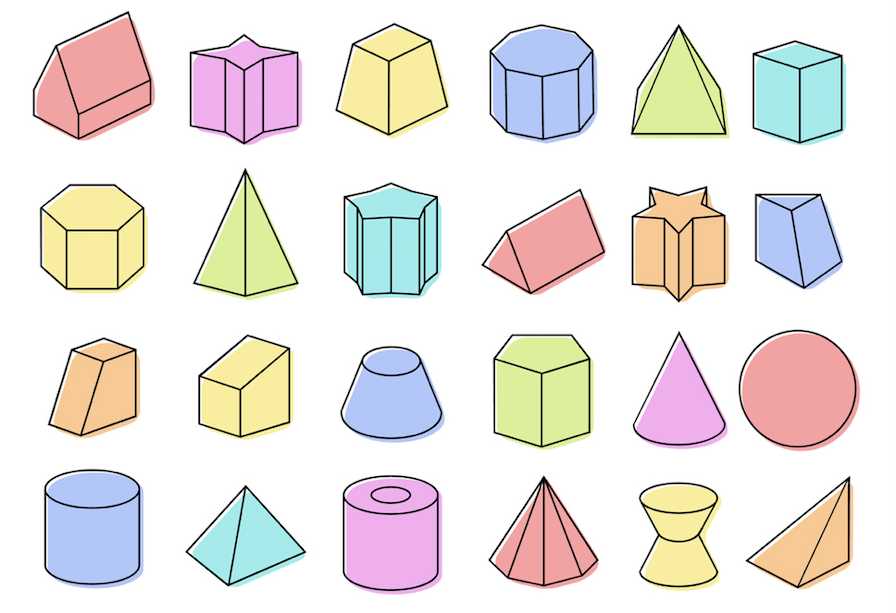 Определите, какие линии на рис. 21 являются пересекающимися, а какие непересекающимися. ________________________________________________
Определите, какие линии на рис. 21 являются пересекающимися, а какие непересекающимися. ________________________________________________ 25
25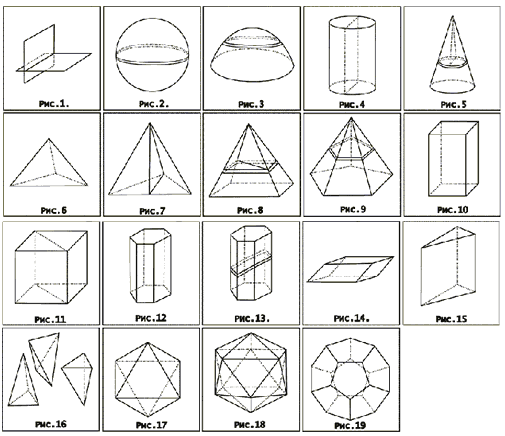
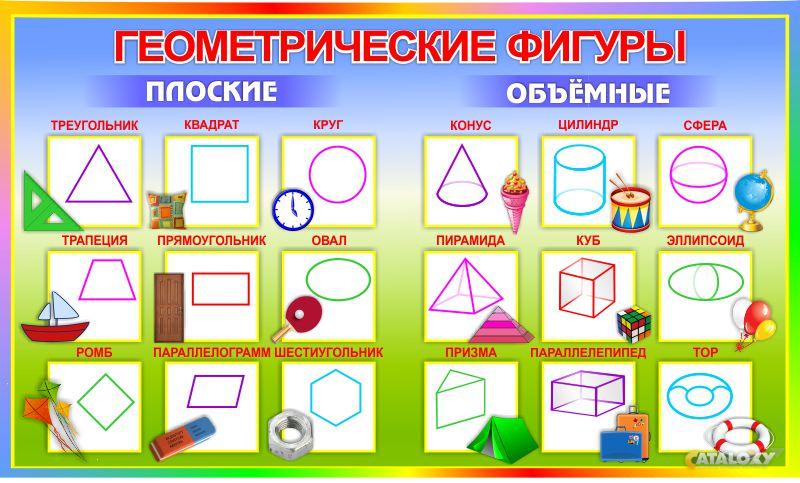 Обозначьте их. Выделите противоположные стороны в прямоугольнике и квадрате. Сделайте вывод о том, как располагаются противоположные стороны в данных фигурах. Закончите предложение:
Обозначьте их. Выделите противоположные стороны в прямоугольнике и квадрате. Сделайте вывод о том, как располагаются противоположные стороны в данных фигурах. Закончите предложение: Рассмотри окружность, изображенную на рис. 32. Чем являются отрезки АС и ВК? Как они расположены? Построй такой же чертеж. Используя знак ║, выпишите параллельные отрезки. _________________________________________
Рассмотри окружность, изображенную на рис. 32. Чем являются отрезки АС и ВК? Как они расположены? Построй такой же чертеж. Используя знак ║, выпишите параллельные отрезки. _________________________________________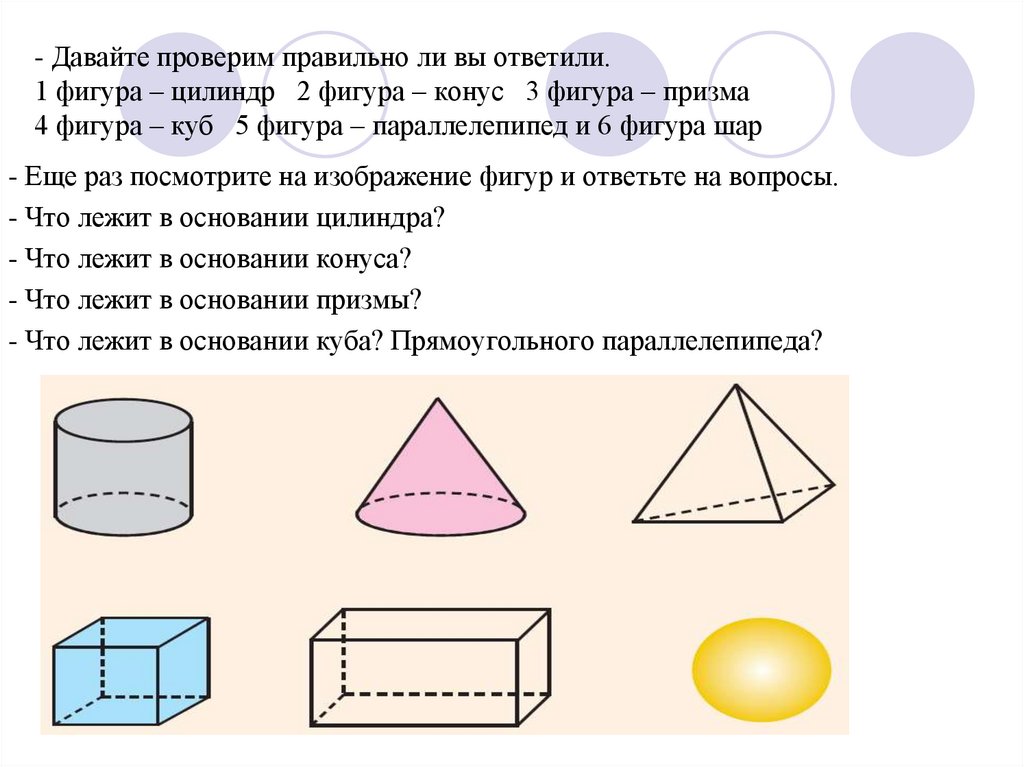
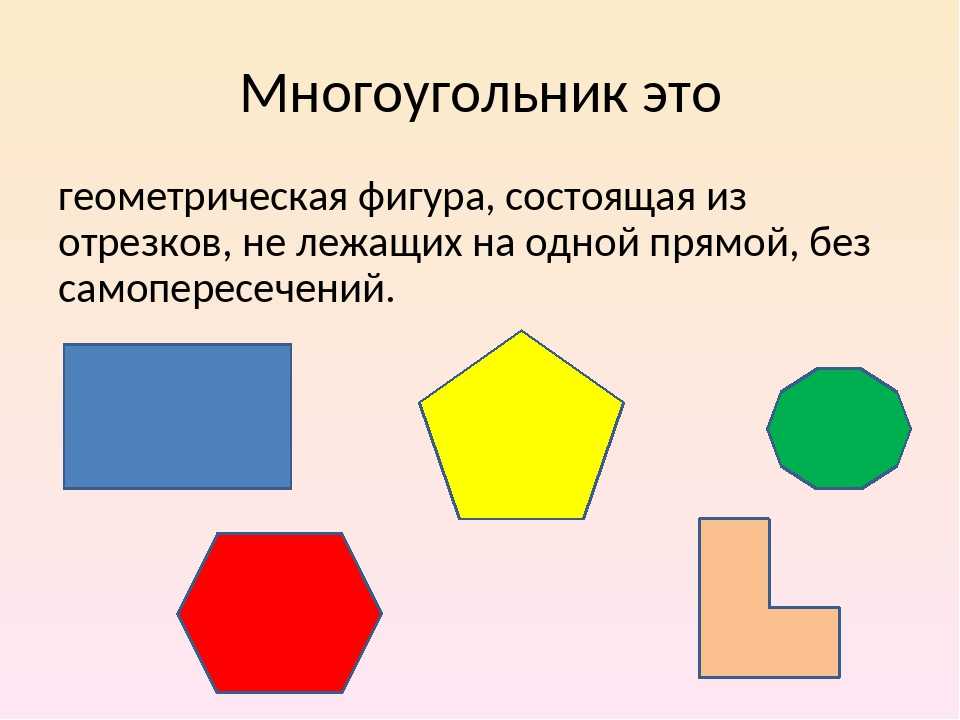
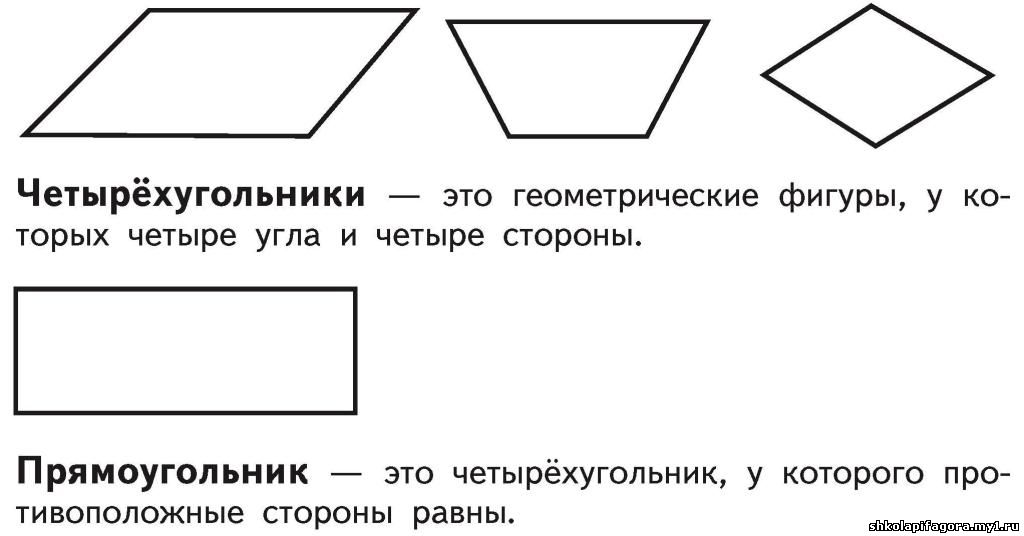 __________________________________
__________________________________ 39
39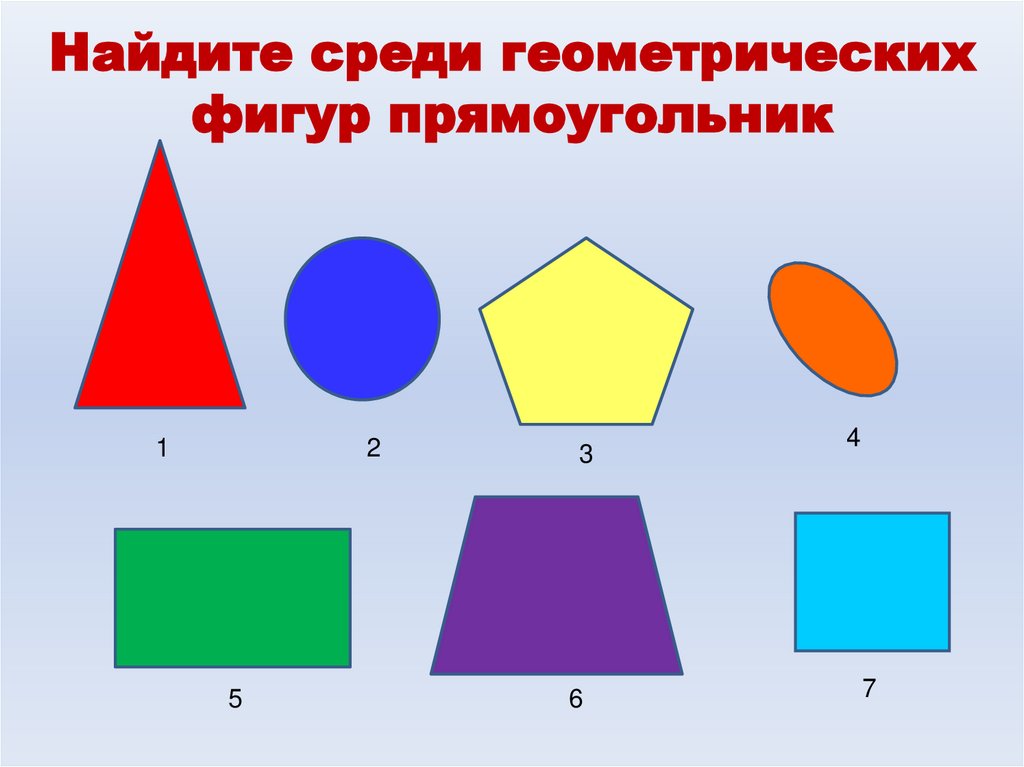
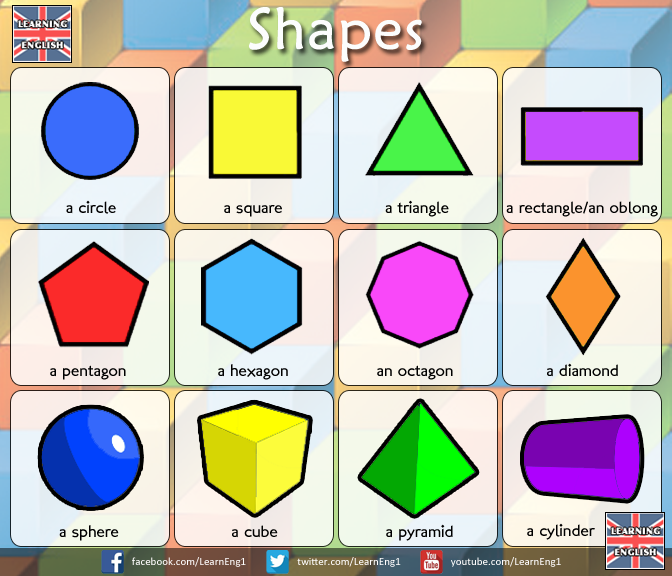
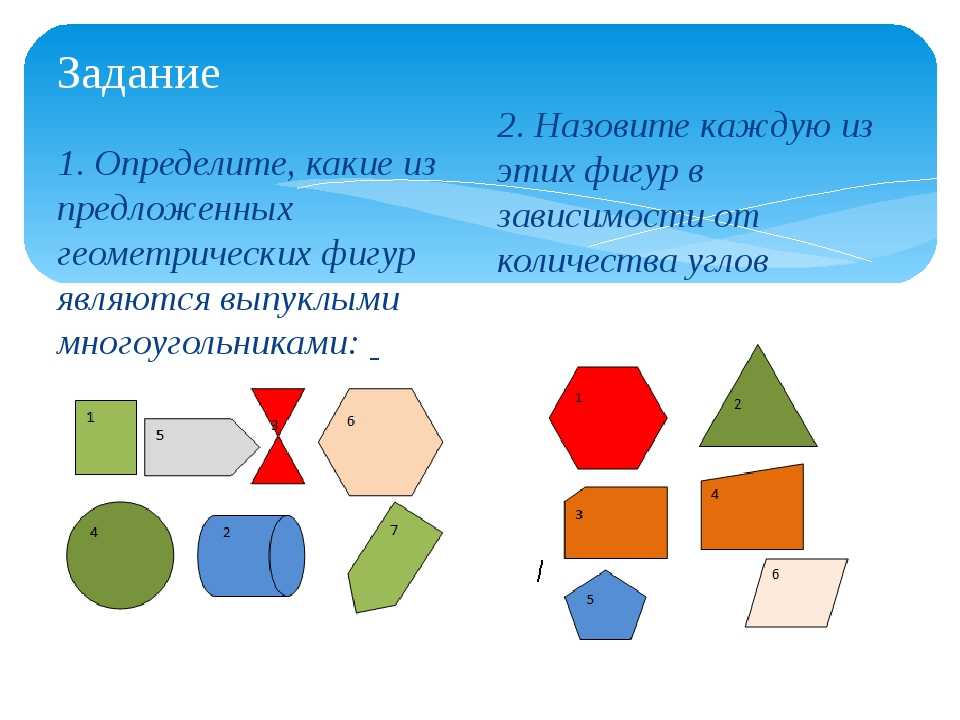 Что забыл написать Саша, чтобы не было ошибки? …………………………………………………………………………………………….
Что забыл написать Саша, чтобы не было ошибки? ……………………………………………………………………………………………. М. Н Перова, Г. М. Капустина “Математика 6 класс. ” Издательство “Просвещение” г. Москва 2004 г.
М. Н Перова, Г. М. Капустина “Математика 6 класс. ” Издательство “Просвещение” г. Москва 2004 г.