Формулы по математике для 3 класса: Математика 2-3 класс (правила, формулы) | Презентация к уроку по математике (2 класс) по теме: – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Основные формулы по математике – Математика – Теория, тесты, формулы и задачи

Главная –
Формулы и прочее –
Математика: Основные формулы

Знание формул по математике является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по математике, которые надежно хранятся в памяти ученика – это основной инструмент, которым он должен оперировать при решении математических задач. На этой странице сайта представлены основные формулы по школьной математике.

Изучать основные формулы по школьной математике онлайн:

Вперёд

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше.
В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

Урок математики 3 класс. Л.Г.Петерсон. Тема “Формула работы”

I. Организационный момент.

– Сейчас урок математики.

II. Мотивация к учебной деятельности.

– Давайте прочитаем хором высказывание

Человек лишь тогда чего-то добивается, когда он верит в свои силы. (немецкий философ Андреас Фейербах)

– О каких качествах идет речь?

– Как эти качества могут нам пригодиться?

III. Актуализация знаний.

– В математике часто используются формулы.

– Какие формулы вы знаете?

– А зачем они нужны? (Чтобы решать похожие и обратные задачи)

– Рассмотрите таблицу. О каких величинах можно составить задачи.

– Составьте задачи по данным таблицы.

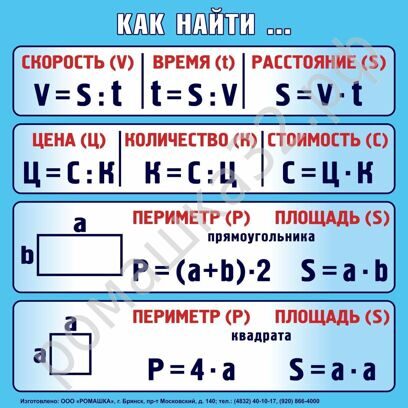
s	v	t
?	60 км/ч	4ч
540 км	?	6ч
57км	19км/ч	?

S=v•t t=s:v v=a•b•c s= a•b v=s:t

– Какие формулы вы будете использовать для решения этих задач? Подчеркнем их и прочитаем.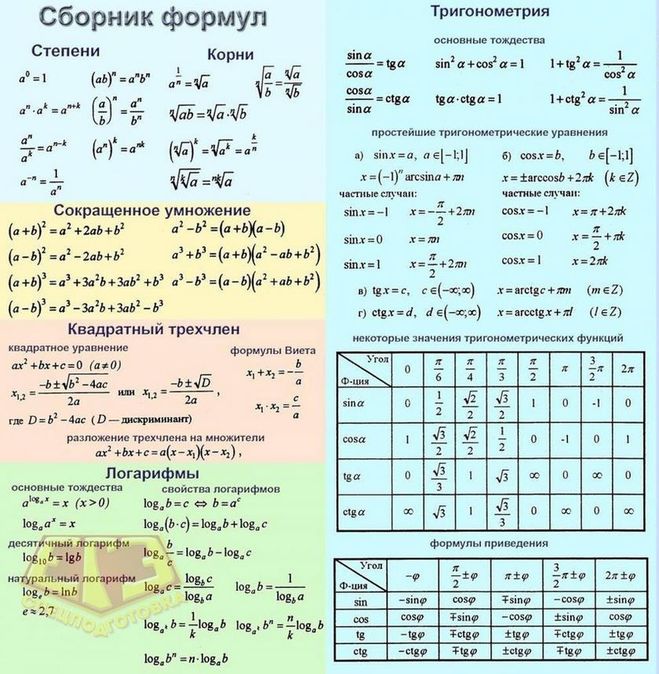

– Запишите в тетради только ответы этих задач.

– Давайте проверим с помощью сигнальных кругов.

-Те, кто не ошибся в решении задач, поставьте на полях +.

IV. Пробное действие.

– Запишите формулу, для решения следующей задачи.

«Одна швея за 5ч сшила 20 фартуков, другая за 4ч сшила 16 таких же фартуков. Какая швея работает быстрее?»

– Какие формулы записали? А кто не записал никакой формулы?

– В чем трудность? (Не могу записать формулу для такой задачи)

– Почему возникло затруднение? (Не знаем такой формулы)

– О чем эта задача? (о работе)

– Какие величины есть в задаче? (время работы, скорость работы)

– Какая новая величина? (работа)

– Как же можно назвать эту формулу? (формула работы)

V. Сообщение темы урока и постановка целей.

– Итак тема урока «Формула работы»

– Какие же цели мы поставим на сегодняшний урок?

Цели урока:

1. Узнать формулу работы.

2. Научиться решать задачи по формуле работы.

VI. Решение учебной задачи. Открытие нового знания.

– Заполним таблицу к задаче.

– О каких величинах идет речь в этой задаче?

(о времени, количестве выполненной работы)

– Если сказано «быстрей», то о какой величине идет речь?

– Какие задачи напоминает? (задачи на движение)

– Как же найти скорость работы? (всю работу разделить на время)

– В математике скорость работы принято обозначать v, так же, как и в задачах на движение.

Вся выполненная работа – А,

Время, затраченное на работу – t, так же, как и в задачах на движение.

– Попробуйте сами записать формулу, по которой можно найти скорость работы. v=A: t

– А теперь выведем формулу работы.

– Чем является А? (А – делимое, чтобы найти делимое, нужно частное умножить на делитель)

– Прочитайте получившуюся формулу. A=v•t

– Какую еще формулу можно вывести? t= A: v

– А теперь сверим с текстом на доске.

– Что нового узнали, почитав текст?

(Скорость еще называют производительностью)

– Что же мы подразумеваем под словом работа?

VII. Физминутка.

– Объясните, как вы понимаете смысл следующих высказываний? (с. 44 № 1)

– Давайте еще раз озвучим цели урока.

– Узнали формулу работы? Прочитайте ее.

– Какие формулы вывели? Прочитайте их.

VIII. Первичное закрепление.

– Какой была вторая цель?

(Научиться решать задачи по формуле работы.)

– Предлагаю выполнить следующие задания:

1. Составить и решить задачи по таблице.

A	v	t
?	4 детали/мин	5 мин
160 скворечников	?	8 дней
120 шт.	60 шт/ч	?

A=v•t v=A: t t= A: v

– Запишите решение этих задач.

-Проверим решение задач через документ-камеру.

– Какую формулы выбрали для решения задач?

– Покажите, какую формулу использовали для нахождения неизвестной величины.

– Те, кто не ошибся в решении задач, поставьте на полях +.

2. Практическая работа (индивидуальные карточки с примерами)

– А сейчас вы попробуете вычислить производительность своего умственного труда.

– Будем решать на время примеры, а данные заносить в таблицу.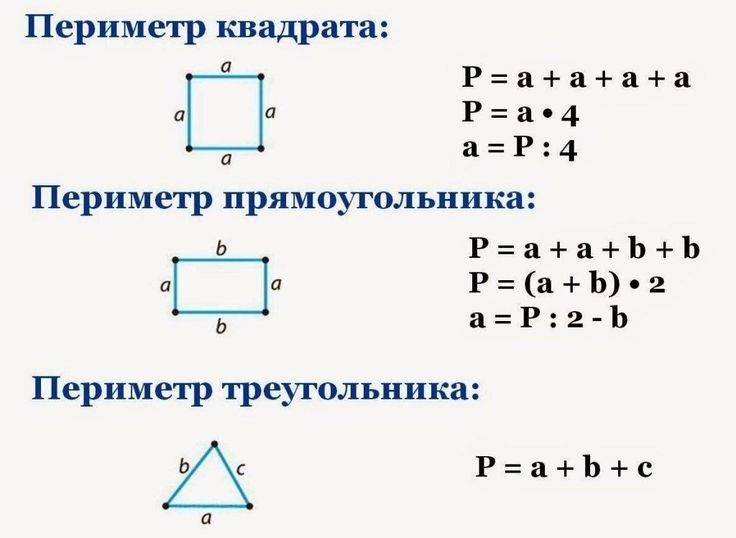

Вся работа A

Производительность

Время работы t

…

2мин

3. Взаимопроверка

– Давайте проверим правильность решения.

– Запишите количество правильных ответов в таблицу.

– Если количество правильных ответов не меньше 10 – поставьте себе +

– Как узнать производительность? Какой формулой воспользуемся? (v=A: t)

– Вычислите свою производительность.

(количество правильных примеров разделить на 2 мин)

-Где в жизни может пригодиться умение находить производительность, объем работы, время работы?

IX. Контроль достижения целей.

– А теперь вернемся к задаче, которая вызвала затруднение.

– Какую же формулу выберем?

– Запишите самостоятельно решение этой задачи в тетрадь.

– Проверим решение.

– Те, кто правильно решил задачу, поставьте на полях +.

X. Рефлексия.

– Итак, какой была тема урока?

– Какие цели мы поставили на урок? Прочитайте формулу работы.

– Достигли этих целей?

– Помогли ли нам в достижении поставленных целей те качества, о которых мы говорили в начале урока.?

XI. Д/з с. 44 № 4, № 5.

Основные математические формулы

Здесь вы найдете исчерпывающий список основных математических формул, обычно используемых при выполнении основных математических вычислений.

n — набор чисел, среднее значение = (a ₁ + a ₂ + a ₃ ,+……+ a _n )/n

Процент:

Процент в дробь: x% = x/100

Формула процента: Ставка/100 = процент/основание

Ставка: процент.
База: Сумма, от которой вы берете процент.
Процент: Ответ, полученный путем умножения основания на скорость

Формулы дробей:

Преобразование неправильной дроби в смешанное число:

Формула пропорции:

В пропорции произведение крайностей (ad) равно произведению средних (bc),

Таким образом, ad = bc

Математические формулы для потребителей:

Скидка = прейскурантная цена × ставка дисконта

Цена продажи = прейскурантная цена − скидка

Ставка дисконтирования = скидка ÷ прейскурантная цена

Налог с продаж = цена товара × налоговая ставка

Проценты = основная сумма × процентная ставка × время

Чаевые = стоимость еды × ставка чаевых

Комиссия = стоимость обслуживания × ставка комиссии

Геометрические формулы:

Периметр :

Периметр квадрата : s + s + s + s
s: длина одной стороны

Периметр прямоугольника : l + w + l + w
l: длина:
ширина

Периметр треугольника : a + b + c

a, b и c: длины трех сторон

Площадь:

Площадь квадрата : s × s
s: длина одной стороны

Площадь a прямоугольник : l × w
l: длина
w: ширина

Площадь треугольника : (b × h)/2
b: длина основания
h: длина высоты

Площадь трапеции : (b ₁ + b ₂ ) × h/2
b ₁ и b ₂ : параллельные стороны или основания
h: длина высота

объем:

объем куба : s × s × s
s: длина одной стороны

объем коробки : l × w5 l : 9003 длина
w: ширина
h: высота

Объем сферы : (4/3) × pi × r ³
pi: 3,14
r: радиус сферы

Объем треугольной призмы : площадь треугольника × высота = (1/2 основания × высота) × высота
основание: длина основания треугольника
height: высота треугольника
Height: высота треугольной призмы

Объем цилиндра :pi × r ² × высота
pi: 3,14
r: радиус окружности основания
Высота: высота цилиндра

Есть вопросы по основным математическим формулам? Отправить мне письмо здесь и задайте мне любые вопросы об этих основных математических формулах

Квадратичная формула: простые шаги
26, 23 января 11:44
Узнайте о квадратичной формуле, дискриминанте, важных определениях, связанных с формулой, и приложениях.
Подробнее
Формула площади — список важных формул
25, 23 января 05:54
Что такое формула площади для двумерной фигуры? Вот список тех, которые вы должны знать!
Подробнее

Основные математические формулы – GeeksforGeeks

Математика предлагает бесконечные возможности для исследований и исследований в области чисел и их операций. Каждая область математики имеет дело с чем-то другим. Филиалы исследуют новые методы и стандарты расчета, чтобы сделать ежедневную торговлю еще более удобной.

Математика делится на различные разделы в соответствии с используемыми способами вычислений и темами, которые они охватывают. Ветви включают геометрию, алгебру, арифметику, проценты, экспоненты и т. Д. Математика также предоставляет стандартные производные формулы, чтобы сделать операции или расчеты точными. В данной статье представлены все основные формулы, имеющиеся в математике по разным ее разделам или областям.

Основные математические формулы

Формула – это математическое выражение или определенное правило, которое выводится из отношения между двумя или более величинами, а полученный конечный продукт выражается в символах. Формулы математики включали числа, известные как константы, буквы, которые представляют неизвестные значения и известны как переменные, математические символы, известные как знаки, и в некоторых случаях экспоненциальные степени.

Арифметика

Арифметика – древнейший метод вычислений, известный до сих пор. Слово арифметика происходит от греческих слов «арифмос», что буквально означает числа. Брахмагупта индийский математик известен как «отец арифметики ». И Фундаментальная теория теории чисел была предложена Карлом Фридрихом Гауссом в 1801 году.

Основными арифметическими операциями являются сложение, вычитание, умножение и деление.

Арифметическая формула

Среднее арифметическое (среднее) = Сумма значений/Количество значений.

Алгебра

Алгебра — это элементарный предмет математики, который занимается изучением оценки чисел и символов. Алгебраические операции выполняются для определения неизвестных значений, которые выражаются буквами. Алгебраические уравнения представляют собой выражения, образованные комбинацией переменных, констант, факторов и коэффициентов переменных.

Базовая алгебраическая формула

а ² – b ² = (а – b)(а + b)
(а + b) ^{2 7 аб 2 7 аб 2
а а ²}
A ² + B ² = (A + B) ² – 2AB
(A – B) ² = A ² – B) ² = A ² – 2 9012 2 9012. 2 9012 2
– 2 9012 2 9012 2
(A – B) ² = A
(A – B) ² = A
(A – B) ² = A
a + b + c) ² = a ² + b ² + c ² + 2ab + 2bc + 2ca
(a – b – c) ² = A ² + B ² + C ² – 2AB + 2BC – 2CA
(A + B) ³ = A ³ + 3A ² = A ³ + 3A ² 2 2 2 2 2 2 2 2 . + b ³
(a – b) ³ = a ³ – 3a ² b + 3ab ² – b ³
a ³ – b ³ = (a – b)(a ² + ab + b ² )
a ³ + b ³ = (a + b)(a ² – ab + b ²)
(A + B) ⁴ = A ⁴ + 4A ³ B + 6A ² B ² + 4Ab ³ + B ² + 4AB ³ + B ² + 4AB ³ + B ² + 4AB ³ + B ² + 4AB ³ + B ² + 4AB ³ + B ^{. ) ⁴ = A ⁴ – 4A ³ B + 6A ² B ² – 4AB ³ + B ⁴}
222222.^{^{^{^{^{^{^{^{^{^{^{^{^{^{^{^{^{^{^{^{4 ^{^{+ ^{^{4 ^{^{+ ^{4 ^{^{+ ^{. )(a + b)(a ² + b ² )}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}
(a ^m )(a ⁿ ) = a ^{m + n}
(ab) ^m = a ^m b ^m
(a ^m ) ⁿ = a ^mn

Geometry

Geometry is a part of mathematics that is concerned with the изучение форм, размеров, параметров, измерений, свойств и размеров. Обычно существует три типа геометрии. Это евклидова геометрия, сферическая геометрия и гиперболическая геометрия.

Формула базовой геометрии

Прямоугольник

Периметр прямоугольника = 2 (L + B)
Площадь прямоугольника = L × B

, где ‘L’ – длина, а ‘B’ – это хлебная ^{8928926292892629 2}

, где ‘L’ – длина.

Площадь квадрата = A ²
Периметр квадрата = 4A

, где ‘A’ – это длина бок 9000

2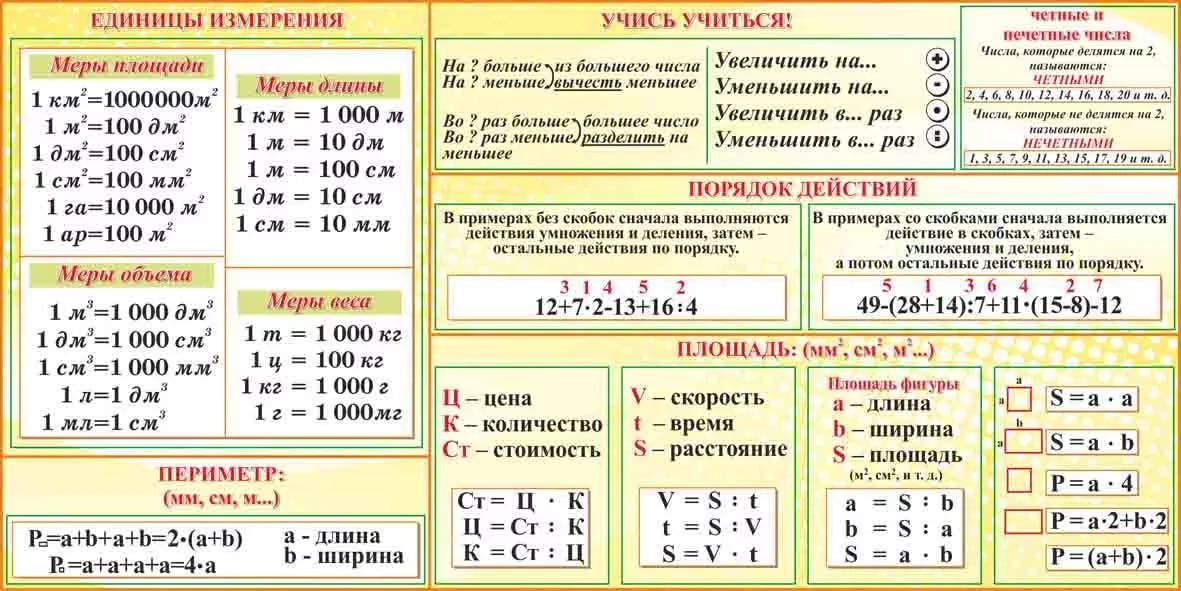22222222222222222222222222222222222222222222222222222222222222222222222222222222222929н. треугольника = 1/2 × b × h
Где «b» — основание треугольника, а «h» — высота треугольника
- Трапеция
Площадь трапеции = 1/2 × (b 2 _{1 909010 + b} ) × h
, где B ₁ и B ₂ являются основаниями трапеции
и, H = высота трапеции
- Circle

0
0
0
0

r ²
Длина окружности = 2πr
Where ‘r’ is the radius of a Circle
Cube
Surface Area of Cube = 6a ²
Where ‘a’ is the length of the sides of the Cube
Цилиндр
Площадь изогнутой поверхности цилиндра = 2πrh
Общая площадь поверхности цилиндра = 2πr (R + H)
Общая поверхность Cylinder = 2πr (R + H)
Общая объем калишера = 2πr (r + h)
. Общая поверхность = vIder = v = v = v = v = v = vder = v = v = v = vder = v = vder = vder = 2πr (r + h)
.
Где «r» — радиус основания цилиндра
А, «h» — высота цилиндра
Конус
Общая площадь криволинейной поверхности конуса = πrl
2 площадь конуса = πr(r + l) = πr[r + √(h
² + r ² )]
Здесь ‘r’ — радиус основания конуса, а h = высота конуса
Сфера
Surface Area of a Sphere = S = 4πr ²
Volume of a Sphere = V = 4/3 × πr ³
Where, r = Radius of the Sphere
Probability
Вероятность — это математический термин, используемый для определения вероятности наступления определенного события. Вероятность можно просто определить как возможность возникновения события. Она выражается по линейной шкале от 0 до 1. Существует три типа теоретической вероятности, экспериментальной вероятности и субъективной вероятности.
Базовая формула вероятности
P(A) = n(A)/n(S)
Где
P(A) — вероятность события.
n(A) — количество благоприятных исходов
n(S) — общее количество событий
Дробь
Дробь — это число, выраженное целыми числами, в котором числитель делится на знаменатель. Дробь – это в основном частное от деления.
Формула основных фракций
(а + b/c) = (a × c) + b/c
(a/b + d/b) = (a + d)/b
(a/b + c/d ) = (a × d + b × c/b × d)
a/b × c/d = ac/bd
(a/b)/(c/d) = a/b × d/c
Процент
Процент — это числовое значение или отношение, выраженное в виде доли от 100. Обычно оно обозначается знаком %.
Основная формула процента
Процент = (Сумма в категории/Общая стоимость) × 100
Примеры задач
Вопрос 1: Определите вероятность получения туза из карты, взятой из колоды.
Решение:
Дано:
Общее количество благоприятных исходов n(S) = 52

Количество лицевых карт в колоде = 12 Теперь
P(A) = n(A)/n(S)
=> 12/52
=> 3/13
Следовательно, вероятность получить лицевую карту из колоды карт равна 3/ 13.
Вопрос 2: Упростить 3/(x – 1) + 1/(x(x – 1) = 2/x
Решение:
=> 3x + 1/x(x – 1) ) = 2(x – 1)/x(x – 1)
=> 3x + 1 = 2(x – 1)
=> x = -3
Вопрос 3: Если x + 1/x = 3. Найдите значение x ² + 1/x ².
=> х ² + 2 × x × 1/x + (1/x) ² = 9
=> x ² + 1/x ² + 2 = 9
=> x ² + 1/ x ² = 7
Вопрос 4: Если радиус окружности равен 21см. Найдите площадь данного круга.

Решение:
Дано:
Радиус круга равен 21см.
Имеем,
Площадь круга (A) = πr ²
=> 22/7 × 21 × 21
=> 1386см ²
Следовательно, площадь данного круга равна 1386см ²
Вопрос 5: Найдите площадь треугольника с основанием 100см и высотой 20см.
Решение:
Дано:
Основание треугольника равно 100см.
Высота треугольника 20см.
У нас есть,
Площадь (A) = 1/2 × b × h
=> 1/2 × 10 × 20
=> 1000 см ²
Вопрос 6: У Пунам есть 4/5 части поля, 2/5 из которых она использует для сельского хозяйства. Какая часть фермы остается для других целей?
Решение:

Дано:
Общая доля земли 4/5.
Общая фракция, используемая для фарма 2/5.