Эйлер круги – Диаграмма Эйлера — Википедия
Диаграмма Эйлера — Википедия
Материал из Википедии — свободной энциклопедии
Пример кругов Эйлера. Буквами обозначены, например, свойства: B{\displaystyle B} — живое существо, A{\displaystyle A} — человек, C{\displaystyle C} — неживая вещьДиагра́ммы Э́йлера (круги́ Э́йлера) — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Первое их использование приписывают Леонарду Эйлеру (подробней см. ниже). Используется в математике, логике, менеджменте и других прикладных направлениях. Не следует их путать с диаграммами Эйлера — Венна (о различии между ними см. ниже).
Диаграммы Эйлера также называют кругами Эйлера. При этом «круги» — это условный термин, вместо кругов могут быть любые фигуры.
На диаграммах Эйлера множества изображаются кругами (или другими фигурами). Причём непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами. Например, диаграмма на рисунке показывает, что множество
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.[1]
Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в со
ru.wikipedia.org
|
www.sites.google.com
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ «КРУГОВ ЭЙЛЕРА»
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ «КРУГОВ ЭЙЛЕРА»
Рыбина Ангелина
Класс 5 «Д», МОУ «СОШ № 59 с УИП», РФ, г. Саратов
Багаева Ирина Викторовнанаучный руководитель, педагог высшей категории, преподаватель математики, МОУ «СОШ № 59 с УИП», РФ, г. Саратов
«… круги очень подходят для того, чтобы облегчить наши размышления»
Леонард Эйлер
Нет ученого, имя которого упоминалось бы в учебной математической литературе столь же часто, как имя Эйлера. Даже в средней школе логарифмы и тригонометрию изучают до сих пор в значительной степени «по Эйлеру».
В 1741 году Эйлер пишет «Письма о разных физических и философических материях, написанные к некоторой немецкой принцессе…», где появились впервые «круги Эйлера». Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления».
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера».
С помощью этих кругов Эйлер изобразил и множество всех действительных чисел:
· N — множество натуральных чисел,
· Z — множество целых чисел,
· Q — множество рациональных чисел,
· R — множество всех действительных чисел.
Рисунок 1. Изображение множества действительных чисел
Что такое множество?
В математике нет точного определения этого понятия. Понятие «множество» не определяется, оно поясняется примерами: множество яблок в корзине; множество точек отрезка прямой. Множество состоит из элементов. В приведенных примерах — это яблоки, буквы, точки.
Множества обозначаются заглавными буквами латинского алфавита: А, В, С, … K, M, N … Х, …; элементы множества — строчными буквами алфавита: а, в, с, … k, m, n … х, у, …. А={а; в; с; d} — множество А состоит из элементов а, в, с, d, или, говорят, что элемент а принадлежит множеству А, записывается: аА (знак читается: «принадлежит»). Элемент 5 не входит в множество А, говорят, что «5 не принадлежит А»: 5 А, или . Если множество В не содержит ни одного элемента, то говорят, что оно пустое, обозначается: В=.
Под множеством можно понимать совокупность каких-либо объектов, называемых элементами множества [1, с. 18]. Примерами множеств могут быть и дома на нашей улице, и алфавит — совокупность букв, и наш 5 «Д» класс — множество учеников.
Множества могут быть:
· Конечное (элементы которого можно пересчитать; например — множество цифр)
· Бесконечное (пересчитать нельзя; например — песчинки в пустыне)
· Пустое (не содержащее ни одного элемента; например — множество зайцев, которые учатся в нашем классе).
Множество K называется подмножеством множества N, если каждый элемент множества K является элементом множества N. Обозначается: KÍN. Говорят, что множество K включается в множество N.
Подмножества можно проиллюстрировать кругами Эйлера.
Рисунок 2. Изображение подмножества
Действия с множествами
В математике существуют несколько операций над множествами. Мы разберем два из них: пересечение и объединение.
1. Пересечение множеств
Пересечением множеств M и N называется множество, состоящее из элементов, одновременно принадлежащих M и N. Пересечение множеств M и N обозначается [1, с. 23].
Пример. Множество N = { А Н Д Р Е Й };
множество K = { А Л Е К С Е Й }; множество M = { Д М И Т Р И Й }
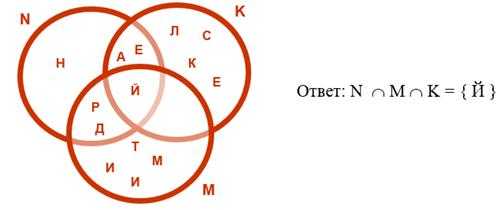
Рисунок 3. Пример пересечения множеств
2. Объединение множеств
Объединение множеств — это множество, содержащее в себе все элементы исходных множеств. Объединение множеств M и N обозначается .
Пример ; 2) объединение множества всех пород собак и множества мопсов есть множество всех собак.
Операции объединения и пересечения множеств очень удобно показывать с помощью кругов Эйлера.
По определению в пересечение двух множеств M и N входят элементы, принадлежащие множествам M и N одновременно
Пример. Пусть D — множество из 12 самых хороших девочек, M — множество из 12 самых умных мальчиков. Получили наш класс.

Рисунок 4. Пример объединения множеств
3. Вложенные множества.
Пример. Имеется три множества: «дети», «школьники», «учащиеся начальной школы». Мы видим, что эти 3 множества находятся одно внутри другого. Про множество, находящееся внутри другого множества, говорят, что оно вложенное.
Рисунок 5. Пример вложенных множеств
Задачи, которые можно решить с помощью диаграмм Эйлера
Задача № 1
На стол бросили две салфетки 10 см х 10 см. Они покрыли площадь стола, равную 168. Какова площадь перекрытия?
Решение
1)168 – 10 х 10 = 68;
2)10 х 10 – 68 = 32.
Ответ: 32 см
Рисунок 6. Рисунок к задаче № 1
Задача № 2
В поход ходили 80 % учеников класса, а на экскурсии было 60 %, причем каждый был в походе или на экскурсии. Сколько процентов класса были и там, и там?
Решение
А — множество учеников, которые ходили в поход
В — множество учеников, которые были на экскурсии
100 % – 80 % = 20 %
60 % – 20 % = 40 %
Ответ: 40 %
Рисунок 7. Рисунок к задаче № 2
Задача № 3
В нашем классе 24 ученика. Все они хорошо провели зимние каникулы.10 человек катались на лыжах, 16 ездили на каток, а 12 — лепили снеговиков. Сколько учеников смогли покататься и на лыжах, и на коньках, и слепить снеговика?
А — множество ребят, катающихся на лыжах
В — множество ребят, катающихся на коньках
С — множество ребят, лепивших снеговиков
Решение
Пусть х — число ребят,
которые успели за эти каникулы всё!
(12 – х) + (16 – х) + (10 – х) + х = 24
Ответ: 7 ребят
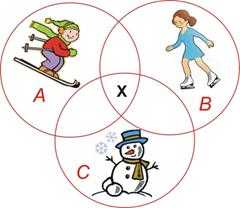
Рисунок 8. Рисунок к задаче № 3
Задача № 4
9 моих друзей любят бананы, 8 – апельсины, а 7 – сливы, 5 – бананы и апельсины, 3 – бананы и сливы, 4 – апельсины и сливы, 2 – бананы, апельсины и сливы. Сколько у меня друзей?
Решение
5 – 2 = 3 3 – 2 = 1 4 – 2 = 2
9 – 6 = 3 8 – 7 = 1 7 – 5 = 2
3 + 1 + 2 + 3 + 2 + 1 + 2 = 14
Ответ: 14 друзей
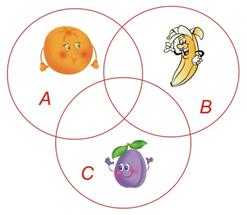
Рисунок 9. Рисунок к задаче № 4
Задача № 5
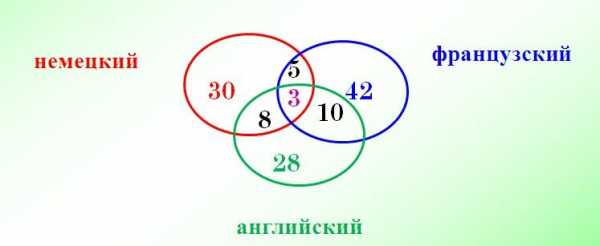
В пионерском лагере «Дубки» в смене актива отдыхали: 30 отличников, 28 победителей олимпиад и 42 спортсмена. 10 человек были и отличниками и победителями олимпиад, 5 — отличниками и спортсменами, 8 — спортсменами и победителями олимпиад, 3 — и отличники, и спортсмены, и победители олимпиад.
Сколько ребят отдыхали в лагере?
А — множество отличников
В — множество победителей олимпиад
С — множество спортсменов
Решение
10 – 3 = 7 5 – 3 = 2 8 – 3 = 5
30 – 12 = 18 28 – 15 = 13 42 – 10 = 32
18 + 13 + 32 + 7 + 2 + 5 + 3 = 80
Ответ: 80 ребят
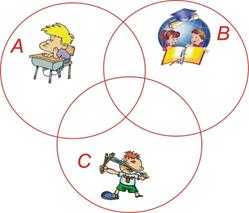
Рисунок 10. Рисунок к задаче № 5
3. Заключение
Диаграммы Эйлера — это общее название целого ряда способов графической иллюстрации , широко используемых в различных областях математики: теория множеств, теория вероятностей, логика, статистика, компьютерные науки, и др. Применение кругов Эйлера позволяет даже пятикласснику легко решать задачи, которые обычным путем решаются только в старших классах.
Список литературы:
1.Александрова Р.А., Потапов А.М. Элементы теории множеств и математической логики. Практикум / Калининград. 1997. — 66 с.
2.Депман И.Я., Виленкин Н.Я. За страницами учебника математики. Пособие для учащихся 5—6 кл. М.: Просвещение, 1999. с. 189—191, 231.
3.Задачи для внеклассной работы по математике в V—VI классах: Пособие для учителей / Сост. В.Ю. Сафонова. Под ред. Д.Б. Фукса, А.Л. Гавронского. М.: МИРОС, 1993. — с. 42.
4.Занимательная математика. 5—11 классы. Как сделать уроки нескучными / Авт. сост. Т.Д. Гаврилова. Волгоград: Учитель, 2005. — с. 32—38.
5.Смыкалова Е.В. Дополнительные главы по математике для учащихся 5 класса. СПб: СМИО Пресс, 2009. — с. 14—20.
6.Энциклопедия для детей. Т. 11. Математика Глав.ред. М.Д. Аксёнова. М.: Аванта +, 2001. — с. 537—542.
sibac.info
Использование метода кругов Эйлера (диаграмм Эйлера–Венна) при решении задач в курсе информатики и ИКТ
Разделы: Информатика
1. Введение
В курсе Информатики и ИКТ основной и старшей школы рассматриваются такие важные темы как “Основы логики” и “Поиск информации в Интернет”. При решении определенного типа задач удобно использовать круги Эйлера (диаграммы Эйлера-Венна).
Математическая справка. Диаграммы Эйлера-Венна используются прежде всего в теории множеств как схематичное изображение всех возможных пересечений нескольких множеств. В общем случае они изображают все 2n комбинаций n свойств. Например, при n=3 диаграмма Эйлера-Венна обычно изображается в виде трех кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
2. Представление логических связок в поисковых запросах
При изучении темы “Поиск информации в Интернет” рассматриваются примеры поисковых запросов с использованием логических связок, аналогичным по смыслу союзам “и”, “или” русского языка. Смысл логических связок становится более понятным, если проиллюстрировать их с помощью графической схемы – кругов Эйлера (диаграмм Эйлера-Венна).
| Логическая связка | Пример запроса | Пояснение | Круги Эйлера |
| & – “И” | Париж & университет | Будут отобраны все страницы, где упоминаются оба слова: Париж и университет | Рис.1 |
| | – “ИЛИ” | Париж | университет | Будут отобраны все страницы, где упоминаются слова Париж и/или университет | Рис.2 |
3. Связь логических операций с теорией множеств
С помощью диаграмм Эйлера-Венна можно наглядно представить связь логических операций с теорией множеств. Для демонстрации можно воспользоваться слайдами в Приложение 1.
Логические операции задаются своими таблицами истинности. В Приложении 2 подробно рассматриваются графические иллюстрации логических операций вместе с их таблицами истинности. Поясним принцип построения диаграммы в общем случае. На диаграмме – область круга с именем А отображает истинность высказывания А (в теории множеств круг А – обозначение всех элементов, входящих в данное множество). Соответственно, область вне круга отображает значение “ложь” соответствующего высказывания. Что бы понять какая область диаграммы будет отображением логической операции нужно заштриховать только те области, в которых значения логической операции на наборах A и B равны “истина”.
Например, значение импликации равно “истина” в трех случаях (00, 01 и 11). Заштрихуем последовательно: 1) область вне двух пересекающихся кругов, которая соответствует значениям А=0, В=0; 2) область, относящуюся только к кругу В (полумесяц), которая соответствует значениям А=0, В=1; 3) область, относящуюся и к кругу А и к кругу В (пересечение) – соответствует значениям А=1, В=1. Объединение этих трех областей и будет графическим представлением логической операции импликации.
4. Использование кругов Эйлера при доказательстве логических равенств (законов)
Для того, чтобы доказать логические равенства можно применить метод диаграмм Эйлера-Венна. Докажем следующее равенство ¬(АvВ) = ¬А&¬В (закон де Моргана).
Для наглядного представления левой части равенства выполним последовательно: заштрихуем оба круга (применим дизъюнкцию) серым цветом, затем для отображения инверсии заштрихуем область за пределами кругов черным цветом:
Рис.3 Рис.4
Для визуального представления правой части равенства выполним последовательно: заштрихуем область для отображения инверсии (¬А) серым цветом и аналогично область ¬В также серым цветом; затем для отображения конъюнкции нужно взять пересечение этих серых областей (результат наложения представлен черным цветом):
Рис.5 Рис.6 Рис.7
Видим, что области для отображения левой и правой части равны. Что и требовалось доказать.
5. Задачи в формате ГИА и ЕГЭ по теме: “Поиск информации в Интернет”
Задача №18 из демо-версии ГИА 2013.
В таблице приведены запросы к поисковому серверу. Для каждого запроса указан его код – соответствующая буква от А до Г. Расположите коды запросов слева направо в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
| Код | Запрос |
| А | (Муха & Денежка) | Самовар |
| Б | Муха & Денежка & Базар & Самовар |
| В | Муха | Денежка | Самовар |
| Г | Муха & Денежка & Самовар |
Решение:
Для каждого запроса построим диаграмму Эйлера-Венна:
| Запрос А Рис.8 |
Запрос Б Рис. 9 |
Запрос В Рис. 10 |
Запрос Г Рис. 11 |
Ответ: ВАГБ.
Задача В12 из демо-версии ЕГЭ-2013.
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысяч) |
| Фрегат | Эсминец | 3400 |
| Фрегат & Эсминец | 900 |
| Фрегат | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Эсминец?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Пусть
Ф – количество страниц (в тысячах) по запросу Фрегат;
Э – количество страниц (в тысячах) по запросу Эсминец;
Х – количество страниц (в тысячах) по запросу, в котором упоминается Фрегат и не упоминается Эсминец;
У – количество страниц (в тысячах) по запросу, в котором упоминается Эсминец и не упоминается Фрегат.
Построим диаграммы Эйлера-Венна для каждого запроса:
| Запрос | Диаграмма Эйлера-Венна | Количество страниц |
| Фрегат | Эсминец | Рис.12 | 3400 |
| Фрегат & Эсминец | Рис.13 | 900 |
| Фрегат | Рис.14 | 2100 |
| Эсминец | Рис.15 | ? |
Согласно диаграммам имеем:
- Х+900+У = Ф+У = 2100+У = 3400. Отсюда находим У = 3400-2100 = 1300.
- Э = 900+У = 900+1300= 2200.
Ответ: 2200.
6. Решение логических содержательных задач методом диаграмм Эйлера-Венна
Задача 1.
В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический – 14 человек, химический – 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек – и математический и физический, 5 и математический и химический, 3 – и физический и химический.
Сколько учеников класса не посещают никаких кружков?
Решение:
Для решения данной задачи очень удобным и наглядным является использование кругов Эйлера.
Самый большой круг – множество всех учеников класса. Внутри круга три пересекающихся множества: членов математического (М), физического (Ф), химического (Х) кружков.
Пусть МФХ – множество ребят, каждый из которых посещает все три кружка. МФ¬Х – множество ребят, каждый из которых посещает математический и физический кружки и не посещает химический. ¬М¬ФХ – множество ребят, каждый из которых посещает химический кружок и не посещает физический и математический кружки.
Аналогично введем множества: ¬МФХ, М¬ФХ, М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.
Известно, что все три кружка посещают 2 человека, следовательно, в область МФХ впишем число 2. Т.к. 8 человек посещают и математический и физический кружки и среди них уже есть 2 человека, посещающих все три кружка, то в область МФ¬Х впишем 6 человек (8-2). Аналогично определим количество учащихся в остальных множествах:
| Круги Эйлера с названиями
непересекающихся множеств: Рис. 16 |
Круги Эйлера с количественной
информацией: Рис. 17 Например, количество человек, которые посещают физический кружок 2+6+1+5=14 |
Просуммируем количество человек по всем областям: 7+6+3+2+4+1+5=28. Следовательно, 28 человек из класса посещают кружки.
Значит, 36-28 = 8 учеников не посещают кружки.
Ответ: 8.
Задача 2.
После зимних каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников класса двое не были ни в кино. ни в театре, ни в цирке. В кино побывало 25 человек, в театре – 11, в цирке 17 человек; и в кино, и в театре – 6; и в кино и в цирке – 10; и в театре и в цирке – 4.
Сколько человек побывало и в кино, и в театре, и в цирке?
Решение:
Пусть х – количество ребят, которые побывали и в кино, и в театре, и в цирке.
Тогда можно построить следующую диаграмму и посчитать количество ребят в каждой области:
Рис.18. |
В кино и театре побывало 6 чел., значит,
только в кино и театре (6-х) чел. Аналогично, только в кино и цирке (10-х) чел. Только в театре и цирке (4-х) чел. В кино побывало 25 чел., значит, из них только в кино были 25 – (10-х) – (6-х) – х = (9+х). Аналогично, только в театре были (1+х) чел. Только в цирке были (3+х) чел. Не были в театре, кино и цирке – 2 чел. Значит, 36-2=34 чел. побывали на мероприятиях. С другой стороны можем просуммировать количество человек, которые были в театре, кино и цирке: (9+х)+(1+х)+(3+х)+(10-х)+(6-х)+(4-х)+х = 34 33+х = 34. Отсюда следует, что только один человек побывал на всех трех мероприятиях. |
Ответ: 1.
Таким образом, круги Эйлера (диаграммы Эйлера-Венна) находят практическое применение при решении задач в формате ЕГЭ и ГИА и при решении содержательных логических задач.
Литература
- В.Ю. Лыскова, Е.А. Ракитина. Логика в информатике. М.: Информатика и Образование, 2006. 155 с.
- Л.Л. Босова. Арифметические и логические основы ЭВМ. М.: Информатика и образование, 2000. 207 с.
- Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и ИКТ для 8 класса: БИНОМ. Лаборатория знаний, 2012. 220 с.
- Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и ИКТ для 9 класса: БИНОМ. Лаборатория знаний, 2012. 244 с.
- Сайт ФИПИ: http://www.fipi.ru/
6.05.2013
urok.1sept.ru
Iteach
Материал из ИнтеВики — обучающей площадкой для проведения тренингов программы Intel
|
wiki.iteach.ru
Круги Эйлера – это… Что такое Круги Эйлера?
Круги́ Э́йлера[1] — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.
Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна, изображающие все комбинаций свойств, то есть конечную булеву алгебру. При диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц. Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.[2]
Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествамиНо достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна, подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют Диаграммы Эйлера — Венна.
Множества А и BСм. также
Примечания
- ↑ «Круги…» — это условный термин, вместо кругов могут быть любые многомерные фигуры, иерархически расположенные в пространстве, то есть одни фигуры поглощают либо часть других фигур, либо полностью.
- ↑ Leibniz G. W. Opuscules et fragments inédits de Leibniz. — Paris, 1903. — p. 293—321.
| Логика | |
|---|---|
| Формальная | Логические операции с понятиями Изменение содержания понятия: отрицание • ограничение • обобщение • деление |
| Математическая (теоретическая, символическая) | Логические связки (операции) над высказываниями Высказывание – построение над множеством {B, , , , 0, 1} |
dic.academic.ru
Круги Эйлера онлайн – 4 Июля 2016 – Примеры решений задач
Круги Эйлера, диаграммы Венна
Геометрическое моделирование множеств. Калькулятор.
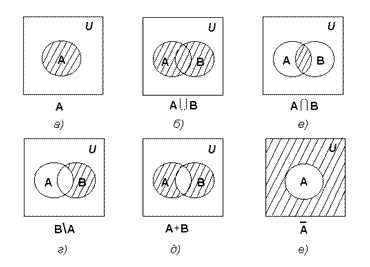
Для наглядного представления множеств и отношений между ними используется диаграммы Венна (иногда их называют кругами Эйлера или диаграммами Эйлера – Венна).
Универсальное множество изображают в виде прямоугольника, а множества, входящие в универсальное множество, – в виде кругов внутри прямоугольника; элементу множества соответствует точка внутри круга.
С помощью диаграмм Венна удобно иллюстрировать операции над множествами.
Калькулятор для построения кругов Эйлера.
Правила вввода основных обозначений операций над множествами:
| Операция | Обозначение | |
| математическое | в калькуляторе | |
| Дополнение | $\bar{A}$ | A’ |
| Пересечение | (A∩B) | (A intersection B) |
| Объединение | (А⋃B) | (A union B) |
| Симметрическая разность | (A∆B) | (symmetric difference of A and B) |
| Относительное дополнение | (A\B) | (A\B) |
Пример. Изобразить множество D с помощью кругов Эйлера (нарисовать диаграмму Эйлера-Венна):
№ | Множество D | Вводим в калькулятор |
1 | (А∩B’) ∪ C | (A intersection B’) union C |
2 | (А∩B) ∪C’ | (A intersection B’) union C’ |
3 | (А∪B) ∩ C | (A union B’) intersection C |
4 | (А∪B) ∩C’ | (A union B’) intersection C’ |
5 | (А∩B) ∪ C | (A intersection B) union C |
6 | (А∩B) ∪ (А∩C) | (A intersection B) union (A intersection C) |
В таблице показано: как правильно вводить в калькулятор выражения для операций над множествами.
www.reshim.su