Деление трехзначного числа на однозначное примеры в столбик: Деление трёхзначного числа на однозначное | Методическая разработка по математике (3 класс) по теме:

Деление трёхзначного числа на однозначное | Методическая разработка по математике (3 класс) по теме:

Опубликовано 18.03.2012 – 16:48 – Сикорская Валентина Аристафовна

Дидактический раздаточный материал для самостоятельной работы по математике

Скачать:

Предварительный просмотр:

486 : 2

642 :2

693 : 3

848 : 4

 936 : 3

 264 : 2

 996 : 3

555 : 5

966 : 3

 484 : 4

488 : 2

963 : 3

 448 : 4

639 : 3

684 : 2

777 : 7

674 : 2

896 : 2

678 : 3

 892 : 4

 676 : 2

 954 : 3

490 : 2

 860 : 4

 580 : 5

 678 : 6

 896 : 8

798 : 7

 476 : 4

 687 : 3

 585 : 5

654 : 2

 876 : 4

298 : 2

 675 : 3

 468 : 4

595 : 5

 684 : 6

872 : 4

146 : 2

219 : 3

196 : 2

332 : 4

335 : 5

 288 : 4

 370 : 5

291 : 3

 408 : 8

 426 : 6

 330 : 6

 455 : 7

 567 : 7

 549 : 9

 684 : 9

504 : 8

 486 : 6

728 : 8

595 : 7

 531 : 9

168 : 4

189 : 3

 405 : 5

260 : 4

 232 : 4

504 : 6

592 : 8

 252 : 3

432 : 9

539 : 7

516 : 6

376 : 8

570 : 2

  672 : 4

 792 : 3

 828 : 6

 840 : 5

 936 : 6

 920 : 8

 912 : 4

 882 : 7

 965 : 5

 738 : 6

 801 : 3

708 : 4

 903 : 7

822 : 6

895 : 5

984 : 8

 852 : 6

 973 : 7

 936 : 4

875 : 5

572 : 4

855 : 3

 976 : 2

 918 : 6

 966 : 7

 992 : 8

792 : 3

 996 : 4

 894 : 6

889 : 7

952 : 8

612 : 2

927 : 3

540 : 5

828 : 4

648 : 6

921 : 3

742 : 7

963 : 9

864 : 8

745 : 5

 872 : 8

954 : 9

 536 : 8

 861 : 7

576 : 6

436 : 4

530 : 5

856 :  8

 648 : 6

836 : 4

972 : 9

 675 : 5

 954 : 6

896 : 7

Предварительный просмотр:

 

592 : 8

 252 : 3

432 : 9

539 : 7

516 : 6

376: 8

 672 : 4

 828 : 6

840 : 5

912 : 4

882 :7

570 : 2

 936 : 6

 920 : 8

828 : 6

 840 : 5

 936 : 6

 920 : 8

 

 278 х 3

 157 х 6

186 х5

124 х 8

 128 х 7

182 х 4

293 х 3

171 х5

 238 х 4

147 х 7

136 х 6 

374 х 2

204 х 3

103 х 8

107 х 6

 269 х 3

253 х 3

151 х 5

204 х 3

103 х 8

107 х 6

 269 х 3

374 х 2

128 х 7

По теме: методические разработки, презентации и конспекты

Математика.

Деление трёхзначного числа на двузначное

Дорогие ребята! В этой презентации вашему вниманию представлены тренировочные примеры на деление трёхзначных чисел на двузначные. Удачи!   Для скачивания нажмите “скачать”!…

3-4 класс, Интерактивная игра-тренажёр «Африка» (деление трёхзначного числа на однозначное)

Цель: отработка умения делить трёхзначное число на однозначное число.[[{“type”:”media”,”view_mode”:”media_large”,”fid”:”3188798″,”attributes”:{“alt”:””,”class”:”media-image”,”height”:”351″,”width”:”46…

Карточка “Деление трёхзначного числа на однозначное”

Письменные приёмы деления…

Интерактивная игра “Деление трёхзначного числа на однозначное”

Интерактивная игра “Деление трёхзначного числа на однозначное” по математике создана для учащихся 3-4 класса, УМК любой. Игру можно использовать на этапе изучения или повторения в ходе …

Технологическая карта урока математики ” Деление трёхзначного числа на однозначное ” 3 класс

Технологическая карта разработана для урока математики по теме “Деление трёхзначного числа на однозначное ” в 3 классе УМК “Школа 2100”. …

Интерактивная игра – Деление трёхзначного числа на однозначное

Интерактивная игра – Деление трёхзначного числа на однозначное…

Алгоритм письменного деления трёхзначного числа на однозначное.

Алгоритм письменного деления трёхзначного числа на однозначное. Математика 3 класс….

Поделиться:

 

Деление трехзначного числа на однозначное – примеры

4.3

Средняя оценка: 4.3

Всего получено оценок: 138.

4.3

Средняя оценка: 4.3

Всего получено оценок: 138.

Деление трехзначного числа на однозначное, как правило, выглядит достаточно угрожающе. Но оно так только выглядит. Понимание природы и свойств деления, а также навыки деления в столбик с остатком и без него помогут без проблем справится с подобной задачей.

Природа деления

Деление подразумевает операцию, обратную операции умножения. Например выражение:

45:5=9 – показывает следующее: чтобы получить число 45 число 5 умножили на число 9.

Свойства деления аналогичны свойствам умножения, поэтому зачастую их разучивают вместе.

Деление различных чисел

Важно понимать, что делить можно любые числа, включая иррациональные и комплексные. Но в результате деления рациональных чисел всегда подучаются рациональные числа. В результате деления иррациональных – иррациональные и так далее.

Не может быть ситуации, когда рациональное число, делится на рациональное, а в ответе получается иррациональное число. Но может быть ситуация, когда рациональное число делится на иррациональное или наоборот. Конкретно этот момент мы и обсудим, чтобы не теряться при виде таких примеров.

В этом случае, рациональное число возводится в степень корня и вносится под знак радикала. После этого выполняется операция деления. Если из конечного результата можно извлечь корень, то операция выполняется и результатом будет рациональное число.
Если корень извлечь невозможно, то результатом станет иррациональное число. Если результат обязательно нужно записать без знака радикала, то при помощи калькулятора извлекается приблизительное значение корня.

Однозначные и трехзначные числа

Прежде чем перейти непосредственно к делению, давайте разберемся, какое число считается однозначным, а какое многозначным: двухзначным, трехзначным и так далее.

Дело в том, что в математике четко разделяют понятия цифры и числа. Цифры это обозначения от 0 до 9. Числа состоят из нескольких разрядов: единицы, десятки, сотни и так далее. Однозначное число содержит один разряд: единицы, а значит не может быть больше 9.

Двухзначное число содержит уже 2 разряда: единицы и десятки, следовательно, не может быть больше 99. Следуя той же логике трехзначные числа это числа от 100 до 999

Деление трехзначного числа на однозначное

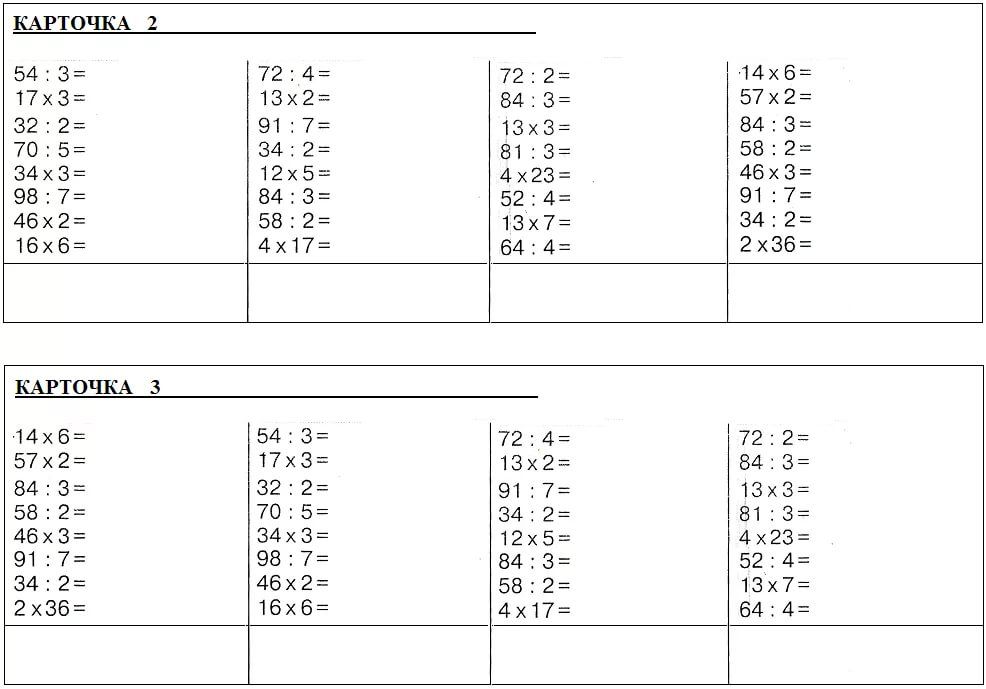
Такие операции, как правило, выполняют в столбик для простоты расчета. Рассмотрим пример деления трехзначного числа на однозначное: 967 поделим на 23.

Столбик это вертикальная линия, к середине которой проводится горизонтальная. Над горизонтальной чертой пишется делитель, с другой стороны вертикальной черты, рядом с делителем записывают делимое.

Под горизонтальной чертой будет записываться результат.

Первым этапом нужно среди первых цифр числа 967 найти число, которое больше 23. Рассматриваем по порядку: 9 – меньше 23, а вот 96 уже больше. Значит первым шагом мы делим число 96 на число 23. Обязательно с остатком.

96:23=8, ост. 4 – в столбике под 96 записывается результат произведения 8*23=92. Число 92 подчеркивается и под ним записывается результат разности: 96-92=4. Рядом с 4 сносится цифра 7. Получается число 47, которое таким же образом делится на 23. А число 8 будет первой цифрой в результате.

47:23=2, ост. 1 – цифра 2 будет второй цифрой результата.

Рядом с 1 можно снести 0 и считать уже дробную часть частного, но мы поделим число с остатком.

Результат: 967:23=82, ост.

Что мы узнали?

Мы узнали, что такое деление, поговорили о свойствах деления и отдельно обсудили деление трехзначного числа на однозначное. Привели небольшой пример подобного деления в столбик с остатком.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

• Мадия Аманджолова

  10/10

• Денис Бедарев

  8/10

• Игорь Пронькин

  10/10

• Елена Зябрева

  10/10

• Жека Нихейма

  10/10

• Артём Мещеряков

  9/10

Оценка статьи

4.3

Средняя оценка: 4.3

Всего получено оценок: 138.

---

А какая ваша оценка?

Трехзначное умножение — Метод, шаги

Трехзначное умножение в математике — это процесс умножения трехзначных чисел на двузначные, однозначные или трехзначные числа путем размещения чисел в столбцах в соответствии с их значения места. Трехзначное умножение идет на шаг впереди по сравнению с двузначным или однозначным умножением.

В этой статье мы изучим 3-значное умножение на 1-значное , 3-значное на 2-значное умножение и 3-значное умножение на 3-значное и решить несколько примеров для лучшего понимания концепции.

1.	Что такое трехзначное умножение?
2.	3-значное умножение на 1-значное
3.	3-значное умножение на 2-значное
4.	3-значное умножение на 3-значное
5.	Часто задаваемые вопросы по 3-значному умножению

Что такое трехзначное умножение?

Трехзначное умножение

— это метод умножения трехзначных чисел на другие числа. Когда мы умножаем трехзначные числа, мы располагаем числа в столбцах в соответствии со значениями разрядов цифр. Мы знаем, что трехзначные числа располагаются в соответствии со своими разрядными значениями как единицы, десятки и сотни. Когда у нас есть набор из двух чисел для умножения, мы обычно держим большее число сверху, а меньшее число — под ним. Число, которое находится сверху, становится множимое на и число, написанное ниже, является множителем . Когда числа расположены в соответствии с их разрядными значениями, мы умножаем множитель со всеми цифрами множимого один за другим, начиная с цифры единиц, затем следует цифра десятков, а затем цифра сотен. Все эти продукты написаны вместе, и они приводят к конечному продукту.

Например, если нам нужно умножить 123 × 3, мы размещаем их, как показано ниже, где 123 — множимое, а 3 — множитель. После умножения этих чисел мы получаем произведение 269.

Давайте теперь научимся умножать трехзначные числа с разными числами.

3-значное умножение на 1-значное

Когда трехзначное число умножается на однозначное число, у нас есть два сценария.

• Первый относится к умножению, при котором однозначное число просто умножается на трехзначное число без каких-либо переносов, и мы получаем произведение. Это 3-значное умножение без перегруппировки .
• Второй относится к умножению, при котором мы умножаем 3-значное число на 1-значное число, и нам нужно перенести лишнюю цифру произведения в следующий столбец. Это трехзначное умножение с перегруппировкой . Рассмотрим оба случая на примерах.

3-значное умножение без перегруппировки

Чтобы найти произведение 3-значного числа на 1-значное число, мы умножаем 1-значное число на каждую цифру 3-значного числа. Если произведение однозначного числа на каждую цифру числа является однозначной цифрой, то нет необходимости переносить какое-либо число. Рассмотрим пример.

Пример: Умножить 214 × 2

Решение: Следующие шаги показывают процедуру умножения 214 на 2. показано на рисунке, приведенном ниже.

Шаг 2: Теперь сначала мы умножаем однозначное число (2) на каждую цифру трехзначного числа (214)

• Если 2 умножить на 4, получится 8.
• Если 2 умножить на 1, получится 2.
• Если 2 умножить на 2, получится 4.

Шаг 3: Следовательно, произведение, которое мы получаем, равно 428.

Умножение трехзначного числа с перегруппировкой

В этом разделе мы умножим трехзначное число на однозначное число и посмотрим, как работает перегруппировка. Давайте решим пример, чтобы продемонстрировать это.

Пример: Умножьте 347 на 3.

Решение: Умножим 347 на 3, используя шаги, описанные ниже.

• Шаг 1: Расположите числа 347 и 3 в столбцах в соответствии с их разрядностью, как показано ниже.
• Шаг 2: Умножьте 3 на каждую цифру 347.
  • Если 3 умножить на 7, получится 21. Поскольку 21 — двузначное число, мы пишем 1 в столбце единиц и переносим 2 в столбец десятков над 4.
  • Когда 3 умножается на 4, мы получаем 12. Теперь нам нужно прибавить перенос (2) к 12, и мы получим 14. Поскольку 14 — двузначное число, мы записываем 4 под столбцом десятков и переносим 1 в столбец сотен выше 3.
  • Когда 3 умножается на 3, мы получаем 9. Теперь нам нужно добавить перенос 1 к 9, и мы получим 10. Поскольку для умножения не осталось другой цифры, мы пишем 10.
• Шаг 3: Следовательно, мы получаем произведение как 1041.

3-значное умножение на 2-значное

Чтобы умножить 3-значные числа на 2-значные числа, мы сначала записываем 3-значное число сверху, а 2-значное число под ним. Давайте обсудим умножение трехзначного числа на двузначное без перегруппировки и с перегруппировкой в ​​следующих разделах.

Умножение 3-значного числа на 2-значное без перегруппировки

Когда мы умножаем 3-значное число на 2-значное число, мы умножаем разряд единиц множителя на множимое, затем умножаем разряд десятков множителя с множителем. Затем мы добавляем оба этих продукта, чтобы получить конечный продукт. Давайте обсудим процесс шаг за шагом с помощью следующего примера.

Пример: Умножить 411 на 31.

Решение: Умножим 411 на 31 пошагово.

• Шаг 1: Расположите числа 411 и 31 в столбцах в соответствии с их разрядностью, как показано ниже.
• Шаг 2: умножьте 1 на каждую цифру 411.
  • Если 1 умножить на 1, получится 1.
  • Если 1 умножить на 1, получится 1.
  • Когда 1 умножается на 4, мы получаем 4. Таким образом, у нас есть 411 как первое частичное произведение.
• Шаг 3: Теперь мы ставим ноль под первым частичным произведением, то есть непосредственно перед записью второго частичного произведения в следующей строке. Этот 0 помещен здесь, потому что на этом шаге мы фактически умножаем 411 на 30.
• Шаг 4: Умножьте 3 на каждую цифру 411.
  • Если 3 умножить на 1, получится 3.
  • Если 3 умножить на 1, получится 3.
  • Если 3 умножить на 4, получится 12. Таким образом, у нас есть 12330 в качестве второго частичного произведения.
• Шаг 5: Добавьте эти продукты, чтобы получить окончательный ответ.
• Шаг 6: 411 + 12330 = 12741. Следовательно, конечный продукт равен 12741.

Умножение трехзначного числа на двузначное с перегруппировкой

Теперь, когда мы умножили трехзначное число на двузначное, давайте попробуем решить другую задачу, связанную с перегруппировкой или переносом.

Пример: Умножьте 573 на 46.

Решение: Умножим 573 на 46, выполнив следующие шаги:

• Шаг 1: Расположите числа 573 и 46 в столбцах в соответствии с их разрядами, как показано ниже. .
• Шаг 2: Умножьте 6 на каждую цифру 573.
  • Когда 6 умножается на 3, мы получаем 18. Поскольку 18 — двузначное число, мы пишем 8 под колонкой единиц и переносим 1 в колонку десятков над 7.
  • Когда 6 умножается на 7, мы получаем 42. Теперь нам нужно добавить перенос (1) к 42, и мы получим 43. Поскольку 43 — двузначное число, мы записываем 3 в столбце десятков и переносим 4 в столбец сотен выше 5.
  • При умножении 6 на 5 получается 30. Теперь прибавим перенос (4) к 30, получим 34. Так как других цифр для умножения не осталось, запишем 34. Итак, имеем 3438 в первой строке (частичное произведение) ответа.
• Шаг 3: Теперь поставим ноль под первым частичным произведением, то есть перед записью второго частичного произведения в следующей строке. Это потому, что на этом шаге мы фактически умножаем 573 на 40.
• Шаг 4: Умножьте 4 на каждую цифру 573.
  • Если 4 умножить на 3, получится 12. Поскольку 12 — двузначное число, мы записываем 2 под столбцом десятков и переносим 1 в столбец десятков над 7.
  • Когда 4 умножается на 7, мы получаем 28. Теперь мы добавим перенос 1 к 28, чтобы получить 29. Поскольку 29 — двузначное число, мы пишем 9 в столбце сотен и переносим 2 в столбец сотен выше 5.
  • Когда 4 умножается на 5, мы получаем 20. Теперь мы прибавим перенесенное число 2 к 20, и мы получим 22. Поскольку для умножения не осталось другой цифры, мы запишем 22. Итак, мы имеем 22920 как Вторая линия продукта.
• Шаг 5: Сложите эти частичные произведения, чтобы получить окончательный ответ.
• Шаг 6: Это означает 3438 + 22920 = 26358. Следовательно, конечный продукт равен 26358.

3-значное умножение на 3-значное

В этом разделе мы научимся умножать трехзначное число на трехзначное число. Этот процесс аналогичен тому, что мы обсуждали в предыдущих разделах. Давайте разберемся с трехзначным умножением на трехзначное с помощью следующего примера.

Пример: Умножьте 123 на 456.

Решение: Умножим 123 на 456, выполнив следующие действия.

• Шаг 1: Расположите числа 123 и 456 в столбцах в соответствии с их разрядностью, как показано ниже.
• Шаг 2: Умножьте 6 на каждую цифру 123.
  • Когда 6 умножается на 3, мы получаем 18. Поскольку 18 — двузначное число, мы пишем 8 под колонкой единиц и переносим 1 в колонку десятков над 2.
  • Когда 6 умножается на 2, мы получаем 12. Теперь мы прибавляем перенесенную 1 к 12 и получаем 13. Поскольку 13 — двузначное число, мы записываем 3 в столбце десятков и переносим 1 в следующий столбец. столбец выше 1.
  • Когда 6 умножается на 1, мы получаем 6. Теперь прибавляем перенесенную 1 к 6, чтобы получить 7. Поскольку для умножения не осталось другой цифры, мы пишем 7. Итак, у нас есть 738 в первой строке как частичный продукт.
• Шаг 3: Теперь поместите ноль под этим частичным произведением в столбце единиц. Это потому, что на этом шаге мы фактически умножаем 123 на 50.
• Шаг 4: Умножьте 5 на каждую цифру 123.
  • Когда 5 умножается на 3, мы получаем 15. Поскольку 15 — двузначное число, мы пишем 5 в столбце десятков и переносим 1 в следующий столбец над 2.
  • Когда 5 умножается на 2, мы получаем 10. Теперь прибавляем перенесенный 1 к 10, чтобы получить 11. Поскольку 11 — двузначное число, мы пишем 1 в столбце сотен и переносим 1 в следующий столбец над 1.
  • Когда 5 умножается на 1, мы получаем 5. Теперь прибавляем перенесенную 1 к 5, чтобы получить 6. Так как для умножения не осталось другой цифры, мы пишем 6. Итак, у нас есть 6150 во второй строке частичный продукт.
• Шаг 5: Теперь поместите два нуля (0) в столбце единиц и десятков под частичным произведением, полученным на предыдущем шаге. Это потому, что на этом шаге мы фактически умножаем 123 на 400.
• Шаг 6: Умножьте 4 на каждую цифру 123.
  • Если 4 умножить на 3, получится 12. Поскольку 12 — двузначное число, мы записываем 2 под столбцом сотен и переносим 1 в следующий столбец над 2.
  • Когда 4 умножается на 2, мы получаем 8. Теперь прибавляем перенесенный 1 к 8, чтобы получить 9. Мы пишем 9 в следующем столбце.
  • При умножении 4 на 1 получается 4. Так как другой цифры для умножения не осталось, пишем 4. Итак, в третьей строке имеем 49200 как частичное произведение.
• Шаг 7: Добавьте все 3 частичных продукта, чтобы получить конечный продукт. Это означает 738 + 6150 + 49200 = 56088.
• Шаг 8: Таким образом, конечный продукт равен 56088.

☛ Связанные темы

• Вычитание двух цифр
• 2-значное дополнение
• Трехзначное дополнение
• 3-значное вычитание
• 2-значное умножение
• 4-значное дополнение
• 4-значное вычитание
• Умножение и деление целых чисел

Часто задаваемые вопросы о 3-значном умножении

Что такое трехзначное умножение?

Трехзначное умножение в математике представляет собой процесс умножения трехзначных чисел на однозначные, двузначные и трехзначные числа путем размещения чисел в столбцах в соответствии с их порядковыми номерами.

Как сделать трехзначное умножение?

Трехзначное умножение можно легко выполнить, если числа расположены в соответствии с их разрядностью. Когда у нас есть набор из двух чисел для умножения, мы обычно держим большее число сверху, а меньшее число — под ним. Число, расположенное сверху, становится множимым, а число, написанное ниже, — множителем. Когда числа расположены в соответствии с их разрядными значениями, мы умножаем множитель со всеми цифрами множимого один за другим, начиная с цифры единиц, затем следует цифра десятков, а затем цифра сотен. Все эти продукты написаны вместе, и они приводят к конечному продукту.

Как умножить трехзначное число на однозначное?

Чтобы умножить 3-значное число на 1-значное число, мы умножаем 1-значное число на каждую цифру 3-значного числа, чтобы получить произведение. Например, давайте умножим 314 × 2. Мы умножим 2 на 4, чтобы получить 8, которые будут помещены под колонку единиц. Затем мы умножим 2 на 1, чтобы получить 2, которые будут помещены в столбец десятков. После этого мы умножим 2 на 3, чтобы получить 6. Следовательно, произведение 314 × 2 = 628,

Что такое 3-значное умножение на 2-значное?

Когда 3-значное число умножается на 2-значное число, мы умножаем каждую цифру 2-значного числа на каждую цифру 3-значного числа. Мы располагаем числа в столбцах в соответствии с их разрядными значениями, пишем частичные произведения одно под другим и складываем их, чтобы получить конечный продукт.

Что такое 3-значное умножение на 3-значное?

Умножение 3-значного на 3-значное означает, что 3-значное число умножается на другое 3-значное число. Это делается путем размещения чисел в столбцах, а затем умножения каждой цифры одного числа на каждую цифру другого числа. Частичные продукты записываются один под другим, а затем продукты добавляются, чтобы получить окончательный ответ.

Видеоурок: Деление трехзначного числа на однозначное число: Вычитание неполных частных

Расшифровка видео

Деление трехзначного числа на Однозначное число: вычитание неполных частных

В этом видео мы научимся как делить трехзначные числа на однозначные. И для этого мы будем использовать то, что называется частичными частными.

Теперь один из методов, которые мы используем когда мы учимся делить, это многократное вычитание. Вы помните, как это работает? Если мы хотим найти ответ на 24 разделить на три, например, мы можем начать с 24 и посмотреть, сколько троек вписывается в Это. И мы можем сделать это, забрав по три за раз или многократно вычитая. 24 отнять три равно 21. 21 отнять три равно 18. И мы просто продолжаем вычитать тройки пока, в конце концов, мы не достигнем нуля. И в этот момент нет больше троек убрать. И поскольку мы вычли три восемь раз, чтобы добраться до нуля, мы можем сказать, что 24 разделить на три равно восьми. И такое повторение вычитание работает довольно хорошо, когда мы думаем о двузначных числах.

Но что, если нам нужно разделить большее число? Как мы сказали в начале в этом видео, мы будем думать о делении трехзначных чисел на однозначные цифры. Так что, если вы хотите найти ответ на 138 разделить на три? Это заставит нас навсегда Продолжайте вычитать тройки, не так ли? И нам нужно очень длинное число линия. Там должно быть быстрее, больше эффективный метод, который мы могли бы использовать. Ну, есть, и это касается используя то, что мы называем частичными частными, что звучит сложно, но на самом деле это не так. Слово «частное» просто означает ответ на расчет деления. Это то, что мы получаем, когда мы делим один номер другим. И слово «частичный» просто говорить о части чего-либо. Так что это на самом деле означает, что мы будет находить ответ на 138 разделить на три понемногу за раз.

Мы поделим 138 на три, но мы собираемся делать это по частям. Давайте покажем, что мы имеем в виду под это. Теперь, когда мы используем этот метод, мы можем записать вычисление 138 разделить на три вот так. Это способ записи делений, но интересно, не так ли? В нем нет знака деления там вообще. Здесь мы пишем число мы делимся. И здесь мы пишем число, на которое мы делим, или делитель. Таким образом, мы могли бы прочитать это как, сколько тройки в 138? Теперь, как мы уже сказали, мы можем несколько раз вычитать тройки, но это заняло бы так много времени, чтобы получить ответ нуль.

Существует ли большее число, кратное трем мы могли бы вычесть, чтобы добраться до нуля быстрее? Ну, мы знаем, что 10 троек 30. Что, если мы вычтем 10 лотов из три сразу? Другими словами, что, если мы расстанемся 138 на куски, которые стоят 10 раз по три? Частичные частные, которые определенно быстрее, чем вычитать три каждый раз, не так ли? Посмотрим, куда это нас приведет. Теперь у 138 уже есть тройка в столбец десятков. Итак, если мы отнимем от этого 30, это довольно быстро сделать. Ответ 108. Теперь, когда мы используем этот метод, будет становиться все более и более важным вести учет того, что мы вычитано. Итак, рядом с 30 нам нужно написать вниз, что это то же самое, что и 10 лотов из трех.

Мы точно знаем, что их 10 много три в 138. И поскольку у нас осталось 108, мы можно увидеть, что мы можем забрать еще 10 лотов из трех тоже. На этот раз мы можем считать в обратном порядке в десятках три раза из 108. Итак, 108, а затем 98, 88, 78. 108 отнять 30 будет 78. И знаете, мы могли бы продолжать, продолжая убирать эти частичные частные, эти куски 10 троек. 78 убери 30 приведи нас к 68, 58, 48. И у нас осталось как раз достаточно, чтобы уберите еще один лот из 10 троек. 48 забери 30 оставь нам 38, 28, 18.

Помните, все дело в сведение к нулю. А у нас осталось всего 18. И мы должны знать таблицу умножения факт, который поможет нам вычесть все эти 18 за один раз. Шесть троек — это 18, не так ли? Поэтому вместо того, чтобы делать много меньшие прыжки из трех, мы сделали один, два, три, четыре прыжка по 10 раз по три и затем прыжок шесть раз по три. Так сколько же было троек вообще? Другими словами, сколько будет 10 плюс 10? плюс 10 плюс 10 плюс шесть? Итак, четыре десятки стоят 40. А если мы добавим шесть, это даст нам 46. ​​Итак, мы можем сказать 138 разделить на три равно 46. И просто чтобы показать вам часто с этот тип деления, мы пишем ответ сверху так, 46.

Это было довольно эффективно, не так ли? Мы нашли ответ довольно быстро. Нам нужно было только вычесть пять раз, что намного меньше, чем мы сделали бы, если бы нам пришлось убрать тройки. Но, знаете, мы могли бы даже работать еще эффективнее. И способ сделать это – дать заранее подумал, посмотреть на расчет, сколько троек в 138, и задать себе вопрос: «Какое наибольшее кратное трем я знаю это меньше 138? Другими словами, насколько близко я могу подобраться до 138? Я мог забрать 30 каждый раз. Но есть ли какие-то большие кратные чем я знаю?

Здесь есть ручка и Бумага может помочь, потому что мы можем записать некоторые факты, прежде чем начать. Потому что если я знаю, что 10 троек 30, я мог бы удвоить это и знать, что 20 троек стоят 60, поэтому я мог бы взять прочь 20 лотов по три за раз. Но что, если мы удвоим факт опять таки? Мы видим, что 40 троек должны быть стоит удвоить 60 или 120. И это действительно близко к 138. Посмотрим, как быстро мы сможем найти ответ, вычитая 40 лотов из трех первых.

У нас осталось восемь штук место. Три 10-ки берут две 10-ки, оставляя нас. с одной 10. А сотен у нас нет, потому что мы отнимаем 100 от 100. Итак, мы нашли частичное частное 40 лотов по три. А у нас осталось всего 18. И, как и прежде, мы знаем, что в 18 есть шесть партий по три. Итак, если мы уберем шесть партий из три, у нас останется ноль. На этот раз мы получили ответ в два шага. Нам не станет намного лучше чем мы? Сначала мы вычли 40 лотов из три, а затем шесть лотов по три, и 40 плюс шесть равно 46. Мы получили тот же ответ, но много быстрее. И причина, по которой мы смогли получить так быстро, потому что мы взяли несколько минут, прежде чем мы начали, и спросили себе: «Какое наибольшее из известных мне кратных трем меньше 138?» Чем больше кратность, тем меньше шаги, которые вам нужно будет сделать.

Теперь, чтобы лучше использовать этот метод, а также для того, чтобы действительно понять, как он работает, нам имеет смысл попрактикуйтесь в нескольких вопросах. Мы собираемся пройти через три вопросы теперь, где мы должны разделить трехзначные числа на одну цифру. И каждый раз мы будем использовать этот метод частичного частного. Мы будем делать это довольно медленно, чтобы начать с, потому что это совершенно новое для нас. Но, надеюсь, к концу мы будем работать намного быстрее. И вы сможете увидеть, как полезный этот метод может быть. Итак, начнем с вопроса один.

Бенджамин вычисляет 450 разделить на пять с использованием метода частичного частного. Помогите ему найти частное из его расчет.

В этом вопросе нам говорят, что Бенджамин пытается найти ответ на вопрос о делении. Мы знаем это, потому что нам это дано в первом предложении. Нам говорят, что он рассчитывает 450 разделить на пять. Но вы знаете, мы также можем видеть расчет написан ниже здесь. может не иметь деления символ, но везде, где мы видим числа, написанные так или иногда так, мы знаю, что нам нужно разделить, чтобы найти ответ. Нам нужно найти, сколько пятерок там 450. Теперь, как и при любом расчете, есть несколько способов, которыми Бен мог найти ответ. Но нам говорят, что он использует Метод частичного частного.

Теперь этот метод проще понять, что это выглядит. Слово «частичный» просто означает часть чего-либо. И частное – это просто ответ к дивизии. Другими словами, Бенджамин находит сколько пятерок в 450 части ответа за раз. Он разбивает 450 на куски. И нам говорят, что мы должны помочь ему найти частное из его вычислений. Теперь один из способов узнать, сколько пятерок в 450 было бы продолжать вычитать пятерки. 450 убери пять, оставь нам 445. И если мы уберем еще много пять, это 440. Нам понадобится довольно много времени, чтобы свести все к нулю, не так ли?

Таким образом, когда мы используем частичное частное Метод, мы задаем себе вопрос. Каково наибольшее кратное, которое я может придумать что бы я мог вычесть из этого числа? Вместо того, чтобы забрать одну партию пять каждый раз, можете ли вы придумать что-то еще, что мы могли бы вычесть? Ну, мы знаем, что 10 пятерок – это 50, чтобы мы могли забрать 10 лотов по пять штук за раз, забрать 50 шиллингов. Но мы могли бы даже пойти еще лучше чем это. Что, если мы удвоим факт? Если 10 пятерок — это 50, то 20 пятерок — это стоит удвоить 50 или 100. Если мы уберем 100, мы собираемся получить ответ гораздо быстрее, не так ли? Итак, давайте попробуем вычесть это частичное частное. И это может помочь нам рассмотреть о чем Бен думает на каждом шагу.

Итак, для начала он собирается посмотри на его число 450 и подумай про себя: «Ну, я знаю, что точно есть 20». лотов пять из 450, так что я уберу 20 лотов по пять или 100». Ну и конечно 450 убери 100 оставляет ему 350. Теперь он может смотреть на 350 и думать, сам себе: «Ну, я могу забрать еще кучу 25-х». 350 забрать 100 отдать ему 250. И у него еще достаточно, чтобы держать собирается. 250 убери 100 оставь его с 150. 150 убери 100 оставь его с 50. И теперь уже не отнять куски 25s, может он? У него осталось всего 50. Но Бенджамин знает, сколько пятерок есть по 50. А если он отнимет 10 лотов пять, он вернется к нулю.

Итак, вычитая часть за раз, Бенджамин разделил ответ на это вычисление деления или частное на биты. Он знает, что есть раз, два, три, четыре лота по 25 и один лот из 10 пятерок. Теперь, сколько пятерок это вообще? Ну, мы знаем, что четыре лота по 20 стоят 80. И если мы прибавим 10, мы получим ответ 90.

Мы вычли кратные пяти найти ответ. Это называется частичным частным метод. И мы обнаружили, что нам пришлось забрать 90 много пять, чтобы вернуться к нулю. И вот откуда мы знаем, что 450 разделить на пять равно 90.

Вычислите 848, разделенное на четыре, используя метод частных частных.

В этом вопросе нас просят оцените или найдите значение 848, деленное на четыре. Или другими словами, сколько четверок есть в 848? Теперь, когда мы могли бы использовать времена таблицы фактов, которые мы уже знаем, делили ли мы двузначное число на четыре или даже использовать повторное вычитание, каждый раз отбирая четыре, нам нужно использовать метод это немного быстрее, когда мы делим трехзначное число, подобное этому, на четыре. Вот почему нам говорят использовать метод частных частных. А это предполагает разрыв число 848 на более мелкие части. Мы можем не знать, сколько четверок их сразу в 848-м, но мы знаем, сколько их в части 848-го. Тогда мы можем посмотреть, что осталось, и посмотреть другую часть и так далее.

Итак, прежде чем мы начнем, давайте подумаем о некоторых кратных четырем, которые мы могли бы убрать. Мы не хотим вычитать четыре, потом четыре, потом четыре, а потом четыре, не так ли? Теперь мы знаем, что 10 четверок стоит 40. Теперь это может пригодиться. Но 848 все равно довольно большой число, которое будет забирать 40 из каждого раза. Что, если мы умножим этот факт на 10? Что такое 100 четверок? Ну, это довольно тоже простой факт. 100 четверок — это 400. Что, если мы начнем с того, что уберем 100 четверок за раз? Это вернет нас к нулю довольно быстро, не так ли? Итак, мы начнем с вычитания порция четверок, 100 партий четверок или 400.

Теперь в нашем числе 848 восемь сотен. в этом. И если мы уберем четыре из них 100, у нас останется 448. Теперь мы видим, что у нас есть только осталось более 400, не так ли? Так что должно быть еще 100 четверок мы могли бы вычесть. 448 забрать 400 оставляет нас с только десятки и единицы, 48. Итак, что мы можем вычесть из 48? Что ж, если мы используем факты, мы уже знаете, мы могли бы забрать все 48 разом. Мы знаем, что 10 четверок — это 40. Это означает, что 11 четверок должны равняться 44 и 12 четверок должны стоить 48. Итак, если мы уберем эти 12 четверок, это вернет нас к нулю. Итак, сколько четверок мы там нашли были в 848? Было 100, еще 100 и 12 более. И 100 плюс 100 плюс 12 равно 212.

Мы нашли ответ на 848 разделенный на четыре, используя метод частичного частного. Количество четверок в 848 равно 212.

Вычислите 216, разделенное на восемь. Подсказка: используйте частичные частные, чтобы помочь ты.

В этом вопросе нам нужно найти ответ на 216 разделить на восемь. И нам дают подсказку. Нам говорят, что мы можем использовать частичный коэффициенты нам в помощь. Другими словами, вместо того, чтобы думать о том, сколько восьмерок в 216 по восемь, мы можем разделить число 216 на части. И мы можем найти ответ один кусок за раз. Итак, для начала напишем наш расчет. И способ, которым мы это делаем, опускание делителя. Это число, на которое мы делим первый. Затем рисуем серию линий. Он всегда будет выглядеть точно так же, как это. Это один из способов рисования. А затем под верхней строкой, мы пишем большое число, которое мы делим.

Таким образом, этот расчет спрашивает нас: «Как сколько восьмерок в числе 216?» Теперь то, что кратно восьми может мы отнимаем от 216, чтобы быстро довести нас до нуля? Мы могли бы вычесть восемь, тогда восемь, потом восемь, потом восемь и так далее, но это займет очень много времени. время. Факт, который мы могли бы использовать, чтобы помочь нам составляет 10 восьмерок. 10 восьмерок стоят 80. Но знаете, мы могли бы поквитаться ближе к 216, если удвоить этот факт. Если мы знаем, что 10 восьмерок стоят 80, тогда 28 должно стоить двойных 80 или 160. Теперь мы ясно видим, что в числе 216 20 восьмерок. Итак, отнимем 160 сразу.

Теперь 216 забери 100 оставит нас со 116. А если отнять 60, получится нас обратно к 56. И так можно сказать 216 отнять 160 равно 56. Теперь мы знаем, сколько восьмерок в 56, не так ли? Это таблица умножения, которую мы уже выучил. В числе 56 семь восьмерок. Итак, если мы отнимем наш последний семь восьмерок, мы останемся ни с чем.

Мы использовали частичные частные для помогите найти сколько восьмерок в числе 216. А мы отобрали 20 лотов восьмерок а затем еще семь лотов по восемь.