Деление на пальцах: Таблица умножения на 6, 7, 8 и 9 на пальцах
Устный счет на пальцах – основные приемы
Человека ежедневно окружает множество цифр. Работа и учеба, походы в магазин и банковские операции – во всех сферах жизни необходимо уметь считать в уме, ведь калькулятор не всегда бывает под рукой. Желая упростить себе жизнь, многие люди хотят научиться проводить различные операции с числами с помощью подручных средств. Одним из подобных методов и является счет на пальцах.
Искусство устного счета
С древнейших времен и до наших дней люди стремились развить способность быстро производить математические вычисления в уме. Этот навык полезен в самых разных сферах нашей жизни: от покупок в магазине до профессиональной деятельности. Возможность устно выполнять сложение и вычитание, умножение и деление позволяет человеку продуктивнее справляться с повседневными задачами.
Обычные знания, которые мы получаем на уроках математики в школе, не позволяют человеку научиться выполнять операции с большими числами без помощи тетради или калькулятора.
Неудивительно, что человечество находится в поиске методов для качественного устного счета.
Существует множество самых разных подходов, позволяющих производить вычисления в уме. Многие из них все же подразумевают использование некоторых подручных средств. Так существует методика, основы которой знакомы нам с самого раннего детства – счет на пальцах. Но мало кто знает, что, помимо сложения и вычитания, также можно освоить умножение и деление больших чисел в уме.
Сложение и вычитание в уме
С самого детства человек учится сложению и вычитанию простейших чисел. Родители и воспитатели детских садов, а затем и учителя в школе открывают для ребенка бескрайний мир математики.
Сначала ребенку предлагают складывать и вычитать с использованием подручных средств. Так многие дети сначала учатся считать на пальцах, что позволяет им легче понять, как происходит то или иное арифметическое действие. Если на начальном этапе этот метод даже полезен, то позже он отпадает за ненадобностью.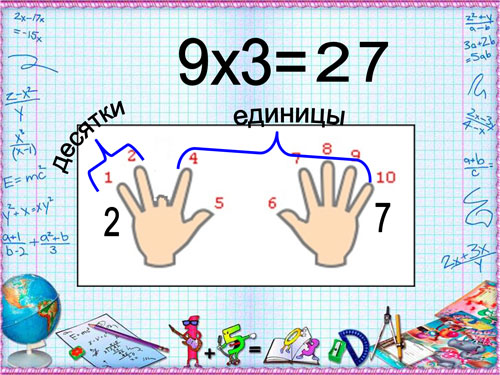
При поступлении в первый класс ребенок учится производить вычисления устно, без использования пальцев или счетных палочек.
Различные подручные материалы только тормозят скорость счета, не дают своевременно раскрыть способности детей. По этой причине, арифметические вычисления на пальцах подходят только для того, чтобы ввести для ребенка понятие цифр, чисел и простейших операций с ними.
Как выучить таблицу умножения на пальцах
С умножением и делением ситуация обстоит немного иначе. Есть методика, позволяющая производить подобные вычисления с использованием пальцев на левой и правой руке. К сожалению нельзя сказать, что подобный подход позволяет быстро умножать и делить числа. Такой вид счета на пальцах скорее направлен на общее развитие интеллекта человека, чем на широкое применение в быту.
К тому же, сложно запомнить и выучить подобную таблицу умножения и деления, так как она видоизменяется в зависимости от размера чисел, с которыми проводятся операции. С помощью калькулятора или листка бумаги считать намного проще, чем на пальцах, а потому этот метод не получил широкого распространения.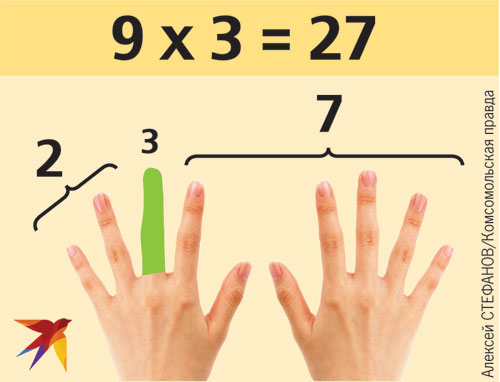
Популярные методики
Конечно, изучение различных методик устного счета на пальцах полезно для общего развития, но существуют и другие способы проводить вычисления в уме за более короткое время. Пожалуй, самым ярким из них является ментальная арифметика – программа, которая позволит научиться выполнять сложение, вычитание, умножение и деление в уме практически мгновенно. Количество операций, которые может производить человек, обученный по данной методике, поражает воображение, счет на пальцах не позволяет считать с подобной скоростью.
Ментальная арифметика не является новшеством. Известно, что она использовалась еще пять тысяч лет назад. За ее основу взяты вычисления на специальных счетах – абакусе. Если в начале занятий еще используется данное приспособление, то потом человек учится представлять счеты в уме и устно проводить на них вычисления.
Неудивительно, что курсы ментальной арифметики сегодня так популярны. Особенно это актуально для детей, ведь умение быстро считать в уме позволяет повысить успеваемость в школе по множеству дисциплин.
К тому же, ребенка легче научить выполнять вычисления по данной методике, так как ее изучение во взрослом возрасте не приносит таких высоких результатов.
Существует множество детских центров дополнительного образования, обучающих детей ментальной арифметике. Нужно выбирать такой, занятия в котором проходят в небольших группах и по уникальной методике. Так удастся научить ребенка быстро считать, а также сохранить изучаемый навык на всю жизнь, что не раз поможет в профессиональной и повседневной деятельности.
Как умножить на 7 на пальцах. Умножение на пальцах
В жизни люди, способные вычислять в уме, смотрятся как «суперумники», хотя в этом ничего сложного нет. Калькулятор калькулятором, а считать в уме полезно!
Как помочь ребенку выучить таблицу умножения?
Ниже описаны некоторые простые приемы
Умножение на 2 или удваивание.
Удваивать довольно легко, достаточно что-то сложить с самим собой. Вначале я показал на своей левой и правой руке одновременно по одному, двум, трем, четырем, пяти пальцам – так мы получили 2, 4, 6, 8, 10.
Вместе с пальцами моего ученика мы дошли до двадцати, а потом я показывал на разные штуки в комнате, и предлагал сосчитать и удвоить – число букв в плакате, число символов на циферблате часов, сосчитать число спиц на одной стороне колеса велосипеда, и проверить, сойдется ли общее число с удвоенным и так далее.
Умножение на 4 и 8, 3 и 6
Когда умеешь умножать на два, это сущие пустяки. Умножить на четыре это то же, что удвоить ответ для того, что уже удвоено, например 7×4 это 7×2х2, а что 7×2 это 14 мы уже хорошо запомнили на предыдущем уроке про удваивания, так что и само 14 превратить в 28 не составит труда. Когда разобрался с четверкой, не так уж сложно разобраться и с большими числами восьмерки. По пути мы заметили, что, например, 16 это и 2×8, и 4×4. Так мы узнали, что есть числа, сплошь состоящие из двоек: 2, 4, 8, 16, 32, 64.
Умножая на 3 и 6, мы выучили старый пиратский метод «дележки на три».
Если сложить цифры в числе, умноженном на 3, 6 или любом другом, которое делится на тройку, то результат сложения цифр ответа всегда кратен трем.
Например, 3×5 = 15, 1+5 = 6. Или 6×8 = 48, а 4+8 = 12, кратно трем. А можно и в 12 цифры сложить, получится тоже 3, так что, если так дойти до конца, то всегда получается одно из трех чисел: 3, 6 или 9.
Так мы превратили это в еще одну игру. Я задавал какое-нибудь число, даже трех- или четырехзначное, и спрашивал, делится ли оно на 3. Для ответа достаточно сложить цифры, что довольно просто. Если число делилось на 3, то я спрашивал – «а на 6?» – и тогда нужно было просто посмотреть четное ли оно. А потом (в специальном случае небольших чисел из таблицы) иногда еще хотел узнать, что же получится при таком делении на 3 или 6. Это было очень веселое занятие.
Умножение на 5 и 7, простые числа
И вот остались у нас умножение на пятерку, семерку, и девятку. А это значит, что мы выучили умножение их на многие другие числа – на 1, 2, 3, 4, 6, 8 и 10. С пятеркой мы разобрались очень быстро – она легко запоминается: на конце либо нолик, либо пять, точно также как умножаемое число: либо четно, либо нечетно.
В качестве предмета, на котором с пятерками удобно заниматься, отлично подходит циферблат часов, можно придумать множество задач про путешествия во времени и пространстве. Заодно я рассказал почему в часе шестьдесят минут, и мы поняли чем это удобно.
Мы увидели, что 60 удобно делить на 1, 2, 3, 4, 5, 6, а на 7 делить неудобно. Поэтому было самое время присмотреться к этому числу. Из умножения на семерку оставалось запомнить лишь 7×7 и 7×9. Теперь мы знали почти все, что нужно. Я объяснил, что семь просто очень гордое число – такие числа называются простые, они делятся только на 1 и на себя.
Таблица умножения – те необходимые в жизни каждого человека знания, которые требуется элементарно заучить, что на первых школьных порах даётся совсем не элементарно. Это потом уже с легкостью мага мы «щелкаем » примеры на умножение: 2·3, 3·5, 4·6 и т.д., но со временем все чаще забываемся на множителях ближе к 9, особенно если счетной практики давно не ведали, отчего отдаемся во власть калькулятора или надеемся на свежесть знаний друга.
Однако, овладев одной незамысловатой техникой «ручного » умножения, мы можем запросто отказаться от услуг калькулятора. Уточнение: речь идет о школьной таблице умножения, т.е. для чисел от 2 до 9, умножаемых на числа от 1 до 10.
Умножение для числа 9 – 9·1, 9·2 … 9·10 – легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится» на пальцах». Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).
Допустим, хотим умножить 9 на 7. Загибаем палец с номером, равным числу, на которое мы будем умножать 9. В нашем примере нужно загнуть палец с номером 7. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа – количество единиц.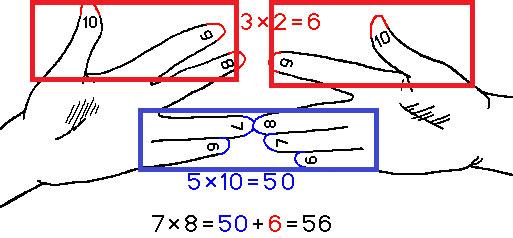
Слева у нас 6 пальцев не загнуто, справа – 3 пальца. Таким образом, 9·7=63. Ниже на рисунке детально показан весь принцип «вычисления ».
Еще пример: нужно вычислить 9·9=? По ходу дела скажем, что в качестве « счетной машинки » не обязательно могут выступать пальцы рук. Возьмите к примеру 10 клеточек в тетради. Зачеркиваем 9-ю клеточку. Слева осталось 8 клеточек, справа – 1 клеточка. Значит 9·9=81. Все очень просто.
Умножение для числа 8 – 8·1, 8·2 … 8·10 – действия здесь похожи на умножение для числа 9 за некоторыми изменениями. Во-первых, поскольку числу 8 не хватает уже двойки до круглого числа 10, нам необходимо каждый раз загибать сразу два пальца – с номером х и следующий палец с номером х+1. Во-вторых, тотчас же после загнутых пальцев мы должны загнуть еще столько пальцев, сколько осталось не загнутых пальцев слева.
В-третьих, это напрямую работает при умножении на число от 1 до 5, а при умножении на число от 6 до 10 нужно отнять от числа х пятерку и выполнить расчёт как для числа от 1 до 5.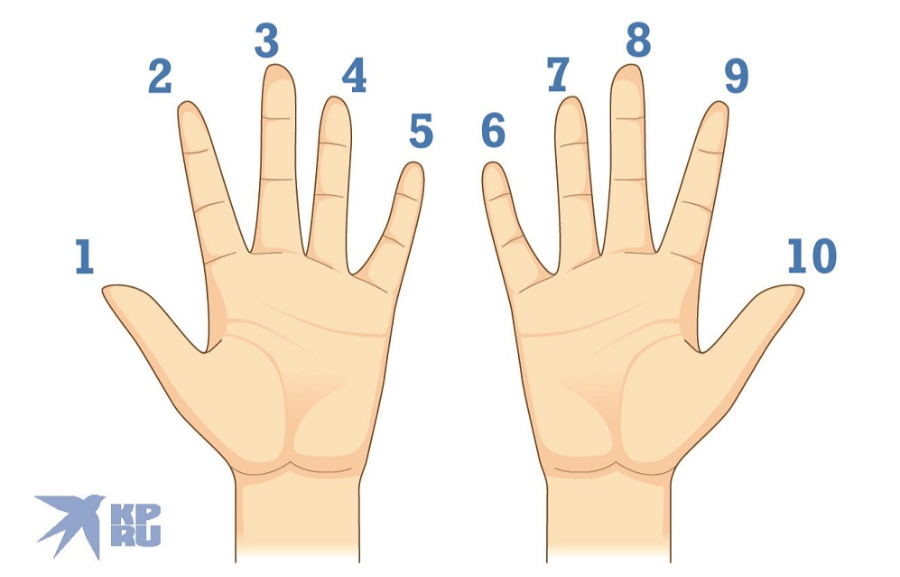
, а к ответу затем добавить число 40, потому что иначе придется выполнять переход через десяток, что не совсем удобно «
Теперь рассмотрим пример умножения для числа 8. Допустим, хотим умножить 8 на 3. Загибаем палец с номером 3 и за ним палец с номером 4 (3+1). Слева у нас осталось 2 незагнутых пальца, значит нам необходимо загнуть еще 2 пальца после пальца с номером 4 (это будут пальцы с номерами 5, 6 и 7). Осталось 2 пальца не загнуто слева и 4 пальца – справа. Следовательно, 8·3=24.
Еще пример: вычислить 8·8=? Как было сказано выше, при умножении на число от 6 до 10 нужно отнять от числа х пятерку, выполнить расчет с новым число х-5, а затем добавить к ответу число 40. У нас х=8, значит загибаем палец с номером 3 (8-5=3) и следующий палец с номером 4 (3+1). Слева два пальца остались не загнуты, значит загибаем еще два пальца (с номером 5,6).
1.5 Люди – феномен быстрого счёта
Феномен особых способностей в устном счёте встречается с давних пор. Как известно, ими обладали многие ученые, в частности Андре Ампер и Карл Гаусс. Однако, умение быстро считать было присуще и многим людям, чья профессия была далека от математики и науки в целом.
До второй половины XX века на эстраде были популярны выступления специалистов в устном счёте. Иногда они устраивали показательные соревнования между собой. Известными российскими «суперсчетчиками » являются Арон Чиквашвили, Давид Гольдштейн, Юрий Горный, зарубежными – Борислав Гаджански, Вильям Клайн, Томас Фулер и другие.
Хотя некоторые специалисты уверяли, что дело во врожденных способностях, другие аргументировано доказывали обратное: «
Истина как обычно, оказалась на некоей «золотой середине » сочетания природных способностей и грамотного, трудолюбивого их пробуждения, взращивания и использования. Те, кто следуя Трофиму Лысенко уповают исключительно на волю и напористость, со всеми уже хорошо известными способами и приемами устного счёта обычно при всех стараниях не поднимаются выше очень и очень средних достижений.
Более того, настойчивые попытки «хорошенько нагрузить » мозг такими занятиями как устный счёт, шахматы вслепую и т.п. легко могут привести к перенапряжению и заметному падению умственной работоспособности, памяти и самочувствия (а в наиболее тяжелых случаях – и к шизофрении). С другой стороны и одаренные люди при беспорядочном использовании своих талантов в такой области как устный счёт быстро « перегорают » и перестают быть в состоянии длительно и устойчиво показывать яркие достижения. Один из примеров удачного сочетания обоих условий (природной одаренности и большой грамотной работы над собой) показал наш соотечественник, уроженец Алтайского края Юрий Горный.
Пожалуй, единственная научно обоснованная и достаточно подробно разработанная система резкого повышения быстроты устного счёта создана была в годы второй мировой войны цюрихским профессором математики Я. Трахтенбергом. Она известна под названием «Система быстрого счёта ». История ее создания необычная. В 1941г. гитлеровцы бросили Трахтенберга в концлагерь.
Чтобы уцелеть в нечеловеческих условиях и сохранить нормальной свою психику, Трахтенберг начал разрабатывать принципы ускоренного счета. За четыре страшных года пребывания в концлагере профессору удалось создать стройную систему ускоренного обучения детей и взрослых основам быстрого счёта. Уже с самого начала результаты были самые отрадные. Учащиеся радовались вновь приобретенным навыкам и с воодушевлением двигались вперед. Если раньше их отталкивала монотонность, то сейчас их привлекало разнообразие приёмов. Шаг за шагом, благодаря достигнутым ими успехам, рос интерес к занятиям. После войны Трахтенберг создал и возглавил Цюрихский математический институт, получивший мировую известность.
Также разработкой приёмов быстрого счёта занимались другие ученые: Яков Исидорович Перельман, Георгий Берман и другие.
Это потом уже с легкостью мага мы “щелкаем” примеры на умножение: 2·3, 3·5, 4·6 и так далее. С возрастом, правда, все чаще забываемся на множителях ближе к 9, особенно если счетной практики давно не ведали, отчего отдаемся во власть калькулятора или надеемся на свежесть знаний друга. Однако, овладев одной незамысловатой техникой “ручного” умножения, мы можем запросто отказаться от услуг калькулятора. Но сразу уточним, что говорим только о школьной таблице умножения, то есть для чисел от 2 до 9, умножаемых на числа от 1 до 10.
Умножение для числа 9 – 9·1, 9·2 … 9·10 – легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится “на пальцах”. Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).
Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа – количество единиц. Слева у нас 5 пальцев не загнуто, справа – 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип “вычисления”.
Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в качестве “счетной машинки” не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа – 2 клеточки. Значит 9·8=72. Все очень просто.
Теперь несколько слов тем любознательным детям, которые кроме механического применения сказанного хотят понять, из-за чего это работает. Здесь все основано на таком наблюдении, что числу 9 не хватает всего лишь единицы до круглого числа 10, в котором разряд единиц содержит число 0.
Умножение можно записать как сумму одинаковых слагаемых. Например, 9·3=9+9+9. Всякий раз, прибавляя следующую девятку, мы знаем, что еще одной единички в ответе не будет доставать до круглого числа. Следовательно, сколько раз прибавлялась девятка (или, по-другому, на какое число x выполнялось умножение), столько же единичек будет не доставать в ответе. Поскольку разряд единиц исчисляет не более 10 чисел (от 0 до 9), а при умножении 9·x=? в разряде единиц не будет хватать ровно x единичек, то и число в разряде единиц будет равно 10-x. Это отражено в примере с руками: мы загибали палец с номером x и для разряда единиц подсчитывали оставшиеся пальцы справа, а на самом деле из 10 пальцев просто исключали пальцы с номерами от 1 до x, выполняя таким образом операцию 10-x.
В то же время с каждой прибавленной девяткой увеличивается на 1 число в разряде десятков, причем изначально этот разряд был пустым (равным нулю). То есть для первой девятки разряд десятков равен нулю, прибавление второй девятки увеличивает его на 1, третьей девятки – еще на 1, и так далее.
А значит число десятков равно x-1, поскольку отсчет десятков начинался с нуля. В примере с руками мы загибали палец с номером x, обеспечивая этим действие “минус один”, и считали количество пальцев слева от загнутого, а их там оказывается ровно x-1. Таков секрет этой нехитрой методики.
Отсюда следуют дополнительные соображения. Мало того, что пример 9·x=? легко вычислять через число x (разряд десятков равен x-1, разряд единиц равен 10-x), так еще такой пример можно вычислять как x·10-x. Другими словами, дописываем справа к числу x один нулик и вычитаем из получившегося числа число x. Например, 9·5=50-5=45, или 9·6=60-6=54, или 9·7=70-7=63, или 9·8=80-8=72, или 9·9=90-9=81. Таким необычным шагом мы превращаем пример на умножение в пример на вычитание, который значительно проще решается.
Умножение для числа 8 – 8·1, 8·2 … 8·10 – действия здесь похожи на умножение для числа 9 за некоторыми изменениями. Во-первых, поскольку числу 8 не хватает уже двойки до круглого числа 10, нам необходимо каждый раз загибать сразу два пальца – с номером x и следующий палец с номером x+1.
Во-вторых, тотчас же после загнутых пальцев мы должны загнуть еще столько пальцев, сколько осталось незагнутых пальцев слева. В-третьих, это напрямую работает при умножении на число от 1 до 5, а при умножении на число от 6 до 10 нужно отнять от числа x пятерку и выполнить расчет как для числа от 1 до 5, а к ответу затем добавить число 40, потому что иначе придется выполнять переход через десяток, что не совсем удобно “на пальцах”, хотя в принципе это не так сложно. Вообще надо заметить, что умножение для чисел ниже 9 тем неудобнее выполнять “на пальцах”, чем ниже число расположено от 9.
Теперь рассмотрим пример умножения для числа 8. Допустим, хотим умножить 8 на 4. Загибаем палец с номером 4 и за ним палец с номером 5 (4+1). Слева у нас осталось 3 незагнутых пальца, значит нам необходимо загнуть еще 3 пальца после пальца с номером 5 (это будут пальцы с номерами 6, 7 и 8). Осталось 3 пальца не загнуто слева и 2 пальца – справа. Следовательно, 8·4=32.
Еще пример: вычислить 8·7=?.
Как было сказано выше, при умножении на число от 6 до 10 нужно отнять от числа x пятерку, выполнить расчет с новым числом x-5, а затем добавить к ответу число 40. У нас x=7, значит загибаем палец с номером 2 (7-5=2) и следующий палец с номером 3 (2+1). Слева один палец остался не загнут, значит загибаем еще один палец (с номером 4). Получаем: слева 1 палец не загнут и справа – 6 пальцев, что обозначает число 16. Но к этому числу нужно еще добавить 40: 16+40=56. В итоге 8·7=56.
И на всякий случай разберем пример с переходом через десяток, где никаких пятерок предварительно вычитать не нужно и никаких 40 после прибавлять тоже не нужно. Вдруг вам так окажется проще. Попробуем вычислить 8·8=?. Загибаем два пальца с номерами 8 и 9 (8+1). Слева осталось 7 незагнутых пальцев. Запомним, что у нас уже есть 7 десятков. Теперь начинаем справа загибать 7 пальцев. Поскольку там остался только один незагнутый палец, загибаем его (осталось еще 6 загнуть), затем переходим через десяток (это значит, что все пальцы разгибаем), и загибаем слева направо 6 недозагнутых пальцев.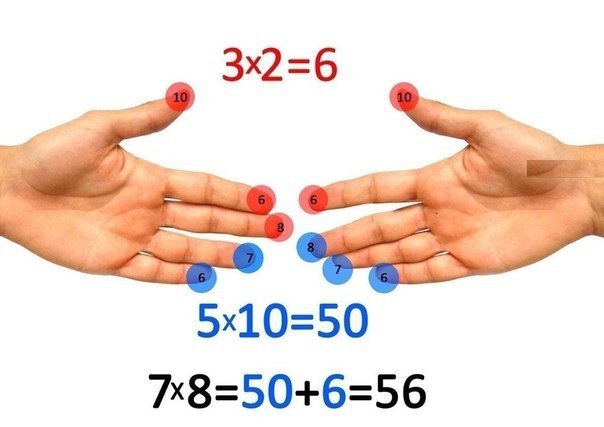
Справа осталось 4 пальца не загнуто, значит в разряде единиц в ответе будет число 4. Ранее мы запомнили, что было 7 десятков, но так как нам пришлось перейти через десяток, то один десяток нужно отбросить (7-1=6 десятков). В итоге 8·8=64.
Дополнительные соображения: здесь также можно вычислять примеры просто через число x в форме выражения на вычитание x·10-x-x. То есть дописываем справа к числу x один нулик и два раза вычитаем из получившегося числа число x. Например, 8·5=50-5-5=40, или 8·6=60-6-6=48, или 8·7=70-7-7=56, или 8·8=80-8-8=64, или 8·9=90-9-9=72.
Умножение для числа 7 – 7·1, 7·2 … 7·10. Здесь без переходов через десяток не обойтись. Числу 7 на хватает тройки до круглого числа 10, следовательно загибать придется сразу по 3 пальца. Сразу же запоминаем получившееся количество десятков по количеству незагнутых слева пальцев. Следом справа загибается столько пальцев, сколько насчитано десятков. Если во время загибания пальцев требуется переход через десяток, делаем его.
Затем второй раз загибается столько же пальцев, то есть одна операция выполняется два раза. И вот теперь количество оставшихся справа незагнутых пальцев записывается в разряд единиц, количество ранее насчитанных десятков (минус количество переходов через десяток) – в разряд десятков.
Видите, как тут уже становится сложнее посчитать “на пальцах”, чем выудить эти сведения из памяти. И потом, для чисел 7, 8 и 9 забывчивость элементов таблицы умножения еще как-то оправдательна, но для чисел ниже грешно не помнить. Потому на этом месте остановим рассказ в надежде на то, что саму нить “вычислений” вы ухватили и, если будет на то крайняя надобность, сможете самостоятельно спуститься к числам ниже 7, хотя человек, считающий “на пальцах” нечто в духе “пятью пять”, должно быть, выглядит крайне глупо.
С удовольствием разместим Ваши статьи и материалы с указанием авторства.
Информацию присылайте на почту
Возможность умножения на пальцах — это ценный навык, и человечеству известно как считать на пальцах таблицу умножения, по крайней мере, с XV века.
У нас могут быть мобильные калькуляторы, но во многих случаях, на самом деле, проще держать телефон в кармане и умножать на пальцах. Эта методика также может оказаться полезной для малышей, которые столкнулись с проблемами во время заучивания бесконечных математических формул.
Учить таблицу умножения на пальцах можно начинать после того, как ребенку будет известно умножение от одного до пяти. Уже на основе этих знаний можно развить навык в прямом смысле ручного умножения. Итак, приступим?
Таблица умножения на пальцах рук: девять
Держите руки перед собой ладонями вверх. Каждый из ваших десяти пальцев представляет собой число. Перемещаясь от большого пальца левой руки к большому пальцу правой руки, подсчитайте числа от одного до десяти.
Направьте палец, цифра которого соответствует числу, которое вы хотите умножить на девять, вниз к вашему телу. Так, например, если вы хотите решить, сколько будет 9×3, вам нужно будет удерживать средний палец левой рукой. Средний палец представляет номер три, потому что, если вы считаете свои пальцы от одного до десяти, начиная с большого пальца левой руки, ваш средний палец является третьим по счету.
Производим подсчет
Решается задача посредством подсчета пальцев в левую и в правую сторону. Сначала подсчитайте пальцы слева от вашего согнутого пальца — в этом случае их будет два. Затем подсчитайте пальцы справа от вашего согнутого пальца — в этом случае должно быть семь. Первая цифра ответа равна двум, а вторая цифра — семи. В итоге ответ равен 27!
Так работает таблица умножения на 9 на пальцах. Попробуйте это с другими числами кратными девяти. Как бы вы умножили 9 на 2? Как насчет 9 на 7? Этот метод невероятно прост и понятен даже малышам. Как показывает практика, дети более охотно и успешно изучают математику, зная этот интересный способ подсчета произведения двух чисел!
Таблица умножения на пальцах на шесть, семь, восемь и десять
Держите руки так, чтобы ваши ладони были обращены к вашему телу, а ваши пальцы обращены друг к другу. Снова каждый палец будет представлять собой число. Ваш мизинец представляет собой номер шесть. Безымянный палец будет иметь значение семи, средний — восьми.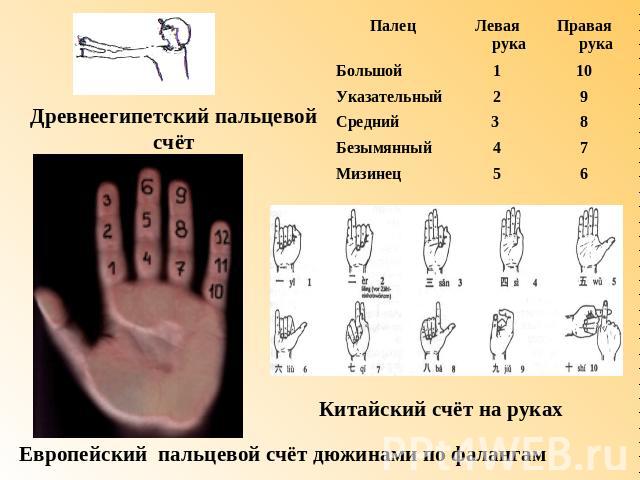
Указательные пальцы ваших рук будут символизировать девятку, а большие пальцы — десятку. Итак, как выучить таблицу умножения на пальцах?
Схема расчета
Например, если вы хотите высчитать, чему будет равно 7 * 6, вам необходимо коснуться безымянным пальцем левой руки (поскольку она представляет цифру слева) мизинца правой руки, поскольку он означает цифру справа. Опять же, помните, что каждый палец представляет собой число, и в этом случае ваш безымянный палец представляет семь, а ваш мизинец представляет шесть. Поэтому вам нужно соединить их чтобы решить эту математическую проблему.
Возможно, вам придется странным образом сгибать свое запястье, чтобы подсчитать произведение двух чисел! А кто говорил, что будет легко?
Для того чтобы убедиться, что вы правильно поняли технику таблицы умножения на пальцах на шесть, семь, восемь и десять, проверьте себя. Если вам необходимо вычислить, чему будет равно произведение 9 и 7, то какие пальцы вы бы соединили? Подумайте! Ответ будет в следующем предложении.
Итак, считайте, что вы выучили таблицу умножения на пальцах на шесть, семь, восемь и десять, если в качестве ответа, какие пальцы вам необходимо соединить, чтобы высчитать, чему равно произведение 9 и 7, вы выбрали указательный палец вашей левой руки и безымянный палец правой руки. Дело за малым!
Как считать?
Следующий шаг — просто подсчитать пальцы, что соприкасаются, а также пальцы под ними. Они будут представлять десятичные числа. В этом случае вы будете считать безымянный палец на левой руке, мизинец на левой руке и мизинец на правой руке. Каждый палец, который вы учитываете будет равняться 10. В этом случае общая сумма составляет 30.
Умножьте оставшиеся пальцы. Следующим шагом будет сложить количество пальцев на каждой руке, не считая пальцы, которые соприкасаются друг с другом. Сначала подсчитайте количество пальцев на левой руке, которые находятся над касающимися пальцами — в этом случае их будет 3. Затем подсчитайте количество пальцев правой руки над касающимися пальцами — в этом случае их будет 4.
3 * 4 = 12. Сложите два полученных числа вместе, чтобы найти свой ответ. В этом случае вам необходимо добавить 30 к 12. Общая сумма будет равна 42. Если 7 умножить на 6, то ответ совпадет и будет равняться 42!
Таблица умножения на пальцах может поначалу показаться сложной, однако, если тщательно разобраться, то выучить ее намного проще, чем бесконечные формулы в настоящей математической таблице.
Умножьте на 10, прибегая к помощи этого же метода. Например, если вы хотите найти ответ, чему будет равняться 10, умноженная на 7, то начните с касания большим пальцем левой руки безымянного пальца правой руки. Подсчитайте количество пальцев под соединяющимися пальцами, включая пальцы, которые касаются друг друга. В общей сложности у вас должно получиться 7, что означает 70. Затем подсчитайте количество пальцев над касающимися пальцами правой и левой руки. Здесь должно быть 0 слева и 3 справа от вас. Теперь умножьте 3 на 0 = 0 и добавьте 70 к 0 для ответа. Ответ 10 на 7 = 70!
Итог
Попробуйте это с другими кратными шести, семи, восьми и десяти.
Как бы вы умножали 8 и 8 пальцами? Что насчет 8 и 10? Если вас интересует вопрос, как научить таблице умножения на пальцах своего ребенка, то просто постарайтесь включить практику подсчета произведения различных чисел в ежедневную рутину. Вы и не заметите, как малыш начнет не только быстро считать произведение двух чисел, но и в конечном итоге запомнит таблицу умножения.
В этом и заключается вся привлекательность данного способа — он веселый, заставляет думать логически, включать математические способности и при этом развивает память. Что может быть лучше для ребенка? Давайте напоследок подсчитаем, чему будет равно произведение 6 и 10? А 8 и 9? Что насчет 7 и 8? Вот такая вот занимательная математика.
Сравнение систем классификации отпечатков пальцев— NY DCJS
Первичные классификации отпечатков пальцев имеют форму дроби, например 1/13, 23/2 и т. д. Числитель и знаменатель дроби получаются путем сложения значений, связанных с каждым из 10 пальцев.
Всякий раз, когда на пальце появляется паттерн завитка, связанное значение этого пальца прибавляется к базовому значению 1.
Основные различия между американской системой и системой Генри заключаются в значениях, которые присваиваются каждому из пальцев, и способе в котором эти vaules накапливаются.
Чтобы продемонстрировать разницу, мы составим набор шаблонов отпечатков пальцев.
Образцы отпечатков пальцев (пример):
................Большой палец..Указатель...Средний..Кольцо...Мало |------------------------------------------------- ---| |.Finger.Number|...1...|...2..|...3...|...4...|...5..| |.ПРАВАЯ.РУКА...|.......|......|.......|.......|......| |.Finger.Pttrn.|.Loop..|.Loop.|.Arch..|.Worl.|.Loop.| |--------------|-------|------|-------|-------|--- ---| |.Finger.Number|...6...|...7..|...8...|...9...|..10..| |.ЛЕВАЯ.....|.......|......|.......|.......|......| |.Finger.Pttrn.|.Worl.|.Loop.|.Worl.|.Loop..|.Loop.| |------------------------------------------------- ---|
Система Генри суммирует все значения в каждом из ЧЕТНЫХ пальцев, где появляется завиток.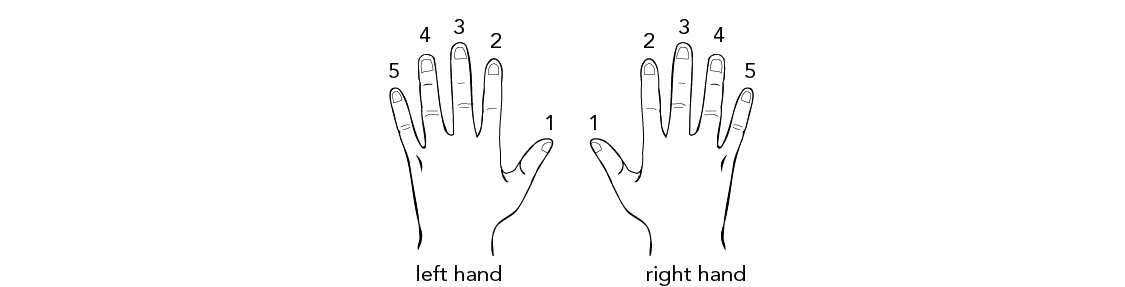
Это число используется в качестве числителя. Затем все значения для пальцев с нечетными номерами, в которых появляется завиток, складываются и используются в качестве знаменателя.
Генри Значения классификации:
................Большой палец..Указательный...Средний..Кольцо...Маленький |------------------------------------------------- ---| |.Finger.Number|...1...|...2..|...3...|...4...|...5..| |.Finger Pttrn.|.Loop..|.Loop.|.Arch..|.Worl.|.Loop.| |.Finger.Value.|..16...|..16..|...8...|...8...|...4..| |--------------|-------|------|-------|-------|--- ---| |.Finger.Number|...6...|...7..|...8...|...9...|..10..| |.Finger Pttrn.|.Worl.|.Loop.|.Worl.|.Loop..|.Loop.| |.Finger.Value.|...4...|...2..|...2...|...1...|..1...| |------------------------------------------------- ---|
Приведенный выше пример будет иметь классификацию Генри 15/1.
Глядя на четные пальцы, вы найдете Завитки в:
пальцы номер 4 (значение = 8), 6 (значение = 4) и 8 (значение = 2).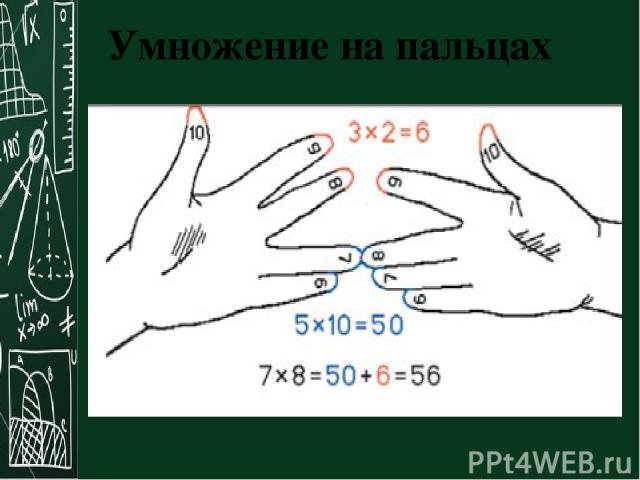
Числитель: 1 (базовое значение) + 8 + 4 + 2, что равняется 15.
Ни в одном из пальцев с нечетными номерами нет завитков, поэтому демилитор будет:
1 (базовое значение) + 0, что равно 1.
Вместе эти числа образуют первичную классификацию Генри 15/1
В американской системе первичный результат достигается аналогичным образом, но сначала добавляются значения пальцев для правой руки, а затем для левой.
Американская система классификации. |————————————————- —| |.Finger.Number|…1…|…2..|…3…|…4…|…5..| |.Finger Pttrn.|.Loop..|.Loop.|.Arch..|.Worl.|.Loop.| |.Finger.Value.|..16…|…8..|…4…|…2…|…1..| |————–|——-|——|——-|——-|— —| |.Finger.Number|…6…|…7..|…8…|…9…|..10..| |.Finger Pttrn.|.Worl.|.Loop.|.Worl.|.Loop..|.Loop.| |.Finger.Value.|..16…|…8..|…4…|…2…|.. 1..| |————————————————- —|
Глядя на пальцы ПРАВОЙ руки, вы видите завиток в пальце номер 4, значение которого равно 2.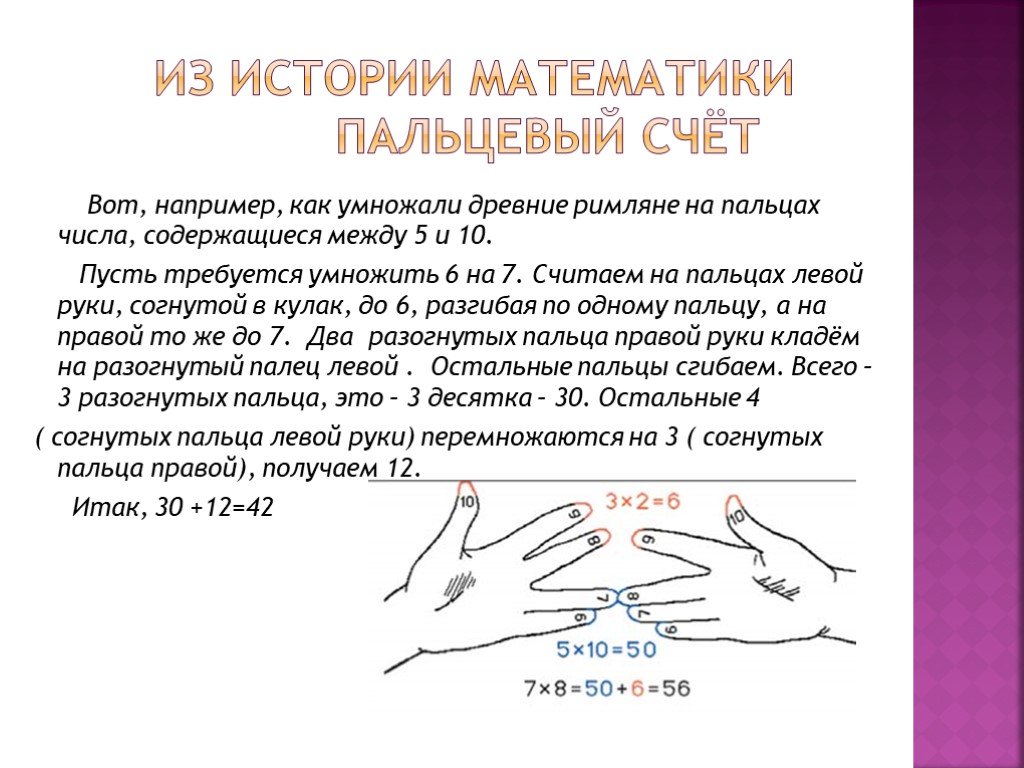
Числитель будет:
1 (базовое значение) + 2, что равняется 3.
ЛЕВАЯ рука имеет узоры завитков на пальцах номер 6 (значение 16) и 8 (значение 4). в
Знаменатель будет:
1 (базовое значение) + 16 + 4, что равняется 21.
Американская первичная система в приведенном выше примере будет 3/21.
Для того, чтобы Первичная классификация Генри соответствовала Первичной системе Американской системы, завитки должны быть на всех 10 пальцах (32/32) или вообще на пальцах (1/1).
Дом легкой атлетики муниципального колледжа Фингер-Лейкс
Женский баскетбол
VS Общественный колледж SUNY Broome
L, 58-40
Баскетбол, мужской
VS SUNY Broome Community College
L, 73-70
Женский баскетбол
VS Общественный колледж Джефферсона
L, 86-29
Мужской баскетбол
VS Общественный колледж Джефферсона
L, 60-54
Баскетбол среди мужчин
AT Университет Альфреда СП
L, 72-69
Женский баскетбол
AT Erie Community College
L, 65-30
https://www.
youtube.com/channel/UCobEfXCoEZRZqcknae5IDOA/featured
Мужской баскетбол
AT Erie Community College
L, 92-52
Женский баскетбол
AT Общественный колледж Томпкинса Кортленда
L, 66-33
Баскетбол, мужской
AT Tompkins Cortland Community College
L, 66-65
Мужской баскетбол
AT Columbia-Greene Community College
L, 80-69
Мужской баскетбол
VS СП Университета Альфреда
Мужской баскетбол
VS Брайант и Стрэттон Рочестер
Женский баскетбол
VS Колледж Mohawk Valley Community College
L, 75-27
Мужской баскетбол
VS Колледж Mohawk Valley Community College
L, 108-59
Женский баскетбол
VS Fulton-Montgomery Community College
L, 92-38
Мужской баскетбол
VS Общественный колледж Фултон-Монтгомери
L, 107-70
Баскетбольный мяч для мужчин
AT
St.