Деление целого на равные части в дошкольном возрасте: Деление целого на равные части | Учебно-методический материал по математике (старшая, подготовительная группа):
Методика ознакомления с делением целого на равные части, установления отношений целое и часть.
В старшей группе дети учатся делить целое (геометрические фигуры, предметы) на равные части. Это необходимо в качестве пропедевтики к усвоению долей и дробных чисел в школе, углубления понимания детьми элементарных математических отношений: «больше», «меньше», «равны».
Обучение строится на общих и функциональных зависимостях целого и части:
– часть всегда меньше целого, а целое больше части;
– равенство частей целого между собой;
– функциональная зависимость между количеством и размером частей: чем больше количество частей, на которое делится целое, тем меньше каждая часть, и, наоборот, чем больше часть, тем на меньшее количество частей разделено целое.
Деление целого на части осуществляется практически путем складывания с последующим разрезанием или путем разрезания.
Освоение детьми способов деления целого на равные части и отношения «целое — часть» способствует
Слово один они относят к разным величинам: то к целому, то к его части, причем разного размера.Обучение делению целого на части осуществляется с учетом особенностей понимания детьми отношения «целое — часть».
К старшему дошкольному возрасту у детей накапливается опыт деления целого на части (в играх, конструировании, быту). У них складывается бытовое понимание целого как неделимого и восприятие каждой части целого как нового, самостоятельного объекта.
Задачи обучения состоят в следующем:
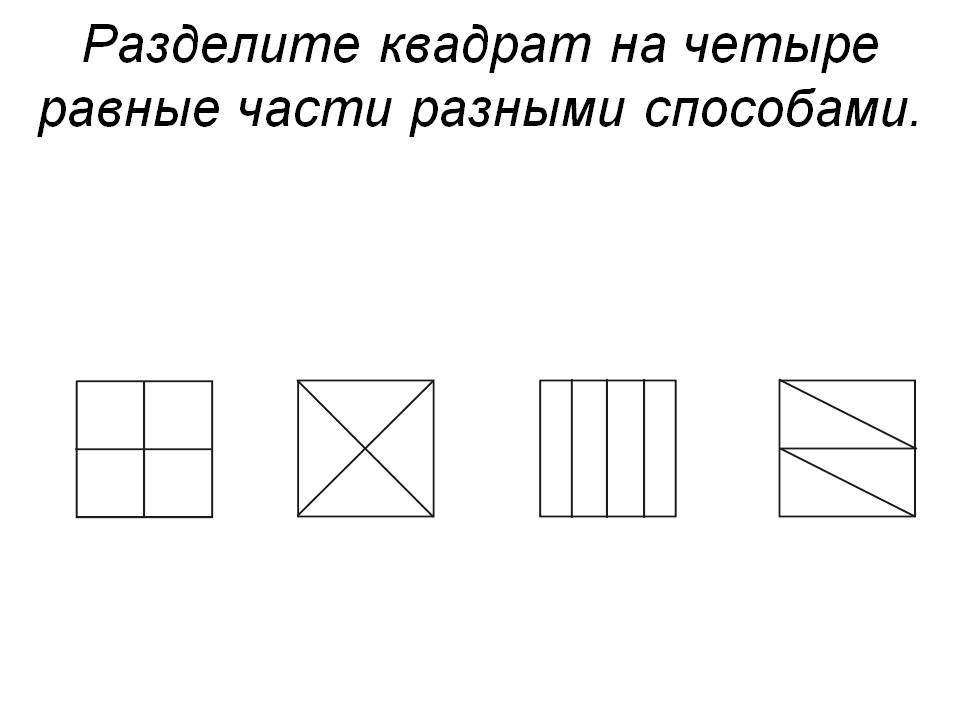
—научить детей делить предмет на две, четыре равные части путем разрезания или последовательного складывания плоских предметов пополам;
— сформировать представление о зависимости целого и части, уметь воспринимать как целое не только неразделенный предмет, но и воссозданный из частей;
— упражнять в способе сравнения частей, полученных при делении целого на равные части, путем наложения, уточнить значение слова равенство;
— способствовать развитию самостоятельности мышления, сообразительности, упражнять детей в нахождении новых способов деления, выявления зависимостей.
В ходе обучения у детей формируется понимание половины как части целого, деленного на две равные части, четверти — на четыре равные части. Они учатся выражать в речи способ деления, складывания, соотношение частей.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.
Расчет стоимостиГарантииОтзывы
Обучение делению предметов на равные части является основной задачей 3-4 занятий.
Вначале детей знакомят со способами деления целого на равные части (две и четыре) путем сгибания без разрезания, что дает возможность обнаружить части внутри целого, их количество и соотношение с целым, каждая из частей меньше целого, целое больше части. С этой целью берутся плоские предметы: круги, полоски бумаги, шнуры, тесьма и др.
Детям свойственно определять полученные в результате решения части, пользуясь названиями геометрических фигур (квадраты, треугольники), а не признаком формы. Они не выделяют форму частей: части квадратной, треугольной формы. Слово часть в своей речи они заменяют названиями геометрических фигур.
Предупреждению данной ошибки и упражнению в употреблении слов часть, часть целого, половина, четверть способствуют упражнения на деление таких предметов, когда в результате получаются части, не имеющие прямого сходства с геометрическими фигурами.
В процессе деления путем складывания дети убеждаются в том, что одноразовое перегибание листа бумаги ведет к получению двух равных частей, двухразовое — четырех.
В дальнейшем педагог упражняет детей в делении путем складывания с разрезанием и последующим склеиванием частей для воссоздания целого.
С целью уточнения зависимостей целого и частей используется прием деления на равные и неравные части и воссоздания целого из них.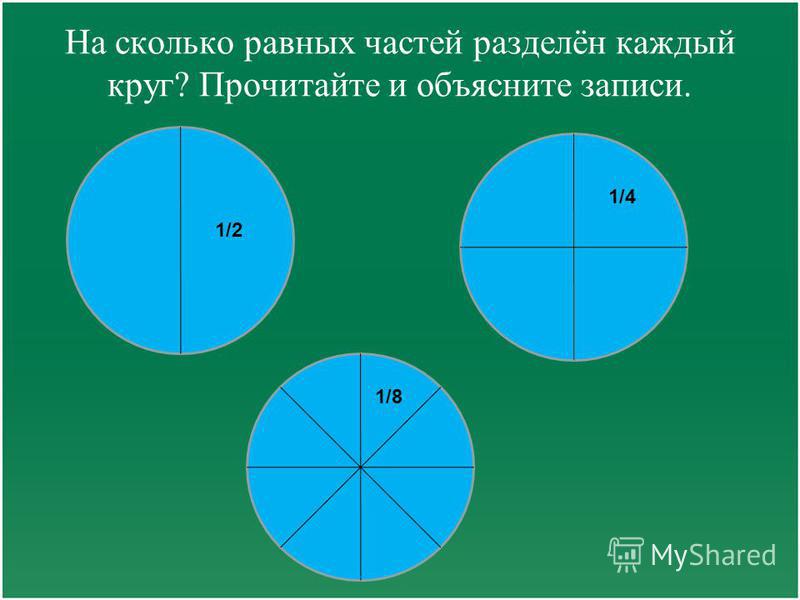
Педагог, указывая на часть, спрашивает детей, можно ли ее назвать частью целого: половиной, одной четвертой частью, предлагает использовать практические приемы для убеждения в этом: наложение частей, воссоздание целого.
Для обобщения знаний воспитатель использует вопросы-задачи
Припоминая вместе с детьми факты деления предметов на части, которые им приходилось наблюдать у себя дома, в детском саду, в магазине и т.д. педагог обогащает и уточняет представления детей о делении предметов на части.
Дети, обучаясь делению предметов (яблока, пряника) в бытовых для них ситуациях на равные и неравные части путем разрезания, уточняют, что только при делении на равные части каждую из них можно назвать долей.
В игровой ситуации при соблюдении требований к делению каждый из участников получает предназначенную ему долю целого предмета.
Поможем написать любую работу на аналогичную тему
Реферат
Методика ознакомления с делением целого на равные части, установления отношений целое и часть.
От 250 руб
Контрольная работа
Методика ознакомления с делением целого на равные части, установления отношений целое и часть.
От 250 руб
Курсовая работа
Методика ознакомления с делением целого на равные части, установления отношений целое и часть.
От 700 руб
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Обучение старших дошкольников делению целого на равные части
1.
Введение
К моменту поступления в школу
дети должны усвоить относительно широкий
круг взаимосвязанных знаний о множестве
и числе, форме и величине, научиться ориентироваться
в пространстве и во времени. Практика
показывает, что затруднения первоклассников
связаны, как правило, с необходимостью
усваивать абстрактные знания, переходить
от действия с конкретными предметами,
их образами к действию с числами и другими
абстрактными понятиями. Такой переход
требует развитой умственной деятельности
ребенка. Поэтому в подготовительной к
школе группе особое внимание уделяют
развитию у детей умения ориентироваться
в некоторых скрытых существенных математических
связях, отношениях, зависимостях: «равно»,
«больше», «меньше», «целое и часть», зависимостях
между величинами, зависимости результата
измерения от величины меры и др. Дети
овладевают способами установления разного
рода математических связей, отношений,
например способом установления соответствия
между элементами множеств (практического
сопоставления элементов множеств один
к одному, использования приемов наложения,
приложения для выяснения отношений величин).
Умение ориентироваться
в существенных математических связях
и зависимостях и овладение соответствующими
действиями позволяют поднять на
новый уровень наглядно-
Не менее важно в этом возрасте развитие умственных способностей, самостоятельности мышления, мыслительных операций анализа, синтеза, сравнения, способности к отвлечению и обобщению, пространственного воображения.
У детей должны быть воспитаны устойчивый интерес к математическим знаниям, умение пользоваться ими и стремление самостоятельно их приобретать.
Программа по развитию элементарных
математических представлений подготовительной
к школе группы предусматривает
обобщение, систематизацию, расширение
и углубление знаний, приобретенных
детьми в предыдущих группах.
Одними из самых сложных
знаний, умений и навыков, включенных
в содержание общественного опыта,
которым овладевают подрастающие поколения,
являются математические. Они носят
отвлеченный характер, оперирование
ими требует выполнения системы
сложных умственных действий. В повседневной
жизни, в быту и в играх ребенок
достаточно рано начинает встречаться
с такими ситуациями, которые требуют
применения, хотя и элементарного, но все
же математического решения (приготовить
угощение для друзей, накрыть стол для
кукол, разделить конфеты поровну и т.
д.), знания таких отношений, как много,
мало, больше, меньше, поровну, умения определить
количество предметов в множестве, выбрать
соответствующее количество элементов
из множества и т. д. Сначала с помощью
взрослых, а затем самостоятельно дети
разрешают возникающие проблемы. Таким
образом, уже в дошкольном возрасте дети
знакомятся с математическим содержанием
и овладевают элементарными вычислительными
умениями, а формирование у них элементарных
математических представлений является
одним из важных направлений работы дошкольных
учреждений.
2.Ознакомление детей с делением целого на равные части
При отсутствии специально
организованного обучения математическое
развитие в дошкольном возрасте проходит
медленно и не достигает того уровня,
который требуется для
Содержание математических представлений, формируемых у детей дошкольного возраста, очень разнообразно. Особое место в нем занимают количественные представления.
Дальнейшему развитию понятия о числе служат упражнения в делении предметов на равные части. Дети учатся видеть части в целом предмете, выявляют отношение целого и части.
Делению предметов на равные части отводят 6—7 (последовательно проводимых) занятий, а затем до конца года к этому периодически возвращаются
На первом занятии создают
ситуации, при которых возникает
необходимость разделить 
п. Воспитатель показывает, как
надо делить предметы на 2 равные части,
т. е. пополам, подчеркивает, что он точно
складывает и разрезает предмет посередине,
потом сравнивает полученные части, накладывая
одну на другую или прикладывая одну к
другой. Дети считают части, убеждаются,
что они равные. Воспитатель говорит, что
любую из 2 равных частей обычно называют
половиной.
Следующий предмет воспитатель намеренно делит на 2 неравные части и спрашивает: «Можно ли такую часть назвать половиной? Почему нет?»
Дети видят, что предметы
могут быть разделены как на равные,
так и на неравные части. Половиной
1 из 2 частей можно назвать лишь тогда,
когда части равны. Постепенно дети
убеждаются в том, как важно точно
складывать, разрезать предметы, чтобы
получились равные части. Выполнив действие,
они проверяют (наложением и приложением),
равные ли получились части, считают
их и, соединив вместе, получают целый
предмет, обводят его контур и
части рукой, сравнивают размер целого
и части.
На втором занятии воспитатель расширяет круг предметов, которые дети делят пополам. Можно использовать крупу, воду. Их распределяют поровну в 2 прозрачных стакана одинаковых размеров. На третьем занятии показывают способы деления предметов на 4 равные части, т. е. пополам и еще раз пополам. Устанавливают отношения между целым и частью: часть меньше целого, целое больше части. Если в подготовительную к школе группу поступило много новых детей целесообразно начать с деления предметов на части путем складывания. Дети получают по 2 предмета одинаковых размеров, в чем они убеждаются, накладывая 1 предмет на другой. Они делят 1 предмет на 2 равные части, другой — на 4. Соединив части вместе, они получают целый предмет, пересчитывают части, показывают 1 из 2 частей, 2 из 2 частей, соответственно 1 (2, 3, 4) из 4 равных частей. Сравнивают размер 1 части и целого.
Аналогичным образом на следующем
занятии показывают взаимосвязи
между разными частями единого
целого.
Дети получают по 3—4 листа бумаги
одинакового размера, первый кладут
перед собой, второй делят на 2 равные
части, а третий — на 4 (можно четвертый
лист разделить на 8 равных частей).
Соединяя части (как бы оставляя листы целыми), дети раскладывают их один под другим, показывают 1 из 2 частей, 1 из 4 частей, сравнивают размер 1/2 и 1/4 части и их количество. Что меньше: целый лист или половина? Что больше: половина или 1 из 4 частей, 1/4? Какая часть меньше всех? Почему? И т. п.
Полезно установить связь между количеством действий разрезания и количеством получившихся частей. Например, воспитатель спрашивает:
«Сколько раз надо сложить
квадрат пополам, чтобы получились
2 равные части? А 4 части?» Для обобщения
знаний можно использовать схемы
деления того или иного предмета
на равные части (яблока, круга, квадрата
и пр.). Рассматривая с детьми схему,
воспитатель спрашивает: «На сколько
равных частей сначала разделили
яблоко? Сколько получилось таких
частей? На сколько равных частей потом
разделили яблоко? Сколько получилось
частей? Что больше и что меньше:
половина или целое яблоко? 2 половины
или целое яблоко? 1 из 4 частей (1/4)
или половина (1/2)?» И т.
д. Такие
упражнения дети обычно воспринимают
как игру и с удовольствием
отвечают на вопросы.
На последующих занятиях проводят упражнения в делении геометрических фигур на 2, 4, 8 частей и в составлении целых фигур из частей, например: «Как надо сложить и разрезать квадрат, чтобы получились 2 равных прямоугольника? Чтобы получились 2 равных треугольника?» (Надо согнуть квадрат стороной к стороне или сложить уголок с уголком.) Дети рассказывают о том, какие фигуры и как они разделили и, что получилось в результате деления, какой формы части, сколько их.
Проводят и специальные упражнения в составлении фигур из частей: «Сколько кругов можно сложить из 4 полукругов?» Можно показать части фигур: «Это 1 из 4 (1 из 2, 4 из 8) частей квадрата. Догадайтесь, сколько было квадратов. Составьте их».
Полезно побуждать детей
находить наиболее удобные (рациональные)
способы деления предметов на
части с учетом их размера, формы,
пропорций. Например, надо сравнить, как
легче разделить на 4 части узкую
полоску (ленту) и квадрат (кусок
ткани).
Дети решают, что узкую полоску
удобнее складывать по длине пополам
и еще раз пополам, а квадрат
— последовательно сложить
Предметы были разных размеров,
и их части тоже разных размеров.
Целесообразно здесь же противопоставить
результаты деления на части предметов,
равных по величине.
При проведении упражнений
в делении предметов на равные части воспитатель
постоянно следит за тем, чтобы дети точно
выполняли действия, проверяли равенство
частей, пользуясь приемами наложения
и приложения, а также измерения условной
меркой, приучает детей употреблять в
речи следующие слова и выражения: разделить
на равные части, целое, половина, пополам,
одна из двух частей, одна из четырех частей,
а несколько позднее — одна вторая, одна
четвертая. Последние выражения не следует
специально заучивать, дети постепенно
их запоминают. Каждый раз ребята пересчитывают
части, а соединяя их вместе, получают
1 целый предмет, устанавливают отношение
между целым и частью.
После того как дети овладевают
приемами измерения, им можно предложить
разделить палку, рейку, дощечку, нарисованный
на доске прямоугольник и пр.
на
2; 4, 8 равных частей. Ребята видят, что
данные предметы не сгибаются, усвоенные
способы деления не подходят. Как
быть? Воспитатель не спешит с подсказкой.
Он раскладывает перед детьми предметы,
которыми можно воспользоваться
в качестве мерки. Здесь детям и помогает
понимание взаимосвязи между размером
предметов и размером их соответствующих
частей. 1—2 наводящих вопроса и дети догадываются,
что надо выбрать подходящую мерку, отмерить
кусок, равный длине предмета, разделить
мерку (сложить) на соответствующее количество
частей и затем отмерить эти части на предмете,
сделать отметки карандашом, мелком и
др. Полезно поупражнять детей в делении
геометрических фигур, нарисованных на
бумаге в клетку. Дети рисуют фигуры заданного
размера, а затем по указанию воспитателя
делят их на 2, 4 равные части, измеряя по
клеткам. По указанию воспитателя они
проводят отрезки длиной от 2 до 10 клеток
сверху вниз или слева направо и делят
их на части, равные длине 1, 2, 3, 4, 5 клеток.
Благодаря делению целого предмета
на части, устанавливаются связи
между величиной мерки и
Деление на части позволяет показать
детям возможность дробления
предметов на равные доли, наглядно
выявлять отношение целого и части,
и, таким образом, создается условие
для осознания детьми процесса измерения
величин. При измерении предмет
как бы дробится на части, сумма которых
и характеризует его величину.
Обучение делению предмета на равные доли является основной задачей 3—4 занятий. Начинать его следует с деления предмета на части путем складывания (сгибания), но не разрезания: разрезав предмет, дети каждую его часть воспринимают как отдельный объект, независимый от целого. Например, на вопрос, что больше: целое или его часть, некоторые из них отвечают, что «частей больше, потому что их 2, а целое только одно». Установление связи между размером и принадлежностью целому его части подменяется поштучным сопоставлением объектов. Не понимая существа вопроса, дети не могут дать соответствующий ответ.
На первом
занятии педагог показывает
способ деления прямоугольного
листа бумаги на равные
части путем складывания (сгибания)
его пополам (на 2 части)
и еще раз пополам (на 4
части). Материалом для
этой работы, кроме листа
бумаги, могут служить
модели геометрических
фигур из бумаги. Демонстрируя
возможность деления
предмета как на 2 равные,
так и на 2 неравные части,
детям дают представление
о том, что 1 из 2 равных
частей целого называется
половиной, половинами
являются обе равные
части.
Если предмет
разделен на 2 неравные
части, то их нельзя
назвать половинами.
В таком случае говорят:
предмет разделен на 2 (4)
неравные части.
С самого начала детей убеждают в необходимости точно складывать (в дальнейшем и разрезать) предмет, чтобы получились равные части. Равенство частей проверяется наложением или приложением. Складывая предмет пополам, а потом каждую часть еще раз пополам (дважды пополам), дети делят его на 4 равные части. Воспитатель постоянно побуждает ребят отражать в слове способ и результат деления. («Что сделали? Что получилось? Равны ли части?»)
Когда
предметы разрезаются
на части, полезно предлагать
детям то соединить их
вместе («Как будто остался
целый предмет»), то
разделить предмет на
части (отодвинуть их
друг от друга). Устанавливают
связь между действием
и его результатом: разделили
предмет пополам (дважды
пополам) — получились 2 (4)
равные части, соединили
их вместе — получился
целый предмет. По просьбе
педагога дети показывают 1
из 2 частей (половину), 1
из 4 частей, 2 половины, 2 (3, 4)
из 4 частей.
Они обводят
контур предмета и каждую
из его частей пальцем,
сравнивают размер целого
и части и выясняют,
что целое больше части,
а часть меньше целого.
Пди этом педагог постоянно
следит за тем, чтобы
дети правильно употребляли
следующие слова и выражения:
пополам, половина, равные
части, целое, одна из
двух, одна из четырех
частей. Деление на части
моделей геометрических
фигур позволяет уточнить
знание о них. Детям
предлагают не только
определить, какой формы
получились части (сложили
— перегнули квадрат,
получили 2 равных прямоугольника),
но и самостоятельно
получать части указанной
формы. («Как надо сложить
квадрат (прямоугольник),
чтобы получились 2 равных
треугольника?») Дети
выполняют упражнения
в составлении целых
фигур из частей.
Разрежьте круги на равные части и назовите их дробями Третьи и Четвертые
- Уроки
- 2 класс
- Математика
- Фракции и формы
Мероприятие 1 / Круг Третьи Рабочий лист
Во-первых, напомните своим детям, как можно разделить фигуры.
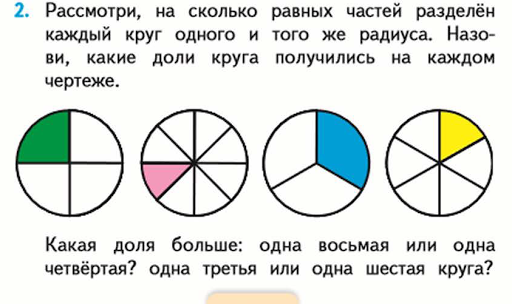Когда форма завершена, они называются целыми. Когда фигура разделена на две равные части, они называются половинками. Точно так же формы, которые были разделены на три части, называются терциями, а четыре части называются четвертями. Теперь посмотрите вместе с детьми на фигуры на этом листе. Обведите печенье, разрезанное на три части.Заполнить онлайн
Отметить как выполненное
Добавить в избранное
Мероприятие 2 / Рабочий лист «Найти четвертые круги»
Нахождение дробей в наборе может быть очень простым и интересным для изучения с помощью этого рабочего листа «Найти четвертые числа с кругами». Красочный PDF-файл дает вашему ребенку возможность увидеть осязаемое графическое представление кругов, разделенных на разные части.
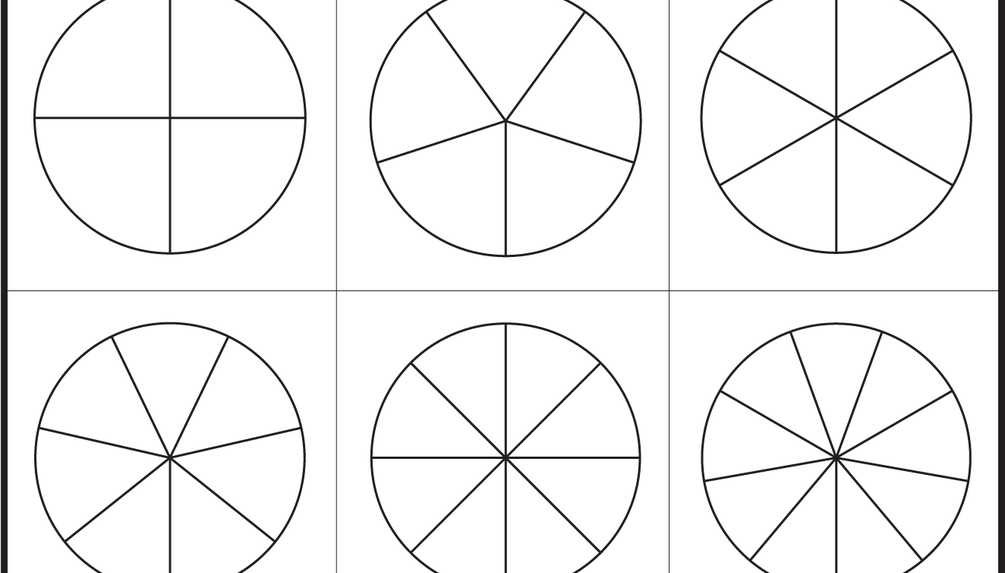Затем они обводят гнезда, разделенные на четверти. Вместе со своим веселым другом-птицей они будут искать гнезда, которые разделены на четыре равные части, и добьются успеха в выборе правильного гнезда.Заполнить онлайн
Отметить как выполненное
Добавить в избранное
Мероприятие 3 / Шина Третьи и Четвертые Рабочий лист
Изучение геометрии — очень важный аспект образования вашего ребенка. Самое первое, чему они должны научиться, это как определять и называть формы, которые были разрезаны на разные части. Спросите своих детей, могут ли они сказать вам, как называются фигуры, разрезанные на 2, 3 и 4 части соответственно.
Теперь проверьте свои знания с помощью этого простого рабочего листа. Шины на этой распечатке разделены. Попросите детей обвести пунктирную линию, чтобы обозначить каждую из них как третью или четвертую.Заполнить онлайн
Отметить как выполненное
Добавить в избранное
Мероприятие 4 / Разрезать лист на четверти четвертей
Когда дело доходит до обучения тому, как идентифицировать дроби и работать с ними, всегда лучше, если у детей есть хорошее визуальное представление, к которому можно обращаться, когда они пытаются идентифицировать разные группы. С помощью этого бесплатного рабочего листа они увидят, как различные круги делятся на трети и четверти.
Затем у них будет возможность выбрать фигуры, которые разделены как на трети, так и на четверти. Они узнают, что дроби нужно делить на равные части, а не только на определенное количество наборов, и добьются успеха в выборе правильных цветных кругов.Заполнить онлайн
Отметить как выполненное
Добавить в избранное
Когда форма завершена, они называются целыми. Когда фигура разделена на две равные части, они называются половинками. Точно так же формы, которые были разделены на три части, называются терциями, а четыре части называются четвертями. Теперь посмотрите вместе с детьми на фигуры на этом листе. Обведите печенье, разрезанное на три части.
Затем они обводят гнезда, разделенные на четверти. Вместе со своим веселым другом-птицей они будут искать гнезда, которые разделены на четыре равные части, и добьются успеха в выборе правильного гнезда.
Теперь проверьте свои знания с помощью этого простого рабочего листа. Шины на этой распечатке разделены. Попросите детей обвести пунктирную линию, чтобы обозначить каждую из них как третью или четвертую.
Затем у них будет возможность выбрать фигуры, которые разделены как на трети, так и на четверти. Они узнают, что дроби нужно делить на равные части, а не только на определенное количество наборов, и добьются успеха в выборе правильных цветных кругов.Попробуйте Детскую Академию БЕСПЛАТНО!
Посмотреть полную программу обучения
Да, я хочу добавить
Электронный блок
– совместимый с кирпичом
конструктор для построения 3D схем с подсветкой, звуками, движением и т.
д.
19,99 $
Введите код купона
Примечание. Вам не будет выставлен счет, пока не закончится бесплатная пробная версия. и может отменить в любой момент. Безвоздмездно.
Отличное приложение
Вау! Это приложение действительно отличное. Впервые моим детям действительно нравится изучать математику и читать. Игры в Kids Academy образовательные и очень веселые.
Кимберлихо
Отличное приложение!
Это был действительно интересный способ заставить моих детей попрактиковаться в математике. Я обычно изо всех сил пытаюсь вовлечь их в это, и Kids Academy делает это легко.
Фернанндас Стоун
Так увлекательно
Нам нравится, как мы можем сосредоточиться на математике с помощью этого приложения.
Это увлекательно, и нам нравится, как мы можем настраивать и адаптировать уровни в соответствии со знаниями и навыками нашего сына!
Мама Анна
Отлично подходит для детей
Наша 7-летняя дочь любит чтение и все офлайн-игры, которые предлагает Kids Academy. Это очень хорошее приложение, я очень рекомендую его!
ТониТан
Любимец дочери
По-прежнему самый любимый для нашего 7-летнего ребенка. Ей нравится зарабатывать звезды, когда она учится выводить буквы и цифры. Окраска и звуки привлекают внимание и соответствуют ее возрастной группе и уровню Pre K.
Выживание5Дети
Отличное приложение!
Это замечательное приложение для моего 7-летнего сына! 🙂 Он фокусируется на базовых навыках чтения, письма и математики.
Система вознаграждений отличная и последовательная!
Лилбиттигарза
Обучение дробям с пониманием: концепция часть-целое
В своих исследованиях детей, изучающих рациональные числа, Грейс Лопес-Чарльз [см. примечание 1 ниже] определила несколько различных точек зрения, с которых дети видят дроби. Эта статья начинает рассмотрение некоторых из этих точек зрения, во-первых, с рассмотрения того, что происходит в ситуациях, когда учащиеся пытаются создать равные доли. От совместного использования половинок учащиеся переходят к разделению используя другие деления, такие как пятые или шестые. Это приводит к необходимости развивать понимание эквивалентности, которое обсуждается во втором разделе этой статьи. Наконец, мы рассмотрим некоторые способы более эффективного обучения дробям, основанные на работе Грейс.
Равные доли
Работа с половинками
Похоже, что эта стратегия основана на половинках, потому что дети уверены в этой концепции.
Этот подход более распространен среди детей младшего возраста, хотя в своих исследованиях Грейс видела, что многие дети в возрасте от 7 до 10 долларов также применяют его. Используя этот метод, ребенок начинает с разделения каждой области или составной единицы на две части. Таким образом, разделив три плитки шоколада между четырьмя
детей можно было бы получить, сначала уменьшив вдвое все бары. В этом случае четыре половины могут быть разделены, и останется один целый стержень (две половины). Части третьего такта снова разделены пополам, и теперь их можно использовать совместно. Если бы справедливая доля была невозможна на этом этапе, произошло бы дальнейшее деление пополам. В этот момент учитель может спросить ребенка: «Сколько получил каждый?» и в предложении
описание ребенок может ответить «Два», потому что он считает фрагменты, а не видит равную долю как часть целого.
Застрял на счете
При фрагментации ребенок рассматривает части как отдельные единицы. Таким образом, на вопрос, какую долю получит каждый ребенок, если три плитки шоколада будут поровну разделены между четырьмя детьми, некоторые 7-летние дети ответят, что ребенок получит две.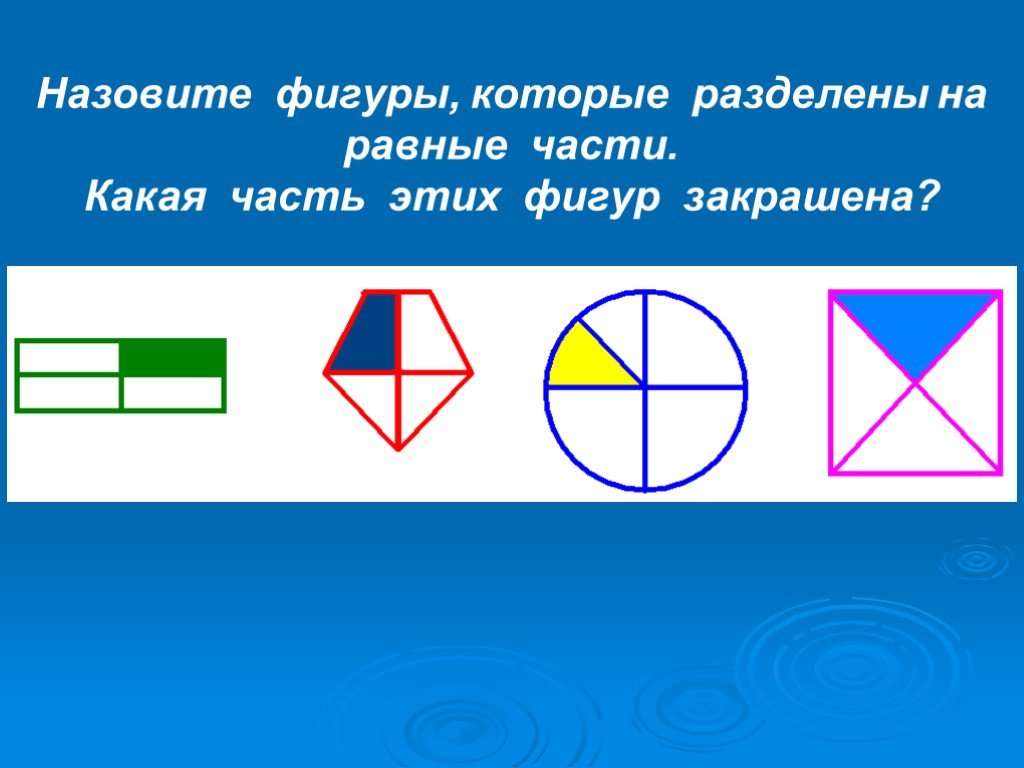
Не делается никакого концептуального различия между «двумя» как числом частей и «двумя» частями как частями каждой единицы, или
целое (три такта), которое используется совместно. Эти дети осознают фрагменты только как отдельные единичные элементы. Сложность здесь также заключается в том, относится ли «целое» к отдельным тактам, и в этом случае каждый ребенок получает три четверти такта, или «целое» относится к трем тактам. В последнем случае ответом будет «Четверть шоколада». Здесь учитель пытался бы
подчеркнем, что мы не всегда можем успешно описать количество счетом. Было бы необходимо, чтобы порции были равны по размеру для подсчета, чтобы предложить путь вперед.
Разделение
Даже маленькие дети могут разделить регионы или составные единицы примерно поровну между двумя или тремя реципиентами. Более старший, более математически зрелый ребенок может разделить область на $x$ частей, а затем обозначить $y$ частей, чтобы указать $\frac{y}{x}$, где $x$ больше, чем $2$.
Например: 8$-летних детей попросили разделить прямоугольник на восемь частей, а затем раскрасить две части в красный цвет на схеме, подобной приведенной ниже.
Проблема здесь становится вопросом эквивалентности. Грейс обнаружила, что когда учащихся спрашивают, какая дробь не заштрихована, они отвечают $\frac{6}{8}$. Ни один ребенок в исследовании не идентифицировал окрашенную часть как $\frac{1}{4}$ целого или неокрашенную часть как $\frac{3}{4}$. Это выдвигает на первый план вопрос учителей о том, как они могут повысить осведомленность об этих эквивалентности. Это может быть достигнуто с помощью вопросов, предлагающих учащимся описать одну и ту же дробь по-разному, или путем выявления проблем с одинаковыми ответами. Например, в последнем случае, разделив плитку шоколада по 6$ между 8$, вы получите такое же количество шоколада, что и поделив плитку по 3$ между 4$. «Можно ли получить тот же ответ другим способом?»
Рассматривая дробь как разбиение и определяя, что общего и что различается в $\frac{3}{4}$ и $\frac{6}{8}$, учащиеся начинают видеть дробь как сравнение между числителем и знаменателем (то, что Грейс называет сравнением «один ко многим» или «многие ко многим»).
Это основано на концепции отношения, и Грейс утверждает, что это также указывает на более глубокое понимание дробей. Как в
предыдущий пример, ребенок, указывающий, что неокрашенная дробь квадрата равна трем четвертям, упрощает знаменатель и числитель, чтобы получить эквивалентную дробь, без потери значения дроби, хотя некоторая информация теряется.
Как это может повлиять на то, как мы учим детей лучше понимать дроби?
Идеи для обучения дробям
При обучении дробям в школах акцент часто делается на ситуации, когда предмет можно легко разрезать, сложить, разделить или раскрасить на равные части. Хотя есть некоторая потребность в такого рода деятельности, дети должны быть подвержены широкому разнообразию ситуаций, некоторые из которых такие стратегии складывания или разделения не будут успешными. Испытывая различные ситуации, когда дроби могут
быть найдены, учащиеся будут иметь возможность отражать и абстрагировать критические отношения в различных контекстных ситуациях.
Иными словами, дети должны видеть целое во всех его репрезентативных формах. Это поможет им лучше усвоить понятие дроби. Грейс описывает некоторые из этих ситуаций в терминах дискретности или непрерывности, определенности или
неопределенный (см. ниже). Таким образом, цель состоит в том, чтобы работать в ситуациях, которые дают возможность исследовать дроби в каждой из этих ситуаций.
Отдельные целые – конфеты, шарики, вишни, бусы и т. д.
Непрерывные целые – пирожные, шоколадные батончики, пицца и т. д.
Определенные целые – где объем целого ясен, например: степень целого не ясна, например, мы не знаем, как долго шаблон простирается в любом направлении на изображении ниже:
При развитии правильного понимания концепции дробей часть-целое учителям необходимо представьте ситуации справедливого разделения, когда ребенок должен обдумать последствия различных действий. Например, с очень маленькими может быть необходимо начать с безчислового подхода;
- Покажите детям сладости; задайте им вопрос: – Как вы думаете, у меня достаточно конфет, чтобы каждый ребенок получил по одной конфете?; Что будет, если каждую конфету разрезать пополам?; Будет ли больше или меньше детей получать сладости?
- Поощряйте детей проводить осмысленные сравнения, например. «3 пиццы, 4 ребенка», «Все ли получают больше или меньше половины пиццы?» Все получают больше или меньше целой пиццы?
«3 пиццы, 4 ребенка», «Все ли получают больше или меньше половины пиццы?» Все получают больше или меньше целой пиццы?Качественно представляя проблему, учителя могут проводить полезные дискуссии, которые побуждают детей использовать, подвергать сомнению и развивать свои собственные подходы.
Типы заданий, которые учитель устанавливает для индивидуальной или групповой работы, должны быть направлены на развитие концепции дробей с целью преодоления некоторых трудностей с дробями. Представляя детям целое, которое явно не разделено на равные части, они поощряются к анализу отношений часть-целое.
Например:
Для каждой цифры запишите представленную дробь:
(a) Какая дробь равна K?
(б) Какая часть фигуры не окрашена?
(c) Какая часть целого отсутствует?
При явном разделении целого на равные части дети могут определить долю указанной части/частей, подсчитав количество частей в целом и количество указанных частей (двойной счет).
На рисунках, представленных выше, детям труднее принять этот «разделительный» подход. Дети должны проанализировать отношения
конкретная часть/части, указанные по отношению ко всему целому.
Дроби, преподаваемые как часть-целое, как указано в этой статье, могут гарантировать, что у детей есть прочная основа для осмысления других понятий в виде дробей. Однако следует отметить, что, несмотря на обилие возможных примеров, подход к дробям, основанный исключительно на «часть-целое», слишком ограничен — дает только правильные дроби. Поэтому другие понятия дробей необходимо изучить, если дети хотят иметь более полное и лучшее понимание рациональных чисел.
Примечание 1. Эта статья основана на исследовании Грейс Лопез-Чарльз «Оценка понимания детьми рациональных чисел» — докторская диссертация.
Ссылки:
- Азис, Н. и Па, Н. (1991), Знание дробей учащимися начальной школы, Журнал исследований в области образования, 45
- Nunes, T. (1996), Понимание рациональных чисел, в T.
