Деление целого на части: ДЕЛЕНИЕ ЦЕЛОГО НА ЧАСТИ

ДЕЛЕНИЕ ЦЕЛОГО НА ЧАСТИ

• Предыдущая
• К оглавлению
• Следующая

Главная страница =>библиотека=>оглавление

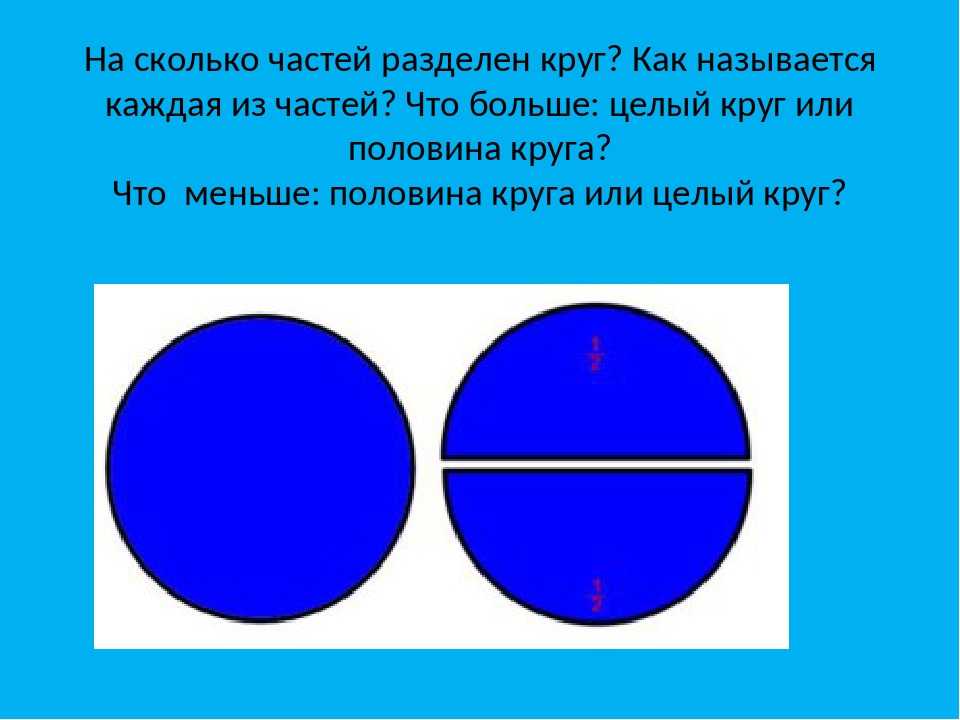
Детям шестого года жизни показывают возможность дробления предмета на равные доли, их учат устанавливать отношения между целым и частью. Разделив предмет, они получают 2—4 равные части, а соединив их вместе,— 1 целый предмет.
8 качестве единицы счета выступает то предмет, то его часть. Понятие о единице углубляется, соответственно развивается и понятие о числе
Обучение делению предмета на равные доли является основной задачей 3—4 занятий. Начинать его следует с деления предмета на части путем складывания (сгибания), но не разрезания: разрезав предмет, дети каждую его часть воспринимают как отдельный объект, независимый от целого. Например, на вопрос, что больше: целое или его часть, некоторые из них отвечают, что «частей больше, потому что их 2, а целое только одно».

Установление связи между размером и принадлежностью целому его части подменяется поштучным сопоставлением объектов. <Не понимая существа вопроса, дети не могут дать соответствующий ответе
– На первом занятии педагог показывает способ деления прямоугольного листа бумаги на равные части путем складывания (сгибания) его пополам (на 2 части) и еще раз пополам (на 4 части). Материалом для этой работы, кроме листа бумаги, могут служить модели геометрических фигур из бумаги. Демонстрируя возможность деления предмета как на 2 равные, так и на 2 неравные части, детям дают представление о том, что
1 из 2 равных частей целого называется половиной, половинами являются обе равные части. Если предмет разделен на 2 неравные части, то их нельзя назвать половинами. В таком случае говорят: предмет разделен на 2 (4) неравные частиц
//, С самого начала детей убеждают в необходимости точно складывать (в дальнейшем и разрезать) предмет, чтобы получились равные части. Равенство частей проверяется наложением или приложением вкладывая предмет пополам, а потом каждую часть еще раз пополам (дважды пополам), дети делят его на 4 равные части. Воспитатель постоянно побуждает ребят отражать в слове способ результат деления. («Что сделали? Что получилось? Равны ли части?»)
 Когда предметы” разрезаются на части, полезно предлагать детям то соединить их вместе («Как будто остался целый предмет»), то разделить предмет на части (отодвинуть их друг от друга). Устанавливают связь между действием и его результатом: разделили предмет пополам (дважды пополам) — получились 2 (4) равные части, соединили их вместе — получился целый предмет. По просьбе педагога дети показывают 1 из
2 частей (половину), 1 из 4 частей, 2 половины, 2 (3, 4) из 4 частей. Они обводят контур предмета и каждую из его частей пальцем, сравнивают размер целого и части и выясняют, что целое больше части, а часть меньше целого. При этом педагог постоянно следит за тем, чтобы дети правильно употребляли следующие слова и выражения: пополам, половина, равные части, целое, одна из двух, одна из четырех частей
 Деление, на части моделей геометрических фигур позволяет уточнить знание о них. Детям предлагают не только определить, какой формы получились части (сложили — перегнули квадрат, получили 2 равных прямоугольника), но и самостоятельно получать части указанной формы. («Как надо сложить квадрат (прямоугольник), чтобы получились 2 равных треугольника?») Дети выполняют упражнения в составлении целых фигур из частей.)
Для обобщения знаний воспитатель использует вопросы-задачи. Например: «Мне надо поровну разделить ленту между 2 девочками. Какую часть ленты получит каждая из них? Если эту ленту надо будет разделить между 4 девочками, что я должна сделать?» Или: «Вечером я пойду в булочную за хлебом. Мне нужна половина буханки хлеба. Как продавец разрежет буханку хлеба и почему? А если мне достаточно будет четвертушки хлеба, что сделает продавец и почему?» Правильность ответов проверяют соответствующими действиями.
У Припоминая вместе с детьми факты деления предметов на части, которые им приходилось много раз наблюдать у себя дома, в детском саду, в магазине и т. д., педагог обогащает и уточняет представления детей о делении предметов на части.

Л.С. Метлина. Математика в детском саду. М.:Просвещение, 1984.

Главная страница =>библиотека=>оглавление

Л.С. Метлина. Математика в детском саду. М.:Просвещение, 1984.

Добавить в закладки:

• Предыдущая
• К оглавлению
• Следующая

Смотрите еще:

• ОБУЧЕНИЕ ДЕТЕЙ ИЗМЕРЕНИЮ
• ФОРМА
• ФОРМА
• ФОРМА
• СОСТАВ ЧИСЛА ИЗ ЕДИНИЦ
• СОСТАВ ЧИСЛА ИЗ 2 ЧИСЕЛ, МЕНЬШИХ ЭТОГО ЧИСЛА
• ОРИЕНТИРОВКА В ПРОСТРАНСТВЕ
• ДЕЛЕНИЕ ЦЕЛОГО НА ЧАСТИ     
• ПРИМЕРНЫЕ КОНСПЕКТЫ ЗАНЯТИЯ
• МЕТОДЫ И ПРИЕМЫ ОБУЧЕНИЯ

Деление целого на части

Главная страница =>библиотека=>оглавление

Дальнейшему развитию понятия о числе служат упражнения делении предметов на равные части. Дети учатся видеть части целом предмете, выявляют отношение целого и части. Делению предметов на равные части отводят 6—7 (последовательно проводимых) занятий, а затем до конца года к этому периодически возвращаются.

На первом занятии создают ситуации, при которых возникает необходимость разделить предмет на 2 равные части, например разделить угощение между 2 куклами или 2 детьми (гостями), мочь 2 Жадным медвежатам разделить сыр и т. п. Воспитатель показывает, как надо делить предметы на 2 равные части, т. е. пополам, подчеркивает, что он точно складывает разрезает предмет посередине, потом сравнивает полученные части, накладывая одну на другую или прикладывая одну к другой.  Дети считают части, убеждаются, что они равные. Воспитатель говорит, что любую из 2 равных частей обычно называют половиной.
Следующий предмет воспитатель намеренно делит на 2 неравные части и спрашивает- «Можно ли такую часть назвать половиной? Почему нет?»
Дети видят, что предметы могут быть разделены как на равные, так и на неравные части.

Половиной 1 из 2 частей можно назвать лишь тогда, когда части равны.
Постепенно дети убеждаются в том, как важно точно складывать, разрезать предметы, чтобы получились равные части. Выполнив действие, они проверяют (наложением и приложением), равные ли получились части, считают их и, соединив вместе, получают целый предмет, обводят его контур и части рукой, сравнивают размер целого н части
На втором занятии воспитатель расширяет круг предметов, которые дети делят пополам Можно использовать крупу, воду Их распределяют поровну в 2 прозрачных стакана одинаковых размеров
На третьем занятии показывают способы деления предметов на 4 равные части, т е пополам и еще раз пополам. Устанавливают отношения между целым и частью: часть меньше целого, целое больше части.
Дети получают по 2 предмета одинаковых размеров, в чем они убеждаются, накладывая 1 предмет на другой. Они делят 1 предмет на 2 равные части, другой — на 4. Соединив части вместе, они получают целый предмет, пересчитывают части, показывают 1 из 2 частей, 2 из 2 частей, соответственно 1 (2, 3, 4) из 4 равных частей. 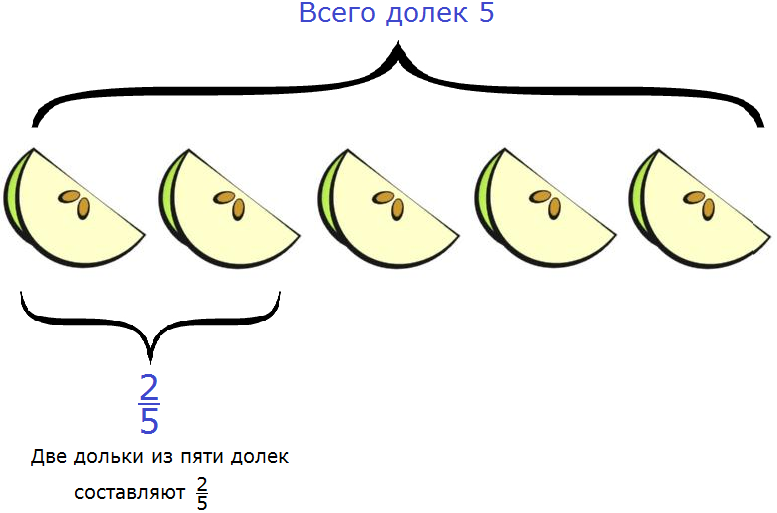Сравнивают размер 1 части и целого.
Аналогичным образом на следующем занятии показывают взаимосвязи между разными частями единого целого. Дети получают по 3—4 листа бумаги одинакового размера, первый кладут перед собой, второй делят на 2 равные части, а третий — на 4 (можно четвертый лист разделить на 8 равных частей).
Соединяя части (как бы оставляя листы целыми), дети раскладывают их один под другим, показывают 1 из 2 частей, 1 из 4 частей, сравнивают размер /г и /« части и их количество. Что меньше: целый лист или половина? Что больше: половина или 1 из 4 частей, /4? Какая часть меньше всех? Почему? И т. п.
Полезно установить связь между количеством действий разрезания и количеством получившихся частей. Например, воспитатель спрашивает: «Сколько раз надо сложить квадрат пополам, чтобы получились 2 равные части? А 4 части?»
Для обобщения знаний можно использовать схемы деления того или иного предмета на равные части (яблока, круга, квадрата и пр.). Рассматривая с детьми схему, воспитатель спрашивает: «На сколько равных частей сначала разделили яблоко? Сколько получилось таких частей? На сколько равных частей потом разделили яблоко? Сколько получилось частей? Что больше и что меньше: половина или целое яблоко? 2 половины или целое яблоко? 1 из 4 частей (/4) или половина (/2)?» И т. д. Такие упражнения дети обычно воспринимают как игру и с удовольствием отвечают на вопросы.
На последующих занятиях проводят упражнения в делении геометрических фигур на 2, 4, 8 частей и в составлении целых фигур из частей, например: «Как надо сложить и разрезать квадрат, чтобы получились 2 равных прямоугольника? Чтобы получились 2 равных треугольника?» (Надо согнуть квадрат стороной к стороне или сложить уголок с уголком.) Дети рассказывают о том, какие фигуры и как они разделили и что получилось в результате деления, какой формы части, сколько их.
Проводят и специальные упражнения в составлении фигур из частей: «Сколько кругов можно сложить из 4 полукругов?» Можно показать части фигур: «Это 1 из 4 (1 из 2, 1 из 8) частей квадрата. Догадайтесь, сколько было квадратов. Составьте их».
Полезно побуждать детей находить наиболее удобные (рациональные) способы деления предметов на части с учетом их размера, формы, пропорций. Например, надо сравнить, как легче разделить на 4 части узкую полоску (ленту) и квадрат (кусок ткани). Дети решают, что узкую полоску удобнее складывать по длине пополам и еще раз пополам, а квадрат — последовательно сложить противоположными сторонами. На одном из последних занятий по этой теме целесообразно сравнить результаты деления на равные части предметов разных размеров. Детям предъявляют 2 предмета контрастных размеров, например большой и маленький круг или квадрат. Воспитатель делит фигуры на 2 (4) равные части, берет по 1 из частей каждой фигуры и просит детей сказать, как можно назвать эти части («Половина, 1 из 2 частей, /г»-) «Это половина и это половина. Объясните, почему они разных размеров». Помогая детям, воспитатель показывает запасные фигуры соответствующего размера. Делает вывод: половина большого круга больше половины маленького, а половина маленького круга меньше половины большого круга.
Предметы были разных размеров, и их части тоже разных размеров. Целесообразно здесь же противопоставить результаты деления на части предметов, равных по величине.
При проведении упражнений в делении предметов на равные части воспитатель постоянно следит за тем, чтобы дети точно выполняли действия, проверяли равенство частей, пользуясь приемами наложения и приложения, а также измерения условной меркой, приучает детей употреблять в речи следующие слова и выражения: разделить на равные части, целое, половина, пополам, одна из двух частей, одна из четырёх частей, а несколько позднее — одна вторая, одна четвертая. Последние выражения не следует специально заучивать, дети постепенно их запоминают. Каждый раз ребята пересчитывают части, а соединяя их вместе, получают 1 целый предмет, устанавливают отношение между целым и частью.
В итоге ряда занятий можно задать детям вопросы, позволяющие обобщить знания: «Сколько раз надо сложить круг, чтобы разделить его на 2 (4, 8) равные части? Если квадрат сложить 1 (2, 3) раз пополам, сколько частей получится? Если я вас прошу дать мне половину груши, на сколько частей вы ее разделите? А если попрошу /4? Сколько таких частей в целой груше? На сколько частей я разделила целое, если это 1 часть из 4 (из 2)? Если мы разделим пополам большой предмет и маленький, половина какого предмета будет больше? А меньше? Почему?»
Деление на части позволит показать детям возможность дробления предметов на равные доли, наглядно выявить отношение целого и части, и, таким образом, создается условие для осознания детьми процесса измерения величин. При измерении предмет как бы дробится на части, сумма которых и характеризует его величину.
После того как дети овладевают приемами измерения, им можно предложить разделить палку, рейку, дощечку, нарисованный на доске прямоугольник и пр. на 2, 4, 8 равных частей. Ребята видят, что данные предметы не сгибаются, усвоенные способы деления не подходят. Как быть? Воспитатель не спешит с подсказкой. Он раскладывает перед детьми предметы, которыми можно воспользоваться в качестве мерки. Здесь детям и помогает понимание взаимосвязи между размером предметов и размером их соответствующих частей. 1—2 наводящих вопроса — и дети догадываются, что надо выбрать подходящую мерку, отмерить кусок, равный длине предмета, разделить мерку (сложить) на соответствующее количество частей и затем отмерить эти части на предмете, сделать отметки карандашом, мелком и др.
Полезно поупражнять детей в делении геометрических фигур, нарисованных на бумаге в клетку. Дети рисуют фигуры заданного размера, а затем по указанию воспитателя делят их на 2, 4 равные части, измеряя по клеткам. По указанию воспитателя они проводят отрезки длиной от 2 до 10 клеток сверху вниз или слева направо и делят их на части, равные длине 1, 2, 3, 4, 5 клеток. Устанавливают связи между величиной мерки и количеством получившихся частей: «На сколько частей разделится отрезок, если каждая часть будет равна 2 клеткам? Если мы разделим отрезок на 3 равные части, чему будет равна 1 часть?»
Упражнения в делении предметов на равные части позволяют перейти к обучению измерению, а умение измерять дает возможность делить на части самые разнообразные предметы.

Л.С. Метлина. Математика в детском саду. М.:Просвещение, 1984.

Главная страница =>библиотека=>оглавление

Деление дроби на целое число

Деление дроби на целое число: Введение

Предположим, вам нужно разделить половинку пиццы между 6 друзьями. Чтобы найти долю каждого друга, вам нужно разделить дробь $\frac{1}{2}$ на целое число 6. На следующем рисунке показаны две половинки целой пиццы. Каждая половина далее делится на 6 равных частей. Таким образом, если вы выберете любой небольшой фрагмент, он представляет собой $\frac{1}{12}$ долю целого.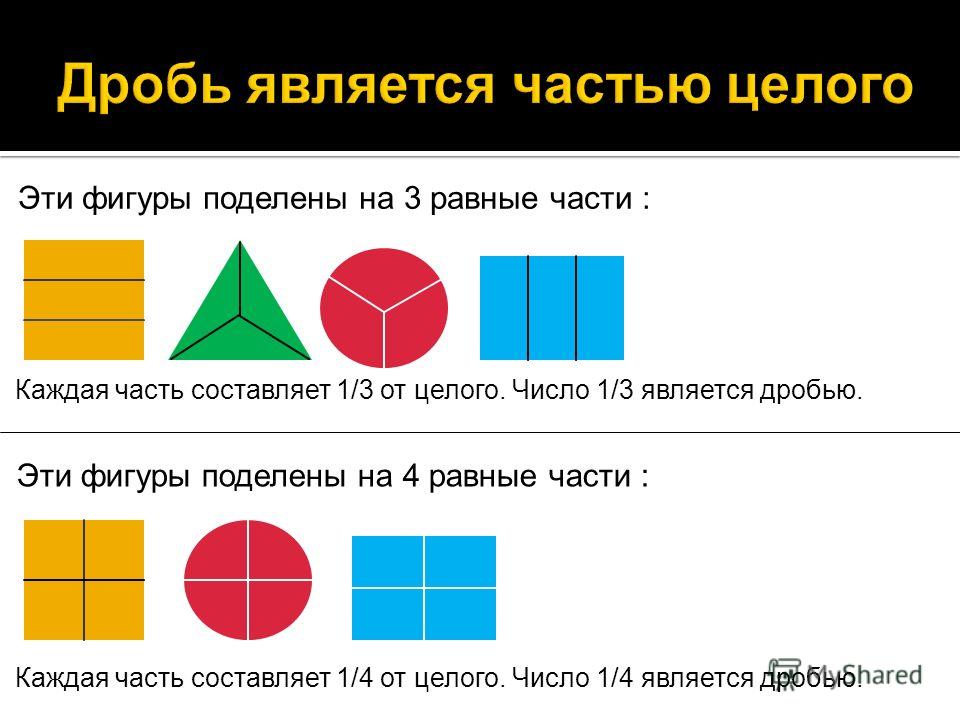

Деление дроби на целое число требует понимания некоторых основных понятий, таких как дроби, смешанные дроби, обратные дроби и целые числа.

• Целые числа включают натуральные числа и 0.

Целые числа: 0, 1, 2, 3, 4 . . .

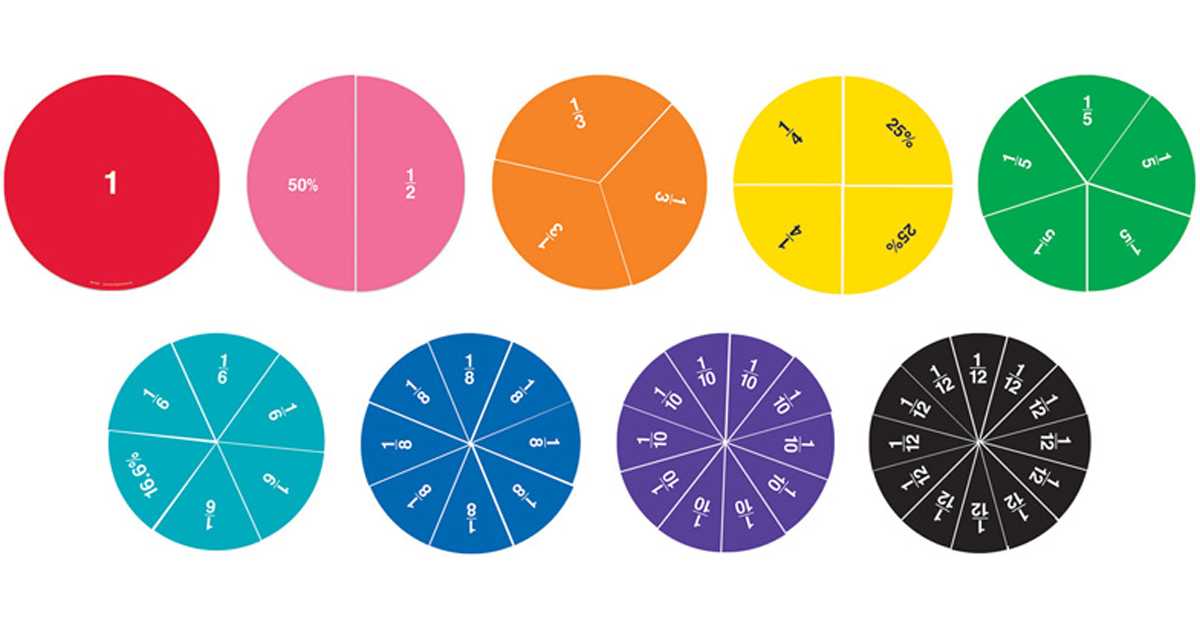
• Дробь является частью целого. Например, один целый круг, разделенный на две равные части, дает нам две половины. Если круг разделить на 4 равные части, каждая часть равна $\frac{1}{4}$ или четверти.

В дроби $\frac{1}{2}$ 1 — числитель, 2 — знаменатель.

Родственные игры

Обратная дробь

Обратная дробь получается путем перестановки числителя и знаменателя.

Например: обратная дробь $\frac{5}{7}$ будет равна $\frac{7}{5}$.

Мы также можем найти обратную величину целого числа.

Например: обратная величина целого числа 2 будет $\frac{1}{2}$.

Дополнительные примеры обратных величин смотрите на изображении ниже:

Произведение дроби на обратную всегда равно единице.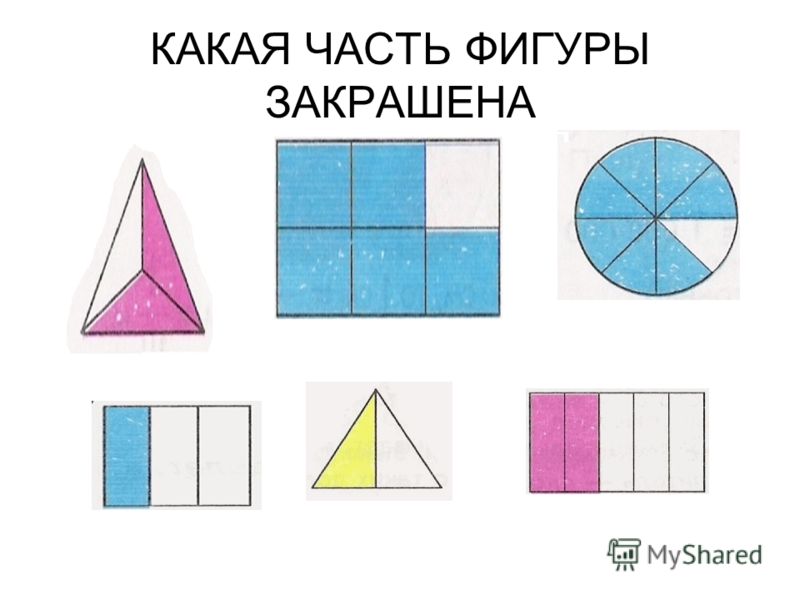

Например, $\frac{3}{2} \times \frac{2}{3} = 1$.

Связанные рабочие листы

Как разделить дробь на целое число?

Давайте разберемся с концепцией деления дроби на целое число на примере.

Предположим, что яблоко нужно разделить между двумя друзьями поровну. Его разрежут на две части, и каждый друг получит по половинке яблока.

Теперь предположим, что присоединяются еще два друга. В этом случае каждая половинка будет разделена на две равные части, что эквивалентно делению дроби $\frac{1}{2}$ на 2. Таким образом, каждый друг теперь получит одну четвертую или $\frac{1 {4}$ целого яблока.

$\frac{1}{2} \div 2 = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4}$

Итак, деление дроби на 2 эквивалентно умножению дроби на обратную 2, которая равна $\frac{1}{2}$.

В обычно используются три шага деления дроби на целое число .

• Шаг 1. Запишите задачу  в формате уравнения.
• Шаг 2: Измените знак деления на умножение и замените делитель его обратным числом.
• Шаг 3: Умножьте числитель на числитель и знаменатель на знаменатель, чтобы получить требуемый ответ.

Давайте обсудим еще два примера.

Пример 1: Разделить a/b на u.

Шаг 1: $\frac{a}{b} \div u$  

Шаг 2: $\frac{a}{b} \times \frac{1}{u}$

Шаг 3: $ \frac{a \times 1}{b \times u}= \frac{a}{bu}$

Пример 2. Разделите $\frac{3}{5}$ на 6.

Шаг 1: $\frac{3}{5} \div 6$.

Шаг 2: $\frac{3}{5} \times \frac{1}{6}$.

Шаг 3: $\frac{3 \times 1}{5 \times 6} = \frac{3}{30} = \frac{1}{10}$

Как разделить смешанную дробь на целое Число?

Прежде чем мы научимся делить смешанную дробь на целое число, давайте быстро повторим некоторые важные понятия.

Смешанные дроби

Смешанная дробь — это дробь, состоящая из целого числа и дроби.

Например, 7 — это целое число, а $1/3$ — это дробь, поэтому $7\frac{1}{3}$ является смешанной дробью.

Также можно записать как $\frac{22}{3}$ (неправильная дробь).

Смешанные и неправильные дроби

Дробь, у которой числитель больше знаменателя, называется неправильной дробью. Смешанные дроби и неправильные дроби в основном представляют одно и то же. Мы просто пишем их в разных форматах.

Например: Чтобы преобразовать смешанную дробь 347 в неправильную дробь:

                       $3\frac{4}{7} =\frac{(7 \times 3) + 4}{7}= \frac{(7 \times 3) + 4}{7}= \frac{25}{7}$

Теперь давайте разберемся, как разделить смешанную дробь на целое число с помощью примера.

Разделим $4\frac{5}{3}$ на 7.

Сначала запишем смешанную дробь   $4\frac{5}{3}$ как неправильную дробь, т. е. $\ доля{17}{13}$.

Теперь мы выполняем те же три шага, которые обсуждались выше.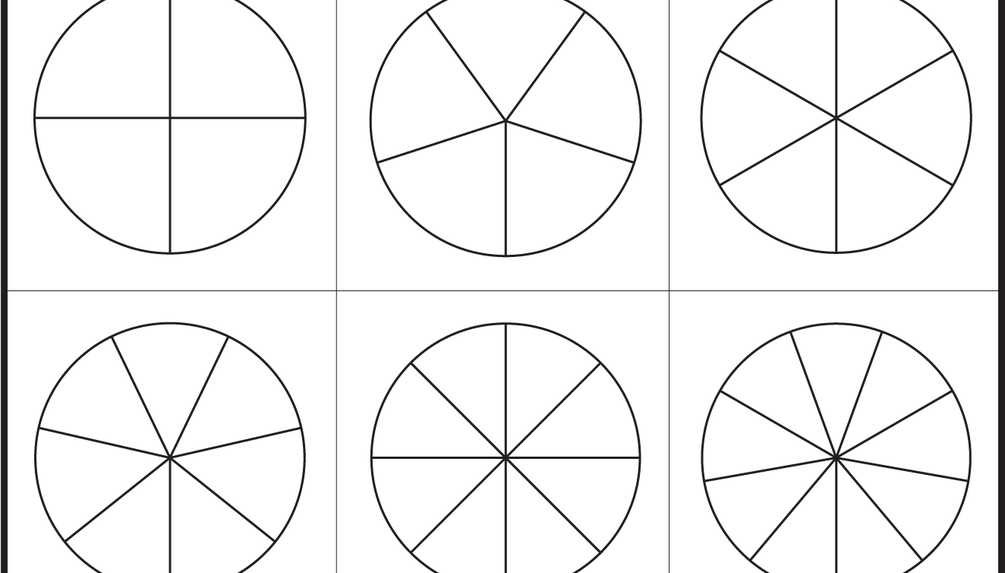

Запишите задачу в виде $4\frac{5}{3} \div \frac{7}{1}$.

$= \frac{17}{13} \times \frac{1}{7}$

$= \frac{17 \times 1}{13 \times 7}$

$= \frac{17 }{91}$

Как разделить целые числа на дробь?

Поскольку вы познакомились с делением дроби на целое число , давайте теперь разберемся с его обратным случаем.

Деление целого числа на дробь требует следующих шагов:

1. Запишите целое число в виде неправильной дроби.
2. Выполните три шага деления дроби на целое число.

Пример: Разделите 12 на $\frac{4}{5}$.

Сначала мы преобразуем 12 в неправильную дробь, т. е. в $\frac{12}{1}$.

Затем запишем задачу $\frac{12}{1} \div \frac{4}{5}$.

$= \frac{12}{1} \times \frac{5}{4}$

$= \frac{12 \times 5}{1 \times 4}$

$= \frac{60 {4}$

$ = 15$

Интересный факт!

• Деление целого числа на дробь дает либо целое число, либо неправильную дробь.

Заключение

Деление дроби на целое число предполагает использование понятий, связанных с дробями и целыми числами. Таким образом, иметь базовое понимание этого имеет решающее значение, поскольку оно помогает вам понять и следовать трем шагам, связанным с делением дробей.

Деление целого числа на дробь состоит из тех же трех шагов с небольшим изменением преобразования целого числа в неправильную дробь.

В общем, знание деления дробей необходимо, так как оно закладывает основу для понимания сложных задач на дроби в старших классах.

Решенные примеры

1. Преобразовать смешанную дробь $7\frac{2}{3}$ в неправильную дробь.

Решение: Сначала возьмем произведение целого числа 7 со знаменателем 3 и прибавим к нему числитель 2. Знаменатель 3 остается прежним.

$7\frac{2}{3} = \frac{(7 \times 3) + 2}{3}$

         $= \frac{23}{3}$

Тогда получим числитель как 23.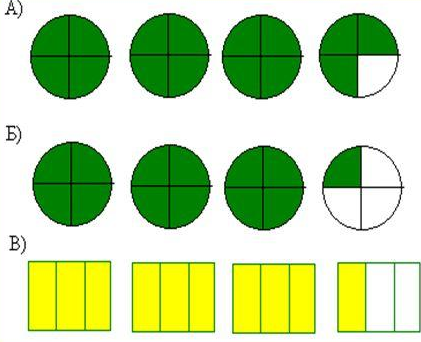 Знаменатель останется прежним.

Таким образом, $\frac{23}{3}$ будет полученной неправильной дробью.

2. Разделить $\frac{5}{8}$ на 12.

Решение:  Для деления дроби (58) на целое число (12) запишем:

$\frac{5}{8} \div 12$

$= \frac{5}{8} \times \frac{1}{12}$

$= \frac{5}{96} $

3. Разделите $5\frac{4}{9}$ на 7.

Решение:  Сначала преобразуем смешанную дробь в неправильную, т. е. $5\frac{4}{9} = \frac{49}{9}$

Затем запишем задачу в виде $49/9 \div 7$

$= \frac{49}{9} \times \frac{1}{7}$

$= \frac{49 \times 1}{9 \times 7})$

$= \frac{ 49}{63}$

$= \frac{7}{9}$

4. Разделите 24 на $\frac{3}{2}$ .

Решение:  Сначала преобразуем число в неправильную дробь, т.  е. $\frac{24}{1}$.

Затем запишем задачу в виде $\frac{24}{1} \div \frac{3}{2}$.

$= \frac{24}{1} \times \frac{2}{3}$

$= \frac{24 \times 2}{1 \times 3}$

$= \frac{48 }{3}$

$= 16$

5.   Бен должен разделить $\frac{5}{4}$ на 25 в рамках своего задания. Помогите ему, разделив дробь на целое число.

Решение: Для деления дроби  $\frac{5}{4}$  на целое число  25, нам нужно записать задачу в следующем виде:

$\frac{5}{4} \div 25$

$= \frac{5}{4} \times \frac{1}{25}$

$= \frac{5 \times 1} {4 \times 25}$

$= \frac{5}{100}$

Практические задачи

1

Разделить $\frac{5}{9} $ на 10.

$\frac{15}{9}$

$\frac{50}{9}$

$\frac{1}{18}$

$\frac{9}{50 }$

Правильный ответ: $\frac{1}{18}$
Сначала мы запишем задачу в виде уравнения, а затем умножим данную дробь на обратную величину целого числа, чтобы получить ответ.
$\frac{5}{9} \div 10$
$= \frac{5}{9} \times \frac{1}{10}$
$= \frac{5}{90}$
$ = \frac{1}{18}$

2

Преобразуйте $3\frac{5}{9}$ в неправильную дробь.

$\frac{15}{9}$

$\frac{32}{9}$

$\frac{8}{9}$

$\frac{9}{15}$

Правильный ответ: $\frac{32}{9}$
$3\frac{5}{9}= \frac{(9 \times 3)+5}{9}= \frac{32}{9}$
Неправильная дробь $= \frac{32}{9}$

3

Разделить $2\frac{5}{8}$ на 15,

$\frac{7}{40}$

$\frac{50}{23}$

$\frac{25}{18}$

$\frac{22}{120}$

Правильный ответ: $\frac{7}{40}$
Преобразуйте смешанную дробь в неправильную дробь.
$2\frac{5}{8}=\frac{(8 \times 2) + 5}{8}= \frac{21}{8}$
Неправильная дробь $= \frac{21}{8}$
Сейчас,$\frac{21}{8} \div 15$
$= \frac{21}{8} \times \frac{1}{15}$
$= \frac{21}{120}$
$= \frac{7}{40}$

4

Обратная величина смешанной дроби $2\frac{3}{5}$:

$\frac{13}{5}$

$3\frac{2}{5}$

$\frac{5}{13}$

$\frac{5}{17}$

Правильный ответ: $\frac{5}{13}$
Преобразуйте смешанную дробь в неправильную.
$2\frac{3}{5}=\frac{(5 \times 2) + 3}{5}= \frac{13}{5}$
Неправильная дробь $= \frac{13}{5}$
Обратная величина $= \frac{5}{13}$

5

Разделите 35 на $\frac{5}{7}$.

$49$

$25$

$\frac{25}{49}$

$\frac{49}{25}$

Правильный ответ: $49$
Теперь $\frac{35}{1} \div \frac{5}{7}$
$= \frac{35}{1} \times \frac{7}{ 5}$
$= \frac{35 \times 7}{1 \times 5}$
$= \frac{175}{5}$
$= 35$

Часто задаваемые вопросы

В чем важность деления дробей на целые числа?

Научиться делить дробь на целое число важно, потому что это помогает решать сложные математические задачи, основанные на дробях, отношениях и пропорциях, десятичных дробях и т. д., в старших классах.

Включают ли целые числа отрицательные числа?

Нет, целые числа не включают отрицательные числа.

Что является обратным числом 0 и 1?

Обратная величина 0 не существует, а обратная 1 всегда равна 1.

Почему при делении дробей используется обратная величина?

Обратное число используется для упрощения процесса деления путем преобразования знака деления в умножение.

Деление дробей на целые числа

Деление дробей на целые числа

ExampleVideoQuestionsLesson

Отправить в Google Classroom

ExampleVideoQuestionsLesson

Отправить в Google Classroom

Умножьте знаменатель дроби на целое число, на которое вы делите.

• Чтобы разделить дробь на целое число, умножьте нижнюю часть дроби на целое число.
• Основание дроби равно 2, а целое число равно 3.
• 2 × 3 = 6.
•   ¹ / ₂   ÷ 3 =   ¹ / ₆  .
• Мы делим дробь на 3, чтобы увеличить нижнюю часть дроби в 3 раза.
• Число внизу дроби говорит нам, на сколько она делится.
• Большее число внизу дроби означает, что она разделена на большее количество частей.

• При делении дроби на целое число становится еще меньше.
• Здесь одна половина делится на 3 равные части.
• После деления у нас получается 1 из 6 частей.
•   ¹ / ₂   ÷ 3 =   ¹ / ₆  .
• Изначально круг был разделен на 2 части. Дальнейшее деление на 3 означало, что оно было разделено на 6 частей.
• Дробь   ¹ / ₂   стала меньше при делении на 3.

Как делить дроби на целые числа

Чтобы разделить дроби на целые числа, выполните следующие действия:

1. Разделить верхнюю часть дроби на целое число, если она делится точно.
2. Если нет, умножьте нижнюю часть дроби на целое число.

Если вы использовали шаг 2, возможно, вам придется упростить ответ, разделив верхние и нижние части дроби на одно и то же число.

Например, вычислите ⁴ / ₅   ÷ 3.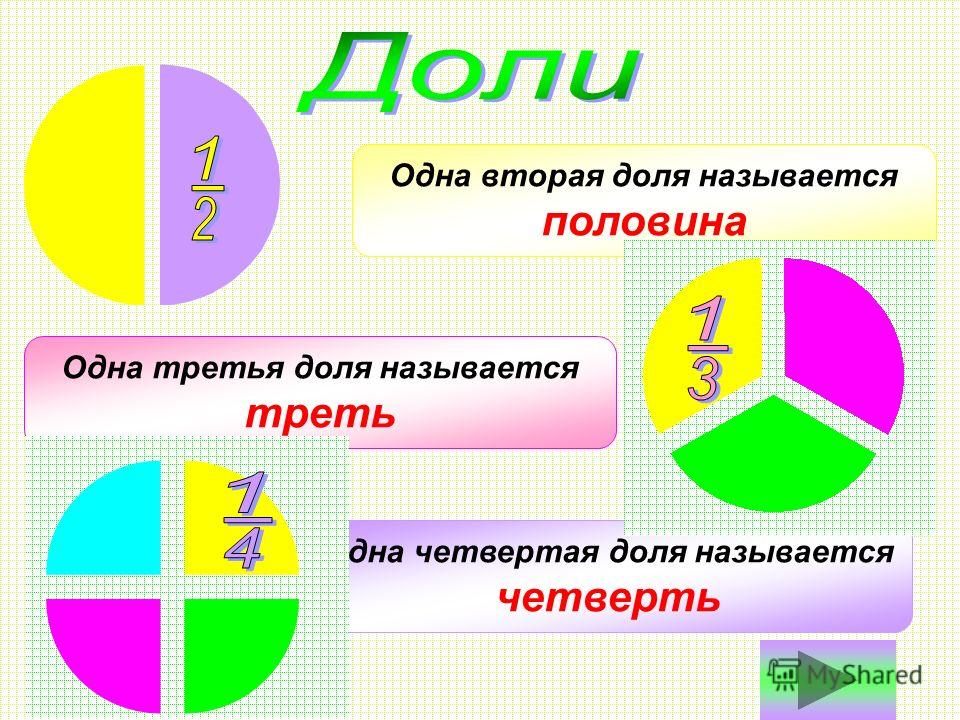

Сначала мы смотрим, можем ли мы разделить верхний числитель на 3.

У нас есть 4 в верхней части дроби, и 4 нельзя разделить точно на 3, чтобы получить целое число.

Это означает, что вместо этого мы используем шаг 2, чтобы разделить дробь.

Умножаем нижний знаменатель на целое число, на которое делим. 5 – знаменатель дроби.

5 × 3 = 15, значит, 15 — знаменатель в нижней части ответа.

⁴ / ₅   ÷ 3 =   ⁴ / ₁₅  .

Мы умножили знаменатель на 3, чтобы разделить всю дробь на 3.

Вычислить ⁶ / ₇ ÷ 2.

Мы можем следовать методу, показанному в предыдущем примере, где мы можем умножить знаменатель на 2.

⁶ / ₇   ÷ 2 =   ⁶ / _{(7 × 2)}  .

⁶ / ₇   ÷ 2 =   ⁶ / ₁₄  .

Затем это можно упростить, потому что и 6, и 14 можно разделить на 2.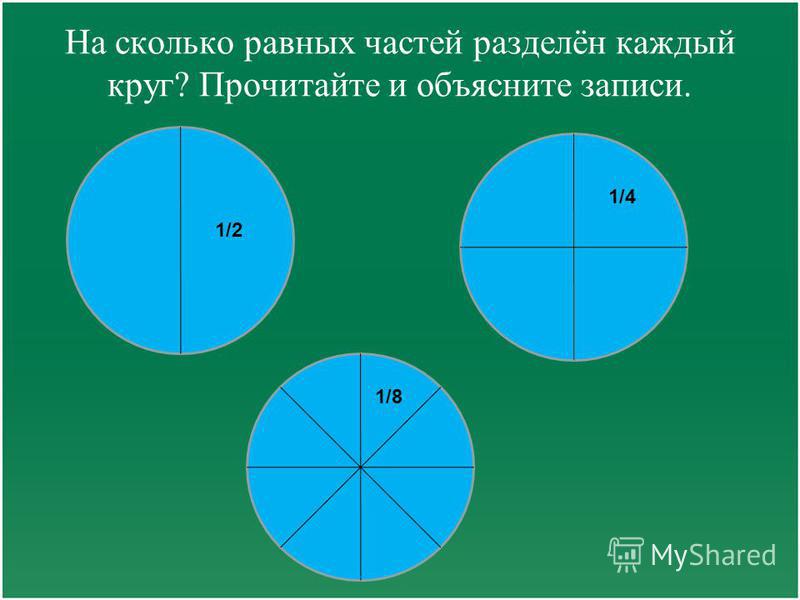

⁶ / ₁₄   =   ³ / ₇  .

Однако гораздо проще использовать шаг 1 в наших шагах для деления дробей на целые числа.

Мы видим, что числитель сверху можно делить сразу.

6 ÷ 2 = 3, значит, числитель можно разделить точно.

Мы можем просто разделить числитель на ⁶ / ₇   на 3, чтобы получить ответ   ³ / ₇  .

Легче сделать этот метод, так как впоследствии не требуется упрощение.

Чтобы разделить дробь на целое число, мы можем либо умножить знаменатель на целое число, либо разделить числитель на целое число.

Обратите внимание, что нам нужно использовать только тот или иной метод.

Вот еще один пример использования этого метода для деления дроби на целое число.

У нас есть ⁹ / ₁₀ ÷ 3.

Сразу видно, что 9 ÷ 3 = 3 и делится точно. Используем метод 1.

Делим числитель, а знаменатель оставляем прежним.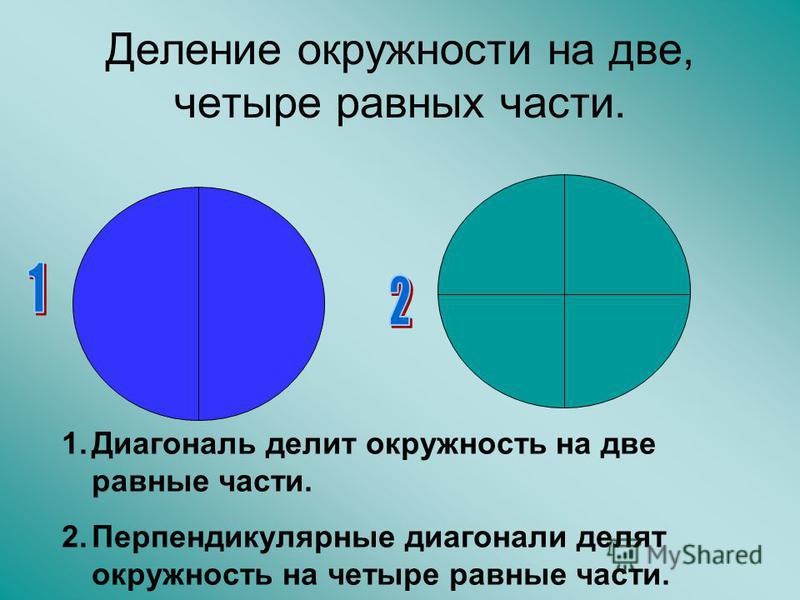

⁹ / ₁₀   ÷ 3 =   ³ / ₁₀  .

Обратите внимание, что мы делим 9 только на 3. Мы не умножаем 10 внизу на 3, потому что мы уже выполнили наше деление, разделив 9.на 3.

Модель деления дробей на целые числа

Когда мы делим, мы делим сумму на равные части. Разделить дробь на целое число означает также разделить его на равные части.

Когда мы делим дробь на целое число, оно становится меньше.

Вот пример деления дроби ¹ / ₂ на 3.

¹ / ₂   означает, что у нас есть 1 из 2 равных частей.

Когда мы делим одну половину на 3, мы делим ее на 3 равные части.

Ответ меньше половины.

Это 1 из 6 равных частей.

Мы говорим, что ¹ / ₂ ÷ 3 = ¹ / ₆ .

Мы можем видеть в визуальной модели, что окончательная заштрихованная область представляет собой меньшую долю, чем мы начали, но число в нижней части дроби увеличилось с 2 до 6.

Мы умножили знаменатель в нижней части дроби на 3, чтобы разделить дробь на 3.

Без рисования визуальной модели метод заключается в простом умножении нижней части дроби на 3.

Вот еще один пример деления дроби на целое число.

У нас есть ³ / ₄ ÷ 2 = показано с визуальной моделью.

³ / ₄   означает, что у нас есть 3 из 4 равных частей. Это показано ниже.

Когда мы разделим ³ / ₄ на 2, у нас будет только половина исходной заштрихованной дроби.

Мы можем разделить каждую четвертинку на две части, чтобы всего получилось 8 частей. 3 четверти это то же самое, что 6 из 8 частей.

Если мы разделим на 2, у нас будет только 3 из 8 частей.

Мы видим, что половина от ³ / ₄ составляет ³ / ₈ .

Круг был разделен на вдвое больше частей. Вместо 3 из 4 у нас теперь только 3 из 8 частей.