Деление числа на части: Пропорциональное деление. Деление на пропорциональные части

Пропорциональное деление. Деление на пропорциональные части

• Деление числа на пропорциональные части
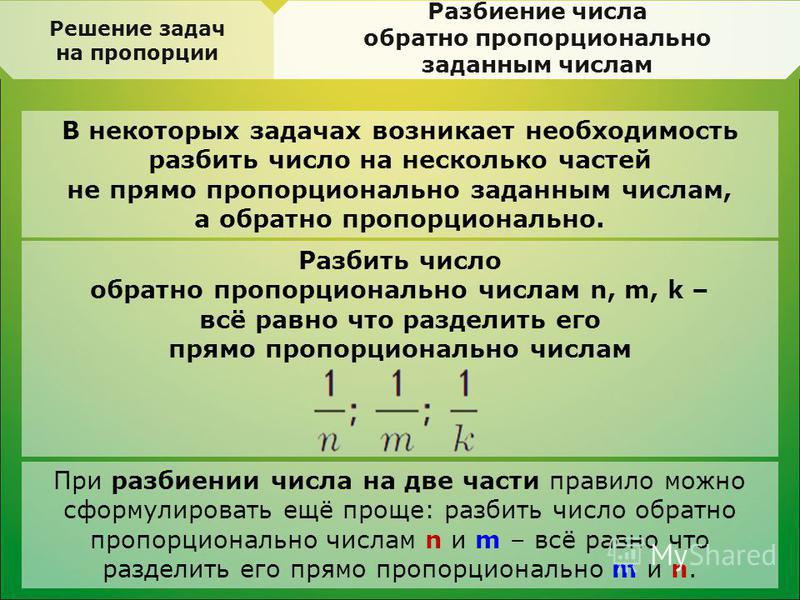
• Деление на части, обратно пропорциональные числам

Пропорциональное деление — деление какой-нибудь величины на части, прямо или обратно пропорциональные данным числам.

Чтобы разделить число на части пропорционально нескольким данным числам, надо разделить его на сумму этих чисел и частное умножить на каждое из них.

Деление числа на пропорциональные части

Пример 1. Разделить число  50  на части пропорционально числам  2  и  3.

Решение: Надо найти такие два слагаемых числа  50,  которые будут относиться друг к другу так, как  2:3.  Первое слагаемое должно содержать  2  части числа, а второе  3,  значит, число  50  содержит  5  таких частей (2 + 3 = 5), следовательно, каждая такая часть будет равна:

50 : 5 = 10.

Число  10  — одна часть. Теперь надо умножить эту часть на числа, пропорционально которым требовалось разделить число  50:

10 · 2 = 20;

10 · 3 = 30.

Ответ:  2:3 = 20:30.

Пример 2. Разделить число  90  на три слагаемых пропорционально числам  1,  2  и  3.

Решение:

90 : (1 + 2 + 3) = 90 : 6 = 15;

1 · 15 = 15;

2 · 15 = 30;

3 · 15 = 45.

Ответ:  1:2:3 = 15:30:45.

Длинные отношения вида  1:2:3  называются сложными. Сложные отношения — это условные записи, показывающие, сколько долей содержит каждая часть. Если члены сложного отношения дробные, то, приведя их к общему знаменателю и умножив на него, можно заменить отношение дробных чисел отношением целых.

Пример. Разделить число  66  на такие три части, чтобы первая относилась ко второй, как  3:2,  а вторая к третьей, как  5:4.

Решение:

Первый способ: обозначим искомые части буквами  a,  b  и  c.  Так как отношение не изменится, если оба члена умножить на одно и то же число, то умножим члены первого отношения на  5,  а второго на  2:

a:b = 3:2 = 15:10;

b:c = 5:4 = 10:8;

значит  a:b:c = 15:10:8.   Так как  15 + 10 + 8 = 33,  то

a = (66 : 33) · 15 = 30;

b = (66 : 33) · 10 = 20;

c = (66 : 33) · 8 = 16.

Второй способ: обозначим искомые части буквами  a,  b  и  c:

a:b = 3:2;

b:c = 5:4.

Если первая часть  a  равна  3,  вторая  b  равна  2,  то третью часть  c  можно определить из пропорции:

2:c = 5:4.

Следовательно,  c  равно:

c =	2 · 4	=	8	,
	5		5

поэтому

a:b:c = 3:2:	8	.
	5

Умножив все члены полученного сложного отношения на 5, чтобы избавиться от дробного члена, получим:

a:b:c = 15:10:8,

так как 15 + 10 + 8 = 33, то

a = (66 : 33) · 15 = 30;

b = (66 : 33) · 10 = 20;

c = (66 : 33) · 8 = 16.

Деление на части, обратно пропорциональные числам

Пример. Разделить число  62  на три части обратно пропорционально числам  2,  3  и  5,  то есть разложить на три части, которые относились бы между собой, как

1	:	1	:	1	.
2		3		5

Решение: Обозначим искомые части буквами  a,  b  и  c.  Приведём члены отношения к общему знаменателю и заменим дробные члены на целые числа:

a:b:c =	1	:	1	:	1	=	15	:	10	:	6	= 15:10:6,
	2		3		5		30		30		30

так как  15 + 10 + 6 = 31,  то

a = (62 : 31) · 15 = 30;

b = (62 : 31) · 10 = 20;

c = (62 : 31) · 6 = 12.

Повторяем и систематизируем школьный курс алгебры и начал анализа

Повторяем и систематизируем школьный курс алгебры и начал анализа

Крамор В. С. Повторяем и систематизируем школьный курс алгебры и начал анализа.—М.: Просвещение, 1990.— 416 с. В книге в конспективной форме изложен теоретический материал по алгебре и началам анализа. К каждому пункту теоретического материала приведены упражнения с решениями и упражнения трех уровней сложности для самостоятельного решения. Она может быть использована при подготовке к экзаменам в высшие учебные заведения. Оглавление ПРЕДИСЛОВИЕ ГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3. ВЫЧИТАНИЕ § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 5. ДЕЛЕНИЕ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ § 5. СТЕПЕНЬ ДРОБИ Контрольные вопросы ГЛАВА VI § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросы ГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2. ПРЕДЕЛ ФУНКЦИИ § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1. ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА § 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление

Разделить число на случайные части онлайн-инструмент

Главная > Разделить номер

С помощью этого инструмента вы можете мгновенно разделить любое число или числа на равные или случайные группы чисел (части).

6

014 #1 Введите номер: Название строки/столбца (необязательно): Distributed Values ​​:  Equal     Random Round to Integer :  Value Gap :  Almost Equal Bigger Gap #2 УДАЛИТЬ (-) Введите номер :  Название строки/столбца (необязательно) :  Row / Column Count (Max 200) :  Distributed Values ​​:  Equal     Random Round to Integer :  Value Gap :  Almost Equal Большой зазор 9 #3 СНЯТЬ (-) Введите номер: Строка / заголовок столбца (необязательно): Строка / Количество столбцов (макс 200): Распределенные значения Равные Целое число: Разрыв значений:  Почти равно Больший разрыв

#4	REMOVE (-)
Enter Number :
Row / Column Title (Optional) :
Row / Column Count (Max 200) :
Распределенные значения:	Равно Случайно
Округлить до целого числа
Разрыв значений0013 Большой зазор

---

#5	REMOVE (-)
Enter Number :
Row / Column Title (Optional) :
Row / Column Count (Max 200) :
Распределенные значения:	Равно     Случайное
Округление до целого числа:
Разрыв значений:	Почти равно Больший разрыв

9

Distribute Into :

Rows     Columns

(+) ADD NUMBERS TO DIVIDE (1/5)

OR

Нравится FunctionCube?

У вас есть предложение, запрос или сообщение об ошибке? Пожалуйста, напиши мне.

Как делить в Excel и обрабатывать #DIV/0! ошибка

В этом учебном пособии показано, как использовать формулу деления в Excel для разделения чисел, ячеек или целых столбцов, а также как обрабатывать ошибки Div/0.

Как и в случае других основных математических операций, Microsoft Excel предоставляет несколько способов деления чисел и ячеек. Какой из них использовать, зависит от ваших личных предпочтений и конкретной задачи, которую необходимо решить. В этом руководстве вы найдете несколько хороших примеров использования формулы деления в Excel, которые охватывают наиболее распространенные сценарии.

• Знак отдела в Excel
• Функция деления в Excel (ЧАСТНОЕ)
• Как разделить столбцы в Excel
• Как разделить столбец на число
• Как разделить на проценты в Excel
• Ошибка деления Excel на ноль (#DIV/0!)
• Как выполнить деление в Excel с помощью Ultimate Suite

Обычный способ деления — использование знака деления. В математике операция деления представлена ​​символом обела (÷). В Microsoft Excel символ деления — это косая черта (/).

При таком подходе вы просто пишете выражение вида =a/b без пробелов, где:

• a — делимое , — число, которое нужно разделить, а
• b – это делитель – число, на которое нужно разделить делимое.

Как разделить числа в Excel

Чтобы разделить два числа в Excel, введите в ячейке знак равенства (=), затем введите число, которое нужно разделить, затем косую черту, а затем число, на которое нужно разделить и нажмите клавишу Enter, чтобы вычислить формулу.

Например, чтобы разделить 10 на 5, введите в ячейку следующее выражение: =10/5

На снимке экрана ниже показаны еще несколько примеров простой формулы деления в Excel:

Когда формула выполняет более одной арифметической операции, важно помнить о порядке вычислений в Excel (PEMDAS): сначала круглые скобки, затем возведение в степень (возведение в степень), затем умножение или деление, в зависимости от того, что наступит раньше, затем сложение или вычитание, в зависимости от того, что приходит первым.

Как разделить значение ячейки в Excel

Чтобы разделить значения ячейки, вы используете символ деления точно так же, как показано в приведенных выше примерах, но вместо чисел укажите ссылки на ячейки.

Например:

• Чтобы разделить значение в ячейке A2 на 5: =A2/5
• Чтобы разделить ячейку A2 на ячейку B2: =A2/B2
• Чтобы разделить несколько ячеек последовательно, введите ссылки на ячейки, разделенные символом деления. Например, чтобы разделить число в A2 на число в B2, а затем разделить результат на число в C2, используйте следующую формулу: =А2/В2/С2

Функция деления в Excel (ЧАСТНОЕ)

Сразу скажу: функции деления в Excel нет. Всякий раз, когда вы хотите разделить одно число на другое, используйте символ деления, как описано в приведенных выше примерах.

Однако, если вы хотите вернуть только целое число часть деления и отбросить остаток, используйте функцию ЧАСТНОЕ:

ЧАСТНОЕ(числитель, знаменатель)

Где:

• Числитель (обязательно) – делимое, т. е. число, которое нужно разделить.
• Знаменатель (обязательно) – делитель, т.е. число, на которое нужно делить.

Когда два числа делят нацело без остатка , символ деления и формула ЧАСТНОЕ возвращают один и тот же результат. Например, обе приведенные ниже формулы возвращают 2.

=10/5

=ЧАСТНОЕ(10, 5)

Когда есть остаток после деления знак деления возвращает десятичное число, а функция ЧАСТНОЕ возвращает только целую часть. Например:

=5/4 возвращает 1,25

=ЧАСТНОЕ(5,4) дает 1

имеет несколько предостережений, о которых вы должны знать:

1. Аргументы числителя и знаменателя должны предоставляться в виде чисел, ссылок на ячейки, содержащие числа, или других функций, возвращающих числа.
2. Если какой-либо из аргументов не является числом, формула ЧАСТНОЕ возвращает ошибку #ЗНАЧ! ошибка.
3. Если знаменатель равен 0, ЧАСТНОЕ возвращает ошибку деления на ноль (#ДЕЛ/0!).

Как разделить столбцы в Excel

Разделить столбцы в Excel также легко. Это можно сделать, скопировав обычную формулу деления вниз по столбцу или используя формулу массива. Зачем кому-то использовать формулу массива для такой тривиальной задачи? Вы узнаете причину через мгновение 🙂

Как разделить два столбца в Excel, скопировав формулу

Чтобы разделить столбцы в Excel, просто сделайте следующее:

1. Разделите две ячейки в самой верхней строке, например: =A2/B2
2. Вставьте формулу в первую ячейку (скажем, C2) и дважды щелкните маленький зеленый квадрат в правом нижнем углу ячейки, чтобы скопировать формулу вниз по столбцу. Сделанный!

Поскольку мы используем относительные ссылки на ячейки (без знака $), наша формула деления будет меняться в зависимости от относительного положения ячейки, в которую она копируется:

Совет. Аналогичным образом вы можете разделить две строки в Excel. Например, чтобы разделить значения в строке 1 на значения в строке 2, вы помещаете 90 354 = A1/A2 90 355 в ячейку A3, а затем копируете формулу вправо в необходимое количество ячеек.

Как разделить один столбец на другой с помощью формулы массива

В ситуациях, когда вы хотите предотвратить случайное удаление или изменение формулы в отдельных ячейках, вставьте формулу массива во весь диапазон.

Например, чтобы построчно разделить значения в ячейках A2:A8 на значения в B2:B8, используйте следующую формулу: =A2:A8/B2:B8

Чтобы правильно вставить формулу массива, выполните выполните следующие действия:

1. Выберите весь диапазон, в который вы хотите ввести формулу (в данном примере C2:C8).
2. Введите формулу в строке формул и нажмите Ctrl + Shift + Enter, чтобы завершить ее. Как только вы это сделаете, Excel заключит формулу в {фигурные скобки}, указывая, что это формула массива.

В результате вы получите числа в столбце A, разделенные на числа в столбце B одним махом. Если кто-то попытается изменить вашу формулу в отдельной ячейке, Excel покажет предупреждение о том, что часть массива нельзя изменить.

Чтобы удалить или изменить формулу, вам нужно сначала выбрать весь диапазон, а затем внести изменения. Чтобы расширить формулу до новых строк, выберите весь диапазон, включая новые строки, измените ссылки на ячейки в строке формул, чтобы разместить новые ячейки, а затем нажмите Ctrl + Shift + Enter, чтобы обновить формулу.

Как разделить столбец на число в Excel

В зависимости от того, хотите ли вы вывести формулы или значения, вы можете разделить столбец чисел на постоянное число, используя формулу деления или функцию Специальная вставка .

Разделить столбец по номеру с помощью формулы

Как вы уже знаете, самый быстрый способ выполнить деление в Excel — использовать символ деления. Итак, чтобы разделить каждое число в данном столбце на одно и то же число, вы помещаете обычную формулу деления в первую ячейку, а затем копируете формулу вниз по столбцу. Вот и все!

Например, чтобы разделить значения в столбце A на число 5, вставьте следующую формулу в A2, а затем скопируйте ее в любое количество ячеек: =A2/5

Как объяснено выше Например, использование относительной ссылки на ячейку (A2) гарантирует правильную корректировку формулы для каждой строки. То есть формула в B3 становится =A3/5 , формула в B4 становится =A4/5 и так далее.

Вместо того, чтобы указывать делитель непосредственно в формуле, вы можете ввести его в какую-нибудь ячейку, например D2, и разделить на эту ячейку. В этом случае важно заблокировать ссылку на ячейку знаком доллара (например, $D$2), сделав ее абсолютной ссылкой, поскольку эта ссылка должна оставаться постоянной независимо от того, куда копируется формула.

Как показано на снимке экрана ниже, формула =A2/$D$2 возвращает точно такие же результаты, что и =A2/5 .

Разделить столбец на тот же номер с помощью специальной вставки

Если вы хотите, чтобы результаты были значениями, а не формулами, вы можете выполнить деление обычным способом, а затем заменить формулы значениями. Или вы можете добиться того же результата быстрее с помощью опции Специальная вставка > Разделить .

1. Если вы не хотите переопределять исходные числа, скопируйте их в столбец, где вы хотите получить результаты. В этом примере мы копируем числа из столбца A в столбец B.
2. Поместите делитель в какую-нибудь ячейку, скажем, D2, как показано на скриншоте ниже.
3. Выберите ячейку делителя (D5) и нажмите Ctrl + C, чтобы скопировать ее в буфер обмена.
4. Выберите ячейки, которые вы хотите умножить (B2:B8).
5. Нажмите Ctrl + Alt + V, затем I, что является ярлыком для Специальная вставка > Разделить , и нажмите клавишу Enter.

Либо щелкните правой кнопкой мыши выбранные числа, выберите Специальная вставка… из контекстного меню, затем выберите Разделить под Операция и нажмите OK.

В любом случае каждое из выбранных чисел в столбце A будет разделено на число в D5, и результаты будут возвращены в виде значений, а не формул:

Как разделить на проценты в Excel

Поскольку проценты части больших целых вещей, некоторые люди думают, что для вычисления процента от заданного числа нужно разделить это число на проценты. Но это обычное заблуждение! Чтобы найти проценты, нужно умножать, а не делить. Например, чтобы найти 20% от 80, нужно умножить 80 на 20% и получить в результате 16: 80*20%=16 или 80*0,2=16.

В каких случаях вы делите число на проценты? Например, чтобы найти X, если определенный процент X равен Y. Чтобы было понятнее, давайте решим такую ​​задачу: 100 составляет 25% от какого числа?

Чтобы получить ответ, преобразуйте задачу в это простое уравнение:

X = Y/P%

Если Y равно 100, а P равно 25%, формула примет следующий вид: = 100/25%

Так как 25% это 25 частей от ста, можно смело заменить процент десятичным числом: =100/0,25

Как показано на снимке экрана ниже, результатом обеих формул является 400:

Дополнительные примеры процентных формул см. в разделе Как рассчитать проценты в Excel.

Ошибка Excel DIV/0

Деление на ноль — это операция, для которой не существует ответа, поэтому она запрещена. Всякий раз, когда вы пытаетесь разделить число на 0 или на пустую ячейку в Excel, вы получите ошибку деления на ноль (#DIV/0!). В некоторых ситуациях эта индикация ошибки может быть полезна, предупреждая вас о возможных ошибках в вашем наборе данных.

В других сценариях ваши формулы могут просто ожидать ввода, поэтому вы можете заменить обозначения ошибок Excel Div 0 пустыми ячейками или своим собственным сообщением. Это можно сделать с помощью формулы ЕСЛИ или функции ЕСЛИОШИБКА.

Подавить ошибку #DIV/0 с помощью IFERROR

Самый простой способ справиться с ошибкой #DIV/0! ошибка в Excel состоит в том, чтобы обернуть формулу деления в функцию ЕСЛИОШИБКА следующим образом:

=ЕСЛИОШИБКА(A2/B2, "")

Формула проверяет результат деления и, если она дает ошибку, возвращает пустая строка (“”), иначе результат деления.

Пожалуйста, взгляните на два рабочих листа ниже. Какой из них более эстетичен?

Примечание . Функция ЕСЛИОШИБКА в Excel маскирует не только #ДЕЛ/0! ошибки, но и все другие типы ошибок, такие как #Н/Д, #ИМЯ?, #ССЫЛКА!, #ЗНАЧ! и т. д. Если вы хотите подавить конкретные ошибки DIV/0, используйте формулу ЕСЛИ, как показано на следующий пример.

Обработка ошибки Excel DIV/0 с помощью формулы ЕСЛИ

Чтобы скрыть только ошибки DIV/0 в Excel, используйте формулу ЕСЛИ, которая проверяет, равен ли делитель (или не равен) нулю.

Например:

=ЕСЛИ(B2=0,"",A2/B2)

Или

=ЕСЛИ(B2<>0,A2/B2,"")

Если делитель любое число, отличное от нуля, формулы делят ячейку A2 на B2. Если B2 равен 0 или пуст, формулы ничего не возвращают (пустая строка).

Вместо пустой ячейки вы также можете отобразить пользовательское сообщение, подобное этому:

=ЕСЛИ(B2<>0, A2/B2, "Ошибка в расчете")

Как разделить с помощью Ultimate Suite для Эксель

Если вы делаете свои первые шаги в Excel и пока не чувствуете себя комфортно с формулами, вы можете выполнить деление с помощью мыши. Все, что для этого нужно, — установить наш Ultimate Suite в ваш Excel.

В одном из рассмотренных ранее примеров мы разделили столбец на число с помощью специальной вставки Excel. Это включало много движений мыши и два ярлыка. Теперь позвольте мне показать вам более короткий способ сделать то же самое.

1. Скопируйте числа, которые вы хотите разделить, в столбец «Результаты», чтобы предотвратить переопределение исходных чисел.
2. Выберите скопированные значения (C2:C5 на скриншоте ниже).
3. Перейдите на вкладку инструментов Ablebits > группу Calculate и выполните следующие действия:
   • Выберите знак деления (/) в поле Операция .
   • Введите число для деления в поле Значение .
   • Нажмите кнопку Вычислить .

Готово! Весь столбец в мгновение ока делится на указанное число:

Как и в случае специальной вставки Excel, результатом деления является значений , а не формул.