Что такое состав чисел 1 класс: Что такое – состав числа ? – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Состав чисел от 1 до 5

10.05.2020

Что такое состав числа и нужно ли его изучать? Знание его позволяет ребенку лучше понимать, как проводить одно из основных арифметических действий – сложение. С составом чисел от 1 до 5 детям целесообразно познакомиться в возрасте около пяти лет.

Содержание:

Составляем число из единичек
Каждое число можно составить из двух чисел
Выучив состав чисел, приступаем к сложению

Составляем число из единичек

Это самое простое действие: составлять числа из отдельных единиц: двойка – это 1 и 1, три – это 1 и 1 и 1. По такой же аналогии из единичек составляют четверка и пятерка. Объяснять ребенку это действие лучше с помощью однородных предметов: карандашей, конфет, игрушек или пальцев руки.

Каждое число можно составить из двух чисел

Следующий шаг обучения – дать понять малышу, что каждое число может быть составлено из двух чисел, каждое из которых меньше, чем оно само. К примеру, двойка – это 1 и 1, а четыре – это 1 и 3 или 2 и 2. Составляйте все возможные комбинации, например, пятерку можно представить как 2 и 3 или как 3 и 2. На этом же этапе включите в состав чисел нуль: каждое из них можно посчитать как сумму самого его и нуля: тройка – это 0 и 3 или 3 и 0.

Пусть ребенок запомнит одно из первых арифметических правил: Любое число можно представить как сумму 0 и этого же числа.

В обучении также используйте предметы – так дошкольнику будет проще понять принцип разложения чисел на отдельные составляющие, а в дальнейшем он будет без проблем считать. Позже можно перейти к письменным упражнениям. Одно из самых известных – «Числовой домик». На каждом этаже этого условного домика – по две квартиры, а жить в них может только определенное число людей, например, только по 4. Вместе с ребенком «заселяйте» жильцов по квартирам, следя, чтобы их общее количество (цифра в окошке) не превышало указанное в задании. Писать числа в окошках сначала может взрослый, но такие занятия – отличная возможность для ребенка познакомиться с тем, как выглядят цифры на бумаге или экране компьютера, потренироваться в их написании.

В этих домиках жили-были капитаны. Как-то раз все капитаны поссорились и вышли из своих «квартирок». Мы их должны помирить, и снова поселить в свои «квартиры».

Посмотрите, какая цифра написана на крыше этого дома? (5)

Сколько капитанов должны жить на каждом этаже? (5)

(Каждый ребенок работает над составом числа 5. А ребенок, справившийся быстрее всех, выставляет этот состав числа в большом домике).

Вместо домика можно использовать другие картинки, например, елку с новогодними игрушками. Изображения можно нарисовать самостоятельно, скачать из сети интернет или адаптировать для занятий обычные книжки-раскраски.

После графических упражнений ребенок будет готов выполнять подобное разложение в уме, без использования пальцев или других предметов. Значит, в дальнейшем в математике устный счет будет ему даваться без проблем.

Приятный бонус: Упражнение Недостающие числа (76.2 KB)

Выучив состав чисел, приступаем к сложению

Когда ребенок без заминки начинает раскладывать числа от 1 до 5 на составляющие во всех комбинациях, можно вместо занятий в формате игры начинать выполнять примеры на сложение.

Начинайте с простых, где участвуют только единицы, например: «В саду растет одна яблоня, садовник посадил рядом еще одну. Сколько теперь яблонь растет на участке?». Позже можно переходить к более сложным упражнениям.

Урок математики в 1-м классе по теме: “Состав числа 9”

Цель: изучить состав числа 9, закрепить навыки счета в пределах 9, умение составлять числовые выражения по рисунку, сравнивать выражение и число; развивать мыслительные операции.

Оборудование.

Числовой ряд от 0 до 20 (над классной доской),
числовой лабиринт Винни Пуха (на доске, рис.1, рис. 4),

елочка, картонные елочные игрушки с примерами, разрезанные пополам (на доске, рис.2, рис. 5),

горшочки с медом разной величины и цвета (на доске, рис.3).

На партах у каждого ребенка: карточки с числами от 1 до 8, листы с “математическими гирляндами” (рис. 6), карточки с примерами для первичного контроля усвоения знаний; а так же учебник математики для 1 класса, автор Истомина Н.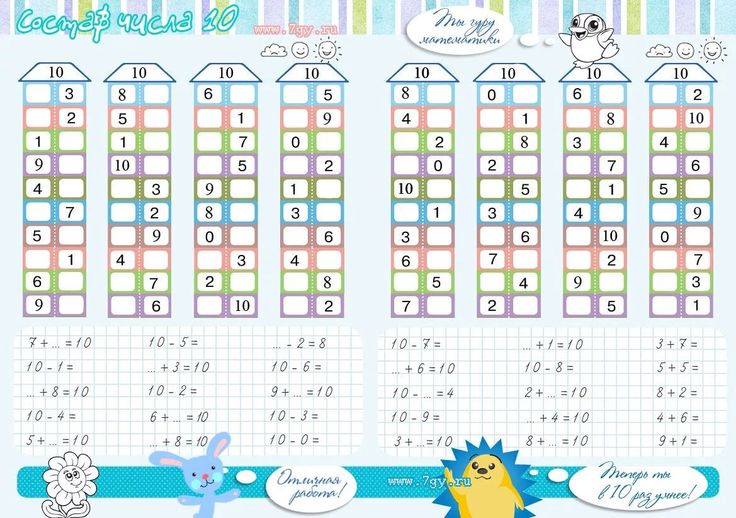

Б., тетрадь.

Ход урока.

1. Организационный момент.

– Сегодня урок математики нам помогут провести Винни-Пух и его друзья. Вместе с ними мы будем составлять математические выражения, складывать числа, учиться считать быстро, используя числовой ряд.

2. Работа с числовым рядом.

Винни-Пух и Пятачок договорились встретиться. Но Винни-Пух что-то запаздывает. Прогуляемся вместе с Пятачком по числовой дорожке.

счет до 20 и обратно;
сосчитайте от 9 до 16, от 10 до3;

назовите последующее число 8, 14;

назовите предыдущее число 10, 20;

какое число стоит между 8 и 10, 18 и 20?

Какое число стоит слева от 10, справа от8?

Назовите соседей числа 8.

3. Сложение чисел с опорой на числовой ряд.

К Пятачку подошел Тигр. Ему трудно устоять на одном месте. Он все время прыгает. Постараемся не отстать от Тигра.

-“Встаньте” глазками на число 2, сделайте три шага вправо. На каком числе оказались? Как математическим выражением записать это действие?

-“Встаньте” глазками на число 4. Сколько шагов вам нужно сделать, чтобы оказаться на числе 6?

Приготовьте карточки с числами. Кто из вас сосчитает быстрее и первым покажет ответ?

К 4 прибавить 3;

К 3 прибавить 4;

К 6 прибавить 1;

К 1 прибавить 6;

К 5 прибавьте 2, прибавьте еще 3.Сколько получилось?

4. Повторение состава чисел 6, 7 и 8.

Друзья вышли на полянку и увидели красивую ёлочку. Кто-то хотел нарядить её к Новому году. Но вот беда – игрушки сломались. Подумайте и соедините половинки игрушек правильно.

-Что вы заметили?

(На желтых игрушках при сложении получается число 6, на синих – 7, на красных – 8).

Повторение состава чисел 6, 7 и 8 хором.

5. Решение примеров на сложение.

-Перед каждым из вас лежит листочек с математическими гирляндами. Вставьте числа правильно и мы украсим гирляндами нашу ёлочку (рис.4).

Взаимопроверка в парах.

Физкультминутка.

Ритмическая игра “Счет через 3”.

Коснуться руками ног (1), хлопнуть в ладоши (2), прикоснуться друг к другу ладонями и сказать “три” (3),коснуться руками ног (4), хлопнуть в ладоши (5), прикоснуться друг к другу ладонями и сказать “шесть”(6) и т.

д. [1]

6. Нахождение ошибок в числовых выражениях.

-Но где же Винни-Пух? Наверное, по дороге с ним что-то приключилось . Может быть ему нужна помощь?

Игра “Лабиринт Винни-Пуха”.

-Найдите и исправьте ошибки в числовых равенствах по-разному, если они есть.

(Дети читают равенства и, если находят ошибки, исправляют одним из способов: 5+2=7, 5+2>6, 5+1=6, 4+2=6)

7. Знакомство с составом числа 9.

-Посмотрите, в конце лабиринта медвежонок нашел подарок. Вам интересно, что там лежит? (В подарке 9 горшочков мёда). Как выдумаете, Винни-Пух обрадуется такому подарку?

– Пересчитаем горшочки, запишем цифрой. (9)

-Что вы знаете о числе 9?

(Дети называют, на что похожа цифра 9, рассказывают о положении числа 9 в числовом ряду, называют “соседей” числа и т. д.)

Винни-Пух решил расставить горшочки на 2 полки. Как по-разному можно расставить их на полки?

Дети называют количество и записывают выражения:

1+8=9 3+6=9 0+9=9

2+7=9 4+5=9

Физкультминутка (дети выполняют движения, проговаривая стихотворение)

Мы проверили осанку
И свели лопатки.
Мы походим на носках,

А потом на пятках.
Пойдем мягко, как лисята,
И как мишка косолапый.
И как заинька трусишка,
И как серый волк-волчишка.
Вот свернулся еж в клубок,
Потому что он продрог.
Лучик ежика коснулся,
Ежик сладко потянулся.

7. Работа по учебнику (страница 84).

№ 193 – составление и запись числовых равенств по рисунку.

(Дети называют равенство, соответствующее каждому рисунку, и записывают в тетрадь. )

№198 – работа в парах.

(Задание на повторение. Дети в парах проверяют друг друга.)

-Кто ни разу не ошибся?

-Какая пара быстрее справилась с заданием?

№ 201 – самостоятельно.

(Дети дополняют до 9 число.)

Решение примеров на карточках (первичная проверка усвоения состава числа 9).

1+8 = 2+7= 3+6=

4+5= 8+1= 5+4=

6+3= 7+2= 1+7=

9. Итог. Рефлексия.

-Состав какого числа изучили?

-Кому из вас было интересно на уроке?

-Кто узнал на уроке что-то новое?

Литература

1. Л. Г. Петерсон Методические рекомендации, математика, 1 класс, “Баласс”, 1996

Изучение состава числа

Когда ребенок понимает состав числа, он понимает, что числа состоят из других чисел. Они «видят числа внутри» других чисел: во-первых, что все числа состоят из единиц, а затем, что их можно составить из пар больших чисел.

Так, например, 5 состоит из «пяти единиц», или из «1 и 4», или из «2 и 3».

Символы CBeebies Numberblocks демонстрируют это своей способностью разделяться на другие символы, как показано в этом клипе:

Понимание состава числа имеет основополагающее значение для понимания структуры отношений часть-часть-целое, которые могут быть представлены с помощью модели часть-часть-целое, как показано ниже:
Если 5 разделить на 3 и 2, то 3 будет частью, 2 будет частью, а 5 будет целым.
Концепция композиции позволяет детям развивать беглость с числовыми связями — не только числовыми связями 10, но и все число облигаций внутри числа. Итак, вернемся к примеру с числом 5: числовые связи числа 5: 0 и 5, 1 и 4, 2 и 3.
Понимание состава также поддерживает понимание коммутативности: если вы узнали, что 2+3=5, то вы также знаете, что 3+2=5 без необходимости заучивать это как новый факт.
Композиция также имеет решающее значение для понимания сложения и вычитания и их обратных отношений. Для тех, кто понимает состав числа, помните, что 2 + 3 = 5 и 5-2 = 3, и то, как соотносятся эти два факта, — это не столько повторение и запоминание, сколько применение структурного понимания. Когда мы складываем, мы составляем: когда мы вычитаем, мы разлагаем.
В рамках программы NCETM/Maths Hubs Mastering Number, занятия предназначены для понимания состава числа для детей в приемной, 1-го и 2-го классов. рекомендуется «субитизировать» (см. без подсчета) меньшие числа «внутри» больших чисел.
Что ты видишь? Может 4 в квадрате, а нечетная 1?
Что вы видите, если они окрашены в такой цвет? Вероятно, 2 и 3.
Детей можно попросить сказать: «Я знаю, что это 5, потому что я вижу 3 красные точки и 2 черные точки».
Различное расположение цветных точек в венгерских числовых рамках помогает развивать распознавание различных конфигураций 3 и 2 и, следовательно, 5.
Перемещение птиц между разными проводами позволяет детям увидеть, что разные пары чисел составляют 5.
Для чисел от 5 до 10 детям предлагается, опять же с помощью используемых представлений, увидеть структуру «5 с небольшим». Понимание чисел по отношению к 5 и 10 важно для разработки эффективных стратегий расчета. Так что увидеть 5 (и немного) в 6, 7, 8 и 9 особенно полезно.
Помимо определения того, что 5 является частью чисел 6,7,8 и 9, другие связи этих чисел также исследуются отдельно.
Различные представления 6 используются для демонстрации различных композиций 6: «5 и немного», а также «3 и 3» или «2 и 2 и 2».
Рисунок кубика подчеркивает «3 и 3»:
Сетка из 9 позволяет переместить одиночные фишки из знакомой схемы игры в кости, чтобы увидеть, что у нас все еще есть 6. Исследуются различные способы деления чисел в пределах 6 для составления 6.
Использование ящика для яиц позволяет разделить яйца на коричневые и белые и использовать истории о яйцекладке, чтобы увидеть разные числа в пределах 6.
Более подробная информация о композиции, в том числе идеи для занятий, графики прогресса, типичные ошибки и то, на что следует обращать внимание при работе с маленькими детьми, содержится на странице «Композиция для детей младшего возраста». Вас также могут заинтересовать другие статьи из этого набора: «Количественность и числовой смысл» и «Обучение порядкового порядка — больше, чем просто первая, вторая и третья».
NCETM и Maths Hubs рассматривают программу освоения чисел на 2022/23 год. Если вы заинтересованы в участии, пожалуйста, заполните Форму выражения заинтересованности.
Что такое составные числа? Определение, список, примеры, факты
В математике составные числа можно определить как числа, имеющие более двух делителей. Числа, которые не являются простыми, являются составными числами, потому что они делятся более чем на два числа.
Тест на делимость — это стандартный метод, используемый для нахождения составного числа. В этом тесте данное число делится на меньшее простое или составное число. Если оно полностью делится, число является составным числом.
Составные числа с нечетной цифрой на месте единицы являются нечетными составными числами. Проще говоря, все нечетные числа, не являющиеся простыми, являются нечетными составными числами. Например: 9, 15, 21 и т. д.
Составные числа с четной цифрой на месте единицы являются четными составными числами.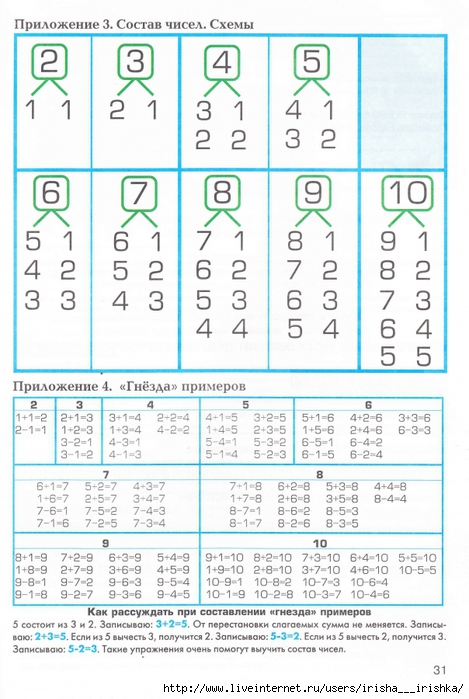 Проще говоря, все четные числа, кроме 2, являются четными составными числами. Это потому, что никакое четное число (кроме 2) никогда не может быть простым числом.
Среди заданных чисел 179 не делится ни на одно число, кроме 1 и 179.; следовательно, это не составное число. 144 делится на 2, значит, это составное число.
1
Какое из следующих составных чисел является наименьшим?
9
11
14
2
Правильный ответ: 9
9 — наименьшее составное число. Оно имеет более двух делителей: 1, 3 и 9.
2
Какое из следующих чисел не является составным?
15
21
25
23
Правильный ответ: 23
23 не является составным числом. Он делится только на 1 и самого себя.
3
Какое из следующих чисел является составным?
11
13
17
20
Правильный ответ: 20
20 — составное число. Оно делится более чем на два множителя: 1, 2, 4, 5, 10 и 20.
4
Какое самое большое составное число из следующих?
47
33
35
39
Правильный ответ: 39
39 — наибольшее составное число среди всех вариантов, делителями которых являются 1, 3, 13 и 39. 47 — простое число.
Заключение
Составное число — это положительное целое число, которое делится на меньшие положительные целые числа, кроме 1 и самого себя. Составные числа можно определить с помощью метода делимости. Посетите SplashLearn, игровую обучающую платформу, чтобы найти больше интересных упражнений на составные числа.
Может ли число быть одновременно простым и составным?
Нет, число не может быть одновременно простым и составным. Простое число имеет ровно два делителя, 1 и само себя, а составное число имеет более двух делителей. Итак, все натуральные числа (кроме 1) либо простые, либо составные, но не то и другое вместе.