Число 15 четное или нечетное число: Число 15 чётное или нет ? – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Натуральные числа /qualihelpy

Натуральными числами называют числа, с помощью которых определяется количество предметов того или иного множества. Ряд натуральных чисел бесконечен: , , , , , , , , , , , , … Множество всех натуральных чисел обозначают .

Любое натуральное число можно записать с помощью десяти цифр: , , , , , , , , , . Цифры , , , , называют четными, а цифры , , , , – нечетными.

Числа, запись которых оканчивается четной цифрой, называют четными числами.

Числа, запись которых оканчивается нечетной цифрой, называют нечетными числами.

Например, натуральные числа , , , , , , , , , , … – четные, а натуральные числа , , , , , , , , , , … – нечетные.

Четные числа записывают в виде , где – любое натуральное число. Нечетные числа записывают в виде , если – любое натуральное число, или в виде , если – любое натуральное число и число .

Над натуральными числами можно производить арифметические действия:

1) сложение: , где и – слагаемые, – сумма;

2) вычитание: , где – уменьшаемое, – вычитаемое, – разность;

3) умножение: , где и – множители, – произведение;

4) деление: , где – делимое, – делитель, – частное.

Чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое.

Чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое.

Чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность.

Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель.

Чтобы найти неизвестное делимое, необходимо частное умножить на делитель.

Чтобы найти неизвестный делитель, необходимо делимое разделить на частное.

Законы сложения:

1) переместительный: от перестановки слагаемых значение суммы не изменится, т. е. ,

например, ;

2) сочетательный: чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего, т. е. ,

например, .

Законы умножения:

1) переместительный: от перестановки множителей значение произведения не изменится, т. е. ;

2) сочетательный: чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего, т. е. ;

3) распределительный закон умножения относительно сложения: чтобы умножить сумму на число, можно каждое слагаемое умножить на это число и полученные произведения сложить, т. е. ;

4) распределительный закон умножения относительно вычитания: чтобы умножить разность на число, можно уменьшаемое и вычитаемое умножить на это число и из первого произведения вычесть второе, т. е. .

Например:1) ;

2) ;

3) ;

4) .

Делимость натуральных чисел

Если натуральное число делится без остатка на натуральное число , то число называют кратным числа , а число – делителем числа . Например, . Говорят, что число кратно числу , а число является делителем числа .

Если число кратно числу , то записывают: .

Признаки делимости натуральных чисел на , , , , , , , и .

1. Число делится на , если его запись оканчивается четной цифрой. Например, числа , и делятся на .

2. Число делится на , если сумма цифр числа делится на . Например, делится на , так как сумма цифр этого числа и число делится на .

3. Число делится на , если его запись оканчивается цифрой или цифрой Например, числа и делятся на .

4. Число делится на , если сумма цифр числа делится на . Например, число делится на , так как сумма цифр этого числа и число делится на .

5. Число делится на , если его запись оканчивается цифрой . Например, число делится на .

6. Число делится на , если две последние цифры его записи образуют число, которое делится на . Например, число делится на , так как число делится на .

7. Число делится на , если три последние цифры его записи образуют число, которое делится на . Например, число делится на , так как число делится на .

8. Число делится на , если разность сумм цифр, стоящих на четных и нечетных местах, делится на . Например, число делится на , так как и число делится на .

9. Число делится на , если две последние цифры его записи образуют число, которое делится на . Например, числа , , и делятся на .

Деление с остатком

Разделить натуральное число на натуральное число с остатком – значит представить число в виде , где – неполное частное, а – остаток от деления на и меньше .

Если же остаток равен нулю, то говорят, что число делится нацело на число .

Например, при делении натуральных чисел на , будем получать один из остатков: или , или , или , или .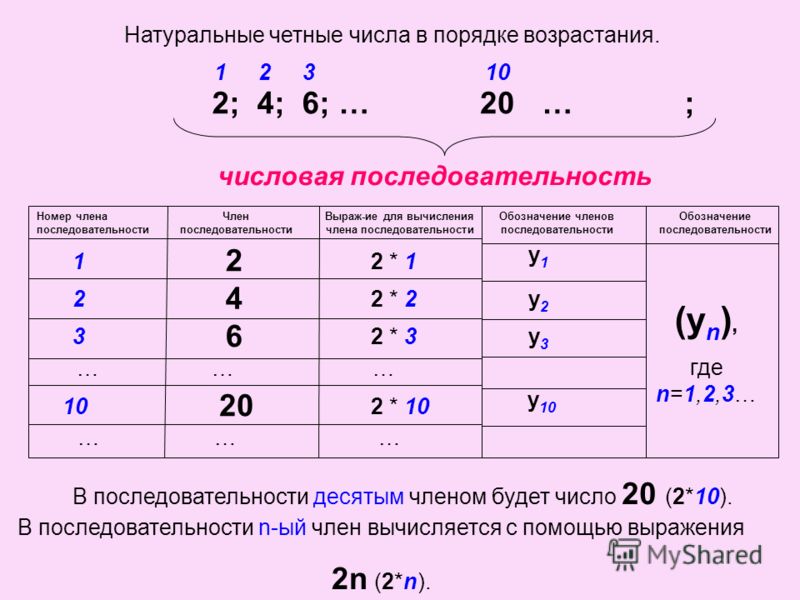

Простые и составные числа

Числа, которые имеют только два различных делителя (делятся только сами на себя и на число 1), называют простыми.

Например, простыми являются числа , , , , , , , , , …. .

Числа, которые имеют более двух различных делителей, называют составными. Составные числа можно представить в виде произведения двух и более простых множителей.

Например, число составное, так как .

Натуральные числа называются взаимно простыми, если они не имеют общих делителей, за исключением числа .

Например, числа и взаимно простые;

Наибольший общий делитель и наименьшее общее кратное

Общим делителем нескольких чисел называют число, которое является делителем каждого из этих чисел. Среди всех общих делителей всегда имеется наибольший. Это число называется наибольшим общим делителем (НОД).

Например, числа , , и являются общими делителями чисел и , а число – их наибольший общий делитель;

Общим кратным нескольких чисел называют число, которое является кратным каждого из этих чисел. Среди всех общих кратных всегда есть наименьшее. Это число называется наименьшим общим кратным (НOК).

Например, числа и кратны числам , , , и , а число – наименьшее общее кратное чисел и .

Чтобы найти НОД нескольких чисел, необходимо разложить их на простые множители и найти произведение только тех множителей, которые имеются в разложениях всех чисел.

Чтобы найти НOК нескольких чисел, необходимо разложить их на простые множители, найти произведение всех множителей, входящих в разложение одного из чисел и недостающих множителей из разложений оставшихся чисел.

Пример 1. Найдите наибольший общий делитель и наименьшее общее кратное чисел , и .

Решение. Разложим эти числа на простые множители:

Найдем наибольший общий делитель чисел , и :

НОД .

Найдем наименьшее общее кратное чисел , и :

НОК .

Ответ: и .

Пример 2. При делении пятизначного числа на в остатке получается . Найдите это число, если известно, что оно делится на .

Решение. Согласно условию задачи число делится на , следовательно, оно делится и на и на .

Если искомое число делится на , то число делится на . Тогда может принимать одно из значений: или , или , или . Поскольку при делении числа на в остатке получается , то .

Если же число делится на , то сумма цифр этого числа делится на , то есть . Тогда при условии, что число будет делиться на .

Запишем искомое число: .

Ответ: .

1. Число не является ни простым и ни составным.

2. В результате сложения и умножения натуральных чисел всегда будем получать натуральное число.

3. В результате вычитания натуральных чисел получим натуральное число только в том случае, если уменьшаемое больше вычитаемого.

4. Деление одного натурального числа на другое не всегда выполнимо. В этом случае имеет место деление с остатком.

5. Множество делителей числа конечно, а множество чисел, кратных числу, бесконечно. Например, число имеет делителя: ; ; ; ; ; . Числу кратны числа: , , и т. д.

6. Числа, кратные числу , записывают в виде , где – любое натуральное число. Например, все числа, кратные числу , можно записать так: где – натуральное число.

7. Рассмотрим буквенную запись чисел в десятичной позиционной системе счисления. Так, например, если – цифра десятков, – цифра единиц некоторого двузначного числа, то запишем: . Аналогично запишем трехзначное число, у которого – цифра сотен, – цифра десятков, – цифра единиц: .

30 четное число или нет. Чётные и нечётные числа. Умножение четных и нечетных чисел

Ответы к с. 66

212. Какое число получится: чётное или нечётное, если нечётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи три примера, подтверждающих твоё предположение.

При делении нечётного числа на нечётное число результат всегда будет нечётным числом.
45 : 5 = 9 55 : 11 = 5 63 : 7 = 9

213. Какое число получится: чётное или нечётное, если чётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи несколько примеров, подтверждающих твоё предположение. Обсуди результат с соседом по парте.

При делении чётного числа на нечётное число результат всегда будет чётным числом.
54 : 9 = 6 50 : 5 = 10 96 : 3 = 32

214. Можешь ли ты привести пример такого случая деления, когда нечётное число делится нацело на чётное число? Почему? Вспомни, как можно получить делимое из делителя и значения частного.

Делимое можно получить, умножив делитель на значение частного. По условию делитель является чётным числом. Мы знаем, что если чётное число умножить на чётное или нечётное число, то результатом будет всегда чётное число. В нашем же случае делимое должно быть нечётным числом. Это означает, что никакое значение частного в этом случае подобрать нельзя и привести пример такого случая деления невозможно.

215. Представь число 2873 в виде суммы круглых десятков и однозначного числа. Чётным или нечётным числом является каждое из слагаемых? Чётным или нечётным числом будет значение их суммы? На какую цифру может оканчиваться запись чётного числа? А нечётного?

2873 = 2870 + 3
Первое слагаемое – чётное число, второе слагаемое – нечётное число.

2873 – нечётное число.
Нечётное число 2873 заканчивается на нечётную цифру 3, запись чётного числа 2870 — на чётную цифру 0.
Запись чётного числа может оканчиваться чётными цифрами (0, 2, 4, 6, 8), а запись нечётного числа — нечётными числами (1, 3, 5, 7, 9).

216. Выпиши чётные числа в один столбик, а нечётные — в другой.

2844 57893
67586 9231
10050 9929

217. Сколько существует чётных двузначных натуральных чисел? А сколько таких же нечётных чисел?

Самое маленькое двузначное чётное число 10, а самое большое – нечётное число 99. Всего их 99 – 10 + 1 = 90. Чётные и нечётные числа в натуральном ряду чередуются, поэтому чётных двузначных чисел столько же сколько и нечётных, то есть 45, поскольку 90 : 2 = 45.

218. Запиши самое большле чётное шестизначное число.

Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным.

Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.

Например: -24, 0, 6, 38 — все это четные числа.

m = 2k — общая формула написания четных чисел, где k – целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.

Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.

Пример нечетных чисел: 3, 1, 7 и 35.

n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k – целое число.

Сложение и вычитание четных и нечетных чисел

В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.

Операция	Результат	Пример
Четное + Четное
Четное + Нечетное	Нечетное
Нечетное + Нечетное

Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.

Умножение четных и нечетных чисел

При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.

Операция	Результат	Пример
Четное * Четное
Четное * Нечетное
Нечетное * Нечетное	Нечетное

А теперь рассмотрим дробные числа.

Десятичная запись числа

Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.

Например: 3,14; 5,1; 6,789 — это все

С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.

Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.

Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.

А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом – дробную.

Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.

Определения

Чётное число – целое число, которое делится без остатка на 2: …, −4, −2, 0, 2, 4, 6, 8, …
Нечётное число – целое число, которое не делится без остатка на 2: …, −3, −1, 1, 3, 5, 7, 9, …

В соответствии с этим определением нуль является чётным числом.

Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .

В разных странах существуют связанные с количеством даримых цветов традиции.

В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли.

Например, вполне допустимо подарить юной даме букет из 12 или 14 цветов или срезов кустового цветка, если они имеют множество бутонов , у которых они, в принципе, не подсчитываются.
Тем более это относится к б́ольшему количеству цветов (срезов), даримых в других случаях.

Примечания

Wikimedia Foundation . 2010 .

Смотреть что такое “Чётные и нечётные числа” в других словарях:

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Слегка избыточное число, или квазисовершенное число избыточное число, сумма собственных делителей которого на единицу больше самого числа. До настоящего времени не было найдено ни одного слегка избыточного числа. Но со времён Пифагора,… … Википедия

Целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные С. ч. можно… …

Целые (0, 1, 2,…) или полуцелые (1/2, 3/2, 5/2,…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы.… … Большая советская энциклопедия

Книги

Математические лабиринты и ребусы, 20 карточек , Барчан Татьяна Александровна, Самоделко Анна. В наборе: 10 ребусов и 10 математических лабиринтов на темы: – Числовой ряд; – Чётные и нечётные числа; – Состав числа; – Счёт парами; – Упражнения на сложение и вычитание. В комплекте 20…

Что означают чётные и нечётные числа в духовной нумерологии. В изучении это очень важная тема! Чем по своей СУТИ чётные числа отличаются от нечётных чисел?

Чётные числа

Общеизвестно, что чётные числа — те, которые делятся на два. То есть, числа 2, 4, 6, 8, 10, 12, 14, 16, 18 и так далее.

А что означают чётные числа относительно ? Какова нумерологическая суть деления на два? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.

У несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств — точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».

А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии. Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.

Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?

Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.

Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе… надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.

Нечётные числа

Нечётные числа — те, которые не делятся на два: числа 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 и так далее. С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.

Что, кстати, даёт пищу для размышления: почему число цветов в букете для живого человека нечётное, а для мёртвого — чётное… Не потому ли, что материальная логика (логика в рамках «да-нет») мертва относительно души человека?

Видимые совпадения материальной логики и духовной происходят очень часто. Но пусть это не вводит вас в заблуждение. Логика духа, то есть логика нечётных чисел , никогда в полной мере не прослеживается на внешних, физических уровнях человеческого бытия и сознания.

Возьмём для примера — число любви. Мы разглагольствуем о любви на каждом шагу. Мы признаёмся в ней, мечтаем о ней, украшаем ею свою жизнь и чужую жизнь.

Но что на самом деле мы знаем о любви? О той всепроникающей Любви, которая пронизывает собой все сферы Мироздания. Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!

Парадоксальность — вот одно из ключевых свойств нечётных чисел. В толковании нечётных чисел надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них…

Кстати, зрелость ума характеризуется способностью воспринимать парадоксы. Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.

Чётные и нечётные числа в нумерологии

Подведём итоги. В чём главное отличие чётных чисел от нечётных?

Чётные числа более предсказуемы (кроме числа 10), основательны и последовательны. События и люди, связанные с чётными числами, более устойчивы и объяснимы. Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел…

Нечётные числа — взбалмошны, свободолюбивы, неустойчивы, непредсказуемы. Они всегда преподносят сюрпризы. Вот вроде и знаешь смысл какого-то нечётного числа, а оно, это число, вдруг начинает вести себя так, что заставляет тебя заново пересмотреть чуть ли не всю твою жизнь…

Обратите внимание!

В магазины уже поступила моя книга под названием «Духовная нумерология. Язык чисел». На сегодняшний день это самое полное и востребованное из всех существующих эзотерических пособий о смысле чисел. Подробнее об этом, а также для заказа книги пройдите по следующей ссылке: ««

———————————————————————————————

в каких странах дарят четное, а в каких нечетное количество цветов?

Почему в одних странах принято дарить четное, а в других- нечетное количество цветов, и откуда у разных народов появилось такое суеверие? Задумывались ли вы, как давно появилась эта традиция?

В одной из версий появления этой традиции, говорится о том, что ещё в древности, языческие племена верили в магию чисел. Каждому из них присваивалось своё значение и особая ритуальная сила. Чаще всего это было значение жизни и смерти. Например, Волхвы на Руси говорили о том, что числа четные олицетворяют завершенный жизненный цикл, это предвестники и проводники смерти. Нечетное же число считалось символом противоположным – знаком жизни и развития, движения и стремлений.

Это суеверие распространилось позднее и на цветочный этикет! На Руси в похоронный день стали приносить два цветка. Один – в память об ушедшем человеке, а второй предназначался проводнику, который защитит душу «по ту сторону» жизни.

Вторая версия опровергает первую. Говорят, что традиция дарения нечетного числа цветов живым, а четного – мертвым, пришла к нам из Японии. А произошло это потому, что написание иероглифа четной цифры четыре очень схоже с иероглифом, означающим у японцев «смерть».

Древние пифагорейцы тоже верили в нумерологию и её влияние на судьбу человека. Нечетные числа считались символом жизни и добра, занимали сторону удачи (правую сторону). Четные – наоборот! Это были числа лжи, неудачи, обмана и потерь – символ левой стороны. Возможно, выражение встать не с той ноги (с левой), появилось именно благодаря этой символике?

Несмотря на мрачные легенды прошлого, в наше время многое изменилось. В том числе и отношение к суевериям о четных и нечетных числах.

Какое количество цветов принято дарить сегодня и какое значение этому придают в мире?

Россия

Традиции народа с древних времен передаются в нашей стране от прадедов и дедов к внукам. Поэтому нет ничего удивительного в том, что в России по случаю праздничных событий принято дарить букеты только из нечетного количества цветов! Четное число – символ скорби и потери.

УКРАИНА, КАЗАХСТАН и УЗБЕКИСТАН

Так же придерживаются обычаев прошлого. Здесь, как и в России, принято дарить по случаю праздников только нечетное количество цветов.

ГРУЗИЯ

Здесь все наоборот! Четное количество цветов в букете – признак расположения, пожелание удачи и благополучия. А вот нечетное количество бутонов приносят в похоронные дни, чтобы ушедшие не забрали счастье у живых.

США

Самыми популярными букетами на территории США согласно статистическим данным, считаются букеты из10 или 12 роз. Здесь принято дарить четное количество цветов. Зато здесь есть другое суеверие. Букеты из 13 цветов считаются пожеланием неудачи и несчастий, ведь это число несчастливое.

ИЗРАИЛЬ

Здесь принято дарить четное количество цветов. Традиции преподносить цветы по случаю дней памяти и скорби в Израиле нет. Цветы олицетворяют только жизнь, радость и благополучие.

ГЕРМАНИЯ

Раньше здесь существовало определенное правило для флористов: составлять букеты только с четным количеством цветов. Это было продиктовано вовсе не суевериями или традициями. Любовь немцев к точности и геометрии нашла свое выражение и во флористике! На сегодняшний день цветочные композиции собирают без оглядки на точное количество цветов но, как и в США избегают «чертовой дюжины».

КАНАДА

Четное количество цветов не несет в себе никакого негатива и не связано с ритуальными обычаями в этой стране. Букеты из 10, 20 и 30 цветов – вполне обычное дело!

АФРИКА

Жаркий континент, где относительно традиций по вручению цветов можно выделить два направления:

В современной традиции этикет не предъявляет никаких требований к количеству цветов в букете, поэтому дарить четное количество- вполне нормально.
Жители некоторых отдаленных провинций и определенных народностей Африки и вовсе не имеют традиции преподносить друг другу цветы!

АВСТРАЛИЯ

Четное количество цветов – вполне уместный подарок. Но не стоит дарить букет(как и любой другой сувенир), если нет особого повода! Здесь не любят делать и принимать подарки, ставящие в неловкое положение и не соответствующие событию.

ФРАНЦИЯ

Четное число цветов в букете французы считают неприемлемым. Такой букет символизирует скорбь, беду и разлуку.

ЯПОНИЯ

Здесь вполне допустимо четное количество цветов и преподнести такой букет не считается правилом плохого тона или оскорблением. Наоборот! Японцы дарят четное количество бутонов, считая, что человек не должен быть один и ему нужно разделить с кем-то то, что у него есть! Исключение лишь четыре цветка – как мы и говорили раньше, у японцев этот символ схож со знаком смерти.

ТАЙЛАНД

Здесь, как и в России существует правило дарения нечетного количества цветов. Но, согласно данным статистических исследований более половины населения не придают особого значения тому, из какого количества цветов собран букет.

КИТАЙ

В этой стране принято дарить четное количество цветов. Особое отношение здесь только к разновидности цветов в букете. Есть праздник, когда принято дарить только ирисы, а белые хризантемы ассоциируются только с похоронами (как в Японии и Корее).

БРАЗИЛИЯ

Территория радости, танцев, карнавала и, конечно, цветов! Бразилия -страна, где не обращают внимания на такие мелочи, как количество цветов в букете! Подарите цветы красиво, сделайте комплимент и улыбнитесь – вот и все правила цветочного этикета!

В мире так много условностей, традиций и обычаев! Каждый житель планеты, так или иначе, сталкивается с ними. А что думаете о цветочных традициях вы? На какой стороне мира вам комфортнее : четная или нечетная? Выбор за вами!

Четные и нечетные числа. Понятие о десятичной записи числа

Определения

Чётное число – целое число, которое делится без остатка на 2: …, −4, −2, 0, 2, 4, 6, 8, …
Нечётное число – целое число, которое не делится без остатка на 2: …, −3, −1, 1, 3, 5, 7, 9, …

В соответствии с этим определением нуль является чётным числом.

Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .

В разных странах существуют связанные с количеством даримых цветов традиции.

Примечания

Wikimedia Foundation . 2010 .

Смотреть что такое “Чётные и нечётные числа” в других словарях:

Целые (0, 1, 2,…) или полуцелые (1/2, 3/2, 5/2,…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы. … … Большая советская энциклопедия

Книги

Математические лабиринты и ребусы, 20 карточек , Барчан Татьяна Александровна, Самоделко Анна. В наборе: 10 ребусов и 10 математических лабиринтов на темы: – Числовой ряд; – Чётные и нечётные числа; – Состав числа; – Счёт парами; – Упражнения на сложение и вычитание. В комплекте 20…

Чётные числа

Общеизвестно, что чётные числа — те, которые делятся на два. То есть, числа 2, 4, 6, 8, 10, 12, 14, 16, 18 и так далее.

Нечётные числа

Чётные и нечётные числа в нумерологии

Подведём итоги. В чём главное отличие чётных чисел от нечётных?

Обратите внимание!

———————————————————————————————

Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.

Например: -24, 0, 6, 38 — все это четные числа.

Пример нечетных чисел: 3, 1, 7 и 35.

n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k – целое число.

Сложение и вычитание четных и нечетных чисел

Операция	Результат	Пример
Четное + Четное
Четное + Нечетное	Нечетное
Нечетное + Нечетное

Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.

Умножение четных и нечетных чисел

Операция	Результат	Пример
Четное * Четное
Четное * Нечетное
Нечетное * Нечетное	Нечетное

А теперь рассмотрим дробные числа.

Десятичная запись числа

Например: 3,14; 5,1; 6,789 — это все

Ответы к с. 66

При делении нечётного числа на нечётное число результат всегда будет нечётным числом.
45 : 5 = 9 55 : 11 = 5 63 : 7 = 9

При делении чётного числа на нечётное число результат всегда будет чётным числом.
54 : 9 = 6 50 : 5 = 10 96 : 3 = 32

2873 = 2870 + 3
Первое слагаемое – чётное число, второе слагаемое – нечётное число.
2873 – нечётное число.
Нечётное число 2873 заканчивается на нечётную цифру 3, запись чётного числа 2870 — на чётную цифру 0.
Запись чётного числа может оканчиваться чётными цифрами (0, 2, 4, 6, 8), а запись нечётного числа — нечётными числами (1, 3, 5, 7, 9).

216. Выпиши чётные числа в один столбик, а нечётные — в другой.

2844 57893
67586 9231
10050 9929

217. Сколько существует чётных двузначных натуральных чисел? А сколько таких же нечётных чисел?

218. Запиши самое большле чётное шестизначное число.

Новый инвариант числа. Исследование натурального ряда чисел (НРЧ) / Хабр

&nbsp &nbsp &nbsp &nbsp &nbsp В арифметике натуральных чисел иногда возникает необходимость поиска делителей составного числа N. Простая операция, обратная умножению чисел, на сегодняшний день неизвестна. Ее отсутствие создает определенные трудности при решении некоторых практических задач, особенно, если манипулировать приходится с числами высокой и очень высокой разрядности (сотни и даже тысячи цифр, представляющих числа).

&nbsp &nbsp &nbsp &nbsp &nbsp В работе «Фундаментальные структуры натурального ряда чисел» Ваулин А.Е., Пилькевич С.В.– Интеллектуальные системы. Труды Седьмого международного симпозиума. Под ред. К.А. Пупкова.– М.: РУСАКИ, 2006. – с.384-387. Приводятся сведения об оригинальной концепции моделирования натурального ряда чисел и отдельного числа с целью установления свойств, слабо зависящих или вообще не зависящих от разрядности чисел. Дальнейшему развитию и уточнению деталей этого подхода посвящена настоящая работа.

&nbsp &nbsp &nbsp &nbsp &nbsp Независимость некоторых свойств чисел от их разрядности явилась одной из основных идейных посылок предлагаемого аналитического подхода к моделированию чисел. Наличие таких свойств у чисел подтверждает существование признаков делимости чисел. Например, какой бы величины не было заданное число, если свертка (сумма) его цифр делится на три, то и исходное число делится на три. От разрядности числа делимость на три практически не зависит. Аналогично и для других признаков делимости. Это свидетельство того, что некоторые свойства чисел могут не зависеть от их разрядности. Поиск таких свойств и разработка теории их использования в различных направлениях, в частности, при разработке алгоритмов факторизации, установлении простоты числа, и других не менее трудных задач является актуальной и важной проблемой современной математики.

&nbsp &nbsp &nbsp &nbsp &nbsp В работе описывается новый обнаруженный признак-свойство чисел. Этот признак оказывается полезным для разработки алгоритмов решения как новых, так и традиционных задач теории и практики. Приведем вначале качественные содержательные рассуждения о сущности предлагаемой работы.

&nbsp &nbsp &nbsp &nbsp &nbsp Натуральный ряд. Будем далее рассматривать натуральный ряд чисел как математический объект, имеющий сложное строение. НРЧ можно рассматривать как совокупность различных рядов с разными свойствами, например, составленным из двух арифметических прогрессий четных и нечетных чисел. Эти прогрессии имеют совпадающие разности d, равные d=2, но с разными начальными элементами: а=1 для прогрессии нечетных чисел и а=2 для прогрессии четных чисел. Загрузим все числа НРЧ в ячейки (разряды) регистра и тогда НРЧ можно представить регистром с бесконечным числом ячеек. Обратим внимание на ряд нечетных чисел.

&nbsp &nbsp &nbsp &nbsp &nbsp Рассмотрим в НРЧ три смежных последовательных числа 2n–1, 2n, 2n+1, среднее из которых четное. Возведем их в квадрат. Между квадратами крайних нечетных чисел всегда лежит четное число разрядов регистра вида 8k, которое четным квадратом разбивается на два последовательных (смежных) нечетных числа вида 4k–1 слева и 4k+1 справа. Ячейку самого четного квадрата отнесем к правому числу.

&nbsp &nbsp &nbsp &nbsp &nbsp Таким образом, любое нечетное число вида N=4k±1, k>0 – произвольное натуральное число, в НРЧ лежит всегда между квадратами чисел N=x₁²–x₀² с разной четностью. В определенных ячейках НРЧ размещаются квадраты натуральных чисел. Такому размещению соответствует ряд закономерностей. Нечетные квадраты чередуются с четными квадратами. При этом, если больший квадрат x₁² четный, то N=4k–1 и N≡3(mod4), а если больший квадрат x₁² нечетный, то N=4k+1 и N≡1(mod4).

&nbsp &nbsp &nbsp &nbsp &nbsp Представим регистр НРЧ линейкой с движком по типу логарифмической. Для заданного числа N в движке создадим окно размером в N+1 позиций (разрядов). Путем перемещения движка вдоль НРЧ-линейки будем находить и фиксировать его положения парой чисел (x₀², x₁²), которые размещены в крайних позициях окна (x₀² – левая и x₁² – правая) и оба значения будут соответствовать числовым квадратам. Разность между квадратами в крайних позициях окна, очевидно, будет совпадать с числом N=x₁²–x₀².

&nbsp &nbsp &nbsp &nbsp &nbsp Контуры НРЧ. Расстояние между квадратами двух последовательных нечетных чисел назовем контуром. Расстояние между ячейками с квадратами несмежных чисел назовем интервалом в НРЧ. Если сумма смежных нечетных чисел кратна числу 8, то она образует длину интервала, называемого контуром, а значение k является номером этого контура. Так смежные числа 11 и 13 образуют контур (11+13=24=3•8) с номером k=3 и длиной L(k)=24=k•8, а смежные нечетные числа 13 и 15 контур не образуют (13+15=28≠k•8).

&nbsp &nbsp &nbsp &nbsp &nbsp Расстояния между нечетными квадратами-границами смежных чисел всегда образуют контуры и содержат число регистровых ячеек, равное 8k. Контуры в НРЧ образуют непрерывную последовательность с номерами k=1(1)∞, т. е. НРЧ образован заполненными числами ячейками последовательности контуров, длины которых кратны числу 8. Первый контур имеет длину L(1)=3²–1²=1•8, второй контур – L(2)=5²–3²=2•8=16, и т.д. Длины контуров образуют арифметическую прогрессию с разностью d=8 и а=8.

&nbsp &nbsp &nbsp &nbsp &nbsp Заполнение всех позиций окна числами (интервалов) в каждом из фиксированных парой чисел (x₀², x₁²) положений обладает закономерностью и характеризуется некоторым числовым инвариантом, устанавливаемым в работе. Так как пар (x₀², x₁²) может быть больше одной, то будем снабжать ее числа индексом i.

&nbsp &nbsp &nbsp &nbsp &nbsp

Пример 1

&nbsp &nbsp &nbsp &nbsp &nbsp Для N=105 (размер окна — 1) имеется 4 положения (4 пары квадратов разной четности), которые фиксируются. Контролировать будем положение левой границы окна. Начинаем перемещение движка от 1 вправо. Первое положение (остановка) возникает с появлением на левой границе окна числа x₀²=4, но правая граница при этом равна 109 – не квадрат, затем на левой границе окна оказывается квадрат x₀²=9, но справа число 114 – не квадрат, после прохода позиции с числом 15 в окне слева появляется число x₀²=16 – квадрат. Останавливаемся и проверяем число на правой границе окна. Там видим число x₁²=121 – тоже квадрат. Фиксируем это положение с контролем разности между квадратами:

x₁₁²–x₀₁²=11²–4²=105

.
&nbsp &nbsp &nbsp &nbsp &nbsp Продолжаем движение до прихода левого края окна в позиции 25, 36, 49 и видим, что для них правая граница на квадрат не попадает. Но когда в окне слева появляется число 64, справа видим число 169 – квадрат. Фиксируем это положение и выполняем контроль

x₁₂²–x₀₂²=13²–8²=105

.
&nbsp &nbsp &nbsp &nbsp &nbsp Следующее фиксируемое положение окна: слева число x_о²=256, а справа x₁²=361, оба квадраты. Фиксируем и выполняем контроль разности между квадратами

x₁₃²–x₀₃²=19²–16²=105

.
&nbsp &nbsp &nbsp &nbsp &nbsp И, наконец, четвертое положение окна дает разность квадратов равную

x₁₄²–x₀₄²=53²–52²=105

.
&nbsp &nbsp &nbsp &nbsp &nbsp Дальнейшее движение прекращается, так как больше не существует пары квадратов, разность между которыми равна числу N=105, разность всех пар будет больше 105. Четвертую пару x₁₄², x₀₄² назовем предельной парой.

&nbsp &nbsp &nbsp &nbsp &nbsp Полуконтуры. Место каждого четного квадрата вида (2k)² во внутренней ячейке k-го контура. Эта ячейка делит длину L(k) контура на два m(k)=4k–1 и М(k)=4k+1 смежных нечетных числа (левое и правое), называемых полуконтурами. Заметим, что контуры и полуконтуры – это множества ячеек, заполненных натуральными числами, а m(k) и M(k) – мощности этих множеств. Множества ячеек последовательно следующих полуконтуров формируют НРЧ. Все множество нечетных чисел образуют два класса: левые числа N≡3(mod4) и правые числа N≡1(mod4). Длины полуконтуров первого контура, левое нечетное число 4•1–1=3 и правое нечетное число 4•1+1=5, в сумме образуют длину L(k=1)=3+5=8 контура с номером k=1.

&nbsp &nbsp &nbsp &nbsp &nbsp Границы контура. При заданном номере k контура он полностью определяется, полуконтуры с длиной m(k)=4k–1 левый и М(k)=4k+1 правый, границы этого контура левая Г_л(k)=(2k–1)² и правая Г_п(k)=(2k+1)². Длина контура L(k)=m(k)+M(k)=Г_п(k)–Г_л(k)=8k. Четный квадрат Г_ч(k)=(2k)² — общая граница полуконтуров.
&nbsp &nbsp &nbsp &nbsp &nbsp Действительно, разность границ Г_п(k)–Г_л(k)=(2k+1)²–(2k–1)²=~~4k²~~+2•2k+1–~~4k²~~+2•2k–1=8k.

&nbsp &nbsp &nbsp &nbsp &nbsp Предельный контур. Любое нечетное число N можно представить как полуконтур в некотором контуре с номером k_п. Такой контур единственный, так как контур слева от предельного имеет полуконтуры меньшие N, а справа — большие N. Число N левое или правое определяется с использованием четного квадрата предельного контура. Для левогоN=x₁²–x₀², и x₁ четное, для правого N=x₁²–x₀² и x₁ нечетное. Здесь роль границ полуконтуров играют значения x₁² и x₀². Эти границы определяются из выражений x₁=(N+1)/2 и x_о=(N–1)/2. Длина предельного контура с номером k_п для числа N определяется по формуле

&nbsp &nbsp &nbsp &nbsp &nbsp Номер k_п предельного контура числа N вычисляется через длину предельного контура k_п=L(k_п)/8. Теперь самое время пояснить введенные понятия числовым примером. Это специально подобранный пример, очень простой, способствующий лучшему пониманию изучаемого явления.

&nbsp &nbsp &nbsp &nbsp &nbsp

Пример 2

&nbsp &nbsp &nbsp &nbsp &nbsp Пусть задано составное нечетное натуральное число (сннч)

N=105=3•5•7

. Для этого числа требуется найти предельный контур, его границы и определить его номер k_п. Указать все пары квадратов

(x_i1², x_i0²)

, i=1(1)… разной четности, разность между которыми равна числу N=105.

&nbsp &nbsp &nbsp &nbsp &nbsp Решение. Для лучшего усвоения содержания примера рекомендуется воспользоваться карандашом и бумагой. Известно, что сннч лежит между квадратами разной четности N=x₁²–x₀². Определим левое или правое число заданногоN=105≡1(mod4). Число N правое, т.е. это больший полуконтур в предельном контуре. Определим границы предельного контура через значение N, x₁=(N+1)/2=(105+1)/2=53 и x_о=(N–1)/2=(105–1)/2=52. Квадраты чисел 52 и 53 являются границами полуконтура.
&nbsp &nbsp &nbsp &nbsp &nbsp Длина контура L(k_п)=2•105–2=208=8•k_п, откуда k_п=208/8=26. Меньший (левый) полуконтур имеет длину m(k_п)=L(k_п)–М(k_п)=208–105=103, является простым числом.
&nbsp &nbsp &nbsp &nbsp &nbsp Находим через k_п границы предельного контура: левая Г_л(k_п)=(2k_п–1)²=(2•26–1)²=51²=2601 и правая Г_п(k_п)=(2k_п+1)²=(2•26+1)²=53²=2809. Длина контура через его границы определяется выражением L(k_п)=Г_п(k_п)–Г_л(k_п)=2809–2601=208=8k_п.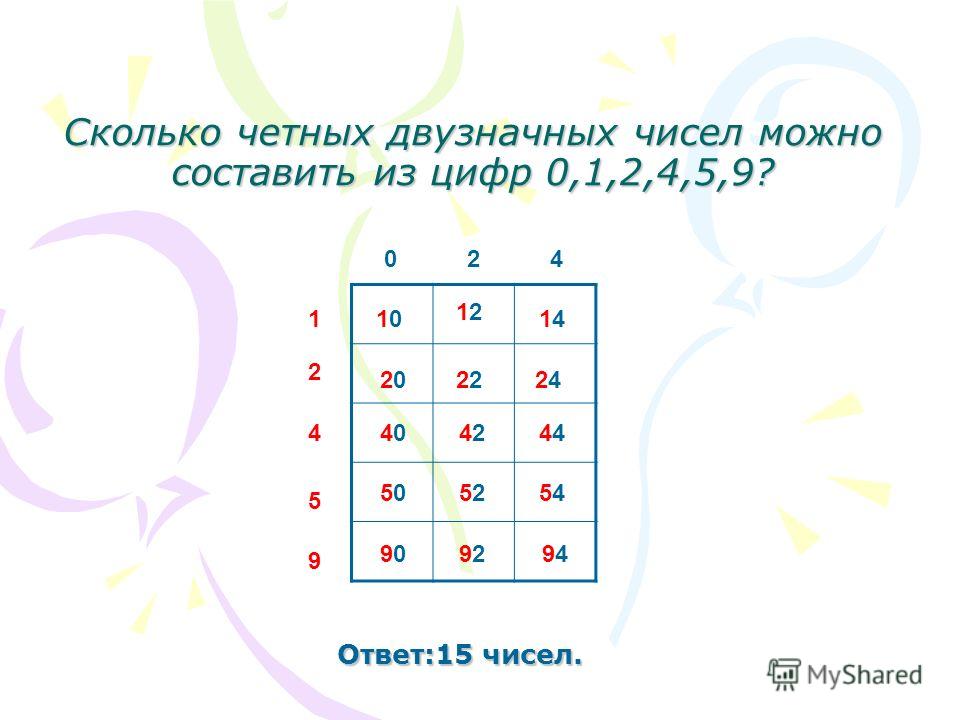
&nbsp &nbsp &nbsp &nbsp &nbsp Поскольку заданное сннч N=105 является полуконтуром в предельном контуре, то будем полагать, что ему соответствует лишь половина номера предельного контура, т.е. k_п(N)/2=26/2=13.

&nbsp &nbsp &nbsp &nbsp &nbsp Инвариант числа. Характеристику числа N в форме k_п(N)/2 назовем инвариантом числа N, а дальше покажем, почему выбрано такое название. Инвариант может быть целым или дробным числом в зависимости от четности номера k_п предельного контура.

&nbsp &nbsp &nbsp &nbsp &nbsp Интервалы НРЧ для числа N. Далее рассмотрим возможности представления сннч N=105 разностями других пар квадратов разной четности. Число 105, как впрочем, и любое другое нечетное число можно представить суммой нечетного количества меньших смежных нечетных чисел. Полезность такого представления N следует из того, что границы всех нечетных чисел в НРЧ – квадраты, следовательно, и непрерывный интервал, представляющий N=105 из смежных нечетных чисел, будет иметь на границах квадраты. Количество слагаемых в сумме должно быть нечетным числом.

Допустим, что таких слагаемых будет три. Очевидно, 105:3=35 и первое слагаемое будет равно 35–2=33, второе 35, а третье 35+2=37. Числа 33, 35, 37 образуют непрерывную последовательность нечетных смежных чисел, а 35 и 37 являются полуконтурами одного контура, так как их сумма 35+37=72 кратна 8. Этот контур имеет номер k=72/8=9. Число 33 принадлежит другому предшествующему контуру с номером k=8 и в нем является правым, т.е. большим. Этому числу 33 соответствует половина номера его контура, т.е. k/2=8/2=4. Интервалу из трех примыкающих друг к другу нечетных чисел длиной в 105 ячеек в НРЧ соответствует сумма номеров контуров в виде k_п(N)/2=8/2+9=4+9=13.
Для этого интервала определим границы. Большая граница интервала совпадает с правой границей большего контура с номером k=9, т. е. Г_п(k)=(2•k+1)²=(2•9+1)²=19²=x₁²=361. Меньшая граница интервала совпадает с левой границей меньшего из трех полуконтура, т.е. числа 33, находящегося в контуре с номером k=8, его граница – это четный квадрат удвоенного номера контура Г_ч(k)=Г_л(k)=(2k)²=(2•8)²=x₀²=256. Проверка: N=Г_п(9)–Г_л(8/2)=361–256=105.
Теперь для N=105 можем записать факторы N=x₁²–x₀²=(19+16)(19–16)=35•3=105.
Пусть представление N имеет полуконтурами в сумме пять нечетных слагаемых. Очевидно, 105:5=21 и первое слагаемое будет равно 21–4=17, второе 21–2=19, третье 21, четвертое 21+2=23 и, наконец, пятое 21+4=25. Числа 17, 19, 21, 23, 25 образуют непрерывную последовательность нечетных смежных чисел, а 19, 21 и 23, 25 из них являются полуконтурами двух смежных контуров, так как их сумма 19+21=40=5•8 и 23+25=48=6•8 кратна 8. Эти контуры имеют номера k=40/8=5 и k=48/8=6.
Число 17 является большим (правым) полуконтуром предшествующего контура с номером k=(15+17)/8=4. Этому числу соответствует половина номера меньшего контура k/2=4/2=2. Интервалу из пяти примыкающих друг к другу нечетных чисел длиной в 105 ячеек в НРЧ соответствует сумма номеров контуров k_п(N)/2=4/2+5+6=2+5+6=13.
Для этого интервала определим границы. Большая граница интервала совпадает с правой границей большего контура с номером k=6, т.е. Г_п(k)=(2•k+1)²=(2•6+1)²=13²=x₁²=169. Меньшая левая граница интервала совпадает с левой границей меньшего полуконтура, т.е. числа 17, находящегося в контуре с номером k=4. Меньшая граница – это четный квадрат удвоенного номера контура Г_ч(k)=Г_л(k)=(2k)²=(2•4)²=x₀²=64.Проверка на разность квадратов: N=Г_п(6)–Г_ч(4)=169–64=105. Теперь для N=105 можем записать факторы N=x₁²–x₀²=(13+8)(13–8)=21•5=105.
Пусть слагаемых в представляющей число N сумме будет семь. Очевидно, 105:7=15 и первое слагаемое будет равно 15–6=9, второе 15–4=11, третье 15–2=13, четвертое 15, пятое 15+2=17, шестое 15+4=19 и, наконец, седьмое 15+6=21. Числа 9, 11, 13, 15, 17, 19, 21 образуют непрерывную последовательность нечетных смежных чисел, а 11, 13; 15, 17 и 19, 21 являются полуконтурами трех смежных контуров, так как их суммы 11+13=24=3•8; 15+17=32=4•8 и 19+21=40=5•8 кратны 8. Эти контуры имеют номера k=24/8=3, k=32/8=4 и k=40/8=5.
Число 9 является большим (правым) полуконтуром предшествующего контура с номером k=(7+9)/8=2. Этому числу соответствует половина номера меньшего контура, т. е. k/2=2/2=1. Интервалу из семи примыкающих друг к другу нечетных чисел длиной в 105 ячеек в НРЧ соответствует сумма номеров контуров k_п(N)/2=2/2+3+4+5=1+3+4+5=13.
Для этого интервала определим границы. Большая граница интервала совпадает с правой границей большего контура с номером k=5, т.е. Г_п(k)=(2•k+1)²=(2•5+1)²=11²=x₁²=121. Меньшая граница интервала совпадает с левой границей меньшего полуконтура, т.е. числа 9, находящегося в контуре с номером k=2, это четный квадрат удвоенного номера контура Г_ч(k)=Г_л(k)=(2k)²=(2•2)²=x₀²=16.Проверка: N=Г_п(5)–Г_ч(2)=121–16=105.
Теперь для N=105 можем записать факторы N=x₁²–x₀²=(11+4)(11–4)=15•7=105.

&nbsp &nbsp &nbsp &nbsp &nbsp Рассмотренный пример показывает, что для числа N=105 существуют четыре пары квадратов разной четности, расстояние в НРЧ между которыми равно 105. Каждая из найденных пар квадратов позволяет решить задачу факторизации сннч N=105, исключая предельную пару – она дает тривиальное разложение на множители.

&nbsp &nbsp &nbsp &nbsp &nbsp Остается открытым очень важный вопрос, где брать, как получать для произвольного числа N пары (x_о², x₁²) квадратов?

&nbsp &nbsp &nbsp &nbsp &nbsp Анализ результатов примера 2 показывает, что разные пары квадратов (x_оi², x_1i²), i=1(1)4, получаются при разных представлениях инвариантаk_п(N)/2=13 в виде суммы с разным числом слагаемых. Сами такие суммы можно рассматривать как разбиения числа 13 специального вида. Все слагаемые суммы представляют собой отрезок НРЧ, в котором одно из крайних слагаемых в сумму включается лишь своей половиной. Определение такого слагаемого диктуется принадлежностью числа N к классу левых или правых нечетных чисел.

Если N – левое, то половина берется от большего слагаемого:

N=183 – левое нечетное, 183≡3(mod4), половина берется от большего слагаемого в представлении инварианта суммой k_п(183)/2=23=15+16/2; инвариант целое число;
N=203 – левое нечетное, 203≡3(mod4), половина берется от большего слагаемого в представлении инварианта суммой k_п(203)/2=25.5=6+7+8+9/2; инвариант не целое число;

Если N – правое, то половина берется от меньшего слагаемого:

N=213 – правое нечетное, 213≡1(mod4), половина берется от меньшего слагаемого в представлении инварианта суммой k_п(213)/2=26.5=17/2+18; инвариант не целое число;
N=217 – правое нечетное, 217≡1(mod4), половина берется от меньшего слагаемого в представлении инварианта суммой k_п(217)/2=27=6/2+7+8+9; инвариант целое число;

Таким образом, из рассмотренных фактов следует алгоритм решения задачи факторизации чисел:

Для заданного сннч N найти инвариант k_n/2.
Инвариант представить разбиением специального вида k_n/2=a+(a+1)+(a+2)+…+(a+t-1)+k_д/2, где k_д – дополнительный номер крайнего контура, левый или правый.
Для крайних слагаемых вычислить границы: левую Г_л=x₀² и правую Г_п=x₁².
Разность границ представить произведением скобок N=x₁²–x₀²=(x₁+x₀)(x₁–x₀)=pq.

Рассмотренный материал позволяет сделать следующие выводы.

Модель составного нечетного натурального числа, представляемого в понятиях контуров – полуконтуров НРЧ позволяет установить инвариант такого числа, как функцию номеров представляющих число контуров. Инвариант k_п(N)/2 сохраняет значение независимо от того разностью какой пары квадратов ( при наличии нескольких пар квадратов ) представляется сннч N=x_i1²–x_i0², i=1(1)t, где t – число представляющих пар. N=105=x_i1²–x_i0²=53²–52²=19²–16²=13²–8²=11²–4²
Значение инварианта устанавливается элементарной обработкой заданного числа N при установлении номера предельного контура. Инвариант может быть как целым, так и дробным числом. Относительно предельного контура сформулированы и доказаны теоремы, которые в посте не приводятся, но используются.
Предлагаемая модель НРЧ в терминах и понятиях контуров – полуконтуров открывает возможность формулирования и исследования задачи факторизации нечетных чисел за приемлемое для практических приложений время.

Гадание по часам онлайн. На что обращать внимание. Четные и нечетные числа

Чтобы гадание правдиво рассказало о будущем, необходимо соблюдать несколько несложных правил:

Предсказание лучшего всего проводить на старинных часах по циферблату с наличием часовой и минутной стрелок. Однако в современном мире люди чаще пользуются электронными ходиками. Они также подойдут для гадания.
Если человеку важно узнать ближайшие перспективы будущего, важно обратить внимание на день недели. Лучше всего проводить предсказание во вторник и субботу. Гадание в эти дни будет наиболее точным.
Нельзя специально стараться подгадать нужное время. В таком случае полученная информация не будет иметь никакого смысла и силы. Лучше просто присматриваться и стараться запоминать комбинации цифр, которые чаще всего попадаются на глаза.

Кроме дня недели, следует обращать внимание на то, в какое время суток встречаются комбинации, так как значения гадания могут совершенно отличаться друг от друга:

С утра – подсказывает о нежелательных в этот день действиях.
Днем гадание по часам подскажет о необходимых изменениях в отношениях с родными людьми, хорошими друзьями, коллегами во избежание возможных конфликтов.
Вечером предсказание поможет узнать о личной жизни, есть ли будущее у этих отношений.

Ночью люди могут узнать информацию о возможных путях достижения успеха в профессиональном плане.

Значение цифр в нашей жизни преуменьшать не стоит. Наука нумерология по времени рождения может предсказать характер человека и основные моменты его будущей жизни. И в повседневности числа сопровождают нас всегда – от появления на свет до самой смерти.

Нумерологи утверждают, что когда человек видит на часах похожие цифры (они могут быть двойными, повторяющимися или парными) – это неспроста. Таким образом он получает послания от своего ангела-хранителя. И пренебрегать информацией, идущей к нам из тонкого мира, по меньшей мере неразумно. Нумерология времени способна открыть каждому из нас глаза на неочевидные, но от того не менее важные вещи.

На что обращать внимание

Следует внимательно приглядеться ко всем встречающимся на нашем пути повторам цифр – на табло часов или экране монитора, на номерных знаках встречных машин или на рекламных стендах. Нумерология по дате времени дает возможность читать послания наших невидимых защитников – ангелов-хранителей, которые беспокоятся о нас и норовят предупредить о надвигающихся неприятностях. Или же наоборот – оповестить о грядущем радостном событии, настроить на нужный лад, подсказать правильное решение в сложной ситуации.

Наш невидимый защитник

Считается, что каждый из нас обладает своим собственным ангелом-хранителем. Он дается нам при рождении, и задача его – сопровождать и охранять нас на протяжении всей жизни. Ангел-хранитель незримо стоит за плечом, отгоняет напасти, а порой и призывает на помощь силы, более влиятельные.

Каждый день наш защитник пытается “подбросить” нам какую-то немаловажную информацию. Чаще всего мы не слышим этих подсказок, но порой они звучат вполне явственно и прорываются к нам в виде вещих снов, интуитивных озарений, внезапных звонков знакомых людей, кстати мелькнувшей строчки в газете или услышанной фразы.

Это правда работает?

Люди с развитой интуицией научились считывать эти подсказки и достаточно верно интерпретировать их. Другие же, сугубые материалисты, упрямо отрицают наличие во всём этом смысла, не считают нужным прислушаться к внутреннему голосу и списывают всё на случайное совпадение. А зря! Ведь задача ангела-хранителя – помогать нам. Когда мы просим вашего небесного защитника о защите и поддержке, чаще всего результат бывает налицо.

Конечно, если речь не идет о плохом деле. Причинять зло другому человеку, наносить вред, делать прочие нехорошие вещи упрашивать ангела-хранителя не стоит – тут он вам не помощник. Но в “мирных целях” или о помощи в безвыходной ситуации следует просить его от души, с чистым сердцем, и тогда желаемое почти наверняка исполнится.

Чего можно ожидать

Не следует рассчитывать на моментальное исполнение желания – нашему небесному защитнику всегда виднее, в какой момент оно должно сбыться. Запаситесь терпением – и в конечном итоге всё сложится, как надо.

Чтобы заручиться поддержкой и расположением своего хранителя, следует общаться к нему почаще и всегда произносить слова благодарности за оказанную помощь. Это можно делать и не вслух, довольно мысленно проговаривать то, что, по вашему мнению, следует донести. Приступая к важному делу, попросите ангела не покидать вас и направлять в нужное русло.

Как нам общаться с ними?

Ангелы – нежные существа, они не выносят скверного поведения подопечного, грубости, нецензурщины, дурных привычек, запаха алкоголя. Все эти негативные проявления человека заставляют его болеть и страдать от отрицательной энергетики.

Каким же образом ангел-хранитель может стараться передать нам информацию из тонкого мира? Очень часто для этого используются самые обычные цифры, которые мы ежедневно видим вокруг себя. А точнее, их комбинации. Нумерология по времени на часах способна делать далеко идущие выводы. Если при взгляде на циферблат вы регулярно замечаете одно и то же сочетание, например, три или четыре одинаковые цифры подряд, парные либо симметричные, то следует понять: случайных совпадений не бывает.

Когда цифры выстроились в ряд.

Попробуйте выяснить, что всё это означает. О чём вас хотят предупредить? Какое событие из будущего скрывается за данным сочетанием?

Рассмотрим вначале, как нумерология времени интерпретирует повторяющиеся цифры. При этом следует знать, что чем длиннее ряд одинаковых цифр (две подряд, три или четыре), тем важнее послание, и тем настойчивее ангел-хранитель пытается донести до вас определённую информацию. Итак, о чем скажут нам конкретные цифры?

Ангельская нумерология времени – от единицы до девятки

Если в вашей жизни часто повторяется цифра 1, это прямой намек на то, что пора уделить внимание собственному внутреннему миру, заняться саморазвитием. Повторяющиеся двойки говорят о различиях в характерах между вами и вашим избранником. Следует попытаться подкорректировать отношения или при необходимости найти разумный компромисс.

Цифра 3 говорит о том, что у вас проблемы с самоопределением. Пора вспомнить случившиеся в прошлом события, разобраться с текущим моментом и утвердить планы на будущее. Важно настроиться на четкую цель, чтобы не допустить тех ошибок, от которых ваш небесный защитник пытается предостеречь.

Когда речь идёт о четверке, это намек на чрезмерную погруженность в сферу карьеры и работы. Разумеется, трудолюбие – замечательное качество, но следует уделять внимание и прочим сторонам собственной жизни. Возможно, вам требуется отдых и забота о здоровье.

Регулярно попадающиеся на глаза пятёрки говорят о зачастую необоснованной жажде риска и приключений. Похоже, настала пора воспринимать жизнь более серьезно.

Шестерка символизирует гармонию и существование в мире с себе подобными. Вам следует упорядочить отношения с окружающими.

Семерка почти у всех народов несет в себе мистических колорит. Нумерология времени утверждает: тот, кто часто сталкивается с этой цифрой, возможно, обладает способностью к ясновидению и очень развитой интуицией. Такой человек в состоянии постичь многие тайны вселенной и серьезно влиять на окружающих.

Восьмерка – символ бесконечности. Эта цифра скажет о том, что нельзя терять время, его потом не вернешь. Уже сейчас следует предпринять конкретные шаги для того, чтобы будущее стало спокойным и счастливым.

Если же часы часто показывают нам цифру 9, следует набраться твердости, перестать бросать незавершённые дела и огорчаться из-за пустяков.

Сигналом личного ангела-хранителя может быть такое время на циферблате часов, как 11:11 или 12:12

Что означают определенные сочетания цифр?

Ангельская нумерология: время на часах

00.00 — если желание загадывалось с чистым сердцем, ему суждено сбыться.

01.01 — вас ожидает хорошее известие со стороны мужчины.

01.10 — к сожалению, затеянное вами кончится ничем.

01.11 — не спешите в этот день отвергать любые предложения.

02.02 — вас могут пригласить в ресторан или в гости.

02.20 — следите за речью, не поддавайтесь раздражению.

02.22 — небеса приоткроют вам какую-то тайну.

03.03 — вас ожидает новая любовь.

03. 30 — ваши чувства не взаимны.

03.33 — впереди – удача и счастье.

04.04 — попробуйте взглянуть на текущие дела с другой точки зрения.

04.40 — удача отвернулась от вас – похоже, это не ваш день.

04.44 — на работе навлечете гнев начальника.

05.05 — против вас плетутся интриги, враги затеяли нечестную игру.

05.50 — бойтесь огненной стихии, а также воды.

05.55 — скоро вам повезет встретить мудрого человека.

06.06 — впереди – женитьба или замужество.

07.07 — остерегайтесь человека в военной форме.

08.08 — можно ожидать карьерного взлета.

09.09 —берегитесь кражи, позаботьтесь о собственном кошельке или сумочке.

10.01 — вы познакомитесь со значительным человеком (мужчиной), обладающим серьезным влиянием.

10.10 — время приходит.

11.11 — вам грозит зависимость от кого-либо (или чего-либо).

12.12 — ждите удачу в делах сердечных.

12.21 — встреча с незнакомцем, новые отношения.

13.13 — соперники могут напакостить.

13.31 — наконец-то добьетесь желаемого.

14.14 — любовь захватит вас целиком.

14.41 — возможна крайне неприятная ситуация.

15.15 — мудрый человек даст совет, которому стоит последовать.

15.51 — вас ожидает короткий и яркий роман.

16.16 — берегите себя в пути.

17.17 — угроза от уличных хулиганов.

18.18 — в дороге соблюдайте осторожность.

19.19 — в делах можно рассчитывать на успех.

20.02 — поссоритесь с близким вам человеком.

20.20 — в семье возможны скандалы.

21.12 — в скором будущем вас ожидает новый проект или рождение малыша.

21.21 — яркое романтическое увлечение.

22.22 — вероятность нового знакомства, встречи.

23.23 — речь идет об опасной связи.

23.32 — поберегите здоровье, возможны проблемы.

Возможно, вы считаете, что нумерология времени – типичная лженаука, что-то вроде несерьезного развлечения для скучающих домохозяек. Но попробуйте все же приглядеться к якобы “случайным” совпадениям и проанализировать последующие за этим события. Быть может, вашему мнению суждено измениться!

С очень древних времен люди всматриваются в свое будущее и анализируют прошлое, его связь с настоящим и с различными событиями, в надежде найти закономерность, связь, которая поможет ориентироваться в будущем и менять свою судьбу по желанию. Как говорится: информирован – значит вооружен, соответственно человек, знающий своё будущее – готов к нему, так или иначе он его ждет, и оно не станет для него роковой неожиданностью.

Из покон веков люди обращаются за информацией о себе и будущем к специалистам в этой области – колдунам магам и звездочетам, за любой имеющейся информацией, любой ниточкой, что укажет в будущее как путеводная звезда.

Порой нам не нужно обращаться к гадалкам или мы просто не можем физически к ним попасть, но ответ на важный вопрос необходим! В таком случае можно просто присмотреться к мелочам – , сны или же время на часах. Сегодня мы поговорим о последнем случае – гаданию по часам. Разные мастера своего дела предлагают различные способы гадания, мы собрали лучшие из них и представили Вам.

Внимание! Для наиболее точного результата стоит точно соблюдать последовательность действий, иначе результат может быть непредсказуем.

Гадание по часам – прекрасная возможность узнать о своем будущем, она появилась на свет ровно тогда же, когда и первые часы, но сегодня это проверенный годами метод, который заслуживает большого внимания.

Гадание на часах – одинаковые цифры

Гадание по часам предполагает трактовку одинаковых цифр, но магическое значение также имеют еще некоторые комбинации. Просто посмотрите на часы и узнайте, что сулит увиденная комбинация (конечно, если это сочетание чисел имеет магическое значение).

Гадание по часам – штука простая и многим привычная, и большинство людей даже как-то неосознанно, интуитивно загадывают желание, если видят на часах красивое число или одинаковые цифры. К примеру, 20:02, или 12:21. И правильно делают!

На самом деле, это не простое совпадение, это – очень тонкий момент, когда у человека действительно может всего на несколько мгновений установиться связь с высшими силами, а желание может осуществиться. Особенно у того, кто в гадание по часам верит!
К таким «совпадениям» нужно относиться внимательнее, чем к счастливым комбинациям, ведь в предостережении может содержаться и руководство к действию, рекомендации, позволяющие выйти из любого сложного положения. В любом случае, если вы посмотрели на часы и увидели повторяющуюся четную комбинацию, вам нужно задуматься: о чем именно высшие силы хотят вас предупредить, о каком испытании и каких трудностях говорят вам часы.
Но смысл кроется не только в совпадении чисел, но и в любой другой комбинации. В некоторых случаях, значение имеет какое-то одно число, которое постоянно попадается вам на глаза. Если вы постараетесь, то обязательно сможете вспомнить, хотя бы один момент из жизни, когда несколько раз подряд, глядя на часы, вы видели одну и туже цифру.
К примеру, вы несколько раз за день увидели минутную стрелку на отметке «12», вы можете не обратить на это никакого внимания, но если вам известны значения чисел, то вы сразу поймете, что высшие силы говорят вам о том, что в скором времени вам предстоит знакомство с интересным человеком, которое способно коренным образом изменить всю вашу жизнь.
Особое значение имеют также зеркальные отражение чисел, к примеру, если вы увидели на часах значение: 10:01, то это явный знак, и не стоит пропускать его, ведь зная о своем будущем, вы сможете упростить свою жизнь и не пропустить свой счастливый шанс.
Именно поэтому многие эзотерики крайне серьезно относятся к часам и гаданию по этому механизму.
Который час? Что сбудется?
Существует гадание по времени на часах, помимо простого загадывания желаний при виде одинаковых циферок. Есть особенные комбинации чисел, которые не только очень красивы и гармоничны, но и имеют особое магическое значение.
Это гадание получится на любых часах с электронным циферблатом – не только на наручных, но даже на мониторе компьютера. Узнайте, что вас ждет!
00:00 – если вы взглянули и увидели эти цифры, ровно в полночь, высшие силы предостерегают вас – день будет не самым удачным для новых начинаний. Не планируйте на этот день никаких новых проектов или смелых действий, если возможно, отложите это. Постарайтесь провести день спокойно и тихо.
3:33 – эта красивая комбинация троек очень удачна для того, кто ее увидел. Тройки говорят о том, что сегодня начатые вами дела непременно завершатся очень удачным образом, или же будут правильно и удачно развиваться.Сегодня можно начинать новые дела, строить смелые планы и делать решительные шаги. Это ваш день!
10:01 – комбинация, которую сложно не заметить. Если вы увидели на часиках 10:01, будьте уверены, сегодняшний день будет очень удачным во всем.Таким образом, высшие силы как бы подбадривают вас и подталкивают к смелым действиям – стройте свою судьбу, ничего не бойтесь, у вас все получится! Сегодня удача стоит на вашей стороне.
10:10 – еще одно счастливое утреннее совпадение. Эти цифры на часах указывают на удачу в рабочей и деловой сфере, так что, если вы увидели их, будьте смелее и решительнее! Все проекты будут развиваться отлично, а переговоры пройдут в вашу пользу.
11:11 – сегодня вам предстоит получать подарки от судьбы. Кстати, о материальных подарках со стороны близких людей тоже идет речь, потому что сегодня такое время, когда вам предстоит получить сюрпризы и приятные неожиданности. Вы будете приятно удивлены не один раз!
12:12 – это необычная комбинация, и нечасто именно ее приходится заметить. Если вам повезло, и на циферблате часов вы обнаружили 12:12, радуйтесь! Сегодня абсолютно все, за что вы ни возьметесь, будет идти наилучшим образом, все получится, никакие трудности вам мне помешают.
12:21 – тоже красивая комбинация из единиц и двоек, ее трудно пропустить, ведь что-то она должна означать! Разумеется, как и другие необычные и редкие комбинации, 12:21 – особенная.Это знак, что сегодня вам предстоит влюбиться, или же вы целый день проведете в романтический мыслях о ком-то. Возможно, сегодня вас ожидает очень романтичный сюрприз от любимого человека, свидание или приятное предложение.
14:41 – это удачная комбинация, которая может иметь несколько значений. К примеру, для молодых людей и незамужних девушек 14:41 означает любовные приключения, новые знакомства, флирт и все самое приятное, связанное с романтической сферой.Для людей же семейных и взрослых, цифры 14:41 сулят приятное общение, отдых, примирение в семье, гармоничный и спокойный день, полный радости.
15:15 – не самое удачное сочетание цифр. Это гадание говорит, что если на часах вы увидели 15:15, будьте осторожны сегодня – не рискуйте и не начинайте новых дел. Может случиться неприятный сюрприз или нежеланная встреча, старайтесь ко всему относиться максимально спокойно и мудро.
15:51 – напротив, хорошее сочетание. Комбинация 15:51 сулит вам приятный сюрприз и хороший вечер. Даже если этот день трудный и полный разных нежеланных событий, стрессов и неудач, знайте, что к вечеру все изменится в лучшую сторону.
20:02 – необычное число. Это не предсказание, а совет вам, если вы увидели 20:02 на часах, то будьте сдержаннее в этот вечер. Комбинация 20:02 состоит из двоек и нолей, и может сулить ссору с любимым или близким человеком. Держите эмоции под контролем, умейте промолчать.
21:12 – будет для вас успешным и принесет новую радость.
21:21 – предупреждение, будьте осторожны и взвешивайте свои поступки. Возможно, вы уже совершили ошибку, о которой придется жалеть – обдумайте это.
23:23 – Завтра вас ждет большая удача и радость. Засыпайте с хорошими мыслями!
Гадания по часам и цифрам – это то, что поможет вам ориентироваться в своей реальности, не забывать о том, что жить и действовать надо по совести, и избегать ошибок.
Дополнительные значения
Некоторые народы уверены, что счастливой комбинацией совпадение чисел на часах будет лишь та, в которой присутствуют только нечетные числа. Однако люди, проживающие на Востоке, полагали, что стоит опасаться чисел, в которых присутствует цифра 9, ведь она говорит о скорых изменениях в жизни. Но никто не может точно сказать, положительными они будут или отрицательными.
Также некоторые народы считают, что если в комбинации повторяется много четных, это говорит о том, что человек находится в опасной ситуации.
Четные цифры пытаются предупредить человека, что у них есть недоброжелатели, которые могут в скором будущем нанести урон. Это говорит о том, что стоит оградить себя от потенциальных врагов и на время «залечь на дно».
Правила проведения гадания с часами
В любых гаданиях, на бумаге, с монетами, на палочках, на картах Таро, есть свои правила, которых необходимо придерживаться для того, чтобы получить точный результат. Это – не исключение.
Помните, точный результат можно получить только во вторник и в четверг. Другие дни недели не несут особую ценность и любые совпадения чисел, которые вы увидели не в указанные дни, не несут логического значения.
Также не следует специально подбирать нужное время. Это будет всего лишь искусственное совпадение и не будет иметь никакой реальной силы.
Гадание по количеству часов в доме
Помимо распространенного ритуала, который позволяет узнать ваше будущее по одинаковым цифрам на электронных часах, есть еще это, менее распространенное гадание. Узнать энергетику дома и хозяина можно по тому, сколько в помещении находится часов.
Одни – дом наполнен любовью, пониманием, благополучием.
Двое – помещение сохраняет положительную энергетику, хозяева находятся в гармонии с собой.
Трое – хозяин дома очень прагматичный человек, реалист, который любит отстаивать свою правоту.
Четверо – в этом помещении мало тепла и любви.
Пять – хозяин дома любит гостей, он всегда дружелюбен, рад новым встречам и знакомствам.
Шесть – в этом доме тяжело расслабиться, везде спешка и суета, хозяин помещения возможно очень занятой и скандальный человек.
Семь – в помещении нет энергетики спокойствия и благополучия, хозяину дома необходимо наладить отношения со своими близкими людьми.
Восемь – также говорит об отсутствие энергетики комфорта и уюта. Хозяева дома обеспокоены мелкими хлопотами, мало времени уделяет друг другу.
Девять – в помещении царит атмосфера спокойствия и благополучия, здесь любой гость может чувствовать себя как дома.
Если в помещении более 9 часов, то для получения результата необходимо сложить цифры например: 14 = 1+4 = 5.
Если вы решили провести любое гадание, заранее настройтесь на положительный результат. Потому что, даже если цифры предупредят о чем-то негативном, это всего лишь руководство к тому, чтобы быть более осторожными, но не гарантия того, что случится что-либо плохое.
grimuar.ru/gadanie/gadanie-na-chasah.html
Гадание на электронных часах
Гадания сегодня разные и много примет, некоторые гадания пришли к нам с древности, некоторые мы сами приобрели в современном мире. Часы и время – это вечное, которое было всегда, возможно изначально и не было у людей часов, но так они определяли время по солнцу, но все равно множество гаданий и примет связано с часами. Но так как мы с вами живем в современном мире, то рассмотрим гадание по электронным часам, которые мы можем наблюдать не только в офисе или дома, но и в магазинах, на вокзалах, на улицах, в метро и т.д.
Очень много примет уже связано с цифрами и на электронных часах оно то и дело меняются, и каждый человек интуитивно смотри на время и видит разные цифры не случайно.
Доказано, что какие – то высшие силы пытаются донести до человека что-то важное, подсказать или предупредить его с помощью цифр. А электронные часы – это именно тот предмет, где цифры есть постоянно и постоянно они несут разную информацию.
Какие вы для себя делаете выводы, когда смотрите на электронные часы несколько раз в день и не обязательно на одни и те же и цифры попадают на глаза все время 12 или 48 ? Скорее всего, вы ответите на этот вопрос так: я вообще не замечаю этого, не придаю значения или не акцентирую на этом внимание.
А ведь напрасно это высшие силы пытаются вам что-то подсказать и предупредить. К примеру, те же 12 все время перед вашими глазами не просто говорят вам, а «кричат» о том, что вас ждет новое интересное знакомство, а цифра 48 – это уже предвещает бурный роман.
Но магическое значение по многим мнениям магов и экспертов имеют цифры зеркально отражающие т.е. это, к примеру, такие 12,21 или те которые повторяются 13:13, которые и напоминают электронные часы даже когда записаны. Поэтому гадание по электронным часам есть смысл изучать и применять каждый день для того чтобы знать что в ближайшем будущем нас ждет.
Единственное вам нужно учитывать два всего лишь простых правила, для того, чтобы гадания были правдивыми и действительно исполнялись. Если их не учитывать, то гадания не будут правдивыми и вы вскоре скажите, что гадание по электронным часам – это ерунда, поэтому соблюдайте правила и убедитесь сами на личном опыте, что гадание действительно правдивое и действительно говорит нам правду.
Итак, правило номер один. Вы можете прибегать к помощи электронных часов и их цифр только два раза в неделю – это вторник и четверг, когда цифры более всего настроен на то, чтобы говорить правду.
Правило номер два. Не нужно специально подгадывать время или мухлевать, так как врятли специально что-то получиться и часы вам скажут правду, только случайно увиденные цифры парные или одинаковые могут правду на будущее время тебе напророчить.
Когда увидели те самые цифры, смотрите интерпретацию на нашем сайте и открывайте для себя завесу будущего.
Но не забывайте два заветных правила, только интуитивный взгляд может сказать вам правду и посоветовать, то чего нужно опасаться или наоборот что хорошее вас ждет.
Интерпретация значений цифр, гадания по электронным часам.

00.00 – если ваше желание идет от чистого сердце без злых помыслов оно обязательно сбудется
01.01 – ожидай хорошей новости от мужчины
01.10 – к сожаленью, то дело, которое ты начала не принесет желаемого результата
01.11 – звезды советую не отказываться ни от каких-либо предложений сегодня
02. 02 – тебя ждет приглашение или в клуб или просто в гости
02.20 – предостережение для тебя: следи за тем, что ты говоришь, не раздражайся
02.22 – тебе откроется секрет или тайна
03.03 – к тебе спешит любовь на своих крыльях, открой ей двери
03.30 – к сожалению, если твое желание связано с переменами в жизни, оно на данный момент не исполниться
03.33 – счастье и удача у тебя на пороге
04.04 – попытайся посмотреть на сложившуюся ситуацию с другой стороны
04.40 – это не твой день. Фортуна не на твоей стороне
04.44 – от начальства тебе попадет
05.05 – враги что-то замыслили против тебя
05.50 – бойся воды и огня
05.55 – скоро ждет тебя встреча с умным человеком
06.06 – скоро свадьба
07.07 – относись осторожно к людям в военной форме
08.08 – карьерный взлет
09.09 – береги деньги и сумочку
10.01 – тебя ждет знакомство с мужчиной очень влиятельным
10. 10 – твое время наступает
11.11 – будешь зависима от кого-то или же чего-то
12.12 – тебя ждет большой успех в любви.
12.21 – тебя ждет знакомство с красивой девушкой
13.13 -соперники будь осторожней
13.31 – наконец то ты получишь, то чего долго хотела
14.14 – балом твоим правит любовь
14.41 – тебя ждет неприятная ситуация
15.15 – послушай совет умного человека
15.51 – тебя ждет короткий но бурный роман
16.16 – осторожней на дороге
17.17 – осторожней на улице могут быть хулиганы
18.18 – на дороге осторожней
19.19 -в делах тебя ждет успех
20.02 – ссора с человеком, который тебе дорог
20.20 – в твоей семье ссора
21.12 – у тебя родиться в голове новый проект или же эти цифры предвещают рождение ребенка
21.21 – роман бурный страстей
22.22 – новое знакомство.
23.23 – у тебя может быть опасная связь.
23.32 – со здоровьем могут возникнуть проблемы.

Как только люди создали настенные и наручные циферблаты, гадание по цифрам на часах стало пользоваться популярностью. Самой большой магической силой наделены одинаковые и зеркальные числа. Каждая комбинация является маленьким предсказанием.

Суть ворожбы

Узнать будущее можно не только благодаря картам Таро и . Вы можете заниматься ворожбой, не привязываясь к лунному циклу.

Цифры, которые вы видите на циферблатах часов, являются не только констатацией реального времени, но и подсказкой судьбы.

Относясь к необычным цифровым значениям как к совпадению, вы не разгадаете послание . Современное гадание на циферблате отличается высокой информативностью и не требует от вас сложной подготовки.

Вы можете проигнорировать часто повторяющуюся комбинацию чисел и , но с помощью гадания вы узнаете: такое сочетание сулит вам знакомство с харизматичным и богатым поклонником.

Увидев одинаковые значения чисел () на часовой и минутной стрелке, вы должны внимательно проанализировать собственную жизнь. В вашу судьбу стучатся важные открытия или перемены.

Проводя гадание по наручным часам, помните, что значение одинаковых чисел может быть таким:

вам предстоит разочароваться в своем супруге или в ком-то из близких друзей, но это событие освободит вас от возможных потерь и потрясений в будущем;
наступает удачное время для поиска своей половинки;
ваши таланты раскроются на полную силу;
благодаря счастливому совпадению, вы получите престижную должность;
удвоение чисел и «10» сообщает, что вам необходимо проявить упорство, чтобы выйти на благоприятную полосу жизни.

Зеркальные комбинации цифровых значений ( :41) нередко указывают, что вы неправильно видите ситуацию. Они сообщают о невозможности решить проблему привычным для вас способом.

Правила гадания по часам

Есть два вида гадания по часам.

Спонтанная ворожба. Посмотрев на часы, вы случайно увидели одинаковые значения на часовой и минутной стрелке.
Запланированное гадание. В начале дня сформулируйте вопрос, который больше всего вас тревожит. Вы можете спросить: «Будем ли мы с (таким-то парнем) встречаться?». В течение дня смотрите на часы как обычно. Заметив зеркальные цифры или одинаковую числовую комбинацию, смотрите в толкование.

Правила ворожбы:

наиболее удачные дни для гадания по времени – вторник и четверг;
незамужние барышни и одинокие дамы могут заниматься ворожбой в пятницу;
если вы доверили электронным часикам миссию прорицателя, позаботьтесь, чтобы они выглядели презентабельно – наличие царапин на циферблате недопустимо;
не стоит навязывать свою волю и специально смотреть на циферблат по несколько раз, чтобы получить нужное значение, в таком случае правдивых предсказаний можете не ждать;
откажитесь от идеи гадать, когда вы расстроены или пьяны;
не рассказывайте никому о магических таинствах.

Ворожба на разных часах

Не имеет значения, по каким часам вы будете гадать: по электронным или по механическим. Главное, чтобы техника была исправной. Гадание по электронным часам удобно для путешественников. Где бы вы ни находились, вы сможете уделить несколько секунд, чтобы посмотреть на циферблат.

Еще один нюанс: благодаря светящемуся циферблату электронные часы больше подходят для ночной ворожбы, чем механические. Желая знать, что ожидает вас в пункте назначения, воспользуйтесь таким вариантом гадания. Когда вы будете ехать в поезде или лететь на самолете, среди ночи посмотрите, что показывают часы.

Числа и на минутной стрелке предостерегают: вам предстоит встреча с хитрыми людьми. Не исключено, что вас попытаются втянуть в нечестную сделку. Хорошим знаком являются числа и 41. Ваша поездка будет благополучной, и вы вернетесь домой с ценным приобретением.

Если верить примете, для гадания можно использовать только собственные часы, которые никто, кроме вас, не носил.

Существует старинный способ узнать ближайшее будущее своей семьи. Лучший период для ворожбы – первые 20 дней после Нового года. В четверг посмотрите время на настенных часах. Увидев на минутной стрелке число 55, 15 или 31, готовьтесь к позитивным событиям: рождению ребенка, улучшению жилищных условий. Если вам встретится повторяющееся число , вам стоит приложить усилия для реализации в профессиональной сфере.

Значения распространенных комбинаций

Колоссальным магическим смыслом наделены 5 комбинаций.

00:00. Сочетание говорит, что вскоре может исполниться ваша заветная мечта. Чтобы осуществиться, ваше желание должно быть добрым. Если вы захотите причинить вред своим коллегам или сопернице, двойное сочетание сыграет против вас. Все попытки повысить свою значимость за счет других, обернутся проигрышем.

11:11. Тревожное предзнаменование. Не относитесь к появлению 4 единиц на циферблате, как к совпадению. Такая комбинация предупреждает: в будущем вы попадете в зависимость от влиятельных людей (богатых родственников, начальника или непорядочного возлюбленного). Не позволяйте втянуть себя в финансовые авантюры. Второй вариант толкования: вас ожидает болезнь. Иногда двукратное повторение цифры «11» показывает, что гадающая особа попала в плен своих пагубных пристрастий (игромании, курения).

Благоприятный знак. Одиноким парням и девушкам он предвещает встречу с половинкой. Супругам, чьи отношения проходят проверку бытовыми проблемами, повторение числа 12 сулит возрождение любви и страсти. Родителям, которые переживают за детей-подростков, эта комбинация обещает: все трудности и недоразумения унесет река времени. Главное, не навязывать младшему поколению свои взгляды на жизнь.

14:14. Судьба приготовила гадающей особе щедрый подарок – любовь. Если в этот момент избранник не отвечает вам взаимностью, вскоре в его сердце вспыхнет влюбленность. Одно из значений цифры «14» – стабильность, устойчивость. Чтобы новая любовь приносила вам радость, не спешите менять себя в угоду страсти.

22:22. Увидев эти значения, ждите встречи с необычной и яркой личностью, которая изменит вашу жизнь. На вашем пути повстречается человек, который поможет вам построить головокружительную карьеру. Вместе с влиятельным другом (коллегой) вам суждено сделать важные открытия.

Другие цифровые сочетания

Выполняя гадание по любым часам, по одинаковым цифрам можно узнать многое, но будьте готовы к неожиданностям. Ответ Высших Сил покажется вам неправильным или слишком запутанным. Все, что вам необходимо делать – принять к сведению информацию, полученную в результате гадания. В этих цифровых комбинациях скрывается точное предсказание:

01:01 – девушкам и женщинам эта комбинация обещает головокружительный роман, для представителей сильного пола в этом значении закодирован иной смысл – приятель или бывший сослуживец, живущий в другом городе или за границей, предложит вам прибыльный проект;

02:02 – если вы увидели это сочетание чисел, ждите выгодного предложения – оно может поступить от вашего руководства или от старого друга;
10:10 – эта комбинация чисел призывает вас мобилизовать свои силы, если вы хотите добиться успехов в работе, проявите настойчивость и смекалку;
13:13 – вскоре у вас появится соперник;
17:17 – проявите осторожность, вам предстоит провести некоторое время в обществе завистливых или агрессивных людей – чтобы не навлечь на себя беду, оградите себя от злобного окружения;
18:18 – если вы гадаете по часам, эта комбинация вас не обрадует, она предупреждает вас о возможной автокатастрофе – постарайтесь реже пользоваться личным автомобилем и общественным транспортом;
19:19 – вам суждено стать любимцем Фортуны, во всех начинаниях вас ожидает успех;
21:21 – судьба предсказывает вам начало новой любви, у вашего романа будет много шансов перерасти в счастливый брак;
23:23 – знак, что вам необходимо пересмотреть свой круг общения, среди ваших знакомых есть злобный и коварный тип, не исключено, что он попытается навредить вашей репутации.

Приступать к повторному гаданию по часам можно через неделю после первого сеанса ворожбы.

Четные и нечетные числа

В славянской магической традиции нечетным числам приписывалась роль удачливых символов. Числа , считались символами достатка, радости и любви. Повторение нечетного числа (55) сулит крупный выигрыш или новую денежную работу.

Единица символизирует активность, напор, здоровый риск. В сложных цифровых комбинациях (2121) нечетное число обещает избавление от проблем. Числа 51 и 31 можно назвать символами семейного счастья.

Увидеть четные числа на циферблате считалось дурным предзнаменованием. Некоторые люди уверены: цифры 2 и 4 зазывают беду в дом.

В наши дни отношение к числам изменилось. Четное может приносить удачу. Главное – в какой комбинации оно вам встретилось: число 23 предупреждает вас об опасности, а его зеркальное отражение (число 32) символизирует освобождение от проблем.

Неоднозначные толкования вызывает цифра . Во многих культурах она предсказывает бесповоротные изменения, жертвы ради достижения цели. Увидеть 9 или 19 на часах – значит, получить предсказание, что вскоре вам придется порвать с прежними привычками и связями и начать новую жизнь.

Подсказки для гадания Гадая по электронным часам, не забывайте записывать результаты в блокнот. Если в течение месяца вам несколько раз попалась на глаза одна и та же комбинация чисел, будьте внимательны. Гадание по часам сообщает о ваших дремлющих талантах или о скрытых проблемах.

В одном из увиденных вами цифровых значений может скрываться число или месяц вашего рождения. Если вы родились на свет 1 мая, это число на часах – послание вашего ангела. Вы слишком увлеклись достижением чужих целей и забыли о собственных планах.

Каждая единица времени несет в себе большое значение, но ворожба не является окончательным решением. Если вас не устраивает предсказание, не впадайте в уныние. Получив предупреждение о возможных опасностях, вы сможете повернуть ситуацию в свою пользу.

Самый простой и безопасный способ узнать будущее – гадание по времени на часах. Ориентируясь по числам, которые попадаются вам на глаза, вы можете избежать опасности и получить подсказку в интересующем вас вопросе.

Некоторые привычки детства остаются на всю жизнь. Мы можем быть трижды взрослыми и серьёзными, со своими семьями, карьерами и важными жизненными устремлениями… И при этом так же торопиться загадать желание, оказавшись между двумя тёзками. Или встретив на улице машину с приметным номером 777. Или увидев на табло электронных часов необычную комбинацию цифр. Впрочем, к чему стесняться? Это так замечательно и мило – сохранить в себе хоть кроху детской веры в чудеса! И потом, кто сказал, что она вредна? Если всей душой ждать от «удачных» циферок добра, они действительно работают!

Что означают одни и те же цифры или зеркальные числа на часах

Постоянно сменяя друг друга, спеша вперёд, светящиеся циферки наших электронных часов то и дело складываются в разнообразные комбинации. Чаще всего они ничем не примечательны. В самом деле, кого удивишь, например, указанным на табло временем 16:15? Но порой цифры складываются весьма интересным образом – 05:05, 12:12, 13:31. Ещё поразительнее, если они начинают попадаться на глаза не разово, а день за днём, словно пытаются обратить на себя внимание! Человек, далёкий от суеверий, и тот почувствует себя сбитым с толку. А любитель примет обязательно увидит в этом событии прямой намёк на грядущее и тут же попытается разгадать: чего ждать, как себя вести и как использовать обстоятельства себе на пользу.

00:00 – время загадывать любые желания, планировать перемены и начинать сначала то, что когда-то не получилось. Лишь бы вы действовали с чистым сердцем и поменьше думали о корысти.

Впрочем, есть прямо противоположная точка зрения, убеждающая: если на часах мелькнули четыре нуля, лучше в этот день ничего не планировать и новых проектов не начинать. Какому из толкований верить, решайте сами.

01:01 – появление этих цифр сулит хорошие новости и оставляет надежду на исполнение заветной мечты. Правда, считается, что эта комбинация отличается меньшей силой, чем предыдущая.

01:10 – к сожалению, «зеркальные» цифры не принесут удачи. Начатое дело либо захиреет, либо зайдёт в тупик, поэтому лучше немного повременить с ним.

01:11 – три единицы подряд обещают интересное предложение, которое вскоре вам поступит. Не оставляйте его без внимания!

02:02 – богатая на предсказания комбинация. Первое: судьба усиленно посылает вам знаки, которые нужно научиться видеть. Внимательнее смотрите по сторонам. Второе: если получите приглашение в гости или просьбу о помощи, не отказывайте. Результат будет неожиданным и приятным. Третье: не оставляйте без внимания здоровье, с ним возможны проблемы.

02:20 – воспользуйтесь зеркальным временем, чтобы взглянуть на себя со стороны. Кажется, вы слишком бурно реагируете на обстоятельства и людей, позволяя себе неоправданные вспышки гнева.

02:22 – три двойки подряд символизируют тайну, которая вам сегодня приоткроется.

Тройка – знак удачи

03:03 – Судьба ведёт вас самым прямым путём к счастью и любви. Если в данный момент вы заняты каким-то важным проектом, тройки обещают его успешное завершение и неплохие дивиденды в итоге.

03:30 – «зеркальная» пара из тройки и нуля, увы, не сулит удачу. В жизни намечается период застоя, а в чувствах – охлаждение.

03:33 – зато три тройки очень приятный знак, сулящий успехи, радостные события и настоящее счастье.

04:04 – если вам кажется, что вы зашли в тупик, просто оглядитесь по сторонам. Выход рядом, нужно лишь посмотреть на него под другим углом. Возможно, обстоятельства заставят вас изменить своё мнение по какому-либо вопросу. Не сопротивляйтесь и доверьтесь судьбе, она выведет вас на верный путь.

04:40 – зеркальный день, по традиции не обещает золотых гор. Ведите себя осторожнее, не планируйте серьёзных перемен в жизни. Но можете осмелиться на знакомство с симпатичным представителем противоположного пола, если представится возможность.

04:44 – появление трёх четвёрок предупреждает о конфликте с человеком, занимающим более высокое положение. Возможно, предстоит визит на ковёр к начальнику?

05:05 – недруги придут в движение, плетя заговоры против вас. Не волнуйтесь, их интриги не увенчаются успехом, так как день обещает быть благоприятным. Тем же, кто пока одинок, он может подарить встречу со своей будущей половинкой.

05:50 – опасайтесь несчастных случаев, связанных с водой и огнём.

05:55 – судьба пошлёт вам мудрого советчика, не отмахнитесь о него.

06:06 – в большинстве случаев эта цифра намекает на то, что вы уделяете слишком много внимания материальному, забывая о душе. Но некоторым две шестёрки рядышком предсказывают скорую свадьбу.

07:07 – круговорот событий захватит вас с головой. Если поблизости окажутся верные друзья, сообща вы горы свернёте и осуществите все мечты. Окружите себя недостойными людьми – увы, добра не ждите. И постарайтесь избежать столкновений с теми, кто носит форму, это может плохо кончиться.

08:08 – день располагает к трудовым подвигам, получению прибыли и продвижению вверх по карьерной лестнице. Но только если вы сумеете не поддаться на провокации злопыхателей и не ввяжетесь в конфликт.

09:09 – сочетание девяток и нулей предупреждает о потерях. Что бы это ни было – кошелёк, который ловко вытащит из вашей сумочки воришка, или завершившиеся разрывом отношения – примите случившееся спокойно. Всё, что вам действительно нужно, останется при вас.

Кто-то умудряется строить свою жизнь по показаниям часов!

10:01 – ждите знакомства с влиятельным человеком, вероятнее всего, мужчиной.

10:10 – удача и новые возможности у вас на пороге. Самое время для реализации давно вынашиваемых идей и планов.

11:11 – подсчитывая подарки судьбы, которые вам сегодня обещаны, не теряйте головы. Велик риск угодить в зависимость от нечистоплотного в моральном плане субъекта.

12:12 – удачный час и удачный день. Звёзды собираются устроить вам встречу с родственным по духу человеком! Не упустите шанс обрести друга, с которым можно будет разделить свои взгляды и убеждения. Впрочем, отчего только друга? Счастливая комбинация цифр предсказывает вам сегодня колоссальный успех у противоположного пола.

12:21 – знакомство с обаятельной женщиной. Дамы обретут интересную собеседницу, мужчины – надежду на увлекательный роман.

13:13 – если научитесь действовать рассудительно и держать эмоции под контролем, сумеете осуществить потаённое желание. Вы движетесь в верном направлении, но не забывайте о соперниках, которые не упустят случая подставить вам подножку. Будьте осмотрительнее.

13:31 – зеркальная комбинация тройки и единицы означает избавление от преград и конец периода застоя. Вы наконец-то обретёте то, что так жаждете получить.

14:14 – прагматичная четвёрка в компании единицы изменяет своим обычным принципам и советует вам поддаться новому романтичному чувству. Лёгкая влюблённость, огненная страсть или крепкий брачный союз – когда на часах эта удачная комбинация, возможно всё.

14:41 – следует вести себя осмотрительней, вам грозит несчастный случай, болезнь или другие неприятности.

15:15 – из неловкой ситуации поможет выбраться дельный совет опытного человека, возможно, родственника.

15:51 – готовьтесь потерять голову от любви.

16:16 – судьба постоянно подбрасывает вам возможности изменить то, чем вы недовольны в своей жизни. Но научиться видеть их вы сможете, лишь поработав над своими моральными качествами. Слегка приструните эгоизм, научитесь видеть проблемы других людей, и удача не обойдёт вас стороной. Тем, кто в этот день находится в пути, следует поберечься: возможны травмы или встреча с грабителями.

17:17 – ваш девиз на сегодня «Кто не рискует, тот не пьёт шампанского!» Однако не забывайте, что мудрый человек просчитывает все возможные варианты развития событий и успевает подстелить соломку в самых опасных местах. Рискуя, не забывайте о здравомыслии.

18:18 – две восьмёрки символизируют значительную финансовую поддержку или рост доходов. Но вместе с тем вы можете лишиться хорошего друга или пострадать в путешествии.

Что бы ни сулили часы, верьте в удачу

19:19 – двойственная комбинация. Одни толкователи считают тандем девятки и единицы несомненным знаком полосы везения в жизни, другие, наоборот, советуют собрать силы в кулак и стойко переждать неудачный период. Чтобы мрачные прогнозы гарантированно не сбылись, действуйте обдуманно. А лучше постарайтесь взять несколько дней отдыха от забот.

20:02 – зеркальные цифры предсказывает разлад с близкими…

20:20 – …да и прямая комбинация прогнозами не радует: вам грозят ссоры, дрязги и бурное выяснение отношений. Не идите на поводу у эмоций, даже если очень захочется!

21:12 – время обновления: новый образ, новое мировоззрение, новые интересные идеи в голове. Нацеленные на карьеру граждане начнут выдавать одну креативную мысль за другой, а занятые семьёй имеют все шансы на появление желанного малыша.

21:21 – удержать себя в разумных рамках будет сложно, ибо звёзды заготовили для вас незабываемое любовное приключение. Но придётся придерживать сердце в узде и почаще обращаться к разуму, иначе очень скоро вы будете горько сожалеть о своих действиях.

22:22 – осторожность, осторожность и ещё раз осторожность. Ведите себя осмотрительно, но не отказывайтесь от общения с новыми людьми. Именно в это непростое время вам дано заводить выгодные знакомства и находить настоящих друзей.

23:23 – отношения, недавно появившиеся в вашей жизни, несут с собой опасность. Обдумайте как следует, всё ли вас в них устраивает, а заодно поразмыслите над своими ошибками в общем. Чем скорее вы поймёте, в чём были неправы, тем быстрее начнёте двигаться к намеченным целям.

23:32 – следите за здоровьем.

Девичьи приметы: что обозначает одинаковое время для дам

Помимо всего перечисленного есть ещё одно, чисто женское поверье. Увидели на часах одинаковые цифры? Назовите имя мужчины, который вам нравится, и он перед вами не устоит. Даже если «магия чисел» подкачает, подействует ваше женское обаяние, подкреплённое верой в добрую примету. Как выглядит девушка, уверенная в своей неотразимости для желанного мужчины? Блеск в глазах, улыбка победительницы на губах, шаг летучий и чуть-чуть кошачий… Как говорила Верочка из «Служебного романа», мужчины такую женщину не пропускают! Кто знает, вдруг и сердце любимого пронзит стрела Амура?

Знатоки человеческой психики считают, что в появлении на часах одних и тех же необычных цифр виноваты мы сами. Подметив их раз, мы подсознательно начинаем бросать взгляды в сторону табло в нужное время и не очень-то отмечаем в памяти цифры, которые не «вписываются» в примету. Чистая психология и никакой мистики! А может быть, дело обстоит иначе. К примеру, для вас сочетание двойки и нуля означает что-то своё, не отмеченное традиционным толкованием. Если подсознание привлекло внимание именно к этому числу, не торопитесь шуршать листиками таблички в поисках ответа. Обратитесь к собственным ощущениям и интуиции. Что они говорят вам? О чём предупреждают? Ответ может оказаться очень ясным и очень неожиданным!

Что такое четные числа? Определение и примеры — 1 класс

Обзор

Четные числа — это суммы, которые могут быть точно равны , разделенным на на два . Вы всегда можете создать две равные группы из четного количества объектов!

Четные числа легко узнать, потому что они заканчиваются на…

0, 2, 4, 6 или 8

Взгляните на числовую таблицу ниже. Четные числа заштрихованы разными цветами.

Когда вы считаете только четные числа, начинающиеся с нуля, вы Считаете с пропуском на два . Как высоко вы можете сосчитать только четными числами? Вы можете использовать приведенную ниже числовую таблицу, чтобы помочь вам.

Мы очень часто используем четные числа. Например, при подсчете большого количества предметов, чтобы мы могли двигаться быстрее, считая по два за раз. Кроме того, нас окружает множество четных вещей: у бабочки 2 крыла, у автомобиля 4 колеса, у нас 10 пальцев, и это лишь некоторые из них.

Но как определяются четные числа? и каковы их основные свойства? Это то, что мы собираемся обнаружить.

Что такое четные числа?

Интуитивно мы думаем о четном числе как о числе, которое можно разделить на две равные части. Давайте представим группу морских животных где-то в глубинах океана… Прямо как на картинке!

Можем ли мы разделить группу рыб на две подгруппы одинакового размера? Да мы можем! Как на картинке ниже. Это означает, что 6 (количество рыб) равно 9.0005 четное число , потому что его можно разделить на две группы по 3 размера каждая.

А количество морских звезд? Это даже? Что ж, если мы разделим группу из 3 морских звезд на две подгруппы, мы всегда получим еще одну звезду в одной из подгрупп, как показано ниже. Таким образом, 3 не является четным числом, потому что его нельзя разделить на две равные части.

Другими словами, когда мы разделяем 3 морские звезды на две части, они кажутся «странными», потому что не выглядят гармоничными или сбалансированными. Так мы называем нечетные числа: они нечетные числа.

Кстати, 4 тоже четное число! Чтобы убедиться в этом, попробуйте разделить набор из 4 морских коньков на две равные части: как показано ниже, в каждой части по 2 морских конька.

Формально мы говорим, что целое число равно , если при делении на 2 мы получаем 0 в остатке. Или, что то же самое, целое число четно, если 2 — один из его множителей. Как в примере с океаном: 6 = 2 × 3 означает, что когда мы делим 6 на 2, мы получаем 3 как частное.

Это частное соответствует количеству рыб в каждой равной части. Кроме того, 4 = 2 × 2, то если мы разделим 4 на 2 части, то в каждой части будет по 2 элемента.

Мы знаем, что при делении целого числа на 2 возможно два остатка: 0 или 1. Что происходит, когда остаток равен 1? Ну, в таком случае мы говорим, что число нечетное. Другими словами, целое число является нечетным , если 2 не является одним из его множителей. Как то, что произошло с морскими звездами: 2 не является фактором 3, поэтому 3 нечетно, а не четно!

Другими четными числами являются, например, 10, 36 и 568, потому что 10 = 2 × 5, 36 = 2 × 18 и 568 = 2 × 284. Можем ли мы увидеть закономерность в этих выражениях? Давайте обсудим это дальше.

Как распознать четные числа?

Прежде всего, поскольку любое четное число имеет 2 в качестве одного из своих делителей, любое четное число имеет вид

, где k — целое число.

Посмотрите на примеры выше: 10 = 2 × 5, таким образом, k = 5; и 36 = 2 × 18, таким образом, k = 18 в этом случае. На самом деле мы получаем четное число для каждого значения k.

Например, если k = 25, то 50 = 2 × 25 четно. Кроме того, значение k может быть отрицательным; например, если k = -7, то -14 = 2 × (-7) — четное число.

Мы можем распознавать четные числа и в числовой строке, где они расположены попеременно. На картинке ниже мы видим четные числа: -8, -6, -4, -2, 0, 2, 4, 6, 8 и 10.

Да! 0 — четное число, поскольку его можно записать как 0 = 2 × 0. Кроме того, интуитивно понятно, если мы начнем с 0 элементов и разделим их на две части, каждая часть будет иметь одинаковый размер: 0 элементов.

Мы видим в числовой строке, что каждое четное число имеет два нечетных числа в качестве соседей с обеих сторон.

Например, 4 имеет 3 и 5 с обеих сторон, которые являются нечетными числами. Точно так же у -6 есть -7 и -5 с обеих сторон, которые также являются нечетными числами.

Первые четные целые числа: 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22 и так далее.

Обратите внимание, что в числовой строке между 6 и 8, например, нет другого четного числа. Когда это происходит, числа называются последовательных четных чисел . Точно так же 2 и 4, -6 и -4 являются последовательными четными числами.

Однако числа 4 и 8 не являются последовательными, так как 6 является еще одним четным числом между ними. Любое целое число между двумя последовательными четными числами является нечетным числом. Например, 7 находится между последовательными четными числами 6 и 8.

Что, если мы хотим перечислить четные числа между 105 и 120? Ну а так как 2 × 52 = 104 и 2 × 53 = 106, то 104 и 106 — последовательные четные числа, а 105 — нечетное. Таким образом, первое число в списке равно 106.

Точнее, числа в списке имеют вид 2 × k, где k больше 52 и меньше или равно 60, как показано в таблице.

Теперь рассмотрим большое число, например 3 187 074. Это даже? Чтобы определить, является ли какое-либо заданное число четным, достаточно посмотреть на цифру, стоящую на разряде единиц. Если разряд единиц в числе равен 0, 2, 4, 6 или 8, то число четное.

Таким образом, наше большое число 3 187 074 четное, потому что цифра в разряде единиц равна 4. И наоборот, 24 046 243 не является четным, потому что цифра в разряде единиц равна 3, что отличается от 0, 2, 4, 6 и 8.

Знаете ли вы, что…?
Почти всегда кукуруза имеет четное число рядов в каждом початке? На самом деле, кукуруза с нечетным числом рядов более странная, чем четырехлистный клевер! В среднем большинство початков имеют 16 рядов.

Давайте попрактикуем то, что мы узнали, на следующем примере.

Практический вопрос 1

На дне рождения было нечетное количество детей. Каждый ребенок съел одинаковое четное количество кексов. Среди всех детей было съедено 60 кексов.

Сколько детей было на вечеринке?

Тренировочный вопрос 2

Продолжаем считать по четным числам!

Какие четные числа идут дальше?

2, 4, 6, ___, ___, ___

См. соответствующие листы:

2-й класс

Даже снеговики могут быть причудливыми

Рабочие листы

Снеговик на этом листе определенно прикольный! Студентам понравится охотиться с ним за четными числами. Это …

2 класс

Поквитаемся!

Рабочие листы

“Даже” детям, которые не любят снег, понравится этот рабочий лист! Они будут скатываться из снежка в снежок, решив…

2 класс

Странно уютные снеговики

Рабочие листы

Могут ли снеговики быть уютными? Этот может! Мы знаем, что это «странно»! На этих снегоходах школьники будут “кататься”. ..

2-й класс

Санта-Снеговик спасает нечетное число

Рабочие листы

Этот рабочий лист “Снег” очень весело! Учащиеся рассмотрят каждое число и решат, од…

Просмотреть все рабочие листы

Соответствующие темы:

Попробуйте ArgoPrep для

БЕСПЛАТНО Учить больше Попробуйте ArgoPrep за БЕСПЛАТНО

Поделитесь хорошим контентом с друзьями и получите скидку 15% на 12-месячную подписку

Поделиться в фейсбуке Поделиться в твиттере

Четные числа от 1 до 100, определение, примеры и решенные вопросы

Четные числа

Четные числа: Целое число можно разделить на четное и нечетное. Если число при делении на 2 не оставляет остатка, то число называется четным. Если целое число при делении на 2 оставляет какой-либо остаток, то это число idd. Чтобы понять четные числа намного проще и лучше, вы должны знать таблицы/кратные 2 и основные методы деления. Например:

Давайте поговорим о числах 4, 19, 54 и 488.

Вы можете легко узнать, что 4 — четное число, если знаете таблицы 2. Точно так же вы можете легко узнать, что 19 — нечетное число, так как оно не делится на 2. 19÷2 = 9, оставляя 1 в качестве остатка или частного.

Если у нас есть такие числа, как 54 и 488, Так что в приведенных выше примерах только 19не четное число. Вы можете легко определить четное число, прочитав эту статью. В этом уроке мы расскажем все о четных числах, определениях, примерах, свойствах и важных моментах.

Четное число Определение

Четным числом считается любое число, которое полностью делится на 2, или число, которое можно разделить на две равные группы или пары без остатка, называется четным числом. Ниже приведены некоторые примеры. Проверьте, является ли число четным или нет.

8, если мы разделим 8 на 2, т.е. 8 ÷ 2=4, а в остатке 0. Таким образом, данное число 8 является четным числом.

12, если мы разделим 12 на 2, т. е. 12 ÷ 2 = 6, то снова в остатке будет 0. Таким образом, данное число 12 является четным числом.

15, если мы разделим 15 на 2, то есть 15 ÷ 2, то в остатке получится 1, поэтому данное число 15 не является четным числом. Это нечетное число.

21, Если мы проверим делимость 21 тем же методом, то есть 21 ÷ 2 дает остаток 1. Таким образом, 21 не является четным числом. Это нечетное число.

Как вы заметили, те числа, которые не делятся на 2, оставляют остаток, поэтому они нечетные числа, а не четные.

Четное число также может быть определено как четное целое число в форме n=2k , где k — целое число.

Как легко найти четные числа?

Самый простой способ определить, является ли данное число четным или нет. Мы должны сначала посмотреть на последнюю цифру данного числа:

Если последняя цифра числа заканчивается на 0, 2, 4, 6 или 8. Это четное число.
Если последняя цифра числа заканчивается на 1, 3, 5, 7 или 9. Это нечетное число.

Например,

58 — четное число, поскольку последняя цифра числа 58 — 8.

366 — четное число, поскольку последняя цифра числа 366 равна 6. последняя цифра 987654 — 4.

23 — нечетное число, так как последняя цифра 23 — 3, поэтому 23 — нечетное число.

487 тоже нечетное число, так как последняя цифра 7, а значит, это тоже нечетное число.

Even Numbers 1 to 100

List of Even Numbers 1 to 100
2	22	42	62	82
4	24	44	.0006	46	66	86
8	28	48	68	88
10	30	50	70	90
12	32	52	72	92
14	34	54	74	94
16	36	56	76	96
18	38	58	78	98
20	40	60	80	100

Even Numbers 1 to 200

44444444444444444444444444444444444444444444444444944444449н0005 108 9000

List of Even Numbers 1 to 200
2	22	42	62	82	102	122	142	162	182
4	24	44	64	84	104	124	144	164	184
6	26	46	66	86	106	126	146	166	186
8	28	48	68	9000 88 9 9	128	148	168	188
10	30	50	70	90	110	130	150	170	190
12	32	52	72	92	112	132	152	172	192
14	34	54	74	94	114		9	9		. 0244	154	174	194
16	36	56	76	96	116	136	156	176	196
18	38	58	78	98	118	138	158	178	198
20	40	60	80	100	120	14066	160		160	160	160 4747	160 4747	0006	200

Свойства четных чисел

1. Свойства сложения:

а) Сложение двух четных чисел всегда дает четное число.

Например, 8+6=14, 14+82=96, 12+6=18

б) Сложение четного числа с нечетным или наоборот дает нечетное число.

Например, 4+9=13, 11+10=21, 22+3=25

c) Сумма двух нечетных чисел всегда дает четное число.

Например, 7+3=10, 9+9=18, 43+65=108

2. Свойства вычитания:

а) Разница между двумя четными числами дает четное число.

Например, 16-4=12, 88-8=80, 442-322=120

б) Разница между четным числом и нечетным числом или наоборот дает нечетное число.

Например, 32-9=23, 19-10=9, 40-7=33

c) Разница между двумя нечетными числами дает четное число.

Например, 7-3=4, 11-9=2, 47-5=42

3. Свойства умножения.

а) Умножение двух четных чисел всегда является четным числом.

Например, 8 X 2 = 16, 14 X 4 = 56, 2 X 2 = 4

б) Произведение четного числа на нечетное дает четное число.

Например, 4 х 7 = 28, 3 х 6 = 18, 12 х 5 = 60

c) Умножение двух нечетных чисел всегда дает нечетное число. Иногда это не будет считаться свойством четных чисел.

Например, 5 x 5 = 25, 11 x 11 = 121, 13 x 3 = 39

Сводка свойств равномерных чисел

4.9

Свойства Добавления:
,1,
,
,
Even + Even	Even
2.	Even + Odd	Odd
3.	Odd + Odd	Even
Properties of Subtraction:
1.	Even – Even	Even
2.	Even – Odd	ODD
3.	ODD – ODD	даже
Properties Multiplation			5.0245
1.	Even X Even	Even
2.	Even X Odd	Even
3.	Нечетные X Нечетные	Нечетные

Четные простые числа

Знаете ли вы, что простое число имеет только два делителя: 1 и само себя. Принимая во внимание, что четное число делится на 2. Если число считается четным простым числом, оно должно соответствовать обоим вышеуказанным критериям. Следовательно, только 2 может быть четным простым числом. Поскольку все остальные четные числа делятся на 2, они не могут быть простыми числами.

Важные моменты по четным числам:

При счете каждое альтернативное число является четным числом, начиная с 2, и нечетным числом, начиная с 1.
0 «Ноль» — это четное число.
Наименьшее четное число – 2.
Единственное четное простое число – 2.

Четные числа – Решенные вопросы

Q1: Как узнать сумму n

Ответ: Сумма n четных чисел вычисляется по формуле S= n (n+1)

Q2: Найдите сумму первых десяти четных чисел.

Ответ: Сумма первых десяти четных чисел вычисляется по формуле S= n(n+1)

Итак, здесь нам нужно найти сумму первых десяти четных чисел, т. е. n =10

Подставляя n=10 в формулу

S=10(10+1)

=10(11)

= ответ 110. , 10, 12, 14, 16, 18 и 20.

2+4+6+8+10+12+14+16+18+20=110, следовательно, сумма первых десяти четных чисел равна 110

Q3: Найдите четное число из заданного набора чисел 633, 524, 873, 448, 87, 222, 65, 14872, 8945, 25648.

Ответ: Четные числа из списка: 524, 448, 222, 14872 и 25648.

Итак, общее количество бутылок с водой в их доме равно 84 (четным) + 60 (четным) = четным, т.е. 144

Q4. Запишите любые восемь последовательных четных чисел от 50 до 70.

Ответ: Все числа от 50 до 70 равны 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69 и 70. Восемь последовательных четных чисел от 50 до 70: 52, 54, 56, 58, 60, 62, 64 и 68.

Q5: Камаль покупает 84 новые бутылки с водой, а его брат Сатьям также приносит домой 60 новых бутылок с водой. Является ли общее количество бутылок с водой в их доме четным числом?

Ответ: Камаль купил 84 бутылки с водой, т.е. четное число.

Количество бутылок с водой, принесенных Satyam, равно 60, что также является четным числом.

Итак, общее количество бутылок с водой в их доме равно

84 (четные) + 60 (четные) = четные, т. е. 144

Q6: Найдите сумму всех четных чисел от 1 до 20?

Ответ: Всего между числами от 1 до 200 находится 100 четных чисел.

Здесь n = 100

Используя формулу S = n(n+1), , мы можем вычислить сумму всех четных чисел от 1 до 200.

Так как n= 100

S = N (N+1)

S = 100 (100+1)

S = 100 (101)

Итак, здесь S = 100 x 101

= 10100

Следовательно, сумма четные числа от 1 до 200 равны 10 100.

Q7: Какое утверждение является правильным?

Произведение двух четных чисел всегда является четным числом.
Сумма двух четных чисел всегда является нечетным числом.

Ответ: Правильным ответом является Утверждение 1.

Здесь, если мы рассмотрим утверждение 1, т.е. Четный X Четный = Четный, что верно. Например, 6 X 6 = 36, 8 X 6 = 48.

Но утверждение 2 неверно, так как Чет + Чет = Чет,

Например, 4+8=12, 10+12=22. После сложения двух четных чисел сумма также будет четным числом, а не нечетным.

Q8: Выберите правильный вариант. Разница между двумя четными числами:

а) Всегда четное число

б) Всегда нечетное число

в) Может быть как нечетным, так и четным

г) Ничего из вышеперечисленного правильно.

Ответ: Правильный ответ вариант а). Как четное число – четное число = четное. Например, 8 – 4 = 4, 18 – 6 = 12

Q9: Является ли ноль (0) четным числом? Обосновать ответ.

Ответ: Да, ноль (0) — четное число. Четное число всегда должно делиться на 2. Итак, когда 0 делится на 2, результирующий остаток в частном также равен нулю, который является целым числом, тем самым классифицируя его как четное число .

Вопрос 10. Какова сумма 4 последовательных четных чисел от 20 до 30? , сумма первых четырех последовательных четных чисел от 20 до 30 равна 22 + 24 + 26 + 28 = 100.

Читайте также:

Что такое четное число?

Определение четного числа

: целое число, которое можно разделить на два на два равных целых числа Числа 0, 2, 4, 6 и 8 являются четными числами.

Посмотреть полный ответ на byjus.com

Что такое четный ответ?
Что такое четное число? Любое число, которое можно точно разделить на 2, называется четным числом. Четные числа всегда заканчиваются последней цифрой 0, 2, 4, 6 или 8. Некоторые примеры четных чисел: 2, 4, 6, 8, 10, 12, 14, 16.
Просмотр полный ответ на byjus.com
Что такое четное нечетное число?
Что такое нечетные и четные числа с примерами? Нечетные числа — это те числа, которые нельзя разделить на две равные части, тогда как четные числа — это те числа, которые можно разделить на две равные части. Примеры нечетных чисел: 3, 5, 7, 9, 11, 13, 15,… Примеры четных чисел: 2, 4, 6, 8, 10, 12, 14,…
Посмотреть полный ответ на byjus.com

4 четное число?
Почему 4 четное число? Поскольку 4 кратно 2 и его можно разделить на две равные группы, это четное число. Другими словами, это четное число, потому что оно полностью делится на 2.
Посмотреть полный ответ на cuemath.com
Является ли 6 четным числом?
Отвечать. 6 – четное число.
Посмотреть полный ответ на mathwarehouse. com

Определение четного числа

Является ли 7 нечетным числом?
Список нечетных чисел от 1 до 100: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59 , 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99.
Посмотреть полный ответ на cuemath.com
Является ли 10 нечетным числом?
10 не нечетное число.
Посмотреть полный ответ на mathwarehouse.com
Является ли ноль нечетным числом?
Так что же это — нечетное, четное или ни то, ни другое? Для математиков ответ прост: ноль — четное число.
Просмотр полный ответ на bbc.com
Является ли 2 нечетным числом?
2 не нечетное число.
Посмотреть полный ответ на mathwarehouse.com

Является ли 0 наименьшим четным числом?
Четное число: Все числа, оканчивающиеся на 0, 2, 4, 6 и 8, называются четными. 0 – четное число и целое число. Итак, наименьшее четное целое число равно 0.
Посмотреть полный ответ на vedantu.com
Какое число является нечетным?
Нечетные числа — это числа, которые нельзя разделить на 2 без остатка. Его нельзя разделить на два отдельных целых числа поровну. Если разделить нечетное число на 2, то останется остаток. Примеры нечетных чисел: 1, 3, 5, 7 и т. д.
Просмотр полный ответ на byjus.com
Является ли ноль четным числом?
Когда 0 делится на 2, результирующее частное также оказывается равным 0 — целому числу, что классифицирует его как четное число. Хотя многие поспешили осудить ноль как вовсе не число, некоторые быстрые арифметические расчеты проясняют путаницу, связанную с числом, причем четным числом.
Посмотреть полный ответ на britannica.com
Что такое нечетные кратные?
Нечетные числа — это те, которые не делятся на 2. Нечетные кратные в списке — 3, 9., 15, 21, 27. Следовательно, нечетные кратные 3 = 3, 9, 15, 21, 27. Пример 3: Монике дан список чисел, разделенный на 4 группы.
Посмотреть полный ответ на cuemath.com

Что такое нечетное натуральное число?
Натуральные числа — это счетные числа, начинающиеся с 1. Они включают в себя все положительные целые числа, начинающиеся с 1 до бесконечности. Некоторые примеры натуральных чисел: 0, 5, 13, 32, 45, 57, 69 и т. д. Нечетные числа — это целые числа, которые не делятся на 2.
Просмотр полный ответ на geeksforgeeks.org
Как вы находите нечетные числа?
Чтобы определить, является ли число четным или нечетным, посмотрите на число в разряде единиц. Это единственное число скажет вам, является ли все число нечетным или четным. Четное число оканчивается на 0, 2, 4, 6 или 8. Нечетное число оканчивается на 1, 3, 5, 7 или 9.
Посмотреть полный ответ на factmonster.com
Является ли 6 нечетным числом?
6 не нечетное число.
Посмотреть полный ответ на mathwarehouse.com
Какое 100-е нечетное число?
Ответ: 100-е нечетное число равно 199.
Посмотреть полный ответ на brainly.in

Является ли 8 нечетным числом?
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30 — четные числа. Нечетные числа всегда заканчиваются цифрой 1, 3, 5, 7 или 9. 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31. являются нечетными числами.
Посмотреть полный ответ на aaamath.com
Может ли отрицательное число быть четным?
Конечно да. Отрицательные числа могут быть нечетными или четными. Это очень простой ответ, если вы знаете определения нечетных и четных чисел. Целые числа, кратные 2, являются четными числами.
Посмотреть полный ответ на quora.com
0,2 четно или нечетно?
0,2 не четно и не нечетно!
Посмотреть полный ответ на gmatclub.com
Бесконечность четная или нечетная?
Я объяснил, что бесконечность не четна и не нечетна. Это не число в обычном смысле, и оно не подчиняется правилам арифметики. Если бы это произошло, последовали бы всевозможные противоречия. Например, «если бы бесконечность была нечетной, бесконечность, умноженная на 2, была бы четной.
Просмотр полный ответ на mindator.blogs.nytimes.com

Является ли 4 нечетным числом?
4 не нечетное число.
Посмотреть полный ответ на mathwarehouse.com
Является ли минус 3 нечетным числом?
1 и 3 — нечетные числа, не превышающие 3, как и любые отрицательные нечетные числа (например, -5). Да, -3 — нечетное число, потому что нечетные числа — это целые числа, которые не делятся на 2 или которые при делении на 2 дают в остатке 1 в каждом случае независимо от положительного или отрицательного знака.
Просмотр полный ответ на quora.com
Является ли минус 4 четным числом?
Да, -4 – четное число. Отрицательные числа также могут быть классифицированы как четные и нечетные числа.
Посмотреть полный ответ на Meritnation.com
← Предыдущий вопрос
Как долго должны болеть имплантаты?
Следующий вопрос →
Как сделать волосы блестящими?
Нечетные и четные числа | Определение, примеры, свойства, отличия
Введение
Математика — это мир чисел. У нас есть различные типы чисел, такие как натуральные числа, целые числа, десятичные числа и дроби, которые основаны на определенных характеристиках чисел. У всех этих типов чисел есть одна общая черта. Все они имеют нечетные числа и четные числа. Итак, что такое нечетные числа и четные числа и как мы их классифицируем? Давайте узнаем.
Что такое четные и нечетные числа?
Рассмотрим числа 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9и 10. Это полностью натуральные числа. Если вы посмотрите на них внимательно, некоторые из чисел, такие как 2, 4, 6, 8 и 10, делятся на 2, а остальные числа 1, 3, 5, 7 и 9 не делятся на 2. Итак, можем ли мы составить группа чисел по признаку их делимости на 2? Да, именно так мы определяем нечетные числа и четные числа.
Четные числа — это числа, которые делятся на 2, оставляя в остатке 0. Например, в приведенном выше примере 2 , 4 , 6 , 8 и 10 — четные числа.
Нечетные числа — это числа, которые не делятся на 2 и всегда оставляют остаток 1 при делении на 0. Например, в приведенном выше примере 1 , 3 , 5 , 7 и 9 являются нечетными числами.
Нечетные и четные числа от 1 до 100
Ниже представлена таблица четных и нечетных чисел. Он показывает числа до 100. Числа, заштрихованные синим цветом, являются четными числами, а числа, заштрихованные желтым цветом, — нечетными числами.
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
Do we always have look at the number table to identify whether the number is an нечетное число или четное число, или мы можем определить число любым другим способом? Давайте узнаем.
Как отличить четные числа от нечетных
Теперь мы знаем, что число, которое делится на 2 и дает в остатке 0, называется четным числом. С другой стороны, нечетное число — это число, которое не делится на 2. Также остаток в случае нечетного числа всегда равен «1». Итак, можем ли мы определить, является ли число четным или нечетным, просто взглянув на само число?
Рассмотрим числа от 1 до 10. У нас есть 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10. Из них мы знаем, что числа 1, 3, 5, 7 и 9 — нечетные числа, а числа 2, 4, 6, 8, 10 — четные числа. Аналогично рассмотрим теперь числа от 11 до 20. У нас есть 11, 12, 13, 14, 15, 16, 17, 18, 18 и 20. Из них 11, 13, 15, 17 и 19 нечетные числа. а числа 12, 14, 16, 18 и 20 четные? Вы видите здесь закономерность? Запишем отдельно нечетные и четные числа. У нас будет
Нечетные числа – 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
Четные числа – 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
Посмотрите на последние цифры нечетных чисел. Нечетные числа заканчиваются любой из пяти цифр 1, 3, 5, 7 и 9. Следовательно, мы можем сказать, что все нечетные числа имеют любую из пяти цифр 1, 3, 5, 7 и 9 на своих единицах. Следовательно, мы можем сказать, что числа, имеющие любую из пяти цифр 1, 3, 5, 7 и 9, являются нечетными числами.
Теперь посмотрите на последние цифры четных чисел. Четные числа заканчиваются любой из пяти цифр 0, 2, 4, 6 и 8. Следовательно, мы можем сказать, что все четные числа имеют любую из пяти цифр 0, 2, 4, 6 и 8 на своем месте единиц. Следовательно, мы можем сказать, что числа, имеющие любую из пяти цифр 0, 2, 4, 6 и 8, являются четными числами.
Давайте теперь посмотрим на свойства нечетных и четных чисел.
Свойства нечетных чисел
Когда мы складываем два нечетных числа, всегда получается четное число. Например, если мы сложим 7 и 15, мы получим 7 + 15 = 22. Точно так же, когда мы сложим 13 и 17, мы получим 13 + 17 = 30, что является четным числом.
Когда мы вычитаем два нечетных числа, результатом всегда будет нечетное число. Например, когда мы вычитаем 9из 17 мы получим 17 – 9 = 8. Точно так же, когда мы вычтем 21 из 37, мы получим 37 – 21 = 16, что является четным числом.
При умножении двух нечетных чисел всегда получается нечетное число. Например, если мы умножим 3, которое является нечетным числом, на 5, которое также является нечетным числом, результатом будет 3 x 5 = 15, что также является нечетным числом. Точно так же, если мы умножим 7, которое является нечетным числом, на 9, которое также является нечетным числом, результатом будет 7 x 9 = 63, что также является нечетным числом.
Когда мы умножаем четное число на нечетное, всегда получается четное число. Например, если мы умножим 3, являющееся нечетным числом, на 6, являющееся четным числом, результатом будет 3 x 6 = 18, что является четным числом. Точно так же, если мы умножим 9, которое является нечетным числом, на 4, которое является четным числом, результатом будет 9 x 4 = 36, что является четным числом.
Свойства четных чисел
Когда мы складываем два четных числа, всегда получается четное число. Например, если мы сложим 8 и 6, то получим 8 + 6 = 14, то есть четное число. Точно так же, если мы сложим 24 и 12, мы получим 24 + 12 = 36, что является четным числом.
Когда мы вычитаем два четных числа, всегда получается четное число. Например, если мы вычтем 8 из 14, мы получим 14 – 8 = 6. Точно так же, когда мы вычтем 24 из 36, мы получим 36 – 24 = 12.
Когда мы складываем четное число и нечетное число, результат всегда нечетное число. Например, если мы добавим 3, что является нечетным числом, и 6, которое является четным числом, мы получим 3 + 6 = 9, что является нечетным числом. Точно так же, если мы добавим 9, что является нечетным числом, и 16, что является четным числом, мы получим 9.+ 16 = 25, что является нечетным числом.
Когда мы вычитаем четное число из нечетного, всегда получается нечетное число. Например, если мы вычтем 3, которое является нечетным числом, из 6, которое является четным числом, мы получим 6 – 3 = 3, которое является нечетным числом. Точно так же, если мы вычтем 12, что является четным числом, из 17, которое является нечетным числом, мы получим 17 – 12 = 5, что является нечетным числом.
Когда мы умножаем два четных числа, всегда получается четное число. Например, если мы умножим 6, что является четным числом, на 12, что также является четным числом, результатом будет 6 x 12 = 78, что также является четным числом. Точно так же, если мы умножим 4, которое является четным числом, на 8, которое также является четным числом, результатом будет 4 x 8 = 32, что также является четным числом.
Ноль — четное число. Ноль — четное число, потому что оно является целым числом, кратным 2, а именно 0 × 2.
Представление наборов четных и нечетных чисел
Теперь, когда мы узнали, что мы подразумеваем под нечетными и четными числами, можем ли мы обобщить их в операторе, чтобы представить их в форме построителя множества? Давайте узнаем.
Чтобы представить нечетные и четные числа в обобщенной форме, важно понимать условие, определяющее нечетные и четные числа. Мы знаем, что основным условием для того, чтобы число было четным, является то, что оно делится на 2. Поэтому, если мы хотим обобщить его и представить в форме построителя множеств, мы будем иметь
Набор четных чисел = { x : x = 2k, где k — любое целое число }
Точно так же мы знаем, что основное условие для того, чтобы число было нечетным, состоит в том, что оно не делится на 2. Также , мы знаем, что любое число, которое не делится на 2, оставит в остатке 1 при делении на 2. Следовательно, такое число должно иметь вид 2x + 1, где x — целое число. Поэтому, если мы хотим обобщить его и представить в форме построителя набора, мы будем иметь
Множество нечетных чисел = { x : x = 2k + 1, где k любое целое число }
Решенные примеры
Пример 1 Найдите сумму
a) Первые 5 нечетных натуральных чисел.
б) Первые 5 четных натуральных чисел
Решение Нас попросили найти
а) Первые 5 нечетных натуральных чисел.
б) Первые 5 четных натуральных чисел
Выполним их последовательно.
Чтобы получить сумму первых пяти нечетных натуральных чисел, мы должны сначала перечислить первые 5 нечетных натуральных чисел. Мы знаем, что натуральные числа начинаются с 1 и продолжаются 1, 2, 3, 4, 5 и так далее.
Следовательно, первые 5 нечетных натуральных чисел — это 1, 3, 5, 7 и 9. Сумма этих чисел будет 1 + 3 + 5 + 7 + 9 = 25
Следовательно, сумма первых 5 нечетных натуральные числа = 25
Далее найдем сумму первых 5 четных натуральных чисел.
Первые 5 четных натуральных чисел 2, 4, 6, 8 и 10.
Сумма этих чисел будет 2 + 4 + 6 + 8 + 10 = 30
Следовательно, сумма первых 5 нечетных натуральные числа = 25
Пример 2 Перечислите все нечетные числа больше 3 и меньше 30.
Решение Нас попросили перечислить все нечетные числа больше 3 и меньше 30. Давайте сначала перечислим все числа больше than 3 and less than 30 in the table below –
4 5 6 7 8
9 10 11 12 13
14 15 16 17 18
19 20 21 22 23
24 25 26 27 28
29 30
Далее мы выделим нечетные числа в этой таблице и пометим их желтым цветом. Получим,
4 5 6 7 8
9 10 11 12 13
14 15 16 17 18
19 20 21 22 23
24 25 26 27 28
29 30
Therefore, all odd numbers greater than 3 and smaller than 30 are
Пример 3
3 – наименьшее четное число.
4-значное наименьшее четное число с 6 на разряде тысяч.
2-значное нечетное число меньше 40
4-значное наибольшее нечетное число с 3 на разряде сотен.
Наименьшее четное число, использующее все 4 цифры.
Решение а) Нам даны цифры – 3 , 4 6 и 7.
Нам нужно найти трехзначное наименьшее четное число. Наименьшее трехзначное четное число будет 3 4 6.
б) Опять же, нам даны цифры — 3 , 4 6 и 7
нам нужно найти 4-значное наименьшее четное число с 6 на разряде тысяч.
Наименьшее четырехзначное четное число с 6 в разряде тысяч равно 6 3 7 4.
c) Нам даны цифры – 3 , 4 6 и 7.
Нам нужно найти двузначное число нечетное число меньше 40. Двузначное нечетное число меньше 40 равно 3 7.
г) Нам даны цифры – 3 , 4 6 и 7.
Нам нужно найти 4-значное наибольшее нечетное число с 3 на месте сотен. 4-значное самое большое нечетное число с 3 на разряде сотен будет 6 3 4 7
e) Нам даны цифры – 3 , 4 6 и 7.
Нам нужно найти наименьшее четное число, используя все 4 цифры. Наименьшее четное число при использовании всех 4 цифр будет 3 4 7 6
Ключевые факты и резюме
Четные числа — это числа, которые делятся на 2, оставляя остаток 0.
Нечетные числа — это числа которые не делятся на 2 и всегда оставляют остаток 1 при делении на 0.
Набор четных чисел = {x : x = 2k, где k — любое целое число}
Набор нечетных чисел = {x : x = 2k + 1, где k — любое целое число}
При сложении двух четных чисел , результатом всегда будет четное число.
Когда мы вычитаем два четных числа, всегда получается четное число.
При умножении двух нечетных чисел всегда получается нечетное число.
Когда мы умножаем четное число на нечетное, всегда получается четное число.
Когда мы складываем два четных числа, всегда получается четное число.
Когда мы вычитаем два четных числа, всегда получается четное число.
Когда мы складываем четное число и нечетное число, результатом всегда будет нечетное число.
Когда мы вычитаем четное число из нечетного, всегда получается нечетное число.
Когда мы умножаем два четных числа, всегда получается четное число.
Ноль — четное число.
Числа, содержащие любую из пяти цифр 1, 3, 5, 7 и 9все нечетные числа.
Числа, содержащие любую из пяти цифр 0, 2, 4, 6 и 8, являются четными числами.
Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Определение нечетных чисел, типы, свойства и примеры
Числа являются строительными блоками математики. Их можно использовать для подсчета или измерения чего-либо. Он играет очень важную роль в нашей повседневной жизни и математике .
Десять математических цифр (от 0 до 9) используются для обозначения возраста, веса, дня рождения, времени, результатов, банковских счетов и телефонных номеров. Без этих десяти чисел невозможно представить свою жизнь.
Числа бывают различных типов, такие как натуральные числа (N), целые числа (W), целые числа (Z), рациональные числа (Q), действительные числа (R) и т. д.
Натуральные числа, целые числа и целые числа могут быть далее классифицируются на нечетные и четные числа.
Четные и нечетные числа играют важную роль в изучении многих математических понятий. Понимание четных и нечетных чисел важно для освоения некоторых из самых сложных математических понятий.
ЧТО ТАКОЕ НЕЧЕТНЫЕ НОМЕРА?
Нечетные числа — это целые числа, которые не делятся на 2. Если мы разделим нечетное число на 2, то в остатке останется 1. Нечетные числа оканчиваются цифрами 1, 3, 5, 7 или 9. Нечетные числа противоположны четным числам. Нечетные числа не могут быть расположены парами. Нечетные числа не кратны 2.
Примерами нечетных чисел являются 1, 3, 5, 7,31, 43 и т. д.
Например, 13 не делится точно на 2, потому что в остатке остается 1, когда мы разделите его на 2, и оно оканчивается на 3. Итак, 13 — нечетное число.
СПИСОК НЕЧЕТНЫХ ЧИСЕЛ ОТ 1 до 100:
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35 , 37, 39, 41, 43, 45, 47, 49,51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85 , 87, 89, 91, 93, 95, 97, 99
ПРИМЕЧАНИЕ:
Наименьшее нечетное число – 1.
Каждое число, следующее за четным, является нечетным.
Каждое число, следующее за нечетным, является четным числом.
Дроби и десятичные дроби не являются четными или нечетными числами, потому что они не являются целыми числами.
ЧТО ТАКОЕ ЧЕТНЫЕ ЧИСЛА?
Четные числа — это те числа, которые точно делятся на 2. Четные числа всегда заканчиваются последней цифрой 0, 2, 4, 6 или 8. Любое число, которое делится на 2 без остатка, называется четным числом. .
Примеры четных чисел: 24, 56, 88, 102 и т. д.
Что такое собственность?
Свойство целого числа, независимо от того, является оно четным или нечетным, называется четностью.
Целое число является четным, если оно делится на два без остатка, и его четность является нечетной, если оно не делится на 2 и его остаток равен 1.
Любые два последовательных целых числа имеют противоположную четность.
Четные и нечетные числа имеют противоположную четность.
Например, 15 — нечетное, а 16 — четное, имеет противоположную четность
29нечетно, а четное 14 имеет противоположные четности.
ОБЩАЯ ФОРМА НЕЧЕТНЫХ ЧИСЕЛ
Нечетное число – это целое число вида 2k+1, где k ∈ Z (т.е. целые числа) называются нечетными числами.
Если мы подставим любое значение k, мы получим нечетное число.
Например: Если мы возьмем k за 2, получим 2 x 2 + 1 = 5, что является нечетным числом.
Четное число — это целое число вида 2k, где k ∈ Z (т. е. целые числа) называются нечетными числами.
Если мы подставим любое значение k, мы получим четное число.
Например: Если мы возьмем k за 2, получим 2 x 2 = 4, что является четным числом.
КАК ПРОВЕРИТЬ ЧЕТНОЕ ИЛИ НЕЧЕТНОЕ ЧИСЛО?
Существует два метода определения четности или нечетности числа. Это:
1. Проверяя цифру числа на месте единиц:
Чтобы проверить, является ли число нечетным или четным, мы должны проверить число на «единицы» или «единицы». «место или конечная цифра числа.
Числа, оканчивающиеся цифрами 1,3,5,7 и 9, являются нечетными.
Пример: 7,11,283,5735,9859 и т.д.
Поскольку число 2835 заканчивается цифрой 5 (нечетное число), данное число является нечетным.
А,
Числа, оканчивающиеся цифрами 0,2,4,6 и 8, являются четными числами.
Поскольку число 2838 заканчивается цифрой 8 (четное число), данное число является четным числом.
2. По группировке:
Здесь у нас всего 11 точек. Все точки не спарены. Одна точка остается непарной. Такие числа, которые нельзя составить парами, называются 9.0168 нечетные числа.
Те числа, которые не делятся точно на 2, называются нечетными.
Теперь
12 точек. Мы видим, что все точки спарены и не осталось непарных точек, поэтому 12 — четное число.
Мы можем сделать вывод, что все те числа, которые можно сложить в пары, называются четными числами.
СВОЙСТВА НЕЧЕТНЫХ ЧИСЕЛ
Свойство сложения двух нечетных чисел
Когда мы складываем два нечетных числа, результаты всегда четные.
Пример: 7(нечетное) + 5(нечетное) = 12 (четное)
Когда мы складываем одно нечетное число и одно четное, результат всегда будет нечетным.
Пример: 9(нечетное) + 2(четное) = 11(нечетное)
Свойство вычитания нечетных чисел
Когда мы вычитаем два нечетных числа, результаты всегда четные.
    Пример: 9(нечетное) – 3(нечетное) = 6(четное)
Когда мы вычитаем одно нечетное число и одно четное, результат всегда будет нечетным.
   Пример: 15(нечетное) – 10(четное) = 5(нечетное)
Свойство умножения нечетных чисел
1. При умножении двух нечетных чисел результат всегда нечетный.
Пример: 3(нечетное) x 5(нечетное) = 15(нечетное)
2. Когда мы умножаем одно нечетное число на одно четное, результаты всегда четные.
Пример: 5(нечетное) x 2(четное) = 10(четное)
Свойство деления нечетных чисел
1. При делении двух нечетных чисел получается нечетное число, только если знаменатель является множителем числителя.
Пример: Когда мы делим 15 на 5 и 5 делят на 15, мы получаем 3, то есть целое число.
Когда мы делим два нечетных числа и знаменатель не является множителем числителя, то результат может быть дробным или десятичным (заканчивающимся или не завершающимся).
Пример: когда мы делим 5 на 15, мы получаем 1/3 (дробь) или 0,3333 (неконечная десятичная дробь). .
Составные нечетные числа : Составные числа, которые нельзя разделить на 2, являются составными нечетными числами, а все положительные целые числа, имеющие множитель, отличный от 1, называются составными числами. Эти типы нечетных чисел образованы произведением двух меньших положительных нечетных целых чисел.
Список составных нечетных чисел от 1 до 50 выглядит следующим образом.
        9, 15, 21, 25, 27, 33, 45, 49.
Последовательные нечетные числа : Последовательные нечетные числа — это нечетные числа, следующие друг за другом в последовательном порядке. Между ними разница 2. Если n нечетное число, то числа n и n+2 являются последовательными нечетными числами.
Последовательные нечетные числа от 1 до 20:
1, 3, 5, 7, 9, 11, 13, 15, 17, 19
СУММА НЕЧЕТНЫХ ЧИСЕЛ ОТ 1 ДО 1000
Согласно формуле суммы нечетных чисел, сумма первых n нечетных чисел равна n2, где n — натуральное число, представляющее количество слагаемых.
Таким образом, сумма первых n нечетных чисел будет представлена как 1 + 3 + 5 +…+ n слагаемых = n2
ИНТЕРЕСНЫЕ ФАКТЫ:
Если сложить все нечетные числа от 1 до любое число, сумма всегда будет полным квадратом.
Сумма всех нечетных чисел от 1 до 100 равна 2500, и эта сумма представляет собой полный квадрат.
Четные числа создают симметрию, а нечетные вызывают интерес и их легче запомнить
Некоторые суеверные люди считают, что четные числа не приносят счастья. Частично это связано с тем, что они делимы, что уменьшает или уменьшает их силу. Нечетные числа обладают большей силой, потому что их нельзя уменьшить таким образом.
The Amazing 5 Even Numbers
Представляем Четные и нечетные числа
Различать четные и нечетные числа — важный навык, который необходим детям. помочь им понять нашу систему счисления и помочь в их подготовке к группированию операции с целыми числами. Это также поможет подготовить их к обучению делению, простые числа и даже квадратные корни.
Некоторым детям трудно понять четные и нечетные числа. Этот концепция важна, потому что она помогает учащемуся увидеть закономерность в числа. Это предшественник для подсчета пропусков, деления и простых чисел. Так, важно убедиться, что дети понимают это на раннем этапе.
Четные числа — это целые числа, которые делятся на 2 без остатка. Этот означает, что число можно разделить на пары или две равные группы без остатки. Примеры четных чисел: 2, 6, 10, 20, 50 и т. д.
Что такое четное число в математике?
Число, которое можно разделить на две половины, т.е. на две равные части. Это называется четное число. Другими словами, четные числа точно делится на 2. Это означает, что остаток будет равен 0.
Что такое четные числа вообще?
Целые числа, в которых вместо единицы стоят цифры 0, 2, 4, 6 или 8, считаются четные числа. Четные числа всегда заканчиваются последней цифрой 0, 2, 4, 6 или 8. Некоторые примеры четных чисел: 2, 4, 6, 8, 10, 12, 14 и 16.
Это четные числа, так как они легко делятся на 2. Это следует отметить, что наименьшее положительное четное натуральное число равно 2. Если вы выберите число, которое не может делиться на 2,
оно будет известно как нечетное число Например: 1, 3, 5, 7, 9 и т. д.
Как узнать, четное число или нечетное?
Чтобы узнать, является ли заданное число четным или нечетным, необходимо проверить число на месте единицы (или единицы). Это конкретное число на своем месте скажет вам, является ли число нечетным или четным.
Четный числа заканчиваются на 0, 2, 4, 6, 8
Нечетный Номера заканчиваются на 1, 3, 5, 7, 9
Если цифра единицы (или цифра единицы) равна 1, 3, 5, 7 или 9, то число набрал нечетный номер . Если устройство цифра 0, 2, 4, 6 или 8, то число называется четным номер . Это простые приемы для определения чисел четные они или нечетные.
Подумайте о следующих числах 3, 845 и 917, которые оканчиваются на нечетную число, то есть 3, 5 и 7. Следовательно, данные числа 3, 845 и 917 нечетные числа. Таким образом, эти числа не являются четными числами. Точно так же 8 и 322 являются четными числами, поскольку они заканчиваются на 8 и 2.
Ноль
Ноль — четное число, потому что нечего спаривать и ничего не осталось над. Значит, четно. Для математиков ноль — четное число. потому что любое число, которое можно разделить на два, чтобы получить другое целое число, даже. Ноль проходит этот тест, потому что если вы разделите ноль пополам, вы получите ноль. Нам следует запомнить 0,2,4,6,7 и 8 как четные и 1, 3,5,7 и 9как то странно.
Список четных чисел до 100
Список четных чисел до 100 приведен ниже:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100
Свойства четных чисел
Свойство добавления
Ниже приведены три важных свойства четных чисел: Добавление четного и другого четного числа всегда приведет к четному номер
Пример: четный + четный = четный, 14 + 6 = 20
Свойство вычитания
Вычитание четного числа из другого четного числа всегда приводит к четное число.
Пример: четный – четный = четный, 16 – 6 = 10
Свойство умножения
Умножение четного числа на другое четное число всегда приводит к четное число.
Пример: четное × четное = четное, 6 × 4 = 24

Краткое изложение фактов
Сумма из двух или более четных чисел всегда четно
Четный числа при делении на 2 не оставляют остатка
Четный числа кратны двум
Есть не являются остатком. Да, это правда!
Четный числа при умножении на любое число всегда дают четное число
произведение двух и более четных чисел всегда четно
Свойство дополнения
Когда сложение четного и нечетного числа (или наоборот), в результате число всегда будет нечетным.
Примеры:
9 + 4 = 13
3 + 20 = 23
Добавление четное число и другое четное число, приведет к числу, которое всегда даже.
Примеры:
14+6 =20
Добавление нечетное число и другое нечетное число всегда будут приводить к числу это даже.
Примеры:
11 + 13=24
Свойство вычитания
Если вы вычесть четное число из четного числа, ответ будет четным числом
Если вы вычесть нечетное число из нечетного числа, ответ будет четным числом
Если вы вычесть четное число из нечетного числа, ответ будет нечетным числом
Если вы вычесть нечетное число из четного числа, ответ будет нечетным числом
Вычитание четное число из нечетного числа (или наоборот) приведет к числу это всегда странно.
Примеры:
7 – 4= 3
8 – 5= 3
Вычитание четное число из другого четного числа приведет к числу, которое всегда даже.
Пример:
12 – 8= 4
Вычитание нечетное число из другого нечетного числа, приведет к числу, которое всегда даже.
Примеры:
23 –11 = 12
Свойство умножения
Умножение четное число и другое четное число всегда приводят к четному количество.
Примеры:
8 × 2= 16
10 × 6= 60
Умножение четное число и нечетное число всегда будут давать четное число.
Примеры:
4 × 5= 20
8 × 5= 40
Умножение нечетное число и другое нечетное число всегда дадут вам нечетное число.
Примеры:
3 × 5= 15
3 × 5= 15
Четные числа от 40 до 60
Давайте посмотрим на список четных чисел между 40 и 60. 42, 44, 46, 48, 50, 52, 54, 56, 58 Таким образом, всего 9 четных чисел находятся между 40 и 60. Пройдите примеры и решения четного числа, приведенные ниже, для лучшее понимание.
Пример 1:
Некоторые четные числа решили задачи
Все ли числа четные?
Решение:
Нет, список целых чисел, которые точно делятся на два, называется четные числа.
Пример 2:
Запишите любые четыре последовательных четных числа между числами от 13 до 21.
Решение:
Пусть А = {13, 14, 15, 16, 17, 18, 19, 20, 21}
Следовательно, 14, 16, 18, 20 — это 4 последовательных четных числа.
Пример 3:
Выберите правильный ответ. Сумма двух четных чисел
А) Всегда четное число
B) Всегда нечетное число
C) иногда бывает нечетным, а иногда четным
г) Может быть ни нечетным, ни четным Решение:
Правильный ответ – вариант а). Четное число + Четное число = Четное число
Пример 4: −24, 0, 6 и 38 — все четные числа?
Да, все числа -24, 0, 6 и 38 четные.
Пример 5: Является ли 2 четным числом?
Да, 2 — четное число, так как 2 точно делится на 2.
Пример 6: Какие четные числа находятся между 1 и 50?
Список четных чисел от 1 до 50: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48
Пример 7: Какое четное простое число?
2 — единственное четное простое число.
Пример 8. Если сложить два четных числа, получится:
Всегда даже
Всегда нечетное
Иногда четные и иногда нечетные
0
четный + четный = четный Например, 2 + 6 = 8.

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100