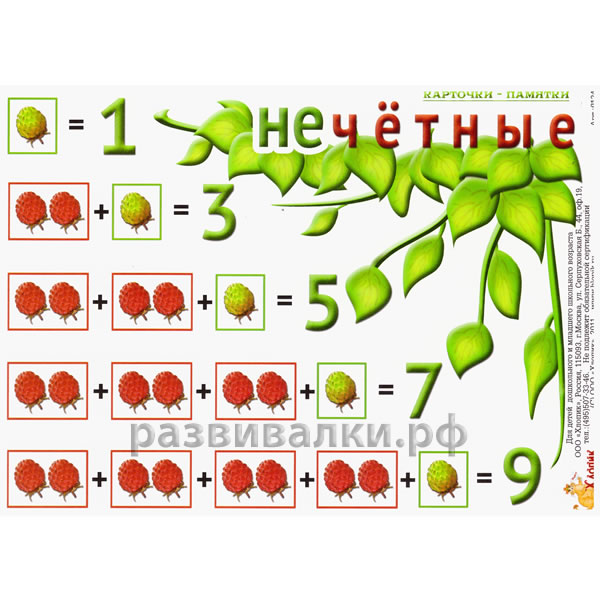
Четные и нечетные цифры: Чётные и нечётные числа — урок. Математика, 2 класс.
Главная → Видеоуроки → Математика. 5 класс. Натуральные числа. Описание видеоурока: Четные и нечетные числа – это целые числа. Если число может быть разделено на 2 без остатка, то число чётное. Если же целое число разделить на 2 и в итоге мы получим число с остатком, то значит число нечетное. Валерий Волков 13 17.09.2015 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математике Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 23 Задача 24 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
5 класс.
10 – 11 класс.
Как объяснить 5-ти летке что такое четные числа?
- Форум
- Архив
- Детская психология и развитие
Педагоги, воспитатели, пожалуйста, подскажите, как корректно объяснить ребенку что такое четное число? Ребенку 5.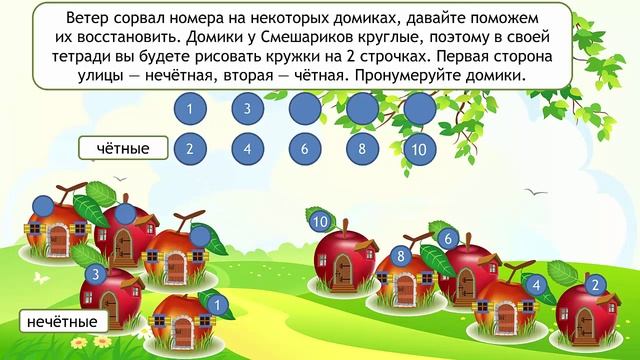
Да именно так, четное число можно поделить на 2, на две равных части. Хватило одного раза, чтобы ребенок понял. Сейчас может сразу про любое число в пределах первой сотни сказать четное оно или не четное. Сыну 5,3.
А вашего объяснения про зайцев даже я не поняла
Объясните на уровне “делится на 2 одинаковые кучки” и поделите-таки конфеты, например В принципе мы научились делить на 2 кучки числа до 10ти включительно. Этого достаточно. Дальше ведь просто: если число заканчивается на чётное, значит точно можно на 2 равные кучки поделить.
Я своей 4-летке объясняла, что чётное количество можно распределить группами по 2 штуки без остатка.
Нарисовала, к примеру, 5 точек, две обвела кругом, ещё 2 обвела кругом, осталась одна без пары – значит, 5 – нечётное число. Дочь поняла сразу.
Ещё очень помогла таблица сотни, дочка сообразила, что чётные и нечётные чередуются, и что весь столбик под числом 1 ( 21, 31 и т.д.) – нечётные, так как заканчиваются на 1. То же самое со всеми остальными числами.
+1 так же объясняла. Ребенок все понял.
Если можно все разделить на двоих так, чтобы получилось у обоих одинаковое количество. Лучше всего объяснять на конфетах
Мои делили, “чтоб маме не досталось”
А зачем это знать 5-летке???…числа до 20 но не знает деления…
Зачем гнать если в 7лет можно рассказать за пару минут и ребенок сразу все поймет?
Которые кончаются на 0,2,4,6,8.
А зачем вам это объяснять???? В школе научат. Господи, не отнимайте у ребенка детство.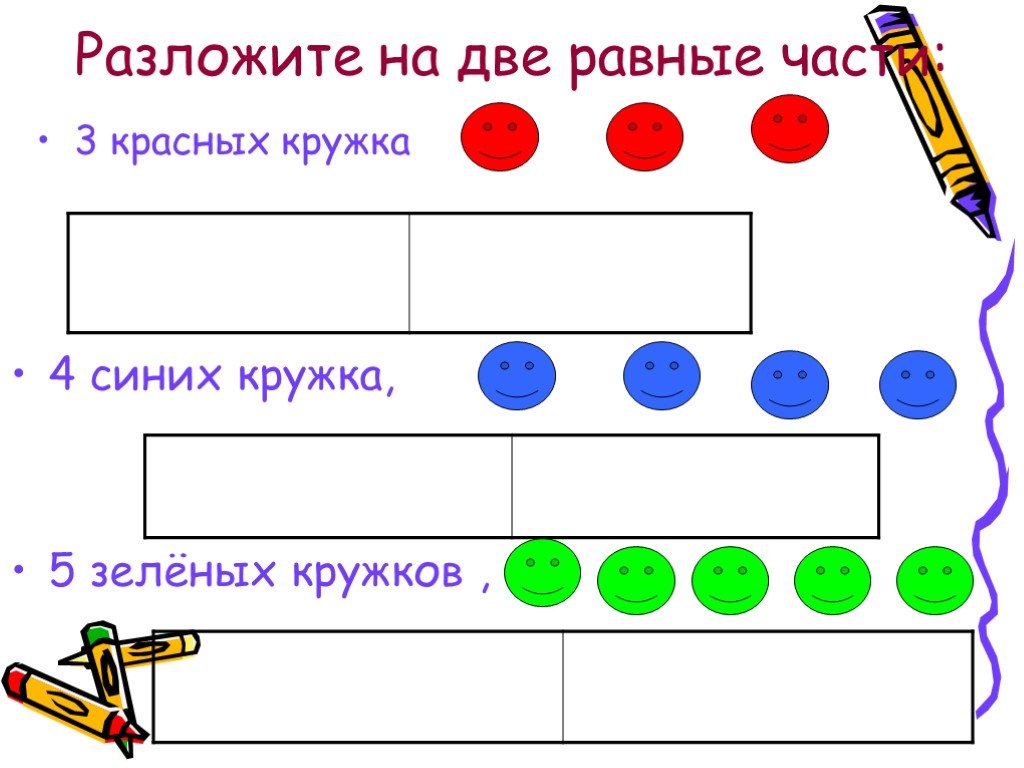
…
Зачем???
Потому что когда есть желание учиться и бесконечное любопытство – надо его удовлетворять. И если моих педагогических способностей не хватает чтобы объяснить, надо лезть в Инет, и разбираться, как такие вещи доносят до детей.
Я бы объяснила так (хоть и не педагог) ,четные числа -это то количество(допустим яблок) которое всегда можно поделить поровну с другом(допустим)
как объяснить маме пятилетки не бежать впереди паровоза?!
оно делится на 2
в свое время объясняла дочке, что четные числа те, корорые можно “разделить поровну” разделить на 2 маленькому ребенку не понятно, а поровну понятно.
Четное количество предметов можно “постоить” по парам.
Т.е. все книжки, где упоминаются четные/нечетные – забрать (или страницы, где про ЭТО есть, вырезать?), и на вопросы не отвечать?
Разумеется. Дать пирамидку, сказку про репку и пусть с ними до школы сидит.
Остальному научат без Вас…
разложите на примере на кучки пополам.
Почему отнимать детство?Если ребенок сам интересуется?Мою было от математики не оторвать в 5 лет.
вот у нас такая есть одна девочка со сказкой про репкусамая тупая в школе в 1 нашем классе.Единственная,что пришла и ничего не знала, включая чтение.Учитель ругает на каждом уроке.Моя вон сколько всего выучила, а и то тяжеловато, такие у нас нагрузки.Учитель так и сказала на собрании, что “официально до школы учить не надо- а на деле, сами видите, как кому что дается.Так что выбирайте”
Напишите в топике плз., зачем ему эта информация. Интересно и понять хочется
А Вам зачем этот навык? … В данный момент операции с числами это один из видов развлечений наряду скучей других
У меня тоже есть дети 6 и 4 года – вот и интересно как и зачем может ребенок в этом возрасте использовать такие знания.
Мне кажется, что для того чтобы усвоить эту информацию ребенок должен свободно делить и умножать, а потом уже обратить его внимание на четность и нечетность чисел. Так ему легче будет понять и усвоить. Но эта задача явно не для пятилетнего ребенка, тем более в качестве развлечения. В этом возрасте физиология мозга не готова адекватно принимать такую информацию. Хотя, конечно, есть исключения, но их мало. Если ребенок хорошо усваивает новый материал, получает удовольствие от подобных занятий – тогда конечно такие развлечения и интересны, и полезны для малыша. Это мое мнение. Если Вам не сложно, дайте ссылочку где можно посмотреть эти упражнения\задания. Хочу попробовать с сыном 6,5 лет полистать. Вдруг он меня удивит?
Согласна про физиологию мозга Не дам. Сами на ходу придумываются.
Понятно.
Моему 5-и летке это просто интересно, ему интересны разные операции с цифрами интересно считать туда и обратно, интересно счет через единицу, как раз сначала считает все нечетные, затем четные цифры , считает десятками, любит писать большие (4,5,6,7 и т.
а за что ругает??? за то, что научить не может??? в сад таких учителей, которые могут “учить” только тех, кто уже все знает!
Да-да, а вес класс будет сидеть, деградировать и ждать когда там эту единственную девочку читать научат и дотянут до уровня остальных детей.
Умница Ваш малыш. А он умеет умножать и делить? И как он понимает четные и нечетные числа? Вот если его спросить: Какие ты знаешь четные\нечетные числа? Почему они четные\нечетные? Ведь для того, чтобы ответить на этот вопрос он должен хорошо знать умножение\деление.
Нет, умножать делить пока не учили, хотя он и интересуется таблицей умножения, если найду хорошее пособие обучающее, при случае куплю ему.
Четные числа это те, которые можно разделить на 2, на 2-е равные части, не четные соответственно нельзя. Про то, что может быть остаток у числа мы не разбирали, разбирали только числовую прямую -1, 0, 1 объясняли про бесконечность (ребенок задался этим вопросом после взгляда на уличный градусник), ну и на уроках в школе они уже разбирают такие понятия как отрезок, линия, ломаная линия, луч это, кстати, из Патерсона для 5-6 леток.
а так весь класс получает ценнейшие знания, пока учтель ругает девочку.
Ну а пойдет он в школу – все это знает и умеет. Ему там станет скучно и не интересно.
Мир безграничен – зачем обязательно изучать школьную программу?
Занимаемся по книжкам изд-ва Стрекоза (серия с Дружком, 6+, Математика, Считаем до 20 и пр.) – и там есть это понятие. Ответ “тебе рано про это знать, зайка” ребенка не удовлетворяет Вообще книжки улетные – когда деть болеет, это мое спасение. Пока занята – готовлю, убираюсь, дела делаю, ребенка не видно и не слышно – сидит сам разбирается. Правда хватает ненадолго – одна книжка 3-4 занятия максимум.
Собственно, вопрос как объяснить, а не зачем изучать.
Вот мы зайцам уши и пририсовывали, чтобы построить по парам. Только уж больно муторно, “отоварить” десяток зайцев ))
Будем пробовать с конфетами, спасибо
на конфетах или машинках покажите, через что им нравится они быстро понимают.
Ну просто знаете, некоторые пятилетки интересуются такими вещами. Что, не отвечать?
Открыть тему в окнах
Знаменитости в тренде
Наталья Сергунина: «Московские сезоны» в честь Дня народного единства представят на ВДНХ патриотическую программу
Инсульт отразился на внешности Елены Прокловой
Семь идей для активного досуга школьника на осенних каникулах
четных и нечетных чисел | Определение, факты и примеры
Этот урок посвящен двум широким категориям чисел в математике: четным и нечетным.
Что такое четные и нечетные числа?
Число четное, если его можно разделить поровну на два, и нечетное, если его нельзя разделить поровну.
Чтобы лучше понять классификацию, давайте рассмотрим следующий сценарий:
Грег и Джейк покупают 6 кексов.
Если разделить кексы поровну, каждый получит по 3.
Доля Грега
Доля Джейка
Поскольку Грег и Джейк могут разделить кексы поровну, мы знаем, что 6 — четное число.
Теперь давайте попробуем разделить эти 9 конфет между Амандой и Сандрой.
После того, как Аманда и Сандра получат по 4 конфеты, останется 1 конфета.
Доля Аманды
Доля Сандры
Остаток
Мы не могли разделить конфеты поровну между двумя, поэтому 9является нечетным числом.
Можете ли вы определить четные и нечетные числа с помощью пары?
Сопряжение — это еще один способ узнать, является ли число четным или нечетным. Число является четным, если его можно сгруппировать в пары или двойки, и нечетным, если его нельзя сгруппировать в пары.
Возьмем, к примеру, эти пары носков:
У нас здесь 6 пар носков, значит, 12 — четное число.
Теперь проверим, четное или нечетное количество здесь варежек.
Разобьем их на пары и посмотрим, не остались ли они непарными.
У нас здесь 7 пар и одна непарная варежка. Это показывает, что 15 – нечетное число.
Можете ли вы определить четные и нечетные числа, используя крайнюю правую цифру?
Самый простой способ определить четное или нечетное число — посмотреть, на что оно заканчивается.
Числа, оканчивающиеся на 0, 2, 4, 6 или 8, четные.
Числа, оканчивающиеся на 1, 3, 5, 7 или 9, являются нечетными.
Если расставить числа по порядку, то обязательно заметите закономерность.
Да, нечетные и четные числа чередуются друг с другом. Этот чередующийся узор продолжается и продолжается, независимо от того, сколько цифр в числе! На самом деле цифры — это просто комбинация цифр от 0 до 9, не так ли?
Теперь твоя очередь!
Щелкайте по кругу, чтобы найти шесть четных чисел
Сброс
Как видите, на самом деле имеет значение крайняя правая цифра числа. Вам не нужно беспокоиться о других цифрах.
На этот раз больше!
Проверьте, являются ли следующие числа четными или нечетными.
1) 1 564 – даже
2) 256 789 – ODD
3) 899 251 – ODD
4) 39,857 – ODD
5) 996 966 – даже
Hide
. независимо от того, насколько велико число, это эмпирическое правило определенно сработает.
Краткий обзор
Если вы можете разделить количество элементов на две группы с одинаковым количеством элементов в каждой, число будет четным.
Если у вас остались какие-либо остатки при делении количества предметов на две равные группы, число будет нечетным.
Если вы можете соединить предметы в наборе, значит, в наборе четное количество объектов. Если остались какие-либо остатки, набор имеет нечетное количество объектов.
В целой числовой последовательности четные и нечетные числа чередуются друг с другом.
Число с 0, 2, 4, 6 или 8 в качестве крайней правой цифры является четным. Число с 1, 3, 5, 7 или 9так как крайняя правая цифра нечетная.
Пройди тест на четные и нечетные числа прямо сейчас!
Прогресс
Перезапустить тест
Извините, ваш ответ неверен.
Ответ:
Медоносные пчелы умеют различать четные и нечетные числа
- Медоносные пчелы — первые существа, не являющиеся людьми, которые продемонстрировали способность различать четные и нечетные числа.
- Эксперимент с медоносной пчелой может привести к лучшему пониманию того, как люди выполняют задачи на четность (четное или нечетное число).
- Задачи четности могут быть не такими сложными, как считалось ранее.
Люди настолько умны, что легко различают четные и нечетные числа. И пока не появилось новое исследование, люди считали, что мы единственный вид, способный на этот подвиг, известный как задача на паритет.
Все может измениться, когда станет известно, что медоносные пчелы могут научиться различать четные и нечетные группы. Мозг размером лишь в несколько раз меньше нашего — человеческий мозг состоит из 86 миллиардов нейронов, а 9Мозг 0159 медоносной пчелы отстает от одного миллиона нейронов — либо игра на четность не так сложна, как мы когда-то думали, либо у медоносных пчел просто другой способ обучения четности.
Исследование , опубликованное на прошлой неделе в журнале Frontiers in Ecology and Evolution, показало, как медоносные пчелы «продемонстрировали способность изучать понятия четных и нечетных», а затем применяли эти понятия к числам, большим, чем считали исследователи.
мог понять. Все это было довольно впечатляюще для летающего насекомого.
«Результаты должны стимулировать дальнейшее тестирование обработки паритета у более широкого круга животных, чтобы получить информацию о его потенциальных биологических корнях, эволюционных движущих силах и потенциальных технологических инновациях для обработки понятий», — пишут авторы. «Эти результаты показывают, что задачи обработки нечетных и четных чисел потенциально имеют биологическую основу в том, как числа обрабатываются за пределами культурной передачи».
Больше животных + математика
- Эти рыбы умеют считать, но никто не знает почему
- Жемчуг может содержать секрет более прочной брони
В ходе исследования наши доблестные пчелы-герои были разделены на две контрольные группы. Показывая пчелам карточки с напечатанными фигурами от одной до десяти, одну группу обучали ожидать, что приземление на карточки с четными номерами принесет им приятное лакомство с сахарной водой.
Напротив, приземление на карты с нечетными номерами приводило к горькому на вкус хинину. Другая группа узнала обратное. Урок чет-нечет продолжался до тех пор, пока пчелы не могли выбрать правильный ответ по крайней мере в 80% случаев.
В то время как люди доказали, что они могут быстрее обрабатывать четные числа, медоносные пчелы показали обратное; группа, получавшая сахарную воду для групп с нечетными номерами, училась быстрее.
Посмотреть полную публикацию на Youtube
Затем исследование резко продвинулось вперед, превысив предыдущий предел в десять и включив группы из 11 или 12. Пчелы сохранили более чем 70-процентную точность в мастер-классе.
Авторы говорят, что им потребуются дальнейшие исследования, чтобы понять, как медоносные пчелы научились классифицировать числа по четности, и является ли это когнитивно сложным, простым или позволяет ли им это делать ранее существовавший нейронный механизм.