Четные и нечетные числа таблица: Четные и нечетные числа — как объяснить ребенку четные и нечетные числа?
Этапы урока |
Деятельность учителя |
Деятельность ученика |
Комментарии |
| I. Орган-й момент. | – Прозвенел звонок и смолк. Начинается урок. И как всегда с нами будут учиться наши друзья: Катя и Вова. |
Слушают учителя. | Регулятивные УУД: – волевая; саморегуляция. |
| II. Актуализация знаний.
III.
IV. Формулирование темы и цели урока.
V.
VI. Самостоятельное применение знаний.
VII. Итог урока. Рефлексия.
VIII. Домашнее задание. |
– Начнём урок с математической
разминки. Важна она? Чем? – Задания вам
приготовили наши друзья. – Кто справился с заданием? – А теперь выполним Катино задание (часть ребят работает по карточкам, часть с “цепочками”. Далее открываем “секретик” в “цепочке” (там-конечный результат – число 10). – Назовите результат в “цепочке”. – Кто справился с заданием? – Ребята, а что мы можем рассказать об этом числе? Какое оно? Обсудите в парах. – Молодцы, мы многое можем рассказать о числах (на доске появляются карточки под табличкой ЗНАЕМ: – круглые, – однозначные – многозначные). – Ребята, а почему не открыта ещё одна карточка? – Предлагаю это узнать. Работать будем по рядам в парах. А помогут нам счётные палочки. 1 ряд – положите перед собой 8 палочек, 2 ряд – 6
палочек, 3 ряд – 10 палочек. – Что можно сказать про числа 8 (6,10)? – Теперь положите перед собой 5 (7,9) палочек и разложите их по 2. – Все палочки разложили? – Что можно сказать про числа 5, 7, 9? – Давайте сделаем вывод: какими могут быть числа? (Слайд)
– Какая же тема нашего урока? Назовите её. – А как в математике называются числа, которые делятся (не делятся) на 2?
– Что нам поможет найти ответ на этот вопрос? – Откройте учебник на с.66. Назовите тему урока. (Тема – на доске + слайд). А теперь давайте определим цель нашего урока, чему научимся к концу урока?
– А в жизни нам эти знания пригодятся? Где?
– А теперь найдите и прочитайте, какие числа
будут чётными и нечётными.
– Достаточно ли только знать знать про эти числа? – Для этого в парах выполним задание № 3 с.66. – Теперь нечётные числа умно-жим на два и запишем равенства. (Один ученик у доски) – Какие числа умножали на 2? – Каким получился результат? – Какой вывод можно сделать? – Как вы думаете, если я чётное число умножу на два, каким числом будет произведение? Проверим? (Слайд). Выпишите равенства, в которые вместо звёздочки можно вставить знак умножения. Какие равенства выписали? – Какие числа умножали на 2? – Каким получился результат?
– Наш урок подходит к концу. – Давайте подведём итоги. – Какая была тема урока? – Объясните, пользуясь схемой, что нового вы
узнали про числа (слайд). – Кто теперь может предположить, что записано на карточке? – Какую цель мы ставили перед собой в начале урока? Достигли мы её? – Кто из ребят помогал открывать знания? – Оцените свою работу. С.67, №5 (любая задача), №8 (любой пример), №9 (кого заинтересовала новая тема). – Спасибо за урок. |
– Да, мы повторим то, что знаем, и
подготовимся к тому, что будем узнавать.
Дети оценивают свою работу.
Ребята выполняют работу. – Число 10. (Поднимают руку) – Оно двузначное, круглое.
– Наверно, мы что-то про числа не знаем.
Ребята выполняют работу в парах.
– Они делятся по 2.
– Нет, палочки остались. – Они не делятся по 2
– Числа, которые делятся и не делятся на 2.
Дети затрудняются с ответом. – Учебник.
– Чётные и нечётные числа.
– Мы научимся различать чётные числа и нечётные. (Появляется карточка на доске). Дети предлагают свои ответы (врач принимает по
чётным и нечётным дням, расположение домов:
чётная сторона – нечётная сторона). Идёт работа с правилом.
– Нет, надо закрепить полученные знания. Дети выполняют задание и самопроверку (слайд). Один ученик у доски (1*2=2, 3*2=6, 5*2=10, 7*2=14, 9*2=18) – Нечётные. – Чётным. – Когда нечётное число умножаем на 2, получаем чётное число. Дети выполняют задание и проверяют его.
– Чётные. – Чётным. – Когда чётное число умножаем на 2, получаем чётное число.
Дети отвечают на вопросы учителя, оценивают работу своих товарищей с помощью символов. (Приложение 3) |
Коммуникат-е УУД: -
формируем умение строить речевое высказывание в
соответствии с поставленными задачами.
Регулятивные УУД: – формируем умение определять цель своей работы. Коммуникативные УУД: 1) формируем умение оформлять свои мысли в устной форме; 2) формируем умение слушать и понимать других. Познавательные УУД: – формируем умение работать со схемами, таблицами Регулятивные УУД: – формируем умение осуществлять личностную рефлексию.
Регулятивные УУД: – формируем умение определять цель своей работы. Коммуникативные УУД: – формируем умение слушать и понимать других. Познавательные УУД: – формируем умение на основе анализа
результатов работы делать выводы.
Регулятивные УУД: – формируем умение определять цель деятельности на уроке.
Познавательные УУД: 1) формируем умение извлекать информацию из текста; 2) формируем умение на основе анализа объектов делать выводы. Личностные УУД: – опора на жизненный опыт.
Регулятивные УУД: – формируем умение оценивать учебные действия в соответствии с поставленной задачей.
Познавательные УУД: 1) формируем умение извлекать информацию из текста; 2) формируем умение выявлять сущность явлений; 3) формируем умение на основе анализа объектов
делать выводы. Коммуникативные УУД: 1) формируем умение слушать и понимать других; Познавательные УУД: – формируем умение выполнять умозаключение.
Регулятивные УУД: – формируем умение осуществлять познавательную и личностную рефлексию. Познавательные УУД: – формируем умение выявлять сущность явлений – формируем умение на основе анализа объектов делать выводы.
Регулятивные УУД: – формируем умение определять успешность своей работы в диалоге с учителем. |
Упражнение 8. Четные-нечетные. Супертренажер мозга для развития сверхспособностей [Активизируй «зоны гениальности»]
Упражнение 8. Четные-нечетные. Супертренажер мозга для развития сверхспособностей [Активизируй «зоны гениальности»]
Четные-нечетные. Супертренажер мозга для развития сверхспособностей [Активизируй «зоны гениальности»]ВикиЧтение
Супертренажер мозга для развития сверхспособностей [Активизируй «зоны гениальности»]
Могучий Антон
Содержание
Упражнение 8. Четные-нечетные
Назовите в первом ряду чисел все нечетные числа в порядке возрастания, во втором ряду – все четные в порядке возрастания, а в третьем ряду называйте поочередно: одно четное, одно нечетное, также в порядке возрастания, следя за тем, чтобы не пропустить ни одного.
18 234 87 95 46 3 871 114 55 29 11
78 45 332 90 123 84 99 657 73 12 3
67 451 23 129 61 95 34 37 48 57 88
Данный текст является ознакомительным фрагментом.
Упражнение 7
Упражнение 7
Таблица фиксированных образных кодов двузначных чисел от 41 до 60
Выучите образные коды представленные в таблице фиксированных образных кодов двузначных чисел от 41 до 60. Тренируйтесь в перекодировании по таблице случайных чисел. Таблица случайных чисел от 41
Тренируйтесь в перекодировании по таблице случайных чисел. Таблица случайных чисел от 41
Упражнение 8
Упражнение 8 Таблица фиксированных образных кодов двузначных чисел от 61 до 80 Переведите в образные коды числа из таблицы. Тренируйтесь до тех пор, пока преобразование одного числа в буквенный код не будет составлять одну секунду. Таблица случайных чисел от 61 до
Упражнение
Упражнение Запомните несколько списков слов разными способами. Сравните, какой метод эффективнее лично для вас.Список 1КофеМореЭкранДверьКранКоньГромДроздКрайМифСписок
Упражнение
Упражнение Запомните постепенно вашу личную числовую информацию: номера и пин-коды банковских карт, номера документов, телефоны родных и друзей, даты их
Упражнение
Упражнение
Как известно, самые надежные компьютерные пароли содержат в себе буквы, числа и специальные знаки. Заведите и запомните сложные пароли, защитив тем самым свои данные. Буквы можно закодировать словами, которые начинаются с этой буквы. Специальные символы –
Заведите и запомните сложные пароли, защитив тем самым свои данные. Буквы можно закодировать словами, которые начинаются с этой буквы. Специальные символы –
Упражнение
Упражнение Прочитайте небольшую статью. Выделите в ней смысловые блоки. Запишите основные идеи этих блоков с помощью тезисов. Выделите ключевые слова и запомните их. Попробуйте пересказать статью, после чего сверьте рассказ с оригиналом.Почаще проделывайте это
Упражнение
Упражнение Составьте интеллект-карту, описывающую метод мест. Визуальное конспектирование поможет вам лучше освоить эту
Упражнение
Упражнение
Опишите с помощью интеллектуальной карты ваш вчерашний или завтрашний день. Пусть размер элементов карты отражает затраты времени, а цвет обозначает важность того или иного дела.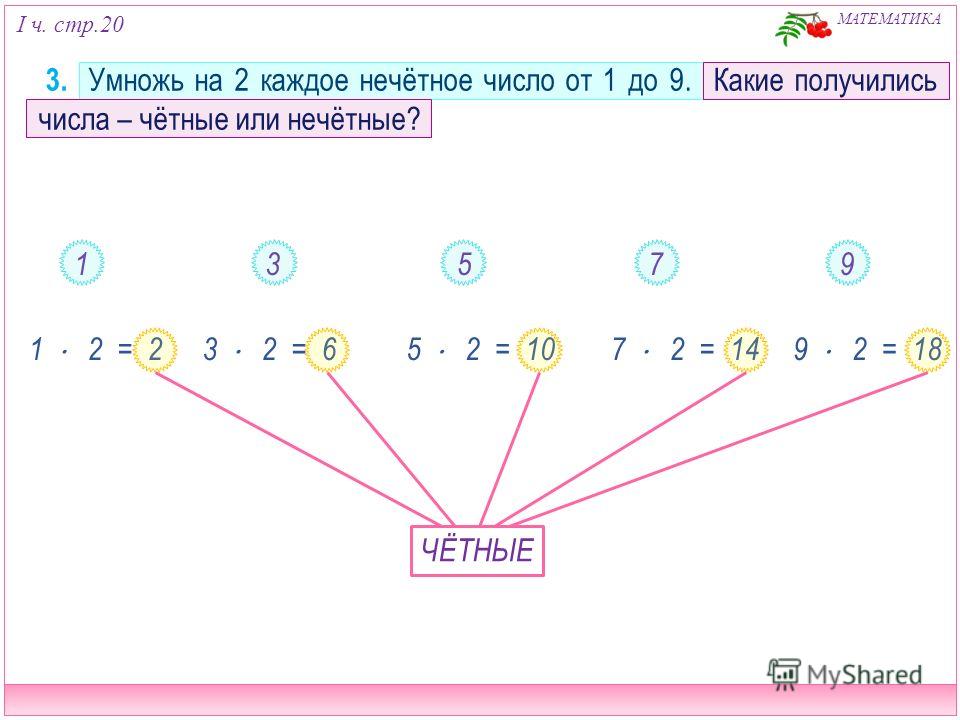 Секретно
Из дела оперативной разработки на гражданина Аргентины Хосе Альвареса
Секретно
Из дела оперативной разработки на гражданина Аргентины Хосе Альвареса
Упражнение
Упражнение Понаблюдайте за собой в течение одной-двух недель. Оценивайте свою работоспособность по семибалльной шкале от –3 до +3 и записывайте данные о ней несколько раз в день. Обобщив графики, вы получите средний суточный цикл работоспособности. После этого
Упражнение
Упражнение Чтобы тренировать способность концентрироваться, работайте иногда в трудных, отвлекающих условиях. Включите телевизор, откройте окно или пойдите в шумное место. Со временем усложняйте задачу: включите телевизор и радио одновременно.Это трудное упражнение –
Упражнение
Упражнение
Находите необычные черты в фотографиях самых разных людей в газетах, журналах и в Интернете. Навык быстрого восприятия лица и определения необычной черты должен быть доведен до автоматизма.Начните с лиц того типа, который распространен в вашей стране. Затем
Навык быстрого восприятия лица и определения необычной черты должен быть доведен до автоматизма.Начните с лиц того типа, который распространен в вашей стране. Затем
Упражнение
Упражнение Продолжайте изучать портреты людей в журналах, газетах и на сайтах. Можете взять справочник «Кто есть кто?» в своей профессиональной области. Изучайте внешность интересующих вас людей и запоминайте информацию о них. Эти знания вам пригодятся. Установки.
Упражнение
Упражнение Продолжайте работать с фотографиями людей. Составляйте их словесные портреты по приведенной системе. Делайте это при просмотре фильмов, новостей, наблюдении за окружающими людьми. Наблюдательность разведчика складывается из двух вещей: знания признаков, на
Упражнение
Упражнение
Усложните предыдущее задание. Попробуйте описать собеседнику общего знакомого, известного актера или политика так, чтобы он узнал его по словесному портрету. При составлении портрета придерживайтесь последовательности. Потом поменяйтесь ролями.
Установки.
Попробуйте описать собеседнику общего знакомого, известного актера или политика так, чтобы он узнал его по словесному портрету. При составлении портрета придерживайтесь последовательности. Потом поменяйтесь ролями.
Установки.
Упражнение № 15: Ароматное упражнение
Упражнение № 15: Ароматное упражнение Вы знаете ее любимые духи? Или запахи, которые она любит?Узнайте, если вы еще не в курсе. Поисследуйте ее полку в ванной комнате.К большинству парфюмов продают сопровождающие средства по уходу. Кремы, скрабы для тела, масла – продавец
Программа на Python для вывода четных чисел из списка
Имея список чисел, напишите программу на Python для вывода всех четных чисел в заданном списке.
Пример:
Ввод: список1 = [2, 7, 5, 64, 14] Вывод: [2, 64, 14]
Ввод: список2 = [12, 14, 95, 3] Вывод: [12, 14]
Метод 1: Использование цикла for
Перебрать каждый элемент в списке с помощью цикла for и проверить, соответствует ли num % 2 == 0.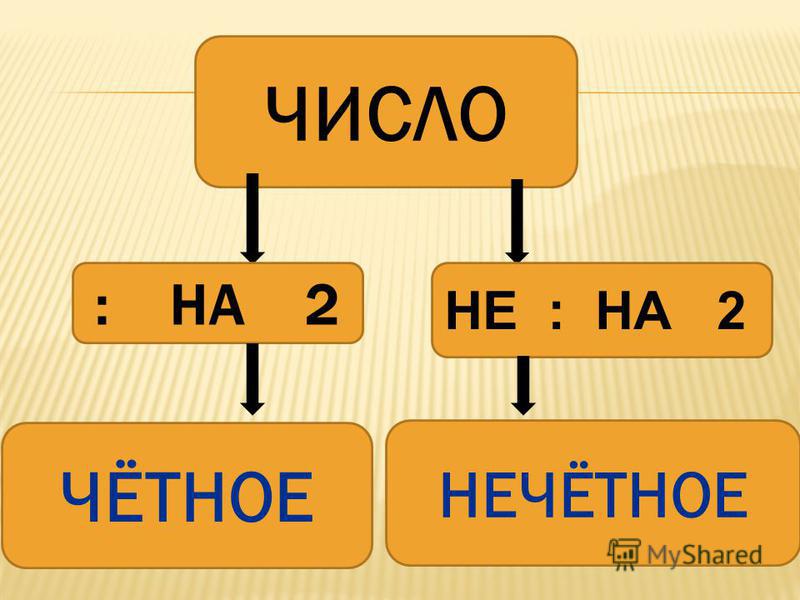 Если условие выполняется, то вывести только число .
Если условие выполняется, то вывести только число .
Python3
Я0036 |
Вывод
10 4 66
Временная сложность: O(N)
Вспомогательное пространство: O(1), поскольку постоянное дополнительное пространство используется.
Метод 2: Использование цикла while
Python3
|
Выход
10 24 4 66
Временная сложность: O(N)
Вспомогательное пространство: O(1), поскольку постоянное дополнительное пространство используется.
Method 3: Using list comprehension
 Открытие нового знания.
Открытие нового знания. Первичное закреп ление.
Первичное закреп ление. Начнём с задания
Вовы.(“в парах проверить таблицу умножения и
деления на 2”).
Начнём с задания
Вовы.(“в парах проверить таблицу умножения и
деления на 2”). Разложите ваши палочки
по 2. Сколько пар получилось?
Разложите ваши палочки
по 2. Сколько пар получилось?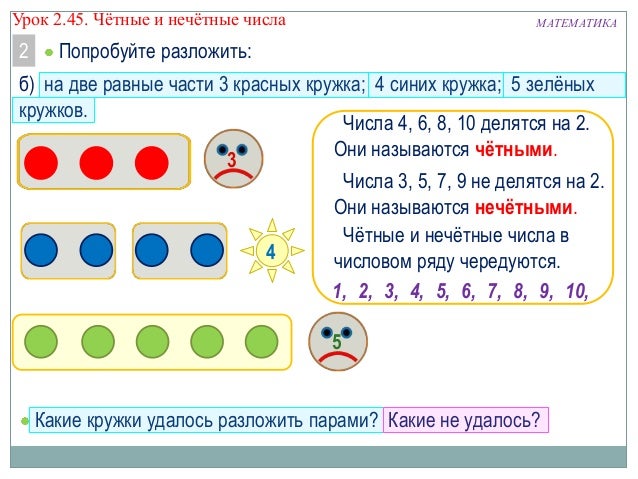






 0036
0036 Давшие номера в списке: 10 4 669
Давшие номера в списке: 10 4 669 

 Мы обходим все элементы в списке и проверяем, не элемент&1 . If condition satisfied then we say it is an even number
Мы обходим все элементы в списке и проверяем, не элемент&1 . If condition satisfied then we say it is an even number

 . . .
. . . 

 Если вычесть 2, мы получим 2\left( {a + b + 1} \right).
Если вычесть 2, мы получим 2\left( {a + b + 1} \right).