Четные и нечетные числа правило: Четные и нечетные числа — как объяснить ребенку четные и нечетные числа?

Играем в математику. Чётные? Нечётные? О чём это вы?: janemouse — LiveJournal

У меня сегодня был очень интересный урок – в рамках семинара для учителей.
Группа учителей подобралась отличная – все активные, заинтересованные, улыбающиеся!
Если бы во всех начальных школах были такие учителя, можно было бы с куда большим оптимизмом смотреть на развитие образования в этом городе и его окрестностях.

В самом начале семинара у меня был открытый урок с семилетками – на час примерно.
Из шести детей – три Сони )
Очень мне понравилось с ними играть.

Начали мы с простых вещей, чтобы точно у всех получилось.
Я тебе кидаю мяч и говорю число,
а ты мне мяч кидай обратно и говори число на 1 больше.
-Семь. – Восемь!
-Одиннадцать? – двенадцать!
-19 – 20.
39 – 40

Это всем легко, и в 6 лет тоже, потому что надо просто сказать следующее число, следующее слово в скороговорке.

Теперь я тебе число, а ты мне – число на 2 больше.
Это сложнее, но тоже справляются.
-14 – 16
11 – 13
9 – 11
16 – 18

Отлично,
а теперь я тебе число, а ты мне – число на один меньше.
Это уже половине не то, чтобы сложно, но требуется время для ответа (пробормотать тихонько ряд числительных до нужной точки)

Я тебе число, а ты мне – число на 2 меньше.
Это сложнее, и не все могут.
Но некоторые рвутся в бой. Хорошо же ))
Я тебе говорю число, а вы мне – число на 10 больше моего.
(Родители и учителя считают, что я дала очень простое задание. Ха-ха. Как бы не так!)
-Уууу, – тянут дети. – Это сложно.
-Ну, кто готов попробовать?
-Ну давайте, я попробую, – вызывается Соня.
-Четыре.
-Щас. – Соня начинает перебирать пальцами и бормотать. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14. Ага, будет 14!

Я тем временем выписываю на доске ряд чисел, один десяток под другим, чтобы было удобнее отсчитывать.
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25…

Тогда и другие дети решают попробовать, и некоторые даже, кажется, в итоге поняли идею.
Ну, не на сто процентов поняли, но хоть немного приблизились к пониманию.

После этого похлопали по коленкам – громко-тихо, громко-тихо, называя числа
ОДИН – два – ТРИ – четыре – ПЯТЬ – шесть
Это всем легко, идею все поняли, отлично.

Тогда давайте нарисуем улицу, и с одной стороны улицы у нас дома 12, 14, 16, а какой следующий дом на той же стороне?

А на другой стороне улицы дома с номерами 11, 13, 15, а потом?
Кому-то это уже не настолько очевидно…

А потом мы делили шоколадки – и дети пытались выяснить, почему одни шоколадки можно поровну на двоих поделить, а другие – не получается.

Потом делили бумажные шоколадки из 12, 14, 24 клеточек.
Эти все делились без проблем.
А вот можно ли разделить поровну 32 клеточки?
Тут мнения разделились…

Я предполагала дать и несколько задач более сложных, но вскоре обнаружила, что некоторые дети считают, что 100 – это аж два десятка. то есть, ой, четыре.
После этого я решила в такие дебри не лезть )

Некоторые задачи в итоге у нас остались без ответа,
мы их пообсуждали, но до решения сходу не добрались.
Мне очень нравится идея из книги А. З. Звонкина, что вопросы и задачи куда важнее, чем ответы и “разжевывание” решения.
Именно этим, по-моему, полезны олимпиады.
Правда, взрослым, увы, бывает страшно сложно удержаться и не подсказывать детям…

Если бы не было открытого урока в самом начале семинара, многие учителя бы мне не поверили, боюсь,
что у детей могут возникать сложности … на ровном месте.
Но эти дети играли активно, старались, и было очень хорошо видно, какие именно сложности у них возникают.

Альбом: семнар_учителям

Как объяснить детям знаки “больше” и меньше”, чтобы они их не путали?

На столе у меня сидел маленький “Квантик”, и помогал мне объяснять правила игры в чёрный ящик.
Мне очень нравится, как эту идею реализовали на сайте “дети и наука”, там и видео, и задачки для детей…

Заодно поговорили про учи.ру и про “олимпиаду “плюс”

Можно ли объяснить первоклашкам, что значит, что мы перебрали все варианты?
По-моему, нет. ..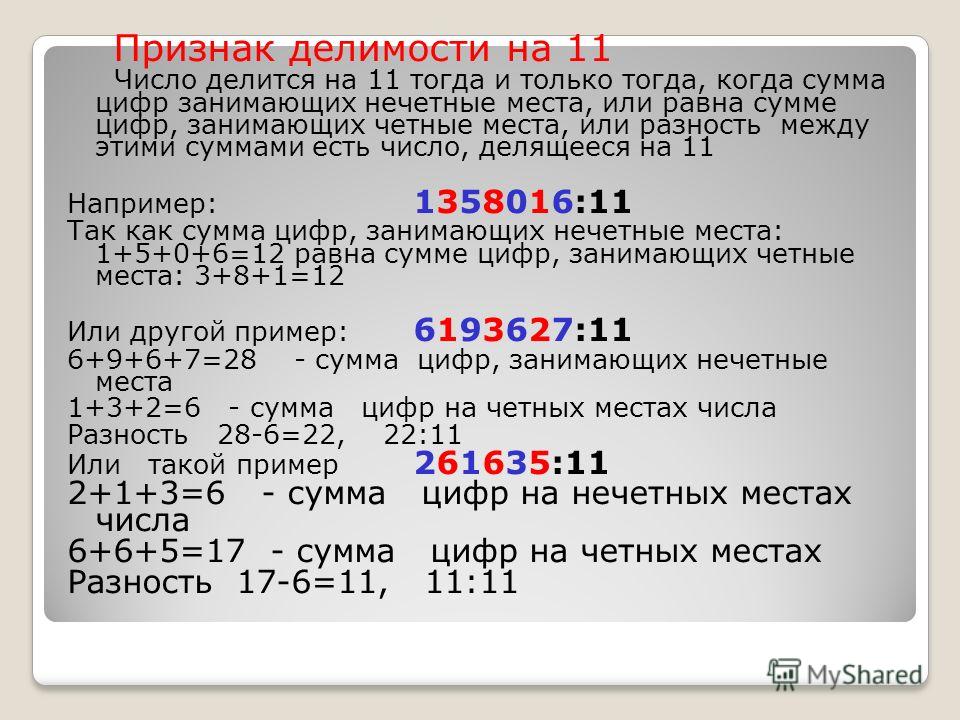

вредно ли считать на пальцах

А ещё у меня вышла новая книжка,
“Математика вприпрыжку”,
но про это я ещё потом подробнее напишу!

В следующие выходные – мат игротека
регистрация ведущих и участников

Четные и нечетные числа – презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Урок: Математика

тема:
Четные и
нечетные числа

2. Чему мы должны научиться:

• Познакомиться с понятиями
«Четные и нечетные числа»
• Научиться определять
четное число или нет;
• Закрепить наши знания
таблицы умножения и
деления на 2

3.

Устный счет: Что неизвестно? Как найдем?множитель
2
2
множитель
9
9
произведение
7
2
16
5
6
14
12
10
Разложите по два:
6 красных кружков
9 синих кружков,

5. Разложите на две равные части:

• 3 красных кружка
• 4 синих кружка,
• 5 зелёных кружков ,

6. Числа которые можно разделить на 2

2, 4, 6, 8, 10,
12, 14, 16, 18, 20,
22, 24, 26, 28, 30,
32, 34, 36, 38, 40,
42, 44, 46, 48, 50,
52, 54, 56, 58, 60,
62, 64, 66, 68, 70,
72, 74, 76, 78, 80……….

7. Я правило запомни меня!

Числа, которые делятся
на 2, называются
четными,
а которые не
делятся на
2 – нечетными.

8. Запиши по порядку числа от 10 до 19

10 11 12 13 14 15 16 17 18 19
Обведи кружками четные числа
Подчеркни нечетные числа
Откройте учебник на
странице 20
• Посмотрите на поля, какое там
задание?
• Какие четные номера домов
пропущены?
• Какие нечетные номера
домов пропущены?

10.

Умножь на 2 каждое нечетное число от 1 до 9. Какие получились числа четные или нечетные?Умножь на 2 каждое нечет ное
число от 1 до 9. Какие
получились числа чет ные или
нечет ные?
Умножь на 2 каждое чет ное
число от 1 до 10. Какие
получились числа чет ные или
нечет ные?
• 1 *2 =2
• 2*2 =2
• 3 *2 =6
• 4*2 =8
• 5 *2 =10
• 6 *2 =12
• 7 *2 =14
• 9 *2 =18
• 8*2 =16
• 10 *2=20

11. Сделайте вывод:

При умножении и
четных и нечетных
чисел на 2 в результате
получаются четные
числа

12. Задача №4

13. Выполните Задание №6

2*6 =
18:9=
•12 : 2 * 3 =

14. Что нового вы узнали на этом уроке?

• Что есть числа четные и нечетные
Какие числа называются четными?
• Числа которые делятся на 2,
называются ЧЕТНЫМИ
Какие числа называются нечетными?
• Числа которые не делятся на
называются НЕЧЕТНЫМИ
2,

15. Запишите домашнее задание

• С. 21 №3,4,7
СПАСИБО
ЗА
УРОК

English     Русский Правила

ChemTeam: Округление

ChemTeam: округление

Правила округления

Вернуться в меню важных цифр

---

Теперь, когда “у всех” есть калькулятор, который выдает результат до шести-восьми (или более) цифр, важно, чтобы мы знали, как правильно округлять ответ. Типичное правило, которому учат, состоит в том, что вы округляете до пяти или более и округляете до четырех или менее.

ЭТО ПРАВИЛО НЕПРАВИЛЬНОЕ!

Однако, пожалуйста, не спешите бежать к своему учителю начальных классов и читать им акт о бунте!

Проблема заключается в округлении “в большую сторону” (увеличении) числа, за которым следует 5. Например, такие числа, как 3,65 или 3,75, округляются до ближайшей десятой.

Хорошо, посмотрим, смогу ли я это объяснить. Когда вы округляете, вы меняете значение числа, за исключением случаев, когда вы округляете до нуля. Следуя старым правилам, вы можете округлить число в меньшую сторону четыре раза (округление на единицу, два, три, четыре) по сравнению с пятикратным округлением в большую сторону (пять, шесть, семь, восемь, девять). Помните, что «округление» до нуля не меняет значение округляемого числа.

Предположим, вам нужно округлить очень большую выборку чисел. В среднем вы будете изменять значения в выборке вниз в 4/9 случаев по сравнению с изменением значений в выборке в сторону увеличения в 5/9 случаев.

Это означает, что среднее значение ПОСЛЕ округления будет больше, чем среднее значение ДО округления.

Это неприемлемо.

Мы можем решить эту проблему, изменив правило округления 5 округление «в меньшую сторону» (сохранение числа тем же) в пятидесяти процентах округлений — четные числа, за которыми следует 5. Тогда, в среднем, округление «в сторону» отменит округление «в большую сторону».

Следующие правила определяют порядок округления чисел до указанного числа цифр. Первые два правила более или менее старые. Правило третье — изменение по-старому.

При округлении вы проверяете цифру, следующую (т. е. справа) от цифры, которая должна быть последней цифрой в округленном числе. Цифра, которую вы изучаете, является первой цифрой, которую нужно отбросить.

1. Если первая отбрасываемая цифра меньше 5 (то есть 1, 2, 3 или 4), отбросить ее и все цифры справа от нее.
2. Если первая отбрасываемая цифра больше 5 (то есть 6, 7, 8 или 9), увеличьте на 1 округляемое число, то есть предыдущую цифру (до отбрасываемой цифры).
3. Если первая отбрасываемая цифра равна 5, округлите округляемую цифру до четной. Имейте в виду, что ноль считается четным при округлении.

---

Приведенные выше правила немного технические, поэтому вот несколько примеров.

Пример №1. Предположим, вы хотите округлить 62,53 4 7 до четырех значащих цифр. Посмотрите на пятую цифру. Это 4, число меньше 5. Следовательно, вы просто отбросите каждую цифру после четвертой, и исходное число округляется до 62,53.

(правило №1 выше)

Пример #2 — округлить 3,78 7 21 до трех значащих цифр. Посмотрите на четвертую цифру. Это 7, число больше 5, поэтому вы округляете исходное число до 3,79. (правило №2 выше)

Пример №3. Округлите 726,83 5 до пяти значащих цифр. Для этого необходимо посмотреть на шестую цифру. Это 5, так что теперь вы должны посмотреть и на пятую цифру. Это 3, а это нечетное число, поэтому вы округляете исходное число до 726,84. (правило №3 выше)

Пример №4. Округлите 24,8 5 14 до трех значащих цифр. Посмотрите на четвертую цифру. Это 5, так что теперь вы должны также посмотреть на третью цифру. Это 8, четное число, так что вы просто отбрасываете 5 и цифры, которые следуют за ним. Исходное число становится 24,8. (правило №3 выше)

Вот еще несколько примеров для правила №3.

Пример №5. Округлите 23,55 до 0,1 места. Для этого вы должны смотреть на сотые места (помните, мы собираемся сохранить десятые места в нашем ответе).

Это пятерка, поэтому теперь мы смотрим на следующую цифру внутрь (десятое место) и видим, что это пятерка, нечетное число. Поскольку мы округляем 5 (в сотых долях), мы должны округлить до четного числа. Ответ 23,6.

Пример №6. Округлите 23,65 до 0,1 места. Для этого вы должны смотреть на сотые места (помните, мы собираемся сохранить десятые места в нашем ответе). Это пятерка, поэтому теперь мы смотрим на следующую цифру внутрь (десятое место) и видим, что это шестерка, четное число. Поскольку мы округляем 5 (в сотых долях), мы должны округлить до четного числа. Ответ 23,6.

---

Обратите внимание на разные формулировки задач. Один говорит округлить до определенного числа значащих цифр, а другой тип говорит округлить до определенного десятичного разряда. В обоих случаях вам нужно смотреть на цифру справа от того места, где вы собираетесь закончить свой ответ. Например, если вы хотите округлить цифры до трех знаков, вы должны смотреть на четвертую значащую цифру. Если вы хотите округлить 0,01-е место, вы также должны посмотреть на 0,001-е место.

Цифра в этом месте указывает на округление в большую сторону (если это 6, 7, 8 или 9).) или округлить в меньшую сторону (если это 1, 2, 3 или 4).

Если значение, которое вы хотите округлить, составляет пять, вы ДОЛЖНЫ ТАКЖЕ просмотреть предыдущее значение. Если оно четное, вы округляете в меньшую сторону. Если это нечетно, вы округляете. Распространенный вопрос: «Считается ли ноль четным или нечетным?» Ответ четный.

Вот еще несколько примеров «правила пяти». Округлите до пяти. (Ответы внизу файла.)

3,075

3,85

22.73541

0,00565

2,0495

Последнее сложно (по крайней мере, для старшеклассников, сталкивающихся с этим впервые!). Девять округляется до десяти (не нуля), поэтому правильный ответ — 2,050, а НЕ 2,05.

Ваш учитель был бы настолько груб, чтобы включить задачи, подобные этой, в контрольную? В классе ChemTeam страдальцы (упс, я имею в виду студентов) научились кричать «ДА» в унисон на такие простые вопросы.

Наконец, прежде чем мы перейдем к проблемам. Студенты, когда они узнают это правило, любят применять его по всем направлениям. Например, в 2.0495, допустим, мы хотим округлить до ближайшего 0,01. Много раз студент ответит 2.04. Когда вас попросят объяснить, будет процитировано правило относительно пяти. Однако важным числом в этой задаче является девятка, поэтому правило заключается в округлении в большую сторону, и правильный ответ — 2,05.

---

Практические задачи

Округлите следующие числа, как указано.
До четырех цифр: С точностью до 0,1: С точностью до 0,01: С точностью до целого числа:
1) 2,16347 x 10  5  13) 3,64 25) 6,675 37) 56,912
2) 4,000574 x 10  6  14) 4,55 26) 0,4203 38) 3,4125
3) 3,682417 15) 7,250 27) 0,03062 39) 251,7817
4) 7,2518 16) 0,0865 28) 4,500 40) 112,511
5) 375,6523 17) 0,5182 29) 2,473 41) 63,541
6) 21,860051 18) 2,473 30) 7,555 42) 7,555
До двух цифр: До одного десятичного знака: До ближайшего 0,001: Округлить крайнюю правую цифру
7) 3,512 19) 54,7421 31) 5,687524 43) 2,473
8) 25,631 20) 100,0925 32) 39,861214 44) 5,396
9) 40,523 21) 1,3511 33) 104,97055 45) 8,235
10) 2,751 х 10  8  22) 79. 2588 34) 41.86632 46) 3,05
11) 3,9814 x 10  5  23) 0,9114 35) 0,03765 ​​47) 8,25
12) 22,494 24) 0,2056 36) 0,0045 48) 8,65
 

Ответы

Ответы на правило “округление до 5”

3,08

3,8

22,74

0,0056

---

Вернуться к меню «Значимые цифры»

Закон нечетных чисел, который можно использовать для пространственного проектирования в 3DCG

VR-сцена

Четверг, 30 апреля 2020 г.

В этой статье я хотел бы представить закон нечетных чисел, который можно использовать для пространственного проектирования в 3DCG.

Законы нечетных чисел, которые используются в композиции фотографий и расстановке мебели, будут объяснены в контексте 3DCG. Пожалуйста, проверьте это, если вы хотите думать о размещении логически.

В этой статье я расскажу о законе нечетных чисел, используя пространство, созданное в STYLY.

• 1 Что такое закон нечетных чисел?
• 2 Различия в композиции между четными и нечетными числами
  • 2.1 Композиция с четным числом предметов
  • 2.2 Композиция с нечетным числом предметов
• 3 Нечетная правильная композиция в 2D
• 4 Композиция по закону нечетные числа в трехмерном пространстве
• 5 Резюме впечатления, которое производят нечетные числа в космическом дизайне

Что такое закон нечетных чисел?

Закон нечетных чисел — это закон, согласно которому нечетные числа выглядят более стабильными, чем четные.

Он основан на трехчастном методе, используемом в фотографии, но это только одно из правил размещения и композиции, поэтому старайтесь использовать его, сохраняя хороший баланс.

Это правило не работает, если у вас большое количество объектов.

Правило нечетных чисел больше проявляется, когда объектов меньше, поэтому важно помнить об этом при размещении объектов.

Различия в композиции между четными и нечетными числами

Сначала давайте посмотрим на различия между композициями, расположенными в четных и нечетных числах.

Композиция с четным количеством объектов

На следующем эталонном изображении показан случай с четным количеством объектов.

Бывают случаи, когда четное число играет хорошую роль, но когда в ряд выстраивается четное количество объектов, люди склонны смотреть на остальные или на поля.

Это эффективный прием, когда вы хотите выразить настроение или мировоззрение .

Even low_picture

Источник ссылки на изображение: https://unsplash.com/photos/jzG_6EWvDyc

 

Композиция с нечетным количеством объектов

Это эталонное изображение с нечетным количеством объектов.

Объект, который вы хотите больше всего выделить в композиции, называется фокусом. Помня об этом и сводя общее количество объектов к нечетному числу, вы можете создать композицию, отражающую фокус.

Это эффективный метод , когда вы хотите выделить объект.

Нечетное low_picture

Источник ссылки на изображение: https://unsplash.com/photos/rvhn6_Y_Cmg

Состав правила нечетных чисел в 2D

Теперь мы сосредоточимся на законе нечетных чисел.

Закон нечетных чисел в 2D следует помнить как основное правило, используемое в фотографии.

На следующем изображении показано понимание этого правила. Объект (1) является фокальной точкой, а (2) и (3) служат для усиления фокальной точки.

Композиция закона нечетных чисел в 2D

Композиция закона нечетных чисел в 3D пространстве

На этом изображении показан пример пространственного дизайна, в котором мебель размещается в пространстве 3DCG с учетом закона нечетных чисел.

В случае с пространственным дизайном, если вы слишком внимательно относитесь к фокусам в каждой точке, вы получите слишком много элементов, и впечатление станет тяжелым.

В этом случае луна и три огонька помещаются в сумме. Вы можете видеть, что освещение придает комнате трехмерный эффект и стабилизирует размещение. Я осознаю цветовой тон, который не мешает другим объектам.

Spatical design_room_01

 

В этом случае окно, стол и книжная полка окрашены в более темные тона, чтобы отразить закон нечетных чисел. Диван немного белый, но расстановка черной мебели очень стабильная.

В данном случае я использовал монохромную мебель, чтобы не слишком сильно зависеть от цвета, но, учитывая цвет, вы можете логически подумать о расположении ближе к изображению.

Обе эти схемы используют закон нечетных чисел. Даже если цвета одинаковые, впечатление будет немного меняться в зависимости от того, где они выделяются.

Пространственное проектирование_комнаты_02

Краткий обзор впечатления, которое производят нечетные числа при проектировании пространства

Давайте еще раз повторим то, что я уже объяснял.

1. Закон нечетных чисел — одно из основных правил фотографии и верстки.
2. При использовании закона нечетных чисел в 2D помните о фокусе
3. В пространстве 3DCG посмотрите на общий баланс, чтобы добиться ощущения стабильности

Основные правила 2D могут не отражаться напрямую в 3D. Поэтому в космическом дизайне я чувствовал, что важнее помнить о балансе и использовать нечетные числа, чем о фокусных точках.

Источник ссылки на изображение: https://unsplash.com/photos/lyGKZzp-tb8

 

При рендеринге для композиции, как и в 2D, если учитывать закон нечетных чисел, баланс будет выглядеть более стабильным . При просмотре пространства распределение по точкам закона нечетных чисел стабилизирует размещение.

Законы нечетных чисел в трехмерных изображениях _ Резюме

 

Как вам?

Композиция, используемая в фотографии, также может быть применена к пространственному дизайну в 3DCG. В этой статье я сосредоточился на пространственном дизайне, но его также можно применить к постановке модели и композиции анимации.