Большая буква е в математике: как называется буква E в математике 11 класса.
Число е | Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия
С замечательным числом e мы впервые встречаемся, начиная изучать показательную функцию, логарифмы и производные. Поэтому для лучшего понимания мы рекомендуем вам прочитать наши статьи «Показательная функция» и «Геометрический смысл производной».
В статье «Показательная функция» мы говорили о важнейшем свойстве функции — при эта функция очень быстро растет. И не просто «быстро растет» — чем больше x, тем больше скорость ее роста, тем круче идет график. Можно сказать, что с увеличением x растут и значения показательной функции, и ее производная. А если аргументом показательной функции является время, то при такая функция является математическим выражением стремительно развивающегося процесса.
Среди показательных функций есть особенная. Называется она экспонента, ее формула . Особенность ее в том, что в каждой точке скорость роста этой функции равна значению самой функции в этой точке.
Другими словами, , то есть производная функции равна ей самой.
Нарисуем несколько графиков функции при , а также при . Среди этих графиков есть такой, что касательная к нему, проведенная в точке , идет ровно под углом к положительному направлению оси OX.
Это и есть график функции . Само число e — иррациональное, то есть выражается бесконечной непериодической десятичной дробью. Приблизительно оно равно 2,718.
Логарифм по основанию e называется натуральным и обозначается . Если в уравнении или неравенстве вам встретились такие логарифмы, вы работаете с ними так же, как и с любыми другими, у которых основание больше 1.
Функция также обладает интересным свойством:
Это значит, что с ростом x график логарифмической функции идет более и более полого, скорость роста его уменьшается, что мы и видим.
Формулы для производных функций и содержат в себе выражение :
Число e, как и число , является одной из мировых констант.
Число известно людям с глубокой древности. Оно равно отношению длины окружности к ее диаметру. А вот с числом e (названным так в честь великого математика Леонарда Эйлера) человечество познакомилось намного позже. Впервые его вычислил математик Якоб Бернулли в начале XVIII века, причем сделал это, решая чисто практическую задачу о начислении процентов на банковский вклад.
В заданиях вариантов ЕГЭ вам встречались задачи, где вклад величиной x помещен в банк под p % годовых. Найти нужно было, например, каким станет вклад через два года. Рассказывая о решении таких задач, мы вывели удобные формулы:
- если величину x увеличить на p процентов, получится
- если вклад пролежит в банке n лет, его величина станет равной
Итак, если вклад поместить банк под 10% годовых, он вырастет за год в 1,1 раз, за два года — в 1,21 раза, за десять — примерно в 2,6 раза.
Значит, рост вклада зависит от того, сколько он пролежит в банке, то есть сколько раз начисляются проценты. А что будет через сто лет? А если найти такой банк, где процент начисляется не раз в год, а раз в день? И пусть даже каждый день начисляется совсем небольшой процент, но ведь дней-то много! Верно ли, что можно положить в такой банк один доллар под одну сотую процента в день, а через пару десятков лет забрать из банка миллион?
Давайте так и сформулируем задачу. Пусть банк начисляет каждый день по одной сотой процента. Во сколько раз вырастет вклад через 10000 дней (это двадцать семь с лишним лет)? Иными словами, чему приближенно равна величина ? И к чему будет стремиться величина , если n стремится к бесконечности?
Вот такую задачу и решал Бернулли. Если n будет очень большим, или, как говорят математики, бесконечно большим, будет стремиться к бесконечности (то есть больше миллиона, больше миллиарда, больше двух миллиардов. . . ) — то величина будет, наоборот, очень малой.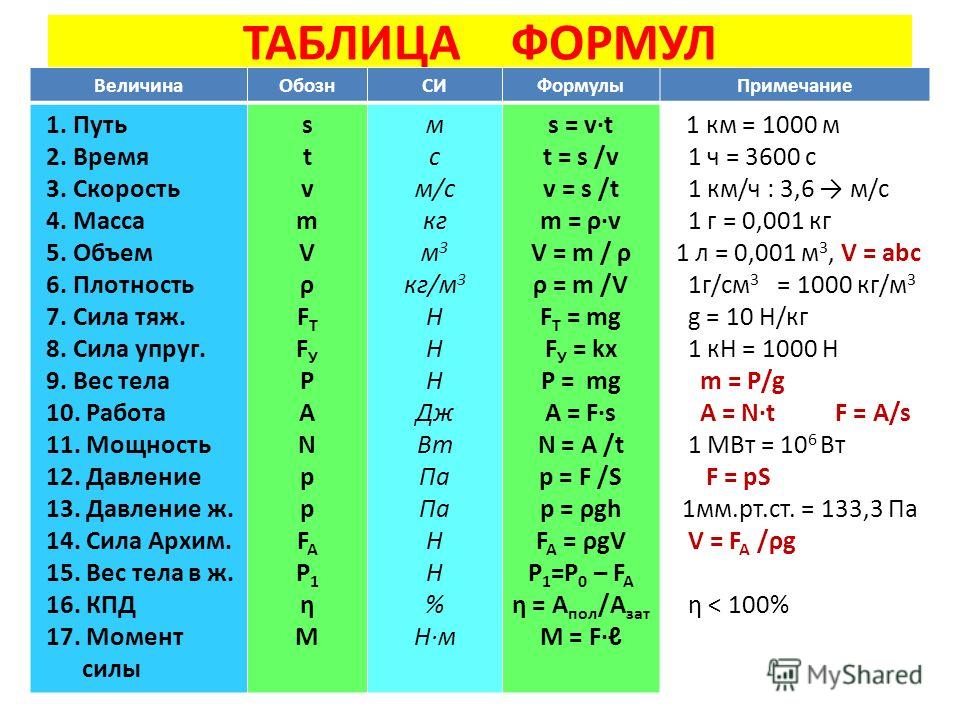
Можно сказать, что будет стремиться к нулю.
Оказывается, что в этом случае величина будет стремиться к числу e. Если банк каждый год начисляет по 1%, через 100 лет вклад увеличится примерно в e раз (напомним, что e ≈ 2,718). Еще большая точность будет достигнута, если каждый день банк начисляет по 0,01 процента. Через 10000 дней вклад увеличится примерно в e раз. Итак, если n стремится к бесконечности, то величина стремится к числу
Этот неожиданный факт называется вторым замечательным пределом. Вы встретитесь с ним в курсе математического анализа.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Число е» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена: 08.04.2023
Решение высшей математики онлайн
‹– Назад
В математике для записи сумм, содержащих много слагаемых, или в случае, когда число слагаемых обозначено буквой, применяется следующая запись:
которая расшифровывается так
| (14.1) |
где — функция целочисленного аргумента. Здесь символ (большая греческая буква “сигма”) означает суммирование. Запись внизу символа суммирования показывает, что переменная, которая меняет свои значения от слагаемого к слагаемому, обозначена буквой и что начальное значение этой переменной равно .
Запись вверху обозначает последнее значение, которое принимает переменная .
Пример 14.2 Вычислим несколько сумм:
1) .
2) . Так как в правой части стоит сумма геометрической прогрессии с первым членом равным и знаменателем прогрессии равным , то эту сумму легко найти
3) .
4) .
5) .
В курсе линейной алгебры чаще всего будут встречаться суммы вида . Здесь переменная с индексом рассматривается как функция от своего индекса. Поэтому
С помощью знака суммы формулу (10.1) скалярного произведения векторов можно записать так:
(14. 2) |
где для трехмерного пространства , для плоскости .
Для единообразия будем считать, что
и говорить, что это сумма, содержащая одно слагаемое.
Замечание 14.1 Буква, стоящая внизу под знаком суммы (индекс суммирования), не влияет на результат суммирования. Важно лишь, как от этого индекса зависит суммируемая величина. Например,
Или
в правой части никакой буквы нет, значит, и результат от не зависит.
Предложение 14.1 Множитель, не зависящий от индекса суммирования, может быть вынесен за знак суммы:
Доказательство этого предложения предоставляется читателю.
Предложение 14.
2
| (14.3) |
Это предложение является частным случаем следующего утверждения.
Предложение 14.3
| (14.4) |
Доказательство. Пусть
Тогда
Раскроем скобки в правой части этого равенства. Получим сумму элементов при всех допустимых значениях индексов суммирования. Слагаемые сгруппируем по-другому, а именно, сначала соберем все слагаемые, у которых первый индекс равен 1, потом, у которых первый индекс равен 2 и т.
д. Получим
Заменив в этом равенстве в левой части его выражением через знаки суммирования, получим формулу (14.4).
Замечание 14.2 Двойные суммы из равенства (14.4) можно записывать и без использования скобок
Нужно помнить, что двойная сумма означает сумму элементов для всех допустимых значений индексов суммирования. По этой же причине, если встречается запись, содержащая подряд три или более символов суммирования, то порядок расстановки этих символов можно менять произвольно.
Если границы изменения всех индексов суммирования одинаковы, то можно для суммирования по нескольким индексам использовать запись вида
Иногда под символом суммы указывают дополнительные условия, налагаемые на индексы суммирования. Так запись
означает, что в сумму не включаются величины , ,…, , то есть с равными индексами.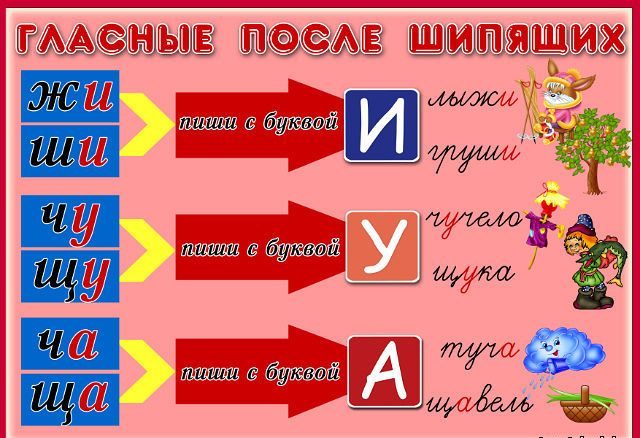
Иногда в записи суммы не указываются границы изменения индексов, например,
Такая запись используется, когда значения, которые могут принимать индексы, очевидны из предыдущего текста или будут оговорены сразу после окончания формулы.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Что означает E в математике?
Обновлено 20 декабря 2020 г.
Автор Chris Deziel
Буква E может иметь два разных значения в математике, в зависимости от того, является ли она заглавной E или строчной e. Обычно на калькуляторе вы видите заглавную букву Е, которая означает возведение следующего за ней числа в степень 10. Например, 1E6 будет означать 1 × 10 6 , или 1 миллион. Обычно буква E используется для чисел, которые были бы слишком длинными для отображения на экране калькулятора, если бы они были написаны от руки.
Математики используют строчную букву e для гораздо более интересной цели — для обозначения числа Эйлера. Это число, как и π, является иррациональным числом, потому что оно имеет неповторяющуюся десятичную дробь, простирающуюся до бесконечности. Подобно иррациональному человеку, иррациональное число кажется бессмысленным, но число, которое обозначает e, не обязательно должно иметь смысл, чтобы быть полезным. На самом деле, это одно из самых полезных чисел в математике.
E в научной записи и значение 1E6
Вам не нужен калькулятор, чтобы использовать E для выражения числа в экспоненциальном представлении.
Вы можете просто позволить E обозначать основной корень экспоненты, но только тогда, когда основание равно 10. Вы не будете использовать E для обозначения основания 8, 4 или любого другого основания, особенно если основание является числом Эйлера, e.
Когда вы используете E таким образом, вы записываете число x E y , где x — первый набор целых чисел в числе, а y — показатель степени . Например, число 1 миллион можно записать как 1E6. В обычных научных обозначениях это 1 × 10 6 или 1 с 6 нулями. Точно так же 5 миллионов будут 5E6, а 42 732 будут 4,27E4. При написании числа в экспоненциальном представлении, независимо от того, используете ли вы E или нет, вы обычно округляете число до двух знаков после запятой.
Откуда взялось число Эйлера e?
Число, представленное буквой e, было открыто математиком Леонардом Эйлером как решение проблемы, поставленной другим математиком, Якобом Бернулли, 50 лет назад.
Проблема Бернулли была финансовой. 9n
, где r равно 1, а n – период оплаты.
Оказывается, по мере того, как n приближается к бесконечности, результат становится все ближе и ближе к e, который равен 2,7182818284 с точностью до 10 знаков после запятой. Вот как это открыл Эйлер. Максимальный доход, который вы можете получить от инвестиций в размере 1000 долларов в год, составит 2718 долларов.
Число Эйлера в природе
Показатель степени с основанием e известен как натуральный показатель степени, и вот почему. Если построить график 9x
вы получите кривую, которая увеличивается экспоненциально, точно так же, как если бы вы построили кривую с основанием 10 или любым другим числом. Однако кривая y = e x обладает двумя особыми свойствами. Для любого значения x значение y равно значению наклона графика в этой точке, а также равно площади под кривой до этой точки.
Это делает e особенно важным числом в исчислении и во всех областях науки, которые используют исчисление. 9{bθ}
встречается повсюду в природе, в морских раковинах, окаменелостях и цветах. Кроме того, е появляется во многих научных контекстах, включая исследования электрических цепей, законов нагревания и охлаждения и демпфирования пружин. Несмотря на то, что оно было открыто 350 лет назад, ученые продолжают находить новые примеры числа Эйлера в природе.
Что означает буква «Е» на калькуляторе?
Обновлено 9 апреля 2023 г.
Автор Chris Deziel
Прописная буква «E» означает «показатель степени» на дисплеях калькулятора. Производители калькуляторов используют его для отображения чисел в экспоненциальном представлении, потому что длинную версию трудно отобразить и еще труднее прочитать. Чтобы усложнить ситуацию, некоторые производители калькуляторов используют строчную букву «е» для обозначения показателей степени, вызывая путаницу между научной записью и числом Эйлера, что совершенно другое.
Не обманывайтесь. Если на выходе вашего дисплея появляется прописная или строчная буква «e», это обозначает показатель степени. Единственное место, где вы увидите число Эйлера, — это число на клавиатуре или в виде константы, которую вы вводите.0003
TL;DR (слишком длинно, не читал)
На дисплее калькулятора E (или e) обозначает показатель степени 10, и за ним всегда следует другое число, которое является значением показателя степени. Например, калькулятор покажет число 2,5 триллиона как 2,5E12 или 2,5E12. Другими словами, E (или e) — это краткая форма научного обозначения.
Что такое научная запись?
Наука полна очень больших чисел и очень маленьких чисел, которые трудно читать и записывать. Например, масса земли 5,970 000 000 000 000 000 000 000 кг, а масса атома водорода 0,000000000000000000000000000167 кг. Научная нотация упрощает работу с этими числами, выражая 0 как степень десяти. Это помогает сжать многие десятичные знаки или несколько порядков в меньшее математическое выражение, которое легче читать.
Используя эти обозначения, масса Земли становится равной 5,97 × 1024 кг, а масса атома водорода становится равной 1,67 × 10-27 кг. Вместо чисел с длинными цепочками нулей, которые трудно сосчитать и еще труднее отобразить на маленьком экране, у вас есть более удобные десятичные дроби и показатели степени 10.
Научная нотация работает путем уменьшения числа, чтобы только одно число было меньше 10 перед запятой. Мы делаем это путем деления на определенную величину 10. В научной записи показатель степени множителя (10) почти всегда будет целым числом.
Выражение степени на калькуляторе
В своей письменной форме научная запись выглядела бы странно на калькуляторе. Это было бы запутанно и не поместилось бы на маленьком дисплее. Чтобы избежать этих проблем, производители создали символ «X 10». Этот символ либо E, либо e, в зависимости от калькулятора. За этой буквой всегда следует число, которое является показателем степени, до которой возводится 10.
На дисплее калькулятора масса Земли будет отображаться как 5,97E24 (или 5,97e24). Число 5,97 — это аргумент, а число 24 — показатель степени. Точно так же масса атома водорода будет равна 1,67E-27 (или 1,67e-27).
Другим примером из чистой математики может быть факториал числа. Например, ввод 20! (двадцать факториал) в калькулятор, скорее всего, вернет 2,432902E18. Указание, что это примерно 2,432902 квинтиллиона.
Ввод экспоненциального представления с клавиатуры
Набирать длинные цепочки нулей на блокноте калькулятора так же сложно, как и записывать их на бумаге, поэтому в калькуляторах есть ярлык. Это ключ ЕЕ. Чтобы ввести число в экспоненциальном представлении, сначала введите аргумент, затем нажмите клавишу EE и введите показатель степени. Например, чтобы ввести массу Земли, введите 5,97, затем нажмите клавишу EE и введите 24. На дисплее появится 5,97E24 (или 5,97e24). Обратите внимание, что число будет отображаться со всеми нулями, если они помещаются на экране.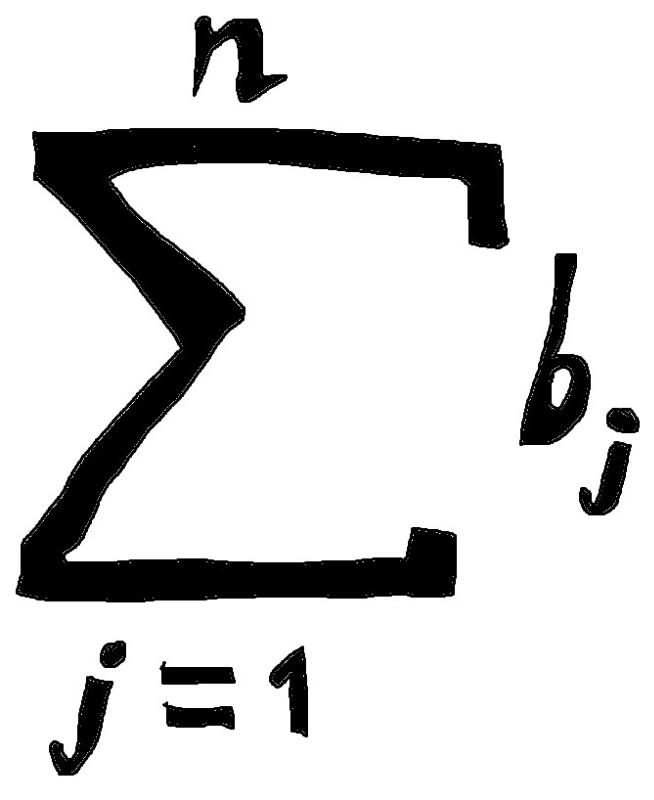
Например, если вы наберете 1.2 EE 5, на дисплее отобразится 120 000.
Не путайте экспоненты с числом Эйлера
Большинство научных калькуляторов выделяют специальный ключ для числа Эйлера, потому что это одно из самых важных иррациональных чисел в математике, которое используется во всех видах научных вычислений. Это клавиша «е». Нажмите ее, и число Эйлера появится на вашем дисплее с точностью, которую позволяет дисплей. Научный калькулятор на iPhone, например, показывает 2,718281828459045. Кроме того, в большинстве калькуляторов есть клавиша “e x“. Введите число, нажмите эту клавишу, и на дисплее отобразится значение 9.0019 e возводится в степень, которую вы ввели, как выражение экспоненциальной функции. В обоих этих случаях математическая константа e имеет особое значение как выражение научной записи.
Обычно вы можете выбрать варианты использования числа e по сравнению с буквой E (используемой для научного обозначения) по контексту, или вы можете найти букву «E», которая будет зажата между двумя другими числами.