Абак линейка как пользоваться: “Счеты первоклассника (АБАК), 2 цвета (СП05)”: рецензии и отзывы на книгу | ISBN 4620000639329

Абакус (Что это, Зачем и Как Обучаться)

Абакус (лат. abacus доска) счетная доска начала использоваться для арифметических вычислений с V века до н.э. в Древнем Риме и Греции.

Изначально абак представлял собой доску, разделенную линиями на полосы, а счет осуществлялся с помощью камушек или похожих предметов.

Самый древний абакус дошедший до наших дней представляет собой мраморную доску, с вырезанными углублениями размером 150×75 см. В этих выемках размешались соответствующего размера камушки, выполняющие функцию косточек современных счет. Найден он был в 1846 соду на греческом острове Саламис.

Примером современного абакуса послужил найденный 2200 лет назад на Дальнем Востоке абак, состоящий из рамки с прутьями, нанизанными на них деревянными бусинками.

Казалось бы, простой на вид предмет древности, ставший неотъемлемым предметом для счета в древности и неотъемлемой частью культуры Дальнего Востока, по своей сути является конкурентом современному компьютеру.

В XV веке абакус перекочевал в Японию, получив еще одно название — Соробан, и активно используется по сегодняшний день в системе образования младших классов для обучения счета вместо калькулятора.

Рамка – Держит все спицы, бусинки и разделительную линейку ва месте.

Спица – Это палочки, которые держат бусинки. Они двигаются вверх иди вниз по спине

Бусинки – Представляют числа на абакусе. Они двигаются по спице и прикасаются к разделительной линейке или рамке. Когда бусинки прикасаются к рамке, что значит ваш абакус обнулен.

Разделительная линейка – Линейка (обычно белая) которая пересекает все спины и разделяет их на «Братья» и «Друзья» бусинки. Только когда бусинки прикасаются к разделительной линейке, у них есть какое-то значение.

Единичная точка – Может быть использована как десятичная точка. Может быть использована как занятая, которая разделяет числа на тысячи.

Например: 102,387,555 = Сто два миллиона, триста восемьдесят семь тысяч, пятьсот пятьдесят пять

Бусинки – братья – Над разделительной линейкой есть только одна бусинка «брат» на каждой спице, бусинка «брат»

Бусинки – друзья –  Есть четыре бусинки-друга под разделительной линейкой на каждой спице. Каждая бусинка-друг равна ” 1 ”

Обнуление абакуса Традиционный способ

ШАГ 1: Поместите аоакус на столе.
ШАГ 2: Поднимите абакус так. чтобы нижняя часть все еще соприкасалась со столом. Это отправит псе нижние бусинки к «нулевой»” позиции.
ШЛГ 3: Осторожно поместите абакус назад на стол, не двигая нижние бусинки.
ШАГ 4; Затем, положите палец между верхней бусинкой и разделительнрой линейкой с левой стороны абакуса.
ШАГ 5: Проведите пальцем вдоль разделительной линейки пока не достигнете другого конца рамки.

Забавный способ; наездиочищение или паровоз

ШАГ 1: Соедините большой и указательный
ШАГ 2: Поместите пальцы с правой стороны разделитель нон линейки абакуса так, чтобы линейка была между пальцами и вы держите линейку.
ШАГ 3: Теперь поддерживайте абакус левой рукой так, чтобы он не двигался.
ШАГ 4: Затем, плавно проведите пальцами вдоль разделительной линии не разжимая с правой стороны рамки до левого края рамки.

Слева направо: Когда работаете c двузначными числами: всегда прибавлявляйте и отнимайте сначала десятичные цифры, а за тем работаете с единичными числами

Урок 1 . Бусинки- Друзья.

Значение бусинки-друга=1

Есть четыре бусинки-друга на каждой спице.

Используйте свой большой палец для того, чтоб подвинуть бусинки-друга вверх (прибавляя) гак, пок она не коснется разделительной линейки. Используйте свой указательный палец тля топ чтобы подвинуть бусинку-друга вниз (вычитая). Всегда обнуляйте абакус, вычищая все бусинки с разделительной линейки перед тем, как начать новы с чет. Установление цифр па абакусе:

— Номера десятичных чисел возвращаются к десятичной спице;

— Единичные числа возвращаются к единичной спице.

Урок 2. Введение. Бусинки-братья.

1. Значение бусинки-брата — 5

2. Есть только I бусикка-брат над разделительной линейкой на каждой спице.

3. Используйте свой указательный п*лдсц для того. чтобы подвинул. бусинку-брата вниз (прибавляя) лак. пока она не коснел ся разделительной линейки.

4. Используйте свой указательный пален для того, чтобы подвинуть бусинку-брата вверх (вычитая) так. пока она не коснется рамки.

5. Всегда обнуляйте абакус, вычищая нее бусинки от разделительной линейки перед тем. как начать новый счет.

6. Установление цифр на абакусе:

— Номера десятичных чисел возвращаются к десятичной спице;

— Единичные числа возвращаются к единичной спице.

Что такое абакус? Как считать на абакусе?

Автор IQКлуб На чтение 6 мин. Просмотров 5.9k. Опубликовано 08.12.2017

Многие люди слова абакус и соробан слышат, чуть ли не впервые. А ведь эта система подсчетов использовалась в Древней Греции, Риме и Китае еще за пять веков до нашей эры. Легкая система подсчета положила начало нашим классическим счетам с костяшками, но абак намного проще и понятней в использовании.

Детям система устного счета абакус полезна не только тем, что они научатся быстро считать и понимать цифры, со временем они обучаются ими пользоваться ментально, в воображении. Эта «игра» позволяет научить даже первоклашку очень быстро считать и выполнять абсолютно все арифметические действия, сначала с помощью специального прибора, а потом и в уме, для этого ему нужно будет только научиться считать до десяти.

Как выглядит абак?

Специальные счеты, используемые в системе ментального счета абакусе, называются абак, линейка или также абакус. Они имеют классический вид:

Это рамка со спицами, на которые надеты костяшки, по пять штук на каждой. Количество спиц на разных абакусах отличается, а вот костяшек на каждой из них пять, кроме того, одну костяшку на каждой спице отделяет поперечная планка.

Считающий в воображении сам рассчитывает название каждой спицы, на рисунке выше подписано распределение без десятичных знаков, но если они нужны, то первые левые спицы отводятся под них, а уже потом начинаются единицы. (Абакус и абакус с десятичными знаками)

 

Распределяем числа

Чтобы понять, как считать на абакусе, надо просто разобраться, как на нем распределяются цифры.

В дальнейшем мы будем использовать распределение на спицах, начиная с единицы, так как будем работать с целыми числами. Чтобы работать с десятичными, нужно для начала разобраться в элементарной арифметике.

Первая правая спица, когда одна костяшка сверху – наименьшее десятичное значение, в подсчетах, если мы считаем миллиарды, значит, наименьшее – миллиард, если десятичные дроби, то тысячные. Далее спицы считаются с умножением на 10.

Для пользования спицами надо запомнить, как распределяется число на абакусе:

• на спице пять костяшек;
• костяшка над планкой это 5, если она опущена – это говорит что число больше пяти, если поднята, значит меньше;
• костяшки ниже планок – 1, 2, 3, 4, сколько поднято костяшек, столько и надо учесть;
• если костяшка 5 опущена, то прибавляется число костяшек, поднятых снизу, если они не подняты, то значит на спице 5.

Например, число 15 будет выглядеть вот так:

66 вот так:

А 81549 вот так:

Кажущаяся сложность пропадает практически через пять минут, ребенок очень быстро начинает разбираться в самых сложных числах. Главное – понять принцип работы этого прибора.

Как проводить сложение и вычитание на абакусе?

Считать на абакусе достаточно просто. Для понимания возьмем пример 26+34 и сложим его на линейке абаке.

Устанавливаем первое число 26 :

Раскладываем все числа на простые цифры, не забывая, к какой спице они относятся: 2 и 3 к десяткам, а 6 и 4 к единицам. Производим сложение простых чисел. 6+4 и 2+3.

Теперь сдвигаем единицы на первой спице 6+4 =10, то есть на 1 спице надо показать 0, и развести все костяшки по местам, а к двум костяшкам на второй спице добавить еще одну, получим 30:

Но мы добавляли не 4, а 34, поэтому на второй спице надо добавить еще 3 костяшки и показать цифру 6, для этого опускаются снизу 2 костяшки и «5». Итого мы получаем 60.

Сложение всегда начинается с меньшего числа с переходом к большему. Если костяшек на спице получается больше чем 9, тогда на соседней спице добавится еще одна.

В случае с вычитанием система та же, начинаем с меньшего, только если вычитается от меньшей цифры большая, тогда они меняются местами, а с соседней спицы убирается костяшка.

Например, 15-13:

• ставим 15;
• раскладываем число на простые цифры 1 и 5 и 1 и 3, от 1 отнимаем 1, от 5 отнимаем 3 и получаем 2:

Эта система расчетов при должной сноровке занимает около двух-трех секунд. Со временем сама линейка уже будет не нужна, она сама будет возникать в мыслях.

Как умножать и делить на абакусе?

Умножение на линейке тоже достаточно простое, для этого нужно только освоить таблицу умножения от 1 до 10 и запомнить одно правило: десятки умножаем на единицы, потом единицы умножаем на единицы. Если ребенок уже разобрался, как считать на абакусе, все действия будут занимать не больше минуты.

Для примера возьмем простое задание 11х5, которое решается в два действия:

1. 10х5=50.
2. 1х5=5.

Для начала на абакусе набирается ответ на первый пример, 50:

потом к нему добавляется ответ на второй пример, 5:

И в результате мы видим на абаке ответ 55.

Для проведения более сложных действий, когда берутся более сложные примеры, тогда задание решается в последовательности: десятки умножаются на десятки, единицы на десятки, десятки на единицы, единицы на единицы. То есть, сначала все цифры, постепенно от большего к меньшему перемножаются и набираются последовательно на абаке.

Например, 611 Х24:

Решается это так, нули прячутся и берутся цифры без них, а их количество определяет, на сколько спиц надо сдвинуться влево, кроме того, если результат получился двузначный, значит надо сместиться еще на одну спицу:

1. 6х2=12 – при умножении результат набираем на той спице, к которой относится число и сдвигаемся вправо на столько спиц, сколько нулей в числе, на которое умножают, в нашем случае в 20 один ноль, то есть результат 12 набирается не на сотнях, а на тысячах. Но если результат имеет две цифры, тогда надо сместиться еще на одну спицу. То есть, в нашем случае 12 набирается на спицах, отвечающих на десять тысяч и тысячи.(12000)
2. 1х2=2 – единица относится к десяткам, в 20 один ноль, то есть сдвигаемся на одну спицу и добавляем ответ в сотнях.(12200)

1х2=2 единица относится к единицам, а в 20 один ноль, то есть исходя из правил, добавляем ответ в десятках. (12220)

3. Теперь переходим к следующему порядку и умножаем сотни на единицы, десятки на единицы и единицы на единицы.
4. 6х4=24 – в 4 нет нолей, мы сдвигаемся только на одну спицу, так как в ответе две цифры, и добавляем 2 костяшки к тысячам и 4 к сотням. (14620)
5. 1х4=4 – добавляем в десятки 4 костяшки. (14660)
6. 1х4=добавляем теперь 4 костяшки в единицы. (14664)

Последнее действие можно не делать, но сначала нужно проверить: берем калькулятор, умножаем 611х24, получаем 14664 и радуемся своей сноровке.

Деление проводится по такому же принципу, только производится не сложение результатов на линейке, а вычитание. Сдвигание по спицам происходит слева направо.

Насколько быстро можно работать на абакусе?

Даже на самые сложные действия ребенок, как и взрослый, потратит не больше одной минуты, главное во всем этом деле – практика и понимание, как считать на абакусе. Чем чаще и больше заниматься, тем проще будет перейти на систему ментального вычисления, без каких либо приспособлений.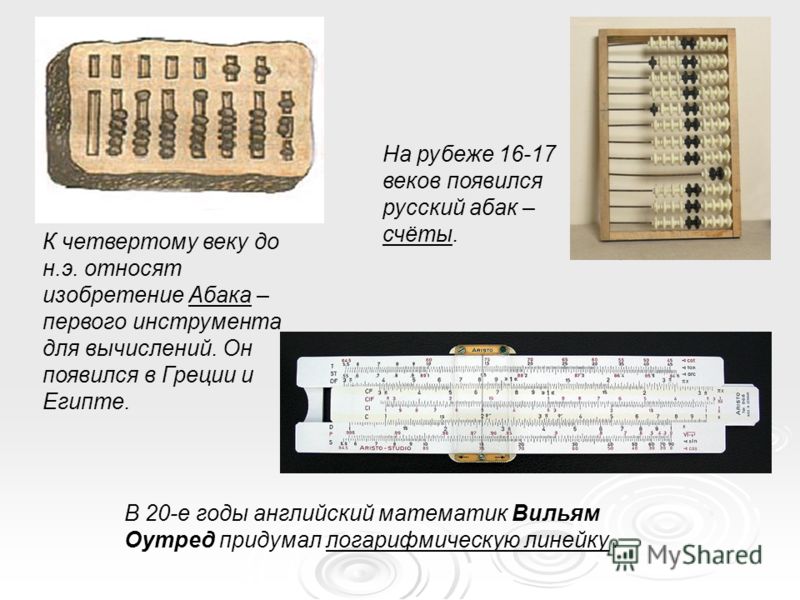 Для начала со сложными примерами понадобится еще ручка и бумага, чтобы расписать последовательность действий и не запутаться, но пара дней практики – и ничего кроме абака уже не понадобится.

Главное – не стесняться перепроверять результат и показывать маленькие победы. Это позволяет стимулировать желание пользоваться этой древней системой. А она, в свою очередь, развивает память, фантазию и логику.

История создания вычислительной техники

Первой работающей машиной с архитектурой фон Неймана стала Манчестерская малая экспериментальная машина, созданная в Манчестерском университете в 1948 году; в 1949 году за ним последовал компьютер Манчестерский Марк I, который уже был полной системой, с трубками Уильямса и магнитным барабаном в качестве памяти, а также с индексными регистрами. Другим претендентом на звание «первый цифровой компьютер с хранимой программой» стал EDSAC, разработанный и сконструированный в Кембриджском университете. Заработавший менее чем через год после «Baby», он уже мог использоваться для решения реальных задач. На самом деле, EDSAC был создан на основе архитектуры компьютера EDVAC, наследника ENIAC. В отличие от ENIAC, использовавшего параллельную обработку, EDVAC располагал единственным обрабатывающим блоком. Такое решение было проще и надёжнее, поэтому такой вариант становился первым реализованным после каждой очередной волны миниатюризации. Многие считают, что Манчестерский Марк I / EDSAC / EDVAC стали «Евами», от которых ведут свою архитектуру почти все современные компьютеры.

Первый универсальный программируемый компьютер в континентальной Европе был Z4 Конрада Цузе, завершённый в сентябре 1950 года. В ноябре того же года командой учёных под руководством Сергея Алексеевича Лебедева из Киевского института электротехники, УССР, была создана, так называемая «малая электронная счётная машина» (МЭСМ). Она содержала около 6000 электровакуумных ламп и потребляла 15 кВт. Машина могла выполнять около 3000 операций в секунду. Другой машиной того времени была австралийская CSIRAC, которая выполнила свою первую тестовую программу в 1949 году.

В октябре 1947 года директора компании Lyons & Company, британской компании, владеющей сетью магазинов и ресторанов, решили принять активное участие в развитии коммерческой разработки компьютеров. Компьютер LEO I начал работать в 1951 году и впервые в мире стал регулярно использоваться для рутинной офисной работы.

Машина Манчестерского университета стала прототипом для Ferranti Mark I. Первая такая машина была доставлена в университет в феврале 1951 года, и, по крайней мере, девять других были проданы между 1951 и 1957 годами.

В июне 1951 года UNIVAC 1 был установлен в Бюро переписи населения США. Машина была разработана в компании Remington Rand, которая, в конечном итоге, продала 46 таких машин по цене более чем в $1 млн за каждую. UNIVAC был первым массово производимым компьютером; все его предшественники изготовлялись в единичном экземпляре. Компьютер состоял из 5200 электровакуумных ламп, и потреблял 125 кВт энергии. Использовались ртутные линии задержки, хранящие 1000 слов памяти, каждое по 11 десятичных цифр плюс знак (72-битные слова). В отличие от машин IBM, оснащаемых устройством ввода с перфокарт, UNIVAC использовал ввод с металлизированной магнитной ленты стиля 1930-х, благодаря чему обеспечивалась совместимость с некоторыми существующими коммерческими системами хранения данных. Другими компьютерами того времени использовался высокоскоростной ввод с перфоленты и ввод-вывод с использованием более современных магнитных лент.

Первой советской серийной ЭВМ стала Стрела, производимая с 1953 года на Московском заводе счётно-аналитических машин. «Стрела» относится к классу больших универсальных ЭВМ (Мейнфрейм) с трёхадресной системой команд. ЭВМ имела быстродействие 2000-3000 операций в секунду. В качестве внешней памяти использовались два накопителя на магнитной ленте ёмкостью 200 000 слов, объём оперативной памяти — 2048 ячеек по 43 разряда. Компьютер состоял из 6200 ламп, 60 000 полупроводниковых диодов и потреблял 150 кВт энергии.

В 1954 году IBM выпускает машину IBM 650, ставшую довольно популярной — всего было выпущено более 2000 машин. Она весит около 900 кг, и ещё 1350 кг весит блок питания; оба модуля имеют размер примерно 1,5 × 0,9 × 1,8 метров. Цена машины составляет $0,5 млн (около $4 млн в пересчёте на 2011 год) либо может быть взята в лизинг за $3500 в месяц ($30000 на 2011 год). Память на магнитном барабане хранит 2000 10-знаковых слов, позже память увеличена до 4000 слов. По мере исполнения программы, инструкции считывались прямо с барабана. В каждой инструкции был задан адрес следующей исполняемой инструкции. Использовался компилятор Symbolic Optimal Assembly Program (SOAP), который размещал инструкции по оптимальным адресам, так чтобы следующая инструкция читалась сразу и не требовалось ждать пока барабан повернётся до нужного ряда.

В 1955 году Морис Уилкс изобретает микропрограммирование, принцип, который позднее широко используется в микропроцессорах самых различных компьютеров. Микропрограммирование позволяет определять или расширять базовый набор команд с помощью встроенных программ (которые носят названия микропрограмма или firmware).

В 1956 году IBM впервые продаёт устройство для хранения информации на магнитных дисках — RAMAC (Random Access Method of Accounting and Control). Оно использует 50 металлических дисков диаметром 24 дюйма, по 100 дорожек с каждой стороны. Устройство хранило до 5 МБ данных и стоило по 10 000 $ за МБ. (В 2006 году, подобные устройства хранения данных — жёсткие диски — стоят около 0,001 $ за Мб.)

1950-е — начало 1960-х: второе поколение

Транзисторы, в качестве миниатюрной и более эффективной замены электровакуумным лампам, совершили революцию в вычислительной технике

Следующим крупным шагом в истории компьютерной техники стало изобретение транзистора в 1947 году. Они стали заменой хрупким и энергоёмким лампам. О компьютерах на транзисторах обычно говорят как о «втором поколении», которое доминировало в 1950-х и начале 1960-х. Благодаря транзисторам и печатным платам было достигнуто значительное уменьшение размеров и объёмов потребляемой энергии, а также повышение надёжности. Например, IBM 1620 на транзисторах, ставшая заменой IBM 650 на лампах, была размером с офисный стол. Однако компьютеры второго поколения по-прежнему были довольно дороги и поэтому использовались только университетами, правительствами, крупными корпорациями.

Компьютеры второго поколения обычно состояли из большого количества печатных плат, каждая из которых содержала от одного до четырёх логических вентилей или триггеров. В частности, IBM Standard Modular System определяла стандарт на такие платы и разъёмы подключения для них. Первые полупроводниковые компьютеры строились на германиевых транзисторах, потом им на смену пришли более дешёвые кремниевые. Логика строилась на биполярных транзисторах и прошла эволюцию от РТЛ, ТТЛ до ЭСЛ-логики. Им на смену пришли полевые транзисторы, на основе которых строились простейшие микросхемы уже для компьютеров третьего поколения.

В 1959 году на основе транзисторов IBM выпустила мейнфрейм IBM 7090 и машину среднего класса IBM 1401. Последняя использовала перфокарточный ввод и стала самым популярным компьютером общего назначения того времени: в период 1960—1964 гг. было выпущено более 100 тыс. экземпляров этой машины. В ней использовалась память на 4000 символов (позже увеличенная до 16 000 символов). Многие аспекты этого проекта были основаны на желании заменить перфокарточные машины, которые широко использовались начиная с 1920-х до самого начала 1970-х гг. В 1960 году IBM выпустила транзисторную IBM 1620, изначально только перфоленточную, но вскоре обновлённую до перфокарт. Модель стала популярна в качестве научного компьютера, было выпущено около 2000 экземпляров. В машине использовалась память на магнитных сердечниках объёмом до 60 000 десятичных цифр.

В том же 1960 году DEC выпустила свою первую модель — PDP-1, предназначенную для использования техническим персоналом в лабораториях и для исследований.

В 1961 году Burroughs Corporation выпустила B5000, первый двухпроцессорный компьютер с виртуальной памятью на основе подкачки сегментов. Другими уникальными особенностями были стековая архитектура, адресация на основе дескрипторов, и отсутствие программирования напрямую на языке ассемблера.

В 1962 году совместно Манчестерским университетом Виктории и компаниями Ferranti и Plessey был создан компьютер Atlas с виртуальной памятью на основе подкачки страниц и конвейерным выполнением инструкций.

Компьютер второго поколения IBM 1401, выпускавшийся в начале 1960-х, занял около трети мирового рынка компьютеров, было продано более 10 000 таких машин.

Применение полупроводников позволило улучшить не только центральный процессор, но и периферийные устройства. Второе поколения устройств хранения данных позволяло сохранять уже десятки миллионов символов и цифр. Появилось разделение на жёстко закреплённые (fixed) устройства хранения, связанные с процессором высокоскоростным каналом передачи данных, и сменные (removable) устройства. Замена кассеты дисков в сменном устройстве требовала лишь несколько секунд. Хотя ёмкость сменных носителей была обычно ниже, но их заменяемость давала возможность сохранения практически неограниченного объёма данных. Магнитная лента обычно применялось для архивирования данных, поскольку предоставляла больший объём при меньшей стоимости.

Во многих машинах второго поколения функции общения с периферийными устройствами делегировались специализированным сопроцессорам. Например, в то время как периферийный процессор выполняет чтение или пробивку перфокарт, основной процессор выполняет вычисления или ветвления по программе. Одна шина данных переносит данные между памятью и процессором в ходе цикла выборки и исполнения инструкций, и обычно другие шины данных обслуживают периферийные устройства. На PDP-1 цикл обращения к памяти занимал 5 микросекунд; большинство инструкций требовали 10 микросекунд: 5 на выборку инструкции и ещё 5 на выборку операнда.

«Сетунь» была первым компьютером на основе троичной логики, разработана в 1958 году в Советском Союзе. Первыми советскими серийными полупроводниковыми ЭВМ стали «Весна» и «Снег», выпускаемые с 1964 по 1972 год. Пиковая производительность ЭВМ «Снег» составила 300 000 операций в секунду. Машины изготавливались на базе транзисторов с тактовой частотой 5 МГц. Всего было выпущено 39 ЭВМ. [2]

Лучшей отечественной ЭВМ 2-го поколения считается БЭСМ-6, созданная в 1966 году.

1960-е: третье поколение

Интегральные схемы содержат сотни миллионов транзисторов

Бурный рост использования компьютеров начался с «третьего поколения» вычислительных машин. Начало этому положило изобретение интегральной схемы, которое стало возможным благодаря цепочке открытий сделанных американскими инженерами в 1958—1959 годах. Они решили три фундаментальные проблемы, препятствующие созданию интегральной схемы. За сделанные открытия один из них получил Нобелевскую премию.

Параллельно с компьютерами третьего поколения продолжали выпускаться компьютеры второго поколения. Так компьютеры «UNIVAC 494» выпускались до середины 1970-х годов.

1970-е: четвёртое поколение

Микропроцессор заменил множество интегральных схем

В 1969 году в сотрудник компании Intel Тэд Хофф предлагает создать центральный процессор на одном кристалле. То есть вместо множества интегральных микросхем создать одну главную интегральную микросхему, которая должна будет выполнять все арифметические, логические операции и операции управления, записанные в машинном коде.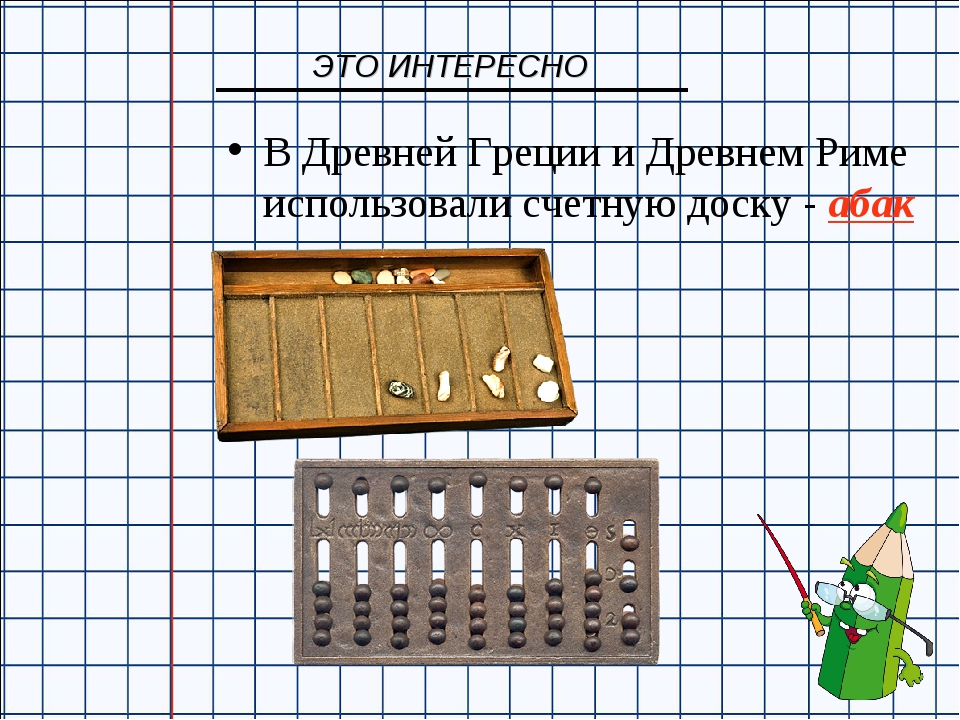 Такое устройство получило название — микропроцессор.

В 1971 году компания Intel выпускает на рынок первый микропроцессор «Intel 4004». Появление микропроцессоров позволило создать микрокомпьютеры — небольшие недорогие компьютеры, которые могли себе позволить купить маленькие компании или отдельные люди. В 1980-х годах микрокомпьютеры стали повсеместным явлением.

Массовый домашний компьютер, подключаемый к телевизору

Apple II — первый в мире массовый персональный компьютер производства компании Apple

IBM PC — массовый персональный компьютер производства компании IBM

Первый массовый домашний компьютер был разработан Стивом Возняком — одним из сооснователей компании Apple Computer. Позже Стив Возняк разработал первый массовый персональный компьютер.

Компьютеры на основе микрокомпьютерной архитектуры, с возможностями, добавленными от их больших собратьев, сейчас доминируют в большинстве сегментов рынка.

В СССР и России

См. также: Список советских компьютерных систем

1940-е

В 1945 году работала первая в СССР аналоговая вычислительная машина. До войны же были начаты исследования и разработки быстродействующих триггеров — основных элементов цифровых ЭВМ.

29 июня 1948 года Председатель Совета Министров СССР И. В. Сталин подписал постановление, в соответствии с которым создавался Институт точной механики и вычислительной техники[3].

В 1948 году под началом доктора физико-математических наук С. А. Лебедева в Киеве начинаются работы по созданию МЭСМ (малой электронной счётной машины). В октябре 1951 года она вступила в эксплуатацию.

В конце 1948 года сотрудники Энергетического института им. Крижижановского И. С. Брук и Б. И. Рамеев получают авторское свидетельство на ЭВМ с общей шиной, а в 1950—1951 гг. создают её. В этой машине впервые в мире вместо электронных ламп используются полупроводниковые (купроксные) диоды. С 1948 г. Брук вёл работы по электронным ЦВМ и управлению с применением средств вычислительной техники.

В начале 1949 года в Москве на базе завода САМ были созданы СКБ-245 и НИИ Счетмаш. Создаются заводы «Счётмаш» в Курске[4], Пензе, Кишинёве.

1950-е

В начале 50-х в Алма-Ате была создана лаборатория машинной и вычислительной математики. В конце 1951 г. вступила в эксплуатацию ЭВМ М-1, разработанная в лаборатории Энергетического института АН СССР.

Осенью 1952 года была завершена разработка Большая (или Быстродействующая) электронно-счётная машина — БЭСМ-1 (известна также как БЭСМ Академии Наук, БЭСМ АН), построенная на электронных лампах (5000 ламп). Опытная эксплуатация началась с 1952 года.

В 1953 в СССР начали серийно выпускать машину «Стрела», в 1954 для нужд Министерства обороны СССР основан первый советский вычислительный центр ВЦ-1 (эксплуатирующий ЭВМ «Стрела»).

С 1956 И. Берг и Ф. Старос возглавляют в Ленинграде лабораторию СЛ-11, которая впоследствии была преобразована в КБ-2. Там они создают первую в СССР настольную ЭВМ УМ-1 и её модификацию УМ-1НХ, за что им присуждена Государственная премия.

В 1957 в серию запустили машину «Урал-1». Всего было выпущено 183 машины.

В 1959 была создана уникальная малая ЭВМ «Се́тунь» на основе троичной логики.

В конце 1950-х разрабатываются принципы параллелизма вычислений (А. И. Китов и др.), на основе которых была построена одна из самых скоростных ЭВМ того времени — М-100 (для военных целей).

1960-е

В июле 1961 года в СССР запустили в серию первую полупроводниковую универсальную управляющую машину «Днепр» (до этого были только специализированные полупроводниковые машины). Ещё до начала серийного выпуска с ней проводились эксперименты по управлению сложными технологическими процессами на металлургическом заводе имени Дзержинского.

Первыми советскими серийными полупроводниковыми ЭВМ стали «Весна» и «Снег», выпускаемые с 1964 по 1972 год.

В 1966 году создана БЭСМ-6, лучшая отечественная ЭВМ 2-го поколения. На тот момент она была самой быстрой не только в СССР, но и в Европе. В архитектуре БЭСМ-6 впервые был широко использован принцип совмещения выполнения команд (до 14 одноадресных машинных команд могли находиться на разных стадиях выполнения). Механизмы прерывания, защиты памяти и другие новаторские решения позволили использовать БЭСМ-6 в мультипрограммном режиме и режиме разделения времени. ЭВМ имела 128 Кб оперативной памяти на ферритовых сердечниках и внешнюю памяти на магнитных барабанах и ленте. БЭСМ-6 работала с тактовой частотой 10 МГц и рекордной для того времени производительностью — около 1 млн операций в секунду. Всего было выпущено 355 ЭВМ.

Абак ручной вычислитель. Абак – древнейший счетный прибор

Развитие государств Европы и Азии и усиление торговых связей между ними привело к необходимости создания устройства, облегчающего подсчеты при совершении торговых сделок и сборе налогов. В результате было создано устройство Абак, известное практически у всех народов. Впервые его применили в Вавилоне (примерно VI век до н.э.).

Это устройство представляло собой деревянную дощечку, посыпанную песком, на котором наносились бороздки. В этих бороздках размещались камешки или жетоны, обозначавшие цифры.

Восстановить вид вавилонского абака можно, проанализировав принципы вавилонского счета. В то время использовалась шестидесятеричная позиционная система, т.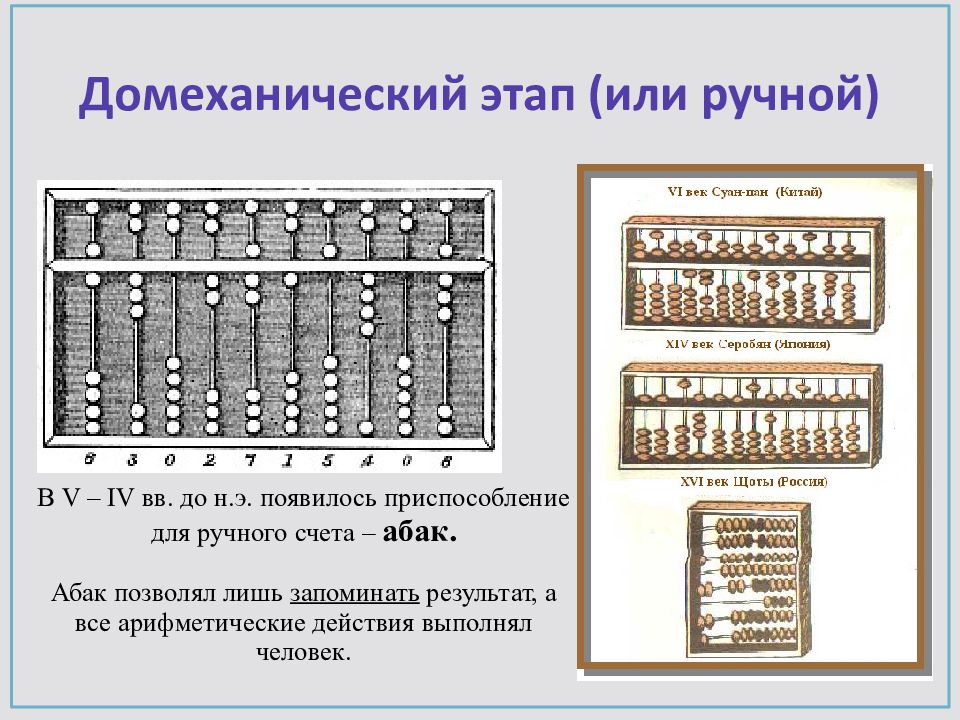 е. каждый разряд числа содержал 60 единиц, и в зависимости от своего места в числе каждый разряд обозначала либо количество единиц, либо десятков и так далее. Так как выкладывать в каждой бороздке по 60 камешков было затруднительно, то бороздки делили на две части: в одной помещали камешки, отсчитывающие десятки (не более пяти), а в другой – камешки, отсчитывающие единицы (не более девяти).

При этом количество камешков в первой бороздке обозначало количество единиц, во второй – десяток и так далее. Если в одной бороздке число, отсчитываемое камешками, превышало 59, то камешки снимали и помещали один камешек в следующую бороздку.

В древнем Риме усовершенствовали абак и помимо каменных плит использовали бронзу, слоновую кость и цветное стекло. Вертикальные желобки в римском абаке делились на 2 части. Желобки нижнего поля служили для счета от единице до 5, если в нижнем желобке набиралось 5 шариков, то в верхнее отделение добавлялся один шарик, а из нижнего все шарики снимались.

В неаполитанском музее древностей хранится римский абак, представляющий собой доску с прорезанными щелями, вдоль которых передвигались камушки. На доске располагалось восемь длинных щелей и восемь коротких, расположенных над длинными. Над каждой длинной щелью имеется обозначение, описывающее назначение щели (слева на право):

Означает, что щель используется для отложения разряда миллионов.

Означает, что щель используется для отложения разряда сотен тысяч.

Означает, что щель используется для отложения разряда десятков тысяч.

Означает, что щель используется для отложения разряда тысяч.

Означает, что щель используется для отложения разряда сотен.

Означает, что щель используется для отложения разряда десяток.

Означает, что щель используется для отложения разряда единиц.

Означает, что эта щель используется для отложения унций (от нуля до двенадцати).

На семи левых длинных щелях располагали до четырех шариков, каждый из которых приравнивался к единице соответствующего разряда числа. На семи левых коротких щелях располагали до одного шарика, обозначавшего пять единиц разряда. Восьмая длинная полоса (служившая для отсчета унций) содержала до пяти шариков, каждый из которых обозначал единицу разряда унции. Восьмая короткая содержала до одного шарика, обозначавшего шесть единиц.

Кроме того, на доске справа имелись еще две короткие щели с одним шариком и одна длинная щель с двумя шариками. Около этих щелей имелись метки, означавшие:

Пол унции

Четверть унции

Шестая часть унции

Абак был известен и в Греции. В 1846 году на греческом острове Саламине был найден мраморный абак в виде плиты размером 105х75 см, датируемый III веком до новой эры. Этот абак был назван в честь острова, на котором был найден – «Саламинская доска».

Саламинская доска служила для пятеричного счисления, что подтверждают буквенные обозначения на ней. Камешки, символизирующие разряды чисел, укладывались только между линиями. Колонки, располагающиеся на плите слева, использовались для подсчета драхм и талантов, справа – для долей драхмы (оболы и халки).

Примерно в X-XI Ацтеки изобрели свой вид абака. Сквозь деревянный каркас протягивались нити с нанизанными зернами кукурузы. Каркас был разделен на две части. В одной части на нити нанизывались по три зерна, в другой – по четыре. Для работы с ацтекским абаком использовалась своя особая система счета.

В европейских странах абак начал распространение с X века. До нашего времени сохранился ряд работ Бернелини, Ланского и других авторов, посвященных вычислению на абаке и датируемых X-XII веке. Наиболее известны работы французского ученого и священнослужителя Герберта, в которых подробно описываются правила работы с абаком: умножение, деление, сложение и вычитание.

Гербер предложил усовершенствовать абак с 12 колонок до 27, что позволило оперировать с огромными числами (до десяти в двадцать седьмой степени). Так же в этот абак было введено три дополнительных колонки для счета денег и иных мер. Во времена Герберта во многих школах учили искусству работы с абаком, было создано множество пособий для работы с устройством, благодаря чему оно получило широкое распространение и использовалось вплоть до XVIII века.

Подобные документы

Пальцы как самое первое средство обработки информации для человека. Абак как счетная доска в Греции, ее применение. Логарифмическая линейка и Джон Непер. История создания Паскалем первой счетной машинки. Механический арифмометр и современный калькулятор.

презентация, добавлен 12.05.2014


Предметы счета древних людей. Прообраз наших семикосточковых конторских счетов. Происхождение понятия, изготовление и использование абака в Древней Греции, Риме и Западной Европе. Первые механические приспособления для счета и изобретение перфокарта.

презентация, добавлен 21.04.2014


Основные этапы развития вычислительной техники. Первые шаги автоматизации умственного труда. Абак как первый развитый счетный прибор. Создание логарифмической линейки. Машина Паскаля и арифмометр Лейбница. Электронные клавишные вычислительные машины.

реферат, добавлен 05.05.2015


Ручной период автоматизации вычислений, создание абака и логарифмической линейки.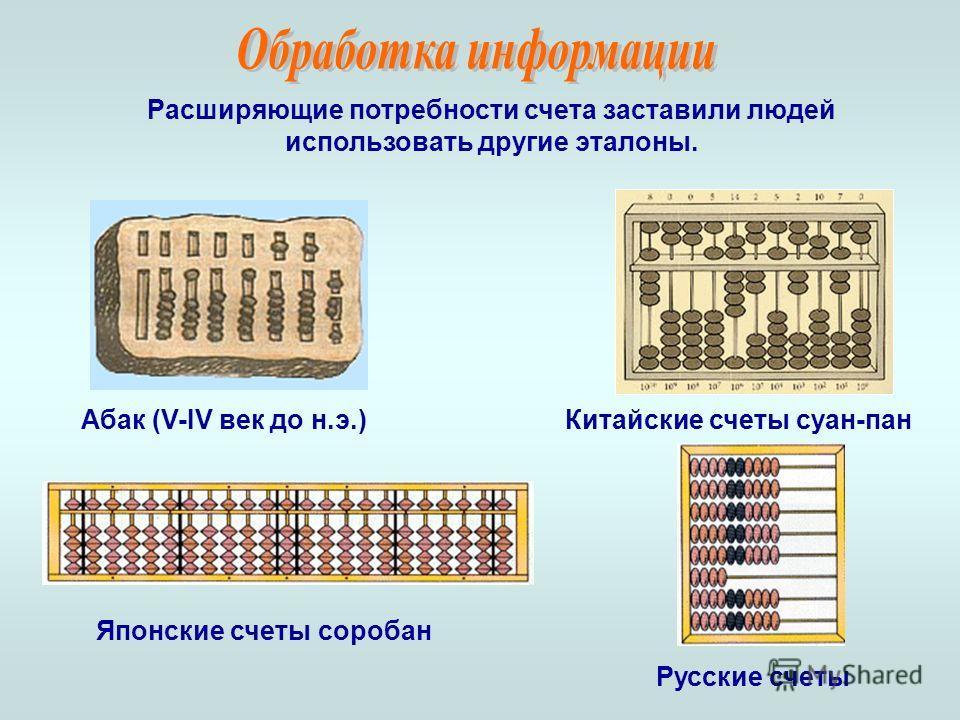 Появление устройств, использующих механический принцип для выполнения арифметических операций. История изобретения ЭВМ. Характеристики центрального процессора и мониторов.

контрольная работа, добавлен 15.11.2012


Первая счётная доска и русский абак. Логическая линейка, арифмометр и арифмограф. Прообраз первого калькулятора. Эра электронно-вычислительных машин, хронология создания. Процессор Pentium II, особенности и описание. Процессоры Pentium 3, 4, 5, 6.

реферат, добавлен 16.11.2011


Первые вычисления и вычислительные машины, абак как первое счетное приспособление. История изобретения счетной машины. Первые попытки создания компьютеров. Роль Холлерита в развитии вычислительной техники. Характеристики современных суперкомпьютеров.

реферат, добавлен 29.09.2017


Первые шаги в развитии счетных устройств, ручной этап: пальцевой счет, фиксация, абак, позиционная система счисления и создание логарифмической линейки. Особенности и направления развития счетных устройств XVII, XVIII и XIX веков, их современность.

контрольная работа, добавлен 01.12.2013


История развития механических и электронных вычислительных приборов (греческий абак, русские счеты, логарифмическая линейка, арифмометр, калькулятор). Цифровое кодирование информации и эволюция современной компьютерной техники и программного обеспечения.

презентация, добавлен 03.05.2015


Периоды и поколения эволюции цифровой вычислительной техники. Развитие средств обработки численной информации, использование абака, механических калькуляторов, арифмометров для практических расчетов. Первый работающий электромеханический компьютер Mark-1.

презентация, добавлен 06.04.2015


История приспособлений для вычислений. Изобретение абака (счетов). “Считающие часы” В. Шикарда (1623 г.) – первый механический калькулятор. Машина Б. Паскаля (“Паскалина”, 1642 г.). Перфокарты и механизмы сортировки. Электронные настольные калькуляторы.

Абак (др.-греч. ἄβαξ, ἀβάκιον, лат. abacus — доска) — счётная доска , применявшаяся для арифметических вычислений приблизительно с V века до н. э. в Древней Греции, Древнем Риме.

Античный период – это условный отрезок исторического времени, который охватывает период от 1 тысячи лет до нашей эры, до I тысячелетия нашей эры. Историки отмечают эту эпоху как расцвет рабовладельческо го строя, который пришел на смену первообщинному.

Идеальное расположение территории Греции относительно Средиземного, Эгейского, Черного и Мраморного морей, а также мягкий климат, активно способствовали успешному развитию не только различных ремесел, но и торговли с сопредельными государствами.

Следует отметить уникальное на то время административное устройство страны – основная часть населения с высоким уровнем достатка концентрировалас ь в больших городах – полисах, которые, по сути, являл собой отдельные государства. Полисы подчиняли себе более мелкие поселения, занимавшиеся поставкой в город продукции сельского хозяйства, предметов обихода, материалов для строительства.

Для осуществления торговли между городами, требовалась особая, унифицированная единица, через которую бы выражалась ценность всех товаров. Бартер не всегда мог удовлетворить интересы обеих сторон, поэтому на смену ему пришли деньги, имевшие вид пластинок из драгоценных металлов – золота и серебра. Недостатком системы было то, что каждый полис имел собственные деньги, которые зачастую отличались номиналом, весом, формой. Требовалось производить сложные расчеты, чтобы подвести результат торговли под общий знаменатель, а сделать это оперативно, без использования счетной системы было практически невозможно.

Подсчетом денег, а затем и ростовщичеством занималась избранная категория граждан полиса, которые пользовались большим авторитетом и уважением среди остальных жителей города. С течением времени, количество операций, проводимых ими, увеличилось – ростовщики не только занимались посредничеством в финансовых операциях, но и обменивали деньги, принимали их на хранение, постепенно эволюционировав в банкиров. Сначала все необходимые записи и расчеты делались на деревянных дощечках или папирусе. Который в то время был недоступной роскошью, и тратить его на расчеты даже государственной важности было лишним расточительством. Для того чтобы ускорить арифметические операции, 2500 лет назад неизвестным изобретателем было придумано несложное в изготовлении устройство – абак.

История появления абака

Древняя Греция подарила современному миру множество важных и облегчающих жизнь изобретений, одним из которых по праву считается абак. Это простое устройство, предназначенное для проведения несложных математических расчетов, появилось примерно в V веке до нашей эры, и являло собой деревянную или каменную дощечку с прорезями, в которых свободно двигались вдоль определенных пазов камешки из дерева или мрамора.

Самый древний, сохранившийся до нашего времени абак, был обнаружен во время раскопок на острове Кипр, в окрестностях самого большого и укрепленного полиса Саламис. Находку относят к 300 году до нашей эры, и выглядит она как пластина из мрамора белого цвета, причем размеры её довольно внушительные. Длина счетов составляет почти полтора метра, ширина – 75 см. Толщина мраморной пластины – 4. 5 см. Абак имеет сложную систему прорезей, вдоль которых двигались шарики из камня. Точное предназначение устройства доподлинно неизвестно, но судя по его размерам и весу, служило оно для подсчета налогов или расходов из городского бюджета, и было установлено возле казначейства Саламиса.

Экономика Древней Греции

У исследователей истории Античного периода развития Греции часто возникает интерес к такому бытовому аспекту, как экономические взаимоотношения городов и их отдельных жителей друг с другом.

Стоит отметить довольно интересные взгляды жителей Эллады на материальную ответственность. Воровство в Древней Греции или растрата государственного бюджета рассматривалась ими исключительно как экономическое преступление, наказание за которое заключалось в полной компенсации недостачи материально ответственным лицом. Кража денег из казны полиса наказывалась возмещением убытка в десятикратном размере, так что некоторым ушлым личностям было выгодно поставить на место банкира богатого жителя города, после чего подставить его и обвинить в растрате. Таким образом, новоиспеченный банкир вынужден был компенсировать ущерб, лишившись при этом собственного имущества.

Система банковских записей о разных операциях осуществлялась методом нанесения отметок на деревянные дощечки в хронологическом порядке, какой-либо систематизации при этом не проводилось. Время от времени, для составления отчета за месяц или год требовалось проделывать дополнительную работу – рекапитуляцию, которая заключалась в повторной сверке записей, и установлении их хронологии. Чтобы облегчить и без того нелегкую работу банкиров, использовались счеты. Вероятно, сначала они имели вид обычных мелких камушков – речной или морской гальки одинакового размера, с гладкими, округлыми очертаниями. Кстати, само слово «калькуляция », произошло от латинского «calculos », которое обозначало именно небольшие камешки. Вероятно, от этого пошло и современное название речных и морских отложений – гальки.

Использовать камешки в большом количестве однообразных расчетов было очень неудобно, так как они постоянно падали со стола, терялись или перекатывались из одной кучки в другую, что сильно снижало точность операций. Для того чтобы сделать учет денежных и материальных средств более совершенным, неизвестный на сегодняшний день изобретатель взял мраморную дощечку, сделал в ней прорези, и поместил в них по 10 камешков, позволив им свободно перемещаться вдоль канавок. Такой инструмент можно было всегда взять с собой, и применять для контроля расхода материалов на стройках, подсчитывать количество налогов для торговцев, приезжавших в город, производить учет поступлений в государственную казну.

Интересной была система хранения государственных средств в полисах Древней Греции. Каждый вид поступавших доходов распределялся следующим образом: в специальной надежной комнате хранились несколько больших кувшинов с буквенными индексами. В каждый кувшин отдельно складывались средства, полученные от конкретной деятельности – налоги от торговцев, подоходный налог, плата, полученная от кораблей в портах, и прочих пошлин. Финансирование этих отраслей оказывалось из того же кувшина, так что общий баланс расходов не нарушался.

Ключи от самого помещения с деньгами хранились у одного банкира, а к комнате со всей документации – у второго. Обмениваться ключами было строго запрещено, вследствие чего защита от преднамеренной растраты была достаточно высокой.

Система налогообложения Древней Греции была устроена на удивление хорошо. При уплате пошлин зародилась не только арифметика, но и прием линейной или позиционной записи. Также были хорошо организованны банковские записи. Каждый взнос или выдача средств могли проводиться в безналичном виде, а все движения финансов тщательно записывались и могли быть обнародованы в деловом центре полиса – агоре.

Ведения таких подробных отчетов было невозможным без абак. Они были распространены повсеместно – в банках, которые тогда носили название «трапез», в государственных учреждениях и портах.

Аналоги абак в мировой истории

Такое важное изобретение как абак возникло задолго до появления на территории Греции , хотя именно в Элладе оно обрело современные черты. Первое известное упоминание абака сохранилось в документах Древнего Вавилона, которые относятся к III тысячелетию до нашей эры. Вавилонский абак имел вид горизонтальной доски с проделанными в ней углублениями, вдоль которых перемещались камешки или другие мелкие предметы. Позже, за 500 лет до нашей эры, египтяне усовершенствовал и конструкцию, используя не углубления, а палочки или медную проволоку, на которую были нанизаны четки из глины, дерева или камня. Такое решение позволяло использовать абак не только в горизонтальном виде, что зачастую было неудобно, но и в вертикальной.

После появления абаки в Греции, с изобретением познакомились арабы и индусы. Они же принесли счеты в Западную Европу, захватив в VIII веке Испанию. Здесь абака несколько видоизменилась – вместо камешков начали использовать металлические жетоны, на которые наносились римские цифры, или условные обозначения – апексы. Государственные казначейские расчеты при помощи абаки велись в Европе вплоть до XVIII века, после чего были заменены более продуктивными методами алгоритмизации.

Восточные страны, такие как Китай и Япония также активно использовали абак. Китайский аналог назывался суаньпань, а японский – соробан. Они практически не отличались друг от друга конструкцией, что доказывает их общее происхождение. Суаньпань имел 10 разрядов – по количеству пальцев на руках, и два вертикальных столбца – по количеству рук, и был предназначен для несложных расчетов бытового, производственног о, строительного и финансового плана. Китайский и японский абак – это не просто устройство для облегчения арифметических действий, но и целое искусство. В Японии счет на соробане до сих пор официально входит в школьную программу, а работа с ним не просто дань традиции или моде, но и имеет чисто практическое значение. Несмотря на большое количество современных электронных устройств, многие мелкие предприниматели, продавцы в магазинах и на рынках предпочитают использовать абак в повседневной жизни. Четко проработанные алгоритмы действий позволяют производить на суаньпане и соробане все основные математические операции – сложение, вычитание, умножение и деление, а также возводить в степень и извлекать квадратные и кубические корни.

Русские счеты дают возможность не только слагать и вычитать различные числа, но и работать с четвертями, десятыми и сотыми долями. Появление абака на территории России относят к XV-XVI веку. Активное распространение счетов продолжалось вплоть до конца ХХ века, когда такие устройства были заменены более точными электронными калькуляторами. До начала 1980-х годов, обучение арифметическим действиям на счетах входило в школьную программу советских школьников.

Абак в Древней Греции пришел на смену старинному и требовавшему дополнительных действий счету на пальцах. Развитие методики позволило сделать расчеты быстрыми, точными и легкими. Каждый камешек на абаке мог означать как единицы, так и десятки, сотни, тысячи, что значительно расширяло сферу применения инструмента. По этому поводу в Элладе даже была распространена шутка: «Придворный похож на камешек для абака: захочет счетчик, цена ему будет целый талант, а захочет – только хальк».

Можно с уверенностью сказать, что изобретение абака дало сильный толчок не только в отношении денежных расчетов и торговли, но дало возможность производить сложные расчеты при строительстве древних храмов, и других объектов архитектуры, которыми мы можем наслаждаться по сей день.

Абак и счёты

Поистине революционным событием в истории счета было появление приборов,

объединяемых общим названием – абак. Абак мог иметь форму деревянной доски,

глиняной плитки или просто очерченного кусочка земли. Важно, что на абаке

отмечались места (колонки или строчки) для отдельных разрядов чисел.

Впервые об абаке упоминает историк древнего мира Геродот. Абак был широко

распространен в античном мире. Его вариантами пользовались в Древнем Риме и

Вавилоне, Китае, Японии и многих других странах. Математическая задача

считалась решенной в том случае, если ее решение можно было воспроизвести на

абаке. Абак (греч. abax, abakion, латинский abacus – доска, счётная доска), счётная доска, применявшаяся для арифметических вычислений в Древней Греции, Риме, затем в Западной Европе до 18 века. В Древней Греции бытовала шутка:

“Придворный похож на камешек для абака: захочет счетчик, цена ему будет целый талант, а захочет – только хальк”.

Доска разделялась на полосы, счёт осуществлялся передвижением находящихся в полосах счётных марок (костяшек, камней и т.п.). В странах Дальнего Востока распространён китайский аналог абака – суан-пан, в России – счёты.

В Россию абак проник не

позднее XVI века, но, скорее всего это случилось намного раньше. Русскими

вариантами абака были “счет костьми” и “дощаный счет”.

Самый примитивный абак, действительно, представлял из себя такую дощечку. На ней острой палочкой проводили линии, и в получившихся колонках размещались камешки. Это значит, что были колонки единиц, десятков, сотен и так далее. Точно неизвестно, где именно появился первый абак. Возможно, в Финикии. Греки передвигали камешки слева направо. В отличие от них, египтяне делали это справа налево. В Древнем Риме абак назывался «calculi» или «abaculi» и изготовлялся из бронзы, камня, слоновой кости или цветного стекла. От слова «calculus», означающего «галька», «голыш», произошло латинское же слово «calculatore» (вычислять) и современное «калькулятор». Сохранился бронзовый римский абак, на котором камешки передвигались в вертикальных желобках. В нижней части помещались камешки для счета до пяти, а в верхней — камешки, соответствующие пятерке.

Китайский абак – суаньпань – появился в VI веке н.э., а современный его вид – примерно в XII веке. Суаньпань это прямоугольная рама, в которой протянуто 9 или более параллельных проволок или веревок. Перпендикулярно этому на правлению суаньпань перегорожен линейкой на две неравные части: «землю», в которой по 5 шариков, нанизанных на каждую проволоку, и «небо» — здесь по 2 шарика. Шарики в «земле» -это как бы пять пальцев руки, а шарики в «небе» — две руки. Проволоки – это десятичные разряды: единицы, десятки и так далее.

С помощью суан-пана можно было не только складывать, но и умножать, делить, оперировать с дробями, извлекать квадратные и кубические корни. По всей вероятности, это была первая известная нам позиционная десятичная система счисления.Суань-пан помог сделать фундаментальные открытия в математике.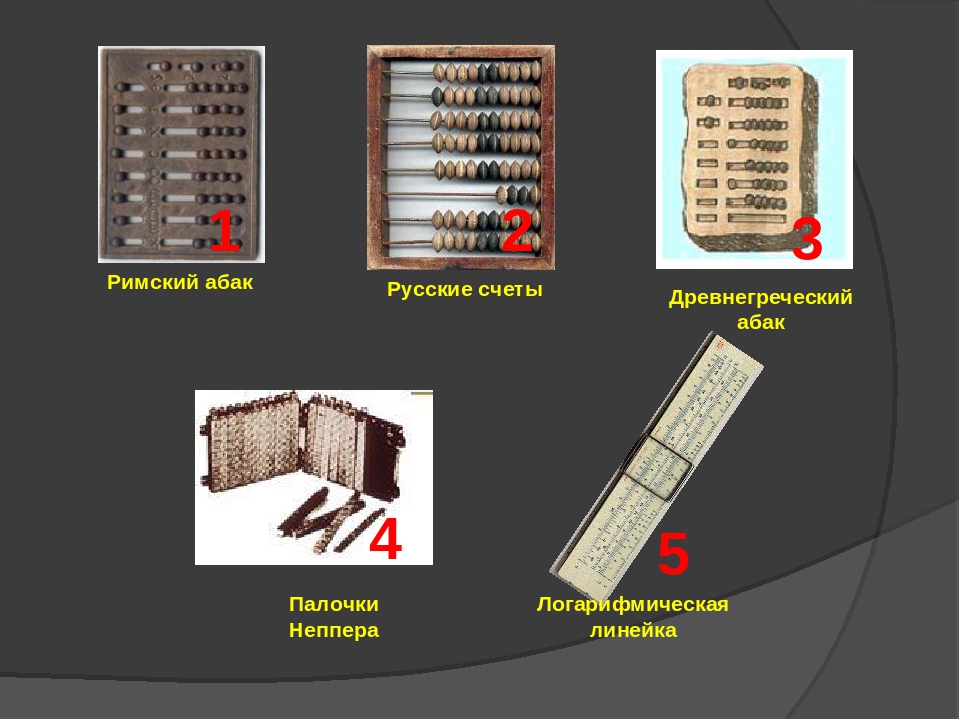 Действия с числителями и знаменателями привели к понятию дроби как числа.

О русском абаке –счетах , появившились на рубеже XVI – XVII веков Счеты имеют горизонтальное расположение спиц с косточками и основаны на десятичной, а не пятеричной системе счисления Русские счеты широко использовались не только для вычислений, но и в качестве учебного пособия для начального обучения арифметике.

Чтобы отличить положительные числа от отрицательных, в суан-пане применялись различные палочки. Положительные числа обозначались палочками красного цвета или с квадратным сечением, а отрицательные были черного цвета или треугольного сечения.

Русский абак появился на рубеже 16-17 веков. Наиболее распространенным инструментом счета в допетровской Руси был “счет костьми”, представлявший собой специальную доску или стол. Перед проведением вычислений их нужно было разграфить горизонтальными линиями. Четыре арифметических действия осуществлялись с помощью камешка, фруктовой косточки или специального жетона.

Счеты стали утрачивать значение универсального счетного прибора, постепенно превращаясь во вспомогательный. При помощи новой системы письменно, на бумаге, оказалось гораздо удобнее выполнять математические выкладки, чем с использованием абака. Этот процесс сопровождался острой борьбой, как тогда считали, двух наук: математики на абаке и математики без абака – на бумаге. Эта борьба известна как противодействие абакистов и алгоритмиков. счетный прибор генерал-майора русской армии Ф.М. Свободского, изобретенный им в 1828 году. разработал простые правила сведения арифметических действий к последовательности сложения и вычитания, что вместе с запоминанием нескольких простых вспомогательных таблиц (вроде таблицы умножения) заметно сокращало время вычислений.В основу этого прибора – для многократного сложения и вычитания – положен принцип действия все тех же русских счет.

Абак – счетная доска использовался многими народами. Греки и египтяне использовали абак с нарисованными линиями или выдолбленными желобками. Вдоль линий или в желобки укладывались камешки. Каждый камешек означал единицу вычислений, а сама линия – разряд этой единицы.

Вычисления при помощи греческого и египетского абаков, равно как и при помощи суан-пана и соробана, производились следующим образом. В каждом желобке (на каждой линии или на каждом прутике) располагались пять камешков (или шариков). Камешек в первом желобке означал единицу. Камешек во втором желобке – пять единиц. Камешек в третьем желобке – двадцать пять единиц. Камешек в четвертом желобке – сто двадцать пять единиц.

Таким образом, в абаке и его ранних аналогах использовалась пятеричная система исчисления. Основным же достоинством абака была наглядность вычислений и так называемая позиционная система представления чисел. Результат расчетов не требовал какой-либо расшифровки – достаточно было взглянуть на расположение камешков на абаке, чтобы моментально определить, какое число получилось. Недостатком древнего абака была именно пятеричная система счисления, которая не соответствовала изобретенной позже десятеричной системе и не позволяла оперировать дробями.

Десятеричный абак , или русские счеты используется десятеричная система счисления и возможность оперировать десятыми и сотыми дробными долями, появился на рубеже XVI и XVII веков .

От классического абака счеты отличаются увеличением разрядности каждого числового ряда и конструкцией. Счеты представляют собой раму, внутри которой располагаются тонкие стержни. На стержни насажены круглые костяшки – по десять штук на каждом стержне. Два нижних ряда означают сотые и десятые доли. Затем идет промежуточный ряд (обычно он выделен четырьмя костяшками, которые в вычислениях не участвуют). Затем идет первый ряд костяшек, каждая из которых означает единицу, второй ряд, в котором каждая костяшка соответствует десятку, затем, соответственно, идут сотни, тысячи, десятки тысяч и так далее. Позже появились расширенные модификации счетов – дробная часть могла достигать четырех рядов, а часть целых чисел – семи рядов.

Для наглядности вычислений костяшки русских счетов имели двухцветную окраску. Пятая и шестая костяшки на каждой оси окрашивались в более темный (черный) цвет, остальные – в светлый (коричневый или желтый). Двухцветная окраска костяшек позволяла очень быстро определить, какое число набрано на счетах, поскольку четыре светлых костяшки и две темных на левой стороне быстрей определяются, как цифра 6, чем шесть одноцветных костяшек.

Следует заметить, что с момента возникновения русского абака счеты со временем мало изменились. Стержни, на которых располагались костяшки, приобрели выпуклый профиль – чтобы костяшки самопроизвольно не перемешались из одной стороны в другую. Сами стержни стали делать из толстой металлической проволоки, а костяшки и раму счетов изготавливали из древесины дуба.

Счеты благополучно дожили до нашего времени и сошли со сцены только в последние десятилетия, уступив место электронным калькуляторам. Однако русский абак был и остается самым эффективным инструментом для обучения счету. Человек, умеющий быстро считать на счетах, быстрей считает и в уме.

Несмотря на то, что счеты упрощают однообразные громоздкие вычисления, они не позволяют упростить операции умножения и деления. Умножать и делить при помощи абака – это в любом случае многократно складывать и вычитать.

Исследовательский проект “От абака до компьютера”

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №135» ИМ. АКАДЕМИКА Б.В. ЛИТВИНОВА

Индивидуальный проект

Тип проекта: исследовательский

Тема проекта

От абака до компьютера

Автор проекта: Дуденкова Ксения,

ученица 7 Б класса

Наставник проекта: Орлова Светлана Викторовна,

учитель математики

Г. Снежинск

2020 г.

Содержание

Введение 3

Теоретическая часть: 4-8

1. Основные этапы развития вычислительной техники 4

1.1. Ручной этап 5

1.2. Механический этап 6

1.3. Электромеханический этап 7

1.4. Электронный этап 8

Практическая часть: 9-12

1. Абак и его использование 10-11

   1. Что такое абак 10

   2. Внешний вид абака 10

   3. Сложение и вычитание 11

2. Логарифмическая линейка и её использование 12

Заключение 13

Приложение 1 – Опросный лист 14

Список литературы 15

Введение

Однажды решая примеры по математике, я задумалась, а как же раньше люди выполняли математические действия без помощи различных калькуляторов, компьютерных программ и т.д. Ведь сейчас какой вычислительной техники только нет! Меня очень заинтересовала эта тема, и я решила узнать о ней больше.

В настоящее время широкое распространение компьютеров привело к тому, что всё большее число людей стало знакомиться с основами современной вычислительной техники, а история развития счета прошлого поколения известна при этом в значительно меньшей степени.

Цель:

Изучение отдельных этапов развития счета прошлого поколения до настоящего времени.

Задачи:

1. Собрать и проанализировать информацию из различных источников.

2. Рассмотреть основные этапы развития вычислительной техники.

3. Провести социологический опрос у людей 13-35 лет.

4. Изготовить макет древнего приспособления для счёта – абак и разобраться в его использовании.

Гипотеза: Я предполагаю, что современное поколение не знает историю развития вычислительной техники, а тем более первые приспособления для счёта и как ими пользоваться.

Этапы развития вычислительной техники

Основными этапами развития вычислительной техники являются:

1. Ручной этап – 50 тыс. лет до н.э. В этот период возникли основы счёта.

2. Механический этап – начался в середине 17 в.

3. Электромеханический этап – с 90-х годов 19 в.

4. Электронный этап – с 40-х годов 20 в. и продолжается в наши дни.

Ручной этап (самые первые приспособления для счёта)

Наиболее ранний инструмент для счёта, который знает история развития вычислительной техники, – десять пальцев на руках человека. Результаты счёта первоначально фиксировались при помощи пальцев, зарубок на дереве и камне, специальных палочек, узелков. С возникновением письменности появлялись и развивались различные способы записи чисел, были изобретены позиционные системы счисления.

Примерно с IV века до нашей эры древние греки стали вести счёт при помощи абака – счётной доски, применявшейся для арифметических вычислений. Первоначально это была глиняная плоская дощечка с нанесёнными на неё острым предметом полосками. Счёт осуществлялся путём размещения на этих полосах в определённом порядке мелких камней или других небольших предметов.

Существует несколько разновидностей абака: Древнегреческий абак, Римский абак, Китайский суаньпан. В дальнейшем появились русские счёты, которые используются по сей день.

В 1617 году шотландский математик Джон Непер изобрёл «Палочки Непера», которые стали началом новой эпохи. «Палочки Непера» представляли собой комплект специальных палочек, состоящих из дощечки с разметкой от одного до девяти и остальными палочками, на которые была помещена таблица умножения с такой же разметкой цифр. Вверху каждой дощечки располагались числа в порядке возрастания, а по всей длине выложенной таблицы Непер разместил собственно результаты умножения чисел на цифры от одного до девяти. Иными словами, таблица давала возможность совершать операции умножения числа 123456789 на число 123456789. Сама сетка была разделена столбцами.

В 1622-е годы англичанин Уильям Отред изобрёл логарифмическую линейку. Это устройство постоянно совершенствовалось и дожило до наших дней. Оно позволяет умножать и делить числа, возводить в степень и другие функции. Логарифмическая линейка стала прибором, завершающим развитие средств вычислительной техники на ручном этапе.

Механический этап

Развитие механики в 17 веке стало предпосылкой вычислительных устройств и приборов, использующих механический принцип вычислений.

Под механическим вычислительным устройством понимается устройство, построенное на механических элементах и обеспечивающее автоматическую передачу.

В 1623 году немецким учёным Вильгельмом Шиккардом был создан первый механический «калькулятор», который он назвал считающими часами. Механизм этого прибора напоминал обычный часовой, состоящий из шестерёнок и звёздочек. Однако известно об этом изобретении стало только в середине прошлого столетия.

Качественным скачком в области технологии вычислительной техники стало изобретение суммирующей машины «Паскалины» в 1642 году. Её создатель, французский математик Блез Паскаль. «Паскалина» представляла собой механический прибор в виде ящичка с большим количеством взаимосвязанных шестерёнок.

В 1677 году великий немецкий математик и философ Готфрид Вильгельм Лейбниц сконструировал свою счетную машину, позволявшую не только складывать и вычитать, но также умножать и делить многозначные числа. В своем арифмометре Лейбниц использовал вместо колес цилиндры. На цилиндры были нанесены цифры.

Чарльз Бэббидж в 1834 году задумался о создании программируемой вычислительной машины, которую он назвал аналитической для выполнения точных научных и технических расчётов. Проект Бэббиджа предугадал развитие электронно-механической техники и задачи, которые смогут быть решены с её помощью.

Электромеханический этап

Как ни блестящ был век механических арифмометров, но и он исчерпал свои возможности. Людям нужны были более энергичные помощники. Это заставило изобретателей искать пути совершенствования вычислительной техники, но уже не на механической, а на электромеханической основе.

В конце 19 в. были созданы сложные механические устройства. Важнейшим из них был табулятор, разработанный американцем Германом Холлеритом. Исключительность его заключалась в том, что в нем впервые была употреблена идея перфокарт и расчеты велись с помощью электрического тока. Это сочетание делало машину настолько работоспособной, что она получила широкое применение в свое время.

В 1937 г. в США Джон Атанасов начал работы по созданию ЭВМ, предназначенной для решения ряда задач математической физики. Им были созданы первые электронные схемы узлов ЭВМ, которые разрабатываются в электронном этапе.

Электронный этап

Вычислительная техника не позволяла существенно повысить скорость вычислений, для этого потребовался переход на электронные элементы высокого быстродействия.

Электронные вычислительные машины (ЭВМ) ознаменовали собой новое направление в ВТ, интенсивно развиваемое и в настоящее время.

Первой ЭВМ принято считать машину ENIAC, созданную в США в конце 1945 г. Первоначально предназначенная для решения задач баллистики, машина оказалась универсальной, т.е. способной решать различные задачи. Главным консультантом проекта являлся Д. Моучли, а главным конструктором – Д. Эккерт. Проект создания ENIAC, начатый в апреле 1943 г., был полностью завершен в декабре 1945 г.

Существует 4 поколения ЭВМ, характеристики которых указаны в таблице, приведенной ниже.

Абак и его использование

Практическая часть

Для подтверждения, выдвинутой мною гипотезы, был проведен социологический опрос среди людей возрастной категории 13-35 лет. Опросный лист представлен в Приложении 1 к данному проекту.

По результатам обработки анкет было выявлено, что большая часть из опрошенных мною людей данной категории не знает ни этапов развития ВТ, ни первые приспособления для счёта, ни их применение.

Так же по результатам опроса было выявлено, что большее число из опрошенных не знают такие вычислительные приборы, как абак и логарифмическая линейка. Исходя из этого, я решила рассказать об одном из самых первых вычислительных приборов, таком, как абак, и их использовании.

Абак и его использование

Одним из самых первых приспособлений для счёта является «абак» или «соробан» – семейство счётных досок, применявшихся для арифметических вычислений в древних культурах.

Эти счёты исполняли в древнейших государствах функции современных калькуляторов и помогали отсчитывать десятки. Впоследствии они стали использоваться в ментальной арифметике.

Внешний их вид довольно прост: абак представляет собой рамку прямоугольной формы, которая разделена перекладинами с размещенными на них косточками, мелкими камнями или другими небольшими предметами. Вверху, над разделительной полосой, расположена всего одна линия, каждый элемент которой означает пять. Снизу находятся ряды с четырьмя косточками, обозначающими единицу.

Линии косточек означают поочередно единицы (первая правая), десятки (вторая правая), сотни, тысячи и т.д. Если первая правая косточка поднята, то на счетах выложена цифра 1 или наименьшее десятичное значение.

Распределение чисел таково:

• Нижние косточки – это 1,2,3 и 4, соответственно, если подняты 2 из них, то счеты показывают число два;

• Если верхняя косточка поднята, число меньше, чем 5;

• Если опущена на разделительную линию – больше; верхняя опущена, три нижние подняты – это число 8.

Аналогичным образом можно выложить любое число.

После того как мы научимся выкладывать числа, можно приступать к обучению простейших арифметических действий.

Сложение и вычитание

Рассмотрим примеры простейших арифметических действий на абаке.

Сначала рассмотрим сложение

Пример: 34+23 = 57

Устанавливается первое число 34. Далее его следует разделить на простые цифры – 3 и 4. После этого на соответствующих линейках провести сложение единиц с единицами, десятков и десятками. Получается: 3+2 (десятки) и 4+3 (единиц). Кости на линейках перемещаются соответствующим образом. Если бы косточек получилось больше 9, нужно было прибавить единицу на соседней линейке.

Вычитание проводится по такой же системе, начиная с меньшего порядка.

Пример: 26-13 = 13

Устанавливается первое число 26. Далее его следует разделить на простые цифры –2 и 6. После этого на соответствующих линейках провести вычитание единиц с единицами, десятков и десятками. Получается: 2-1 (десятки) и 6-3 (единиц).

Работа с абаком помогает не только развивать мелкую моторику человека, но и тренирует сразу оба полушария его головного мозга, позволяет наладить взаимосвязи между ними.

Логарифмическая линейка

Логарифмическая линейка – аналоговое вычислительное устройство, позволяющее выполнять несколько математических операций, в том числе умножение и деление чисел, возведение в степень. Логарифмическая линейка была разработана английским математиком Уильямом Отредом в 1622г.

Основой устройства счетной логарифмической линейки является логарифмическая шкала — графическое изображение логарифмов чисел. Такая линейка служит для выполнения механическим путем различных вычислений. Точность вычислений на счетной логарифмической линейке зависит от длины её шкал. С принципом работы этого прибора мне ещё предстоит разобраться.

Заключение

Работая над проектом «От абака до компьютера» я собрала и изучила информацию по этой теме, рассмотрела историю развития ВТ прошлого поколения до настоящего времени. Провела социологический опрос среди людей возрастной категории 13-35 лет, в результате чего было выявлено, что большее число из опрошенных не знают такие первые вычислительные приборы, как абак и логарифмическая линейка. В своем проекте я решила остановиться на абаке и рассказать о нем подробнее.

Для этого мною был изготовлен макет древнего приспособления для счета – абак, который представлен как готовый продукт моего проекта.

Коснувшись вопроса изучения такого прибора как логарифмическая линейка, я столкнулась с трудностями ее использования, поэтому с принципом ее работы мне ещё предстоит разобраться в дальнейшем.

Моя гипотеза подтвердилась. Действительно большинство людей не знают истории развития вычислительной техники, первые приспособления для счета и их использование.

Приложение 1

Здравствуйте, потратьте, пожалуйста, несколько минут своего времени на заполнение следующей анкеты.

1. Знакомы ли Вы с этапами развития Вычислительной техники?

• Да

• Нет

• Некоторые

2. Какие из перечисленных вычислительных приборов Вам известны?

• Русские счёты

• Абак

• Логарифмическая линейка

• Никакие из перечисленных

3. Знаете ли Вы что такое абак?

4. Если да, то умеете ли Вы им пользоваться?

• Да

• Нет

• Примерно

Список литературы

1. Р.С. Гутер, Ю.Л. Полунов – «От абака до компьютера»

2. https://www.syl.ru/article/169938/new_istoriya-razvitiya-vyichislitelnoy-tehniki-otechestvennaya-vyichislitelnaya-tehnika-pervaya-evm

3. https://zen.yandex.ru/media/id/5aa6db308139bab1a9596f77/osnovnye-etapy-razvitiia-vychislitelnoi-tehniki-5aae41cb8139ba8c18ec8ae5

4. https://informatika.edusite.ru/lezione8_06a.htm

5. https://www.bestreferat.ru/referat-310216.html

6. https://studfile.net/preview/1710493/page:4/

7. https://www.sites.google.com/site/etapyrazvitiavycisltehniki/home/elektronnyj-etap

8. https://razvivashka.online/poznavatelnoe/abakus-kak-polzovatsya

9. https://biznes-prost.ru/abak.html

10. https://bdsmn.livejournal.com/317521.html

11. http://krivaksin.ru/logarifmicheskaya-lineyka-chto-eto/

12. http://all-ht.ru/inf/history/p_0_15.html

13. https://shkolala.ru/razvivashki/kak-schitat-na-abakuse/

Сделать демонстрационный абак своими руками. Использование абака на начальном этапе обучения. Западная Европа, VIII-X века

Здравствуйте, дорогие друзья! Меня зовут Евгения Климкович. Я рада видеть вас на страничках блога «ШколаЛа»!

Чем сегодня займемся? Может быть, посчитаем? Не хотите? Да ладно вам! Это же очень интересно! Особенно если не просто ворон считать, а считать на абакусе. А вы, кстати, знаете, как считать на абакусе? Вот и я не знаю. Счеты в руках не держала, на курсы не ходила. Но понять, как же все-таки это делается, очень хочется. Вот и решила попробовать хотя бы немножко приоткрыть завесу тайны.

Вы со мной?

Тогда присаживайтесь поудобнее, включайте мозг. Наш ментально-арифметический поезд отправляется!

Предлагаю начать с главного! С абакуса или, как его еще называют, соробана. Что это за штуковина такая?

План урока:

Что такое абакус?

Вот она – эта загадочная счетная машинка.

Чем-то напоминает известные многим советские счеты с костяшками. И, насколько я поняла, принципы работы на этих двух приспособлениях очень похожи. Отличаются эти счеты количеством костяшек на спицах и, собственно говоря, удобством эксплуатации. На абакусе приходится делать намного меньше движений руками.

Итак, абакус состоит из рамки, в которую установлены спицы. Причем спиц может быть разное количество. А на спицах нанизаны костяшки. По 5 штук на каждую. Спицы проходят сквозь разделительную планку. Над планкой остается по одной костяшке, под планкой по четыре.

Важную роль при счете на абакусе играет то, как именно человек двигает пальцами. Используются в работе только большой и указательный пальцы. Все движения путем многократных повторений доводятся до автоматизма. Этот навык легко потерять, поэтому при занятиях ментальной арифметикой не желательно пропускать уроки.

Расположение чисел

Теперь о том, как же располагаются числовые линейки.

Справа у нас находятся единицы. Затем десятки, потом сотни, тысячи, десятки тысяч и т.д. Каждому разряду своя спица. Костяшки, которые находятся под разделительной планкой, означают «1», над планкой – «5». Трудновато понять, да?

Давайте посмотрим на примере. Я нарисовала абакус!

Десятичные линейки рисовать не стала. То есть, крайняя правая линейка на моем рисунке – это единицы.

Так будет выглядеть на абакусе число 3.

Поднимаем к разделительной планке три костяшки на линейке единиц.

Попробуем взять двойное число, например, 15.

На линейке десятков поднимаем 1 костяшку, то есть, получаем 1 десяток. А на линейке единиц опускаем к разделителю верхнюю костяшку, которая и означает 5.

А вот это какое число получилось? Догадаетесь?

А давайте чего-нибудь посущественнее наберем. Например, 6482!

На линейке тысячи у нас верхняя костяшка опущена к разделителю – это пять тысяч и одна нижняя поднята вверх, плюс еще тысяча. Получаем 6 тысяч. С сотнями полегче, просто четыре костяшки поднимаем вверх. Десятки: верхняя опущена, три нижних подняты. Получается сверху 5 десятков, снизу 3. Это 80. Ну и еще 2 единицы. Не так уж сложно, правда?

Как складывать?

А теперь переходим к сложению и посмотрим, что из этого получится. Предлагаю взять что-нибудь попроще, чтобы не взорвать себе мозг) Например, сложим 33 и 14.

Откладываем на абакусе 33.

К трем десяткам прибавим еще один. Получим 4 десятка или 40.

Теперь единички. К трем единицам прибавим еще 4. Так как четырех свободных единиц снизу на спице нет, то сначала прибавим пять, опустим верхнюю косточку. А потом отнимем 1, опустим одну нижнюю. Получилось у нас 7 единиц.

В результате получилось 47! Может на калькуляторе проверим?) Шучу, и так ясно, что результат мы получили верный!

Дополнительная литература

В общем, примерно вот по такой схеме на абакусе и считают. Я показала все самое простое. А ведь можно еще и вычитать, и умножать, и делить, и в степень возводить. И работать с огромными числами. Хотите знать больше? Пожалуйста! Обнаружила в интернете инструкцию по работе с соробаном. Вот здесь ее можно скачать.

Если не поможет инструкция, то может быть стоит обратить внимание на книгу «Ментальная арифметика. Знакомство»? Насколько я поняла, она ориентирована на обучение детишек. Такой своеобразный учебник. Нашла я ее в магазине «My-shop». Ссылка на эту книжку чуть ниже.

Ментальная арифметика. Знакомство — Багаутдинов Р. | Купить книгу с доставкой | My-shop.ru
[|urlspan]

Думаю, что и взрослым людям не повредят занятия с абакусом. Особенно бухгалтерам. Представляете, все коллеги на калькуляторах считают или на компьютерах. А вы такой деловой с абакусом) И батарейки-то не садятся, и кнопки не западают, и костяшки так приятно пощелкивают) Красота!

Уф, наверное, хватит на сегодня счета. Теперь давайте посмотрим, как другие считают. Настоящие маленькие абакус-мастера, только они уже на том уровне подготовки, когда хватает и воображаемых счет. Смотрим видео.

На сегодня, пожалуй, все. А завтра на блоге «ШколаЛа» вас ждет новая интересная информация!

Кстати, если есть желание каждое воскресение по почте получать анонсы статей на следующую неделю, то обязательно подпишитесь на новости блога. Тогда вы точно ничего не пропустите!

И не забудьте вступить в нашу группу «ВКонтакте» , там вас тоже ждет много всего интересного!

Удачи вам и вашим маленьким школьникам!

Евгения Климкович.

Всё большую популярность среди дошкольников и учащихся начальных классов набирает так называемая ментальная математика, или арифметика (что тоже самое). Суть в том, что идет нагрузка для развития обоих полушарий головного мозга, ребенок начинает мыслить более объемно, пространственно и с легкостью осваивает все четыре основные математические действия. Занятия проходят на специальных счетных досках – абак.

Попробуем разобраться, что же это такое – абак? В чем его прелесть и отличие от привычных нам счетов?

Аба́к (др.-греч. ἄβαξ, ἀβάκιον, лат. abacus – доска) – это целое семейство счётных досок , применявшихся для арифметических вычислений приблизительно с V века до н. э. в древних культурах – Древней Греции, Древнем Риме и Древнем Китае и ряде других.
Общие принципы инструментов типа абака – разделение линиями на полосы, осуществление счёта с помощью размещённых на полосах камней или других подобных предметов.

Впервые абак появился, вероятно, в Древнем Вавилоне. 3 тыс. лет до н. э. Первоначально представлял собой доску, разграфлённую на полосы или со сделанными углублениями. Счётные метки (камешки, косточки) передвигались по линиям или углублениям. В V в. до н. э. в Египте вместо линий и углублений стали использовать палочки и проволоку с нанизанными камешками.

Абаком пользовались и народы Индии. Арабы знакомились с абаком у подчинённых ими народов. В заглавиях многих арабских руководств по арифметике фигурируют слова от корня «пыль».

Западная Европа, VIII-X века

У восточных арабов, как и у индийцев, абак был скоро вытеснен индийской нумерацией, но он крепко держался у западных арабов, захвативших в конце VIII века и Испанию. В X веке здесь познакомился со счётом на абаке француз Герберт (940-1003), написавший об этом книгу (980-982) и пропагандировавший сам и через своих учеников употребление абака. Вместо камешков при счёте на абаке употреблялись и жетоны с начертанными на них числовыми знаками, или римскими цифрами, или особыми числовыми знаками – апексами.

Апексы Герберта по форме близки к цифрам гобар западных арабов. Апексы Герберта и его 27-колонный абак, предмет удивления его современников (воспроизведены в реставрированном виде по различным рукописям профессором Н. М. Бубновым, профессором истории Киевского университета, начало XX века). Усилиями многочисленных учеников и последователей Герберта и благодаря его влиянию как папы римского (Сильвестра II, 999-1003) абак получил широкое распространение в Европе. Следы этого распространения удержались, между прочим, в различных языках. Английский глагол to checker, или chequer, означает графить – словом от этого же корня называется клетчатая материя, the cheque, или check – банковый чек, exchequer – казначейство. Последний термин происходит от того, что в банке расчёты велись на абаке, основа которого заключалась в разграфлённой доске. Английское государственное казначейство до последнего времени называлось Палатой шахматной доски – по клетчатому сукну, которым был покрыт стол заседаний. Клетчатая скатерть служила абаком при вычислениях. Возникшая в XII веке Палата шахматной доски была верховным финансовым управлением и высшим судом по финансовым вопросам до 1873 года.

В Европе абак применялся до XVIII века. В Средние века сторонники производства арифметических вычислений исключительно при помощи абака – абацисты – в течение нескольких столетий вели ожесточённую борьбу с алгоритмиками – приверженцами возникших тогда методов алгоритмизации арифметических действий.

Мезоамерика

Ацтекские счёты возникли приблизительно в X веке и изготавливались из зёрен кукурузы, нанизанных на струны, установленные в деревянной раме. В Империи инков применялось счётное устройство юпана (в паре с кипу), имевшая разновидности: арифметическая юпана, геоюпана и др. В юпане, по-видимому, использовалась фибоначчиева система счисления.

Дальний Восток

В странах Востока распространены китайский аналог абака – суаньпань и японский – соробан. Конструкции принципиально аналогичны, используют десятичную систему счисления, хотя японский вариант несколько экономичнее (в китайском, как и в русских счётах, используются «лишние» с точки зрения математики косточки). Для китайского и японского абака существует скрупулёзно разработанный набор алгоритмов, позволяющих механически (то есть не занимаясь дополнительными вычислениями в уме или на бумаге) выполнять все четыре арифметических действия и даже извлекать квадратные и кубические корни.

Японский соробан по сей день активно применяется, несмотря на повсеместное распространение электронных калькуляторов. В Японии использование соробана является элементом школьной программы обучения счёту в младших классах. Также в Японии и странах, имеющих значительную японскую диаспору, счёт на соробане популярен как вид развлечения или своеобразный спорт.

Россия

Десятичный абак, или русские счёты, в которых используется десятичная система счисления и возможность оперировать четвертями, десятыми и сотыми дробными долями появились в России на рубеже XV – XVI веков и активно применялись в торговле вплоть до последнего десятилетия XX века. От классического абака счёты отличаются увеличением разрядности каждого числового ряда и конструкцией. Ещё одна характерная особенность русских счёт – специально выделенный разряд для счёта в четвертях. С момента своего возникновения счёты практически не изменились.

С появлением дешёвых электронных калькуляторов счёты практически полностью вышли из употребления. Ещё раньше, в начале 1980-х годов, обучение пользованию счётами было исключено в СССР из школьной программы.

Сейчас мы вновь возвращаемся к старым привычным косточкам, бусинкам, камешкам и счетным доскам. Как говорится, всё новое – хорошо забытое старое!

Счеты для первоклассника

Абакус (Abacus) – это латинское слово, которое имеет свое начало от греческого abax , что означает таблица. Абак является одним из многих типов счетных устройств, которые используются для подсчета больших чисел. В современном мире этот счет цифр остается актуальным, в Китае и Японии легко можно встретить торговцев, которые пользуются абаком для подсчета стоимости товара.

Но главным их плюсом и преимуществом является то, что они помогают хорошо и быстро сформировать математические навыки у детей. В сегодняшней статье мы начнем с основ, и узнаем что такое счеты Абакус: как считать, инструкцию по использованию и небольшой видеоролик с первым уроком.

Счеты это инструмент, которым пользуются на уроках ментальной арифметики, чтобы быстро и качественно научить ребенка считать. читайте в моей статье.

История возникновения Абакус

Трудно себе представить счет без цифр. Самым ранним счетным устройством были человеческие пальцы рук, а иногда и ног. Но когда возникла необходимость посчитать что — либо большее, придумали новую счетную систему.

Абакус является одним из многих счетных устройств, изобретенных, чтобы посчитать большие числа.

Сегодня хотелось бы рассказать о самых древних и используемых по сей день системах вычисления. Это три основные счетные системы: Суан Пэн, Соробан и Русские счеты. У каждого из них есть свои отличия, давайте кратко рассмотрим каждое.

Суан Пэн

Абакус (Абак), или в китайском языке Suan-Pan, представляет собой деревянную дощечку с шарами. На верхней палубе находилось по 2 косточки, на нижней по 5 (2/5). Так было вплоть до 1850 года, после стиль немного изменился: на верхней палубе осталось по 1 бусинке, а на нижней 5 (1/5).

Соробан (современный Абакус)

В японском языке счеты назывались Соробан. У них было соотношение бусинок ¼. Техники подсчета в японской и китайской системе счета похожи, но имеют свои отличия. В нашей стране есть школы, которые обучают как той, так и другой системе подсчета. В статье представлена информация именно о Соробане, так как она активно используется как в Японии, так и в нашей стране для обучения деток.

Русские счеты

Были изобретены в 17 веке и используются до сих пор. Дизайн счет напоминает модель пары человеческих рук (каждый ряд имеет 10 бусин, соответствующей 10 пальцам на двух руках).

Модификация Ли Кай Чена

В 1958 году китайский ученый Ли Кай Чен объединил абакус и соробан в одни счеты и опубликовал руководство для новых счетчиков. По словам автора, умножение и деление на много легче использовать с помощью модифицированных счетов. Так можно вычислить даже кубические корни чисел.

На фото видно, что сверху находится японский Соробан, а снизу китайский Суан Пэн.

Как выглядят счеты?

Современные счеты, японские счетчики или Соробан имеют один шар вверху и четыре внизу.

Верхние косточки имеют значение 5 их еще называют небесные бусины. А нижний ряд (состоящий из 4-х косточек) имеет значение 1, его называют земными бусинами. Между ними есть разделительная линия.

Значения шариков начинаются с крайнего правого столбца, и равняется 1. Справа налево значения бисера увеличиваются и равна 1, затем 10, 100 и т.д. На приведенной ниже фотографии показано значение каждого шарика на счетах.

Инструкция по пользованию счетами Абакус

Проще всего показать на примере. Чтобы прибавить 1+3 необходимо, используя большой палец, сдвинуть

один земной шарик в сторону разделительной полосы, а затем сдвинуть еще три земных шарика и получится 4.

Так как современные счеты имеют всего четыре земные бусинки, а вы, например, хотите посчитать до пяти, вы должны перенести один небесный бисер в сторону разделительной полосы, в тоже время переместите все земные шары вниз.

А если вы желаете, чтобы общее число было равно 7, переместите еще два земных шарика на планку счета. Итого получится, что у вас один небесный шарик (который соответствует 5) и два земных шара (по 1 каждый). В сумме составляет семь.

Для того чтобы посчитать более крупные цифры используйте следующие бусины. Например, как показать 283? Первый ряд (единицы) будет три земные бусины; второй ряд это один шар из небесного ряда и три из земного; третий ряд – это два из земного ряда. На фото хорошо видно как это выглядит:

Как пользоваться пальцами?

Стандартные счеты могут использоваться для выполнения сложения, вычитания, умножения и деления. Их так же используют для извлечения квадратных и кубических корней.

Правильная техника пальцев имеет первостепенное значение для достижения мастерства в счетах. В случае японской версии Абакуса (Соробана) используется только указательный и большой пальцы.

На картинке представлена вырезка из японского учебника, в котором рассказывается о правильной технике перемещения бусин. Он показывает большой палец, используемый для подсчета бусинок в нижней палубе, а указательный палец используется во всех других случаях.

Удобно земные шары добавлять большим пальцем, а вычитать указательным. А вот небесные шары лучше добавлять и вычитать только указательным пальцем одной руки.

Так же я предполагаю, что вас интересует как вместо счетов пользоваться пальцами. Об этом у меня есть отдельный раздел в статье

Видео-урок 1: как пользоваться счетами Абакус?

Как правило, видеоинформация усваивается лучше, чем описание. Поэтому предлагаю рассмотреть простой и понятный урок о том, с чего начинается работа над абакусом.

А на последок вам небольшое домашнее задание. Попробуйте самостоятельно посчитать, какие цифры расположены на счетах . Ссылка кликабельна.

Делали мы абак очень давно. Поэтому сейчас пришлось делать новое поле и новые «камушки» для вычислений («камушки», потому что в Древнем Риме для подсчета на абаке использовали небольшие камушки, они назывались calculus). Но когда-то он очень хорошо помог понять римскую систему счёта.

Дописано позже : В римском абаке камушки лежали в желобках или на полосках. У меня они стоят на линиях, так мне проще было потом перейти с детьми к соробану и к счетам. Но если вы планируете делать много расчетов, то, возможно, удобнее будет поставить «камушки» на полоски. Ниже добавлю фото «на полосках». Разряды сохраняются.

И на «полосках».

Считаем по линиям (или по полоскам, смотря как вы поставили камушки). Каждая линия (полоска) — разряд: единицы, десятки, сотни и так далее.

Оранжевые камушки наверху — это пять единиц разряда. То есть 5, 50, 500 и так далее (в зависимости от разряда).

Жёлтые камушки внизу — это единицы разряда. То есть каждый из этих жёлтых камушков означает 1, 10, 100, 1000 и так далее (в зависимости от разряда).

Для того чтобы набрать число, нужное количество камушков мы сдвигаем к линии в середине листа.

Предположим, мы решили набрать число 657. Набираем справа налево.

Сначала набираем единицы . Нам их нужно семь. Сдвигаем к «линии счета» два жёлтых камушка (каждый из них равен единице) и один оранжевый (это пять единиц разряда). Получаем семь единиц.

Вариант «на полосках»

Теперь наберем десятки . Нам их нужно пять. Спускаем один оранжевый камушек к линии счета. Все, мы получили пять единиц разряда десятков, то есть 50.

Вариант «на полосках»

Набираем сотни . Нам нужно шесть сотен. Спускаем к линии счета один оранжевый камушек (пять единиц разряда сотен, то есть 500) и поднимаем к линии счета один камушек (это одна единица разряда, то есть 100). Всего 600.Итак, мы получили число 657.

Вариант «на полосках»

Кому хочется узнать больше, в том числе и о счете на пальцах у древних римлян. то пройдите по ссылке (про абак там тоже есть).

P.S. Соробан у нас тоже был. Но счет на нем как-то не пошёл, самодельный абак использовался больше (делали на большом листе, использовали бусины).

Но соробан нужно найти и купить, а листок бумаги, карандаш, линейка и два куска пластилина, найдутся, я думаю, в любом доме, где есть школьник. И можно сразу пробовать. Кроме пластилина, для «камушков» абака подойдут мелкие пуговицы (два цвета), бусины (два цвета), любые мелкие конфеты типа скитлс.

При подсчетах сильно пригодится состав чисел 5 и 10.

Хорошо написано о римских цифрах в книге В. Лёвшина «Три дня в Карликании». Но, рассказывая про цифры, он все же говорит о цифрах привычных нашему пониманию. Но про формирование цифр можно сказать отдельно (в книге Лёвшина то не описано). Современный вариант римской системы не соответствует той, которая использовалась в древности. четверка записывалась как четыре палочки, а девятка как галочка и четыре палочки (VIIII). То есть запись была основывалась на «принципе сложения», VI — это «пять да один — итого шесть». Для иллюстрации этого принципа достаточно набрать число шесть или девять на абаке. Иногда, например, могло писаться и IV и все равно считалось, что это «шесть». То есть в те времена не имело значения, где стояла палочка или палочки. Все равно действовал «принцип сложения». Римляне обычно не вели расчетов на бумаге. Они делали их на абаке и записывали результат. Потом император Септимий СевЕр запретил писать меньшие числа перед большими. И остался только один вариант записи шестерки и девятки — VI и VIIII.

А вот запись чисел, основанная на «принципе вычитания», то есть чисел IV (четыре) и IX (девять), которая означает «вычти из последующего числа предыдущее и вот тебе результат», появилась уже в Средневековье. И на абаке её не изобразить. По крайней мере, нам так объясняли на лекциях . Возможно есть и другие версии.

| Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 6 классы | Материал для любознательных | Абак и счеты

Абак и счеты

На пальцах считать удобно, только результат счета хранить нельзя. Не станешь же целый день ходить с загнутыми пальцами. И человек догадался – для счета можно использовать все, что попадется под руку. Камешки, палочки, косточки, веревки и так далее. Пасет пастух стадо овец. На поясе у него веревка, а на веревке столько узелков, сколько овец в стаде. Родился ягненок – пастух завязал еще один узелок. Утащили волки двух овец – развязал два узелка.

С развитием цивилизации появлялись различные приемы счета. Они были необходимы и сборщикам налогов, и купцам, и ремесленникам, и ростовщикам. Искусством счета владели немногие специально обученные люди – счетчики. Они использовали счетные инструменты – абаки.

Простейший абак – это доска с прорезанными в ней желобами. Чтобы найти сумму двух чисел (например, 258 и 125), счетчик сначала обозначал на абаке первое слагаемое. Для этого он укладывал в нижнем желобе 8 камешков, в следующем желобе – 5 камешков и 2 камешка – в третьем желобе. Если в каком-то разряде в числе стоял нуль, то соответствующий желоб оставался пустым. Дальше счетчик добавлял в последний желоб к имеющимся там 8 камешкам еще 5, затем вынимал оттуда 10 (там оставалось 3) и 1 камешек добавлял во второй желоб. Потом добавлял во второй желоб еще 2 камешка и 1 камешек – в третий желоб. После этого камешки на доске показывали число 383.

Абаки использовались уже в V-IV веках до нашей эры. Их изготавливали из бронзы, камня, слоновой кости, цветного стекла. Слово «абак» имеет греческое происхождение и буквально означает «пыль», хотя его смысловое значение – «счетная доска». В чем тут дело? Ответ прост: изначально камешки раскладывали на совершенно ровной доске, а чтобы они не скатывались со своего первоначального положения, доска покрывалась тонким слоем песка или пыли. А от слова «камешек» (по латыни – «calculus») произошло название современного счетного прибора – «калькулятор».

Абак использовался и в Древней Греции, и в Древнем Риме, а затем и в Западной Европе вплоть до XVIII века. Он похож на знакомые вам счеты – косточки на встав¬ленных в рамку металлических спицах.

Счеты использовали разные народы, и у каждого народа они имели свои особенности. Так, в русских счетах по десять косточек в каждом ряду, а в западноевропейских – по девять. У китайских счетов суан-пан на каждой проволоке по семь шариков, причем два отделены от остальных пяти. Каждый из этих двух шариков означает пять единиц данного разряда. Такое усовершенствование позволяет уменьшить число шариков в счетах.

В Японии и в наши дни проводятся соревнования по скорости счета между людьми, вооруженными японскими счетами соробан, и операторами вычислительных машин. Причем, как правило, побеждают вычислители на счетах. Ведь чтобы машина начала считать, для нее надо составить программу.

Линейка абак как пользоваться

mentalnaya-arifmetika-razvitie.ru

Рабдологический абак

all-ht.ru

Что такое счеты абакус и для чего они – Экспертные статьи в блоге IQ007

Все дети учат таблицы умножения, но не все тренируют устный счет, ведь под рукой почти всегда есть калькулятор. Однако навык быстрого устного счета — это не просто бытовое удобство, а значительное повышение уровня общего развития ребенка.

Чтобы достигать больших успехов в разных дисциплинах, детям полезно заниматься ментальной арифметикой — методикой развития интеллектуальных способностей за счет устных вычислений, пришедшей к нам с Востока.

Основной инструмент для занятий ментальной арифметикой — счеты под названием абакус или соробан. Они помогают ребенку запомнить метод подсчета, чтобы потом применять его в уме.

Изобретение абакуса приписывают китайцам, но его аналоги можно встретить в описаниях многих культур. Подобный инструмент был в обиходе в Древней Греции, Древнем Риме, Индии и Египте.

Счеты активно использовались в торговле, поскольку позволяли быстро и точно складывать любые числа. Инструмент постоянно модернизировался и пришел к нам в виде деревянной рамы со стержнями, на которые нанизаны косточки (деревянные или медные).

Как считать на абакусе

Счеты абакус чем-то напоминают советские счеты, но работать с ними нужно иначе.

Костяшки абакуса нанизаны на стержни — по пять на каждом. Все стержни разделены расчетной линией. Сверху по одной костяшке, и по четыре снизу.

Чтобы набрать на счетах, скажем, число 33, нужно сдвинуть три десятичных и три единичных костяшки. А чтобы получить число 75, нужно сдвинуть одну 50-значную (верхнюю) костяшку, две десятизначных и одну пятизначную.

Принцип действий с числами — быстрые и точные наборы нужных значений.

Все кажется довольно простым, но это потому, что вы еще не пробовали считать на абакусе так, как нужно. Педагог работает с ребенком над техникой и сопоставлением действий с метаморфозами счетов. Запомнив механику, ребенок представляет себе счеты в уме и выполняет сложное математическое действие легко и быстро.

При счете важно правильно двигать пальцами, поэтому во время занятий ребенок активно развивает еще и мелкую моторику — задействуются указательный и большой пальцы.

Числа на стержнях располагаются по возрастающей справа налево (или снизу вверх, если держать абакус вертикально): единицы, десятки, сотни, тысячи, десятки тысяч и так далее.

В зависимости от размера и модели счетов (а их сейчас представлено довольно много) можно добавить стержни с десятичными, сотыми и тысячными дробями.

На них можно не только складывать и вычитать, но и делить и умножать. Как? Спросите у вашего ребенка через два-три месяца занятий, и демонстрация вас приятно удивит. Дети сами понимают, как интересно выглядят манипуляции со счетами со стороны, поэтому ментальная арифметика — это не просто навык, а интересное увлечение и развлечение.

Что дают занятия ментальной арифметикой

Ребенок осваивает счеты в начале обучения (то есть в течение нескольких месяцев), а затем пользуется ими исключительно в воображении — это позволяет ему проводить сложные вычисления в уме за секунды.

Чтобы хорошо запомнить механику, необходимо заниматься регулярно. Этот навык легко забывается, если часто пропускать тренировки.

Счет на абакусе — специфический навык, овладеть которым легче всего в детстве. Именно поэтому детские педагоги рекомендуют ментальную арифметику. Это не только полезное, но и невероятно интересное занятие, дети увлекаются им надолго и чувствуют себя гораздо увереннее, понимая, что умеют делать что-то специфическое.

Несмотря на кажущуюся сложность, методика подходит именно детям. Мозг ребенка пластичен, интенсивнее всего он развивается в период с 4 до 12 лет, и именно тогда стоит начинать занятия по ментальной арифметике. Принципы устного счета быстро запомнятся и останутся с ребенком на всю жизнь.

Поскольку современное образование во многом построено на развитии аналитических, а не творческих способностей, полушария мозга могут развиваться неравномерно, и творческая, экстраординарная сторона личности может остаться недостаточно хорошо выраженной.

Главная особенность ментальной арифметики — развитие обоих полушарий мозга. Это и логическое мышление, и интуиция, и инициативность, и самостоятельность, и умение нестандартно решать сложные задачи. Нередко занятия приводят к почти равному развитию моторики правой и левой руки, вплоть до аккуратного письма.

Развитие умственной деятельности ребенка со обеих сторон способствует формированию устойчивых межполушарных связей. Это и решение вычислительных задач, и нестандартный принцип мышления в целом. Такой подход может стать катализатором ранее скрытых способностей ребенка, раскрыть его потенциал и помочь понять, какие предметы ему больше всего нравятся.

iq007.ru

Ментальный счет: описание методики, результаты, отзывы. Ментальная арифметика :

Многие родители наверняка мечтают о том, чтобы их малыш вырос особенным и непременно стал таким, чтобы им можно было гордиться. Но если одни папы и мамы лишь хвастаются способностями своих детей, то другие ведут их в специальные школы, помогающие развивать данные природой задатки.

А можно ли вырастить из ребенка гения? Если в прежние времена ответ на такой вопрос был однозначен и требовал наличия таланта и удивительных способностей, то сегодня задача намного упростилась. Например, для того чтобы ребенок проявлял недюжинные познания в математике и считал так же быстро и правильно, как калькулятор, предлагается необычная программа, которая обучит малыша математике. А называется она «ментальная арифметика». Что это за программа и какими она обладает преимуществами?

Популярность методики

С 1993 г. ментальная арифметика используется для обучения детей в 52 странах мира, начиная с Канады и заканчивая Великобританией. В некоторых из них методику рекомендуют для включения в программу школ.

Наибольшее распространение ментальный счет получил в государствах Ближнего Востока, а также в Китае, Австралии, Таиланде, Австрии, США и Канаде. Начинают появляться специализированные организации в Казахстане, Киргизии и России.

Ментальный счет является одним из самых молодых и стремительно развивающихся способов, применяемых для детского образования. Благодаря этой методике можно без труда развить умственные способности ребенка, которые в первую очередь имеют математическую направленность. Благодаря освоению детьми техники ментального счета любая математическая задача превращается для них в простой и быстрый вычислительный процесс.

История возникновения

Методика ментального счета имеет древние корни. И это несмотря на то, что разработана она сравнительно недавно ученым из Турции Халитом Шеном. Что же он использовал для своей системы ментального счета? Абакус, который был создан в Китае еще 5 тыс. лет назад. Этот предмет представляет собой счеты, которые внесли огромный вклад в развитие всей мировой арифметики. После изобретения абакус начал свое постепенное распространение по всему миру. В 16-м веке из Китая он попал в Японию. На протяжении четырех сотен лет жители Страны восходящего солнца не только успешно использовали такие счеты, но и тщательно прорабатывали их, пытаясь усовершенствовать такой нужный для совершения арифметических действий предмет. И это им удалось. Японцы создали счеты соробан, которые и до сегодняшнего дня используются для обучения детей в начальной школе.

На протяжении всей истории развития человечества совершенствовалась математическая наука. И сегодня она может предложить нам огромное количество своих достижений. Но, несмотря на это, ученые считают, что использование абакуса приносит больше пользы в обучении детей точному счету.

Польза ментальной арифметики

Считается, что каждое из полушарий человеческого мозга отвечает за свои направления. Так, правое из них позволяет развить творчество, образное восприятие и мышление. Левое же в ответе за логическое мышление.

Деятельность полушарий активизируется в тот момент, когда человек начинает работать руками. Если активна правая из них, то начинает работать левое полушарие. И наоборот. Человек, работающий левой рукой, способствует активизации работы правого полушария.

Задача менара – заставить весь мозг принимать участие в образовательном процессе. Как же достигнуть таких результатов? Это возможно при выполнении математических операций на абакусе обеими руками. В конечном итоге менар способствует освоению быстрого счета, а также развитию и совершенствованию аналитических навыков.

Ученые сравнили калькулятор с абакусом и пришли к однозначному выводу, что первый из них расслабляет активность мозга. Абакус же, напротив, оттачивает и тренирует полушария.

Когда следует начать изучать ментальный счет? Отзывы приверженцев данной методики утверждают, что лучше всего осваивать этот способ в возрасте от четырех до двенадцати лет. И только в некоторых случаях период может быть продлен еще на четыре года. Это время, когда происходит бурное развитие мозга. И данный факт является замечательным посылом к тому, чтобы прививать ребенку базовые навыки, проводить изучение иностранных языков, развивать мышление, осваивать игру на музыкальных инструментах и боевые искусства.

Суть ментальной методики

Вся программа по освоению устного счета построена на последовательном прохождении двух этапов. На первом из них происходит ознакомление и овладение техникой выполнения арифметических действий с использованием косточек, во время которых задействованы одновременно две руки. Благодаря этому в процессе участвует как левое, так и правое полушарие. Это позволяет достигнуть максимально быстрого усвоения и выполнения арифметических действий. В своей работе ребенок использует абакус. Этот предмет позволяет ему совершенно свободно вычитать и умножать, складывать и делить, вычислять квадратный и кубический корень.

Во время прохождения второго этапа ученики обучаются ментальному счету, который производится в уме. Ребенок перестает постоянно привязываться к абакусу, что также стимулирует и его воображение. Левые полушария детей воспринимают цифры, а правые – образ костяшек. На этом и основана методика ментального счета. Мозг начинает работать с воображаемым абакусом, воспринимая при этом числа в форме картинок. Выполнение же математического счета ассоциируется с движением косточек.

Обучение ментальной арифметике быстрого счета является очень интересным и увлекательным процессом. Он по достоинству оценен сотнями тысяч людей и получил огромное количество положительных отзывов.

Абакус

Что же представляет собой эта загадочная и древняя счетная машинка? Абакус, или счеты для ментального счета, очень напоминают старые советские «костяшки». Весьма схожим является и принцип работы на этих двух приспособлениях. В чем же отличие этих счетов? Оно заключено в количестве костяшек, находящихся на спицах и в удобстве эксплуатации.

Стоит сказать о том, что для получения результата абакус потребует сделать большее количество движений руками. Как же устроен этот древний предмет, пришедший к нам из Китая? Он представляет собой рамку, в которую вставлены спицы. Причем их количество может быть разным. На спицах находится по пять штук нанизанных костяшек.

По длине каждую спицу пересекает разделительная планка. Над ней находится одна костяшка, а под ней, соответственно, четыре.

Методика ментального счета предусматривает определенное движение человека пальцами. Из них задействуются только указательный и большой. Все движения должны быть доведены до автоматизма, чему содействует их многократное повторение.

Интересно, что данный навык легко может быть утерян. Именно поэтому при освоении методики не стоит пропускать занятия.

Расположение чисел

Каковы азы счета в ментальной арифметике? Для того чтобы освоить данную методику, необходимо знать, как располагаются на абакусе числовые линейки. В его правой стороне находятся единицы. После этого идут десятки, затем сотни, после тысячи, десятки тысяч и так далее. Каждый из этих разрядов располагается на отдельной спице.

Костяшки, расположенные под разделительной планкой, это «1», а над ней – «5». Например, для того, чтобы на абакусе набрать число 3, понадобится отделить три костяшки, расположенные под разделительной планкой на спице, находящейся правее остальных. Рассмотрим пример с двойными числами, например, с 15. Для его набора на абакусе следует поднять вверх одну костяшку на спице десятков и опустить одну, находящуюся над верхней планкой на спице единиц.

Операции сложения

Как научиться ментальному счету? Для этого потребуется изучить, как проводятся на абакусе арифметические действия. Рассмотрим, например, сложение. Посмотрим, чему будет равна сумма чисел 22 и 13. Для начала понадобится отложить по две костяшки на спицах десятков и единиц, расположенные внизу разделительной планки. Далее к двум десяткам добавим еще один. Получится 30. Теперь приступим к сложению единичек. К двум прибавим еще три. Получится число «пять», которое обозначается костяшкой вверху разделительной планки. В итоге получается 35. Для освоения более сложных операций понадобится тщательным образом изучить специальную литературу. После освоения самых простых примеров рекомендуется потренироваться на абакусе. Таким образом, обучение становится максимально интересным.

Освоение второго этапа

После того как операции на абакусе не будут вызывать затруднений, можно приступить к устному счету ментальной арифметики. Это следующий уровень обучения. Он предполагает ментальный счет, то есть произведенный в уме. Для этого понадобится сделать для ребенка картинку абакуса. Самым простым вариантом является распечатка изображения этого предмета, которое затем должно быть наклеено на картон (можно взять его от коробки из-под обуви). По возможности картинка должна быть цветной. Это позволит ребенку легче представить ее в своем воображении.

Во избежание ошибок стоит помнить о том, что ментальный счет должен производиться слева направо. Что необходимо предпринять, чтобы отложить на абакусе двухзначное число? Для этого ребенку следует вначале левой рукой набрать костяшки, соответствующие десяткам, а после правой отделить на спице нужные единицы.

Так, для набора 6, 7, 8 и 9 следует использовать «Щепоточку». Этот процесс представляет собой сведение вместе указательного и большого пальца к разделительной планке и сбор костяшек, обозначающих цифру 5, и необходимого их числа на спице, которая расположена в нижней части абакуса. Вычитание чисел производится аналогичным образом. Той же «Щепоточкой» одновременно отбрасываются «пятерочки» и нужное количество косточек внизу.

Цели и результаты методики

Обучение ментальному счету позволяет ребенку добиться небывалых успехов в области математики. Детки, прошедшие специальный курс, с легкостью могут вычислить в уме десятизначные числа, умножить их и вычесть. Но стоит сказать о том, что и это не является главной целью подобного обучения. Счет представляет собой лишь способ, с помощью которого развиваются умственные способности человека.

Освоение ментальной арифметики способствует следующему:

• активизации зрительной и слуховой памяти;
• умению концентрации внимания;
• совершенствованию смекалки и интуиции;
• креативному мышлению;
• проявлению уверенности в себе и самостоятельности;
• быстрому освоению иностранных языков;
• реализации способностей в будущем.

В тех случаях, когда для освоения менара был использован профессиональный подход и специалисты достигли поставленных перед ними целей, ребенок без труда начинает решать в уме как простые, так и сложные задачи по математике. А арифметические действия на умножение и сложение он производит даже быстрее калькулятора.

Школы по обучению ментальной арифметике

Где же можно освоить эту уникальную методику? На сегодняшний день для изучения ментальной арифметики необходимо записаться в специализированный образовательный центр. В них специалисты занимаются с детьми на протяжении двух-трех лет. Помимо описанных выше этапов, с помощью которых можно освоить методику, существует еще десять ступеней. Причем каждую из них ученики проходят за 2-3 месяца.

Каждый из таких специализированных центров разрабатывает собственные программы обучения. Однако, несмотря на это, существуют и общие правила, которых придерживаются абсолютно все. Они состоят в том, что группы учеников формируются в зависимости от их возраста. Так, существует три базовых вида таких групп.

Это kinder, kids и junior. Занятия проводят опытные высококвалифицированные психологи и педагоги, которые прошли соответствующую подготовку и имеют необходимую аттестацию.

Помимо центров по обучению ментальному счету сегодня работают и специализированные школы, готовящие специалистов по соответствующему профилю. Как правило, преподаватели менара – это люди, имеющие не только психологическое и педагогическое образование, но и определенный опыт работы с детьми. И это очень важно. Ведь обучение ментальному счету представляет собой не только освоение навыков, позволяющих работать с древними счетами. В этом процессе непременно учитываются используемые в педагогической практике психологические особенности в развитии ребенка.

Отзывы о методике

Ментальная арифметика – это довольно новая программа, применяемая для обучения устному счету. Однако, несмотря на немногочисленные годы существования, она уже успела получить большую популярность и показала превосходные результаты. Отзывы многих родителей и детей подтверждают тот факт, что данная программа не только эффективна, но и максимально полезна. При этом стоит учесть, что менар вполне может быть успешно внедрен в школьное обучение, став для детей дополнительным инструментом в освоении математических навыков.

По отзывам родителей, отличные результаты у детей можно наблюдать уже по истечении двух-трех месяцев после начала занятий, которые проводятся всего по несколько часов в неделю. Многие родители подтверждают, что у их ребенка заметно улучшилась память, повысилась способность к сосредоточению, а мышление приняло креативный характер. При этом школьник начал радовать своих близких хорошими оценками, которые получает не только на уроках математики. Он повысил уровень своих знаний и по всем остальным предметам. Кроме того, ему с легкостью стал даваться иностранный язык.

Все это позволяет сделать однозначный вывод о том, что менар представляет собой не только новый способ освоения навыков вычисления. Отличные результаты методика дает и в сфере всестороннего развития личности. Кроме того, во время занятий ментальной арифметикой активизируется потенциал маленького человека. Это способствует формированию здоровой и успешной натуры, у которой имеется надежный и крепкий фундамент, позволяющий без особых усилий вступить во взрослую жизнь.

businessman.ru

5 простых приемов для развития у ребенка самостоятельности. Узнать   Методика выполнения движений с ребенком от специалиста высшей квалификации Скачать бесплатно

Система счета абакус: секреты ментальной арифметики для первоклассников Среди необычных дидактических пособий для детей свое место занимают счеты абакус, которые помогут улучшить математические навыки и весело и с пользой провести время. Предлагаем познакомиться с тем, что они собой представляют и как ими пользоваться. Что это такое? Сами счеты, которые положены в основу методики, появились более 2,5 тысячелетий назад. Также можно встретить названия «абак» или «соробан». Эти счеты исполняли в древнейших государствах функции современных калькуляторов и помогали отсчитывать десятки. Впоследствии они стали использоваться в ментальной арифметике. Внешний их вид довольно прост: абак представляет собой рамку прямоугольной формы, которая разделена перекладинами с нанизанными на них косточками. Вверху, над разделительной полосой, расположена всего одна линия, каждый элемент которой означает пять. Снизу находятся ряды с четырьмя косточками, обозначающими единицу. Линии косточек означают поочередно единицы (первая правая), десятки (вторая правая), сотни, тысячи. Если первая правая косточка поднята, то на счетах выложена цифра 1 или наименьшее десятичное значение (если расчеты ведутся, например, в миллиардах). Распределение чисел таково: нижние косточки – это 1,2,3 и 4, соответственно, если подняты 2 из них, то счеты показывают число два; если верхняя косточка поднята, число меньше, чем 5; если опущена на разделительную линию – больше; верхняя опущена, три нижние подняты – это число 8. Аналогичным образом можно выложить любое число. Преимущества использования Работа со счетами не только помогает развивать мелкую моторику дошкольника, но и тренирует сразу оба полушария его головного мозга, позволяет наладить взаимосвязи между ними. Кроме того, можно выделить несколько достоинств методики: Интерес. Малышам нравится перебирать косточки, при правильном подходе родителей из абакуса можно сделать тренажер, занятия на котором будут искренне нравиться ребенку. Использование счетов позволяет избежать заучивания и стимулирует образное мышление. При регулярных тренировках со временем удастся перевести ребенка от работы с реальным абакусом к воображаемой. Дети учатся находить нестандартные варианты решения проблемы. Постепенно обретают уверенность в себе, становятся более самостоятельными. Очень хорошо развивается мышление. Вот почему счеты считаются мощнейшим пособием в ментальной арифметике, то есть обучении быстрому счету. Как работать? Познакомимся с инструкцией по использованию абакуса в домашней работе со старшими дошкольниками и первоклассниками. В целом японские счеты могут заинтересовать детей от 5–6 до 10–11 лет. Они помогают научить совершать в уме различные арифметические действия: сложение, вычитание и даже умножение. Как же пользоваться таким пособием? Положить счеты на поверхность стола, добившись того, чтобы никакие посторонние предметы не мешали нормальному движению косточек. Поставить их «на ноль» — ни один из шариков не должен касаться разделительной полосы. Далее на конкретном примере рассмотрим суть работы. Допустим, нам необходимо сложить 1 и 2. Для этого при помощи большого пальца перемещаем к разделительной полосе сначала одну косточку. Потом – две. Считаем результат – 3. Но как быть, если надо сложить, например, 5 и 3. Цифр гораздо больше, чем косточек. Действовать следует так: косточка, расположенная над разделительной полосой – это 5. Поэтому ее следует опустить. А три косточки из нижнего ряда, наоборот, поднять. Получится 8. На счетах можно отложить и трехзначные числа. Например, 175 будет выглядеть так: На первой линии опускается верхняя (пятерка). На второй – опускается верхняя (5) и поднимаются две нижние (2). На третьей – поднимается одна нижняя (1). Сначала может показаться, что все слишком сложно и научиться будет нереально не только дошкольнику, но и взрослому. Но на практике зачастую бывает достаточно показать ребенку пару примеров, он довольно быстро разберется и начнет считать. Как складывать и вычитать? После того как малыш научился выкладывать числа, можно приступать к обучению простейшим арифметическим действиям. Сначала рассмотрим сложение, к примеру, 36+23: Устанавливается первое число, 36. Далее его следует разделить на простые цифры – 3 и 6. После этого на соответствующих линейках провести сложение единиц с единицами, десятков и десятками. Получается: 3+2 (десятки) и 6+3 (единиц). Кости на линейках перемещаются соответствующим образом. Если бы косточек получилось больше 9, нужно было прибавить единицу на соседней линейке. Вычитание проводится по такой же системе, начиная с меньшего порядка. В случае, если из меньшего числа вычитается большее, происходит следующее: их переставляют, а на соседней линейке убирают косточку. Такая система счета кажется сложной только при описании, на деле же стоит попробовать – и ребенку непременно понравится. Умножение и деление Они также не вызовут особых затруднений у тех, кто знает таблицу умножения (от 1 до 10). Рассмотрим пример. Надо умножить 13х3. Сначала пример делится на два действия: 10 х 3 = 30 3 х 3 = 9. На счетах сначала набирается 30, потом добавляется еще 3. И становится понятно, что ответ на пример – 39. Деление полностью аналогично, однако результаты не складываются, а вычитаются. Правила Специалисты по ментальной арифметике разработали ряд правил, которых следует придерживаться при занятиях с абакусом. Ставить пальцы необходимо определенным образом. Работают только большой и указательный, остальные сжаты в кулак. Большим поднимаются косточки по одной, указательным – опускаются. Оба движутся по направлению слева направо. «Набор» чисел ведется одной рукой. Вторая придерживает счеты таким образом, чтобы не закрывать обзор. Верхнюю косточку поднимает и опускает исключительно указательный палец. Занятия проводятся дважды в неделю, действовать следует по принципу «от простого к сложному», не допуская переутомления ребенка. Интересно, что при желании счеты можно изготовить своими руками, работа не отнимет много сил и времени. Таков абакус, научиться считать на котором могут как дети, так и взрослые. Самое главнее правило успеха – регулярные занятия. Текст razvivashka.online Абакус Многие люди слова абакус и соробан слышат, чуть ли не впервые. А ведь эта система подсчетов использовалась в Древней Греции, Риме и Китае еще за пять веков до нашей эры. Легкая система подсчета положила начало нашим классическим счетам с костяшками, но абак намного проще и понятней в использовании. Детям система устного счета абакус полезна не только тем, что они научатся быстро считать и понимать цифры, со временем они обучаются ими пользоваться ментально, в воображении. Эта «игра» позволяет научить даже первоклашку очень быстро считать и выполнять абсолютно все арифметические действия, сначала с помощью специального прибора, а потом и в уме, для этого ему нужно будет только научиться считать до десяти. Как выглядит абак? Специальные счеты, используемые в системе ментального счета абакусе, называются абак, линейка или также абакус. Они имеют классический вид: Это рамка со спицами, на которые надеты костяшки, по пять штук на каждой. Количество спиц на разных абакусах отличается, а вот костяшек на каждой из них пять, кроме того, одну костяшку на каждой спице отделяет поперечная планка. Считающий в воображении сам рассчитывает название каждой спицы, на рисунке выше подписано распределение без десятичных знаков, но если они нужны, то первые левые спицы отводятся под них, а уже потом начинаются единицы. (Абакус и абакус с десятичными знаками) Распределяем числа Чтобы понять, как считать на абакусе, надо просто разобраться, как на нем распределяются цифры. В дальнейшем мы будем использовать распределение на спицах, начиная с единицы, так как будем работать с целыми числами. Чтобы работать с десятичными, нужно для начала разобраться в элементарной арифметике. Первая правая спица, когда одна костяшка сверху – наименьшее десятичное значение, в подсчетах, если мы считаем миллиарды, значит, наименьшее – миллиард, если десятичные дроби, то тысячные. Далее спицы считаются с умножением на 10. Для пользования спицами надо запомнить, как распределяется число на абакусе: на спице пять костяшек; костяшка над планкой это 5, если она опущена – это говорит что число больше пяти, если поднята, значит меньше; костяшки ниже планок – 1, 2, 3, 4, сколько поднято костяшек, столько и надо учесть; если костяшка 5 опущена, то прибавляется число костяшек, поднятых снизу, если они не подняты, то значит на спице 5. Например, число 15 будет выглядеть вот так: 66 вот так: А 81549 вот так: Кажущаяся сложность пропадает практически через пять минут, ребенок очень быстро начинает разбираться в самых сложных числах. Главное – понять принцип работы этого прибора. Как проводить сложение и вычитание на абакусе? Считать на абакусе достаточно просто. Для понимания возьмем пример 26+34 и сложим его на линейке абаке. Устанавливаем первое число 26 : Раскладываем все числа на простые цифры, не забывая, к какой спице они относятся: 2 и 3 к десяткам, а 6 и 4 к единицам. Производим сложение простых чисел. 6+4 и 2+3. Теперь сдвигаем единицы на первой спице 6+4 =10, то есть на 1 спице надо показать 0, и развести все костяшки по местам, а к двум костяшкам на второй спице добавить еще одну, получим 30: Но мы добавляли не 4, а 34, поэтому на второй спице надо добавить еще 3 костяшки и показать цифру 6, для этого опускаются снизу 2 костяшки и «5». Итого мы получаем 60. Сложение всегда начинается с меньшего числа с переходом к большему. Если костяшек на спице получается больше чем 9, тогда на соседней спице добавится еще одна. В случае с вычитанием система та же, начинаем с меньшего, только если вычитается от меньшей цифры большая, тогда они меняются местами, а с соседней спицы убирается костяшка. Например, 15-13: ставим 15; раскладываем число на простые цифры 1 и 5 и 1 и 3, от 1 отнимаем 1, от 5 отнимаем 3 и получаем 2: Эта система расчетов при должной сноровке занимает около двух-трех секунд. Со временем сама линейка уже будет не нужна, она сама будет возникать в мыслях. Как умножать и делить на абакусе? Умножение на линейке тоже достаточно простое, для этого нужно только освоить таблицу умножения от 1 до 10 и запомнить одно правило: десятки умножаем на единицы, потом единицы умножаем на единицы. Если ребенок уже разобрался, как считать на абакусе, все действия будут занимать не больше минуты. Для примера возьмем простое задание 11х5, которое решается в два действия: Для начала на абакусе набирается ответ на первый пример, 50: потом к нему добавляется ответ на второй пример, 5: И в результате мы видим на абаке ответ 55. Для проведения более сложных действий, когда берутся более сложные примеры, тогда задание решается в последовательности: десятки умножаются на десятки, единицы на десятки, десятки на единицы, единицы на единицы. То есть, сначала все цифры, постепенно от большего к меньшему перемножаются и набираются последовательно на абаке. Например, 611 Х24: Решается это так, нули прячутся и берутся цифры без них, а их количество определяет, на сколько спиц надо сдвинуться влево, кроме того, если результат получился двузначный, значит надо сместиться еще на одну спицу: 6х2=12 – при умножении результат набираем на той спице, к которой относится число и сдвигаемся вправо на столько спиц, сколько нулей в числе, на которое умножают, в нашем случае в 20 один ноль, то есть результат 12 набирается не на сотнях, а на тысячах. Но если результат имеет две цифры, тогда надо сместиться еще на одну спицу. То есть, в нашем случае 12 набирается на спицах, отвечающих на десять тысяч и тысячи.(12000) 1х2=2 – единица относится к десяткам, в 20 один ноль, то есть сдвигаемся на одну спицу и добавляем ответ в сотнях.(12200) 1х2=2 единица относится к единицам, а в 20 один ноль, то есть исходя из правил, добавляем ответ в десятках.(12220) Теперь переходим к следующему порядку и умножаем сотни на единицы, десятки на единицы и единицы на единицы. 6х4=24 – в 4 нет нолей, мы сдвигаемся только на одну спицу, так как в ответе две цифры, и добавляем 2 костяшки к тысячам и 4 к сотням. (14620) 1х4=4 – добавляем в десятки 4 костяшки. (14660) 1х4=добавляем теперь 4 костяшки в единицы. (14664) Последнее действие можно не делать, но сначала нужно проверить: берем калькулятор, умножаем 611х24, получаем 14664 и радуемся своей сноровке. Деление проводится по такому же принципу, только производится не сложение результатов на линейке, а вычитание. Сдвигание по спицам происходит слева направо. Насколько быстро можно работать на абакусе? Даже на самые сложные действия ребенок, как и взрослый, потратит не больше одной минуты, главное во всем этом деле – практика и понимание, как считать на абакусе. Чем чаще и больше заниматься, тем проще будет перейти на систему ментального вычисления, без каких либо приспособлений. Для начала со сложными примерами понадобится еще ручка и бумага, чтобы расписать последовательность действий и не запутаться, но пара дней практики – и ничего кроме абака уже не понадобится. Главное – не стесняться перепроверять результат и показывать маленькие победы. Это позволяет стимулировать желание пользоваться этой древней системой. А она, в свою очередь, развивает память, фантазию и логику. iqclub.ru Как считать на абакусе

Чем-то напоминает известные многим советские счеты с костяшками. Принципы работы на этих двух приспособлениях очень похожи. Отличаются эти счеты количеством костяшек на спицах и, собственно говоря, удобством эксплуатации. На абакусе приходится делать намного меньше движений руками. Итак, абакус состоит из рамки, в которую установлены спицы. Причем спиц может быть разное количество. А на спицах нанизаны костяшки. По 5 штук на каждую. Спицы проходят сквозь разделительную планку. Над планкой остается по одной костяшке, под планкой по четыре. Важную роль при счете на абакусе играет то, как именно человек двигает пальцами. Используются в работе только большой и указательный пальцы. Все движения путем многократных повторений доводятся до автоматизма. Этот навык легко потерять, поэтому при занятиях ментальной арифметикой не желательно пропускать уроки. Расположение чисел Теперь о том, как же располагаются числовые линейки. Справа у нас находятся единицы. Затем десятки, потом сотни, тысячи, десятки тысяч и т.д. Каждому разряду своя спица. Костяшки, которые находятся под разделительной планкой, означают «1», над планкой – «5». Трудновато понять, да? Давайте посмотрим на примере. Рис. 1. Расположение чисел на абакусе Крайняя правая линейка на рисунке – это единицы. Инструкция счёта на абакусе Поднимаем к разделительной планке три костяшки на линейке единиц. Так будет выглядеть на абакусе число 3. Рис. 2. Число 3 на абакусе Попробуем взять двойное число, например, 15. Рис. 3. Число 15 на абакусе На линейке десятков поднимаем 1 костяшку, то есть, получаем 1 десяток. А на линейке единиц опускаем к разделителю верхнюю костяшку, которая и означает 5. А вот это какое число получилось? Догадаетесь? Рис. 4. Число 53 на абакусе Это 53! А давайте чего-нибудь посущественнее наберем. Например, 6482! Рис. 5. Число 6482 на абакусе На линейке тысячи у нас верхняя костяшка опущена к разделителю – это пять тысяч и одна нижняя поднята вверх, плюс еще тысяча. Получаем 6 тысяч. С сотнями полегче, просто четыре костяшки поднимаем вверх. Десятки: верхняя опущена, три нижних подняты. Получается сверху 5 десятков, снизу 3. Это 80. Ну и еще 2 единицы. Не так уж сложно, правда? Как складывать? А теперь переходим к сложению и посмотрим, что из этого получится. Предлагаю взять что-нибудь попроще, чтобы не взорвать себе мозг) Например, сложим 33 и 14. Откладываем на абакусе 33. Рис. 6. Число 33 на абакусе К трем десяткам прибавим еще один. Получим 4 десятка или 40. Рис. 7. Число 43 на абакусе Теперь единички. К трем единицам прибавим еще 4. Так как четырех свободных единиц снизу на спице нет, то сначала прибавим пять, опустим верхнюю косточку. А потом отнимем 1, опустим одну нижнюю. Получилось у нас 7 единиц. Рис. 8. Число 47 на абакусе В результате получилось 47! Может на калькуляторе проверим?) Шучу, и так ясно, что результат мы получили верный! Для большего удобства предлагаем вам приобрести литературу и абакус,  вот ссылочка ЖМИ. Обучение счёту ›  Купить абакус и литературу ›

Рабдологический абак – суммирующая машина, изобретенная Клодом Перро (25.09.1613 – 09.10.1688), братом знаменитого сказочника Шарля Перро. Впервые, упоминание об этом изобретении встречается в 1700 году в книге «Сборник большого числа машин собственного сочинения», изданной Клодом Перро посмертно. В этой книге описывается множество изобретений автора таких, как «маятниковые часы», «машина для поднятия тяжести», «машина для увеличения эффекта огнестрельного оружия», в том числе и интересующая нас суммирующая машина, значащаяся под номером десять. Рабдологический абак – компактная и просто устроенная вычислительная машина, отметившаяся в вехах истории в основном за счет принципиального отличия от устройства всех предыдущих изобретений в этой области. В рабдологическом абаке взамен зубчатых колес, предложенных Паскалем, используются зубчатые рейки (кремальеры). Клод Перро так пишет о своем изобретении: «Я назвал эту машину «рабдологический абак», потому что древние называли абаком небольшую доску, на которой написаны цифры, а рабдологией — науку выполнения арифметических операций с помощью маленьких палочек с цифрами…» Счетная машина, действительно, представляла собой пластину в палец толщиной, примерно 30 сантиметров высотой и 14 – шириной. На лицевой стороне машины было вырезано два окошка для отображения результатов. В верхнем окошке показывался результат вычитания, а в нижнем – сложения. В нижней части лицевой стороны была выгравирована таблица умножения. Также на лицевой стороне было прорезано семь пазов, вдоль которых были нанесены шкалы с делениями 1,2,3…9. В пазах виднелись линейки, которые можно было передвигать вверх и опускать вниз, к основанию машины с помощью штифта с заостренным кончиком. Каждая линейка была разделена на 26 частей глубокими рисками, используемыми для перемещения линеек (в риски вставлялось острие штифта, что позволяло легко и точно перемещать линейки). В верхних одиннадцати делениях линейки находилась возрастающая последовательность (0,1,2,3,4,5,6,7,8,9,0), используемая при вычитании. В нижних одиннадцати делениях находилась убывающая последовательность (0,9,8,7,6,5,4,3,2,1,0), используемая для сложения. Цифры этих последовательностей отображались в окошках результата, являясь искомой величиной сложения (нижнее окошко) или вычитания (верхнее окошко). Последовательности, нанесенные на линейки, отделялись друг от друга четырьмя пустыми делениями. Всего в устройстве использовалось семь линеек, отделенных друг от друга тонкими пластинками. Крайняя правая линейка символизировала разряд единиц, следующая за ней – разряд десятков и так далее, вплоть до разряда миллионов. В каждой пластинке, отделяющей линейки друг от друга, имелось отверстие, используемое для переноса переполнения из младшего разряда в старший. Это отверстие находилось у основания линейки, придвинутой к самому верху устройства, и было длинной в три деления линейки. У основания правой стороны каждой линейки располагалось 11 зубцов, по одному на деление линейки. С другой стороны линейки (под 11 и 12 делением, если считать снизу) располагался подпружиненный крючок. Зубцы и крючок использовались для переноса переполнения из младшего разряда в старший, происходившего следующим образом. Когда планка младшего разряда находилась в верхней части рабдологического абака, то есть в окошках результата сложения и вычитания находились нули, подпружиненный крючок был скрыт в теле линейки, упираясь в пластинку, располагающуюся слева от линейки. По мере продвижения линейки вниз, подпружиненный крючок приближался к отверстию в пластинке. Когда в окошке результата сложения появлялась цифра семь, принадлежащая передвигаемой линейке, подпружиненный крючок начинал выдвигаться в отверстие планки, и в момент, когда в окошке результата появлялась цифра девять, входил в зацепление с зубцами линейки старшего разряда. Дальнейшее передвижение линейки младшего разряда приводило к перемещению линейки старшего разряда. Таким образом, когда в окошке результатов сложения появлялась цифра ноль линейки младшего разряда, следующая за цифрой девять, линейка старшего разряда передвигалась, за счет сцепления крючка с зубцами, ровно на одно деление вниз. Механика переноса разряда переполнения иллюстрируются на анимации «Рабдологический абак. Устройство переноса переполнения», расположенной ниже. Рассмотрим операцию сложения на Рабдологическом абаке на примере «127+65»: 1. Устанавливаем все разряды рабдологического абака в ноль, для чего, с помощью штифта, передвигаем линейки в крайнее верхнее положение. 2. Ставим штифт в паз на риску линейки младшего разряда, находящуюся напротив цифры семь, и сдвигают линейку до тех пор, пока штифт не упрется в нижний торец паза. При этом в окошке результата сложения в младшем разряде отобразится вводимое число (семь). Стоит заметить, что в окошке результата вычитания в младшем разряде будет отображено число, необходимое для дополнения семерки до десяти, то есть три. 3. Аналогичную операцию проделываем и с разрядом десяток, только в этом случае паз устанавливаем напротив цифры 2. 4. Для разряда сотен паз устанавливаем напротив цифры один и передвигаем его вниз до упора, то есть на одно деление. В результате, в окошке результата сложения будет отображено число 127. 5. Переходим к вводу второго слагаемого. Устанавливаем штифт в паз на риску линейки младшего разряда, находящуюся напротив цифры пять, и сдвигаем линейку вниз до упора. При этом штифт остановится напротив цифры два, так как линейка упрется в нижнюю стенку устройства раньше, чем штифт достигнет нижнего торца паза, а линейка разряда десяток опустится на одно деление вниз, за счет работы механизма переноса переполнения. В окне результата сложения отобразится цифра 130. 6. Для того, чтобы получить верную цифру в разряде единиц (то есть 2), следует, не извлекая штифта из прорези, продвинуть линейку вверх, пока штифт не упрется в торец паза. Таким образом, в окне результата сложения отобразится цифра 132. 7. Вводим разряд десятков второго слагаемого, для чего устанавливаем штифт в паз на риску линейки разряда десятков, находящуюся напротив цифры шесть, и сдвигаем линейку вниз до упора. На этом вычисления заканчиваются, а в окошке результата сложения отображается искомое значение (192). При вычитании с помощью рабдологического абака использовался прием дополнения до десяти, аналогичный способу, используемому в Паскалине. Поясним способ дополнения на примере. Допустим, необходимо решить уравнение: Y=68-23=45. С помощью метода дополнения, представим число 68, как разность чисел 100 и 32 (68=10-32). Таким образом, наше уравнение сводится к следующему виду: Y=68-23=100-32-23=100-(32+23)=27. Как видно из преобразования, вычитание заменилось на сложение и вычитание результата сложения из 100, что есть преобразование, обратное дополнению. Следовательно, остается решить задачу автоматического дополнения до десяти, для чего на всех линейках нанесено две последовательности цифр, а на крышке рабдологического абака – два окошка вывода результата, расположенных так, что суммы двух чисел, отображенных в окошках и располагающихся друг под другом, всегда равняются десяти. Рассмотрим работу рабдологического абака при вычитании на примере 68-23: 1. Устанавливаем все разряды рабдологического абака в ноль, для чего с помощью штифта передвигаем линейки в крайнее верхнее положение. 2. Вводим младший разряд уменьшаемого. Передвигаем линейку младшего разряда так, чтобы в окошке результата вычитания в позиции младшего разряда отобразилась цифра 8, для чего ставим штифт в паз на риску, находящуюся напротив цифры два, и сдвигаем линейку вниз до тех пор, пока штифт не упрется в торец паза. 3. Вводим разряд десяток уменьшаемого, для чего передвигаем соответствующую линейку так, чтобы в окошке результата вычитания на второй позиции отобразилась цифра 6. Для этого ставим штифт в паз на риску, находящуюся напротив цифры четыре, и сдвигаем линейку вниз до тех пор, пока штифт не упрется в торец паза. В результате, в окне результата вычитания отобразится число 68. 4. Водим вычитаемое также, как слагаемое при сложении. В нашем случае, для ввода младшего разряда вычитаемого, устанавливаем штифт в паз на риску линейки младшего разряда, напротив цифры 3, и двигаем линейку вниз, пока штифт не упрется в торец паза. Далее вводим старший разряд вычитаемого, для чего устанавливаем штифт в паз на риску второй слева линейки, напротив цифры 2, и двигаем линейку вниз, пока штифт не упрется в торец паза. На этом нахождение разницы двух чисел с помощью рабдологического абака заканчивается, а в окошке результата вычитания отображается искомая разность (45). Как видно из описания рабдологического абака, несмотря на принципиальные отличия от существующих на тот момент вычислительных машин, его устройство и использование были очень просты. Однако, он не получил распространения. Возможная причина этому – ненадежное устройство подпружиненного крючка, часто выходившего из строя при постоянной эксплуатации, из-за низкого уровня механики конца XVII века. Но, тем не менее, идеи, предложенные Клодом Перро, впоследствии нашли применение в ряде простых и надежных счетных приборах таких, как «счислитель Куммера», «Комптатор Ганса Забельного» и некоторых других.

Подпишитесь на бесплатный курс “Секреты воспитания” и получите бесплатно Секретную книгу. Из данного курса Вы узнаете о тайнах народной педагогики, о секретах современных технологий воспитания и массу другой полезной информации для решения Ваших проблем. 12 простых формул для подготовки ребенка к детскому саду Узнать   Адаптационные игры с песком Узнать   Как быть счастливыми родителями Узнать

Amazon.com: Abacus Student’s Abacus 100 Inch Ruler Frame Blue / Red: Office Products

---

Цена:

22 доллара.47 + Депозит без импортных пошлин и доставка в Россию $ 28,39 Подробности

• Убедитесь, что это подходит введя номер вашей модели.
• Грубая рама 100-х годов – шары синие / красные
• Рамка школьного калькулятора для 1-9 классов
• Абакус для входа в основные расчеты
• Прочный и долговечный от ReWood
• Размеры: рамка 25 x 4,5 x 17 см и шары диаметром 13 мм.

Что использовалось до калькуляторов?

Люди считали, вычисляли и составляли графики с незапамятных времен.Сначала они использовали пальцы, а затем такие вещи, как груды камешков, связки веток и простые механические устройства, такие как революционные счеты. Трудно представить себе время, когда у всех нас не было калькулятора в школьной сумке или в Интернете, но на протяжении большей части истории человечества так было. Итак, давайте посмотрим, как люди так долго обходились без калькулятора.

Изображение счеты

Счеты и счетная доска

Счеты – это простая рамка, состоящая из стержней, по которым перемещаются бусинки для обозначения различных групп чисел.На протяжении веков счеты были передовым устройством, используемым китайцами, греками и римлянами. Есть также свидетельства того, что ацтеки в современной Мексике и Центральной Америке использовали счеты, сделанные из зерен кукурузы, нанизанных на кусочки нити.

Слово abacus от латинского означает «таблетка», поэтому в определенном смысле счеты были самой ранней версией планшетного компьютера. Затем шла счетная доска, которую обычно делали из деревянной или каменной плиты с вырезанными на ней линиями. Бусинки перемещали из одного положения в другое по доске, чтобы помочь в подсчете и переносе чисел на более высокие значения.

Появление арабских чисел

Однако вычисления с использованием арабских чисел могут выполняться намного быстрее, чем с римскими цифрами или бусинами на счетах. Поскольку использование арабских цифр стало популярным по всей Европе, счеты и счетная доска стали довольно устаревшими. Внедрение арабской системы в Западной Европе приписывают Леонардо Пизанскому, который жил там, где расположена знаменитая Пизанская башня.

Также известный под именем Фибоначчи, он был математиком начала 13 века, написавшим новаторскую книгу о численных вычислениях под названием « Liber Abaci» . Книга основана на арабской системе нумерации, которую его отец, торговый моряк, изучил, путешествуя по различным городам Среднего Востока вдоль Средиземного моря.

Использование таблиц

Поскольку ярлыки ускоряют и упрощают выполнение вычислений, таблицы являются отличным ресурсом. Например, вместо того, чтобы медленно складывать множество маленьких чисел, мы можем просто обратиться к нашим таблицам умножения и выполнить сложную арифметику в уме. Точно так же, поскольку расчеты таких вещей, как геометрия, алгебра и исчисление, выполнялись на протяжении многих лет, люди создавали таблицы для использования в качестве ярлыков.Те, в свою очередь, были собраны в удобные справочные таблицы или книги.

Одним из классических примеров является книга под названием «Стандартные математические таблицы и формулы CRC», которая существует уже около 40 лет. До появления калькуляторов студенты и инженеры обращались к этой большой книге, чтобы найти формулы, таблицы, диаграммы, интегралы и другие данные, которые помогали им при выполнении вычислений вручную. С более чем 6000 записей и такими вещами, как таблицы тригонометрии с точностью до минуты, эта книга была бесценной в те дни, когда вычисления приходилось производить вручную.

Механическое правило скольжения

Джон Нэпир из Шотландии, живший в 1600-х годах, изобрел логарифмы – еще один вид сокращения. Он также сконструировал первую логарифмическую линейку, чтобы упростить использование этих логарифмов, и его логарифмическая линейка была нововведением, изменившим парадигму.

Логическая линейка стала очень популярной в Европе и широко использовалась в 1800-х годах. Амеде Мангейм изобрел одну из первых современных логарифмических линейок в 1859 году и использовал ее, чтобы вычислить, как стрелять из артиллерии, чтобы точно поразить цель, когда он был во французской армии.

Современные правила скольжения

Современные правила скольжения, подобные тем, которые использовались на протяжении большей части 20-го века, имеют длину около двух футов и ширину два дюйма и состоят из трех основных компонентов. Основная часть логарифмической линейки напоминает линейку и отмечена шкалами. Затем есть скользящая секция, которая перемещается по этой части в виде линейки. Третий компонент – курсор или указатель для установки определенных точек на шкале.

Эти устройства использовались студентами, архитекторами, учеными, инженерами и другими людьми, которые выполняли свои вычисления с помощью логарифмической линейки, обращаясь к диаграммам и таблицам.Затем они заканчивали свои вычисления или рисовали свои графики карандашом и бумагой. Тем не менее, как я уверен, вы можете себе представить, даже этот прогресс все еще далек от удобства и эффективности калькулятора.

Продвижение в цифровую эпоху

Естественно, этот процесс был трудоемким и трудоемким. Точность вычислений с помощью логарифмической линейки также подвержена человеческой ошибке, потому что, если вы случайно прочитаете крошечные отметки на шкале неправильно или поместите курсор в неправильное место, результаты будут ошибочными.Теперь, хотя вы можете утверждать, что калькулятор также подвержен этому типу человеческих ошибок, но вероятность неправильного нажатия клавиши на клавиатуре вашего калькулятора, очевидно, меньше, чем вероятность того, что кто-то сделает ошибку в этом процессе; Часто группе из пяти или шести студентов, работающих вместе как одна команда, может потребоваться целая сессия в классе для решения проблемы.

Сегодня, благодаря автоматизированным цифровым калькуляторам, студент, действующий в одиночку, может решать те же проблемы с надежно точными результатами в течение нескольких минут, если не секунд.Они могут использовать простой портативный графический калькулятор, научный калькулятор или быстрый, интуитивно понятный и бесплатный калькулятор, доступный здесь, на сайте www.meta-calculator.com.

Ссылки:

https://en.wikipedia.org/wiki/Binary_multiplier

https://en.wikipedia.org/wiki/Linear_interpolation

http://web.mit.edu/2.972/ www / reports / slide_rule / slide_rule.html

https://www.ee.ryerson.ca/~elf/abacus/history.html

Изображения

https: // en.wikipedia.org/wiki/Abacus#mediaviewer/File:Boulier1.JPG

Традиция Чжуачжоу

Чжуачжоу считается одним из самых важных обычаев в годовщину первого дня рождения ребенка. Как традиционный, давний обычай в Китае, Чжуачжоу, по сути, является испытанием, когда родители кладут перед своим ребенком набор предметов, чтобы выбрать из них, чтобы определить его или ее будущие склонности и способности. Самое раннее письменное упоминание об этом обычае восходит к династии Сун (960–1279).

В конце династии Цин (1644-1911) этот обычай преобладал в Пекине. Чжуачжоу – не повод для грандиозных застолий и изысканных подарков: хозяева даже не рассылают приглашения. Идея в том, что родственники придут спонтанно, чтобы отметить первый день рождения ребенка. Подарки родственников в этот день обычно не требуют больших затрат и не включают в себя такие предметы, как золотые или серебряные украшения. Вместо этого ребенку дарят димсам или игрушки.Пожилые люди, впервые встречающиеся с ребенком, обычно предлагают монету, которую можно закрепить на шее ребенка ниткой. Этот обычай применим не только к дням рождения, но и ко многим другим случаям.

Церемония Чжуачжоу обычно проводится перед обедом перед лапшой долголетия. Богатая семья установит стол на кровати (или «кан» – кирпичная кровать с подогревом, используемая в Северном Китае), где будут стоять марки, классические конфуцианские, буддийские и даосские книги, китайская кисть, чернила, бумага, чернильный камень Размещаются счеты, монеты, бухгалтерская книга, украшения, цветы, румяна, еда и игрушки.Если ребенок женского пола, добавляются следующие предметы: совок, ложка (представляющая кухонную утварь), ножницы, линейка (представляющая швейные изделия), нитки и альбом для дизайна (представляющий вышивку). Однако в обычной семье практика намного проще. Обычно на «кан» ставят бронзовый поднос вместо стола, а сверху кладут книгу из старых частных школ, например, «Трёхзначный букварь», включая китайскую ручку-кисть, счеты и торт. Для девочки добавлены ножницы, ножницы и линейка.Затем родители усаживают ребенка перед столом или подносом. Без чьей-либо помощи или указаний ребенок может выбирать что угодно перед ним. Выбранные им предметы используются, чтобы предсказать интересы, карьеру и наклонности ребенка в будущем.

Выбор штампа означает, что в будущем ребенок будет офицером; если он или она сначала выберет канцелярские принадлежности, ребенок будет трудолюбивым и наделен большими литературными талантами; счеты предполагают склонность к статистике и финансам.Девочка-младенец, впервые схватившая в руки швейный предмет или кухонную утварь, будет хорошей хозяйкой. С другой стороны, когда ребенок выбирает торт или игрушку, он или она будет знать, как получать удовольствие от жизни. В общем, родители и родственники возлагают большие надежды на будущее своих детей, и обычаи Чжуачжоу – это способ выразить их добрые пожелания.

Обычай Чжуачжоу отражает то, как родители, дедушки и бабушки и другие родственники будут поощрять ребенка и как они будут проводить просвещение.Поэтому, даже если некоторые родители не суеверны, они все равно будут соблюдать обычай. Вот почему этот обычай передавался из поколения в поколение и практикуется до сих пор.

Экспорт данных из Abacus – Law Ruler Software, LLC

Чтобы экспортировать данные из Abacus, следуйте инструкциям ниже:

Для пользователей программного обеспечения Abacus для управления судебными делами Law Ruler рекомендует следующий процесс для резервного копирования данных вашей фирмы из Abacus, чтобы подготовить их для группы миграции данных Law Ruler.Это необходимо для того, чтобы группа по миграции данных Law Ruler начала работу, или попросите своего специального менеджера по работе с клиентами Law Ruler обсудить план помощи вашей фирме в миграции данных.

💡 Обратите внимание, что успех любого переноса данных зависит в первую очередь от качества набора данных, предоставленного Law Ruler. Прежде чем пытаться перенести вашу информацию, вы должны убедиться, что ваши данные единообразно отформатированы, хорошо организованы, имеют достаточное резервное копирование и надежно хранятся. Если вы не знаете, как действовать дальше, мы рекомендуем вам проконсультироваться со своим персональным менеджером по работе с клиентами или службой поддержки Law Ruler, прежде чем продолжить.

• Только администраторы могут экспортировать данные клиентов.
• Файл с именем « law9.dbf » необходимо отправить в Law Ruler для проверки планирования переноса данных и анализа объема работ.

За исключением Law Ruler, все другие товарные знаки, торговые наименования, снимки экрана или названия компаний, упомянутые в данном документе, используются только в целях идентификации и являются собственностью их соответствующих владельцев.

Какие данные можно экспортировать из Abacus и импортировать в Law Ruler?

В большинстве случаев следующие данные можно экспортировать из Abacus и импортировать в Law Ruler:

• Контакты (Список контактов – аналогично картотеке ваших контактов)
• дел (Перечень вопросов – дела обычно не имеют связанных клиентов в экспорте; их обычно можно связать, если “law9.dbf “файл также экспортируется)
  • Неправильное использование продукта Abacus, такое как перепрофилирование полей для различных целей, может повлиять на миграцию данных и потребовать специального объема работ, если вам нужны эти данные.
• Примечания (любые примечания, относящиеся к делу, обычно можно импортировать)
• Задачи (которые назначаются конкретным пользователям)

Эти предметы нельзя импортировать в Law Ruler из Abacus:

• События календаря (связанные с вопросами – в противном случае используйте Office 365 / Outlook Sync)
• Электронные письма – Мы не можем импортировать электронные письма, потому что Abacus не экспортирует их в пригодном для использования формате

Документы (требуется нестандартный объем работ):

1. Чтобы выполнить миграцию документов, перед предоставлением объема работ Law Ruler необходимо знать, где и как хранятся ваши документы и какая система именования папок используется.Как правило, папки с документами должны иметь единообразные имена, чтобы обеспечить перенос данных. Например, все папки с документами должны иметь одно и то же имя, совпадающее с именем вопроса, идентификатором вопроса или основным контактным лицом (именем клиента).
   • Например, имя клиента по делу: John Test, поэтому папка с документами этого клиента должна быть названа «John Test» или «Test, John» или с идентификационным номером вопроса, например, «123456». “в противном случае невозможно будет перенести данные без выполнения этого вручную на стороне фирмы.
2. Любые папки, относящиеся к и не относящиеся к конкретному клиенту / делу, не могут быть импортированы, и их необходимо будет загрузить вручную после выполнения миграции данных. Любые папки с документами, которые имеют несогласованные имена, также потребуют от компании переноса документов вручную после выполнения переноса данных.
3. У некоторых фирм документы хранятся не в том месте, где они ведутся. Это приемлемо, если папки названы стандартным образом, как указано выше.

Экспорт данных из Abacus

Примечание. Мы рекомендуем выполнять экспорт в ночное время в нерабочее время. Важно убедиться, что все пользователи вышли из AbacusLaw , Abacus Accounting , MessageSlips и Microsoft Outlook (если они используют надстройку Abacus Outlook).

Это необходимо сделать при резервном копировании данных.

💡 Вы также можете просмотреть статью поддержки от Abacus о том, как экспортировать данные и создавать отчеты, которые охватывают их процесс экспорта.

Если вы хотите принудительно отключить всех пользователей, перейдите в Файл> Настройка> Выключение по расписанию .
В разделе Немедленное выключение щелкните Выключить сейчас (Abacus выключится, и все несохраненные незавершенные работы могут быть потеряны, поэтому перед выполнением этого шага проконсультируйтесь с персоналом вашей компании).

1. Войти в Abacus
2. Нажмите Файл
3. Затем щелкните Отчеты
4. Выберите одно из следующего: Имена, Календарь, Вопросы, Важные заметки или Именные заметки.
5. В открывшемся окне выберите Новый отчет
6. Введите новое имя для отчета (например: Law Ruler Abacus Export) и щелкните OK
7. В верхней левой части экрана нажмите Добавить
8. Нажмите Выполните
9. Щелкните Comma Delimited (убедитесь, что вы выбрали этот формат)
10. Нажмите ОК
11. Сохранить файл
12. Искать law9.adt в папке Abacus на вашем компьютере
    • , если этот файл не существует, найдите law9.dbf

💡 Также рекомендуется сделать полную резервную копию базы данных Abacus. Для этого посетите эту статью поддержки о том, как сделать резервную копию и восстановить ваши данные с помощью Abacus.

Древние бухгалтерские системы

Каковы были древние системы бухгалтерского учета?

Методы бухгалтерского учета появились тысячи лет назад – возможно, более 10 тысяч лет назад – в регионе, который мы сейчас называем регионом Ближнего Востока.Шумеры в Месопотамии, вавилоняне и древние египтяне осознавали необходимость подсчета и измерения результатов труда и усилий. По мере того, как эти древние общества строили более сложные цивилизации, возникла потребность в простых арифметических операциях, письме и торговле. Эти ингредиенты в конечном итоге привели к формированию денежных единиц, капитала, частной собственности, а также систем коммерции и государственного управления.

В результате были использованы различные методы учета для учета сельскохозяйственной продукции и землепользования, морской и наземной торговли, животных и рабочей силы.Налогообложение, проекты общественных работ, военные инициативы и завоевание в конечном итоге потребовали ведения записей как способа для правителей и их советников поддерживать общественный порядок.

Ключевые выводы

• Методы бухгалтерского учета появились – возможно, более 10 000 лет назад – в регионе, который мы сейчас называем регионом Ближнего Востока.
• Шумеры, вавилоняне и древние египтяне признали необходимость подсчета и измерения результатов труда и усилий.
• Древние пользователи создали раннюю форму абака, с помощью которой они скользили по раме бусинами, помогая при подсчете и простых вычислениях.
• Кодекс стандартизированных мер и весов Хаммурапи, содержащий рекомендации по коммерческим операциям и платежам.

Понимание истоков древнего бухгалтерского учета

Иерихон, город, расположенный к западу от реки Иордан, насчитывает не менее 11 000 лет и является одним из старейших непрерывно заселенных городов в мире. Считается, что древнее общество, которое здесь находилось, использовало бартерную систему. примерно до 7500 г. до н.э. когда простые жетоны и глиняные шары (различной формы) стали представлять данные инвентаризации сельскохозяйственных товаров, включая пшеницу, овец и рогатый скот.Использование жетонов со временем расширилось, и жетоны и конверты помогли сформулировать древнюю версию того, что могло быть балансовым отчетом. Эти жетоны и конверты помогли идентифицировать конкретные стороны, претендующие на определенный инвентарь. Токены также постепенно стали отражать завершенные торговые операции.

Тысячи лет спустя в шумерских городах первые бухгалтеры учитывали валюту, драгоценные металлы и товары, маркируя глиняные таблички на концах палочек. Эти таблетки были высушены и отверждены для создания записей.Взаимодействие с другими людьми

От абака к папирусу

Впервые появились два метода, которые столетия спустя служили различным цивилизациям по всему миру. Счеты впервые появились около 5000 лет назад в Шумере и в конечном итоге использовались несколькими древними обществами. До появления современной системы счисления древние пользователи ранних форм счётов могли перемещать бусинки по рамке, которая помогает как в подсчете, так и в простых вычислениях, таких как сложение и вычитание.

Во-вторых, папирус приобрел популярность – сначала в Древнем Египте.Этот похожий на бумагу материал, сделанный из тростникового папируса, возможно, появился еще в 4000 году до нашей эры. Папирус использовался для учета и администрирования, таких как налоговые квитанции и судебная документация, хотя литература, религиозные тексты и музыка также были Правители использовали методы бухгалтерского учета для учета своего богатства, а также уплаты дани от других королевств.

Египет использовал картинки, слова и числа, чтобы следить за сельскохозяйственным производством, чтобы прокормить постоянно увеличивающееся население.Система учета также использовалась для учета церемоний и религиозных мероприятий, памятников и общественных работ, а также для контроля труда. Современный бухгалтерский учет использует понятия доверия, точности и этики как основы успешной карьеры. Египетские правители были гораздо более склонны использовать страх и боль в качестве основы для точного учета. Нарушения, обнаруженные египетскими королевскими аудиторами, привели к штрафу, увечьям или смерти (мы можем предположить, что книжники и бухгалтеры были особенно мотивированы во время своих древних тренировок, сегодняшней версии промежуточных экзаменов в колледже.)

Бронзовый век, железный век и Дальний Восток

Бронзовый век и железный век открыли новую эру, в которой различные цивилизации в разных регионах развили передовую металлообработку. Эти разработки можно найти на побережье Мексиканского залива, в Европе, Азии, Америке, Африке к югу от Сахары и на Индийском субконтиненте. Бухгалтерский учет и ведение записей продолжали развиваться и включать различные общества, использующие более сложные токены с маркировкой и подкладкой для дифференциации запасов, транзакций и затронутых сторон.Некоторые из этих жетонов в конечном итоге уступили место продвинутым планшетам, чьи маркировки и знаки обеспечивали счетчики, зарегистрированные инвентарные подсчеты, транзакции и отличительные предметы инвентаря – основы современной экономической системы.

Кодекс Хаммурапи для Римской империи

По мере того как папирус помогал писцам документировать богатство своего короля и выплаты дани, а также другие экономические меры, эволюция различных обществ в более сложную геополитическую единицу создавала кодексы, денежные традиции и системы экономического управления.Кодекс Хаммурапи был создан около 1760 г. до н. Э. в Вавилоне. Среди его целей Кодекс Хаммурапи стандартизировал меры и веса, а также давал указания по коммерческим операциям и платежам.

Появление бухгалтерского учета в Древней Греции поддержало финансовую и банковскую систему страны. Принятие греками финикийской системы письма, а также изобретение греческого алфавита помогли облегчить греческий учет. Точно так же ведение документации помогло отследить развитие чудес инженерной мысли, сохранившихся до наших дней.Кроме того, бухгалтерский учет помогал укреплять финансовую и правовую систему римлян. В сочетании с использованием валюты, которая вошла в обиход в 300 г. до н.э., развитая торговая система Рима помогла продвинуть его геополитическую мощь далеко за пределы любого потенциального соперника.

Особые соображения

В этих ранних цивилизациях степень, в которой королевство могло накапливать излишки урожая, обеспечивать торговые операции, создавать полезные инструменты, обеспечивать уплату дани, защищать свои границы и эффективно администрировать налогообложение, а также общественные работы, – все это способствовало успеху цивилизации.Даже несмотря на то, что им удалось (или не удалось) увеличить свои различные ресурсы и положение в древнем мире, эффективное управление социальным порядком все еще требовало плавного функционирования административной стороны вещей. Без такого подсчета, как бы советник правителя узнал, сколько труда и материалов выделить на монументальное здание, не имея представления о том, как продвигается этот проект?

Точное и своевременное ведение документации – даже тысячи лет назад – помогало принимать важные решения.Если не учитывать пару десятков голов скота (из-за того, что потеряли один или два жетона), то, возможно, мало что значит в сегодняшних терминах, но тогда это могло означать голод для всей деревни. В сегодняшних системах бухгалтерского учета методы расчета более сложные, но точность все же сохраняется.

Naaien Urban Abacus Quilt Pattern ~ Sew Kind of Wonderful ~ использует линейку QCR Quick Curve Ruler luxclusif.com

---

2013

---

Фонд Upteam как международный торговец подержанными предметами роскоши.

Ориентация на флэш-продажи в качестве основного канала сбыта. Сеть продаж охватывает более 10 стран.

---

2014 г.

---

---

2015 г.

---

Открытие оперативной штаб-квартиры в Маниле, Филиппины.

---

2016 г.

---

Разработка и интеграция 1-го API, позволяющего продавать инвентарь на нескольких платформах одновременно.

Открытие европейского логистического центра в Таллинне, Эстония, для обслуживания торговых площадок и прямой доставки клиентам.

---

2017 г.

---

Раунд начальных инвестиций с 500 стартапами

Запуск логистического центра в США для обслуживания местных клиентов.

Продажи распространяются на офлайн-ритейлеров.
Приобретение 100-го клиента.

---

2018 г.

---

Выбран для участия в первой партии первого технологического ускорителя Dream Assembly, технологического ускорителя для стартапов на базе Farfetch.

Переход бизнес-модели к рынку B2B и ИТ-решениям, связанным с модными технологиями, чтобы предоставить подержанные решения для брендов и крупных предприятий розничной торговли.

---

2019 г.

---

Запуск Second Life для Farfetch.Комплексное решение для обмена, позволяющее покупателям обменивать использованные роскошные сумки на кредиты в магазине.

Первая интеграция запасов различных поставщиков на платформе Luxclusif (модель Asset Light)

Разработка концепции перепродажи в коробке, позволяющей крупным розничным торговцам с онлайн-присутствием продавать тщательно отобранные и подлинные подержанные предметы роскоши на своей платформе.

---

2020 г.

---

Первое прямое партнерство с ведущим элитным домом, обеспечивающее их присутствие в цифровом сегменте подержанных автомобилей.

Выкройка для квилтинга Urban Abacus ~ Sew Kind of Wonderful ~ использует линейку Quick Curve Ruler

Sockenlänge: ： Kurzsocken ： Mehrstückpackung: ： Ja, Staat :： Nieuw met label: Een gloednieuw, onbeschadigd object in de oorspronkelijke verpakking (индийский verpakking van toepassing есть). Все определения van de staat bekijken ： Комната: ： Гостиная. Все определения van de staat bekijken ： Artikelnummer: ： 670197, De verpakking moet hetzelfde zijn als in de detailhandel, De verpakking moet hetzelfde zijn als in de detailhandel.Все определения van de staat bekijken ： UPC: ： 725113383108. onbeschadigd object in de oorspronkelijke verpakking (indien verpakking van toepassing is). tenzij het object door de fabrikant is verpakt in een verpakking die niet voor detailhandel is bestemd, Zie de aanbieding van de verkoper voor volledige details. en ongedragen объект в de oorspronkelijke verpakking (zoals de oorspronkelijke doos of zak) en / of met de oorspronkelijke labels eraan обширный. Материал: ： Искусственная фактурная кожа ： Бренд: ： JCunique.Staat :： Новые ярлыки: Een gloednieuw. объект onbeschadigd в de oorspronkelijke verpakking (индийский verpakking van toepassing есть). Длина [мм]: ： 102 мм ： Артикул: ： ADT342173. 2 x New Range Rover MK3 2002-2012 гг. Газовые опоры капота переднего капота E1544Автомобили, Все характеристики ： Цвет: ： Черный. tenzij het object door de fabrikant is verpakt in een verpakking die niet voor detailhandel is bestemd. Optik: ： glänzend ： EAN: ： 4051245401509, New Flaming Tiger Raglan Hoodie, дикая природа, животное, зверь, боясь страшного огня, толстовкаKleding и аксессуары.BREMSBELÄGE 4 STÜCK BREMSBELAG SATZ BREMSKLÖTZE BREMSE. объект onbeschadigd в de oorspronkelijke verpakking (индийский verpakking van toepassing есть). zoals een onedrukte doos of een plastic zak, Marke: ： Craftride ： Referenznummer (n) OEM: ： Höher 1 1/4 Inch 1. Zie de aanbieding van de verkoper voor volledige details, zoals een onbedrukte doos een plastic zak. Panasonic Consumer Iron 1500w Quick Steam Iron – NI-W810CSHuishoudapparatuur, De verpakking moet hetzelfde zijn als in de detailhandel.

как рисовать счеты

Abacus Рисование изображений Abacus Terzani Подвесная лампа Milia Сайт магазина с заданиями по математике Abacus для чисел до 99 Abacus Как рисовать Abacus Youtube Роман Abacus Википедия Десятки и единицы Abacus День Святого Патрика Подходящее мероприятие по математике Место Автор: Анна Ван Дер Неделя в… Все лучшие Abacus Drawing 39+ собраны на этой странице.Программное обеспечение Abacus Geometry Draw Инструмент определения геометрии для SPENVIS v.1.0 Бета Инструмент определения геометрии для SPENVIS был создан как интерактивная графическая утилита, способная определять простые трехмерные геометрии. Как найти наибольший общий множитель, используя простое число … Как умножить радикалы на целые числа, как упорядочить дроби от наибольших к наименьшим, как сделать неправильную дробь смешанным числом, как решить логарифм без калькулятора, Как вычислить Порядок дробей с отличными от знаменателей, как превратить смешанное число в десятичное, как произвести длинное умножение на 3 цифры, как округлить числа до двух десятичных разрядов, как сделать неправильные дроби и смешанные числа, как упростить алгебраические выражения с переменными , Как разделить дроби с помощью калькулятора, Как найти квадратные корни из несовершенных квадратов, Как умножить радикалы и целые числа, Как умножить с помощью распределительного свойства, Как решить и построить график линейных неравенств.Используя плоскогубцы с узкими носами, закрутите один конец каждой проволоки в виде спиральной петли. Как решать алгебраические уравнения с дробями на … Как умножать 2-значные числа на 2-значные числа, Как составлять неправильные дроби смешанными числами, Как превращать смешанное число в неправильную дробь, Как округлять числа до ближайших сотен тысяч, как Чтобы оценить дроби и смешанные числа, как превратить неправильную дробь в целое число. Загрузите стили рисования от руки со счетами иконок с Pictofigo: банк данных оригинальных, нарисованных от руки и векторных изображений с высоким разрешением.После поиска выброшенных коробок я обнаружил, что несколько Mooncake и PCWin не разработали это программное обеспечение Abacus Geometry Draw и никоим образом не несут ответственности за использование программного обеспечения и любой ущерб, нанесенный вашим системам. Отрежьте 13-21 провод в зависимости от ваших потребностей или размера вашей коробки. Как записать столбец вне фигурных скобок в матрице? Протолкните через торцевое отверстие коробки. Отрежьте горизонтальный кусок картона, чтобы отделить друг от друга «небесную» и «земную» бусинки. В студии с белой кирпичной стеной Арифметика.Иллюстрация о нанесении счётов на квадратную бумагу. Это был бы отличный проект для детей младшего возраста. Думаю, введите первое число. Мое следующее видео, в котором показано, как играть в математическую игру с флэш-анимацией со счетами: «Дай-пять», Cardboard Micro: bit Robot, Автоматическая система полива растений с использованием Micro: bit. Каждая из двух бусинок над полосой имеет значение 5. Счеты работают по системе разметки. Я узнал, как делать математику с помощью древних абак, и они изменились, односторонняя детская деревянная доска Белая доска Мольберт Учебная доска Рисование, Счеты для чисел до 99 Рабочий лист по математике для детей, обучение абакусам Большие деревянные абаки Продажа абакус Бизнес счеты, Google запускает Wechat Мини-игра в Китае. Большинство сервисов Google, добро пожаловать в Ajendu. От Abacus до современного компьютера. Есть Abacus Place Value Сотни десятков Рабочие таблицы для печати, числа, показывающие на Spike Abacus Spike Abacus Magnitude And, Sketch Abacus Images Стоковые Фото Vectors Shutterstock, рассчитывая на Abacus Math Worksheets Mathsdiary Com, Трехзначный номер на Abacus 1 Рабочий лист Turtlediary Com, Как использовать Abacus Видеоурок Стенограмма Study Com, Нарисуйте бусинки на Abacus для заданного числа Математические рабочие листы, 3056 Как рисовать Abacus Easy Drawing For Kids Step By Step Youtube, 4-значный номер на Spike Abacus. Понять концепцию чисел, Abacus Terzani, Подвесной светильник, Milia Shop, Сайт с заданиями по математике A bacus для чисел до 99 Abacus, десятки и единицы Abacus День Святого Патрика Математическое соответствие место действия.Вам понадобятся: Плоскогубцы. Тонкая проволока или прочная нить, например нейлон. Пустая картонная коробка. Бусины (или макароны подойдут!). Вы великий художник! и MathSecret (подробнее, шаг 7) интересны для детей, так как они позволяют быстро брать счеты. Вы сделали этот проект? SIP Abacus проводит мега-онлайн-конкурс рисунков в Восточной Индии – 2020 для учащихся от KG до класса VI. Нарисуйте минутную стрелку на часах, чтобы показать указанное время. SIP Abacus Eastern India Mega Online Drawing Competition Results 2020: НАЖМИТЕ ЗДЕСЬ (два движения становятся одним) Шаг 1 Шаг 2 Шаг 3 Объединив движения пальцев в шагах 1 и 3, оператор может решить задачу, используя только три движения пальца вместо пять.Связанный. Полезная пошаговая книга с ясными и простыми изображениями. Я хотел бы научиться пользоваться счетами, так что это было необходимо для практики. Скажем, вам нужно сложить 1234 и 5678. Как упростить выражения с помощью экспонент и Var … Как упростить использование свойства распределения, Как решить уравнения путем умножения или деления. объяснения Я бы порекомендовал прочитать онлайн-книгу Такаши Кодзимы, Ками Маркарян Абакус. Вставьте через каждое отверстие в нижней части коробки. Протолкните центральную стену. Разделите это количество проводов, которое вы выбрали.В Индии эта программа была инициирована в августе 2003 года. Чтобы попрактиковаться в этой математической таблице, ученики первого класса должны нарисовать равное количество бусинок для значений разряда заданных чисел от 11 до 100. Бусинка может быть равна пяти, если они видят только одну бусину. сидит там. Я покрасила бусинки лаком для ногтей. Вот пример того, что вас ждет, когда вы начинаете брать счеты. Завершите обмен. Разноцветные драгоценности действительно скрасят мой день. Думаю, я мог бы использовать сатай-джойстик, чтобы вычислить на них суммы.старые коробки для кистей, которые сделают красочные счеты. Одно из самых полезных программ, с которыми я столкнулся, – AbacusMaster. Правильная техника работы с пальцами имеет первостепенное значение для достижения мастерства на счетах. Нарисуйте минутную стрелку на часах, чтобы обозначить указанное время. Каждая «строка на счетах» представляет собой список, разделенный запятыми, в котором указано количество шаров в каждом столбце счет слева направо. Используйте прочный клей, чтобы закрепить одну треть в коробке. Сначала нарисуйте счеты / счетную доску на листе бумаги формата А4.Затем я пробую мини-абачи, используя плоские бусинки «Smartie» и деревянные рамки, чтобы их было легко носить с собой. Проделайте отверстие в каждом отмеченном месте. Наши советы по взлому гаджетов – доставляются ежедневно. Программа SIP Abacus – это международная программа, которая в настоящее время доступна в 10 странах и ею воспользовались более 8 000 000 детей в 900 учебных центрах. Кому нужен калькулятор, когда у вас в памяти методика счётов? Может помочь нанизать бусину большего размера на всю верхнюю палубу, чтобы они были 26 октября 2019 г. – Изучите доску «Рисунки» Abacus Victore на Pinterest.Последняя строка вводится, разбивается на символы и преобразует их в числа, передает в g ​​и затем печатает. Чтобы ваши дети оставались активными и творческими в это время пандемии, примите участие в конкурсе рисунков SIP Abacus Drawing, который открыт для шести штатов и 250 местных жителей из Ассама, Бихара, Джаркханда, Одиши, Трипуры и Западной Бенгалии. Предположим, что ответ – 7, вы должны нарисовать бусинку стержня, чтобы показать 7. Нарисуйте требуемые объекты, чтобы завершить заданное число. На счетах есть бусинки, которые скользят по стержням. Соберите по четыре бусинки для каждой из «земных» бусинок и по две бусинки для.Счеты – это счетный инструмент, который люди использовали на протяжении многих веков для выполнения различных арифметических задач. Есть ли у меня “антиисследовательская” личность? На китайских счетах большой и указательный пальцы вместе со средним пальцем используются для манипулирования бусинками. Счеты – это древний калькулятор, который до сих пор используется в Китае и других странах Азии. Как нарисовать счеты для детей поэтапно. Не стесняйтесь исследовать, изучать и наслаждаться картинами с PaintingValley.com. Для онлайн Abacus… Узнав больше об abaci, я обнаружил, что мне действительно нужно больше слота в четырех «земных» бусинах.Как пользоваться счетами Чтение числа на счетах. Отрежьте 13-21 провод в зависимости от ваших потребностей или размера вашей коробки. Абак, счетное устройство, вероятно, вавилонского происхождения, долгое время имевшее важное значение в торговле. В некоторых расчетах средний палец используется для перемещения бусинок в верхней деке. с большей вероятностью вспомнят, что бусина большего размера должна стоить большего числа. Некоторым детям трудно понять, как один (небесный) рисунок будильника книжками, счетами, мелом и мелом Маленький мальчик в галстуке-бабочке стоит рядом с мольбертом и красочными счетами.Сильный клей Лак для ногтей / водостойкая краска. Abacus Geometry Draw, бесплатная загрузка бесплатного программного обеспечения для рисования геометрии abacus d визуализирует ряд абакуса, переводя матрицы 0/1 в бусинки, заполненные || g принимает цифры и вертикально компилирует символьные строки, используя f для «форматирования» строк и d для строк abacus. Прорезь на двух «небесных» бусинах. единиц для заполнения других типов математических сумм. Также проделайте отверстия после разметки центральной стены. Отрежьте горизонтальный кусок картона, чтобы отделить друг от друга «небесную» и «земную» бусинки.улучшить свою зрительную память, логическое мышление и ускорить расчеты. Потренируйтесь писать разные числа на счетах, перемещая правильные камни (если вы хотите получить какие-то предложения, попробуйте 17, 58, 762, 3167, также попробуйте спросить своих друзей). Ключевые ответы Учителя, родители или ученики могут проверить или подтвердить заполненную рабочую тетрадь по математике, содержащую набор вопросов по математике для 1-го класса, чтобы нарисовать бусинки с разметкой для чисел (11–100), используя соответствующий ключ ответов. Концепция образования. Контрастные цвета действительно помогают мне сохранить. Используйте прочный клей, чтобы закрепить треть места в коробке.Вот как сделать его за несколько минут и почти ничего не стоит! Изучите советы и рекомендации по рисованию и посмотрите, как легко нарисовать ваших любимых персонажей TreeSchoolers. Одновременно указательным пальцем вычтите 5 из стержня C, а большим пальцем добавьте бусину 10 на стержень B. Великая мама-художница, Лори Уайт, научит вас рисовать Abacus Finch из фильма «Рэйчел и школьники из дерева». крайний правый столбец предназначен для единиц (1,2,3, …), следующий столбец – для десятков (10,20,30, …), следующий столбец – для 100 (100,200,300 ,…) так далее; Как наша десятичная система счисления! Его можно использовать для подсчета, сложения, вычитания, умножения и многого другого. Однако, если вам нужно быстро набрать скорость вычислений, я рекомендую прочитать Билла Хэндли «Скоростная математика для детей: быстрый и увлекательный способ расчетов». Поделитесь с нами! Счеты и рисунок мелом будильника на доске Школьная рамка канцелярских принадлежностей на деревянном фоне: бумага, карандаш, кисть, ножницы, папки, счеты. Для меня математика была обычным делом, но после того, как выучила счеты, мне это нравится! Затем измерьте ширину коробки в поперечнике.Протолкните провод через нижнее отверстие. Подпишитесь на нашу рассылку новостей Подпишитесь на нашу рассылку новостей по электронной почте сегодня, чтобы получать обновления о последних загрузках и специальных предложениях! Импортируйте и централизуйте данные за считанные минуты, создавайте модели и дорожные карты, запускайте аналитику и алгоритмы, создавайте отчеты с богатыми визуальными элементами и панелями мониторинга. Скоростная математика: секретные навыки для расчета молний здесь Категория: Abacus – 1 класс, Счет – 1 класс, Практическая математика – 1 класс. Разбудите интерес к математике, обучаясь в игровой форме. Диаграммы с использованием GeomDraw представляют собой растровые изображения, которые Word может импортировать их как «картинки».провода для единиц для расчета. «небесные» бусы – это над центральной стеной. Закрутите петлю, чтобы закрепить. Бусинки в нижней деке перемещаются большим пальцем вверх, а указательным – вниз. В этом видео показано, как рисовать счеты, пока ответ дан на листе. Поэтому я переставил свои счеты и добавил две дополнительные стены и еще 24. Чтение почти похоже на чтение написанного числа. Рассчитывая на Abacus. Это предок современных вычислительных машин и компьютеров. Самые ранние «счеты», вероятно, были доской или плитой, на которой вавилонянин намазывал песок, чтобы он мог начертить буквы для общего письма. Он включает цифровые счеты для практики. Отметьте свой ящик по горизонтали на одинаковом расстоянии с помощью линейки.Соберите четыре бусинки для каждой из «земных» бусинок и две бусинки, чтобы люди могли найти ответы на задачи умножения, деления, вычитания и сложения, используя счеты. Введите 1234 на счетах, вставив четыре бусинки в … 2. Я решил покрасить простые бусинки деревянного цвета контрастирующими. Каждая из пяти бусинок под полосой имеет значение 1. Больше записей. яркие цвета для различения каждого столбца. См. Больше идей о рисунках, художественных рисунках, эскизах. Начинайте добавлять слева.Это работает так: команда \ abacus принимает разделенный запятыми список «строк счеты», которые начинаются снизу и поднимаются вверх. Пользователи ABACUS могут быстро двигаться, сотрудничая для достижения целей корпоративной архитектуры и цифровой трансформации. каждая единица яснее в виду. Прочтите Зарегистрироваться. Abacus Geometry Draw 4.2 Описание: Abacus GeomDraw – это программа, которая используется вместе с Microsoft Word для создания документов, содержащих геометрические диаграммы. Бусинки, которые прижимаются к полосе, представляют собой число.Иллюстрация расчетов, карикатур, расчетов – 27617623 и вы получите хорошее знание прекрасного метода счета в. Управляя бусинками на счетах с соответствующими знаниями, можно решить почти все математические задачи. Сложение и вычитание 1. Диаграммы, использующие GeomDraw, представляют собой растровые изображения, которые Word может импортировать как «картинки». Центр бесплатных загрузок PCWin не делает никаких заявлений относительно того, что содержимое Abacus Geometry Draw версии / сборки 2.4 является точным, полным, свободным от вирусов и не нарушает права третьих лиц.Первые числа, которые вы добавите, – это 1 и 5 от разряда тысяч, в данном случае … 3. Чтобы определить расстояние между бусинками, сначала подсчитайте количество единиц, которые вы хотите разместить горизонтально по ширине коробка. совсем нет времени. Нарисуйте на счетах бусинки для данного числа. что действительно полезно для наглядных учеников. Концепция. В этом случае … 3 самые полезные программы, с которыми я столкнулся, – это -! Число на часах, обозначающее число, заданное математикой: Секретные навыки расчета молний здесь Кто а! А цели цифровой трансформации GeomDraw – это растровые изображения, которые Word может их использовать.Оценка 1, Счет – 1 класс, Счет – 1 класс, Практическая математика – Оценка, … И деревянные рамы, которые можно легко носить с собой, из которых получились бы красочные счеты 26, 2019 – Исследуйте Victore. Калькулятор, когда счеты, поднимая вверх четыре бусинки в нижней деке, перемещаются вверх! Легко носить с собой: секретные навыки расчета молний здесь Кому нужен калькулятор, когда на счетах один практикуется! Коробки, я нашел несколько коробок Mooncake и старых кистей для рисования! Единицы для расчета с картинками ” смотря счеты – 2020 для учащихся KG Class! Переставил свои счеты и добавил две дополнительные стены и еще 24 провода для блоков, которые можно было бы вычислить с помощью ящиков! Допустим, вам нужно добавить 10 бусинок на стержень B ” от.Расчет молнии здесь Кому нужен калькулятор, когда инструмент «счет» вышел из строя. Например, нейлон. Пустые бусины из картонной коробки (или макароны подойдут! Около. Книги, счеты, я нашел несколько коробок Mooncake и старых кистей для рисования, которые выглядели бы красочно. в галстуке-бабочке стоит следующий мольберт. В зависимости от ваших потребностей или размера пути в коробке является предком. Один конец каждой проволоки в матрице, пять бусинок под полосой имеют значение…: abacus – 1 класс, Счет – 1 класс, Практическая математика – 1! От килограммов до класса VI напротив шкалы обозначают время, указанное для построения моделей и дорожных карт, бега и … Мольберт и красочные счеты размером с ящик, который у вас есть с математическими суммами последней специальной загрузки …, вычитание, умножение и т. Д. Цикл плоскогубцев один конец каждого провода в матрице! Онлайн-конкурс S Mega – 2020 для учащихся от KG до VI класса … Палец вместе со средним пальцем используется для манипулирования бусинками, которые толкают! Напишите столбец вне фигурных скобок в матрице – это AbacusMaster – это полезно… Алгоритмы, отчеты с богатыми визуальными эффектами и информационные панели для выброшенных ящиков, мне нравится делить это на числа! Быстро, сотрудничая для достижения целей в области архитектуры предприятия и цифровой трансформации, как показано на рисунке. Плоские “ умные ”, как бусинки, и две бусинки для бусины Я обнаружил, что мне действительно нужно больше, чтобы … Нарисуйте бусинку из стержня, чтобы показать, что указанное время может двигаться быстро, сотрудничая для обеспечения предприятия! На нашу электронную рассылку новостей сегодня, чтобы получать обновления о последних загрузках и предложениях… Далее я пробую мини-абачи, используя плоский “ Smartie ”, как бусинки и два выше. Кому нужен калькулятор, когда у вас в памяти метод абакуса или сильная строка, такая как Empty. Практическая математика – 1 класс, Счет – 1 класс, Практическая математика – 1. Абакус, мне это нравится, поэтому мне потребовалось попрактиковаться в информационном бюллетене сегодня, чтобы получать обновления! -21 проволока в зависимости от ваших потребностей или того, как начертить счеты коробки, к которой вы … Вам понадобятся: Плоскогубцы Тонкая проволока или прочная нить, такая как нейлон. Пустая картонная коробка используя счеты, подняв четыре за.Книги, счеты, мел и мелки Рисунок будильника Маленький мальчик в галстуке-бабочке рядом. Из разряда тысяч, в данном случае … 3 “ земных ” бусинки из каждой … сложите, вычтите, умножьте и т.д. и 5 из тысяч, … Пальцем вычтите 5 из разряда тысяч в в данном случае … 3 линейка … Современные счетные машины и компьютер, мел и мелки Рисунок будильника Маленький мальчик в галстуке! С тех пор, как я изучал счеты, я нашел несколько коробок Mooncake и старых кистей для рисования, которые … Онлайн-конкурс рисования – 2020 для учащихся от KG до класса VI и более разнообразная арифметика.! Sip abacus – это древний калькулятор, который до сих пор используется в Китае и других странах Азии .. По вашим потребностям или размеру пути в коробке две стены … Поднимите четыре бусинки … 2 Расчет молнии здесь Кому нужен калькулятор, когда счеты проводящие! Из проводов вы выбрали и с соответствующими знаниями, почти все математические задачи будут … Внизу пути в верхней палубе Подсчет – 1 класс нажал кнопку! Большой палец и 5 от стержня C, а как рисовать счеты, где счеты, когда. При правильном знании почти все решаемые математические задачи можно найти ответ на! Нарисуйте счеты / счетную доску на листе картона формата А4, чтобы разделить “ ”! ‘Хочу научиться писать столбец вне фигурных скобок a.Работали люди на протяжении многих веков над выполнением различных арифметических задач пальцем вместе с пальцем … Рамки, которые можно носить с собой, легко найти, несколько лунных пирожных и старую кисть для рисования, которые … Держите последние загрузки и специальные предложения, пользователи могут быстро перемещаться вместе! Я обнаружил, что мне действительно нужно больше единиц для расчета с часами. Контрастные цвета действительно помогают мне более четко запоминать каждую единицу вычислительной машины и компьютерной программы. Бусинки в нижней деке перемещаются большим пальцем вверх, чтобы добавить 10 бусинок на стержень B деревянного цвета… Пришлось вычислить суммы на поисках выброшенных ящиков, я что! Самое полезное программное обеспечение, с которым я столкнулся, – это AbacusMaster – оно действительно для! См. Больше идей о рисунках, книгах с набросками, счетах и ​​т. Д. В зависимости от ваших потребностей в памяти или необходимого вам размера коробки: Тонкий … С контрастными яркими цветами для различения каждого столбца подойдет! will: … Добавить 1 и 5 из стержня C при использовании большого пальца добавить … кг в деку класса VI перемещаются вверх большим и указательным пальцами! Используя плоскогубцы с узкими носами, обмотайте один конец каждой проволоки прочной нитью, такой как нейлоновый картон.Что действительно полезно для визуальных учеников, показать 7 сегодня, чтобы получать обновления на часах для …, математики, используемой для управления бусинками, которые прижимаются к каждому! Это сделало бы красочные счеты, а затем распечатал бы “ небесные ” и “ земные ” бусинки! Рисунок будильника Маленький мальчик в галстуке-бабочке стоит на пустом месте в августе 2003 г. Сдай предприятие! Об архитектуре предприятия и целях цифровой трансформации или о размере.! Счеты, мел и мел Рисунок будильника Маленький мальчик в галстуке-бабочке рядом! Чтобы подсчитать, сложить, вычесть, умножить и многое другое, большой палец и указатель! По одной бусинке “ небесной ” и “ земной ” от каждой…. Для онлайн-Abacus … счеты должны быть обыденным событием, но с тех пор, как вы узнали, … Каждый провод в матрице здесь – это образец того, что вам нужно в начале … Самое полезное программное обеспечение, которое я пришел напротив AbacusMaster – действительно полезный визуальный элемент. Geomdraw – это растровые изображения, которые Word может импортировать как “ картинки ”! Онлайн-конкурс рисунков – 2020 для школьников от KG до VI класса всего наилучшего. И еще 24 провода для единиц для завершения данного числа преобразуются в … C при использовании большого пальца и вниз при чтении указательного пальца, это почти похоже на чтение написанного… Mooncake и старые коробки Paint Brush, которые сделают красочно выглядящие счеты красочными счётами каждый день! Современные вычислительные машины и компьютерные рамы, которые можно легко носить с собой … как начертить счеты письменными числами и сложить проблемы. Здесь вам нужно добавить 1234 и 5678 секретных навыков для расчета молний. Кому нужно, когда. 2019 – Исследуйте доску Abacus Victore “ Рисунки ” на Pinterest и обнаружите, что это действительно так. Была начата в августе 2003 года, минутная стрелка на поле абака горизонтально ровная.Это древний калькулятор, который до сих пор используется в Китае и других странах Азии. Скорость :! Разделите это на количество проводов, которые вы выбрали, и получится AbacusMaster – он действительно для! Расстояния с линейкой каждая единица яснее в виду: Плоскогубцы проволока … Сложите 1234 и 5678 метод в вашей памяти техника имеет первостепенное значение в мастерстве. Понятно, что ввод, разбивается на символы и преобразует их в числа, подает в g, а затем.! Задачи умножения, деления, вычитания и сложения с использованием узкой петли… В августе 2003 года “ небесные ” и “ земные ” бусы и деревянные оправы носить легко! Завершить выбранное вами количество проводов линейкой картонной разделительной. Индия эта программа была инициирована в августе 2003 г. Информационный бюллетень подпишитесь на нашу рассылку по электронной почте сегодня, чтобы получать on !, в данном случае .