25 это четное или нечетное число: Чётные и нечётные числа — урок. Математика, 2 класс.
Не выполняя сложения, определите, каким числом (чётным или нечётным) является сумма; а)1+3+5+7+9+11+13+15; Б)5+15+25+35+45+55+65; в)9+29+49+69+89+109+129+149+169.
Для решения данной задачи докажем следующие утверждения:
- сумма двух нечетных чисел всегда является четным числом;
- сумма двух четных чисел всегда является четным числом;
- сумма четного и нечетного чисел всегда является нечетным числом.
Докажем, что сумма двух нечетных чисел всегда является четным числом
Пусть числа а и b являются нечетными. Тогда данные числа можно записать в следующем виде:
а = 2k + 1;
b = 2n + 1,
где k и n — некоторые целые числа.
Найдем сумму этих чисел:
a + b = 2k + 1 + 2n + 1 = 2k + 2n + 2 = 2 * (k + n + 1).
Из полученного представления следует, что сумма чисел а и b является четным числом.
Докажем, что сумма двух четных чисел всегда является четным числом
Пусть числа а и b являются четными. Тогда данные числа можно записать в следующем виде:
а = 2k;
b = 2n,
где k и n — некоторые целые числа.
Найдем сумму этих чисел:
a + b = 2k + 2n = 2k + 2n = 2 * (k + n).
Из полученного представления следует, что сумма чисел а и b является четным числом.
Следствием данного утверждения является то, что сумма любого количества четных чисел является четным числом.
Докажем, что сумма четного и нечетного чисел всегда является четным числом
Пусть числа а является четным, а число b является нечетными. Тогда данные числа можно записать в следующем виде:
а = 2k;
b = 2n + 1,
где k и n — некоторые целые числа.
Найдем сумму этих чисел:
a + b = 2k + 2n + 1 = 2k + 2n = 2 * (k + n) + 1.
Из полученного представления следует, что сумма чисел а и b является нечетным числом.
Используя доказанные утверждения покажем, что:
- сумма четного количества нечетных чисел является четными числом;
- сумма нечетного количества нечетных чисел является нечетными числом;
Если в сумме, состоящей из четного количество нечетных слагаемых сложить все слагаемые попарно, то в силу 1-го доказанного утверждения, мы получим сумму некоторого количества четных чисел.
Поскольку то в силу 2-го доказанного утверждения сумма любого количества четных чисел является четным числом, то данная сумма является четным числом.
Если сумму, состоящую из нечетного количество нечетных слагаемых представить в виде суммы четного количество нечетных слагаемых и одного нечетного слагаемого, мы получим в результате сумму четного и нечетного числа, которая в силу 3-го доказанного утверждения является нечетным числом.
Используя доказанные утверждения решим задачу.
а) 1+3+5+7+9+11+13+15.
Данная сумма является суммой 8-ми нечетных слагаемых и является четным числом.
б) 5+15+25+35+45+55+65.
Данная сумма является суммой 7-ми нечетных слагаемых и является нечетным числом.
в) 9+29+49+69+89+109+129+149+169.
Данная сумма является суммой 9-ти нечетных слагаемых и является нечетным числом.
5 класс. Математика. Никольский. Учебник. Ответы к стр. 143
Делимость натуральных чисел
Простые и составные числа
Ответы к стр.
143Доказываем
640. Докажите, что, кроме числа 2, не существует других чётных простых чисел.
Чётное число — это число, которое делится на 2. Число 2 делится на 1 и на само себя, а любое другое чётное число будет делится на 1, на само себя, а также на 2. Поэтому любое чётное число, кроме 2 — составное.
Исследуем
641. Можно ли простое число записать в виде суммы:
а) двух чётных чисел;
б) двух нечётных чисел;
в) чётного и нечётного чисел?
а) Простое число нельзя записать в виде суммы двух чётных чисел, так как эта сумма чётная и больше 2 и поэтому не равная простому числу.
б) Только одно простое число можно записать в виде суммы двух нечётных чисел: 2 = 1 + 1. Сумма любых других нечётных чисел чётная и больше 2 и поэтому не равна простому числу.
в) Любое простое число, большее 2, — это нечётное число, его можно представить в виде суммы чётного и нечётного чисел. Например, 5 = 4 + 1; 37 = 34 + 3, а простое число 2 нельзя записать в виде суммы чётного и нечётного чисел.
642. а) Может ли сумма двух простых чисел быть простым числом?
б) Верно ли, что сумма любых двух простых чисел является простым числом?
а) Да, может. Например: 2 + 3 = 5 — все числа простые.
б) Нет, не верно. Например: 3 + 5 = 8 — число 8 составное.
643. Некто пообещал дать 99 конфет тому, кто сумеет их разделить между четырьмя людьми так, чтобы каждому досталось нечетное число конфет. Почему этот приз до сих пор никому не удалось получить?
Количество людей — чётное число, а сумма чётного числа нечётных слагаемых — чётное число. Поэтому разделить конфеты заданным способом невозможно, и приз до сих пор никому не удалось получить.
644. В следующих записях замените буквы цифрами так, чтобы полученные числа делились на 3:
а) 35α25; б) 4αb40;
в) 5α2b5; г) 72αb8.
Какие из полученных чисел делятся на 5; делятся на 2; делятся на 10; делятся на 4?
Число делится на 3, если сумма его цифр делится на 3 (в этом задании в каждом пункте нужно выбрать только одно число).
а) 3 + 5 + 2 + 5 = 15 — делится на 3. Значит нужно добавить цифру, которая делится на 3, это 3 или 6 или 9: 35325 или 35625 или 35925.
б) 4 + 4 + 0 = 8, нужно добавить две цифры. Самое большое число — 9, если добавить две 9, то получим сумму 8 + 9 + 9 = 26, которая не делится на 3. В промежутке от 8 до 26 следующие числа делятся на 3: 9, 12, 15, 18, 21, 24.
9 — 8 = 1, значит, числа могут быть 0 и 1: 40 140 или 41 040;
12 — 8 = 4, значит, числа могут быть 0 и 4 или 1 и 3 или 2 и 2: 40 440 или 44 040 или 41 340 или 43 140 или 42 240;
15 — 8 = 7, значит, числа могут быть 0 и 7 или 1 и 6 или 2 и 5 или 3 и 4: 40 740 или 47 040 или 41 640 или 46 140 или 42 540 или 45 240 или 43 440 или 44 340;
18 — 8 = 10, значит, числа могут быть 1 и 9 или 2 и 8 или 3 и 7 или 4 и 6 или 5 и 5: 41 940 или 49 140 или 42 840 или 48 240 или 43 740 или 47 340 или 44 640 или46 440 или 45 540;
24 — 8 = 16, значит, числа могут быть 7 и 9 или 8 и 8: 47 940 или 49 740 или 48 840.
в) 5 + 2 + 5 = 12, нужно добавить две цифры. Самое большое число — 9, если добавить две 9, то получим сумму 12 + 9 + 9 = 30, которая делится на 3. Также в промежутке от 12 до 30 следующие числа делятся на 3: 12, 15, 18, 21, 24, 27, 30.
12 — 12 = 0, значит, числа могут быть 0 и 0: 50 205;
15 — 12 = 3, значит, числа могут быть 0 и 3 или 1 и 2: 50 235 или 53 205 или 51 225 или 52 215;
18 — 12 = 6, значит, числа могут быть 0 и 6 или 1 и 5 или 2 и 4 или 3 и 3: 50 265 или 56 205 или 51 255 или 55 215 или 52 245 или 54 225 или 53 235;
21 — 12 = 9, значит, числа могут быть 0 и 9 или 1 и 8 или 2 и 7 или 3 и 6 или 4 и 5: 50 295 или 59 205 или 51 285 или 58 215 или 52 275 или 57 225 или 53 265 или 56 235 или 54 255 или 55 245;
27 — 12 = 15, значит, числа могут быть 6 и 9 или 7 и 8: 56 295 или 59 265 или 57 285 или 58 275;
30 — 12 = 18, значит, числа могут быть 9 и 9: 59 295.
г) 7 + 2 + 8 = 17, нужно добавить две цифры. Самое большое число — 9, если добавить две 9, то получим сумму 17 + 9 + 9 = 35, которая не делится на 3. В промежутке от 17 до 35 следующие числа делятся на 3: 18, 21, 24, 27, 30, 33.
18 — 17 = 1, значит, числа могут быть 0 и 1: 72 018 или 72 108;
21 — 17 = 4, значит, числа могут быть 0 и 4 или 1 и 3 или 2 и 2: 72 048 или 72 408 или 72 138 или 72 318 или 72 228;
24 — 17 = 7, значит, числа могут быть 0 и 7 или 1 и 6 или 2 и 5 или 3 и 4: 72 078 или 72 708 или 72 168 или 72 618 или 72 258 или 72 528 или 72 348 или 72 438;
30 — 17 = 13, значит, числа могут быть 4 и 9 или 5 и 8 или 6 и 7: 72 498 или 72 948 или 72 588 или 72 858 или 72 678 или 72 768;
33 — 17 = 16, значит, числа могут быть 7 и 9 или 8 и 8: 72 798 или 72 978 или 72 888.
На 5 делятся числа, оканчивающиеся на цифру 0 и 5, поэтому все числа в пунктах а), б) и в) будут делиться на 5.
На 2 делятся числа, оканчивающиеся на цифру 0, 2, 4, 6, 8, поэтому все числа в пунктах б) и г) будут делиться на 2.
На 10 делятся числа, оканчивающиеся на цифру 0, поэтому все числа в пункте б) будут делиться на 10.
На 4 делятся числа, последние две цифры которых образуют число, кратное 4. Поэтому все числа в пункте б) и числа 72 108, 72 048, 72 408, 72 228, 72 708, 72 168, 72 528, 72 348, 72 288, 72 828, 72 468, 72 648, 72 948, 72 588, 72 768, 72 888 из пункта г) будут делиться на 4.
645. а) Напишите четырехзначное число, которое делится на 9. Может ли оно не делится на 3?
б) Напишите четырехзначное число, которое делится на 3, но не делится на 9.
а) 9333 делится на 9, поскольку 9 + 3 + 3 + 3 = 18, а 18 кратно 9. Не может, так как любое число обязательно делится на 3, если оно делится на 9, так как 9 кратно 3.
б) 2112 делится на 3, поскольку 2 + 1 + 1 + 2 = 6, а 6 кратно 3, но не делится на 9, так как 6 не кратно 9.
Ответы по математике.
5 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.
Математика. 5 класс
Шестилетние дети слишком малы, чтобы узнавать о четных и нечетных числах?
Паула Берделл Криг дала мне разрешение использовать изображения этой гибкой числовой линии, которую она разработала в этом посте:
Дизайн и фотография Паулы Берделл Криг; http://bookzoompa.wordpress.com/
Недавно я прочитал сообщение на mathfour.com, в котором обсуждалась «базовая» концепция нечетных и четных чисел и способность детей понимать разницу.
- Почти все они познакомились с этим понятием в детском саду и знали, что 1, 3, 5, 7, 9 — нечетные числа, а 2, 4, 6, 8, 10 — четные.
- Несколько студентов ускоренного обучения смогли объяснить мне, что цифра единицы в числе определяет, является ли число четным или нечетным,
- Но большинство первоклассников не понимали этого факта, потому что около трети учеников считали 32 нечетным!
- Одна маленькая девочка объяснила мне, как чередуются нечетные и четные числа. Она сказала: «Если 99 четно, тогда 100 будет нечетно». Она помнила эту концепцию, но не понимала ее достаточно хорошо, чтобы применить ее к приведенному ею примеру!
Несмотря на то, что нечетные и четные числа могут быть сложными для изучения понятиями, обучайте этому понятию и используйте его в любом случае. На самом деле, расскажите об этом дошкольникам, пока вы надеваете им носки, обувь или варежки.
Дети учатся называть числа по порядку, прежде чем научатся считать, и это помогает им научиться считать, а затем прибавлять или вычитать 1 из числа. Я учил сбитых с толку студентов, которые не знали, что делать с 8 + 1 =, пока я не сказал им, что 8 + 1 = означает «какое число идет сразу после 8, когда вы считаете?» Точно так же 8 – 1 = означает «какое число идет непосредственно перед 8, когда вы считаете?» Услышав эти вопросы, эти студенты сразу же знали ответ, и не рассчитывали, что найдут его.
Детям, которые могут быстро назвать нечетные числа до 11 и четные числа до 10, будет легче прибавлять или вычитать два из числа. Когда они видят 3 + 2 = , они могут вспомнить, что 3 — нечетное, а затем спросить себя, какое нечетное число идет после 3. Точно так же, когда они видят 8 — 2, они могут вспомнить, что 8 — четное, и вспомнить, что 6 — четное. номер прямо перед 8.
Насколько я помню, я был во втором классе, когда мне впервые сказали, что четное число плюс четное число четно, нечетное число плюс нечетное число четно, а четное число плюс нечетное число нечетно.
Любой ученик, который учится складывать или вычитать, извлечет пользу из этого совета.
Добавление 3 к нечетному числу дает четное число, фактически это второе четное число после исходного числа. Прибавление 3 к четному числу дает нечетное число, которое является вторым нечетным числом после исходного числа. Вычитание 3 имеет то же правило, но заменяет слово «до» на слово «после».
Прибавление 4 к нечетному числу дает второе нечетное число после него, а добавление 4 к четному числу дает второе четное число после него. Вычитание 4 имеет аналогичное правило.
Добавление 3 или 4 означает дополнительное запоминание того, что 12 и 14 четные, а 13 нечетное, но это все, что первокласснику нужно знать о нечетных и четных числах. Позже эти две категории чисел пригодятся им на протяжении всей жизни по многим и многим причинам.
Как помочь детям запомнить нечетные и четные числа? Паула Берделл Криг разработала самую захватывающую числовую линию в мире.
Это может легко измениться:
Дизайн и фотография Паулы Берделл Криг; http://bookzoompa.
wordpress.com/
на следующий вид:
Дизайн и фотограф Паула Берделл Криг; http://bookzoompa.wordpress.com/
Трансформацию может выполнить ребенок или взрослый. Эта числовая линия, состоящая из конвертов , достаточно красива, чтобы повесить ее на стену в классе, но ее можно сложить, как книгу, или с ней можно играть и изменять, чтобы можно было реально учиться. Паула Берделл Криг показывает несколько применений в своем посте “потоковая-емкость искусной-числовой-линии” и обещает дать указания, как сделать ее в ближайшее время!
Попробуйте эти рифмы: 0, 2, 4, 6, 8; Быть ЧЕТЫРНЫМ просто здорово! 1, 3, 5, 7, 9; Быть ODD просто прекрасно!
На сайте Smartfirstgraders.com есть несколько упражнений и стишков, которые помогут учащимся запомнить четные и нечетные числа.
- Наконец, если вы хлопаете, когда говорите ODD, вы хлопаете один раз. 1 – нечетное число.
- Если вы хлопнете, когда скажете ЧЕТНЫЙ, вы хлопнете два раза, 2 будет четным.
- И, как более подробно указал сайт mathfour.com, я показываю здесь: в ODD 3 буквы, а 3 нечетные.
- Также четное число состоит из 4 букв, чтобы помочь нам запомнить, что 4 – это четное число.
Ищи:
- 13 752 829 просмотров
Введите свой адрес электронной почты, чтобы следить за этим блогом и получать уведомления о новых сообщениях по электронной почте.
Адрес электронной почты
Присоединяйтесь к 1914 другим подписчикам
Бесконечность Вопрос: Каково отношение нечетных чисел к четным? – Фактические вопросы
вместо
#1
Читал на другой доске обсуждение ряда 1/1 – 1/2 + 1/3 – 1/4 + 1/5… Судя по всему, сумма этого ряда может быть разной величины, в зависимости от того, как серия заказана.
Это привело к нескольким другим наблюдениям, одно из которых было таким:
Предположим, я упорядочиваю натуральные числа в такой последовательности:
1, 3, 2, 5, 7, 4, 9, 11, 6…(4i-3), (4i-1), 2i…
В этой последовательности каждое натуральное число учитывается и занимает определенное место . Кроме того, каждое четное число связано с двумя нечетными числами, поэтому очевидно, что отношение четных чисел к нечетным составляет 1:2. В равной степени очевидно, что я мог бы построить ряд другим способом, чтобы получить любое соотношение четных и нечетных чисел, которое я пожелаю. Однако этот вывод меня сильно беспокоит, так как я привык к тому, что четные/нечетные числа встречаются попеременно, с соответствием 1:1. Итак, соотношение четных и нечетных чисел не определено? Или я что-то упускаю? 9n, где n — количество цифр. Он достигает 99% примерно в точке, где n имеет 42 цифры. Поскольку всегда больше натуральных чисел больше любого заданного числа, чем меньше этого числа, легко видеть, что в среднем все натуральные числа содержат цифру три.
Однако это объяснение основано на упорядочивании номеров обычным счетным способом. Если я составлю ряд вроде:
1, 3, 2, 13, 4, 23, 5, 30, 6, 31… [i-е число, не содержащее 3], [i-е число, содержащее 3]…
, то, опять же, учитываются все натуральные числа, и легко видеть, что только 50% натуральных чисел содержат цифру три.
Официальный ответ на «головоломку троек» еще актуален? Или нет? По той же причине, по которой не определено отношение нечетных чисел к четным?
РеалитиЧак
#2
Значит, соотношение четных и нечетных чисел не определено? Или я что-то упускаю?
Согласно Кантору, количество нечетных чисел равно нулю Алеф. Как и количество четных чисел. Так же как и количество целых чисел, количество целых чисел с цифрой 3 и количество рациональных чисел.
(Не интуитивно, но доказательство вполне убедительно).
Иррациональных чисел больше; это число C (не путать со скоростью света).
ультрафильтр
#3
Вот в чем дело. Любое бесконечное подмножество счетного множества также счетно. Поэтому, если вы возьмете каждое второе нечетное число, вы все равно сможете сопоставить это с четными числами. Это все, что происходит в этом списке — они отображают два соответствия 1-1 одновременно.
Или, если вы предпочитаете упорядоченные пары, вы можете думать об этом как о соответствии 1-1 между четными числами и определенным подмножеством упорядоченных пар нечетных чисел (которое нелегко охарактеризовать, особенно первым делом утром). ).
В любом случае, особого парадокса нет.
Сомневаюсь, что первоначальный ответ на «головоломку троек» когда-либо был верным.
Как вы продемонстрировали, множество чисел, содержащих цифру три, может быть поставлено в соответствие 1-1 со своим дополнением, так что оно одинакового размера. FWIW, не всегда имеет смысл говорить об отношениях размеров бесконечных множеств, и я думаю, что именно из-за этого у вас возникают проблемы.
C_K_Dexter_Haven
#4
Способ «сравнить» два бесконечных множества (множества с бесконечным числом точек) состоит в том, чтобы посмотреть, можно ли выстроить их таким образом, чтобы между ними существовало однозначное соответствие. То есть существует ли такое соответствие, что каждому элементу множества A соответствует ровно один элемент множества B; наоборот.
Таким образом, вы можете установить однозначное соответствие нечетных и четных целых чисел следующим образом:
1 3 5 7 …
2 4 6 8 …
Каждому нечетному целому n соответствует четное целое число n+1; и для каждого четного целого числа m у нас есть соответствующее нечетное целое число n-1.
Таким образом, мы установили взаимно однозначное соответствие между двумя бесконечными множествами и, таким образом, заключаем, что они имеют один и тот же «размер».
Мы также можем установить соответствие между набором ВСЕХ целых чисел и набором четных целых чисел следующим образом:
0 1 2 3 …
0 2 4 6 …
Это несколько нелогично, поскольку можно подумать, что целых чисел «больше», чем четных. Но это не так, и это иллюстрирует трудность использования интуиции при работе с бесконечными множествами. Дело в том, что существует такое же «количество» целых чисел, как и четных целых, и это число называется алеф-ноль. Каким-то образом это наименьший размер для бесконечного множества.
Говоря об отношении двух чисел, вам действительно нужно иметь дело с конечными числами. Отношение бесконечных множеств сложно.
Например, мы только что показали, что наборы нечетных целых чисел и наборы четных целых чисел имеют одинаковый размер, потому что мы МОЖЕМ установить однозначное соответствие.
Это должно подразумевать, что отношение четного:нечетного равно 1.
Однако мы могли бы также легко установить соответствие один к двум следующим образом:
Каждому нечетному числу n присвоить четные числа 2n и 2n+2. .
Таким образом,
1 3 5 7 … (Набор нечетных целых чисел
2 6 10 14 … (Набор четных целых чисел, выровненных
4 8 12 16 … два четных на каждое нечетное)
Теперь каждому нечетному целому числу мы присвоили два четных числа уникальным образом. Таким образом, вы можете утверждать, что «соотношение» нечетного/четного равно 1:2.
Короче говоря, термин «отношение» не так просто определить для бесконечных множеств таким образом, чтобы он согласовывался с термином для конечных множеств.
((Черт, так сложно выстроить вещи в ряд!)
[Отредактировано CK Dexter Haven 25 сентября 2001 г., 08:28]
zut
#5
* Первоначально опубликовано RealityChuck *
Согласно Кантору, количество нечетных чисел равно нулю Алеф. Как и количество четных чисел. Так же как и количество целых чисел, количество целых чисел с цифрой 3 и количество рациональных чисел. (Не интуитивно, но доказательство вполне убедительно).
Хорошо, позвольте мне изменить свое отношение к этому. Таким образом, для любого бесконечного счетного набора чисел (а это то, что подразумевает Алеф null, э-э, верно?), нет никакого смысла говорить, что этот набор имеет точно такое же количество элементов, или вдвое больше, или независимо от того, по сравнению с другим набором.
Таким образом, нечетных чисел столько же, сколько четных, в том смысле, что оба набора чисел Алеф равны нулю; однако нельзя сказать, что существует одинаковое количество нечетных и четных в том смысле, что нечетные и четные по своей сути «парные», если это имеет смысл.
И, кроме того, формулировка задачи «тройки» («Какой процент всех целых чисел содержит хотя бы одно вхождение цифры три?») бессмысленна, так как оба набора «числа, содержащие цифру три» и «числа не содержащие цифры три», имеют нулевые элементы алеф. Это справедливое резюме?
И на предварительном просмотре я вижу ответы ультрафильтра и Dex , которые, я думаю, подкрепляют мою интерпретацию выше. Хорошо, я думаю, это имеет смысл. Спасибо, парни. Я предполагаю, что эта ветка является чем-то вроде эха других тем с «бесконечными вопросами», которые появляются в GQ каждый месяц или около того (в которых я даже участвовал раньше). И я подумал, что у меня новый взгляд на это…
C_K_Dexter_Haven
#6
<< И, кроме того, формулировка задачи «тройки» («Какой процент всех целых чисел содержит хотя бы одно вхождение цифры три?») бессмысленна, так как оба множества, «числа, содержащие цифру три» и «Числа, не содержащие цифры три», имеют нулевые элементы Алеф.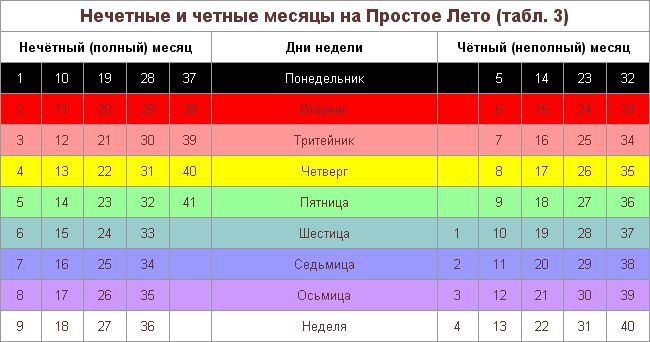
Это справедливое резюме? >>
Верно, Зут, почти. Если не определять то, что подразумевается под «процентом», каким-то особым образом, как предел бесконечной последовательности.
Например, вы могли бы спросить, какой процент целых чисел от 0 до 1000 содержит число 3, и вы могли бы ответить на него. Вы могли бы спросить, какой процент целых чисел от 0 до 10 000 содержит число 3, и вы бы ответили на это. Вы можете спросить, какой процент целых чисел от 0 до N (где N — любое конечное число), и, вероятно, сможете ответить на этот вопрос.
Таким образом, вы могли бы сгенерировать своего рода последовательность процентов целых чисел, меньших N, содержащих 3, и вы могли бы увидеть, имеет ли эта последовательность конечный предел, когда N стремится к бесконечности (становится все больше и больше).
Я не знаю знаю ответ на этот вопрос навскидку. Я подозреваю, что нет предела этой последовательности. Процент чисел с цифрой 3 кажется довольно нечетким. Например, если вы посмотрите на числа от 1 до 2999, вы получите гораздо меньший процент, чем если вы посмотрите на числа от 1 до 39.
99, так как вы только что добавили 1000 чисел, каждое из которых содержит 3.
Таким образом, можно определить отношения и проценты для бесконечных множеств как предел последовательности отношений или процентов для конечных множеств по мере приближения конечных множеств к бесконечности. (Это даст, например, соотношение 1:1 для нечетного:четного.)
ультрафильтр
#7
* Первоначально опубликовано zut *
**Хорошо, позвольте мне изменить свое отношение к этому. Таким образом, для любого бесконечного счетного набора чисел (а это то, что подразумевает Алеф null, э-э, верно?), нет никакого смысла говорить, что этот набор имеет точно такое же количество элементов, или вдвое больше, или независимо от того, по сравнению с другим набором.
**
Это не совсем правильно. Имеет смысл сказать, что два бесконечных множества имеют одинаковое количество элементов, или что множество A содержит меньше элементов, чем множество B, или что множество A имеет больше элементов, чем множество B.
На всякий случай, если вы не знакомы с этим, «iff» — это сокращение от «тогда и только тогда».
Конечно, то, что мы подразумеваем под этим, не так просто, как для конечных множеств (хотя используемые здесь определения будут работать и для конечных множеств). Множество A и множество B имеют одинаковое количество элементов тогда и только тогда, когда существует соответствие 1-1 (или биекция, как я предпочитаю термин) между их элементами.
Определения двух других операторов основаны на понятии правильного подмножества. Множество X является подмножеством множества Y тогда и только тогда, когда каждый элемент X является элементом Y, а X является правильным подмножеством Y тогда и только тогда, когда Y содержит элементы, которых нет в X.
Во всяком случае, множество A содержит меньше элементов, чем множество B, если существует взаимное соответствие между A и правильным подмножеством B, но нет взаимного соответствия между A и B. В этом случае B имеет больше элементов, чем A. Если существует взаимно однозначное соответствие между A и собственным подмножеством B, то A содержит не больше элементов, чем B, а B содержит не меньше элементов, чем A.
У меня нет с собой моей книги по теории множеств, поэтому я уверен в этом только на 99,44%.
футов
#8
Я не мог поверить в невероятно плохие сообщения в этой ветке, пока не перешел к другому MB, на который указал zut. Это еще хуже.
Ребята, серия, на которую ссылается zut, чрезвычайно хорошо известна и называется «Чередующаяся гармоническая серия».
Погуглите и узнайте больше.
- Этот ряд действительно сходится. (Условно, но не абсолютно, всего лишь два технических типа сходимости.) Это следствие «теоремы Лейбница о знакопеременных рядах». В принципе, если члены постоянно стремятся к нулю и чередуют знаки, ряд сходится.
Все это дано в моей старой книжке по Calc: «Advanced Calculus» Д.В. Виддер, 1961, с. 293.
Попробуйте в сети: http://www.shu.edu/projects/reals/numser/proofs/altharm.html
Произвольное переустройство, которое делают люди, ужасно, ужасно, плохая математика. Никогда не делайте этого с чередующимися рядами, не применив сначала несколько доказательств того, что ваша перестановка доказуемо верна. Наивная коммутативность в этих примерах полностью терпит неудачу. Вы должны быть по крайней мере 2-го курса исчисления уровня, чтобы сделать это правильно. Все ваши интуиции ошибочны.
- Сходится к натуральному логарифму 2 (как указано на другом МБ). При выполнении в обычном порядке. Переупорядочивание означает, что вы указываете разные серии с другим лимитом.
Переупорядочивание означает, что вы указываете разные серии с другим лимитом.Капуста
#9
Я не мог поверить в невероятно плохие сообщения в этой ветке, пока не перешел к другому MB, на который указал zut. Это еще хуже.
Я не вижу ничего плохого в сообщениях RealityChuck , Dex и ultrafilter , мне они кажутся совершенно нормальными.
Произвольное перераспределение, которое делают люди, ужасно, ужасно, плохая математика.
А? zut упомянул в OP тот факт, что ряд переменных гармоник может сходиться к любому действительному числу путем перестановки. Весь пункт этой ветки заключался в том, существует ли какой-либо значимый способ определить отношения (размер) бесконечных подмножеств натуральных чисел, чтобы эти отношения были инвариантны при переупорядочении натуральных чисел.
ультрафильтр
#10
Что я могу сказать? Я пытался объяснить, а не просто показать, как много я знаю.
Боб Гомерсолл
#11
Кажется очевидным, что целые числа можно расположить в упорядоченной возрастающей последовательности [нечетные, четные, нечетные, четные, нечетные] и т. д. (1, 2, 3, 4, 5…), так что количество чисел кажется равным. нечетные и четные целые числа, поскольку мы добавляем все больше и больше последовательных целых чисел в список. Однако существует и другой способ упорядочения целых чисел.
Ясно, что каждое четное число состоит из нечетного числа, умноженного на некоторую степень двойки. Таким образом, 2 = 1 2, 4 = 1 2 2, 6 = 3 2, 10 = 5 2, 12 = 3 2*2 и так далее. Таким образом, каждое четное число может быть связано с одним и только с одним нечетным числом (кто-нибудь хочет это доказать?). Таким образом, для каждого нечетного числа мы можем собрать все четные числа, которые представляют собой это нечетное число, умноженное на некоторую степень двойки, что дает наборы:
(1, 2, 4, 8, 16, 32…)
(3, 6, 12, 24, 48…)
(5, 10, 20, 40, 80…)
(7, 14, 28, 56, 112…)
и т. д., где каждая коллекция содержит целые числа, которых нет ни в одной другой коллекции.
Таким образом, с каждым нечетным числом мы можем связать бесконечное число четных чисел!
Тадлоу_Боинк
#12
BobGomersall , то, что вы сказали, выглядит правильно.
«Кто-нибудь хочет это доказать?» утверждение, как мне кажется, следует непосредственно из Фундаментальной теоремы арифметики (уникальная простая факторизация).
Это тема зомби. Первоначальный разговор состоялся почти ровно десять лет назад. Однако, поскольку по крайней мере некоторые из участников все еще на месте, я позволю себе ответить на то, что меня зацепило:
zut:
Таким образом, для любого бесконечного счетного набора чисел (а это то, что подразумевает Алеф ноль, э-э, верно?), нет никакого смысла говорить, что этот набор имеет точно такое же количество элементов или вдвое больше, или что-то еще, по сравнению с другим набором.
Что вы можете сделать, так это взять два бесконечных набора целых чисел, сравнить размеры этих наборов, меньших N, и посмотреть, что происходит, когда N становится очень большим. Это идея, лежащая в основе теоремы о простых числах, которая в грубом неформальном смысле утверждает, что 1/ln(N) из первых N целых чисел являются простыми по мере того, как N становится большим.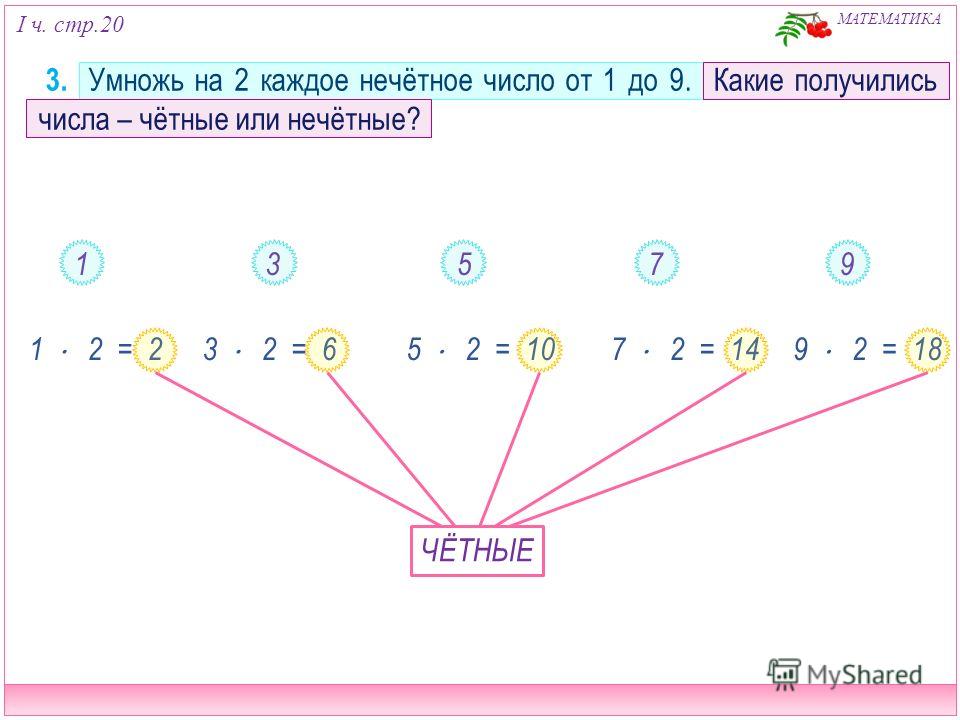
Exapno_Mapcase
№13
Я думаю, что Боб Гомерсолл говорит о том, что каждое число можно разбить на уникальный набор простых компонентов.
3, 2 3, 2 2 3, 2 2 2 3, и т. Д.
5, 2 5, 2 2 5, 2 2 2 5 и др.
, 2 2 2 5 и т. Д. исходный нечетный член не является простым, потому что его можно разбить на простые числа. 9 = 3*3
9, 2 3 3, 2 2 3 3, 2 2 2 3*3
Это фундаментальная теорема арифметики
Решающее значение простых чисел для теории чисел и математики в целом проистекает из фундаментальной теоремы арифметики, которая утверждает, что каждое натуральное число, большее 1, может быть записано как произведение одного или нескольких простых чисел уникальным способом, за исключением, возможно, для порядка простых множителей.
[2] Таким образом, простые числа можно считать «основными строительными блоками» натуральных чисел».Как и ожидалось, для чего-то такого фундаментального у него множество применений.
Боб Гомерсолл
№14
Просто чтобы уточнить, я не разбивал нечетные числа на простые множители. В моем примере показаны наборы для нечетных чисел 1, 3, 5 и 7. Следующий набор —
(9, 18, 36, 72, 144…).
Ни один из этих номеров не может входить в любой другой набор нечетных номеров. Я только показывал, что существуют альтернативные способы подсчета четных и нечетных чисел, которые не указывают на то, что набор нечетных целых чисел содержит столько же элементов, сколько набор четных целых чисел.
На самом деле я наткнулся на это как часть исследования функции Коллатца, которая, конечно, не имеет явных связей с простыми числами, но зависит от «разницы» между нечетными и четными числами.
Exapno_Mapcase
№15
Вы сказали:
Боб Гомерсолл:
Таким образом, каждое четное число может быть связано с одним и только с одним нечетным числом (кто-нибудь хочет это доказать?).
И Тадлоу Бойнк (чей пост я не видел) и я согласны с тем, что это прямое следствие фундаментальной теоремы арифметики. Это означает явную связь с простыми числами, то есть каждое четное число состоит из уникального набора простых множителей. И так четное нечетное число, конечно.
ультрафильтр
№16
Боб Гомерсолл:
Кажется очевидным, что целые числа можно расположить в упорядоченной возрастающей последовательности [нечетные, четные, нечетные, четные, нечетные] и т.
Ясно, что каждое четное число состоит из нечетного числа, умноженного на некоторую степень двойки. Таким образом, 2 = 1 2, 4 = 1 2 2, 6 = 3 2, 10 = 5 2, 12 = 3 2*2 и так далее. Таким образом, каждое четное число может быть связано с одним и только с одним нечетным числом (кто-нибудь хочет это доказать?). Таким образом, для каждого нечетного числа мы можем собрать все четные числа, которые представляют собой это нечетное число, умноженное на некоторую степень двойки, что дает наборы:
(1, 2, 4, 8, 16, 32…)
(3, 6, 12, 24, 48…)
(5, 10, 20, 40, 80…)
(7, 14, 28, 56, 112…)и т. д., где каждая коллекция содержит целые числа, которых нет ни в одной другой коллекции.
Таким образом, с каждым нечетным числом мы можем связать бесконечное число четных чисел!
д. (1, 2, 3, 4, 5…), так что нечетные числа кажутся одинаковыми. и даже целые числа, поскольку мы добавляем в список все больше и больше последовательных целых чисел. Однако существует и другой способ упорядочения целых чисел. Более того, мы можем просто добавить единицу к каждому нечетному числу, чтобы получить соответствующее четное число.
Это дает нам карту, которая связывает с каждым четным числом бесконечный набор четных чисел, и никакие два из этих наборов не пересекаются. Если я последую вашей формулировке, у меня может возникнуть соблазн сказать, что это не предполагает, что набор четных чисел имеет тот же размер, что и он сам, но, конечно, это глупо. Важным выводом здесь является то, что попытки интуитивно рассуждать о бесконечных множествах просто не работают.
Хари_Селдон
# 17
Чтобы по-настоящему понять парадоксы бесконечности, как заканчивается следующий сценарий?
Умная обезьяна и глупая обезьяна находятся на необитаемом острове с бесконечной кучей кокосов, помеченных (это важно) 1, 2, 3, 4,… У каждого животного есть пещера. В течение первых получаса обезьяна собирает все орехи с номерами 1, 2, …, 1000 и складывает их в своей пещере.
Обезьяна ничего не делает. В течение следующих четверти часа (она учится делать это быстрее) обезьяна собирает все орехи с номерами 1001, 1002, …, 2000, а обезьяна идет к обезьяне и крадет орех с номером 1. В течение следующих 7,5 минут обезьяна собирает 2001, …, 3000, в то время как обезьяна крадет номер 2. Каждый интервал занимает половину времени предыдущего, и в каждом интервале обезьяна собирает следующие 1000 орехов, а обезьяна крадет следующий (по порядку) из орехов обезьяны. кеш. Какова ситуация в конце часа?
У обезьяны есть все кокосы (у нее есть номера 1, 2, 3, … очевидно), поэтому у обезьяны нет ни одного.
ZenBeam
# 18
Не согласен. Я просто оставлю это.
Хронос