2 задачи по математике: Задачи по математике для 2 класса | Материал по математике (2 класс) по теме:
Задачи для 1 – 2 класса
Меню раздела
- Математика
Рейтинг: 3 / 5
Пожалуйста, оцените Оценка 1Оценка 2Оценка 3Оценка 4Оценка 5Примеры решения задач по математике
Задача №1
В шкафу стояло 39 книг. Когда на полку переставили несколько книжек, их там осталось 25.
Сколько книг переставили на полку?Решение:
39 – 25 = 14 (кн.)Ответ: на полку переставили 14 книг.
Задача №2
Когда со стоянки уехало 4 машины, там осталось ещё 26.
Сколько машин было на стоянке?Решение:
26 + 4 = 30 (маш.)Ответ: на стоянке было 30 машин.
Задача №3
У Олега было 15 почтовых марок. 5 марок он использовал.
Сколько марок осталось у Олега?Решение:
15 – 5 = 10 (мар.)Ответ: у Олега осталось 10 марок.
Задача №4
На элеватор привезли 45 т ржи, а пшеницы 15 т.
Сколько всего зерна привезли на элеватор?Решение:
45 + 15 = 60 (т)Ответ: на элеватор привезли 60 тонн зерна.
Задача №5
Петя собрал по теме «Космос» 25 марок, а по теме «Флот» только 9.
Сколько всего марок в Петиной коллекции?Решение:
25 + 9 = 34 (мар.)Ответ: в Петиной коллекции 34 марки.
Задача №6
В ларёк привезли 15 ящиков яблок и 8 ящиков слив.
Сколько всего привезли ящиков с фруктами?Решение:
15 + 8 = 23 (ящ.)Ответ: в ларёк привезли 23 ящика с фруктами.
Задача №7
Бабушка посадила 16 кустиков клубники, а внучка 5.
Сколько всего кустиков клубники они посадили?Решение:
16 + 5 = 21 (кус.)Ответ: они посадили 21 куст клубники.
Задача №8
В школьную столовую привезли 15 кг картофеля, через 2 дня ещё 10 кг.
Сколько всего килограммов картофеля привезли?Решение:
15 + 10 = 25 (кг)Ответ: всего привезли 25 кг картофеля.
Задача №9
На стройку привезли 5 ящиков больших гвоздей и 8 ящиков маленьких.
Сколько всего привезли ящиков с гвоздями? Решение:
5 + 8 = 13 (ящ.)
Ответ: на стройку привезли 13 ящиков с гвоздями.
)Задача №10
Дедушка налил в бочку 18 вёдер воды и привёз в сад. Из бочки, под кусты, вылили 7 вёдер воды.
Сколько вёдер воды осталось бочке?Решение:
18 – 7 = 11 (вёд.)Ответ: в бочке осталось 11 вёдер воды.
Домашнее задание
Чтобы легко и быстро решать аналогичные задачи нужно закрепить знания выполнив несколько заданий самостоятельно. Реши задачу и дай ответ.
Пример 1
На праздник 9 Мая дети читали стихи. Девочки прочитали 7 стихов, а мальчики 9. Сколько всего прочитали стихотворений?
Пример 2
Оля помогала маме мыть посуду. Мама помыла 6 тарелок, а Оля помыла 3 чашки. Сколько всего вымыто посуды?
Пример 3
К новогоднему празднику ученики украсили школьный класс.
Пример 4
В классе на подоконниках стоят 36 горшков с цветками. На первом подоконнике стоят 12 горшков, на втором 14. Сколько горшков на третьем подоконнике?
Пример 5
У Коли в аквариуме 18 рыбок – 7 скалярий и 11 барбусов. Коля подарил Ване 4 скалярия, а Пете 4 барбуса. Сколько рыбок каждой породы осталось у Коли?
Девочки вырезали из бумаги 15 снежинок, а мальчики 20 хлопушек. Сколько всего украшений сделали ученики?Коротко:
Известные и великие математики
ученые древности, средневековья и современности, и их вклад в мировую науку
Жозеф Луи Лагранж
математик, астроном и механик
Дата рождения: 25 января 1736 г.
Место рождения: Турин, Сардинское королевство
Дата смерти: 10 апреля 1813 г. (77 лет), Париж, Первая империя
Биография
Лагранж родился 25 января 1736 в Турине.
Из-за материальных затруднений семьи он был вынужден рано начать самостоятельную жизнь. Сначала Лагранж заинтересовался филологией. Его отец хотел, чтобы сын стал адвокатом, и поэтому определил его в Туринский университет. Но в руки Лагранжа случайно попал трактат по математической оптике, и он стал увлечённо изучать математическую литературу.
В 1755 году Лагранж послал Эйлеру (швейцарский, немецкий и российский учёный, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук) свою работу об изопериметрических свойствах, ставших впоследствии основой вариационного исчисления. В этой работе он решил ряд задач, которые сам Эйлер не смог одолеть. Эйлер включил похвалы Лагранжу в свою работу и (вместе с д’Аламбером) рекомендовал молодого учёного в иностранные члены Берлинской Академии наук (избран в октябре 1756 года).
В 1755 году Лагранж был назначен преподавателем математики в Королевской артиллерийской школе в Турине, где пользовался, несмотря на свою молодость, славой прекрасного преподавателя.
Лагранж организовал там научное общество, из которого впоследствии выросла Туринская академия наук, издаёт труды по механике и вариационному исчислению (1759). Здесь же он впервые применяет анализ к теории вероятностей, развивает теорию колебаний и акустику.
В 1764 году Французская академия наук объявила конкурс на лучшую работу по проблеме движения Луны. Лагранж представил работу, посвящённую либрации Луны (см. Точки Лагранжа), которая была удостоена первой премии. В 1766 году Лагранж получил вторую премию Парижской Академии за исследование, посвященное теории движения спутников Юпитера, а до 1778 года был удостоен ещё трёх премий.
В 1766 году по приглашению прусского короля Фридриха II Лагранж переехал в Берлин (тоже по рекомендации Д’Аламбера и Эйлера). Здесь он вначале руководил физико-математическим отделением Академии наук, а позже стал президентом Академии.
В 1772 году избран иностранным членом Парижской академии наук. Берлинский период (1766—1787) был самым плодотворным в жизни Лагранжа.
Здесь он выполнил важные работы по алгебре и теории чисел, в том числе строго доказал несколько утверждений Ферма и теорему Вильсона.
В Берлине была подготовлена и «Аналитическая механика», опубликованная в Париже в 1788 году и ставшая вершиной научной деятельности Лагранжа. Гамильтон назвал этот шедевр «научной поэмой». В основу всей статики положен т. н. принцип возможных перемещений, в основу динамики — сочетание этого принципа с принципом Д’Аламбера. Введены обобщённые координаты, разработан принцип наименьшего действия. Впервые со времён Архимеда монография по механике не содержит ни одного чертежа, чем Лагранж особенно гордился.
В 1787 году, после кончины Фридриха II, Лагранж по приглашению Людовика XVI переехал в Париж, где был принят с королевскими почестями и стал членом Парижской Академии наук (уже не иностранным членом).
В 1795 году открылась Нормальная школа, и Лагранж преподаёт там математику. В 1797 году, после создания Политехнической школы, вёл там преподавательскую деятельность, читал курс математического анализа.
В эти годы Лагранж публикует свою знаменитую интерполяционную формулу для приближения функции многочленом. Издаёт книгу «Теория аналитических функций», без актуальных бесконечно малых. Там же Лагранж дал формулу остаточного члена ряда Тейлора, указал метод множителей Лагранжа для решения задач на условный экстремум.
Наполеон любил обсуждать с деликатным и ироничным Лагранжем философские вопросы. Он пожаловал Лагранжу титул графа, должность сенатора и орден Почётного легиона.
Лагранж внёс существенный вклад во многие области математики, включая вариационное исчисление, теорию дифференциальных уравнений, решение задач на нахождение максимумов и минимумов, теорию чисел, алгебру и теорию вероятностей. Формула конечных приращений и несколько других теорем названы его именем. В двух своих важных трудах — «Теория аналитических функций» (1797 г.) и «О решении численных уравнений» (1798 г.) — подытожил всё, что было известно по этим вопросам в его время, а содержавшиеся в них новые идеи и методы были развиты в работах математиков XIX века.
Умер Лагранж 10 апреля 1813 года, похоронен в парижском Пантеоне.
Его труды:
- Аналитическая механика
- Вариационное исчисление
- Дифференциальное уравнение Лагранжа
- Математический анализ
- Формула конечных приращений
- Теория аналитических функций
- О решении численных уравнений
- Метод множителей Лагранжа
В его честь названы:
- Кратер на Луне
- астероид (1006) Лагранжея, открытый в 1923 году советским астрономом Белявским Сергеем Ивановичем
- Улицы в Париже и Турине
- Множество научных понятий и теорем в математике, механике и астрономии
- Имя Лагранжа внесено в список 72 величайших учёных Франции, помещённый на первом этаже Эйфелевой башни.
- Назад
- Вперед
Если заметили ошибку, выделите фрагмент текста и нажмите Ctrl+Enter
Запомнить меня
Регистрация
Задания по математике для 2 класса — задачи по математике для детей 2 класса
Четыре причины изучать математику во 2 классе
Развитие логического мышления
Математика учит анализировать данные, устанавливать взаимосвязи и находить оптимальное решение.
Эти навыки помогут справиться не с одной жизненной задачей.
Достижение успеха в любой профессии
Умение оперировать цифрами нужно не только экономистам. Математика необходима даже в таких творческих профессиях, как архитектор и фотограф.
Повышение авторитета в своем окружении
В школе разбирающийся в математике ребенок будет пользоваться уважением сверстников, а вне учебы не позволит обмануть себя, например, на кассе в магазине.
Развитие коммуникативных навыков
Неочевидно, но факт: те, у кого все хорошо с математикой, более стройно, логично и последовательно излагают свои мысли.
А значит, с ними приятнее общаться.
Какой должна быть математика для учеников 2 класса?
Интересные задачи вместо
длинных примеров
Задачи даются в игровой форме. Школьник просто следит за ходом интересной истории, как в мультфильме, и помогает продвигаться сюжету, решая несложные и увлекательные математические задачи на логику.
Развитие логики вместо
оперирования числами
Математика учит не только быстро считать, но и думать, рассуждать, анализировать и искать решения, опираясь на логику. Лучше всего развивать нужные навыки с детства — они пригодятся как в школе, так и в жизни.
Занятия всего от нескольких
минут в день
Каждый урок курса математики длится 30-40 минут и посвящен отдельной теме.
Ребенок может делить занятия, как удобно, занимаясь хоть по 5-10 минут в день, и возвращаться к задачам в любое время.
Какие задачи по математике для 2 класса предлагает Умназия?
Задачи на классификацию
Поиск закономерностей
Математические задачи на логику
Задачи на истину и ложь
Волшебные квадраты
Математические ребусы
Задачи на переливание
Задачи на взвешивание
Задачи, решаемые с конца
Задачи на скорость
Задачи, решаемые методом перебора
Геометрические задачи
Начать заниматься
Примеры заданий по математике для 2 класса
Задача 1
Иван-Царевич заметил, что перед избушкой Бабы-яги спят несколько трёхголовых Горынычей и стадо гусей.
Всего Иван насчитал 9 голов и 5 хвостов.
Сколько гусей в стаде?
Решить задачу
Задача 2
Лягушки на пруду соревновались в ловле мух. Соревнования длились 20 минут. Известно, что Квакша поймала на 7 мух меньше, чем Тревор, Тревор и Аква вместе поймали 100 мух, а Квакша ловила по 2 мухи в минуту.
Кто занял первое место, а кто — последнее?
Решить задачу
Задача 3
На новогоднем утреннике веселилось 20 малышей. Каждый из них был одет в костюм либо зайчика, либо снежинки, либо пирата. Второклассник Петя заметил, что зайчиков на празднике было в 6 раз больше, чем снежинок, а пиратов оказалось меньше, чем зайчиков.
Сколько пиратов было на этом празднике?
Решить задачу
Решать задачи по математике для 2 класса
Познакомьтесь с форматом курса “Математическое мышление”.
Пройдите сюжетную игру и решите три математические задачи!
Решать задачи
В Умназии дети развивают логическое мышление, решая увлекательные сюжетные задачи по математике
Продуманная программа
Курсы математического мышления разработаны на базе множества источников, экспертизы методистов и педагогов, разделены на 10 тем с теорией и игровыми заданиями с объяснением
Увлекательные задания
Ребенок решает сюжетные игровые задачи по математике для изучения новых тем и закрепления пройденного по каждому курсу.
Никакой скуки! Ни одно задание не повторяется!
Дипломы и награды
В конце каждого курса ребенок решает тест или проходит игру, получая сертификат в случае успешного выполнения. Вы будете уверены в его знаниях!
Решение задач по математике во 2 классе
Во втором классе дети начинают учить таблицу умножения и получают первые оценки по итогам уроков и выполнения домашних заданий. Ученикам впервые приходится запоминать определенный объем информации.
Но зубрежка без логики не имеет смысла: заученные наизусть цифры и параграфы быстро забываются. Интерактивные сюжетные задания по математике помогут развить логическое мышление, научат ребенка анализировать и структурировать материал.
Купите курс математики для детей со скидкой 40 % уже сейчас
Задачи математики для 2 класс
Описание
Помогает вам практиковаться и улучшать свои математические навыки.
Веселитесь, решая задачи. Все задачи в вашем распоряжении без дополнительной оплаты.
Более 500 математических проблем для второго класса с разной сложностью.
Все категории задач бесплатны. Если вы оцениваете нашу работу или хотите прекратить рекламу, вы можете сделать это, нажав кнопку «Остановить рекламу». Таким образом, мы сможем добавить новые задачи.
Приложение содержит:
+ Сложение
+ Вычитание
+ Умножение
+ Сплит
+ Пропущенные номера подряд
+ Текстовые задачи
+ Часы
+ Умножение, сложение и вычитание
Задачи делятся на категории сложности.
Языки:
Болгарский, русский, английский, испанский, немецкий, французский, итальянский, польский, турецкий, китайский (традиционный), китайский (упрощенный), хинди, португальский, украинский, индонезийский, японский, вьетнамский, иврит, греческий, голландский, чешский, корейский, Норвежский, арабский, венгерский, румынский, шведский, тайский, малайский, датский.
По вопросам и комментариям: ios@uponex.
com
Используются следующие ресурсы: http://www.freepik.com”>Designed by brgfx / Freepik
Версия 3.4
New content
Bug fixes
Оценки и отзывы
Оценок: 234
Разработчик Kalin M указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.
Данные, используемые для отслеживания информации
Следующие данные могут использоваться для отслеживания информации о пользователе в приложениях и на сайтах, принадлежащих другим компаниям:
- Геопозиция
- Идентификаторы
- Данные об использовании
- Диагностика
Связанные с пользователем данные
Может вестись сбор следующих данных, которые связаны с личностью пользователя:
- Геопозиция
- Идентификаторы
- Данные об использовании
- Диагностика
Не связанные с пользователем данные
Может вестись сбор следующих данных, которые не связаны с личностью пользователя:
Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов.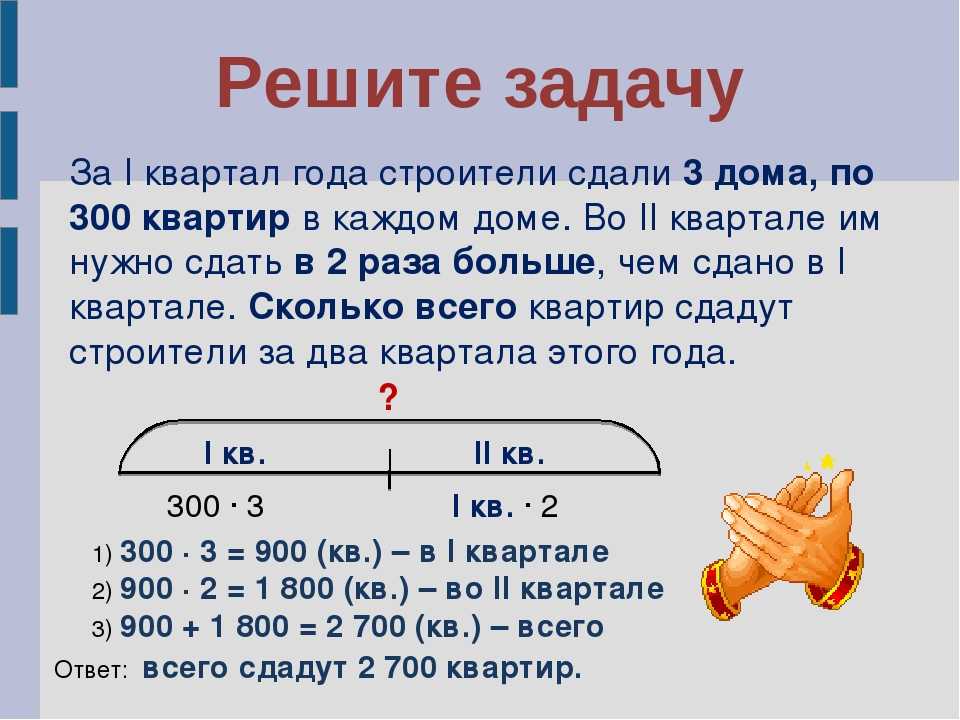
Подробнее
Информация
- Провайдер
- Kalin M
- Размер
- 37,9 МБ
- Категория
- Образование
- Возраст
- 4+
- Copyright
- © Ina Mihaleva
- Цена
- Бесплатно
- Поддержка приложения
- Политика конфиденциальности
Другие приложения этого разработчика
Вам может понравиться
Две задачи на неделю от 9 до 99 лет
от 9 до 99 лет
Поможем расшевелить мозги и поддерживать их в тонусе с помощью математических задач
0 ₽
3280 ₽
бесплатно
Записаться на курс
Когда
Круглый год
Идет набор
Продолжительность
• 10 недель
• записаться на курс можно в любое время
Формат
• задание на онлайн-платформе
• видео с разборами заданий
• проверка преподавателем (опционально)
• видео с теорией и объяснениями
Когда
Круглый год
Идет набор
Продолжительность
• 10 недель
• записаться на курс можно в любое время
Формат
• задание на онлайн-платформе
• видео с разборами заданий
• проверка преподавателем (опционально)
• видео с теорией и объяснениями
Что дает курс
Пробуждает интерес к математике
Курс помогает внести в жизнь математику, показывает ее красоту и вызывает интерес к ней.
Поддерживает мозг в тонусе
Это возможность расшевелить свой мозг, развить логику и воображение в легком формате — 10-15 минут в неделю найдутся у каждого.
Помогает провести время вместе
Надеемся, что этот курс станет поводом для совместного досуга всей семьи. Присоединяйтесь! Будет интересно!
Интересные задачи
Интересное объяснение
Спортивный интерес
У меня получается
Интерес к математике у вашего ребенка
Я заметил, что даже пятилетние дети решают подобные задачи лучше школьников, испорченных натаскиванием, которым они даются легче, чем студентам, подвергшимся зубрежке в университете, но все же превосходящим своих профессоров. Хуже всех решают эти простые задачи нобелевские и философские лауреаты.
Владимир Арнольд
Академик, в предисловии к своему сборнику олимпиадных задач
Как проходят занятия
1
Получаете две интересные олимпиадные задачи
Часто это будут известные красивые задачи, но мы переформулируем их, чтобы нельзя было загуглить.
Одна будет посложнее, а вторая попроще.
2
Решаете задачи в течение недели
По желанию присылаете ответы нам на проверку. Если решение неверное, даем подсказку.
3
Смотрите видеоразбор
Через неделю вам открывается видео с разбором этих задач. Покажем не только, как решать задачи, но и как догадаться до решения. Вместе с разбором открываются задачи на следующую неделю.
4
Выдаем сертификат
Каждый ученик в конце курса получает именной сертификат — он будет доступен по ссылке на нашем сайте. Также сертификат можно самостоятельно распечатать.
Получаете две интересные олимпиадные задачи
Часто это будут известные красивые задачи, но мы переформулируем их, чтобы нельзя было загуглить. Одна будет посложнее, а вторая попроще.
Решаете задачи в течение недели
По желанию присылаете ответы нам на проверку. Если решение неверное, даем подсказку.
Смотрите видеоразбор
Через неделю вам открывается видео с разбором этих задач.
Покажем не только, как решать задачи, но и как догадаться до решения. Вместе с разбором открываются задачи на следующую неделю.
Выдаем сертификат
Каждый ученик в конце курса получает именной сертификат — он будет доступен по ссылке на нашем сайте. Также сертификат можно самостоятельно распечатать.
Выдаем сертификат
Каждый ученик в конце курса получает именной сертификат. Сертификат о прохождении онлайн-курса будет доступен по ссылке на нашем сайте, а также его можно будет самостоятельно распечатать.
Преподаватели курса
У нас преподают выпускники и студенты старших курсов Мехмата МГУ и МФТИ. Курс ведут только организаторы, призёры и победители математических олимпиад.
Места преподавания Основатель и руководитель проекта «Систематика»
Преподаватель математики в выездных лагерях и математических кружках
Записаться на курс
20 задач
10 недель
Доступ на 3 месяца
от 0 ₽
3280 ₽
10000 учеников
уже прошли курс
400 отзывов читать отзывы →
читать отзывы →
Ученики о нас
Нажмите на имя, чтобы посмотреть пройденные учеником курсы
Пустов Всеволод
Россия, г.
Москва и Московская область
Занимается
2 года 10 месяцев
Здравствуйте! Ребята, спасибо от всей души за такой качественный и полезный продукт! Для ребенка (9 лет, 4-й класс) это ЕДИНСТВЕННЫЙ тренинг, в котором он участвует добровольно и с удовольствием, каждый раз с нетерпением ждет результатов, разбора, новых задач! Я, конечно, проверяю, где-то подсказываю, но больше с оформлением, по сути в основном справляется сам, и сложность — та, что надо. Не неподъемная (чтобы не отбить интерес), но и не легкая (было бы бесполезно). Задачи разнообразные, интересные, необычные! Улучшить, на мой взгляд, можно только, если вы не ограничитесь 10 занятиями, а продлите курс!
читать полностьюсвернуть
о курсе Две задачи на неделю
Эмиль Кюльян
Россия, Ростовская область. Пос. Октябрьский
Занимается
3 года 9 месяцев
Здравствуйте! Задачи интересные, спасибо! Пару раз советовался с папой, но в основном решаю сам.
Самое трудное для меня, это письменные ответы. Привык всё решать в уме, а тут ещё надо текст составить. Знаю, что в олимпиадах для более старших классов всегда нужны письменные ответы, поэтому это для меня тренировка.
Также большое спасибо за видео разборы.
читать полностьюсвернуть
о курсе Две задачи на неделю
Николай Суслин
Россия, Зеленоград
Занимается
3 года 6 месяцев
Здравствуйте! Спасибо за такой замечательный курс! Сын стал решать задачи сам!!! Причём, делает это с удовольствием. Некоторые задачи решаем всей семьей и даже с друзьями семьи (монеты и сёстры), а последние две недели Николай все решает сам. Это означает прогресс в развитии его математического мышления. Занятия сын очень любит и ждёт с удовольствием вечера пятницы. Спасибо за Ваш невероятно полезный труд!
читать полностьюсвернуть
о курсе Две задачи на неделю
Светлана
Россия, Москва
Занимается
2 года 8 месяцев
Очень интересно, замечательно помогает снять эмоциональное напряжение.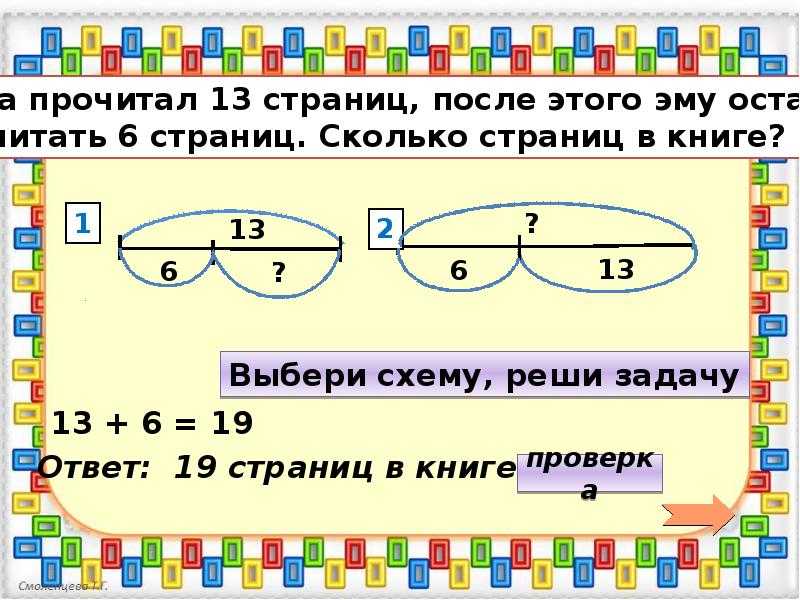
Сложновато, но когда что то получается это такой заряд позитива… Решаю без участия семьи, к сожалению. Мне 43 года и мне очень нравится. Спасибо : )
читать полностьюсвернуть
о курсе Две задачи на неделю
Максим Валавин
Россия, Можайск
Занимается
2 года 6 месяцев
Мне очень понравился курс. Интересные задачи, которые заставляют поработать мозг.
Решение задач у нас происходит так: сначала мы с сыном читаем условие задач, размышляем на эту тему, если решение не приходит сразу, то откладываем решение на следующий день. Как правило, если в течение недели не пришло озарение, то в выходные рисуем, чертим, чтобы понять и найти ответ. Задачи интересные, иногда кажется, что решения нет, а потом оказывается, что ответ на поверхности. На работе тоже всем читаю задачи и предлагаю подумать над решением.
В итоге, я очень рада, что увидела этот курс и решила поучаствовать.
Спасибо авторам курса и разработчикам задач.
читать полностьюсвернуть
о курсе Две задачи на неделю
Добрый день!
Спасибо за ваш труд! Задачи у нас семиклассник решает самостоятельно. Очень полезен разбор задач, который вы предоставляете: как писать решение, как записывать ответ, каким способом легче решить задачу. К сожалению, не везде можно не только узнать эти важные моменты, часто даже нельзя узнать, правильно ли ты решил ту или иную задачу. Хочу также ответить прекрасно придуманные награды за достижения. Казалось бы, мелочь, а как приятно смотреть на свои медальки! Интересные задачи в вашем курсе, понятный и при этом важный видео разбор с наглядным решением, обратная связь — всё это делает ваш курс очень привлекательным для родителей и детей, и вызывает у ребёнка желание и дальше заниматься математикой.
Спасибо вам огромное от всей нашей семьи!!!
читать полностьюсвернуть
о курсе Две задачи на неделю
Inna Guterman
Великобритания
Занимается
3 года 4 месяца
Здравствуйте, большое Вам спасибо за возможность познакомиться с нестандартными задачками.
Мы решаем с сыном, ему 6 лет. Нравится то, что объяснения, которые вы даете, доступны даже 6ти летнему ребенку. Я сама не всегда могу придумать решение, которое будет ему понятно, а у Вас получается! Спасибо большое, что даете возможность проходить курс бесплатно.
читать полностьюсвернуть
о курсе Две задачи на неделю
Victoria
Занимается
2 года 2 месяца
Большое спасибо за этот курс!!!
Очень понятный разбор!
С нетерпением ждём ответов и разборов! Подключили даже соседей! Есть бабушка 80 лет — пока решила все задачи, что давали, правда иногда думает несколько дней, но ключевое слово — решает. И очень ждёт новых!!!
читать полностьюсвернуть
о курсе Две задачи на неделю
Радует, что такие мероприятия проводятся даже в условиях ограничений.
Задания (5 класс) заинтересовали всех членов семьи, Но, главное, ребенок продемонстрировал высшую степень увлеченности и мотивацию. Полина впервые принимала участие в олимпиаде, да и занимается в Систематике совсем недолго, радует полученный опыт и укрепившееся желание продолжать.
читать полностьюсвернуть
об Олимпиаде по математике
Александр Донецков
Россия, г.Москва и Московская область
Занимается
3 года 9 месяцев
Прекрасная организация олимпиады в просторном помещении недалеко от метро, спокойная обстановка, доброжелательное отношение. Задания интересные, ребёнку очень понравилось. Спасибо!
читать полностьюсвернуть
об Олимпиаде по математике
Курс отличный! Спасибо за ваш бесценный энтузиазм и желание дать детям возможность выйти за рамки школьной программы, за ту почву, что позволяет развить интерес к математике, логике и саморазвитию! Спасибо за бесплатный курс! Задачи интересные, достаточно сложные для самостоятельного решения детками первых трех классов.
Задачи хорошо подобраны, интересно составлены, заставляют думать и рассматривать разные варианты решений. В большинстве случаев ребенок решает задачи самостоятельно, но при проверке результатов помогаем искать иные, где возможно и не стандартные, пути решения, предлагаем к решению аналогичные задачи, но с измененными условиями, чтобы ребенок могу увидеть разные грани одного типа задач ))
Очень рады, когда наши предложения и пожелания встречают поддержку и отлично реализовываются (как с электронной формой дипломов) 🙂
Спасибо!
читать полностьюсвернуть
о курсе Две задачи на неделю
Ребенок доволен. После олимпиады смогла рассказать все задания — и те которые решила и те, которые не решила. Это важно для меня. Что она все поняла. Очень часто на олимпиадах много странных названий и дети занимаются тем, что пытаются их понять, вместо решения математической (логической ) составляющей.
Здесь таких вопросов не было — за что Вам спасибо огромное.
читать полностьюсвернуть
об Олимпиаде по математике
Евгений Шуев
Россия, Коломна
Занимается
2 года 6 месяцев
Здравствуйте! Большое спасибо за курс. Начала заниматься сама, но сразу же подключила сына (7 лет), т.к. его очень заинтересовали «мамины» задачки. Сейчас решаем параллельно: некоторые задачки сын решает с уточняющими и наводящими вопросами, а для меня сложностей пока не нашлось. Главное для нас- научиться рассуждать и объяснить решение письменно. Видеоразборы помогают графически представлять решения и выстраивать логику размышлений. Огромное спасибо!
читать полностьюсвернуть
о курсе Две задачи на неделю
Мы очень довольны курсом.
Главное что почерпнули, самоуверенность это для ребенка. Рассказал сыну о математической школе в России, знаменитых математиках. Сын очень гордится тем, что решает задачи повышенного уровня. Это придает мотивации в школе. Пишет что математика его любимый предмет. По математике он в самой продвинутой группе в классе. Online занятия придают колоссальную уверенность в классе! Больше времени сидели вместе.
читать полностьюсвернуть
о курсе Олимпиадной математики
Алеша Боднарчук
В целом мнение хорошее. Есть вопросы в информации об условиях оформления решений. Их надо изложить в более легкой и доступной форме для тех, кто участвует впервые. Опытным итак все понятно. А вот если входишь в дверь впервые…Так мы потеряли на баллах. А в целом все хорошо. Спасибо за отличную и , немаловажно, бесплатную возможность испытать свои силы
читать полностьюсвернуть
об Олимпиаде по математике
Давид Втюрин
Португалия
Занимается
1 год 7 месяцев
Увлекательные занятия для креативных творческих детей.
Любое занятие — это маленькое достижение к поставленной задаче и, как результат, — интересные работы.
читать полностьюсвернуть
Мне очень понравилось участвовать в мероприятии подобного уровня. Задания были трудные, но интересные. Организация на высоком уровне. Я приобрёл колоссальный опыт. Очень переживаю за результат. Всё было замечательно. Буду участвовать сам и рекомендовать своим одноклассникам.
читать полностьюсвернуть
об Олимпиаде по математике
Екатерина Громова
Россия, Санкт-Петербург
Занимается
3 года 10 месяцев
Третий раз участвуем в ваших олимпиадах. Организация хорошая, родителей не держат на улице, что в нашу питерскую погодку очень актуально. Ребёнку понятны правила проведения олимпиады. И, конечно, призы у вас приятные. Для моего ребёнка ваша самая лучшая в рейтинге олимпиад! С нетерпением ждёт следующую!
читать полностьюсвернуть
об Олимпиаде по математике
Игнатович Екатерина
Россия, г.
Санкт-Петербург и Ленинградская область
Занимается
3 года 10 месяцев
Прошло замечательно! Всё в организации было понятно. Сдвигов по времени не было. Остались очень приятные впечатления
читать полностьюсвернуть
об Олимпиаде по математике
Другие занятия Систематики
Курс от студии Артгайка
Архитектура и дизайн для 3-7 классов
Креативное мышление. Рисование. Макетирование. Графика. Бумагопластика. Дизайн. Архитектура
Курс в записи
Научный онлайн-клуб
Эксперименты, исследования и интересные задачи каждую неделю. Для детей от 9 лет и их семей.
Идёт набор
Курс от студии Артгайка
Архитектура и дизайн для 3-7 классов
Архитектура и дизайн для 3-7 классов
Креативное мышление. Рисование. Макетирование. Графика. Бумагопластика. Дизайн. Архитектура
Курс в записи
Научный онлайн-клуб
Научный онлайн-клуб
Эксперименты, исследования и интересные задачи каждую неделю. Для детей от 9 лет и их семей.
Идёт набор
Показать все
Логические и математические задачи с собеседований
Разомнем мозг! В этой статье собраны логические и математические задачи, которые нередко встречаются на собеседованиях и могут попасться вам.
Основные проблемы, которые часто возникают в процессе интервью, не в отсутствии опыта или подготовки. Даже по-настоящему опытный разработчик может легко “споткнуться” о решение какой-нибудь хитро скроенной задачки. Поэтому мы поговорим не о том, как составлять резюме и выгодно презентовать себя. Фокусируемся на решении нетривиальных задач, которые включают в себя решение логического и/или математического характера.
Помните загадку из третьего фильма? Если нет, то вспоминайте, так как этим вопросом любят потчевать в Microsoft.
Задача:
Есть 2 пустых ведра: первое объемом 5 л, второе – 3 л. Как с их помощью отмерить 4 литра воды?
[spoiler title=’Ответ:’ collapse_link=’true’]Сперва наполните пятилитровое ведро. Далее перелейте из него воду в трехлитровое так, чтобы в пятилитровом осталось 2 л воды (полностью заполнив трехлитровое). Вылейте из меньшего ведра всю воду и перелейте в него оставшиеся в большем 2 л. Снова наполните пятилитровое и перелейте один литр в трехлитровое (оно как раз заполнится): так в большем ведре останется 4 л воды.[/spoiler]
Задача:
Есть двадцать баночек с таблетками. Почти во всех таблетки весят по 1 г, и только в одной – по 1,1 г. У нас есть точные весы, с помощью которых нужно определить баночку, каждая таблетка которой весит 1,1 г. Как это сделать, если можно взвесить только 1 раз?
[spoiler title=’Ответ:’ collapse_link=’true’]Давайте абстрагируемся и представим, что у нас 2 баночки, в одной из которых таблетки более тяжелые. Даже если мы поставим их обе на весы, мы ничего не узнаем. Но если мы достанем из одной баночки 1 таблетку, из другой – 2 и положим их на весы – вот тогда-то и откроется истина 🙂 В данном случае вес будет 2,1 или 2,2 (в зависимости от того, сколько каких таблеток мы взяли). Так и определяем нашу баночку.
Вернемся к задаче. Из каждой баночки нужно доставать разное количество таблеток. То есть из первой баночки 1 таблетку, из второй – 2, из третьей – 3 и так далее. Если бы каждая таблетка весила по 1 г, общий вес составил бы 210 г. Но поскольку в одной из баночек таблетки тяжелее, вес будет больше. Для определения нужной баночки просто воспользуемся формулой:
№ тяжелой баночки = (вес - 210) * 10[/spoiler]
Но на этом интересные логические и математические задачи не заканчиваются. Идем дальше!
Задача:
Парень и девушка договорились встретиться ровно в 21:00. Проблема в том, что у обоих часы идут неправильно. У девушки часы спешат на 2 мин. , но она думает, что они на 3 мин. отстают. У парня же часы отстают на 3 мин., но он считает, что они на 2 мин. спешат. Кто из пары опоздает на свидание?
[spoiler title=’Ответ:’ collapse_link=’true’]Ничего сложного: чистая математика. Если у девушки часы спешат, а она думает, что они отстают, то поторопится и придет на 5 мин. раньше. Парень, наоборот, посчитает, что у него еще 5 минут времени в запасе, отчего на эти самые 5 мин. опоздает.[/spoiler]
Задача:
Длина курицы при измерении от головы до хвоста составит 45 см, а вот от хвоста до головы (если измерять вдоль брюха) – 53 см. По статистике плотность курицы на единицу боковой проекции составляет 8 г/см2. Усредненная высота курицы, если мерить ее вдоль боковой поверхности, – 21 см. Сколько весит килограмм курицы?
[spoiler title=’Ответ:’ collapse_link=’true’]Килограмм курицы весит 1 килограмм.[/spoiler]
Да, математические задачи с подвохом тоже встречаются 🙂
Задача:
Книга содержит N страниц, которые пронумерованы стандартно: от 1 до N.
Если сложить количество цифр (не сами числа), что содержатся в каждом номере страницы, выйдет 1095. Так сколько в книге страниц?
[spoiler title=’Ответ:’ collapse_link=’true’]Каждый номер страницы имеет цифру на месте единицы, так что есть N цифр, расположенных на месте единицы. А вот после 9 начинаются двухзначные числа, и нам нужно добавить N-9 цифр. То же самое с трехзначными, которые начинаются после 99: добавляем N-99 цифр. Продолжать нет смысла, так как сумма не предполагает более 999 страниц. Получаем следующую формулу:
N + (N-9) + (N-99) = 1095
Далее просто решаем:
3N - 108 = 1095
3N = 1203
N = 401
Итого 401 страница.[/spoiler]
Задача:
Математические задачи на собеседованиях бывают и довольно простыми, но зачастую только на первый взгляд. Попробуйте в уме разделить 30 на 1/2 и прибавить 10. Каким будет результат?
[spoiler title=’Ответ:’ collapse_link=’true’]Первое решение, которое обычно приходит на ум, ошибочно:
30/2 + 10 = 25
Если мы делим на дробь, ее нужно переворачивать и производить умножение:
30*2 + 10 = 70[/spoiler]
Задача:
Сколько целых чисел в диапазоне 1-1000 вмещают в себя цифру 3? При подсчете нельзя пользоваться компьютером.
[spoiler title=’Ответ:’ collapse_link=’true’]Запомните, что нам нужно учесть просто факт содержания в числе тройки. Если, например, это 33 – мы не считаем цифру 2 раза. В числе должна быть по крайней мере одна тройка, чтобы его учесть. Например, числа в диапазоне 300-399 дают нам сразу 100 чисел. Еще 10 мы получаем от 30-39. То же касается 130-139, 230-239, etc. Десяток этих чисел уже был учтен при подсчете 330-339, так что убираем его и получаем:
100 + 90 = 190
А еще есть группа чисел (их 100), которые заканчиваются на тройку: 2-993. Мы исключаем из нее такие 10 чисел, как 303, 313 … 393 (они учтены ранее). Получаем еще +90 чисел. У 1/10 из этих 90 на месте десяток также расположилась тройка: 33, 133 … 933. Убираем еще 9, оставляя 81 число. Дальше простая математика:
100 + 90 + 81 = 271
А вот более изящное решение данной задачи. Сперва мы считаем, сколько чисел не включает в себя тройку (на каждое из 3-х мест ставится 9 цифр, которые не тройки):
9 * 9 * 9 = 729
1000 - 729 = 271[/spoiler]
Ну что, размялись? Надеемся, вам понравились собранные логические и математические задачи.
Если этого мало, можете заглянуть сюда + ниже вы найдете еще больше задач, специально подобранных Библиотекой программиста 🙂
- Логика в программировании: логические задачи с собеседований
- Тренируй свои мозги или ТОП-15 логических задач
- Спортивное программирование и 5 ресурсов для решения задач
- Задачи с IT-собеседований
10 увлекательных задач от советского математика
12 сентября 2021Отдых
Попробуйте решить головоломки от популяризатора математики Бориса Кордемского, не пользуясь подсказками.
Поделиться
01. Переправа через реку
Небольшой воинский отряд подошёл к реке, через которую необходимо было переправиться. Мост сломан, а река глубока. Как быть? Вдруг офицер замечает у берега двух мальчиков в лодке. Но лодка так мала, что на ней может переправиться только один солдат или только двое мальчиков — не больше! Однако все солдаты переправились через реку именно на этой лодке.
Каким образом?
Показать ответ
Скрыть ответ
2. Сколько деталей?
В токарном цехе завода вытачиваются детали из свинцовых заготовок. Из одной заготовки — деталь. Стружки, получившиеся при выделке шести деталей, можно переплавить и приготовить ещё одну заготовку. Сколько деталей можно сделать таким образом из тридцати шести свинцовых заготовок?
Показать ответ
Скрыть ответ
3. Во время прилива
Недалеко от берега стоит корабль со спущенной на воду верёвочной лестницей вдоль борта. У лестницы десять ступенек; расстояние между ступеньками 30 см. Самая нижняя ступенька касается поверхности воды.
Океан сегодня очень спокоен, но начинается прилив, который поднимает воду за каждый час на 15 см. Через какое время покроется водой третья ступенька верёвочной лесенки?
Показать ответ
Скрыть ответ
4. Девяносто девять
Сколько нужно поставить знаков «плюс» (+) между цифрами числа 987 654 321, чтобы в сумме получилось 99?
Показать ответ
Скрыть ответ
5.
Для Цимлянского гидроузлаВ выполнении срочного заказа по изготовлению измерительных приборов для Цимлянского гидроузла приняла участие бригада в составе опытного бригадира и девяти молодых рабочих.
В течение дня каждый из юных рабочих смонтировал по 15 приборов, а бригадир — на 9 приборов больше, чем в среднем каждый из десяти членов бригады. Сколько всего измерительных приборов было смонтировано бригадой за один рабочий день?
Показать ответ
Скрыть ответ
6. Попробуйте отвесить
В пакете находится 9 кг крупы. Попробуйте при помощи чашечных весов с гирями 50 и 200 г распределить всю крупу по двум пакетам: в один — 2 кг, в другой — 7 кг. При этом разрешается произвести только 3 взвешивания.
Показать ответ
Скрыть ответ
7. Смышлёный малыш
Три брата получили 24 яблока, причём каждому досталось столько яблок, сколько ему было лет три года назад. Самый младший, мальчик очень смышлёный, предложил братьям такой обмен яблоками:
— Я, — сказал он, — оставлю себе только половину имеющихся у меня яблок, а остальные разделю между вами поровну.
После этого пусть средний брат тоже оставит себе половину, а остальные яблоки даст мне и старшему брату поровну, а затем и старший брат пусть оставит себе половину всех имеющихся у него яблок, а остальные разделит между мной и средним братом поровну.
Братья, не подозревая коварства в таком предложении, согласились удовлетворить желание младшего. В результате… у всех оказалось яблок поровну. Сколько же лет было малышу и каждому из остальных братьев?
Показать ответ
Скрыть ответ
8. Раздробить на части
Раздробите 45 на четыре части так, что если к первой части прибавить 2, от второй отнять 2, третью умножить на 2, а четвёртую разделить на 2, то все результаты будут равными. Сумеете сделать?
Показать ответ
Скрыть ответ
9. Посадка деревьев
Пятиклассникам и шестиклассникам было поручено посадить деревья по обе стороны улицы по равному количеству на каждой стороне.
Чтобы не ударить лицом в грязь перед шестиклассниками, пятиклассники вышли на работу пораньше и успели посадить 5 деревьев, пока пришли старшие ребята, но оказалось, что они сажали деревья не на своей стороне.
Пришлось пятиклассникам идти на свою сторону и вновь начинать работу. Шестиклассники, конечно, справились с задачей раньше. Тогда учитель предложил:
— Пойдём, ребята, поможем пятиклассникам!
Все согласились. Перешли на другую сторону улицы, посадили 5 деревьев, отдали, значит, долг, да ещё успели посадить 5 деревьев, и вся работа была закончена.
— Хоть вы пришли раньше нас, а всё-таки мы вас обогнали, — посмеялся один шестиклассник, обращаясь к младшим ребятам.
— Подумаешь, обогнали! На 5 деревьев только, — возразил кто-то.
— Нет, не на 5, а на 10, — зашумели шестиклассники.
Спор разгорался. Одни настаивают на том, что на 5, другие пытаются как-то доказать, что на 10. Кто же прав?
Показать ответ
Скрыть ответ
10. Четыре теплохода
В порту пришвартовались 4 теплохода. В полдень 2 января они одновременно покинули порт. Известно, что первый теплоход возвращается в этот порт через каждые 4 недели, второй — через каждые 8 недель, третий — через 12 недель, а четвёртый — через 16 недель.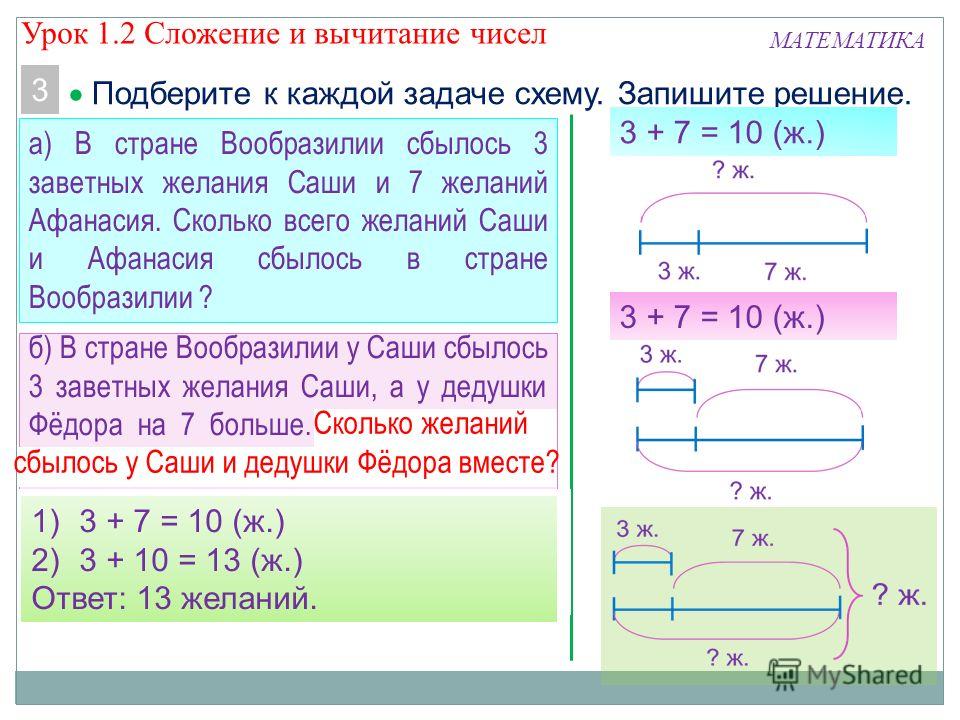
Когда в первый раз теплоходы снова сойдутся все вместе в этом порту?
Показать ответ
Скрыть ответ
Задачи для этой подборки взяты из сборника «Математическая смекалка» Бориса Кордемского, который выходил в издательстве «Альпина Паблишер».
Читайте также 🔥
- 15 занимательных задач для тренировки ума и сообразительности
- 11 хитрых советских головоломок для проверки логики и сообразительности
- 5 задач, которые предлагают решить на собеседованиях в Google и других компаниях
Решатель математических задач | Решение задач Word
Ниже представлен решатель математических задач, который позволяет вам вводить самые разные математические задачи и дает окончательный ответ бесплатно.
Этот калькулятор также может помочь решить упрощенные математические задачи. Нажмите на ответ, чтобы зарегистрироваться и посмотреть пошаговое решение!
Math Solver
Отказ от ответственности: IntMath.com не гарантирует точность результатов. Решатель задач предоставлен Mathway.
Темы решения проблем
Математический калькулятор может решить ряд задач по широкому кругу предметов, не только строго по математике. Ниже приведен список доступных предметов на выбор. Вы можете переключить тему калькулятора, щелкнув или коснувшись меню в верхнем левом углу калькулятора.
- Базовая математика
- Предварительная алгебра
- Алгебра
- Тригонометрия
- Предварительный расчет
- Исчисление
- Статистика
- Конечная математика
- Линейная алгебра
- Химия
- Физика
- Графики
Вот примеры математических задач по каждому предмету, которые можно ввести в калькулятор и решить.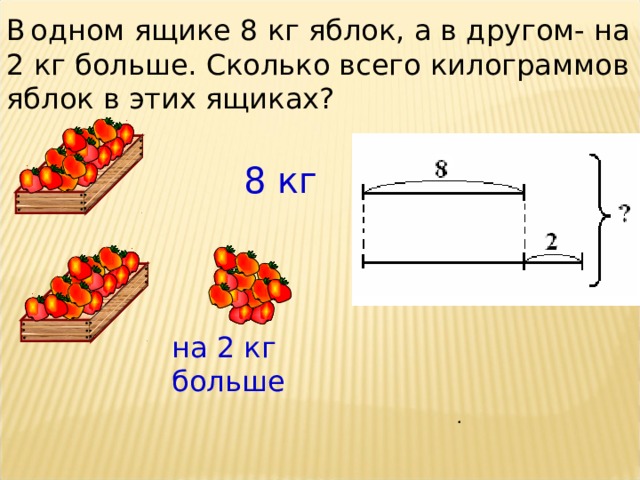
Этот список постоянно пополняется по мере добавления функциональности калькулятору.
Базовая математика
Ниже приведены примеры задач, которые можно решить с помощью Basic Math.
- Длинная арифметика
- Рациональные числа
- Операции с дробями
- Соотношения, пропорции, проценты
- Измерение, площадь и объем
- Факторы, дроби и показатели степени
- Преобразование единиц измерения
- Измерение данных и статистика
- Точки и сегменты линии
Предварительная алгебра
Ниже приведены примеры задач, которые можно решить в Pre-Algebra.
- Переменные, выражения и целые числа
- Упрощение и оценка выражений
- Решение уравнений
- Многошаговые уравнения и неравенства
- Факторы, дроби и показатели степени
- Операции с дробями
- Рациональные числа
- Соотношения, пропорции и проценты
- Точки и сегменты линии
- Линейные уравнения и неравенства
- Преобразование единиц измерения
- Измерение, площадь и объем
- Измерение данных и статистика
Алгебра
Ниже приведены примеры задач, которые можно решить с помощью алгебраической математики.
- Понятия и выражения алгебры
- Точки, линии и сегменты линий
- Упрощающие многочлены
- Факторные полиномы
- Линейные уравнения
- Выражения и уравнения абсолютных значений
- Основные выражения и уравнения
- Системы уравнений
- Квадратные уравнения
- Неравенства
- Отношения
- Функции
- Комплексные числа и векторный анализ
- Логарифмические выражения и уравнения
- Экспоненциальные выражения и уравнения
- Матрицы
- Конические секции
- Векторы
- Векторные пространства
- Трехмерная система координат
- Собственные значения и собственные векторы
- Линейные преобразования
- Наборы номеров
- Таблицы
- Аналитическая геометрия
Тригонометрия
Ниже приведены примеры задач, которые можно решить с помощью тригонометрии.
- Обзор понятий и выражений алгебры
- Тригонометрия прямоугольного треугольника
- Радианное измерение и круговые функции
- Графики тригонометрических функций
- Упрощение тригонометрических выражений
- Проверка тригонометрических тождеств
- Решение тригонометрических уравнений
- Комплексные числа
- Аналитическая геометрия в полярных координатах
- Экспоненциальные и логарифмические функции
- Векторная арифметика
- Векторы
Предварительный расчет
Ниже приведены примеры задач, которые можно решить в Precalculus.
- Понятия и выражения алгебры
- Отношения
- Функции
- Операции над функциями
- Точки, линии и сегменты линий
- Выражения и уравнения абсолютных значений
- Рациональные выражения и уравнения
- Полиномиальные и рациональные функции
- Факторные полиномы
- Конические секции
- Экспоненциальные и логарифмические функции
- Тригонометрия
- Аналитическая тригонометрия
- Неравенства
- Линейные уравнения
- Системы уравнений
- Квадратные уравнения
- Матрицы
- Последовательности и серии
- Аналитическая геометрия в прямоугольных координатах
- Аналитическая геометрия в полярных координатах
- Пределы и введение в исчисление
- Векторов
- Наборы номеров
Исчисление
Ниже приведены примеры задач, которые можно решить в исчислении.
- Понятия и выражения алгебры
- Функции
- Операции над функциями
- Полиномиальные и рациональные функции
- Экспоненциальные и логарифмические функции
- Последовательности и серии
- Оценка пределов
- Производные
- Применение дифференциации
- Интегралы
- Приложения интеграции
- Методы интеграции
- Параметрические уравнения и полярные координаты
- Дифференциальные уравнения
Статистика
Ниже приведены примеры задач, которые можно решить в статистике.
- Обзор алгебры
- Средняя описательная статистика
- Статистика дисперсии
- Вероятность
- Распределения вероятностей
- Распределение частот
- Нормальные распределения
- т-распределения
- Проверка гипотез
- Оценка и размер выборки
- Корреляция и регрессия
Конечная математика
Ниже приведены примеры задач, которые можно решить в рамках конечной математики.
- Полиномы и выражения
- Соотношения, пропорции и проценты
- Уравнения и неравенства
- Линейные функции и точки
- Функции
- Отношения
- Матрицы
- Системы линейных уравнений
- Математика финансов
- Средняя описательная статистика
- Статистика дисперсии
- Статистические распределения
- Распределение частот
- Нормальные распределения
- т-распределения
- Проверка гипотез
- Оценка и размер выборки
- Корреляция и регрессия
- Векторы
Линейная алгебра
Ниже приведены примеры задач, которые можно решить с помощью линейной алгебры.
- Введение в матрицы
- Комплексные числа
- Матрицы
- Системы линейных уравнений
- Векторы
- Линейная независимость и комбинации
- векторных пробелов/li>
- Собственные значения и собственные векторы
- Линейные преобразования
- Наборы номеров
Химия
Ниже приведены примеры задач, которые можно решить в рамках программы «Химия».
- Преобразование единиц измерения
- Атомная структура
- Молекулы и соединения
- Химические уравнения и реакции
- Поведение газов
- Растворы и концентрации
Физика
Ниже приведены примеры задач, которые можно решить в рамках физики.
- Статическое равновесие
- Динамическое равновесие
- Уравнения кинематики
- Электричество
- Энергия
- Волны
- Термодинамика
Графики
Ниже приведены примеры задач, которые можно решить с помощью Graphing.
- Пошаговая графика
- Точки, линии и сегменты линий
- Линейные уравнения и функции
- Конические секции
- Полярные уравнения
Ознакомьтесь с этими 50 задачами дня по математике для второклассников
Начните свой ежедневный урок математики со словесной задачи дня по математике — это отличный способ подготовить почву для обучения.
Все мы знаем, что юным ученикам трудно понять текстовые задачи, даже если часть задачи, связанная с математическими операциями, является базовой. Включайте эти задачи по математике для второго класса один день за раз в начале вашего математического блока, чтобы укрепить уверенность, навыки критического мышления и обучающееся сообщество!
Рассматриваемые темы включают сложение, вычитание, умножение, четные/нечетные числа, трехзначные числа и время. Все, что вам нужно сделать, это опубликовать одну из этих математических задач второго класса на доске или экране проектора. Тогда пусть дети взять его оттуда!
Хотите весь этот набор задач по математике для второго класса в одном простом документе? Получите бесплатный пакет PowerPoint, отправив сообщение электронной почты здесь.
1. У Трея есть 5 мягких игрушек. Он получает еще 4 на свой день рождения. Сколько мягких игрушек у него всего?
2. Стефани приносит пончики, чтобы раздать ее одноклассникам на ее день рождения.
Она приносит 8 порошковых пончиков, 8 глазированных пончиков и 10 шоколадных пончиков. Сколько всего пончиков она принесла?3. Сара идет в библиотеку. Ей разрешено просмотреть 10 книг. Она выбирает 5 иллюстрированных книг и 3 книги с главами. Сколько еще книг она может выбрать?
4. Дэвид сажает 8 семян ананаса, 5 семян клубники и 2 семена черники. Сколько всего семян он посадил?
5. У Пейдж есть 10 мелков. У Майка на 6 мелков больше, чем у Пейдж. У Джона 9 мелков. Сколько всего у них карандашей?
6. В коллекции Джеффа 21 шарик. В коллекции Эдди 39 шариков. Сколько шариков у них всего?
7. Вики идет в зоопарк и видит 8 фламинго. Затем она видит 15 уток, прежде чем увидеть 22 ибиса. Сколько всего птиц она увидела?
8. Джошуа продает 26 билетов на школьный спектакль. Нина продает 39билеты на школьный спектакль. Сколько всего билетов было продано?
9. Второклассник отправляется на экскурсию в океанариум.
В школе 7 учителей, 62 девочки и 59 мальчиков. Сколько всего людей отправится на экскурсию?10. Несколько яблок в яблоневом саду. Собрано 38 яблок. Сейчас осталось 52. Сколько яблок было в начале?
11. В понедельник Блейк проплыл 18 кругов. Во вторник он проплыл 22 круга. В среду он проплыл 27 кругов. Сколько кругов он проплыл всего?
12. Энцио читает 25 минут в понедельник. Во вторник он читает 33 минуты. Он читает 35 минут в среду. Сколько всего минут он читает?
13. У Даны есть 15 вкусных печенек. Он ест немного печенья. У Даны осталось 7 печений. Сколько печенья съела Дана?
14. У Эрика было 12 игрушечных машинок. Он подарил 5 машин своему другу Даррену. Сколько игрушечных машинок у него сейчас?
15. Каролин увидела 15 красивых птиц на дереве. Некоторые птицы улетели. Теперь на дереве 4 птицы. Сколько птиц улетело?
16. Кристина продала 32 коробки печенья для девочек-скаутов.
Леа продала 44 коробки печенья для девочек-скаутов. На сколько больше коробок продала Лея, чем Кристина?17. У Мими на 23 мелка больше, чем фломастеров. У нее 15 маркеров. Сколько у неё карандашей?
18. У Кэрри 36 конфет. Она дает 13 штук Томми. Сколько конфет осталось у Кэрри?
19. У Далии на полке 28 кукол. Она перемещает некоторых в свой кукольный домик. Сейчас на полке 15 кукол. Сколько она переместилась на кровать?
20. У Джерри 12 футбольных мячей. У Боба было 17 футбольных мячей, но он отдал 8 из них Филу. Сколько теннисных мячей сейчас у Джерри и Боба?
21. У Джона 54 конфеты. Он съедает 7 штук в понедельник. Во вторник он съедает 11 штук. В среду он раздает 17 штук друзьям. Сколько конфет у него осталось?
22. У Марии 29 шариков. У Сэма 56 шариков. У Рэйчел 67 шариков. На сколько шариков больше у Рэйчел, чем у Эллы?
23. Стивен покупает 52 клубники.
Он съедает 12 из них на закуску. Вечером того же дня он съедает 15 из них на десерт. Сколько клубники осталось?24. Диана собирает стикеры. У нее 48 наклеек в альбоме. Она покупает еще 27 наклеек. Затем она дает 18 наклеек своей подруге Джуди. Сколько наклеек у нее сейчас?
25. В коллекции Хантера 47 бейсбольных карточек. В коллекции Райана 39 карт. Сколько еще карт у Хантера?
26. В поезде 95 человек. На первой остановке вышли 19 человек. На второй остановке вышли 24 человека. Сколько человек еще в поезде?
27. Дэрил любит собирать комиксы с супергероями. У него на столе 5 комиксов. У него в рюкзаке 3 комикса. У Дэрила четное или нечетное количество комиксов?
28. Ким собирает на пляже особые ракушки. Она кладет 8 ракушек в ведро. В банку она кладет еще 7 ракушек. У Ким четное или нечетное количество ракушек?
29. Лесли сажает красный перец в своем саду. В ее саду 6 рядов по 5 перцев в каждом ряду.
Сколько помидоров в ее саду?30. Марк помещает 16 фотографий в альбом. Если в каждом столбце по 4 карточки, сколько столбцов?
31. Мисс Сандерс хотела угостить свой класс пиццей. В каждом пироге пиццы 8 кусочков пиццы. Если у нее 29 учеников, сколько пицц ей нужно заказать?
32. Четверо друзей хотят разделить тыквенный пирог. Как они могли разрезать пирог, чтобы каждый друг получил равную долю? Нарисуйте картинку, чтобы показать свое мышление.
33. Выберите трехзначное число. Нарисуйте модели, чтобы показать сотни, десятки и единицы, чтобы объяснить свое мышление.
34. Лиам думает о трехзначном числе. В нем 7 сотен, 4 десятка и 6 единиц. Какой у него номер? Нарисуйте модель, чтобы объяснить свое мышление.
35. В коллекции Юлианы 257 наклеек. Она хочет исследовать это число дальше. Сначала она рисует модель числа, рисуя блоки с основанием десять. Затем она выписывает его в развернутом виде.
Наконец, она записывает это в словесной форме. Покажите, как она использует все три способа, чтобы объяснить 257.36. Калеб пропускает счет. Он пишет 160, 165 и 170 на доске. Каковы следующие 5 чисел в его образце?
37. Футбольная команда Florida Gators выиграла свои последние 4 футбольных матча. Они набрали 25 очков в первой игре, 58 очков во второй игре, 33 очка в третьей игре и 77 очков в четвертой игре. Сколько очков они набрали всего?
38. Нолан коллекционирует карты покемонов. В его коллекции 402 карты. Он дает 25 карт своей подруге Шарлотте. Затем он дает 32 карты своей подруге Марии. Сколько карт у него осталось?
39. В школе распродажа выпечки. Мама Домини приносит 82 кекса. Папа Амелии приносит 75 печенек. Мама Лоренцо приносит 100 пирожных. Сколько предметов на распродаже выпечки всего?
40. Кристелла читает книгу «Волшебный домик на дереве» для своего отчета о книге. Она читает 24 страницы в понедельник.
Она читает 39страницы во вторник. Она читает 37 страниц в среду. Сколько всего страниц она прочитала?41. Эрика читает «Джеймс и гигантский персик». В книге 144 страницы. Она читает 30 страниц в понедельник. Она читает 42 страницы во вторник. Сколько страниц у нее осталось в книге?
42. Алана и ее семья собираются в Disney World на ее день рождения. Это в 425 милях от ее дома. Ее отец проезжает 127 миль, прежде чем они останавливаются перекусить. Он проезжает еще 233 мили, прежде чем они останавливаются на обед. Сколько еще миль им осталось до прибытия в Диснейуорлд?
43. Школьная группа дает праздничный концерт. Пегги продает 75 билетов. Диана продает 101 билет. Джуди продает 135 билетов. Сколько билетов они продали всего?
44. Класс мистера Аксельрода отслеживает, сколько книжек с картинками они читают каждый месяц. В марте они прочитали 329 книг. В апреле они прочитали 471 книгу. В мае они прочитали 450 книг.
Сколько всего книг они прочитали?45. За выходные музей посетило 792 человека. В субботу музей посетили 382 человека. Сколько человек посетило музей в воскресенье?
46. Луна продает экземпляры школьной газеты. Есть 500 экземпляров. В понедельник она продала 122 копии. Во вторник она продала 198 копий. Сколько копий осталось?
47. Второклассники собираются на экскурсию на спектакль. В классе госпожи Анастасио 29 учеников. В классе мистера Гордона учится 31 ученик. В классе мистера Фишмана 33 ученика. В классе мисс МакКоннелл 30 учеников. Сколько всего студентов отправится на экскурсию?
48. Карлос едет в Нью-Йорк в отпуск. Его самолет вылетает из аэропорта в 14:30. Полет длится 3 часа 30 минут. Во сколько он приземлится в Нью-Йорке?
49. Хуанита смотрит фильм «Гарри Поттер и Философский камень». Она начинает фильм в 5 часов вечера. Продолжительность фильма 2 часа 32 минуты. Во сколько заканчивается фильм?
50.
Гарри, Рон и Гермиона едут в Хогвартс. Поезд отправляется с вокзала в Лондоне в 9 утра. Дорога до Хогвартса занимает 7 часов. Во сколько они прибывают в Хогвартс?Наслаждаетесь математическими задачками второго класса? Посетите наш центр второго уровня, чтобы получить еще больше ресурсов.
Получите версию этих текстовых задач в формате PPT.
Практические вопросы по математике 2
1. Каждый из двух углов треугольника равен 70°. Чему равен третий угол в градусах?
- 40°
- 80°
- 100°
- 120°
- 140°
2. Если Джеку нужно 2 ½ пинты сливок, чтобы приготовить десерт. Сколько пинт ему понадобится, чтобы приготовить 3 десерта?
- 2 ½
- 3
- 4
- 5
- 7 ½
3. Дисконтный магазин снимает 50% от розничной цены письменного стола. На праздничную распродажу в магазине действует дополнительная скидка 20% на всю мебель. Розничная цена стола составляла 320 долларов.
Сколько стоит стол во время праздничной распродажи?- 107 долларов
- 114 долларов
- 128 долларов
- 136 долларов
- 192 долларов
4. Какое место отдыха чаще всего посещают студенты?
- Пляж
- Исторические места
- Круизы
- Горы
- Другое
5. Если 500 учащихся посещают среднюю школу Вашингтона, сколько поедет в горы на каникулы?
- 25
- 60
- 75
- 100
- 125
6. Если ¼ чайной ложки составляет 1 мл, то сколько в 6 миллилитрах чайной ложки?
- 10 мл
- 12,5 мл
- 15 мл
- 20 мл
- 24 мл
7. Какой из следующих графиков является правильным для x≥3 или x≤ -2?
8. Масштаб на карте показывает, что каждые ¼ дюйма соответствуют 20 милям. Если два города находятся на расстоянии 3 ½ дюйма друг от друга, сколько миль на самом деле разделяет эти два города?
- 14 миль
- 20 миль
- 125 миль
- 230 миль
- 280 миль
клумба быть, если L и W представляют собой исходные размеры клумбы в длину и ширину?
- 2 LW
- 2 (L+W)
- 2L +2W
- (L+2) (W+2)
- LW/2
10.
У Мелинды погас свет. У нее в ящике 3 пары красных носков, 2 пары черных носков и 5 пар белых носков. Какое минимальное количество пар она должна вынуть из ящика, чтобы у нее была пара каждого цвета?- 3
- 5
- 7
- 9
- 10
11. Какие из следующих дробей правильно расположены от наименьшей по значению к наибольшей по значению?
- 1 / 4 , 17 / 25 , 3 / 4 , 11 / 16
- 17 / 25 , 1 / 4 , 11 / 16 , 3 / 4
- 1 / 4 , 17 / 25 , 11 / 16 , 3 / 4
- 1 / 4 , 17 / 25 , 3 / 4 , 11 / 16
- 3 / 4 , 17 / 25 , 11 / 16 , 1 / 4
12.
Каково среднее математическое число дней в типичном году, количество дней в неделе и количество часов в сутках?- 100
- 115
- 132
- 158
- 224
13. 1,75 x 10
5 =- 175 000
- 17 500
- 1,750
- 0.00175
- 0,000175
- 0.-HORSHORVER. Джордж использовал 2800 киловатт-часов в апреле, 3200 киловатт-часов в мае и 3600 киловатт-часов в июне. Какова была его средняя стоимость электроэнергии за 3 месяца?
- 72 долл. США
- 88 долл. США
- 96 долл. США
- 102 долл. США
- 113 долл. США
15. На карте
1 / 3 дюйм равен 15 милям. Расстояние между двумя городами на карте равно 3 2/3 дюйма. Сколько миль на самом деле между двумя городами?- 11
- 16
- 88
- 132
- 165
16. Джеймс инвестировал 4000 долларов под 5% годовых; сколько времени потребуется ему, чтобы заработать 200 долларов в виде простых процентов?
- 1 год
- 2 года
- 3 года
- 4 года
- 5 лет
17.
Джон платит 650 долларов налога на недвижимость. Какова оценочная стоимость его имущества, если налог на имущество составляет 1,2% от оценочной стоимости?- $ 28 800,27
- $ 41,328,90
- $ 43,768,99
- $ 54,166,67
- $ 64,333,39 9065 3
- $ 64 333,39 9065 3
- $ 64,333,39 9065 3 40015 $ 64,333,39. Какова обычная цена?
- 26 долларов
- 28 долларов
- 30 долларов
- 32 доллара
- 43 $
- 550,75 $
- 562,50 $
- 573,75 $
- 637,50 $
- 675,00 $
- 160
- 170
- 180
- 190
- 220
- 10
- 15
- 20
- 25
- 30
- Произведение двух отрицательных чисел отрицательно.
- Произведение одного отрицательного и одного положительного числа является положительным.
- При делении положительного числа на отрицательное число результат отрицательный.
- При делении отрицательного числа на положительное число результат положительный.
- При делении отрицательного числа на отрицательное число результат отрицательный.
- 1 / 4
- 2 / 9
- 1 / 5 9776 1 / 5
- 7 / 5
- / 5
- / 5
- / 5 / 5
- 9 1 / 5 1 /0777 / 8
- 2 / 7
- 23 / 5
- 7 / 5
- 12 / 20
- 20 / 12
- 12 / 5
- 10
- 12
- 13
- 14
- 15
- 6 часов 15 минут
- 6 часов 35 минут
- 7 часов 5 минут
- 7 часов 15 минут
- 7 часов и 35 минут
- 2 / 3
- 3 / 8
- 4 / 5
- 3 / 4
- 7 / 16
- 0,53935
- 0,053935
- 0,0053935
- 10,195652
- 101,95652
- 32:24
- 4:3
- 3:4
- 4:7
- 3:7
- 5 / 12
- 10 / 6
- 20 / 30
- 15 / 24
- 15 / 18
- 180 долларов
- 225 долларов
- 245 долларов
- 280 долларов
- 310 долларов
- 1998 и 1999
- 1998 и 2000
- 1998 и 2001
- 1999 и 2000
- 2000 и 2001
- 1998
- 1999
- 2000
- 2001
- Такого не происходило в течение 4 лет.
- 9 000
- 9 375
- 9 545
- 9 770
- 9,995
- 50%
- 100%
- 150%
- 200%
- 250%
- 10
- 15
- 20
- 25
- 30
- 2
- 5
- 10
- 16
- 17
- 40 °
- 50 °
- 60 °
- 65 °
- 75 °
- 3
- 15
- 17
- 35
- 42
- $ 3,75
- $ 5,45
- $ 6,34
- $ 7,77
- $ 8,12
- 1 Вопросы по математике для детского сада
- 2 Задачи на сложение и вычитание для детского сада:
- 3 Забавные математические вопросы для первого класса
- 4 Математические вопросы для второго класса
- post являются партнерскими ссылками. Это означает, что если вы нажмете на ссылку и купите товар, я получу небольшую комиссию без каких-либо дополнительных затрат для вас. Все мнения остаются моими.
Вы ищете забавные математические вопросы, чтобы задать своим детям? Если да, то этот список — отличный способ начать. Здесь вы найдете сочетание текстовых задач, головоломок и математических рассуждений для детского сада, первого и второго класса.
Дети привыкли думать о математическом вопросе как об уловке – почти невозможно найти правильный ответ или решить математическое уравнение так, как от них ожидают.
Но с новой волной математических стандартов учителя находят творческий способ поощрять и поддерживать детей в решении сложных задач.Вопросы по математике для детского сада
Основные математические навыки начинаются до детского сада. Сортировка и счет вместе с детьми — лучший способ начать обучение основам понимания чисел. В раннем детском саду маленькие дети находят математику развлечением. Типичная учебная программа детского сада начинается с классических игр для обучения фигурам, расположению слов, простой последовательности чисел и числам до 5. Затем, во второй половине года, учащиеся детсадовского возраста начинают учиться решать задачи на сложение и вычитание.
Вопросы по математике для детского сада
Вот несколько примеров вопросов, используемых в моих беседах по математике для детского сада в первой половине учебного года.
Эти математические беседы — идеальный способ вовлечь детей в хорошие разговоры о любой математической концепции.- Сколько мелков помещается в коробку?
- Сколько колес у автобуса?
- Оцените, сколько салфеток в коробке.
- Сколько книг вы можете поместить в свой рюкзак?
- Осмотрите комнату. Сколько стульев вы видите?
- У пряничного человечка два глаза. Если бы было 4 пряничных человечка, сколько было бы глаз?
- Назовите мне число больше 4 и меньше 11.
- Сколько цветов в радуге?
- 3 друга играют под дождем. Сколько резиновых сапог им нужно?
- Сколько у тебя сегодня карманов?
- Что бы вы предпочли использовать для измерения елки: моток ленты или леденец? Почему?
Ознакомьтесь с ежемесячными тематическими докладами по математике, ЗДЕСЬ
Задания на сложение и вычитание для детского сада:
Ниже приведены несколько простых задач для урока математики, чтобы повторить основные факты математики.
- У Ноя восемь штук, а у Элайджи — две. Сколько pop-it у них всего вместе?
- На столе лежат три красных и три зеленых шарика. Сколько шариков на столе?
- Есть четыре маленьких зефира и два больших зефира. Сколько всего зефира вместе?
- У Бена четыре персика. У Сары три персика. Сколько персиков у них всего?
- У Уильяма есть три апельсина. У Майкла на четыре апельсина больше, чем у Уильяма. Сколько апельсинов у Майкла?
- У Джеймса три шарика. Джеймс дает Мейсону два шарика. Сколько шариков осталось у Джеймса?
- Уильям такие же игрушки, как и Бобби. У Бобби есть две игрушки. Сколько игрушек у Уильяма?
- Четыре шарика в корзине. Три красные, а остальные зеленые. Сколько шариков зеленого цвета?
- У Бена 8 мелков. Он дает 7 мелков Миа. Сколько мелков осталось у Бена?
- У Брэда семь камней. У Ноя на пять камней меньше, чем у Брэда. Сколько камней у Ноя?
- На столе две пиццы. Если четверо детей съедят пиццу, сколько останется? Откуда вы знаете?
- В корзине девять мячей. Из корзины достают три мяча. Сколько мячей осталось в корзине?
- 19 персиков на столе. Затем Эллисон врезается в стол, и с него падают шесть персиков. Сколько персиков осталось на столе?
Забавные математические вопросы для первоклассников
В 1-м классе учитель математики повторит основные математические факты, такие как определение и запись чисел до 20, подсчет наборов объектов, на один больше, на один меньше и десятки кадров. В течение всего года можно использовать простые математические загадки и веселые игры в качестве увлекательного способа обучения математике.
Вот образцы открытых карточек с математическими беседами из комплекта «Разговоры о математике для первоклассников». Они идеально подходят для детей, у которых есть трудности с навыками решения проблем. Когда они слышат, как их сверстники выражают свои стратегии, это дает им стратегии, не чувствуя, что им нужно решать сложные математические задачи.
Наиболее важной частью обучения математике в начальной школе является поощрение критического мышления, а не традиционного мышления «только один способ решить проблему».
Вопросы по математике для первоклассников
Вот несколько примеров из сборника «Разговоры по математике для первоклассников». Опять же, это открытые математические вопросы, чтобы больше сосредоточиться на решении проблем и критическом мышлении, а не на правильном/неправильном ответе.
- Пришло время поиграть в настольную игру. Какой спиннер тебе нужен? Тот, у которого 2 номера, или спиннер с 6 номерами. Почему?
- Для постройки чего требуется больше снега: одного иглу или 20 снежков?
- Какое число больше 50 и меньше 62?
- Что вы заметили в этой последовательности чисел: 15, 20, 25, 30, 35
- У нас есть коробка с 25 мелками. Это четное или нечетное?
- Что займет меньше времени: уборка комнаты или чтение книги?
- Какие фигуры вы видите в классе?
1-й класс Дополнительные задания:
- В холодильнике 4 стопки шоколадных пудингов, 7 стопок пирожных и 5 стопок салата из макарон. Сколько стопок десерта?
- Есть 9 кастрюль супа с лапшой и 8 кастрюль овощного супа. Сколько кастрюль с супом?
- На качелях 4 девочки, на горке 6 мальчиков. Сколько детей на детской площадке?
- Мы отправляемся на экскурсию. 15 детских бутербродов. 3 детских упакованных обеда. Сколько обедов мы возьмем на экскурсию?
- Напишите соответствующее дополнение: «Скайлер прочитала 15 книг. 7 были книгами Dogman, а 8 были книгами Джуни Б. Джонс».
Вопросы для 1-го класса:
- Школа начинается в 9 часов утра и заканчивается на 6 часов позже. Во сколько заканчивается школа?
- Второй перерыв в 1 час дня, то есть через 2 часа после первого перерыва. Когда первый перерыв?
- Директор начал собрание в понедельник в 10 часов утра. Заседание закончилось в 1 час дня. Сколько длилась встреча?
- Все ученики вышли из школы в 3 часа. Учитель остался еще на 3 часа. Когда учитель ушел из школы?
- Дети пошли на экскурсию в 9 утра. Им потребовалось 2 часа, чтобы все увидеть и вернуться в школу. Как вы думаете, во сколько они вернулись?
Контрольные вопросы для 1-го класса:
В каждом наборе «Разговоров по математике для первоклассников» есть контрольные вопросы. Эти вопросы являются открытыми и основаны на изображениях, используемых на карточках и слайдах. Однако приведенные ниже вопросы более прямолинейны и требуют конкретного ответа.
- Ножницы Джейкоба имеют длину 7 дюймов. Ножницы Шона на 2 дюйма короче, чем ножницы Джейкоба. Какой длины ножницы Шона?
- Мать дает мальчикам две веревки. Нить Шона имеет длину 8 дюймов, а Джейкоба — 5 дюймов. Какова общая длина их строк?
- Желтый мелок израсходован больше, чем серый. Серый мелок на 3 дюйма длиннее желтого. Если длина желтого мелка 1 дюйм, то какой длины серый мелок?
- Клюшка Холдена имеет длину 9 дюймов, а клюшка Бруклина — 5 дюймов. У кого палка длиннее?
- Есть 3 тюбика с краской. Синий – 5 дюймов в длину. Красный – 3 дюйма в длину, а желтый – 7 дюймов в длину. На сколько длиннее желтый по сравнению с синим?
- Есть два клеевых стержня. Самый длинный из них имеет длину 5 дюймов. Более короткая на 2 дюйма короче. Какой длины более короткий клей-карандаш?
Вопросы по математике для второго класса
Вот примеры вопросов из Сборника математических бесед для второго класса:
- Поезд прибывает на Северный полюс в 9 вечера. Если дорога займет 5 часов, во сколько мы должны выйти?
- Что такое 640 в развернутом виде? Какое еще число можно составить, используя цифры 6, 4 и 0?
- Что бы вы купили? Дюжина больших пончиков за 6 долларов или 2 дюжины мини-пончиков за 7 долларов?
- У нас есть 20 конфет. Некоторые части синие, а некоторые оранжевые. Сколько у нас может быть каждого?
- Назовите мне уравнение, которое соответствует вашему возрасту.
Фракции второго сорта:
- В аквариуме 15 золотых рыбок. 4 золотых рыбки оранжевые, а 11 серебристые. Какая часть рыб серебряная?
- На выставке 5 кроликов. 3 кролика белые и 2 серых. Какая часть кроликов серая?
- Есть 6 кошек, ожидающих усыновления. 4 из них котята. Какую часть кошек составляют котята?
- На полке 9 упаковок корма для животных. 5 из них для кошек, а остальные для собак. Какая часть корма предназначена для собак?
- В зоомагазине работает 8 человек. Две восьмых людей работают в груминг-центре. Три восьмых из них работают на кассе. Остальные помогают покупателям в магазине. Сколько сотрудников помогает клиентам?
Задачи на счет денег 2-го класса:
- У Лукаса есть 2 однодолларовых купюры, 3 десятицентовика и 3 пятицентовых монеты. Сколько денег у Лукаса?
- У Скарлетт есть 5 долларов 60 центов, и ее сестра дает ей 2 четвертака. Сколько денег у Скарлетт?
- У Оуэна есть 2,35 доллара, и он тратит 1 цент и 3 никеля. Сколько у него денег?
- У Итана есть 1 пятидолларовая купюра и 4 четвертака. Сколько денег у него останется после того, как он потратит 60 центов?
- У Эллы есть 4 однодолларовых купюры, 3 четвертака и 5 десятицентовиков. У Логана есть 1 пятидолларовая купюра и 1 пятицентовая монета. У кого больше денег?
- У Дэна 2 однодолларовых купюры, 1 четверть и 2 десятицентовика. У Джо 3 однодолларовых купюры и 3 пятицентовых монеты. После того, как Джо отдаст Дэну все свои монеты, у кого останется меньше денег?
2-й класс Вопросы на сложение и вычитание:
- Пластиковая новогодняя елка состоит из 3 частей. Нижняя часть имеет 8 ответвлений. Средняя часть имеет 6 ветвей, а верхняя часть имеет 4 ветви. Сколько всего отделений?
- У нас есть 9 цепочек серебряных огней и 6 цепочек золотых огней. 2 серебряные световые нити оборваны. Сколько хороших световых цепочек осталось?
- На прошлой неделе мы купили две коробки леденцов. В каждой коробке есть 4 красных и 4 синих всплывающих окна. Сколько попсов у нас есть?
- В гирлянде 16 лампочек, но 8 из них сломаны. У Джека всего 4 запасные лампочки. Сколько лампочек работает?
- В коробке конфет девять шоколадных батончиков и девять леденцов. Три кольца сломались. Сколько конфет у нас осталось?
- Напишите подходящее числовое предложение: «Джек сделал 5 украшений, чтобы повесить их на елку, а Эмма сделала 9.украшения, чтобы повесить на елку. Эмма сделала на 4 украшения больше, чем Джек».
Веселые математические игры для детей
Вот небольшая коллекция игр для занятий математикой. Есть простые математические вопросы, логические головоломки, магические квадраты и многое другое.
- Волшебные магнитные строительные блоки
- Тетрадь-головоломка «Волшебный квадрат»
- Простые математические загадки для умных детей Игра Бинго
- Чисел
- Магнитные дроби для пиццы
Перед тем, как вы пойдете, вот статьи по математике, которые вам понравятся:
Лучшая оценка по математике в детском саду
Как научить составлять и разлагать числа
Преимущества Math Talks для детей
22 Лучшие образовательные приложения для детей
45 апреля Вы бы предпочли Вопросы для детей
Забавные математические вопросы для детей
Математические задачи от Good Will Hunting, с решениями | Йорген Вейсдал
Фото : © 1997 Miramax PicturesЦель этой статьи — рассказать вам о решениях двух математических задач, решенных вымышленным персонажем Уиллом в фильме «Умница Уилл Хантинг», получившем премию «Оскар» в 1997 году.
Повествование в значительной степени основано на превосходной статье «Математика в охоте за доброй волей II: проблемы с точки зрения студентов » Хорвата, Коранди и Сабо (2010).Музыка для настроения Spotify. Приятного чтения!
Краткое изложение Умница Уилл Хантинг рассказывает историю вымышленного персонажа Уилла Хантинга, который, несмотря на свой исключительный интеллект, работает уборщиком в Массачусетском технологическом институте в Бостоне. Там он однажды замечает задачу на доске в коридоре, поставленную профессором Джеральдом Ламбо, обладателем медали Филдса. Обладая эйдетической памятью, Уилл запоминает задачу и решает ее перед зеркалом в своей ванной дома в Южном Бостоне. Вернувшись на следующий день в Массачусетский технологический институт, он не может ничего с собой поделать, но анонимно излагает свое решение на доске.
Когда на следующий день ни один из студентов Ламбо не претендует на зачет, профессор ставит другую, более сложную задачу. Уилл снова решает ее, но профессор ловит его в момент написания своего решения, который потрясен, узнав, что самый блестящий молодой математик в Массачусетском технологическом институте – необразованный уборщик.
Профессор Джеральд Ламбо (в исполнении Стеллана Скарсгарда) просматривает предложенное Уиллом решение. Фото : © 1997 Miramax PicturesЗадача 1: По графу G найти 1. Матрица смежности, A
Рис. 1: График G
2. Матрица, задающая количество 3-шаговых блужданий
3. Производящая функция для блужданий от i → j
4. Производящая функция для блужданий от 1 → 3Первая задача теории графов требует количества обходов от вершины i до вершины j в графе G. Для этого пусть G граф с множеством вершин V = {1, 2 , 3, 4} и множество ребер E = {(1,2), (1,4), (2,4), (2,3),(2,3)}, где (2,3) — обоюдоострый.
Решения задачи 1
Задача 1.1
Для заданного графа G найдите матрицу смежности AМатрица смежности — это квадратная матрица, используемая для представления конечного графа. Элементы матрицы смежности L указывают, являются ли пары вершин в графе смежными или нет.
Решение 1.1. Реберные элементы от вершин i до j и матрица смежности графа G, показывающая количество ребер между вершинами i и j Для простого графа с набором вершин V матрица смежности представляет собой квадрат |L| × |Л| матрица такая, что ее элемент L ᵢⱼ равен 1, когда есть одно ребро из вершины i до вершины j , 2, когда их два, и ноль, когда нет ребер из вершины i в вершину j. Все диагональные элементы матрицы равны нулю, поскольку ребра из вершины i в саму себя (петли) не допускаются в простых графах. Для всех ступенчатых обходов длины 1 вдоль множества ребер E это дает нам следующую матрицу смежности для графа G:Задача 1.2
Найдите матрицу, определяющую количество трехшаговых прогулокВторая задача в задаче 1 состоит в том, чтобы найти матрицу, которая кодирует все возможные прогулки длины 3 (Knill, 2003). То есть найти количество различных последовательностей ребер, соединяющих каждую отдельную последовательность вершин.
n + 1 шаг от i до j состоит из n шагов от i до k и затем 1 шаг от 9от 1554 к 91 555 до 91 554 j 91 555 . То есть запись ij L ⁿ⁺¹ задается суммой:
Equation 1Что на английском языке для этой задачи гласит, что «количество обходов длины 3 из вершины i в j» равно сумма «количества прогулок длины 2 от вершины i до 91 554 k» 91 555, умноженная на «количество прогулок длины 1 от вершины 91 554 k 91 555 до j» для 91 554 k 91 555 = 1,2. Путем матричного умножения, для всех ступенчатых обходов длины 3 от i до j это дает следующую матрицу:
Решение 1.2. Матрица, представляющая количество 3 обходов из вершины i в j в графе GЗадача 1.3
Найти производящую функцию для обходов из i → jТретья задача в задаче 1 запрашивает производящую функцию из вершины i от до j . Чтобы ответить на этот вопрос, Хорват и др. (2010) рассматривают аналитическую производящую функцию, определяемую степенным рядом
Уравнение 2Где коэффициент zⁿ обозначает число n шагов с i до j .
Уравнение 3 Из задачи 1.3 мы нашли, что ω_n(i → j) является ij элементом матрицы Lⁿ . В задаче требуется производящая функция, которая дает все элементы одновременно, поэтому имеет смысл рассмотреть матрицу L , заданную знакомым степенным рядом (Horváth et al, 2010):Где Lⁿ — это матрица, содержащая количество ступенчатых обходов от каждой вершины i до j (общий случай решения задачи 1.2). Сумма может быть рассчитана с использованием известного тождества для геометрического степенного ряда, а именно:
Уравнение 4Чтобы вычислить обратное выражение ( I − z × L) , мы можем использовать правило Крамера. Согласно Horváth et al (2010) для матрицы M пусть Mᵢⱼ обозначает матрицу, полученную из M удалением i -го столбца и j -й строки. Если мы это сделаем, мы получим матрицу N, ij запись равна
Уравнение 5По правилу Крамера, если M обратима (существует некоторая матрица N размера n×n такая, что M × N = N × M =
- 4 I_n 91, то 9 5 5 54 I_n 91 Уравнение 6
То есть ij запись обратной матрицы M: 8
Замена М:
Решение 1. 3. 9(i+j) (вероятно, из-за обозначений), и он обозначает единичную матрицу с 1 вместо более распространенного I .Задача 1.4
Найти производящую функцию для блужданий от 1 → 3Для решения задачи 1.4 просто применим общую формулу для блужданий от i к j (из задачи 1.3) к случаю блужданий от 1 → 3 :
Уравнение 9.Определители которого несложно найти:
Уравнения 10 и 11. Определители ( I − zL ) и его младший/приведенный определитель ( I ₁₃ − zL ₁₃)Задав следующие выражения, получим, используя определение определителя:
Уравнение 12. Формула для определения производящей функции для блужданий из вершины 1 в вершину 3. Уравнение 830. 13. Формула для определения значений производящей функции для блужданий из вершины 1 в вершину 3, решеннаяДля получения коэффициентов этого степенного ряда вычисляется ряд Тейлора функции:
Уравнение 14.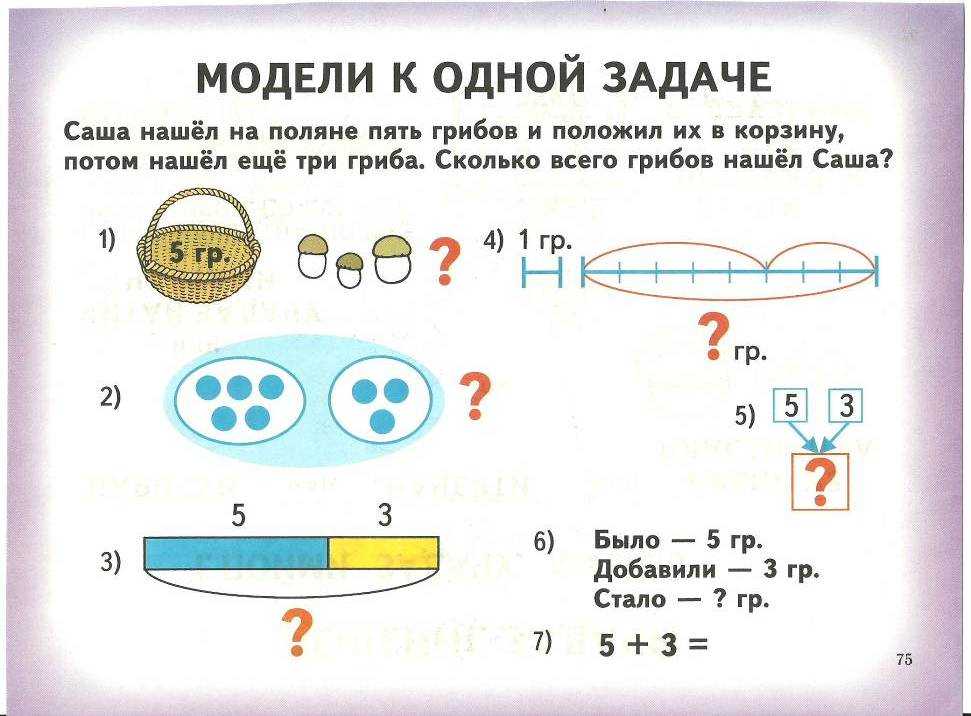 f(z) — ряд Маклорена, где fⁿ(0) — n-я производная от f при 0,Для нашего выражения f(z) мы можем использовать правило частных, где g(z) = 2z² и h(z) = 4z³− 6z² −z +1. В фильме Уилл приводит значения первых шести производных разложения f(z):
Решение 1.4. Разложение Тейлора для определения значений производящей функции для блужданий из вершины 1 в вершину 3В шоке профессор Ламбо смотрит на правильное решение второй задачи, данное анонимным уборщиком, которого он только что прогнал. Фото : © 1997 Miramax PicturesПоскольку Уилл не расписался на доске за решение первой задачи, профессор Ламбо поставил вторую задачу, о которой он сообщает своему классу , что «нам потребовалось более двух лет, чтобы доказать» . Задача снова касается древовидных структур:
Задача 2
a. Сколько существует деревьев с n помеченными вершинами?
б. Нарисуйте все гомоморфно неприводимые деревья с n = 10Решения задачи 2
Как указывают Horváth et al (2010), задача 2a на самом деле просто запрашивает формулу Кэли, которая для каждого положительного целого числа n число деревьев на n -помеченных вершинах равно nⁿ⁻².
Формула названа в честь Артура Кэли, но известна с тех пор, как была открыта Карлом Вильгельмом Борхардтом в 1860 году. учитывайте степени вершин, и поэтому с тех пор он носит его имя. Есть несколько известных доказательств результата.Заключительное задание, задача 2б требует рисунков все гомоморфно неприводимых деревьев с n = 10. Гомоморфно неприводимое дерево — это дерево, не имеющее точек степени 2. Проблема, вероятно, была навеяна статьей «Число гомоморфно неприводимых деревьев и других видов » Харари и Принса ( 1959).
Мы можем сгруппировать гомоморфно неприводимые деревья, пометив их вершины цифрами 1,…., 10 и степени их вершин цифрами d₁, …,d₁₀ (Horváth et al, 2010). Поскольку у деревьев 10 вершин, мы знаем, что у них 9края. Мы можем классифицировать эти различные деревья по количеству их листьев (узлов/вершин степени вершины 1):
- Если есть 9 листьев и 1 нелист, то мы получаем «звезду», единственную вершину, соединенную с каждым листом :
- Если 8 листьев и 2 нелиста, то d₁ + d₂ = 10 и d₁ ≥ d₂ ≥ 3, поэтому либо: a) d₁ =7 и d₂ = 3 (одно дерево), или b ) d₁ = 6 и d₂ = 4 (одно дерево), или c) d₁ = d₂ = 5 (одно дерево).
- Если листьев 7 , то d₁ + d₂ + d₃ = 11 и d₁ ≥ d₂ ≥d₃ ≥ 3, поэтому либо а) d₁ = d₂ = 5 и d₃ = 3 (два дерева), либо б) d₁ = 5 и d₂ = d₃ = 3 (три дерева).
- Если листьев 6, то d₁ + d₂ + d₃ +d₄ = 3.
Итого получается 10 деревьев с n=10. На доске в фильме появляется только 8, либо потому, что Уилла прервал профессор Ламбо, либо из-за недосмотра со стороны создателей фильма.
В ранних версиях сценария «Умница Уилл Хантинг» персонаж Уилл был вундеркиндом в области физики, но Шелдон Глэшоу из Гарварда предположил, что речь идет о математике, поскольку современная физика — это «обычно групповой проект», тогда как «делает какая-то математическая теорема очень часто является единичным предприятием» (Лондон, 2016).
Консультантом по математике фильма был профессор физики Университета Торонто, покойный Патрик О’Доннелл.Было высказано предположение, что персонаж Уилла основан на вундеркинде Уильяме Сидисе (1898–1944), известный своими исключительными математическими способностями.
Повествование, представленное в этом эссе, в значительной степени основано на замечательной статье «Математика в охоте за доброй волей II: проблемы с точки зрения студентов» Хорвата, Коранди и Сабо (2010). Я призываю всех заинтересованных прочитать их оригинальную, подробную статью, доступную здесь, которая также включает обсуждение других частей математики, показанных в различных сценах на протяжении всего фильма.
Алгебра 2
Алгебра 1
Исчисление
Также известен как «Алгебра колледжа»
ОК. Итак, что вы собираетесь здесь изучать?
Вы узнаете о числах, полиномах, неравенствах, последовательностях и суммах, многих типах функций и о том, как их решать .
Вы также получите более глубокое представление о математике, попрактикуетесь в использовании новых навыков с множеством примеров и вопросов и в целом улучшите свой ум.
С вашими новыми навыками вы сможете составлять математические модели, чтобы находить качественные решения многих сложных реальных ситуаций.
В конце большинства страниц находится раздел “Твоя очередь”… сделайте это! Вам нужно сбалансировать свое чтение с , делая . Ответы на вопросы помогают разобраться в себе. И не угадывайте ответ: используйте ручку и бумагу и постарайтесь изо всех сил, прежде чем увидеть решение.
Язык
Так что это за штука называется Математика? И как вы собираетесь его изучать?
- Добро пожаловать в математику
- Изучение математики
- Язык математики
- Символы в алгебре
Наборы
Далее нам нужно подумать о математике с точки зрения множеств .
- Знакомство с наборами
Номера
Теперь, когда мы знаем, что такое множество, давайте посмотрим на различные полезные наборы чисел:
- Эволюция чисел
- Простые и составные числа
- Основная теорема арифметики
- Целые числа и целые числа
- Рациональные числа
- Использование рациональных чисел
- Иррациональные числа
- 0,999. .. = 1
- Реальные числа
- Воображаемые числа
- Комплексные числа
- Умножение комплексных чисел
- Сложный самолет
- Наборы общих номеров
Неравенства
“Равно” хорош, но не всегда доступен. Может быть, мы знаем только, что что-то меньше или больше. Итак, давайте узнаем о в равенствах.
а≥б
- Введение в неравенства
- Свойства неравенств
- Решение неравенств
- Решение словесных вопросов о неравенстве
- Интервалы
Экспоненты
Мы будем часто использовать экспоненты, поэтому давайте познакомимся с ними поближе.
- Экспоненты
- Переменные с показателями степени
- Использование экспонент в алгебре
- Квадраты и квадратные корни
- Квадраты и квадратные корни в алгебре
- -й корень
- Дробные показатели степени
- Законы показателей
- Экспоненты отрицательных чисел
Многочлены
Многочлены были одними из первых вещей, которые когда-либо изучались в алгебре.
Они просты, но мощны в своей способности моделировать ситуации реального мира.- Что такое многочлен?
- Сложение и вычитание многочленов
- Умножение многочленов
- Многочлены — длинное умножение
- Деление многочленов
- Многочлены — длинное деление
- Степень (выражения)
- Специальные биномиальные продукты
- Разность двух кубиков
- Факторинг в алгебре
- Решение многочленов
- Корни многочленов: суммы и произведения
- Рациональные выражения
- Использование рациональных выражений
- Основная теорема алгебры
- Теорема об остатках и теорема о факторах
- Общая форма многочлена
Графические многочлены
- Как ведут себя многочлены
- Полиномы: правило знаков
- Полиномы: границы нулей
Уравнения
И, конечно же, нам нужно знать об уравнениях.
.. и о том, как их решать.- Уравнения и формулы
- Решение уравнений
- Упростить
- Решение словесных вопросов
- Свойство нулевого продукта
- Импликация и случайность
- Теоремы, Следствия, Леммы
Графики
Графики могут нас спасти! Они являются отличным способом увидеть, что происходит, и могут помочь нам решить многие проблемы. Но нам нужно быть осторожными, так как иногда они не дают полной информации.
- Декартовы координаты
- Теорема Пифагора
- Расстояние между 2 точками
- График уравнения
- Поиск пересечений в уравнении
- Симметрия в уравнениях
Линейные уравнения
Это просто уравнения для линий. Но они бывают разных форм.
- Уравнение прямой
- Линейные уравнения
- Уравнение точки-наклона линии
- Общая форма уравнения линии
- Уравнение прямой из 2 точек
- Середина сегмента линии
- Параллельные и перпендикулярные линии
Функции
Функция связывает вход с выходом.
Но из этого простого фундамента можно построить много полезных вещей.- Что такое функция?
- Домен, диапазон и кодовый домен
- Оценка функций
- Функции возрастания и убывания
- Максимумы и минимумы функций
- Четные и нечетные функции
- Обозначение Set-Builder
Общие функции Ссылка:
- Квадратная функция
- Функция извлечения квадратного корня
- Функция куба
- Обратная функция
- Функция абсолютного значения
- Функция пола и потолка
- Преобразование функций
- Графическое устройство уравнений
- Операции с функциями
- Состав функций
- Обратные функции
Уравнения второй степени
“Вторая степень” просто означает, что переменная имеет показатель степени 2, например x 2 . Это следующий важный шаг после линейных уравнений (где показатель степени равен 1, как и x).
- Квадратные уравнения
- Факторинг Квадратика
- Завершение квадрата
- Вывод квадратной формулы
- Графики квадратных уравнений
- Квадратные уравнения в реальном мире
- Уравнения окружности
Решение
У нас уже есть опыт решения, но теперь мы можем узнать больше!
- Математические модели и математические модели 2
- Приблизительные решения
- Теорема о промежуточном значении
- Решение радикальных уравнений
- Изменение переменных
- Ошибки в алгебре
Решение неравенств
О неравенствах мы узнали выше, теперь научимся их решать.
- Решение неравенств
- Графики линейных неравенств
- Инструмент для построения графиков неравенства
- Решение квадратных неравенств
- Решение рациональных неравенств
- Абсолютное значение в алгебре
Экспоненты и логарифмы
Мы уже знаем о показателях степени.
.. ну логарифмы просто идут в другую сторону. И вместе они могут быть очень сильными.- Введение в логарифмы
- Экспоненты, корни и логарифмы
- Работа с экспонентами и логарифмами
- Экспоненциальная функция
- Логарифмическая функция
- Экспоненциальный рост и упадок
Системы линейных уравнений
Что произойдет, если у нас есть два или более линейных уравнения, которые работают вместе? Их часто можно решить! Это не очень сложно, но может потребовать много вычислений.
- Системы линейных уравнений
- Матрицы
- Типы матриц
- Как умножать матрицы
- Определитель матрицы
- Инверсия матрицы:
- Использование элементарных операций со строками (Гаусса-Жордана)
- Использование миноров, кофакторов и адъюгатов
- Скаляр, Вектор, Матрица и Векторы
- Матричный калькулятор
- Еще в Matrix Index
- Решение систем линейных уравнений с использованием матриц
- Системы линейных и квадратных уравнений
Вероятность
Возможно ли это? Ты будешь судьей!
- Вероятность
- Основной принцип счета
- Комбинации и перестановки
Последовательности, ряды и частичные суммы
Последовательность — это набор элементов (обычно чисел), расположенных по порядку.
Джон платит 650 долларов налога на недвижимость. Какова оценочная стоимость его имущества, если налог на имущество составляет 1,2% от оценочной стоимости?19. Магазин матрасов продает свои запасы со скидкой 15% от розничной. Если кто-то платит наличными, он получает дополнительную скидку 10% от цены со скидкой. Если розничная цена матраса составляет 750 долларов, какова цена после скидки в магазине и скидки за наличные?
20. 851% от 3 какого числа?
21.
Здание высотой 150 футов отбрасывает тень длиной 20 футов. При этом дерево отбрасывает тень длиной 2 м. Какой высоты дерево?22. Какое из следующих утверждений является верным?
23. Чему равен дробный эквивалент 12,5%?
24.
Замените 4 3 / 5 на неправильную дробь.25 , Штраф для водителя, едущего по полосе для автобазы без пассажиров, составляет 133 доллара. Водителю выдан судебный ордер на сумму 2,29 доллара США.4.25, который включает сбор в размере 15% за просроченные платежи и судебные издержки. Сколько билетов не оплатил водитель?
Сколько времени потребовалось Бретту, чтобы закончить гонку?
27. Какой дроби соответствует заштрихованная область в следующем круге?
28.
Умножить 2,345 * 0,02329. Мужская баскетбольная команда выиграла 24 игры и проиграла 32. Каково отношение количества проигранных игр к количеству сыгранных игр?
30. Which of the following choices is equivalent to
5 / 6 ?31. 31. $ № 120. При той же ставке заработной платы, сколько она заработает за 15 часов работы?
32. В какие два года было продано наименьшее количество шин?
33.
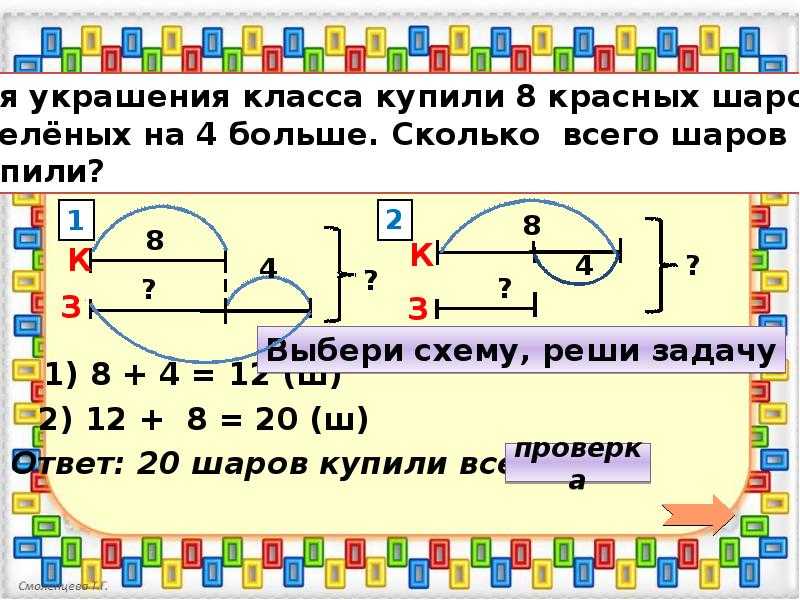В каком году магазин продал шин на 1/3 больше, чем годом ранее?34. Сколько в среднем шин было продано магазином с 1998 по 2001 год?
35. Продавец продал 20 автомобилей в июле и 40 автомобилей в августе. На сколько процентов увеличилось количество автомобилей, проданных продавцом?
36. Если одна сторона квадрата равна 5 единицам?
37. Если 8x + 5 = 21, то 3x + 4 =
38. В треугольнике ABC угол AB=BC, а угол C равен 65°.
39.
Если среднее среднее арифметическое среднее из 8, 12, 15, 21, x и 11 – 17.40. У Сары есть 20-долларовая и 5-долларовая купюры. Если она купит две вещи, одну за 11,23 доллара, а другую за 8,32 доллара, то сколько денег у нее останется?
Ответы и объяснения
1. ANGELS
. Мера третьего угла равна разности 180° и 140°, или 40°.
2. E
Количество, которое ему понадобится для 3 десертов, равно произведению 2 1/2 и 3, или 7 1/2.
3. C
Применение скидки 50 % дает выражение 320 – 0,50(320), что равно 160. Применение дополнительной скидки 20 % к этой сумме дает выражение 160 – 0,20(160), что равно 128. Таким образом, цена продажи стола составила 128 долларов.
4. A
25% больше, чем любой процент, указанный для других направлений, поэтому пляж является наиболее распространенным направлением.
5. B
Количество студентов, отправляющихся в горы, равно произведению 0,12 на 500, что равно 60.
6. E
Можно составить следующую пропорцию: (1/4)/1 =6/х. Решение для x дает x = 24. Таким образом, 6 чайных ложек содержат 24 миллилитра.
7. D
Правильный график должен показывать один луч с замкнутой точкой на целом числе -2, который указывает влево, и другой луч с замкнутой точкой на целое число 3, который указывает на Правильно.
8. E
Можно записать следующую пропорцию: (1/4)/20=(3 1/2)/x, которая упрощается до 1/4 x=70, где x = 280. Таким образом, существует на самом деле 280 миль между двумя городами.
9. D
Новая длина может быть представлена выражением L + 2, а новая ширина может быть представлена выражением W + 2. Таким образом, площадь равна произведению двух измерений, или (L + 2)(W + 2).
10. D
Удаление 9 пар гарантирует, что у нее будет по одной паре каждого цвета, потому что будут представлены все 3 цвета.
Удаление 7 пар может включать только пары черных и белых носков, но не включая красную пару.
11. C
Дроби в варианте C могут быть преобразованы в следующие десятичные числа: 0,25, 0,68, 0,6875, 0,75, которые действительно расположены в порядке от наименьшего к наибольшему.
12. C
Среднее значение может быть записано как (365+7+24)/3, что равняется 132.
13. A
Перемещение десятичной дроби на 5 знаков вправо дает 175 000.
14. C
Среднее значение можно записать как (0,03(2800+3200+3600))/3, что равно 96.
15. E
Можно записать следующую пропорцию: (1/3)/ 15=(3 2/3)/x, что упрощается до 1/3 x=165/3, где x = 165. Таким образом, фактически между двумя городами 165 миль.
16. A
Простые проценты можно рассчитать по формуле I = Prt, где представляет собой основную сумму, r представляет собой ставку, а t представляет период времени. Замена 200 на I, 4000 на P и 0,05 на r дает 200 = (4000) (0,05) t.
Таким образом, t = 1. Ему понадобится 1 год, чтобы заработать 200 долларов в виде простых процентов.
17. D
Для x можно решить следующее уравнение: 650 = 0,012x. Разделив обе части уравнения на 0,012, мы получим x = 54 166,67. Таким образом, оценочная стоимость его имущества составляет 54 166,67 долларов.
18. B
Задачу можно смоделировать с помощью уравнения 23,80 = x – 0,15x, которое упрощается до 23,80 = 0,85x. Разделив обе части уравнения на 0,85, мы получим x = 28. Таким образом, обычная цена лампы составляет 28 долларов.
19. C
Выражение 750 – 0,15(750) может использоваться для представления цены после первой скидки. Эта сумма составляет 637,50 долларов США. Дополнительная скидка 10% от цены со скидкой представлена выражением 637,50 – 0,10(637,50), что равняется 573,75. Таким образом, цена после обеих скидок составляет $573,75.
20. A
Задачу можно смоделировать и решить, используя уравнение 0,85x = 136. Решение для x дает x = 160.
21. B
Можно записать следующую пропорцию: 150/20= х/2. Решение для x дает x = 15. Таким образом, высота дерева составляет 15 футов.
22. C
Деление положительного числа на отрицательное дает отрицательное частное. Например, 4/(-2)=-2.
23. D
1/8=0,125, что соответствует 12,5%.
24. А
Чтобы превратить смешанное число в неправильную дробь, нужно сначала умножить знаменатель на целое число. Далее к этому произведению следует прибавить числитель. Полученное значение следует поместить над исходным знаменателем дробной части смешанного числа. 4 3/5=23/5, потому что (5 х 4) + 3 = 23, а 23, деленное на 5, записывается как 23/5.
25. E
Для решения задачи можно использовать следующее уравнение: 133x + 0,15(133x) = 2294,25. Решение для x дает x = 15. Итак, водитель не оплатил 15 билетов.
26. B
Прошло шесть часов, с 6:30 утра. до 12:30 С 12:30 минуло еще тридцать пять минут. до 13:05 Итак, ему потребовалось 6 часов 35 минут, чтобы финишировать в гонке.
27. A
Круг разделен на 3 равные части, причем 2 из них заштрихованы. Таким образом, представленная дробь равна 2/3.
28. B
Десятичные дроби можно умножать как целые числа. Однако десятичная дробь будет иметь шесть разрядов справа от десятичной дроби.
29. D
Соотношение может быть записано как 32/56, что сокращается до 4/7. Таким образом, отношение проигранных игр к сыгранным составляет 4:7.
30. E
5/6=15/18, потому что числитель и знаменатель первой дроби умножаются на 3.
31. B
Можно написать следующую пропорцию: 120/8=x/15. Решение для x дает x = 225. Она зарабатывает 225 долларов за 15 часов работы.
32. B
В каждый год было продано 7500 шин, 1998 и 2000. Это число было наименьшим количеством, проданным за год, о чем свидетельствуют полторы шины, показанные для этих лет, по сравнению с двумя и двумя с половиной для двух других лет.
33. B
Используя указанное количество шин, 1999 год можно представить выражением 1 1/2+1/3 (1 1/2), что равно 2.
Поскольку 2 равно 1/3 более 1 1/2, количество шин, проданных в 1999 году, было на 1/3 больше, чем количество, проданное в 1998 году. , что равно 9,375.
35. B
Увеличение в процентах может быть представлено как (40-20)/20, что равно 1,1 = 100%. Таким образом, процентное увеличение составило 100%.
36. D
A=s2, поэтому площадь можно записать как A=52; A = 25. Площадь квадрата 25 квадратных единиц.
37. C
Первое уравнение можно решить относительно x. Это дает x = 2. Подстановка 2 вместо x во второе уравнение дает 3(2) + 4 или 10.
38. B
Каждый из углов при основании равен 65°, поскольку треугольник равнобедренный. Таким образом, один из углов при основании равен 130°. Мера угла В равна разности 180° и 130°, или 50°.
39. D
Среднее значение может быть записано как (8+12+15+21+x+11)/6=17, что упрощается до (67+x)/6=17. Умножение обеих частей уравнения на 6 дает 67 + x = 102. Вычитание 67 из обеих частей уравнения дает решение x = 35.
40. B
Решение может быть представлено выражением, 25 – ( 11,23 + 8,32), что равно 5,45. Таким образом, у нее осталось 5,45 доллара.
70 занимательных математических вопросов для детей (K-2)
Содержание
Но с новой волной математических стандартов учителя находят творческий способ поощрять и поддерживать детей в решении сложных задач.
Эти математические беседы — идеальный способ вовлечь детей в хорошие разговоры о любой математической концепции.
Из корзины достают три мяча. Сколько мячей осталось в корзине?
Сколько стопок десерта?
Им потребовалось 2 часа, чтобы все увидеть и вернуться в школу. Как вы думаете, во сколько они вернулись?
Синий – 5 дюймов в длину. Красный – 3 дюйма в длину, а желтый – 7 дюймов в длину. На сколько длиннее желтый по сравнению с синим?
4 золотых рыбки оранжевые, а 11 серебристые. Какая часть рыб серебряная?
Сколько денег у него останется после того, как он потратит 60 центов?
У Джека всего 4 запасные лампочки. Сколько лампочек работает?
Повествование в значительной степени основано на превосходной статье «Математика в охоте за доброй волей II: проблемы с точки зрения студентов » Хорвата, Коранди и Сабо (2010).
Для простого графа с набором вершин V матрица смежности представляет собой квадрат |L| × |Л| матрица такая, что ее элемент L ᵢⱼ равен 1, когда есть одно ребро из вершины i до вершины j , 2, когда их два, и ноль, когда нет ребер из вершины i в вершину j. Все диагональные элементы матрицы равны нулю, поскольку ребра из вершины i в саму себя (петли) не допускаются в простых графах. Для всех ступенчатых обходов длины 1 вдоль множества ребер E это дает нам следующую матрицу смежности для графа G:
Из задачи 1.3 мы нашли, что ω_n(i → j) является ij элементом матрицы Lⁿ . В задаче требуется производящая функция, которая дает все элементы одновременно, поэтому имеет смысл рассмотреть матрицу L , заданную знакомым степенным рядом (Horváth et al, 2010):
3. 9(i+j) (вероятно, из-за обозначений), и он обозначает единичную матрицу с 1 вместо более распространенного I .
f(z) — ряд Маклорена, где fⁿ(0) — n-я производная от f при 0,
Формула названа в честь Артура Кэли, но известна с тех пор, как была открыта Карлом Вильгельмом Борхардтом в 1860 году. учитывайте степени вершин, и поэтому с тех пор он носит его имя. Есть несколько известных доказательств результата.
Консультантом по математике фильма был профессор физики Университета Торонто, покойный Патрик О’Доннелл.
.. = 1
Они просты, но мощны в своей способности моделировать ситуации реального мира.
.. и о том, как их решать.
Но из этого простого фундамента можно построить много полезных вещей.
.. ну логарифмы просто идут в другую сторону. И вместе они могут быть очень сильными.