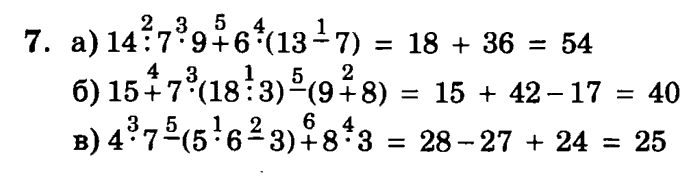2 класс математика примеры со скобками: Выражения со скобками – 2 класс, примеры, порядок действия

Как раскрывать скобки в выражениях и уравнениях. Правила математики.

ГДЗ 1 класс

ГДЗ 10 класс

  

Категория: Математика

Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Этот прием носит название раскрытия скобок.

Раскрыть скобки означает избавить выражение от этих скобок.

Отдельного внимания заслуживает еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения
3−(5−7) мы получаем выражение 3−5+7. Оба этих выражения мы можем записать в виде равенства 3−(5−7)=3−5+7.

И еще один важный момент. В математике для сокращения записей принято не писать знак плюс, если он стоит в выражении или в скобках первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не +7+3, а просто 7+3, несмотря на то, что семерка тоже положительное число. Аналогично если вы видите, например, выражение (5+x) – знайте, что и перед скобкой стоит плюс, который не пишут, и перед пятеркой стоит плюс +(+5+x).

Правило раскрытия скобок при сложении

При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.

Пример. Раскрыть скобки в выражении 2 + (7 + 3) Перед скобками плюс, значит знаки перед числами в скобках не меняем.

2 + (7 + 3) = 2 + 7 + 3

Правило раскрытия скобок при вычитании

Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но слагаемые, которые были в скобках, меняют свой знак на противоположный.

 Отсутствие знака перед первым слагаемым в скобках подразумевает знак +.

Пример. Раскрыть скобки в выражении 2 − (7 + 3)

Перед скобками стоит минус, значит нужно поменять знаки перед числами из скобок. В скобках перед цифрой 7 знака нет, это значит, что семерка положительная, считается, что перед ней знак +.

2 − (7 + 3) = 2 − (+ 7 + 3)

При раскрытии скобок убираем из примера минус, который был перед скобками, и сами скобки 2 − (+ 7 + 3)  , а знаки, которые были в скобках, меняем на противоположные.

2 − (+ 7 + 3) = 2 − 7 − 3

Раскрытие скобок при умножении

Если перед скобками стоит знак умножения, то каждое число, стоящее внутри скобок, умножается на множитель, стоящий перед скобками. При этом умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.

Таким образом, сскобки в произведениях раскрываются в соответствии с распределительным свойством умножения.

Пример. 2 · (9 – 7) = 2 · 9 – 2 · 7

При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй скобки.

(2 + 3) · (4 + 5) = 2 · 4 + 2 · 5 + 3 · 4 + 3 · 5

На самом деле, нет необходимости запоминать все правила, достаточно помнить только одно, вот это: c(a−b)=ca−cb. Почему? Потому что если в него вместо c подставить единицу, получится правило (a−b)=a−b. А если подставить минус единицу, получим правило −(a−b)=−a+b. Ну, а если вместо c подставить другую скобку – можно получить последнее правило.

Раскрываем скобки при делении

Если после скобок стоит знак деления, то каждое число, стоящее внутри скобок, делится на делитель, стоящий после скобок, и наоборот.

Пример.  (9 + 6) : 3=9 : 3 + 6 : 3

Как раскрыть вложенные скобки

Если в выражении присутствуют вложенные скобки, то их раскрывают по порядку, начиная с внешних или внутренних.

При этом важно при раскрытии одной из скобок не трогать остальные скобки, просто переписывая их как есть. 

Пример.    12 – (a + (6 – b) – 3) = 12 – a – (6 – b) + 3 = 12 – a – 6 + b + 3 = 9 – a + b

• Назад
• Вперед

 
умножить наподелить на

 

• Уроки
• Математика

Вам может пригодиться:

Тест: Порядок действий в выражениях со скобками

Тест: Порядок действий в выражениях со скобками – Математика 2 класс

Английский язык

Астрономия

Белорусский язык

Биология

География

ИЗО

Информатика

История

Итальянский язык

Краеведение

Литература

Математика

Музыка

Немецкий язык

ОБЖ

Обществознание

Окружающий мир

ОРКСЭ

Русский язык

Технология

Физика

Физкультура

Химия

Черчение

Для учителей

Дошкольникам

VIP – доступ

• Предметы
»
• Математика
»
• 2 класс
»
• Порядок действий в выражениях со скобками

Порядок действий в выражениях со скобками

Цель: проверить знания учащихся по теме “Порядок действий в выражениях со скобками “

Математика 2 класс | Автор: Кошелева Анастасия Васильевна | ID: 14884 | Дата: 1. 11.2021

Помещать страницу в закладки могут только зарегистрированные пользователи

Зарегистрироваться

Вопрос № 1

Найди значения выражений 19-(8-1)=

12
10
9

Вопрос № 2

Найди значения выражения 9-(6-2)=

2
5
1

Вопрос № 3

Если в выражении есть скобки,то ….

сначала вычесляют значение в скобках
вычесляют по порядку,слева направо.

Вопрос № 4

Как правильно прочитать данное числовое выражение: 12 – (6 + 4)?

к 12 прибавить сумму чисел 6 и 4
из 12 вычесть сумму чисел 6 и 4

из 12 вычесть 6 плюс 4
разность чисел 12 и 6 плюс 4

Вопрос № 5

Какую из данных записей можно прочитать так: «К 14 прибавить разность чисел 8 и 7»

14 – (8 + 7)
14 + (8 + 7)
14 + (8 – 7)
14 – (8 – 7)

Вопрос № 6

К разности чисел 10 и 6 прибавить 8. Сколько получится?

12
24
10
4

Вопрос № 7

Из 15 вычесть сумму чисел 8 и 2. Сколько получится?

9
8
6
5

Вопрос № 8

Значение какого из данных выражение равно 15?

(39 + 1) + 7
10 + (12 – 7)
4 + (34 – 30)
16 – (10 – 8)

Вопрос № 9

Значение какого из данных выражений равно 0?

(12 – 10) – 1
15 – (10 + 3)
(18 – 8) – 8
14 – (7 + 7)

Вопрос № 10

В каком из данных примеров первым действием нужно выполнить вычитание?

5 – (14 – 10)
7 + (9 + 1)
(12 + 1) – 3
(25 + 1) — 20

Показать ответы

Получение сертификата
о прохождении теста

Доступно только зарегистрированным пользователям

© TestEdu.

ru 2013-2022

E-mail администратора: [email protected]

Дополнение с рабочим листом по математике в скобках для детей 2-го класса – PDF для печати

во 2-м классе, Дополнение / by math5childrenplus

Дополнение со скобками, рабочий лист для детей 2-го класса. Это математический PDF-лист с несколькими упражнениями, который можно распечатать. На второй странице прикреплен ключ ответа. Этот рабочий лист является дополнительным ресурсом для второго класса, который поможет учителям, родителям и детям дома и в школе.

Печать рабочего листа

Связанные рабочие листы

Математическая таблица на сложение и вычитание для детей 2-го класса – PDF для печати

30 ноября 2013 г.

Таблица на сложение и вычитание для детей 2-го класса.…

https://math5childrenplus.com/wp-content/uploads/2013/11/дополнение-и-вычитание-matchup-0021.png 237 168 математика5детиплюс https://math5childrenplus. com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-30 05:45:352013-11-30 05:45:35Математическая таблица сложения и вычитания для детей 2-го класса – PDF для печати

Рабочий лист по уравнениям сложения и уравновешивания для детей 2-го класса – PDF для печати

27 ноября 2013 г.

Рабочий лист по уравнениям сложения и уравновешивания для детей 2-го класса…

https://math5childrenplus.com/wp-content/uploads/2013/11/addition-and-balancing-equations-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-27 07:03:422013-11-27 07:03:42Математическая таблица сложения и балансировки уравнений для детей 2-го класса – PDF для печати

Дополнительное круговое упражнение 1 лист по математике для детей 2-го класса – PDF для печати

27 ноября 2013 г.

Дополнительное круговое упражнение 1 рабочий лист для детей 2-го класса. Это…

https://math5childrenplus.com/wp-content/uploads/2013/11/addition-circle-drill-sheet-1-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-27 07:02:312013-11-27 07:02:31Сложение с круговым упражнением 1 математический лист для детей 2-го класса – PDF для печати

Рабочий лист по математике с уравнениями на сложение для детей 2-го класса – PDF для печати

27 ноября 2013 г.

Рабочий лист с задачами на сложение уравнений для детей 2-го класса.…

https://math5childrenplus.com/wp-content/uploads/2013/11/addition-equations_word-problems-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-27 06:58:142013-11-27 06:58:14Сложение уравнений словесные задачи математический лист для детей 2-го класса – PDF для печати

Дополнение «Найти пропущенное число по математике для детей 2-го класса» – PDF для печати

27 ноября 2013 г.

Дополнение «Найти пропущенное число» для детей 2-го класса.…

https://math5childrenplus.com/wp-content/uploads/2013/11/дополнение-find-missing_number-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-27 06:57:512013-11-27 06:58:59Дополнение «Найди отсутствующее число» по математике для детей 2-го класса – PDF для печати

Дополнение по горизонтали 5 по математике для детей 2-го класса – PDF для печати

27 ноября 2013 г.

Дополнение по горизонтали 5 заданий для детей 2-го класса…

https://math5childrenplus.com/wp-content/uploads/2013/11/дополнение-горизонтально-расположенный-лист-5-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-27 06:57:132013-11-27 06:57:13Дополнение по горизонтали 5 листов по математике для детей 2-го класса – PDF для печати

Дополнение к упражнению 2 по математике для детей 2-го класса – PDF для печати

27 ноября 2013 г.

Дополнение к упражнению 2 для занятий по математике для детей 2-го класса.…

https://math5childrenplus.com/wp-content/uploads/2013/11/дополнение-matchup-exercise-2-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-27 06:56:462013-11-27 06:56:46Дополнительное упражнение по математике 2 для детей 2-го класса – PDF для печати

Дополнительный лист с математическими упражнениями для детей 2-го класса – PDF для печати

27 ноября 2013 г.

Дополнительный лист с упражнениями для детей 2-го класса. Это…

https://math5childrenplus.com/wp-content/uploads/2013/11/дополнение-matchup-exercise-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-27 06:56:262013-11-27 06:56:26Дополнительное задание по математике для детей 2-го класса – PDF для печати

Дополнительный рабочий лист по математике с несколькими операциями для детей 2-го класса – PDF для печати

27 ноября 2013 г.

Дополнительный рабочий лист с несколькими операциями для детей 2-го класса. Это…

https://math5childrenplus.com/wp-content/uploads/2013/11/Addition-multi-operations-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-27 06:51:162013-11-27 06:51:16Дополнительный математический лист с несколькими операциями для детей 2-го класса – PDF для печати

Добавление 3-, 4- и 5-значных математических заданий для детей 2-го класса – PDF для печати

27 ноября 2013 г.

Добавление 3-, 4- и 5-значных чисел для 2-го класса…

https://math5childrenplus.com/wp-content/uploads/2013/11/дополнение-из-3-4-и-5-значных-чисел-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-27 06:50:582013-11-27 06:50:58Сложение 3-х, 4-х и 5-значных чисел математический лист для детей 2-го класса – PDF для печати

ПредыдущийСледующий

Похожие сообщения:

Поделитесь этой записью

https://math5childrenplus. com/wp-content/uploads/2013/11/дополнение-с-скобками-002.png 237 168 математика5детиплюс https://math5childrenplus.com/wp-content/uploads/2013/04/logo.png math5childrenplus2013-11-27 06:12:032013-11-27 06:12:03Дополнение со скобками по математике для детей 2-го класса – PDF для печати

© Copyright – Math 4 Children Plus

Дополнение с иллюстрациями до 10. Рабочие листы по математике для детей 2-го класса –… Таблица сложения. Рабочие листы по математике для детей 2-го класса – PDF для распечатки…

Что такое правило PEMDAS? Определение, примеры

PEMDAS — это аббревиатура, используемая для обозначения порядка операций, которым необходимо следовать при решении выражений, состоящих из нескольких операций. PEMDAS означает P-круглые скобки, E-экспоненты, M-умножение, D-деление, A-сложение и S-вычитание. В разных странах для обозначения порядка операций используются разные аббревиатуры. Например, в Канаде порядок операций указан как BEDMAS (скобки, возведение в степень, деление, умножение, сложение и вычитание). Некоторые люди предпочитают говорить BODMAS (B-скобки, O-порядок или Off), в то время как некоторые другие называют это GEMDAS (G-группировка).

На этом уроке вы узнаете о правиле PEMDAS для решения арифметических выражений, за которым следуют решенные примеры и практические вопросы.

1.	Знакомство с PEMDAS
2.	Что такое PEMDAS?
3.	Правила PEMDAS
4.	BODMAS против PEMDAS
5.	Когда использовать PEMDAS?
6.	Распространенные ошибки при использовании правила PEMDAS
7.	Часто задаваемые вопросы о PEMDAS

Введение в PEMDAS

PEMDAS или порядок операций — это набор правил для выполнения операций в арифметическом выражении. Существуют разные сценарии, в которых все проходит через различные этапы в фиксированной последовательности.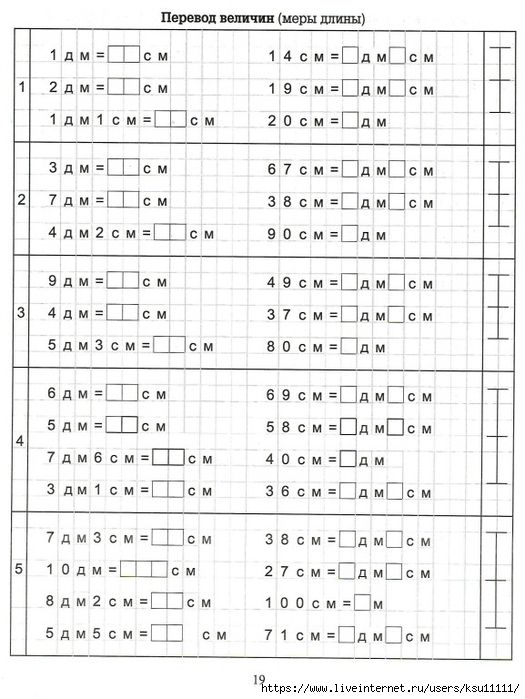 Рассмотрим следующий сценарий. Рон и Рейвен посетили фабрику игрушек. Они оба наблюдали за процессами, которым следовали на фабрике по производству игрушек. Сначала создаются игрушки. Далее они строятся и упаковываются в коробки. Наконец, они проверяются на качество перед отправкой в ​​магазины. Все делается в установленном порядке.

Точно так же арифметические операции выполняются упорядоченным образом. Давайте узнаем порядок операций в математике. Найти ответ на математические операции довольно просто, когда задействован только один оператор. Что делать, если задействовано несколько операторов? Это может стать немного сложнее! Посмотрим, как.

Рон и Рейвен по отдельности решили математическое выражение 5+2×3. Вот как они решили это.

Метод Рона	Метод Ворона
5+2×3 = 7×3 = 21	5+2×3 = 5+6 = 11

Как видите, Рон и Рейвен дали разные ответы. На это выражение в математике может быть только один правильный ответ! Сможете решить, кто прав?

Не волнуйтесь! PEMDAS здесь, чтобы помочь вам найти правильный ответ.

Что такое PEMDAS?

PEMDAS — это порядок операций, используемый в математике для облегчения выполнения сложных вычислений. В нем говорится, что мы начинаем решать любое арифметическое выражение с решения членов, написанных в скобках или скобках, а затем упрощаем экспоненциальные члены и переходим к операциям умножения и деления, а затем, наконец, мы можем найти ответ, решая операции сложения и вычитания.

Правила PEMDAS

PEMDAS — это набор правил, которым следуют при решении математических выражений. Эти правила начинаются с 90 194 скобок 90 195 , а затем операции выполняются над 90 194 показателями степени 90 195 или степенями. Далее выполняем операции над умножением или делением слева направо. Наконец, операции сложения или вычитания выполняются слева направо.

П	[{()}]	Скобки
Е	х 2	Экспоненты
М Д	× ИЛИ ÷	Умножение ИЛИ Раздел
А С	+ ИЛИ –	Дополнение ИЛИ Вычитание

Если вы будете придерживаться этого порядка операций в правиле PEMDAS, вы всегда получите правильный ответ. Следующая аббревиатура поможет вам запомнить правило PEMDAS.

P аренда E извините M y D ухо A unt S союзник

Давайте разберемся с PEMDAS на примере.

BODMAS против PEMDAS

Правило PEMDAS аналогично правилу BODMAS . В аббревиатуре есть разница, потому что некоторые термины известны под разными именами в разных местах.

Когда использовать PEMDAS?

Когда в математическом выражении имеется более одной операции, мы используем метод PEMDAS. PEMDAS в математике дает вам правильную структуру для получения уникального ответа для каждого математического выражения. Существует ряд определенных правил, которые необходимо соблюдать при использовании метода PEMDAS. Как только вы освоите эти правила, вы сможете выполнять несколько шагов одновременно.

На заметку

• Операции в скобках следует выполнять в первую очередь.
• Затем решите показатели степени в выражении.
• Двигайтесь слева направо и выполняйте умножение или деление, в зависимости от того, что наступит раньше.
• Двигайтесь слева направо и выполняйте сложение или вычитание, в зависимости от того, что наступит раньше.

Распространенные ошибки при использовании правила PEMDAS в математике

Наличие нескольких скобок обычно вызывает путаницу. Если мы не знаем, какую скобку решить первой, это может привести к неправильному ответу. Теперь мы узнаем, как решить это выражение с несколькими скобками.

4+3[8-2(6-3)]÷2

Начнем с внутренней стороны скобок. Сначала мы решим самую внутреннюю скобку, а затем переместимся наружу.

• Начиная с 6 – 3 = 3, получаем: 4 + 3[8 – 2(3)] ÷ 2
• Далее, умножая 2(3)=6 или 2×3=6, получаем: 4 + 3[8 – 6] ÷ 2
• Осталась одна скобка, [8 – 6] = 2, получаем: 4 + 3[2] ÷ 2
• Решив 3[2] или 3 × 2 = 6, мы получим: 4 + 6 ÷ 2

Мы видим, что все выражения в скобках решены. Опираясь на PEMDAS, мы знаем, что затем следует деление, следовательно, 6 ÷ 2 = 3, то есть 4 + 3. И, наконец, сложение 4 + 3 = 7,9.0003

☛Статьи по теме

Ознакомьтесь с еще несколькими интересными статьями, связанными с PEDAS и правилами. Узнайте разницу между BODMAS и PEMDAS с помощью следующих статей.

• Правило БОДМАС
• Порядок операций — PEMDAS и BODMAS
• Рабочие листы PEMDAS

 

Примеры PEMDAS

1. Пример 1:

   Упростите выражение, используя правило PEMDAS: 18÷(8-2×3).

   Решение:

   Полученное выражение: 18÷(8-2×3)

   Согласно правилу PEMDAS, сначала нужно решить скобки. Но здесь, внутри скобок, у нас есть две операции, умножение и вычитание. Итак, мы должны сначала умножить, прежде чем оно станет первым в PEMDAS. Итак, (8-2×3)= 8-6 = 2

   Теперь мы можем переписать выражение как 18÷2 как 18÷2= 9

   ∴ 18÷(8-2×3)= 9.

2. Пример 2:

   Упростите выражение, используя правило PEMDAS: (4×3÷6+1)×3 ²

   Решение:

   Шаг 1. Сначала нам нужно умножить 4 на 3 в данном выражении. ,​​(4×3÷6+1)×3 ² , получаем, (12÷6+1)×3 ²

   Шаг 2- Теперь нам нужно разделить 12 на 6 внутри скобки, таким образом, мы получаем, (2+1)×3 ²

   Шаг 3- Снимите скобки после добавления 2 и 1, мы получим, 3×3 ²

   Шаг 4- Решите экспоненту , то есть 3 ² , что равно 9, 3×9

   Шаг 5- Умножьте 3 на 9, чтобы получить окончательный ответ, то есть 3×9= 27

   ∴ ​(4×3÷6+1)×3 ² = 27.

перейти к слайдуперейти к слайду

Готовы увидеть мир глазами математика?

Математика — это жизненный навык. Помогите своему ребенку усовершенствовать его с помощью реального приложения.

Запись на бесплатный пробный урок

Практические вопросы по PEMDAS

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о PEMDAS

Что означает PEMDAS?

PEMDAS означает порядок операций для математических выражений, включающих более одной операции. Это означает P-круглые скобки, E-экспоненты, M-умножение, D-деление, A-сложение и S-вычитание.

Как работает правило Пемдаса?

В любом арифметическом выражении, если используется несколько операций, мы должны сначала решить члены, записанные в скобках. После избавления от круглых скобок решаем операции умножения и деления, что стоит первым в выражении слева направо. Тогда мы получим упрощенное выражение только с операциями сложения и вычитания. Мы решаем сложение и вычитание в порядке слева направо, что наступит раньше, и получаем окончательный ответ. Вот как работает PEMDAS.

Как сделать Пемдас с дробями?

В выражении с дробями нет изменений в использовании правила PEMDAS. Это должно быть сделано так же, как и любое целочисленное выражение.

Что означает буква P в слове Пемдас?

В PEMDAS буква P означает круглые или квадратные скобки. Порядок решения скобок задается как [{()}]. Это означает, что мы всегда сначала решаем самую внутреннюю скобку, а затем переходим к фигурным скобкам и квадратным скобкам.

Для чего нужен калькулятор PEMDAS?

Все мы очень хорошо разбираемся в наборе арифметических операций, таких как сложение, вычитание, умножение и деление. PEMDAS — это набор правил, которым следуют при решении математических выражений. Чтобы легко и быстро упростить любое арифметическое выражение, мы используем калькулятор PEMDAS. Попробуйте калькулятор Cuemath PEMDAS — бесплатный онлайн-инструмент, который поможет вам решать математические выражения и получать ответы одним щелчком мыши.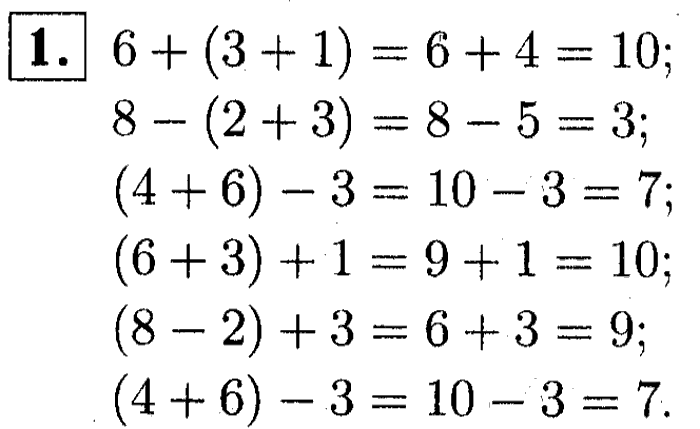

Вы сначала умножаете или делите в PEMDAS?

В правиле PEMDAS мы решаем операции умножения и деления слева направо. Мы можем выполнять любую операцию, умножение или деление, что бы ни стояло первым в выражении.

Когда мы применяем правило PEMDAS?

Правило PEMDAS применяется для решения сложных математических выражений, включающих несколько операций, таких как сложение, вычитание, умножение или деление.

☛Также проверьте:

Попробуйте эти БЕСПЛАТНЫЕ рабочие листы прямо сейчас, чтобы попрактиковаться в правилах PEMDAS.

• Рабочие листы PEMDAS 5-й класс
• Порядок операций — рабочие листы PEMDAS

Каково правило для PEMDAS?

Правило PEMDAS дает нам правильную последовательность для решения математического выражения. В правиле PEMDAS операции сначала выполняются в круглых скобках. Далее выполняются операции над показателями или степенями. Далее следуют операции умножения или деления слева направо, в зависимости от того, что наступит раньше.