2 это четное число или нечетное: Чётные и нечётные числа — урок. Математика, 2 класс.
Четное число | это… Что такое Четное число?
ТолкованиеПеревод
- Четное число
Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет — нечётным (примеры: 1, 3, 75, −19). Нуль считается чётным числом. [1]
Чётное число — целое число, которое делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…
Нечётное число — целое число, которое не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…
Иными словами, чётные и нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.
Содержание
- 1 Признак чётности
- 2 Арифметика
- 3 История и культура
- 4 Примечания
Признак чётности
Если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.

42, 104, 11110, 9115817342 — чётные числа.
31, 703, 78527, 2356895125 — нечётные числа.Арифметика
- Сложение и вычитание:
- Чётное ± Чётное = Чётное
- Чётное ± Нечётное = Нечётное
- Нечётное ± Чётное = Нечётное
- Нечётное ± Нечётное = Чётное
- Умножение:
- Чётное × Чётное = Чётное
- Чётное × Нечётное = Чётное
- Нечётное × Нечётное = Нечётное
- Деление:
- Чётное / Чётное — однозначно судить о чётности результата невозможно (если результат целое число, то оно может быть как чётным, так и нечётным)
- Чётное / Нечётное = если результат целое число, то оно Чётное
- Нечётное / Чётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
- Нечётное / Нечётное = если результат целое число, то оно Нечётное
История и культура
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение.
 Так, в древнекитайской мифологии нечётные числа соответствовали Инь, а чётные — Ян.
Так, в древнекитайской мифологии нечётные числа соответствовали Инь, а чётные — Ян.В разных странах существуют связанные с количеством даримых цветов традиции, например в США, Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье. В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.
Примечания
- ↑ «Чётные числа» в БСЭ.
Wikimedia Foundation. 2010.
Игры ⚽ Поможем сделать НИР
Синонимы:
чет
- Четмэн Вернон
- Четность функции
Полезное
Как определить четное или нечетное число в Python
Главная » Python для начинающих
На чтение 2 мин Просмотров 83.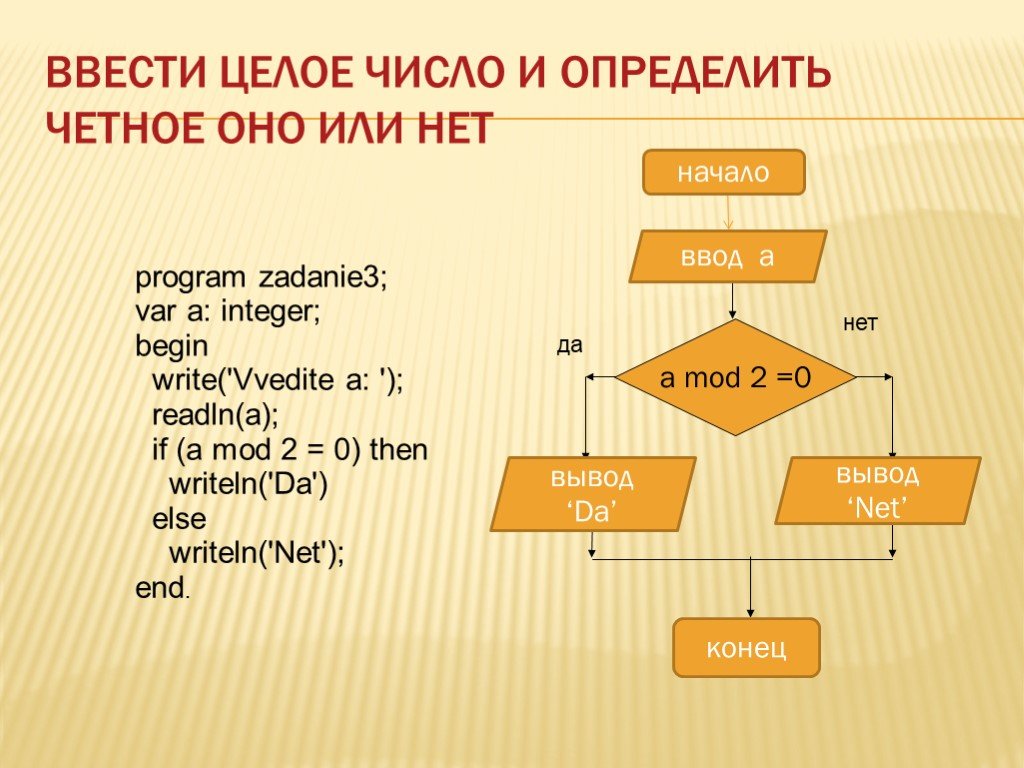 8к. Опубликовано
8к. Опубликовано
Для того чтобы определить четное число введено или нет в Python необходимо воспользоваться оператором «Остаток деления» и написать условие.
Содержание
- Оператор вычисления остатка от деления
- Определения четности числа с помощью оператора остатка от деления
- Написание функции для определения четности числа
В языке программирования Python, также как и в других языках программирования, есть команда — оператор (%), который вычисляет остаток от деления на число. Приведем примеры:
4 % 2 >>>0 5 % 2 >>>1 20 % 10 >>>0 25 % 10 >>>5
При делении числа 4 на 2 — остаток 0. При делении числа 5 на 2 — остаток 1. При делении числа 20 на 10 — остаток 0. При делении числа 25 на 10 — остаток 5.
Определения четности числа с помощью оператора остатка от деления
Мы знаем, что при делении четного числа на 2 у нас в остатке остается 0. Поэтому для определения четного и нечетного числа можем воспользоваться оператором остатка от деления. Напишем для этого условие:
Поэтому для определения четного и нечетного числа можем воспользоваться оператором остатка от деления. Напишем для этого условие:
a = 5
if a % 2 == 0:
print('Четное число')
else:
print('Нечентное число')
>>> Нечетное числоВ начале присваиваем переменной a число, четность которого хотим проверить. Далее пишем условие: если остаток деления переменной a на 2 равно 0, то вывести на экран «Четное число», в противном случае вывести «Нечетное число».
При запуске написанного кода, мы увидим «Нечетное» число.
Написание функции для определения четности числа
Можем написать функцию, которая на входе будет получать число, а на выходе выводить на экран «Четное число» или «Нечетное число» в зависимости от четности полученного числа.
def even_or_odd(a):
if a % 2 == 0:
print('Четное число')
else:
print('Нечентное число')
even_or_odd(10)
>>> Четное число
even_or_odd(11)
>>> Нечетное числоРазберем написанный код.
Как видим, определить четность числа — это довольно простая задача, которая быстро решается с помощью оператора остатка от деления (%).
( 23 оценки, среднее 3.96 из 5 )
Сумма двух нечетных чисел четна
Мы хотим показать, что если мы сложим два нечетных числа , то сумма всегда будет четным числом .
Прежде чем мы даже напишем фактическое доказательство, нам нужно убедиться, что в данном утверждении есть доля правды. Мы можем проверить утверждение на нескольких примерах.
Я подготовил таблицу ниже, чтобы собрать результаты некоторых чисел, которые я использовал для проверки утверждения.
Похоже, что утверждение, что сумма двух нечетных чисел четна, верно. Однако простое приведение бесконечного множества примеров не является доказательством. Невозможно перечислить все возможные случаи.
Вместо этого нам нужно показать, что утверждение справедливо для ВСЕХ возможных случаев. Единственный способ добиться этого — выразить нечетное число в его общей форме. Затем мы складываем два нечетных числа, записанных в общей форме, чтобы получить сумму четного числа, также выраженную в общей форме.
Чтобы написать доказательство этой теоремы, вы уже должны иметь четкое представление об общих формах как четных, так и нечетных чисел.
- Четные числа
Число n равно и даже , если его можно выразить как
n=2k
, где k — целое число.
- Нечетные числа
С другой стороны, число n равно нечетному , если его можно записать как
n=2k+1
, такое что k — некоторое целое число.
Примечание: Цель мозгового штурма при письменном доказательстве состоит в том, чтобы мы поняли, что пытается передать теорема; и соберите достаточно информации, чтобы соединить точки, которые будут использоваться для соединения гипотезы и заключения.
Возьмем два произвольных нечетных числа 2a + 1 и 2b + 1, где a и b — целые числа.
Поскольку нам нужна сумма, мы хотим добавить 2a + 1 и 2b + 1.
\left( {2a + 1} \right) + \left( {2b + 1} \right)
что дает us
\left( {2a + 1} \right) + \left( {2b + 1} \right) = 2a + 2b + 2.
Обратите внимание, что мы не можем объединить 2a и 2b, потому что они не похожи условия. Однако нам удалось объединить константы, таким образом, 1 + 1 = 2,
.Что нам делать дальше? Если подумать, то в 2a + 2b + 2 есть общий делитель 2. Если вычесть 2, мы получим 2\left( {a + b + 1} \right).
Что дальше? Что ж, если мы заглянем внутрь скобок, станет очевидно, что перед нами просто целое число. Сначала оно может не отображаться как целое число, потому что мы видим, как складываются несколько целых чисел.
Сначала оно может не отображаться как целое число, потому что мы видим, как складываются несколько целых чисел.
Вызов свойства замыкания сложения для набора целых чисел.
Предположим, что a и b принадлежат множеству целых чисел. Сумма a и b, равная {a+b}, также является целым числом.
На самом деле, вы можете расширить это свойство замыкания сложения до более чем двух целых чисел. Например, сумма целых чисел -7, -1, 0, 4 и 10 равна 6, что также является целым числом. Таким образом,
(-7)+(-1)+0+4+10=6.
Возвращаясь к тому месту, где мы остановились, в 2\left( {a + b + 1} \right) выражение внутри круглых скобок является просто целым числом, поскольку сумма целых чисел a, b и 1 является просто другим целым числом . Для простоты назовем его целым числом k.
Итак,
а+б+1=к
Это означает, что 2\left( {a + b + 1} \right) может быть выражено как
2\влево( {а + б + 1} \вправо) =2k
, где 2k — это общая форма четного числа. Похоже, мы успешно добились того, что хотели показать, что сумма двух шансов четная.
Похоже, мы успешно добились того, что хотели показать, что сумма двух шансов четная.
НАПИШИТЕ ДОКАЗАТЕЛЬСТВО
ТЕОРЕМА: Сумма двух нечетных чисел является четным числом.
ДОКАЗАТЕЛЬСТВО:
Другие доказательства, которые могут вас заинтересовать:
Доказательство: сумма двух четных чисел является четным числом
Основы работы с четными и нечетными числами
Начнем с основных определений:
Четное : любое целое число, которое делится на 2. Примеры: 2, 4, 14.
Примеры: 2, 4, 14.
Нечетное : любое целое число, которое делится на 2. не делится на 2, т. е. оставляет в остатке 1 при делении на 2. Примеры: 1, 3, 5, 7, 9
Пока все хорошо. Рассмотрим это потенциальное заблуждение:
0 четный или нечетный? При делении 0 на 2 получается 0 ÷ 2 = 0. Другими словами, 0 делится на 2. Следовательно, ноль соответствует критериям, установленным для четных целых чисел. Следовательно, ноль четный. Ноль нейтрален, когда речь идет о положительных и отрицательных числах, т.е. ноль не является ни положительным, ни отрицательным — он нейтрален. Не путайте это с четным и нечетным. Но ноль делится на 3, 5 и 7…. также? Тот факт, что ноль делится и на другие нечетные целые числа (и да, ноль делится на 3, 5, 7 или любое другое целое число, кроме самого себя), не имеет значения. Определение четного или нечетного числа имеет отношение только к делимости на 2. |
Запомните этот факт: Ноль четен.
Нечетные и четные целые числа также могут быть отрицательными; например, ?7 нечетно, а ?18 четно.
Четные числа: {…., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ….}
Нечетные числа: {…., -9 , -7, -5, -3, -1, 1, 3, 5, 7, 9, ….}
Какое из следующих чисел НЕ является четным?
|
- 117 — нечетное число, поскольку оно не делится на 2.
- -4,222 — десятичное число. Десятичные значения не являются ни четными, ни нечетными.
- -2 — четное число, так как оно делится на 2.
- 0 — четное число, поскольку оно делится на 2.

- -2.2 — десятичное число. Десятичные значения не являются ни четными, ни нечетными.
- 100,002 — десятичное число. Десятичные значения не являются ни четными, ни нечетными.
- 498 — четное число, так как оно делится на 2.
Как и у большинства людей, сдающих GRE, ваши знания по математике могут быть немного заржаветыми. Хорошей новостью является то, что GRE проверяет вас только по математике, которую вы уже выучили в старшей школе. Если вы переживаете, что забыли большую часть того, что выучили в старшей школе, вы…
подробнее
Стандартное отклонение – важный статистический термин, проверенный на GRE. Это дает вам представление об отклонении или разбросе набора чисел от его среднего значения; следовательно, низкое стандартное отклонение означает, что числа очень близки к среднему, и наоборот….
читать дальше
Каждое целое число больше 1 является либо простым, либо составным числом. Все составные числа можно представить в виде произведения простых чисел. Например, 6 можно выразить как 2 × 3. Простые делители числа 6 — это 2 и 3. Тогда как выражение 2 × 3 называется…
Все составные числа можно представить в виде произведения простых чисел. Например, 6 можно выразить как 2 × 3. Простые делители числа 6 — это 2 и 3. Тогда как выражение 2 × 3 называется…
подробнее
Давайте посмотрим, как мы используем диаграмму, чтобы ответить на этот вопрос: сколько положительных факторов имеет 100? Настройте диаграмму: 100 Левая колонка Правая колонка 1 100 2 50 4 25 5 20 10 10 Помните правило: как только факторы повторяются (например, 10 и 10), остановитесь. С…
читать далее
Вы уже видели прекрасную таблицу множителей — простой способ найти все множители целого числа. Давайте посмотрим, как мы используем диаграмму, чтобы ответить на этот вопрос: сколько положительных факторов имеет число 140? Вопрос касается факторов, поэтому таблица факторов…
подробнее
Некоторые целочисленные вопросы могут потребовать от вас найти множители целого числа. Таблица множителей — это основной метод нахождения всех множителей любого целого числа. Этот метод также может быть полезен для вопросов о том, сколько множителей имеет конкретное целое число. Техника…
Таблица множителей — это основной метод нахождения всех множителей любого целого числа. Этот метод также может быть полезен для вопросов о том, сколько множителей имеет конкретное целое число. Техника…
подробнее
Простые числа играют центральную роль в целочисленных вопросах. Излишняя самоуверенность здесь опасна: в то время как почти каждый может без труда назвать определение простого числа, поле на самом деле изобилует неправильными представлениями. Мы здесь, чтобы убедиться, что вы знаете все…
подробнее
Сформулируем правила сложения, вычитания, умножения и деления четных и нечетных чисел. Вот правила сложения/вычитания четных и нечетных чисел: Четные ± четные = четные (например, 2 + 2 = 4; -4 – 2 = -6) Нечетные ± нечетные = четные (например, 1 + 1 = 2; -31 – 1 = -32)…
подробнее
Найдите остаток от деления 5 142 376 298 на 9? Метод длинного деления точно скажет вам остаток от деления 5 142 376,29.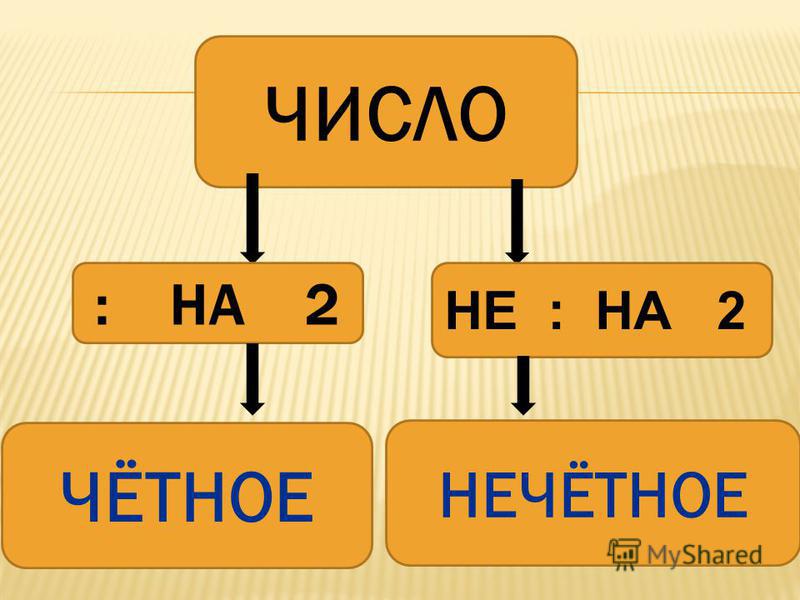

 Например, 6 является четным числом, потому что оно делится на 2. 6 также делится на 3, но это не имеет значения.
Например, 6 является четным числом, потому что оно делится на 2. 6 также делится на 3, но это не имеет значения.