2 число это четное или нечетное: Чётные и нечётные числа — урок. Математика, 2 класс. – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Назовите два нечетных числа, которые в сумме дают нечетное число. — Спрашивалка

А.

Акира …………

Назовите два нечетных числа, которые в сумме дают нечетное число. число сумма

6 лет

998

Ответы

Александр Себихов

Хм… Порассуждаем… Если говорится о нечётных числах, то речь идёт ТОЛЬКО о целых числах. Формула нечётных чисел z=2k +1 или 2n+1, где k и n – целые числа! Сложим их: 2k+1 + 2n+1= 2(k+n)+2=2(k+n+1) – получилось чётное число, поскольку k+n+1=m – целое число, а 2m – чётное число! ВЫВОД: Сумма двух любых нечётных чисел всегда является чётным числом! (На всякий случай напомню, что 0 – чётное число! Ну и ещё то, что сумма целых чисел тоже всегда целое число!)

6 лет

Александр Кузнецов

нет таких при данной формулировке! а вот если бы вы составили примерно так: “назовите два числа, которые не являются четными и которые в сумме дают нечетное число!”, вот тогда они существуют (0 и любое нечетное! а в вашем вопросе нельзя использовать 0, т. к. он не является ни четным ни нечетным!)

6 лет

Алексей Кучеренко

Любое нечетное число можно представить в виде 2n+1 или 2n-1, где n — целое число.
Сложение и вычитание:
Чётное ± Чётное = Чётное
Чётное ± Нечётное = Нечётное
Нечётное ± Нечётное = Чётное

Умножение:
Чётное × Чётное = Чётное
Чётное × Нечётное = Чётное

Нечётное × Нечётное = Нечётное

6 лет

А.

Акира …………

Долго гуглил?)

6 лет

Алексей Кучеренко

не люблю много писать, а так это за первый класс материал – удивила безграмотность народа.

6 лет

ВД

Вячеслав Дамер

Четные и нечетные числа обладают замечательными свойствами:

а) сумма двух четных чисел четна;

б) сумма двух нечетных чисел четна;

в) сумма четного и нечетного чисел — нечетное число

6 лет

Раджа

Так как в условии Вы не уточнили, числа целые или дробные, то могу предположить, что это могут быть числа 1 и 1,5. В сумме дают нечётное дробное число. Или два одинаковых числа, например 1,5+1,5=3

6 лет

ТП

Ту Пой

по определению, нечетное число это четное плюс один. т.е. два нечетных в сумме дадут два четных плюс два.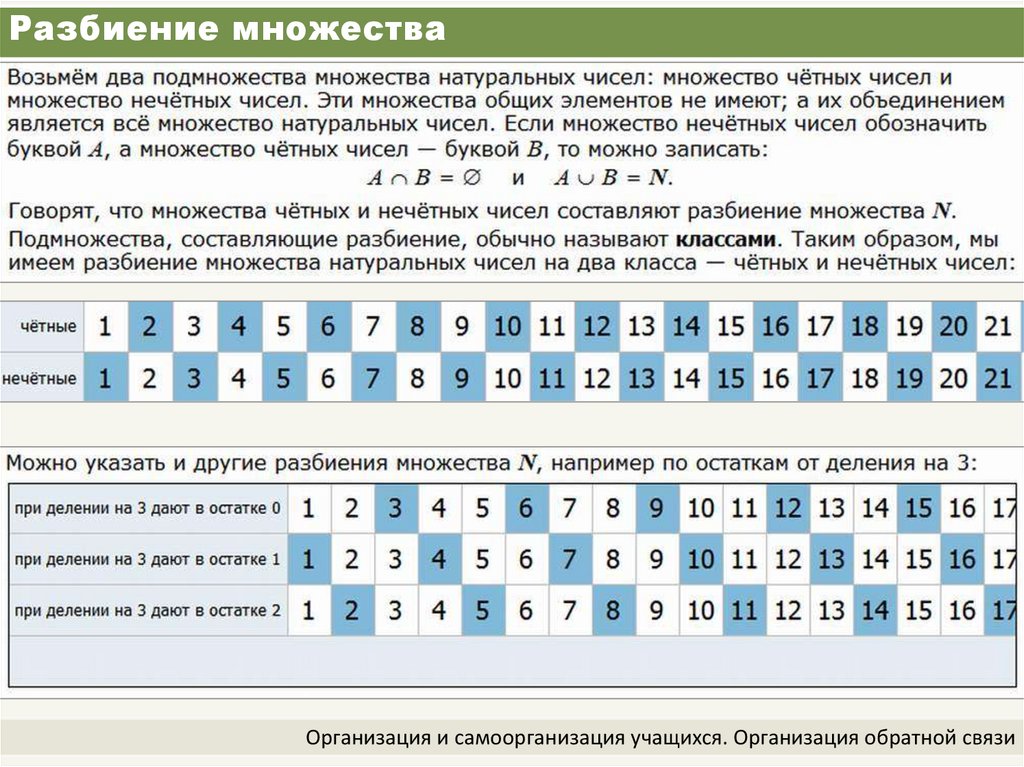 так что фигу.

6 лет

бн

бофайтер нагато

Адын адын

6 лет

(((Сергей))) *

Ноль четное число, а значит такого не может быть )))) Ну если только не выдуманное какое – нибудь….. )))))

6 лет

А.

Акира …………

Листайте ответы

6 лет

Крысанов Андрей

жмоты они , нечетные, как по 2 соберутся, никогда не дадут нечетное в сумме

6 лет

Кручинин Владимир

две единички образуют тройку в двоичной системе счисления

6 лет

Александр Жук Эстония Таллин

Без уловки не получится такое ,а уловку не вспомнить никак

6 лет

А.

Акира …………

Печально

6 лет

Александр Жук Эстония Таллин

Значит не возможнно назвать такие числа

6 лет

Юрий Наумов

Сумма двух нечётных чисел всегда есть число чётное.

6 лет

Игорь Крылов

меня знакомые от водки полегли, а от наркотиков сидят.

6 лет

Геннадий Сергеевич (Ни С Кем Не Знакомлюсь Пошли Все Нах.

это могут быть не полные числа 2,5+2,5 1,5+1,5 и так далее

6 лет

Дмитрий Самойленко

Нет таких. Сумма двух нечетных чисел вроде четная.

6 лет

СБ

Станислав Бондаренко

Я не математик, но наверное с “нулём” любое……….

6 лет

А.

Акира …………

нет

6 лет

СБ

Станислав Бондаренко

Извиняюсь…….

6 лет

ДБ

Диана Белова

Не существует

6 лет

Олег Плохотник

нет таких чисел ,если только считать 0 нечетным

6 лет

Алемжан

В десятичном исчислении не бывает

6 лет

ВВ

Василий Васильев

Просвети. .. а то спать не смогу…

6 лет

А.

Акира …………

ШТО? Ты ломаешь мой мозг

6 лет

ВВ

Василий Васильев

А он там есть?

6 лет

А.

Акира …………

Да

6 лет

ВВ

Василий Васильев

Везёт…

6 лет

А.

Акира …………

Канешно

6 лет

Люцифер Морнингстар

таких чисел нет . (2а+1)+(2б+1)=2(а+б+1)

6 лет

Карлсон

Неприменимо для целых чисел.

6 лет

Денис Розов(Эксперт, Модератор)

ОО математика пошла.-1 +-2 =-3.

6 лет

А.

Акира …………

2-четное число

6 лет

Денис Розов(Эксперт, Модератор)

ААА.)..А в чем прикол то.Полтора.можно пременить.

6 лет

Ник Ци

1 и любое другое нечётное

6 лет

А.

Акира …………

Получается четное

6 лет

ВМ

Виталий Михальченко

Прости! Заябала ! Ты меня!

6 лет

Василий Про

С целыми это невозможно.

6 лет

Наталия Васильевна

ну, например 3,5 + 5,5 =9

6 лет

Следующая страница

Другие вопросы

Что можно поделать: D. Я одна дома ( Мне очень очень скучно, только не пишите погуляй, покушай, поспи: Р

Как приготовить филе индейки

LG sinema smart 3D можно-ли записать фильм на флешку

Есть ли 4 часть книги Алексея Доронина Чёрный День?

кто помнит мультик когда был по айситиви про парня из помпей, что-то такое. подскажите пожалуйста название….

из какого аниме эта картика

Привет! сегодня прочитал про усыпление человека (оно же ”мультики посмотреть”). говорят классно и отрубаешься на 1 мин

Что делать? Подскажите пожалуйста

Можно ли есть варёную рыбу с свежей сметаной?

Как сделать некачественные мыльны пузыри?

Как то давно в школе ..-

хочу сделать напробу капусту вот рецепт посоветуйте

4 фотки 1 слово помогите <noindex> http://s019.radikal.ru/i632/1303/98/c849eeb749c5.jpg </noindex>

надо написать рассказ на тему что я пожилел? лпмл

Добавляете ли вы в замес для драников оливковое масло?

Четные и нечетные числа | Образовательная социальная сеть

Районная научно – практическая конференция учащихся и педагогов

Предмет «математика»

Номинация «Реферат проблемно – поискового характера»

Тема: «Четные и нечетные числа»

Автор: Шнякина Алина учащаяся 5 класса

МОБУ «Рыбкинская средняя общеобразовательная школа»

Учитель: Окшина Л. А.

2011 – 2012 учебный год

МОБУ «Рыбкинская средняя общеобразовательная школа»

Чётные и нечётные числа.

/Реферат/

Работу выполнила

ученица 5 класса

Шнякина Алина.

Работу проверил

учитель математики

Окшина Л. А.

с. Рыбкино 2012г.

Оглавление

Введение 4

Основная часть 5

Определение. Свойства. 5

Традиции 6

Пифагорейская теория чисел 8

Нумерология 10

Вывод 12

Литература 13

Введение.

Цель: узнать, почему четным и нечетным числам приписывают различный смысл.

Задачи:

Найти определение и свойства четных и нечетных чисел.
Какие традиции в различных странах связаны с числами?
Как четные и нечетные числа применяются в нумерологии?

План:

Введение.
Основная часть.

Определение. Свойства;

Традиции;
Пифагорейская теория чисел;
Нумерология.

Вывод.

Актуальность.

Еще в древности люди отмечали влияние чисел и зависимость судьбы от совпадения или, наоборот, невыпадения определенных чисел, а также цикличность всего происходящего в мире. Не философы и не мыслители, скорее всего, вообще в своей массе простые и не слишком образованные люди очень верно выражали это в сказках и мифах, где чаще всего фигурируют тройка и семерка.

В сказках жили-были три богатыря, трое или семеро сыновей, семь гномов, а царство числилось тридевятым! Чтобы не сглазить свою удачу, люди традиционно трижды сплевывали (и сейчас тоже!) через левое плечо или стучали по дереву. Особо любимые числа часто встречаются в пословицах и поговорках: «Бог троицу любит», «семеро одного не ждут», «семь раз отмерь, один раз отрежь»…

Почему в основном в сказках применяются нечетные числа?

Почему на день рождения дарят нечетное число цветов? И еще много вопросов встало передо мною.

Я решила узнать об этом. Нашла материал и начала своё исследование.

Основная часть.

Определение.

Чётное число — целое число, которое делится без остатка на 2: например: 2, 4, 6, 8, …
Нечётное число — целое число, которое не делится без остатка на 2: например: 1, 3, 5, 7, 9, …

В соответствии с этим определением нуль является чётным числом.

Если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.

42, 104, 11110, 9115817342 — чётные числа.

31, 703, 78527, 2356895125 — нечётные числа

Свойства.

Сложение и вычитание:

Чётное ± Чётное = Чётное
Чётное ± Нечётное = Нечётное
Нечётное ± Чётное = Нечётное
Нечётное ± Нечётное = Чётное

Умножение:

Чётное × Чётное = Чётное
Чётное × Нечётное = Чётное
Нечётное × Нечётное = Нечётное

Деление:

Чётное / Чётное — однозначно судить о чётности результата невозможно (если результат целое число, то оно может быть как чётным, так и нечётным)
Чётное / Нечётное = если результат целое число, то оно Чётное
Нечётное / Чётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
Нечётное / Нечётное = если результат целое число, то оно Нечётное.

Традиции.

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. В разных странах существуют традиции, связанные с количеством даримых цветов.

Например, в Европе, США и некоторых государствах востока существует поверье, что четное количество цветов приносит счастье.

По российским традициям четное количество цветов приносят на похороны, а живому человеку пристало дарить цветы только в нечетном количестве.
Существует несколько версий о происхождении этой традиции.
Языческие верования трактуют четные числа – как символы смерти и зла. Помните поговорку «беда не приходит одна»? Именно из следования этой традиции и пошел обычай дарить живым людям только четное количество цветов.

Многими древними культурами, парные числа связывались с законченностью, завершением, в данном случае – жизненного пути. Нечетное число, (кроме 13) напротив, символ счастья, успеха, везения. Нечетные числа нестабильны, они символизируют движение, жизнь, смех. Четные – символ умиротворенности и покоя.

Для древних пифагорейцев олицетворением добра, жизни, света были нечетные числа, а еще они символизировали правую сторону (сторону удачи). Неудачливую же левую сторону, и вместе с ней смерть, зло, тьму – символизировали четные числа.

Не отсюда ли пошло знаменитое «встать с левой ноги», символизирующее неудачное начало дня? В японской культуре числа 1,3,5 обозначают мужское начало «янь» и говорят о жизни, силе, движении. Числа 2,4,6, – это женское начало «инь», покой, пассивность. В Японии не принято дарить живым людям четыре цветка, потому что число 4 символизирует смерть.

Израильтяне, наоборот – дарят четное количество цветов, а вот на похороны цветы не приносят. В Грузии считают, что все связанное с семейными ценностями приносит счастье, поэтому два цветка (пара) – удачное сочетание, а на кладбище несут нечетное количество цветов «чтобы покойный пару не забрал с собой». Европеец и американец может с наилучшими намерениями подарить русской девушке 8 или 10 роз, и искренне удивиться ее реакции.

Стоит отметить, что столь придирчивый счет цветов имеет место лишь до дюжины. После этого количества не имеет значение четное или нет количество стеблей в букете. Ведь, пресловутый «миллион алых роз» – имеет четное количество цветов.

Во многих сказках^[1] мы встречаем разные числа. Чаще всего это числа ТРИ и СЕМЬ.

Число «3» издревле считали магическим. Даже в библии бог предстает в триедином лице. 3- это божественное совершенство. Известно выражение: Бог троицу любит.

Цифра «3» в сказках наталкивает читателя на мысль о волшебстве, о совершенстве. Ведь в русских сказках всегда желания исполняются только в третий раз.

«Три девицы под окном

Пряли поздно вечерком».

«И очутятся на бреге,

В чешуе как жар горя,

Тридцать три богатыря.»

7 – число особое. Так, известно, что жрецы Вавилона поклонялись семи богам. Символика числа 7 характерна и для библейских сюжетов. Богословы трактуют это число как соединение числа 3-божественного совершенства и 4 –мирового порядка.

В русских поговорках и пословицах слово «семь» часто выступает в значении «много»: «Семеро одного не ждут», «Семь раз отмерь – один раз отрежь», «Семь бед – один ответ», «Лук от семи недуг» и т. д. В сказке А.С. Пушкина число 7 тоже имеет значение «много»: «семь богатырей, семь румяных усачей».

В приданое царевне было дано «семь торговых городов да сто сорок теремов».

А вот с четными числами есть суеверное представление: оно связано со смертью, с нечистой силой.

Значит, выбор числительных в сказках основан на народном представлении о значении чисел.

Пифагорейская теория чисел.

Пифагор^[2] определяя число как энергию и считал, что через науку о числах раскрывается тайна Вселенной, ибо число заключает в себе тайну вещей.

Проникая в свойства чисел, объясняя их различные сочетания, Пифагор пытался создать науку всех наук. Все числа он разделил на два вида: четные и нечетные, и с удивительной чуткостью выявил свойства чисел каждой группы. Четные числа обладают следующими свойствами: любое число может быть разделено на две равные части, обе из которых либо четны, либо нечетны. Например, 14 делится на две равные части 7 + 7, где обе части нечетные; 16 = 8 + 8, где обе части четные. Пифагорейцы рассматривали четное число, прототипом которого была дуада^[3], неопределенным и женским.

Четные числа Пифагор делил на 3 класса: четно-четные, четно-нечетные, нечетно-нечетные.

Четно – четные – числа, которые представляют собой удвоение чисел, начиная с единицы. Таким образом, это 1,2,4,8,16,32,64,128,512 и 1024. Совершенство этих чисел Пифагор видел в том, что они могут делиться пополам и еще раз, и так далее до получения единицы.

Четно-нечетные числа – это числа, которые будучи разделены пополам не делятся.

Нечетно-нечетные числа неоднократно делятся пополам, но при делении не придут к 1.

Нечетные числа не могут быть разделены равным образом, то есть поровну. Пифагор объяснял неспособность таких чисел делится пополам следующим образом: поскольку 1 всегда остается не делимой, нечетное число таким же образом не может быть делимым. Если нечетное число попытаться разделить поровну, то получается два четных числа, а последнее из них единица, которая является неделимой. Например, 9 есть 4+4+1.

Нечетные числа имеют и такое свойство – если какое-либо нечетное число разделить на две части, одна всегда будет четной, а другая – всегда нечетной.

Пифагорейцы рассматривали нечетное число, прототипом которого была монада^[4], определенным и мужским, хотя по поводу 1 (единицы) среди них существовали определенные разногласия.

Нечетные числа делятся на 3 общих класса: несоставные, составные и несоставные – составные.

Несоставные числа – это такие числа, которые не имеют других делителей, кроме себя самого и единицы. Это числа 3,5,7,11,13,17 и т.д.

Составные числа – это числа, делимые не только сами на себя, но и на некоторые другие числа. Такими числами являются те из нечетных чисел, которые не входят в группу несоставных. Это числа 9,15,21,25,27,33,39 и т.д.

Несоставные – составные числа – эта числа, не имеющие общего делителя, хотя каждое из них делимо.

Обычаем у пифагорейцев было приношение высшим богам нечетного числа предметов, в то время как богиням и подземным духам приносить четное число.

Все числа представляют собой чет и нечет, точно так же и все вещи и процессы соединяют в себе противоположности – начало и конец, предел и бесконечность. Каждое явление или вещь Пифагор рассматривал как примирение противоположностей – гармонию. Поиск внутреннего различия и гармонии всей реальности посредством числа объединял Бога, душу и природу в единое целое. Знать природу и числа, ее определяющие, значит, по мнению ученого, знать Бога.

Нумерология.^[5]

А можно ли узнать, сколько радостей, счастливых дней, бед и несчастий предназначено в жизни каждому из нас? В поисках ответа люди издавна по своим наблюдениям стали приписывать цифрам особый магический смысл. Это позволило растолковать зависимость явлений от чисел и объяснить их законы. Так зарождалась наука о числах – нумерология. Особая роль в становлении нумерологии принадлежит великому Пифагору – древнегреческому философу и математику, который объединил математику с науками о природе человека.

Нумерология утверждает, что числа обладают определенными свойствами, которые они распространяют на все предметы и явления мира.

Чётные и нечётные числа применяются в нумерологии.

Во вселенной существуют пары противоположностей, которые являются важным фактором ее устройства. Основные свойства, которые нумерология приписывает нечетным (1, 3, 5, 7, 9) и четным (2, 4, 6, 8) числам, как парам противоположностей, следующие:

1 – активный, целеустремленный, властный, черствый, руководящий, инициативный;

2 – пассивный, восприимчивый, слабый, сочувствующий, подчиненный;

3 – яркий, веселый, артистичный, удачливый, легко добивающийся успеха;

4 – трудолюбивый, скучный, безынициативный, несчастный, тяжелый труд и частое поражение;

5 – подвижный, предприимчивый, нервный, неуверенный;

6 – простой, спокойный, домашний, устроенный; материнская любовь;

7 – уход от мира, мистика, тайны;

8 – мирская жизнь; материальная удача или поражение;

9 – интеллектуальное и духовное совершенство.

Нечетные числа обладают гораздо более яркими свойствами. Рядом с энергией “1”, блеском и удачливостью “3”, авантюрной подвижностью и многогранностью “5”, мудростью “7” и совершенством “9” четные числа выглядят не столь ярко. Насчитывается 10 основных пар противоположностей, существующих во Вселенной. Среди этих пар: четное – нечетное, один – много, правое – левое, мужское – женское, добро – зло. Один, правое, мужское и доброе ассоциировалось с нечетными числами; много, левое, женское и злое – с четными.

Мужские свойства нечетных чисел вытекают из того факта, что они сильнее четных. Если четное число расщепить пополам, то, кроме пустоты, посередине ничего не останется. Нечетное число разбить непросто, потому что посередине остается точка. Если же соединить вместе четное и нечетное числа, то победит нечетное, так как результат всегда будет нечетным. Именно поэтому нечетные числа обладают мужскими свойствами, властными и резкими, а четные – женскими, пассивными и воспринимающими.

Нечетных чисел нечетное число: их пять. Четных чисел четное число – четыре.
Нечетные числа – солнечные, электрические, кислотные и динамичные. Они являются слагаемыми; их с чем либо складывают. Четные числа – лунные, магнетические, щелочные и статичные. Они являются вычитаемыми, их уменьшают. Они остаются без движения, потому что имеют четные группы пар (2 и 4; 6 и 8).

Если мы сгруппируем нечетные числа, одно число всегда останется без своей пары (1 и 3; 5 и 7; 9). Это делает их динамичными. Два подобных числа (два нечетных числа или два четных) не являются благоприятными.

четное + четное = четное (статичное) 2+2=4

четное + нечетное = нечетное (динамичное) 3+2=5

нечетное + нечетное = четное (статичное) 3+3=6

Некоторые числа дружественны, другие – противостоят друг другу. Взаимоотношения чисел определяются отношениями между планетами, которые ими управляют (подробности в разделе “Совместимость чисел”). Когда два дружественных числа соприкасаются, их сотрудничество не очень продуктивно. Подобно друзьям, они расслабляются – и ничего не происходит. Но когда в одной комбинации находятся враждебные числа, они заставляют друг друга быть настороже и побуждают к активным действиям; таким образом, эти два человека работают намного больше. В таком случае, враждебные числа оказываются на самом деле друзьями, а друзья – настоящими врагами, тормозящими прогресс. Нейтральные числа остаются неактивными. Они не дают поддержки, не вызывают и не подавляют активность.

Вывод.

В ходе работы я выяснила, что не зря Пифагор сказал «Число есть всё». Нечетные числа, особенно 3 и 7, являлись символом полноты, счастья. В сказках часто встречается тройка персонажей. А в радуге не случайно семь цветов, на свете семь чудес света, в неделе 7 дней. В Библии есть упоминание о семи светильниках, семи ангелах, о семи годах изобилия и семи – голода.

Еще с древних времен остались обычаи дарить четное или нечетное количество цветов, хотя в разных странах по – разному.

И еще я выяснила, что есть целая наука, которая занимается числами. Это нумерология. Числовые совпадения встречаются сплошь и рядом – в номерах телефонов и автомобилей, в адресах и номерах этажей, в датах рождения. Это не случайные совпадения, а вполне определенная зависимость, так называемая магия чисел. Числа не только позволяют измерять количества, но и обозначают свойства и качественные характеристики, обращают наше внимание на различные явления и могут о многом рассказать. Числа магическим, неотвратимым образом влияют на нашу жизнь, на самые разные события, и невозможно отрицать, что магия чисел существует. Надо только найти ключ к их тайному коду.

Я поняла, что, изучая числа и их роль, можно лучше понять историю своего народа по сказкам. Зная дату рождения, можно определить характер человека. Поэтому работа над этим рефератом мне очень понравилась.

Литература.

Людмила Большедворова. Нумерология. Коды жизни и судьбы. Введение. Немного о нумерологии.
Пропп В.Я. «Исторические корни Волшебной сказки»
http://ru. wikipedia.org
http://www.opakyl.ru/number.php?id=10
http://numerology.astrostar.ru/number/133702.html
http://ru.math.wikia.com/wiki/
http://skazvikt.ucoz.ru

[1] Пропп В.Я. «Исторические корни Волшебной сказки»

[2] Пифагор Самосский ( 570—490 гг. до н. э.) – древнегреческий философ, математик и мистик, создатель религиозно – философской школы пифагорейцев.

[3] Дуада – символ деления единого на противоположности.

[4] Монада (греч. monas – единица, единое)

[5] Людмила Большедворова. Нумерология. Коды жизни и судьбы. Введение. Немного о нумерологии.

Четное число и нечетное в экселе. Как четные и нечетные числа выделить разным цветом в Excel. Функция остат в excel для поиска четных и нечетных чисел

Четное число и нечетное в экселе. Как четные и нечетные числа выделить разным цветом в Excel. Функция остат в excel для поиска четных и нечетных чисел

Excel для Office 365 Excel для Office 365 для Mac Excel для Интернета Excel 2019 Excel 2016 Excel 2019 для Mac Excel 2013 Excel 2010 Excel 2007 Excel 2016 для Mac Excel для Mac 2011 Excel Starter 2010 Меньше

В этой статье описаны синтаксис формулы и использование функции ЕЧЁТН в Microsoft Excel.

Описание

Возвращает значение ИСТИНА, если число четное, и значение ЛОЖЬ, если число нечетное.

Синтаксис

ЕЧЁТН(число)

Аргументы функции ЕЧЁТН описаны ниже.

Число Обязательный. Проверяемое значение. Если число не является целым, оно усекается.

Замечания

Если значение аргумента “число” не является числом, функция ЕЧЁТН возвращает значение ошибки #ЗНАЧ!.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем – клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.

Например: -24, 0, 6, 38 — все это четные числа.

m = 2k — общая формула написания четных чисел, где k – целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.

Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.

Пример нечетных чисел: 3, 1, 7 и 35.

n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k – целое число.

Сложение и вычитание четных и нечетных чисел

В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.

Операция	Результат	Пример
Четное + Четное
Четное + Нечетное	Нечетное
Нечетное + Нечетное

Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.

Умножение четных и нечетных чисел

При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.

Операция	Результат	Пример
Четное * Четное
Четное * Нечетное
Нечетное * Нечетное	Нечетное

А теперь рассмотрим дробные числа.

Десятичная запись числа

Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.

Например: 3,14; 5,1; 6,789 — это все

С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.

Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.

Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.

А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом – дробную.

Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.

Стандартные функции

Первый способ возможен при использовании стандартных функций приложения. Для этого необходимо создать два дополнительных столбца с формулами:

Четные числа – вставляем формулу «= ЕСЛИ (ОСТАТ(число;2) =0;число;0)», которая вернет число, в случае если оно делится на 2 без остатка.
Нечетные числа – вставляем формулу «= ЕСЛИ (ОСТАТ(число;2) =1;число;0)», которая вернет число, в случае если оно не делится на 2 без остатка.

Затем необходимо определит сумму по двум столбцам с помощью функции «=СУММ()».

Плюсы данного способа в том, что он будет понятен даже тем пользователям, которые профессионально не владею приложением.

Минусы способа – приходится добавлять лишние столбцы, что не всегда удобно.

Пользовательская функция

Второй способ, является более удобным, чем первый, т.к. в нем применяется пользовательская функция, написанная на VBA – sum_num(). Функция возвращает сумму чисел в виде целого числа. Суммируются либо четные числа, либо нечетные, в зависимости от значения ее второго аргумента.

Синтаксис функции: sum_num(rng;odd):

Аргумент rng – принимает диапазон ячеек, по которым необходимо произвести суммирование.
Аргумент odd – принимает логическое значение ИСТИНА для четных чисел или ЛОЖЬ для нечетных.

Важно: Четными и нечетными числа могут являться только целые числа, поэтому числа, которые не соответствуют определению целого числа, игнорируются. Также, если значением ячейки является срока, то данная строка не участвует в расчете.

Плюсы: нет нужны добавлять новые столбцы; лучший контроль над данными.

Минусы заключаются в необходимости перевода файла в формат. xlsm для версий Excel, начиная с версии 2007. Также функция будет работать только в той книге, в которой она присутствует.

Использование массива

Последний способ является самым удобным, т.к. не требует создания дополнительных столбцов и программирования.

Его решение схоже с первым вариантом – они используют одни и те же формулы, но данный способ, благодаря использованию массивов, производит подсчет в одной ячейке:

Для четных чисел – вставляем формулу «=СУММ (ЕСЛИ (ОСТАТ(диапазон_ячеек;2) =0;диапазон_ячеек;0))». После ввода данных в строку формул нажимаем одновременно клавиши Ctrl + Shift + Enter, чем сообщаем приложению, что данные необходимо обрабатывать как массив, и оно заключит их в фигурные скобки;
Для нечетных чисел – повторяем действия, но изменяем формулу «=СУММ (ЕСЛИ (ОСТАТ(диапазон_ячеек;2) =1;диапазон_ячеек;0))».

Плюсом способа является то, что все рассчитывается в одной ячейке, без дополнительных столбцов и формул.

Минусом является лишь то, что неопытные пользователи могут не понять Ваших записей.

На рисунке видно,что все способы возвращают один и тот же результат, какой лучше, необходимо выбирать под конкретную задачу.

Скачать файл с описанными варианта можно по данной ссылке.

· Четные числа – это те, которые делятся на 2 без остатка (например, 2, 4, 6 и т.п.). Каждое такое число можно записать в виде 2K, подобрав подходящее целое K (например, 4 = 2 х 2, 6 = 2 х 3, и т.д.).

· Нечетные числа – это те, которые при делении на 2 дают в остатке 1 (например, 1, 3, 5 и т.п.). Каждое такое число можно записать в виде 2K + 1, подобрав подходящее целое K (например, 3 = 2 х 1 + 1, 5 = 2 х 2 + 1, и т.д.).

Сложение и вычитание:

- Ч ётное ± Ч ётное = Ч ётное
- Ч ётное ± Н ечётное = Н ечётное
- Н ечётное ± Ч ётное = Н ечётное
- Н ечётное ± Н ечётное = Ч ётное
Умножение:
- Ч ётное × Ч ётное = Ч ётное
- Ч ётное × Н ечётное = Ч ётное
- Н ечётное × Н ечётное = Н ечётное
Деление:
- Ч ётное / Ч ётное – однозначно судить о чётности результата невозможно (если результат целое число , то оно может быть как чётным, так и нечётным)
- Ч ётное / Н ечётное -– если результат целое число , то оно Ч ётное
- Н ечётное / Ч ётное – результат не может быть целым числом, а соответственно обладать атрибутами чётности
- Н ечётное / Н ечётное —если результат целое число , то оно Н ечётное

Сумма любого числа четных чисел – четно.

Сумма нечетного числа нечетных чисел – нечетно.

Сумма четного числа нечетных чисел – четно.

Разность двух чисел имеет ту же четность, что и их сумма .
(напр. 2+3=5 и 2-3=-1 оба нечетные)

Алгебраическая (со знаками + или -) сумма целых чисел имеет ту же четность, что и их сумма .
(напр. 2-7+(-4)-(-3)=-6 и 2+7+(-4)+(-3)=2 оба четны)

Идея четности имеет много разных применений. Самые простые из них:

1. Если в некоторой замкнутой цепочке чередуются объекты двух видов, то их четное число (и каждого вида поровну).

2. Если в некоторой цепочке чередуются объекты двух видов, а начало и конец цепочки разных видов, то в ней четное число объектов, если начало и конец одного вида, то нечетное число. (четное число объектов соответствует нечетному числу переходов между ними и наоборот !!! )

2″. Если у объекта чередуются два возможных состояния, а исходное и конечное состояния различны , то периодов пребывания объекта в том или ином состоянии – четное число, если исходное и конечное состояния совпадают – то нечетное . (переформулировка п.2)

3. Обратно: по четности длины чередующийся цепочке можно узнать, одного или разных видов ее начало и конец.

3″. Обратно: по числу периодов пребывания объекта в одном из двух возможных чередующихся состояний можно узнать, совпадает ли начальное состояние с конечным. (переформулировка п.3)

4. Если предметы можно разбить на пары, то их количество четно.

5. Если нечетное число предметов почему-то удалось разбить на пары, то какой-то из них будет парой к самому себе, причем такой предмет может быть не один (но их всегда нечетное число).

(!) Все эти соображения можно на олимпиаде вставлять в текст решения задачи, как очевидные утверждения.

Примеры:

Задача 1. На плоскости расположено 9 шестеренок, соединенных по цепочке (первая со второй, вторая с третьей… 9-я с первой). Могут ли они вращаться одновременно?

Решение: Нет, не могут. Если бы они могли вращаться, то в замкнутой цепочке чередовалось бы два вида шестеренок: вращающиеся по часовой стрелке и против часовой стрелки (для решения задачи не имеет никакого значения, в каком именно направлении вращается первая шестеренка ! ) Тогда всего должно быть четное число шестеренок, а их 9 штук?! ч. и.т.д. (знак “?!” обозначает получение противоречия)

Задача 2. В ряд выписаны числа от 1 до 10. Можно ли расставить между ними знаки + и -, чтобы получилось выражение, равное нулю?
Решение: Нет, нельзя. Четность полученного выражения всегда будет совпадать с четностью суммы 1+2+…+10=55, т.е. сумма всегда будет нечетной . А 0 – четное число?! ч.т.д.

Определите нечетное и четное число

Несколько дней назад, когда пользователи вводили основную информацию, чтобы посмотреть, какой метод заполнения у пользователя выше при заполнении информации, был проведен тест: он разделен на два случая: обязательное заполнение и пропуск, если он не завершен. По конечному номеру мобильного телефона пользователя определите четность, чтобы различить сцену, поэтому выходит тема этой статьи, метод определения нечетного и четного числа (всего два):
Метод 1: Найдите оставшийся%

1.if( x % 2 == 0)
         //Четный
      else
         //Странный
 2.  (x% 2 == 0)? Четное число: нечетное число

анализ:
Согласно определению нечетных и четных чисел, если целое число делится на 2 без остатка, это четное число, в противном случае – нечетное число.
Следовательно, остаток от четного числа равен 0, а остаток от нечетного числа не равен нулю.
В суждении if (условие), если условие не равно нулю, это означает, что условие выполнено, в противном случае это означает, что условие не выполняется (то есть оператор после if () не выполняется)
?: ситуация аналогичная.
Метод 2: И 1 фаза и (& 1)

1.if( x & 1 == 0)
    //Четный
      else
         //Странный
 2. (x & 1 == 0)? Четное число: нечетное число

анализ:
Во-первых, вы должны знать, как использовать побитовую операцию И &
побитовая операция И a & b
Соответствующими двоичными битами двух чисел, участвующих в операции, является И, только если оба соответствующих двоичных бита равны 1, бит результата равен 1, в противном случае – 0. 0, то есть десятичное число является нечетным числом Четный он или нет, зависит от того, является ли младшая цифра в двоичном коде 0 или 1.

Наконец, в этой статье упоминаются:http://blog.csdn.net/u013162593/article/details/17473331

Интеллектуальная рекомендация

Решите метод «Доступ к базе данных метаданных IIS»

Доступ к метаданным IIS потерпел неудачу. иллюстрировать:Во время текущего веб -запроса возникают необработанные аномалии. Пожалуйста, проверьте информацию о отслеживании стека, чтобы понять подробную…

JMeter Обзор (4) Отчет

1. Просмотр результата с формой(View Results in Tables) Щелкните правой кнопкой мыши на соответствующем меню – Add-Listener – Просмотр результатов Пример #: номер серии. Время начала: Время начала каж…

Понимание шаблонов проектирования MVC и MVVM

Понимание шаблонов проектирования MVC и MVVM Шаблон проектирования MVC (без прямого взаимодействия между представлением и моделью) MVC – это архитектурный шаблон, M означает модель, V означает предста. ..

Используйте VirtualBox для установки эталонной тестовой среды Ubuntu10 (ZZ)

Окружающая среда: Хост операционная система Windows XP sp3 Программное обеспечение для виртуальных машин VirtualBox VirtualBox Операционная система виртуальной машиныUbuntu(Linux) 1. Сделать ви…

Программирование NIO (использование отметки и сброса)

Отметить и сбросить использование Метка является индексом.Конкретная позиция в буфере указывается методом mark () в буфере, а затем ее можно восстановить в эту позицию, вызвав метод reset (). Пример и…

Проект 2: система управления и обслуживания Linux

Трещина и обслуживание задачи четыре пароля корневой учетной записи [Описание задания] Учет корневого аккаунта является супер администратором в операционной системе Linux, и если новые п…

“#Ifdef __cplusplus extern” C “{#endif” определение

Основной эффект: Чтобы вызвать файл библиотеки, написанный с C в коде C ++, вам нужно сказать компилятору с Extern «C»: это файл библиотеки, написанный с C, пожалуйста, свяжите их в. ..

Эффекты простых частиц Unity3d

Цели Добейтесь простого эффекта частиц Процесс внедрения Сначала создайте пустой объект, затем добавьте систему частиц Скрипт для управления движением частиц инициализировать параметры, которые необхо…

887. Projection Area of 3D Shapes

887. Projection Area of 3D Shapes 887. Projection Area of 3D Shapes титульный решить титульный Название Leetcode On a N * N grid, we place some 1 * 1 * 1 cubes that are axis-aligned with the x, y, and…

POJ 3683 Самый загруженный день священника Иоанна (схема вывода 2-SAT) Определите, перекрываются ли интервалы

Источник вопроса: http://poj.org/problem?id=3683 Заглавие: Есть N пар, которые проводят свадьбы, и каждая свадьба должна длиться d раз, от s до t, и можно выбирать только от s до s + d или от td до t….

Четные и нечетные числа — определение, признаки и свойства » Kupuk.net

Одной из характеристик числа является его кратность двум. Простое арифметическое свойство стало основой для мистических верований древних людей, служит фундаментом для быстрых алгебраических вычислений и геометрических формул. Нечетные и четные числа широко используются современным человеком в повседневной жизни.

Арифметические свойства

Четными называют числа, которые при делении на 2 образуют целое число. Нечетные при том же действии дают результат с остатком (дробное число). Чтобы быстро проверить на четность двузначную цифру, нужно определить параметр для последней его цифры в десятичной записи. Если она делится на два, число является четным, в противном случае — нечетным. Метод работает для любых многозначных чисел.

Арифметические правила четных и нечетных чисел при различных операциях описаны древнегреческим математиком Пифагором до нашей эры и используются для вычислений современниками. Они помогают составлять формулы для оптимизированных расчетов в задачах с большим рядом переменных. Алгоритмы многих онлайн-калькуляторов запрограммированы с помощью таких функций.

Закономерности арифметических операций с целыми числами:

Если оба слагаемых или множителя четные, сумма также будет четной.

При вычитании четного из четного получится четное, при вычитании нечетного — наоборот.

Сложение и вычитание нечетных чисел дает в результате четное.

При умножении двух нечетных чисел результат также будет нечетным, если один из множителей четный — наоборот.

Четное при делении на нечетное может образовать либо четное число, либо дробное.

Деление нечетных чисел образует нечетное либо дробное.

Формула четного числа: m = 2k. Формула нечетного числа: m = 2k + 1.

При уменьшении или увеличении четного числа на единицу получается нечетное и наоборот. При начертании оси с нулем в центре будет сохраняться чередование четных и нечетных чисел. Наглядно продемонстрировать феномен школьникам можно, предложив записать последовательный ряд четных чисел через запятую.

Характеристика парности у ноля

Не бывает целых чисел, которые не принадлежат к одной из групп по признаку кратности двум. Ноль, который разделяет отрицательные и положительные значения последовательного ряда, не является целым. Из-за этого большинство предполагает, что ноль стоит особняком, т. е. не относится ни к одному виду или же одновременно представляет оба.

В науке ноль — это аддитивный нейтральный элемент четной группы. Он является логическим началом для рекурсии последовательного ряда кратных двум объектов. Исследования, проведенные в учебных заведениях Великобритании, показали, что 2/3 преподавателей не знают верного ответа, а ученики пятого класса ошибаются реже, чем из шестого и старше.

Признаки четности ноля:

элемент гармонично вписывается в логику порядка последовательной оси натуральных и обратных числительных;

полное соответствие всем арифметическим законам для группы;

если объект, для которого нужно определить парность, двузначный и больше, цифра в конце явно указывает на кратность его двум;

принадлежность цифры к группе обеспечивает мультипликативность функции Мебиуса и не нарушает логику работы формулы вращения.

Маленьким слушателям легче пояснить феномен с помощью двух таблиц — по одной для каждой группы. Элементы кратных схематически изображаются в первом столбце, во втором — остаток. Олицетворяемая нолем пустота при делении на два остается пустотой, что соответствует признаку кратности двум. Вышеприведенный список доказательств содержит другие примеры для наглядной демонстрации логики принадлежности знака к группе элементов, кратных двум.

Свойства группы для вычислений

Когда требуется вычислить сумму множества слагаемых из натурального ряда последовательных нечетных чисел, можно отказаться от длительных монотонных операций. Известно, что сумма любого количества элементов всегда соответствует квадрату их количества. Проверку можно осуществить путем сложения двух, трех и четырех элементов последовательного ряда. Аналогичное выражение можно составить для любого количества слагаемых.

Алгоритм оптимизированного решения:

к последнему элементу ряда добавляют 1;

результат делят на два;

полученное значение возводят в квадрат, т. е. определяют произведение умножения его на самое себя.

Количество складываемых элементов последовательного ряда некратных двум числительным всегда соответствует квадратному корню суммы.

Примеры логических задач для решения через характеристику парности:

Можно ли доску, разбитую на определенное количество клеток, заполнить костями домино, чтобы каждое значение располагалось в отдельной ячейке?

Группа детей, среди которых пять мальчиков, встали в круг, взявшись за руки. Сколько всего малышей, если известно, что соблюдено чередование девочек и ребят?

Могут ли 11 шестеренок, расположенных на плоскости, вращаться одновременно?

Получится ли разменять купюру в 25 единиц с помощью банкнот значением 1, 3 и 5?

Ответ на каждую из задач можно получить методом проб и подбора. Понимание законов парности позволяет существенно сократить время на поиск верного решения. Школьникам нравится изящное решение головоломки о маленьком кузнечике. Детям сообщают, что за один скачок он преодолевает 1 метр. Учащимся предлагают доказать, что насекомое совершило парное количество прыжков, если в результате движений оно оказалось в исходной точке.

Ответ становится очевидным при понимании, что пройденный путь, равен расстоянию, которое необходимо пройти для возвращения к стартовой позиции. Таким образом суммарное расстояние обязано быть парным.

История и значение в культуре

Неоценимое влияние на развитие арифметики оказали труды Пифагора. Ученый посвятил много труда и времени, чтобы выявить закономерности свойств чисел и объединить их в логичную систему. Математические законы и наблюдения он связал с мировосприятием и теорией самопознания человека.

Каждой цифре математик отвел свое значение. Нечетные обладают более сильными, активными характеристиками. Именно они в воссозданной мистической системе являлись олицетворением мужского начала, динамики и солнца. Четные же, наоборот, олицетворяли женское естество, статичность и луну.

Аналогичное деление характерно для китайской философии, в которой нечетные числительные относят к светлой мужской субстанции Ян, а Инь — к теневому, негативному, женскому. В учении о материи тайцзи противоположности представлены как единые и неделимые стороны одного целого.

У каждого этноса существуют свои поверья. Самое популярное суеверие у славян запрещает преподносить букеты с парным количеством цветов. В США и Европе такой подарок, наоборот, трактуется как пожелание счастья и благополучия. Нечетность приглашенных гостей, дней празднования, даты события также считается обязательным по свадебным традициям Руси.

Практическое применение

Возможность разделить все числительные на парные и непарные широко используется в повседневной жизни. В зависимости от того, кратен ли двум порядковый номер месяца, по правилам дорожного движения может быть запрещена или разрешена стоянка в определенных зонах. Четные и нечетные недели помогают запомнить расписание вузов с многочисленной аудиторией.

В расписании железнодорожных поездов на кратности двум числа месяца завязаны маршруты с расписанием через день. Чтобы не нарушать установленный порядок, после 31 числа поезд может пропустить один выезд. Тот же принцип используется для нумерации вагонов — парность содержит информацию о направлении пути. В плацкартах и купе места с верхними полками всегда обозначены четным числом, а нижние — нечетным.

Парность строк помогает проверить созвучность стиха поэтам. Если мысленно пронумеровать слоги, можно подобрать слово в соответствии с ритмом произведения, так как ударные и безударные гласные являются основным ориентиром.

3 четное или нечетное число. Нумерология

Нечётное число – целое число , которое не делится на без остатка : …, −3, −1, 1, 3, 5, 7, 9, …

Если m чётно, то оно представимо в виде m = 2 k, а если нечётно, то в виде m = 2 k + 1, где k \in \mathbb Z.

История и культура

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. В китайской космологии и натурософии чётные числа соответствуют понятию «инь », а нечётные – «ян » .

В разных странах существуют связанные с количеством даримых цветов традиции. Например в США , Европе и некоторых восточных странах считается, что чётное количество даримых цветов приносит счастье . В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т. д. цветов или срезов кустового цветка, имеющих множество бутонов , у которых они, в принципе, не подсчитываются. Тем более это относится к бо́льшему количеству цветов (срезов), даримых в других случаях.

Практика

В высших учебных заведениях со сложными графиками учебного процесса применяются чётные и нечётные недели. Внутри этих недель отличается расписание учебных занятий и в некоторых случаях время их начала и окончания. Такая практика применяется для равномерности распределения нагрузки по аудиториям, учебным корпусам и для ритмичности занятий по дисциплинам с малой аудиторной нагрузкой (1 раз в 2 недели)

В графиках движения поездов применяются чётные и нечётные номера поездов, зависящие от направления движения (прямое или обратное). Соответственно чётностью/нечётностью обозначается направление, в котором проходит поезд через каждую станцию.

С чётными и нечётными числами месяца иногда увязаны графики движения поездов, которые организованы через день.

Напишите отзыв о статье “Чётные и нечётные числа”

Примечания

Ссылки

Последовательность A005408 в OEIS : нечётные числа
Последовательность A005843 в OEIS : чётные числа
Последовательность A179082 в OEIS : чётные числа с чётной суммой цифр в десятичной записи

Отрывок, характеризующий Чётные и нечётные числа

– Так, так, – сказал князь Андрей, обращаясь к Алпатычу, – все передай, как я тебе говорил. – И, ни слова не отвечая Бергу, замолкшему подле него, тронул лошадь и поехал в переулок.

От Смоленска войска продолжали отступать. Неприятель шел вслед за ними. 10 го августа полк, которым командовал князь Андрей, проходил по большой дороге, мимо проспекта, ведущего в Лысые Горы. Жара и засуха стояли более трех недель. Каждый день по небу ходили курчавые облака, изредка заслоняя солнце; но к вечеру опять расчищало, и солнце садилось в буровато красную мглу. Только сильная роса ночью освежала землю. Остававшиеся на корню хлеба сгорали и высыпались. Болота пересохли. Скотина ревела от голода, не находя корма по сожженным солнцем лугам. Только по ночам и в лесах пока еще держалась роса, была прохлада. Но по дороге, по большой дороге, по которой шли войска, даже и ночью, даже и по лесам, не было этой прохлады. Роса не заметна была на песочной пыли дороги, встолченной больше чем на четверть аршина. Как только рассветало, начиналось движение. Обозы, артиллерия беззвучно шли по ступицу, а пехота по щиколку в мягкой, душной, не остывшей за ночь, жаркой пыли. Одна часть этой песочной пыли месилась ногами и колесами, другая поднималась и стояла облаком над войском, влипая в глаза, в волоса, в уши, в ноздри и, главное, в легкие людям и животным, двигавшимся по этой дороге. Чем выше поднималось солнце, тем выше поднималось облако пыли, и сквозь эту тонкую, жаркую пыль на солнце, не закрытое облаками, можно было смотреть простым глазом. Солнце представлялось большим багровым шаром. Ветра не было, и люди задыхались в этой неподвижной атмосфере. Люди шли, обвязавши носы и рты платками. Приходя к деревне, все бросалось к колодцам. Дрались за воду и выпивали ее до грязи.
Князь Андрей командовал полком, и устройство полка, благосостояние его людей, необходимость получения и отдачи приказаний занимали его. Пожар Смоленска и оставление его были эпохой для князя Андрея. Новое чувство озлобления против врага заставляло его забывать свое горе. Он весь был предан делам своего полка, он был заботлив о своих людях и офицерах и ласков с ними. В полку его называли наш князь, им гордились и его любили. Но добр и кроток он был только с своими полковыми, с Тимохиным и т. п., с людьми совершенно новыми и в чужой среде, с людьми, которые не могли знать и понимать его прошедшего; но как только он сталкивался с кем нибудь из своих прежних, из штабных, он тотчас опять ощетинивался; делался злобен, насмешлив и презрителен. Все, что связывало его воспоминание с прошедшим, отталкивало его, и потому он старался в отношениях этого прежнего мира только не быть несправедливым и исполнять свой долг.
Правда, все в темном, мрачном свете представлялось князю Андрею – особенно после того, как оставили Смоленск (который, по его понятиям, можно и должно было защищать) 6 го августа, и после того, как отец, больной, должен был бежать в Москву и бросить на расхищение столь любимые, обстроенные и им населенные Лысые Горы; но, несмотря на то, благодаря полку князь Андрей мог думать о другом, совершенно независимом от общих вопросов предмете – о своем полку. 10 го августа колонна, в которой был его полк, поравнялась с Лысыми Горами. Князь Андрей два дня тому назад получил известие, что его отец, сын и сестра уехали в Москву. Хотя князю Андрею и нечего было делать в Лысых Горах, он, с свойственным ему желанием растравить свое горе, решил, что он должен заехать в Лысые Горы.
Он велел оседлать себе лошадь и с перехода поехал верхом в отцовскую деревню, в которой он родился и провел свое детство. Проезжая мимо пруда, на котором всегда десятки баб, переговариваясь, били вальками и полоскали свое белье, князь Андрей заметил, что на пруде никого не было, и оторванный плотик, до половины залитый водой, боком плавал посредине пруда. Князь Андрей подъехал к сторожке. У каменных ворот въезда никого не было, и дверь была отперта. Дорожки сада уже заросли, и телята и лошади ходили по английскому парку. Князь Андрей подъехал к оранжерее; стекла были разбиты, и деревья в кадках некоторые повалены, некоторые засохли. Он окликнул Тараса садовника. Никто не откликнулся. Обогнув оранжерею на выставку, он увидал, что тесовый резной забор весь изломан и фрукты сливы обдерганы с ветками. Старый мужик (князь Андрей видал его у ворот в детстве) сидел и плел лапоть на зеленой скамеечке.
Он был глух и не слыхал подъезда князя Андрея. Он сидел на лавке, на которой любил сиживать старый князь, и около него было развешено лычко на сучках обломанной и засохшей магнолии.
Князь Андрей подъехал к дому. Несколько лип в старом саду были срублены, одна пегая с жеребенком лошадь ходила перед самым домом между розанами. Дом был заколочен ставнями. Одно окно внизу было открыто. Дворовый мальчик, увидав князя Андрея, вбежал в дом.
Алпатыч, услав семью, один оставался в Лысых Горах; он сидел дома и читал Жития. Узнав о приезде князя Андрея, он, с очками на носу, застегиваясь, вышел из дома, поспешно подошел к князю и, ничего не говоря, заплакал, целуя князя Андрея в коленку.

Как мы видели выше, любая подстановка разлагается в произведение транспозиций. Вообще говоря, одну и ту же подстановку можно представить в виде произведения транспозиций многими различными способами. Например, очевидно, что

(формулы (1) и (2) выражают, как легко видеть, один и тот же факт, но в различных обозначениях).

Лемма. Если произведение нескольких транспозиций равно тождественной подстановке, то число этих транспозиций четно.

Мы докажем эту лемму индукцией по числу s различных чисел, входящих в записи данных транспозиций.

Наименьшее возможное значение числа s равно, очевидно, двум. Если , то рассматриваемое произведение является степенью некоторой транспозиции и поэтому равно тождественной подстановке только тогда, когда показатель степени четен (ибо любая транспозиция имеет порядок 2). Таким образом, в случае лемма доказана.

Предполагая теперь, что лемма уже доказана для любого произведения транспозиций, записи которых содержат менее s различных чисел, рассмотрим некоторое, равное тождественной подстановке произведение транспозиций

в записи которых входит ровно s различных чисел. Пусть I – одно из этих чисел. Пользуясь соотношением (1) и тем, что независимые транспозиции перестановочны, мы можем «переместить вперед» все транспозиции, в запись которых входит число i, т. е. перейти от произведения (3) к равному произведению вида

в котором все числа отличны от числа l. Если , то, пользуясь соотношением (2) или соотношением

мы можем от произведения (4) перейти к произведению такого же вида, но с меньшим . В результате ряда таких преобразований мы либо полностью уничтожим все транспозиции, в записи которых входит число l, либо получим произведение, содержащее только одну такую транспозицию:

Но это произведение переводит, очевидно, число в число l и потому не может быть тождественной подстановкой. Следовательно, последний случай невозможен. Таким образом, в результате наших преобразований мы получим равное тождественной подстановке произведение транспозиций, записи которых не содержат числа l. Никаких новых чисел записи этих подстановок, очевидно, не содержат. Следовательно, согласно предположению индукции, в это произведение входит четное число транспозиций.

Остается заметить, что при описанных преобразованиях число транспозиций либо не меняется (когда мы пользуемся соотношениями (1), (2)), либо уменьшается на две единицы (когда мы пользуемся соотношением . Поэтому исходное произведение (3) также состоит из четного числа транспозиций. Тем самым лемма полностью доказана.

Пусть теперь некоторая подстановка а двумя способами разложена в произведение транспозиций:

(первое разложение содержит транспозиций, а второе q). Тогда

и, следовательно, по доказанной лемме, число четно.

Таким образом, числа и q либо одновременно четны, либо одновременно нечетны. Другими словами, при всех разложениях подстановки в произведение транспозиций четность числа этих транспозиций будет одна и та же.

Подстановка называется четной, если она разлагается в произведение четного числа транспозиций, и нечетной – в противном случае. Согласно доказанной теореме, четность подстановки не зависит от выбора ее разложения в произведение транспозиций.

Любая транспозиция, или вообще любой цикл четной длины, является нечетной подстановкой, а любой цикл нечетной длины, в частности любой цикл длины 3, является четной подстановкой. Тождественная подстановка, очевидно, четна.

Разложение подстэновки а в произведение транспозиций, то

откуда следует, что подстановка, обратная – четной подстановке, четна, обратная нечетной – нечетна.

Например: -24, 0, 6, 38 — все это четные числа.

Пример нечетных чисел: 3, 1, 7 и 35.

n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k – целое число.

Сложение и вычитание четных и нечетных чисел

Операция	Результат	Пример
Четное + Четное
Четное + Нечетное	Нечетное
Нечетное + Нечетное

Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.

Умножение четных и нечетных чисел

Операция	Результат	Пример
Четное * Четное
Четное * Нечетное
Нечетное * Нечетное	Нечетное

А теперь рассмотрим дробные числа.

Десятичная запись числа

Например: 3,14; 5,1; 6,789 — это все

Определения

Чётное число – целое число, которое делится без остатка на 2: …, −4, −2, 0, 2, 4, 6, 8, …
Нечётное число – целое число, которое не делится без остатка на 2: …, −3, −1, 1, 3, 5, 7, 9, …

В соответствии с этим определением нуль является чётным числом.

Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .

В разных странах существуют связанные с количеством даримых цветов традиции.

В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли.

Например, вполне допустимо подарить юной даме букет из 12 или 14 цветов или срезов кустового цветка, если они имеют множество бутонов , у которых они, в принципе, не подсчитываются.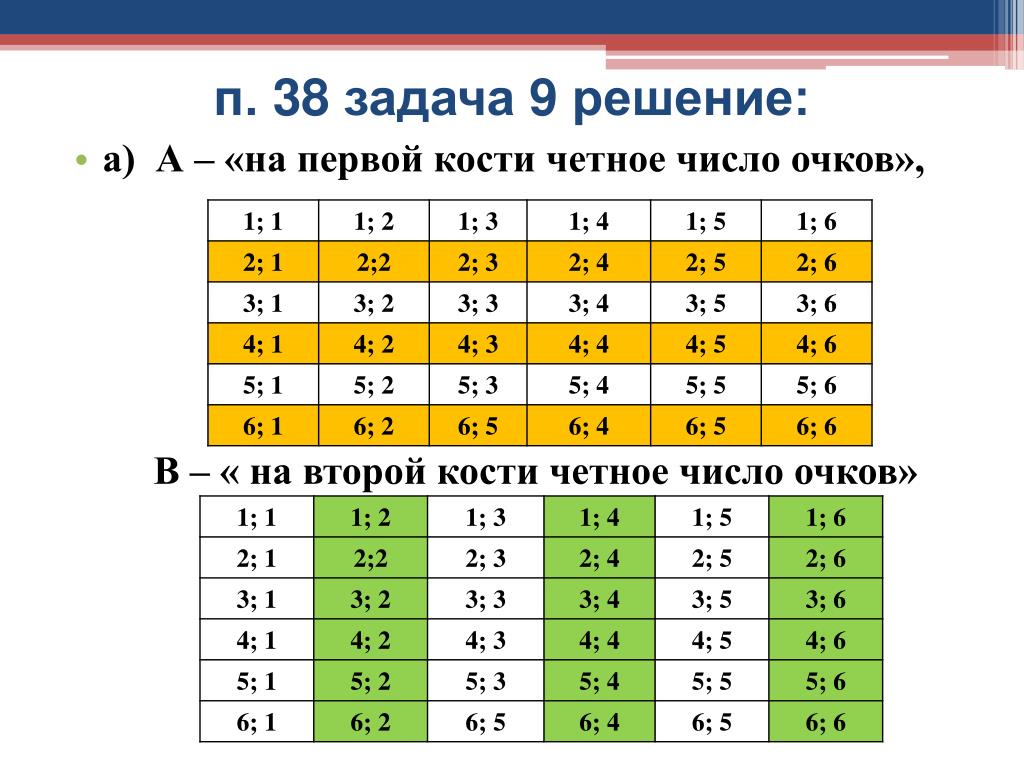
Тем более это относится к б́ольшему количеству цветов (срезов), даримых в других случаях.

Примечания

Wikimedia Foundation . 2010 .

Маарду
Сверхпроводимость

Смотреть что такое “Чётные и нечётные числа” в других словарях:

Нечётные числа

Чётные числа – Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Нечётное – Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Нечётное число – Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Нечетные числа – Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Четные и нечетные числа – Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Четные числа – Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19). … … Википедия

Слегка избыточные числа – Слегка избыточное число, или квазисовершенное число избыточное число, сумма собственных делителей которого на единицу больше самого числа. До настоящего времени не было найдено ни одного слегка избыточного числа. Но со времён Пифагора,… … Википедия

Совершенные числа – целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные С. ч. можно… …

Квантовые числа – целые (0, 1, 2,…) или полуцелые (1/2, 3/2, 5/2,…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы.… … Большая советская энциклопедия

Книги

Математические лабиринты и ребусы, 20 карточек , Барчан Татьяна Александровна, Самоделко Анна. В наборе: 10 ребусов и 10 математических лабиринтов на темы: – Числовой ряд; – Чётные и нечётные числа; – Состав числа; – Счёт парами; – Упражнения на сложение и вычитание. В комплекте 20…

Что означают чётные и нечётные числа в духовной нумерологии. В изучении это очень важная тема! Чем по своей СУТИ чётные числа отличаются от нечётных чисел?

Чётные числа

Общеизвестно, что чётные числа — те, которые делятся на два. То есть, числа 2, 4, 6, 8, 10, 12, 14, 16, 18 и так далее.

А что означают чётные числа относительно ? Какова нумерологическая суть деления на два? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.

У несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств — точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».

А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии. Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.

Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?

Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.

Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе… надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.

Нечётные числа

Нечётные числа — те, которые не делятся на два: числа 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 и так далее. С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.

Что, кстати, даёт пищу для размышления: почему число цветов в букете для живого человека нечётное, а для мёртвого — чётное… Не потому ли, что материальная логика (логика в рамках «да-нет») мертва относительно души человека?

Видимые совпадения материальной логики и духовной происходят очень часто. Но пусть это не вводит вас в заблуждение. Логика духа, то есть логика нечётных чисел , никогда в полной мере не прослеживается на внешних, физических уровнях человеческого бытия и сознания.

Возьмём для примера — число любви. Мы разглагольствуем о любви на каждом шагу. Мы признаёмся в ней, мечтаем о ней, украшаем ею свою жизнь и чужую жизнь.

Но что на самом деле мы знаем о любви? О той всепроникающей Любви, которая пронизывает собой все сферы Мироздания. Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!

Парадоксальность — вот одно из ключевых свойств нечётных чисел. В толковании нечётных чисел надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них…

Кстати, зрелость ума характеризуется способностью воспринимать парадоксы. Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.

Чётные и нечётные числа в нумерологии

Подведём итоги. В чём главное отличие чётных чисел от нечётных?

Чётные числа более предсказуемы (кроме числа 10), основательны и последовательны. События и люди, связанные с чётными числами, более устойчивы и объяснимы. Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел…

Нечётные числа — взбалмошны, свободолюбивы, неустойчивы, непредсказуемы. Они всегда преподносят сюрпризы. Вот вроде и знаешь смысл какого-то нечётного числа, а оно, это число, вдруг начинает вести себя так, что заставляет тебя заново пересмотреть чуть ли не всю твою жизнь…

Обратите внимание!

В магазины уже поступила моя книга под названием «Духовная нумерология. Язык чисел». На сегодняшний день это самое полное и востребованное из всех существующих эзотерических пособий о смысле чисел. Подробнее об этом, а также для заказа книги пройдите по следующей ссылке: ««

———————————————————————————————

Основы четных и нечетных чисел

Начнем с основных определений:

Четное : любое целое число, которое делится на 2. Примеры: 2, 4, 14.

Нечетное : любое целое число, которое делится на 2. не делится на 2, т.е. оставляет остаток 1 при делении на 2. Примеры: 1, 3, 5, 7, 9

Пока все хорошо. Рассмотрим это потенциальное заблуждение:

0 четный или нечетный?

При делении 0 на 2 получается 0 ÷ 2 = 0. Другими словами, 0 делится на 2. Следовательно, ноль соответствует критериям, установленным для четных целых чисел. Следовательно, ноль четный.

Ноль нейтрален, когда речь идет о положительных и отрицательных числах, т. е. ноль не является ни положительным, ни отрицательным — он нейтрален. Не путайте это с четным и нечетным.

Но ноль делится на 3, 5 и 7…. также?

Тот факт, что ноль делится и на другие нечетные целые числа (и да, ноль делится на 3, 5, 7 или любое другое целое число, кроме самого себя), не имеет значения.

Определение четного или нечетного числа имеет отношение только к делимости на 2. Например, 6 является четным числом, потому что оно делится на 2. 6 также делится на 3, но это не имеет значения.

Запомните этот факт: Ноль четен.

Нечетные и четные целые числа также могут быть отрицательными; например, ?7 нечетно, а ?18 четно.

Четные числа: {…., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ….}

Нечетные числа: {…., -9 , -7, -5, -3, -1, 1, 3, 5, 7, 9, ….}

Какое из следующих чисел НЕ является четным?

-117
-4,222
-2
0
2,2
100. 002
498

117 — нечетное число, поскольку оно не делится на 2.
-4,222 — десятичное число. Десятичные значения не являются ни четными, ни нечетными.
-2 — четное число, так как оно делится на 2.
0 — четное число, поскольку оно делится на 2.
-2,2 — десятичное число. Десятичные значения не являются ни четными, ни нечетными.
100,002 — десятичное число. Десятичные значения не являются ни четными, ни нечетными.
498 — четное число, так как оно делится на 2.

Как и у большинства людей, сдающих GRE, ваши знания по математике могут быть немного заржаветыми. Хорошей новостью является то, что GRE проверяет вас только по математике, которую вы уже выучили в старшей школе. Если вы беспокоитесь, что забыли большую часть того, что выучили в старшей школе, вы…

Стандартное отклонение – важный статистический термин, проверенный на GRE. Это дает вам представление об отклонении или разбросе набора чисел от его среднего значения; следовательно, низкое стандартное отклонение означает, что числа очень близки к среднему, и наоборот…

подробнее

Каждое целое число больше 1 является либо простым, либо составным числом. Все составные числа можно представить в виде произведения простых чисел. Например, 6 можно выразить как 2 × 3. Простые делители 6 — это 2 и 3. Тогда как выражение 2 × 3 называется…

Давайте посмотрим, как мы используем диаграмму, чтобы ответить на этот вопрос: сколько положительных факторов имеет 100? Настройте диаграмму: 100 Левая колонка Правая колонка 1 100 2 50 4 25 5 20 10 10 Помните правило: как только факторы повторяются (например, 10 и 10), остановитесь. С…

подробнее

Вы уже видели прекрасную таблицу множителей — простой способ найти все множители целого числа. Давайте посмотрим, как мы используем диаграмму, чтобы ответить на этот вопрос: сколько положительных факторов имеет число 140? Вопрос касается факторов, поэтому таблица факторов…

Некоторые целочисленные вопросы могут потребовать от вас найти множители целого числа. Таблица множителей — это основной метод нахождения всех множителей любого целого числа. Этот метод также может быть полезен для вопросов о том, сколько множителей имеет конкретное целое число. Техника…

подробнее

Простые числа играют центральную роль в целочисленных вопросах. Излишняя самоуверенность здесь опасна: в то время как почти каждый может без труда назвать определение простого числа, поле на самом деле изобилует неправильными представлениями. Мы здесь, чтобы убедиться, что вы знаете все…

Сформулируем правила сложения, вычитания, умножения и деления четных и нечетных чисел. Вот правила сложения/вычитания четных и нечетных чисел: Четные ± четные = четные (например, 2 + 2 = 4; -4 – 2 = -6) Нечетные ± нечетные = четные (например, 1 + 1 = 2; -31 – 1 = -32)…

подробнее

Найдите остаток от деления 5 142 376 298 на 9? Метод длинного деления определенно покажет вам остаток от деления 5 142 376 298 на 9, но вы можете себе представить, сколько времени это займет. Хорошая новость заключается в том, что, как и делимость…

Делится ли 5 142 376 298 на 3? Калькулятор не помешал бы в этом вопросе. К сожалению, калькулятор отображает до восьми цифр. Если число больше восьми цифр, то будет отображаться ERROR. С 5 142 376,298 больше восьмерки…

корректуры – Откуда мы знаем, что все числа чередуются между нечетными и четными числами?

Спросил 9 лет, 6 месяцев назад

Изменено 9 лет, 4 месяца назад

Просмотрено 9к раз

$\begingroup$

По сути, я пытался доказать моему другу, что умножение нечетного и четного числа дает четное число. Это то, что я сказал. 92 + k)$, умноженное на $2$, так что это четное число (по определению четного числа).

Мой друг тогда сказал, что мы делаем предположение, что $2k \pm 1$ нечетно, потому что на числовой прямой чередуются нечетные и четные числа, как узнать, что это правда?

Я думал, как это доказать. Будет ли это какой-то формой индукции?

РЕДАКТИРОВАТЬ: я думаю, мне нужно изменить «число» на «целое число» в этом посте, не так ли?

элементарная теория чисел
корректура

$\endgroup$

$\begingroup$

Я бы не стал апеллировать к тому факту, что целые числа чередуются между четными и нечетными.

Я бы сказал так:

Четное число — это , определяемое как как любое целое число вида $2k$ для $k$ любого целого числа (возможно, за исключением $k=0$).

Нечетное число — это , определяемое как как любое целое число вида $2k +1$ для любого целого числа $k$.

Вы можете просто принять это как определение. И тогда (как и у вас) доказательство того, что четное, умноженное на нечетное, равно четному, просто $$ 2к(2к’+1) = 2[к(2к’+1)] $$ где, конечно, $k(2k’+1)$ — просто целое число.

$\endgroup$

$\begingroup$

Да, это можно доказать по индукции.

Претензия. $2\nсредний 1$.

Доказательство. Для натуральных чисел верно, что $k\mid n$ влечет $k\leq n$, поскольку $1<2$, мы имеем $2\nmid 1$. Кроме того, $1$ является преемником $0$, а $2$ является преемником $1$, поэтому единственными неотрицательными числами, меньшими $2$, являются $0,1$, и поэтому они являются единственными возможными остатками при делении положительного целого числа $. k$ на $2$. $\квадрат$

Лемма. Если $k$ четно, то $k+1$ нечетно, а если $k$ нечетно, то $k+1$ четно.

Доказательство. Если $k$ четно, то $2\mid k$, а затем $2\nmid k+1$, потому что $2\nmid 1$; поэтому $k+1$ нечетно. Если $k$ нечетно, то $2\nmid k$, поэтому остаток от $k$ при делении на $2$ равен $1$, значит, $2\mid k+1$, и он четен. $\square$

Претензия. Каждое число $n\in\Bbb N$ либо нечетно, либо четно.

Доказательство. Докажем по полной индукции. Предположим, что для каждого $k

Претензия. Каждый $k\in\Bbb Z$ либо нечетен, либо четен.

Доказательство. По предыдущему утверждению оно выполняется для $k\geq 0$ и $2\mid k\iff 2\mid -k$, поэтому утверждение верно для любого целого числа. $\квадрат$

$\endgroup$

$\begingroup$

По индукции можно доказать, что все неотрицательные целые числа имеют вид $2n$ или $2n+1$ для некоторого $n$. Тогда вы можете доказать это и для отрицательных целых чисел.

Это означает, что нечетные целые числа имеют вид $2n+1$.

$\endgroup$

$\begingroup$

Пусть $a$ четно.

Используйте тот факт, что $2\; \не \середина 1$. Итак, если $2 \mid a$ (т. е. если a четно), $2 \not\mid (a + 1)$. Следовательно, $a + 1$ нечетно.

Тогда как насчет $(a + 1) + 1$, числа, непосредственно следующего за нечетным $(a + 1)$, которое, в свою очередь, следует непосредственно за четным $a$.

Итак, $(a + 1) + 1 = a + 2$, а так как $a$ четно, то оно может быть выражено как $a = 2k$ для некоторого целого числа $k$. Тогда $a + 2 = 2k + 2 = 2(k+1).$ И ясно, что $2\mid 2(k+1).$

Следовательно, $a$ четное $\имеет (a + 1)$ нечетное $\имеет (a + 2)$ четное…

$\endgroup$

$\begingroup$

Обратите внимание, что по определению целое число $a\in{\mathbb{Z}}$ является нечетным , если оно не делится на два. n\,$ имеет период $\,2.$

$\endgroup$

$\begingroup$

Как вы говорите, четное число делится на 2. А если $a$ и $b$ делятся на $d$, скажем, это означает $a = d \cdot m$ и $b = d \cdot n $, поэтому $a – b = d (m – n)$ также делится на $d$.

Теперь возьмем $2k + 1$, предположим, что оно делится на 2. Поскольку $2k$ явно делится на $2$, если $2k + 1$ делится на 2, то $1 = (2k + 1) – 2 k$ делится на 2, а это нонсенс.

$\endgroup$

$\begingroup$

Пусть $m$ — нечетное число, а $n$ — четное число.

Таким образом, по определению нечетного и четного у нас есть целые числа $k_1$ и $k_2$ такие, что: $$m = 2k_1 + 1$$ $$n = 2k_2$$

Отсюда следует, что: $$\begin{выравнивание} м \cdot n &= (2k_1 + 1)\cdot(2k_2)\\ &= 4k_1k_2+2k_2 \\ &= 2(2k_1k_2 + k_2) \end{align}$$

Так как $(2k_1k_2 + k_2)$ является целым числом, то $m\cdot n$ четно.

$\endgroup$

$\begingroup$

Индукция не требуется как для доказательства того, что произведение нечетного целого числа на четное число является четным, так и для доказательства того, что целые числа попеременно являются нечетными и четными.

Мне нравится доказательство Томаса о мультипликативном результате (в настоящее время ответ с наивысшим рейтингом), хотя я думаю, что важно явно указать, что здесь мы полагаемся на ассоциативное свойство умножения. (Это важно, потому что не все операции, подобные умножению в алгебраических структурах, ассоциативны.)

Для доказательства чередования четных и нечетных чисел я бы просто сделал следующие наблюдения:

Поскольку «четность» определяется как кратность 2, а «нечетность» определяется как нечетность, все числа либо четны, либо или нечетный.

Любое четное число $k$ может быть представлено как $2j$ для некоторого целого числа $j$. Обратите внимание, что по дистрибутивному свойству $\frac{1}{2}(2j+1) = j + \frac{1}{2}$. Таким образом, $k+1$ не делится на 2 и, следовательно, нечетно. Точно так же $k-1$ нечетно.

Любое нечетное число $n$ может быть представлено как $2i+1$ для некоторого целого числа $i$. Обратите внимание, что $n-1 = 2i$, поэтому перед $n$ стоит четное число. $n+1 = 2i+2 = 2(i+1)$, опять же по свойству дистрибутивности, так что за $n$ следует четное число.

Следовательно, перед каждым нечетным числом и за ним следует четное число, и наоборот, перед каждым четным числом и за ним следует нечетное число. Таким образом, целые числа попеременно нечетные и четные.

$\endgroup$

$\begingroup$

Индукция не нужна, требуется только ассоциативность.

Четное число имеет вид 2k . Для любого j произведение (2k)j имеет форму 2(kj) .

Или, по-английски, произведение четного числа и любого числа является четным. Следовательно, произведение четного числа на нечетное число должно быть четным.

$\endgroup$

$\begingroup$

$2k+1$ нечетно, потому что 2 делится на 2k и не делится на 1. Четное число, умноженное на нечетное, будет четным, потому что $2m\times (2n+1) = 4mn+2n = 2(2mn+n )$, что является четным.

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie 93 6 Решить для ? cos(x)=1/2 7 Найти x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти x cos(x)=(квадратный корень из 3)/2 11 Найти x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2 шт. 92-3sin(x)+1=0 43 Найти x tan(x)+ квадратный корень из 3=0 44 Найти x sin(2x)+cos(x)=0 45 Упростить (1-cos(x))(1+cos(x)) 92=25 59 График f(x)=- натуральный логарифм x-1+3 60 Найдите значение с помощью единичного круга угловой синус(-1/2) 61 Найти домен квадратный корень из 36-4x^2 92=0 66 Найти x cos(2x)=(квадратный корень из 2)/2 67 График у=3 68 График f(x)=- логарифмическая база 3 x-1+3 92 71 Найти x квадратный корень из x+4+ квадратный корень из x-1=5 72 Решить для ? cos(2x)=-1/2 73 Найти x логарифмическая база x из 16=4 9х 75 Упростить (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) 76 Упростить сек(х)sin(х) 77 Упростить кубический корень из 24 кубический корень из 18 92=0 96 Найти x 3x+2=(5x-11)/(8г) 97 Решить для ? sin(2x)=-1/2 98 Найти x (2x-1)/(x+2)=4/5 92+n-72)=1/(n+9)

Четные/нечетные числа — ACT Math

Все ресурсы ACT Math

14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 Следующая →

ACT Math Help » Арифметика » Целые числа » Четные/нечетные числа

Решение:

Возможные ответы:

Правильный ответ:

Объяснение:

Добавьте цифры единиц:

Так как нет цифры десятков для переноса, продолжайте добавлять цифры десятков:

Ответ: .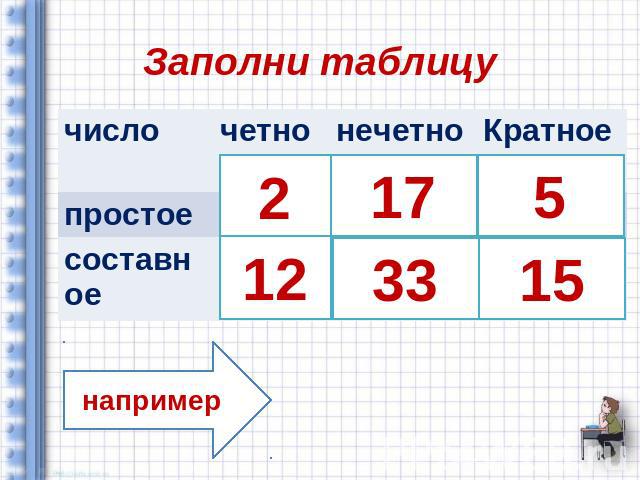

Сообщить об ошибке

В одной средней школе каждый должен сдавать латынь или греческий. Студентов, изучающих латынь, больше, чем студентов, изучающих греческий. Если есть студенты, изучающие греческий язык, сколько всего студентов?

Возможные ответы:

Правильный ответ:

Объяснение:

Если есть студенты, изучающие греческий язык, значит, есть или студенты, изучающие латынь. Однако вопрос спрашивает, сколько всего учеников в школе, поэтому вы должны сложить эти два значения вместе, чтобы получить:

или всего учеников.

Сообщить об ошибке

Найти сумму 13 и 19.

Возможные ответы:

Правильный ответ:

Объяснение:

Перепишите вопрос в виде математического выражения.

Добавьте цифру единиц.

Так как это число больше чем , при добавлении следующего члена перенесите разряд десятков.

Добавьте цифру десятков с переносом.

Объедините цифру десятков и цифру единиц. Ответ .

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы получить нечетный результат от сложения, у нас должно быть одно нечетное и одно четное число, таким образом, вы знаете из первого пункта о том, что только одно из двух значений является нечетным. Теперь, чтобы получить четный результат, у вас может быть два четных или два нечетных. Итак, предположим, что имеет два нечетных значения, это означает, что должно быть четным. Таким образом, у вас есть:

Теперь, если мы предположим, что имеет два четных значения, мы должны тогда знать, что это нечетное. Таким образом, мы имеем:

Прежде всего, вы можете исключить два ответа, которые говорят, что данное значение является положительным или отрицательным. Этого нельзя сказать по нашим данным. Далее, не может быть четного случая. Оно всегда будет нечетным (следовательно, правильный ответ таков). Наконец, не может быть, чтобы даже всегда было . Во втором вышеприведенном случае у вас будет два четных числа, сложенных вместе, что даст вам четное число. Затем вы добавите нечетное, что даст вам нечетное.

Сообщить об ошибке

Выберите ответ, который лучше всего решает следующее уравнение:

Возможные ответы:

Правильный ответ:

6 3 Объяснение:
Есть два способа решить эту проблему. Сначала вы можете сделать это алгебраически, разделив обе части на 13:
Но есть и другой способ, который, если вы понимаете нечетные числа, еще быстрее. Из всех ответов выше только один нечетный. Вы знаете, что данное уравнение должно быть нечетным — любое нечетное число, умноженное на нечетное число, даст нечетное число. Если вы умножите нечетное число на четное число, вы получите четное число.
Сообщить об ошибке
Найдите в следующем уравнении:
Возможные ответы:
Правильный ответ:
6 Объяснение:
Есть два способа решить эту задачу:
1. Используйте правило, согласно которому любые два нечетных числа, умноженные вместе, дадут еще одно нечетное число.
Используя это правило, только один ответ является нечетным числом (29), которое даст другое нечетное число (493) при умножении на заданное нечетное число (17).
2. Решить алгебраически:
Отчет о ошибке
Решение для уравнения в Фоллвинге:
Возможные ответы:
Правильный ответ:
9003
. Правильный ответ:

696
. Объяснение:
Есть два способа решить эту задачу:
1. Используйте правило, согласно которому любые два нечетных числа, умноженные вместе, дадут еще одно нечетное число.
Используя это правило, только один ответ является нечетным числом (85), которое даст другое нечетное число (7,735) при умножении на заданное нечетное число (91).
2. Решите алгебраически:

Сообщить об ошибке
Если и  являются нечетными целыми числами, какое из следующих чисел не обязательно нечетное?
Возможные ответы:
Правильный ответ:
Объяснение:
Во многих подобных вопросах может быть проще подставить числа, чем иметь дело с теоретическими переменными. Однако, учитывая, что этот вопрос требует выражения, которое не всегда является четным или нечетным, а только не обязательно нечетным, теоретический путь может быть нашим единственным выбором.
Поэтому лучше всего просто анализировать каждый вариант ответа.
: Поскольку  нечетное, тоже нечетное, так как и нечетное число, умноженное на нечетное число, дает нечетный продукт. Так как  также является нечетным, умножение его на  даст снова нечетный продукт, поэтому это выражение всегда нечетное.
: Поскольку  нечетное число, умножив его на 2, вы получите четное число. Вычитание этого числа из  также даст нечетный результат, поскольку нечетное число минус четное число дает нечетное число. Поэтому этот ответ тоже всегда нечетный.
: Поскольку оба числа нечетные, их произведение также всегда будет нечетным.
: Поскольку  нечетное число, умножив его на 2, вы получите четное число. Поскольку это нечетное число, вычитание его из нашего четного числа даст нечетное число, поскольку четное число минус нечетное число всегда будет нечетным. Поэтому этот ответ всегда будет нечетным.
: Поскольку оба числа нечетные, сумма будет четной. Однако деление четного числа на другое четное число (в нашем случае на 2) не всегда дает четное или нечетное число. Например, 5 и 7 оба нечетные. Их сумма 12 четна. Деление на 2 дает 6, четное число. Однако числа 5 и 9 тоже нечетные. Их сумма, 14, четна, но деление на 2 дает 7, нечетное число. Следовательно, это выражение не обязательно всегда нечетное или всегда четное, и поэтому является нашим ответом.
Сообщить об ошибке
У Теодора есть драже. У Порции в три раза больше. У Харви их в пять раз больше, чем у нее. Каково общее количество драже во всей группе?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти ответ на этот вопрос, подсчитайте общее количество мармеладок на каждого человека:
Порция:   * <количество мармеладок Теодора>, то есть  или
Харви:   * <количество мармеладок у Порции>, то есть   или
Итого:
(Не забывайте, что эти оригиналы нужны для Теодора!)
Сообщить об ошибке 3 Найдите произведение и .
Возможные ответы:
Правильный ответ:
Объяснение:
Преобразуйте произведение в выражение и умножьте на единицу оба числа.
Цифра единиц окончательного ответа — это цифра единиц от умножения 3 и 7, то есть 1. Цифра десятков, 2, будет перенесена в следующий расчет.
Умножьте число десятков от 13 до 7 и прибавьте перенос.

Значение 9 — это разряд десятков окончательного ответа.
Объедините цифру десятков с цифрой единиц. Ответ .
Сообщить об ошибке
← Предыдущая 1 2 3 Следующая →
Уведомление об авторских правах
Все математические ресурсы ACT
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept
Изучаем четные и нечетные числа
В математике четные числа — это целые числа, делящиеся на 2, то есть при делении целого числа на два не остается остатка. С другой стороны, нечетные числа являются целыми числами, при делении на 2 в остатке будет 1. Нечетные числа всегда находятся между четными числами и наоборот. Каждое целое число либо четное, либо нечетное, и ни одно целое число не является одновременно четным и нечетным.
Важность изучения четных и нечетных чисел

Определение четных и нечетных чисел является важным математическим навыком, которым должны овладеть учащиеся. Расширенная программа обучения математике будет предоставляться учителями в классах, где учащиеся изучают эту концепцию, а не просто относиться к этому уроку как к «нестандартному». Студенты упускают важные знания, которые имеют решающее значение для овладения математическими понятиями на более высоком уровне. Учителя должны изучить более глубокие подходы к четным и нечетным числам, т. е. четность отрицательных целых чисел.

Учащиеся больше оценят урок, если усвоят его через конкретное исследование. В зависимости от того, в каком классе он изучается, этот урок можно проводить с творческими идеями. Например, вместо того, чтобы учить первоклассников четным и нечетным числам путем деления, более уместно и более творчески говорить, что число четное, если все его можно соединить без остатка, в противном случае оно будет нечетным. Учителя также могут использовать наглядные материалы для представления этого определения.

Четные и нечетные числа также можно изучать в старших классах, и они могут иметь такой же уровень важности. В этом блоге Learn ZOE будут рассмотрены такие понятия, как четность и краткое определение четных и нечетных чисел.

Что такое четность?
Свойство того, является ли целое число четным или нечетным, называется четностью. Любые два последовательных целых числа имеют противоположную четность. Например, 15 нечетно, а 16 четно. Четные числа можно формально определить как целые числа вида n=2k, где k — целое число. Отсюда следует, что нечетные числа — это целые числа вида n=2k+1 или n=2k-1. Обратите внимание, что эти определения четности применимы только к целым числам. Рациональные числа, такие как 25 и -5,369, и иррациональные числа, такие как π и 5, не имеют четности. Эти краткие определения представляют собой формулы для создания четных и нечетных чисел, а также для доказательства четности целых чисел.
Пример 1. Укажите, является ли число 18 596 четным или нечетным.
Четность 18 596 можно определить, разделив на 2.
Поскольку остатка нет, четность 18 596 четна. Мы также можем использовать правило делимости на 2, чтобы определить четность числа. 18 596 оканчивается на 6, поэтому оно делится на 2 и, следовательно, является четным числом.
Пример 2: Определить четность 458 963.
Разделите 458 963 на 2.
458 963 нечетно, так как мы получили остаток от 1. Число также заканчивается на 3, нечетное число, поэтому наше решение должно быть правильным.
Четность целых чисел также включает следующие свойства.
четный четный = четный
четный нечетный = нечетный
нечетный нечетный = четный
четный × четный = четный
четный × нечетный = четный
нечетный × нечетный = нечетный 17+863 даст четную или нечетную сумму.
Поскольку 17 нечетно, 863 четно, а сумма четного и нечетного числа четна, мы можем заключить, что их сумма нечетна. Проверьте, найдя сумму двух чисел.
880 заканчивается нулем, четным числом, поэтому сумма действительно четная.
Пример 4: Определить четность произведения 27 и 15.
27 и 15 нечетные. Следовательно, их произведение также должно быть нечетным. Проверьте, найдя произведение двух чисел.
405 заканчивается четным числом. Поэтому продукт действительно странный.
Четность отрицательных целых чисел
Многие, вероятно, скажут, что отрицательные целые числа нельзя классифицировать как четные или нечетные. Но оказывается, мы действительно можем! Четность отрицательных целых чисел кажется озадачивающей, но это довольно простая концепция, которую должны знать учащиеся. Чтобы понять концепцию четных и нечетных отрицательных целых чисел, мы должны начать с обобщения отношения чисел в делении.
Любой делитель n равен сумме произведения делителя d на частное q и остатка r.
n=dq+r,
, где 0r
Это обобщение можно перевести на определение четных и нечетных чисел. Поскольку мы определяем четность целых чисел делением на 2, d=2. Значение r может быть либо 0, либо только 1.
n=2q+1 или n=2q.
Мы можем использовать эти два определения для проверки четности любого отрицательного целого числа.
Пример 5. Докажите, что четность -37 нечетна.
Пусть n= -37. Мы будем использовать n=2q+1, чтобы доказать его нечетную четность. Мы покажем, что q существует
-37=2q+1
q=-19
Поскольку мы можем показать, что существует целое число q такое, что -37=2q+1, мы видим, что -37 нечетно. .
Образцы текстовых задач
Вот несколько примеров текстовых задач, которые можно использовать для улучшения навыков определения четных и нечетных чисел.
x и y — целые числа, такие что x четно, а y нечетно. Какова четность xy?
Мы знаем, что четное нечетное = четное. Следовательно, xy должно быть четным.
Какова четность произведения простых чисел на интервале (2,1001]?
Поскольку на интервале есть четные числа, мы можем сказать, что произведение простых чисел на интервале (2,1001]? интервал также должен быть четным
Если a нечетно, а b четно, что из следующего должно быть верно относительно (a2+b)3+ab? Выберите все подходящие варианты.
Четность (a2+b)3+ab четна.
абис даже.
Четность (a2+b)3+abadd.
(a2+b)3четно.
Упрощая выражение, используя свойства четных и нечетных чисел, получаем:
[(нечетное)2+четное]3+(нечетное)(четное)
=[нечетное+четное]+четное 0 900
=нечетный+четный
= нечетный
Следовательно, варианты B и C верны.
Если x — целое число, какое из следующих чисел всегда нечетное?
2x+8
3x-5
10×2-6
34x+17
Вариант A можно переписать как 2(x+4). Умножение на любое четное число всегда дает четное произведение.
Вариант B четный, если x нечетный.
Вариант выбора можно переписать как 2(5×2-3). Умножение на любое четное число всегда дает четное произведение.
Вариант D можно переписать как 17(2x+1). (2x+1) — это определение нечетного числа, а 17 — нечетное. Произведение двух нечетных чисел всегда нечетно. Следовательно, правильный ответ — вариант D.
Докажите: если x — нечетное целое число, то 15x+5 — четное.
Любое нечетное целое число x может быть записано как 2n+1, где n — целое число. Следовательно,
15x+2=15(2n+1)+2
=30n+15+5
=30n+20
Обратите внимание, что 30n+20 можно переписать в 2(15n+10), где 15n+10 — элемент множества целых чисел. Поскольку 15x+2=2(15n+10), мы можем заключить, что 15x+2, поскольку любое целое число, умноженное на два, дает четное целое число.
Итог
Число четное, если оно делится на 2 без остатка, в противном случае оно нечетное. Остаток при делении нечетного на 2 всегда равен 1.
Мы можем формально определить четные числа как 2k, а нечетные числа как 2k+1. Мы можем использовать эти два определения для генерации четных и нечетных чисел.
Понимание четных и нечетных чисел важно для освоения некоторых из самых сложных математических понятий.
Четность — это свойство того, является ли число четным или нечетным. Только целые числа имеют четность.
Отрицательные целые числа также имеют четность. Обратите внимание, что остаток при делении отрицательных целых чисел на два также должен быть равен 0 или 1.
Резюме
Определение, различие, свойства и примеры решения
Четные и нечетные числа являются дальнейшими классификациями целых чисел по математике. И нечетные, и четные числа уникальны, то есть не существует числа, которое было бы одновременно четным и нечетным. Число либо четное, либо нечетное. Чтобы выразить определение четных и нечетных чисел простыми словами, мы можем сказать, что четные числа — это те числа, которые полностью делятся на число 2, а нечетные числа — это те числа, которые не делятся полностью на два. Кроме того, ноль считается четным числом, поскольку он является целым числом, кратным 2, то есть 0 x 2 = 0,9.0003
Содержание
Что такое четные и нечетные числа?
Набор представлений четных и нечетных чисел
Разница между четными и нечетными числами
Свойства четных и нечетных чисел
Как найти четные и нечетные числа?
Что такое четные и нечетные десятичные дроби?
Почему ноль четное число?
Вещи, чтобы запомнить
Вопросы выборки
Ключевые термины: ровные числа, нечетные числа, целые числа, целые числа, равенные группы, раздел. , Остаток
Что такое четные и нечетные числа?
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Четные числа — это числа, которые можно разделить на две равные группы. Точно так же нечетные числа — это те числа, которые нельзя разделить на две равные группы. Более четко их можно определить следующим образом:
Четное число — это число, которое делится на 2 с 0 в остатке, то есть полностью делится на 2.
Нечетное число — это число, которое не делится на 2, оставляя 1 в остатке, то есть не полностью делится на 2.
ровные числа и нечетные числа
Читать ДЛЯ СОЗДАНИЯ: Система номеров
Установить представление ровных и нечетных чисел
Примеры вопросов]
Наборы четных и нечетных чисел могут быть представлены следующими способами:
Набор четных чисел записывается как {x : x = 2k, где k ∈ W}, где k — любое целое число, а W — множество целых чисел.
Множество нечетных чисел записывается как {x : x = 2k + 1, где k ∈ W}, где k — любое целое число, а W — множество целых чисел.
Надлежащее определение четного числа имеет вид n = 2k, где n и k — любые целые числа, а правильное определение нечетного числа имеет вид n = 2k + 1, где n и k — любые целые числа .
Разница между четными и нечетными числами
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Ниже приведены наиболее важные различия между четными и нечетными числами:
Все четные числа делятся на 2 без остатка нечетное число полностью делится на 2.
Если цифра в разряде единиц любого заданного числа четная, то это число считается четным числом. Точно так же, если цифра в разряде единиц любого заданного числа нечетная, то это число считается нечетным числом.
В то время как четные числа могут быть разделены на пары, нечетные числа не могут быть разделены на пары.
Подробнее: Сложение и вычитание целых чисел
Свойства четных и нечетных чисел
[Нажмите здесь, чтобы просмотреть примеры вопросов]
полезно при решении задач. Они
Сумма двух четных чисел является только четным числом, например, 2 + 4 = 6, четное число.
Сумма четного числа и нечетного числа является нечетным числом. Например, 1 + 8 = 9, нечетное число.
Сумма двух нечетных чисел является четным числом, например, 3 + 5 = 8, четное число.
Разница между двумя четными числами является четным числом. Например, 14 – 10 = 4, четное число.
Разница между четным числом и нечетным числом является нечетным числом. Например, 12 – 7 = 5, нечетное число; или, например, 19 – 16 = 3, нечетное число.
Разность двух нечетных чисел является четным числом. Например, 13 – 9 = 4, четное число.
Произведение двух четных чисел является четным числом. Например, 18 х 20 = 360, четное число.
Произведение четного числа на нечетное число является четным числом. Например, 11 х 22 = 242, четное число.
Читайте также: Действительные числа
Таблица четных и нечетных чисел
синие – все четные числа. С помощью этой таблицы легко увидеть, что все четные числа заканчиваются на 0, 2, 4, 6 или 8, а все нечетные числа заканчиваются на 1, 3, 5, 7 или 9..
Таблица четных и нечетных чисел
Как найти четные и нечетные числа?
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Существует ряд простых способов определить, является ли заданное число четным или нечетным.
Все четные числа оканчиваются на 0, 2, 4, 6 или 8, а все нечетные числа оканчиваются на 1, 3, 5, 7 или 9. Поэтому, взглянув на цифру, стоящую в единицах любого данного числа, мы можно определить, четное это число или нечетное.
В наборе всех счетных чисел каждое альтернативное число, начинающееся с 1, является нечетным числом, а каждое альтернативное число, начинающееся с 2, является четным числом.
Мы также можем узнать, является ли данное число четным или нечетным, проверив его делимость на 2. Если оно полностью делится на 2, оно четное число, а если оно не делится полностью на 2, оно является нечетным числом.
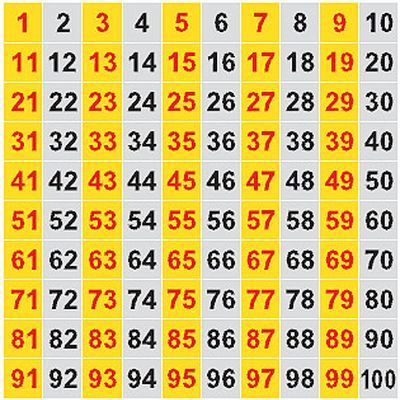
Все нецелые числа не могут быть отнесены ни к множеству четных чисел, ни к множеству нечетных чисел.
6
Умножение и деление целых чисел
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Десятичные числа не являются ни четными, ни нечетными числами, поскольку они не являются целыми числами или целыми числами. Только целые числа или целые числа могут быть либо четными, либо нечетными числами. Ноль — это целое число, которое делится на 2, поэтому 0 считается четным числом.
Подробнее: Десятичное разложение рациональных чисел
Почему ноль — четное число?
[Щелкните здесь, чтобы просмотреть примеры вопросов]
Ноль считается четным числом, поскольку он является целым числом, кратным 2, то есть 0 x 2 = 0. Вот примеры вопросов]
Четные и нечетные числа являются исключающими множествами, то есть данное число не может быть одновременно четным и нечетным.
Четное число может быть определено как число, которое точно делится на 2.
Нечетное число может быть определено как число, которое не делится точно на 2.
Ноль является четным числом, поскольку является целым кратным числа 2, то есть 0 x 2 = 0.
Десятичная дробь не может быть ни четной, ни нечетной.
Примеры вопросов
Вопросы. Всего у Гарри было 45 ручек. Он подарил своему другу 34 мяча. Количество мячей, оставшихся у него, четное или нечетное? (3 балла)
Ответ. У Гарри 45 ручек, а поскольку он отдал своему другу 34 мяча, то
Осталось мячей = 45-34 = 11.
У Гарри осталось 11 мячей, а 11 — нечетное число.
Вопросы. Найдите пары последовательных четных чисел из следующих. (3 балла)
a.30 и 34 b. 97 и 99 в. 90 и 92 д. 45 и 48
Ответ. Ответ – вариант (с).
90 и 92 — это пара последовательных четных чисел.
Остальные пары – 30 и 34, 97 и 99, 45 и 48 не являются последовательными четными числами.
Вопросы. Когда вы покупаете дюжину апельсинов, они четные или нечетные? (3 балла)
Отв. Десяток апельсинов – это 12 апельсинов.
Итак, 12/2 = 6, а остаток равен нулю.
Следовательно, они четны, поскольку делятся на 2.
Ques. Бесконечность – это нечетное или четное число? Какое самое маленькое семизначное четное число? (3 балла)
Отв. Поскольку бесконечность — это всего лишь представление числа, а не действительное число, ее нельзя разделить ни на четные, ни на нечетные числа.
Наименьшее семизначное четное число — 10 00 000.
Вопросы. Выясните, является ли 27 x 12 четным или нечетным числом. (3 балла)
Ответ.

Назовите два нечетных числа, которые в сумме дают нечетное число. — Спрашивалка

Четные и нечетные числа | Образовательная социальная сеть

Четное число и нечетное в экселе. Как четные и нечетные числа выделить разным цветом в Excel. Функция остат в excel для поиска четных и нечетных чисел

Описание

Синтаксис

Замечания

Пример

Умножение четных и нечетных чисел

Десятичная запись числа

Стандартные функции

Пользовательская функция

Использование массива

Определите нечетное и четное число

Интеллектуальная рекомендация

Решите метод «Доступ к базе данных метаданных IIS»

JMeter Обзор (4) Отчет

Понимание шаблонов проектирования MVC и MVVM

Используйте VirtualBox для установки эталонной тестовой среды Ubuntu10 (ZZ)

Программирование NIO (использование отметки и сброса)

Вам также может понравиться

Проект 2: система управления и обслуживания Linux

“#Ifdef __cplusplus extern” C “{#endif” определение

Эффекты простых частиц Unity3d

887. Projection Area of 3D Shapes

POJ 3683 Самый загруженный день священника Иоанна (схема вывода 2-SAT) Определите, перекрываются ли интервалы

Четные и нечетные числа — определение, признаки и свойства » Kupuk.net

Арифметические свойства

Характеристика парности у ноля

Свойства группы для вычислений

История и значение в культуре

Практическое применение

3 четное или нечетное число. Нумерология

История и культура

Практика

Напишите отзыв о статье “Чётные и нечётные числа”

Примечания

Ссылки

Отрывок, характеризующий Чётные и нечётные числа

Умножение четных и нечетных чисел

Десятичная запись числа

Определения

Примечания

Смотреть что такое “Чётные и нечётные числа” в других словарях:

Книги

Чётные числа

Нечётные числа

Чётные и нечётные числа в нумерологии

Основы четных и нечетных чисел

корректуры – Откуда мы знаем, что все числа чередуются между нечетными и четными числами?

Твой ответ

Зарегистрируйтесь или войдите

Опубликовать как гость

Опубликовать как гость

Четные/нечетные числа — ACT Math

Все ресурсы ACT Math

6

Все математические ресурсы ACT

Изучаем четные и нечетные числа

Образцы текстовых задач

Итог

Определение, различие, свойства и примеры решения

6

Добавить комментарий Отменить ответ