15 число четное или нечетное: Четные и нечетные числа — как объяснить ребенку четные и нечетные числа?

Понятие о десятичной записи числа. Четные и нечетные числа

Что означают чётные и нечётные числа в духовной нумерологии. В изучении это очень важная тема! Чем по своей СУТИ чётные числа отличаются от нечётных чисел?

Чётные числа

Общеизвестно, что чётные числа — те, которые делятся на два. То есть, числа 2, 4, 6, 8, 10, 12, 14, 16, 18 и так далее.

А что означают чётные числа относительно ? Какова нумерологическая суть деления на два? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.

У несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств — точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».

А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии.

Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.

Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?

Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.

Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе… надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.

Нечётные числа

Нечётные числа — те, которые не делятся на два: числа 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 и так далее. С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.

Что, кстати, даёт пищу для размышления: почему число цветов в букете для живого человека нечётное, а для мёртвого — чётное… Не потому ли, что материальная логика (логика в рамках «да-нет») мертва относительно души человека?

Видимые совпадения материальной логики и духовной происходят очень часто. Но пусть это не вводит вас в заблуждение. Логика духа, то есть логика нечётных чисел , никогда в полной мере не прослеживается на внешних, физических уровнях человеческого бытия и сознания.

Возьмём для примера — число любви. Мы разглагольствуем о любви на каждом шагу. Мы признаёмся в ней, мечтаем о ней, украшаем ею свою жизнь и чужую жизнь.

Но что на самом деле мы знаем о любви? О той всепроникающей Любви, которая пронизывает собой все сферы Мироздания. Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!

Парадоксальность — вот одно из ключевых свойств нечётных чисел. В толковании нечётных чисел надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них…

Кстати, зрелость ума характеризуется способностью воспринимать парадоксы. Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.

Чётные и нечётные числа в нумерологии

Подведём итоги. В чём главное отличие чётных чисел от нечётных?

Чётные числа более предсказуемы (кроме числа 10), основательны и последовательны. События и люди, связанные с чётными числами, более устойчивы и объяснимы. Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел…

Нечётные числа — взбалмошны, свободолюбивы, неустойчивы, непредсказуемы. Они всегда преподносят сюрпризы. Вот вроде и знаешь смысл какого-то нечётного числа, а оно, это число, вдруг начинает вести себя так, что заставляет тебя заново пересмотреть чуть ли не всю твою жизнь…

Обратите внимание!

В магазины уже поступила моя книга под названием «Духовная нумерология. Язык чисел». На сегодняшний день это самое полное и востребованное из всех существующих эзотерических пособий о смысле чисел. Подробнее об этом, а также для заказа книги пройдите по следующей ссылке: «

«

———————————————————————————————

Ответы к с. 66

212. Какое число получится: чётное или нечётное, если нечётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи три примера, подтверждающих твоё предположение.

При делении нечётного числа на нечётное число результат всегда будет нечётным числом.
45 : 5 = 9 55 : 11 = 5 63 : 7 = 9

213. Какое число получится: чётное или нечётное, если чётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи несколько примеров, подтверждающих твоё предположение. Обсуди результат с соседом по парте.

При делении чётного числа на нечётное число результат всегда будет чётным числом.
54 : 9 = 6 50

: 5 = 10 96 : 3 = 32

214. Можешь ли ты привести пример такого случая деления, когда нечётное число делится нацело на чётное число? Почему? Вспомни, как можно получить делимое из делителя и значения частного.

Делимое можно получить, умножив делитель на значение частного. По условию делитель является чётным числом. Мы знаем, что если чётное число умножить на чётное или нечётное число, то результатом будет всегда чётное число. В нашем же случае делимое должно быть нечётным числом. Это означает, что никакое значение частного в этом случае подобрать нельзя и привести пример такого случая деления невозможно.

215. Представь число 2873 в виде суммы круглых десятков и однозначного числа. Чётным или нечётным числом является каждое из слагаемых? Чётным или нечётным числом будет значение их суммы? На какую цифру может оканчиваться запись чётного числа? А нечётного?

2873 = 2870 + 3
Первое слагаемое – чётное число, второе слагаемое – нечётное число.

2873 – нечётное число.
Нечётное число 2873 заканчивается на нечётную цифру 3, запись чётного числа 2870 — на чётную цифру 0.
Запись чётного числа может оканчиваться чётными цифрами (0, 2, 4, 6, 8), а запись нечётного числа — нечётными числами (1, 3, 5, 7, 9).

216. Выпиши чётные числа в один столбик, а нечётные — в другой.

2844 57893
67586 9231
10050 9929

217. Сколько существует чётных двузначных натуральных чисел? А сколько таких же нечётных чисел?

Самое маленькое двузначное чётное число 10, а самое большое – нечётное число 99. Всего их 99 – 10 + 1 = 90. Чётные и нечётные числа в натуральном ряду чередуются, поэтому чётных двузначных чисел столько же сколько и нечётных, то есть 45, поскольку 90 : 2 = 45.

218. Запиши самое большле чётное шестизначное число.

Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.

Например: -24, 0, 6, 38 — все это четные числа.

m = 2k — общая формула написания четных чисел, где k – целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.

Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.

Пример нечетных чисел: 3, 1, 7 и 35.

n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k – целое число.

Сложение и вычитание четных и нечетных чисел

В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.

Операция	Результат	Пример
Четное + Четное
Четное + Нечетное	Нечетное
Нечетное + Нечетное

Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.

Умножение четных и нечетных чисел

При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.

Операция	Результат	Пример
Четное * Четное
Четное * Нечетное
Нечетное * Нечетное	Нечетное

А теперь рассмотрим дробные числа.

Десятичная запись числа

Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.

Например: 3,14; 5,1; 6,789 — это все

С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.

Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.

Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.

А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом – дробную.

Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.

Определения

• Чётное число – целое число, которое делится без остатка на 2: …, −4, −2, 0, 2, 4, 6, 8, …
• Нечётное число – целое число, которое не делится без остатка на 2: …, −3, −1, 1, 3, 5, 7, 9, …

В соответствии с этим определением нуль является чётным числом.

Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .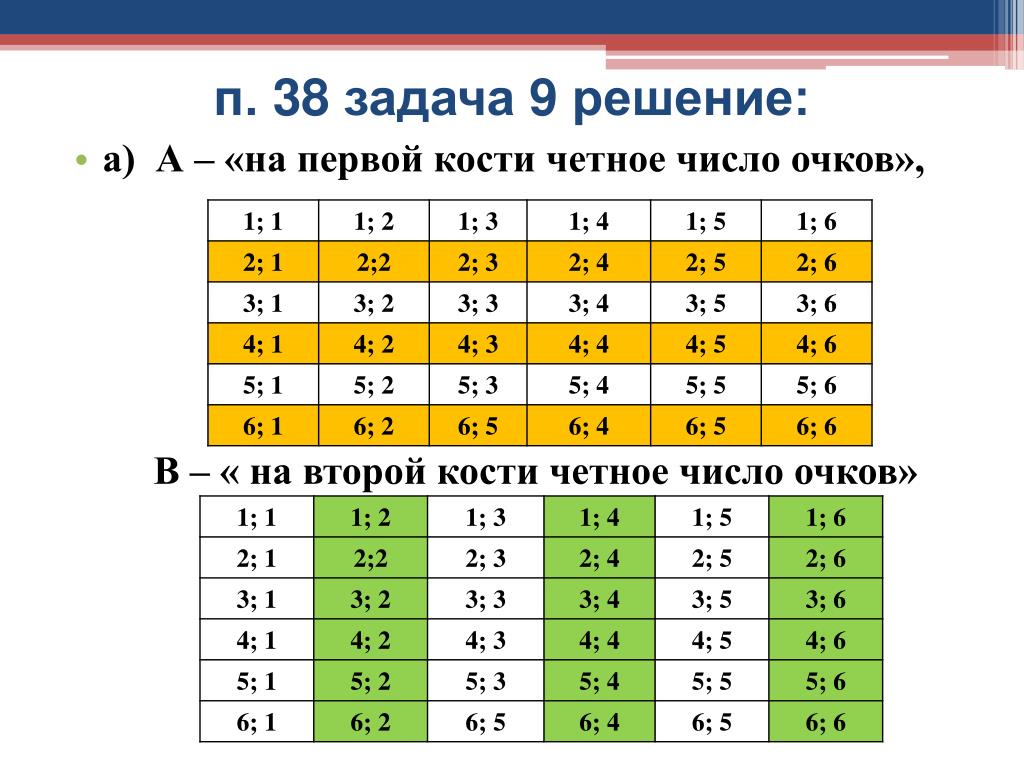

В разных странах существуют связанные с количеством даримых цветов традиции.

В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли.

Например, вполне допустимо подарить юной даме букет из 12 или 14 цветов или срезов кустового цветка, если они имеют множество бутонов , у которых они, в принципе, не подсчитываются.
Тем более это относится к б́ольшему количеству цветов (срезов), даримых в других случаях.

Примечания

Wikimedia Foundation . 2010 .

Смотреть что такое “Чётные и нечётные числа” в других словарях:

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Слегка избыточное число, или квазисовершенное число избыточное число, сумма собственных делителей которого на единицу больше самого числа. До настоящего времени не было найдено ни одного слегка избыточного числа. Но со времён Пифагора,… … Википедия

Целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные С. ч. можно… …

Целые (0, 1, 2,…) или полуцелые (1/2, 3/2, 5/2,…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы.… … Большая советская энциклопедия

Книги

• Математические лабиринты и ребусы, 20 карточек , Барчан Татьяна Александровна, Самоделко Анна. В наборе: 10 ребусов и 10 математических лабиринтов на темы: – Числовой ряд; – Чётные и нечётные числа; – Состав числа; – Счёт парами; – Упражнения на сложение и вычитание. В комплекте 20…

КОНСПЕКТ УРОКА ПО МАТЕМАТИКЕ НА ТЕМУ “ЧЁТНЫЕ И НЕЧЁТНЫЕ ЧИСЛА”

Четные и нечетные числа

(Урок введения нового знания)

Основные цели:

1. Познакомиться с понятиями четности-нечетности

(учить видеть, что:

• сумма двух четных чисел – четное число;

• сумма двух нечетных чисел – четное число;

• сумма четного и нечетного чисел – нечетное число).

Продолжить работу с простыми задачами на умножение, основываясь на знании смысла действия умножения и таблицы умножения числа 2.

Решать простые задачи на деление, основываясь на знании взаимосвязи умножения и деления.

Продолжать учить таблицу умножения числа 2 и соответствующих ей случаев деления.

Развивать умение решать комбинаторные задачи на перестановку.

Развивать интеллектуальные и коммуникативные общеучебные умения.

Развивать организационные общеучебные умения, в том числе самостоятельно оценивать результаты своих действий, самого себя, находить и исправлять собственные ошибки.

Ход урока

I. Актуализация знаний

1. Организационный момент

Повторение таблицы умножения числа 2 и соответствующих ей случаев деления.

2. Индивидуальная работа (4 ученика получают карточки с заданиями)

1 карточка

Какое число пропущено?

7 + 8 = 15

6 + 8 = 14

9 + 4 = 13

2 + 10 = 12

Найди и исправь ошибки

18 – 9 = 7 (9)

9 + 6 = 15

13 – 6 = 8 (7)

7 + 6 = 13

15 – 8 = 9 (7)

16 – 9 = 7

5 + 7 = 12

11 – 2 = 8 (9)

3 карточка

Между некоторыми числами поставь знаки действий: «+» «-» или «*», чтобы выполнялись равенства:

2 4 6 8 = 4

2 4 6 8 = 6

2 4 6 8 = 8

2 4 6 8 = 10

4 карточка

Составь выражение и посчитай:

• сколько лапок у 3 гусят? 2*3 = 6

• сколько лапок у 2 котят? 4*2 = 8

• сколько крыльев у 4 кутят? 2*4 = 8

3. Фронтальная работа

а) соревнования по группам

«Кто первый решит?»

18 : 9 = 2 4 – 2 = 8 5 – 2 = 10

8 : 2 = 4 12 : 2 = 6 10 : 5 = 2

2 – 3 = 6 2 – 2 = 4 6 – 2 = 12

16 : 2 = 8 14 : 7 = 2 16 : 8 = 2

6 : 2 = 3 18 : 2 = 9 2 – 8 = 16

10 : 2 = 5 14 : 2 = 7 9 – 2 = 18

Что можно сказать об ответах, которые получились в 1, 2, 3 столбиках? Что это за числа?

б) составьте слова, найдите лишнее:

ПОКТА ЧАТРЕПКА

СОКОН ПКАША

РЕЖВАКА ФРША

Какие из этих предметов используются только по два? Верно ли выполнено задание? Какой вопрос был самым трудным? Самым легким? Какую оценку заслужили?

II. «Открытие» нового знания

Работа с учебником

1. Задание 1 (стр. 66)

Как разложить варежки по 2 (парами)?

Проанализировать вместе с детьми задание и рисунок. Сделать вывод, как должны производить деление: варежки разложить парами в соответствии с их цветами, при этом варежка останется без пары.

Варежки разложить в классе не можем, заменим их кругами.

Практическая работа

Возьми 7 кружков и разложи их по 2.

Дети раскладывают на партах 7 кружков по 2. Делают вывод: 7 по 2 не делится, один кружок остается.

2. Задание 2 (стр. 66)

а) по два 6 красных кружков, 9 синих кружков, 10 зеленых кружков;

б) на две равные части 3 красных кружка, 4 синих кружка, 5 зеленых кружков.

Практическая работа

Дети самостоятельно на партах раскладывают кружки, а два человека работают у доски. После того, как задание выполнено, они объясняют, как делили кружки «по 2» и «на 2 равные части». Делают вывод. Остальные ребята оценивают выполненное задание, выставляют оценку.

а) дети раскладывают красные, синие, зеленые кружки по 2;

б) дети раскладывают красные, синие, зеленые кружки на 2 равные части.

3. Работа с текстом учебника со знаком вопроса:

Дети отвечают на вопросы, делают вывод, записывают на доске числа, которые можно (нельзя) разделить по два

6, 4, 10 9, 3, 5, 7

Как называются эти числа? (ответы детей)

4. Работа с текстом учебника с восклицательным знаком:

Вывод: Числа 4, 6, 10 делятся на 2. Они называются четными.

Числа 3, 5, 7, 9 не делятся на 2. Они называются нечетными.

5. Задание 3 (стр. 66).

Прочитайте сначала четные, потом нечетные числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18.

(дети читают по очереди).

6. Работа с текстом учебника со знаком вопроса:

Что ты заметил?

7. Работа с текстом учебника с восклицательным знаком:

Вывод: Четные и нечетные числа в числовом ряду чередуются.

8. Выполнение задания 4.

Выполни действия:

а) умножь на 2 все четные числа в числовом ряду от 1 до 10. Расскажи, какие получились числа – четные или нечетные?

б) умножь на 2 все нечетные числа в этом же ряду. Расскажи, какие получились числа – четные или нечетные?

Дети записывают в тетрадь

а) 2 4 6 8 10

4 8 12 16 20

б) 1 3 5 7 9

2 6 10 14 18

Делают вывод: записанные числа четные и нечетные.

9. Работа с текстом учебника с восклицательным знаком:

Какое число, четное или нечетное получается при умножении любого числа на 2?

Вывод: При умножении любого числа на 2 получается четное число.

III. Формулирование темы и целей урока

Как вы думаете, для чего нам может пригодиться то, что мы сейчас узнали? Чем мы сегодня будем заниматься?

(ответы детей)

Сейчас узнаем тему:

«Четные и нечетные числа» (запись на доске)

Физминутка

Мы устали, засиделись

Мы устали, засиделись,

Нам размяться захотелось.

Отложили мы тетрадки,

Приступили мы к зарядке

(Одна рука вверх, другая вниз, рывками менять руки. )

То на стену посмотрели,

То в окошко поглядели.

Вправо, влево поворот.

(Повороты корпусом.)

А потом наоборот.

Приседанья начинаем,

Ноги до конца сгибаем.

Вверх и вниз, вверх и вниз,

Приседать не торопись!

(Приседанья.)

И в последний раз присели,

А теперь за парты сели.

(Дети садятся за парты.)

IV. Первичное закрепление

(использование нового знания при решении задач)

Задание 5 (а) стр. 67.

Сделайте рисунок и решите задачу.

Восемь ребят разделились в группы по 2 человека. Сколько групп получилось.

Практическая работа

Просчитайте и объясните задание. Как будем его выполнять?

(ответы детей, составление плана действий, выполнение задания в тетрадях, на доске)

Какую оценку заслужили?

V. Самостоятельная работа в парах

Задание 5 (б) стр. 67

Восемь ребят разделились на 2 группы поровну. Сколько человек в одной группе?

Можно ли по нашему плану выполнить это задание? Почему? В чем отличие?

(дети самостоятельно работают по плану:

Верно выполнено задание? Чем отличаются решения этих задач? Сравни их решения.

Какую оценку заслужили?(пара получает оценку за правильность работы, за точность формулировок).

Придумайте и решите похожие задачи.

(заслушивается несколько вариантов подобных задач).

VI. Систематизация и повторение

1. Работа в парах (по вариантам)

1 в – № 6 (1, 2 столбик)

2 в – № 6 (3, 4 столбик)

Вставь вместо «*» знаки «·» или «:».

8 * 2 = 4 2 * 5 = 10

6 * 2 = 12 4 * 2 = 2

7 * 2 = 14 18 * 9 = 2

16 * 8 = 2 3 * 2 = 6

Выполняется самостоятельно с последующей взаимопроверкой и обсуждением. Правильность полученных результатов обсуждается классом.

Физминутка

Рисуй треугольник

Рисуй глазами треугольник.

Теперь его переверни

Вершиной вниз.

И вновь глазами

Ты по периметру веди.

Рисуй восьмерку.

Ты головою не крути,

А лишь глазами осторожно

Ты вдоль по линиям води.

И на бочок ее клади.

Теперь следи горизонтально,

И в центре ты остановись.

Зажмурься крепко, не ленись.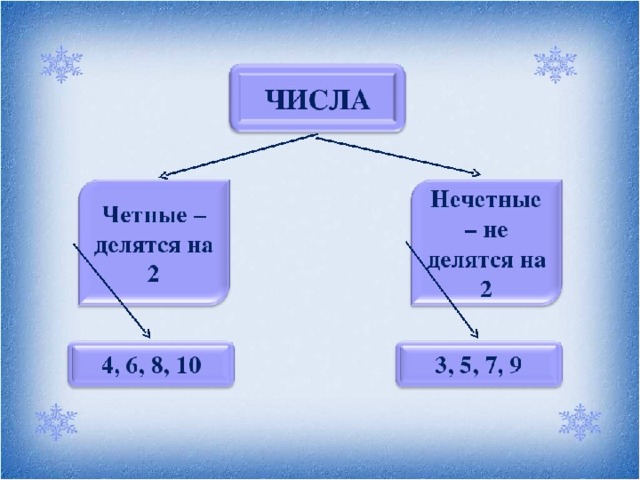

Глаза открываем мы наконец.

Зарядка окончилась.

Ты молодец!

(Дети представляют внешний вид геометрических фигур)

2. Фронтальная работа, на перестановку четырех элементов.

№ 9 (стр. 67)

Сколько различных четных и двузначных чисел можно написать с помощью цифр 1, 3, 2, 0, если:

а) цифры в числе могут повторяться;

б) цифры в числе не повторяются.

Последовательность работы:

а) на доске записаны цифры 1, 3, 2, 0

Детям предлагается назвать все возможные способы получения двухзначных чисел, когда цифры в числе повторяются, отобрать из них только четные. Получается, что возможен только один вариант – 22.

б) устанавливается закономерность, по которой записываются двузначные числа, когда цифры в числе не повторяются (фиксируется первая цифра, а вторые меняются), при этом двузначные числа должны быть четными. Из всех возможных вариантов выбираются следующие числа: 10, 12, 20, 30, 32.

VII. Итоги урока

Чем занимались на уроке?

Какое задание понравилось больше всего?

Какое задание захотелось выполнить еще раз?

Чтобы убедиться, что материал вами усвоен, предлагаю «блиц-опрос»

а) сложить два четных числа;

три четных числа;

два нечетных числа;

три нечетных числа.

б) из четного вычесть четное;

из нечетного вычесть четное;

из нечетного вычесть нечетное.

Обоснуйте свои ответы

(после каждого ответа на доске выставляются карточки с буквами Ч – четное, Н – нечетное)

ч ч ч н ч н ч

А теперь получите оценку за урок.

(карточки переворачиваются, там слово МОЛОДЦЫ)

VIII. Предполагаемая домашняя работа

(включая вариант и инвариант)

Задание 7, 8.

Четные и нечетные числа | План-конспект урока по математике (2 класс) по теме:

План урока математики

во 2 «А» классе МОУ «СОШ № 51»

г. Саратова

учитель Кузьмина М.В.

Четные и нечетные числа

(Урок введения нового знания)

Основные цели:

1. Познакомиться с понятиями четности-нечетности

(учить видеть, что:

1. сумма двух четных чисел – четное число;
2. сумма двух нечетных чисел – четное число;
3. сумма четного и нечетного чисел – нечетное число).

2. Продолжить работу с простыми задачами на умножение, основываясь на знании смысла действия умножения и таблицы умножения числа 2.
3. Решать простые задачи на деление, основываясь на знании взаимосвязи умножения и деления.
4. Продолжать учить таблицу умножения числа 2 и соответствующих ей случаев деления.
5. Развивать умение решать комбинаторные задачи на перестановку.
6. Развивать интеллектуальные и коммуникативные общеучебные умения.
7. Развивать организационные общеучебные умения, в том числе самостоятельно  оценивать  результаты  своих  действий, самого себя, находить и исправлять собственные ошибки.

Ход урока

I. Актуализация знаний

1. Организационный момент

Повторение таблицы умножения числа 2 и соответствующих ей случаев деления.

2. Индивидуальная работа (4 ученика получают карточки с заданиями)

1 карточка

Какое число пропущено?

7 + 8 = 15

6 + 8 = 14

9 + 4 = 13

2 + 10 = 12

Найди и исправь ошибки

18 – 9 = 7 (9)

9 + 6 = 15

13 – 6 = 8 (7)

7 + 6 = 13

15 – 8 = 9 (7)

16 – 9 = 7

5 + 7 = 12

11 – 2 = 8 (9)

3 карточка

Между некоторыми числами поставь знаки действий: «+» «-» или «*», чтобы выполнялись равенства:

2   4   6   8 = 4

2   4   6   8 = 6

2   4   6   8 = 8

2   4   6   8 = 10

4 карточка

Составь выражение и посчитай:

1. сколько лапок у 3 гусят? 2*3 = 6
2. сколько лапок у 2 котят? 4*2 = 8
3. сколько крыльев у 4 кутят? 2*4 = 8

3. Фронтальная работа

а) соревнования по группам

«Кто первый решит?»

18 : 9 = 2                 4 – 2 = 8                     5 – 2 = 10

8 : 2 = 4                       12 : 2 = 6                    10 : 5 = 2

2 – 3 = 6               2 – 2 = 4                      6 – 2 = 12

16 : 2 = 8              14 : 7 = 2                     16 : 8 = 2

6 : 2 = 3                       18 : 2 = 9                     2 – 8 = 16

10 : 2 = 5              14 : 2 = 7                     9 – 2 = 18

Что можно сказать об ответах, которые получились в 1, 2, 3 столбиках? Что это за числа?

б) составьте слова, найдите лишнее:

ПОКТА                 ЧАТРЕПКА

СОКОН                     ПКАША

РЕЖВАКА             ФРША

Какие из этих предметов используются только по два? Верно ли выполнено задание? Какой вопрос был самым трудным? Самым легким? Какую оценку заслужили?

II.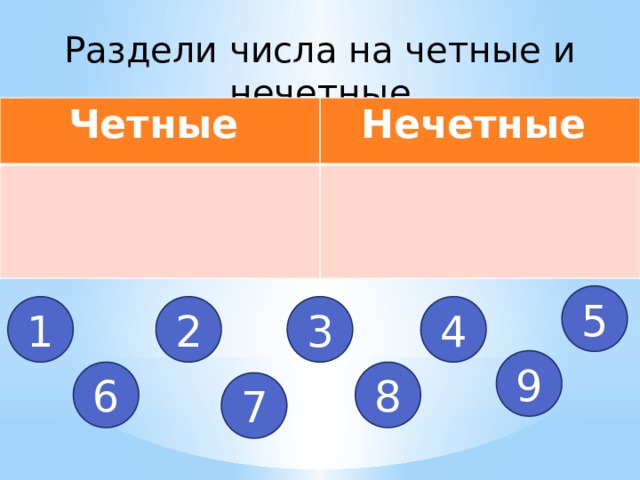 «Открытие» нового знания

Работа с учебником

1. Задание 1 (стр. 66)

Как разложить варежки по 2 (парами)?

Проанализировать вместе с детьми задание и рисунок. Сделать вывод, как должны производить деление: варежки разложить парами в соответствии с их цветами, при этом варежка останется без пары.

Варежки разложить в классе не можем, заменим их кругами.

Практическая работа

Возьми 7 кружков и разложи их по 2.

Дети раскладывают на партах 7 кружков по 2. Делают вывод: 7 по 2 не делится, один кружок остается.

2. Задание 2 (стр. 66)

а) по два 6 красных кружков, 9 синих кружков, 10 зеленых кружков;

б) на две равные части 3 красных кружка, 4 синих кружка, 5 зеленых кружков.

Практическая работа

Дети самостоятельно на партах раскладывают кружки, а два человека работают у доски. После того, как задание выполнено, они объясняют, как делили кружки «по 2» и «на 2 равные части». Делают вывод.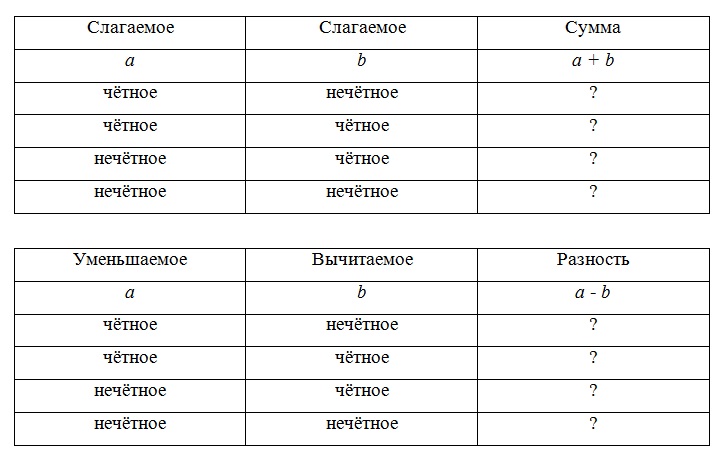 Остальные ребята оценивают выполненное задание, выставляют оценку.

а) дети раскладывают красные, синие, зеленые кружки по 2;

б) дети раскладывают красные, синие, зеленые кружки на 2 равные части.

3. Работа с текстом учебника со знаком вопроса:

1. какие кружки удалось разложить парами?
2. какие не удалось?
3. почему?

Дети отвечают на вопросы, делают вывод, записывают на доске числа, которые можно (нельзя) разделить по два

6, 4, 10                 9, 3, 5, 7

Как называются эти числа? (ответы детей)

4. Работа с текстом учебника с восклицательным знаком:

Вывод:         Числа 4, 6, 10 делятся на 2. Они называются четными.

Числа 3, 5, 7, 9 не делятся на 2. Они называются нечетными.

5. Задание 3 (стр. 66).

Прочитайте сначала четные, потом нечетные числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18.

(дети читают по очереди).

6. Работа с текстом учебника со знаком вопроса:

Что ты заметил?

7. Работа с текстом учебника с восклицательным знаком:

Вывод: Четные и нечетные числа в числовом ряду чередуются.

8. Выполнение задания 4.

Выполни действия:

а) умножь на 2 все четные числа в числовом ряду от 1 до 10. Расскажи, какие получились числа – четные или нечетные?

б) умножь на 2 все нечетные числа в этом же ряду. Расскажи, какие получились числа – четные или нечетные?

Дети записывают в тетрадь

а)         2         4         6         8         10

4         8         12         16         20

б)         1         3         5         7         9

2         6         10         14         18

Делают вывод: записанные числа четные и нечетные.

9. Работа с текстом учебника с восклицательным знаком:

Какое число, четное или нечетное получается при умножении любого числа на 2?

Вывод: При умножении любого числа на 2 получается четное число.

III. Формулирование темы и целей урока

Как вы думаете, для чего нам может пригодиться то, что мы сейчас узнали? Чем мы сегодня будем заниматься?

(ответы детей)

Сейчас узнаем тему:

«Четные и нечетные числа» (запись на доске)

Физминутка

Мы устали, засиделись

Мы устали, засиделись,

Нам размяться захотелось.

Отложили мы тетрадки,

Приступили мы к зарядке

(Одна рука вверх, другая вниз, рывками менять руки.)

То на стену посмотрели,

То в окошко поглядели.

Вправо, влево поворот.

(Повороты корпусом.)

А потом наоборот.

Приседанья начинаем,

Ноги до конца сгибаем.

Вверх и вниз, вверх и вниз,

Приседать не торопись!

(Приседанья.)

И в последний раз присели,

А теперь за парты сели.

(Дети садятся за парты.)

IV. Первичное закрепление

(использование нового знания при решении задач)

Задание 5 (а) стр. 67.

Сделайте рисунок и решите задачу.

Восемь  ребят  разделились  в  группы  по  2  человека.  Сколько  групп получилось.

Практическая работа

Просчитайте и объясните задание. Как будем его выполнять?

 (ответы детей, составление плана действий, выполнение задания в тетрадях, на доске)

Какую оценку заслужили?

V. Самостоятельная работа в парах

Задание 5 (б) стр. 67

Восемь ребят разделились на 2 группы поровну. Сколько человек в одной группе?

Можно ли по нашему плану выполнить это задание? Почему? В чем отличие?

(дети самостоятельно работают по плану:

1. разъясняют друг другу задание;
2. записывают решение;
3. взаимопроверка;
4. презентация результата одним учеником из пары)

Верно выполнено задание? Чем отличаются решения этих задач? Сравни их решения.

Какую оценку заслужили?(пара получает оценку  за правильность  работы, за точность формулировок).

Придумайте и решите похожие задачи.

(заслушивается несколько вариантов подобных задач).

VI. Систематизация и повторение

1. Работа в парах (по вариантам)

1 в – № 6 (1, 2 столбик)

2 в – № 6 (3, 4 столбик)

Вставь вместо «*» знаки «·» или «:».

8 * 2 = 4           2 * 5 = 10

6 * 2 = 12          4 * 2 = 2

7 * 2 = 14         18 * 9 = 2

16 * 8 = 2         3 * 2 = 6

Выполняется самостоятельно с последующей взаимопроверкой и обсуждением. Правильность полученных результатов обсуждается классом.

Физминутка

Рисуй треугольник

Рисуй глазами треугольник.

Теперь его переверни

Вершиной вниз.

И вновь глазами

Ты по периметру веди.

Рисуй восьмерку.

Ты головою не крути,

А лишь глазами осторожно

Ты вдоль по линиям води.

И на бочок ее клади.

Теперь следи горизонтально,

И в центре ты остановись.

Зажмурься крепко, не ленись.

Глаза открываем мы наконец.

Зарядка окончилась.

Ты молодец!

(Дети представляют внешний вид геометрических фигур)

2. Фронтальная работа, на перестановку четырех элементов.

№ 9 (стр. 67)

Сколько различных четных и двузначных чисел можно написать с помощью цифр 1, 3, 2, 0, если:

а) цифры в числе могут повторяться;

б) цифры в числе не повторяются.

Последовательность работы:

а) на доске записаны цифры 1, 3, 2, 0

Детям предлагается назвать все возможные способы получения двухзначных чисел, когда цифры в числе повторяются, отобрать из них только четные. Получается, что возможен только один вариант – 22.

б) устанавливается закономерность, по которой записываются двузначные числа, когда цифры в числе не повторяются (фиксируется первая цифра, а вторые меняются), при этом двузначные числа должны быть четными. Из всех возможных вариантов выбираются следующие числа: 10, 12, 20, 30, 32.

VII. Итоги урока

Чем занимались на уроке?

Какое задание понравилось больше всего?

Какое задание захотелось выполнить еще раз?

Чтобы убедиться, что материал вами усвоен, предлагаю «блиц-опрос»

1. какое число получится, если

а)         сложить два четных числа;

три четных числа;

два нечетных числа;

три нечетных числа.

б)         из четного вычесть четное;

из нечетного вычесть четное;

из нечетного вычесть нечетное.

Обоснуйте свои ответы

(после каждого ответа на доске выставляются карточки с буквами Ч – четное, Н – нечетное)

ч        ч        ч        н        ч        н        ч

А теперь получите оценку за урок.

(карточки переворачиваются, там слово МОЛОДЦЫ)

VIII. Предполагаемая домашняя работа

(включая вариант и инвариант)

Задание 7, 8.

Видео-урок: Определение нечетных и четных чисел: Пропустить счет

Стенограмма видео

Определение нечетных и четных чисел: Пропустить счет

В этом видео мы научимся как определить, является ли число до 20 нечетным или четным. И мы собираемся сделать это, пропустив считая двойками. Давайте начнем с практики нашего пропуска навыки счета. Мы знаем, что когда мы пропускаем счет, мы назовите число, затем пропустите несколько, затем произнесите другое число, пропустите еще несколько и так далее. на. И в этом видео мы собираемся пропустить счет двойками.

Давайте построим из них башню ледяные кирпичи. Чтобы помочь нам пропустить счет двойками, мы будем класть по два кирпича за раз. Какие числа мы скажем? ну там кирпичей нету начать с, так что мы можем начать считать с нуля, а затем два, четыре, шесть, восемь, 10, 12. Что вы заметили в числа, которые мы сказали? Если мы начнем с нуля и пропустим счет в двойках все числа, которые мы произносим, ​​будут четными: два, четыре, шесть, восемь, 10, 12. Продолжим считать в двоек, так что мы произносим все остальные четные числа до 20. После 12 идут 14, 16, 18 и 20. Возможно, вы также заметили, что все эти четные числа являются числами в таблице умножения на два. Один раз два два, две двойки четыре, трижды два — шесть и так далее. И поэтому мы можем сказать, что все четные числа кратны двум.

А как насчет чисел в между? Мы все еще могли бы сказать эти числа по пропустим счет двойками, но нам придется начинать с единицы, а не с нуля. Это будет немного похоже на положить один ледяной кирпич для начала, а затем считать по два, как до. Мы бы закончили тем, что сказали бы цифры один, три, пять. Кстати, вы можете посмотреть, что происходит с нашей башней каждый раз? Всегда остается один кирпич на вершине. Семь, девять, 11. Мы называем эти числа нечетными числа. Начнем с последнего нечетного числа что мы сказали, 11, и давайте продолжим считать двойками, чтобы мы сказали все нечетные числа до 20,

Итак, у нас есть 11, а затем 13, 15, 17 и 19. Посмотрите, как каждое из наших нечетных чисел на единицу больше, чем четное число. Три на один больше, чем два, пять на на единицу больше четырех, семь на единицу больше шести. Вот почему, когда мы пытаемся сделать нашу башня, это выглядело так интересно. Всегда был еще один кирпич осталось сверху. Итак, теперь, когда мы попробовали считая ледяные кирпичи по двое. Давайте попробуем ввести вопрос, где мы должны посчитать другой тип объекта двойками. Посмотрим, сможем ли мы справиться является ли число нечетным или четным.

Майкл считает своих медведей в двойки. Он доходит до 12 и затем видит, что он осталось сосчитать только одного медведя. У него четное или нечетное число медведей?

Похоже, у Майкла довольно коллекция игрушечных медведей здесь, не так ли? И нам говорят в первую предложение этой задачи, что он их считает. Но он не считает их в таким же образом, как, может быть, мы могли бы обычно считать группу предметов, один, два, три и т. д. на. Нам говорят, что он их считает в двойках. И, подсчитав их по группам два, как это, это гораздо более быстрый способ подсчета. Мы называем это пропуском счета, потому что мы не обязательно говорить каждое число. Некоторые цифры пропускаем. Чтобы понять, что сделал Майкл вот и попробуем сами.

Итак, вот наша коллекция медведей. Начнем считать двойками. Два, четыре, шесть, восемь, 10, 12. Но подождите минутку. Мы больше не можем считать двойками. Остался только один медведь. Давайте поставим ее с другие. Теперь, делая это для себя, мы может понять, что говорит нам следующее предложение в нашей задаче. Нам говорят, что Майкл доходит до 12 лет. а потом видит, что ему осталось сосчитать только одного медведя. Теперь вы можете подумать, что это Теперь нас спросят, сколько медведей у ​​Майкла? И чтобы найти ответ, нам нужно думать о том, что один больше, чем 12. Но нас об этом не спрашивают. Нам не нужно считать, сколько медведи у Майкла есть вообще. Вместо этого нам нужно сказать, является ли он имеет четное или нечетное количество медведей.

Теперь, когда Майкл пересчитал свои медведи, он начал без медведей. Пометим ноль, просто чтобы показать, что он начал считать отсюда. Теперь мы знаем, что если мы начнем с ноль, и мы пропускаем счет двойками, каждое число, которое мы произносим, ​​будет четным количество. Итак, если бы у Майкла было только два медведя, у него будет четное количество медведей, или четыре медведя, или шесть, восемь, 10 или 12. Это все четные числа.

Но мы знаем, что Майкл не был способен считать своих медведей по двое. Он дошел до числа 12, но потом у него остался один. У Майкла нет четного числа медведей. У него нечетное количество медведей. Если мы пропустим счет двойками от нуля но у нас остался один, у нас нечетное число. Другой способ сказать то же самое Дело в том, что на единицу больше, чем четное число, является нечетным числом. Количество медведей, которое Майкл имеет странное.

Ты помнишь наш номерной трек которые мы раскрасили, чтобы показать нечетные и четные числа? Ну, давайте нарежем его на квадраты и мы сложим все нечетные числа вместе и все четные числа вместе. Итак, у нас есть нечетные числа: один, три, пять, семь, девять, 11, 13, 15, 17, 19. И у нас есть четные числа: два, четыре, шесть, восемь, 10, 12, 14, 16, 18, 20. Теперь вы заметили что-нибудь о эти группы чисел теперь, когда мы собрали их все вместе? Давайте поиграем в игру, которая может помочь ты что-то замечаешь.

Этот медведь держит двузначный карты, и они составляют число. Но является ли это загадочное число четным или странный? А теперь приходит вызов. Чтобы найти ответ, вам нужно всего лишь разрешено перевернуть одну из карт. Что это будет? Во-первых, мы знаем, что наша номер состоит из двух цифр. Но если мы перевернем цифру на левые здесь, это на самом деле не поможет нам. Представьте, что мы посмотрели на это, и это показал цифру один. Ну там много нечетных чисел с единицей в разряде десятков: 11, 13, 15 и так далее. Но есть и четные числа с единицей в разряде десятков: 12, 14, 16.

В этом разряде десятков есть много нечетных и четных чисел, сидящих рядом. Итак, чтобы решить нашу задачу, один карта, на которую нам нужно взглянуть, находится справа. Это цифра единиц. И цифра единиц – ноль. Теперь мы не знаем, что другое цифра есть, но нам это не нужно знать. Это может быть один, делая число 10, или это может быть двойка, что дает число 20. На самом деле это не имеет значения. И причина, почему это не так все дело в схеме, которую мы можем видеть в цифрах. Если мы начнем с рассмотрения нашего четные числа, мы можем видеть, что они всегда заканчиваются одним и тем же набором цифр. Это может быть цифра два, как в числа два или 12, четыре, как в числах четыре или 14, шесть, восемь или ноль.

Теперь мы знаем, потому что решили посмотрите на эту вторую карту, число, которое показывает нам медведь, заканчивается нулем. Это должно быть даже. И хотя любое число, оканчивающееся на два, четыре, шесть, восемь или ноль четны, мы можем сказать, что любое число, оканчивающееся на один, три, пять, семь или девять — нечетное число. Итак, если бы наш друг медведь перевернул свою карточку, а на ней была семерка вместо нуля, мы бы знали что его номер был бы нечетным.

И, знаете ли, знание закономерностей и подобные последовательности могут помочь нам расширить наши знания о нечетных и четных числах за пределы 20. 28 оканчивается цифрой восемь. Это должно быть четное число. Мы знаем, что один странный цифра. Поэтому любое число, оканчивающееся на единицу также должно быть нечетным. тогда 31 нечетное число, как и 21. Давайте сейчас ответим на несколько вопросов где мы должны применить на практике эти два факта, которые мы только что узнали. Четные числа всегда заканчиваются на ноль, два, четыре, шесть или восемь. А нечетные числа всегда заканчиваются на один, три, пять, семь или девять.

Запишите следующие два нечетных числа: семь, девять, 11, 13, что, что.

В этом вопросе нам дается последовательность нечетных чисел. Мы знаем, что один из способов подсчета нечетные числа, чтобы начать с нечетного числа и пропустить счет по двое. Итак, если мы начнем с семи, наш следующий нечетное число девять, затем 11, и 13. И вы можете видеть, пропуская счет в двойки, мы пропускаем четные числа между восьмерками, 10 и 12? Итак, какие следующие два странных числа в нашей последовательности? Какое нечетное число идет после 13? Ну, если мы продолжим пропускать счет по двойке от 13 доходим до числа 15 и затем до числа 17. Мы знаем, что нечетные числа по порядку всегда следуйте шаблону. Последняя цифра единица, затем три, пять, семь и девять.

Хотя мы начали с цифры семь, мы можем продолжить этот шаблон и просто проверить правильность нашего ответа. Итак, у нас есть семь, девять, а затем снова к началу, раз, три, пять, семь. Мы пропускаем счет по двое, чтобы найти следующие два нечетных числа в нашей последовательности. Полная последовательность: семь, девять, 11, 13, а затем два недостающих числа, 15, 17.

Найдите большее нечетное число чем 93 и меньше 97.

В этом вопросе мы на охоте для нечетного числа. И нам дают две подсказки о нашем количество. Нам говорят, что это больше, чем 93, а также меньше 97. Если сказать по-другому, то нужно найти нечетное число между 93 и 97. Теперь в между 93 и 97, но только одно нечетное число. Чтобы узнать, что это такое, мы можем использовать наше знание некоторых моделей, которые мы можем видеть в четных и нечетных числах. Как мы могли определить даже номер, если мы видели один? Мы могли бы сказать, просто глядя на последнюю цифру, потому что четные числа всегда заканчиваются на ноль, два, четыре, шесть, или восемь.

Так что же это говорит нам о нечетных числа? Ну, они всегда заканчиваются цифрами между. Нечетные числа всегда заканчиваются на цифры один, три, пять, семь или девять. Итак, если мы посмотрим на два нечетных числа, которые нам дали в нашем вопросе, 93 оканчивается на тройку, 97 оканчивается на Семь. Вот откуда мы знаем, что они странные. Знаешь, может быть полезно обозначьте цифру три и цифру семь в нашем списке здесь, потому что если мы посмотрим в наших нечетных цифрах по порядку мы можем увидеть цифру между ними. Между тремя и семью пять. Итак, нечетное число между 93 а 97 равно 95.

Если мы знаем, какая последняя цифра в число, мы всегда можем сказать, четное оно или нечетное. Четные числа всегда заканчиваются на ноль, два, четыре, шесть или восемь. И нечетные числа всегда заканчиваются на единицу, три, пять, семь или девять. И вот как мы знаем нечетное число больше 93 и меньше 97 равно 95.

Что мы узнали из этого видео? Мы научились решать, число является нечетным или четным при пропуске счета двойками.

Суммирование последовательных чисел

Возраст от 11 до 14 лет

Уровень сложности

Свати из Международной школы сада начала с перечисления чисел до 15 и попытки представить их в виде суммы последовательных чисел:

2
3 = 1+ 2
4
5 = 2+3
6 = 1+2+3
7 = 3+4
8
9 = 4+5 = 2+3+4
10 = 1+2+3+4
11 = 5+6
12 = 3+4+5
13 = 6+7
14 = 2+3+4+5
15 = 7+8 = 4+5+6 = 1+2+3+4+5

Мы не можем записать каждое число в виде суммы последовательных чисел — например, 2, 4 и 8 нельзя записать в виде суммы последовательных чисел. В вышесказанном 9и 15 были единственными числами, которые я мог найти, которые можно было записать более чем одним способом.

Многие заметили закономерность, согласно которой все нечетные числа (кроме 1) можно записать как сумму двух последовательных чисел. Например, Матильда и Тамарис написали:

Если сложить два последовательных числа вместе, сумма будет нечетным числом, например.
1+2=3    
2+3=5      
3+4=7      
4+5=9     
5+6=11     
6+7=13
и так далее…

Молодцы ученики Kenmont Primary School, которые заметили это и объяснили, что нечетное плюс четное всегда является нечетным.

Некоторые заметили аналогичную закономерность для чисел, кратных 3. Джулия и Лиззи сказали:

Если сложить вместе любые 3 последовательных числа, оно всегда будет кратно 3, например.
1+2+3=6
2+3+4=9
3+4+5=12
4+5+6=15
5+6+7=18

Продолжая выкройки, Lumen Christi Команда программы повышения квалификации по математике для 5/6 классов прислала нам:

Мы обнаружили, что сумма четырех последовательных чисел дает нам числовую последовательность 10, 14, 18, 22, 26, 30 и так далее. Все они были четными числами, половина которых составляла нечетное число.
1+2+3+4=10
2+3+4+5=14
3+4+5+6=18…

Хизер из Уоллингтонской средней школы для девочек объяснила эту закономерность:
10   – 1 +2+3+4
14   – 2+3+4+5
18   – 3+4+5+6
22   – 4+5+6+7
Во всех столбцах каждое место добавляет 1 каждый раз, поэтому в общей сложности вы добавляете 4 каждый раз.

Руби сказал:

Числа, кратные 5, начиная с 15, являются суммами 5 последовательных чисел:
1+2+3+4+5=15
2+3+4+5+6=20
3+4+5+6+7=25…

Фергус и Сами заметили аналогичную закономерность:

Если разрешены отрицательные числа, можно легко найти сумму для любого числа, кратного 7. Каждый раз, когда вы добавляете одно число по обе стороны от суммы, ваша сумма увеличивается на 7, например.
3+4=7
2+3+4+5=14
1+2+3+4+5+6=21
0+1+2+3+4+5+6+7=28
– 1+0+1+2+3+4+5+6+7+8=35…

Отлично! (Есть способ заставить этот паттерн работать даже без использования отрицательных чисел — вы его заметили?) Почему возникают все эти паттерны?

Бекки заметила другой тип шаблона:

Мы обнаружили, что степени двойки (2, 4, 8, 16. ..) никогда нельзя получить, сложив вместе последовательные числа.

Интересно! Интересно, почему?

Команда Lumen Christi предложила способ построения множества кратных нечетных чисел:

Мы выяснили, что если разделить число, кратное 3, на 3 и назвать ответ n, то исходное число будет суммой (n -1), n ​​и (n+1).

Затем мы обнаружили, что числа, кратные 5, можно записать как 5 последовательных чисел. Это то же самое, что правило для 3 последовательных чисел. Возьмите число и разделите его на 5, назовите его n, и тогда ваше число будет суммой (n-2), (n-1), n, (n+1) и (n+2).

Затем мы сделали предположение, что, поскольку это верно для 3 и 5, оно также будет работать для 7, 9 и любого другого нечетного числа. Мы проверили это, и это сработало. Например, 63 кратно 7 и 9:

7 чисел: 6+7+8+ 9 +10+11+12=63
(63/7 = 9)
9 чисел: 3+4+ 5+6+ 7 +8+9+10+11=63
(63/9 = 7)

Как мы можем продолжить это исследование? Артур спросил:

Есть ли другие шаблоны?
Можем ли мы продолжить изучение силы двоих?
Есть ли хороший способ записать определенные числа (например, все остальные четные числа) в виде суммы последовательных чисел?

Оттилия предложила:

Вместо сложения вы могли бы умножить последовательные числа и посмотреть, какие закономерности появятся.