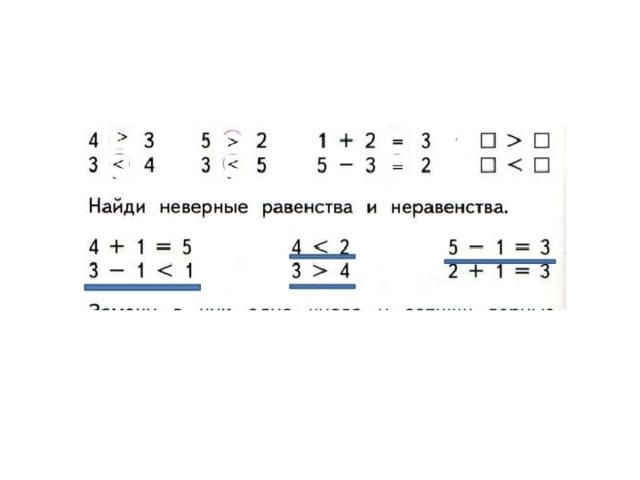
1 класс математика равенства и неравенства: Математика 1 класс Моро

Урок математики ” Равенство и неравентсво”(1 класс(

Конспект урока  Равенство, неравенство

по математике в 1 классе «А»
по теме: «Равенства и неравенства»
Составила учитель начальных классов первой квалификационной категории Мальшакова Н. П.

Дата: «19» ноября 2018г.
ФИО учителя: Мальшакова Н. П
Класс: 1 «А» класс.

Цель:
1. Цель: создать условия для ознакомления с терминами «равенство», «неравенство».
Задачи:
Формировать представление о равенстве и неравенстве.
Формировать умение сравнивать числа и правильно использовать знаки сравнения «больше», «меньше», «равно».
Совершенствовать умение составлять равенство, используя связь целого и частей.
Способствовать развитию математической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышления.
Планируемые результаты:
Предметные:
Формирование представления о равенстве и неравенстве.
Умение сравнивать числа и правильно использовать знаки сравнения «больше», «меньше», «равно».

Умение составлять равенство, используя связь целого и частей.
Способствование развитию математической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышления.
Метапредметные:
Познавательные УУД:
Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя, добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.
Регулятивные   УУД:
уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность  действий на уроке, работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной оценки, планировать своё действие в соответствии с поставленной задачей

Коммуникативные УУД:
Уметь оформлять свою мысль в устной форме (на уровне одного предложения или небольшого текста).
Уметь слушать и понимать речь других.

Совместно договариваться о правилах поведения и общения в школе и следовать им
Личностные УУД:
Соблюдают организованность, дисциплинированность на уроке.
Уметь проводить самооценку на основе критерия успешности учебной деятельности.
Основные понятия: равенство, неравенство, сравнение.
Образовательные ресурсы:
– Моро М. И. Математика. Учебник для 1-го класса. Часть 1. Стр. 49
– электронное приложение к учебнику М. И. Моро «Математика» 1 класс

                                                          Сценарий урока
Этапы урока

 Ход урока

Формируемые УД
1. Организация начала урока
1.1 Приветствие.
-Ребята, прозвенел звонок. Станьте ровно, красиво чтобы на вас приятно было смотреть.
– Садитесь.

Мы пришли сюда учиться,

Не лениться, а трудиться,

Работаем старательно

Слушаем внимательно.

 Сегодня к нам на урок пришёл наш дружок Кузя. Он тоже хочет учиться. И сегодня он пришёл к нам в гости, чтобы найти ответы на некоторые вопросы. Вам потребуется внимание, творчество, взаимовыручка и взаимопомощь.  Я тоже желаю вам всего хорошего.

Кто с работой дружен,
Нам сегодня нужен?. .. (Нужен)
Кто с учёбой дружен,
Нам сегодня нужен?… (Нужен)
С математикой кто дружен,
Нам сегодня нужен?…(Нужен)
Таким ребятам хвала и честь!
Такие ребята в классе есть?
Есть!
Учащиеся приветствуют учителя.
Организуют свое рабочее место, проверяют наличие индивидуальных учебных принадлежностей на столе.
Хором отвечают на вопрос учителя:

2. Актуализация опорных знаний.

Повторение  нумерации чисел в пределах 10.

Тогда проведем небольшую разминку.

·        Фронтальная работа.
Счет цепочкой от 1 до 10 и обратно.
Игра « Продолжай ,не зевай»

·        Работа с математическим набором. Учитель задает вопрос, дети подни­мают карточку с ответом.

На одной улице с Кузей построили новый дом для чисел, чтоб они жили вместе, и им не было скучно. Когда все числа перезнакомились, то они стали жить дружно. А вот Кузя не знает, какие соседи у каждого числа, и решил спросить об этом вас.
Покажите соседей числа 4, (3, 5)

Какие числа живут рядом с числом 5, (4,6)

Какое число следует за числом 3? 5?
Какое число предшествует числу 4? 5? 2.

Кузя благодарит Вас.

Чему мы с вами учимся на уроках математики?(считать, писать цифры, сравнивать, решать примеры задачи)

Что уже узнали на прошлом уроке? (познакомились со знаками.)

3. Определение темы  и цели урока.
Создаётся проблемная ситуация.
Заполните пропуски в карточках с записью, найти «лишнюю» запись, прийти к выводу.
-Посмотрите на карточки с записью. Заполните пропуски.

1+3…4
5-1…4
3+2…4
-Что можно сказать о последней записи?
-Кто знает, как называется эта запись? (Если дети не смогут дать название записи, то учитель сам высказывает своё мнение)

Ученики называют «лишний пример» (Отличается цветом, левая часть не равна правой)

Какой знак надо поставить? Появилась проблема. Как её решить?

Значит  ставим знак больше, он похож на клюв птицы, а клюв раскрыт в сторону большего количества.

Исправьте ошибку. Давайте разобьем эти выражения на группы. По какому признаку вы их можете разделить?

1+3=4               3+2>4
          5-1=4
        Учитель через поставленные вопросы подводит учащихся к формулированию темы и целей урока.

– Как бы вы назвали запись в левом столбике?

(Если дети не смогут дать название записи, то учитель сам высказывает своё мнение)

-Как бы вы назвали запись в правом столбике?

«Со знаком «=» – это равенство, а со знаком «>» или  «<»- неравенство»

Давайте прочитаем, как  эти  записи  предлагают  назвать авторы учебника? Учебник, стр. 48

– Можете ли вы сформулировать тему урока?

На доске появляется запись:

ТЕМА: Равенство.Неравенство.

– Какую цель вы поставите перед собой на уроке?

Я думаю …

Я считаю …

Тогда скажите, что мы будем делать на уроке?

Сегодня на уроке мы будем сравнивать числа и выражения, узнаем,что такое равенство и  неравенство.

4. Физминутка.

5. Открытие новых знаний.

Ребята, давайте  вместе с вами выясним, что такое равенство и неравенство, и поможем в этом разобраться нашему другу Кузе.

1.     Работа со счетным материалом.

У доски работает один ученик, остальные дети работают на местах.
Положите 3 красных квадрата, рядом  положите столько же синих.

 Сколько положили?

– Что можете сказать о количестве красных и синих квадратов? (Красных и синих квадратов поровну. Красных столько же, сколько и синих)

Обозначим цифрами. Какой знак поставим между цифрами?(Равно)
Как это записать? (3 =3)

– Прочитайте выражение. Как назовём это выражение?(равенство)

 – Правильно, это равенство.

    – Как думаете, почему мы  называем это выражение равенство?

 (Если количество равное, то такое математическое выражение  называется равенством)

  2. Положите 3 красных круга. Рядом 2 желтых треугольника.

– Что можно сказать о количестве красных и желтых треугольников?

(кругов больше, чем треугольников)

 Давайте покажем это на доске, обозначьте  цифрами. Какой знак поставим между цифрами? (больше)

Появляется запись 3 > 2.

Прочитайте выражение. Как назовём это выражение?

Это неравенство.
– Как думаете, почему мы называем это выражение неравенством?

(Если количество больше или меньше, то  такое математическое выражение называется неравенством)

– Какой можно сделать вывод?( если между числами стоит знак  «равно», то это равенство, если между числами стоит знак « больше» или «меньше», то это неравенство.

 6. Учитель проверяет степень понимания учащимися нового

материала. Закрепление изученного материала.

Фронтальная работа. Первичное закрепление. Игра.

1.     Учитель показывает карточки ( 2=2, 4>2, 4=4, 1 <3, 1 = 1, 4> 3). Если я показываю равенство, то вы стоите ровно, если  неравенство, делаете наклон)

2.     Составление равенств и неравенств по рисунку.(работа у доски)

У Кузи был друг Почемучка. Почемучка любил задавать вопросы. Он спрашивает : А как сравнить число и выражение?

Давайте попробуем вместе с вами ответить на этот вопрос.

– Сколько звездочек слева? Запишите. ( 2)

– Сколько справа красных? А жёлтых?( 2 красные и 2 желтые)

– Какое выражение запишем?(2+2)

– Как сравнить число и выражение?( Надо найти сначала значение выражения и сравнить полученные числа)

– Сколько всего звездочек справа?

– Какой знак поставим  2 < 2+2.

-Как называется это выражение? (неравенство)Почему называем это выражение неравенством?( Стоит знак  меньше)

– Сколько солнышек? Запишите. (3)

– Сколько было тучек?

– Что сделали с одной тучкой?

– Какое выражение запишем? ( 4-1)

– Сравните. Какой знак поставим? (3=4-1)

Как называется это выражение?( равенство). Почему это выражение называем равенством?. Стоит знак «равно».

1.     Учитель предлагает задание:

«Катя написала равенства, а Петя – неравенства. Прочитайте сначала записи  Кати, а потом записи Пети»

Работа в парах. .

Надо разложить записи в группы:

7+1=8           3+3=6

4-2=2            9-1>6

8-1< 9           10-1<10

Проверка.

2.     Самостоятельная работа.

Ребята, Незнайка не мог справиться с заданием, он не знает какие нужно поставить знаки. А вы можете выполнить задание? У каждого учащегося карточки с заданием.

-Поставь знаки сравнения.

4*3      2*4

1*3     3*3

2*2      3*1

Проверка работы.

-Прочитайте равенства.

– Какой математический знак использовали при записи равенства?

– Прочитайте неравенства.

— Какие математические знаки  использовали при записи неравенства?

7. Итог урока. Рефлексия.

– С какими математическими выражениями мы познакомились сегодня на уроке?

Скажите ребята, чем мы сегодня занимались на уроке?

– Что особенно понравилось?

Оцените свою работу на уроке.

– Кто сегодня справился со всеми заданиями без ошибок?

– Кому нужна помощь товарищей?

Какое задание вам было интересно выполнять?

– Кто доволен своими успехами?

 

Я благодарю вас за работу на уроке. Поднимите руки, положите их на голову и погладьте себя. Все вы молодцы!

А теперь покажите мне, с каким настроением вы уходите с урока. Если все получилось, вы довольны собой –нарисуйте улыбку.

Если недовольны собой и у вас ничего не получалось, нарисуйте грустного человечка. Поднимите свои рисунки. У нас много улыбок, а это значит, что мы все на уроке потрудились очень хорошо и еще сможем многое. Молодцы!

 

 

Презентация к уроку математики в 1 классе.

Равенство, неравенство. Презентация к уроку математики в 1 классе. Равенство, неравенство.

12+  Свидетельство СМИ ЭЛ № ФС 77 – 70917 Лицензия на образовательную деятельность №0001058

Пользовательское соглашение     Контактная и правовая информация

 

Педагогическое сообщество УРОК.РФ

Бесплатные всероссийские конкурсы

Бесплатные сертификаты за публикации

Нужна помощь? Инструкции для новых участников

Бесплатная   онлайн-школа для 1-4 классов

Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости

Библиотека

▪Учебно-методические материалы

▪Презентации

Материал опубликовала

10

#1 класс #Математика #Учебно-методические материалы #Презентация #Учитель начальных классов #Школьное образование

Пояснительная записка. Математика
DOCX / 14.6 Кб
22 урок. Равенство. Неравенство
PPTX / 3.94 Мб

Опубликовано 09.10.19 в 17:19 в группе «Учителя начальных классов»

сменить сортировку

Ильина Оксана Геннадьевна, 09.10.19 в 17:33 2ОтветитьПожаловаться

Спасибо,Ольга Игоревна,отличная презентация!

Горбачёва Марина Юрьевна, 09.10.19 в 17:33 2ОтветитьПожаловаться

Благодарю за интересный ресурс!

Кадырова Ольга Игоревна, 09.10.19 в 17:36 1ОтветитьПожаловаться

Спасибо, коллеги, за постоянное внимание!

Перминова Елена Федоровна, 09.10.19 в 18:02 1ОтветитьПожаловаться

Отличная работа, спасибо!

Кадырова Ольга Игоревна, 09. 10.19 в 18:20 0ОтветитьПожаловаться

Очень рада!

Ахметшина Наталья Юрьевна, 09.10.19 в 20:31 1ОтветитьПожаловаться

А вот сегодня девчонка весёлая!!!

Кадырова Ольга Игоревна, 10.10.19 в 07:13 0ОтветитьПожаловаться

Конечно, поменяла, раз вчера грустный был!!!

Чтобы написать комментарий необходимо авторизоваться.

Закрыть

мат-гр. 1. Равенство и неравенство, гр. 2. Округление – г-жа Чин

1-й класс: равенство и неравенство 

Сегодня я хочу, чтобы вы попрактиковались в определении, является ли уравнение равным или нет. Например, вы привыкли видеть такие уравнения, как 5+5=10 и 8-5=3. Теперь представьте, что знак = похож на стену. Когда мы пытаемся увидеть, равны ли вещи в математических уравнениях, мы хотим знать, одинаковы ли значения чисел на каждой стороне стены со знаком =. Например, для уравнения 5+5=10. С левой стороны 5+5, мы знаем, что это равно 10. С правой стороны у нас есть число 10. Таким образом, на каждой стороне стены значение одинаковое. Опять же, с 8-5=3. Представьте, что знак = — это стена. На левой стороне стены у нас есть 8-5, что, как мы знаем, равно 3. На правой стороне стены у нас есть 3, поэтому на каждой стороне стены значение одинаково. В обеих этих ситуациях есть равенство.

А как насчет 4+5=10? С левой стороны стены мы знаем, что 4+5=9. Таким образом, на левой стороне стены значение чисел равно 9. На правой стороне стены со знаком = 9. Равно ли это уравнение? Ответ – нет. 4+5 не равно 10. Значения на каждой стороне стены неравны, поэтому возникает неравенство . Для этого уравнения мы покажем, что это неравенство, используя этот знак: ≠.

Мы также можем сделать это с помощью простых уравнений.

Если у меня 5+5=6+4, это правильно? Должен ли быть знак = или знак ≠?

С левой стороны стены со знаком = есть 5+5, что, как мы знаем, равно 10. С правой стороны есть 6+4, что тоже равно 10. Так есть ли равенство или неравенство? Существует равенство, потому что обе стороны равны 10. 

Попробуйте эти рабочие листы и посмотрите, сможете ли вы выяснить, используете ли вы знак = или знак ≠!

Рабочие листы:

Введение Рабочий лист равенства и неравенства

Равенство и неравенство Простые уравнения

2 класс: Округление

Сегодня мы попрактикуемся в округлении до десятых. Что такое округление? Округление — это когда мы берем число и находим ближайшее число 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, рядом с которым оно находится. Мы делаем это, когда оцениваем измерение или нуждаемся в общем представлении о том, сколько чего-то есть или какова его длина. Например, если у меня есть число 26, я должен подумать, между какими числами оно находится или близко к ним (которые кратны десяти)? Что ж, на числовой прямой 26 находится между 20 и 30. Теперь, какова середина пути между 20 и 30?

20, 21, 22, 23, 24, 25 , 26, 27, 28, 29, 30.

25 находится прямо между ними. Теперь я должен подумать, 26 ниже или выше, до или после 25? Оно выше 25, потому что 26 больше 25, оно стоит после него на числовой прямой. На числовой прямой видно, что 26 ближе к 30. Поэтому, если бы я округлял до ближайших десяти, 26 округлилось бы до 30.

Мы также можем округлить до ближайших сотых. Например, если у меня есть число 123. Я должен подумать, ближе ли оно к 100 или 200? На числовой прямой это число было бы ближе к 100, чем к 200.

Посмотрите это видео, чтобы получить полное объяснение того, что такое округление и как это сделать!

Округление до ближайших 10

Вот диаграмма, которая может вам помочь.

Округление до ближайших 10 и 100 Диаграмма

Теперь я хочу, чтобы вы попробовали. Вот несколько рабочих листов, чтобы попробовать. Если у вас нет принтера, попробуйте сделать это устно. Используйте числовые линии, чтобы помочь вам, если вам это нужно!

Округлить до ближайшей десятки Введение

Округление до ближайшего 10-го рабочего листа

Значение, расчет, решение, построение графиков неравенств

В математике уравнения не всегда сбалансированы с обеих сторон с помощью символа «равно». Иногда речь может идти об отношениях «не равно», например, что-то больше, чем другое или меньше. В математике неравенство относится к отношениям, которые делают неравное сравнение между двумя числами или другими математическими выражениями. Эти математические выражения относятся к алгебре и называются неравенствами.

Давайте изучим правила неравенств, а также способы их решения и построения графика.

1.	Что такое неравенство?
2.	Правила неравенств
3.	Решение неравенств
4.	Графические неравенства
5.	Решение полиномиальных неравенств
6.	Решение абсолютных неравенств
7.	Решение рациональных неравенств
8.	Часто задаваемые вопросы о неравенствах

Что такое неравенство?

Неравенства   – это математические выражения, в которых обе стороны не равны. В неравенстве, в отличие от уравнений, мы сравниваем две величины. Знак равенства между ними заменяется знаком меньше (или меньше или равно), больше (или больше или равно) или не равно.

Оливия выбрана в софтболе 12U. Сколько лет Оливии? Вы не знаете, сколько лет Оливии, потому что там не сказано “равный”. Но вы знаете, что ее возраст должен быть меньше или равен 12, поэтому его можно записать как Возраст Оливии ≤ 12. Это практический сценарий, связанный с неравенством.

Неравенство Значение

Неравенство означает, что две вещи НЕ равны. Одна из вещей может быть меньше, больше, меньше или равна или больше или равна другим вещам.

• p ≠ q означает, что p не равно q
• p < q означает, что p меньше q
• p > q означает, что p больше q
• p ≤ q означает, что p меньше или равно q
• p ≥ q означает, что p больше или равно q

Существуют различные типы неравенств. Некоторые из важных неравенств:

• Полиномиальные неравенства
• Неравенства абсолютного значения
• Рациональные неравенства

Правила неравенств

Правила неравенств особенные. Вот некоторые из них с примерами неравенств.

Неравенства Правило 1

Когда неравенства связаны, вы можете перепрыгнуть через среднее неравенство.

• Если p < q и q < d, то p < d
• Если p > q и q > d, то p > d

Пример: Если Огги старше Мии, а Миа старше Черри, то Огги должен быть старше Черри.

Неравенство Правило 2

Перестановка чисел p и q приводит к:

• Если p > q, то q < p
• Если p < q, то q > p

Пример: Огги старше Мии, значит, Мия моложе Огги.

Неравенства Правило 3

Добавление числа d к обеим частям неравенства: Если p < q, то p + d < q + d

Пример: У Огги меньше денег, чем у Мии. Если и Огги, и Миа получат по 5 долларов больше, то у Огги все равно будет меньше денег, чем у Миа.

Аналогично:

• Если p < q, то p − d < q − d
• Если p > q, то p + d > q + d, и
• Если p > q, то p − d > q − d

Таким образом, прибавление и вычитание одного и того же значения как к p, так и к q не изменит неравенство.

Неравенства Правило 4

Если числа p и q умножить на положительное число, неравенство не изменится. Если вы умножаете и p, и q на отрицательное число, неравенство меняется местами: p

Вот правила:

• Если p < q и d положительно, то pd < qd
• Если p < q и d отрицательно, то pd > qd (обмен неравенством)

Положительный пример: оценка Огги, равная 5, ниже, чем оценка Мии, равная 9 (p < q). Если Огги и Миа удвоят свои оценки «×2», оценка Огги все равно будет ниже, чем оценка Миа, 2p < 2q. Если баллы станут минусами, то баллы будут -p > -q.

Правило неравенств 5

Постановка минусов перед p и q меняет направление неравенства.

• Если p < q, то −p > −q
• Если p > q, то −p < −q
• Это то же самое, что умножение на (-1) и изменение направления.

Неравенства Правило 6

Взятие обратного значения 1/от p и q изменяет направление неравенства. Когда p и q оба положительны или оба отрицательны:

• Если p < q, то 1/p > 1/q
• Если p > q, то 1/p < 1/q

Неравенства Правило 7

Квадрат числа всегда больше или равен нулю p ²  ≥ 0,

Пример: (4) ² = 16, (−4) ² = 16, (0) ² = 0

Неравенства Правило 8

Извлечение квадратного корня не изменит неравенство. Если p ≤ q, то √p ≤ √q (при p, q ≥ 0).

Пример:
р=2, д=7
2 ≤ 7, тогда √2 ≤ √7

Правила неравенств сведены в следующую таблицу.

Операция, применяемая при решении неравенств	Смена знака?
Дополнение с обеих сторон	№
Вычитание с обеих сторон	№
Умножение или деление обеих частей на положительное число	Нет
Умножение или деление обеих частей на отрицательное число	Да
Замена обеих сторон	Да
Упростить одну сторону	№

Решение неравенств

Вот шаги для  решения неравенств :

• Шаг – 1: Запишите неравенство в виде уравнения.
• Шаг – 2: Решите уравнение для одного или нескольких значений.
• Шаг – 3: Представьте все значения в числовой строке.
• Шаг – 4: Кроме того, обозначьте все исключенные значения на числовой строке с помощью незакрашенных кружков.
• Шаг – 5: Определите интервалы.
• Шаг – 6: Возьмите случайное число из каждого интервала, подставьте его в неравенство и проверьте, выполняется ли неравенство.
• Шаг – 7: Удовлетворяющие интервалы являются решениями.

Но для решения простых неравенств (линейных) мы обычно применяем алгебраические операции, такие как сложение, вычитание, умножение и деление. Рассмотрим следующий пример:

2x + 3 > 3x + 4

Вычитание 3x и 3 с обеих сторон,

2x – 3x > 4 – 3

-x > 1

Умножение обеих сторон на -1,

5

2 х

< -1

Обратите внимание, что мы заменили символ «>» на символ «<». Почему? Это потому, что мы умножили обе части неравенства на отрицательное число. Процесс решения упомянутых выше неравенств работает для простого линейного неравенства. Но чтобы решить любое другое сложное неравенство, мы должны использовать следующий процесс.

Применим эту процедуру для решения неравенств разных типов.

Графические неравенства

Пока графически изображая неравенства , мы должны помнить о следующих вещах.

• Если включена конечная точка (т. е. в случае ≤ или ≥), используйте замкнутый кружок.
• Если конечная точка НЕ ​​включена (т. е. в случае < или >), используйте открытый кружок.
• Используйте открытый круг на ∞ или -∞.
• Нарисуйте линию от конечной точки, которая продолжается вправо, если переменная больше числа.
• Нарисуйте линию от конечной точки до левой стороны, если переменная меньше числа.

Запись неравенств в интервальной записи

При записи решения неравенства в интервальной записи мы должны помнить о следующих вещах.

• Если включена конечная точка (т. е. в случае ≤ или ≥), используйте закрывающие скобки ‘[‘ или ‘]’
• Если конечная точка не указана (например, в случае < или >), используйте открытые скобки ‘(‘ или ‘)’
• Всегда используйте открытую скобку либо в ∞, либо в -∞.

Вот несколько примеров, чтобы понять то же самое:

Неравенство	Интервал
х < 2	(-∞, 2)
х > 2	(2, ∞)
х ≤ 2	(-∞, 2]
х ≥ 2	[2, ∞)
2 < х ≤ 6	(2, 6]

Графики неравенств с двумя переменными

Для построения графиков неравенств с двумя переменными вам нужно будет построить линию «равно», а затем заштриховать соответствующую область. Есть три шага:

• Напишите уравнение, например, “у” слева, а все остальное справа.
• Постройте линию “y=” (нарисуйте сплошную линию для y≤ или y≥ и пунктирную линию для y< или y>)
• Закрасьте область над линией для «больше чем» (y> или y≥) или под линией для «меньше чем» (y< или y≤).

Давайте рассмотрим пример: Это график линейного неравенства: y ≤ x + 4

Вы можете видеть, y = x + 4 линия и заштрихованная область (желтым цветом) находится там, где y меньше или равно x + 4.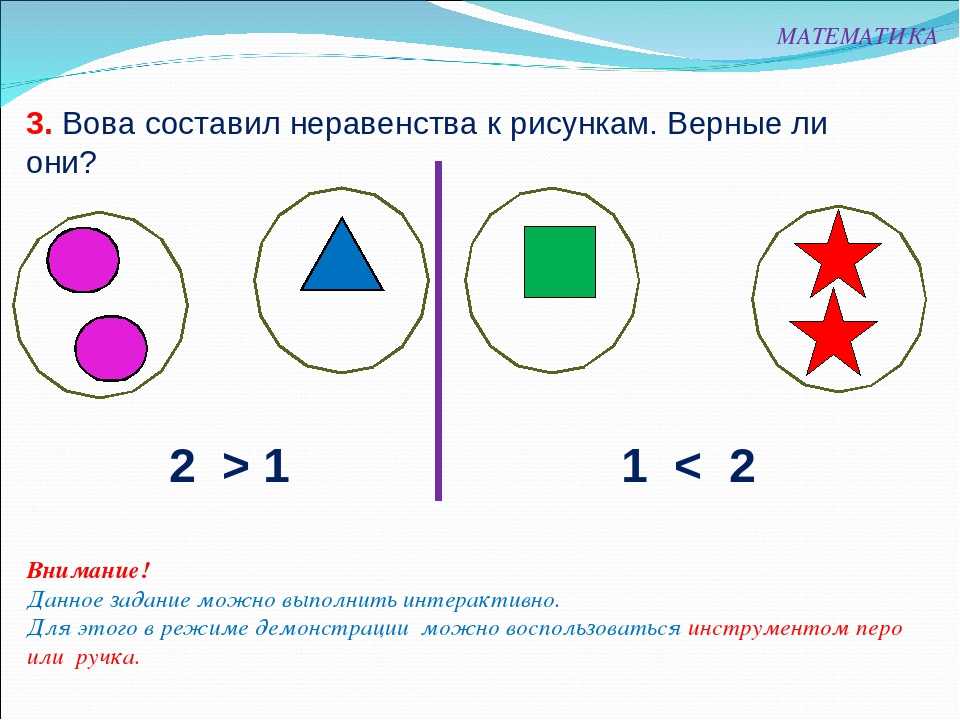 Давайте теперь посмотрим, как решать различные типы неравенств и как графически отображать решение в каждом случае.

Решение полиномиальных неравенств

Полиномиальные неравенства — это неравенства, которые могут быть выражены полиномом с одной стороны и 0 с другой стороны неравенства. Существуют различные типы полиномиальных неравенств, но наиболее важными из них являются:

• Линейные неравенства
• Квадратные неравенства

Решение линейных неравенств

Линейное неравенство — это неравенство, которое может быть выражено линейным выражением с одной стороны и 0 с другой. Решение линейных неравенств аналогично решению линейных уравнений, но следует соблюдать только правила решения неравенств (которые были объяснены ранее). Давайте посмотрим на некоторые примеры.

Решение одношаговых неравенств

Рассмотрим неравенство 2x < 6 (линейное неравенство с одной переменной). Чтобы решить это, достаточно всего одного шага, который делит обе части на 2. Тогда мы получаем x < 3. Следовательно, решение неравенства x < 3 (или) (-∞, 3).

Решение двухшаговых неравенств

Рассмотрим неравенство -2x + 3 > 6. Чтобы решить его, нам нужно выполнить два шага. Первым шагом является вычитание 3 из обеих сторон, что дает -2x > 3. Затем нам нужно разделить обе части на -2, и в результате x < -3/2 (обратите внимание, что мы изменили знак неравенства). Таким образом, решением неравенства является x < -3/2 (или) (-∞, -3/2).

Решение составных неравенств

Составные неравенства относятся к набору неравенств, между которыми есть «и» или «или». Для решения неравенств в этом случае просто решите каждое неравенство независимо, а затем найдите окончательное решение по следующим правилам:

• Окончательное решение является пересечением решений независимых неравенств, если между ними есть «и».
• Окончательное решение — это объединение решений независимых неравенств, если между ними есть «или».

Пример: Решите составное неравенство 2x + 3 < -5 и x + 6 < 3.

Решение:

По первому неравенству:
2x + 3 < -5
2x < -8
x < -4

По второму неравенству,
х + 6 < 3
x < -3

Так как между ними есть “и”, мы должны найти пересечение множеств x < -4 и x < -3. В этом случае может помочь числовая линия. Тогда окончательное решение:

х < -3 (или) (-∞, -3).

Решение квадратных неравенств

Квадратное неравенство включает в себя квадратное выражение. Вот процесс решения квадратных неравенств. Процесс поясняется на примере, где мы собираемся решить неравенство x ² – 4x – 5 ≥ 0.

Мы можем использовать тот же процесс для решения кубических неравенств, биквадратичных неравенств и т. д.

Решение абсолютных неравенств

Неравенство абсолютного значения включает алгебраическое выражение внутри знака абсолютного значения. Вот процесс решения абсолютного неравенства, где процесс объясняется на примере решения абсолютного неравенства |x + 3| ≤ 2. Если вы хотите узнать о различных методах решения абсолютных неравенств, нажмите здесь.

Решение рациональных неравенств

Рациональные неравенства — это неравенства, включающие рациональные выражения (дроби с переменными). Чтобы решить рациональные неравенства (неравенства с дробями), мы просто используем ту же процедуру, что и другие неравенства, но мы должны позаботьтесь об исключенных точках . Например, решая рациональное неравенство (x + 2)/(x – 2) < 3, следует отметить, что рациональное выражение (x + 2)/(x - 2) НЕ определено при x = 2 (положим знаменатель х - 2 = 0 ⇒ х = 2). Пошагово решим это неравенство.

• Шаг 5: Интервалы, получившие «истину» в Шаге 4 , являются решениями.
  Следовательно, решением рационального неравенства (x + 2)/(x – 2) < 3 является (-∞, 2) U (4, ∞).

Важные примечания о неравенствах:

Вот примечания о неравенствах:

• Если у нас строго меньше или строго больше чем символ, то мы никогда не получим никакого замкнутого интервала в решении.
• Мы всегда получаем открытые интервалы в символах ∞ или -∞, потому что они НЕ являются числами для включения.
• При решении рациональных неравенств всегда записывать открытые интервалы на исключенных значениях.
• Исключенные значения следует учитывать только в случае рациональных неравенств.

☛  Похожие темы:

• Калькулятор линейных неравенств
• Калькулятор теоремы о неравенстве треугольника
• Калькулятор рациональных неравенств

Часто задаваемые вопросы о неравенствах

Что такое неравенства в математике?

Когда два или более алгебраических выражения сравниваются с использованием символов <, > ≤ или ≥, они образуют неравенство. Они   являются математическими выражениями, в которых обе стороны не равны.

Как решать неравенства на числовой прямой?

Чтобы построить неравенство в математике, например, x>3, на числовой прямой,

• Шаг 1: Нарисуйте кружок над числом (например, 3).
• Шаг 2: Проверьте, включает ли знак равно (≥ или ≤) или нет. Если знак равенства стоит вместе с > или <, то закрасьте кружок, в противном случае оставьте кружок незаполненным.
• Шаг 3: В числовой строке удлините линию от 3 (после ее обведения), чтобы показать, что она больше или равна 3.

Как вычислять математические неравенства?

Чтобы вычислить неравенства :

• просто составьте уравнение
• решить
90 149 отметьте нули на числовой прямой, чтобы получить интервалы 90 150
• проверить интервалы, взяв из него любое число против неравенства.

Объясните процесс решения неравенств графически.

Графическое решение неравенств возможно при наличии системы двух неравенств с двумя переменными. В этом случае мы рассматриваем оба неравенства как два линейных уравнения и изображаем их на графике. Тогда мы получим две строки. Закрасьте верхнюю/нижнюю часть каждой из линий, удовлетворяющих неравенству. Общая часть обеих заштрихованных областей является областью решения.

В чем разница между уравнениями и неравенствами?

Вот различия между уравнениями и неравенствами.

Уравнения	Неравенства
1. В уравнениях есть символ “=”.	1. Неравенства содержат «>», «<», «≥» или «≤»
2. Количество решений уравнения зависит от степени уравнения.	2. Неравенство может иметь единственное, единственное решение или не иметь решения. Это не зависит от степени.
3. Применяя любую операцию с обеих сторон, уравнение остается верным.	3. Если мы умножим/разделим обе части неравенства на отрицательное число, знак изменится.

Что произойдет, если возвести в квадрат неравенство?

Квадрат числа всегда больше или равен нулю p ² ≥ 0. Пример: (4) ² = 16, (−4) ² = 16, (0) ² = 0

Каковы шаги для расчета неравенств с дробями?

Вычисление неравенств с дробями так же, как решение любого другого неравенства. Одним из простых способов решения таких неравенств является умножение каждого члена с обеих сторон на LCD всех знаменателей, чтобы все дроби стали целыми числами. Например, чтобы решить (1/2) x + 1 > (3/4) x + 2, умножьте обе части на 4. Тогда мы получим 2x + 4 > 3x + 8 ⇒ -x > 4 ⇒ x < -4.

Каковы шаги для решения неравенств с переменными с обеих сторон?

Когда неравенство имеет переменную с обеих сторон, мы должны попытаться изолировать переменную. Но в этом процессе переворачивайте знак неравенства всякий раз, когда мы делим или умножаем обе части на отрицательное число. Вот пример. 3x – 7 < 5x - 11 ⇒ -2x < -4 ⇒ x > 2.

Как найти диапазон неравенства?

Вы можете найти диапазон значений x, решив неравенство, рассматривая его как нормальное линейное уравнение.