Знак меньше и равно – Таблица математических символов. Сокращённая запись математического текста, математические обозначения. Математический алфавит. Математическая скоропись. Негламурный эксклюзив от Проекта DPVA.info
Как пишется знак больше и знак меньше
 Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как знак больше и знак меньше, а также знак равно.
Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как знак больше и знак меньше, а также знак равно.
Однако, если с последним что-то напутать достаточно сложно, то о том, как и в какую сторону пишутся знаки больше и меньше (знак менее и знак более, как ещё их иногда называют) многие сразу после этой же школьной скамьи и забывают, т.к. они довольно редко используются нами в повседневной жизни.
Но практически каждому рано или поздно всё равно приходится столкнуться с ними, и “вспомнить” в какую сторону пишется нужный им символ получается лишь обратившись за помощью к любимой поисковой системе. Так почему бы не ответить развернуто на этот вопрос, заодно подсказав посетителям нашего сайта как запомнить правильное написание этих знаков на будущее?
Именно о том, как правильно пишется знак больше и знак меньше мы и хотим напомнить вам в этой небольшой заметке. Также будет не лишним рассказать и том, как набрать на клавиатуре знаки больше или равно и меньше или равно, т.к. этот вопрос тоже довольно часто вызывает затруднения у пользователей, сталкивающихся с такой задачей очень редко.
Содержание:
- Как пишется знак больше
- Как пишется знак меньше
- Знак “больше или равно”/«меньше или равно” (как набрать на клавиатуре)
Перейдем сразу к делу. Если вам не очень интересно запоминать всё это на будущее и проще в следующий раз снова “погуглить”, а сейчас просто нужен ответ на вопрос “в какую сторону писать знак”, тогда для вас мы приготовили краткий ответ – знаки больше и меньше пишутся так, как показано на изображении ниже.
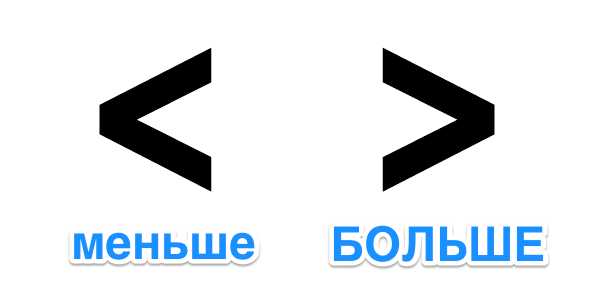
А теперь расскажем немного подробнее о том, как это понять и запомнить на будущее.
Как и в какую сторону пишется знак больше

В общем и целом логика понимания очень проста – какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону – такой и знак. Соответственно, знак больше влево смотрит широкой стороной – большей.
Пример использования знака больше:
- 50>10 – число 50 больше числа 10;
- посещаемость студента в этом семестре составила >90% занятий.
Как и в какую сторону пишется знак меньше
 Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной – меньшей, то перед вами знак меньше.
Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной – меньшей, то перед вами знак меньше.
Пример использования знака меньше:
- 100<500 – число 100 меньше числа пятьсот;
- на заседание явилось <50% депутатов.
Как видите, все довольно логично и просто, так что теперь вопросов о том, в какую сторону писать знак больше и знак меньше в будущем у вас возникать не должно.
Знак больше или равно/меньше или равно
Если вы уже вспомнили, как пишется необходимый вам знак, то дописать к нему одну черточку снизу вам не составит труда, таким образом вы получите знак “меньше или равно” или знак “больше или равно”.
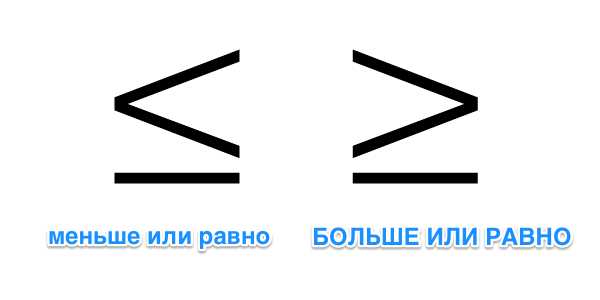
Однако относительно этих знаков у некоторых возникает другой вопрос – как набрать такой значок на клавиатуре компьютера? В результате большинство просто ставят два знака подряд, к примеру, “больше или равно” обозначая как “>=”, что, в принципе, часто вполне допустимо, но можно сделать красивее и правильнее.
На самом деле для того, чтобы напечатать эти знаки, существуют специальные символы, которые можно ввести на любой клавиатуре. Согласитесь, знаки “≤” и “≥” выглядят значительно лучше.
Знак больше или равно на клавиатуре
Для того, чтобы написать “больше или равно” на клавиатуре одним знаком даже не нужно лезть в таблицу специальных символов – просто поставьте знак больше с зажатой клавишей “alt”. Таким образом сочетание клавиш (вводится в английской раскладке) будет следующим.
alt+ю
Или же вы можете просто скопировать значок из этой статьи, если вам нужно воспользоваться им один раз. Вот он, пожалуйста.
≥
Знак меньше или равно на клавиатуре
Как вы наверное уже смогли догадаться сами, написать “меньше или равно” на клавиатуре вы можете по аналогии со знаком больше – просто поставьте знак меньше с зажатой клавишей “alt”. Сочетание клавиш, которое нужно вводить в английской раскладке, будет следующим.
alt+б
Или просто скопируйте его с этой страницы, если вам так будет проще, вот он.
≤
Как видите, правило написания знаков больше и меньше довольно просто запомнить, а для того чтобы набрать значки больше или равно и меньше или равно на клавиатуре достаточно просто нажать дополнительную клавишу – всё просто.
© OchProsto.com
ochprosto.com
Знаки: «>» больше, «
Однажды решили Белочка и Ёжик проверить, что птицы любят есть больше всего: пшеничные зерна или крошки белого хлеба. На один пень насыпали зерна, а на другой крошки хлеба и стали наблюдать.
– Ежик, ну что ты там видишь?
– Пока ничего.
– О, теперь вижу. Два воробья прилетели. Сейчас зерна будут клевать.
– А крошки клюют?
– Пока нет.
– Ой. Ко второму пню, ну там где крошки, сорока наша прилетела.
– Так где птиц больше?
– На пне с зернышками птиц больше, чем около пня с крошками.
– Белочка, кажется дядя Филя прилетел.
– Ну, и где сейчас птиц стало больше?
– Теперь птиц стало одинаково.
– Любик, а ты знаешь, что в математике, чтобы сравнивать объекты или предметы используют специальные математические знаки: больше, меньше и равно.
Например, вот у нас одно яблоко и одна груша, т.е. яблок столько же сколько и груш. Значит между ними можно поставить знак равно. А записать это можно так: два равно двум.
Теперь мы сравним грибы: три боровика и две лисички. Что больше?
– Три боровика больше, чем две лисички.
– Правильно. В этом случае мы между грибами поставим знак больше. А записать это можно так: три больше чем два.
– А сейчас сравним жёлуди и орехи. Чего меньше?
– Ага… Желудей у нас три, а орехов пять. Значит желудей меньше, чем орехов.
– Правильно, в этом случае мы поставим знак меньше. А записать это можно так: пять меньше чем три.
А теперь мы посмотрим, как пишутся эти знаки.
– Я помню как пишется знак равно. Он состоит из двух палочек, которые пишутся друг под другом. Вот.
– Правильно. Знаки больше и меньше тоже состоят из двух палочек. В знаке больше палочки расходятся к большему числу, а записывается этот знак так.
В знаке меньше палочки сходятся к меньшему числу и записывается он так.
– Ежик, допиши пожалуйста знаки в строчку, в пустые клеточки.
– Ага… Сейчас, сейчас. Сначала допишу знак равно, теперь больше и меньше.
А чтобы ты не запутался, запомни: левая рука, согнутая в локте даст нам знак меньше, а правая рука согнутая в локте даст нам знак больше.
Если между двумя числами поставить знак равно, то получится числовое равенство. А если между двумя числами поставить знаки больше или меньше, то получится числовые неравенства.
Ежик, а теперь проверь пожалуйста, верные ли равенства и неравенства.
Так, так, так. Ага. Два больше чем один – все верно, три больше, чем четыре…ага…
что-то не так, три обозначает большее количество предметов, чем четыре и при счете
идет раньше, чем четыре значит это неравенство не верное. Мы его зачеркнем.
– А давай лучше исправим, чтобы у нас не было ошибок.
– Давай. Значит здесь надо поставить знак меньше. Вот.
– Так-так. Пять равно пяти. Все верно.
– Ага, а здесь совсем сложно.
– Ничего сложного. Смотри, чтобы проверить, надо сначала посчитать, сколько будет два да один.
– Это будет три.
– А сколько будет два да три.
– Пять. Значит три меньше пяти. Здесь опять ошибка. Надо поставить знак меньше.
– Ну молодец Ежик. Ты все правильно выполнил. Итак, ты должен запомнить:
1. Чтобы сравнить числа в математике используют знаки больше, меньше или равно.
2. Знак больше, расходится палочками к большему числу. И если согнуть правую руку в локте, то получится знак больше. Выражение, в котором стоит знак больше называется неравенство.
3. Знак меньше, сходится палочками к меньшему числу. И если согнуть левую руку в локте, то получится знак меньше. Выражение, в котором стоит знак меньше тоже называется неравенство.
4. Знак равно состоит из двух палочек, которые пишутся друг под другом, а выражение, в котором стоит знак равно называется числовым равенством.
– Белочка, а давай посмотрим, что там наши птицы делают?
– Все склевали и улетели. Да, теперь мы не сможем определить, что же птицы любят больше. Ничего не осталось.
– Наверное, Ежик, одни птицы больше любят есть зерна, а другие хлебные крошки.
videouroki.net
| Символ (TeX) | Символ (Unicode) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒ → ⊃ | Импликация, следование | означает «если верно, то также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). | верно, но неверно (так как также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает « верно тогда и только тогда, когда верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда и оба истинны. | , если — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий и истинно. | , если — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| ¬ | Отрицание | истинно тогда и только тогда, когда ложно . | ||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает « верно для всех ». | ||
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один такой, что верно » | (подходит число 5) | |
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | обозначает « и обозначают одно и то же значение». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| := :⇔ | Определение | означает « по определению равен ». означает « по определению равносильно » | (Гиперболический косинус) (Исключающее или) | |
| «равно/равносильно по определению» | ||||
| везде | ||||
| { , } | Множество элементов | означает множество, элементами которого являются , и . | (множество натуральных чисел) | |
| «Множество…» | ||||
| Теория множеств | ||||
| { | } { : } | Множество элементов, удовлетворяющих условию | означает множество всех таких, что верно . | ||
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅ {} | Пустое множество | и означают множество, не содержащее ни одного элемента. | ||
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈ ∉ | Принадлежность/непринадлежность к множеству | означает « является элементом множества » означает « не является элементом множества » | ||
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆ ⊂ | Подмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇ ⊃ | Надмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋ | Собственное надмножество | означает и . | ||
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪ | Объединение | означает множество элементов, принадлежащих или (или обоим сразу). | ||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ⋂ | Пересечение | означает множество элементов, принадлежащих и , и . | ||
| «Пересечение … и … », «…, пересечённое с …» | ||||
| Теория множеств | ||||
| \ | Разность множеств | означает множество элементов, принадлежащих , но не принадлежащих . | ||
| «разность … и … », «минус», «… без …» | ||||
| Теория множеств | ||||
| → | Функция | означает функцию с областью определения и областью прибытия (областью значений) . | Функция , определённая как | |
| «из … в», | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом после применения функции будет . | Функцию, определённую как , можно записать так: | |
| «отображается в» | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или реже (в зависимости от ситуации). | ||
| «Эн» | ||||
| Числа | ||||
| Z или ℤ | Целые числа | означает множество | ||
| «Зед» | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| «Ку» | ||||
| Числа | ||||
| R или ℝ | Вещественные числа, или действительные числа | означает множество всех пределов последовательностей из | ( — комплексное число: ) | |
| «Эр» | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| «Це» | ||||
| Числа | ||||
| < > | Сравнение | обозначает, что строго меньше . означает, что строго больше . | ||
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| ≤ или ⩽ ≥ или ⩾ | Сравнение | означает, что меньше или равен . означает, что больше или равен . | ||
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до означает, что 2,718 отличается от не больше чем на . | с точностью до . | |
| «приблизительно равно» | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает неотрицательное действительное число, которое в квадрате даёт . | ||
| «Корень квадратный из …» | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов . | ||
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма, сумма ряда | означает «сумма , где принимает значения от 1 до », то есть . означает сумму ряда, состоящего из . | ||
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает «произведение для всех от 1 до », то есть | ||
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| ! | Факториал | означает «произведение всех натуральных чисел от 1 до включительно, то есть | ||
| « факториал» | ||||
| Комбинаторика | ||||
| ∫ | Интеграл | означает «интеграл от до функции от по переменной ». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
| df/dx f'(x) | Производная | или означает «(первая) производная функции от по переменной ». | ||
| «Производная … по …» | ||||
| Математический анализ | ||||
| Производная -го порядка | или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ». | |||
| «-я производная … по …» | ||||
| Математический анализ |
dic.academic.ru
Как правильно ставить знак больше меньше
Вконтакте
Google+
Одноклассники
Как пишется знак больше и знак меньше?
При обучении математике детям обычно называют знаки больше и меньше клювиком, так им проще запоминать образное понятие. А вот чтобы запомнить в какую сторону пишется меньше, а в какую больше приводят другой пример — закрытый клювик всегда смотрит в сторону меньшего числа, открытый в сторону большего. То есть у нас получается такая жадная уточка, которая разевает клюв только на действительно стоящее. Возможно поэтому еще этот знак сравнивают с крокодилом. Теперь если слева стоит большее число, клювик к нему открыт и мы имеем знак quot;большеquot;, а если слева стоит меньшее число, клювик налево закрыт, то у нас получается знак quot;меньшеquot;.
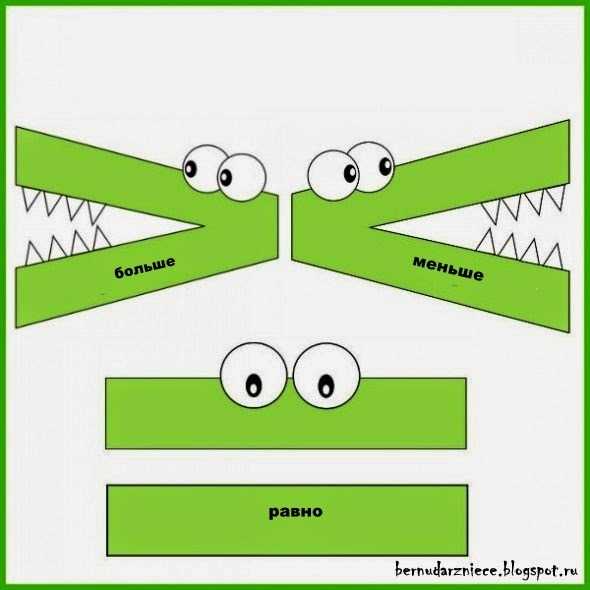
Знак quot;большеquot; и quot;меньшеquot; при письме изображаются галочкой, которая поврнута на девяносто градусов. При этом если носик галочки смотрит направо, то это знак больше. В противном случае, если узкий кончик галочки смотри налево, то меньше.
В математике часто приходится сравнивать числа по величине, для чего и были придуманы графические символы. Вместо слова quot;большеquot; используется знак quot;>quot;, а вместо слова quot;меньшеquot; — символ quot;lt;quot;.
Если, например, нам нужно сравнить между собой цифры 5 и 3, то это будет выглядеть так: 5 > 3. Между цифрами стоит знак quot;большеquot;, который повернут своей открытой стороной в сторону большей величины. Запомнить обозначение очень просто: quot;носикquot; всегда повернут своим острием в сторону меньшего числа.
Математические знаки запомнить легко: вот этот знак quot;>quot; обращен к буквам перед ним широкой частью и означает quot;большеquot;, а этот знак quot;lt;quot; обращен тонким углом и означает меньше. Оба знака могут быть усложнены знаком равно.
Если вы хотите запомнить как пишется знак больше и знак меньше, то в первую очередь нужно запомнить о том, что у знака больше острый кончик направлен вправо:>. У знака меньше наоборот, острый кончик направлен влево: lt;.
В первом классе нас учили (и я теперь так же 3х летней дочке легко объяснила), что этот знак похож на открытый клювик уточки, которая смотрит в сторону большего числа, то есть если левое число больше правого, то пишем > (больше), если наоборот- то lt; (меньше). Также можно запомнить что широкой (большой) своей стороной он смотрит в сторону большего числа.
Если quot;открытой пастьюquot; знак поврнут влево — это больше.
А если вправо — это знак меньше.
Запомнить легко, если считать, что quot;открытая пасть — большаяquot;, значит БОЛЬШЕ.
Острый угол на знаке показывает на число — маленькая стрелка — знак МЕНЬШЕ.
sovetydljavseh.ru
Символ | ASCII-код / | Назначение |
Буквы и знаки препинания | ||
| &nbsp; | Неразрывный пробел | |
| @ | &#64; | Коммерческое “эт” (“собака”) |
| & | &amp; | Амперсенд |
| “ | &quot; | Простые кавычки |
| “ | &#147; | Открывающая кавычка (“лапочка”) |
| ” | &#148; | Закрывающая кавычка (“лапочка”) |
| « | &laquo; | Открывающая кавычка (“елочка”) |
| » | &raquo; | Закрывающая кавычка (“елочка”) |
| — | &mdash; | Длинное тире |
| – | &ndash; | Короткое тире |
| … | &hellip; | Многоточие |
| ¦ | &brvbar; | Вертикальная черта |
| ¤ | &curren; | “Солнышко” |
| § | &sect; | Параграф (раздел) |
| ¶ | &para; | Параграф |
Математические символы | ||
| < | &lt; | Знак “меньше” |
| > | &gt; | Знак “больше” |
| ≤ | &le; | Знак “меньше или равно” |
| ≥ | &ge; | Знак “больше или равно” |
| ≈ | &asymp; | Примерное равенство |
| ≠ | &ne; | Неравенство |
| ≡ | &equiv; | Тождество |
| − | &minus; | Знак минуса (аналог короткого тире) |
| × | &times; | Знак умножения |
| ÷ | &divide; | Знак деления |
| ± | &plusmn; | Плюс/минус |
| ¬ | &not; | Логическое отрицание |
| ¯ ‾ | &macr; &oline; | Надчеркивание (два варианта разной длины) |
| ° | &deg; | Градус |
| ƒ | &fnof; | Функция |
| ∑ | &sum; | Сумма |
| ∏ | &prod; | Произведение |
| ∫ | &int; | Интеграл |
| ∂ | &part; | Символ дифференциала |
| √ | &radic; | Знак радикала |
| ∞ | &infin; | Знак бесконечности |
| Ø | &Oslash; | Зачеркнутое “О” (в качестве “пустого множества”) |
| ∩ | &cap; | Пересечение |
| µ | &micro; | Обозначение “10-6” (визуально отличается от греческой “мю”) |
| ² ³ | &sup2; &sup3; | Квадрат и куб |
Греческие буквы | ||
| Α α | &Alpha; &alpha; | Альфа |
| Β β | &Beta; &beta; | Бета |
| Γ γ | &Gamma; &gamma; | Гамма |
| Δ δ | &Delta; &delta; | Дельта |
| Ε ε | &Epsilon; &epsilon; | Эпсилон |
| Ζ ζ | &Zeta; &zeta; | Дзета |
| Η η | &Eta; &eta; | Эта |
| Θ θ | &Theta; &theta; | Тэта |
| Ι ι | &Iota; &iota; | Иота (йота) |
| Κ κ | &Kappa; &kappa; | Каппа |
| Λ λ | &Lambda; &lambda; | Лямбда (ламбда) |
| Μ μ | &Mu; &mu; | Мю (ми) |
| Ν ν | &Nu; &nu; | Ню (ни) |
| Ξ ξ | &Xi; &xi; | Кси |
| Ο ο | &Omicron; &omicron; | Омикрон |
| Π π | &Pi; &pi; | Пи |
| Ρ ρ | &Rho; &rho; | Ро |
| Σ σ | &Sigma; &sigma; | Сигма |
| Τ τ | &Tau; &tau; | Тау |
| Υ υ | &Upsilon; &upsilon; | Ипсилон |
| Φ φ | &Phi; &phi; | Фи |
| Χ χ | &Chi; &chi; | Хи |
| Ψ ψ | &Psi; &psi; | Пси |
| Ω ω | &Omega; &omega; | Омега |
Прочие символы | ||
| · | &middot; | Точка посередине строки |
| • | &bull; | Жирная точка (“буллет”) |
| ™ | &#153; | Торговая марка |
| © | &copy; | Копирайт |
| ® | &reg; | Зарегистрированный торговый знак |
| ← | &larr; | Стрелка влево |
| ↑ | &uarr; | Стрелка вверх |
| → | &rarr; | Стрелка вправо |
| ↓ | &darr; | Стрелка вниз |
| ↔ | &harr; | Двунаправленная горизонтальная стрелка |
| ‰ | &#137; | Промилле |
| † | &#134; | Крест |
| ‡ | &#135; | Двойной крест |
| ◊ | &loz; | Ромб |
| ♠ | &spades; | “Пики” |
| ♣ | &clubs; | “Крести” |
| ♥ | &hearts; | “Червы” |
| ♦ | &diams; | “Бубны” |
konreal.livejournal.com
Математика для блондинок: Знак больше и меньше
Здесь мы рассмотрим элемент математического неравенства, при помощи которого в математике обычно выражается несправедливость. Если знак равенства можно считать отражением справедливости, то знаки “больше” и “меньше” отражают отсутствие таковой. Справедливость – это понятие относительное. То, что я считаю справедливым по отношению к вам, вы можете считать не справедливым по отношению к себе. И наоборот. То, что считаете справедливым вы, другие могут называть вопиющей несправедливостью. Каждый смотрит со своей колокольни. В математике всё это можно выразить при помощи знаков “больше” и “меньше”.Наблюдая за процессом сравнения со стороны, мы будем получать разные результаты в зависимости от того, в каком порядке мы выполняем сравнение. Небоскреб БОЛЬШЕ хибарки. Хибарка МЕНЬШЕ небоскреба. Как видите, результат сравнения зависит от того, что мы ставим на первое место при сравнении.
В математике неравенство возникает из-за того, что при записи математических выражений принят определенный порядок выписывания символов на бумаге. При этом один из символов обязательно будет на первом месте, второй символ – на втором. Это приводит к определенному результату при сравнении того, что эти символы обозначают. Если мы изменим порядок записи символов, то есть второй символ запишем на первом месте, а первый – после него, тогда у нас изменится результат сравнения. Математики очень удачно подобрали графические символы для обозначения понятий “больше” и “меньше”. Вот смотрите.
Что такое неравенство? Это почти то же самое, что и уравнение. Решаются они практически одинаково. Единственное, о чем нужно помнить при решении неравенств, что знаки “больше” и “меньше” могут выворачиваться на изнанку, а знак равенства – нет. Собственно, знак равенства тоже можно вывернуть, но никаких отличий вы не увидите. Другое дело со знаками “больше” и “меньше”. Если такой знак вывернуть на изнанку, тогда его нос будет смотреть в другую сторону. Знак “больше” превратится в знак “меньше”, знак “меньше” превратится в знак “больше”.
Никакой шаманской магии в этом нет. Обыкновенная относительность или, как её ещё называют в математике, зеркальная симметрия. Посмотрите на рисунок ниже.

Нижняя половина рисунка является зеркальным отражением верхней половины. Или наоборот. Теперь возьмите зеркало. Приставьте его перпендикулярно к экрану монитора так, чтобы одновременно видеть картинку на экране монитора и её отражение в зеркале. В зеркале нижняя и верхняя половины картинки поменяются местами. Если бы не надпись на картинке “математика для блондинок”, то вообще нельзя было бы точно сказать, где сама картинка, а где её отражение. Кстати, применение на уроках математики прозрачной стеклянной доски, вращающейся вокруг вертикальной оси, поможет понять очень многие вещи в математике.
Так вот, если мы в математическом неравенстве меняем местами левую и правую части неравенства, то знак меняется на противоположный. Знак “больше” меняется на знак “меньше” и наоборот. То же самое происходит, когда мы умножаем всё неравенство на минус единицу. При этом меняются все знаки в левой и правой частях неравенства. Умножение на минус единицу мы можем использовать при решении неравенств.
Нужно помнить, что если мы переносим всего один элемент из одной части неравенства в другую и при этом МЕНЯЕМ ЗНАК “плюс” или “минус”, то знак неравенства “больше” или “меньше” остается неизменным. Всё, как в уравнении. Если при переносе математического элемента через знак сравнения мы изменяем знак, результат сравнения не изменяется: равенство сохраняется, знак “больше” остается знаком “больше”, знак “меньше” остается знаком “меньше”.
www.webstaratel.ru
| ЗНАК | ЗНАЧЕНИЕ | ПРИМЕР |
| = | равно | 5 = 5 |
| ≠ | не равно | 7 ≠ 5 |
| ≈ | приблизительно | 3,57 ≈ 3,6 |
| >, | больше, меньше | 8 > 5 |
| ≥ | больше или равно | a ≥ b |
| ≤ | меньше или равно | c ≤ b |
| + | плюс | 6 + 4 = 10 |
| – | минус | 10 – 6 = 4 |
| * | умножение | 5 * 3 = 15 |
| : | деление | 15 : 3 = 5 |
| ! | факториал | 3! = 1*2*3 = 6 |
| ∑ | сумма | |
| ⋅ | Оператор точка | |
| ⋆ | Оператор звезда | |
| ⊙ | Оператор точка в круге | |
| ⊚ | Оператор круг в круге | |
| ⊛ | Оператор звездочка в круге | |
| − | Знак минус | |
| ± | Знак плюс-минус | |
| ∓ | Знак минус-плюс | |
| ∔ | Знак точка-плюс | |
| × | Знак умножения | |
| ÷ | Знак деления | |
| ∞ | Знак бесконечность | |
| ˔ | Знак перпендикулярно | |
| ∼ | Оператор тильды (подобно) | |
| ∽ | Знак обратная тильда | |
| ≁ | Знак не тильда | |
| ≂ | Знак минус тильда | |
| ≃ | Знак асимптотически равный | |
| ≄ | Знак асимптотически равный | |
| ≈ | Знак почти равный (приблизительно) | |
| ≉ | Знак почти не равный | |
| ≊ | Знак равный или почти равный | |
| ≋ | Тройная тильда | |
| ≌ | Знак все равны | |
| ≅ | Знак приблизительно равный | |
| ≆ | Знак фактически равный | |
| ≇ | Знак фактически не равный | |
| ≠ | Знак не равно | |
| > | Знак больше | |
| < | Знак меньше | |
| ≤ | Знак меньше или равно | |
| ≥ | Знак больше или равно | |
| ≦ | Меньше, чем над равно | |
| ≧ | Больше, чем над равно | |
| ≨ | Менее чем, но не равны | |
| ≩ | Больше чем, но не равны | |
| ≮ | Не меньше чем | |
| ≯ | Не больше чем | |
| ⋦ | Меньше чем, но не эквивалентны | |
| ⋧ | Больше чем, но не эквивалентны | |
| ⋖ | Меньше чем с точкой | |
| ⋗ | Больше чем с точкой | |
| ≰ | Ни меньше, ни равный | |
| ≱ | Ни больше, ни равный | |
| ⋜ | Равно или меньше чем | |
| ⋝ | Равно или больше чем | |
| ≲ | Меньше чем или эквивалентно | |
| ≳ | Больше чем или эквивалентно | |
| ≶ | Меньше чем или больше чем | |
| ≷ | Больше чем или меньше чем | |
| ≸ | Ни меньше чем, ни больше чем | |
| ≹ | Ни больше чем, ни меньше чем | |
| ⋚ | Меньше или равно или больше чем | |
| ⋛ | Больше или равно или меньше чем | |
| ≡ | Знак тождественно | |
| ≢ | Знак не идентично | |
| ≀ | Сплетение | |
| ≍ | Знак эквивалентно | |
| ≏ | Знак различие между | |
| ≣ | Строго эквивалентный | |
| ≪ | Гораздо меньше чем | |
| ≫ | Гораздо больше чем | |
| ⋘ | Много меньше чем | |
| ⋙ | Много больше чем | |
| ¬ | Знак отрицания (скобка) | |
| ∀ | Для всех | |
| ∂ | Частичный дифференциал | |
| ∃ | Существует | |
| ∄ | Не существует | |
| ∆ | Инкремент | |
| ∇ | Оператор набла | |
| ∈ | Элемент из | |
| ∉ | Не элемент из | |
| ∋ | Содержит в качестве члена | |
| ∌ | Не содержит как член | |
| √ | Квадратный корень | |
| ∛ | Кубический корень | |
| ∜ | Четвертый корень | |
| ∝ | Знак пропорционально | |
| ∠ | Знак угол | |
| ∟ | Прямой угол | |
| ⊾ | Прямой угол с дугой | |
| ∡ | Измеренный угол | |
| ∣ | Разделять | |
| ∤ | Не разделять | |
| ∥ | Параллельно | |
| ∦ | Не параллельно | |
| ∧ | Логическое “И” | |
| ∨ | Логическое “Или” | |
| ∩ | Пересечение | |
| ∪ | Союз (объединение) | |
| ∫ | Интеграл | |
| ∬ | Двойной интеграл | |
| ∭ | Тройной интеграл | |
| ∮ | Контурный интеграл | |
| ∯ | Поверхностный интеграл | |
| ∴ | Следовательно | |
| ∵ | Поскольку | |
| ∶ | Соотношение | |
| ∷ | Пропорция | |
| ∸ | Точка минус | |
| ∹ | Избыток | |
| ∺ | Геометрическая прогрессия | |
| ⊂ | Подмножество | |
| ⊃ | Супермножество | |
| ′ | Штрих | |
| ″ | Двойной штрих | |
| ‴ | Тройной штрих | |
| ½ | Одна вторая | |
| ℃ | Знак градуса по Цельсию | |
| N | натуральные числа | 1,2,3,4,5…. |
| Z | целые числа | -1,0,+1,+2 |
| R | рациональные числа |
spishy-u-antoshki.ru