Задачи кенгуру прошлых лет – Задания и ответы Кенгуру 2016 года : Скачать задания Кенгуру : Конкурсы и олимпиады школьников

Кенгуру 2017 для 2 класса

Элен нарисовала бабочку с белыми крыльями и хочет украсить ее шестью наклейками (см. рисунок справа). Что может у нее получиться?

Правильно!

Неправильно!

–

Джим и Бен катаются на колесе обозрения. Где окажется Джим, когда кабинка с Беном займет то место, где сейчас находится Джим?

Правильно!

Неправильно!

–

Даша назвала число, Петя прибавил к нему 5 и записал результат на доске. Вася прибавил к Дашиному числу 2 и записал свой результат под Петиным числом. Что могло получиться?

Правильно!

Неправильно!

–

Брусок склеен из двух белых и двух черных кубиков (см. рисунок справа). Какая фигура сложена из четырех таких брусков?

Правильно!

Неправильно!

–

Стопка карточек с дырками нанизана на нитку (см. рисунок). Каждая карточка с одной стороны белая, а с другой тёмная. Вася разложил карточки на столе. Что у него могло получиться?

Правильно!

Неправильно!

–

shkolnaiapora.ru

Кенгуру 2018 для 3 – 4 класса: задания, решение, ответы

На одном из рисунков А-Д божья коровка отличается от других четырех. На каком?

Правильно!

Неправильно!

–

У Алика есть много наклеек пяти разных видов. Он вклеивает их по одной в каждую клетку квадрата так, чтобы фигурки в каждом столбце и в каждой строчке не повторялись. Какая наклейка должна оказаться в закрашенной клетке?

Правильно!

Неправильно!

–

Вася, Коля, Митя и Петя взяли синий, красный, желтый и зеленый мячи, каждый по одному.

— У меня мяч не красный, — сказал Вася.
— У меня мяч не синий, — сказал Петя.
— У меня мяч не зеленый, — сказал Коля.
— У меня мяч не желтый и не синий, — сказал Митя.
Соврал только тот, у кого красный мяч. Какой мяч у Коли?

синий

красный

зеленный

желтый

невозможно определить

Правильно!

Неправильно!

–

shkolnaiapora.ru

О тестированиях | Конкурс Кенгуру

Тестирования «от Кенгуру» являются естественным соединением технологии, отработанной за годы существования конкурса, и педагогического опыта, накопленного в Лаборатории проблем школьного математического образования, созданной под руководством М.И. Башмакова. 

В основу методики оценки математической подготовки участников тестирований положена система параметров, разработанная сотрудниками лаборатории. Отличительной чертой этой системы является внимание не только к знаниям и навыкам по конкретным темам школьного курса математики, но, кроме того, к целому ряду показателей более широкого плана (развитию логических навыков, умению использовать наглядные представления и т.п.). Система прошла апробацию в учебных заведениях с различными уровнями преподавания математики и получила высокую оценку специалистов как у нас в стране, так и за рубежом.

Важно отметить, что все тестирования этой серии не привязаны к каким-то конкретным учебникам. Их содержание нацелено на Федеральные образовательные стандарты с упором на те навыки и знания, которые в наибольшей степени будут востребованы на следующих ступенях обучения.

Все наши тестирования объединены общими чертами:

• Каждый тест содержит большое количество вопросов, что позволяет охватить все значимые разделы курса.
• Все вопросы тестов предполагают только ответы «Да» или «Нет». За верный ответ баллы добавляются, за неверный — снимаются. Впрочем, есть еще одна возможность — не отвечать на вопрос. При проверке это рассматривается как ответ «Не знаю», и за него баллы не начисляются, но и не снимаются.
• Самая главная особенность тестирований – это комплексная оценка математической подготовки каждого участника, основанная на упомянутой системе параметров (в зависимости от возраста участника, такая оценка содержит от 12 до 19 параметров). В настоящее время тестирования проводятся в следующих возрастных категориях:
• 4-й класс: «Кенгуру — выпускникам» в январе;
• 5-й класс: входное интеренет-тестирование в сентябре;
• 7-й класс: входное интеренет-тестирование в сентябре;
• 9-й класс: «Кенгуру — выпускникам» в январе;
• 11-й класс: «Кенгуру — выпускникам» в январе.

На следующий день после завершения каждого тестирования организаторы проводят видео-разбор всех заданий. Доступ к записи уже проведенных разборов можно получить в разделах Видео-разборы заданий «Кенгуру — выпускникам» (4, 9, 11 классы) и Видео-разборы заданий интернет-тестирования (5, 7 классы).

mathkang.ru

архив задач и ответов |

Задачи “Кенгуру” : архив задач и ответов

Международный математический конкурс “”Кенгуру” с каждым годом привлекает к себе все больше и больше участников. Причин несколько. И одна их них- задачи “Кенгуру”.

Их классификация уже была рассмотрена в этой статье. Нестандартность и многообразие математических

задач “Кенгуру”, фантазия авторов  этих задач делает этот конкурс массовым и популярным среди школьников разных возрастных категорий.

Ученики все больше заинтересованы в высоких результатах. Поэтому участие в конкурсе-игре “Кенгуру”  требует заранее определенной подготовки.

Цель данной статьи: предоставить учащимся возможность ознакомиться с задачами “Кенгуру” прошлых лет и ответами к ним. 

Содержание статьи будет пополняться новыми ссылками для скачивания . Таким образом будет сформирован архив задач “Кенгуру”.

Задачи “Кенгуру”: архив задач и ответов

“Кенгуру ” в России.

Сейчас можно скачать:

(Файлы временно отсутствуют)

 

 

“Кенгуру ” в Украине.

Сейчас можно скачать:

Задачі “Кенгуру” 2012-2013:

ЗадачІ “Кенгуру” 2013-2014:

Задачі “Кенгуру” 2014-2015 (ІІ етап): 19 березня

Успехов в учебе!

Татьяна Бурмистренко, автор сайта http://repetitor-problem.net

repetitor-problem.net

Задачи олимпиады Кенгуру, решения и ответы

С 1997 по 2012 годы, за пятнадцать лет проведения в Украине олимпиады Кенгуру, собралась обширная база нестандартных математических задач. Они печатаются в ежегодном вестнике олимпиады, кроме того, к юбилею конкурса вышел сборник «10 років разом. Міжнародний математичний конкурс «Кенгуру»», в котором собраны условия всех задач за 1997-2006 годы.

Решение таких задач – хороший интеллектуальный досуг, вне зависимости от возраста. Помимо этого, в свете современных образовательных требований, решение задач Кенгуру может оказаться отличным подспорьем в подготовке к Независимому внешнему оцениванию.

Здесь мы представляем свои варианты решения интересных на наш взгляд задач. Раздел регулярно пополняется. В пакет задач входит по одной задачи для каждого возраста, как правило, наивысшего (третьего) уровня сложности.

Краткие правила олимпиады

Участники олимпиады в зависимости от возраста делятся на следующие группы:

Малюк	3, 4 класс
Школярик	5, 6 класс
Кадет	7, 8, 9 класс
Юніор	10, 11 класс, 9 класс с углублённым изучением математики
Студент	10, 11 класс с углублённым изучением математики

C 2007 года были введены уровни “Малюк 2”: 2 класс и “Випускник”: все 11-е классы.

Для каждой возрастной группы предлагаются задачи трёх уровней сложности:

1й уровень	3 балла
2й уровень	4 балла
3й уровень	5 баллов

Всего предлагется 30 задач, на решение отводится 75 минут. В ходе олимпиады запрещается пользоваться калькулятором и литературой.

Желаем успехов в решении!

Задачи на сайте формируются в виде пакетов. В каждый пакет входит по одной задаче каждого возрастного уровня. Уровень сложности, как правило, третий.

• Пакет 1: комбинаторика, логика, взвешивания
• Пакет 2: комбинаторика, логика, выражения
• Пакет 3: взвешивания, логика, делимость
• Пакет 4 : делимость, последовательности, рассуждения
• Пакет 5: вероятность, геометрия, логика
• Пакет 6: целая и дробная часть, делимость, цифры
• Пакет 7: комбинаторика, среднее арифметическое, дроби
• Пакет 8: числовые процессы, выбор, множества
• Пакет 9: комбинаторика, проценты, ребус
• Пакет 10: целые числа, уравнения, логика
• Пакет 11: целые числа, делимость, палиндромы
• Пакет 12: последовательности, проценты, уравнения
• Пакет 13: принцип Дирихле, цифры, множества
• Пакет 14: комбинаторика, делимость, геометрия
• Пакет 15: системы счисления, геометрия, арифметика
• Пакет 16: целые числа, логика, геометрия
• Пакет 17: тригонометрия, неравенства, геометрия
• Пакет 18: тригонометрия, последовательность, цифры
• Пакет 19: тригонометрия, последовательность, цифры

 

Далее>

Задайте вопрос на блоге о математике

intelmath.narod.ru

Моя ГАЛАктика: Кенгуру-2013: несколько задач с решениями!

       Задачи «Кенгуру» 2013 года активно обсуждаются в интернете: кто-то приводит свои варианты (часто неправильные) ответов к задачам, кто-то просто ругает конкурс за сложность предлагаемых задач. Думаю, что раз  конкурс международный, то снижать уровень сложности заданий нецелесообразно. А вот учителям математики стоило бы поактивнее включиться в обсуждение вариантов решений, таким образом повышая интерес учащихся, неравнодушных к математике. Хочу предложить несколько решений к понравившимся мне задачам разного уровня сложности для учеников 7-8 классов.

Задача 1. (5 баллов) Задачку про попугаев (с решением) можно прочитать в комментариях к моей предыдущей  статье  читать>> Задача 2. (3 балла) Чему может быть равно среднее количество котят у пяти кошек? Варианты ответов (А) 3,3  (Б) 4,2  (В) 4,5  (Г) 4,75  (Д) 5,7. Так как кошек пять, то получить среднее количество котят можно разделив их число на пять. Умножив все приведенные значения на 5, получаем, что только вариант (Б)  не даст нам дробного значения. 4,2×5=21. Итак, 21 котенок. Задача 3. (4 балла)  Марк и Лиза стартуют одновременно из диаметрально противоположных точек круговой аллеи и бегут по этой аллее в одном направлении. Скорость Марка в 9/8 раза больше скорости Лизы. Сколько полных кругов пробежит Лиза, когда Марк догонит её в первый раз? Между Лизой и Марком половина круга (1/2). Скорость Марка на 1/8 больше скорости Лизы. За каждый круг Марк будет преодолевать  1/8 расстояния, которое их разделяет. Разделив это расстояние 1/2 на 1/8 получим:  1/2 :1/8=4. Четыре полных круга. Задача 4. (3 балла)  Маша придумала новую операцию с числами: a × b= 2a + 3b. Чему равно 3 × (4×5)? 4×5= 2×4+3×5=23;  3×23= 2×3+3×23=75. Задача 5. (4 балла)  У Васи 9 черных и 18 белых кубиков одинакового размера. Из них он хочет сложить куб (3 на 3 на 3). Какое наибольшее количество граней черных кубиков может оказаться на поверхности получившегося куба? Чтобы получилось максимальное количество черных граней, надо расположить черные кубики по углам, заняв все 8 углов: 8×3=24. Останется один кубик, который располагаем на ребре, т.о. будет видно ещё две грани: 24+2=26. Задача 6. (5 баллов)  Джон задумал пятизначное число. Вычеркнув из него одну цифру, он сложил полученное четырехзначное число с исходным пятизначным числом. Сумма оказалась равна 52713. Чему равна сумма цифр задуманного Джоном пятизначного числа? Опущу свои абстрактные рассуждения, так как моим ученикам всегда нужны конкретные примеры, а в данном случае хочу привести сразу конкретные цифры. Возьмем пятизначное число 47921 ( как я его получила попробуйте  догадаться сами, расположив числа другом под другом, как при сложении). Вычеркнем из него последнюю цифру 1. Сложим 47921 и 4792: 47921+4792=52713. Теперь посчитаем сумму цифр исходного пятизначного  числа, получим 23.
Задача 7. Геометрическая задача (5 баллов)  Условие см. на чертеже.

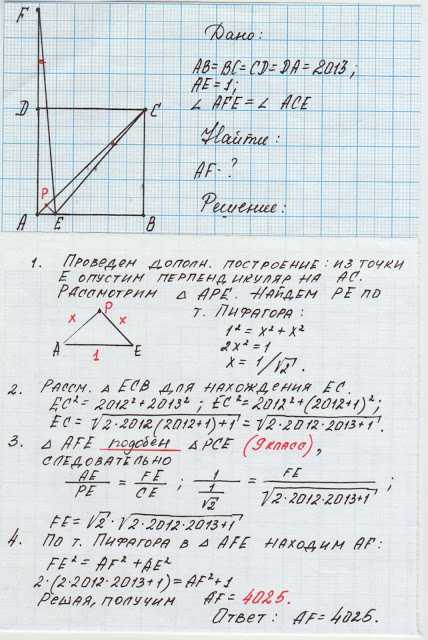
solodenkovagalina.blogspot.com

Об интернет-тестированиях | Конкурс Кенгуру

Интернет-тестирования соединяют методические подходы наших традиционных тестирований с оперативностью интернет-технологий. В рамках этого проекта предлагаются входные тесты для учащихся 5-х и 7-х классов (конец сентября – начало октября).

Выбор классов обусловлен тем, что именно в эти моменты серьезно меняется характер преподавания математики в школе, и именно к этим моментам школьники, обучающиеся по различным программам и учебникам, подходят с более или менее сопоставимым багажом знаний.

Тестирования организованы по следующей схеме.

• За 2–4 недели до проведения тестирования на сайте начинается регистрация учителей, желающих принять в нем участие. Зарегистрировавшись, учитель получает личную страничку на нашем сайте. На этой страничке он может создавать списки своих учеников, редактировать их и тренироваться в заполнении таблицы ответов (это желательно сделать заранее, без спешки). Доступ к персональной страничке учителя кроме него имеют только организаторы тестирования.
• В заранее указанный день на персональных страничках становится доступным текст задания. Учитель распечатывает его, в течение недели в удобное для себя время проводит тестирование и вводит выбранные учениками ответы в заранее подготовленные таблицы.
• Через неделю после открытия заданий возможность редактирования данных закрывается, и через 2–3 дня после этого на персональных страничках появляются отчеты с результатами тестирования. Эти отчеты содержат оценку математической подготовки каждого участника тестирования по широкому кругу параметров, а также средние данные по классу и средние данные по всему массиву тестируемых. Кроме отчета каждый учитель получает возможность распечатать сертификат, подтверждающий его участие в тестировании.

Пока эти тестирования проводятся в экспериментальном режиме, участие в них бесплатное.

---

• 12 сентября 2018 открывается регистрация учителей математики для участия в двух проектах: «Входной контроль в 5-м классе» и «Входной контроль в 7-м классе».
• 24 сентября на личных страничках появляются тексты заданий. До 3 октября надо эти задания распечатать, провести в своих классах тестирование и ввести ответы учеников в таблицы на личных страничках.
• 3 октября возможность редактирования данных на личных страничках закрывается.
• с 8 октября доступны результаты тестирования.

mathkang.ru