Примеры круги эйлера логика – описание, примеры, для дошкольников, для школьников

почему один раз увидеть лучше, чем сто раз услышать

Если вы думаете, что ничего не знаете о кругах Эйлера, вы ошибаетесь. На самом деле вы наверняка не раз с ними сталкивались, просто не знали, как это называется. Где именно? Схемы в виде кругов Эйлера легли в основу многих популярных интернет-мемов (растиражированных в сети изображений на определенную тему).

Давайте вместе разберемся, что же это за круги, почему они так называются и почему ими так удобно пользоваться для решения многих задач.

Происхождение термина

Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.

Пока не очень понятно, верно? Посмотрите на этот рисунок:

На рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал. Это часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей). Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.

Ну что, так стало понятнее? Именно поэтому круги Эйлера – это тот метод, который наглядно демонстрирует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ.

Автор метода – ученый Леонард Эйлер (1707-1783). Он так и говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки.

До него подобным принципом при построении своих умозаключений руководствовался немецкий математик и философ Готфрид Лейбниц.

Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли на свой лад. Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами.

Свою лепту внес также немецкий математике Эрнест Шредер. Но главные заслуги принадлежат англичанину Джону Венну. Он был специалистом в логике и издал книгу «Символическая логика», в которой подробно изложил свой вариант метода (использовал преимущественно изображения пересечений множеств).

Благодаря вкладу Венна метод даже называют диаграммами Венна или еще Эйлера-Венна.

Зачем нужны круги Эйлера?

Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только.

Если говорить о видах кругов Эйлера, то можно разделить их на те, что описывают объединение каких-то понятий (например, соотношение рода и вида) – мы их рассмотрели на примере в начале статьи.

А также на те, что описывают пересечение множеств по какому-то признаку. Таким принципом руководствовался Джон Венн в своих схемах. И именно он лежит в основе многих популярных в интернете мемов. Вот вам один из примеров таких кругов Эйлера:

Забавно, правда? И главное, все сразу становится понятно. Можно потратить много слов, объясняя свою точку зрения, а можно просто нарисовать простую схему, которая сразу расставит все по местам.

Кстати, если вы не можете определиться, какую профессию выбрать, попробуйте нарисовать схему в виде кругов Эйлера. Возможно, чертеж вроде этого поможет вам определиться с выбором:

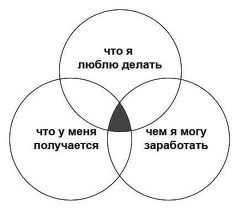
Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и будет вам нравиться.

Решение задач с помощью кругов Эйлера

Давайте рассмотрим несколько примеров задач, которые можно решить с помощью кругов Эйлера.

Вот на этом сайте – http://logika.vobrazovanie.ru/index.php?link=kr_e.html Елена Сергеевна Саженина предлагает интересные и несложные задачи, для решения которых потребуется метод Эйлера. Используя логику и математику, разберем одну из них.

Задача про любимые мультфильмы

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым – «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

Решение:

Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:

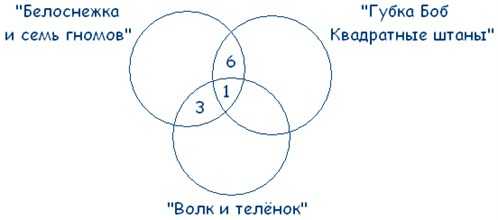
Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу:

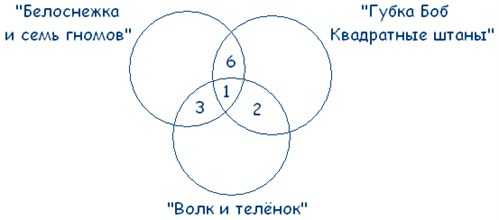
Выходит, что:

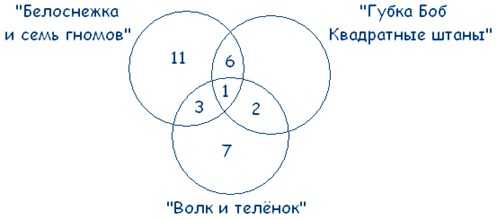
21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».

13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».

Осталось только разобраться, сколько шестиклассников двум другим вариантам предпочитает мультфильм «Губка Боб Квадратные Штаны». От всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:

38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».

Теперь смело можем сложить все полученные цифры и выяснить, что:

мультфильм «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек. Это и есть ответ на поставленный в задаче вопрос.

А еще давайте рассмотрим задачу, которая в 2011 году была вынесена на демонстрационный тест ЕГЭ по информатике и ИКТ (источник – http://eileracrugi.narod.ru/index/0-6).

Условия задачи:

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Запрос	Найдено страниц (в тысячах)
Крейсер | Линкор	7000
Крейсер	4800
Линкор	4500

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?

Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.

Опираясь на условия задачи, составим уравнения:

1. Крейсер | Линкор: 1 + 2 + 3 = 7000
2. Крейсер: 1 + 2 = 4800
3. Линкор: 2 + 3 = 4500

Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:

4800 + 3 = 7000, откуда получаем 3 = 2200.

Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:

2 + 2200 = 4500, откуда 2 = 2300.

Ответ: 2300 – количество страниц, найденных по запросу Крейсер & Линкор.

Как видите, круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.

Заключение

Полагаю, нам удалось убедить вас, что круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Причем не только абстрактных задач на школьный уроках, но и вполне себе житейских проблем. Выбора будущей профессии, например.

Вам еще наверняка будет любопытно узнать, что в современной массовой культуре круги Эйлера нашли отражение не только в виде мемов, но и в популярных сериалах. Таких, как «Теория большого взрыва» и «4исла».

Используйте это полезный и наглядный метод для решения задач. И обязательно расскажите о нем друзьям и одноклассникам. Для этого под статьей есть специальные кнопки.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Круги Эйлера: примеры и возможности

Математика по своей сути наука абстрактная, если отойти от элементарных понятий. Так, на паре-тройке яблок можно наглядно изобразить основные операции, что лежат в основе математики, но, как только плоскость деятельности расширяется, этих объектов становится недостаточно. Кто-нибудь пробовал изобразить на яблоках операции над бесконечными множествами? В том-то и дело, что нет. Чем сложнее становились понятия, которыми оперирует математика в своих суждениях, тем проблематичнее казалось их наглядное выражение, которое было бы призвано облегчить понимание. Однако, на счастье как современных студентов, так и науки в целом, были выведены круги Эйлера, примеры и возможности которых мы рассмотрим ниже.

Немного истории

17 апреля 1707 года мир подарил науке Леонарда Эйлера – замечательного ученого, чей вклад в математику, физику, кораблестроение и даже теорию музыки не переоценить. Труды его признаны и востребованы по сей день во всем мире, несмотря на то что наука не стоит на месте. Особо занимательным является тот факт, что господин Эйлер принял непосредственное участие в становлении российской школы высшей математики, тем более что волею судеб он дважды возвращался в наше государство. Ученый обладал уникальной способностью выстраивать прозрачные в своей логике алгоритмы, отсекая все лишнее и в кратчайшие сроки переходя от общего к частному. Не станем перечислять все его заслуги, так как это займет немалое количество времени, и обратимся непосредственно к теме статьи. Именно он предложил использовать графическое изображение операций над множествами. Круги Эйлера решение любой, даже самой сложно составленной задачи, способны изобразить наглядно.

В чем же суть?

На практике круги Эйлера, схема которых изображена ниже, могут применяться не только в математике, так как понятия “множества” присущи не только данной дисциплине. Так, они с успехом применяются и в менеджменте.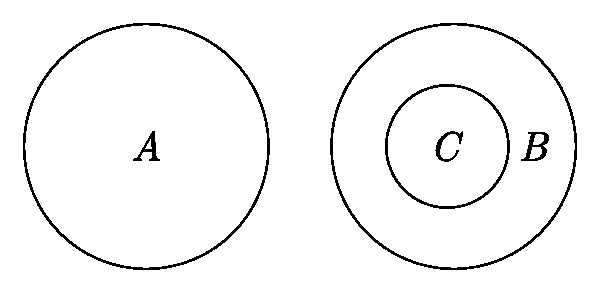

Схема выше показывает отношения множеств А (иррациональные числа), В (рациональные числа) и С (натуральные числа). Круги показывают, что множество С включено в множество В, тогда как множество А с ними никак не пересекается. Пример простейший, но наглядно объясняет специфику “взаимоотношений множеств”, которые слишком абстрактны для реального сравнения хотя бы в силу их бесконечности.

Алгебра логики

Данная область математической логики оперирует высказываниями, которые могут носить как истинный, так и ложный характер. Например, из элементарного: число 625 делится нацело на 25, число 625 делится нацело на 5, число 625 является простым. Первое и второе утверждения – истина, тогда как последнее – ложь. Конечно, на практике все сложнее, но суть показана ясно. И, конечно же, в решении опять участвуют круги Эйлера, примеры с их использованием слишком удобны и наглядны, чтобы их игнорировать.

Немного теории:

• Пусть множества А и В существуют и не являются пустыми, тогда для них определены следующие операции пересечения, объединения и отрицания.
• Пересечение множеств А и В состоит из элементов, что принадлежат одновременно как множеству А, так и множеству В.
• Объединение множеств А и В состоит из элементов, что принадлежат множеству А или множеству В.
• Отрицание множества А – это множество, что состоит из элементов, которые не принадлежат множеству А.

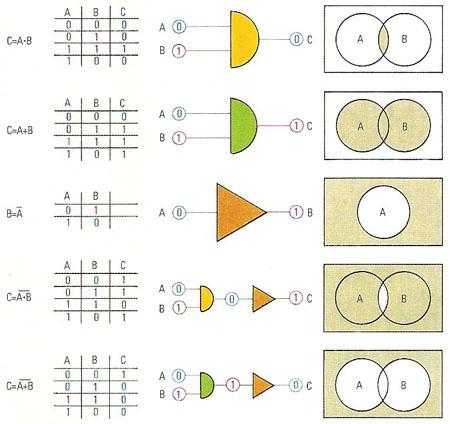
Все это изображают опять же круги Эйлера в логике, так как с их помощью каждая задача, вне зависимости от степени сложности, становится очевидной и наглядной.

Аксиомы алгебры логики

Положим, что 1 и 0 существуют и определены во множестве А, тогда:

• отрицание отрицания множества А есть множество А;
• объединение множества А с не_А есть 1;
• объединение множества А с 1 есть 1;
• объединение множества А с самим собой есть множество А;
• объединение множества А с 0 есть множество А;
• пересечение множества А с не_А есть 0;
• пересечение множества А с самим собой есть множество А;
• пересечение множества А с 0 есть 0;
• пересечение множества А с 1 есть множество А.

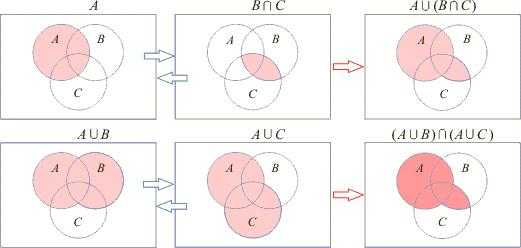
Основные свойства алгебры логики

Пусть множества А и В существуют и не являются пустыми, тогда:

• для пересечения и объединения множеств А и В действует переместительный закон;
• для пересечения и объединения множеств А и В действует сочетательный закон;
• для пересечения и объединения множеств А и В действует распределительный закон;
• отрицание пересечения множеств А и В есть пересечение отрицаний множеств А и В;
• отрицание объединения множеств А и В есть объединение отрицаний множеств А и В.

Ниже показаны круги Эйлера, примеры пересечения и объединения множеств А, В и С.

Перспективы

Работы Леонарда Эйлера обоснованно считаются базой современной математики, однако сейчас их с успехом применяют в областях человеческой деятельности, что появились относительно недавно, взять хотя бы корпоративное управление: круги Эйлера, примеры и графики описывают механизмы моделей развития, будь то российская или англо-американская версия.

fb.ru

1.6. Круговые схемы Эйлера. Логика. Учебное пособие

1.6. Круговые схемы Эйлера

Как мы уже знаем, в логике выделяется шесть вариантов отношений между понятиями. Два любых сравнимых понятия обязательно находятся в одном из этих отношений. Например, понятия писатель и россиянин находятся в отношении пересечения, писатель и человек – подчинения, Москва и столица России – равнозначности, Москва и Петербург

– соподчинения, мокрая дорога и сухая дорога – противоположности, Антарктида и материк – подчинения, Антарктида и Африка – соподчинения и т. д. и т. п.

Надо обратить внимание на то, что если два понятия обозначают часть и целое, например месяц и год, то они находятся в отношении соподчинения, хотя может показаться, что между ними отношение подчинения, ведь месяц входит в год. Однако, если бы понятия месяц и год были подчиненными, то тогда надо было бы утверждать, что месяц – это обязательно год, а год – это не обязательно месяц (вспомним отношение подчинения на примере понятий карась и рыба: карась – это обязательно рыба, но рыба – это не обязательно карась). Месяц – это не год, а год – это не месяц, но и то, и другое – отрезок времени, следовательно, понятия месяц и год, так же, как и понятия книга и страница книги, автомобиль и колесо автомобиля, молекула

и атом и т. п., находятся в отношении соподчинения, т. к. часть и целое – не то же самое, что вид и род.

В начале говорилось о том, что понятия бывают сравнимыми и несравнимыми. Считается, что рассмотренные шесть вариантов отношений применимы только к сравнимым понятиям. Однако возможно утверждать, что все несравнимые понятия находятся между собой в отношении соподчинения. Например, такие несравнимые понятия, как пингвин и небесное тело возможно рассматривать как соподчиненные, ведь пингвин – это не небесное тело и наоборот, но в то же время объемы понятий пингвин и небесное тело входят в более широкий объем третьего понятия, родового по отношению к ним: это может быть понятие объект окружающего мира или форма материи (ведь и пингвин и небесное тело – это различные объекты окружающего мира или различные формы материи). Если же одно понятие обозначает что-то материальное, а другое – нематериальное (например, дерево и мысль), то родовым для этих (как возможно утверждать) соподчиненных понятий является понятие форма бытия, т. к. и дерево, и мысль, и что угодно еще – это различные формы бытия.

Как нам уже известно, отношения между понятиями изображаются круговыми схемами Эйлера. Причем до сих пор мы изображали схематично отношения между двумя понятиями, а это можно сделать и с большим количеством понятий. Например, отношения между понятиями боксер, негр и человек изображаются следующей схемой:

Взаимное расположение кругов показывает, что понятия боксер и негр находятся в отношении пересечения (боксер может быть негром и может им не быть, а также негр может быть боксером и может им не быть), а понятия боксер и человек, так же как и понятия негр и человек находятся в отношении подчинения (ведь любой боксер и любой негр – это обязательно человек, но человек может не быть ни боксером, ни негром).

Рассмотрим отношения между понятиями дедушка, отец, мужчина, человек с помощью круговой схемы:

Как видим, указанные четыре понятия находятся в отношении последовательного подчинения: дедушка – это обязательно отец, а отец – не обязательно дедушка; любой отец – это обязательно мужчина, однако не всякий мужчина является отцом; и, наконец, мужчина – это обязательно человек, но человеком может быть не только мужчина. Отношения между понятиями хищник, рыба, акула, пиранья, щука, живое существо изображаются следующей схемой:

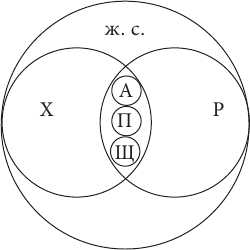
Попробуйте самостоятельно прокомментировать эту схему, установив все имеющиеся на ней виды отношений между понятиями.

Подытоживая сказанное, отметим, что отношения между понятиями – это отношения между их объемами. Значит, для того, чтобы было возможно установить отношения между понятиями, их объем должен быть резким, а содержание, соответственно, ясным, т. е. эти понятия должны быть определенными. Что касается неопределенных понятий, о которых шла речь выше, то установить точные отношения между ними достаточно сложно, фактически невозможно, ведь из-за неясности их содержания и нерезкости объема два каких-нибудь неопределенных понятия можно будет характеризовать как равнозначные или как пересекающиеся, или как подчиняющиеся и т. д. Например, возможно ли установить отношения между неопределенными понятиями неаккуратность и небрежность? То ли это будет равнозначность, то ли подчинение – точно сказать невозможно. Таким образом, отношения между неопределенными понятиями являются так же неопределенными. Понятно поэтому, что в тех ситуациях интеллектуально-речевой практики, где требуется точность и однозначность в определении отношений между понятиями, использование неопределенных понятий является нежелательным.

Поделитесь на страничке

Следующая глава >

fil.wikireading.ru

Использование метода кругов Эйлера (диаграмм Эйлера–Венна) при решении задач в курсе информатики и ИКТ

Разделы: Информатика

---

1. Введение

В курсе Информатики и ИКТ основной и старшей школы рассматриваются такие важные темы как “Основы логики” и “Поиск информации в Интернет”. При решении определенного типа задач удобно использовать круги Эйлера (диаграммы Эйлера-Венна).

Математическая справка. Диаграммы Эйлера-Венна используются прежде всего в теории множеств как схематичное изображение всех возможных пересечений нескольких множеств. В общем случае они изображают все 2ⁿ комбинаций n свойств. Например, при n=3 диаграмма Эйлера-Венна обычно изображается в виде трех кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

2. Представление логических связок в поисковых запросах

При изучении темы “Поиск информации в Интернет” рассматриваются примеры поисковых запросов с использованием логических связок, аналогичным по смыслу союзам “и”, “или” русского языка. Смысл логических связок становится более понятным, если проиллюстрировать их с помощью графической схемы – кругов Эйлера (диаграмм Эйлера-Венна).

Логическая связка	Пример запроса	Пояснение	Круги Эйлера
& – “И”	Париж & университет	Будут отобраны все страницы, где упоминаются оба слова: Париж и университет	Рис.1
| – “ИЛИ”	Париж | университет	Будут отобраны все страницы, где упоминаются слова Париж и/или университет	Рис.2

3. Связь логических операций с теорией множеств

С помощью диаграмм Эйлера-Венна можно наглядно представить связь логических операций с теорией множеств. Для демонстрации можно воспользоваться слайдами в Приложение 1.

Логические операции задаются своими таблицами истинности. В Приложении 2 подробно рассматриваются графические иллюстрации логических операций вместе с их таблицами истинности. Поясним принцип построения диаграммы в общем случае. На диаграмме – область круга с именем А отображает истинность высказывания А (в теории множеств круг А – обозначение всех элементов, входящих в данное множество). Соответственно, область вне круга отображает значение “ложь” соответствующего высказывания. Что бы понять какая область диаграммы будет отображением логической операции нужно заштриховать только те области, в которых значения логической операции на наборах A и B равны “истина”.

Например, значение импликации равно “истина” в трех случаях (00, 01 и 11). Заштрихуем последовательно: 1) область вне двух пересекающихся кругов, которая соответствует значениям А=0, В=0; 2) область, относящуюся только к кругу В (полумесяц), которая соответствует значениям А=0, В=1; 3) область, относящуюся и к кругу А и к кругу В (пересечение) – соответствует значениям А=1, В=1. Объединение этих трех областей и будет графическим представлением логической операции импликации.

4. Использование кругов Эйлера при доказательстве логических равенств (законов)

Для того, чтобы доказать логические равенства можно применить метод диаграмм Эйлера-Венна. Докажем следующее равенство ¬(АvВ) = ¬А&¬В (закон де Моргана).

Для наглядного представления левой части равенства выполним последовательно: заштрихуем оба круга (применим дизъюнкцию) серым цветом, затем для отображения инверсии заштрихуем область за пределами кругов черным цветом:

Рис.3 Рис.4

Для визуального представления правой части равенства выполним последовательно: заштрихуем область для отображения инверсии (¬А) серым цветом и аналогично область ¬В также серым цветом; затем для отображения конъюнкции нужно взять пересечение этих серых областей (результат наложения представлен черным цветом):

Рис.5 Рис.6 Рис.7

Видим, что области для отображения левой и правой части равны. Что и требовалось доказать.

5. Задачи в формате ГИА и ЕГЭ по теме: “Поиск информации в Интернет”

Задача №18 из демо-версии ГИА 2013.

В таблице приведены запросы к поисковому серверу. Для каждого запроса указан его код – соответствующая буква от А до Г. Расположите коды запросов слева направо в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.

Код	Запрос
А	(Муха & Денежка) | Самовар
Б	Муха & Денежка & Базар & Самовар
В	Муха | Денежка | Самовар
Г	Муха & Денежка & Самовар

Решение:

Для каждого запроса построим диаграмму Эйлера-Венна:

Запрос А Рис.8

Запрос Б Рис. 9

Запрос В Рис. 10

Запрос Г Рис. 11

Ответ: ВАГБ.

Задача В12 из демо-версии ЕГЭ-2013.

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысяч)
Фрегат | Эсминец	3400
Фрегат & Эсминец	900
Фрегат	2100

Какое количество страниц (в тысячах) будет найдено по запросу Эсминец?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

Пусть

Ф – количество страниц (в тысячах) по запросу Фрегат;

Э – количество страниц (в тысячах) по запросу Эсминец;

Х – количество страниц (в тысячах) по запросу, в котором упоминается Фрегат и не упоминается Эсминец;

У – количество страниц (в тысячах) по запросу, в котором упоминается Эсминец и не упоминается Фрегат.

Построим диаграммы Эйлера-Венна для каждого запроса:

Запрос	Диаграмма Эйлера-Венна	Количество страниц
Фрегат | Эсминец	Рис.12	3400
Фрегат & Эсминец	Рис.13	900
Фрегат	Рис.14	2100
Эсминец	Рис.15	?

Согласно диаграммам имеем:

1. Х+900+У = Ф+У = 2100+У = 3400. Отсюда находим У = 3400-2100 = 1300.
2. Э = 900+У = 900+1300= 2200.

Ответ: 2200.

6. Решение логических содержательных задач методом диаграмм Эйлера-Венна

Задача 1.

В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический – 14 человек, химический – 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек – и математический и физический, 5 и математический и химический, 3 – и физический и химический.

Сколько учеников класса не посещают никаких кружков?

Решение:

Для решения данной задачи очень удобным и наглядным является использование кругов Эйлера.

Самый большой круг – множество всех учеников класса. Внутри круга три пересекающихся множества: членов математического (М), физического (Ф), химического (Х) кружков.

Пусть МФХ – множество ребят, каждый из которых посещает все три кружка. МФ¬Х – множество ребят, каждый из которых посещает математический и физический кружки и не посещает химический. ¬М¬ФХ – множество ребят, каждый из которых посещает химический кружок и не посещает физический и математический кружки.

Аналогично введем множества: ¬МФХ, М¬ФХ, М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.

Известно, что все три кружка посещают 2 человека, следовательно, в область МФХ впишем число 2. Т.к. 8 человек посещают и математический и физический кружки и среди них уже есть 2 человека, посещающих все три кружка, то в область МФ¬Х впишем 6 человек (8-2). Аналогично определим количество учащихся в остальных множествах:

Круги Эйлера с названиями непересекающихся множеств: Рис. 16

Круги Эйлера с количественной информацией: Рис. 17 Например, количество человек, которые посещают физический кружок 2+6+1+5=14

Просуммируем количество человек по всем областям: 7+6+3+2+4+1+5=28. Следовательно, 28 человек из класса посещают кружки.

Значит, 36-28 = 8 учеников не посещают кружки.

Ответ: 8.

Задача 2.

После зимних каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников класса двое не были ни в кино. ни в театре, ни в цирке. В кино побывало 25 человек, в театре – 11, в цирке 17 человек; и в кино, и в театре – 6; и в кино и в цирке – 10; и в театре и в цирке – 4.

Сколько человек побывало и в кино, и в театре, и в цирке?

Решение:

Пусть х – количество ребят, которые побывали и в кино, и в театре, и в цирке.

Тогда можно построить следующую диаграмму и посчитать количество ребят в каждой области:

Рис.18.

В кино и театре побывало 6 чел., значит, только в кино и театре (6-х) чел. Аналогично, только в кино и цирке (10-х) чел. Только в театре и цирке (4-х) чел. В кино побывало 25 чел., значит, из них только в кино были 25 – (10-х) – (6-х) – х = (9+х). Аналогично, только в театре были (1+х) чел. Только в цирке были (3+х) чел. Не были в театре, кино и цирке – 2 чел. Значит, 36-2=34 чел. побывали на мероприятиях. С другой стороны можем просуммировать количество человек, которые были в театре, кино и цирке: (9+х)+(1+х)+(3+х)+(10-х)+(6-х)+(4-х)+х = 34 33+х = 34. Отсюда следует, что только один человек побывал на всех трех мероприятиях.

Ответ: 1.

Таким образом, круги Эйлера (диаграммы Эйлера-Венна) находят практическое применение при решении задач в формате ЕГЭ и ГИА и при решении содержательных логических задач.

Литература

1. В.Ю. Лыскова, Е.А. Ракитина. Логика в информатике. М.: Информатика и Образование, 2006. 155 с.
2. Л.Л. Босова. Арифметические и логические основы ЭВМ. М.: Информатика и образование, 2000. 207 с.
3. Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и ИКТ для 8 класса: БИНОМ. Лаборатория знаний, 2012. 220 с.
4. Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и ИКТ для 9 класса: БИНОМ. Лаборатория знаний, 2012. 244 с.
5. Сайт ФИПИ: http://www.fipi.ru/

6.05.2013

xn--i1abbnckbmcl9fb.xn--p1ai

Логические задачи и круги Эйлера

Круги Эйлера – это геометрическая схема. С ее помощью можно изобразить отношения между подмножествами (понятиями), для наглядного представления.

Способ изображения понятий в виде кругов позволяет развивать воображение и логическое мышление не только детям, но и взрослым. Начиная с 4-5 лет детям доступно решение простейших задач с кругами Эйлера, сначала с разъяснениями взрослых, а потом и самостоятельно. Овладение методом решения задач с помощью кругов Эйлера формирует у ребенка способность анализировать, сопоставлять, обобщать и группировать свои знания для более широкого применения.

Пример

На рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал. Это часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей). Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.

Вот несколько задач для маленьких детей на логическое мышление:

• Определить круги, которые подходят к описанию предмета. При этом желательно обратить внимание на те качества, которыми предмет обладает постоянно и которыми временно. Например, стеклянный стакан с соком всегда остается стеклянным, но сок в нем есть не всегда. Или существует какое-то обширное определение, которое включает в себя разные понятия, подобную классификацию тоже можно изобразить с помощью кругов Эйлера. Например, виолончель – это музыкальный инструмент, но не каждый музыкальный инструмент окажется виолончелью.

• Определение круга, который не подходит к описанию предмета. Например, баранка – она круглая и вкусная, а определение зеленая к ней не подходит. Можно также придумать, какой предмет подойдет для пересечения другой пары кругов. Пример – круглая и зеленая может быть пуговица.

  

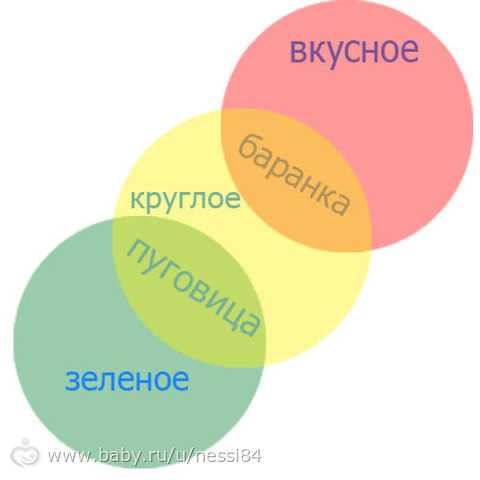
• Определить предмет, который подходит под описание всех кругов. Для каждого круга выбирается какое-либо качество (например – сладкое, оранжевое, круглое). Ребенок должен назвать предмет, который одновременно соответствует всем этим описаниям (в данном примере подойдет апельсин), также можно спросить ребенка, какие предметы могут соответствовать двум описаниям из трех, то есть будут находиться на пересечении каждой пары кругов (например, сладкое и оранжевое – карамелька, оранжевое и круглое – мяч, круглое и сладкое – арбуз).

  

Для детей постарше можно предлагать варианты задач с вычислениями – от достаточно простых до совсем сложных. Причем самостоятельное придумывание этих задач для детей обеспечит родителям очень хорошую разминку для ума.

• 1.Из 27 пятиклассников все изучают иностранные языки – английский и немецкий. 12 изучают немецкий язык, а 19 – английский. Необходимо определить, сколько пятиклассников заняты изучением двух иностранных языков; сколько не изучают немецкий; сколько не изучают английский; сколько изучают только немецкий и только английский?

При этом первый вопрос задачи намекает в целом на путь к решению этой задачи, сообщая, что некоторые школьники изучают оба языка, и в этом случае использование схемы также упрощает понимание задачи детьми.

источник http://shkolazhizni.ru/school/articles/71462/

автор Леонид Серый

Кстати, если вы не можете определиться, какую профессию выбрать, попробуйте нарисовать схему в виде кругов Эйлера. Возможно, чертеж вроде этого поможет вам определиться с выбором:

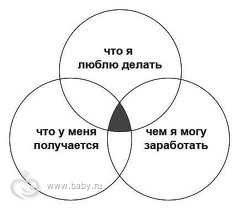
Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и будет вам нравиться.

И еще одна табличка…

www.baby.ru

Решение задач с помощью кругов Эйлера

Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

 Задача №1

В языке запросов поискового сервера для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Торты | Пироги	12000
Торты & Пироги	6500
Пироги	7700

Какое количество страниц (в тысячах) будет найдено по запросу Торты?Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение задачи №1

Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.

Обозначим каждый сектор отдельной буквой (А, Б, В).

Из условия задачи следует:

Торты │Пироги =  А+Б+В = 12000

Торты & Пироги = Б = 6500

Пироги = Б+В = 7700

Чтобы найти количество Тортов (Торты = А+Б), надо найти сектор А, для этого из общего множества (Торты│Пироги) отнимем множество Пироги.

Торты│Пироги – Пироги = А+Б+В-(Б+В) = А = 1200 – 7700 = 4300

Сектор А равен 4300, следовательно

Торты = А+Б = 4300+6500 = 10800

---

Задача №2

В языке запросов поискового сервера для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Пироженое & Выпечка	5100
Пироженое	9700
Пироженое | Выпечка	14200

Какое количество страниц (в тысячах) будет найдено по запросу Выпечка?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.Решение задачи №2

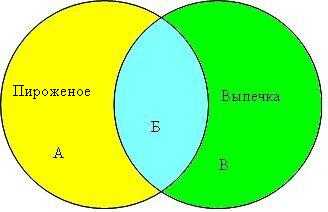
Для решения задачи отобразим множества Пироженых и Выпечек в виде кругов Эйлера.

Обозначим каждый сектор отдельной буквой (А, Б, В).

Из условия задачи следует:

Пироженое & Выпечка = Б = 5100

Пироженое = А+Б = 9700

Пироженое │ Выпечка =  А+Б+В = 14200

Чтобы найти количество Выпечки (Выпечка = Б+В), надо найти сектор В, для этого из общего множества (Пироженое │ Выпечка ) отнимем множество Пироженое.

Пироженое │ Выпечка – Пироженное = А+Б+В-(А+Б) = В = 14200–9700 = 4500

Сектор В равен 4500, следовательно  Выпечка = Б + В = 4300+5100 = 9400

---

Задача №3
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.

1	спаниели | (терьеры & овчарки)
2	спаниели | овчарки
3	спаниели | терьеры | овчарки
4	терьеры | овчарки

Решение задачи №3

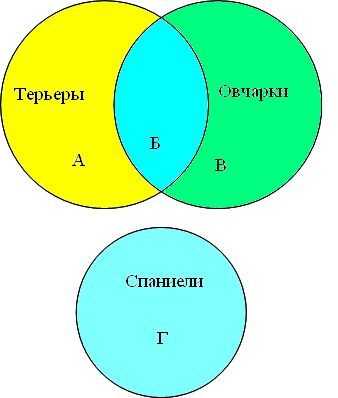
Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).

Преобразим условие задачи в виде суммы секторов:

спаниели │(терьеры & овчарки) = Г + Б

спаниели│овчарки = Г + Б + В

спаниели│терьеры│овчарки = А + Б + В + Г

терьеры & овчарки = Б

Из сумм секторов мы видим какой запрос выдал больше количества страниц.

Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4

---

Задача №4

В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.

1	барокко | классицизм | ампир
2	барокко | классицизм & ампир
3	классицизм & ампир
4	барокко | классицизм

Решение задачи №4

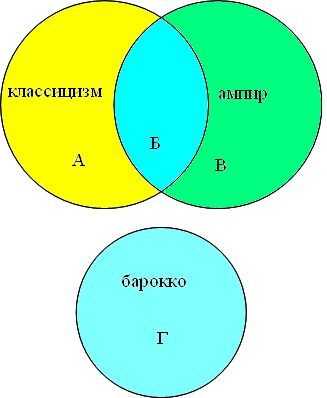Представим множества классицизм, ампир и классицизм в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).

Преобразим условие задачи в виде суммы секторов:

барокко│ классицизм │ампир = А + Б + В + Г
барокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А

Из сумм секторов мы видим какой запрос выдал больше количества страниц.

Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1

---

Задача №5В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.

1	канарейки | терьеры | содержание
2	канарейки & содержание
3	канарейки & щеглы & содержание
4	разведение & содержание & канарейки & щеглы

Решение задачи №5

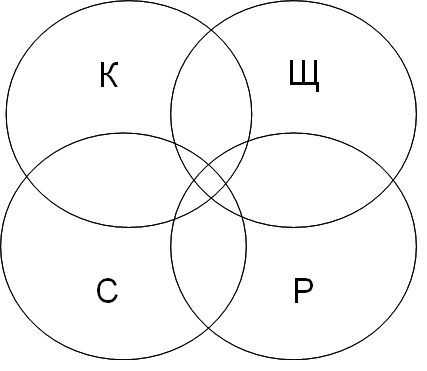
Для решения задачи представим запросы в виде кругов Эйлера.

K –  канарейки,

Щ – щеглы,

С – содержание,

Р – разведение.

Далее будем закрашивать красным цветом сектора согласно запросам, наибольший по величине сектор даст большее количество страниц на запрос.

канарейки | терьеры | содержание	канарейки & содержание	канарейки & щеглы & содержание	разведение & содержание & канарейки & щеглы

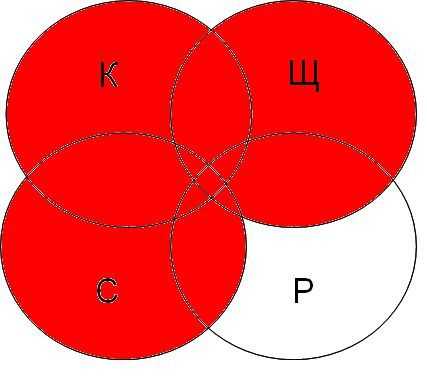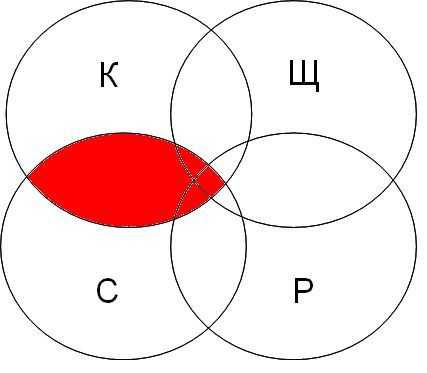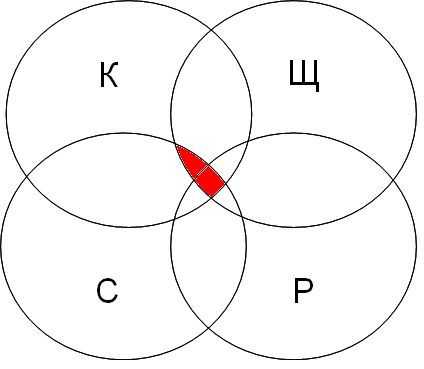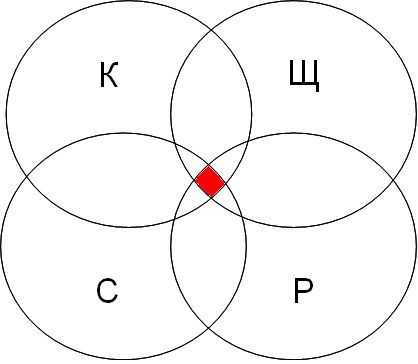Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький.

В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1

Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.

Только при таких условиях мы можем быть уверены, что правильно решили задачу. 

---

Задачи для самостоятельного решения

Задача №6

В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.

1	принтеры & сканеры & продажа
2	принтеры  & продажа
3	принтеры | продажа
4	принтеры | сканеры | продажа

---

Задача №7

В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” используется символ “|”, а для логической операции “И” – символ “&”.

1	физкультура
2	физкультура & подтягивания & отжимания
3	физкультура & подтягивания
4	физкультура | фитнесс

---

Использованные материалы >>> 

Решение подобных задач  по информатике >>>

Ответы к задачам для самостоятельного решения

Номер задачи	Ответ
6	ГБВА
7	БВАГ

saitsewanatalia.blogspot.com

Отношение между понятиями. Круги Эйлера.

Понятие – это форма мысли, отображающая предметы в их наиболее общих и существенных признаках.

Понятие – это форма мысли, а не форма слова, так как слово лишь метка, которой мы помечаем ту или иную мысль.

ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ. КРУГИ ЭЙЛЕРА.

По содержанию между понятиями могут быть два основных вида отношений: сравнимость и несравнимость.

Понятия, имеющие в своих содержаниях общие признаки, называются СРАВНИМЫМИ («адвокат» и «депутат»; «студент» и «спортсмен»).

В противном случае, понятия считаются НЕСРАВНИМЫМИ («крокодил» и «блокнот»; «человек» и «пароход»).

Если кроме общих признаков понятия имеют и общие элементы объёма, то они называются СОВМЕСТИМЫМИ.

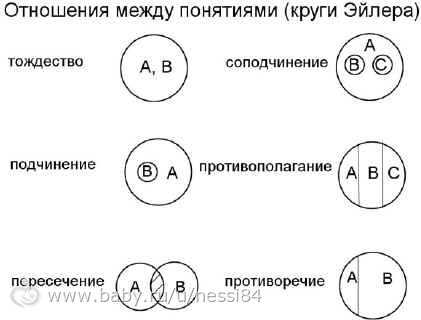
Существует шесть видов отношений между сравнимыми понятиями. Отношения между объёмами понятий удобно обозначать с помощью кругов Эйлера (круговые схемы, где каждый круг обозначает объём понятия).

ВИД ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ	ИЗОБРАЖЕНИЕ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА
РАВНОЗНАЧНОСТЬ (ТОЖДЕСТВЕННОСТЬ)   Объёмы понятий полностью совпадают. Т.е. это понятия, которые различаются по содержанию, но в них мыслятся одни и те же элементы объёма.	1) А – Аристотель В – основатель логики   2) А – квадрат В – равносторонний прямоугольник
ПОДЧИНЕНИЕ (СУБОРДИНАЦИЯ)   Объём одного понятия полностью входит в объём другого, но не исчерпывает его.	1) А – человек В – студент   2) А – животное В – слон
ПЕРЕСЕЧЕНИЕ (ПЕРЕКРЕЩИВАНИЕ)   Объёмы двух понятий частично совпадают. То есть понятия содержат общие элементы, но и включают элементы, принадлежащие только одному из них.	1) А – юрист В – депутат   2) А – студент В – спортсмен
СОПОДЧИНЕНИЕ (КООРДИНАЦИЯ)   Понятия, не имеющие общих элементов, полностью входят в объём третьего, более широкого понятия.	1) А – животное В – кот; С – собака; D – мышь   2) А – драгоценный металл В – золото; С – серебро; D – платина
ПРОТИВОПОЛОЖНОСТЬ (КОНТРАРНОСТЬ)   Понятия А и В не просто включены в объём третьего понятия, а как бы находятся на его противоположных полюсах. То есть, понятие А имеет в своём содержании такой признак, которых в понятии В заменён на противополжный.	1) А – белый кот; В – рыжий кот (коты бывают и чёрными и серыми)   2) А – горячий чай; холодный чай (чай может быть и тёплым)   Т.е. понятия А и В не исчерпывают всего объёма понятия, в которое они входят.
ПРОТИВОРЕЧИЕ (КОНТРАДИКТОРНОСТЬ)   Отношение между понятиями, одно из которых выражает наличие каких-либо признаков, а другое – их отсутствие, то есть просто отрицает эти признаки, не заменяя их никакими другими.	1) А – высокий дом В – невысокий дом   2) А – выигрышный билет В – невыигрышный билет   Т.е. понятия А и не-А исчерпывают весь объём понятия, в которое они входят, так как между ними нельзя поставить никакое дополнительное понятие.

studfiles.net