Названия геометрических тел в картинках – Геометрические фигуры и их названия
шар, куб, пирамида, призма, тетраэдр
Геометрические объемные фигуры – это твердые тела, которые занимают ненулевой объем в евклидовом (трехмерном) пространстве. Эти фигуры изучает раздел математики, который носит название “пространственная геометрия”. Знания о свойствах объемных фигур применяются в инженерии и в науках о природе. Рассмотрим в статье вопрос, геометрические объемные фигуры и их названия.
Геометрические объемные тела
Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:
- Они ортогональны друг другу, то есть перпендикулярны.
- Эти оси нормализированы, то есть базисные вектора каждой оси имеют одинаковую длину.
- Любая из осей координат – это результат векторного произведения двух других.
Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:
- Класс полиэдров. Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань – это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней – это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
- Класс круглых тел или тел вращения. Эти фигуры имеют хотя бы одну поверхность, образующую их, изогнутой формы. Например, шар, конус, цилиндр, тор.
Что касается свойств объемных фигур, то следует выделить два самых важных из них:
- Наличие определенного объема, который фигура занимает в пространстве.
- Наличие у каждой объемной фигуры площади поверхности.
Оба свойства для каждой фигуры описываются конкретными математическими формулами.
Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.
Фигура куб: описание

Под геометрической фигурой куб понимают объемное тело, которое образовано 6-тью квадратными плоскостями или поверхностями. Также эту фигуру называют правильный гексаэдр, поскольку она имеет 6 сторон, или прямоугольный параллелепипед, так как он состоит из 3-х пар параллельных сторон, которые взаимно перпендикулярны друг другу. Называют куб и прямоугольной призмой, у которой основание является квадратом, а высота равна стороне основания.
Поскольку куб является многогранником или полиэдром, то для него можно применить теорему Эйлера, чтобы определить число его ребер. Зная, что число сторон равно 6, а вершин у куба 8, число ребер равно: Р = С + В – 2 = 6 + 8 – 2 = 12.
Если обозначить буквой “a” длину стороны куба, тогда формулы для его объема и площади поверхности будут иметь вид: V = a3 и S = 6*a2, соответственно.
Фигура пирамида

Пирамида – это полиэдр, который состоит из простого многогранника (основание пирамиды) и треугольников, которые соединяются с основанием и имеют одну общую вершину (вершина пирамиды). Треугольники называются боковыми гранями пирамиды.
Геометрические характеристики пирамиды зависят от того, какой многоугольник лежит в ее основании, а также от того, является ли пирамида прямой или косой. Под прямой пирамидой понимают такую пирамиду, для которой перпендикулярная основанию прямая, проведенная через вершину пирамиды, пересекает основание в ее геометрическом центре.
Одной из простых пирамид является четырехугольная прямая пирамида, в основании которой лежит квадрат со стороной “a”, высота этой пирамиды “h”. Для этой фигуры пирамиды объем и площадь поверхности будут равны: V = a2*h/3 и S = 2*a*√(h2+a2/4) + a2, соответственно. Применяя теорему Эйлера для нее, с учетом того, что число граней равно 5, и число вершин равно 5, получаем количество ребер: Р = 5 + 5 – 2 = 8.
Фигура тетраэдр: описание

Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники. Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.
Если все 4-ре треугольника, образующие грани тетраэдра, являются равносторонними и равными между собой, то такой тетраэдр называется правильным. Этот тетраэдр имеет 4 грани и 4 вершины, число ребер составляет 4 + 4 – 2 = 6. Применяя стандартные формулы из плоской геометрии для рассматриваемой фигуры, получаем: V = a3*√2/12 и S = √3*a2, где a – длина стороны равностороннего треугольника.
Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH4, в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.
Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей. Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.
Фигура призма

Эту геометрическую фигуру можно получить, если взять два многогранника, расположить их параллельно друг другу в разных плоскостях пространства, и соединить их вершины соответствующим образом между собой. В итоге получится призма, два многогранника называются ее основаниями, а поверхности, соединяющие эти многогранники, будут иметь форму параллелограммов. Призма называется прямой, если ее боковые стороны (параллелограммы) являются прямоугольниками.
Призма – это полиэдр, поэтому для нее верна теорема Эйлера. Например, если в основании призмы лежит шестиугольник, тогда, количество сторон у призмы равно 8, а количество вершин – 12. Число ребер будет равно: Р = 8 + 12 – 2 = 18. Для прямой призмы высотой h, в основании которой лежит правильный шестиугольник со стороной a, объем равен: V = a2*h*√3/4, площадь поверхности равна: S = 3*a*(a*√3 + 2*h).
Фигура шар

Говоря о простых геометрических объемных фигурах и их названиях, следует упомянуть шар. Под объемным телом под названием шар понимают тело, которое ограничено сферой. В свою очередь, сфера – это совокупность точек пространства, равноудаленных от одной точки, которая называется центром сферы.
Поскольку шар относится к классу круглых тел, то для него не существует понятия о сторонах, ребрах и вершинах. Площадь поверхности сферы, ограничивающей шар, находится по формуле: S = 4*pi*r2, а объем шара можно вычислить по формуле: V = 4*pi*r3/3, где pi – число пи (3,14), r – радиус сферы (шара).
fb.ru
Картинки и названия объемных геометрических фигур
Картинки и названия объемных геометрических фигур
Рубрики Геометрия
Геометрическая фигура: круглый дурак в квадрате.
Первые геометрические понятия возникли в доисторические времена. Различные формы материальных тел наблюдал человек в природе: формы растений и животных, гор и извилин рек, круга и серпа Луны и т. п. Однако исследователи не только пассивно наблюдали природу, но и практически осваивали и использовали ее богатства. Практическая деятельность человека служила основой открытия простейших геометрических зависимостей и соотношений.
Очертания фигур и все возможные действия с ними изучают математические науки геометрия (изучает плоские фигуры) и стереометрия (предмет изучения — объемные фигуры)
Давайте посмотрим какие бывают виды объемных геометрических фигур, какие они имеют названия, а так же поглядим как они выглядят на картинках.
Виды и названия геометрических фигур 3D
Все 3D тела делятся на многогранники и тела вращения.
Тела вращения — это объёмные фигуры, которые возникают следствием вращения плоской геометрической
фигуры, которая ограничена кривой, вокруг оси. Эта ось лежит в той же плоскости.
Если вращать контуры геометрического тела, образуется поверхность вращения (к примеру, сфера, которая
образовывается из окружности), а если вращать заполненные контуры – возникают тела (шар, который
образован из круга).
Многогранник или полиэдр — зачастую замкнутая объемная поверхность, состоящая из многоугольников.
Многогранник – 3D фигура, у которого граница, это объединение ограниченного количества многоугольников.
Изображения объемных правильных многогранников
- Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.

Правильный тетраэдр
- Гексаэдр(куб) — правильный многогранник (шестигранный), каждая грань которого представляет собой квадрат.
Изображение куба
- Октаэдр — многогранник с восемью гранями; грани правильного октаэдра — восемь равносторонних треугольников.
Изображение октаэдра
Изображения тел вращения
- Цилиндр — это тело вращения, которое может быть получено путем вращения прямоугольника вокруг одной из его сторон, как оси.

3D тело вращения: цилиндр
- Конус — это тело вращения, которое может быть получено путем вращения прямоугольного треугольника вокруг одного из его катетов, как оси.

Тела вращения :конус
- Шар — это тело вращения, которое может быть получено путем вращения половины круга вокруг его диаметра, как оси

Тела вращения :шар
df-dt.com
Названия геометрических фигур в картинках (23 ФОТО) |
Поделиться на Facebook
Поделиться в ВК
Поделиться в ОК
Поделиться в Twitter
Геометрия как наука началась с древних греков. Они подстмотрели у египтян землемерные работы и оформили это в виде аксиом и правил. Первым научным трудом в этой области был «Начала» Евклида.
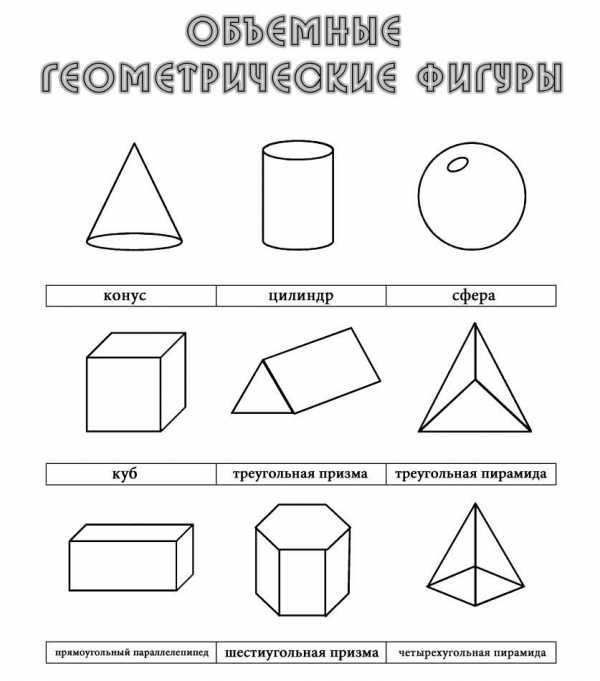
Объёмные геометрические фигуры
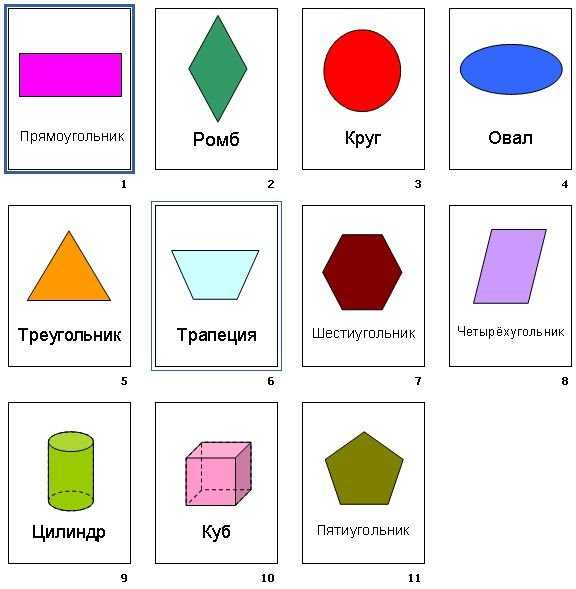
Разноцветные фигуры
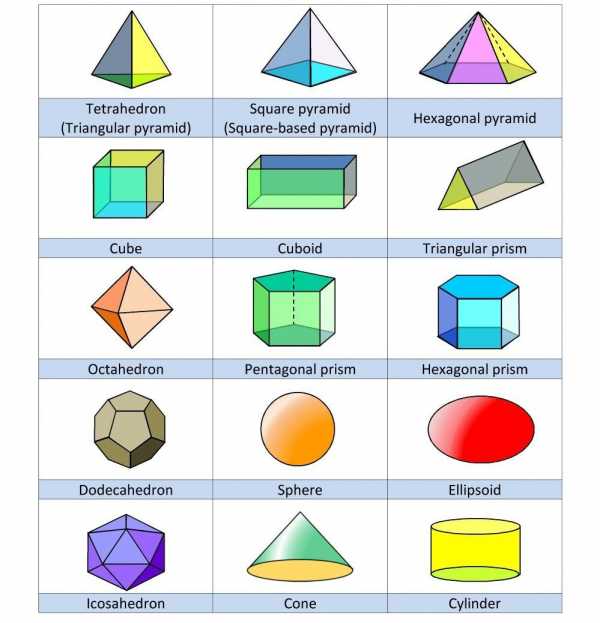
Названия объёмных фигур на английском
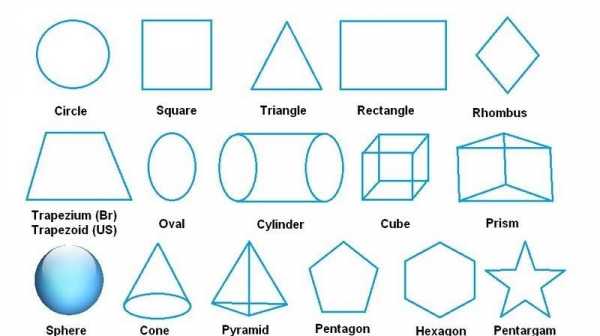
Синие фигуры с английскими названиями

Синие фигуры с русскими названиями
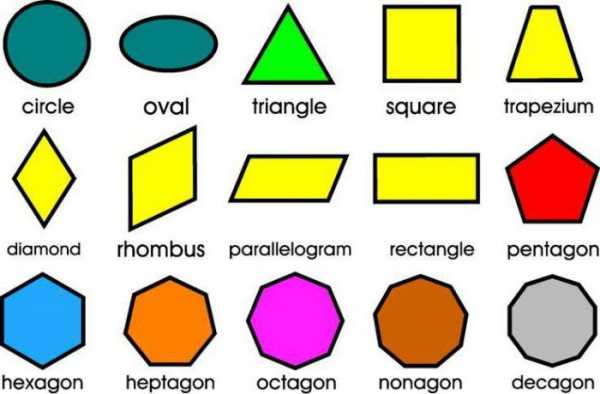
Разноцветные фигуры с английскими названиями
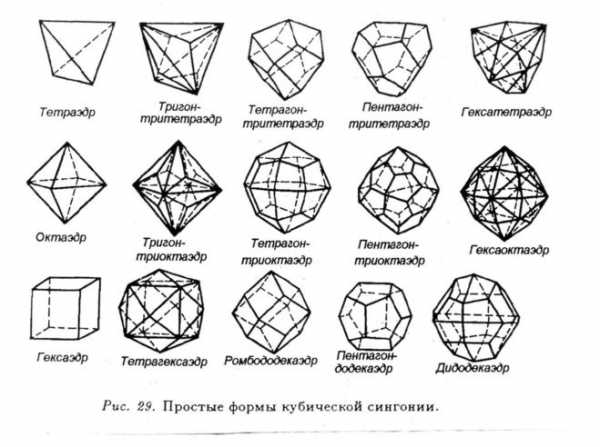
Простые фигуры кубической сингонии
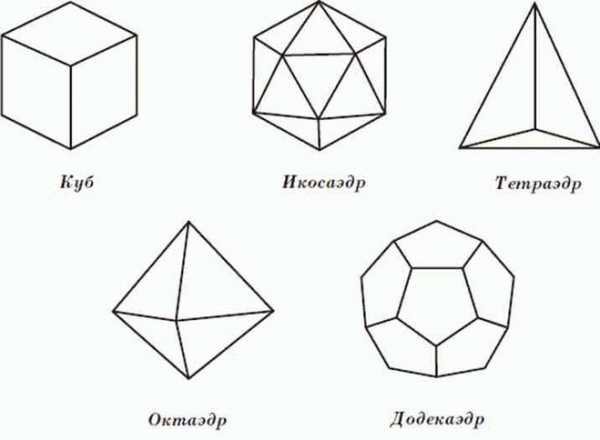
Куб, икосаэдр, тетраэдр, октаэдр, додекаэдр
Урок черчения “Геометрические тела. Комплексные чертежи многогранников”
Разделы: Технология
Цели урока:
- закрепить знания о геометрических телах, умения и навыки по построению чертежей многогранников;
- развивать пространственные представления и пространственное мышление;
- формировать графическую культуру.
Тип урока: комбинированный.
Оснащение урока: интерактивная доска MIMIO, мультимедийный проектор, компьютеры, проект mimo для интерактивной доски, мультимедийная презентация, программа «Компас-3D LT».
ХОД УРОКА
I. Организационный момент
1. Приветствие;
2. Проверка явки учащихся;
3. Проверка готовности к уроку;
4. Заполнение классного журнала (и электронного)
II. Повторение раннее изученного материала
На интерактивной доске открыт проект mimo
Лист 1. На уроках математики вы изучали геометрические тела. Несколько тел вы видите на экране. Давайте вспомним их названия. Учащиеся дают названия геометрическим телам, если есть затруднения – помогаю. (Рис. 1).
Рис. 1
1 – четырехугольная призма
2 – усеченный конус
3 – треугольная призма
4 – цилиндр
5 – шестиугольная призма
6 – конус
7 – куб
8 – усеченная шестиугольная пирамида
Лист 4. Задание 2. Даны геометрические тела и названия геометрических тел. Вызываем ученика к доске и вместе с ним перетаскиваем многогранники и тела вращения под названия, а затем перетаскиваем названия геометрических тел (рис. 2).
Рис. 2
Делаем вывод, что все тела делятся на многогранники и тела вращения.
Включаем презентацию «Геометрические тела» (Приложение). Презентация содержит 17 слайдов. Можно использовать презентацию на нескольких уроках, она содержит дополнительный материал (слайды 14-17). Со слайда 8 есть гиперссылка на Презентацию 2 (развертки куба). Презентация 2 содержит 1 слайд, на котором изображены 11 разверток куба (они являются ссылками на видеоролики). На уроке использована интерактивная доска MIMIO, а также учащиеся работают на компьютерах (выполнение практической работы).
Слайд 2. Все геометрические тела делятся на многогранники и тела вращения. Многогранники: призма и пирамида. Тела вращения: цилиндр, конус, шар, тор. Схему учащиеся перечерчивают в рабочую тетрадь.
III. Объяснение нового материала
Слайд 3. Рассмотрим пирамиду. Записываем определение пирамиды. Вершина пирамиды – общая вершина всех граней, обозначается буквой S. Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды (Рис. 3).
Рис. 3
Слайд 4. Правильная пирамида. Если
основание пирамиды — правильный многоугольник,
а высота опускается в центр основания, то —
пирамида правильная.
В правильной пирамиде все боковые ребра равны,
все боковые грани равные равнобедренные
треугольники.
Высота треугольника боковой грани правильной
пирамиды называется — апофема правильной
пирамиды
Слайд 5. Анимация построения правильной шестиугольной пирамиды с обозначением ее основных элементов (Рис. 4).
Рис. 4
Слайд 6. Записываем в тетрадь определение призмы. Призма – многогранник, у которого два основания (равные, параллельно расположенные многоугольники), а боковые грани параллелограммы. Призма может быть четырехугольной, пятиугольной, шестиугольной и т.д. Призма называется по фигуре, лежащей в основании. Анимация построения правильной шестиугольной призмы с обозначением ее основных элементов (Рис. 5).
Рис.5
Слайд 7. Правильная призма – это прямая призма, в основании которой лежит правильный многоугольник. Параллелепипед – правильная четырехугольная призма (Рис. 6).
Рис. 6
Слайд 8. Куб – параллелепипед, все грани которого квадраты (Рис. 7).
Рис. 7
(Дополнительный материал: на слайде есть
гиперссылка на презентацию с развертками куба,
всего 11 разных разверток).
Слайд 9. Записываем определение
цилиндра. Тело вращения – цилиндр,
образованное вращением прямоугольника вокруг
оси, проходящей через одну из его сторон.
Анимация получения цилиндра (Рис. 8).
Рис. 8
Слайд 10. Конус – тело вращения, образованное вращением прямоугольного треугольника вокруг оси, проходящей через один из его катетов (Рис.9).
Слайд 11. Усеченный конус – тело вращения, образованное вращением прямоугольной трапеции вокруг оси, проходящей через ее высоту (Рис. 10).
Рис. 10
Слайд 12. Шар – тело вращения, образованное вращением круга вокруг оси, проходящей через его диаметр (Рис. 11).
Рис. 11
Слайд 13. Тор – тело вращения, образованное вращением круга вокруг оси, параллельной диаметру круга (Рис. 12).
Рис. 12
Учащиеся записывают определения геометрических тел в тетрадь.
IV. Практическая работа«Построение чертежа правильной призмы»
Переключаемся на проект mimio
Лист 7. Дана треугольная правильная призма. В основании лежит правильный треугольник. Высота призмы = 70 мм, а сторона основания = 40 мм. Рассматриваем призму (направление главного вида показано стрелкой), определяем плоские фигуры, который мы увидим на виде спереди, сверху и слева. Вытаскиваем изображения видов и расставляем на поле чертежа (Рис. 13).
Рис. 13
Учащиеся самостоятельно выполняют чертеж
правильной шестиугольной призмы в программе
«Компас – 3D». Размеры призмы: высота – 60 мм,
диаметр описанной окружности вокруг основания –
50 мм.
Построение чертежа с вида сверху (Рис. 14).
Рис. 14
Затем строится вид спереди (Рис. 15).
Рис. 15
Затем строится вид слева и наносятся размеры (Рис. 16).
Рис. 16
Работы проверяются и сохраняются на компьютерах учащимися.
V. Дополнительный материал по теме
Слайд 14. Правильная усеченная пирамида (Рис. 17).
Рис. 17
Слайд 15. Пирамида, усеченная наклонной плоскостью (Рис. 18).
Рис. 18
Слайд 16. Развертка правильной треугольной пирамиды (Рис. 19).
Рис. 19
Слайд 17. Развертка параллелепипеда (Рис. 20).
Рис. 20
4.01.2012
xn--i1abbnckbmcl9fb.xn--p1ai
Форма простых геометрических тел: многогранники, тела вращения
Любое геометрическое тело состоит из оболочки, т. е. внешней поверхности, и какого-либо материала, его наполняющего (рис. 42). Каждое геометрическое тело имеет свою форму, которая различается по составу, структуре и размерам.
Состав формы геометрического тела — перечень отсеков поверхностей, составляющих его (табл. 4). Так, форма прямоугольного параллелепипеда состоит из шести отсеков, поверхностей (граней): две из них являются основаниями параллелепипеда, а остальные четыре отсека образуют замкнутую выпуклую ломаную поверхность, называемую боковой поверхностью.
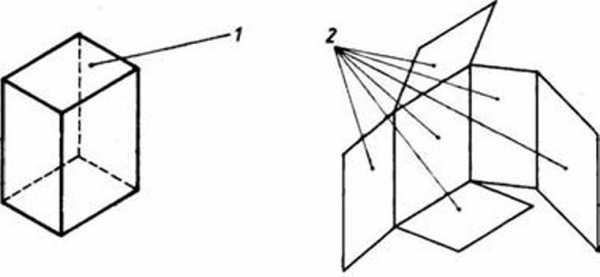
Рис 42. Геометрическое тело: 1 — оболочка; 2 — отсеки поверхностей, образующих оболочку тела
Структура формы геометрического тела — характеристика формы, которая показывает взаимосвязь и расположение отсеков поверхностей относительно друг друга (см. рис. 44).
Эти характеристики взаимосвязаны и в наибольшей степени определяют форму геометрического тела и любого другого объекта.
По форме простые геометрические тела делятся на многогранники и тела вращения.
Плоскость является частным случаем поверхности.
Многогранники — геометрические тела, оболочка которых образована отсеками плоскостей (рис. 43, а).
Грани — отсеки плоскостей, которые составляют поверхность (оболочку) многогранника; ребра — отрезки прямых, по которым пересекаются грани; вершины — концы ребер.
Тела вращения — геометрические тела (рис. 43, б), оболочка которых представляет собой поверхность вращения (например, шар) либо состоит из отсека поверхности вращения и одного (двух) отсека плоскостей (например, конус, цилиндр и т. п.).
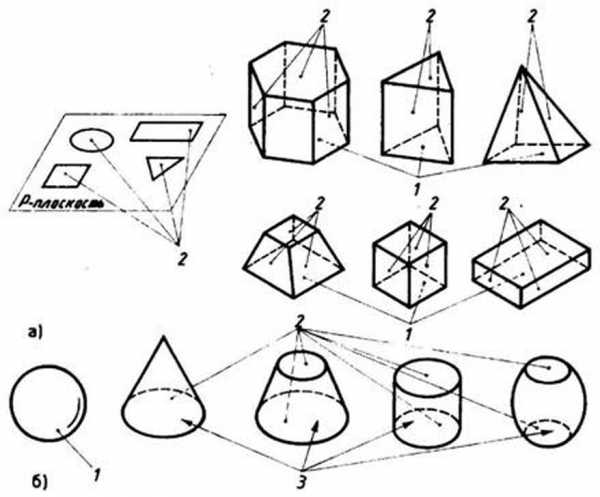
Рис. 43. Многогранники (а) и тела вращения (б): 1 — оболочка геометрического тела;
2 — отсеки плоскостей; 3 — отсеки поверхностей вращения
4. Состав простых геометрических тел
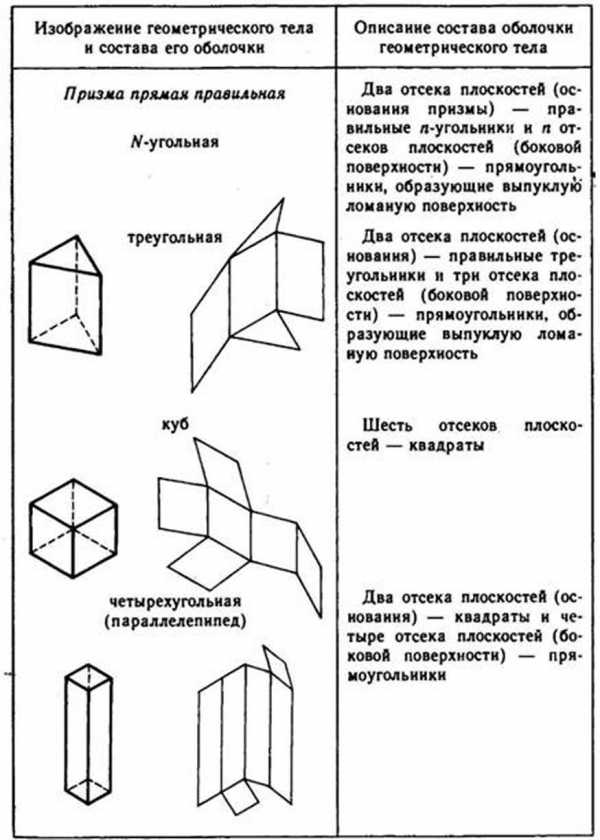
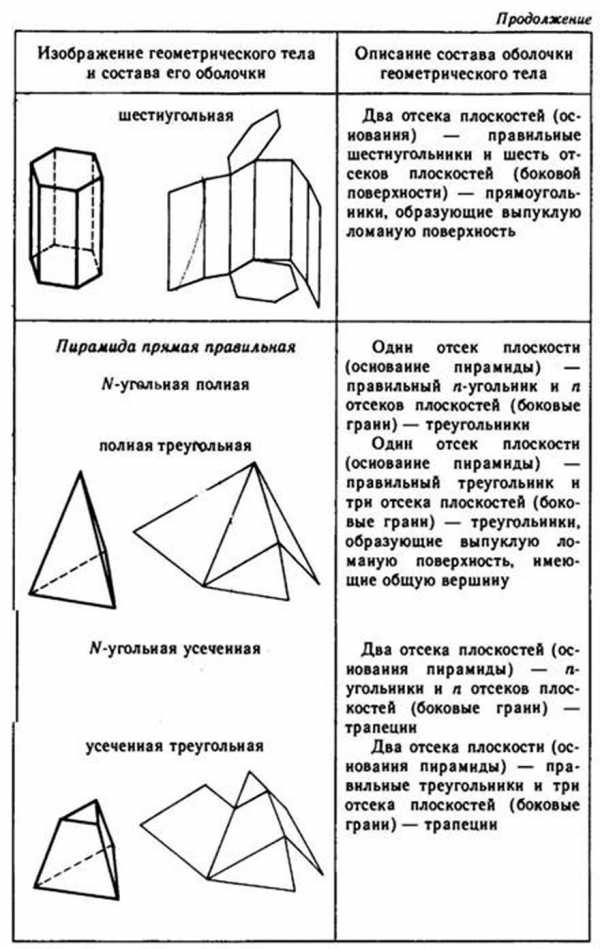
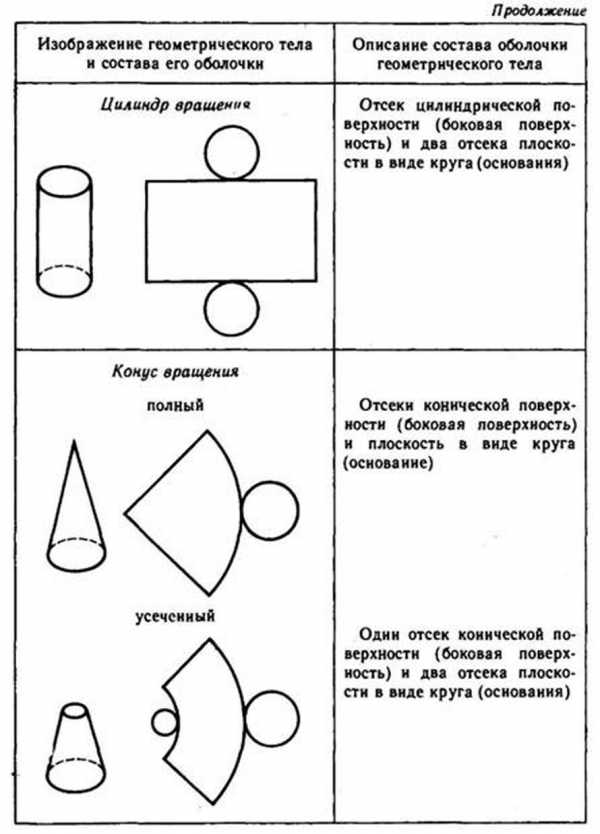
Структура формы влияет на внешний облик геометрического тела. Рассмотрим это на примере прямого и наклонного цилиндров (рис. 44), отсеки оснований которых по-разному расположены относительно друг друга.
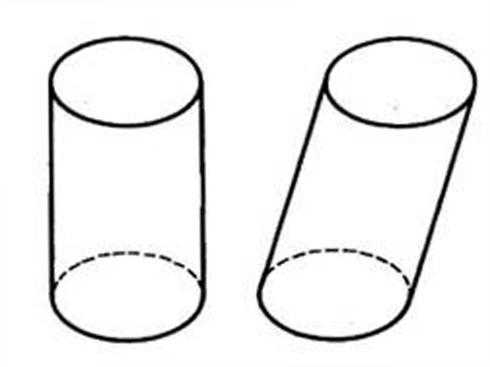
Рис. 44. Структурные различия в форме цилиндров
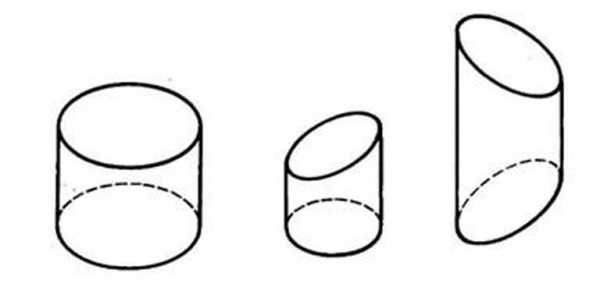
Рис. 45. Изменения формы цилиндров
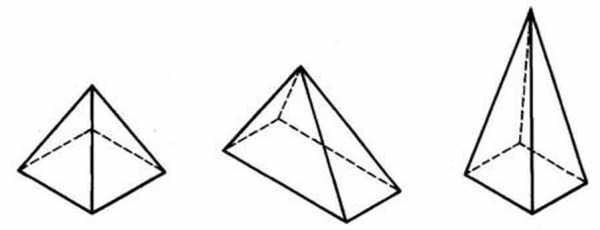
Рис. 46. Четырехугольные пирамиды различной формы
Сравнивая изображения цилиндров на рисунке 45, можно сделать вывод, что изменение положения одного из оснований приводит к изменению формы геометрического тела.
Изменение высоты, ширины, длины, диаметра основания, угла наклона осевой, положение оснований относительно друг друга существенно влияет на форму геометрических тел. Например, рассмотрите четырехугольные пирамиды различной формы (рис. 46).
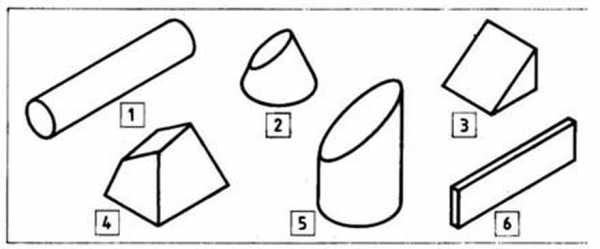
Рис. 47. Геометрические тела
cherch.ru
Удивительные геометрические фигуры
Геометрия – точная математическая наука, которая занимается изучением пространственных и других подобных отношений и форм. Но ее часто называют «сухой», поскольку она не способна описать форму многих природных объектов, ведь облака – это не сферы, горы – не конусы, а молнии распространяются не по прямым линиям. Многие объекты в природе отличаются сложностью форм в сравнении со стандартной геометрией.

Тем не менее, существует ряд удивительных фигур, которые обычно не изучаются на школьных уроках геометрии, но именно они окружают человека в реальном мире: в природе и архитектуре, головоломках, компьютерных играх и т. д.
Фрактал
Главное свойство этой сложной геометрической фигуры – самоподобие, то есть она состоит из нескольких частей, каждая из которых подобна целому объекту. Именно это свойство отличает фракталы от объектов классической (или, как говорят, евклидовой) геометрии.

При этом сам термин «фрактал» не является математическим и не имеет однозначного определения, поэтому может применяться к объектам, которые являются самоподобными или приближенно самоподобными. Его придумал в 1975 г. Бенуа Мандельброт, позаимствовав латинское слово «fractus» (ломанный, дробленный).
Фрактальные формы как нельзя лучше подходят для описания реального мира и часто встречаются среди природных объектов: снежинок, листьев растений, системы кровеносных сосудов человека и животных.
Лента Мебиуса
Это одна из самых необыкновенных трехмерных фигур в геометрии, которую легко сделать в домашних условиях. Для этого достаточно взять бумажную полоску, ширина которой в 5-6 раз меньше ее длины, и, перекрутив один из концов на 180°, склеить их между собой.

Если все сделано правильно, то можно проверить самостоятельно ее удивительные свойства:
- Наличие только одной стороны (без разделения на внутреннюю и внешнюю). Это легко проверить, если попробовать закрасить карандашом одну из ее сторон. Независимо от того, в каком месте и направлении будет начато закрашивание, в результате вся лента будет закрашена одним цветом.
- Непрерывность: если вести ручкой линию вдоль всей поверхности, ее конец соединится с начальной точкой без пересечения границ поверхности.
- Двухмерность (связность): при разрезании ленты Мебиуса вдоль она остается цельной, просто получаются новые фигуры (к примеру, при разрезании надвое получится одно кольцо большего размера).
- Отсутствие ориентированности. Путешествие по такой ленте Мебиуса всегда будет бесконечным, оно приведет к начальной точке пути, только в зеркальном отображении.
Лента Мебиуса широко используется в промышленности и науке (в ленточных конвейерах, матричных принтерах, механизмах для заточки и пр.). Кроме этого существует научная гипотеза, по которой сама Вселенная также представляет собой ленту Мебиуса невероятных размеров.
Полимино
Это плоские геометрические фигуры, которые образуются за счет соединения нескольких квадратов равных размеров по их сторонам.

Названия полимино зависят от количества квадратов, из которых они сформированы:
- мономино – 1;
- домино – 2;
- тримино – 3;
- тетрамино – 4 и т. д.
При этом для каждой разновидности существует разное количество типов фигур: у домино 1 тип, у тримино – 3 типа, у гексамино (из 6 квадратов) – 35 типов. Число различный вариаций зависит от количества используемых квадратов, но при этом еще никому из ученых не удалось найти удивительную формулу, которая будет выражать эту зависимость. Из деталей полимино можно выкладывать как геометрические фигуры, так и изображения людей, животных, предметов. Несмотря на то, что это будут схематичные силуэты, основные признаки и формы предметов делают их вполне узнаваемыми.
Полиамонд
Наряду с полимино, существует еще одна удивительная геометрическая фигура, используемая для составления других фигур – полиамонд. Он представляет собой многоугольник, сформированный из нескольких равносторонних треугольников равного размера.
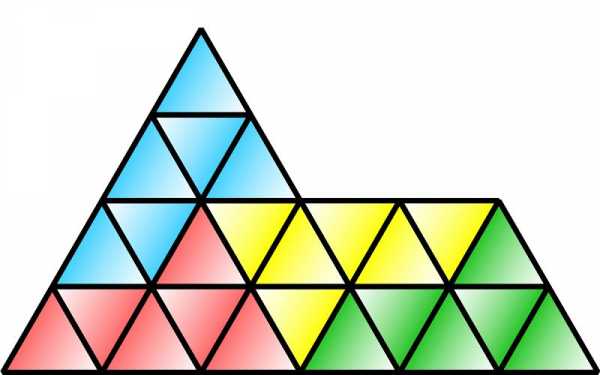
Название придумал математик Т. О’Бейрн на основании одного из названий ромба в английском языке – диамонд, который можно составить из 2-х равносторонних треугольников. По аналогии, фигуру из 3-х равносторонних треугольников О’Бейрн назвал триамондом, из 4-х – тетриамондом и т. д.
Главным вопросом их существования остается вопрос о возможном количестве полиамондов, которые можно составить из определенного количества треугольников. Применение полиамондов в реальной жизни также аналогично использованию полимино. Это могут быть разного рода головоломки и логические задачи.
Треугольник Рело
Как ни удивительно звучит, но с помощью дрели можно просверлить квадратное отверстие, а помогает в этом треугольник Рело. Он представляет собой область, образованную посредством пересечения 3 равных окружностей, центры которых являются вершинами правильного треугольника, а радиусы равны его стороне.
Сам треугольник Рело назван по фамилии немецкого ученого-инженера, который первым наиболее детально исследовал его особенности и использовал для своих механизмов на рубеже XIX-XX в. в., хотя его удивительные свойства были известны еще Леонардо да Винчи. Кто бы ни был его первооткрывателем, в современном мире эта фигура нашла широкое применение в виде:
- сверла Уаттса, которое позволяет сверлить отверстия практически идеальной квадратной формы, только с чуть закругленными краями;
- медиатора, необходимого для игры на музыкальных щипковых инструментах;
- кулачковых механизмов, используемых для создания зигзагообразных швов в швейных машинах, а также немецких часах;
- стрельчатых арок, характерных для готического стиля в архитектуре.
Отдельного внимания заслуживают так называемые невозможные фигуры – удивительные оптические иллюзии, которые на первый взгляд кажутся проекцией трехмерного объекта, но при ближайшем рассмотрении становятся заметны необычные соединения элементов. Наиболее популярными из их числа являются:
Трибар, созданный отцом и сыном Лайонелом и Роджером Пенроузами, который представляет собой изображение равностороннего треугольника, но имеет странные закономерности. Стороны, образующие верхнюю часть треугольника кажутся перпендикулярными, но правая и левая грани в нижней части также кажутся перпендикулярными. Если рассматривать каждую часть этого треугольника по отдельности, еще можно признать их существование, но в действительности такая фигура существовать не может, поскольку при ее создании были неправильно соединены правильные элементы.

Бесконечная лестница, авторство которой также принадлежит отцу и сыну Пенроузам, поэтому ее часто называют по их имени – «лестницей Пенроуза», а также «Вечной лестницей». На первый взгляд, она выглядит как обычная, ведущая вверх или вниз лестница, но при этом человек, шагающий по ней будет непрерывно подниматься (против часовой стрелки) или опускаться (по часовой стрелке). Если визуально путешествовать по такой лестнице, то по окончании «путешествия» взгляд останавливается в точке начала пути. Если бы такая лестница существовала в действительности, по ней пришлось бы подниматься и спускаться бесконечное число раз, что можно сравнить с бесконечным сизифовым трудом.

Невозможный трезубец – удивительный объект, глядя на который невозможно определить, где начинается средний зубец. Он также основан на принципе неправильных соединений, которые могут существовать только в двухмерном, но не трехмерном пространстве. Рассматривая части трезубца по отдельности, с одной стороны видны 3 круглых зуба, с другой стороны – 2 прямоугольных.

Таким образом, части фигуры вступают в своеобразный конфликт: во-первых, происходит смена переднего и заднего плана, во-вторых круглые зубцы в нижней части трансформируются в плоские в верхней.
qwizz.ru
Изучаем геометрические фигуры и их названия
Геометрические фигуры и их названия лучше изучать с ребенком, имея под рукой различные образцы нужных вам фигур. Например: мячики, кубики и т. д., чтобы малышу было более понятно, что представляют собой объемные геометрические фигуры; либо фигуры, вырезанные из бумаги – объясняя на примере, какие бывают плоские геометрические фигуры. Сделайте образцы разных ярких цветов, чтобы заострить на них внимание ребенка.
Геометрические фигуры и их названия – Проводим занятие с ребенком:
Чтобы быстро выучить геометрические фигуры и их названия, нужно уделить время для занятия, которое мы для вас подготовили. Сначала вам нужно будет скачать бланк с фигурами, распечатать на цветном принтере и выполнить указанные ниже пункты:
1. Для того, чтобы малыш быстрее запомнил разницу между объемными и плоскими фигурами, положите все имеющиеся у вас образцы на стол и отойдите на несколько шагов – объемные фигуры будут видны, однако не будет видно плоских. Обязательно обратите на это внимание ребенка.
2. Больше играйте с ребенком во время занятия – предложите ему, например, найти вокруг себя предметы, имеющие форму каких-либо геометрических фигур, либо достать на ощупь из пакета предмет определенной формы…
3. Выложите на стол несколько образцов фигур и покажите их малышу, после чего попросите его на минутку отвернуться и спрячьте одну из них. Повернувшись, ребенок должен озвучить, что именно спрятано.
Скачать геометрические фигуры и их названия в оригинальном размере (для распечатки на компьютере) вы можете во вложениях внизу страницы.
Задания являются авторской разработкой детского портала “Чудо-Юдо”. Копирование и перепубликация задания на других сайтах или в печатных изданиях запрещена законом об авторских правах.
chudo-udo.info