Геометрических фигур из – Аппликации из геометрических фигур для детей с шаблонами
делаем поделку в технике оригами
Геометрические фигуры из бумаги должен научиться делать каждый! Ведь никогда не знаешь, какие знания тебе могут пригодиться в жизни. В последнее время техника оригами набирает широкую популярность среди детей и взрослых. Но перед тем как делать разнообразные поделки (животных, птиц, растений, маленьких домиков), нужно начать с простых геометрических фигур. Такие изделия подойдут для школьников для хорошего визуального представления разных фигур.
Мастерим куб
Итак, для сегодняшнего мастер-класса нам пригодится бумага, схемы, клей, ножницы, линейки и немножечко терпения.
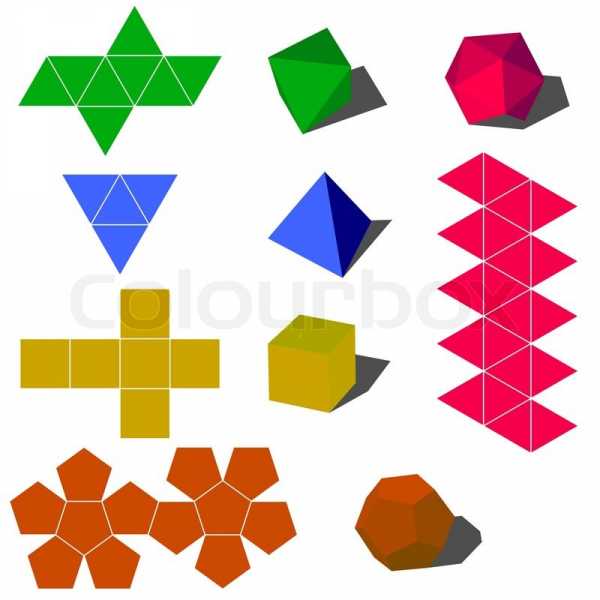


Куб — самая простая фигура для оригами, простой многогранник, в котором каждая грань является квадратом. Схему для создания развертки можно распечатать на принтере, либо начертить самим. Для этого выбрать размеры граней. Ширина листа бумаги должна быть не менее 3 сторон одного квадрата, а длина не более 5 сторон. Начертить в длину листа четыре квадрата, которые станут боковыми сторонами куба. Рисовать строго на одной линии, вплотную. Над и под одним квадратом нарисовать по одному квадрату. Дорисовать полоски для склеивания, благодаря которым грани будут соединяться между собой. Наш куб уже практически готов!
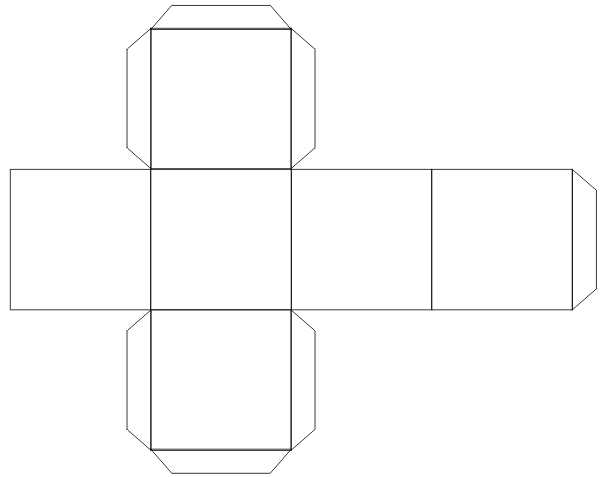
Далее тонким слоем клея равномерно размазать по местам соединения. Склеить эти поверхности и закрепить на некоторое время с помощью скрепки. Клей будет схватываться около 30-40 минут. Таким образом склеить все грани.
Поделка посложнее
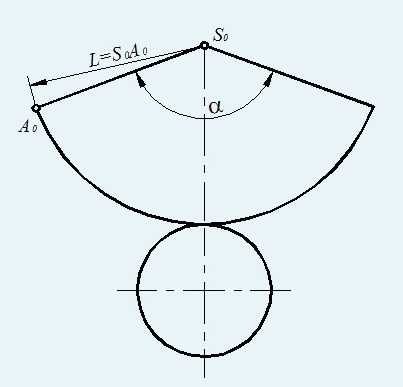
Конус делается немного сложнее. Для начала нарисовать циркулем окружность. Вырезать сектор (часть кружка, ограниченная дугой окружности и двумя радиусами) из этой окружности. Острота конца конуса зависит от вырезанной части большого сектора.
Склеить боковую поверхность конуса. Далее измерить диаметр основания конуса. Циркулем нарисовать окружность на листе бумаги. Затем дорисовать треугольнички для склеивания основы с боковой поверхности. Вырезать. После приклеить основание к боковой поверхности. Поделка готова!
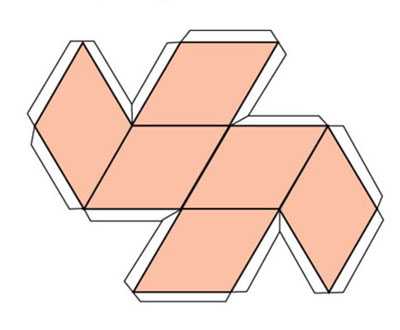
Сложный параллелепипед

Параллелепипед — сложная фигура многогранник, у которого 6 граней и каждая из них параллелограмм.
Чтобы сделать параллелепипед техникой оригами, нужно начертить основание — параллелограмм любого размера. С каждой его стороны нарисовать боковые стороны — тоже параллелограммы. Далее от любой из боковых сторон дорисовать второе основание. Добавить места для склеивания. Параллелепипед может быть прямоугольным, если все стороны имеют прямые углы. Затем вырезать развертку и склеить. Готово!
Пирамида-оригами

Пришло время сделать пирамиду из бумаги. Это многогранник, основание которого — многоугольник, а другие грани — треугольники с общей вершиной.
Для начала нужно выбрать размеры пирамиды и количество граней. Далее нарисовать многогранник — он будет основанием. Смотря на количество граней, это может быть также треугольник, квадрат, пятиугольник.
От одной из сторон нашего многогранника нарисовать треугольник, который будет боковой стороной. Затем нарисовать еще треугольник, чтобы одна его сторона была общей с первым треугольником. Нарисовать их столько, сколько сторон в пирамиде. Далее дорисовать полоски для склеивания в необходимых местах. Вырезать и склеить фигуру. Пирамида готова!
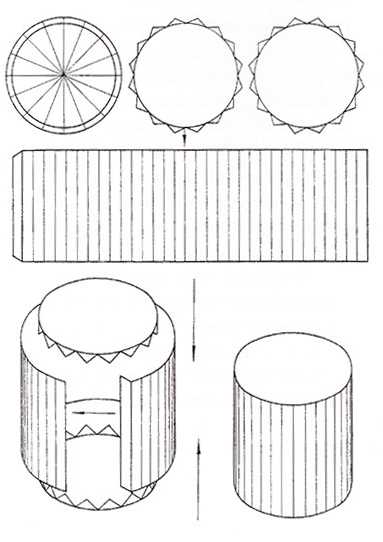
Бумажный цилиндр
Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.
Нарисовать прямоугольник на бумаге, в которой ширина — высота цилиндра, а длина — диаметр. Любители геометрии знают, что отношение длины прямоугольника к диаметру определяется формулой: L=nD, где L — длина прямоугольника, а D — диаметр цилиндра. С помощью этого вычисления узнать длину прямоугольника, которого будем рисовать на бумаге. Дорисовать маленькие треугольнички для склеивания деталей.
Затем нарисовать на бумаге два круга, диаметром как цилиндр. Это будет верхнее и нижнее основания цилиндра. Далее вырезать все детали. Склеить боковую поверхность цилиндра из прямоугольника. Дать детали высохнуть и приклеить к нему нижнее основание. Снова подождать, пока высохнет, и приклеить верхнюю основу. Готово!
Видео по теме статьи
Похожие статьи:
knittochka.ru
Объемные фигуры из бумаги, схемы. Как сделать объемные геометрические фигуры

Лучший способ показать малышу окружающий мир — дать почувствовать его на ощупь, ведь маленькую кроху хлебом не корми — дай дотронуться до заинтересовавших ее предметов, тем более, если это разноцветные геометрические тела оригами, сделанные своими руками.
60 259 т.
Яркие объемные поделки из бумаги привлекут внимание ребенка и уж точно не дадут скучать. А Вы незаметно и с задором проведете горячо любимое чадо в мир занимательной геометрии.

Не знаю, как Вам, дорогие читатели, а мне эти красочные оригами напомнили драгоценные камни . Так почему бы о каждом из них не рассказать малышу что-нибудь интересное, сравнивая очередное геометрическое тело с рубином, сапфиром, турмалином и так далее?
А пока на цветных листах распечатайте схемы поделок и, сделав необходимые изгибы, и склейте в нужных местах. Уверен, у Вас все получится!
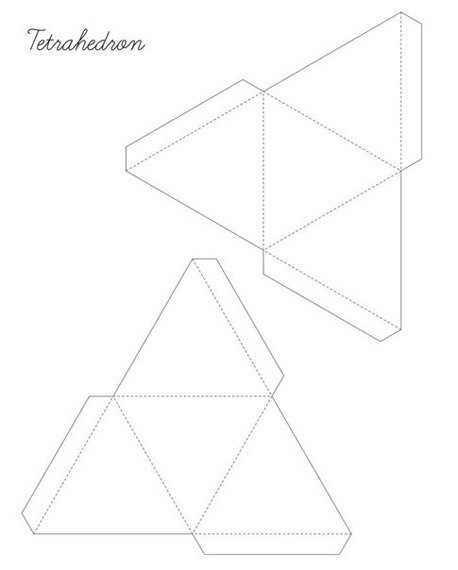
Тетраэдр
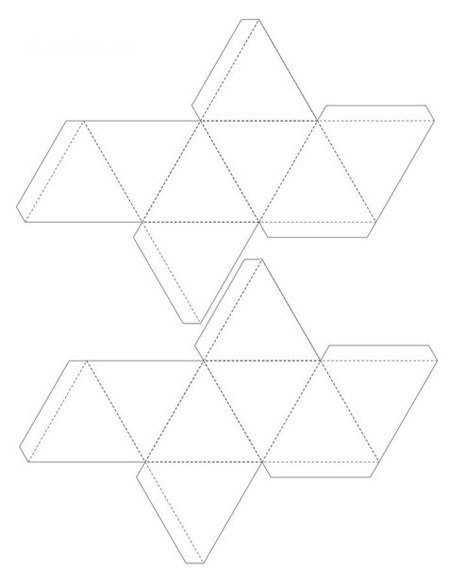
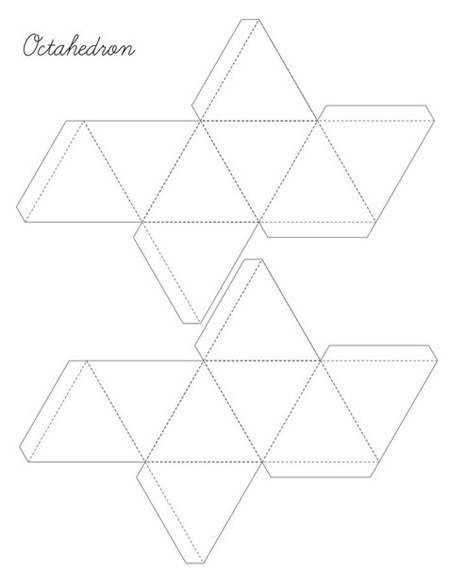
Октаэдр
Икосаэдр
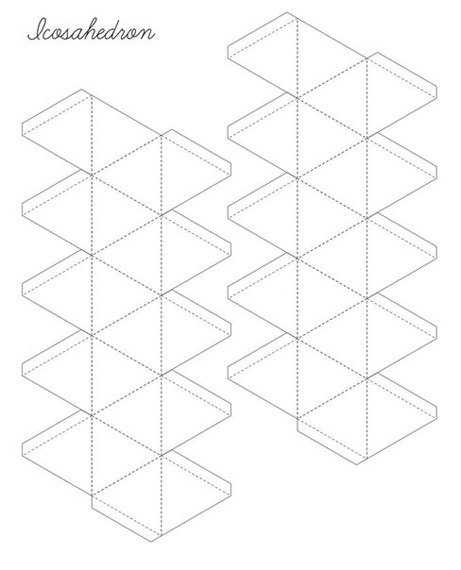
Додекаэдр
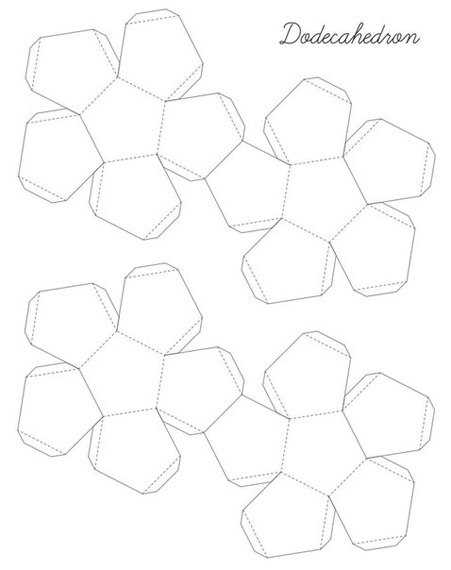
Куб

У Вас должны получиться вот такие заготовки:

А это уже готовые камешки-многогранники. Дерзайте!

Веселых игр, занимательных историй и всестороннего развития Вашему малышу!
Заметили орфографическую ошибку? Выделите её мышкой и нажмите Ctrl+Enter
pustunchik.ua
Игры на воссоздание из геометрических фигур образных и сюжетных изображений
Особое место среди математических развлечений занимают игры на составление плоскостных изображений предметов, животных, птиц, домов, кораблей из специальных наборов геометрических фигур. Наборы фигур при этом подбираются не произвольно, а представляют собой части разрезанной определенным образом фигуры: квадрата, прямоугольника, круга или овала. Они интересны детям и взрослым. Детей увлекает результат – составить увиденное на образце или задуманное. Они включаются в активную практическую деятельность по подбору способа расположения фигур с целью создания силуэта.
Игра “Танграм”
“Танграм” – одна из несложных игр. Называют ее и “Головоломкой из картона”, “Геометрическим конструктором” и др. Игра проста в изготовлении. Квадрат размером 8X8 см из картона, пластика, одинаково окрашенный с обеих сторон, разрезают на 7 частей. В результате получается 2 больших, 1 средний и 2 маленьких треугольника, квадрат и параллелограмм. Используя все 7 частей, плотно присоединяя их одну к другой, можно составить очень много различных изображений по образцам и по собственному замыслу (рис. 60).
Рис. 60
Успешность освоения игры в дошкольном возрасте зависит от уровня сенсорного развития детей. Дети должны знать не только названия геометрических фигур, но и их свойства, отличительные признаки, владеть способами обследования форм зрительным и осязательно-двигательным путем, свободно перемещать их с целью получения новой фигуры. У них должно быть развито умение анализировать простые изображения, выделять в них и в окружающих предметах геометрические формы, практически видоизменять фигуры путем разрезания и составлять их из частей.
Последовательные этапы освоения игры “Танграм” в группе детей 5 лет.
Первый этап – ознакомление с набором фигур к игре, преобразование их с целью составления из 2-3 имеющихся новой.
Примеры (для детей 6-7 лет)
1. Пример
Цель. Упражнять детей в сравнении треугольников по размеру, составлении из них новых геометрических фигур: квадратов, четырехугольников, треугольников.
Материал: у детей наборы фигур к игре “Танграм”, у воспитателя фланелеграф и набор фигур к нему.
Ход работы. Воспитатель предлагает детям рассмотреть набор фигур, назвать их, сосчитать и определить общее количество. Дает задания:
1. Отобрать все треугольники, сосчитать. Сравнить по размеру, накладывая один на другой.
Вопросы для анализа: “Сколько больших, одинаковых по размеру треугольников? Сколько маленьких? Сравните этот треугольник (среднего размера) с большим и маленьким. (Он больше самого маленького и меньше самого большого из имеющихся.) Сколько всего треугольников и какого они размера?” (Два больших, 2 маленьких и 1 средний по размеру.)
2. Взять 2 больших треугольника и составить из них последовательно: квадрат, треугольник, четырехугольник. Один из детей составляет фигуры на фланелеграфе. Воспитатель просит назвать вновь полученную фигуру и сказать, из каких фигур она составлена.
3. Из 2 маленьких треугольников составить те же фигуры, располагая их по-разному в пространстве.
4. Из большого и среднего по размеру треугольников составить четырехугольник.
Вопросы для анализа: “Какую фигуру составим? Как? (Присоединим к большому треугольнику средний или наоборот.) Покажите стороны и углы четырехугольника, каждой отдельной фигуры”.
В итоге воспитатель обобщает: “Из треугольников можно составлять новые различные фигуры – квадраты, четырехугольники, треугольники. Фигуры присоединяются одна к другой по сторонам”. (Показывает на фланелеграфе.)
2. Пример
Цель. Упражнять детей в умении составлять новые геометрические фигуры из имеющихся по образцу и замыслу.
Материал: у детей – наборы фигур к игре “Танграм”. У воспитателя – фланелеграф и таблицы с изображенными на них геометрическими фигурами.
Ход работы. Дети, рассмотрев фигуры, делят их по заданию воспитателя на 2 группы: треугольники и четырехугольники.
Воспитатель поясняет, что это набор фигур к игре, называется она головоломка или танграм; так ее назвали по имени ученого; придумавшего игру. Можно составить много интересных изображений.
Составить четырехугольник из большого и среднего треугольников.
Составить новую фигуру из квадрата и 2 маленьких треугольников. (Сначала – квадрат, затем – четырехугольник.).
Составить новую фигуру из 2 больших и среднего треугольника. (Пятиугольник и четырехугольник.)
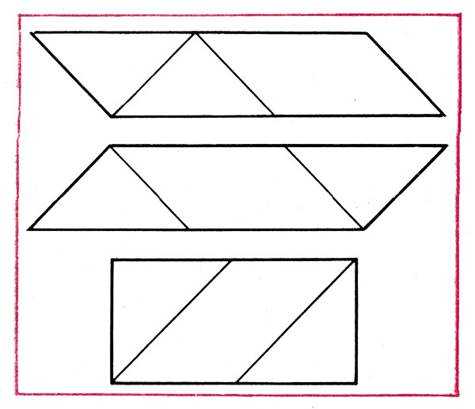
Рис. 61
Воспитатель показывает таблицы и просит детей составить такие же фигуры (рис. 61). Дети последовательно составляют фигуры, рассказывают, как они делали, называют их.
Воспитатель составляет их на фланелеграфе.
Дается задание на составление нескольких фигур по собственному замыслу детей.
Итак, на первом этапе освоения игры “Танграм” проводится ряд упражнений, направленных на развитие у детей пространственных представлений, элементов геометрического воображения, на выработку практических умений в составлении новых фигур путем присоединения одной из них к другой, соотношение сторон фигур по размерам. Задания видоизменяют. Дети составляют новые фигуры по образцу, устному заданию, замыслу. Им предлагают выполнить задание в плане представления, а затем – практически: “Какую фигуру можно составить из 2 треугольников и 1 квадрата? Сначала скажите, а затем составьте”. Эти упражнения являются подготовительными ко второму этапу освоения игры – составлению фигур-силуэтов по расчлененным образцам (Фигурой силуэтом называют предметное плоское изображение, составленное из частей игры). Второй этап работы с детьми является наиболее важным для усвоения ими в дальнейшем более сложных способов составления фигур.
Для успешного воссоздания фигур-силуэтов необходимо умение зрительно анализировать форму плоскостной фигуры и ее частей. Кроме этого, при воссоздании фигуры на плоскости очень важно умение мысленно представить изменения в расположении фигур, которые происходят в результате их трансфигурации. Наиболее простым видом анализа образца является зрительный, но он невозможен без развитого умения видеть пропорциональное соотношение частей фигуры. Способ составления (расположения составных частей) фигуры-силуэта из геометрических фигур играющий вынужден искать, опираясь на данные анализа, в процессе апробирования различных намеченных вариантов составления.
Игры на составление фигур-силуэтов по расчлененным образцам (второй этап работы) должны быть эффективно использованы воспитателем не только с целью упражнения в расположении частей составляемой фигуры, но и в приобщении детей к зрительному и мысленному анализу образца. Детям показывают расчлененный образец (заяц) и объясняют цель: составить такого же: Несмотря на кажущуюся легкость “копирования” способа пространственного расположения частей, дети допускают ошибки в соединении фигур по сторонам, в пропорциональном соотношении. Ошибки объясняются тем, что детям этого возраста недоступен самостоятельный анализ расположения частей. Они затрудняются в определении и назывании относительной величины составных частей, размерных соотношений. Так, дети могут вместо большого треугольника поместить средний по размеру и заметить ошибку только после указания взрослого. Таким образом, исходя из особенностей анализа и практических действий детей, можно определить содержание работы на втором этапе развертывания игр: это усвоение детьми плана анализа предъявляемого образца, начиная с основных частей, и выражение речи способа соединения и пространственного расположения частей.
За анализом следуют упражнения в составлении, ориентируясь на образ. Образец не убирается, дети могут вновь обращаться к нему в случае затруднения. Он должен быть изготовлен в виде таблицы на листе бумаги и равен по размеру фигуре-силуэту, получаемому в результате составления из имеющегося у детей набора фигур к игре. Это облегчает на первых занятиях анализ и сопоставление (проверку) воссозданного изображения с образцом. На следующих занятиях, по мере накопления опыта в составлении фигур, нет необходимости придерживаться этого правила.
Примеры (для детей 6-7 лет)
1. Пример
Составление фигуры-силуэта зайца
Цель. Учить детей анализировать способ расположения частей, составлять, фигуру-силуэт, ориентируясь на образец.
Материал: у детей – набор фигур к игре “Танграм”, образец.
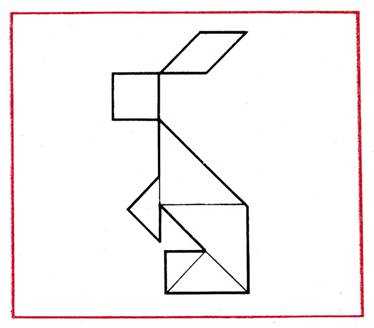
Рис. 62
Ход работы. Воспитатель показывает детям образец фигуры-силуэта зайца (рис. 62) и говорит: “Посмотрите внимательно на зайца и расскажите, как он составлен. Из каких геометрических фигур составлены туловище, голова, ноги зайца?” Надо назвать фигуру и ее величину, так как треугольники, из которых составлен заяц (показывает), разных размеров; предлагает нескольким детям ответить.
Коля. Голова зайца составлена из квадрата, ухо – из четырехугольника, туловище – из двух треугольников, а лапы – тоже из треугольников.
Воспитатель. Правильно ли рассказал Коля? Если заметили ошибки, исправьте их.
Воспитатель просит рассказать другого ребенка.
Игорь. Туловище надо составить из 2 больших треугольников, лапу (вот эту) – из среднего треугольника и маленького, а другую – из маленького треугольника.
Воспитатель. Теперь посмотрите, какую геометрическую фигуру образуют 2 больших треугольника. Покажите стороны, углы этой фигуры.
Лена. Это четырехугольник (показывает его контур, считает углы, стороны).
Воспитатель. А какую фигуру образует вместе средний и маленький треугольник?
Саша. Прямоугольник.
Надя. Нет, это четырехугольник, вот здесь (показывает) не как у прямоугольника.
Воспитатель. Вот мы и рассмотрели, как составлен заяц, из каких фигур составлены туловище, голова, лапы. А теперь возьмите свои наборы и составляйте. Кто выполнит задание, проверьте, правильно ли составил.
После того как фигура составлена, воспитатель просит двоих детей рассказать, как они составили фигуру, т. е. назвать расположение составных частей по порядку.
Света. Я составила так: голову и ухо – из квадрата и четырехугольника, туловище – из 2 больших треугольников, лапы – из среднего и маленького и 1 лапку – из маленького треугольника.
Ира. У меня ухо составлено из четырехугольника, голова – из квадрата, лапа – из треугольника, туловище – из больших треугольников, лапы – вот эти – из 2 треугольников.
Анализ образца в данном случае проводился под руководством педагога. В дальнейшем следует предлагать детям самостоятельно провести анализ фигуры и составить ее. Дети 5 лет составляют наиболее простые фигуры-силуэты: зайца, журавля, кенгуру, лису и др. (рис. 63). В течение 5 занятий с использованием расчлененного образца дети обучаются четкому его анализу, правильному пространственному расположению геометрических фигур при воссоздании плоскостного изображения.
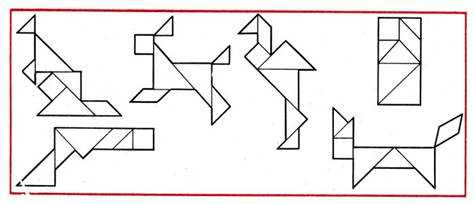
Более сложной и интересной для ребят деятельностью является воссоздание фигур по образцам контурного характера (нерасчлененным) – третий этап освоения игры, что является доступным детям 6-7 лет при условии их обучения.
Воссоздание фигур по контурным образцам требует зрительного членения формы той или иной плоскостной фигуры на составные части, т. е. на те геометрические фигуры, из которых она составлена. Оно возможно при условии правильного расположения одних составных частей относительно других, соблюдения пропорционального соотношения их по величине. Воссоздание осуществляется в ходе выбора (поисков) способа составления на основе предварительного анализа и последующих практических действий, направленных на проверку различных способов взаимного расположения частей. На этом этапе обучения одна из главных задач состоит в развитии у детей умения анализировать форму плоскостной фигуры по контурному ее изображению, комбинаторных способностей.
При переходе от составления фигур-силуэтов по расчлененным образцам к составлению по образцам без указания составных частей важно показать детям, что без предварительного тщательного рассматривания образца составить фигуру на плоскости трудно. Детям предлагают составить 1-2 фигуры силуэтов по образцам контурного характера из числа тех, что составлялись ими ранее по расчлененным образцам. Процесс составления фигуры при этом проходит на основе сформированного представления и проведенного в начале занятия зрительного анализа образца. Такие упражнения обеспечивают переход к воссозданию фигур по более сложным образцам.
Учитывая то, что безошибочно указать расположение составных частей в анализируемом нерасчлененном образце детям сложно, необходимо предлагать им провести предположительный анализ образца. При этом каждый анализирует образец самостоятельно, после чего выслушиваются несколько вариантов расположения частей, правильность или ошибочность которых воспитатель не подтверждает. Это побуждает к практической проверке результатов предварительного анализа расположения частей в составляемой фигуре, поиску новых способов пространственного расположения составных элементов.
2. Пример
Воссоздание фигуры-силуэта бегущего гуся
Цель. Учить детей предположительно рассказывать способ расположения частей в составляемой фигуре, планировать ход составления.
Материал: наборы, фигур к игре “Танграм”, фланелеграф, образец, доска и мел.
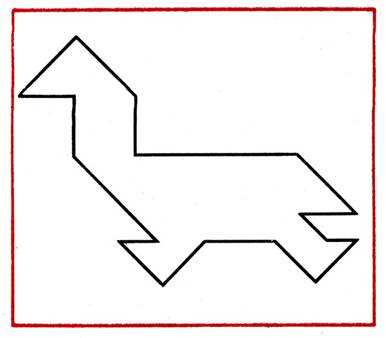
Рис. 64
Ход работы. Воспитатель обращает внимание детей на образец (рис. 64): “Посмотрите внимательно на этот образец. Фигуру бегущего гуся можно составить из 7 частей игры. Надо сначала рассказать, как это можно сделать. Из каких геометрических фигур можно составить туловище, голову, шею, ноги гуся?”
Лена. Я думаю, что туловище составлено из 2 больших треугольников, голова – из маленького треугольника, шея – из квадрата, лапы – треугольники.
Галя. Я думаю, что голова из среднего треугольника составлена, а дальше все так же, как Лена говорила.
Игорь. Голова из среднего треугольника, шея – из квадрата, а туловище – из 2 больших треугольников, вот так они лежат (показывает), и четырехугольника, а ноги – из маленьких треугольников.
Воспитатель. Возьмите фигуры и составляйте. И мы узнаем, кто из ребят прав.
После того как большинство детей составят силуэт гуся, воспитатель вызывает одного ребенка, который мелом на доске рисует расположение частей. Все дети сверяют составленные ими фигуры с изображением на доске.
В ходе работы дети высказывают предположения о способе размещения частей фигуры, подвергая его в дальнейшем практической проверке. Помогая им, педагог подчеркивает необходимость соблюдения определенной последовательности в анализе и процессе составления фигур: от выделения главных частей, составляемых из больших фигур, к выделению других частей, составляемых из маленьких фигур.
В дальнейшем возможно проведение анализа образца составляемой фигуры не в начале занятия, а в ходе его, когда дети апробируют различные пути составления на основе предположительного самостоятельного анализа, но фигура у них не получается. Такой прием особенно оправдывает себя при составлении более сложных фигур, т. е тех, в форме которых трудно определить место расположения мелких частей (четырехугольника, маленьких треугольников). Это плоскостные изображения курицы, елки, рыбки и др. В таких случаях анализ служит как бы подсказкой, которая наиболее эффективна именно в процессе и на определенной стадии выполнения задания, когда решающий задачу исчерпал все возможные способы, но интерес к задаче у него не угас. По мере самостоятельных упражнений совершенствуется умение детей производить зрительный анализ образца, он становится все более точным, конкретным. Поисковые действия, направленные на выбор адекватного способа пространственного расположения фигур на основе предварительного анализа, приобретают целенаправленность. Дети начинают обосновывать свои действия и замыслы.
3. Пример
Составление фигуры-силуэта домика
Цель. Упражнять детей в умении осуществлять предположительный зрительно-мысленный анализ способа расположения фигур, проверяя его практически.
Материалы: наборы фигур к игре “Танграм”. Образец, доска и мел.
Ход работы. Воспитатель. Рассмотрим внимательно домик – стены, крышу, трубу (рис. 65). Расскажите, как бы вы составили его из имеющегося набора фигур.
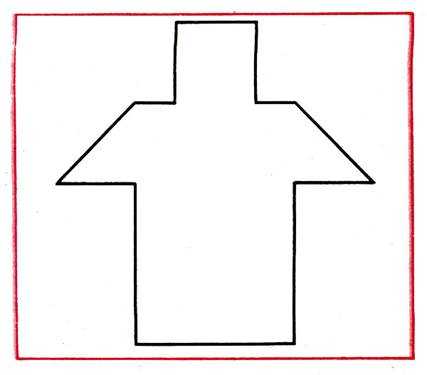
Рис. 65
Коля. Стены домика надо сложить из 2 больших треугольников (пальцем как бы делает разметку на образце), – вот они лежат, получается квадрат. Труба – маленький квадрат, теперь крышу составим. У меня остался треугольник, четырехугольник, еще 1 маленький треугольник. Положу вот так: средний треугольник, затем четырехугольник, надо, чтобы края получились… (задумывается).
Воспитатель. Из каких же, по-твоему, фигур составлена крыша?
Коля. Из среднего и 2 маленьких треугольников да еще четырехугольника.
Радик. Стены – из 2 больших треугольников, труба – из 2 маленьких, а крыша составлена из остальных фигур. Я сейчас составлю, если не получится, значит, надо по- другому, но мне кажется, что так.
После выполнения дети изображают графически, мелом на доске способ расположения фигур в силуэте домика. Отмечается, что многие из детей, еще до составления, зрительно правильно распределили фигуры.
На протяжении ряда занятий дети составляют еще несколько фигур-силуэтов по нерасчлененным образцам (рис. 66).
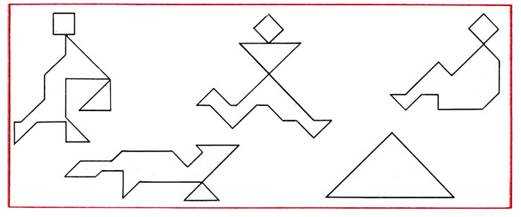
Рис. 66
За играми на составление фигур-силуэтов по образцам следуют упражнения в составлении изображений по собственному, замыслу. На занятии детям предлагают вспомнить, какие плоские фигуры они учились составлять, и составить их. Каждый из детей составляет поочередно по 3-4 фигуры. Эти занятия включают и элемент творчества. При передаче формы некоторых фигур-силуэтов дети воспроизводят общие очертания формы, а составные элементы отдельных частей располагают несколько иначе, чем это делали ранее по образцу.
В играх по самостоятельному придумыванию и составлению фигур-силуэтов дети, задумав составить какое-либо изображение, мысленно, в плане представления, членят его на составные части, соотнося их с формой танграмов., затем составляют. Дети придумывают и составляют интересные фигуры-силуэты, которыми можно дополнить запас образцов к игре “Танграм” (Подробнее см.: Дошкольное воспитание, 1971, № 1).
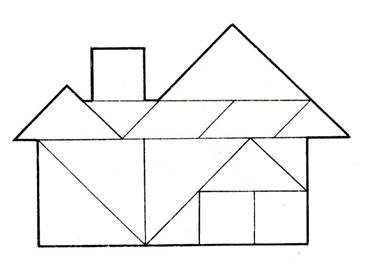
Рис. 67
Детям подготовительной Группы с целью развития творчества можно предложить и более сложные задания. Из 2-3 одинаковых наборов фигур к игре “Танграм” составить фигуру-силуэт, сюжет как по образцам, так и по собственному замыслу (рис. 67). На рисунке дан образец (домик) с указанием составных частей.
4. Пример
Составь фигуру из 2 наборов
Воссоздать фигуру-силуэт или сюжет по образцу из 2 наборов к игре “Танграм, довольно сложно, так как приходится оперировать большим количеством частей (до 14).
Использование же образцов с обозначенным цифрами местом расположения частей в фигуре-силуэте облегчает задачу, хотя ив данном случае легкость только кажущаяся.
Условно пронумеруем (запомним номера) фигуры так: маленькие треугольники – 1, квадраты – 2, четырехугольники – 3, средние по размеру треугольники – 4, большие треугольники – 5.
Составление фигуры-силуэта по образцу с цифровым обозначением места расположения требует активной умственной деятельности. Указано лишь место расположения фигур, например маленьких треугольников цифрой 1, а не способ их расположения (направление, сочетание с другими фигурами). Ребенок, составляющий фигуру-силуэт, должен постоянно ориентироваться на форму фигуры или отдельных ее частей. Так, в ходе составления силуэта человека на коне, изображенного на рисунке 68, вслед за относительным определением места нахождения геометрических фигур следует более тщательное их распределение. Требуется так расположить каждую из фигур в пространстве, чтобы направление линий, соотношение частей по размеру, форме создавало образ. Поэтому в процессе, поисков адекватного способа расположения фигур решающий задачу вынужден постоянно представлять форму составляемой фигуры целостно и члененной на части.
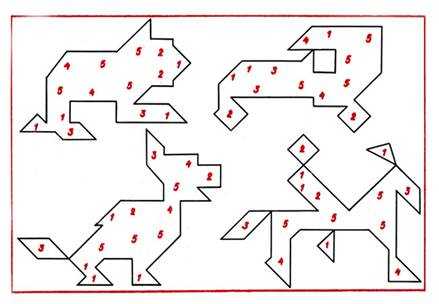
Рис. 68
Руководство процессом составления должно быть направлено на развитие умения предвидеть сочетание фигур, изменения в их расположении и форме составляемого силуэта.
Итак, в обучении детей 5-6 лет воссозданию фигур-силуэтов из частей игры “Танграм” последовательность усложнения заданий можно представить следующим образом: от овладения элементарными способами зрительного анализа дети переходят к усвоению способов мысленных действий.
Усложнение заданий и изменение характера руководства процессом воссоздания со стороны педагога, повышение роли самостоятельных действий детей в ходе поисков составления помогают им овладевать более совершенными способами трансфигурации, на основании чего возможно моделирование предметных изображений по собственному замыслу.
Игра-головоломка “Пифагор”
(Головоломка “Пифагор” выпускается промышленностью с прилагаемым к ней комплектом образцов)
В работе с детьми 6-7 лет игра используется с целью развития мыслительной деятельности, пространственного представления, воображения, смекалки и сообразительности.
Описание игры. Квадрат размером 7X7 см разрезан так, что получается 7 геометрических фигур: 2 разных по размеру квадрата, 2 маленьких треугольника, 2 – больших (в сравнении с маленькими) и 1 четырехугольник (параллелограмм). Дети называют эту фигуру-четырехугольник (рис. 69).
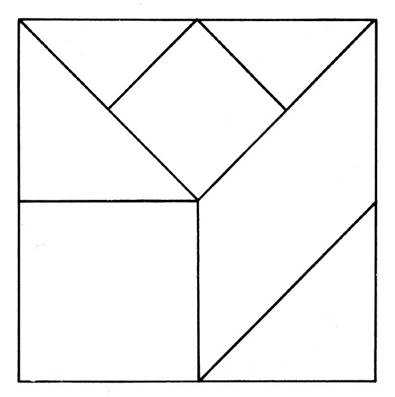
Рис. 69
Цель игры состоит в составлении из 7 геометрических фигур – частей игры, плоских изображений: силуэтов строений, предметов, животных.
Набор к игре представлен фигурами. Поэтому игра может быть использована воспитателем в обучении детей на занятиях с целью закрепления представлений о геометрических фигурах, способах видоизменения их путем составления новых геометрических, фигур из 2-3 имеющихся.
Приобщение детей к игре “Пифагор” начинается с ознакомления с набором фигур, которые потребуются для игры. Необходимо рассмотреть все геометрические фигуры, сосчитать, назвать их, сравнить по размеру, сгруппировать, отобрав все треугольники, четырехугольники. После этого предложить детям из набора фигур составить новые. Из 2 больших, а затем и маленьких треугольников составить квадрат, треугольник, четырехугольник. При этом вновь полученные фигуры равны по размеру имеющимся в наборе. Так, из 2 больших треугольников получается четырехугольник такого же размера, квадрат, равный по величине большому квадрату. Надо помочь детям заметить это сходство фигур, сравнить их по размеру не только на глаз, но и накладывая одну фигуру на другую. После этого можно составлять и более сложные геометрические фигуры – из 3, 4 частей. Например, из 2 маленьких треугольников и маленького квадрата составить прямоугольник; из параллелограмма, 2 больших треугольников и большого квадрата – прямоугольник.
Учитывая опыт, накопленный детьми в процессе освоения игры “Танграм”, воспитатель в ходе обучения новой игре использует ряд методических приемов, способствующих проявлению у детей интереса к ней, помогающих детям быстро освоить новую игру, проявляя при этом творчество и инициативу.
На занятии воспитатель предлагает детям образцы на выбор – расчлененные и контурные. Каждый из детей может выбрать образец по желанию и составить фигуру. Воспитатель указывает, что сложнее и интереснее составлять фигуру-силуэт по образцу без указания составных частей. При этом надо самостоятельно найти способ расположения частей (рис. 70).
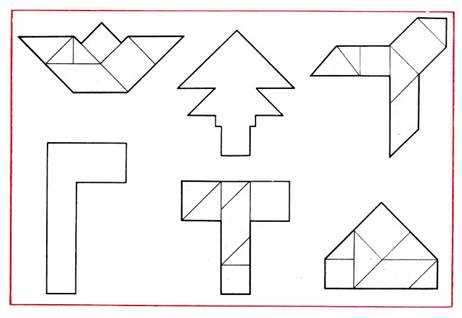
Рис. 70
В процессе руководства деятельностью детей по составлению фигур-силуэтов воспитатель использует разнообразные методы, помогающие поддерживать у ребят интерес, стимулирующие активную умственную деятельность.
1. В случае затруднения в составлении фигуры-силуэта по нерасчлененному образцу предложить ребенку образец с указанием места расположения 1-й и 2-й части игры из заданных 7 частей. Остальные ребенок располагает самостоятельно. Так, в силуэте грибка указывается расположение одного из больших треугольников. В домике – большого квадрата и треугольника (рис. 71). В данном случае решение задачи по составлению фигуры частично подсказывается ребенку взрослым. Это влияет на результативность составления фигур, процесс поиска способа их расположения становится короче и успешнее. Дети могут накладывать части игры прямо на образец.
Рис. 71
2. Взрослый, наблюдая за процессом составления ребенком фигуры, подтверждает правильное расположение отдельных частей игры.
Например, в ходе составления фигуры-силуэта треугольника в зависимости от хода поисков пространственного расположения частей воспитатель указывает на правильное определение места для треугольников или квадратов (рис. 72). В этом случае ребенок оперирует с меньшим количеством фигур, самостоятельно располагая их. Это также влияет на успешность выполнения задания. 3. Анализируя образец, воспитатель предлагает ребенку рассмотреть его, подумать, как расположены в нем части игры. Разрешить ему начертить на бумаге способ расположения частей или сделать разметку непосредственно на образце, на доске мелом. Использование приемов графического изображения, практических путей поиска способов расположения фигур делает анализ более точным. Дети быстро догадываются о способе расположения, дают свои варианты составления фигуры-силуэта.
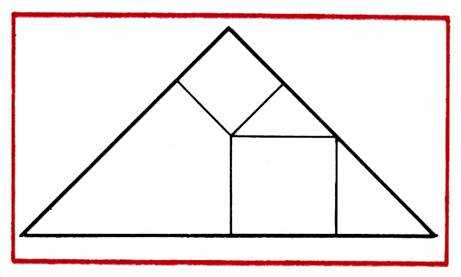
Рис. 72
4. После рассматривания образца, т. е. зрительно-мысленного анализа его, воспитатель просит ребенка рассказать о способе расположения фигур. При этом подчеркивает, чтобы свою догадку он проверял практически, каждый раз отбрасывая неверные пути решения. Такой анализ возможен при условии развитого анализирующего восприятия, гибкости и подвижности мысли, постоянной ориентировки на образ составляемой фигуры-силуэта. Настойчивый поиск новых способов сочетания фигур приводит ребенка к положительному результату.
5. Важна положительная оценка активности поисков способа расположения фигур, осуществляемых детьми практически, мысленно или в сочетании мысленных и практических действий: поощрять, одобрять проявление сообразительности, настойчивости, инициативы, стремление придумать и составить совершенно новую фигуру или частично видоизменить образец.
6. По мере освоения детьми способов составления фигур-силуэтов уместно предлагать им задания творческого характера, стимулировать проявления смекалки, находчивости. Вновь придуманные и составленные детьми фигуры-силуэты зарисовываются в индивидуальный альбом.
В ходе обучения на занятиях дети старшего дошкольного возраста (5-7 лет) быстро осваивают игры на воссоздание из специальных наборов фигур образных, сюжетных изображений, которые становятся для них одним из средств заполнения досуга.
Загадки, задачи-шутки, занимательные вопросы в обучении детей на занятиях
Из многообразия математических игр и развлечений детям в дошкольном возрасте доступны, интересны загадки и задачи-шутки.
В загадках математического содержания анализируется предмет с количественной, пространственной, временной точки зрения, подмечены простейшие математические отношения:
Два конца, два кольца, а посредине гвоздик. (Ножницы.) Четыре братца под одной крышей живут. (Стол.) Пять братцев в одном домике живут. (Варежка.) Стоит Антошка на одной ножке. Где солнце станет, туда он и глянет. (Подсолнух.) Ног нет, а хожу, рта нет, а скажу: когда спать, когда вставать. (Часы.) Сидит дед во сто шуб одет, кто его раздевает, тот слезы проливает. (Лук.) В красном домике сто братьев живут, все друг на друга похожи. (Арбуз.) Нас 7 братьев, летами все равные, а именем разные. Отгадай, кто мы. (Дни недели.) В году у дедушки 4 имени. Кто это? (Весна, лето, осень, зима.) 12 братьев друг за другом ходят, друг друга не находят. (Месяцы.) Кто в году 4 раза переодевается? (Земля.) Много рук, а нога одна. (Дерево.) Пять мальчиков, пять чуланчиков, разошлись мальчики в темные чуланчики. (Пальцы в перчатке.) Чтоб не мерзнуть, 5 ребят в печке вязаной сидят. (Рукавица.) Четыре ноги, а ходить не может. (Стол.)
Задачи-шутки – это занимательные игровые задачи с математическим смыслом. Для решения их надо в большей мере проявить находчивость, смекалку, понимание юмора, нежели познания в математике. Построение, содержание, вопрос в этих задачах необычны. Они лишь косвенно напоминают математическую задачу. Сущность задачи, т. е. основное, благодаря чему можно догадаться о решении, дать ответ, замаскировано внешними условиями, второстепенными (ниже приводятся задачи-шутки для детей 6-7 лет).
Ты да я да мы с тобой. Сколько нас всего? (Двое.)
Как с помощью только одной палочки образовать на столе треугольник? (Положить ее на угол стола.)
Сколько концов у палки? У двух палок? У двух с половиной? (6.)
На столе лежат в ряд 3 палочки. Как сделать среднюю крайней, не трогая, ее? (Переложить крайнюю.)
Как с помощью 2 палочек образовать на столе квадрат? (Положить их в угол стола.)
Тройка лошадей пробежала 5 км. По сколько километров пробежала каждая лошадь? (По 5 км.)
Если курица стоит на одной ноге, то она весит 2 кг. Сколько будет весить курица, если будет, стоять на 2 ногах? (2 кг.)
У трех братьев по одной сестре. Сколько всего детей в семье? (Четверо.)
Надо разделить 5 яблок между 5 девочками так, чтобы одно яблоко осталось в корзине. (Одна должна взять яблоко вместе с корзиной.)
Росло 4 березы. На каждой березе по 4 большие ветки. На каждой большой ветке по 4 маленькие. На каждой маленькой ветке – по 4 яблока. Сколько всего яблок? (Ни одного. На березах яблоки не растут.)
Может ли дождь идти 2 дня подряд? (Не может. Ночь разделяет дни.)
На столе лежало 4 яблока, одно из них разрезали пополам. Сколько яблок на столе? (4.)
Одного человека спросили, сколько у него детей. Ответ был такой; “У меня 6 сыновей, а у каждого есть родная сестра”. (7.)
У какой фигуры нет ни начала, ни конца? (У кольца.)
Как можно сорвать ветку, не спугнув на ней птички? (Нельзя, улетит.)
Назначение загадок и задач-шуток, занимательных вопросов состоит в приобщении детей к активной умственной деятельности, выработке умения выделять главные, существенные свойства, математические отношения, замаскированные внешними несущественными данными. Они могут быть использованы воспитателем в процессе разговоров, бесед, наблюдений с детьми за какими-либо явлениями, т. е. в том случае, когда создается необходимая для этого ситуация.
Изучение особенностей восприятия и понимания детьми старшего дошкольного возраста (5-7 лет) задач-шуток показало, что успех решения их зависит от того, насколько дети понимают шутку, т. е. умеют ли выделять ее в литературных произведениях, придумывать. В противном случае дети, как правило, подходят к решению задач-шуток с позиции арифметики, начинают производить действия с числами. Результат решения детьми задач-шуток зависит от их жизненного опыта, развития представлений об окружающих предметах и явлениях, умения видеть, наблюдать и замечать необычное в обычном. Понять ребенку смысл задачи-шутки поможет создание ситуации, обстановки, аналогичной той, о которой говорится в задаче, практическая проверка, зарисовка и доказательство правильности отгадки, домысла, указание на необходимость размышлять, догадываться, решая подобные задачи.
На занятиях по формированию у детей 6-7 лет элементарных математических представлений задачи-шутки могут быть предложены детям в самом начале занятия в качестве небольшой умственной гимнастики. Назначение их в данном случае состоит в создании у ребят положительного эмоционального состояния, интереса к предстоящей деятельности на занятии, активности. Воспитатель предлагает 1, 2 простые занимательные задачи, которые решаются детьми быстро, с небольшим обоснованием или без него.
Занимательные вопросы, задачи, загадки используются воспитателем и в ходе занятия по математике с целью уточнения, конкретизации знании у детей о числах, их назначении, геометрических формах, временных отношениях. При этом занимательный материал подбирается исходя из цели, занятия и уровня развития детей.
В процессе обучения детей решению арифметических задач применяется прием сравнения задачи-шутки, загадки математического содержания, с арифметической задачей. В ходе анализа задач, нахождения сходства и различия между ними уточняется понимание детьми структуры арифметической задачи, назначения чисел, необходимость выполнения арифметических действий с числами. Задачи-шутки подбираются педагогом согласно цели и содержанию предстоящего занятия, в зависимости от назначения приема сравнения, уровня сформированности у детей представлений об арифметических задачах, развития у них логического мышления.
На протяжений занятия, особенно при переходе от одной части занятия к другой, смене деятельности, занимательные задачи могут служить средством активизации, переключения внимания детей, интеллектуального отдыха.
Так, методически правильно подобранный и к месту использованный занимательный материал (загадки, задачи-шутки, занимательные вопросы) способствуют развитию логического мышления, наблюдательности, находчивости, быстроты реакции, интереса к усвоению “математических знаний и зависимостей, формированию поисковых подходов к решению любой задачи.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Плоские и объемные геометрические фигуры :: SYL.ru
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
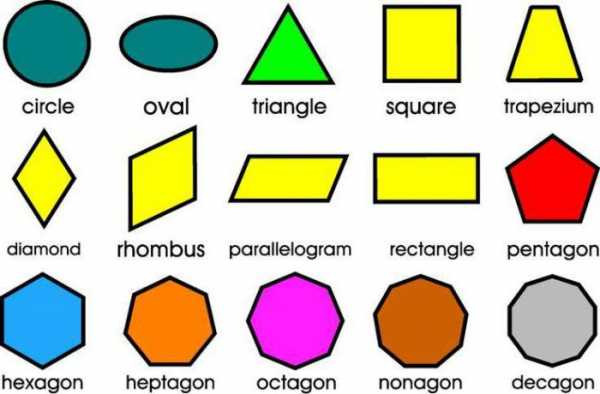
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка – это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка – это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Прямая
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Угол
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.
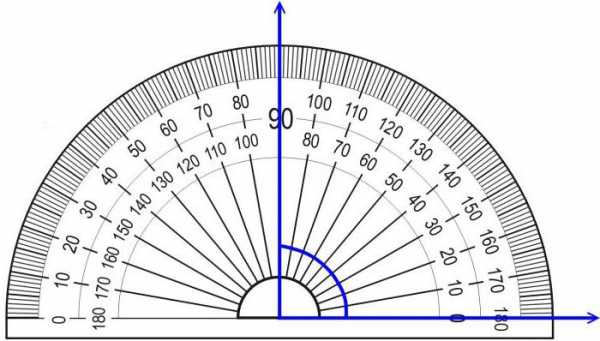
Угол – это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Рассмотрим еще одно первичное понятие. Плоскость – это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Четырехугольники
Параллелограмм – это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник – это параллелограмм, у которого все стороны соприкасаются под прямым углом.
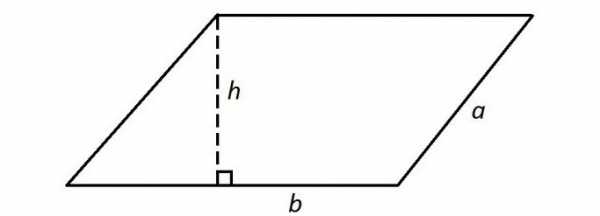
Квадрат – это четырехугольник с равными сторонами и углами.
Ромб – это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция – это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Треугольник
Это простая геометрическая фигура, которая очень часто встречается и изучается.
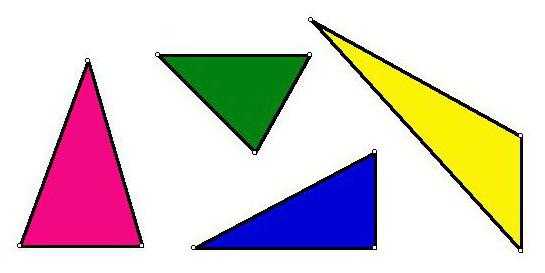
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Многоугольник
К этой категории стоит отнести геометрические фигуры разнообразных форм, ломаная линия контуров которых замыкается.
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
К этой категории причисляют следующие конструкции:
- куб;
- призма;
- сфера;
- конус;
- цилиндр;
- пирамида;
- тор.
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.

Объемные тела изучают не только в геометрии, но и в кристаллографии.
Любопытные факты
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
- Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
- В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
- Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
- В переводе с греческого языка термин «конус» обозначает сосновую шишку.
- Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
www.syl.ru
Игры с геометрическими фигурами. Геометрия. Аппликации из геометрических фигур для малышей.
Your ads will be inserted here by
Easy Plugin for AdSense.
Please go to the plugin admin page to
Paste your ad code OR
Suppress this ad slot.
ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ Более 150 вариантов аппликаций из геометрических фигур на нашем сайте в разделе пособия.

БОЛЕЕ 150 идей для АППЛИКАЦИИ ИЗ ГЕОМЕТРИЧЕСКИХ ФИГУР ТУТ!!!
 БОЛЕЕ 150 идей для АППЛИКАЦИИ ИЗ ГЕОМЕТРИЧЕСКИХ ФИГУР ТУТ!!! ЕЩЕ АППЛИКАЦИИ ИЗ ГЕОМЕТРИЧЕСКИХ ФИГУР ТУТ!!!
БОЛЕЕ 150 идей для АППЛИКАЦИИ ИЗ ГЕОМЕТРИЧЕСКИХ ФИГУР ТУТ!!! ЕЩЕ АППЛИКАЦИИ ИЗ ГЕОМЕТРИЧЕСКИХ ФИГУР ТУТ!!!
ВАРИАНТ 1. Геометрические фигуры. Сложи картинку
Представляем вам игру для детей дошкольного возраста, которая поможет малышам развить зрительное восприятие, произвольное внимание, память и образное мышление, а также закрепить название цветов и геометрических фигур.
Your ads will be inserted here by
Easy Plugin for AdSense.
Please go to the plugin admin page to
Paste your ad code OR
Suppress this ad slot.
Игра состоит из готовых карточек с картинками и материала из геометрических фигур. Распечатайте эти карточки. Геометрические фигуры вырежьте.
Как можно играть:
— Рассмотрите с малышом картинки, расскажите ребенку, из каких геометрических фигур они состоят, сколько их и какого цвета.
— Предложите ребенку выложить такие же картинки из набора геометрических фигур сначала методом наложения на карточку, затем рядом с картинкой, а затем по памяти.
— Покажите ребенку карточку и предложите запомнить, какие фигуры использованы в изображении.
— Предложите ребенку выложить из геометрических фигур любое изображение.
ВАРИАНТ 2. Геометрическая аппликация для детей с 1-3х лет
Рекомендации по проведению занятий
Заниматься аппликацией малышу, конечно же, удобней всего за своим детским столиком, в одежде без длинных рукавов или с подвернутыми рукавами. Занятия должны носить характер игры и продолжаться от 5 до 10 минут.
Предлагая малышу впервые сделать, скажем, неваляшку, покажите ему, какие фигурки нужно для этого взять и как их сложить. Оставьте своё изображение перед ребенком в качестве образца, пока он будет собирать свое.
Несмотря на то, что дети любят все новое, они любят и повторенья. Поэтому во время занятий не следует их избегать, даже если на первый взгляд ребенок усвоил, как складывается то или иное изображение. Можно, например, складывать домик на нескольких занятиях подряд или возвращаться к этому образу спустя какое-то время, внося какие-то усовершенствования — меняя его размер, форму, цвет, или добавляя детали.
Во время занятий комментируйте свои действия и действия ребенка для того, чтобы малыш усваивал названия фигур и названия цвета.
Если вы сделали неваляшку, медвежонка и т.д., то глаза и рот можно сделать из скатанных в комочек цветных ниток.
Перед началом занятия положите перед крохой все фигурки и дайте ему возможность познакомиться и поиграть с ними.
Занимаясь геометрическим конструированием, малыш должен двигаться от простого к сложному.
ПОДЕЛИТЬСЯ В СОЦ СЕТЯХ:
www.mam-club.org
Геометрические фигуры
Самоделки: 21
-
Белый и два цветных тора завязанных в узелок 🙂 + развертки.
Дмитрий ДА 31.03.2009
-
Большой выбор развёрток простых геометрических фигур.
Дмитрий ДА 28.05.2009
-
Тетраэдр (четырёхгранник) – многогранник с четырьмя треугольными гранями, в каждой из вершин которого сходятся по 3 грани.
Дмитрий ДА 28.10.2009
-
Огроменный выбор брендовых товаров для мам и детишек по очень низким ценам.
Только для своих! Тссссс 🙂
Robot
-
Октаэдр – один из пяти выпуклых правильных многогранников.
Дмитрий ДА 28.10.2009
-
Додекаэдр (двенадцатигранник) – правильный многогранник, составленный из двенадцати правильных пятиугольников.
Дмитрий ДА 28.10.2009
-
Икосаэдр – правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел.
Дмитрий ДА 28.10.2009
-
Что вы видите на картинке, параллелепипед? А если внимательно присмотреться 🙂
Дмитрий ДА 19.12.2009
-
Очень интересный видеоролик, с кубиком происходят аномалии или это вообще не куб? 😉
Дмитрий ДА 19.12.2009
-
Сделать флексагон, не трудно, нужна только бумага, ножницы и скотч.
Александр 23.02.2010
-
Готовые развёртки конуса разных размеров.
Дмитрий ДА 08.08.2010
-
Моя первая работа: оригами додекаэдр
Темирлан 13.12.2010
-
Оригами это круто!
Темирлан 02.01.2011
-
Такая коробочка может стать оригинальной упаковкой для ваших подарков.
Дмитрий ДА 01.02.2011
-
В этой статье я покажу вам свой многогранник, отдельные части его, и видео-инструкцию к нему…
Темирлан 16.10.2011
-
Здесь я покажу два вида дадекаэдра и выложил две видеоинструкции по ним…
Темирлан 16.10.2011
-
Думаю, эта статья банальна, но все же, может кому нибудь пригодится, к примеру для геометрии.
Темирлан 19.10.2011
-
Покажу свои икосаэдры, и выложил видео-инструкцию как их сделать.
Темирлан 19.10.2011
-
Это очень простая композиция из геометрических фигур.
ШкоРавоян 16.10.2015
-
Шикарная идея для учителей для создания с детьми на уроках труда, геометрии или черчения в школе! Для изготовления 30 модулей додекаэдра вам понадобится бумага 8*8 см.
Дмитрий ДА 14.10.2017
-
Можно из бумаги делать не только кубики, а ещё строить из нескольких кубов дома, мосты, роботов – всё, на что способна ваша фантазия.
Дмитрий ДА 20.11.2017
-
Сделать шар из бумаги сложно, но сделать шар в технике оригами очень просто. Просто возьмите цветную бумагу и следуйте обучающему видеоуроку.
Дмитрий ДА 20.11.2017
modelmen.ru
Геометрические фигуры, или С чего начинается геометрия
Многие люди ошибочно полагают, что впервые они встречают геометрические фигуры в средней школе. Там они изучают их названия, свойства и формулы. Но на самом деле с самого детства любой предмет, который видит ребенок, ощущает, чувствует его запах или взаимодействует с ним любым другим образом, представляет собой именно геометрическую фигуру. Кушетка, на которой лежит только что родившая женщина – прямоугольник, лампа, что дает акушерам свет – круглая фигура, форточки в окне – квадраты. Этот список можно продолжать бесконечно.
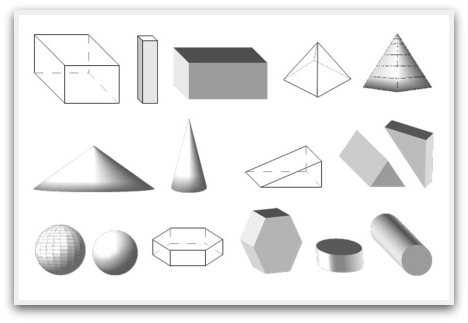
Геометрические фигуры, непосредственно как элемент науки, впервые встречается школьникам в средних классах. Можно даже сказать, что геометрия начинается именно с них. Однако, как уже говорилось выше, первые взаимодействия с ними происходят задолго до этого. Возьмем, к примеру, точку. Она представляет собой самую маленькую фигуру в геометрии. Кроме того, ее принято считать основой всех остальных (как атомы в химии). Все треугольники, квадраты и прочие фигуры на любом чертеже состоят из множества точек. Они обладают определенными свойствами, каждое из которых присуще только одной фигуре (ни одна другая не может быть ими наделена).
Можно предположить, что все геометрические фигуры состоят непосредственно из линий, но чем является она? Это и есть множество точек, расположенных в ряд. Их можно продолжать бесконечно, поскольку прямая линия не заканчивается. Если же она ограничена с двух сторон, то ее принято называть отрезком. Если имеется только одно ограничение, то перед вами луч. Следовательно, все плоские фигуры в геометрии состоят из отрезков, так как составляющие имеют и конец, и начало. Стоит отметить, что прямая, которая была разделена точкой, является двумя лучами, направленными в противоположные друг другу стороны.
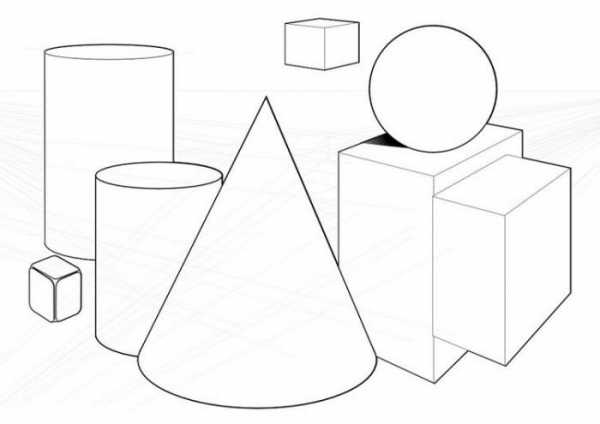
Не только из плоских элементов состоит геометрия, имеются также и объемные геометрические фигуры. К их изучению в школе приступают позже, ближе к окончанию учебы, но сталкивается с ними человек, опять же, гораздо раньше. К примеру, когда ребенок берет в руки кубик, то держит в ладонях куб. Или, если он смотрит на комод, то перед ним прямоугольный параллелепипед. Все объемные фигуры состоят из плоскостей (то есть, она является неопределенным первичным понятием, как и прямая). Тот же самый параллелепипед состоит из шести таких элементов. Наглядно ознакомиться с плоскостью можно, посмотрев на поверхность любого стола. Но это будет только ее часть, поскольку имеются ограничения. Непосредственно плоскость такая же бесконечная, как и прямая линия.
Таким образом, нет сферы, где бы не встречались геометрические фигуры. Названия их различны, они определяют свойства и особенности. К примеру, формула площади треугольника не подойдет для прямоугольника или квадрата.
Желательно приобщать ребенка к геометрическим фигурам еще в дошкольном возрасте. Можно сделать их своими руками, а затем выкладывать ими различные рисунки на бумаге (если это плоские элементы). Однако не стоит отказываться и от объемных фигур. В интернете можно найти множество дидактических игр, связанных с этим. Но нельзя откладывать знакомство с ними, ведь все, что мы видим – геометрические фигуры. Даже человек состоит из них!
fb.ru