10 класс деление с остатком – Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике – Арифметика
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике – Арифметика
Делимость натуральных чисел. Деление с остатком
Определение 1. Говорят, что натуральное число a делится на натуральное число b , если существует такое натуральное число c, что выполняется равенство
a = bc .
В противном случае говорят, что число a не делится начисло b.
Если число a больше, чем число b, и не делится на число b, то число a можно разделить на число b с остатком.
Определение 2. Деление числа a на число b с остатком означает, что найдутся такие натуральные числа c и r , что выполняются соотношения
a = bc + r, r < b .
Число b называется делителем, число c – частным, а число r – остатком от деления a на b .
Еще раз особо подчеркнем, что остаток r всегда меньше, чем делитель b .
Например, число 204 не делится на число 5 , но, разделив число 204 на 5 с остатком, получаем:
Таким образом, частное от деления равно 40 , а остаток равен 4 .
Определение 3. Числа, делящиеся на 2 , называют четными, а числа, которые не делятся на 2 , называют нечетными.
Признаки делимости
Для того, чтобы быстро выяснить, делится ли одно натуральное число на другое, существуют признаки делимости.
| Признак делимости на | Формулировка | Пример |
| 2 | Число должно оканчиваться четной цифрой: 0 , 2 , 4 , 6 , 8 | 1258 |
| 3 | Сумма цифр числа должна делиться на 3 | 745 , (7 + 4 + 5 = 15) |
| 4 | Число, образованное двумя последними цифрами, должно делиться на 4 | 7924 |
| 5 | Число должно оканчиваться цифрой 0 или 5 | 835 |
| 6 | Число должно делиться на 2 и на 3 | 234 , (2 + 3 + 4 = 9) |
| 7 | На 7 должно делиться число, полученное вычитанием удвоенной последней цифры из исходного числа с отброшенной последней цифрой | 3626 , (362 – 12 = 350) |
| 8 | Число, образованное тремя последними цифрами, должно делиться на 8 | 63024 |
| 9 | Сумма цифр должна делиться на 9 | 2574 , (2 + 5 + 7 + 4 = 18) |
| 10 | Число должно оканчиваться 0 | 1690 |
| 11 | Сумма цифр, стоящих на четных местах, либо равна сумме цифр, стоящих на нечетных местах, либо отличается от нее на число, делящееся на 11 | 1408 , (4 + 8 = 12 ; 1 + 0 = 1 ; 12 – 1 = 11) |
| 13 | На 13 должно делиться число, полученное добавлением учетверенной последней цифры к исходному числу с отброшенной последней цифрой | 299 , (29 + 36 = 65) |
| 25 | Число должно оканчиваться на 00 , 25 , 50 или 75 | 7975 |
| 50 | Число должно оканчиваться на 00 или 50 | 2957450 |
| 100 | Число должно оканчиваться на 00 | 102300 |
| 1000 | Число должно оканчиваться на 000 | 3217000 |
| Признак делимости на 2 |
Формулировка признака: Число должно оканчиваться четной цифрой: Пример: 1258 |
| Признак делимости на 3 |
Формулировка признака: Сумма цифр числа должна делиться на 3 Пример: 745 , |
| Признак делимости на 4 |
Формулировка признака: Число, образованное двумя последними цифрами, должно делиться на 4 Пример: 7924 |
| Признак делимости на 5 |
Формулировка признака: Число должно оканчиваться цифрой 0 или 5 Пример: 835 |
| Признак делимости на 6 |
Формулировка признака: Число должно делиться на 2 и на 3 Пример: 234 , |
| Признак делимости на 7 |
Формулировка признака: На 7 должно делиться число, полученное вычитанием удвоенной последней цифры из исходного числа с отброшенной последней цифрой Пример: 3626 , |
| Признак делимости на 8 |
Формулировка признака: Число, образованное тремя последними цифрами, должно делиться на 8 Пример: 63024 |
| Признак делимости на 9 |
Формулировка признака: Сумма цифр должна делиться на 9 Пример: 2574 , |
| Признак делимости на 10 |
Формулировка признака: Число должно оканчиваться 0 Пример: 1690 |
| Признак делимости на 11 |
Формулировка признака: Сумма цифр, стоящих на четных местах, либо равна сумме цифр, стоящих на нечетных местах, либо отличается от нее на число, делящееся на 11 Пример: 1408 , |
| Признак делимости на 13 |
Формулировка признака: На 13 должно делиться число, полученное добавлением учетверенной последней цифры к исходному числу с отброшенной последней цифрой Пример: 299 , |
| Признак делимости на 25 |
Формулировка признака: Число должно оканчиваться на 00 , 25 , 50 или 75 Пример: 7975 |
| Признак делимости на 50 |
Формулировка признака: Число должно оканчиваться на 00 или 50 Пример: 2957450 |
| Признак делимости на 100 |
Формулировка признака: Число должно оканчиваться на 00 Пример: 102300 |
| Признак делимости на 1000 |
Формулировка признака: Число должно оканчиваться на 000 Пример: 3217000 |
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Деление с остатком. Формула деления с остатком и проверка. Примеры
Деление с остатком.
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Решение:
Поделим число 16 на 5 столбиком получим:
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения.
16=5⋅3+1
a=b⋅c+d
a
b – делитель,
c – неполное частное,
d – остаток.
Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.
Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.
Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.
Остаток может быть равен делителю?
Ответ: нет.
Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8
Решение:
а) Делим столбиком:
258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6<7.
Подставим в формулу и проверим правильно ли мы решили пример:
7⋅36+6=252+6=258
б) Делим столбиком: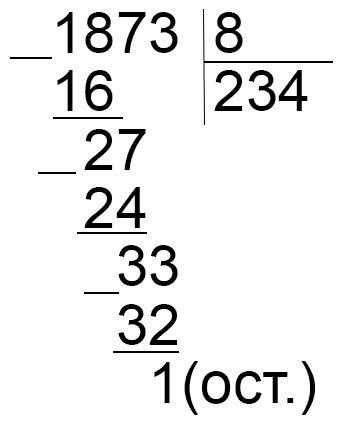
1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1<8.
Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873
Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?
Ответ:
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.
Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.
Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)
Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
Ответ: а=22
б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107
Задача:
Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?
Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400
Ответ: 30 кусков получиться и 10 см. проволоки останется.
tutomath.ru
Деление с остатком | Математика
Если одно натуральное число не делится на другое нацело, можно выполнить деление с остатком.
Как и при делении нацело, числа, которые делим, называются делимое и делитель.
Результат деления называется неполным частным.
Число, которое остаётся от делимого в результате деления (это число меньше делителя), называется остаток.
Чтобы выполнить проверку, надо:
- Неполное частное умножить на делитель.
- К полученному произведению прибавить остаток.
- В результате должно получиться делимое.
Рассмотрим конкретные примеры деления с остатком.
Примеры.
Выполнить деление чисел с остатком и сделать проверку:
1) 29 : 8;
2) 613 : 6;
3) 279 : 10;
4) 784 : 23;
5) 4057 : 35;
6) 8591 : 62;
7) 52779 : 2524;
8) 15 : 79.
Решение: 1)
29 : 8 = 3 (остаток 5).
Проверка:
3 · 8 + 5 = 24 + 5 = 29.
2)
513 : 6 = 85 (остаток 3).
513 — делимое, 6 — делитель, 85 — неполное частное, 3 — остаток.
Проверка:
85 · 6 + 3 = 510 + 3 = 513.
3)
279 : 10 = 27 (остаток 9).
279 — делимое, 10 — делитель, 27 — неполное частное, 9 — остаток.
Проверка:
27 · 10 + 9 = 270 + 9 = 279.
4)
784 : 23 = 34 (остаток 2).
784 — делимое, 23 — делитель, 34 — неполное частное, 2 — остаток.
Проверка:
34 · 23 + 2 = 782 + 2 = 784.
5)
4057 : 35 = 115 (остаток 32).
4057 — делимое, 35 — делитель, 115 — неполное частное, 32 — остаток.
Проверка:
115 · 35 + 32 = 4025 + 32 = 4057.
6)
8591 : 62 = 138 (остаток 35).
8591 — делимое, 62 — делитель, 138 — неполное частное, 35 — остаток.
Проверка:
138 · 62 + 35 = 8556 + 35 = 8591.
7)
52779 : 2524 = 20 (остаток 2299).
52779 — делимое, 2524 — делитель, 20 — неполное частное, 35 — 2299.
Проверка:
20 · 2524 + 2299 = 50480 + 2299= 52779.
8) 15 : 79 = 0 (остаток 15).
15 — делимое, 79 — делитель, 0 — неполное частное, 15 — остаток.
( Если делимое меньше делителя, неполное частное всегда равно нулю, а остаток — делимому).
www.for6cl.uznateshe.ru
Деление. Деление с остатком
Математика, 5 Класcы- 1 класс
- 2 класс
- 3 класс
- 4 класс
- 5 класс
- 6 класс
- 7 класс
- 8 класс
- 9 класс
- 10 класс
- 11 класс
- ЕГЭ
- Алгебра
- Геометрия
- Математика
- Информатика
- Обществознание
- ОБЖ
web-dev01.interneturok.ru
Урок математики на тему “Деление с остатком”
Разделы: Начальная школа
Цели урока: |
1. рассмотреть случаи деления с остатком; |
2. закреплять изученные вычислительные приемы внетабличного умножения и деления; |
|
3. развивать память, логическое мышление, речь, познавательные интересы, творческие способности, положительную учебную мотивацию. |
Ход урока
- Организационный момент
Игра “Цепочка”
Решите задачу:
II. Актуализация знаний.
Математический диктант “Торопись, да не ошибись”.
1. Уменьши 20 в 4 раза. |
|
2. Найди частное 18 и 6 |
|
3. Делимое 32, делитель 8. Найдите |
значение частного |
4. Напишите самое маленькое двузначное |
число. |
| 5. Произведение чисел 35, первый множитель? | множитель 7. Чему равен другой |
6 Уменьши 36 в 9 раз. |
|
7. Найди частное 48 и 6. |
|
8. Делимое 24, делитель. Найдите значение |
частного. |
9. Самое маленькое однозначное число. |
|
10. Произведение чисел 72, первый множитель? |
множитель 7. Чему равен другой |
11. 12 л сока разлили в 2-ух литровые Сколько банок получилось? |
банки. |
– Выполните действия и найдите значения выражений.
( Проверка. Оценивание своей работы на полях.)
42 : 3 36 : 2
17 * 4 18 * 3
Физминутка
Медвежата в роще жили, головой они кружили
Медвежата мед искали, низко – низко приседали
Вот так, вот так, низко – низко приседали.
А потом они плясали, выше ноги поднимали.
Вот так, вот так, выше ноги поднимали.
III. Постановка учебной задачи.
IV. “Открытие” детьми нового знания.
– Ребята, вам знакома считалка: Мы делили апельсин, много нас, а он один”.
– Досчитайте считалку до конца и ответьте на вопрос – почему рассердился волк?
Эта долька – для ежа, стрижа, для утят, для котят, бобра. А для волка – кожура!
Он сердит на нас. Беда! Разбегайтесь кто куда!
– На сколько долек разделили апельсин? (На 5 долек.)
Как догадались?
По сколько долек получил каждый?
: 5 = 1 5 : 5 = 1
– Вспомните, как называются числа при делении.
– Назовите делимое, делитель, частное.
-У меня в коробке 19 конфет.
Как разделить 19 конфет между 9 девочками?
– Мальчики, подскажите, как мне разделить так, чтобы никого не обидеть?
– Можем ли мы выполнить это задание?
– Какие есть мнения?
| -Сначала всем раздать по 1 дольке, потом
еще по 1. В результате оказывается, что всем досталось по 2 конфетки и 1 осталась. |
– Ребята, в некоторых случаях деление поровну выполнить невозможно. В этом случае раздается лишь часть предметов, а часть остается.
– Как назовем то, что осталось? (Остаток.)
Как называется такое деление?
Такое деление называют деление с остатком.
– Какова будет тема нашего урока? (На доске тема.)
V. Первичное закрепление с проговариванием в громкой речи.
– Работаем в тетради. Давайте изобразим деление с остатком на графической схеме.
– Сколько конфет было сначала?
– Что нужно сделать на схеме? (Образовать группы по 9 конфет. Каждый получит столько конфет, сколько образовалось групп.)
– А может ли долек остаться меньше, чем 1? (Нет, иначе бы деление было бы без остатка.)
– Чтобы разделить число с остатком на …, надо узнать, сколько раз по … в нем содержится и сколько остается.
– Что означает выражения: 9* 2 – число долек, которое раздали,
9 * 2 + 1 – число всех долек, т.е. 19 = 9 * 2 + 1.
– Так равенство показывает, что при делении 19 на 9 получается частное 2 и остаток 1.
– Соединим стрелками названия компонентов и числа.
Другими словами: делимое равно произведению делителя и частного плюс остаток.
– Есть и другая запись деления с остатком: 19 : 9 = 2 (ост. 1).
Эта запись используется при решении примеров на деление.
Коллективно составляется памятка для деления с остатком.
Памятка.
- Найди самое большое число до делимого, кратное делителю.
- Разделить это число на делитель. Получаем частное.
- Вычтем из делимого самое большое число, получаем остаток
VI. Обучающая самостоятельная работа с самопроверкой.
| 1 ряд 1 ряд 9 : 2 = 2 ряд 11 : 4 = 3 ряд 8 : 3= |
Задание: найдите частное и остаток, используя рисунок.
– Сравните делители и остатки в каждом примере. Что заметили?
– Какие остатки могли получиться при делении на 5?
– Всегда ли удобен способ деления с остатком изображать на графических моделях? (Нет, не всегда.)
– Для больших чисел графические модели строить неудобно. На следующем уроке мы исследуем способ деления с остатком посредством вычислений.
Коллективно составляется памятка для деления с остатком.
VII. Повторение и закрепление.
Найди соответствие рисунка и записи:
VIII. Самостоятельная работа.
IX. Рефлексия.
– Ребята, какую тему мы сегодня исследовали? (Деление с остатком.)
– Что вы узнали об остатке? (Остаток меньше делителя)
X. Творческое домашнее задание.
– Придумайте 5 примеров на деление с остатком.
– Урок закончился. Всем спасибо за работу.
См. презентацию.
19.04.2012
xn--i1abbnckbmcl9fb.xn--p1ai
примеры в столбик для 4 класса, алгоритм, как научить ребенка разделять в 3 классе
Как научить ребенка делению? Самый простой метод – выучить деление столбиком. Это гораздо проще, чем проводить вычисления в уме, помогает не запутаться, не «потерять» цифры и выработать мысленную схему, которая в дальнейшем будет срабатывать автоматически.
…
Вконтакте
Google+
Мой мир
Как проводится
Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.
Приведем простой пример того, как делить с остатком:
Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:
5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.
Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета и помогает не потерять числа.
Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.
Основные этапы:
- Правильная запись. Делимое (17) – располагается по левую сторону. Правее от делимого пишут делитель (5). Между ними проводят вертикальную черту (обозначает знак деления), а затем, от этой черты проводят горизонтальную, подчеркивая делитель. Основные черты обозначена оранжевым цветом.
- Поиск целого. Далее, проводят первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное.
- Определение остатка. 3*5=15. 15 записываем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.
Обратите внимание! При делении таким образом, остаток всегда должен быть меньше делителя.
Когда делитель больше делимого
Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача: необходимо не разделить, а найти остаток! Дробная часть им не является! Как решить такую задачу?
Обратите внимание! Существует правило для случаев, когда делитель больше делимого: неполное частное равно 0, остаток равен делимому.
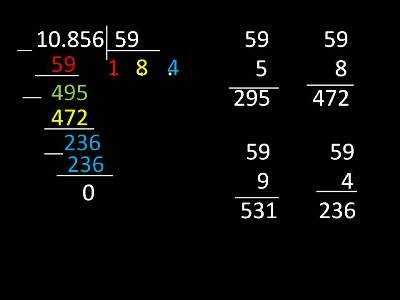Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? Ноль, потому что 6 больше 5.
По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.
Деление начинают изучать в третьем классе школы. К этому времени ученики уже должны освоить таблицу умножения, что позволяет им совершать деление двузначных чисел на однозначные.
Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?
Примеры:
14:3
Находим неполное частное: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.
Остаток: 3*4=12, 14-12=2.
Ответ: неполное частное 4, осталось 2.
Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу.
Еще одна задача: 3 пирожка надо разделить на двоих.
4 пирожка разделить на двоих.
5 пирожков разделить на двоих.
Это интересно! Изучение точного предмета: натуральные числа — это какие числа, примеры и свойства
Работа с многозначными числами
Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами более 100.
Данное действие удобнее всего выполнять в столбик, так как неполное частное также будет двузначным числом (в большинстве случаев), а алгоритм столбика облегчает вычисления и делает их более наглядными.
Разделим многозначные числа на двузначные: 386:25
Данный пример отличается от предыдущих количеством уровней расчета, хотя вычисления проводят по тому же принципу, что и ранее. Рассмотрим подробнее:
386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить остаток.
Первый уровень
Делитель – двузначное число. Делимое – трехзначное. Выделяем у делимого первые две левые цифры – это 38. Сравниваем их с делителем. 38 больше 25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?
25*1=25, 25*2=50. 50 больше 38, возвращаемся на один шаг назад.
Ответ – 1. Записываем единицу в зону не полного частного.
Далее:
38-25=13. Записываем число 13 под чертой.
Второй уровень
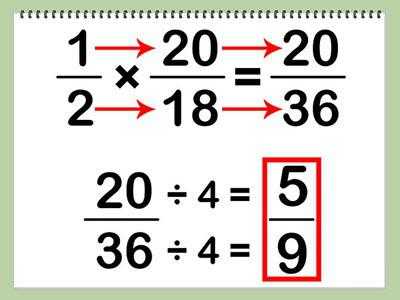13 больше 25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136 больше 25? Да – значит можно его вычесть. Сколько раз 25 поместиться в 136?
25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150 больше 136 – возвращаемся назад на один шаг. Записываем цифру 5 в зону неполного частного, справа от единицы.
Вычисляем остаток:
136-125=11. Записываем под чертой. 11 больше 25? Нет – деление провести нельзя. У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.
Ответ: неполное частное равно 15, в остатке 11.
А если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого? В таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в вычислениях сразу.
Приведем примеры на деление с трех- и четырехзначными числами:
386:75
75 – двузначное число. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38 больше 75? Нет – деление провести нельзя. Берем все 3 цифры. 386 больше 75? Да – деление провести можно. Проводим вычисления.
75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450 больше 386 – возвращаемся на шаг назад. Записываем 5 в зону неполного частного.
Находим остаток: 386-375=11. 11 больше 75? Нет. Еще остались цифры у делимого? Нет. Вычисления закончены.
Ответ: неполное частное = 5, в остатке — 11.
119:35
Выполняем проверку: 11 больше 35? Нет – деление провести нельзя. Подставляем третье число – 119 больше 35? Да – действие провести можем.
35*1=35, 35*2=70, 35*3=105, 35*4=140. 140 больше 119 – возвращаемся на один шаг назад. Записываем 3 в зону неполного остатка.
Находим остаток: 119-105=14. 14 больше 35? Нет. Остались цифры у делимого? Нет. Вычисления закончены.
Ответ: неполное частное = 3, осталось — 14.
1195:99
Проверяем: 11 больше 99? Нет – подставляем еще одну цифру. 119 больше 99? Да – начинаем вычисления.
11<99, 119>99.
99*1=99, 99*2=198 – перебор. Записываем 1 в неполное частное.
Находим остаток: 119-99=20. 20<99. Опускаем 5. 205>99. Вычисляем.
99*1=99, 99*2=198, 99*3=297. Перебор. Записываем 2 в неполное частное.
Находим остаток: 205-198=7.
Ответ: неполное частное = 12, остаток — 7.
Деление с остатком — примеры
Учимся делить в столбик с остатком
Вывод
Таким образом проводятся вычисления. Если быть внимательным и выполнять правила, то ничего сложного здесь не будет. Каждый школьник может научиться считать столбиком, потому что это быстро и удобно.
Это интересно! Легкие правила округления чисел после запятой
uchim.guru
Деление с остатком на 10, 100, 1 000
Привет, ребята!
Сегодня я хочу вам рассказать, как делятся числа на десять, сто, тысячу. Но прежде чем приступить к делению, давайте вспомним несколько примеров из таблицы умножения. Умножим на десять все однозначные числа.
А теперь попробуем составить обратные примеры на деление, в которых делителем будет число десять.
Как видите, на десять делятся те числа, которые оканчиваются нулём, то есть круглые числа. А как вы думаете, можно ли на десять разделить число с двумя нулями в конце? Например, число триста? Ну конечно же можно. Хоть два нуля, хоть три, четыре. Просто в частное записывается то же число, что стояло в делимом, но без последней цифры, то есть в нём нулей становится на один меньше по сравнению с делимым.
300 : 10 = 30
Но иногда на десять надо разделить некруглое число, без нулей в конце. Как это сделать?
Допустим, на десять надо разделить число шестьдесят три. Оно некруглое, значит, на десять без остатка его разделить не получится. Разделить число на десять – это значит узнать, сколько раз по десять в нём содержится.
Давайте на минутку вернёмся во второй класс и вспомним, как мы составляли двузначные числа из счётных палочек. Десять – это один десяток.
В числе шестьдесят три шесть таких десятков и три единицы.
То есть, разделив шестьдесят три на десять, мы получаем частное шесть, а три единицы – это остаток.
А всё ли я вычислила правильно? Надо выполнить проверку.
Проверка: 1) 3 ˂ 10
2) 6 · 10 + 3 = 63
Остаток три меньше делителя. Умножаю частное на делитель и прибавляю остаток. Всё верно. Ответ – шестьдесят три.
А если, к примеру, надо разделить число девяносто восемь на десять. В этом числе девять десятков, то есть, в нём по десять содержится девять раз. Да ещё восемь единиц. Ответ: девять и остаток восемь.
98 : 10 = 9 (ост. 8)
Проверяю:
Проверка: 1) 8 ˂ 10
2) 9 · 10 + 8 = 98
То есть, при делении любого числа на десять, ответом будет то же делимое, но без цифры, которая стояла в разряде единиц. Все единицы перейдут в остаток.
54 : 10 = 5 (ост. 4)
Проверка: 1) 4 ˂ 10
2) 5 · 10 + 4 = 54
Значит, при делении на десять мы определяем, сколько всего десятков в этом числе. Это и будет частным. А все единицы делимого переходят в остаток.
Без остатка на десять делятся только числа, оканчивающиеся нулями.
Ну а если надо какое-нибудь число разделить не на десять, а на сто? В этом случае мы определяем, сколько всего сотен в делимом. Такое число и будет частным.
Надо, например, разделить пятьсот восемьдесят шесть на сто. В делимом пять сотен. Пять и будет частным, а всё, что меньше сотни, то есть десятки и единицы, являются остатком.
А если мы четыре тысячи девятьсот двенадцать разделим на сто. В делимом всего сорок девять сотен. Значит, частное равно сорока девяти, а двенадцать – это остаток.
4 912 : 100 = 49 (ост. 12)
Проверка: 1) 12 ˂ 100
2) 49 · 100 + 12 = 4 912
Без остатка на сто делятся только те числа, у которых в конце не менее двух нулей.
8 700 : 100 = 87
365 000 : 100 = 3 650
Я думаю, вы уже догадались, что если мы делим число на тысячу, то частное равно количеству тысяч в делимом, а всё, что меньше тысячи, то есть сотни, десятки и единицы являются остатком.
139 054 : 1 000 = 139 (ост. 54)
Проверка: 1) 54 ˂ 1 000
2) 139 · 1 000 + 54 = 139 054
Без остатка на тысячу делятся только те числа, у которых в конце не менее трёх нулей.
4 000 : 1 000 = 4
120 000 : 1 000 = 120
Вот и подходит к концу наша встреча. Я надеюсь, вы поняли, что:
* При делении некруглого числа на десять, в частное записываем делимое без единиц. Единицы переходят в остаток. Разрядов в частном по сравнению с делимым становится на один меньше.
* При делении числа на сто, в частное записываем делимое без десятков и единиц. Они переходят в остаток. Разрядов в частном по сравнению с делимым становится на два меньше.
* При делении числа на тысячу, в частное записываем делимое без сотен, десятков и единиц. Они переходят в остаток. Разрядов в частном по сравнению с делимым становится на три меньше.
А я прощаюсь с вами, друзья! До встречи!
videouroki.net