Знаки по математике для 1 класса: Урок математики в 1 классе на тему “Знаки плюс, минус равно”
Знаки плюс, минус, равно. план-конспект урока по математике (1 класс) на тему
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Математические знаки Плюс Минус Равно
В стране Математики живут не только цифры и числа, но и разные математические знаки. Сегодня вы с Лисёнком познакомитесь с ними.
Посмотрите на рисунок. Сколько белочек на рисунке?
2 белочки прибежали. А теперь сколько белочек? На 2 белочки больше.
В математике это действие называется сложением и ставится знак « + ». Вот как это выглядит:
Знак «плюс»
4 белочки + 2 белочки
Я – нужный знак, и я горжусь, Что для сложения гожусь. Я добрый знак соединенья И в том мое предназначенье. Всем людям честно помогаю! Я СКЛАДЫВАЮ и ПРИБАВЛЯЮ!
Но в математике есть ещё один нужный знак. Давайте посмотрим, какой.
П осчитаем, сколько на рисунке белочек?
Но, 2 белочки убежали.
Сколько белочек осталось?
В математике это действие называется вычитание и обозначается знаком « – »
А теперь запишем это действие цифрами
Я – тоже очень нужный знак, Но, только не пойму никак Почему люблю всё отнимать, отнимать и вычитать. Все, что хочу, я забираю! Я ВЫЧИТАЮ! ВЫЧИТАЮ
Скажите, дети, вы знаете, кто это так поёт? Правильно, это Я Математический знак «Минус», а выгляжу я так:
Вы с Лисёнком уже узнали, что в математике самые главные знаки и. Но, есть ещё один очень важный знак. Давайте посмотрим, что это за знак.
Давайте снова вспомним наших белочек. Мы сначала прибавили, но не записали, сколько их всего.
Чтобы записать, сколько всего белочек, нам на выручку придёт ещё один важный знак. Называется он «равно» и выглядит вот так:
Я самый дружный в мире знак, я всех всегда равняю, я всех всегда мирю, ни про кого не забываю, и всех люблю.
Так как вы с Лисёнком уже познакомились с важными знаками, то давайте посмотрим, как будут выглядеть наши примеры.
Спасибо за внимание
Три игривых рыжих кошки Сели рядом у окошка. Тут одна к ним прибежала. Сколько вместе кошек стало?
Пять весёлых медвежат За малиной в лес спешат А один вдруг испугался Дома на печи остался. Сколько смелых медвежат За малиною спешат?
Ёжик стал грибы искать под берёзой было пять под осиной три нашёл, И домой скорей пошёл. Сколько же грибочков, У Ёжика в корзинке?
Сегодня вы с Лисёнком узнали самые важные математические знаки, давайте вспомним их
По теме: методические разработки, презентации и конспекты
Знакомство со знаками ПЛЮС и МИНУС 1 этап
Организованная образовательная деятельность по математике с использованием авторских пособий и рифмовок….
Знакомство со знаками ПЛЮС и МИНУС. 2 этап
Организованная образовательная деятельность по математике с использованием авторских пособий и рифмовок…
В этой статье рассматривается вопрос о “силе родительского слова”. Приводятся примеры самых распространенных фраз – разрушителей.
…
Открытый урок по математике в 1 классе.
Тема урока: знаки «+», «-» и «=».
Цель: познакомить с названием и значением знаков «+», «-» и «=».
Планируемые результаты: учащиеся научатся воспроизводить последовательность чисел от 1 до 10, как в прямом, так и в обратно порядке, начиная с любого числа; обозначать действия знаками; работать с учебными моделями; выполнять мыслительные операции анализа и синтеза и делать умозаключение; оценивать себя, границы своего знания и не знания; работать в паре и оценивать товарища.Оборудование: картинки зверей, демонстрационный материал, компьютор.
Прозвенел опять звонок. Все помчались на урок. Вот вошел учитель в класс, он всему научит нас. Вот и начался урок. Ушки держим на макушке. Сели все – и все молчок.
1.Актуализация знаний.
а) логическая разминка.
Сколько хвостов у трех китов?
Сколько ушей и двух мышей?
У кого больше лап, у утки или у утенка?
Сколько зверей встретил колобок?
Какую песенку пел колобок?
Сколько персонажей в сказке теремок? (6)
б) устный счет.
Сосчитайте:
От 1 до 10 и обратно по цепочке;
От 3 до 5;
От 9 до 5.
Какое число следует за числом 7, 5, 2
Какое число стоит перед числом 8, 6, 4
Назовите числа больше 2, но меньше 5
Назовите числа меньше 9, но больше 7
в) практическая работа.
Работа с полотном.
Положите два красных кружочка на верхнюю линию.
Сколько треугольников нужно положить на вторую линейку, чтобы их было на один меньше, чем кружков? (1)
Положите квадратов на один больше, чем треугольников.
Сколько квадратов положили? (3)
2. Самоопределение к деятельности.
Положите два красных кружка, рядом положите красный квадрат. Сколько красных фигур на полотне?
Какими словами можно заменить слово положили? (прибавили, добавили)
Чтобы записать это выражение в математике используются цифры и математический знак «+».
Посмотрите на этот знак.
На доске запись: 2+1
Плюс – знак добрый, он всем дает, прибавляет и становится больше.
Сейчас я прочитаю вам стихотворение про этот знак.
И этим я горжусь.
Я для сложения гожусь
Я – добрый знак соединенья
И в том мое предназначение.
А теперь от трех красных фигур уберите один квадрат. Сколько фигур осталось? (2)
Слово убрали, тоже можно заменить знаком.
Этот математический знак – минус.
На доске запись: 3-1
Этот знак у всех отбирает, отнимает и становится меньше.
Послушайте стихотворение
Я – минус.
Тоже добрый знак.
Ведь не со зла я отнимаю
Я свою роль лишь выполняю.
А чтобы записать слово получится, используют знак – ровно.(=)
На доске запись: 2+1=3 и 3-1=2
Прочитываем эти примеры хором.
Работа с доской.
На доске три листика.
Сколько листиков? (3)
Один листик убираем.
Что изменилось?
Запишите решение на полотне с помощью цифр и знаков.
Пример: 3-1=2
Читаем хором.
На столе две матрешки.
Поставили еще одну.
Что изменилось?
Запишите с помощью цифр пример.
Пример: 2+1=3
3. Физкультминутка.
Потянулись, потянулись.
И друг другу улыбнулись.
Влево вправо повернулись и еще раз улыбнулись. Повторить два раза.
Как вы думаете, чему мы должны научиться на уроке? (пользоваться знаками: плюс, минус, равно).
4. Работа по теме урока.
Работа по учебнику.
Прочитайте на стр.29 что мы будем делать на уроке.
Верны ли были ваши предположения.
Рассмотрите рисунки с ежиком, прочитайте вопросы к этим рисункам и ответы на них.
Какое слово заменили знаком «плюс». (подбежал). Прочитайте пример. Составьте рассказ. Аналогично разбирается рисунок с зайцами.
Работа в тетради с печатной основой.
Откройте тетрадь на стр.10.
Посмотрите на клеточки, какие знаки написаны.
Гимнастика для мелкой моторики рук.
Медвежонок в гости шел.
К рыжей белки он зашел
И на озеру к бобру
И к ежу зашел в нору
Даже к комаришке заходил наш Мишка. (большой палец по очереди касается всех остальных пальцев)
Это глазки у зайчонка
Это глазки у котенка
Это глазки у бельчонка (большой палец со всеми пальцами делает глазки)
На доске картинки этих животных.
Вопрос: как можно их назвать одним слово? (животные, звери)
Какое животное лишнее? (котенок)
Посмотрите еще раз в тетрадь. Сели правильно. Положите правильно тетрадь.
Какие знаки мы будем писать, обведите знаки и продолжите писать до конца строки.
5. Закрепление изученного материала.
Работа с компьютром.
Нарисованны предметы (геометрические фигуры, яблоки, листья, белочки).
Внизу 6 примеров.
Задание: найди пример соответствующей картинке.
Дети находят пример, а учитель мышкой подводит его к соответствующей картинке.
6.Рефлексия
Учебник (стр.29), самостоятельное выполнение, взаимопроверка.
Прочитай свои записи соседу по парте, один из сильных учеников, читает свои записи всему классу.
Игра «Крестики – нолики»
+ – =
+
= 7. Подведение итогов.
Покажите, какой знак, заменяет слова: взяли, лопнул, съел. Покажите, какой знак заменяет слова: прилетел, дали, положили.
Поднимите руку, кто сегодня на уроке работал весь урок, а кто в чем-то затруднялся, что было вам не понятно? Что вызвало у вас затруднение?
ЗНАКИ «ПЛЮС» (+), «МИНУС» (–), «РАВНО» (=)
Цели урока:
познакомить с новыми математическими знаками «+», «–», «=»; учить понимать значение данных знаков, читать равенства; работать над развитием внимания, логического мышления учащихся; развивать способность качественно выполнять работу, аккуратно.
Планируемые результаты : учащиеся научатся воспроизводить последовательность чисел от 1 до 10, как в прямом, так и в обратно порядке, начиная с любого числа; обозначать математические действия знаками; работать с моделями; выполнять мыслительные операции анализа и синтеза и делать умозаключение; оценивать себя, границы своего знания и не знания; работать в паре.
Ход урока
- Организационный момент.
Прозвенел опять звонок.
Вот и начался урок.
Ушки держим на макушке.
Сели все – и все молчок.
Начинаем наш урок.
- Повторение изученного материала.
Прежде, чем мы приступим к работе, предлагаю вам математическую разминку.
а) логическая разминка.
Сколько хвостов у трех китов?
Сколько ушей и двух мышей?
У кого больше лап, у утки или у утенка?
б) устный счет.
Посчитайте:
От 1 до 10 и обратно по цепочке;
От 3 до 5;
От 9 до 5.
Какое число следует за числом 7, 5, 2
Какое число стоит перед числом 8, 6, 4
- Работа по теме урока.
- Целеполагание.
На доске знаки (+, -, =, 1, 2, 3 и знаки дорожного движения «Автобусная остановка», «место отдыха», пр..)
Что изображено на рисунке?
– Как вы понимаете значение слова «
знак»
?
(Если ребята затрудняются в правильном ответе):
– Представьте, что вы оказались в незнакомом районе города, спросить не у кого, но вы знаете, что в ваш район идет автобус № 1. Что вы будете делать?
(Предлагают найти автобусную остановку.)
– Верно. Посмотрите на доску и найдите этот знак. Он молчит, но и сообщает нам о чем то.
(Ребята отвечают, что он указывает на то место, где находится остановка автобуса.)
А какие еще дорожные знаки вы знаете и что они сообщают?
– Теперь вы можете мне сказать, что такое знак?
Рефлексия:
Знак – это указание или сообщение о каком-либо объекте.
(Версии разные: цифры, числа, знаки.)
Эти записи являются тоже знаками, но
математическими
.
Цифра это тоже математический знак, который используют для записи чисел.
– Какие из этих знаков вам знакомы?
Какие новые? Кто знает, что это за знаки? Проблема?? (Гипотеза, предположение)
Сегодня тема нашего урока: « ЗНАКИ «ПЛЮС» (+), «МИНУС» (–), «РАВНО» (=) ». Вам что-нибудь об этом говорит?
Какую цель поставите себе на урок? Чему ты хотел бы научиться? (…..пользоваться знаками: плюс, минус, равно).
- Знакомство со знаками «плюс» (+), «минус» (–), равно (=).
Практическая работа.
Положите два красных квадрата,
Какой цифрой мы это обозначим? (все на местах работают с веерами цифр, один ученик к доске находит и крепит цифру 2)
Рядом положите синий квадрат
Какой цифрой обозначим?(1).
Квадратов стало больше или меньше? Сколько квадратов получилось?
Какими словами можно заменить слово положили ? (прибавили, добавили)
Чтобы записать это выражение в математике используются цифры и математический знак «+».
На доске запись: 2+1
Плюс – знак добрый, он всем дает, прибавляет и всего становится больше.
Послушайте стихотворение про этот знак.
Я – плюс,
И этим я горжусь.
Я для сложения гожусь
Я – добрый знак соединенья
И в том мое предназначение.
Рефлексия: – Посмотрите на этот знак. Как его имя в математике? (плюс). Какую работу он выполняет? (Он всем дает, прибавляет, всего становится больше.)
Сколько у вас теперь фигур на столе? Возьмите от трех красных фигур уберите синий квадрат. Фигур стало больше или меньше? Сколько фигур осталось? (2)
Слово уберите , тоже можно заменить знаком. Этот математический знак называется – минус.
На доске запись: 3-1
Этот знак у всех отбирает, отнимает и всего становится меньше.
Послушайте стихотворение о нем.
Я – минус.
Тоже добрый знак.
Ведь не со зла я отнимаю
Я свою роль лишь выполняю.
Рефлексия: – Какое имя у математического знака, который все отбирает, и всего становится меньше?
Посмотрите на записи, которые у нас
получились
.
Кто сможет их прочитать? (читают записанные на доске выражения)
Вы произносите слово получится , а как это записать, может кто-нибудь знает?
Чтобы записать слово получится , используют знак равно (=) и такие записи
(показ на доску) называют выражения .
Давайте вместе прочитаем выражения у нас на доске, используя новые термины.
Рефлексия: И так какие же знаки используют математики, для записи выражений?
Какую работу выполняют эти знаки? (+,-)
- Работа в тетради на печатной основе.
Откройте тетрадь на стр.10. «Я тетрадочку открою».
Сели правильно. Правило «Ты сиди за партой стройно».
Посмотрите на клеточки, какие знаки написаны?
Как вы будете работать в тетради? Посмотрите внимательно, а по какому правилу расположены здесь знаки? (через клетку)
Показ, как правильно пишутся знаки «+», «–». Затем учащиеся обводят их по точечным контурам и пишут с а м о с т о я т е л ь н о.
Ребята оцените свою работу.
Посмотрите внимательно, получилось у вас прописать красиво, аккуратно? Сохранили ли вы закономерность, все ли знаки у вас прописаны через клетку? Оцените свою работу по шкале А (аккуратность) и П (правильно). Если вы достигли результата своей работы, то как всегда зажигаете огонек вверху, …
- Закрепление.
- Работа по учебнику .
Посмотрите на стр.28 и скажите, что предлагает нам учебник?
Посмотрите, о ком мы сейчас будем говорить?
Сколько было ежиков сначала? (1 – цифру на доску) Что изменилось потом? (подбежал еще 1) Сколько их стало? (2)
(Чтение под картинкой рассказа) – Правильно вы ответили на вопросы?
Какое слово заменили знаком «плюс» (подбежал). Прочитайте полученное выражение в учебнике.
2) Работа в парах :
Посмотрите на картинку ниже и составьте рассказ. О ком вы будете составлять рассказ? Аналогично разбирается рисунок с зайцами.
Если темп работы класса высокий, то можно провести следующую работу. |
Данное задание закрепляет знание знака сложения «плюс». После выполнения данной работы можно сообщить, что такие записи называются равенствами . А почему?(Если догадаются, то: так как в них есть знак «=», если нет, то – На этот вопрос мы ответим на следующих уроках).
V. Подведение итогов.
– Давайте вспомним, что мы хотели узнать в начале урока?
Вы достигли результата?
Вы теперь знаете, что это за знаки?
Как называются?
– Каким знаком будем пользоваться, если услышим слова: «убежали, убрали»?
Каким знаком будет пользоваться, если услышите слова: «добавили, пришли»?
А какие это знаки….
. + и -? (дорожные или математические)
Спасибо вам большое за урок, завтра мы продолжим учиться пользоваться нашими новыми знаками и познакомимся с новой цифрой.
В течении урока, проводится 2-3 физминутки, в зависимости от возможностей класса. Время проведения первой через 7-10 минут после начала урока, следующие по усмотрению учителя и временной промежуток зависит от работоспособности вашего класса.
КОНСПЕКТ УРОКА МАТЕМАТИКИ1 КЛАСС УМК ПЕРСПЕКТИВА: ТЕМА: ЗНАКИ + (ПЛЮС), – (МИНУС), = (РАВНО). Цели: 1)Познакомить учеников с математическими знаками (+,-,=),узнать их место в математике. Познакомить с новым термином-выражение, научить правильно его читать. 2)Закрепить ведение количественного и порядкового счета предметов, развивать логическое мышление. Оборудование: Корзинка, три яблока, веера цифр, электронное приложение к учебнику Г.В. Дорофеева Математика 1 класс 1.ОРГАНИЗАЦИОННЫЙ МОМЕНТ. Мы начинаем новый день. Прогоняй скорее лень! Почаще улыбайся.
Прилежным быть старайся!
2 .АКТУАЛИЗАЦИЯ ЗНАНИЙ. 1) Счет прямой и обратный от 1 до 10, от 6 до 10, от 7 до 3.Какое число находится между 2 и 4,стоит перед число7, 5,2, следует за числом 3,8.
2) Задание на логику. – В корзине сидят котята. У всех котят 3 пары ушек. Сколько котят в корзине? – У Толи 2 пары варежек. Сколько варежек на левую руку? -По двору ходят куры. У всех кур Петя насчитал 6 ног. Сколько кур? -Бабушка связала Нине две пары носков. Сколько носков связала бабушка Нине?
3.ФИЗМИНУТКА: Мы считали и устали,
Дружно все мы тихо встали.
Ручками похлопали: раз, два, три.
Ножками потопали: раз, два, три.
Сели, встали, встали, сели.
И друг друга не задели.
Мы немножко отдохнем,
И опять считать начнем.
4 . МОТИВАЦИОННО- ЦЕЛЕВОЙ ЭТАП. ПОСТАНОВКА ПРОБЛЕМЫ. РАБОТА ПО ТЕМЕ УРОКА.
Я положу в корзинку 2 яблока. Какой цифрой мы их обозначим? (Ученики работают на местах с веерами цифр, а учитель пишет на доске цифру 2).
Добавлю еще одно яблоко. Какой цифрой мы его обозначим?(1). Ребята, яблок стало больше или меньше? Сколько яблок получилось? -Какими словом можно заменить слово добавить? (Сложить). А кто знает каким математическим знаком можно заменить слова добавить, сложить? (знаком +) – Правильно, чтобы записать это выражение в математике используются цифры и математический знак «+».(Учитель на доске записывает 2+1.Просмотр электронного приложения к учебнику). – Ребята, послушайте стихотворение о знаке плюс:
Я – плюс, И этим я горжусь. Я для сложения гожусь. Я – добрый знак соединения. И в том мое предназначение.
Посмотрите на этот знак. Как его имя в математике? (плюс). Какую работу он выполняет? (Он прибавляет, всего становится больше.)
Сколько у нас теперь яблок в корзинке? (3.Учитель пишет на доске цифру 3) А если я от трех наших яблок уберу одно, сколько их станет: больше или меньше? (Меньше) Сколько яблок осталось? (2. Учитель пишет на доске).- Как вы думаете слово уберу, убрать, можно заменить знаком?(знаком -) – Правильно.
Этот математический знак называется – минус.(Учитель на доске записывает 3-1.Просмотр электронного приложения к учебнику). – Послушайте стихотворение о знаке минус.
Я – минус. Тоже добрый знак. Ведь не со зла я отнимаю. Я свою роль лишь выполняю. – Какое имя у математического знака, который все убавляет, и всего становится меньше? 5.ФИЗМИНУТКА. Ветер дует нам в лицо,
Закачалось деревцо.
Ветер тише, тише, тише –
Деревцо все выше, выше.
6.РАБОТА ПО ТЕМЕ УРОКА . – Посмотрите на записи, которые у нас получились . Кто сможет их прочитать? (Ученики читают записанные на доске выражения) -Вы произносите слово получится, а как это записать, может кто-нибудь знает? (Ответы детей) -Все верно. Чтобы записать слово получится используют математический знак равно (=) и такие записи (показ на доску) называют выражения (Просмотр электронного приложения). – Давайте вместе прочитаем выражения у нас на доске, используя новые термины.
(Хоровое чтение) –Так какие же знаки мы будем использовать для записи выражений?(+,-,=)? А какую работу выполняют знаки + и -?(Ответы учеников)
Работа по учебнику стр.54-55
7.ФИЗМИНУТКА. Можешь пальцы посчитать? Один, два, три, четыре, пять.
На другой руке опять:
Один, два, три, четыре, пять.
Десять пальцев, пара рук –
Вот твое богатство, друг. 8.РАБОТА ПО ТЕМЕ УРОКА . Работа в тетради стр. 42(задание1-2), стр.43 (задание4-5).
9. ПОДВЕДЕНИЕ ИТОГА УРОКА. РЕФЛЕКСИЯ.
Что нового вы узнали на уроке? – С какими новыми математическими знаками познакомились? – Для чего нужен знак «-»,а знак «+»? – Какие умения вы приобрели? – Кто на уроке был самым активным? – Оцените свою работу на уроке? -Хорошо ребята, всем спасибо за урок!
“Ознакомление с действием сложения. Знак « +». Составление примеров на сложение по предметным рисункам”
Урок математики в 1 классе
Тема: Ознакомление с действием сложения.
Знак « +». Составление примеров на сложение по предметным рисункам.
Цель: Ознакомить со знаком «+» и действием сложения. Учить записывать примеры на сложение. Развивать мышление, память, речь. Воспитывать интерес к математике.
Тип: Комбинированный
Оборудование: таблицы по математике для 1 класса. Таблица «Состав чисел первого десятка, счетный материал «желуди », наборное полотно «Дуб»счетные палочки, счетный материал «грибы», наборное полотно «корзинка», микрофон
Ход урока
I.Организация класса
Внимание! Проверь, дружок,
Готов ли ты начать урок.
Все ль на месте, все ль в порядке –
Ручка, книжка и тетрадки.
Проверка готовности к уроку.
II.Повторение и закрепление материала
- Ученики одного ряда называют один за другим свои номера: первый, второй и т. д., от первой парты к последней и наоборот.
- Математический диктант.
д., от первой парты к последней и наоборот.- Запишите цифру 3;
- посчитайте морковки в корзинке, и запишите их количество цифрой;
- запишите соседей числа 2;
- запишите число, которое стоит перед числом 3;
- запишите число, которое следует за числом 4; запишите цифрой, сколько сторон имеет квадрат.
III. Изучение нового материала
1.Подготовительная работа.
«Микрофон»
Учитель:– Ребята, скажите, что вы ожидаете от нашего урока? Чего вы хотите?
Учитель: Сегодня мы с вами познакомимся с новым математическим знаком, с которым вы будете дружить всю жизнь, научимся ним пользоваться.
(Стук в дверь. Входит Красная Шапочка)
Красная Шапочка: Здравствуйте, ребята!
Учитель: Кто это к нам пришел, дети?
(ответы детей)
Учитель: А куда ты идешь, Красная Шапочка?
Красная Шапочка: Я иду к бабушке.
По дороге решила собрать ей грибов, да что-то никак не найду.
Учитель: – А ведь ты идешь не простым лесом, а волшебным. Здесь грибы спрятались, и покажутся только тогда, когда дети будут правильно выполнять задания.
Ребята, давайте продолжим наш урок, будем выполнять разные задания и наполнять корзинку Красной Шапочки волшебными грибами.
Учитель: – Сегодня мы отправляемся с вами в лес. Кто из вас был в лесу? Расскажите, поделитесь впечатлениями.
Здравствуй, лес, дремучий лес,
Полный сказок и чудес!
- Мы будем собирать хворост . Положите на парту 2 палочки.
(Ученики выкладывают на парту 2 палочки).
– Как можно образовать число3? (Прибавить одну палочку)
– Как можно образовать число 4? (Прибавить еще одну палочку)
– Как мы получили числа 3и4?
– Большим или меньшим становилось новое число?(Большим)
Учитель: – В математике это действие можно не только выполнять с помощью палочек, но и записать , используя числа и знаки.
(Запись на доске 3+1=
4+1= )
(Ученик дает Красной Шапочке грибок)
2.Объяснение нового материала
а) Учитель читает примеры, дети повторяют за ним: «к 3 прибавить 1 равняется 4»
б)Учитель рисует на доске слева 4 яблока, а справа 1 яблоко.
– Запишем, сколько мячей вместе. ( 4=1+5)
Учитель: – Эта запись называется пример.
На доску вешается таблица с рисунком, по которому дети придумывают и записывают в тетрадях пример, читают его.
(Ученик дает Красной Шапочке грибок)
3.Физкультминутка
Наши нежные цветки распустили лепестки,
Ветерок чуть дышит, лепестки колышет.
Наши алые цветки закрывают лепестки,
Тихо засыпают, головой качают.
IV.
Первичное закрепление
- Работа с учебником (с. 24, №3)
(Ученик дает Красной Шапочке грибок)
- Работа в парах
Дети составляют примеры. Один говорит: « У меня 4 груши , мне дали еще 1», а другой отвечает: «4+1 =5»
(Ученик дает Красной Шапочке грибок)
Физкультминутка
А теперь, ребята, встали!
Быстро руки вверх подняли,
В стороны, вперед, назад,
Повернулись вправо, влево,
Тихо сели, вновь за дело.
3.Самостоятельная работа (с. 24, №4)
3+1=4
2+2=4
(Ученик дает Красной Шапочке грибок)
4.Работа в тетради (с. 19, №1, 2)
(Ученик дает Красной Шапочке грибок)
5. Письмо цифр (с.19, №5)
(Ученик дает Красной Шапочке грибок)
V.
Итог урока. «Микрофон»
– Чему новому мы научились на уроке?
Красная Шапочка: – Молодцы, ребята! Вы хорошо поработали сегодня и мне помогли собрать бабушке грибов. А я вам за это приготовила угощение! Кушайте на здоровье! До скорой встречи!
Математические символы – Список символов, примеры решения
Математика состоит из чисел, символов и формул. Математические символы используются для разных целей в разных областях математики. Использование символов для представления математической информации облегчает понимание выражений, поскольку эти символы показывают взаимосвязь между величинами. В этой статье давайте рассмотрим общие, которые мы используем в разных областях математики.
| 1. | Общие математические символы |
| 2. | Константы, используемые в качестве математических символов |
| 3. | Математические символы, используемые в логике |
4. | Диаграмма Венна и символы теории множеств |
| 5. | Цифровые символы |
| 6. | Символы геометрии и алгебры |
| 7. | Греческие алфавиты и символы комбинаторики |
| 8. | Решенные примеры |
| 9. | Практические вопросы |
| 10. | Часто задаваемые вопросы о математических символах |
Общие математические символы
Если мы напишем несколько раз слова «прибавление 4 к 2 дает 6», это может усложнить ситуацию. Эти слова также занимают больше места и требуют времени для написания. Вместо этого мы можем сэкономить время и место, используя символы. Язык и словарный запас математики содержат большое количество символов, и этот список бесконечен — некоторые из них более технические, чем другие. У нас есть как минимум 10 000+ символов, и некоторые из них мы редко используем.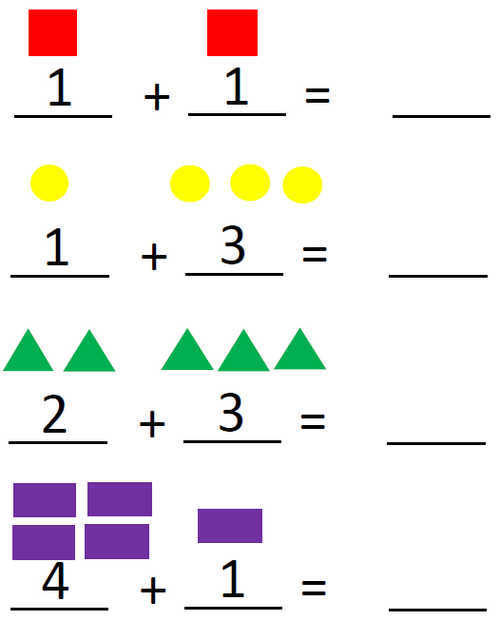
Наиболее распространенные символы перечислены в следующей таблице:
| Символы | Значение | Примеры математических символов |
|---|---|---|
| + | Добавить | 5 + 4 = 9 |
| – | Вычесть | 5 – 4 = 1 |
| = | равно | 1+1 = 2 |
| \(\экв\) | Тождественно равно | (а+б) 2 \(\экв\) а 2 + 2аб +б 2 |
| \(\примерно\) | Приблизительно равно | \(\пи \приблизительно 3,14\) |
| \(\neq\) | Не равно | 5 + 4 \(\neq\) 1 |
| \(\раз\) | Умножить | 5 \(\раз\) 4 = 20 |
| \(\дел\) | Разделить | 10 \(\дел\) 2 = 5 |
| \(<\) | Менее | 10 \(<\) 20 |
| \(>\) | Больше | 20 \(>\) 10 |
| \(\leq\) | Меньше или равно | х + у \(\leq\) г |
| \(\geq\) | Больше или равно | x +y \(\geq\) z |
| \(\%\) | Процент | 50% = \(\begin{align}\frac{50}{100}\end{align}\) |
\(. \) | Десятичная точка или период | \(\begin{align}\frac{1}{2} = 0,5\end{align}\) |
| \(-\) | Винкулум Разделяет числитель и знаменатель | \(\begin{align}\frac{2}{3}\end{align}\) |
| \(\sqrt{} \) | Квадратный корень | \(\sqrt{4} = 2\) |
| \(\sqrt[3]{х}\) | Кубический корень из x | \( \sqrt[3]{27} = 3\) |
| \( \sqrt[n]{x}\) | n th корень \(x\) | \( \sqrt[4]{16} = 2\) |
| \(()\) | Скобки | \(2+(5-3) = 2 +2 = 4\) |
| \([\:\:]\) | Квадратные скобки | \(\ начало {выравнивания} &3\раз[2 +(5 -2)] +1 \\ &3 \раз[2+3] +1 \\ &3 \times5+1\\ &16 \конец{выравнивание}\) |
| \(\{\}\) | Кронштейн для цветов | \(\ начало {выравнивания} &16 \div \{3\times[2 +(5 -2)] +1\} \\ &16 \дел \{3 \раз[2+3] +1\} \\ &16 \дел \{3 \times5+1\}\\ &16 \дел \{16\} \\ &1 \конец{выравнивание}\) |
| \(\в\) | Принадлежит | 0 \(\in\) Целое число |
| \(\нет\в\) | Не принадлежит к | \(\frac{1}{2} \not\in\) Натуральные числа |
| \(\поэтому\) | Поэтому | \(x+1 = 2 \следовательно, x = 1\) |
| \(\потому что\) | Потому что | \(\begin{align}\frac{1}{2} \!\div\! 0. 5 \!= \!1 (\потому что\! \frac{1}{2} \!=\! 0.5)\ конец{выравнивание}\) |
| \(\infty\) | Бесконечность | Бесконечность бесчисленна, \(\begin{align}\frac{1}{3}\end{align}\) при записи в десятичной форме, бесконечно \(0,333…..\) |
| \(!\) | Факториал | \( 5!\ \!\!=\! 5 \!\раз\! 4 \!\раз\!3 \!\раз\! 2\! \раз\! 1\) |
Константы, используемые в качестве математических символов
Мы используем константы в математике для обозначения неизменных объектов. Эти константы могут включать в себя ключевые математические наборы, ключевые числа, ключевые математические бесконечности и другие ключевые математические объекты (например, единичную матрицу). Эти математические константы чаще всего принимают форму буквы алфавита или ее производной. В следующей таблице перечислены некоторые наиболее часто используемые константы, а также их имена, значения и использование.
| Имя символа | Пояснение |
|---|---|
| 0 (ноль) | Аддитивная идентичность общих чисел |
| 1 (один) | Мультипликативная идентичность обычных чисел |
| √2 (квадратный корень из 2) | Положительное число, квадрат которого равен 2. Приблизительно равно 1,41421. |
| e (постоянная Эйлера) | Основание натурального логарифма. Предел последовательности (1 + (1/n) n ). Приблизительно равно 2,71828 |
| \(\pi\) (Pi, постоянная Архимеда) | Отношение длины окружности к ее диаметру. Половина окружности единичного круга. Приблизительно равно 3,14159 |
| \( \phi\) (Phi, золотое сечение) | Отношение между большим числом и p меньшим числом q, когда (p+q)/p = p/q. Положительное решение уравнения y 2 -y-1 = 0 . |
| i (Воображаемая единица) | Главный корень из -1. Основной компонент комплексного числа. |
Математические символы, используемые в логике
В следующей таблице показаны математические символы, используемые в логике.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\существует\) | Существует по крайней мере один | ∃ х: Р(х)∃ х: F(х) Существует хотя бы один элемент p(x), \(x\), , такое что F(x) равно True. |
| \(\существует!\) | Существует один и только один | ∃! х: Ф(х) означает, что существует ровно один \(x\) такое, что F(x) истинно. 92 > 1\) |
| \(\отриц\) | Логический Не | Утверждение A истинно, только если \(\neg\) ложно \(х \neq y \iff\neg(x=y)\) |
| \(\лор\) | Логическое ИЛИ | Утверждение A \(\lor\) B истинно , если A или B верно; , если оба ложны, утверждение неверно. |
| \(\земля\) | Логический И | Утверждение A \(\land\) B истинно , если A и B оба верны; иначе это ложь. |
| \(\подразумевается\) | Подразумевается | х = 2 \(\подразумевается\) x 2 = 4 |
| \(\если\) | Если и только если | х +1 = у +1 \(\ тогда и только тогда) х = у |
| \(\text{|}\) или \(\text{:}\) | Такой, что | { \(х\) | \(х\) > 0} = {1,2,3,…} |
Диаграмма Венна и символы теории множеств
В следующей таблице показаны математические символы, используемые в диаграммах Венна и теории множеств.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\крышка\) | Перекресток | А = {2,3,4} Б = {4,5,6} А \(\заглавная\) В = {4} |
| \(\чашка\) | Союз | А = {2,3,4} В = {4,5,6} А \(\чашка\) В = {2,3,4,5,6} |
| \(\ничего\) | Пустой комплект | Набор без элементов \(\varnothing\) = { } |
| \(\в\) | Является членом | 2 \(\в\) \(\mathbb{N}\) |
| \(\нотин\) | не является членом | 0 \(\нетин\) \(\mathbb{N}\) |
| \(\подмножество\) | Является подмножеством | \(\mathbb{N} \подмножество \mathbb{I}\) |
| \(\расстроен\) | Является надмножеством | \(\mathbb{R} \supset \mathbb{W}\) |
| \(\текст{П(А)}\) | Комплект силовой А | P({1,2}) = {{}, {1}, {2}, {1,2}} |
| \(А=В\) | Равенство (одинаковые элементы в наборе А и наборе В) | А = {1,2}; В = {1,2} \(\ подразумевает \) А = В |
| \( А \раз В\) | Декартово произведение Набор заказанных пар от A и B | А ={5,6}; В = {7,8} \(\ подразумевает \)\( A \times B\) = {(5,7),(5,8),(6,7),(6,8)} |
| \(\текст{|А|}\) | Количество элементов в множестве A | |{1,2,3,4}| = 4 |
Цифровые символы
Цифровые символы с их примерами и соответствующие индийско-арабские цифры перечислены здесь, в таблице.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| Римская цифра I | Значение = 1 | I = 1 , II = 2 , III = 3 |
| Римская цифра V | Значение = 5 | IV = 4 (5-1) ВИ = 6 (5+1) VII = 7 (5+2) VIII = 8 (5+3) |
| Римская цифра X | Значение = 10 | IX = 9 (10-1) |
| Римская цифра L | Значение = 50 | XLIX = 49 (50-1) |
| Римская цифра C | Значение = 100 (столетие) | СС = 200 (100+100) CCLIX = 259 (100+100+50+9) |
| Римская цифра D | Значение = 500 | DCLI = 651 (500+100+50+1) DCCIV = 704 (500+100+100+4) |
| Римская цифра M | Значение = 1000 | ММ = 2000 (1000+1000) |
| R или \(\mathbb{R}\) | Вещественные числа | \(\frac{1}{2} , \frac{1}{4}, 0,5\)\(\sqrt{2},\sqrt{3}\) |
| Z или \(\mathbb{Z}\) | Целое число | -100,-20,5,10,. … |
| N или \(\mathbb{N}\) | Натуральные числа | 1,2,3,…500,… |
| Q или \(\mathbb{Q}\) | Рациональные числа | \(-\frac{1}{2}, \frac{1}{4}, 0,5\) |
| P или \(\mathbb{P}\) | Иррациональные числа | \(\sqrt{2},\sqrt{3}\) |
| C или \(\mathbb{C}\) | Комплексные числа | 5+2i |
Символы геометрии и алгебры
В приведенной ниже таблице показаны часто используемые геометрические символы. Математические символы с названиями и примерами также приведены в таблице.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\угол\) | Укажите угол | \(\угол ABC\) |
| \(\Дельта\) | Символ треугольника | \(\Дельта\текст{PQR}\) |
| \(\конг\) | соответствует | \(\Delta \text{PQR} \cong \Delta \text{ABC}\) 9\цирк\) |
| \(\overline{\rm AB}\) | Отрезок линии AB | Линия из точки А в точку Б |
| \(\overrightarrow{\rm AB}\) | Рэй AB | Линия, начинающаяся из точки А и продолжающаяся через точку В |
| \(\overleftrightarrow{\rm AB}\) | Линия AB | Бесконечная линия, проходящая через точки A и B | 9в\)
Символы алгебры
В следующей таблице показаны наиболее часто используемые алгебраические символы.
2 \)
\(\пропто\)
Греческие алфавиты и символы комбинаторики
В таблице ниже показаны греческие алфавиты, используемые в качестве математических символов. Их имена, использование и примеры также перечислены в таблице.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\альфа\) | Альфа | Используется для обозначения углов, коэффициентов |
| \(\бета\) | Бета | Используется для обозначения углов, коэффициентов |
| \(\гамма\) | Гамма | Используется для обозначения углов, коэффициентов |
| \(\Дельта\) | Дельта | Дискриминантный символ |
| \(\варепсилон\) | Эпсилон | Используется для обозначения универсального набора | .
| \(\йота\) | Йота | Представляет мнимое число |
| \(\лямбда\) | Лямбда | Представляет константу |
| \(\пи\) | Пи | \(\пи \примерно 3,14\) |
| \(\Сигма\) | Сигма | Представляет сумму |
| \(\тета\) | Тета | Представляет углы |
| \(\ро\) | Ро | Статистическая константа |
| \( \фи\) | Фи | Обозначение диаметра |
Символы комбинаторики
В таблице ниже показаны наиболее часто используемые символы комбинаторики. 96{P_4} &= 6 \times 5 \times 4 \times 3 = 360\end{align}
Похожие статьи о математических символах
Ознакомьтесь со следующими страницами, посвященными математическим символам.
- Арифметика
- Алгебраические выражения
- Правила делимости
- Векторы
Важные примечания
Вот несколько моментов, которые следует помнить при изучении математических символов:
- Использование символов для представления информации упрощает понимание математических выражений.
- У нас есть как минимум 10 000+ символов, и некоторые из них мы редко используем.
- Мы используем константы в математике для обозначения неизменяющихся объектов.
Часто задаваемые вопросы о математических символах
Что такое U в математических символах?
Математический символ U используется для обозначения набора, состоящего из элементов двух наборов. Следовательно, объединение двух множеств P и Q будет множеством элементов P и Q. Для обозначения множества используется специальный символ ∪, который выглядит как «U».
Сколько существует математических символов?
Более 10000 математических символов. Некоторые из основных: =,+,−,≠,±, * и так далее. Есть сложные символы, такие как \(\alpha\), \(\varepsilon\) и так далее.
Какой математический символ используется для обозначения периода волны?
Математический символ, который используется для обозначения периода волны, — λ. Он также известен как длина волны, которая измеряется в единицах расстояния.
Для чего используется математический символ сложения?
Символ сложения (+) обычно используется при сложении двух и более чисел, например, 5 + 5. Кроме того, символ (+) также может использоваться для обозначения положительного числа, например, +7.
Перечислите некоторые распространенные арифметические математические символы.
Некоторые из распространенных арифметических математических символов: знак плюс (+), используемый для сложения, знак минус (-), используемый для вычитания, знак звездочки (*) или знак умножения (×), используемый для умножения, и знак деления (÷). или знак косой черты (/), используемый для деления.
Список из 20+ полезных математических символов
Математические символы — это универсальные представления понятий, идей и чисел, которые можно использовать для выражения отношений между величинами. Их можно использовать в различных типах уравнений, и они образуют универсальный язык математики, на который можно ссылаться в любое время.
Учащиеся также могут научиться решать более сложные математические уравнения, интуитивно понимая значения символов, таких как число пи, римские цифры, деление, дроби и т. д.
Математические символы используются различными способами, чтобы помочь извлечь максимальную пользу из уравнений, расчетов и формул. Они упрощают определение математических величин, а также устанавливают отношения между величинами, которые могут быть выражены уникальным образом. Они помогают нам создать логическую последовательность, которую можно использовать для представления любого физического события.
Символы также используются для обозначения предопределенного значения, такого как число пи или постоянная Эйлера. Они используются для обеспечения согласованного стандарта, а также для упрощения расчетов, которые требуют регулярного использования этих чисел. Символы остаются неизменными с течением времени, что делает их лучшим способом представления идеи или стандарта для использования в любых расчетах.
Читать по теме: Лучшие математические трюки, которые превратят ваших детей в математических гениев
Вы также можете использовать символы, чтобы заложить фундамент базовых знаний для учащихся. Математические символы, такие как знаки равенства, знаки больше, скобки и круглые скобки, формируют большую часть предварительных практических знаний обо всех сложных математических уравнениях. Учащиеся должны быть в состоянии привыкнуть к символам, чтобы уверенно решать математические задачи.
Математические символы также значительно облегчают работу со ссылками, так как вы можете вернуться к этим символам, чтобы выяснить взаимосвязь между величинами. Каждый символ, от производных до логарифмов, содержит историю информации, которую можно использовать для решения математических уравнений. Их можно использовать на разных языках, поскольку они являются постоянным справочником для любого математика во всем мире.
Основные математические символы Начнем с основных математических символов, используемых для выражения отношений между величинами.
1. Сложение (+) используется для сложения двух чисел. 9+10 = 19
2. Вычитание (-) используется для вычитания одного числа из другого. 11-2 = 9
3. Знак равенства (=) используется для выражения двух одинаковых значений. X = 33
4. Приближение (≈) используется для обозначения приблизительного равенства. π (пи) ≈3,14
5. Не равно (≠) используется для выражения неравноправия. 15 ≠ Z
6. Умножение (x) используется для умножения двух чисел. 12 x 2 = 24
7. Деление (÷) используется для отделения одного числа от другого. 15 ÷ 5 = 3
Ознакомьтесь с более распространенными математическими символами здесь.
Хотите узнать больше о сложении и вычитании? Эта приключенческая игра учит детей, как использовать дополнение для освещения пещер в темноте – https://www.splashlearn.com/addition-games
Теория множеств и символы диаграмм Венна Теория множеств и представление диаграмм Венна ключ к решению проблемы.
1. Пересечение (∩) обозначает общие числа между множествами.
2. Союз (U) обозначает объединение двух наборов.
3. Равенство (A = B) означает равные элементы в обоих множествах.
4. Декартово произведение (A X B) используется для обозначения наборов упорядоченных пар.
Доступ к другим символам теории множеств и диаграмм Венна здесь.
Римские цифры Математические символыВы также можете встретить римские цифры, особенно в сложных математических уравнениях.
1. I — римская цифра со значением 1. II = 2
2. V — римская цифра со значением 5. V = 5
3. X — римская цифра со значением 10 , XX = 20
4. L — римская цифра со значением 50. L = 50
Чтобы увидеть больше римских цифр, нажмите здесь.
Неизменяемые математические константы Время от времени вам также может понадобиться использовать математические константы, которые можно выразить, как показано ниже.
1. Квадратный корень из двух (√2) используется как положительное число с прибл. значение 1,41421.
2. Постоянная Эйлера (е) используется как основание натурального логарифма.
3. Пи (π) используется как символ для обозначения отношения длины окружности к диаметру круга.
4. Мнимая единица (i), используемая как корень из минус 1 для обозначения комплексных чисел.
Получите доступ к дополнительным математическим константам и их значению.
Алгебраические математические символыАлгебраические символы — одни из наиболее часто используемых символов в математике и естественных науках.
1. Переменные (x, y), используемые для обозначения заполнителей для переменных чисел. х = у + 10,
2. Пропорционально (∝) используется для обозначения пропорционального отношения. X ∝ y ⟹ x = ky
3. Сложение (+) используется для добавления переменных. 2x + 3y = 4z
4. Функциональная карта f(x), используемая для обозначения функции.
f(x) = 2x – 9
Узнайте больше математических символов алгебры здесь.
Нужна дополнительная помощь в решении алгебраических уравнений? Помогите детям обрести интуитивное понимание предмета, нажмите здесь.
Улучшите успеваемость вашего ребенка по математике, записавшись на обширную библиотеку викторин и игр SplashLearn
Вы можете получить доступ к забавным играм, исследовательским викторинам и творческим рабочим листам, позволяющим учащимся раскрыть свой потенциал в математике. С 2046 математическими играми и 51 математическим курсом SplashLearn охватывает весь спектр математических знаний для детей от Pre-K до 5 класса. Используя научно разработанные игры и курсы, созданные в сотрудничестве с ведущими преподавателями, наша программа повышает успеваемость и уверенность в своих математических способностях.
Связанные чтения: Как стать лучше в математике за 10 эффективных шагов
Узнайте больше, посетив – https://www.
splashlearn.com/math-games
Есть вопрос? Отправьте нам электронное письмо по адресу [email protected]
Часто задаваемые вопросыЧто означает ∈ ø в математике?
Символ означает, что элемент этого набора является объектом, содержащимся в нем. Он широко используется в теории множеств и является ключевым математическим символом, используемым для описания отношений.
Что означает U в математике?
Когда два набора имеют объединение, его можно использовать для представления себя как U. В каждом наборе присутствуют значения, которые можно объединить с помощью символа «U». Вы можете узнать больше о союзах, посетив математические игры SplashLearn.
Что такое x и y в математике?
Строчные буквы могут использоваться для обозначения переменных в математике. Буквы x и y широко используются как общие переменные, которые могут быть выражены, чтобы помочь решить проблему. Они также используются в более сложных уравнениях, чтобы установить базовый стандарт для нахождения неизвестных величин.