Знак в математике больше: Больше, меньше, равно — урок. Математика, 1 класс.

2

1

2

1

1

1

2

1

1

2

2

2

2

Прочитай записи, которые сделал Лесовичок.

К каким рисункам они сделаны?

2 = 2

1 = 1

Нажми на число

3

7

6

5

4

0

2

1

10

9

8

Выбери числа больше 4

Подбери ключи к двери.

7

10

9

8

6

5

4

3

2

1

0

Нажми на число

Для этого выбери числа меньше 5 .

5

Выбери верный знак и запиши получившиеся неравенства.

6

7 9

5

Нажми на паровозик

Найди неверное неравенство на вагончиках паровозика и он продолжит свой путь .

М о л о д ц ы !

4 2

2

Чтобы узнать кто здесь живет найди числа меньше 6

Нажми на число

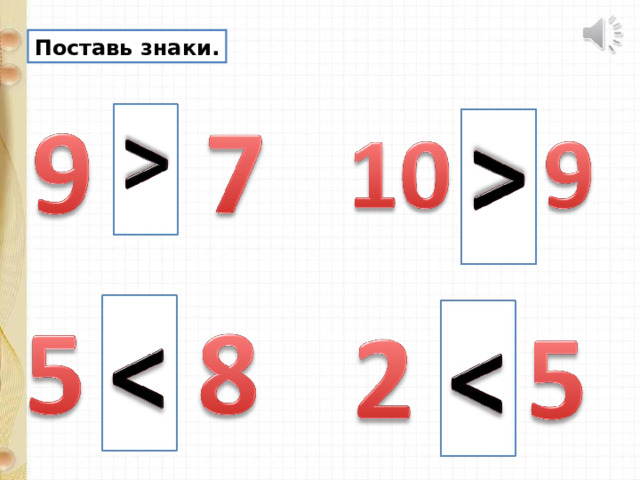
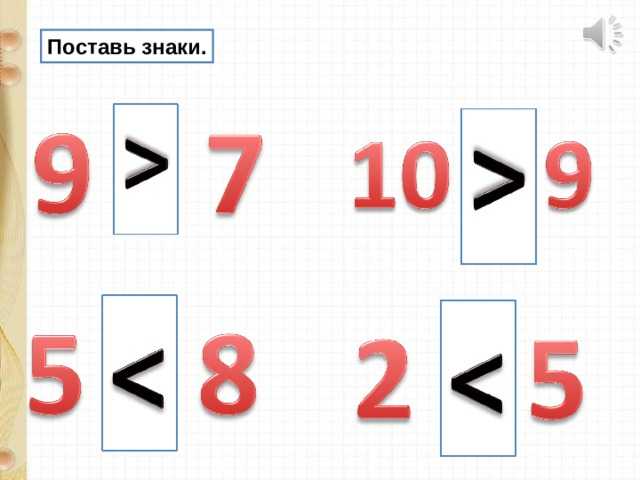
Сравни числа. Поставь правильно знак

4 6

Нажми на знак

Сравни числа. Поставь правильно знак

7 3

Нажми на знак

Сравни числа. Поставь правильно знак 5 9 Нажми на знак “

Сравни числа. Поставь правильно знак

5 9

Нажми на знак

Сравни числа. Поставь правильно знак

8 1

Нажми на знак

Сравни числа. Поставь правильно знак

3 4

Нажми на знак

Спасибо!

1 класс. Математика. Понятия «больше», «меньше» и «равно» – Знакомство с правилом сравнения.

На дан­ном уроке будет рас­смот­ре­но срав­не­ние чисел. Два числа могут быть равны, одно число может быть боль­ше дру­го­го или мень­ше. То есть, если одно число боль­ше, то дру­гое, со­от­вет­ствен­но, – мень­ше. На ри­сун­ке видно, что в одной руке у че­ло­веч­ка ша­ри­ков боль­ше, а в дру­гой – мень­ше. (рис. 1)

Рис. 1 (Ис­точ­ник)

Для луч­ше­го по­ни­ма­ния срав­не­ния чисел рас­смот­рим ис­то­рию о кош­ках.

Ис­то­рия о кош­ках.

Жи­ли-бы­ли маль­чик и де­воч­ка, они были со­се­дя­ми. Они лю­би­ли кошек. Маль­чи­ка звали Петя, а де­воч­ку – Катя. У Пети было 2 кошки и у Кати вна­ча­ле было 2 кошки. (рис. 2)

Рис. 2 (Ис­точ­ник), (Ис­точ­ник)

Это можно за­пи­сать сле­ду­ю­щим об­ра­зом:

То есть ко­ли­че­ство кошек у Пети и у Кати оди­на­ко­вое.

Но Катя по­до­бра­ла на улице еще одну кошку. Она при­нес­ла ее домой, по­мы­ла ее, на­кор­ми­ла. У Кати стало три кошки. (рис. 3)

Рис. 3 (Ис­точ­ник), (Ис­точ­ник)

У Кати стало кошек боль­ше, чем у Пети. А у Пети кошек стало мень­ше, чем у Кати.

Чтобы по­ка­зать, где боль­ше, а где мень­ше, в ма­те­ма­ти­ке при­ду­ма­ли спе­ци­аль­ные знаки: «боль­ше» и «мень­ше».

У Пети 2 кошки, а у Кати – 3. Это можно за­пи­сать сле­ду­ю­щим об­ра­зом:

Два мень­ше чем три.

– знак «мень­ше».

Это нера­вен­ство можно за­пи­сать сле­ду­ю­щим об­ра­зом:

Три боль­ше чем два.

  – знак «боль­ше».

В ма­те­ма­ти­ки можно ис­поль­зо­вать сле­ду­ю­щие знаки:

  – знак «мень­ше».

  – знак «боль­ше».

 – знак «равно».

Чтобы хо­ро­шо раз­би­рать­ся в зна­ках срав­не­ния рас­смот­рим сказ­ку.

Жил-был Ко­те­нок. Это был ма­лень­кий хо­ро­ший пу­ши­стый Ко­те­нок, ко­то­рый любил изу­чать ма­те­ма­ти­ку. Ма­те­ма­ти­ке его учил Куз­не­чик. Куз­не­чик при­ска­ки­вал к до­ми­ку Ко­тен­ка, где про­во­дил ему ин­ди­ви­ду­аль­ные за­ня­тия. Вна­ча­ле они вы­учи­ли числа от 1 до 10. (рис. 4)

Рис. 4

Ко­те­нок на­учил­ся их пи­сать ак­ку­рат­но в тет­ра­ди, на­учил­ся счи­тать пред­ме­ты. Но когда они дошли до зна­ков «боль­ше», «мень­ше», ко­те­нок никак не мог их осво­ить.  То есть он хо­ро­шо по­ни­мал, то зна­чит боль­ше, а что зна­чит мень­ше. К при­ме­ру, когда ему го­во­ри­ли, что есть 1 блю­деч­ко с мо­ло­ком и есть 3 блю­деч­ка с мо­ло­ком, он по­ни­мал, что в трех блю­деч­ках го­раз­до боль­ше мо­ло­ка. Но он пу­тал­ся в самих зна­ках. Он все­гда путал, в какую сто­ро­ну, какой знак пи­шет­ся. Ко­те­нок с тру­дом их раз­ли­чал. Куз­не­чик никак не мог при­ду­мать, как проще объ­яс­нить. Тогда он со­рвал 2 тра­вин­ки и по­лу­чи­лись 2 ко­ро­тень­кие па­лоч­ки. Он сло­жил их в форме знака «боль­ше». (рис. 5)

Рис. 5

Куз­не­чик объ­яс­нил, что там, где острие этого знач­ка, там мень­шее число долж­но сто­ять. (рис. 6)

Рис. 6

Ко­те­нок все понял и по­вто­рил, что куда острие на­прав­ле­но, там и мень­шее число.

С тех пор Ко­те­нок ни­ко­гда не пу­тал­ся со зна­ка­ми «боль­ше» или «мень­ше».

То есть острие на­прав­ле­но в сто­ро­ну мень­ше­го числа.

Пред­ста­вим ряд чисел от 1 до 10. (рис. 7)

Рис. 7

Чем число даль­ше идет по чис­ло­во­му ряду, чем оно пра­вее, тем оно боль­ше. Чем левее число, тем оно мень­ше.

Какое из чисел мень­ше 2 или 7?

Два мень­ше семи.

Какое из чисел мень­ше: 1 или 10?

.

Один мень­ше де­ся­ти.

Срав­ни­те числа 8 и 4.

8 боль­ше чем 4, так как 8 идет даль­ше по чис­ло­во­му ряду. 8 яблок боль­ше чем 4 яб­ло­ка, 8 руб­лей боль­ше чем 4 рубля.

Во­семь боль­ше чем че­ты­ре.

Срав­ни­те числа 9 и 3.

Де­вять на­хо­дит­ся пра­вее чем три.

Если воз­ни­ка­ют со­мне­ния, то можно пред­ста­вить дан­ное вы­ра­же­ние с по­мо­щью точек. (рис. 8)

Рис. 8

Можно уви­деть, что 9 боль­ше чем 3.

Де­вять боль­ше трех.

Срав­ни­те числа 5 и 10. Какое из них боль­ше?

Де­сять боль­ше пяти.

Срав­ни­те числа 6 и 7. Какое из них боль­ше.

Семь боль­ше шести.

Срав­ни­те числа 3 и 3.

Три равно трем.

Знак «равно» очень часто ис­поль­зу­ет­ся в ма­те­ма­ти­ке.

На дан­ном уроке вы узна­ли, что зна­чит срав­не­ние чисел, в какую сто­ро­ну ста­вят­ся знаки «боль­ше» и «мень­ше». Вы по­тре­ни­ро­ва­лись пра­виль­но ис­поль­зо­вать дан­ные знаки на ве­се­лых при­ме­рах.

ИСТОЧНИКИ

http://www.youtube.com/watch?v=aVXblZnEYhQ

http://interneturok.ru/ru/school/matematika/1-klass/nachalnoe-znakomstvo-s-matematikoj/ponyatiya-bolshe-menshe-i-ravno?seconds=0&chapter_id=334

Знак (математика) — Простая английская Википедия, бесплатная энциклопедия

Из Простая английская Википедия, бесплатная энциклопедия

Символы плюс и минус используются для обозначения знака числа. Плюс означает положительный, а минус означает отрицательный.

Не путать с синусоидальной функцией в тригонометрии.

В математике слово знак относится к свойству быть положительным или отрицательным. Каждое действительное число, отличное от нуля, является либо положительным, либо отрицательным и, следовательно, имеет знак. Ноль сам по себе беззнаковый или беззнаковый. В дополнение к нанесению знаков на действительные числа слово «знак» используется в математике для обозначения частей математических объектов, которые означают положительность и отрицательность. Обычно, если числа видны без знака, они воспринимаются как положительное число. В противном случае перед числом добавляется знак минус «−{\ displaystyle -}», чтобы указать, что число является отрицательным по отношению к другому числу. ^{[1] [2]}

Слово «знак» также иногда используется для обозначения различных математических знаков, таких как знаки плюс и минус и знак умножения.

Вещественное число называется положительным, если оно больше нуля, и отрицательным, если меньше нуля. Атрибут быть положительным или отрицательным называется знаком числа. Считается, что сам ноль не имеет знака. ^[3]

В арифметике знак числа часто обозначается знаком плюс или минус перед числом. Например, +3 будет обозначать положительную 3, а -3 будет обозначать отрицательную 3. Когда не указан знак плюс или минус, основной способ увидеть это состоит в том, что число положительное. ^[2]

Знак любого числа, отличного от нуля, можно изменить на положительный с помощью функции абсолютного значения. Например, абсолютное значение −3 и абсолютное значение 3 равны 3. В символах это будет записано как |−3| = 3 и |3| = 3.

Знак нуля[изменить | изменить источник]

Число ноль не является ни положительным, ни отрицательным, и поэтому не имеет знака. ^[3] В арифметике +0 и -0 означают одно и то же число 0.

Поскольку ноль не является ни положительным, ни отрицательным, для обозначения знака неизвестного числа иногда используются следующие выражения:

• Число является положительным , если оно больше нуля.
• Число является отрицательным , если оно меньше нуля.
• Число является неотрицательным , если оно больше или равно нулю.
• Число является неположительным , если оно меньше или равно нулю.

Таким образом, неотрицательное число либо положительно, либо равно нулю, а неположительное число либо отрицательно, либо равно нулю. Например, абсолютное значение действительного числа всегда неотрицательно, но не обязательно положительно.

Это же определение иногда используется для функций, которые принимают действительные или целые значения. Например, функцию можно назвать положительной, если все ее значения положительны, или неотрицательной, если все ее значения неотрицательны.

Знак угла[изменить | change source]

При измерении по оси x углы на единичной окружности считаются положительными в направлении против часовой стрелки и отрицательными в направлении по часовой стрелке.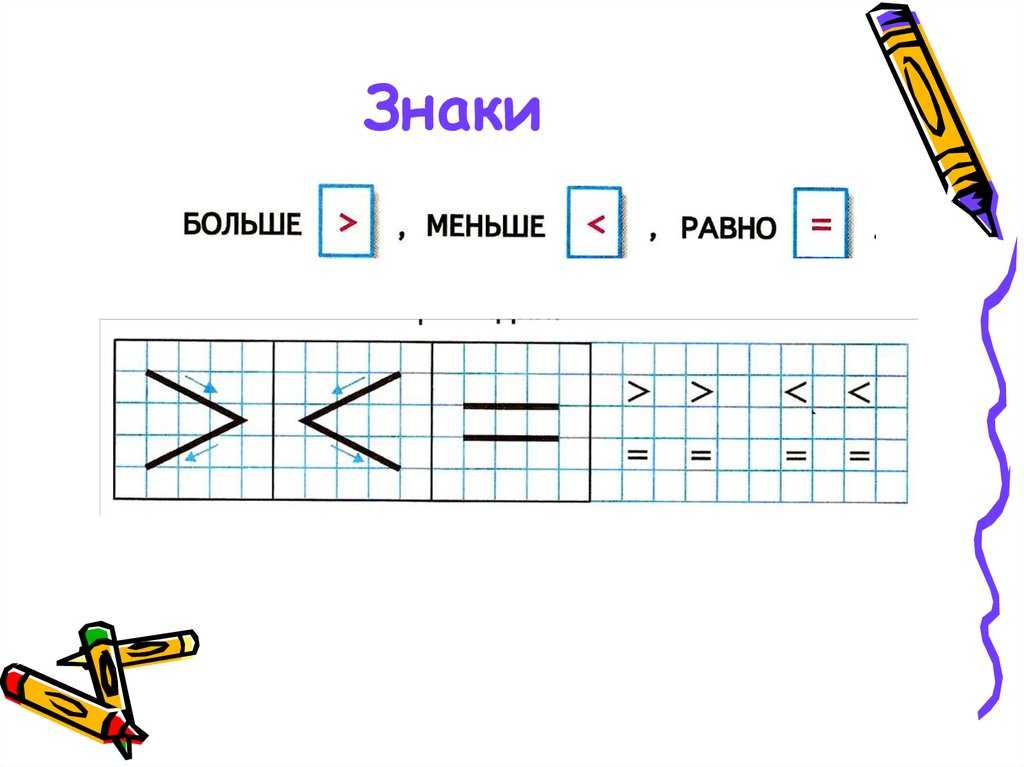

Во многих текстах часто встречается знак вместе с мерой угла, в частности, локализованного угла или угла поворота. В такой ситуации знак говорит, направлен ли угол по часовой стрелке или против часовой стрелки. Хотя могут использоваться разные соглашения, в математике принято считать углы против часовой стрелки положительными, а углы по часовой стрелке – отрицательными.

Также можно поставить знак угла поворота в трех измерениях, предполагая, что ось вращения была ориентирована. В частности, правый поворот вокруг оси обычно считается положительным, а левый поворот считается отрицательным.

Знак направления[изменить | изменить источник]

В арифметике и физике принято обозначать определенные направления как положительные или отрицательные. В качестве базового примера числовая линия обычно рисуется с положительными числами справа и отрицательными числами слева:

На декартовой плоскости направления вправо и вверх обычно считаются положительными, причем вправо является положительным x -направлением, а вверх – положительным y -направлением.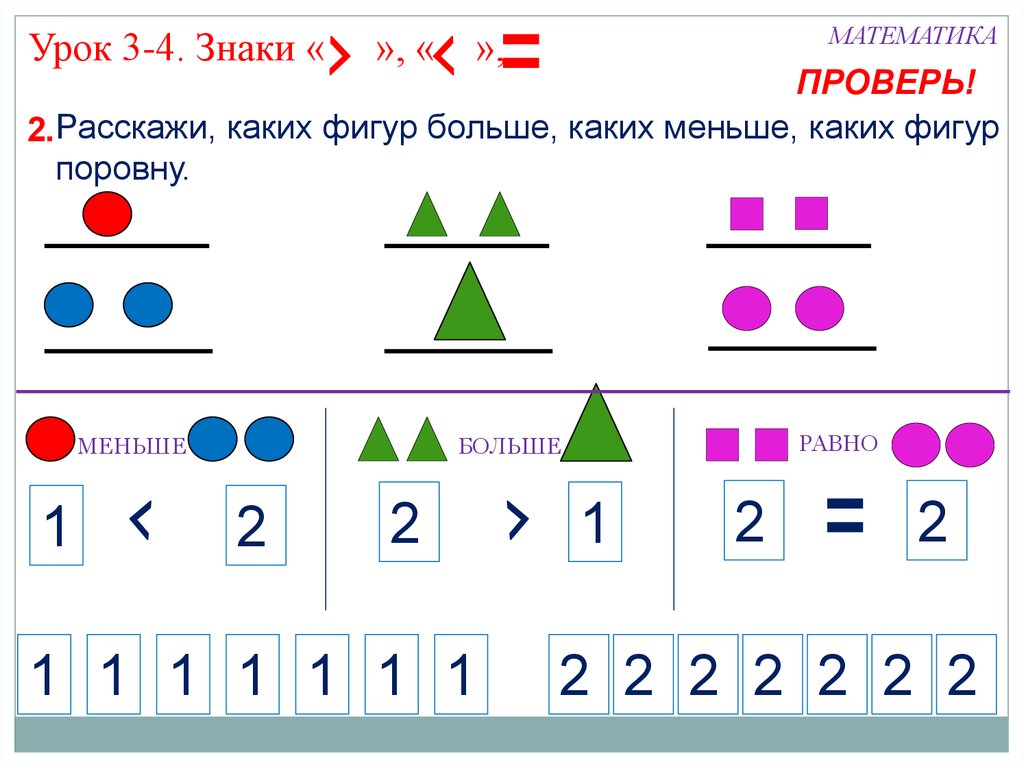

Другие значения[изменить | изменить источник]

Электрический заряд может быть положительным или отрицательным.

В дополнение к знаку действительного числа слово «знак» также используется в различных родственных смыслах в математике и других науках:

• В теории графов граф со знаком — это граф, в котором каждое ребро отмечено положительным или отрицательным знаком.
• В физике любой электрический заряд имеет знак, положительный или отрицательный. По общим правилам положительный заряд — это заряд того же знака, что и у протона, а отрицательный заряд — это заряд того же знака, что и у электрона.

• Список математических символов

1. ↑ «Список арифметических и общепринятых математических символов». Математическое хранилище . 2020-03-17. Проверено 26 августа 2020 г. .
2. ↑ ^{2.0 2.1} «Сложение и вычитание положительных и отрицательных чисел». www.mathsisfun.com . Проверено 26 августа 2020 г. .
3. ↑ ^{3.0 3.1} «Числа — Целые числа со знаком — Подробно». www.math.com . Проверено 26 августа 2020 г. .

404: Страница не найдена

Страница, которую вы пытались открыть по этому адресу, похоже, не существует. Обычно это результат плохой или устаревшей ссылки. Мы извиняемся за любые неудобства.

Что я могу сделать сейчас?

Если вы впервые посещаете TechTarget, добро пожаловать! Извините за обстоятельства, при которых мы встречаемся. Вот куда вы можете пойти отсюда:

• Ознакомьтесь с последними новостями.
• Наша домашняя страница содержит самую свежую информацию о Центре обработки данных.
• Наша страница о нас содержит дополнительную информацию о сайте, на котором вы находитесь, Data Center.
• Если вам нужно, свяжитесь с нами, мы будем рады услышать от вас.

Поиск по категории

SearchWindowsServer

• Советы, как избежать проблем при переходе с Exchange 2010 на Office 365

  Теперь, когда Exchange Server 2010 и Exchange 2013 являются устаревшими продуктами, администраторам следует предпринять усилия по миграции, чтобы избежать …

• Microsoft исправляет нулевой день Windows во вторник с апрельским патчем

  То, что было старым, снова стало новым, так как несколько обновлений безопасности из прошлого вернулись в этом месяце, чтобы увеличить общее количество …

• Разверните WebJEA, чтобы расширить возможности своих пользователей с помощью PowerShell

  Предоставьте своим сценариям автоматизации графический интерфейс, который упростит конечным пользователям получение необходимой им информации с помощью более оптимизированного …

Облачные вычисления

• Преимущества и ограничения Google Cloud Recommender

  Расходы на облако могут выйти из-под контроля, но такие службы, как Google Cloud Recommender, предоставляют информацию для оптимизации ваших рабочих нагрузок. Но…

• Zadara выбирает нового генерального директора, поскольку основатель переходит на роль технического директора

  Йорам Новик, второй генеральный директор облачного стартапа Zadara, привносит в эту должность многолетний опыт руководства ИТ и рассказывает о …

• Как работает маршрутизация на основе задержки в Amazon Route 53

  Если вы рассматриваете Amazon Route 53 как способ уменьшить задержку, вот как работает этот сервис.

Хранение

• Сравните хранилище BLOB-объектов Azure и озеро данных Емкость

  , функции безопасности и цены — это лишь некоторые из многих факторов, которые следует учитывать при сравнении организаций Azure Blob …

• HPE предоставляет многопротокольное хранилище Alletra для GreenLake

  Новейшее дополнение HPE к портфолио Alletra поддерживает блочные, файловые и объектные протоколы.