Знак математика больше: Математические знаки ≈ ∑ ⇒ ∈ ≤ ∞

Содержание

Значение символа

Знак меньше ставится для того, чтобы показать, что одно число (выражение, переменная) меньше другого. Этот математический оператор является одним из знаков неравенства. Неравенство в математике — утверждение об относительной величине двух объектов (один из объектов меньше или не больше другого), или о том, что два объекта не одинаковы (отрицание равенства). В Юникоде, знак больше находится в разделе основная латиница 0000–007F с версии 1.0.0 от 1991 года.

Символ «Знак меньше» был утвержден как часть Юникода версии 1.

1 в 1993 г.

Этот текст также доступен на следующих языках: Español;

Свойства

Версия	1.1
Блок	Основная латиница
Тип парной зеркальной скобки (bidi)	Нет
bmg	003E
Композиционное исключение	Нет
Изменение регистра	003C
Простое изменение регистра	003C

Кодировка

Кодировка	hex	dec (bytes)	dec	binary
UTF-8	3C	60	60	00111100
UTF-16BE	00 3C	0 60	60	00000000 00111100
UTF-16LE	3C 00	60 0	15360	00111100 00000000
UTF-32BE	00 00 00 3C	0 0 0 60	60	00000000 00000000 00000000 00111100
UTF-32LE	3C 00 00 00	60 0 0 0	1006632960	00111100 00000000 00000000 00000000

Наборы с этим символом:

Урок математики в 1 классе по теме «Знаки > (больше), < (меньше), = (равно)» | План-конспект урока по математике (1 класс) на тему:

ОТКРЫТЫЙ УРОК ПО МАТЕМАТИКЕ В 1 КЛАССЕ ПО ТЕМЕ:

« Знаки > (больше),

УМК «Школа России», автор учебника М. И. Моро

Тип урока: изучение нового материала.

Цель урока: в ходе практической работы и наблюдений познакомить со знаками >,

Планируемые результаты: учащиеся научатся сравнивать любые два числа и записывать результат сравнения, используя знаки >,

Познавательные УУД:

Ориентироваться в учебнике.
Понимать информацию, представленную в виде текста, рисунка, схем.
Сравнивать предметы, объекты: находить общее и различие.
Классифицировать предметы, объекты по заданным критериям.

Регулятивные УУД:

Организовывать свое рабочее место.
Осуществлять контроль в форме сличения своей работы с заданным эталоном..
Вносить дополнения, исправления в свою работу.

Коммуникативные УУД:

Соблюдать нормы речевого этикета.
Вступать в диалог.
Сотрудничать с товарищами при выполнении заданий в паре: устанавливать и соблюдать очередность действий, корректно сообщать товарищу об ошибках.
Участвовать в коллективном обсуждении учебной проблемы.

Оборудование: для учителя – интерактивная доска или проектор; магнитный набор цифр и знаков, геометрических фигур; учебник «Математика, 1 класс»; рабочая тетрадь с печатной основой;

для учащихся – геометрический набор; большие карточки с цифрами; учебник; рабочая тетрадь, пенал.

Ход урока

1. Организационный момент

2. Актуализация знаний

1. Логическая разминка.

– Сколько хвостов у четырех щенят?

– Сколько месяцев длится лето?

– Что лишнее: ручка, карандаш, отрезок? Почему?

– Прошли четыре дня после воскресенья. Какой наступил день?

– Сколько букв в слове «книга»?

2. Устный счет.

– Сегодня мы отправимся в математическое путешествие, но сначала нам нужно выбрать транспортное средство. Путешествие сказочное, поэтому, прибывать на станции мы будем всегда одновременно.

Приготовьте счетный набор, выполните задание.

Задание:

Выбрать рисунок и выложить такой же на парте.

– Какое кол-во фигур вы использовали? Положите карточку соответствующую кол-ву. ( На доске также.)

– На каких рисунках столько же фигур? (Корабль, легковая машина.)

– На каких рисунках меньше всего? (Маленький грузовик.)

– На каких больше 6, но меньше 9? (Ракета.)

– Внимание! Путешествие начинается. Чтобы попасть на математическую станцию, необходимо хором вести отсчет. Закрыли глаза. Считаем от1 до 5.

Станция «Быстрый счет»

– Мы прибываем на станцию ( Чтение хором, на доске появляется запись.)

1 задание (Работа с большими карточками, цифры от 1 до 5.)

– Дети, получившие карточки, выходят к доске и строятся по порядку. (Проверка.)

– Делайте шаг вперед, если ответом является число на карточке и называйте его.

1) Какое число следует за числом 3? 4?

2) Какое число стоит между числами 1 и 3? 3 и 5?

3) Какое число предшествует числу 4? 5? 2?

4) Назовите соседей числа 3? 2?

2 задание (Задачи в стихах.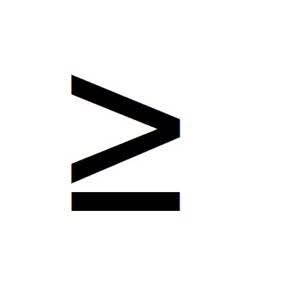 Дети показывают карточку с ответом.)

1) Карандаш один у Миши,

Карандаш один у Гриши.

Сколько всего карандашей у малышей?

2) Четыре краски есть у Сани,

Одна у маленького брата.

Все краски посчитайте сами.

Ну, постарайтесь-ка, ребята!

3) Четыре сороки пришли на уроки.

Одна из сорок не знала урок.

Сколько прилежно трудилось сорок?

4) Два щенка – баловника бегают, резвятся.

К шалунишкам три дружка с громким лаем мчатся.

Вместе лучше – веселей.

Сколько будет всех друзей?

– Вы справились с заданиями, и мы отправляемся на следующую станцию.

Станция «Спортивная»

– Закрываем глаза, путешествие продолжается.

– Хором считаем от 3 до 8.

(Дети встают и выполняют зарядку.)

Мы читали, мы считали,

А теперь тихонько встали.

Раз – присели, два – нагнулись,

На носочках потянулись.

Руки ставим на бочок:

На носочках скок, скок, скок.

А теперь все тихо сели,

Продолжаем наш урок.

Станция «Числовые домики»

– Закрыли глаза. Считаем от 7 до 3.

– Вы должны зажечь окошки в домиках. (Работа ведется около доски и с места, ответ дети показывают карточками.)

– Закрыть глаза – продолжить состав чисел.

2 – это 1 и ?

3 – это 2 и ?

4 – это 2 и ?

4 – это 1 и ?

5 – это 4 и ?

5 – это 2 и ?

3. Работа по теме урока

1) Фронтальная работа

Станция «Математические знаки»

– Закрыли глаза. Считаем от 10 до 5.

– Перечислите знаки, которые вы знаете. (Дети выходят к доске и берут карточки со знаками +, -, =. )

Дети выкладывают на парте примеры (счетный набор)

2 3=5 – Какие карточки перевернуты? Выйти к доске и заполнить

пропуски.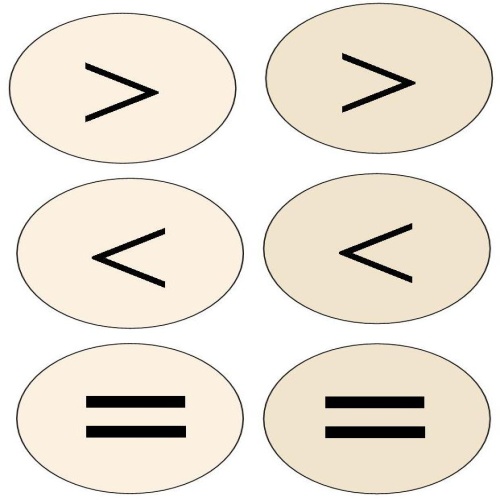

5 1=4

3 1 4

Физкультминутка на внимание.

Покажите, что вы готовы к работе.

– левую руку вверх

– 3 вращения кистью

– правую руку вверх

– 2 хлопка

– правую руку вперед

– 3 вращения кистью

– левую руку вперед

– 2 хлопка

– Сложили руки на столе.

(Вернуться к изображениям транспортных средств. Индивидуальная работа (дети используют счетный набор) и фронтальная (на доске – магнитные цифры).

– Сравните количество фигур корабля и легковой машины. Как это записать? (10=10)

– А теперь сравните по количеству фигуры грузовиков. Где фигур больше? Как же мы запишем сравнение? (Ответы детей.)

– Мы не можем воспользоваться знаком =. Нужен новый знак. В математике этот знак называется больше >.

9 > 6

(Читает учитель. Читают все дети.)

– На каком рисунке фигур меньше? Значит, какое число меньше 6 или 9? В записи мы будем использовать знак меньше

(Читает учитель. Читают все дети.)

– Что вам напоминают эти знаки? (уголки, клювики, ротики)

Открытый ротик направлен к большему числу, уголочек – к меньшему.

Физкультминутка

2) Работа по учебнику

– Откройте учебник на с. 46. Как называются знаки вверху страницы? (Больше, меньше, равно.)

– Прочитайте, что мы будем делать сегодня на уроке.

– Что мы уже узнали? (Как обозначаются слова «больше», «меньше», «равно».)

– Как вы думаете, для чего нужны эти знаки? (Чтобы экономить время при записи.)

– Посмотрите на левый верхний рисунок. Какие фигуры вы видите? (Два зеленых квадрата и три синих круга)

– Чего больше? Как это записать? Чего меньше? Прочитайте запись.

(По аналогии разбираются картинки справа, иллюстрирующие записи 5>4, 4

– Посмотрите на рисунок с птицами. Составьте рассказ по записи.

(Было 3 птицы, прилетела еще 1. Птиц стало 4.)

– Птиц стало больше или меньше? Как это записали?

– Составьте рассказ по второй записи. (Было 4 птицы, одна птица улетела. Осталось 3 птицы.)

– Птиц стало больше или меньше? Прочитайте запись. (Три меньше четырех.)

Работа в паре.

– Вместе с соседом по парте составьте записи к картинкам с вишнями.

(Проверка. Записи приведены на доске: 3+1=4, 4>1, 4-3=1, 1

4. Закрепление изученного материала

1) Работа в тетради с печатной основой.

– Откройте тетрадь на с. 18. Прочитайте первое задание. Самостоятельно запишите, какое время показывают часы.

(Фронтальная проверка.)

– Посмотрите на знаки, приведенные ниже. Как называется знак, который записан первым? Вторым?

(Объяснение, показ, запись знаков в тетради.)

– Посмотрите на рисунок с мячами.

(Записать количество, заполнить пропуски рисунками, с помощью новых знаков составить запись 5>3, 3

2) Работа по учебнику.

– Рассмотрите рисунок на с. 47. вспомните сказку В. Сутеева «Мешок яблок». За что звери принесли зайцу столько подарков? (За доброту. )

Работа в паре.

– Пользуясь рисунком, расскажите соседу по парте, как можно получить число 5.

(Проверка. Выходит к доске пара для ответа. Спросить несколько пар.)

– Посмотрите на следующий рисунок. Сколько желтых полосок нужно положить, чтобы накрыть розовую? А сколько зеленых? Почему получили разные ответы? (Полоски разной длины.) Каких полосок нужно больше?

5. Рефлексия

– Наше путешествие заканчивается.

– Оцените, как вы поняли новую тему, с помощью «Светофора».

6. Подведение итогов урока

– С какими знаками мы сегодня познакомились?

– Покажите знак «больше».

– Покажите знак «меньше».

Таблица знаков (символов) в алгебре и их значения

Символ / знак	Название	Значение / описание	Пример
x	переменная x	неизвестная переменная, которую нужно найти	если 2x = 6, значит x = 3
≡	эквивалентность	логическая равнозначность или эквиваленция	A ≡ B, A эквивалентно B
~	приблизительно равно	приближенное равенство (слабое)	15 ~ 14
≈	приблизительно равно	приближенное равенство	01) ≈ 0.01</nobr>” data-order=”<nobr>sin (0.01) ≈ 0.01</nobr>”>sin (0.01) ≈ 0.01
∝	пропорционально	пропорциональность величин	y ∝ x, если: y = kx, а k – константа
∞	бесконечность	отсутствие границ или количественной меры
≪	намного меньше	A намного меньше, чем B	5 ≪ 50000
≫	намного больше	A намного больше, чем B	50000 ≫ 5
( )	круглые скобки	выражение в скобках считается в первую очередь	4 ⋅ (2+3) = 20
[ ]	квадратные скобки	выражение в скобках считается в первую очередь	[(6-3)⋅(2+7)] = 27
{ }	фигурные скобки	различное применение
⌊x⌋	нижние квадратные скобки	округление числа x до нижнего целого (пол)	3⌋ = 5</nobr>” data-order=”<nobr>⌊5.3⌋ = 5</nobr>”>⌊5.3⌋ = 5
⌈x⌉	верхние квадратные скобки	округление числа x до верхнего целого (потолок)	3⌉ = 6</nobr>” data-order=”<nobr>⌈5.3⌉ = 6</nobr>”>⌈5.3⌉ = 6
x!	восклицательный знак	факториал	5! = 1⋅2⋅3⋅4⋅5 = 120
log	логарифм	log_ab Это степень, в которую нужно возвести a, чтобы получить b	log₂8=3
\| x \|	одиночная вертикальная черта	абсолютная величина (модуль)	\| -7 \| = 7
f (x)	функция с переменной x	величина x определяет значение величины f (x)	f (x) = 5x + 2
(f ∘ g)	композиция функций	е. применение одной функции к результату другой” data-order=”<nobr>(f∘ g) (x) = f (g(x)),</nobr><br>т.е. применение одной функции к результату другой”>(f∘ g) (x) = f (g(x)), т.е. применение одной функции к результату другой	f (x)=5x, g (x)=x-2 ⇒ (f ∘ g (x)) = 5 (x-2)
(a,b)	открытый интервал	(a,b) = {x \| a < x < b}	x ∈ (3,7)
[a,b]	закрытый интервал	[a,b] = {x \| a ≤ x ≤ b}	x ∈ [3,7]
∆	дельта	изменение/разница	∆t = t₂ – t₁
∆	дискриминант	Δ = b² – 4ac	y = x² + 3x – 5 Δ = 3² – 4⋅1⋅(-5) = 29
∑	сигма	сумма всех значений в выбранном диапазоне	..+x<sub>n</sub></em></span></nobr>” data-order=”<nobr><span class="math"><em>∑ x<sub>i</sub>= x<sub>1</sub>+x<sub>2</sub>+…+x<sub>n</sub></em></span></nobr>”>∑ x_i= x₁+x₂+…+x_n
∑∑	сигма	двойная сигма	png" class="stbSkipLazy alignnone size-full" width="230" height="400" data-full="https://microexcel.ru/wp-content/uploads/2020/01/formula-dvoynaya-sigma.png" />” data-order=”<img src="https://microexcel.ru/wp-content/uploads/2020/01/formula-dvoynaya-sigma.png" class="stbSkipLazy alignnone size-full" width="230" height="400" data-full="https://microexcel.ru/wp-content/uploads/2020/01/formula-dvoynaya-sigma.png" />”>
∏	заглавная буква “пи”	произведение множителей в выбранном диапазоне	.. ⋅ x<sub>n</sub></em></span></nobr>” data-order=”<nobr><span class="math"><em>∏ x<sub>i</sub>= x<sub>1</sub> ⋅ x<sub>2</sub> ⋅ … ⋅ x<sub>n</sub></em></span></nobr>”>∏ x_i= x₁ ⋅ x₂ ⋅ … ⋅ x_n
e	e (число) или число Эйлера	718281828…</nobr>” data-order=”<nobr><span class="math"><em>e</em></span> = 2.718281828…</nobr>”>e = 2.718281828…
γ	Постоянная Эйлера — Маскерони	5772156649…</nobr>” data-order=”<nobr><span class="math"><em>γ</em></span> = 0.5772156649…</nobr>”>γ = 0.5772156649…
φ	золотое сечение	golden ratio constant
π	число “пи”	141592654…</nobr><br>Это математическая константа, которая выражает отношение длины окружности к её диаметру.” data-order=”<nobr><span class="math"><em>π</em></span> = 3.141592654…</nobr><br>Это математическая константа, которая выражает отношение длины окружности к её диаметру.”>π = 3.141592654… Это математическая константа, которая выражает отношение длины окружности к её диаметру.

Math.sign () – JavaScript | MDN

Функция Math.sign () возвращает либо положительный или отрицательный +/- 1, указывающий знак число передано в аргумент. Если число, переданное в Math.sign (), равно 0, он вернет +/- 0. Обратите внимание, что если число положительное, явный (+) будет , а не .

Исходный код этого интерактивного примера хранится в репозитории GitHub.Если вы хотите внести свой вклад в проект интерактивных примеров, клонируйте https://github.com/mdn/interactive-examples и отправьте нам запрос на перенос.

Исходный код этого интерактивного примера хранится в GitHub. репозиторий. Если вы хотите внести свой вклад в проект интерактивных примеров, пожалуйста, клонировать https://github.com/mdn/interactive-examples и отправьте нам запрос на перенос.

Параметры

x: Номер. Если этот аргумент не является числом , он неявно преобразуется к одному.

Возвращаемое значение

Число, представляющее знак данного аргумента:

Если аргумент положительный, возвращает 1 .
Если аргумент отрицательный, возвращает -1 .
Если аргумент положительный ноль, возвращает 0 .
Если аргумент отрицательный ноль, возвращает -0 .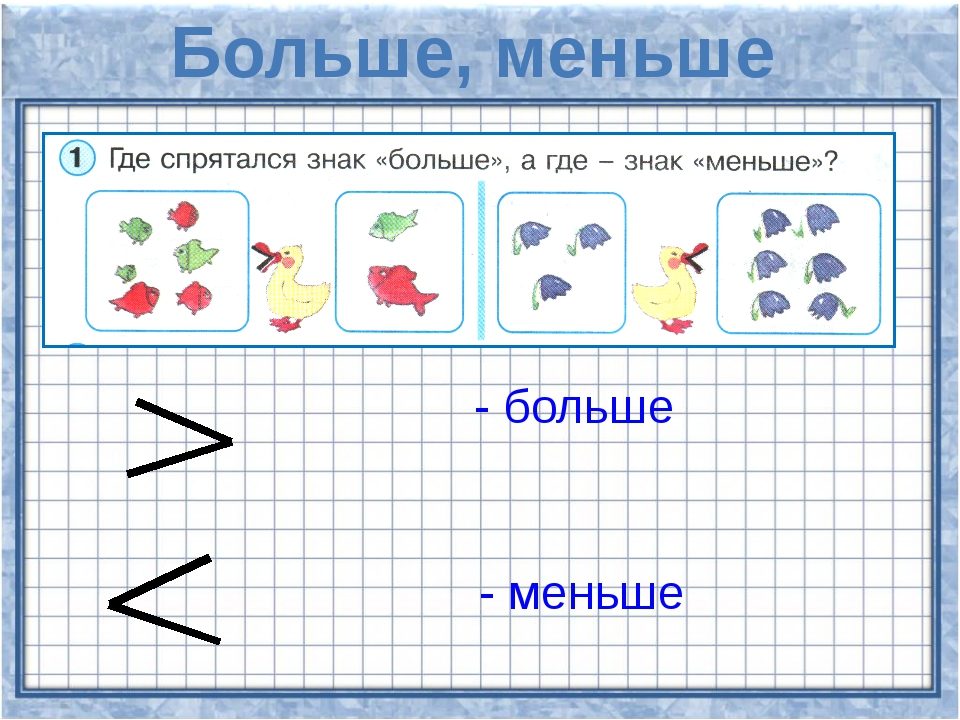
В противном случае возвращается NaN .

Поскольку sign () является статическим методом Math , вы всегда используете его как Math.sign () , а не как метод объекта Math , который вы created ( Math не является конструктором).

  if (! Math.sign) {
  Math.sign = function (x) {
    
    
    
    
    
    return ((x> 0) - (x <0)) || + х;
    
    
    
    
    
    
    
    
  };
}

В приведенном выше полифилле дополнительное приведение типов не требуется для создания (x> 0) или (x <0) чисел, потому что вычитание их друг из друга вынуждает преобразование типов из логических в числа.

Использование Math.sign ()

  Math.sign (3);
Математический знак (-3);
Математический знак ('- 3');
Math.sign (0);
Математический знак (-0);
Математический знак (NaN);
Math.sign ('фу');
Math.sign ();

Таблицы BCD загружаются только в браузере

Math. sign () - JavaScript | MDN

Die Math.sign () Funktion gibt das Vorzeichen einer Zahl zurück, welches angibt, ob eine Zahl positiv, negativ oder 0 ist.

Параметр

Rückgabewert

Eine Zahl, die das Vorzeichen des übergebenen Wertes repräsentiert. Венн дер Parameter eine positive Zahl ist, eine negative Zahl ist oder eine Null (0) ist, wird die Funktion 1 , -1 , 0 или -0 zurückgeben. Andernfalls wird NaN zurückgegeben.

Weil sign () eine statische Funktion von Math ist, wird sie immer als Math.sign () eingesetzt, jedoch nicht als Methode eines erzeugten Math keathin.

Diese Funktion hat die 5 möglichen Rückgabewerte 1 , -1 , 0 , -0 и NaN , welche «положительный Zahlen», «отрицательный Zahlen», «positiv 0», «отрицательный 0» und NaN repräsentieren.

Der Übergebeparameter dieser Funktion wird implizit zu einem number -Type konvertiert.

Einsatz von `Математический знак ()`

  Математический знак (3);
Математический знак (-3);
Математический знак ('- 3');
Math.sign (0);
Математический знак (-0);
Математический знак (NaN);
Math.sign ('фу');
Math.sign ();

  if (! Math.sign) {
  Math.sign = function (x) {
    
    
    
    
    
    return ((x> 0) - (x <0)) || + х;
    
    
    
    
    
    
    
    
  };
}

In diesem Polyfill ist keine weitere Typumwandlung nötig, um aus (x> 0) или (x <0) Zahlen zu machen, weil das Subtrahieren voneinander eine Typkonvertierung von booleanwing zu Zahlen erzahlen.

Таблицы BCD загружаются только в браузере

Знак (математика) - Простая английская Википедия, бесплатная энциклопедия

Символы плюса и минуса используются для обозначения знака числа. Плюс означает положительный, а минус означает отрицательный.

В математике слово знак обозначает свойство быть положительным или отрицательным. Каждое действительное число, отличное от нуля, может быть положительным или отрицательным и, следовательно, имеет знак. Сам по себе ноль без знака или без знака. Помимо добавления знаков к действительным числам, слово "знак" используется в математике для обозначения частей математических объектов, которые означают положительность и отрицательность.Обычно, если числа отображаются без знака, они рассматриваются как положительные числа. В противном случае перед числом добавляется знак минус "- {\ displaystyle -}", чтобы указать, что это число является отрицательным для другого числа.

[1] ^[2]

Слово «знак» также иногда используется для обозначения различных математических знаков, таких как знаки плюс и минус и знак умножения.

Действительное число считается положительным, если оно больше нуля, и отрицательным, если оно меньше нуля.Признак положительности или отрицания называется знаком числа. Сам по себе ноль не считается знаком. ^[3]

В арифметике знак числа часто обозначается путем добавления знака плюс или минус перед числом. Например, +3 будет обозначать положительное число 3, а −3 - отрицательное 3. Когда не указан знак плюс или минус, основной способ увидеть это число - это положительное число. ^[2]

Знак любого числа, отличного от нуля, можно изменить на положительный с помощью функции абсолютного значения.Например, абсолютное значение −3 и абсолютное значение 3 равны 3. В символах это будет записано как | −3 | = 3 и | 3 | = 3.

Знак нуля [изменить | изменить источник]

Число ноль не является ни положительным, ни отрицательным, и поэтому не имеет знака. ^[3] В арифметике +0 и -0 означают одно и то же число 0.

Поскольку ноль не является ни положительным, ни отрицательным, для обозначения знака неизвестного числа иногда используются следующие символы:

Число положительное , если оно больше нуля.
Число отрицательное , если оно меньше нуля.
Число неотрицательное , если оно больше или равно нулю.
Число , неположительное число , если оно меньше или равно нулю.

Таким образом, неотрицательное число может быть положительным или нулевым, а неположительное число - отрицательным или нулем. Например, абсолютное значение действительного числа всегда неотрицательно, но не обязательно положительно.

То же определение иногда используется для функций, которые принимают действительные или целые значения.Например, функция будет называться положительной, если все ее значения положительны, или неотрицательными, если все ее значения неотрицательны.

Знак угла [изменить | изменить источник]

Во многих текстах часто встречается знак вместе с величиной угла, в частности, локализованный угол или угол поворота. В такой ситуации знак говорит, идет ли угол по часовой стрелке или против часовой стрелки. Хотя могут использоваться разные соглашения, в математике принято считать, что углы против часовой стрелки считаются положительными, а углы по часовой стрелке считаются отрицательными.

Также можно поставить знак угла поворота в трех измерениях, предполагая, что ось вращения ориентирована. В частности, правый поворот вокруг оси обычно считается положительным, а левый - отрицательным.

Знак направления [изменить | изменить источник]

В арифметике и физике принято обозначать определенные направления как положительные или отрицательные. В качестве базового примера числовая линия обычно рисуется с положительными числами справа и отрицательными числами слева:

На декартовой плоскости правое и восходящее направления обычно считаются положительными, при этом вправо является положительным направлением x , а вверх - положительным направлением y .

Другие значения [изменить | изменить источник]

Помимо знака действительного числа, слово «знак» также используется по-разному в математике и других науках:

В теории графов граф со знаком - это граф, в котором каждое ребро помечено положительным или отрицательным знаком.
В физике у любого электрического заряда есть знак, положительный или отрицательный. По общим правилам, положительный заряд - это заряд того же знака, что и у протона, а отрицательный заряд - это заряд того же знака, что и у электрона.

↑ «Список арифметических и общих математических символов». Математическое хранилище . 2020-03-17. Проверено 26 августа 2020.
↑ ^2,0 ^2,1 «Сложение и вычитание положительных и отрицательных чисел». www.mathsisfun.com . Проверено 26 августа 2020.
↑ ^3,0 ^3,1 «Числа - целые числа со знаком - подробно». www.math.com . Проверено 26 августа 2020.

Математические символы

Символ	Значение	Пример
+	прибавить	3 + 7 = 10
-	вычесть	5−2 = 3
×	умножить	4 × 3 = 12
÷	делить	20 ÷ 5 = 4
/	делить	20/5 = 4
()	группировки символов	2 (а-3)
[]	группировки символов	2 [a − 3 (b + c)]
{}	набор символов	{1, 2, 3}
π	пи	A = πr ²
∞	бесконечность	∞ бесконечен
=	равно	1 + 1 = 2
	примерно равно	π 3. 14
≠	не равно	π ≠ 2
<≤	меньше, меньше или равно	2 <3
> ≥	больше, больше или равно	5> 1
	корень квадратный («корень»)	√4 = 2
°	градуса	20 °
	следовательно	a = b b = a

math - Математические функции - Python 3.9.1 документация

Этот модуль обеспечивает доступ к математическим функциям, определенным C стандарт.

Эти функции нельзя использовать с комплексными числами; использовать функции то же имя из модуля cmath , если вам требуется поддержка сложных числа. Различие между функциями, поддерживающими комплексные числа, и те, которых не делают, поскольку большинство пользователей не хотят учиться так много математика, необходимая для понимания комплексных чисел.Получение исключения вместо сложного результата позволяет раньше обнаруживать неожиданный комплекс число, используемое в качестве параметра, чтобы программист мог определить, как и почему он был создан в первую очередь.

Этот модуль предоставляет следующие функции. За исключением случаев, когда явно в противном случае все возвращаемые значения являются плавающими.

Теоретико-числовые функции и функции представления

математика. потолок ( x ): Возвращает потолок x , наименьшее целое число, большее или равное x .Если x не является числом с плавающей запятой, делегирует x .__ ceil __ () , который должен вернуть Интегральное значение .

математика.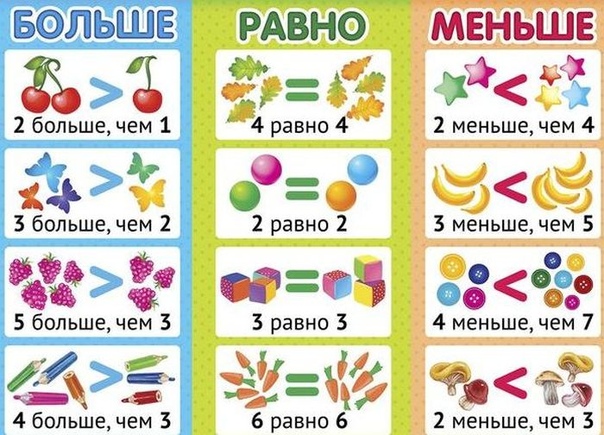 гребень ( n , k )

Вернуть количество способов выбора k элементов из n элементов без повторения и без заказа.

Оценивается как n! / (k! * (n - k)!) , когда k <= n и оценивает к нулю, когда k> n .

Также называется биномиальным коэффициентом, потому что он эквивалентен к коэффициенту k-го члена в полиномиальном разложении выражение (1 + x) ** n .

Вызывает TypeError , если какой-либо из аргументов не является целым числом. Вызывает ValueError , если любой из аргументов отрицательный.

математика. копия ( x , y ): Вернуть число с плавающей запятой с величиной (абсолютным значением) x , но со знаком год .На платформах, поддерживающих нули со знаком, copysign (1.0, -0.0) возвращает -1,0 .

математика. фабрики ( x ): Вернуть абсолютное значение x .

математика. факториал ( x )

Вернуть факториал x как целое число. Вызывает ValueError , если x не является целым или отрицательный.

Не рекомендуется, начиная с версии 3.9: прием чисел с плавающей запятой с целыми значениями (например, 5.0 ) устарел.

математика. этаж ( x ): Возвращает нижний предел x , наибольшее целое число, меньшее или равное x . Если x не является плавающим, делегирует x .__ floor __ () , который должен вернуть Интегральное значение .

математика. fmod ( x , y ): Вернуть fmod (x, y) , как определено библиотекой платформы C.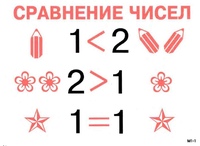 Обратите внимание, что Выражение Python x% y может не возвращать тот же результат. Намерение C стандартным является то, что fmod (x, y) будет точно (математически; до бесконечности точности), равного x - n * y для некоторого целого числа n , так что результат имеет тот же знак, что и x , и величина меньше абс. (y) .Python x% y вместо этого возвращает результат со знаком y и может быть неточно вычислимым для аргументов с плавающей запятой. Например, fmod (-1e-100, 1e100) - это -1e-100 , но результат Python -1e-100% 1e100 будет 1e100-1e-100 , что не может быть представлен в точности как поплавок и округляется до удивительного 1e100 . За по этой причине функция fmod () обычно предпочтительнее при работе с float, тогда как Python x% y предпочтительнее при работе с целыми числами.

математика.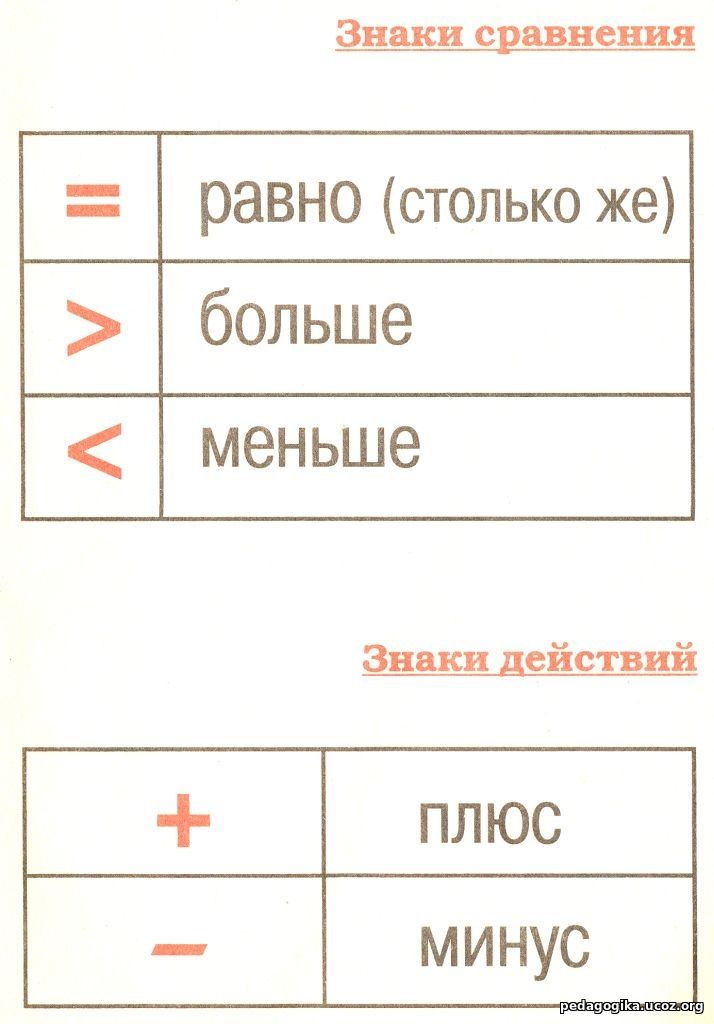 frexp ( x ): Вернуть мантиссу и показатель степени x как пару (m, e) . м - поплавок и e - целое число, такое что x == m * 2 ** e точно. Если x равно нулю, возвращает (0,0, 0) , иначе 0,5 <= abs (m) <1 . Это используется, чтобы «выбрать отдельно »внутреннее представление поплавка портативным способом.

математика. fsum ( итерация )

Вернуть точную сумму значений с плавающей запятой в итерируемом объекте. Избегает потеря точности из-за отслеживания нескольких промежуточных частичных сумм:

 >>> сумма ([. 1, .1, .1, .1, .1, .1, .1, .1, .1, .1])
0,9999999999999999
>>> fsum ([. 1, .1, .1, .1, .1, .1, .1, .1, .1, .1])
1.0

Точность алгоритма зависит от арифметических гарантий IEEE-754 и типичный случай, когда режим округления половинный.На некоторых не-Windows сборки, базовая библиотека C использует сложение расширенной точности и может иногда двойное округление промежуточной суммы, в результате чего ее младший значащий бит.

Значение символа

Свойства

Похожие символы

Кодировка

Урок математики в 1 классе по теме «Знаки > (больше), < (меньше), = (равно)» | План-конспект урока по математике (1 класс) на тему:

Таблица знаков (символов) в алгебре и их значения

Math.sign () – JavaScript | MDN

Параметры

Возвращаемое значение

Использование Math.sign ()

Math. sign () - JavaScript | MDN

Параметр

Rückgabewert

Einsatz von `Математический знак ()`

Знак (математика) - Простая английская Википедия, бесплатная энциклопедия

Знак нуля [изменить | изменить источник]

Знак угла [изменить | изменить источник]

Знак направления [изменить | изменить источник]

Другие значения [изменить | изменить источник]

Математические символы

math - Математические функции - Python 3.9.1 документация

Теоретико-числовые функции и функции представления

Добавить комментарий Отменить ответ

Значение символа

Свойства

Похожие символы

Кодировка

Урок математики в 1 классе по теме «Знаки > (больше), < (меньше), = (равно)» | План-конспект урока по математике (1 класс) на тему:

Таблица знаков (символов) в алгебре и их значения

Math.sign () – JavaScript | MDN

Параметры

Возвращаемое значение

Использование Math.sign ()

Math.<img src='/800/600/https/lh5.ggpht.com/i_onsWYNj2TZZFQpSxRTaM8-a6sxhwoqgKcnW-SJodAI_3tX5D-bq8UaDq0vXHmtj4A' /> sign () - JavaScript | MDN

Параметр

Rückgabewert

Einsatz von Математический знак ()

Знак (математика) - Простая английская Википедия, бесплатная энциклопедия

Знак нуля [изменить | изменить источник]

Знак угла [изменить | изменить источник]

Знак направления [изменить | изменить источник]

Другие значения [изменить | изменить источник]

Математические символы

math - Математические функции - Python 3.9.1 документация

Теоретико-числовые функции и функции представления

Добавить комментарий Отменить ответ

Math. sign () - JavaScript | MDN

Einsatz von `Математический знак ()`