Знак больше и меньше в математике в какую сторону и когда ставить пример: Больше, меньше, равно — урок. Математика, 1 класс.
Скобки в математике: их виды и предназначение
В данной статье рассказывается о скобках в математике, делается своеобразный их анализ, объясняется, зачем они нужны, рассматриваются виды и применения, термины и методы использования при решении или для описания материала. В заключение будем решать подобные математические примеры с подробными комментариями.
Основные виды скобок, обозначения, терминология
Для решения задач или заданий в математике (алгебре и геометрии) и дискретной математике используются три вида скобок: ( ), [ ], { }. И это, на самом деле, немало. Реже встречаются скобки такого вида ] и [, называемые обратными, или < и >, то бывают в виде уголка или треугольные, угловые скобки (первая пара обозначает, в какую сторону пишется знак меньше). Что означает такой знак в математике и в чем их разница? Их применение всегда парное (двойное), то есть имеется открывающаяся и закрывающаяся скобка в любом выражении, тогда оно имеет смысл. Скобки позволяют разграничить и определить последовательность действий.
Фигурная непарная скобка типа { встречается при решении систем уравнений, что обозначает пересечение заданных множеств, а [ скобка используется при их объединении. Далее рассмотрим их применение.
Скобки для указания порядка выполнения действий
Что означает скобка в принципе? Основное предназначение скобок – указание порядка, в котором нужно сделать действия. Тогда выражение может иметь одну или несколько пар круглых скобок. По правилу всегда выполняется первым действие в скобках, после чего умножение и деление, а позже сложение и вычитание.
Пример 1Рассмотрим на примере заданное выражение. Если дан пример вида 5+3-2, тогда очевидно, что действия выполняются последовательно. Когда это же выражение необходимо записать со скобками, тогда их последовательность меняется. То есть при (5+3)-2 первое действие выполняется в скобках. В данном случае изменений не будет. Если выражение будет записано в виде 5+(3-2), тогда в начале производятся вычисления в скобках (их нужно раскрывать), после такого раскрытия пример должен решаться математиком путем сложения с числом 5. На исходное значение в этом случае оно не повлияет.
На исходное значение в этом случае оно не повлияет.
Рассмотрим пример, который покажет, как при изменении положения скобок может перевертываться результат. Если дано выражение 5+2·4, видно, что вначале выполняется умножение, после чего сложение. Когда выражение будет иметь вид (5+2)·4, то вначале выполнится действие в скобках, после чего произведется умножение. Результаты выражений будут отличаться.
Выражения могут содержать несколько пар скобок, тогда выполнения мат-х действий начинаются с первой. В выражении вида (4+5·2)−0,5:(7−2):(2+1+12) видно, что первым делом выполняются действия в скобках, после чего деления, а в конце вычитание.
Существуют примеры, где имеются вложенные сложные скобки вида 4·6-3+8:2 и 5·(1+(8-2·3+5)-2))-4. Тогда начинается выполнение действий с внутренних скобок. Далее производится продвижение к внешним.
Пример 3Если имеется выражение 4·6-3+8:2, тогда очевидно, что в первую очередь выполняются действия в скобках. Значит, следует отнять 3 от 6, умножить на 4 и прибавить 8.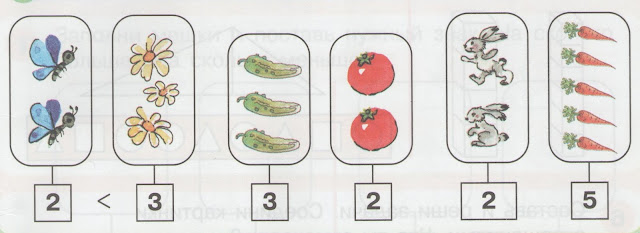
На письме могут быть использованы скобки разных размеров, а не только разновидностей. Это делается для удобства и возможности различия или отличия одной пары от другой. Внешние скобки всегда большего размера, чем внутренние. То есть получаем выражение вида 5-1:2+12+3-13·2·3-4. Редко встречается применение выделенных скобок (2+2·(2+(5·4−4)))·(6:2−3·7)·(5−3) или применяют квадратные скобки, например, [3+5·(3−1)]·7 или фигурные скобки {5+[7−12:(8−5):3]+7−2}:[3+5+6:(5−2−1)].
Перед тем, как приступить к решению, важно правильно определить порядок действий и разобрать все необходимые пары скобок. Для этого следует добавлять разные виды скобок или менять их цвет. Пометка скобки другим цветом удобна для решения, но занимает много времени, поэтому на практике чаще всего применяют круглые скобки, фигурные и квадратные скобки.
Отрицательные числа в скобках
Если необходимо изобразить отрицательные числа, тогда применяют круглые скобки в выражении. Такая запись, как 5+(−3)+(−2)·(−1), 5+-23, 257-5+-673·(-2)·-3,5 предназначена для того, чтобы упорядочить отрицательные числа в выражении.
Такая запись, как 5+(−3)+(−2)·(−1), 5+-23, 257-5+-673·(-2)·-3,5 предназначена для того, чтобы упорядочить отрицательные числа в выражении.
Скобки или кавычки не ставятся для отрицательного числа того, когда оно располагается в начале любого выражения или дроби. Если имеем пример вида −5·4+(−4):2, то очевидно, что символ минуса перед 5 можно не заключать в скобки, а при 3-0,4-2,2·3+7+3-1:2 число 2,2 записано вначале, значит скобки являются нужными. Со скобками может писаться выражение (−5)·4+(−4):2 или 3-0,4-2,2·3+7+3-1:2. Запись, где имеются скобки, считается более строгой.
Знак минуса может находиться не только перед числом, но и перед переменными, степенями, корнями, дробями, функциями, тогда их следует заключить в скобки. Это такие записи, как 5·(−x), 12:(−22), 5·-3+7-1+7:-x2+13, 434–x+2x-1,2·(-(3+2·4), 5·(-log32)-(-2×2+4), sin x·(-cos2x)+1
Скобки для выражений, с которыми выполняются действия
Использование круглых скобок с высокой вероятностью связано с указанием в выражении действий, где имеется возведение в степень, взятие производной, функции. x+3 на выходе получим 2x+3.
x+3 на выходе получим 2x+3.
Основание степени не нуждается в скобках. Поэтому запись принимает вид 03, 5×2+5, y0,5. Если в основании имеется дробное число, тогда будут использоваться круглые скобки. Получаем выражения вида (0,75)2, 22332+1, (3·x+2·y)-3, log2x-2-12x-1.
Если выражение основания степени не взять в скобки, тогда показатель может относиться ко всему выражению, что повлечет за собой неправильное решение. Когда имеется выражение вида x2+y, а -2 – это его степень, то запись примет вид (x2+y)-2. При отсутствии скобок выражение приняло бы вид x2+y-2, что является совершенно другим выражением.
Если основанием степени является логарифм или тригонометрическая функция с целым показателем, тогда запись приобретает вид sin, cos, tg, ctg, arcsin, arccos, arctg, arcctg, log, ln или lg. При записи выражения вида sin2x, arccos3y, ln5e и log52x видим, что скобки перед функциями не меняют значения всего выражения, то есть они равноценны. Получаем записи вида (sin x)2, (arccos y)3, (lne)5и log5 x2. Допустимо опущение скобок.
Допустимо опущение скобок.
Скобки в выражениях с корнями
Использование скобок в подкоренном выражении бессмысленно, так как выражение вида x+1 и x+1 являются равнозначными. Скобки не дадут изменений при решении.
Скобки в выражениях с тригонометрическими функциями
Если имеются отрицательные выражения у функций типа синус, косинус, тангенс, котангенс, арксинус, арккосинус, арктангенс, арккотангенс, тогда необходимо использовать круглые скобки. Это позволит правильно определить принадлежность выражения к имеющейся функции. То есть получим записи вида sin(−5), cos(x+2), arctg1x-223.
При записи sin, cos, tg, ctg, arcsin, arccos, arctg и arcctg при имеющемся числе скобки не используют. Когда в записи присутствует выражение, тогда имеет смысл их поставлять. То есть sinπ3, tgx+π2, arcsinx2, arctg33 с корнями и степенями, cosx2-1, arctg 32, ctgx+1-3 и подобные выражения.
Если в выражении содержатся кратные углы типа х, 2х, 3х и так далее, скобки опускаются. Разрешено записывать в виде sin 2x, ctg 7x, cos 3α. Во избежание двусмысленности скобки можно добавить в выражение. Тогда получаем запись вида sin(2·x):2 вместо sin2·x:2.
Разрешено записывать в виде sin 2x, ctg 7x, cos 3α. Во избежание двусмысленности скобки можно добавить в выражение. Тогда получаем запись вида sin(2·x):2 вместо sin2·x:2.
Скобки в выражениях с логарифмами
Чаще всего все выражения логарифмической функции заключаются в скобки для дальнейшего правильного решения. То есть получаем ln(e−1+e1), log3(x2+3·x+7), lg((x+1)·(x−2)). Опущение скобок разрешено в том случае, когда однозначно понятно, к какому выражению относится сам логарифм. Если есть дробь, корень или функция можно записывать выражения в виде log2x5, lgx-5, ln5·x-53-5.
Скобки в пределах
При имеющихся пределах стоит использовать скобки для представления выражения самого предела. То есть при суммах, произведениях, частных или разностях принято записывать выражения в скобках. Получаем, что limn→51n+n-2 и limx→0x+5·x-3x-1x+x+1:x+2×2+3. Опущение скобок предполагается, когда имеется простая дробь или очевидно, к какому выражению относится знак. Например, limx→∞1x или limx→0(1+x)1x.
Скобки и производная
При нахождении производной часто можно встретить применение круглых скобок. Если имеется сложное выражение, тогда вся запись берется в скобки. Например, (x+1)’ или sin xx-x+1.
Подынтегральные выражения в скобках
Если необходимо проинтегрировать выражение, то следует записать его в круглых скобках. Тогда пример примет вид ∫(x2+3x)dx, ∫-11(sin 2x-3)dx, ∭V(3xy+z)dxdydz.
Скобки, отделяющие аргумент функции
При наличии функции чаще всего применяются круглые скобки для их обозначения. Когда дана функция f с переменной х, тогда запись принимает вид f(x). Если имеются несколько аргументов функций, то такая функция получит вид F (x, y , z, t).
Скобки в периодических десятичных дробях
Использование периода обусловлено применением скобок при записи. Сам период десятичной дроби заключается в скобки. Если дана десятинная дробь вида 0,232323… тогда очевидно, что 2 и 3 мы заключаем в круглые скобки. Запись приобретает вид 0,(23). Это характерно для любой записи периодической дроби.
Это характерно для любой записи периодической дроби.
Скобки для обозначения числовых промежутков
Для того чтобы изобразить числовые промежутки применяют скобки четырех видов: ( ), ( ], [ ) и [ ]. В скобках прописываются промежутки, в каких функция существует, то есть имеет решение. Круглая скобка означает, что число не входит в область определения. Что означает квадратная скобка в математике в таком случае? Что число входит в область определения. При наличии бесконечности принято изображать круглую скобку.
То есть при изображении промежутков получим, что (0, 5), [−0,5, 12), -1012, -523, [5, 700], (−∞, −4], (−3, +∞), (−∞, +∞). Не вся литература одинаково использует скобки. Есть случаи, когда можно увидеть запись такого вида ]0, 1[, что означает (0,1) или [0, 1[, что значит [0, 1), причем смысл выражения не меняется.
Обозначения систем и совокупностей уравнений и неравенств
Системы уравнений, неравенств принято записывать при помощи фигурной скобки вида { . Это означает, что все неравенства или уравнения объединены этой скобкой. Рассмотрим на примере использования скобки. Система уравнений вида x2-1=0x2+x-2=0 или неравенства с двумя переменными x2-y>03x+2y≤3, cos x12x+π3=02×2-4≥5 -система, состоящая из двух уравнений и одного неравенства.
Это означает, что все неравенства или уравнения объединены этой скобкой. Рассмотрим на примере использования скобки. Система уравнений вида x2-1=0x2+x-2=0 или неравенства с двумя переменными x2-y>03x+2y≤3, cos x12x+π3=02×2-4≥5 -система, состоящая из двух уравнений и одного неравенства.
Использование фигурных скобок относится к изображению пересечения множеств. При решении системы с фигурной скобкой фактически приходим к пересечению заданных уравнений. Квадратная скобка служит для объединения.
Уравнения и неравенства обозначаются [ скобкой в том случае, если необходимо изобразить совокупность. Тогда получаем примеры вида (x-1)(x+7)=0x-2=12+x2-x+3 и x>2x-5y=72x+3y≥1
Можно встретить выражения, где имеются и система, и совокупность:
x≥5x<3x>4,5
Фигурная скобка для обозначения кусочной функции
Кусочная функция изображается при помощи одиночной фигурной скобки, где имеются формулы, определяющие функцию, содержащие необходимые промежутки. Посмотрим на примере формулы с содержанием промежутков типа x=x, x≥0-x, x<0, где имеется кусочная функция.
Скобки для указания координат точки
Для того, чтобы изобразить координатные точки в виде промежутков, используют круглые скобки. Они могут быть расположены как на координатной прямой, так и в прямоугольной системе координат или n-мерном пространстве.
Когда координата записывается как А(1), то означает, что точка А имеет координату со значением 1, тогда Q(x, y, z) говорит о том, что точка Q содержит координаты x, y, z.
Скобки для перечисления элементов множества
Множества задаются при помощи перечисления элементов, входящих в его область. Это выполняется при помощи фигурных скобок, где сами элементы прописываются через запятую. Запись выглядит таким образом А={1, 2,3, 4}. Видно, что множество состоит из значений, перечисленных в скобках.
Скобки и координаты векторов
При рассмотрении векторов в системе координат используется понятие координат вектора. То есть при обозначении используют координаты, которые записаны в виде перечисления в скобках.
Учебники предлагают два вида обозначения: a→0; -3 или a→0; -3. Обе записи равнозначны и имеют значение координат 0, -3. При изображении в трехмерном пространстве добавляется еще одна координата. Тогда запись выглядит так: AB→0, -3, 23 или AB→0, -3, 23.
Обозначение координат может быть как со значком вектора на самом векторе, так и без. Но запись координат производится через запятую в виде перечисления. Запись принимает вид a=(2, 4, −2, 6, 12), где вектор обозначается в пятимерном пространстве. Реже можно увидеть обозначение двумерного пространства в виде a=3-7
Скобки для указания элементов матриц
Частое применение скобок предусмотрено в матрицах. Все элементы фиксируются при помощи круглых скобок вида A=423-30012.
Реже можно увидеть использование квадратных скобок в математике в таких примерах.
Тогда матрица приобретает вид A=423-30012.
Конспект по математике
Ұйымдастырылған оқу қызметінің мектепалды даярлық тобының конспектісі
Конспект организованной учебной деятельности в подготовительной группе
Өткізу күні/Дата проведения:
Тәрбиеші/Воспитатель: Нурмаганбетова Л. А.
А.
Білім беру саласы/Образовательная область: «Познание»
Өтпелі тақырып/Сквозная тема: «Мебель»
Пән/Предмет: ФЭМП
Тақырыбы/Тема: Сравнение группы предметов.
Мақсаттары/Цели: Научить сравнивать предметы, определять большее, меньшее или равное количество предметов, обозначая соответствующими знаками “”, “
Ресурстармен қамтамасыз ету/Ресурсное обеспечение: азбука – тетрадь
Көптілділік/полиязычие: ана – мама – mother
1.Ұйымдастырушылық кезеңі/организационный момент:
Для введения в тему занятия, педагог предлагает игру «Помогаю маме».
Педагог предлагает детям накрыть на стол, применяя игрушечную посуду и продукты.
Распределяет роли: мама и дочка, сынок. Дети накрывают на стол, а группа считает вслух предметы на столе.
Педагог вывешивает карточки с числами, результатом счета.
Педагог спрашивает:
– Как можно сравнить чего больше, чего меньше или поровну?
(Дети предлагают два способа – расположить рядом или поставить друг на друга).![]()
Например, чашку на тарелочку. И узнать чего больше. Второй способ – записать число и сравнить числа. Если какое-то число при счете назвали раньше, то оно меньше. Сегодня мы узнаем, как на языке математики можно записать, каких-то предметов больше или меньше, или поровну.
2. Негізі білімі/основная часть:
Кто знает, как записать, что чашек больше (меньше) столько же, сколько тарелочек? Давайте узнаем, какие есть знаки в математике.
Педагог показывает карточки со знаками и просит в воздухе обвести их карандашом или пальчиком. Знаки можно изобразить при помощи трубочек или пластилина. В математике часто приходится сравнивать числа по величине, для чего и были придуманы графические символы. Вместо слова «больше» используется знак «», а вместо слова «меньше» – символ «.
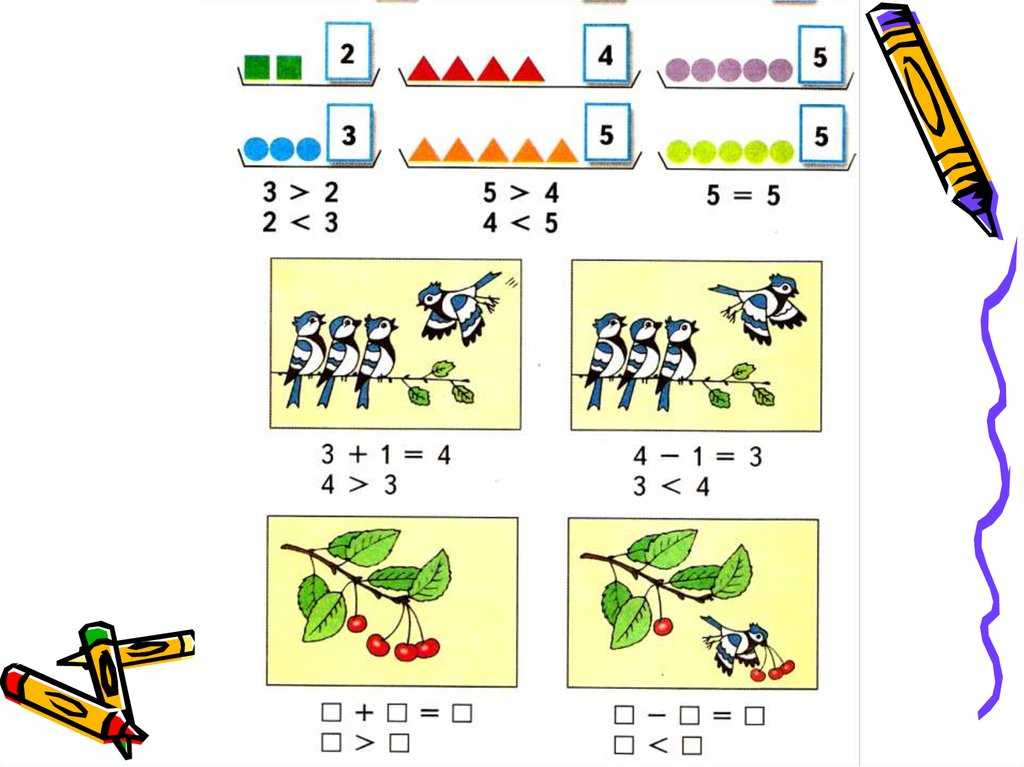
Между карточками из игры «Помогаю маме» педагог предлагает расставить знаки.
Дети вместе с детьми вслух читают новые записи.
Проводит беседу по картинке №1.
– Про что моно сказать больше, меньше, столько же?
Можно составить три записи: 4 6, 64, 5=5 по картинке.
– Как сравнить группы предметов?
– Какой знак можно поставить в записи сравнения двух групп предметов?
– Объясните, какие слова помогли тебе рассказать, как сравнить группы предметов и какие знаки помогли записать это на языке математики.
В задании №2 педагог просит посчитать предметы. Прочитать знак, выложить такую запись при помощи разрезных цифр и знаков.
Аналогичная работа ведется на наборном полотне. Моделирует ситуацию. Тимур и Алия расставляют посуду (или считают шарики), надо помочь им сравнить число предметов.
Детям в парах предлагает достать наугад из
«волшебного мешочка» (непросвечивающий мешочек, откуда наугад дети достают предметы). Затем предметы раскладывают на столе, группа предметов обозначает числом. Далее дети проводят сравнение удобным для них способом. После этого педагог предлагает показать, какой знак можно поставить между числами. Для запоминания знака, можно рассказать сказку.
Для запоминания знака, можно рассказать сказку.
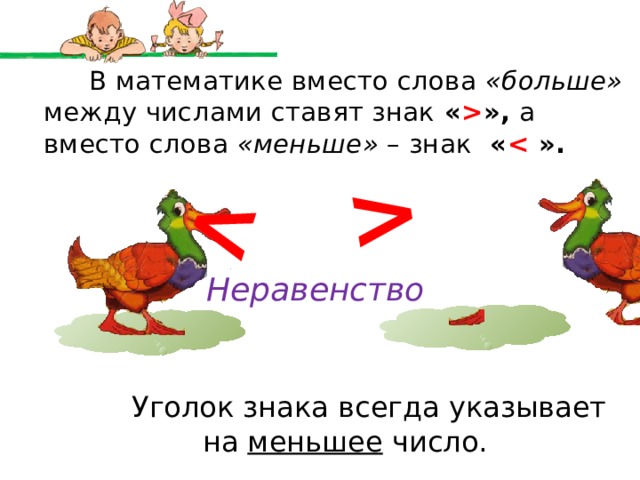
При обучении математике детям обычно называют знаки больше и меньше клювиком, так им проще запоминать образное понятие. А вот чтобы запомнить в какую сторону пишется меньше, а в какую больше приводят другой пример – закрытый клювик всегда смотрит в сторону меньшего числа, открытый в сторону большего.
Педагог может рассказать детям сказку о птенцах, которым мама принесла червячков.
Теперь если слева стоит большее число, клювик к нему открыт, и мы имеем знак «больше», а если слева стоит меньшее число, клювик налево закрыт, то у нас получается знак «меньше».
Еще этот знак сравнивают с крокодилом. Больше открыт рот в ту сторону, где большее число. Затем дети тренируются в обводке знаков в задании №3.
Знаки также можно слепить из пластилина.
После чего педагог может организовать работу с электронным наборным полотном аналогичную первому этапу занятия.
3. Қорытынды/итоговая часть:
Педагог подводит итог, поощряет детей.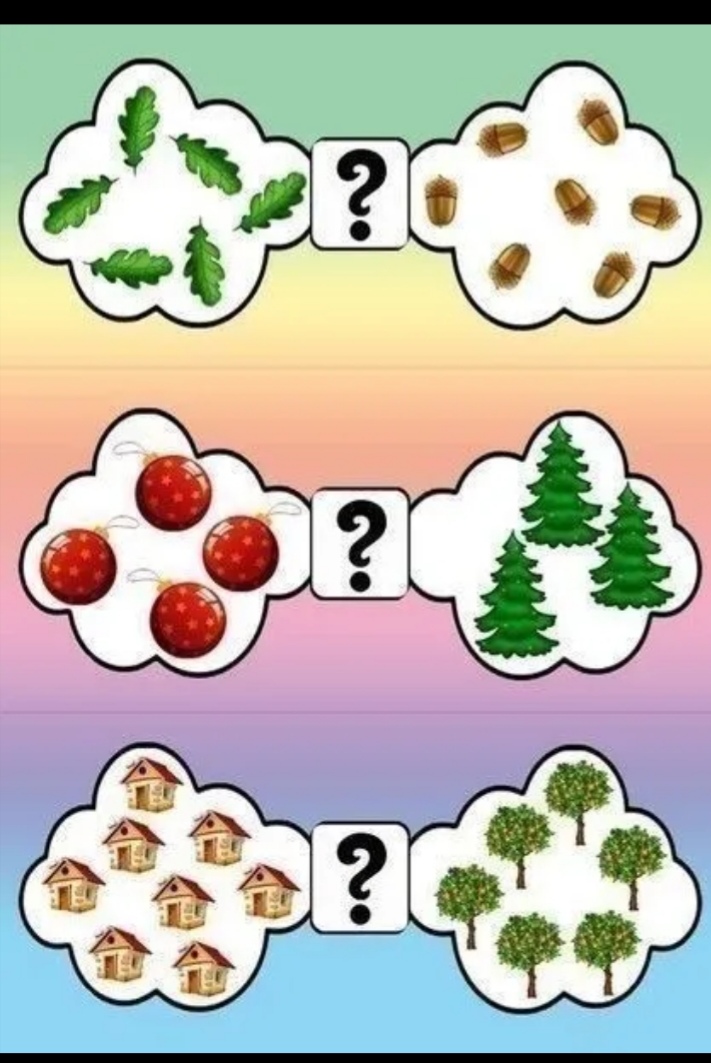
Предлагает оценить свою работу на занятии при помощи «Лесенки успеха».
Педагог поясняет: на нижней ступеньке нужно дорисовать смайлика с грустным ротиком, если у ребенка было много ошибок. На средней ступеньке – с ровным ротиком, если мало ошибок. На верхней ступеньке – с улыбкой, если все было без ошибок, и ребенок хорошо понял тему.
Решите неравенства с помощью Пошагового решения математических задач
В главе 2 мы установили правила решения уравнений с использованием арифметических чисел. Теперь, когда мы изучили операции над числами со знаком, мы будем использовать те же правила для решения уравнений, в которых участвуют отрицательные числа. Мы также изучим методы решения и построения графиков неравенств с одним неизвестным.
РЕШЕНИЕ УРАВНЕНИЙ, ВКЛЮЧАЮЩИХ ЧИСЛА СО ЗНАКОМ
ЗАДАЧИ
По завершении этого раздела вы должны уметь решать уравнения, содержащие числа со знаком.
Пример 1 Найдите х и проверьте: х + 5 = 3 для x и проверьте: – 3x = 12
Решение
Разделив каждую сторону на -3, мы получим
Всегда проверяйте исходное уравнение. |
| Другой способ решения уравнения 3x – 4 = 7x + 8 будет сначала вычесть 3x с обеих сторон, получив -4 = 4x + 8, , затем вычесть 8 с обеих сторон и получить -12 = 4x. Теперь разделите обе части на 4, чтобы получить – 3 = x или x = – 3. |
| Сначала удалите скобки. Затем следуйте процедуре, описанной в главе 2. |
ЛИТЕРАЛЬНЫЕ УРАВНЕНИЯ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Найдите буквальное уравнение.
- Применяйте ранее изученные правила для решения буквенных уравнений.
Уравнение, состоящее из более чем одной буквы, иногда называют буквальным уравнением . Иногда бывает необходимо решить такое уравнение для одной из букв через другие. Пошаговая процедура, рассмотренная и использованная в главе 2, по-прежнему действительна после удаления любых символов группировки.
Пример 1 Решить для c: 3(x + c) – 4y = 2x – 5c
Решение
Сначала удалите скобки.
Здесь мы отмечаем, что, поскольку мы решаем для c, мы хотим получить c с одной стороны и все остальные члены с другой стороны уравнения. Таким образом, мы получаем
| Помните, abx это то же самое, что и 1abx. Делим на коэффициент при x, который в данном случае равен ab. |
| Решите уравнение 2x + 2y – 9x + 9a, сначала вычитая 2.v из обеих частей. Сравните решение с полученным в примере. |
Иногда форма ответа может быть изменена. В этом примере мы могли бы умножить и числитель, и знаменатель ответа на (-l) (это не меняет значения ответа) и получить
Преимущество этого последнего выражения перед первым состоит в том, что много отрицательных знаков в ответе.
| Умножение числителя и знаменателя дроби на одно и то же число является использованием фундаментального принципа дробей. |
Наиболее часто используемые буквенные выражения — это формулы из геометрии, физики, бизнеса, электроники и т. д.
Пример 4 – это формула площади трапеции. Решите для с.
| Трапеция имеет две параллельные стороны и две непараллельные стороны. Параллельные стороны называются основаниями. Удаление скобок не означает просто их стирание. Мы должны умножить каждый член в скобках на множитель, стоящий перед скобками. Изменение формы ответа не обязательно, но вы должны уметь распознавать правильный ответ, даже если форма отличается. |
Пример 5 представляет собой формулу, определяющую проценты (I), полученные за период D дней, когда известны основная сумма долга (p) и годовая ставка (r). Найдите годовую ставку, если известны сумма процентов, основная сумма долга и количество дней.
Найдите годовую ставку, если известны сумма процентов, основная сумма долга и количество дней.
Решение
Задача требует решения для r.
Обратите внимание, что в этом примере r оставлено справа, и поэтому вычисления упростились. Мы можем переписать ответ по-другому, если захотим.
ГРАФИЧЕСКИЕ НЕРАВЕНСТВА
ЦЕЛИ
По завершении этого раздела вы должны уметь:
- Используйте символ неравенства для представления относительного положения двух чисел на числовой прямой.
- Графические неравенства на числовой прямой.
Мы уже обсуждали набор из рациональные числа как те, которые могут быть выражены как отношение двух целых чисел. Существует также набор чисел, называемый иррациональными числами, , которые нельзя выразить как отношение целых чисел. В этот набор входят такие числа как и так далее. Множество, состоящее из рациональных и иррациональных чисел, называется действительных чисел.
Для любых двух действительных чисел a и b всегда можно сказать, что Много раз нас интересует только, равны ли два числа, но бывают ситуации, когда мы также хотим представить относительный размер чисел, которые не равны.
Символы представляют собой символы неравенства или отношений порядка и используются для отображения относительных размеров значений двух чисел. Обычно мы читаем этот символ как «больше чем». Например, a > b читается как «а больше, чем b». Обратите внимание, что мы заявили, что обычно читаем
| Утверждение 2 |
a
| Какое положительное число можно прибавить к 2, чтобы получить 5? |
Проще говоря, это определение утверждает, что а меньше b, если мы должны добавить что-то к а, чтобы получить b. Конечно, «что-то» должно быть положительным.
Если вы думаете о числовой строке, вы знаете, что добавление положительного числа эквивалентно перемещению вправо по числовой строке. Это приводит к следующему альтернативному определению, которое может быть легче визуализировать.
Пример 1 3
| Мы могли бы также написать 6 > 3. |
Пример 2 – 4
| Мы могли бы также написать 0 > – 4. |
Пример 3 4 > – 2, потому что 4 находится справа от -2 на числовой прямой.
Пример 4 – 6
Математическое утверждение x
| Вы понимаете, почему невозможно найти наибольшее число меньше 3? |
На самом деле, назвать число x, которое является наибольшим числом меньше 3, невозможно. Однако это может быть указано в числовой строке. Для этого нам нужен символ, представляющий значение утверждения, такого как x
Однако это может быть указано в числовой строке. Для этого нам нужен символ, представляющий значение утверждения, такого как x
Символы ( и ), используемые на числовой прямой, указывают на то, что конечная точка не включена в набор.
Пример 5 График x
Решение
Обратите внимание, что на графике есть стрелка, указывающая, что линия продолжается без конца влево.
| Этот график представляет каждое действительное число меньше 3. |
Пример 6 График x > 4 на числовой прямой. Пример 7
Решение
| На этом графике представлены все действительные числа больше -5. |
Пример 8 Постройте линейный график, показывающий, что x > – 1 и x
Решение
Утверждение x > – 1 и x
На этом графике представлены все действительные числа от – 1 до 5. |
Пример 9 График – 3
Решение
Если мы хотим включить конечную точку в набор, мы используем другой символ, :. Мы читаем эти символы как «равно или меньше» и «равно или больше».
Пример 10 х >; 4 указывает число 4 и все действительные числа справа от 4 на числовой прямой.
| Что означает x |
Символы [ и ], используемые в числовой строке, указывают, что конечная точка включена в набор.
| Вы обнаружите, что такое использование скобок и квадратных скобок соответствует их использованию в будущих курсах по математике. |
| Этот график представляет число 1 и все действительные числа больше 1. |
Этот график представляет число 1 и все действительные числа, меньшие или равные -3. Пример 14 Напишите алгебраическое выражение для следующего графика.
Пример 15 Напишите алгебраическое выражение для следующего графика.
Пример 16 График на числовой прямой. Решение В этом примере представлена небольшая проблема. Как мы можем указать на числовой прямой? Если мы оценим точку, то другой человек может неправильно понять утверждение. Не могли бы вы сказать, представляет ли точка или, может быть, ? Поскольку целью графика является уточнение, всегда обозначают конечную точку.
РЕШЕНИЕ НЕРАВЕНСТВЗАДАЧИПо завершении этого раздела вы должны уметь решать неравенства с одним неизвестным. Решения неравенств обычно основаны на тех же основных правилах, что и уравнения. Есть одно исключение, которое мы вскоре обнаружим. Однако первое правило аналогично тому, которое используется при решении уравнений. Если к каждой стороне неравенства добавить одинаковое количество, результаты будут неравными в том же порядке. Пример 1 Если 5 Пример 2 Если 7
Мы можем использовать это правило для решения некоторых неравенств. Пример 3 Решить для x: x + 6 Решение Если мы прибавим -6 к каждой стороне, мы получим Отобразив это решение на числовой прямой, мы получим
Теперь мы воспользуемся правилом сложения, чтобы проиллюстрировать важную концепцию умножения или деления неравенств. Предположим, х > а. Теперь добавьте – x к обеим сторонам по правилу сложения.
Теперь добавьте -a с обеих сторон. Последнее выражение -a > -x можно переписать как -x < -a. Поэтому мы можем сказать: «Если х > а, то — х Если неравенство умножить или разделить на отрицательное число, результаты будут неравны в порядке , противоположном .
Пример 5 Найдите x и нарисуйте решение: -2x>6 Решение Чтобы получить x в левой части, мы должны разделить каждый член на – 2.
Обратите внимание на этот факт. Каждый раз, когда вы делите или умножаете на отрицательное число, вы должны изменить направление символа неравенства. Это единственная разница между решением уравнений и решением неравенств.
После того, как мы удалили круглые скобки и в выражении остались только отдельные члены, процедура поиска решения почти такая же, как в главе 2. Теперь рассмотрим пошаговый метод из главы 2 и отметим разница при решении неравенств. Первый Удалите дроби, умножив все члены на наименьший общий знаменатель всех дробей. (Без изменений, когда мы умножаем на положительное число.)
РЕЗЮМЕКлючевые слова
Процедуры
Полный список символов теории множествТеория множеств — это раздел математики, посвященный изучению наборов объектов, их свойств и взаимосвязей между ними. В следующем списке представлены некоторые из наиболее примечательных символов теории множеств, а также их использование и значение. Для удобства чтения эти символы разделены по функциям на таблицы . Другие полные списки символов — с разбивкой по темам и типам — также можно найти на соответствующих страницах ниже (или на панели навигации). Содержание Предпочитаете версию в формате PDF? Получите основную сводку математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX. Да. Это было бы полезно. КонстантыВ теории множеств константы часто представляют собой односимвольные символы, используемые для обозначения ключевых математических наборов . В следующей таблице представлены наиболее заметные из них, а также их соответствующее значение и пример.
Для других ключевых наборов чисел см. ключевые математические наборы в алгебре . ПеременныеКак и в других областях математики, в теории множеств часто используется определенный список переменных символов для обозначения различных объектов и величин. В следующей таблице описаны наиболее распространенные из них, а также их соответствующий пример и значение.
РазделителиВ теории множеств разделители — это символы, используемые для обозначения разделения между независимыми математическими объектами, и часто встречаются в контексте определение наборов . В следующей таблице описаны наиболее распространенные из них, а также их соответствующее использование и значение.
Операторыпозволяют ссылаться на новые наборы через уже существующие наборы — существуют. В следующей таблице представлены наиболее примечательные из них, а также их соответствующий пример и значение.
Следующие диаграммы, известные как диаграммы Венна , обеспечивают визуализацию пяти из упомянутых выше наборов ключей (где $A$ и $B$ представлены левым и правым кругами соответственно).
Реляционная СимволыВ теории множеств реляционные символы часто используются для описания отношений между наборами или отношений между набором и его элементом. В следующей таблице представлены наиболее примечательные из этих символов, а также их соответствующее значение и пример.
Символы, связанные с мощностьюВ теории множеств понятие мощности обеспечивает способ количественной оценки и сравнения размеров различных множеств. В следующей таблице описаны некоторые из наиболее заметных символов, связанных с кардинальностью, а также использование и значение каждого символа. (Для ознакомления с греческими и еврейскими символами см. Греческие, еврейские и латинские символы . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| $\beth_0, \beth_1, \ldots$ | числа Бет | $\beth_0 = |\mathbb{N}|,$ $\beth_1=|\mathcal{P}(\mathbb{ N})|,$ $\beth_2 = |\mathcal{P}(\mathcal{P}(\mathbb{N}))|$ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| $\gimel$ | Функция Гимеля | $ \gimel(\kappa) > \kappa$ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| $\mathfrak{c}$ | Мощность континуума | $|\mathbb{R}| = \mathfrak{c} = |\mathbb{\mathcal{P}(\mathbb{N})}|$ 9+ = \aleph_{\alpha+1}$ |
Основной список символов см. в разделе Математические символы. Списки символов, классифицированных по типу и по теме , см. на соответствующих страницах ниже.
Предпочитаете версию в формате PDF?
Получите основную сводку математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX.
Да. Это было бы полезно.
 Вы всегда должны называть нулевую точку, чтобы показать направление, а также конечную точку или точки, чтобы быть точным.
Вы всегда должны называть нулевую точку, чтобы показать направление, а также конечную точку или точки, чтобы быть точным.
 Обратите внимание, что, поскольку мы делим на отрицательное число, мы должны изменить направление неравенства.
Обратите внимание, что, поскольку мы делим на отрицательное число, мы должны изменить направление неравенства.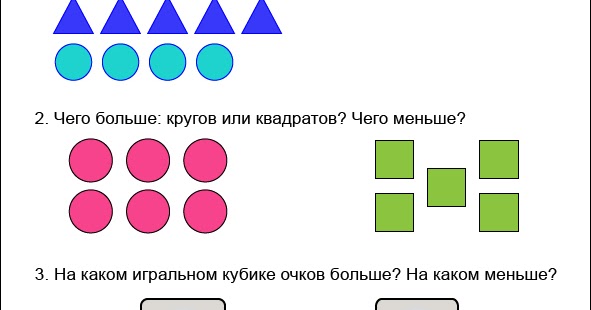

 Если коэффициент положительный, неравенство останется прежним. Если коэффициент отрицательный, неравенство будет обратным.
Если коэффициент положительный, неравенство останется прежним. Если коэффициент отрицательный, неравенство будет обратным. 

 89) \in \mathbb{N} \times \mathbb{R}$
89) \in \mathbb{N} \times \mathbb{R}$
