Знак больше и меньше в математике в какую сторону: Больше, меньше, равно — урок. Математика, 1 класс.

Знаки больше меньше

Занятие по ФЭМП в старшей группе

«Больше. Меньше. Знаки < и >»

Выполнила воспитатель

Маркова Анастасия Игоревна

Цель:закрепить сравнение групп предметов по количеству с помощью составления пар. Познакомить со знаками < и >.

Материалы к занятию:

Демонстрационный – 5 одинаковых котят с разноцветными бантиками; 5 клубков разноцветных, под цвет бантиков; карточки с цифрами от 1 до 5; две полоски бумаги – модели знаков равенства и неравенства.

Ход занятия:

Формирование представлений об отношениях больше, меньше. Знакомство со знаками < и > .

В. – Ребята, давайте встанем в круг и попробуем отгадать загадку про наших гостей.

Он пушистый, он игривый,

Очень-очень шаловливый,

Часто любит хвост ловить,

Молоко парное пить.

Испугаешь – он шипит,

Спинку выгибает,

Приласкаешь – он мурчит,

Весело играет.

               (Котенок)
Д.– Котенок.

В. – Молодцы. Присаживайтесь. Сегодня к нам в гости пришли котята (котята выставлены на магнитной доске). Посмотрите, какие они пушистые, нежные… Они все одинаковые, а бантики у них разных цветов. Котята очень любят играть с клубками (рядом с каждым котенком стоит клубочек по цвету бантика). Как вы думаете, у каждого котенка есть свой клубок? Как нам это узнать?

Д. – Сравнить количество котят и количество клубков.

В. – Правильно. А как вы будете сравнивать?

Д. – Мы посчитаем котят и клубочки. И сравним (если заметят, то скажут, что у каждого котенка есть пара – клубочек по цвету). Котят и клубочков по 5. Значит их поровну.

Ребята считают и делают вывод, что котят и клубочков поровну.

Можно спросить их, какой способ решения проще и почему.

В. – Ребята, положите у себя на листке справа и слева по цифре 5. И поставьте, с помощью счетных палочек, знак равенства.

Затем на доске выставляю две цифры 5 и знак равенства между ними моделирую из 2 полосок.

В. – Молодцы. Правильно посчитали. И котят и клубков поровну. Но вот несколько котят убежали за своими клубочками в сторону (ставлю трех котят с клубками в левую сторону доски, а двух котят, с их клубками, в правую сторону доски). Сколько стало котят справа доски?

Д. – Двое котят.

В. – Правильно. А сколько котят осталось слева?

Д. – Трое котят.

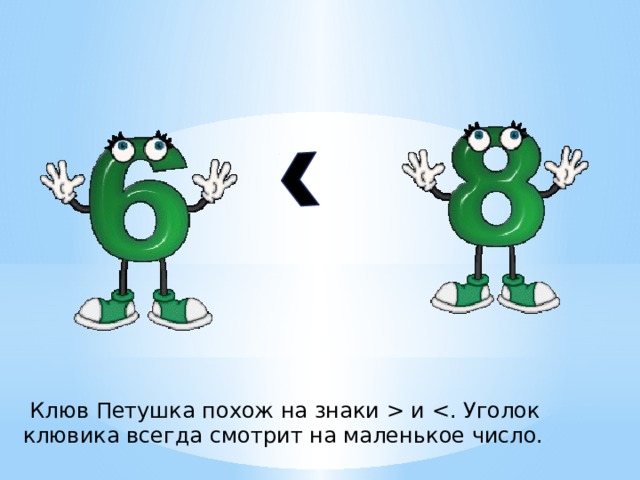
В. – Хорошо. Но тут прилетела птичка и открыла клюв от удивления. Какие красивые котята. Посмотрите на ее клюв – в какую сторону он открыт?

Д. – Птичка открыла клюв в ту сторону, где котят больше. Их трое.

Давайте положим слева цифру 3, а справа цифру 2. Выкладываю на доске цифры 3 и 2 и между ними две полоски, моделирующие знак равенства.

В. – Посмотрите, правильно ли я поставила знак равенства?

Д. – Нет.

В. – Почему? (потому что 3 больше 2). Как превратить полоски в раскрытый клюв птички?

«Раскрываю» полоски в сторону числа три и получаю знак >. Дети делают то же на столах из счетных палочек.

В. – Посмотрите, получается, что три больше двух. Это показывает знак «больше». А сейчас 2 котенка справа перебежали к двум котятам справа. Что произошло?

Д. – Слева остался один котенок, а справа стало четыре котенка.

В. – Давайте положим слева цифру 1, а справа цифру 4. Как вы думаете, как теперь надо положить полоски?

Д. – Так, чтобы клюв открылся на цифру 4.

В. – Что теперь получилось?

Д. – 1 меньше четырех.

В. – Посмотрите, ребята, клюв птички всегда показывает на то число, которое меньше. Ну что устали? Давайте отдохнем.

2.Физминутка «Мы считали, мы считали…»

Мы считали, мы считали,
             А теперь тихонько встали.
             Раз – присели, два – нагнулись,
             На носочках потянулись.
             Руки ставим на бочок:
             На носочках скок, скок, скок.

3.Закрепление представлений о сравнении групп предметов с помощью знаков <, >. (Совместная работа по тетрадям).

4. Итог занятия.

– Понравилось вам занятие? Кому мы помогали? Какие математические знаки мы узнали? (больше, меньше) Куда смотрит носик этих знаков? (всегда на меньшее число). Все вы сегодня были молодцы, помогли котятам найти свои клубочки. Они вам благодарны.

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/431917-znaki-bolshe-menshe

Вся элементарная математика – Средняя математическая интернет-школа

Методы доказательства неравенств.

Решение неравенств. Равносильные неравенства.

Метод интервалов. Системы неравенств.

Доказательство неравенств. Существует несколько методов доказатель ства неравенств. Мы рассмотрим их на примере неравенства:

где a – положительное число.

1). Использование известного или ранее доказанного неравенства.

Известно, что ( a – 1 ) ² 0 .

2). Оценка знака разности между частями неравенства .

Рассмотрим разность между левой и правой частью:

более того, равенство имеет место только при a = 1 .

3). Доказательство от противного.

Предположим противное:

Умножая обе части неравенства на a , получим: a ² + 1 a , т. e .

a

² + 1 – 2 a или ( a – 1 ) ² что неверно. ( Почему ? ) .

Полученное противоречие доказывает справедливость

рассматриваемого неравенства.

4). Метод неопределённого неравенства.

Неравенство называется неопределённым , если у него знак \/ или /\ ,

т.е. когда мы не знаем в какую сторону следует повернуть этот знак,

чтобы получить справедливое неравенство.

Здесь действуют те же правила, что и с обычными неравенствами.

Рассмотрим неопределённое неравенство:

Умножая обе части неравенства на a , получим: a ² + 1 \/ 2 a , т. e .

а ² + 1 – 2 a \/ 0 , или ( a – 1 ) ²

\/ 0 , но здесь мы уже знаем, как повернуть

знак  \/ , чтобы получить верное неравенство ( Как? ). Поворачивая его

в нужном направлении по всей цепочке неравенств снизу вверх, мы
получим требуемое неравенство.

Решение неравенств. Два неравенства, содержащие одни и те же неизвестные, называются равносильными , если они справедливы при одних и тех же значениях этих неизвестных . Такое же определение используется для равносильности двух систем неравенств. Решение неравенств – это процесс перехода от одного неравенства к другому, равносильному неравенству. Для этого используются

основные свойства неравенств (см. параграф “Неравенства: общие сведения” ). Кроме того, может быть использована замена любого выражения другим, тождественным данному. Неравенства могут быть алгебраические ( содержащие только многочлены ) и трансцендентные ( например, логарифмические или тригонометрические ). Мы рассмотрим здесь один очень важный метод, используемый часто при решении алгебраических неравенств.

Метод интервалов.

Решить неравенство:  ( x – 3 )( x – 5 ) x – 3 ). Здесь нельзя делить обе части неравенства на ( x – 3 ), так как мы не знаем знака этого двучлена ( он содержит неизвестное x ). Поэтому мы перенесём все члены неравенства в левую часть:

( x – 3 )( x – 5 ) – 2( x – 3 )

разложим её на множители:

(

x – 3 )( x – 5  – 2 ) ,

и получим: ( x – 3 )( x – 7 ) x = 3 и x = 7 – корни этого выражения. Поэтому вся числовая ось разделится этими корнями на следующие три интервала:

В интервале I ( x ) оба сомножителя отрицательны, следовательно , их произведение

положительно ; в интервале II ( 3 x x – 3 ) положителен, а второй ( x – 7 ) отрицателен, поэтому их произведение отрицательно ; в интервале III ( x > 7 ) оба сомножителя положительны, следовательно, их произведение также положительно . Теперь остаётся выбрать интервал, в котором наше произведение отрицательно . Это интервал II , следовательно, решение неравенства: 3 x двойное неравенство . Оно означает, что x должен быть одновременно больше 3 и меньше 7.

П р и м е р .  Решить следующее неравенство методом интервалов:

( x – 1 )( x – 2 )( x – 3 ) … ( x –100 ) > 0 .

Р е ш е н и е . Корни левой части неравенства очевидны: 1, 2, 3, …, 100.

Они разбивают числовую ось на 101 интервал:

Так как количество скобок в левой части чётно (равно 100), то

при x

положительно.

При переходе через корень происходит смена

знака произведения. Поэтому следующим интервалом, внутри

которого произведение положительно, будет ( 2, 3 ), затем ( 4, 5 ),

затем  ( 6, 7 ), … , ( 98, 99 ) и наконец , x >100.

Таким образом, данное неравенство имеет решение:

x x x x >100.

Итак, чтобы решить алгебраическое неравенство, надо перенести все его члены в левую (или правую) часть и решить соответствующее уравнение. После этого найденные корни нанести на числовую ось; в результате она разбивается на некоторое число интервалов. На последнем этапе решения нужно определить, какой знак имеет многочлен внутри каждого из этих интервалов, и выбрать нужные интервалы в соответствии со знаком решаемого неравенства.

Заметим, что большинство трансцендентных неравенств заменой неизвестного приводятся к алгебраическому неравенству. Его надо решить относительно нового неизвестного, а затем путём обратной замены найти решение для исходного неравенства.

Системы неравенств. Чтобы решить систему неравенств, необходимо решить каждое из них, и совместить их решения. Это совмещение приводит к одному из двух возможных случаев: либо система имеет решение, либо нет.

П р и м е р  1.  Решить систему неравенств:

Р е ш е н и е.  Решение первого неравенства: x x > 6.

Таким образом, эта система неравенств не имеет решения.

( Почему ? )

П р и м е р  2.  Решить систему неравенств:

Р е ш е н и е.  Первое неравенство, как и прежде, даёт: x

второго неравенства в данном примере: x > 1.

Таким образом, решение системы неравенств: 1 x

Назад

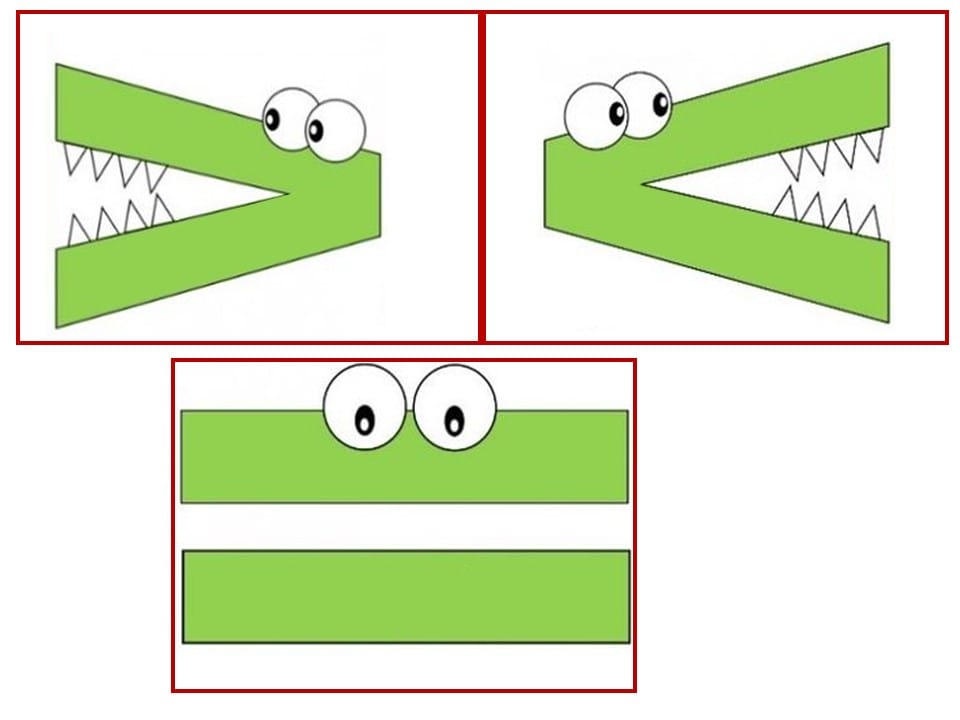
Невероятно, Практика, Больше, меньше, чем Аллигатор Математика

Многим детям трудно запомнить символы больше и меньше. Им не нужно быть. Даже дошкольники могут легко понять концепцию больше, чем аллигатора. Сегодня у меня практическое занятие, в котором используется забавное пение и распечатка из нашего набора крокодилов, вдохновленного Монтессори (бесплатно для подписчиков).

 

Невероятная, практическая, больше, меньше, чем математика аллигатора – YouTube Video

Мне нравится пение в этом коротком видео!

Материалы, используемые в математическом задании «Больше, чем Аллигатор»

Раскрытие информации: Этот пост содержит партнерские ссылки (бесплатно для вас).

Лоток Greater Than, Less Than Alligator с математическими манипуляциями и пением

• Деревянный лоток Multicraft
• Рыбные бусины (это те самые, которые я использовала для нашей темы пингвинов.) Я использовала 17 рыбок, чтобы их хватило, если 9и 8 были выбраны. (Обновление: если рыбные бусины, которые я получил, недоступны, вы найдете похожие здесь.)
• Маленькая чашка для приправы Bambu для рыбных бусин
• Цифры из наждачной бумаги (Мои из набора Элисон Монтессори. Вы также можете получить цифры из наждачной бумаги на Amazon. Или вы можете использовать цифры из кожи аллигатора 0-20 из нашего бесплатного подарка для подписчиков.)
• Free Printable: Greater Than, Less Than Reference Розмари Гэлвин из «Учителя платят учителям»
• Free Printable: Greater Than, Less Than Alligator Photos and Symbols (бесплатный подарок подписчику на набор аллигаторов, вдохновленный Монтессори)

Математическое задание «Больше, меньше, чем аллигатор»

Указание на большее число в математике «Больше, меньше, чем аллигатор»

Дошкольники, умеющие считать предметы, могут выполнить практическую версию «больше, меньше». Зои подсчитывала рыбу для каждого числа, а затем указывала на большее число.

Развлекайтесь с пением «Больше, чем, меньше, чем аллигатор»

Как вы можете видеть на видео, это пение очень весело и является отличным способом представить больше и меньше!

Нахождение большего числа в математике «Больше, меньше, чем аллигатор»

Один из способов выполнить это задание — сначала выложить показанный символ больше или меньше, чтобы он «съел» рыбу.

Больше, меньше, чем Аллигатор Математическая схема для 2 меньше 7

Затем вы можете переместить символ между двумя цифрами и прочитать ответ.

Дети, умеющие читать, могут использовать второй набор символов (показан на коллаже вверху поста). Распечатку также можно разрезать, чтобы ребенок мог сопоставить слова с фотографией аллигатора и математическим символом.

Хотя это, конечно, не обязательно делать с дошкольниками, это веселое занятие, которое устраняет путаницу с символами больше и меньше. Когда позже дети знакомятся только с абстрактными символами, они должны чувствовать себя уверенно и радоваться своему математическому опыту.

Распечатки про аллигаторов и задания для дошкольников-первоклассников

Монтессори-вдохновленный набор про аллигаторов с бесплатными распечатками и заданиями

Бесплатные распечатки про аллигаторов и занятия с аллигаторами по мотивам Монтессори

Распечатки и задания по математике «Больше, меньше, чем у аллигаторов»

Набор «Аллигатор» по Монтессори для карточек и корзин с цифрами или буквами, числами или буквами, числами или числами , Работа с бусинами, Практические математические операции, Работа больше/меньше, Лоток для письма с солью или песком, Отслеживание букв, Подвижный алфавит своими руками и Творческое письмо (бесплатно для подписчиков, так что всего подпишитесь на мою электронную почту, чтобы получить ссылку и пароль  – или проверьте свой почтовый ящик на наличие текущего пароля, если вы уже являетесь подписчиком).

Удачной математики аллигаторов!

Узнайте больше о моей электронной книге Монтессори дома или в школе: как. Учите Изяществу и Вежливости !

Если вы впервые посещаете Living Montessori Now, добро пожаловать! Если вы еще этого не сделали, присоединяйтесь к нам на нашей странице «Жить Монтессори сейчас» в Facebook, где вы найдете бесплатную распечатку дня и много вдохновения и идей для воспитания и обучения! И, пожалуйста, следите за мной в Instagram, Pinterest (множество досок Монтессори, праздников и тематических досок) и YouTube. Пока вы здесь, загляните в магазин Living Montessori Now.

И не забудьте один из лучших способов подписаться на мою еженедельную рассылку. В процессе вы получите потрясающие бесплатные бонусы!

Неравенства – Числовая строка

Числа , которые удовлетворяют неравенству , могут быть изображены на числовой прямой . Например, нам может понадобиться проиллюстрировать все числа, которые удовлетворяют неравенству : \[x показать все числа, подтверждающие истинность неравенства .

Чтобы проиллюстрировать эти числа, мы часто будем использовать числовую строку . Для неравенства \(x

Следующий урок научит нас всему, что нам нужно знать о неравенствах и числовых линиях на данный момент.

---

Резюме – Неравенства и числовая линия

Следуя учебному пособию, которое мы только что видели, ниже мы перечисляем , как проиллюстрировать четыре типа неравенств на числовой прямой.

Больше, чем: \(x > a\)

\(x>a\) представлен стрелкой с пустой точкой над \(a\).
Стрелка указывает на все числа, которые больше \(a\).
Пустая точка подчеркивает тот факт, что \(x\) не может равняться \(a\) :

---

Больше или равно: \(x \geq a\)

\(x \geq a \) представлен стрелкой с цифрой заполненная точка над \(a\).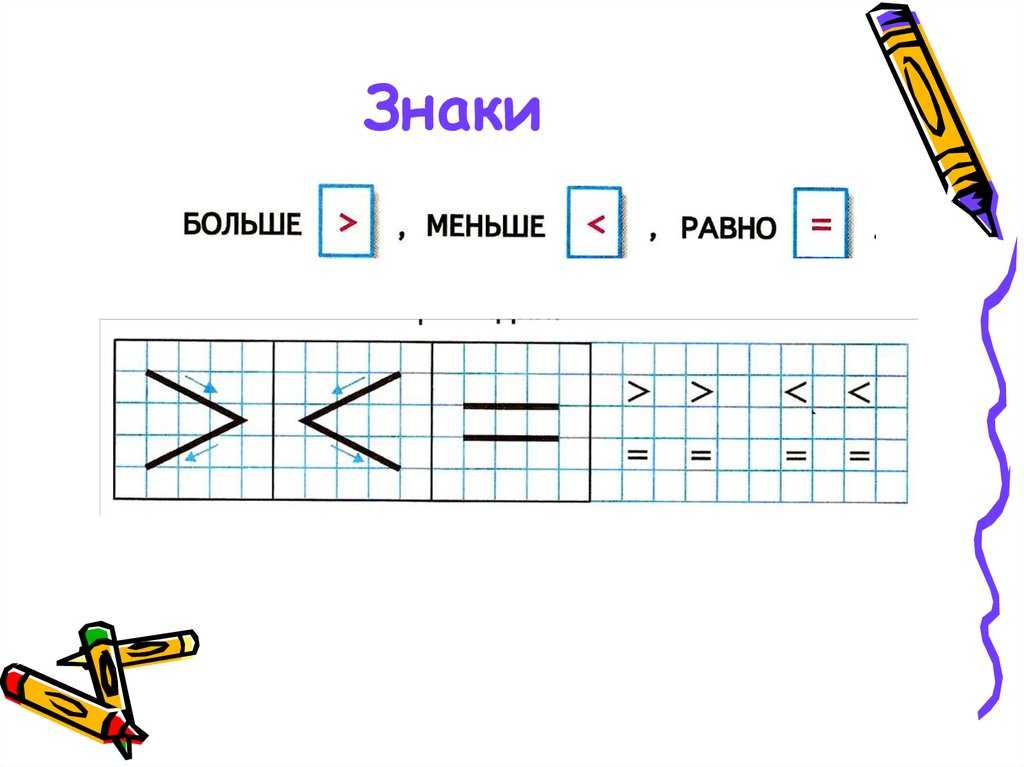
Стрелка указывает на все числа, которые больше \(a\).
заполненная точка подчеркивает тот факт, что \(x\) может быть равно \(a\) :

---

Меньше чем: \(х \(Икс Стрелка указывает в направлении всех чисел, которые меньше \(a\).

Пустая точка подчеркивает тот факт, что \(x\) не может равняться \(a\) :

---

Меньше или равно: \(x \leq a\)

\(x \leq a \) представлен стрелкой с закрашенной точкой над \(a\).
Стрелка указывает на все числа, которые меньше \(a\).
заполненная точка подчеркивает тот факт, что \(x\) может быть равно \(a\) :

Упражнение

Проиллюстрируйте решения каждого из следующих неравенств, используя числовую прямую:

1. \(х \leq 4 \)
2. \(х > -3 \)
3. \(Икс
4. \(х \geq 1\)
5. \(х \leq -1 \)
6. \(х > 2 \)

Ответы без работы

1. Решениями \(x \leq 4 \) являются все числа, меньшие или равные \(4\):


2. Решениями \(x > -3\) являются все числа, большие чем \(-3\):


3. Решения \(x


4. Решениями \(x \geq 1 \) являются все числа, большие или равные \(1\):


5. Решениями \(x \leq -1 \) являются все числа, меньшие или равные \(-1\):


6. Решениями \(x > 2\) являются все числа, большие чем \(2\):

Отсканируйте этот QR-код своим телефоном/планшетом и просмотрите эту страницу на предпочитаемом вами устройстве.