Задания по математике 3 класс с ответами 3 четверть: Контрольная работа по математике 3 класс | 3 четверть
Контрольная работа по математике 3 класс | 3 четверть
Вариант 1
1.
С первого улья собрали 36 кг меда, со второго — на 12 кг больше, чем с первого, а с третьего — в 2 раза меньше, чем со второго. Сколько килограммов меда собрали с третьего улья?
Решение:
- 1) 36 + 12 = 48
- 2) 48 : 2 = 24
- Выражение: (36 + 12) : 2
- Ответ: 24
2.
Железнодорожный мост имеет 3 пролета. Длина первого пролета 31 м, второго 29 м. Найди длину третьего пролета, если длина всего моста 100 м.
Решение:
- 1) 31 + 29 = 60
- 2) 100 – 60 = 40
- Выражение: 100 – (31 + 29)
- Ответ: 40
3.
В одной коробке 36 кг конфет, а в другой в 3 раза меньше. Все конфеты разложили в пакеты, по 4 кг в каждый. Сколько пакетов заняли эти конфеты?
Сколько пакетов заняли эти конфеты?
Решение:
- 1) 36 : 3 = 12
- 2) 36 + 12 = 48
- 3) 48 : 4 = 12
- Выражение: (36 + 36 : 3) : 4
- Ответ: 12
Вариант 2
1.
В одном куске 20 м ткани, а в другом на 8 м меньше. Из всей ткани сшили палатки, расходуя на каждую по 8 м ткани. Сколько палаток сшили?
Решение:
- 1) 20 – 8 = 12
- 2) 20 + 12 = 32
- 3) 32 : 8 = 4
- Выражение: (20 – 8 + 20) : 4
- Ответ: 4
2.
Три ткачихи за смену изготовили 60 м ткани. Первая ткачиха изготовила 22 м ткани, вторая — 18 м. Сколько метров ткани изготовила третья ткачиха?
Решение:
- 1) 22 + 18 = 40
- 2) 60 – 40 = 20
- Выражение: 60 – (22 + 18)
- Ответ: 20
3.

В спортивном клубе гимнастикой занимается 28 человек, плаванием — в 2 раза больше, чем гимнастикой, а теннисом — на 16 человек меньше, чем плаванием. Сколько человек занимается теннисом?
Решение:
- 1) 28 * 2 = 56
- 2) 56 – 16 = 40
- Выражение: 28 * 2 – 16
- Ответ: 40
Вариант 3
1.
В одной корзине было 18 кг черешни, а в другой — в 3 раза меньше. Всю черешню разложили в пакеты, по 2 кг в каждый. Сколько пакетов заняли этой черешней?
Решение:
- 1) 18 : 3 = 6
- 2) 18 + 6 = 24
- 3) 24 : 2 = 12
- Выражение: (18 : 3 + 18) : 2
- Ответ:
12
2.
В коробке 50 карандашей. Из них 17 красных, 13 синих, а остальные зеленые. Сколько зеленых карандашей в коробке?
Решение:
- 1) 13 + 17 = 30
- 2) 50 – 30 = 20
- Выражение: 50 – (13 + 17)
- Ответ: 20
3.
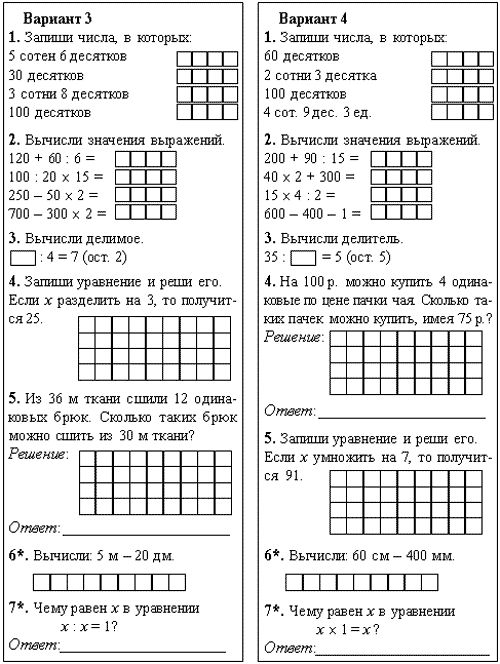
За первый день в кассе театра продали 64 билета, за второй — в 2 раза меньше, чем за первый, а за третий — на 8 билетов больше, чем за второй. Сколько билетов продали за третий день?
Решение:
- 1)64 : 2 = 32
- 2) 32 + 8 = 40
- Выражение: 64 : 2 + 8
- Ответ: 40
Вариант 4
1.
В книге три рассказа. Они занимают 80 страниц. Первый рассказ занимает 34 страницы, а третий — 26 страниц. Сколько страниц занимает второй рассказ?
Решение:
- 1) 34 + 26 = 60
- 2) 80 – 60 = 20
- Выражение: 80 – (34 + 26)
- Ответ: 20
2.
В магазин привезли 5 коробок с елочными гирляндами, по 6 гирлянд в каждой коробке, и 7 коробок с гирляндами, по 9 гирлянд в каждой. Сколько всего гирлянд привезли в этих коробках?
Решение:
- 1) 5 * 6 = 30
- 2) 7 * 9 = 63
- 3) 30 + 63 = 93
- Выражение: (5 * 6) + (7 * 9)
- Ответ: 93
3.

В первый день для актового зала привезли 80 стульев, а во второй — в 8 раз меньше. Все стулья расставили в 9 одинаковых по числу стульев рядов. Сколько стульев в одном ряду?
Решение:
- 1) 80 : 8 = 10
- 2) 80 + 10 = 90
- 3) 90 : 9 = 10
- Выражение: (80 : 8 + 80) : 9
- Ответ: 10
На странице использованы материалы из книги С. И. Волковой «Математика. Контрольные работы. 1-4 классы» 2008г.
Примерная контрольная работа по математике 3 класс 3 четверть | Материал по математике (3 класс) по теме:
Примерная контрольная работа по математике за 3 четверть.
- 12 + 3 · 5 3 · (2 + 7)
(23 +5) : 7 49 : (4 + 3)
56 + 27 – 19 45 – 26 + 38
- В 5 вазах по 7 роз, а в 3 вазах по 5 роз.
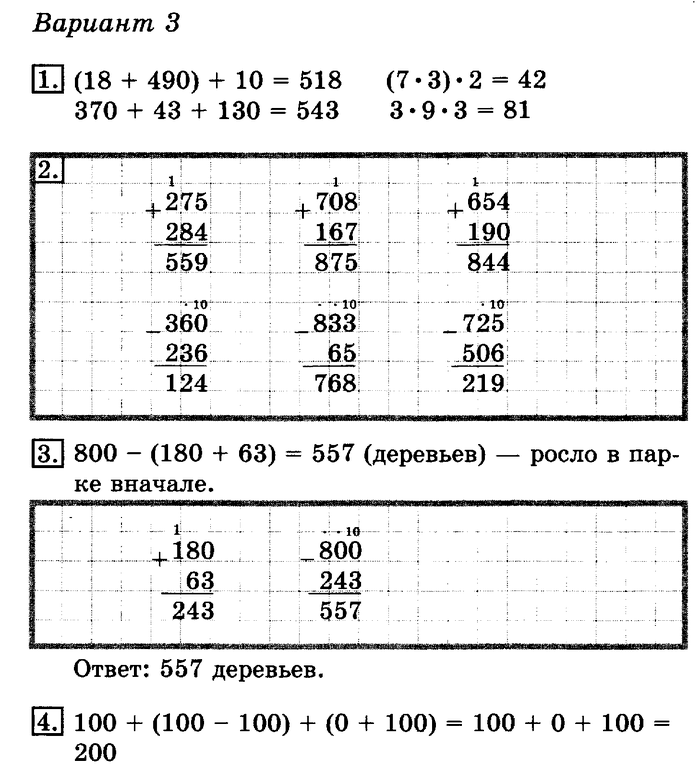 Сколько всего цветов?
Сколько всего цветов? - 5 дм * 4 дм3 см 18 см * 2 дм
12 кг * 21 кг 1 м * 10 дм
- Длина прямоугольника 6 см, ширина 3 см. Найди периметр и площадь этого прямоугольника.
- Начерти два отрезка. Длина первого 4 см, а длина второго на 2 см больше.
6*. Бабушка положила в тарелку 12 груш. После того, как внуки взяли с тарелки по 1 груше, осталось 8 груш. Сколько у бабушки внуков?
Примерная контрольная работа по математике за 3 четверть.
- 12 + 3 · 5 3 · (2 + 7)
(23 +5) : 7 49 : (4 + 3)
56 + 27 – 19 45 – 26 + 38
- В 5 вазах по 7 роз, а в 3 вазах по 5 роз. Сколько всего цветов?
- 5 дм * 4 дм3 см 18 см * 2 дм
12 кг * 21 кг 1 м * 10 дм
- Длина прямоугольника 6 см, ширина 3 см.
 Найди периметр и площадь этого прямоугольника.
Найди периметр и площадь этого прямоугольника. - Начерти два отрезка. Длина первого 4 см, а длина второго на 2 см больше.
6*. Бабушка положила в тарелку 12 груш. После того, как внуки взяли с тарелки по 1 груше, осталось 8 груш. Сколько у бабушки внуков?
Примерная контрольная работа по математике за 3 четверть.
- 12 + 3 · 5 3 · (2 + 7)
(23 +5) : 7 49 : (4 + 3)
- + 27 – 19 45 – 26 + 38
- В 5 вазах по 7 роз, а в 3 вазах по 5 роз. Сколько всего цветов?
- 5 дм * 4 дм3 см 18 см * 2 дм
12 кг * 21 кг 1 м * 10 дм
- Длина прямоугольника 6 см, ширина 3 см. Найди периметр и площадь этого прямоугольника.
- Начерти два отрезка. Длина первого 4 см, а длина второго на 2 см больше.
6*. Бабушка положила в тарелку 12 груш. После того, как внуки взяли с тарелки по 1 груше, осталось 8 груш. Сколько у бабушки внуков?
После того, как внуки взяли с тарелки по 1 груше, осталось 8 груш. Сколько у бабушки внуков?
Примерная контрольная работа по математике за 3 четверть.
- 12 + 3 · 5 3 · (2 + 7)
(23 +5) : 7 49 : (4 + 3)
56 + 27 – 19 45 – 26 + 38
- В 5 вазах по 7 роз, а в 3 вазах по 5 роз. Сколько всего цветов?
- 5 дм * 4 дм3 см 18 см * 2 дм
12 кг * 21 кг 1 м * 10 дм
- Длина прямоугольника 6 см, ширина 3 см. Найди периметр и площадь этого прямоугольника.
- Начерти два отрезка. Длина первого 4 см, а длина второго на 2 см больше.
6*. Бабушка положила в тарелку 12 груш. После того, как внуки взяли с тарелки по 1 груше, осталось 8 груш. Сколько у бабушки внуков?
Ответы на вопросы по 8 классам по математике | Задания по математике
Скачать ответы на вопросы по 8 классу по математике и многое другое Задания по математике в формате PDF только на Docsity! ОТДЕЛ ОБРАЗОВАНИЯ Математика. Четверть 1 — Модуль 6. Иллюстрация прямоугольной системы координат. Математика — 8 класс. Альтернативный режим обучения. Четверть 1. Модуль 6. Иллюстрация прямоугольной системы координат. Работа правительства Филиппин. Однако для использования такого произведения в целях получения прибыли необходимо предварительное одобрение государственного органа или учреждения, в котором создается произведение. Такое агентство или ведомство может, помимо прочего, выдвигать в качестве условия выплату лицензионных отчислений. Заимствованные материалы (т. е. песни, рассказы, стихи, изображения, фотографии, торговые марки, товарные знаки и т. д.), включенные в эту книгу, принадлежат их соответствующим владельцам авторских прав. Были приложены все усилия, чтобы найти и получить разрешение на использование этих материалов у соответствующих владельцев авторских прав. Издатель и авторы не представляют и не претендуют на право собственности на них. Опубликовано Секретарем Департамента образования: Леонор Магтолис Брионес Заместителем секретаря: Диосдадо М.
Четверть 1 — Модуль 6. Иллюстрация прямоугольной системы координат. Математика — 8 класс. Альтернативный режим обучения. Четверть 1. Модуль 6. Иллюстрация прямоугольной системы координат. Работа правительства Филиппин. Однако для использования такого произведения в целях получения прибыли необходимо предварительное одобрение государственного органа или учреждения, в котором создается произведение. Такое агентство или ведомство может, помимо прочего, выдвигать в качестве условия выплату лицензионных отчислений. Заимствованные материалы (т. е. песни, рассказы, стихи, изображения, фотографии, торговые марки, товарные знаки и т. д.), включенные в эту книгу, принадлежат их соответствующим владельцам авторских прав. Были приложены все усилия, чтобы найти и получить разрешение на использование этих материалов у соответствующих владельцев авторских прав. Издатель и авторы не представляют и не претендуют на право собственности на них. Опубликовано Секретарем Департамента образования: Леонор Магтолис Брионес Заместителем секретаря: Диосдадо М. Сан-Антонио Группа разработчиков модулей Авторы: Джейсон Карл Д. Дюма, Винсент Бутч С. Эмболоде, Эммануэль С. Сага Редактор языка: Мерджори Г. Далаган Оценщик макета : Джейк Д. Фрага Оценщик содержания: Элси Мэй М. Перолино Рецензенты: Рея Дж. Ипаррагирре, Нило Б. Монтаджио, Лилибет С. Апат, Ливейвей Дж. Лубанг, Родора С. Луга, Ли С. Апас, Дженни О. Пендика, Иллюстратор: Джейсон Карл Д. Дюма, Винсент Бутч С. Эмболоде Художник-макет: Джейсон Карл Д. Дюма, Винсент Бутч С. Эмболоде, Эммануэль С. Сага Менеджмент: Фрэнсис Сезар Б. Брингас Исидро М. Биол, мл. Марипаз Ф. Magno Josephine Chonie M. Obsefhares Josita B. Carmen Celsa A. Casa Regina Euann A. Puerto Bryan L. Arreo Elnie Anthony P. Barcena Leopardo P. Cortes Напечатано на Филиппинах Министерством образования — Адрес офиса региона Карага: Отдел управления учебными ресурсами (LRMS) JP Rosales Avenue, Butuan City, Ph. Филиппины 8600 Тел. №/телефакса: (085) 342-8207 / (085) 342-5969 Адрес электронной почты: [email protected] Этот модуль состоит из следующих частей и соответствующих значков: Что мне нужно знать Что я знаю Что нового Что нового Что это еще Что я узнал Что я могу сделать Оценка Дополнительно Упражнения Ключ к ответу Это даст вам представление о навыках или компетенциях, которые вы должны освоить в модуле.
Сан-Антонио Группа разработчиков модулей Авторы: Джейсон Карл Д. Дюма, Винсент Бутч С. Эмболоде, Эммануэль С. Сага Редактор языка: Мерджори Г. Далаган Оценщик макета : Джейк Д. Фрага Оценщик содержания: Элси Мэй М. Перолино Рецензенты: Рея Дж. Ипаррагирре, Нило Б. Монтаджио, Лилибет С. Апат, Ливейвей Дж. Лубанг, Родора С. Луга, Ли С. Апас, Дженни О. Пендика, Иллюстратор: Джейсон Карл Д. Дюма, Винсент Бутч С. Эмболоде Художник-макет: Джейсон Карл Д. Дюма, Винсент Бутч С. Эмболоде, Эммануэль С. Сага Менеджмент: Фрэнсис Сезар Б. Брингас Исидро М. Биол, мл. Марипаз Ф. Magno Josephine Chonie M. Obsefhares Josita B. Carmen Celsa A. Casa Regina Euann A. Puerto Bryan L. Arreo Elnie Anthony P. Barcena Leopardo P. Cortes Напечатано на Филиппинах Министерством образования — Адрес офиса региона Карага: Отдел управления учебными ресурсами (LRMS) JP Rosales Avenue, Butuan City, Ph. Филиппины 8600 Тел. №/телефакса: (085) 342-8207 / (085) 342-5969 Адрес электронной почты: [email protected] Этот модуль состоит из следующих частей и соответствующих значков: Что мне нужно знать Что я знаю Что нового Что нового Что это еще Что я узнал Что я могу сделать Оценка Дополнительно Упражнения Ключ к ответу Это даст вам представление о навыках или компетенциях, которые вы должны освоить в модуле. Эта часть включает в себя задание, целью которого является проверка того, что вы уже знаете об уроке, который предстоит пройти. Если вы правильно ответили на все вопросы (100%), вы можете пропустить этот модуль. Это краткое упражнение или повторение, которое поможет вам связать текущий урок с предыдущим. В этой части новый урок будет представлен вам различными способами; рассказ, песня, стихотворение, открытие проблемы, действие или ситуация. В этом разделе дается краткое обсуждение урока. Это направлено на то, чтобы помочь вам открыть и понять новые концепции и навыки. Это включает в себя упражнения для самостоятельной практики, чтобы закрепить ваше понимание и навыки по теме. Вы можете проверить ответы на упражнения, используя Ключ ответов в конце модуля. Сюда входят вопросы или пустые предложения/абзацы, которые необходимо заполнить, чтобы обработать то, что вы узнали из урока. В этом разделе представлено задание, которое поможет вам применить свои новые знания или навыки в реальных жизненных ситуациях или проблемах.
Эта часть включает в себя задание, целью которого является проверка того, что вы уже знаете об уроке, который предстоит пройти. Если вы правильно ответили на все вопросы (100%), вы можете пропустить этот модуль. Это краткое упражнение или повторение, которое поможет вам связать текущий урок с предыдущим. В этой части новый урок будет представлен вам различными способами; рассказ, песня, стихотворение, открытие проблемы, действие или ситуация. В этом разделе дается краткое обсуждение урока. Это направлено на то, чтобы помочь вам открыть и понять новые концепции и навыки. Это включает в себя упражнения для самостоятельной практики, чтобы закрепить ваше понимание и навыки по теме. Вы можете проверить ответы на упражнения, используя Ключ ответов в конце модуля. Сюда входят вопросы или пустые предложения/абзацы, которые необходимо заполнить, чтобы обработать то, что вы узнали из урока. В этом разделе представлено задание, которое поможет вам применить свои новые знания или навыки в реальных жизненных ситуациях или проблемах. Это задание, целью которого является оценка вашего уровня мастерства в достижении учебной компетенции. В этой части вам будет предложено еще одно задание, чтобы обогатить ваши знания или навыки усвоенного урока. Он содержит ответы на все действия в модуле. В конце этого модуля вы также найдете: Ссылки Это список всех источников, использованных при разработке этого модуля. Ниже приведены некоторые напоминания об использовании этого модуля: 1. Используйте модуль с осторожностью. Не ставьте ненужные метки на какую-либо часть модуля. Используйте отдельный лист бумаги, отвечая на упражнения. 2. Не забудьте ответить Что | Узнайте, прежде чем переходить к другим занятиям, включенным в модуль. Внимательно прочитайте инструкцию перед выполнением каждого задания. Соблюдайте честность и добросовестность при выполнении заданий и проверке своих ответов. Завершите текущую задачу, прежде чем переходить к следующей. 6. Верните этот модуль своему учителю/фасилитатору, как только вы закончите с ним. aro Если у вас возникнут трудности с ответами на задания этого модуля, не стесняйтесь проконсультироваться со своим учителем или фасилитатором.
Это задание, целью которого является оценка вашего уровня мастерства в достижении учебной компетенции. В этой части вам будет предложено еще одно задание, чтобы обогатить ваши знания или навыки усвоенного урока. Он содержит ответы на все действия в модуле. В конце этого модуля вы также найдете: Ссылки Это список всех источников, использованных при разработке этого модуля. Ниже приведены некоторые напоминания об использовании этого модуля: 1. Используйте модуль с осторожностью. Не ставьте ненужные метки на какую-либо часть модуля. Используйте отдельный лист бумаги, отвечая на упражнения. 2. Не забудьте ответить Что | Узнайте, прежде чем переходить к другим занятиям, включенным в модуль. Внимательно прочитайте инструкцию перед выполнением каждого задания. Соблюдайте честность и добросовестность при выполнении заданий и проверке своих ответов. Завершите текущую задачу, прежде чем переходить к следующей. 6. Верните этот модуль своему учителю/фасилитатору, как только вы закончите с ним. aro Если у вас возникнут трудности с ответами на задания этого модуля, не стесняйтесь проконсультироваться со своим учителем или фасилитатором. Всегда помните, что вы не одиноки. Мы надеемся, что с помощью этого материала вы получите содержательное обучение и получите глубокое понимание соответствующих компетенций. Ты можешь это сделать! Что мне нужно знать Этот модуль был разработан и написан для вас, чтобы ответить на задание, которое вы пропустили, пока вы не в школе. Он здесь, чтобы помочь вам освоить прямоугольную систему координат и ее использование. Объем этого модуля позволяет использовать его во многих различных учебных ситуациях. Используемый язык признает ваше разнообразие и разнообразный словарный запас. Уроки организованы в соответствии со стандартной последовательностью курса. Но порядок, в котором вы их читаете, можно изменить, чтобы он соответствовал учебнику, которым вы сейчас пользуетесь. Этот модуль содержит: Урок 1. Прямоугольная система координат. После прохождения этого модуля вы должны: дать определение прямоугольной системе координат и другим связанным терминам; нанести точку на координатную плоскость; дать координаты данной точки на координатной плоскости; и использовать координатную плоскость для решения проблем в повседневной жизни.
Всегда помните, что вы не одиноки. Мы надеемся, что с помощью этого материала вы получите содержательное обучение и получите глубокое понимание соответствующих компетенций. Ты можешь это сделать! Что мне нужно знать Этот модуль был разработан и написан для вас, чтобы ответить на задание, которое вы пропустили, пока вы не в школе. Он здесь, чтобы помочь вам освоить прямоугольную систему координат и ее использование. Объем этого модуля позволяет использовать его во многих различных учебных ситуациях. Используемый язык признает ваше разнообразие и разнообразный словарный запас. Уроки организованы в соответствии со стандартной последовательностью курса. Но порядок, в котором вы их читаете, можно изменить, чтобы он соответствовал учебнику, которым вы сейчас пользуетесь. Этот модуль содержит: Урок 1. Прямоугольная система координат. После прохождения этого модуля вы должны: дать определение прямоугольной системе координат и другим связанным терминам; нанести точку на координатную плоскость; дать координаты данной точки на координатной плоскости; и использовать координатную плоскость для решения проблем в повседневной жизни. PON> saaam Прямоугольная система координат ‘1 Исторически карты играли жизненно важную роль для путешественников и исследователей. Эта карта содержит вертикальные и горизонтальные линии, называемые долготой и широтой соответственно. В наши дни картографические приложения и глобальная система позиционирования (GPS) в вашем мобильном телефоне по-прежнему используют горизонтальные и вертикальные линии, чтобы дать вам точное местоположение или координаты места, которое вы ищете. На этом уроке вы изучите концепцию прямоугольной системы координат, нанесение точек и определение координат, которые могут помочь вам в понимании карт, расстояний, экономики, исследований и других повседневных действий. &) Что в действии: НАНЕСИТЕ МЕНЯ! Отметьте заданную точку на числовой прямой. Запишите свой ответ на отдельном листе бумаги. A.0 B.3 <—_—__—_—_—+—-+> <\++_+—++—_++—++-++—> oO o Cc. -1 <—__t— + —+-++> oO Вопросы: 1. Как вам удалось найти положительную и отрицательную точки на горизонтальной числовой прямой? 2.
PON> saaam Прямоугольная система координат ‘1 Исторически карты играли жизненно важную роль для путешественников и исследователей. Эта карта содержит вертикальные и горизонтальные линии, называемые долготой и широтой соответственно. В наши дни картографические приложения и глобальная система позиционирования (GPS) в вашем мобильном телефоне по-прежнему используют горизонтальные и вертикальные линии, чтобы дать вам точное местоположение или координаты места, которое вы ищете. На этом уроке вы изучите концепцию прямоугольной системы координат, нанесение точек и определение координат, которые могут помочь вам в понимании карт, расстояний, экономики, исследований и других повседневных действий. &) Что в действии: НАНЕСИТЕ МЕНЯ! Отметьте заданную точку на числовой прямой. Запишите свой ответ на отдельном листе бумаги. A.0 B.3 <—_—__—_—_—+—-+> <\++_+—++—_++—++-++—> oO o Cc. -1 <—__t— + —+-++> oO Вопросы: 1. Как вам удалось найти положительную и отрицательную точки на горизонтальной числовой прямой? 2. Как вам удалось найти положительную и отрицательную точки на вертикальной числовой прямой? Помните: e« Число, связанное с точкой на числовой прямой, называется координатой этой точки. ¢ Координата начала координат равна нулю. ¢ Координаты точек справа от начала координат на горизонтальной числовой прямой и выше начала координат на вертикальной числовой прямой образуют множество положительных целых чисел. ¢ Координаты точек слева от начала координат на горизонтальной числовой прямой и ниже начала координат на вертикальной числовой прямой образуют множество отрицательных целых чисел. Что нового Упражнение: определение местоположения Предположим, книги на полке расположены следующим образом. Столбец 1 Столбец 2 Столбец 3 Ряд 1 Журналы Ряд 2 Учебники английского языка Ряд 3 Учебники естественных наук Ряд 4 Учебники математики Учебники языка Вопросы: 1. Написав (номер строки, номер столбца), как вы опишете расположение следующего; а. Учебники по математике б. Журналы 2. Используя упорядоченные пары в форме (номер строки, номер столбца), как вы определите положение других книг на полке? Что это такое Упражнение «Определить местоположение» позволяет указать горизонтальное и вертикальное расположение объектов в упорядоченной паре.
Как вам удалось найти положительную и отрицательную точки на вертикальной числовой прямой? Помните: e« Число, связанное с точкой на числовой прямой, называется координатой этой точки. ¢ Координата начала координат равна нулю. ¢ Координаты точек справа от начала координат на горизонтальной числовой прямой и выше начала координат на вертикальной числовой прямой образуют множество положительных целых чисел. ¢ Координаты точек слева от начала координат на горизонтальной числовой прямой и ниже начала координат на вертикальной числовой прямой образуют множество отрицательных целых чисел. Что нового Упражнение: определение местоположения Предположим, книги на полке расположены следующим образом. Столбец 1 Столбец 2 Столбец 3 Ряд 1 Журналы Ряд 2 Учебники английского языка Ряд 3 Учебники естественных наук Ряд 4 Учебники математики Учебники языка Вопросы: 1. Написав (номер строки, номер столбца), как вы опишете расположение следующего; а. Учебники по математике б. Журналы 2. Используя упорядоченные пары в форме (номер строки, номер столбца), как вы определите положение других книг на полке? Что это такое Упражнение «Определить местоположение» позволяет указать горизонтальное и вертикальное расположение объектов в упорядоченной паре. Точно так же точки в прямоугольной системе координат также записываются упорядоченной парой. Прямоугольная система координат, также известная как декартова плоскость, названа в честь французского математика Рене Декарта (159 г.6 — 1650), который известен как «отец современной математики». Он состоит из двух перпендикулярных числовых линий, обычно называемых осью x и осью y соответственно, которые встречаются в исходной точке (0, 0) и делят плоскость на четыре области, называемые квадрантами, которые последовательно пронумерованы как Квадрант I, Квадрант II, Квадрант III и Квадрант IV движутся против часовой стрелки, начиная с верхнего правого угла. 5 Ly C D 4 Ti B A SF 2 (4 7 2 9 4 ~8 5 2 4 3 F 5 Рисунок 2 Помните: в названии координат точки первая координата — это x — координата, а вторая — y — координата. Они нельзя поменять местами Пример 2. Используя декартову плоскость на рисунке 3, найдите координаты следующих точек: a)M b)A c)T d)H 5h y Hah M} 3 2 He 4 ~ | Ba ae att of ae at a £5 Рис.
Точно так же точки в прямоугольной системе координат также записываются упорядоченной парой. Прямоугольная система координат, также известная как декартова плоскость, названа в честь французского математика Рене Декарта (159 г.6 — 1650), который известен как «отец современной математики». Он состоит из двух перпендикулярных числовых линий, обычно называемых осью x и осью y соответственно, которые встречаются в исходной точке (0, 0) и делят плоскость на четыре области, называемые квадрантами, которые последовательно пронумерованы как Квадрант I, Квадрант II, Квадрант III и Квадрант IV движутся против часовой стрелки, начиная с верхнего правого угла. 5 Ly C D 4 Ti B A SF 2 (4 7 2 9 4 ~8 5 2 4 3 F 5 Рисунок 2 Помните: в названии координат точки первая координата — это x — координата, а вторая — y — координата. Они нельзя поменять местами Пример 2. Используя декартову плоскость на рисунке 3, найдите координаты следующих точек: a)M b)A c)T d)H 5h y Hah M} 3 2 He 4 ~ | Ba ae att of ae at a £5 Рис. 3 Ответ: Точка М находится в квадранте II. Он расположен на 2 единицы левее оси у — и на 3 единицы выше оси х. Следовательно, координаты точки М равны (—2,3). Точка А находится в квадранте III. Она расположена на 1 единицу левее оси у — и на 2 единицы ниже оси х. Следовательно, координаты точки А равны (—1,—2). Точка Т находится в квадранте IV. Он расположен на 2 единицы правее оси у и на 4 единицы ниже оси х. Следовательно, координаты точки Т равны (2, —4). Точка H находится в квадранте I. Точка расположена на 3 единицы правее оси у — и на 2 единицы выше оси х. Следовательно, координаты точки H равны (3,2). Пример 3. Нанесите точки на декартову плоскость и определите квадрант. Соедините каждую пару последовательных точек и найдите периметр получившегося четырехугольника. a) L (3,4) b) O (-3,4) c) V (-3,-4) d) E (3,-4) Ответы: Ссылаясь на декартову плоскость на рис. 4 ниже, L (3,4) означает, что точка расположена на 3 единицы правее оси у и на 4 единицы выше оси х. Поскольку знаки обеих координат положительные, точка L находится в квадранте I.
3 Ответ: Точка М находится в квадранте II. Он расположен на 2 единицы левее оси у — и на 3 единицы выше оси х. Следовательно, координаты точки М равны (—2,3). Точка А находится в квадранте III. Она расположена на 1 единицу левее оси у — и на 2 единицы ниже оси х. Следовательно, координаты точки А равны (—1,—2). Точка Т находится в квадранте IV. Он расположен на 2 единицы правее оси у и на 4 единицы ниже оси х. Следовательно, координаты точки Т равны (2, —4). Точка H находится в квадранте I. Точка расположена на 3 единицы правее оси у — и на 2 единицы выше оси х. Следовательно, координаты точки H равны (3,2). Пример 3. Нанесите точки на декартову плоскость и определите квадрант. Соедините каждую пару последовательных точек и найдите периметр получившегося четырехугольника. a) L (3,4) b) O (-3,4) c) V (-3,-4) d) E (3,-4) Ответы: Ссылаясь на декартову плоскость на рис. 4 ниже, L (3,4) означает, что точка расположена на 3 единицы правее оси у и на 4 единицы выше оси х. Поскольку знаки обеих координат положительные, точка L находится в квадранте I. O (—3,4) означает, что точка расположена на 3 единицы левее оси y и на 4 единицы выше оси x. Поскольку знак координаты x или абсцисс отрицательный, а знак координаты y или ординаты положительный, то точка O находится в квадранте II. V (—3,—4) означает, что точка расположена на 3 единицы левее оси y и на 4 единицы ниже оси x. Поскольку знаки обеих координат x и y отрицательные, точка V находится в квадранте III. E (3,—4) означает, что точка расположена на 3 единицы правее оси y и на 4 единицы ниже оси y. ось х. Поскольку знак координаты x или абсцисс положительный, а знак координаты y или ординаты отрицательный, точка E находится в квадранте IV. 5. y loc 3,4 L(3,4) EG3,44) Рисунок 4 10 Соединяя соседние вершины, видим, что точки L, O, V и E образуют прямоугольник. Чтобы найти периметр прямоугольника, мы знаем, что: P=2L+2W Обратите внимание, что каждый интервал на декартовой плоскости представляет собой одну единицу измерения. Это означает, что четырехугольник, образованный точками L, O, V, E, имеет длину 8 единиц и ширину 6 единиц.
O (—3,4) означает, что точка расположена на 3 единицы левее оси y и на 4 единицы выше оси x. Поскольку знак координаты x или абсцисс отрицательный, а знак координаты y или ординаты положительный, то точка O находится в квадранте II. V (—3,—4) означает, что точка расположена на 3 единицы левее оси y и на 4 единицы ниже оси x. Поскольку знаки обеих координат x и y отрицательные, точка V находится в квадранте III. E (3,—4) означает, что точка расположена на 3 единицы правее оси y и на 4 единицы ниже оси y. ось х. Поскольку знак координаты x или абсцисс положительный, а знак координаты y или ординаты отрицательный, точка E находится в квадранте IV. 5. y loc 3,4 L(3,4) EG3,44) Рисунок 4 10 Соединяя соседние вершины, видим, что точки L, O, V и E образуют прямоугольник. Чтобы найти периметр прямоугольника, мы знаем, что: P=2L+2W Обратите внимание, что каждый интервал на декартовой плоскости представляет собой одну единицу измерения. Это означает, что четырехугольник, образованный точками L, O, V, E, имеет длину 8 единиц и ширину 6 единиц. Следовательно, периметр четырехугольника ЛЮБОВЬ равен: P=2L+2W P = 2(8) + 2(6) P=16+12 P = 28 единиц Что еще. Задание 1: Ничего себе, Карага! | 4 s Sirgen ands Surigao Cy Опишите расположение каждой точки, которую Surigao del Norte представляет местом в регионе Карага городом Кабадбаран «Танда Сай», заполнив следующую таблицу. Примером является Z 4, 4 Город Бутуан] | 4 сделано для вас. Запишите свой ответ на отдельном ‘Agusan del Norte Bayugen Cry. [2 листа бумаги. Sarge del NY ‘Agusan del Sur 3 Tig Ciy Место КООРДИНАТЫ КВАДРАНТ/ОСЬ Пример: Острова Динагат (-1,3) Qll 1. Agusan del Norte Город Кабадбаран Город Суригао Город Бислиг 2 3. 4. Агусан-дель-Сур 5 6. Суригао-дель-Норте 7. Город Тандаг 11 Чему я научился Заполните пропуски соответствующего элемента, который сделает предложение правильным Запишите свой ответ в 1. Прямоугольная система координат также названа в честь французского математика, известного как «отец современной математики». 2. Прямоугольная координатная плоскость состоит из двух перпендикулярных числовых линий, которые встречаются на пересечении, называемом и делят плоскость на четыре области, называемые 3.
Следовательно, периметр четырехугольника ЛЮБОВЬ равен: P=2L+2W P = 2(8) + 2(6) P=16+12 P = 28 единиц Что еще. Задание 1: Ничего себе, Карага! | 4 s Sirgen ands Surigao Cy Опишите расположение каждой точки, которую Surigao del Norte представляет местом в регионе Карага городом Кабадбаран «Танда Сай», заполнив следующую таблицу. Примером является Z 4, 4 Город Бутуан] | 4 сделано для вас. Запишите свой ответ на отдельном ‘Agusan del Norte Bayugen Cry. [2 листа бумаги. Sarge del NY ‘Agusan del Sur 3 Tig Ciy Место КООРДИНАТЫ КВАДРАНТ/ОСЬ Пример: Острова Динагат (-1,3) Qll 1. Agusan del Norte Город Кабадбаран Город Суригао Город Бислиг 2 3. 4. Агусан-дель-Сур 5 6. Суригао-дель-Норте 7. Город Тандаг 11 Чему я научился Заполните пропуски соответствующего элемента, который сделает предложение правильным Запишите свой ответ в 1. Прямоугольная система координат также названа в честь французского математика, известного как «отец современной математики». 2. Прямоугольная координатная плоскость состоит из двух перпендикулярных числовых линий, которые встречаются на пересечении, называемом и делят плоскость на четыре области, называемые 3. В упорядоченной паре первое число — это координата x, которая также известна как и второе число — это координата y, которая также известна как 4. Точка попадает в квадрант |, если она имеет знаки (__,__), квадрант II, если (__,__), квадрант III, если (__,__), и квадрант IV if (_,__) 5. Для более легкого построения точек на декартовой плоскости начните двигаться от начала координат либо по оси x, затем по оси y, либо по оси y. 14 © ‘@) DP k Что я могу сделать Упражнение: Найдите спрятанную фигуру Начертите следующие упорядоченные пары на декартовой плоскости, соедините точки и определите образовавшуюся фигуру Запишите ответ на отдельном листе бумаги (Примечание: Соедините точки в порядке номеров ( порядок элементов).Не забудьте соединить цифру 5 с цифрой 1.) 8 1. (6,4) 7 2. (45,5) 6 3. (1,8) 4. (-4, -5) 5 5. (7,2) 91 OPT 2f3t at st ef 778 1 15 Оценка Выберите букву лучшего ответа. Напишите выбранную букву на отдельном листе бумаги. . Точка (9,—1) является примером A. меток C. дробей B. чисел D.
В упорядоченной паре первое число — это координата x, которая также известна как и второе число — это координата y, которая также известна как 4. Точка попадает в квадрант |, если она имеет знаки (__,__), квадрант II, если (__,__), квадрант III, если (__,__), и квадрант IV if (_,__) 5. Для более легкого построения точек на декартовой плоскости начните двигаться от начала координат либо по оси x, затем по оси y, либо по оси y. 14 © ‘@) DP k Что я могу сделать Упражнение: Найдите спрятанную фигуру Начертите следующие упорядоченные пары на декартовой плоскости, соедините точки и определите образовавшуюся фигуру Запишите ответ на отдельном листе бумаги (Примечание: Соедините точки в порядке номеров ( порядок элементов).Не забудьте соединить цифру 5 с цифрой 1.) 8 1. (6,4) 7 2. (45,5) 6 3. (1,8) 4. (-4, -5) 5 5. (7,2) 91 OPT 2f3t at st ef 778 1 15 Оценка Выберите букву лучшего ответа. Напишите выбранную букву на отдельном листе бумаги. . Точка (9,—1) является примером A. меток C. дробей B. чисел D. упорядоченной пары . Точка (—7,—5) находится в каком квадранте? Al C. III B. II D.IV. Что вы называете горизонтальной числовой прямой на декартовой плоскости? A. ось x C. начало координат B. ось y D. квадрант . При построении точки (—8,1), которая описывает движение по оси абсцисс и оси у в правильном порядке? A. 8 единиц вправо, затем 1 единица вверх B. 8 единиц вниз, затем 1 единица влево C. 8 единиц влево, затем 1 единица вверх D.8 единиц вверх, затем 1 единица вправо. В квадранте | значения x и y всегда равны , и , соответственно. A. положительный, положительный C. отрицательный, отрицательный B. положительный, отрицательный D. отрицательный, положительный . Координаты начала координат на координатной плоскости таковы. 2 А. (0,1) В. (1,1) Б. (0,0) Г. (1,0) . Что из следующего верно относительно точки (5, 5)? A. Он лежит на оси x C. Он лежит в квадранте | B. Находится на оси Y D. Находится в квадранте II. Какое из следующих утверждений лучше всего описывает происхождение? A. Точка содержит положительные и положительные целые числа.
упорядоченной пары . Точка (—7,—5) находится в каком квадранте? Al C. III B. II D.IV. Что вы называете горизонтальной числовой прямой на декартовой плоскости? A. ось x C. начало координат B. ось y D. квадрант . При построении точки (—8,1), которая описывает движение по оси абсцисс и оси у в правильном порядке? A. 8 единиц вправо, затем 1 единица вверх B. 8 единиц вниз, затем 1 единица влево C. 8 единиц влево, затем 1 единица вверх D.8 единиц вверх, затем 1 единица вправо. В квадранте | значения x и y всегда равны , и , соответственно. A. положительный, положительный C. отрицательный, отрицательный B. положительный, отрицательный D. отрицательный, положительный . Координаты начала координат на координатной плоскости таковы. 2 А. (0,1) В. (1,1) Б. (0,0) Г. (1,0) . Что из следующего верно относительно точки (5, 5)? A. Он лежит на оси x C. Он лежит в квадранте | B. Находится на оси Y D. Находится в квадранте II. Какое из следующих утверждений лучше всего описывает происхождение? A. Точка содержит положительные и положительные целые числа. B. Точка содержит отрицательные и отрицательные целые числа. C. Точка содержит положительные и отрицательные целые числа. D. Точка не содержит ни положительных, ни отрицательных целых чисел. 16 = Ключ ответа ost ost vo vr {1} tii | tat stl ger va az ot vue sol DoF D6 a6 ae ve Tt DL aL SAL aco 2° Lt vos 275 fo ov vr vee a hel +} 3 az ibe av av quowssassy quoussesse-alg A . ‘паувой адеус 249441U9P1 Ws UR -edeus UoppIT 2uR PUL) =GINRIY re 1 iy ord 9 og ueg 12e4UM i.) (ean 6\4 (Cid”+oo©(g’p)1 exe syoogxe}eBenBueq'(z’z)( 9-2 @ ye ase syooq)xe} ysij6uy (| ‘g ye ae syoogxKe! eoual9g ipo ob yey} Aes am ‘(Jequinu utunjoo ‘yaquunu mos) Buisn Ag Zz SIR) Ese 10 yo 9 8294 UH) 2H cui GACY 3 ) 1>feh_ UCR id USO] ON) «)e . soyutpwods (1’p) I UeAIB auld uerseueD at UI Stulod ey old : NOK e\ceuE MME MRNZe SUL ‘UoRRUESEC SLNIQd SHL 101d ‘$ ALIALLOW uo}2007 84} Aynuep] :AAnOW MON S281 wae N’S2eUN . wae Ek–orvepenesein fp uninkeg esnenna на «smeuipi009»snosuou Busiods 2. AABW SIND x4) ° wo Suey pa er eo) fea Divee la ra ou fed (ed ext i) ‘ et eo inte mam Aue ° ° | _ tt +e ( aso S22UM (= ov ae ca iW ld :Auanoy UL sqeUN 19 Ссылки Абузо, Эммануэль П.
B. Точка содержит отрицательные и отрицательные целые числа. C. Точка содержит положительные и отрицательные целые числа. D. Точка не содержит ни положительных, ни отрицательных целых чисел. 16 = Ключ ответа ost ost vo vr {1} tii | tat stl ger va az ot vue sol DoF D6 a6 ae ve Tt DL aL SAL aco 2° Lt vos 275 fo ov vr vee a hel +} 3 az ibe av av quowssassy quoussesse-alg A . ‘паувой адеус 249441U9P1 Ws UR -edeus UoppIT 2uR PUL) =GINRIY re 1 iy ord 9 og ueg 12e4UM i.) (ean 6\4 (Cid”+oo©(g’p)1 exe syoogxe}eBenBueq'(z’z)( 9-2 @ ye ase syooq)xe} ysij6uy (| ‘g ye ae syoogxKe! eoual9g ipo ob yey} Aes am ‘(Jequinu utunjoo ‘yaquunu mos) Buisn Ag Zz SIR) Ese 10 yo 9 8294 UH) 2H cui GACY 3 ) 1>feh_ UCR id USO] ON) «)e . soyutpwods (1’p) I UeAIB auld uerseueD at UI Stulod ey old : NOK e\ceuE MME MRNZe SUL ‘UoRRUESEC SLNIQd SHL 101d ‘$ ALIALLOW uo}2007 84} Aynuep] :AAnOW MON S281 wae N’S2eUN . wae Ek–orvepenesein fp uninkeg esnenna на «smeuipi009»snosuou Busiods 2. AABW SIND x4) ° wo Suey pa er eo) fea Divee la ra ou fed (ed ext i) ‘ et eo inte mam Aue ° ° | _ tt +e ( aso S22UM (= ov ae ca iW ld :Auanoy UL sqeUN 19 Ссылки Абузо, Эммануэль П. , Брайант, Мерден Л., Кабрелла, Джем Бой Б. и др. (2013). Математика, 8 класс, учебная литература) Module, стр. 109-123.. Philsports Complex, Meralco Avenue, Pasig City, Филиппины Book Media Press, Inc. & Printwell, Inc. -coordinate- system.html Дата получения: 22 декабря 2019 г.20 По вопросам или отзывам, пожалуйста, пишите или звоните: Департамент образования — Бюро учебных ресурсов Первый этаж, здание Бонифачо, Комплекс Депед Мералко Авеню, город Пасиг, Филиппины 1600 Телефакс. №: (632) 8634-1072; 8634-1054; 8631-4985 Адрес электронной почты: [email protected] * [email protected] 21
, Брайант, Мерден Л., Кабрелла, Джем Бой Б. и др. (2013). Математика, 8 класс, учебная литература) Module, стр. 109-123.. Philsports Complex, Meralco Avenue, Pasig City, Филиппины Book Media Press, Inc. & Printwell, Inc. -coordinate- system.html Дата получения: 22 декабря 2019 г.20 По вопросам или отзывам, пожалуйста, пишите или звоните: Департамент образования — Бюро учебных ресурсов Первый этаж, здание Бонифачо, Комплекс Депед Мералко Авеню, город Пасиг, Филиппины 1600 Телефакс. №: (632) 8634-1072; 8634-1054; 8631-4985 Адрес электронной почты: [email protected] * [email protected] 21
Письменные задания
Письменные заданияДомашняя страница На этой странице вы узнаете, как лучше всего выполнять и форматировать письменные задания на моих курсах.Предположим, мы приближаемся к концу курса алгебры, и вот постановка задачи:
| Задание 12: Найдите точки пересечения по оси x следующей функции. \( f(x) = \dfrac{2x+1}{x+1} + \dfrac{3}{2x-4} \) |
Содержимое
Неправильно: Без имени, почти без работы. Хотя это правильный ответ, у меня нет доказательств того, что проблема была решена вами. Выполняйте письменные задания самостоятельно. Я оцениваю правильный ответ, правильные шаги и ясность. Хотя это правильный ответ, у меня нет доказательств того, что проблема была решена вами. Выполняйте письменные задания самостоятельно. Я оцениваю правильный ответ, правильные шаги и ясность. | Правильно: Достаточный баланс работы и объяснения. Можно свернуть несколько шагов в один, но будьте осторожны, чтобы не делать больших прыжков. См. далее. | Правильно, но за бортом: Поскольку мы находимся в последней части алгебры, более ранние темы, такие как FOIL или квадратичная формула, не нуждаются в подробных объяснениях. Однажды я приму многословные решения, если они верны, но в будущем урежу их ради нас обоих! В идеале вы должны уместить свое решение на одной или двух страницах. |
| \( f(x) = 0 \) \( -\dfrac{1}{4}, 1 \) | студентка колледжа 92-3x-1 = 0 \) \( (4x+1)(x-1) = 0 \) \( x = -\dfrac{1}{4}, 1 \) Обе эти значения x находятся в области f (x), поэтому они не являются посторонними решениями. | Колледж J Студент Задание 12 Задача состоит в том, чтобы найти все x-отрезки f(x). Поэтому мне нужно найти все действительные числа x, которые решают следующее уравнение. \( f(x) = \dfrac{2x+1}{x+1} + \dfrac{3}{2x-4} = 0 \) 92 – 4(4)(-1)}}{2(4)} \) |
Но прежде чем я смогу оценить контент, нам нужно поговорить о…
Формат
| Правильное форматирование: Вы можете писать или печатать свои задания. Приведенные выше решения являются примерами правильного форматирования уравнения. (Вы можете использовать LaTeX или редактор уравнений вашего текстового процессора.) Если вы пишете свое решение, я рекомендую вам писать карандашом, чтобы исправить небольшие ошибки сейчас и в будущих попытках. Вы можете отсканировать или сфотографировать его вот так: | Следующие загрузки являются неправильными и должны быть переформатированы и повторно загружены, прежде чем я смогу оценить их содержание: Размытые, слишком темные/светлые, неправильно повернутые, слишком низкое разрешение или нечитаемые по другим причинам. |
| Неизвестное или отсутствующее расширение имени файла (например, .doc). Рабочие форматы: pdf, png, jpg, doc, docx. Всегда предварительно просматривайте загруженное задание, чтобы убедиться, что оно отображается. | |
| Набрано, но не в формате уравнения. Пожалуйста, не делай это! Это мигрень для интерпретации, и она склонна к двусмысленности, которая может изменить весь смысл ваших уравнений. Вот один веб-редактор формул. |
Процесс загрузки
| 1. На боковой панели курса «Доска» слева перейдите на страницу «Задания». | |
| 2. Найдите задание, которое вы выполняете. Нажмите на прикрепленный файл, чтобы увидеть само задание. Щелкните заголовок, чтобы начать процесс загрузки. | |
| 3. Щелкните Обзор моего компьютера и перейдите к файлу, содержащему ваше решение. Затем нажмите «Отправить» в правом нижнем углу. Важно! Вы можете нажать «Сохранить черновик», если хотите просмотреть и внести изменения, но я не смогу просмотреть или оценить ваше задание, пока вы не нажмете «Отправить». | |
| 4. Подтвердите, что ваше решение отображается, затем нажмите OK. | |
| 5. По истечении срока я оценю задание. Отзыв можно найти в синих кружках на самом документе или на боковой панели справа, или и там, и там. Они могут не отображаться на телефонах. Вы можете просматривать отзывы на компьютере. Если вы вовремя сдали попытку, но получили ноль, прочитайте отзыв и внесите исправления, а затем повторно загрузите задание, выполнив эти шаги еще раз. (Нажмите «Начать новый» на экране, где вы видите свое предыдущее решение.) Если есть 0 и нет обратной связи, что-то пошло не так. Дайте мне знать, если это произойдет. |
Почему?
Почему я требую объяснений? Часто упускаемый из виду аспект математики — точная коммуникация. Я имею в виду не просто то, что другой человек знает, что вы имеете в виду, когда говорите «отрицательное значение х в квадрате», а то, почему вы имеете дело с выражением «отрицательное значение х в квадрате».


 Нет ничего плохого в том, чтобы нажать «Отправить»; Вы можете загружать любое задание столько раз, сколько необходимо.
Нет ничего плохого в том, чтобы нажать «Отправить»; Вы можете загружать любое задание столько раз, сколько необходимо.