Задания на логику с ответами по математике 2 класс: Логические задачи для 2 класса

Занимательные задачи на логику с ответами

1. В море плавало 9 пароходов. 2 парохода пристали к пристани. Сколько пароходов в море? (9).

2. Как в решете воды принести? (Когда вода замерзнет и превратится в лед).

3. Из какой посуды нельзя ничего есть? (Из пустой).

4. Наступил долгожданный январь. Сначала зацвела 1 яблоня, а потом еще 3 сливы. Сколько деревьев зацвело? (В январе деревья не цветут).

5. Плитку шоколада разделили на несколько частей. Петя съел 2 части, Нина – 1 часть, осталось еще 3 части. На сколько частей разделили шоколад?(на 6).

6. Строители строили дорогу. Несколько участков выше уровня земли, несколько – ниже. На каких участках земли образуются лужи?( На низких).

7. В физкультурном зале висит канат. Мальчик поднялся на 3 метра и достиг середины. Какой длины канат? (6 м)

8. Неожиданно пошел сильный дождь. Но Таня, Саша, Лена не промокли. Почему?(Они наблюдали из окна; у них были плащи, зонты).

9. У животного 2 правые ноги, 2 левые ноги, 2 ноги впереди, 2 сзади. Сколько у него ног? (4).

10. Сапожник решил починить 2 пары ботинок. На каждый каблук он набьет набойку, каждую набойку он прибьет 2 гвоздями. Сколько набоек и гвоздей ему понадобится?(12)

11. Вода в чайнике закипает через 10 минут. Алеша поставил чайник в 8 часов. Когда он сможет пить чай? ( в 8.10)

12. Костя ссыпал вместе песок из 3 кучек, а Маша ссыпала вместе песок из 4 кучек. Сколько кучек песка получилось?(2, если каждый ссыпал в свою кучку или 1, если ссыпали вместе).

13. На стройке работал каменщик. В первый день работы он построил 2 двадцатиэтажных дома, во второй день – 1 двадцатиэтажный дом. Сколько двадцатиэтажных домов он построил? ( Ни одного, он не мог этого сделать).

14. Сколько орехов в пустом стакане? (Ни одного)

15. По морю плавало 9 акул. Они увидели косяк рыб и нырнули в воду. Сколько акул плавало в море? (9).

16. В вазе 3 тюльпана и 7 нарциссов. Сколько тюльпанов в вазе? (3)

17. 7 мальчиков расчистили по 1 дорожке в саду. Сколько дорожек они расчистили? (7)

18. В стакане 10 ложек меда. На сколько детей его может хватить?

( варианты ответов).

19. В кувшине 10 кружек молока. На сколько детей его может хватить?. ( Варианты ответов)

20. Сестра и брат получили по 4 яблока. Сестра съела 3 яблока, а брат – 2 яблока. У кого яблок осталось больше? (У брата)

21. 2 бригады сеяли горох. Первая бригада засеяла 4 грядки гороха, вторая столько и еще полстолько. Какая бригада стала победителем, сколько грядок она засеяла?

22. Гусь весит 2 кг. Сколько он будет весить, если он встанет на 1 ногу? (2 кг)

23. Один ослик нес 10 кг сахару, а другой – 10 кг ваты. У кого поклажа была тяжелее?( Одинаковая).

24. Бабушка вязала внукам шарфы и варежки. Всего она связала 3 шарфа и 6 варежек. Сколько внуков было у бабушки? (3, объяснить почему).

25. В реке купались дети. Они постоянно ныряли в воду и невозможно их было пересчитать. На берегу были разбросаны кеды, всего 12 штук. Сколько детей купалось в реке? (6).

26. Из-под ворот видно 8 кошачьих лап. Сколько кошек во дворе? (2).

27. Из дупла выглядывают 8 беличьих хвостов. Сколько бельчат в дупле? (8)

28. Кузнец подковал тройку лошадей. Сколько подков ему пришлось сделать?(1ё2).

29. Карандаш разрезали на 3 части. Сколько сделали разрезов? (2).

30. Веревку разрезали в 5 местах. Сколько частей получилось? (6)

31. Повар насыпал рис поровну в 2 стакана. Затем из одного стакана он пересыпал рис в кастрюлю. Где риса больше: во втором стакане или в кастрюле? (Поровну).

32.Одно яблоко разделили поровну между двумя девочками, а второе между 4 мальчиками. Кто из детей получил большую часть? Какую часть получил каждый?

( девочки ½ – большую, мальчики ¼ – меньшую).

33. На столе стоял полный стакан кефира, а рядом стакан, наполненный до половины. Как разделить кефир между 3 детьми?

34. Дедка, бабка, внучка, Жучка, кошка и мышка тянули, тянули и наконец вытянули репку. Сколько глаз увидело репку?(12).

35. В 12 часов ночи шел снег. Может ли через несколько дней в это же время быть солнечная погода? ( Нет, это ночь).

36. Поезд состоит из 12 вагонов. Марат сел в 6 по счёту вагон с головы поезда, а Андрей сел в 6 вагон по счёту с хвоста поезда. В одном ли вагоне ехали Марат и Андрей? (Марат и Андрей ехали в разных вагонах).

37. У трёх девочек по 2 цветных шара: у Оли синий и красный, у Кати зелёный и красный, у Ланы жёлтый и синий. Сколько различных по цвету шаров у детей? (4 разных цвета).

38. Карина гуляла и видела у реки 4 уток, 2 гусей, жука, 4 бабочки и соседскую собаку. Сколько птиц видела Карина? (6 птиц)

39. Лестница состоит из 9 ступенек. На какую ступеньку надо встать, чтобы быть на середине лестницы? (На 5 ступеньку).

40. Мама дала сыновьям по 8 конфет. Вечером у старшего осталось 3 конфеты, а у младшего — 1 конфета. Кто съел больше? (Младший сын).

41. Арбуз и дыня вместе весят 5 кг, а два арбуза и дыня весят 8 кг. Сколько весит один арбуз и одна дыня? (Арбуз 3 кг, дыня 2 кг)

42. Два третьеклассника шли в школу во вторую смену. Они встретили трёх первоклассников — учеников первой смены. Сколько всего учеников шли в школу? (2 ученика).

43. У брата и сестры было орехов поровну. Брат отдал сестре 3 ореха. На сколько орехов стало больше у сестры, чем у брата. (На 6 орехов).

44. Руслан старше Андрея. Кирилл моложе Саши, но старше Руслана. Кто из них самый старший и самый младший? (Старший — Саша, младший — Андрей).

45. Во дворе гуляли собаки и куры. Всего 10 лап. Сколько могло быть кур и сколько собак. Сколько вариантов ответа? (1 собака и 3 курицы или 2 собаки и 1 курица).

46. Колю угостили конфетами. Половину конфет он съел, а оставшиеся 5 конфет отнёс брату. Сколько конфет дали Коле? (10 конфет.)

47. Маме нужно засадить саженцами помидоров ряд длиной 3 м. Расстояние между саженцами 30 см. Сколько саженцев помидоров надо заготовить для посадки? (11 саженцев).

48. Толя, Шурик и Антон были на рыбалке. Каждый из них поймал разное количество рыб. Толя и Шурик вместе поймали 6 рыб, а Антон и Толя — 4 рыбы. Сколько рыб поймал каждый из мальчиков? (Толя — 1 рыбу, Шурик — 5, Антон — 3).

49. На уроке физкультуры дети выстроились в одну шеренгу с интервалом 1 м. Шеренга растянулась на 20 м. Сколько детей было на уроке? (21 ученик).

50. Из красных и жёлтых тюльпанов Ира хочет составить букет так, чтобы в нём было 3 цветка. Сколько разных букетов может составить Ира? (4 букета).

51. Арбуз весит 3 кг и ещё половину арбуза. Сколько весит арбуз? (6 кг)

52. Масса бидона с молоком составляет 34 кг, а масса бидона, наполненного наполовину, равна 18 кг. Какова масса пустого бидона? (2 кг)

53. Как взвесить 4 кг сахара, если имеются гири 3 кг и 5 кг?(Взвесить 5 кг, от этих 5 кг с помощью 3 кг гири отвесить 2 кг.И эту процедуру повторить 2 раза)

54. На одной чаше весов находится 5 одинаковых яблок и 3 одинаковые груши, на другой чаше — 4 яблока и 4 груши. Что легче: яблоко или груша? (Масса яблока и груши одинаковая)

55. Мама закупила продукты: 1 кг соли, 2 кг гречки, 3 кг риса, 4 кг сахара, 5 кг моркови, 6 кг лука, 7 кг картофеля. Как разложить продукты в два пакета, чтобы их масса была одинаковая. (По 14 кг в каждый пакет несколькими различными вариантами)

56. На день рождения Винни-Пуху подарили бочонок с мёдом массой 7 кг. Когда Винни-Пух съел половину мёда, то бочонок с оставшимся мёдом стал весить 4 кг. Какова масса пустого бочонка?(1 кг)

57. Рыбак поймал 29 рыб. Из них карасей на 3 больше, чем щук. Сколько карасей и сколько щук поймал рыбак? (16 карасей и 13 щук)

58. Через 7 лет Данил будет вдвое старше, чем сейчас. Сколько лет Данилу сейчас? Сколько лет будет через 7 лет? (Сейчас 7 лет, будет 14)

59. Магазин при 12-часовом рабочем дне работает с 8 часов до 21 часа. Закрывают ли магазин на обеденный перерыв? (Перерыв 1 час)

60. Аскар дал младшему брату половину своих яблок и ещё одно яблоко, и у него не осталось ни одного яблока. Сколько яблок было у Аскара? (2 яблока)

61. Длина спички 5 см. Как из 13 спичек сложить метр? (сложить слово метр)

62. Сара провела у бабушки понедельник, вторник, среду и четверг, а её младшая сестра в ту же неделю — среду, четверг, пятницу и субботу. Сколько всего дней гостили девочки у бабушки? (6 дней)

63. В автобусе ехало7 человек. На первой остановке вышло 3 пассажира, а село 12. Наследующей — вышли 9 человек, зашли 5. Далее — вышли 7, зашли 8. Сколько было остановок? (3 остановки)

64. В магазин привезли 6 мешков сахара по 50 кг, 8 мешков муки по

25 кг, 4 мешка риса по 10 кг, 2 мешка пшена по 12 кг. Сколько мешков с продуктами привезли? (20 мешков)

65. Автобус с Кушмуруна до Костаная едет 2 часа 10 минут, а обратно — 130 минут. Объясни, почему? (один и тот же участок, 2ч10мин=130мин)

66. Сколько различных трёхзначных чисел можно записать тремя различными цифрами? (6 чисел)

67. Две соседки измеряли длину своих дачных участков. Первая, измеряя длину, поставила 7 колышков через каждые 2 метра, вторая поставила 13 колышков через каждый метр. У кого участок длиннее? (Одинаковые)

68. Как, пользуясь банками в 3 л и 5 л, из крана набрать 1 л воды?(Набрать 5 л, из них отлить 3л, остаток – 2л – вылить в сосуд.Проделать процедуру 2 раза, чтобы в сосуде накопилось 4 л. Затем от этих 4л отлить банкой 3 л, в сосуде останется 1л)

69. На сколько больше наименьшее двузначное число, чем наибольшее однозначное? (На 1)

70. Как разложить 15 карандашей в 5 коробок так, чтобы во всех коробках было разное количество карандашей? (1,2,3,4,5 карандашей)

71. В 3 часа стенные часы отбивают три удара за 6 секунд. За сколько секунд эти часы отобьют шесть ударов в 6 часов? (15 с)

72. Поставьте двух мальчиков так, чтобы Вова стоял сзади Нияза, а Нияз — сзади Вовы. (Спиной друг к другу)

73. Моей сестре сегодня исполнилось 6 лет. Когда она родилась, мне было 3 года 6 месяцев. Сколько лет мне теперь? (9 лет 6месяцев)

74. Врач дал больному 3 таблетки и велел принимать их через каждые полчаса. Больной строго выполнил указания врача. На сколько времени хватило таблеток? (На 1 час)

75. Белочка насушила на зиму 5 целых яблок, 10 половинок и 8 четвертинок. Сколько всего яблок у белочки? (12 яблок)

76. Если один петух закукарекает, то человек проснётся. Сколько петухов должны закукарекать, чтобы проснулись три человека? (Один петух)

77. Брату и сестре вместе 10 лет. Сколько лет им будет вместе через пять лет? (20 лет)

78. Дамир принёс в класс 3 чистые тетради в линейку, Ваня — 6 тетрадей в клетку, а Серёжа забыл принести тетради. Ребята разделили все тетради поровну, каждый из них получил по одной тетради в линейку и по две тетради в клетку. На следующий день Серёжа принёс ребятам 45 тенге за тетради. Как должны разделить деньги между собой Дамир и Ваня, если цена тетрадей в клетку и в линейку одинаковая? (45 тенге Ване)

79. Вы зашли в тёмную комнату, где есть свеча, газовая плита, керосиновая лампа. Что вы зажжёте в первую очередь? (Спички)

80. К празднику ученики должны украсить площадь прямоугольной формы 12 флажками так, чтобы было со всех сторон по 4 флажка. Как это сделать? (По углам флажки и по 2 флажка с каждой стороны)

81. Как наполнить ведро три раза подряд, ни разу не опустошая? (Первый раз наполнить камнями, второй — песком, третий — водой.)

82. В семье несколько детей. Один ребёнок говорит, что у него есть один брат и две сестры. Другой ребенок говорит, что у него одна сестра и два брата. Сколько детей в семье, девочек и мальчиков? (4 человека; 2 девочки и 2 мальчика)

83. По улице шли два отца и два сына, да дедушка с внуком. Сколько всего человек шло по улице? (3 человека)

84. У тебя монеты по 20 тенге. У продавца только монеты по 50 тенге. Как расплатиться за булку хлеба ценой 50 тенге. (5 монет по 20 тенге, сдача — 50 тенге)

85. Бабушке и внуку вместе 65 лет. Бабушке столько лет, сколько месяцев внуку. Сколько лет бабушке и сколько внуку?(60 лет бабушке, 5 лет внуку)

86. Какой знак нужно поставить между 4-мя и 5-ю, чтобы результат оказался больше 4-х и меньше 5-ти? (Запятую)

87. Может ли петух назвать себя птицей? (Нет, т. к. он не умеет говорить)

88. Что можно приготовить, но нельзя съесть? (Уроки)

89. Что становится на треть больше, если его поставить вверх ногами? (Цифра 6)

90. У квадратного стола отпилили один угол. Сколько теперь углов у стола? (Пять)

91. Какой узел нельзя развязать? (Железнодорожный)

92. Какая река самая страшная? (Тигр)

93.Что не имеет длины, глубины, ширины, высоты, а можно измерить? (Температуру, время)

94. Что все люди на земле делают одновременно? (Становятся старше)

95. Как может брошенное яйцо пролететь три метра и не разбиться? (Нужно бросить яйцо более, чем на три метра, тогда первые три метра оно пролетит целым)

96. Что с земли легко поднимешь, но далеко не закинешь? (Тополиный пух)

97. Что может путешествовать по свету, оставаясь в одном и том же углу? (Почтовая марка)

98. Какими нотами можно измерить расстояние? (Ми-Ля-Ми)

99. Что не войдёт в самую большую кастрюлю? (Её крышка)

100. Что считается грязным, когда оно белое, и чистым, когда оно зелёное? (Классная доска)

Урок математики по теме “Решение логических задач”

Цель:

Развивать логическое мышление.

• обучающая – обучать решению логических задач, обучать методу проектной деятельности.
• развивающая – развивать культуры мысли в устной и письменной речи, развивать память, внимание, творчество.
• воспитательная – воспитывать культуру общения, прививать интерес к математике.

Подготовка к уроку.

В классе выбрать три группы, каждой из которых дать домашнее задание: придумать или подобрать задачи, которые решаются методом таблиц или рассуждений.

Оборудование.

На столах карточки с заданиями, листы с самостоятельной работой, с тестами. Для устного счета листы с таблицей чисел от 1 до 20, карточки с заданиям, цветные карточки. Листы с домашним заданием. Коробка и пилотки.

Ход урока

I.

Организационный момент.

Итак, друзья, внимание!
Вновь прозвенел звонок,
Садитесь поудобнее,
Начнем сейчас урок.

II.

Проверка домашнего задания.

К сегодняшнему уроку вы получили задание придумать или подобрать задачи, которые решаются способом таблиц или рассуждений, приготовить презентацию.

Выступление групп (защита мультимедийных презентаций).

1 группа.

Ученики нашего класса Боря, Женя и Миша участвовали в школьных спортивных соревнованиях и заняли первые четыре места.

На вопрос, какие места они заняли трое из них ответили:

1. Женя ни первое, ни последнее;
2. Боря второе;
3. Миша не был последним.

Какое место занял каждый мальчик?

После просмотра презентации учитель предлагает ученикам записать решение в виде таблицы.

2 группа.

Барсук позвал к себе гостей:
Медведя, рысь и белку.
И подарили барсуку
Подсвечник и тарелку.

Когда же он позвал к себе
Рысь, белку мышь и волка,
То он в подарок получил
Подсвечник и иголку.

Им были вновь приглашены
Волк, мышка и овечка.
И получил в подарок он

Иголку и колечко.

Он снова пригласил овцу,
Медведя, волка, белку.
И подарили барсуку
Колечко и тарелку.

Нам срочно нужен ваш совет
(На миг дела отбросьте)
Хотим понять какой предмет
Каким дарился гостем.

И кто из шестерых гостей
Явился без подарка?
Не можем мы сообразить,
Сидим… Мудрим… Запарка…

После просмотра презентации учитель предлагает ученикам записать решение в виде таблицы.

3 группа.

В коробке лежат три пилотки – две синии и одна красная. Учитель вызывает к доске двух учеников, которые становятся лицом к классу и закрывают глаза. Учитель надевает каждому из них на голову пилотку, а оставшиеся прячет в коробку. Ученики открывают глаза и каждый видит пилотку своего товарища, но не видит своей. Может ли кто-нибудь из них определить цвет своей пилотки.

После просмотра презентации учитель предлагает ученикам записать решение задачи.

III.

Актуализация знаний, умений, навыков.

1. Тренируем ум! (интеллектуальная разминка)

– Шла старуха в Москву, а навстречу ей три старика. Сколько человек шло в Москву? (Один человек)

– Что легше: пуд ваты или пуд железа? (Одинаково)

– К 7 прибавить 5. Как правильно записать “одиннадцать” или “адиннадцать”? (12)

– Двое играли в шахматы 4 часа. Сколько времени играл каждый? (4 часа)

2. Тренируем память! (упражнения на развитие памяти)

Учащимся предлагаются цветные карточки с цифрами. Учащиеся рассматривают и запоминают в течении 30 сек. Затем задаются вопросы:

– Какая цифра на зеленой карточке; (3)

– Сколько карточек между коричневой и желтой; (1)

– Сколько цветов начинается на букву “к”; (2)

– Назовите цвет и цифру каждой карточки.

3. Тренируем внимание! (задание на развитие внимания и способности анализировать)

– Работа в парах с числовой таблицей, в которой записаны числа от 1 до 25.

– Перед вами круги с числами, некоторые числа пропущены. Числа расставлены в соответствии с определенными законами. Вставьте пропущенные числа.

4

. Тренируем логику! (логические тесты)

1. Найти неизвестное число

а. геометрия 9,
логика ?

б.

45	(15)	24
29	(21)	37
10	(?)	20

в. Корень х – 6 = 0.
Уравнение 3х – 9 = 0.

IV.

Решение логических задач.

На доске записаны методы решения задач.

Методы:

1. Метод таблиц.
2. Метод рассуждений.
3. Метод граф.
4. Метод кругов Эйлера.
5. Комбинированный.

Сегодня на уроке мы решим несколько задач, которые решаются некоторыми из этих методов. У вас на столах лежит лист № 1 с тремя задачами. Решаем эти задачи.

Задача 1.

В коробке лежат 5 пилоток – 2 синии и три красные. Учитель вызывает к доске трех учащихся, которые становятся лицом к классу и закрывают глаза. Учитель надевает каждому из них га голову пилотку, а оставшиеся прячет в коробку. Ученики открывают глаза и каждый видит пилотку своего товарища, но не видит своей. Может ли кто-нибудь из них определить цвет своей пилотки.

К доске вызываются трое желающих разыграть решение задачи в лицах. Обсуждается решение задачи. Сколько случаев может быть?

1. Синяя, синяя, красная;
2. Синяя, красная, красная;
3. Красная, красная, красная.

Задача 2.

Три друга – Алеша, Боря и Витя – учатся в одном классе. Один из них ездит домой из школы на автобусе, один – на трамвае, один – троллейбусе. Однажды после уроков Алеша пошел проводить своего друга до остановки автобуса. Когда мимо них проходил троллейбус, третий друг крикнул из окна: “Боря ты забыл в школе тетрадку!”. Кто на чем едет?

Обсуждение решения задачи.

– Каким методом решим эту задачу?

– Составим план решения.

1. Выделить ключевые условия.
2. Проанализировать каждое условие.
3. Заполнить таблицу.

Задача 3.

В одной коробке лежат два белых шара, в другой два черных, а в третьей – один белый и один черный. На каждой коробке имеется табличка, но она неправильно указывает содержимое коробки. Из какой коробки, не глядя, надо вынуть шар, чтобы можно было определить содержимое каждой коробки?

Выслушиваются рассуждения учеников, записывается правильное решение.

V.

Решение задач в группах.

У вас на столах лежит лист №2. Решаем эти задачи в группах по 4 человека и заполняем таблицу ответов. (10 мин.) По истечению 10 мин. обсуждаем решение задач. Листы решений с таблицей ответов сдаем учителю.

VI.

Логический тест.

Каждому ученику выдается лист №3 с заданием логического теста. Заполнить тест карандашом и сдать учителю.

VII.

Итог урока.

– Какими методами мы решали на уроке логические задачи?

– Нужно ли решать логические задачи?

– Выставление оценок.

VIII. Дома.

Задача №1, №2 (лист 4)

Приложение

Подумай-пару-поделись | Классные стратегии | Reading Rockets

«Думай в парах и делись» (TPS) — это совместная стратегия обучения, при которой учащиеся работают вместе, чтобы решить проблему или ответить на вопрос о заданном чтении. Эта стратегия требует от учащихся (1) индивидуального обдумывания темы или ответа на вопрос; и (2) поделиться идеями с одноклассниками. Обсуждение с партнером максимизирует участие, концентрирует внимание и вовлекает учащихся в понимание материала для чтения.

Когда использовать:	Перед чтением	Во время чтения	После прочтения
Как использовать:	Индивидуально	С небольшими группами	Установка для всего класса

Дополнительные стратегии понимания

Зачем использовать «думай-пары-разделяй»?

• Это помогает учащимся индивидуально обдумать тему или ответить на вопрос.
• Он учит учащихся делиться идеями с одноклассниками и развивает навыки устного общения.
• Помогает сосредоточить внимание и вовлечь учащихся в понимание прочитанного.

 

Как использовать функцию «думай-пары-обменивайся»

• Определите текст для чтения и разработайте набор вопросов или подсказок, нацеленных на ключевые понятия содержания.
• Опишите цель стратегии и предоставьте рекомендации для обсуждения.
• Смоделируйте процедуру, чтобы учащиеся поняли, как использовать стратегию.
• Наблюдайте за учащимися и поддерживайте их, когда они выполняют следующие задачи:

  T : (Подумайте) Учителя начинают с того, что задают конкретный вопрос по тексту. Студенты «думают» о том, что они знают или узнали по теме.

  P : (Пара) Каждый учащийся должен работать в паре с другим учащимся или небольшой группой.

  S : (Поделиться) Учащиеся делятся своими мыслями со своим партнером. Учителя расширяют «долю» до обсуждения всего класса.

Загрузить пустой шаблон

Смотреть: Think-Pair-Share

Посетите класс второго класса Кэти Дойл в Эванстоне, штат Иллинойс, чтобы понаблюдать за тем, как ее ученики изучают стратегию «думай-пары-поделись». Кэти знакомится с «правилами», а затем вовлекает детей в чтение вслух в классе, Яйцо тихое . Джоан Мейер, наш директор по исследованиям, представляет стратегию и рассказывает о том, как она может помочь укрепить доверие учащихся, которые часто не хотят выступать перед всем классом.

Собрать ресурсы

Language Arts

Используйте функцию «думай в паре», чтобы углубить обсуждение конкретных персонажей в книгах, которые класс читает вместе. Например, если класс читает « Великая Джилли Хопкинс » Кэтрин Патерсон, попробуйте подумать, попарно поделиться, чтобы ответить на такие вопросы, как: «Сможете ли вы подружиться с Джилли? Почему или почему нет?»

Математика

Попробуйте “подумай-пары-поделись” для математических задач с более чем одним правильным ответом, таких как оценка, закономерности и логика.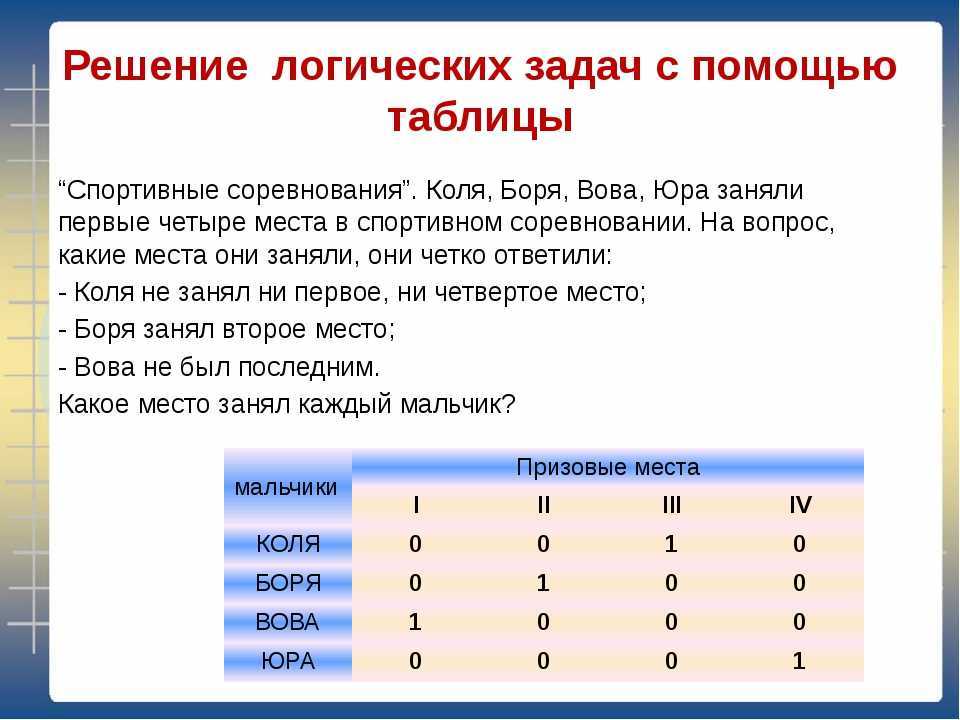 Эту стратегию также можно использовать, когда учащиеся решают, как подойти к решению математической задачи.

Обществознание

Начните дискуссию в паре, задав общий вопрос, относящийся к новой теме исследования, например: «Что вы уже знаете о Гражданской войне?» По мере того, как учащиеся углубляются в более сложные темы, вы можете задавать такие вопросы, как: «Согласились бы вы быть «остановкой» на подземной железной дороге? Почему или почему нет?»

Естествознание

Используйте функцию «думай-пары-рассказы», ​​чтобы помочь учащимся сформулировать гипотезу или обсудить их интерпретацию эксперимента в классе. Например, перед экспериментом с плотностью учащихся можно попросить использовать стратегию «думай парами и разделяй» при принятии решения о том, какие предметы будут плавать в ванне с водой.

 

Дифференцированное обучение

Для изучающих второй язык, учащихся с разными навыками чтения, учащихся с ограниченными возможностями обучения и учащихся младшего возраста

• Учитывайте потребности учащихся (навыки чтения, внимание, языковые навыки) при создании пар.
• Разрешить учащимся выбирать, кто будет делиться со всей группой.
• См. эту статью, Увеличьте взаимодействие учащихся с помощью «Думай, пари, делись» и «Круговые чаты» на Colorín Colorado.

См. исследование, подтверждающее эту стратегию

Gunter, M. A., Estes, T. H., & Schwab, J. H. (1999). Инструкция: Модельный подход , 3-е издание. Бостон: Аллин и Бэкон.

Лайман, Ф. (1981). «Отзывчивое обсуждение в классе». In Anderson, AS (Ed.), Mainstreaming Digest . Колледж-Парк, Мэриленд: Педагогический колледж Мэрилендского университета.

Расински Т. и Падак Н. (1996). Целостные стратегии чтения: обучение детей, которым трудно читать . Энглвуд Клиффс, Нью-Джерси: Меррилл / Прентис Холл.

Детские книги для использования с этой стратегией

Как я изучал географию

Автор: Ури Шулевиц

Возрастной уровень: 6-9

Уровень чтения: Самостоятельный читатель страсть, которая переживает изнурительные времена.

Тихая музыка: История Багдада

Автор: Джеймс Рамфорд

Жанр: Историческая проза, Художественная литература

Уровень возраста: 6-9 лет

Уровень чтения: Самостоятельный читатель

Али, современный мальчик, живущий в Багдаде, увлекается футболом, “громкой, пугающей родителей музыкой” и арабской каллиграфией. Али находит в нем утешение в шуме войны, как каллиграф XIII века Якут. Динамичные, вызывающие воспоминания иллюстрации делают эту книгу запоминающейся и напоминают читателям, что дети во всем мире одинаковы.

Что делать с Алисой?

Автор: Барбара Керли

Жанр: документальная литература, биография

Возрастной уровень: 6-9 лет

Уровень чтения: Начинающий читатель

Какой должна быть жизнь в Белом доме, особенно если вы совсем не похожи на других детей своего времени? Читайте об Элис — старшем ребенке Теодора Рузвельта — и ее нетрадиционном подходе к жизни в Белом доме.

Комментарии

2.

1: Операторы и логические операторы

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

7039

• Тед Сандстром
• Государственный университет Гранд-Вэлли через ScholarWorks @Grand Valley State University

2

ПРОСМОТР \(\PageIndex{1}\): составные операторы

Математики часто разрабатывают способы создания новых математических объектов из существующих математических объектов. Можно сформировать новые утверждения из существующих утверждений, соединив утверждения такими словами, как «и» и «или», или отрицая утверждение. А 9Логический оператор 0051 (или связка ) над математическими утверждениями — это слово или комбинация слов, которые объединяют одно или несколько математических утверждений для создания нового математического утверждения. Составной оператор — это оператор, содержащий один или несколько операторов. Поскольку некоторые операторы так часто используются в логике и математике, мы даем им имена и используем специальные символы для их представления.

• Конъюнкцией утверждений \(P\) и \(Q\) является утверждение «\(P\) и \(Q\)” и обозначается через \(P \клин Q\). Утверждение \(P \клин Q\) верно только тогда, когда оба \(P\) и \(Q\) верны.
• Дизъюнкция операторов \(P\) и \(Q\) есть оператор “\(P\) или \(Q\)” и обозначается через \(P \vee Q\). Утверждение \(P \vee Q\) истинно только тогда, когда хотя бы одно из \(P\) или \(Q\) истинно.
• отрицание ( утверждения ) утверждения \(P\) является утверждением « , а не \(P\) ” и обозначается как \(\urcorner P\). Отрицание \(P\) истинно только тогда, когда \(P\) ложно, а \(\urcorner P\) ложно только тогда, когда \(P\) истинно.
• Импликация или условное является высказыванием « Если \(P\) , то \(Q\)» и обозначается \(P \to Q\). Утверждение \(P \to Q\) часто читается как “\(P\) подразумевает \(Q\), и мы видели в разделе 1.1, что \(P \to Q\) ложно только тогда, когда \ (P\) истинно, а \(Q\) ложно.

Некоторые комментарии о дизъюнкции.
Важно понимать использование оператора «или». В математике мы используем « включительно или », если не указано иное. Это означает, что \(P \vee Q\) истинно, когда оба \(P\) и \(Q\) истинны, а также когда только одно из них истинно. То есть \(P \vee Q\) истинно, когда хотя бы одно из \(P\) или \(Q\) истинно, или \(P \vee Q\) ложно только тогда, когда оба \(P\ ) и \(Q\) ложны.

Другое использование слова «или» — « эксклюзив или ». Для исключающего или результирующее утверждение ложно, когда оба утверждения истинны. То есть «\(P\) исключающее или \(Q\)» истинно только тогда, когда истинно одно из \(P\) или \(Q\). В повседневной жизни мы часто используем исключающее или. Когда кто-то говорит: «На перекрестке поверните налево или идите прямо», этот человек использует исключающее или.

Некоторые комментарии к отрицанию . Хотя утверждение \(\urcorner P\) можно прочитать как «Это не так, что \(P\)», часто есть лучшие способы сказать или написать это на английском языке. Например, мы обычно говорим (или пишем):

• Отрицание утверждения «391 — простое число» равносильно «391 — не простое число».
• Отрицание утверждения «\(12 < 9\)» равно «\(12 \ge 9\)».

1. Для заявлений

   \(P\): 15 нечетно \(Q\): 15 просто
   запишите каждое из следующих утверждений как английские предложения и определите

   , истинны они или ложны.
   (а) \(P \клин Q\). (б) \(P \vee Q\). (c) \(P \клин \urcorner Q\). (d) \(\urcorner P \vee \urcorner Q\).

2. Для заявлений

   P : 15 нечетно R: 15 < 17

   запишите каждое из следующих утверждений в символической форме, используя операторы \(\wedge\), \(\vee\) и \(\urcorner\)

   (a) 15 \(\ge\) 17. (b) 15 нечетно или 15 \(\ge\) 17.
   (c) 15 четно или 15 <17. (г) 15 нечетно и 15 \(\ge\) 17,

ПРЕДВАРИТЕЛЬНАЯ АКТИВНОСТЬ\(\PageIndex{2}\): истинные значения утверждений

Мы будем использовать следующие два утверждения во всех этих предварительных действиях:

• \(P\) — это утверждение «Идет дождь».
• \(Q\) — это утверждение «Дейзи играет в гольф».

В каждой из следующих четырех частей утверждениям \(P\) и \(Q\) будет присвоено значение истинности. Например, в вопросе (1) мы будем предполагать, что каждое утверждение верно. В вопросе (2) мы будем предполагать, что \(P\) истинно, а \(Q\) ложно. В каждой части определите истинностное значение каждого из следующих утверждений:

(a) (\(P \клин Q\)) Идет дождь, а Дейзи играет в гольф.

(b) (\(P \vee Q\)) Идет дождь или Дейзи играет в гольф.

(c) (\(P \to Q\)) Если идет дождь, то Дейзи играет в гольф.

(d) (\(\urcorner P\)) Дождя нет.

Какие из четырех утверждений [(a)–(d)] верны, а какие нет в каждой из следующих четырех ситуаций?

1. Когда \(P\) верно (идет дождь) и \(Q\) верно (Дейзи играет в гольф).
2. Когда \(P\) истинно (идет дождь), а \(Q\) ложно (Дейзи не играет в гольф).
3. Когда \(P\) ложно (дождя нет) и \(Q\) истинно (Дейзи играет в гольф).
4. Когда \(P\) ложно (дождя нет) и \(Q\) ложно (Дейзи не играет в гольф).

В предварительных заданиях для этого раздела мы узнали о составных утверждениях и их значениях истинности. Эту информацию можно обобщить с помощью таблиц истинности, как показано ниже.

\(П\)	\(\угол П\)
Т	Ф
Ф	Т

\(П\)	\(Q\)	\(П \клин Q\)
Т	Т	Т
Т	Ф	Ф
Ф	Т	Ф
Ф	Ф	Ф

\(П\)	\(Q\)	\(P \vee Q\)
Т	Т	Т
Т	Ф	Т
Ф	Т	Т
Ф	Ф	Ф

\(П\)	\(Q\)	\(П\к Q\)
Т	Т	Т
Т	Ф	Ф
Ф	Т	Т
Ф	Ф	Т

Вместо того, чтобы запоминать таблицы истинности, многим людям проще запомнить правила, обобщенные в Таблице 2. 1.

Таблица 2.1: Истинные значения для общих связок

Оператор	Символическая форма	Сводка значений истинности
Соединение	\(П \клин Q\)	Истинно, только если оба \(P\) и \(Q\) истинны
Разделение	\(P \vee Q\)	Ложь, только если обе \(P\) и \(Q\) ложны
Отрицание	\(\угол П\)	Значение истинности, противоположное \(P\)
Условный	\(П\к Q\)	Ложь, только если \(P\) истинно, а \(Q\) ложно

Другие формы условных операторов

Условные операторы чрезвычайно важны в математике, потому что почти все математические теоремы сформулированы (или могут быть сформулированы) в форме условного оператора в следующей форме:

Если «соблюдаются определенные условия», то «что-то происходит».

Крайне важно, чтобы все учащиеся, изучающие математику, полностью понимали значение условного утверждения и таблицу истинности условного утверждения.

Мы также должны знать, что в английском языке есть другие способы выражения условного оператора \(P \to Q\), кроме «If \(P\), then \(Q\)». Ниже приведены некоторые распространенные способы выражения условного оператора \(P \to Q\) в английском языке:

Проверка выполнения 2.1: заявление «Только если»

Напомним, что четырехугольник — это четырехугольник. Пусть \(S\) представляет собой следующее верное условное утверждение:

Если четырехугольник является квадратом, то он является прямоугольником.

Напишите это условное выражение на английском языке, используя

1. слово «когда бы ни»
2. фраза «только если»
3. фраза «необходимо для»
4. фраза «достаточно для»

Ответить

Добавьте сюда текст. Не удаляйте этот текст первым.

Построение таблиц истинности

Таблицы истинности для составных утверждений можно построить, используя таблицы истинности для основных связок. Чтобы проиллюстрировать это, мы построим таблицу истинности для. \((P \клин \urcorner Q) \к R\). Первым шагом является определение необходимого количества рядов.

• Для таблицы истинности с двумя разными простыми утверждениями необходимы четыре строки, поскольку существует четыре различных комбинации значений истинности для двух утверждений. Мы должны быть последовательны в том, как мы настраиваем ряды. В этом тексте мы будем делать это следующим образом: пометим строки для первого утверждения (T, T, F, F), а строки для второго утверждения — (T, F, T, F). Все таблицы истинности в тексте имеют эту схему.
• Для таблицы истинности с тремя различными простыми утверждениями требуется восемь строк, поскольку существует восемь различных комбинаций значений истинности для трех утверждений. Наша стандартная схема для этого типа таблицы истинности показана в таблице 2.2 .

Следующим шагом является определение используемых столбцов. Один из способов сделать это — работать в обратном направлении от формы данного утверждения. Для \((P \wedge \urcorner Q) \to R\) последним шагом является работа с условным оператором \((\to)\). Для этого нам нужно знать истинностные значения \((P \клин \urcorner Q)\) и \(R\). Чтобы определить истинностные значения для \((P \клин \urcorner Q)\), нам нужно применить правила для оператора конъюнкции \((\клин)\) и нам нужно знать истинностные значения для \(P\ ) и \(\urcorner Q\).

Таблица 2.2 представляет собой заполненную таблицу истинности для \((P \клин \urcorner Q) \to R\) с номерами шагов, указанными внизу каждого столбца. Номера шагов соответствуют порядку заполнения столбцов.

Таблица 2.2: Таблица истинности для \((P \клин \urcorner Q) \to R\)

\(П\)	\(Q\)	\(R\)	\(\угол Q\)	\((P \клин \ур угол Q)\)	\((П\клин\уругол Q)\к R\)
Т	Т	Т	Ф	Ф	Т
Т	Т	Ф	Ф	Ф	Т
Т	Ф	Т	Т	Т	Т
Т	Ф	Ф	Т	Т	Ф
Ф	Т	Т	Ф	Ф	Т
Ф	Т	Ф	Ф	Ф	Т
Ф	Ф	Т	Т	Ф	Т
Ф	Ф	Ф	Т	Ф	Т
1	1	1	2	3	4

• Заполняя столбец для \(P \клин \urcorner Q\), помните, что конъюнкция истинна только тогда, когда оба \(P\) и \(\urcorner Q\) истинны.
• Заполняя столбец для \((P \wedge \urcorner Q) \to R\), помните, что единственное время, когда условное утверждение ложно, это когда гипотеза \((P \wedge \urcorner Q)\) верна и заключение \(R\) ложно.

Последний введенный столбец представляет собой таблицу истинности для утверждения \((P \wedge \urcorner Q) \to R\) с использованием настройки в первых трех столбцах.

Проверка выполнения 2.2: построение таблиц истинности

Постройте таблицу истинности для каждого из следующих утверждений:

1. \(P \wedge \urcorner Q\)
2. \(\угол(P\клин Q)\)
3. \(\угол Р \клин \угол Q\)
4. \(\urcorner P \vee \urcorner Q\)

Есть ли среди этих утверждений одинаковая таблица истинности?

Ответить

Добавьте сюда текст. Не удаляйте этот текст первым.

Биусловное утверждение

Некоторые математические результаты формулируются в форме «\(P\) тогда и только тогда, когда \(Q\)» или «\(P\) необходимо и достаточно для \(Q\)». Примером может быть: «Треугольник равносторонний тогда и только тогда, когда три его внутренних угла конгруэнтны». Символическая форма биусловного утверждения «\(P\) тогда и только тогда, когда \(Q\)» — это \(P \leftrightarrow Q\). Чтобы определить таблицу истинности для биусловного утверждения, полезно внимательно посмотреть на форму фразы «\(P\) тогда и только тогда, когда \(Q\)». Слово «и» предполагает, что это высказывание является союзом. На самом деле это конъюнкция утверждений «\(P\), если \(Q\)» и «\(P\), только если \(Q\)». Символическая форма этого соединения: \([(Q \to P) \wedge (P \to Q]\).

Проверка выполнения 2.3: Таблица истинности для биусловного утверждения

Заполните таблицу истинности для \([(Q \to P) \wedge (P \to Q]\). Используйте следующие столбцы: \(P\) , \(Q\), \(Q \к P\), \(P \к Q\) и \([(Q \к P) \клин (P \к Q]\). Последний столбец эта таблица будет истинной для \(P \leftrightarrow Q\).

Добавьте сюда текст. Не удаляйте этот текст первым.

Другие формы биусловного оператора

Как и в случае с условным оператором, существует несколько распространенных способов выражения биусловного оператора \(P \leftrightarrow Q\) в английском языке.

Пример

• \(P\) есть и только если \(Q\).
• \(P\) необходимо и достаточно для \(Q\).
• \(P\) подразумевает \(Q\), а \(Q\) подразумевает \(P\).

Тавтологии и противоречия

Определение: тавтология

тавтология представляет собой составное утверждение S, истинное для всех возможных комбинаций значений истинности составных утверждений, являющихся частью \(S\). А противоречие — это составное утверждение, ложное для всех возможных комбинаций значений истинности составных утверждений, входящих в \(S\).

То есть тавтология обязательно верна при любых обстоятельствах, а противоречие обязательно ложно при всех обстоятельствах.

Проверка прогресса 2.4 (тавтологии и противоречия)

Для утверждений \(P\) и \(Q\):

1. Используйте таблицу истинности, чтобы показать, что \((P \vee \urcorner P)\) является тавтология.
2. Используйте таблицу истинности, чтобы показать, что \((P \клин \urcorner P)\) является противоречием.
3. Используйте таблицу истинности, чтобы определить, является ли \(P \to (P \vee P)\) тавтологией, противоречием или ни тем, ни другим.

Ответить

Добавьте сюда текст. Не удаляйте этот текст первым.

Упражнения к разделу 2.1

1. Предположим, что Дейзи говорит: «Если не будет дождя, я буду играть в гольф». Позже в тот же день вы узнаете, что шел дождь, но Дейзи все еще играла в гольф. Было ли утверждение Дейзи правдой или ложью? Поддержите свой вывод.
2. Предположим, что \(P\) и \(Q\) являются высказываниями, для которых истинно \(P \to Q\) и для которых \(\urcorner Q\) истинно. Какой вывод (если вообще есть) можно сделать об истинности каждого из следующих утверждений?

   (a) \(P\)
   (b) \(P \клин Q\)
   (c) \(P \vee Q\)

3. Предположим, что \(P\) и \(Q\) являются утверждениями, для которых \(P \to Q\) ложно. Какой вывод (если вообще есть) можно сделать об истинности каждого из следующих утверждений?

   (a) \(\угол P \to Q\)
   (b) \(Q \to P\)
   (c) \(P \ vee Q\)

4. Предположим, что \(P\) и \(Q\) являются утверждениями, для которых \(Q\) ложно, а \(\угол P\to Q\) истинно (и неизвестно, если \(R\) истинно или ложно). Какой вывод (если вообще есть) можно сделать об истинности каждого из следующих утверждений?

   (a) \(\угол Q \к P\)
   (b) \(P\)
   (c) \(P \клин R\)
   (d) \(R \к \urcorner P\)

5. Постройте таблицу истинности для каждого из следующих утверждений:

   (a) \(P \to Q\)
   (b) \(Q \to P\)
   (c) \(\urcorner P \to \urcorner Q\)
   (d) \(\urcorner Q \ в \urcorner P\)

   Имеют ли какие-либо из этих утверждений одинаковую таблицу истинности?

6. Постройте таблицу истинности для каждого из следующих утверждений:

   (a) \(P \vee \urcorner Q\)
   (b) \(\urcorner (P \vee Q)\)
   (c) \(\urcorner P \vee \urcorner Q\)
   (d) \(\urcorner P \wedge \urcorner Q\)

   Имеют ли какие-либо из этих утверждений одинаковую таблицу истинности?

7. Построить таблицу истинности для \(P \клин (Q \клин R)\) и \((P \клин Q) \ви (P \клин R)\). Что вы наблюдаете.
8. Предположим, что каждое из следующих утверждений верно.
   • Лаура учится в седьмом классе.
   • ��Лора получила пятёрку за тест по математике или Сара получила пятёрку за тест по математике.
   • ��Если Сара получила пятёрку за контрольную по математике, значит Лора не учится в седьмом классе.

     Если возможно, определите истинность каждого из следующих утверждений. Внимательно объясните свои рассуждения. 92\) четно». Выразите условное утверждение \(P \to Q\) на английском языке, используя

     (a) Форма условного оператора «if then»
     (b) Слово «подразумевает»
     (c) Форма «только если» условного оператора условное утверждение
     (d) Фраза «необходимо для»
     (e) Фраза «достаточно для»

   • Повторите упражнение (9) для условного оператора \(Q \to P\).
   • Для утверждений \(P\) и \(Q\) используйте таблицы истинности, чтобы определить, является ли каждое из следующих утверждений тавтологией, противоречием или ни тем, ни другим.
     (a) \(\urcorner Q \vee (P \to Q)\).
     (b) \(Q \клин (P \клин \urcorner Q)\).
     (c) \((Q \клин P) \клин (P \к \углу Q)\).
     (г) \(\угол Q \к (Р \клин \угол Р)\).
   • Для утверждений \(P\), \(Q\) и \(R\):
     (a) Покажите, что \([(P \to Q) \web P] \to Q\) является тавтологией. Примечание : В символической логике это важная форма логического аргумента, называемая modus ponens .
     (b) Покажите, что \([(P \to Q) \wedge (Q \to R)] \to (P \to R)\) является атавтологией. Примечание : В символической логике это важная форма логического аргумента, называемая силлогизмом .

     Исследования и деятельность

   • Работа с условными операторами. Заполните следующую таблицу:

     Английская форма	Гипотеза	Заключение	Символическая форма
     Если \(P\), то \(Q\)	\(П\)	\(К\)	\(П\к Q\)
     \(Q\) только если \(P\)	\(К\)	\(П\)	\(К\к П\)
     \(P\) необходимо для \(Q\)
     \(P\) достаточно для \(Q\)
     \(Q\) необходимо для \(P\)
     \(P\) подразумевает \(Q\)
     \(P\) только если \(Q\)
     \(P\) если \(Q\)
     если \(Q\), то \(P\)
     если \(\urcorner Q\), то \(\urcorner P\)
     если \(Q\), то \(Q \клин R\)
     если \(P \vee Q\), то \(R\)

   • Работа с истинностными значениями утверждений. Предположим, что \(P\) и \(Q\) являются истинными утверждениями, что \(U\) и \(V\) являются ложными утверждениями, и что \(W\) является утверждением, и неизвестно, если \(W\) истинно или ложно.

     Какие из следующих утверждений верны, какие ложны, и для каких утверждений невозможно определить, истинно оно или ложно? Обоснуйте свои выводы.

     (a) \((P \vee Q) \vee (U \клин W)\) (f) \((\urcorner P \vee \urcorner U) \клин (Q \vee \urcorner V)\)
     (b) \(P \клин (Q \to W)\) (g) \((P \клин \urcorner Q) \клин (U \vee W)\)
     (c) \(P \клин ( W \к Q)\) (h) \((P \vee \urcorner Q) \to (U \клин W)\)
     (d) \(W \to (P \клин U)\) (i) \((P \vee W) \to (U \клин W)\)
     (e) \(W \to (P \клин \urcorner U)\) (j) \((U \клин \urcorner V) \to (P \клин W)\)

Ответить

Добавьте сюда текст. Не удаляйте этот текст первым.

---

Эта страница под названием 2. 1: Операторы и логические операторы распространяется в соответствии с лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Тедом Сандстромом (ScholarWorks @Grand Valley State University) посредством исходного содержимого, которое было отредактировано. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   Тед Сандстром

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   3,0

   Показать страницу Содержание

   нет

2. Метки

   1. Биусловный оператор
   2. составные операторы
   3. источник@https://scholarworks.