Задание 6 математика 3 класс: ГДЗ по математике 3 класс учебник Моро, Волкова 1 часть
ГДЗ по математике 3 класс учебник Моро, Волкова 1 часть
- Тип: ГДЗ, Решебник.
- Автор: Моро М. И., Волкова С. И., Бантова М. А.
- Год: 2020.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
❤️️Ответ к странице 6. Математика 3 класс учебник 1 часть. Автор: М.И. Моро.
Решебник – страница 6Готовое домашнее задание
Номер 1.
Заполни таблицу: найди значения выражений а + 8 и а − 7 при заданных значениях а.
Ответ:
Номер 2.
Вспомни, как называются равенства, которые содержат неизвестное число. Найди и реши их.
Ответ:
Равенства, которые содержат неизвестное число называются уравнениями.
b + 2 = 12 x − 4 = 6 k + 4 = 9
b = 12 − 2 x = 6 + 4 k = 9 − 4
b = 10 x = 10 k = 5
Номер 3.
Из чисел 2, 5, 8, 11 выбери для каждого уравнения такое значение х, при котором получится верное равенство.
Ответ:
18 − х = 10 2 + х = 7 х − 9 = 2 х + 8 = 10 х = 18 − 10 х = 7 − 2 х = 2 + 9 х = 10 − 8 х = 8 х = 5 х = 11 х = 2
Номер 4.
Вычисли удобным способом.
Ответ:
Номер 5.
Найди периметр каждого многоугольника.
Ответ:
1) Р = 2 + 2 + 3 = 7 (см) 2) Р = 3 + 1 + 3 + 1 = 8 (см) 3) Р = 4 + 1 + 5 + 2 = 12 (см)
Номер 6.
Ответ:Номер 7.
В четырехэтажном доме живут четыре друга. Юра живет выше, чем Олег, но ниже, чем Саша, а Дима – ниже, чем Олег. Кто на каком этаже живет?
Ответ:
4 этаж – Саша. 3 этаж – Юра.
2 этаж – Олег.
1 этаж – Дима.
3 этаж – Юра.
2 этаж – Олег.
1 этаж – Дима.
Номер 8.
Начерти ломаную из двух звеньев так, чтобы ее длина была равна 14 см и одно звено было на 2 см короче другого.
Ответ:
(14 − 2) : 2 = 6 (см) – первое звенье.
6 + 2 = 8 (см) – второе звенье.
Задание внизу страницы.
Реши уравнения.
Ответ:
x + 8 = 11 x − 7 = 10 x = 11 − 8 x = 10 + 7 x = 3 x = 17 Проверка Проверка 3 + 8 = 11 17 − 7 = 10 11 = 11 10 = 10
Задание на полях страницы.
Набери 13:
Ответ:
3 + 8 + 2 = 13 4 + 4 + 2 + 3 = 13 8 + 5 = 13 9 + 4 = 13 6 + 7 = 13 4 + 6 + 3 = 13
Рейтинг
Выберите другую страницу
1 часть
| Учебник Моро | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
2 часть
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
ГДЗ по математике 3 класс учебник Моро, Волкова 1 часть
- Тип: ГДЗ, Решебник.

- Автор: Моро М. И., Волкова С. И., Бантова М. А.
- Год: 2020.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
❤️️Ответ к странице 65. Математика 3 класс учебник 1 часть. Автор: М.И. Моро.
Решебник – страница 65Готовое домашнее задание
Номер 1.
Ответ:
64 : 8 = 8 7 ∙ 7 = 49 72 : 9 = 8 8 ∙ 8 = 64 81 : 9 = 9 9 ∙ 9 = 81 56 : 8 = 7 6 ∙ 6 = 36
Номер 2.
Девочка принесла для кроликов 27 морковок, а мальчик – 18 морковок. Все морковки они разложили кроликам в клетки, по 9 морковок в каждую. Объясни, что означают выражения:
27 : 9 18 : 9 27 + 18 (27 + 18) : 9
Ответ:
27 : 9 – в такое количество клеток разложила девочка морковь.
18 : 9 – в такое количество клеток разложил мальчика морковь.
Номер 3.
Длина провода 50 м. Сначала от него отрезали 8 м, потом 7 м. Сколько метров провода осталось?
Реши задачу разными способами.
Ответ:
Было – 50 м
Отрезали сначала – 8 м
Отрезали потом – 7 м
Осталось – ? м
Способ 1:
1) 50 − 8 = 42 (м) – осталось, когда отрезали первый раз.
2) 42 − 7 = 35 (м) – осталось провода.
Ответ: 35 метров.
Способ 2:
1) 8 + 7 = 15 (м) – всего отрезали.
2) 50 − 15 = 35 (м) – провода осталось.
Ответ: 35 метров.
Номер 4.
Ответ:
3 м 9 дм = 39 дм 56 см = 5 дм 6 см 4 см 8 мм = 48 мм 25 мм = 2 см 5 мм
Номер 5.
Даше 14 лет, а Оле 8 лет. Сколько лет было Оле, когда Даше было 9 лет?
Ответ:
1) 14 − 8 = 6 (л. ) – на столько Даша старше Оли.
2) 9 − 6 = 3 (г.) – было Оле.
Ответ: 3 года.
) – на столько Даша старше Оли.
2) 9 − 6 = 3 (г.) – было Оле.
Ответ: 3 года.
Номер 6.
Найди площадь и периметр квадрата, если длина его стороны 7 см; если длина его стороны 4 см; если длина его стороны 9 см.
Ответ:
Площади квадратов:
1) 7 ∙ 7 = 49 см2
2) 4 ∙ 4 = 16 см2
3) 9 ∙ 9 = 81 см2
Периметры квадратов:
1) 7 ∙ 4 = 28 см
2) 4 ∙ 4 = 16 см
3) 9 ∙ 4 = 36 см
Площадь прямоугольника равна произведению его длины и ширины.
Периметр многоугольника – это сумма длин всех его сторон.
Задание внизу страницы
Ответ:
Задание на полях страницы
Вычисли. Найди лишнее выражение:
Ответ:
40 : 5 = 8
64 : 8 = 8
32 : 4 = 8
72 : 9 = 8
80 : 10 = 8
56 : 7 = 8
48 : 6 = 8
24 : 4 = 6 – лишнее выражение.
Рейтинг
Выберите другую страницу
1 часть
| Учебник Моро | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
2 часть
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
Классы 3–8 Стандартные рекомендации по математике после теста
Комментарии общественности: Период общественного обсуждения завершился 31 января 2019 года. Департамент образования штата Нью-Йорк изучил комментарии, которые были получены в отношении проекта обозначений стандартов после тестирования для оценок по математике следующего поколения для 3–8 классов. В целом, комментарии были очень положительными. На основании этих замечаний никаких изменений в проекты обозначений внесено не было. Проект обозначений послетестовых стандартов ниже для 3-8 классов Оценка по математике следующего поколения завершена.
Департамент образования штата Нью-Йорк изучил комментарии, которые были получены в отношении проекта обозначений стандартов после тестирования для оценок по математике следующего поколения для 3–8 классов. В целом, комментарии были очень положительными. На основании этих замечаний никаких изменений в проекты обозначений внесено не было. Проект обозначений послетестовых стандартов ниже для 3-8 классов Оценка по математике следующего поколения завершена.
Обратите внимание: эти обозначения стандартов после тестирования не будут отражаться в оценках штата для 3–8 классов до полного внедрения Стандартов обучения математике нового поколения штата Нью-Йорк, которое начнется в 2022–2023 учебном году.
Эти обозначения стандартов после тестирования должны использоваться по мере того, как округа переходят к этапу наращивания потенциала дорожной карты и графика внедрения стандартов обучения следующего поколения. Первой целью этого этапа является «Поддержка потребностей местного школьного округа в интеграции стандартов обучения математике нового поколения в местную учебную программу». Для округов будет важно учитывать изменения, которые произошли с обозначениями стандартов после тестирования, поскольку они начинают изучать свои текущие учебные материалы и ресурсы округа и определять изменения, необходимые для обеспечения соответствия стандартам обучения математике нового поколения штата Нью-Йорк.
Для округов будет важно учитывать изменения, которые произошли с обозначениями стандартов после тестирования, поскольку они начинают изучать свои текущие учебные материалы и ресурсы округа и определять изменения, необходимые для обеспечения соответствия стандартам обучения математике нового поколения штата Нью-Йорк.
Обратите внимание, что эти обозначения послетестовых стандартов не будут отражаться в оценках 3–8 классов до полного внедрения Стандартов обучения математике нового поколения штата Нью-Йорк, которое начнется в 2022–2023 учебном году.
В 2015 году штат Нью-Йорк (NYS) начал процесс обзора и пересмотра своих текущих математических стандартов, принятых в январе 2011 года. Через многочисленные этапы общественного обсуждения, виртуальных и личных встреч с комитетами, состоящими из Преподаватели штата Нью-Йорк (педагоги специального образования, двуязычного образования и английского как нового языка), родители, специалисты по учебным программам, школьные администраторы, преподаватели колледжей и эксперты в области когнитивных исследований разработали Стандарты обучения математике нового поколения штата Нью-Йорк (2017 г. ). Эти пересмотренные стандарты отражают совместные усилия и опыт всех вовлеченных сторон.
). Эти пересмотренные стандарты отражают совместные усилия и опыт всех вовлеченных сторон.
Чтобы поддержать внедрение этих пересмотренных стандартов, в 2018 году начался процесс определения того, какие стандарты математического содержания для каждого класса (с 3 по 8) будут оцениваться в рамках ежегодной оценки штата Нью-Йорк для этого класса, и поэтому их необходимо преподавать до начала дата оценки и какие стандарты будут преподаваться после даты оценки штата Нью-Йорк каждый год. Этот процесс включал три раунда личных встреч с комитетами, состоящими из преподавателей штата Нью-Йорк. Каждый комитет начал с независимого рассмотрения стандартов и составления первоначальной рекомендации. Затем они рассмотрели рекомендации предшествующих им групп, обсудили достоинства всех вариантов и в завершение представили свою окончательную рекомендацию, в которой учитывались их первоначальные идеи, а также идеи предыдущих групп. Окончательные рекомендации, изложенные в документе, были основаны на всех идеях и обсуждениях каждого из комитетов.
На протяжении всего процесса существовало три основных принципа, которыми руководствовались каждый комитет и окончательные рекомендации; два из которых связаны с поддержанием связи между стандартами во всех возможных пределах. Важно отметить, что на каждом уровне обучения все другие стандарты рассматривались на предмет возможного назначения в качестве пост-тестов, но в конечном итоге они не были перемещены из-за этих трех руководящих принципов.
- Поддержание связи между стандартами в пределах уровня обучения. Стандарты, которые настолько связаны, что их, вероятно, будут преподавать в одной и той же учебной единице, следует рассматривать как группу — либо вся группа проходит предварительное тестирование, либо вся группа — посттестовое.
- Способствуйте установлению связей между классами. Стандарты, которые преподаются в конце одного года обучения (т. е. послетестовое тестирование), должны непосредственно применяться в начале следующего года (т. е. предварительное тестирование).
 Поскольку послетестовые стандарты одного класса проверяются на государственном тесте следующего уровня, этот принцип также помогает гарантировать, что учащиеся готовы ответить на вопросы, относящиеся к послетестовым стандартам.
Поскольку послетестовые стандарты одного класса проверяются на государственном тесте следующего уровня, этот принцип также помогает гарантировать, что учащиеся готовы ответить на вопросы, относящиеся к послетестовым стандартам. - Сбалансируйте и уважайте время, необходимое для обучения и обучения. Стандарты требуют времени, чтобы учить и учиться. Некоторые больше, чем другие. Слишком много стандартов, обозначенных как пост-тест, заставят учителей и учащихся спешить с материалом и не будут выделять время, необходимое для его преподавания и глубокого изучения. Слишком малое количество стандартов, обозначенных как пост-тестовые, вызывает такое же скопление людей и ажиотаж в течение предтестового периода.
Обозначения стандартов после испытаний
Класс 3
Текущие стандарты NYS Common Core Learning Post Test Standards | Стандарты послетестового тестирования следующего поколения | Прямые ссылки в предварительном тесте |
|---|---|---|
| NY-3. | Нет |
3.МД.4 измерить до ¼ дюйма и отобразить на линейном графике | NY-3.MD.4 | NY-4.MD.4 отображать данные измерений с точностью до 1/8 единицы на линейном графике |
3.MD.8 Периметр | NY-3.MD.8 | NY-4.MD.3 применить формулы площади и периметра |
3.G.1 классифицировать многоугольники по количеству сторон | NY-3.G.1 | NY-4.G.2 назовите треугольники и четырехугольники на основе некоторых свойств |
4 класс
Текущие стандарты NYS Common Core Learning Post Test Standards | Стандарты послетестового тестирования следующего поколения | Прямые ссылки в предварительном тесте |
|---|---|---|
4. десятичных знаков | NY-4.NF.5 – 7 | NY-5.NBT.1 – 4 разрядное значение целых чисел и десятичных знаков
NY-5.NBT.7 десятичные операции |
4.MD.1 и 2 преобразование измерений | NY-4.MD.1 и 2 | NY-5.MD.1 преобразование измерений |
5 класс
Текущие стандарты NYS Common Core Learning Post Test Standards | Стандарты послетестового тестирования следующего поколения | Прямые ссылки в предварительном тесте |
|---|---|---|
| NY-5. | NY-6.EE.1 – 4 читать, писать и вычислять алгебраические выражения
NY-6.EE.9 зависимые/независимые переменные |
| NY-5.OA.2 | |
5.ОА.3 анализ закономерностей и взаимосвязей | NY-5.OA.3 | |
5.G.1 и 2 координатный график в квадранте 1 | NY-5.G.1 и 2 | NY-6.G.3 построение графика координат во всех 4 квадрантах
NY-6.NS.6 и 8 построение графика координат во всех 4 квадрантах |
6 класс
Текущие стандарты NYS Common Core Learning Post Test Standards | Стандарты послетестового тестирования следующего поколения | Прямые ссылки в предварительном тесте |
|---|---|---|
6. статистическая изменчивость | NY-6.SP.1 – 3 | NY-7.SP.1 коробчатые диаграммы, IQR и выбросы
NY-7.SP.3 и 4 сравнительные выводы |
6.СП.4 – 5 подвести итоги и описать дистрибутивы | NY-6.SP.4 – 5 | |
| NY-6.SP.6 – 8 | NY-7.SP.8 вероятность сложных событий |
7 класс
Текущие стандарты NYS Common Core Learning Post Test Standards | Стандарты послетестового тестирования следующего поколения | Прямые ссылки в предварительном тесте |
|---|---|---|
7. начертить треугольники, заданные условия – конструкции | NY-7.G.2 | NY-8.G.1 – 4 понимать конгруэнтность и сходство
NY-8.G.6 – 8 понять теорему Пифагора
NY-8.EE.6 подобных треугольника и форма пересечения наклона |
7.G.3 описывают 2D-срезы 3D-тел | NY-7.G.3 |
|
| NY-7.G.4 | NY-8.G.9 объем цилиндров, конусов и сфер |
7.G.5 использовать свойства угла для решения неизвестных углов | NY-7. | NY-8.G.5 свойства угла
NY-8.EE.7 решать линейные уравнения с одной переменной |
7.Г.6 площадь, площадь поверхности и объем | NY-7.G.6 | NY-8.G.6 понять теорему Пифагора
NY-8.G.9 объем цилиндров, конусов и сфер |
8 класс
Текущие стандарты NYS Common Core Learning Post Test Standards | Стандарты послетестового тестирования следующего поколения | Прямые ссылки в предварительном тесте |
|---|---|---|
8. Иррациональные числа
8.EE.2 квадратные и кубические корни
8.Г.6 – 8 Теорема Пифагора |
|
|
| NY-8.EE.3 и 4 | AI-N.Q.3 выберите уровень точности, соответствующий контексту |
| NY-8.EE.8 | АИ-А.РЕИ.6а системы линейных уравнений с двумя переменными
АИ-А.РЕИ.7а системы одного линейного и одного квадратного уравнения с двумя переменными |
Урок 9 | Понимание и представление отношений | Математика 6-го класса
Цель
Используйте рассуждения о соотношениях для решения задачи из трех действий.
Общие базовые стандарты
Основные стандарты
Основные стандарты, рассмотренные в этом уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D89506.РП.А.3 – Используйте рассуждения об отношении и скорости для решения реальных и математических задач, например, рассуждая о таблицах эквивалентных отношений, ленточных диаграммах, линейных диаграммах с двойным числом или уравнениях.
Критерии успеха
Основные концепции, которые учащиеся должны продемонстрировать или понять для достижения цели урока
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- Делайте наблюдения и задавайте вопросы к незавершенной задаче.
- Сделайте образовательную догадку и предложите возможный путь решения.
- Внесите коррективы в соотношение, чтобы создать эквивалентные соотношения.
Советы учителям
Рекомендации для учителей по проведению этого урока
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- однако, будучи первым учеником шестого класса, вы можете захотеть создать в своем классе культуру или процесс в отношении того, как они используются.

- Учащиеся выполняют МР.1 в этом задании из трех действий, анализируя предоставленную им информацию и определяя, как они могут использовать эквивалентные отношения, чтобы исправить путаницу. Они должны разработать свою собственную стратегию и проверить свои ответы, внося коррективы по мере необходимости.
- Учащиеся также узнают, как они могут применять рассуждения об отношениях, чтобы помочь им понять математику в задаче и найти решение (MP.4).
Fishtank Plus
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Проблемы с якорем
Задачи, предназначенные для изучения ключевых моментов урока, и наводящие вопросы, помогающие привлечь внимание учащихся к пониманию Проблема 1
Акт 1: Посмотрите видео-пролог к трехактному заданию «Смешивание красок Наны».
Что вы заметили? Что вам интересно?
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Ссылки
101Questions Смесь красок Наны — Пролог и Акт 1
Смесь красок Nana’s Paint Mixup от Дэна Мейера доступна на 101Questions под лицензией CC BY 3.0. По состоянию на 18 июля 2017 г., 16:33.
Проблема 2
Акт 2: Как мы можем использовать эквивалентные коэффициенты, чтобы исправить эту путаницу?
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Ссылки
101Questions Nana’s Paint Mixup
Nana’s Paint Mixup Дэна Мейера доступен на 101Questions под лицензией CC BY 3.0. По состоянию на 18 июля 2017 г., 16:33.
Изменено Fishtank Learning, Inc.
Проблема 3
Акт 3: Посмотрите видеоответ.
Был ли ваш ответ обоснованным? Почему или почему нет?
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Ссылки
101Questions Nana’s Paint Mixup
Nana’s Paint Mixup Дэна Мейера доступен на 101Questions под лицензией CC BY 3.0. По состоянию на 18 июля 2017 г., 16:33.
Проблема 4
Продолжение: Сколько других способов исправить путаницу вы можете найти?
Наводящие вопросы
Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.
Ссылки
101Questions Nana’s Paint Mixup
Nana’s Paint Mixup Дэна Мейера доступен на 101Questions под лицензией CC BY 3.0. По состоянию на 18 июля 2017 г., 16:33.
Набор проблем
Набор предлагаемых ресурсов или типов задач, которые учителя могут преобразовать в набор задач а Подписка Fishtank Plus.
Целевая задача
Задача, которая представляет собой пик мышления урока – мастерство покажет, была ли достигнута цель
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950 Вы смешиваете ингредиенты для печенья.
 MD.3
MD.3 NF.5 – 7
NF.5 – 7  OA.1
OA.1 СП.1 – 3
СП.1 – 3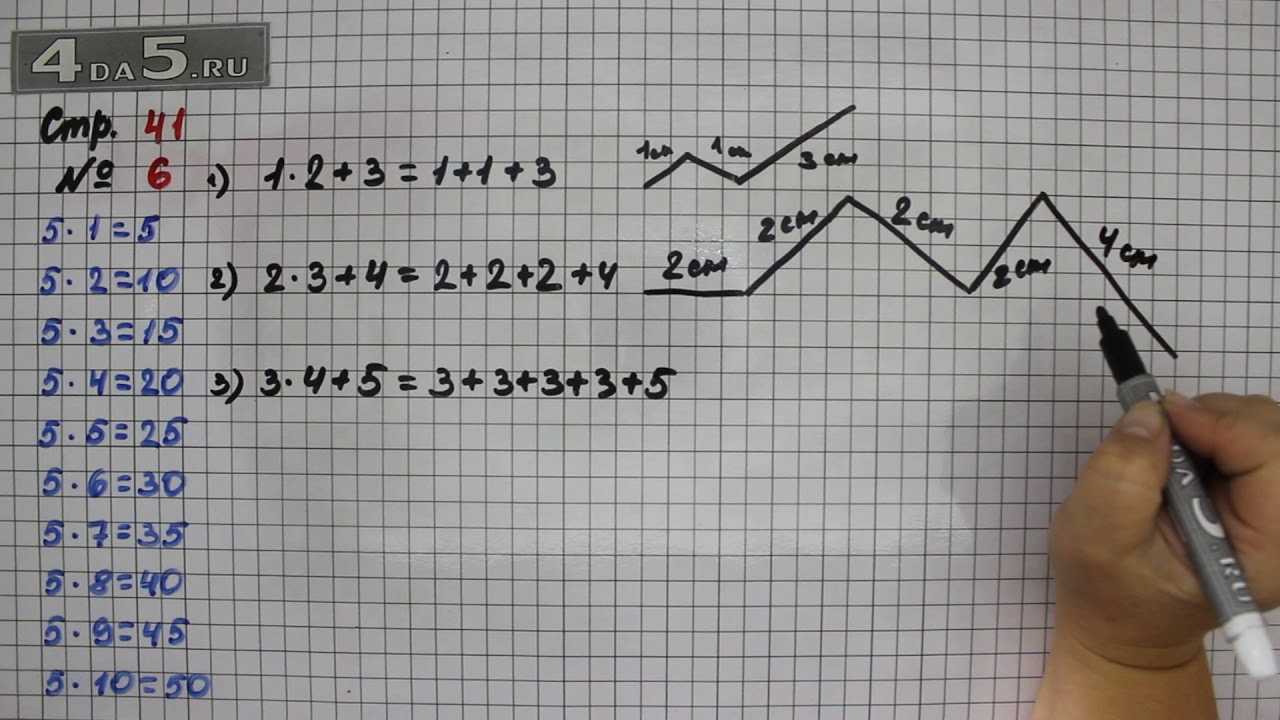 G.2
G.2 G.5
G.5 NS.1 и 2
NS.1 и 2