Задание 2 по математике: Задание 2 ЕГЭ по математике профильного уровня 2023: теория и практика

Задание 2 ЕГЭ по математике профильного уровня 2023: теория и практика

Русский язык Математика (профиль) Математика (база) Обществознание История Биология Физика Химия Английский язык Информатика Литература

Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18

За это задание ты можешь получить

1 балл. На решение дается около 5 минут. Уровень сложности: базовый.
Средний процент выполнения: 66.7%
Ответом к заданию 2 по математике (профильной) может быть целое число или конечная десятичная дробь.

Разбор сложных заданий в тг-канале

Посмотреть

Задачи для практики

Задача 1

Из единичного куба вырезана правильная четырёхугольная призма со стороной основания $0{,}7$ и боковым ребром $1$. Найдите площадь поверхности получившейся фигуры (cм. рис.).

Решение

Поверхность оставшейся части куба состоит из боковой поверхности куба, площадь которой равна 4·1·1=4, боковой поверхности призмы, площадь которой равна 4·0,7·1=2.8, и двух равных фигур (см. заштрихованную фигуру на рисунке), площадь каждой из которых равна 1·1 – 0,7·0,7 = 0.51. Таким образом, площадь поверхности оставшейся части куба равна 4 + 2.8 + 2 · 0.51 = 7.82.

Ответ: 7. 2=6⋅16=96$.

Ответ: 96

Показать решение

Бесплатный интенсив

Задача 6

Длина окружности основания цилиндра равна $6$. Площадь боковой поверхности равна $21$. Найдите высоту цилиндра.

Решение

Площадь боковой поверхности цилиндра вычисляется по формуле $S_{бок} = 2πRH$, где $R$ – радиус основания, $H$ – высота цилиндра. По условию $2πR = 6, S_{бок} = 21$, тогда $H = 21 : 6 = 3.5$.

Ответ: 3.5

Показать решение

Бесплатный интенсив

Задача 7

В основании прямой призмы лежит ромб с диагоналями, равными $20$ и $48$ (см. рис.). Площадь её поверхности равна $1272$. Найдите боковое ребро этой призмы.

Решение

Так как диагонали ромба перпендикулярны и точкой пересечения делятся пополам, то сторону ромба найдём из прямоугольного треугольника $AOD$ по теореме Пифагора. 2} = √{(26 – 24)(26 + 24)} = 10$. Так как $BD = AC$, то $S = 24 · 10 = 240$.

Ответ: 240

Показать решение

Бесплатный интенсив

Задача 10

Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен $7$.

Решение

$V_{цилиндра}=S_{осн}⋅ H$, $V_{конуса}={1} / {3} S_{осн}⋅ H$. По условию конус

и цилиндр имеют общее основание и общую высоту, значит,
$V_{цилиндра}=3V_{конуса}=21$.

Ответ: 21

Показать решение

Бесплатный интенсив

Задача 11

Найдите площадь поверхности правильной четырёхугольной пирамиды, стороны основания которой равны $24$ и высота равна $5$ (см. рис.).

Решение

Площадь $S$ поверхности правильной четырёхугольной пирамиды $SABCD$ равна сумме площади основания $S_{осн}$ и площади боковой поверхности $S_{бок}: S = S_{осн} + S_{бок} = AB^2 + 4S_{SBC}. 2=126$
$ 36а=126-54$
$ 36а=72$
$ а=2$.

Ответ: 2

Показать решение

Бесплатный интенсив

Показать еще

Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.

Включить уведомления

Бесплатный интенсив по математике (профильной)

3 огненных вебинара, домашние задания, беседа курса, личный кабинет, связь с преподавателем и многое другое.

Курс стартует 28 марта. Бесплатный интенсив

Как решать задание 2 из ЕГЭ по математике

Итоговый экзамен по математике сдают все. Те, кто поступает на гуманитарные специальности (филология, юриспруденция, международные отношения) выбирают базовый уровень — вопросы в нем легче, а оценки «3» достаточно для получения аттестата. Профильный уровень сдают будущие экономисты, инженеры и программисты — на этих специальностях без знания математики не обойтись, ее обязательно изучают на первых курсах. Но это непростой предмет. Даже в профильных математических классах не всегда дают достаточно знаний. Если ваша цель — поступление в топовый вуз на техническую специальность, без курсов подготовки к ЕГЭ не обойтись. Это касается не только профильного уровня, но и ЕГЭ по математике базового. «Задание 2, как решать?» — часто спрашивают школьники, сдающие этот экзамен. В этой статье мы проведем разбор задания 2 из ЕГЭ по математике профильного и базового уровня. 

Теория

В задании 2 ЕГЭ по профильной математике теория достаточно простая. Это номер базового уровня сложности, он приносит 1 балл. Выпускникам дается график (иногда — диаграмма), нужно проанализировать его в соответствии с условием. Определение аргумента функции, поиск максимального и минимального значения — навыки, которые нужны для этого задания ЕГЭ. 2 часть математики профильного уровня тоже содержит номера с графиками, поэтому эта теория пригодится и там. То, что нужно знать для решения задания 2 ЕГЭ по математике профильного уровня: 

• функция и ее график;
• оси абсцисс и ординат;
• промежутки возрастания и убывания функции;
• области определения и значения функции;
• максимум и минимум функции;
• наибольшее и наименьшее значения на промежутке;
• диаграммы;
• цена деления на графике. 

Перечисленные понятия нужны для сдачи любого уровня ЕГЭ. Но задание 2 по базовой математике проверяет другие навыки. В нем выпускник должен произвести вычисления со степенями. Этот номер тоже считается легким, однако для его выполнения нужно знать куда больше теории. Формулы для ЕГЭ по базовой математике, к заданию 2:

• определение степени — an = a • a • a … • a, где n — натуральное число. a называют основанием степени, n — показателем. 
• a0 = 1.
• a1 = a.
• a-n = 1 / an.
• anm=man.
• an • am = an+m.
• an • bn = (a • b)n.
• an / am = an-m.
• an / bn = (a / b)n.

Разбор задания 2

Решение задания 2 по математике ЕГЭ мы начнем с профильного уровня. 

Задача. Замеры температуры проводились в течение 3 дней. Какой была минимальная температура 18 апреля? 

Решение. Подобное задание 2 на ЕГЭ по математике профильного уровня кажется очень простым, однако в нем легко ошибиться. Обратим внимание на два момента: «18 апреля» и «минимальная». Для начала отсекаем колонки, относящиеся к 19 и 20 апреля — про них ничего не спрашивают. После этого ищем самую низкую точку и находим ее ординату. 

Ответ: 6.

Задача. В помещении стоит кондиционер с датчиком температуры. Когда она достигает определенного максимального значения, кондиционер включается. Когда комната остужается до необходимой температуры, кондиционер автоматически выключается. На графике показана зависимость температуры от времени. Укажите, сколько минут кондиционер был выключен.

Решение. В этом номере важно умение логически рассуждать. Когда кондиционер отключен, температура увеличивается. На графике это показывается ростом функции вверх. Чтобы определить, сколько минут кондиционер был выключен, нужно найти область возрастания функции. Это промежуток между числами 6 и 9 на оси абсцисс. Теперь мы ищем время: 9 – 6 = 3.

Ответ: 3.

За выполнение такого простого номера можно получить 1 балл на экзамене по математике. Разбор задания 2 ЕГЭ мы продолжим базовым уровнем. Здесь встречаются несколько типов вопросов: степенные выражения с одинаковыми и разными основаниями, поиск частного, произведения и суммы. Чтобы посмотреть все существующие виды заданий, зайдите на «Решу ЕГЭ» по базовой математике. Задание 2 там представлено более чем 40 вариантами. А в рамках этой статьи мы разберем несколько примеров задания 2 из ЕГЭ по математике базового уровня.  

Найти значение выражения

Задача. 4 • 72 + 6 • 72.

Решение. У слагаемых есть общий множитель, который мы можем вынести за скобку. После этого считаем выражение в скобке, потом возводим число в степень и перемножаем: (4 + 6) • 72 = 10 • 72 = 10 • 49 = 490.

Ответ: 490.

Найти значение выражения (разные основания)

Задача. 8^0,76 • 64^0,12.

Решение. Нужно привести степени к одинаковому основанию, представив 64 как 82. После этого их можно перемножить: 8^0,76 • 64^0,12 = 8^0,76 • (8)^2*0,12 = 8^0,76+0,24 = 8¹ = 8.

Ответ: 8.

Найти значение выражения (одинаковые основания)

Задача. 26 • 2-2 / 22.

Решение. В данном примере расчеты можно провести сразу же. Умножение степеней с одинаковым основанием заменяем на сложение показателей, деление — на их вычитание: 26 + (-2) – 2 = 26 – 4 = 22 = 4.

Ответ: 4.  

Найти частное от деления

Задача. 1,6 • 102 : 4 • 10-2.

Решение. У степеней одинаковое основание, поэтому мы можем поделить их, найдя разность показателей. После этого мы делим числа без степеней и выполняем умножение: 1,6 : 4 • 102 – (-2) = 1,6 : 4 • 104 = 1,6 : 4 • 10000 = 0,4 • 10000 = 4000.

Ответ: 4000.

Найти произведение

Задача. 4 • 105 • 2,3 • 10-7.

Решение: Степени имеют одинаковые основания, поэтому мы можем умножить их, сложив показатели. После этого результат умножаем на остальные числа: 4 • 2,3 • 105 + (-7) = 4 • 2,3 • 10-2 = 4 • 2,3 • 0,01 = 9,2 • 0,01 = 0,092. 

Ответ: 0,092.

Найти сумму

Задача. 9,4 • 102 + 2,1 • 103.

Решение. Мы возводим числа в степень, затем выполняем умножение и сложение: 9,4 • 100 + 2,1 • 1000 = 940 + 2100 = 3040.

Ответ: 3040. 

Теперь вы знаете чуть больше теории для ЕГЭ по математике. Задание 2 из профильного уровня достаточно легкое (хотя без практики тут тоже не обойтись), а вот в базе придется рассуждать и выполнять вычисления. Но и его можно выполнить без труда, если должным образом подготовиться к ЕГЭ. Однако, лучший результат всегда дают занятия с опытными преподавателями, знающими специфику экзамена. Если нанимать репетитора для вас дорого, обратите внимание на курсы. Там разбирают не только задание 2 ЕГЭ по математике, но и многие другие номера, в том числе вторую часть. Грамотная подготовка — ключ к хорошим баллам, а значит, и месту на бюджете. 

IELTS Writing Task 2 Sample 773

Детали

Последнее обновление: среда, 08 сентября 2021 г., 12:53

Автор IELTS Mentor

Просмотров: 16380

IELTS Writing Task 2/IELTS Essay:

Вы должны потратить около 40 минут на это задание.

Напишите на следующую тему:

Чтобы устроиться на хорошую работу сегодня детям важнее изучать математику и иностранные языки, чем искусство и музыку.

В какой степени вы согласны или не согласны с этим мнением?

Обоснуйте свой ответ и включите соответствующие примеры из ваших собственных знаний или опыта.

Вы должны написать не менее 250 слов.

---

Модель Ответ 1:
В наши дни возможности трудоустройства становятся очень конкурентоспособными. Навыки в иностранном языке и математике держат человека на лишнюю милю впереди людей со знаниями в музыке и искусстве. Важность искусства и музыки в жизни человека нельзя отрицать, но очевидно, что для большинства профессий гораздо важнее второй язык и математические навыки. Вот почему я полностью согласен с идеей, что ребенок должен уделять больше внимания математике и иностранному языку в академической жизни, чем предметам искусства, если только он не хочет стать художником или музыкантом в профессиональной жизни.

С одной стороны, музыка и искусство важны для нашей личной и общественной жизни. Однако этому может научиться любой, но каждый не может стать художником или музыкантом без врожденного таланта и полной самоотверженности, выходящей за рамки академического обучения.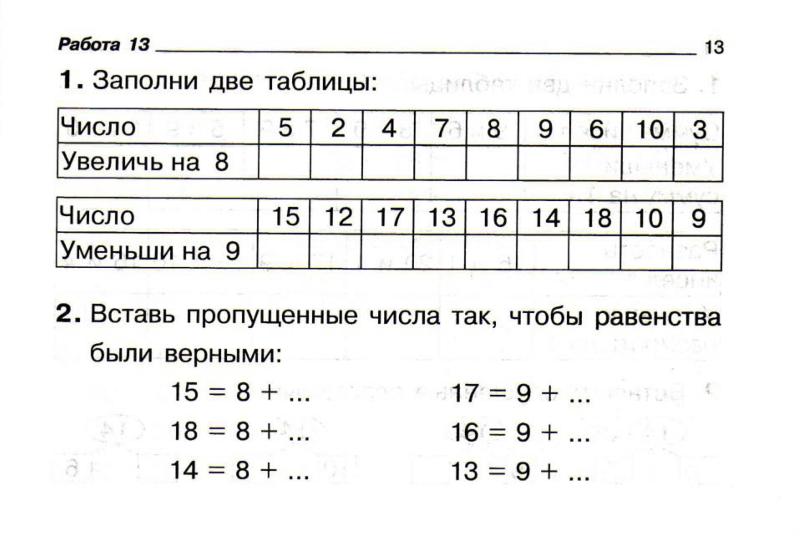 Более того, рынок труда в области искусства и музыки намного меньше по сравнению с профессиями, связанными с технологиями и наукой. Например, если медиа-компании требуется художник, они наймут очень мало артистов, и их коммуникативные и языковые навыки также будут оцениваться. В то же время более низкие ставки оплаты по предметам, связанным с искусством, также следует учитывать при принятии решения о том, какую специальность должен выбрать ребенок в своей академической жизни.

С другой стороны, математика — важный предмет, который должен изучать каждый. Этот предмет побуждает детей думать и улучшать их мозговые способности и память. Более того, в наши дни математика является важной частью каждого сектора труда, включая информационные технологии, автомобилестроение, банковское дело, проектирование, исследования, строительство и так далее. В то же время владение дополнительным языком всегда увеличивает возможности соискателя. Например, когда японская строительная компания ищет специалиста по строительству для своего проекта, она определенно предпочтет среди других кандидатов человека, знающего японский язык.

Поскольку одной из основных целей академических занятий является подготовка детей к их будущей карьере, математика и второй язык всегда должны быть в приоритете.

В заключение, без сомнения, изучение математики и иностранного языка означает способности детей и их будущее. Я не против обучения школьников искусству и музыке, но пока речь идет об их будущей карьере, преподавание математики и второго языка всегда должно иметь приоритет.

[Написано – Ромеш Родриго ]

• IELTS Эссе
• Письменная задача 2

• Пред.
• Следующий

Расследование 1, Задача 2 – Математический сайт Eastman

Алгебра 1> Алгебра 1 Экспоненциальные функции> Экспоненциальные функции, расследование 1>

ШАССОВАЯ ПАССА КОРОЛЕ Индия, крестьянин спас жизнь дочери короля. Король был так благодарен, что сказал крестьянину, что может получить любую награду, которую пожелает. Крестьянин сначала сказал королю, что ему не нужна награда. Но король, будучи гордым человеком, настоял на том, чтобы крестьянин потребовал награду. Крестьянин был мудрым человеком и хотел проучить короля. Он просил об этом в качестве награды. «Я хочу, чтобы вы положили одно зернышко риса на первую клетку шахматной доски, два зернышка риса — на вторую клетку шахматной доски, четыре — на третью клетку, восемь — на четвертую клетку и так далее, пока не получите покрыли все шестьдесят четыре квадрата. На каждом квадрате должно быть в два раза больше рисовых зерен, чем на предыдущем квадрате». Король ответил: “Но рисовое зернышко такое маленькое. Конечно, ты можешь придумать награду получше.” Но крестьянин настоял, и король согласился на его просьбу. (Вот объяснение и рассказ истории из Википедии.) Вот пара видеоверсий этой истории, чтобы вы могли насладиться . Королевская шахматная доска как детская школьная пьеса. (часть 2 видео) Королевская шахматная доска в виде иллюстрированного видео сборника рассказов. Чтение книги Одно зерно риса от Деми. A. Составьте таблицу, показывающую, сколько зерен риса король разместит на клетках с первой по шестнадцатую на шахматной доске. B. Как меняется количество рисовых зерен от одного квадрата к другому? C. Сколько зерен риса будет на квадрате 20? В квадрате 30? В квадрате 64? D. На какой первой клетке король поместит не менее 1 миллиона рисовых зерен? E.  С помощью Desmos постройте график данных (количество квадратов, количество рисовых зерен) для квадратов от 1 до 10.  По мере увеличения номера квадрата, как изменяется количество рисовых зерен? Что этот образец изменений говорит вам о вознаграждении крестьянина? F.  Напишите уравнение зависимости между числом квадратов n и количеством рисовых зерен r . G.  Если бы на шахматной доске было 100 клеток, сколько зерен риса было бы на 100 клетках? H. Характер изменения количества бюллетеней в Задаче 1 и характер изменения количества рисовых зерен в этой задаче демонстрируют экспоненциальный рост . Каковы модели изменений в двух ситуациях  аналогичный ? I.  Напишите уравнение зависимости между количеством бюллетеней b и количеством сокращений n в задании 1. о награде, которую он обещал крестьянину, королева сказала: «Ты обещал ему больше зерна, которое есть у нас в царских амбарах! Ты должен убедить его принять другую награду». После долгих размышлений король придумал план. Он создаст новую доску всего с шестнадцатью квадратами. Он клал 1 зернышко риса на первую клетку, три — на следующую, девять — на следующую и так далее. В каждом квадрате будет в три раза больше рисовых зерен, чем в предыдущем квадрате. A.  В таблице ниже план 1 — это награда, запрошенная крестьянином, а план 2 — новый план короля. Используя Desmos, скопируйте и заполните таблицу, чтобы показать количество рисовых зерен в клетках от 1 до 16 для каждого плана.  Square    Plan 1  Plan 2  1      1  1  2  2  3  3  4 9 4 по плану 1? C.  Напишите уравнение зависимости между количеством клеток n и количеством рисовых зерен r для плана 2. общая награда по крестьянскому плану? Как вы решили? E. С помощью Desmos постройте график плана 2 для n = от 1 до 10. Как ваш график сравнивается с графиком, который вы построили для плана 1? Королева придумала третью награду, которую король мог предложить крестьянину. Согласно плану 3, король должен был сделать доску с 12 клетками. Он начинал с одного рисового зерна на первом квадрате и в четыре раза увеличивал количество рисовых зерен от одного квадрата к другому. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Имя * Email * Сайт Комментарий *