Задачи со схемами 3 класс: занимательные текстовые задачки, примеры и другие задания с ответами и решением

Конспект урока по математике для 3 класса «Решение задач по сумме и разности»

Конспект урока по математике для 3 класса

«Решение задач по сумме и разности»

Стельникович

Юлия Владимировна

учитель начальных классов

ГБОУ ЦО «Школа здоровья» № 2005 г.Москвы

Тип урока: ОНЗ.

Тема: «Решение задач по сумме и разности».

Учебник: Л.Г.Петерсон. «Математика,3 класс»

Основные цели:

1. сформировать способность к решению задач по сумме и разности;

2. актуализировать способность к решению составных текстовых задач на нахождение целого и на разностное сравнение, как их составляющей части;

3. создать условия для самостоятельного (путем подводящего диалога) поиска детьми решения учебной задачи;

4. зафиксировать способ решения задач по сумме и разности в речи и знаково: построить алгоритм решения задач данного типа в ходе обсуждения способа действия с детьми; записать алгоритм в виде опорного конспекта;

5. тренировать способность к устной и письменной нумерации многозначных чисел; развивать вычислительные навыки;

6. сформировать умение использовать открытые знания на практике.

Мыслительные операции: классификация, анализ, синтез, сравнение, обобщение; способность адекватного обобщения.

Раздаточный материал:

1. По две полоски разного цвета и разной длины у каждого;

2. Карточка для этапа актуализации с задачами и схемами к ним;

3. Эталон для самопроверки:

4. Карточка с задачей для пробного действия;

5. Эталон-алгоритм для решения задач по сумме и разности;

6. Карточка для этапа рефлексии.

7. Маркерные дощечки. (5 штук)

СЛАЙД №3.

ХОД УРОКА.

СЛАЙД №4.

1. Мотивация к учебной деятельности.

– Прочитайте незаконченное высказывание. (Последнее слово закрыто.)

«Где есть желание, там всегда найдется путь».

– Как вы думаете, как можно продолжить эту фразу? (…) (Открыть продолжение фразы. )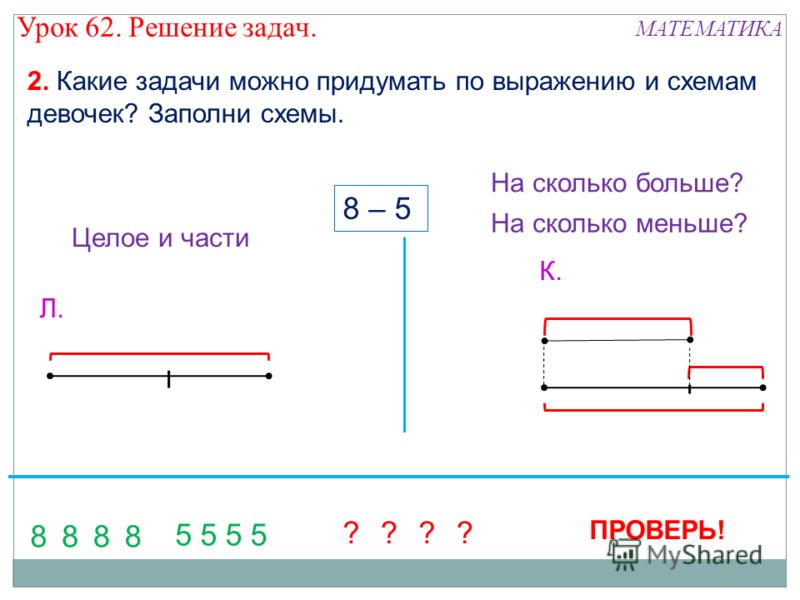

– Как вы понимаете смысл этого высказывания? Подходит ли оно к уроку математики? Почему? (…)

– Попробуйте догадаться, в какую область математики мы сегодня отправимся. Готовясь к встрече с вами и к сегодняшнему уроку математики, я натолкнулась на такое стихотворение:

Хоть ты смейся, хоть ты плачь,

Не люблю решать задач.

Потому что нет удачи

На проклятые задачи.

Может быть, учебник скверный,

Может быть, таланта нет,

Не могу открыть секрет:

Как задаче дать ответ…

– Итак, в какую область математики мы отправляемся? (В область задач.)

– Конечно, вы поняли, что это шуточное стихотворение, но все же, какая проблема у героя этих строк? (…)

– А вы любите решать задачи? Почему? (…)

– Задачи какого типа мы научились решать на уроках математики? (На нахождение части и целого, на разностное сравнение, на приведение к единице.)

– У кого из вас есть желание отправиться дальше в путь по Стране Математики и научиться решать задачи нового типа?

– Тогда все вместе – в путь!

2. Актуализация знаний и фиксация затруднения в пробном действии.

– Путешествуем мы сегодня командами-группами.

– Давайте повторим правила работы в группе. (Не ссориться; выслушивать мнение каждого; и т.д.)

– Сегодня мы будем открывать новые знания.

– Вспомните, как мы это делаем. (Повторяем то, что поможет нам открыть новое; выполняем пробное действие; встречаем затруднение; находим путь; закрепляем то, что открыли)

– Итак, в путь!

СЛАЙД №5.

– Открыли тетради. Запишем число, классная работа.

– Проверим, готовы ли вы к путешествию?

– Задачу нельзя решить, не умея считать.

3. Устный счет

1. Игра «День и Ночь».

Учитель произносит «ночь», и дети кладут головы на парту – «засыпают». В это время учитель диктует цепочку примеров. Дети решают их в уме. Когда учитель говорит «день», дети хором выкрикивают получившийся результат.

1).850 – 50=(800) : 2=(400) – 200=(200) + 100=(300) *2=(600): 100=6 2). 560:7=(80) +120=(200)*3=(600) – 250=(350):50=(7) * 1000=7000

( Взять 2 «цепочки» примеров на случай, если дети в первой ошибутся.)

Если дети ошибутся в первой «цепочке», то пошутить:

– Вы, наверное, так крепко заснули?

-Попробуем решить во сне еще одну «цепочку», будьте «начеку».

СЛАЙД №6.

2. «Математическая разминка».

– Продолжим тренировку в устном счете.

– Ребята, посоветуйтесь, кто из вас лучше всех считает, и выберите в команде счетовода. Услышав выражение, каждый участник команды решает его самостоятельно. Затем вы в группе сравниваете свои результаты, приходите к единому мнению. Счетовод записывает результат на дощечке маркером и показывает ответ. А остальные ребята записывают ответы в тетрадь, в строчку. ( Правильные ответы появляются на экране. Если есть ошибки, разбираем, комментируем, исправляем)

– На сколько 370 больше, чем 90? (280)

– Увеличь 19 в 2 раза. (38)

– Уменьши 640 в 8 раз. (80)

– Из 8 сотен вычти 6 десятков. (740)

– Во сколько раз 100 больше, чем 10? (10)

– Найди произведение 5 и 100. (500)

– Найди частное 120 и 60. (2)

4. Актуализация способности выбора схем к задачам разного типа.

-Мы потренировались в устном счете. Теперь можем приступить к следующему этапу, который поможет нам открыть новое знание. (Повторить то, что уже знаем.)

– Что вам всегда помогает при решении задач? (Схемы.)

СЛАЙД №7.

– Выберите схемы, которыми вы пользовались при решении задач. (1 и 3; схемой №2 мы не пользовались.)

– Назовите типы задач, которые помогают решать эти схемы. (Задачи на разностное сравнение и на нахождение части и целого.)

– На какой схеме можно расставить буквы Б, М, Р, С? (Эти буквы можно расставить на первой схеме.)

– Что они означают? ( Они обозначают: Б – большее число, М – меньшее число, Р – разницу, С – сумму. )

Дети у доски расставляют на схеме буквы.

М

Р

С

Б

Затем учитель закрывает карточкой «?» букву Р.

– Как найти разность? (Чтобы найти разницу, надо из большего числа вычесть меньшее.)

Учитель закрывает карточкой «?» букву Б.

– Проговорите это правило. (Чтобы найти большее число, нужно к меньшему числу прибавить разницу.)

Учитель закрывает карточкой «?» букву М.

– Как найти меньшее число? (Чтобы найти меньшее число, нужно из большего числа вычесть разницу.)

Задание на карточках.

– Молодцы! Я думаю, что вы прекрасно справитесь с заданием на карточках.

– Я диктую условие задачи. Каждый из вас пробует ее устно решить.

– На пальцах покажите участникам своей группы номер схемы, которая подходит к данной задаче. Если ответы не совпадают – обсудите, постарайтесь прийти к общему мнению.

– Счетоводы, покажите всем ваш итоговый ответ. (Можно попросить прокомментировать сначала команду с неверным ответом, если такой будет, а потом ей возразят те, кто решил правильно. )

СЛАЙД №8.

На экране эта карточка и по мере ответов детей появляются правильные ответы.

– Послушайте условие задачи.

Почтовый голубь за день пролетает 500 км, а синица – на 400 км меньше, чем почтовый голубь. Какое расстояние за день пролетает синица?

– Подберите схему к этой задаче. Укажите ее номер. (2)

– Какое выражение выберите для решения? (1.)

– Сколько км за день пролетает синица? (Синица пролетает за день 100 км.)

– Какую величину мы находили? (Мы находили меньшую часть.)

– На карточках соедините линией схему и решение.

– Еще одна задача.

Турист, путешествующий по Африке, на своем пути насчитал 78 баобабов, а пальм – на 22 больше. Сколько всего деревьев увидел путешественник?

– Назовите номер схемы и выражения, соедините линией. (4, 2.)

– Сколько деревьев всего? (178 деревьев.)

– Что мы находили? (Большее значение и сумму.)

– Отлично, рассмотрим еще одну задачу.

Длина шага мужчины 75 см, длина шага мальчика 50 см. На сколько см шаг мальчика короче, чем шаг мужчины?

– Какую схему выбрали? Докажите. (5)

– Какое выражение? (5.)

– Соедините линией.

– Какая из трех задач лишняя? Почему? (Вторая, так как она составная, а остальные простые.)

– Повторение закончилось.

– Что повторили? (Мы повторили правила нахождения разницы, большего и меньшего числа. Повторили способы решения простых и составных задач.)

– Какое задание вы получаете после повторения на уроках открытия нового знания? (Задание с затруднением.)

5. Задание для пробного действия.

– Это задача из жизни. Мы с вами любим ездить на экскурсии. Иногда едут не все ребята из класса, а только группа. В автобусе с нами путешествуют ребята из 3 «Г».

В сентябре мы посетили Парк птиц. Приехав на место, вы все разбежались смотреть птиц. Экскурсовод попросила назвать количество детей в каждой группе, для того, чтобы отдать нам с Ниной Васильевной билеты. Мы забыли, сколько человек в каждой из групп. Но помнили, что всего в автобусе было 46 ребят и в группе 3 «Д» (то есть в нашей) на 4 человека больше, чем в группе 3 «Г». Мы с Ниной Васильевной произвели в уме кое-какие расчеты и назвали экскурсоводу количество детей каждой группы.

-Справитесь ли вы с этой задачей?

– Это задание находится на 2 листе.

– Попробуйте решить задачу самостоятельно.

СЛАЙД №9.

В двух группах – 3 «Г» и 3 «Д» – всего 46 человек. В группе 3 «Д» на 4 человека больше, чем в группе 3 «Г». Сколько человек в каждой группе?

– Проверим. Какой ответ вы получили? Учитель записывает варианты ответов детей на доске.

6. Выявление места и причины затруднения.

– Что же вы видите? (Получили разные ответы, кто-то не приступил к решению, мнения разделились.)

– В чём у вас затруднения? (Мы не смогли решить задачу и не можем доказать, чей ответ верный.)

– А когда возникает затруднение, что надо сделать? (Остановиться и подумать.)

7. Построение проекта выхода из затруднения.

Учитель указывает на схему с буквами на доске.

– Давайте обратимся к известной нам схеме. Может быть, она нам пригодится?

М

Р

С

Б

– Что известно в задаче: большее число, меньшее число, сумма, разность? (Сумма и разность.)

– Что нужно найти? (Большее число и меньшее число.)

– Как бы вы назвали такой тип задач? (…)

– В математике такие задачи называют задачами на нахождение величин по их сумме и разности или короче задачи по сумме и разности.

– Как вы думаете, почему ? (…)

– Давайте вернемся к девизу нашего урока. Какой путь мы должны пройти? Какую цель поставим перед собой на уроке? (Узнать способ решения задач по сумме и разности.)

– Сформулируйте тему урока. (Задачи по сумме и разности.)

Учитель открывает тему на доске.

– Сегодня мы будем узнавать способ решения задач нового типа.

СЛАЙД №10.

8. Реализация проекта выхода из затруднения.

– Давайте обратимся за помощью к нашей схеме.

М

Р С

Б

Учитель возвращает на доску схему №2.

– Давайте заполним нашу схему.

-Что нам дано? (Сумма – 46 и разность – 4.)

Дети у доски заполняют схему.

-Что нужно узнать? (Сколько детей в каждой группе или большее и меньшее значение.)

– Группы не одинаковые. А если бы данные величины были бы одинаковыми, мы бы смогли решить эту задачу? ( Можно из схемы убрать разность, чтобы детям было наглядно видно 2 одинаковых отрезка. )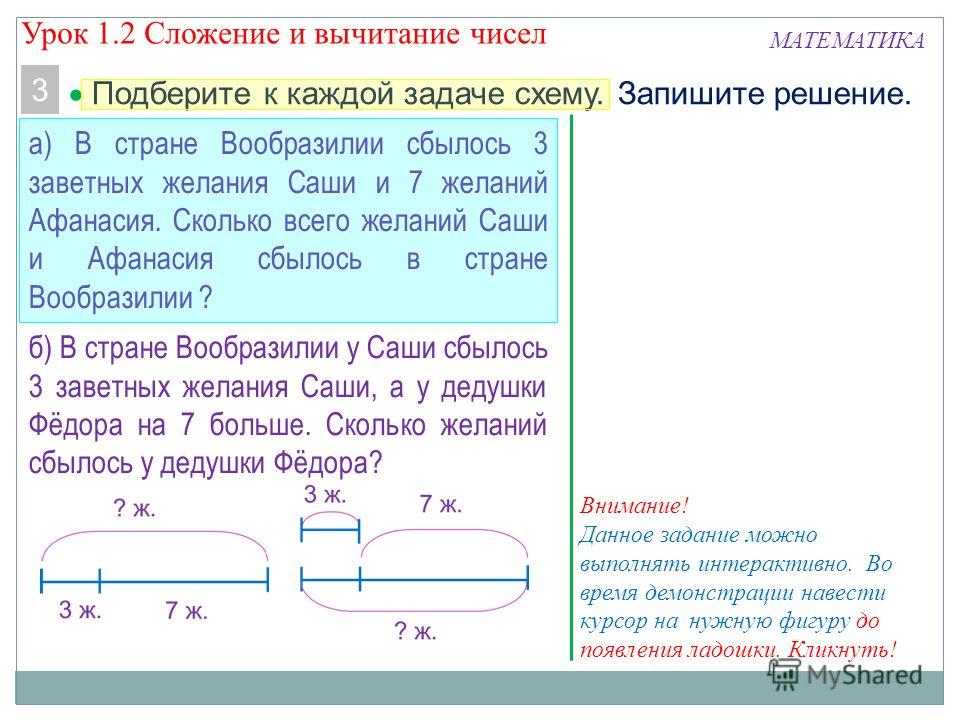

-А как? (Мы бы сумму разделили на 2.)

– А что нужно сделать, чтобы 2 части стали равными? (Вычесть разность.)

– У вас на партах лежат две полоски разной длины. Что можно сделать, чтобы полоски стали равными? (Совместить полоски и отрезать или оторвать лишнее у данной полоски.)

– Покажите.

Учитель производит с демонстрационными полосками те же операции, что и дети. Далее рассуждения идут с опорой на демонстрационные полоски на доске.

– Посмотрите на схему. Что вы сейчас убрали? (Разность.)

Учитель тоже убирает разность со схемы.

– Посмотрите на схему. Со всем ли вы согласны? ( Меняем буквы на схеме и данные.)

– Изменилась ли сумма, когда убрали разность? (Да, она стала меньше.)

– На сколько? (Она стала меньше на разность.)

– Итак, какой первый шаг вы сделали? (Из суммы вычли разность.)

СЛАЙД №10.

На экране появляется карточка.

1. 1. С – Р

– Посмотрите, чему равен каждый из получившихся отрезков? (Меньшему числу.)

– И таких отрезков у нас два, то есть у нас получилось удвоенное меньшее число.

СЛАЙД №10.

На экране появляется карточка.

1. = удвоенное меньшее число

   1. С – Р

– Что вы можете найти, зная сумму одинаковых отрезков? (Длину одного отрезка.)

– Длину какого отрезка вы получили? (Длину меньшего отрезка.)

СЛАЙД №10.

На экране появляется карточка.

2)(С-Р):2=М

– Как теперь найти длину большего отрезка? (Надо к меньшему числу прибавить разницу.)

СЛАЙД №10.

На экране появляется карточка.

3) М + Р = Б

– Итак, алгоритм чего вы сейчас создали? (Алгоритм решения задачи по сумме и разности.)

СЛАЙД №10.

– Сколько действий будет в решении задачи по сумме и разности. (Три действия.)

–Что было известно в условии задачи? (Сумма и разность.)

– Теперь по этому алгоритму давайте решим задачу, которая вызвала у вас затруднение.

1 ученик решает у доски, остальные – в тетради.

1. 46 – 4 = 42(ч.) – удвоенное число учеников в группе 3 «Г».

2. 42 : 2 = 21 (ч.) – в группе 3 «Г».

3. 21+4 = 25 (ч.)

СЛАЙД №11.

Физминутка.

– Настало время немного отдохнуть после напряженного умственного труда.

– На уроках математики физминутки тоже математические.

– На доске записано сегодняшнее число. (29.11.2011)

– Я сотру точки. Прочитайте многозначное число, которое поучилось.(29 112 011– двадцать девять миллионов сто двенадцать тысяч одиннадцать.)

– Цифра, которая стоит в разряде десятков миллионов, подскажет, сколько раз подпрыгнуть. (2 раза)

-Цифра, которая стоит в разряде единиц тысяч, подскажет, сколько раз присесть. (2 раза)

-А цифра в разряде единиц – сколько раз повернуться вокруг себя (1 раз).

-А цифра в разряде единиц миллионов – сколько раз хлопнуть в ладоши (9 раз).

9. Первичное закрепление во внешней речи.

– Мы составили алгоритм, что же можем делать теперь? (Решать задачи.)

– Листочек с алгоритмом лежит у вас на парте. Вставьте его в ваши памятки.

– Итак, давайте попробуем применить наш алгоритм при решении задач.

Работа с учебником.

– С. 8, № 3(а)

– Прочитайте задачу по себя.

– Назовите тип задачи. (Задача по сумме и разности.)

– О чем говорится в задаче? (О марках.)

– Что нам известно? (Всего248 марок, разность 8 марок.)

-Что нужно узнать в задаче? (Большую и меньшую величину.)

– Начертим схему к задаче.

– Объясните первый шаг решения задачи.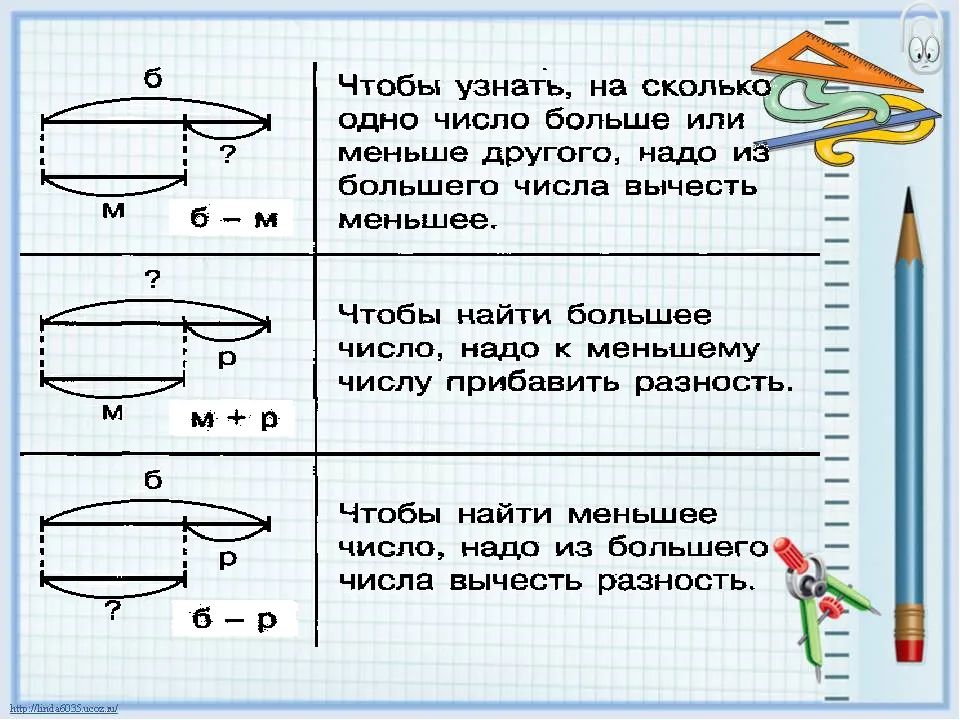 (Из суммы вычитаем разницу, получаем удвоенное меньшее число: 248 – 8 = 240 марок.)

– Объясните второй шаг. (Удвоенное меньшее число делим на 2, получаем меньшее число: 240 : 2 = 120 марок.)

– Объясните третий шаг. (К меньшему числу прибавляем разность, получаем большее число: 120 + 8 = 128 марок.)

По 1 у доски с комментированием, остальные – в тетради.

– Выражение: (248 – 8) : 2 + 8

10. Самостоятельная работа с самопроверкой по эталону.

– Мы замечательно решили задачу вместе. Что теперь предлагаете сделать? (Поработать самостоятельно.)

– С. 8 № 2 (запись в учебнике)

СЛАЙД №12.

– Поверьте себя по эталону. (На экране появляется эталон решения этой задачи.)

– У кого возникли затруднения? С чем они были связаны? (…)

– Кому все удалось?

-У кого были ошибки? Вы их исправили?

-Какие вы молодцы! Благодаря вам мы можем увидеть самые сложные места в решении этого типа задач и ещё раз над ними поработать.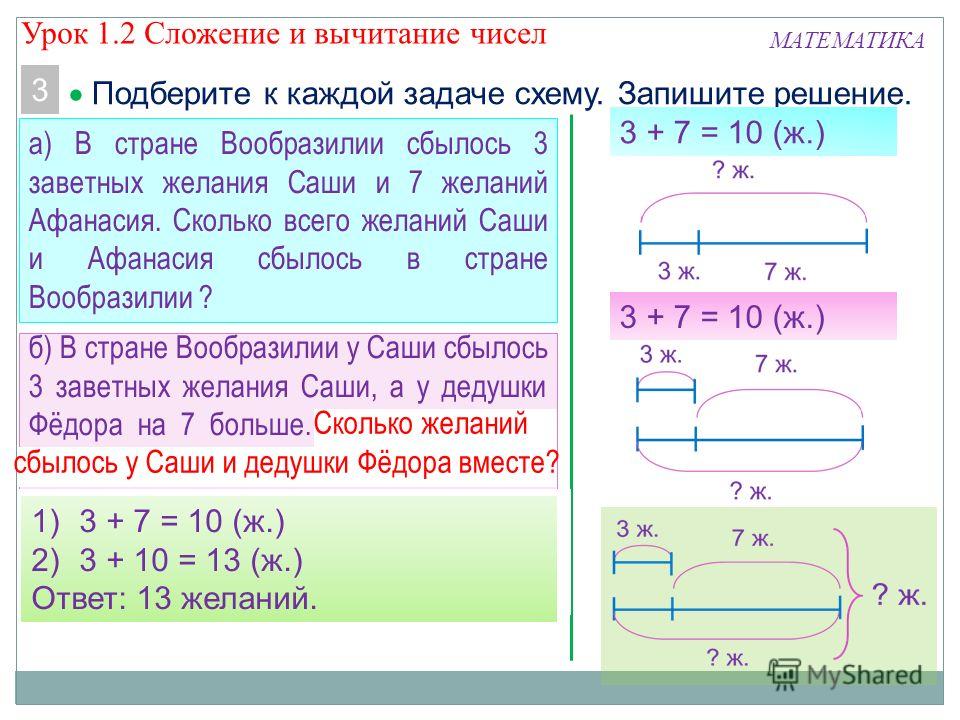

12. Рефлексия учебной деятельности на уроке.

– Ну что ж, наш путь на сегодняшнем уроке подходит к концу. А в конце пути принято подводить итоги и делиться впечатлениями.

– Сначала подведем итоги пути.

– Какую цель мы поставили перед собой в начале пути? (Научиться решать задачи по сумме и разности.)

– Почему так назван этот тип задач? (Потому что мы находим неизвестные величины по их сумме и разности.)

– Достигли ли мы цели? (…)

– Расскажите путь решения задачи по сумме и разности по алгоритму.

– Поделитесь своими впечатлениями об уроке. (Ответы детей.)

-Оцените свои умения знаком + напротив одной из фраз:

СЛАЙД №13.

– Да, я умею решать задачи по сумме и разности.

– Не хватает уверенности в решении задач по сумме и разности.

– Пока я затрудняюсь в решении задач по сумме и разности.

-Поднимите руки те, кто выбрал первую фразу.

– Вторую.

-Третью.

-Возьмите желтую карточку и нарисуйте смайлик, который покажет, какое у вас настроение в конце нашего урока.

Домашнее задание:

-Выйдите к доске 4 девочки и 2 мальчика.

– Сделайте так, чтобы вас стало поровну. (Одна девочка должна перейти к мальчикам.)

– Как по-другому уравнять эти группы? (Добавить из класса 2 человек. И тогда в каждой группе станет по 4 человека.)

– В первый раз мы при уравнивании вычитали, а во втором случае мы увеличивали количество человек в группе.

– Это вам подсказка для выполнения домашнего задания.

СЛАЙД №14.

J Попробуйте найти второй способ решения задачи, которую вы получили для пробного действия .(Задача про нашу экскурсию в Парк птиц.) Условие этой задачи остается у вас на карточке. Запишите этот способ в тетрадь.

J Дома несколько раз проговорите алгоритм решения задач по сумме и разности.

ð № 9 (б), стр. 9.

– Спасибо за работу на уроке и желание добиться успеха!

Список литературы:

1.Кубышева М.А., Селькина Л.В. Сценарии уроков к учебнику математика для начальной школы по программе «Учусь учиться». – М., Ювента, 2008.

2. Мельникова Е.Л., Кузнецова И.В. Я открываю знания. – М., Баласс, 2011.

3.Петерсон Л.Г. Методические рекомендации для учителей. Математика, 3 класс. – М., Ювента, 2009.

4. Петерсон Л.Г. Построй свою математику. Блок-тетрадь эталонов для 3 класса. – М., Ювента, 2007.

5. Петерсон Л.Г. Реализация деятельностного метода обучения на уроках по разным учебным предметам. – М., УМЦ Школа 2000, 2010.

18

Открыта ещё одна группа на курс “Математика 3 класс”

Это зависит от того, чем и как занимался ребёнок до 4 класса. Здесь могут быть варианты:

1 вариант. Ребёнок  занимался дополнительно математикой в 1, 2 и 3 классах, готовился и участвовал в олимпиадах, но в 4 классе решили заниматься по программе А. В. Грецкой. В этом случае с большой долей уверенности можем сказать, что ему хватит нашего курса “Математика 4 класс”, чтобы получить достойный  уровень для поступления и затем учёбы в 5 классе физ-мат лицея. Но в каждом случае надо подходить индивидуально, некоторым детям психологически легче писать вступительную работу, если они потренировались и знают, что у них получается. А другие совершенно спокойно идут на экзамен, даже представления не имея, какие задания там будут.

2 вариант. Ребёнок занимался математикой дополнительно и будет продолжать эти занятия в течение 4 класса. В этом случае, нужен ли наш курс по углублённой программе “Математика 4 класс” или достаточно курса “Подготовка к поступлению. Математика” для тренировки выполнения вступительной работы, решить могут только родители, зная уровень и содержание программы, по которой занимается ребёнок.

3 вариант. Ребёнок ничем не занимался ранее систематически, но успешен на уроках математики, хорошо пишет в школе олимпиаду “Кенгуру”, и родители принимают решение готовиться к поступлению. Тогда мы рекомендуем заниматься у нас на двух курсах – и “Математика 4 класс” , и “Подготовка к поступлению. Математика”. Программы этих курсов различны и дополняют друг друга. 

“Математика 4 класс “ – это программа углублённого изучения математики 4 класса А.В. Грецкой. Она включает в себя все базовые знания и навыки, которые необходимы для подготовки к поступлению и учёбе в 5 классах физико-математических лицеев и гимназий.

“Подготовка к поступлению в 5 классы. Математика” – этот курс направлен на разбор и многократное решений заданий, подобных тем, которые встречаются во вступительных работах в 5 классы лицеев и гимназий. Это тренировочные, репетиционные работы, выполняя которые, ученик познакомится с типами задач и примеров, научится правильно их оформлять и важно – выполнять работу в условиях ограниченного времени. Не занимаясь параллельно на курсе “Математика 4 класс”, не обладая достаточным набором базовых знаний усиленной программы математики 4 класса, ребёнку будет очень сложно.

Таким образом, за 1 год способный ребёнок осваивает всю углублённую программу математики начальной школы и многократно решает задачи, подобные тем, что встречались во вступительных работах. При занятиях на каждом из курсов 1 раз в неделю, выполняя домашнее задание, ребёнок получает 4 занятия математикой в неделю. Нагрузка большая, но для будущего ученика физ-мат лицея – посильная. В нашем Центре такие дети занимаются, к концу 4 класса они осваивают и программу А.В.Грецкой, и успешно пишут тренировочные работы.  

Для подготовки ко второму этапу вступительных испытаний у нас также есть два курса:

– курс “Учимся писать сочинения” даёт фундаментальный подход к изучению литературы на основе классических произведений – от эпоса и мифов через народную сказку к повествованию. Этот курс научит анализировать литературное произведение, писать изложение, сочинение и отзыв. Наряду с изучением литературы много времени уделяется лингвистическим задачам, которые встречаются во вступительных работах в классические гимназии.

– курс “Подготовка к поступлению в 5 классы. Русский язык”  поможет ученику повторить всю орфографию и пунктуацию программы начальной школы, научит определять тему и идею литературного произведения и писать краткое сочинение по предложенному тексту, излагая свои мысли последовательно и обоснованно. Конечно, это нужно всем, но желающим поступать в лицеи и гимназии – просто необходимо, т. к. задание на понимание предложенного текста, ответы на вопросы по тексту и изложение, либо сочинение есть во вступительных работах всех этих школ.   

 

Задания после оценивания для 3–5 классов

Загрузите или распечатайте этот урок

Урок для учащихся третьего, четвертого и пятого классов

Линда Дейси и Джейн Бэмфорд Линч . Хотите знать, как вы можете разработать эффективные задачи после оценивания для ваших студентов? Этот урок предлагает план из четырех шагов, включая 3–5 примеров заданий и соответствующие аутентичные ответы учащихся. Урок адаптирован из Математики для Все: Инструкция по дифференциации, 3–5 классы, Линды Дейси и Джейн Бэмфорд Линч. Посетите www.mathsolutions.com , чтобы узнать больше.

Этап 1I. Разработайте задание, которое позволит получить широкий спектр ответов

Открытые задания позволяют учащимся самостоятельно контролировать некоторые уровни сложности. В приведенном ниже примерном задании учащиеся могут ограничить свое рассмотрение лишь несколькими фигурами или сосредоточиться исключительно на двумерных фигурах. Точно так же учащиеся могут использовать рисунки, схемы или диаграммы для передачи своих идей или они могут больше полагаться на прозу.

Образец 3–5 Задание

Что вы знаете о формах? Пишите и рисуйте, чтобы поделиться своими идеями.

 

Шаг II. Обсудите с учащимися ожидания от задания

Всем классом составьте список, которым учащиеся будут руководствоваться в работе над заданием.

Список образцов 3–5

• Сосредоточьтесь на формах.
• Используйте слова и рисунки, чтобы объяснить, что вы знаете.
• Использовать словарь геометрии.
• Организуйте свои идеи.
• Дайте несколько образцов.
• Подумайте о реальных связях.

 

Шаг III. Предложите учащимся ответить на задание

После краткого обсуждения ожиданий от задания учащиеся обычно готовы приступить к выполнению задания. Некоторые учащиеся могут подумать минуту или около того, прежде чем начать записывать свои идеи, но большинство начинают сразу же. Ниже приведены примеры, в том числе подлинные студенческие работы, того, как учащиеся отреагировали на указанное выше задание.

Некоторые учащиеся использовали шаблоны фигур, в то время как другие предпочитали рисовать от руки. Большинство учеников начинали с того, что рисовали фигуру на бумаге, а затем писали над ней или под ней несколько слов. Несколько студентов начали с того, что написали идею или название фигуры, которую затем проиллюстрировали.

Образец ответа 1: двумерные фигуры

Ответ ученицы третьего класса Лизы был сосредоточен на двухмерных формах. Она классифицировала фигуры по количеству сторон и дала правильные названия трех-, четырех-, пяти-, шести- и восьмигранным фигурам. Хотя она не назвала фигуры, которые нарисовала в своей категории четырехугольников, она включила в нее трапецию, квадрат и параллелограмм. Она привела один пример треугольника, пятиугольника и шестиугольника.

Ответ третьеклассницы Лизы

Четвертоклассница Тай использовала ссылки на вогнутые формы и многоугольники, а также провела связи между двухмерными и трехмерными фигурами. Он также ввел пирамиды, прямые углы и термин параллель. Он был взволнован, когда работал. Он записал одну идею, а затем его глаза загорелись, когда он подумал о другой. Поскольку эти идеи не обязательно были связаны между собой, он часто записывал мысль, а затем обводил ее кольцом, чтобы отделить ее от других своих записей.

Ответ четвероклассника Тая

 

Ответ Рафаэля был особенно интересен. Рафаэль был сильным визуалом. Он часто делал диаграммы, чтобы обобщить события в рассказе, и его язык часто отражал его визуальные предпочтения. Как раз в то утро учительница слушал, как другой ученик объяснял Рафаэлю, почему они должны сегодня днем ​​играть в футбол, а не кататься на велосипеде. Выслушав доводы другого ученика, Рафаэль ответил: «Хорошо, я понимаю, что вы имеете в виду». Наряду с иллюстрацией и обозначением многих геометрических форм и понятий, Рафаэль рисовал инструменты, которые он ассоциировал с геометрией. Обратите внимание на два его изображения, которые соединяют метрические и английские единицы измерения, а также геодоску, розу ветров и транспортир.

Ответ пятиклассника Рафаэля

 

Шаг IV. Анализ ответов учащихся и планирование следующих шагов

Узнайте, что каждый учащийся решил включить; возможно, это то, что он знает лучше всего, или то, что она считает наиболее важным, или то, что он находит наиболее интересным. Также отметьте, для каких концепций

учащиеся не представили доказательства или для которых доказательства являются неполными или неточными. Поделитесь своими выводами с другими учителями. Посмотрите на сходства и различия между уровнями обучения. Ниже приведены наблюдения и планы, сделанные учителями после просмотра ответов на типовое задание.

Примеры отзывов и планов учителей

Учителя были поражены различиями между классами. Учительница третьего класса была удивлена ​​тем, насколько более сложными были ответы учеников старших классов. Он отметил, что в ответе его третьеклассницы Лизы (см. Ответ

Образец 1) стороны внутри ее треугольника, пятиугольника и шестиугольника имели примерно одинаковую длину, а фигуры были нарисованы с основанием, параллельным нижней части страницы. Такие ориентации распространены; на самом деле, многие учащиеся не идентифицируют некоторые из этих фигур, когда их стороны не конгруэнтны или когда они не расположены в традиционном положении.

Учителя решили включить эту работу в портфолио учеников. В следующем году они хотели, чтобы у учителей студентов были эти артефакты, чтобы помочь им определить готовность к будущей работе по геометрии. Им также было интересно наблюдать за эволюцией работы студентов с течением времени. Возможно, они могли бы повторить задание позже в этом году, а в следующем году они могли бы использовать его в качестве предварительной и последующей оценки.

 

Опубликовано в информационном бюллетене Math Solutions Online, выпуск 32

---

 

Связанная публикация:
Математика для всех: дифференциация инструкций, классы 3–5
Линда Дейси и Джейн Бэмфорд Линч .B.3

$3,00

Карточки и гистограммы – Карточки с задачами по математике для 3-го класса – Печатные и цифровые – количество 3.MD.B.3

Добавить в мой список желаний

Категории: 3-й класс, Уроки цифровой математики, Математика, Покупка по классам, Покупка по линейке продуктов, Покупка по навыкам, Покупка по предметам, Предмет 1, Время, ➖ Математика 2-го класса Теги: 3rd, Действия, Гистограммы, Основные операции, Математика, Математические центры, Изображение, Карточки с задачами, Word Problems

• Описание
• Отзывы (0)

⭐️ Этот набор из 30 карточек с заданиями идеально подходит для учащихся 3-х классов, чтобы изучать и практиковать изображения и гистограммы. Этот ресурс включает печатные и цифровые карточки с заданиями (доступные через Google Slides и платформу Boom Learning). Аудио параметры для вопросов также включены. Эти карточки с заданиями для самостоятельной оценки предлагают различные типы вопросов, направленные на построение масштабированного графического изображения и масштабированной гистограммы для представления набора данных с несколькими категориями. Решайте одно- и двухэтапные задачи «насколько больше» и «на сколько меньше», используя информацию, представленную в масштабированных гистограммах. В соответствии с 3.MD.B.3 каждая из карточек требует числового ответа или выбора из нескольких вариантов.

 

⭐️ Цифровые карточки с заданиями Boom Cards™ совместимы с Google Classroom™ и платформой Boom Learning℠ для эффективного дистанционного обучения. Версия для печати идеально подходит для личного и личного использования. Карты для печати можно заламинировать для длительного использования.

 

⭐️ Этот ресурс соответствует 3. MD.B.3. Если вы не используете Common Core, этот пакет по-прежнему идеально подходит для тренировки изображений и гистограмм. Он соответствует многим государственным стандартам, включая TEKS и VA SOL.

 

⭐️ Карточки с заданиями идеально подходят для следующих занятий: центры, охота за мусором, дженга, общеклассная практика, билеты на выход и многое другое!

 

**Чтобы использовать Boom Cards, вам необходимо  быть подключенным к Интернету. Boom Cards можно играть в современных браузерах (Chrome, Safari, Firefox и Edge). Приложения доступны для Android, iPad, iPhone и Kindle Fires. В целях безопасности и конфиденциальности взрослые должны иметь учетную запись Boom Learning, чтобы использовать и назначать карты Boom. Вы сможете назначать карты Boom, которые вы покупаете, с помощью «Fast Pins» (игра обеспечивает мгновенную обратную связь для самооцениваемых карт Boom). Быстрая игра — это всегда свободная дорога для студентов, чтобы они могли взаимодействовать с колодами Boom Cards.

Для дополнительных вариантов заданий вам понадобится премиум-аккаунт. Если вы новичок в Boom Learning, вам будет предложена бесплатная пробная версия нашего премиум-аккаунта.  Подробнее читайте здесь: http://bit.ly/BoomTrial.

 

*** Хотя Boom Cards включены в этот ресурс, версии Google Slides и Print можно использовать в учетной записи Google или в автономном режиме соответственно.

 

Форматы и характеристики:

✏️  Boom Learning  – Этот цифровой интерактивный ресурс использует технологию Boom Card.

• Учащиеся выбирают свои ответы, а вопроса для самостоятельной оценки позволяют в режиме реального времени получать отзывы о правильности своих ответов.
• Учащиеся могут создавать учетные записи, и их ответы передаются учителю с помощью простой функции отчетности .
• Все слайды содержат аудиозапись , которая позволяет учащемуся прослушать отрывок, читаемый вслух.