Разное

Задачи по математике 2 в одно действие класс: Тренажер по математике “Задачи в одно и два действия” 2 класс скачать

Содержание

Краткая запись задачи и её схематический чертёж

- Охо-хо-хо-хо… И куда этот Плюс подевался? Я один с этим заданием не справлюсь. Ну, царица! Каждый раз какое-нибудь новенькое задание подкинет.

- Добрый день, Минус! Прости, я задержался – на природу загляделся. Уж такой сегодня день красивый! Я набрал целую охапку листьев – здесь листья клёна и каштана.

- А что ты с ними делать собираешься?

- Как что – составлю осенний букет. А еще, они помогут нам разобраться в том задании, которое дала нам царица-Математика – научиться выполнять краткую запись задачи и её схематический чертёж.

- Давай скорее начнём, а то ты и так опоздал.

- Ну что же, приступим. Вот смотри – у меня несколько листьев клёна. 5 из них я поставлю в вазу и осталось ещё 4 листа.

- Да-да, я знаю. Если задать вопрос, то получится вот такая задача:

Плюс собрал несколько листьев клёна.

5 из них он поставил в вазу. После этого осталось ещё 4 листа. Сколько всего листьев собрал Плюс?

Ну, и что дальше?

- А дальше составляем краткую запись.

- И как мы это сделаем?

- Выбираем главные, опорные слова. Что происходило в задаче?

- Сначала ты собрал листья, а потом 5 из них поставил в вазу. И у тебя остались 4 листа.

- Вот именно – собрал, поставил, осталось. Вот они, опорные слова. Запишем их:

- Да, но, сколько собрал, в задаче неизвестно. В ней сказано, что собрал несколько листьев.

- Ну, раз неизвестно, мы поставили вопросительный знак. Ведь именно это и надо узнать в задаче. Её вопрос звучит так: «Сколько всего листьев собрал Плюс?» А, чтобы не писать полностью слово листьев, мы поставим только первую букву л. Ведь, если вместо слова ставится одна или, допустим, две буквы, то говорят, что слово сократили, и подсказывает нам это маленькая точка.

Ну, вот. У нас получилась краткая запись задачи. Глядя на неё мы можем вспомнить всё условие задачи.

- Но ведь нам еще надо сделать и схематический чертёж!

- Ну что же. В этом нам помогут отрезки. Мы ведь их уже отлично рисовать научились. Итак, вот первый отрезок.

Он показывает, сколько листьев я поставил в вазу. Второй отрезок мы начнем рисовать от той точки, которая является концом первого отрезка.

Этот отрезок показывает, сколько листьев у меня осталось. То есть, нам известна та часть листьев, которую я поставил в вазу и та часть листьев, которая осталась. А вот, если объединить все листья вместе, то получится уже не часть, а все листья, то есть целое.

Когда мы объединяем, то есть собираем что-то вместе, находим целое, то, конечно, используем действие

сложения. И без меня, Плюса, здесь не обойтись!

Записываю ответ задачи: Плюс собрал 9 листьев клёна.

- Так, отлично, с этой задачей мы справились. Но ведь есть и ещё одна задача.

- Что еще за задача?

- А вот она: На лесной поляне росло 7 мухоморов. Несколько мухоморов съел лось. После этого на поляне осталось 2 мухомора. Сколько мухоморов съел лось?

Теперь моя очередь составлять краткое условие и схематический чертёж. Итак, выделяю числа и опорные слова. Что в задаче происходило? Росло 7 мухоморов. Несколько мухоморов съел лось. Раз несколько, значит, мы не знаем сколько. Дальше написано, что осталось 2 мухомора.

Ну вот, с кратким условием я справился. Так ведь, Плюсик?

- Да, молодец!

- Теперь надо выполнить схематический чертёж.

Росло 7 мухоморов. Рисуем отрезок:

Лось съел, это неизвестно. Пока рисовать не буду, осталось 2 мухомора. Как мне их нарисовать? Откуда начинать? С конца первого отрезка?

Не-е-ет. Ведь семь – это все мухоморы, то есть целое, а два – это часть этих семи. Поэтому откладываем отрезок, обозначающий эти два мухомора от начала первого отрезка. Мы как бы отделим оставшиеся мухоморы от съеденных. А вот тот отрезок, который является второй частью целого отрезка и будет съеденными мухоморами.

Как известно, часть чего-то целого находим действием вычитания. Так что, теперь моя очередь встать в действие:

Ответ: 5 мухоморов съел лось.

- Это у тебя отлично получилось, Минус. Лихо ты справился с такой трудной задачей.

- И ничего трудного тут нет. Чтобы решить любую задачу, надо сначала представить себе все, что в ней происходит. Затем составить

краткое условие, выделив опорные слова, которые нам подскажут, что именно происходит в задаче. А потом нарисовать схематический чертёж. Только надо очень внимательно разобраться, что в задаче целое, а что части.

- Если мы находим наибольшее число, то есть целое, из известных частей, то отрезки рисуем так: сначала первый отрезок, затем второй. При этом, конец первого отрезка одновременно является началом второго отрезка. И такую задачу решаем действием сложения. То есть используем знак плюс.

- А если в задаче надо узнать часть чего либо, то сначала рисуем отрезок, обозначающий самое большое число, то есть целое. Затем от начала первого отрезка рисуем второй отрезок, обозначающий меньшее известное число. Мы как бы разрезаем больший отрезок на части, одна из которых известна, а вторую нужно узнать. И, конечно, если надо узнать часть, то задачу решаем действием

вычитания. То есть используем знак минус.

- Ну что, пойдем к царице сдавать задание?

- Ну да! Побежали! Урра!

ГДЗ по математике 2 класс учебник Моро, Волкова 1 часть

  • Тип: ГДЗ, Решебник.
  • Автор: Моро М. И., Волкова С. И., Бельтюкова Г. В.
  • Год: 2020.
  • Серия: Школа России (ФГОС).
  • Издательство: Просвещение.

Решебник – страница 41Готовое домашнее задание

Номер 1.

Сравни выражения, поставив знак «больше» (>), «меньше» (<) или «равно» (=).

Ответ:

5 – 2 < 1 + 4    5 + 3 = 3 + 5    6 – 2 > 6 – 3

Номер 2.

В буфете было 12 чашек. Из этих чашек на стол поставили сначала 4 чашки, а потом еще 3 чашки. Сколько чашек осталось в буфете? Рассмотри разные способы решения этой задачи и объясни, что узнавали каждым действием.

Ответ:

Задача 1: 12 – 4 – 3 = 5 (ч.) 12 – 4 = 8 (ч.) – осталось сначала. 8 – 3 = 5 (ч.) – осталось.
Задача 2: 12 – (4 + 3) = 5 (ч.) 4 + 3 = 7 (ч.) – достали из буфета. 12 – 7 = 5 (ч.) – осталось. Ответ: 5 чашек.
Обе задачи решались в одно действие, но в первом случае от общего количества отнимались оба вычитаемых сразу, а во втором в скобках нашли сумму чашек, которые поставили на стол и от всех чашек отняли найденное значение.

Номер 3.

Составь по краткой записи задачу и реши ее.

Ответ:

Задача 1: Бабушка собрала 18 кг огурцов. Несколько килограммов она продала на базаре и у неё осталось 8 кг. Сколько килограммов огурцов продала бабушка? 18 – 8 = 10 (кг) – огурцов продала бабушка. Ответ: 10 кг.
Задача 2: В магазин привезли ткань. Когда продали 7 м, осталось 9 м ткани. Сколько метров ткани привезли в магазин? 7 + 9 = 16 (м) – ткани, привезли. Ответ: 16 метров.

Номер 4.

Ответ:

13 – 7 + 6 = 12     80 + 0 + 3 = 83     18 – 9 = 9 12 – 6 + 7 = 13     70 – 0 + 9 = 79     17 – 9 = 8 11 – 5 + 8 = 14     0 + 90 + 5 = 95     17 – 8 = 9

Номер 5.

Начерти такие ломаные и найди длину каждой из них в миллиметрах.

Ответ:

Длина ломаной зелёного цвета: 25 мм + 10 мм + 25 мм + 10 мм = 70 мм.

Ответ: длина зелёной ломаной линии 70 мм.
Длина ломаной розового цвета: 16 мм + 11 мм + 12 мм + 7 мм = 46 мм. Ответ: длина розовой ломаной линии 46 мм.

Задание внизу страницы

Составь по задаче выражение и реши ее. Утром надоили от коровы 6 л молока, а вечером – на 2 л больше. Сколько литров молока надоили утром и вечером вместе?

Ответ:

(6 + 2) + 6 = 14 (л) Ответ: всего надоили 14 литров молока.

Задание на полях страницы

Найди лишнее выражение

Ответ:

12 − 7 = 5     18 − 8 = 5 14 − 9 = 5     15 − 9 = 6 20 − 15 = 5   11 − 6 = 5
Лишнее выражение: 15 − 9 = 6

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро4567891011121314151617181920212223242526272829303132333435363738394041
42		4344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495

2 часть

456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111

Как научить детей решать задачи по математике: советы именитых педагогов и простых мам

Научить детей решать задачи по математике — дело учителя, но и родители не должны оставаться в стороне, если их чадо «тормозит» в этом вопросе. Одним учебником математики сыт не будешь. Ведь если научить ребенка самостоятельно решать задачи в 1-3 классах, дальше он будет щелкать как семечки не только задачи по математике, но и по физике, химии, геометрии и др. И самое главное — этот навык пригодится ребенку в жизни!

vogazeta.ru

В статье Как научить ребенка математике мы подробно писали, из каких 4 частей состоит любая задача и что нужно сделать в первую очередь, чтобы ребенок понял, чего от него хотят и как ответить на вопрос задачи. Уяснив алгоритм решения задач, ребенок сможет самостоятельно решить практически любую задачу, даже несмотря на то, что они все кажутся такими разными. 

Основные типы задач по математике: краткий конспект

Небольшой ликбез, т.к. далеко не все родители учились в педагогических ВУЗах и владеют методикой преподавания. Пробежимся по теории, чтобы понимать, кто, кому и чего «должен». Зная ключевые моменты, вам будет проще помочь ребенку в решении задач, которые вызывают у него сложности, вы сможете определить, где пробелы в знаниях и что нужно «подтянуть» в каждом конкретном случае.

iqsha.ru

Рассмотрим самые распространенные виды задач в начальных классах.

1. Простые задачи на сложение и вычитание

К этой группе относятся несколько задач, но для всех есть общие рекомендации:

  • Решаются в одно действие.
  • Иногда удобно составить уравнение.
  • На их примере ребенок должен научится выполнять краткую запись. 
  • Если краткого условия недостаточно, нарисовать рисунок. Если не помог рисунок, показываем на конкретных предметах и производим действия с ними.
  • Четко усвоить, что «+» — это прибавить, увеличить, а «-» — уменьшить, отнять, вычесть.
  • Хорошо запомнить компоненты арифметических действий:

слагаемое + слагаемое = сумма
уменьшаемое — вычитаемое = разность

  • Понять разницу между словами «стало» и «осталось». Четко понимать, что значит «на … меньше», «на … больше».
  • Важно понять и запомнить: чтобы узнать, НА СКОЛЬКО одно число больше или меньше другого, нужно из большего числа вычесть меньшее.
  • Важно понять и запомнить: чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

 

  • Важно понять и запомнить: чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.

 

  • Важно понять и запомнить: чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.

Задачи с косвенным вопросом

Это самые коварные задачи из этой группы. Внимательно прочитайте условие — и поймете почему.

На стоянке у первого подъезда 7 машин. Это на 2 машины больше, чем на стоянке у второго подъезда. сколько машин на стоянке у второго подъезда.

2. Составные задачи на сложение и вычитание

Эти задачи решаются двумя и более действиями.

Есть несколько способов решения:

  • по действиям с пояснениями;
  • по действиям с вопросами;
  • выражением.

В решении таких задач главное:

  • найти главное и сделать краткую запись;
  • разложить эту задачу на несколько простых и составить план решения;
  • помнить главное: по двум данным находим третье.

3. Задачи на понимание смысла действий умножения и деления
  • Важно запомнить названия компонентов действий и понять их смысл:

1-й множитель х 2-й множитель = произведение
делимое : делитель =частное

  • Ребенок должен понимать, что 1-й множитель показывает, КАКОЕ число повторяется а 2-й множитель показывает — СКОЛЬКО РАЗ оно повторяется.

Это очень важно для правильной записи в задачах, иначе получится бессмыслица.

Советы о том, как научить ребенка осознанно относиться к умножению и делению, вы найдете в нашей статье Как научить детей быстро считать: математика до школы. Если возникли проблемы с решением задач на умножение — сдайте чуть-чуть назад, закрепите осознание этого арифметического действия.

4. Простые задачи на умножение и деление

  • Очень важно понять и запомнить разницу «в «, «на».

«Во сколько раз» или «на сколько»?  Предлог «на» — это сложение или вычитание, а «в» — умножение или деление.

  • Важно понять и запомнить: чтобы узнать, во сколько раз одно число больше или меньше другого, нужно большее число разделить на меньшее.

 5. Составные задачи на все 4 арифметические действия

6. Задачи на цену, количество, стоимость

7. Задачи на движение

Это отдельная обширная тема, вернемся к ней позже.

Типичные ошибки в решении задач

Ошибка №1. Ребенок невнимательно прочитал условие задачи.

Часто бывает так, что ошибки возникают от невнимательности.  Так часто бывает в задачах с косвенным вопросом. Ребенок смотрит на цифры, вроде все логично, но… не верно.

Например: «У Маши 8 конфет, это на 2 меньше, чем у Кати. Сколько конфет у Кати».

Ребенок видит «на 2 меньше» и делает «логичный» вывод, что надо отнять. Отнять можно от бОльшего числа, т.е. сразу напрашивается решение 8-2=6. И ответ: 6 конфет у Кати. А ответ-то не тот! Если внимательно почитать условие, то станет понятно, что у Кати конфет больше чем у Маши. И вовсе тут не отнимать надо.

Как исправить ошибку. Сразу разберитесь с условием, поможет краткая запись.

Ошибка №2. Ребенок допустил ошибку в решении.

Когда в задаче несколько неизвестных, решение затрудняется, требуется выполнить не одно действие, а придумать целую цепочку рассуждений. 

Как исправить ошибку. Для начала определим, каких данных нам не хватает. Решаем по действиям. Находим нужные числа (помним правило: по двум неизвестным находим третье), подставляем их и отвечаем на вопрос задачи.

Ошибка №3. Неправильная запись ответа.

Часто ребенок пишет не то пояснение.

Как исправить ошибку.  Нужно внимательно прочитать вопрос задачи. Уяснить раз и навсегда, что ответ начинается с числа, а дальше пишем, что требовалось найти (переписываем формулировку вопроса задачи). 

Творческий подход в решении задач

www.craftykidsathome.com

  • Учите ребенка рассуждать.
  • Придумывайте задачи с лишними или недостающими данными.

Пусть ребенок сам вычеркнет лишнее, те данные, которые не влияют на решение.

  • Дайте условие, а ребенок пусть сам придумает ответ.
  • Пусть ребенок сам составит обратную задачу.
  • Придумать несколько задач на одно решение.
  • Придумать, как решить задачу другим способом и объяснить его.

На школу надейся, а сам не плошай

Заглянем в педагогику и «расшифруем» мысли умных и заслуженных, исходя из сегодняшних реалий.

В далеком 1867 году К. Ушинский сказал: «У хороших преподавателей дело выходит так, что арифметическая задача есть вместе занимательный рассказ, урок сельского хозяйства или домашней экономии, или историческая или статистическая тема и упражнение в языке».

«Расшифровка» следующая.

  • Ученика нужно поставить в такие условия, чтобы он оказался в эпицентре событий, т.е., решая задачу, видел ее применение в жизни.

Не всегда задачи в школьном учебнике «вдохновляют» современных школьников. Многим не ясно условие по одной простой причине: ребенок не имеет представления о том, что говорится. Например, задача про надои и бидоны с молоком, а городской «деть» и корову-то в глаза не видел, не то, что тонны молока в бидонах. Или в задаче использованы такие значения, которые в жизни нереальны — это затрудняет восприятие, т.к. ребенок все воспринимает буквально.

Задача родителей — помочь ребенку ПОНЯТЬ условие. Любым способом: хоть рисуй, хоть танцуй.

  • К решению задач нужно подходить творчески.

Интерес заставляет ребенка быть активным, а активность в свою очередь усиливает внимание.

В каждодневной жизни нам то и дело приходится решать задачи. Привлекайте ребенка, задавайте вопросы, просите совета. Например, тема ремонта. Вычислить метраж комнаты; просчитать нужное количество краски, зная расход на метр квадратный; купить линолеум, зная длину и ширину комнаты; просчитать, какой метраж выгоднее, если есть напольное покрытие шириной 2, 5 метра и 3 метра, чтобы меньше остатков было и по цене вышло выгоднее. Купить ткань на пошив постельного белья, зная размеры матраса. Примеров масса! И это работает гораздо эффективнее, чем «бездушная» задача в учебнике, которая совершенно не привязана к жизни и не вызывает эмоциональный отклик.

  • При решении жизненных задач у ребенка помимо всего прочего развивается наблюдательность, речь, появляется рабочее настроение, развиваются творческие способности и самостоятельность.

Через некоторое время вы заметите, что ребенок различными способами комбинирует информацию, с легкостью составляет задачи сам, находя идеи в окружающем мире, а не высасывая из пальца.

  • Когда ребенка просят составить собственную задачу, нужно следить и за содержанием, и за решением. Задача должна быть осмысленной и целесообразной.

Например, нельзя допускать таких «ляпов», как «Я съел 13 желтых груш и 20 зеленых яблок. Сколько фруктов я съел?» Задача теряет смысл, если она оторвана от жизни.

  • От задачи надо идти к примеру, а не наоборот.

Дети мыслят не абстрактно, а конкретными образами. Пример 12-6 ни о чем не говорит, а вот ситуация, когда из 12 человек 6 уже купили билеты на футбольный матч — это совсем другое дело. Тут ребенок не задумываясь ответит, что оставшиеся шестеро очень рискуют, нужно поторопиться, иначе билетов может не хватить и придется сидеть у телевизора, вместо того, чтобы активно скандировать на трибунах в поддержку любимой команды.

Лебединцев в своей книге «Введение в современную методику математики» писал: «То влияние, которое может оказывать обучение счислению и вообще математике на умственное развитие детей, находится в прямой зависимости от материала, которым мы пользуемся при обучении; если в учебном материале будут преобладать отвлеченные упражнения в действиях и хитроумные задачи с условиями, лишенными внутренней связи и, по существу, далекими от жизни, то, упражняя учащихся на таком материале, мы, может быть, и выработаем у них формальные навыки в вычислениях и, пожалуй, изощрим их ум для разгадывания разных ребусов и головоломок, но отнюдь не сделаем их более способными к правильному мышлению в жизни или какой-либо области знания…».

Французский педагог Жан Мосе тоже был уверен, что «заставлять ребенка начинать с отвлеченного правила и затем предлагать ему задачи — это значит идти наперекор ходу развития человеческого ума…».

Практические советы по решению задач от реальных мам

fb.ru

Что нам Ушинский, Лебединцев и Мосе, спросим у тех, кто «из нашей песочницы». Как они помогают своим детям решать задачи по математике, что «работает», какие приемы на практике доказали свою эффективность и помогли повысить успеваемость.

Татьяна, мама учеников 4 кл. и 6 кл. 

«Я знаю, что особую сложность у детей вызывают задачи на скорость, поэтому начала готовить своих мальчишек к этому уже с 1 класса. Когда ехали к бабушке в Пинск, говорили о скорости, засекали время, считали сколько мы проехали км, смотрели на знаки и вычисляли сколько нам останется времени, если мы будем ехать с такой же скоростью и сколько, если папа будет ехать с другой. В общем, я очень удивлялась, когда мои пацаны на скорость задачи решали как орехи. Я поняла, что в моем детстве не хватало практического представления того, о чем говорилось в задачах».

Ольга, мама ученика 1 кл. и ученицы 4 кл.

«С задачами старшая плохо дружит))  Почти всегда приходит за помощью. Стараюсь выработать алгоритм решения, но частенько упираюсь в «лень подумать». Если совсем «затык», рисуем схемы. На дополнительные задачи совсем нет времени, а сама по своей воле заниматься ими дочь точно не будет)) Иногда встречаются задачи с некорректно поставленным вопросом, тут приходится помогать с формулировкой ответа.

Младшего усадить за математику очень сложно. В те редкие моменты, когда дело доходит до задач, он их решает в уме и выдает ответ устно).»

Вероника, мама учеников 2 кл. и 4 кл.

«Младший задачи решает без проблем, но ненавидит чертить схемы к ним и писать пояснения. Старший ходит на факультатив по математике, дома домашку сам делает». 

Катерина, мама ученика 2 кл. и ученицы 5 кл.

«Сын отлично справляется сам. Он такие схемы рисует, что я иногда в шоке)). Если за помощью обращается дочь, стараюсь упростить условие задачи до понятных образов, а потом она сама догадывается, как сложную модель решить».

Татьяна, мама ученицы 5 кл.

«Чаще всего прибегаем к рисованию. Прямо вот как по условию… садимся и рисуем, как есть. Так сказать, наглядность помогает. Велосипедист выехал… значит рисуем человечка на велосипеде, город из которого он выехал и тд)))) Если катер плывет по течению, рисуем море, волны)))))) С пояснениями никогда исправлений со стороны учителя не было, да и у нас, собственно, тоже вопросов не возникало. Смотри по условию, что спрашивают — и пиши ответы возле каждого действия».

Наталья, мама ученика 5 кл.

«Приходилось объяснять дроби на примере сломанных карандашей, порванных в клочья бумажек. В гостях в тот момент был друг-проектировщик, он именно так решил наглядно пояснить сыну задачу. Я обычно прибегаю к помощи рисования. В задачах на скорость/время/расстояние рисовали целые истории: кто куда и на чем поехал, кого встретил по дороге и в какой момент. Порой решение задач превращалось в мультфильм, одного черновика обычно мало. Несколько раз решали задачи всей семьей: мама отдельно от папы, потом сравнивали результаты и каждый объяснял ребенку свой «самый рациональный и простой» способ. Как правило, у мужчин своя логика)), мое решение обычно отличается от папиного».

Уважаемые читатели! Делитесь в комментариях своими находками и сложностями в решении задач по математике с детьми. будем разы разобраться вместе и помочь советами и полезными статьями на интересующие вас темы. 

Создать несколько действий в Struts2

Спросил

Изменено 9 лет, 3 месяца назад

Просмотрено 9000 раз

Как создать несколько действий в Struts2 в одном классе действий? Пожалуйста, приведите пример? Я нашел следующий код при поиске в Интернете, но он выдает ошибки ИЛИ Нужно ли мне писать отдельный класс действий для каждого запроса?

  • стойки2

2

Помимо того, что сказал @Quaternion, действия S2 сами по себе являются классом Java, и я не уверен, о чем вы спрашиваете (несколько действий в Struts2 в одном классе действий).

У нас есть несколько способов использования одного класса действий S2 вот некоторые из них

Сопоставьте один класс действий с другим псевдонимом, например.

 <имя действия="А">
  Меню
  /Logon.jsp

<имя действия="B">
  Меню
  /Logon.jsp

Но я полагаю, что вы хотите сопоставить другой запрос действия с другим методом действия. S2 предоставляет способ определить любое количество методов, и мы можем указать S2 вызывать какой метод для какого класса действия из пользовательского интерфейса.

, например, у нас есть класс UserAction, который отвечает за обработку взаимодействия с пользователем, например

  1. Логин
  2. Выход
  3. Регистрация

для этого нам не нужно создавать разные классы действий, но мы можем создать один класс действий, скажем, UserAction, и можем определить в нем разные методы и можем настроить S2 для вызова разных методов, таких как

 <имя действия = "Вход в систему" метод = "вход в систему">
  Меню
  /Logon. jsp


  Меню
  /Logon.jsp


  Меню
  /Logon.jsp

Надеюсь, это поможет развеять ваши сомнения.

В приведенном выше примере использования MyActionClass сопоставлен с двумя псевдонимами A и B, и вы можете сопоставить любой номер.

Я получил ваш вопрос именно о том, что вы хотите написать несколько перенаправлений в одном действии на основе выбранного действия, такого как добавление/редактирование/удаление кода в одном месте. Вы должны искать DispatchAction для вашего требования.

Ниже приведены несколько примеров, на которые вы можете обратить внимание. Все они показывают, как реализовать DispatchAction.

Ссылка1 Ссылка2 Ссылка3

2

Другой метод:

Вот класс действия с 3 действиями (выполнение, действие1, действие2)

 открытый класс MyAction extends ActionSupport{
   публичная строка выполнить () {
     вернуть УСПЕХ;
   }
   общедоступная строка action1 () {
     вернуть УСПЕХ;
   }
   общедоступная строка action2(){
     вернуть УСПЕХ;
   }
}

Вот конфигурация:

 
  <результат>showMe. jsp
  showMe.jsp

Действие “выполнить” будет вызвано по умолчанию. Чтобы вызвать действие «действие1» или «действие2», вы должны указать в запросе параметр с именем «метод: действие1» или «метод: действие2».

  • Вызов действия по умолчанию (выполнить): /path_to_action/myAction.action
  • Вызов action1: /path_to_action/myAction.action?method:action1
  • Вызов action2: /path_to_action/myAction.action?method:action2

Вы можете изменить метод по умолчанию:

 <имя действия = "мое действие" метод = "действие1">
  <результат>showMe.jsp
  showMe.jsp

Итак, когда вы вызовете /path_to_action/myAction.action, действие1 будет выполнено.

Твой ответ

Зарегистрируйтесь или войдите

Зарегистрироваться через Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Каков порядок операций? (Видео и практика)

СтенограммаЧасто задаваемые вопросыИнформационный бюллетеньПрактические рабочие листыКалькулятор

«Пожалуйста, извините, моя дорогая тетя Салли».

Теперь я знаю, о чем вы думаете: «Что на самом деле означает эта фраза?» На самом деле довольно много, потому что это высказывание дает ключ к запоминанию важного математического понятия: порядка операций.

Порядок операций — одно из наиболее важных математических понятий, которое вы изучите, поскольку оно диктует, как мы вычисляем задачи. Он дает нам шаблон, чтобы все решали математические задачи одинаково.

Начнем с простого вопроса. Что такое операция?

Операция — это математическое действие. Сложение, вычитание, умножение, деление и вычисление корня — все это примеры математических операций. Давайте посмотрим на эту задачу:

\(7\times 4-6=?\)

 

Выглядит просто, правда? Что ж, это было бы не так просто, если бы мы не понимали порядок, в котором выполняются математические операции. Если бы у нас не было правил, определяющих, какие вычисления мы должны произвести в первую очередь, мы бы пришли к другим ответам.

Следует ли начать с вычитания 4 минус 6, а затем умножения на 7?

Нет. Порядок операций говорит нам, как решить математическую задачу. И это возвращает нас к тете Салли.

Каков порядок операций?

Операции имеют определенный порядок, и это то, что «Пожалуйста, извините, моя дорогая тетя Салли» помогает нам понять. Это аббревиатура, которая говорит нам, в каком порядке мы должны решать математическую задачу.

«Пожалуйста» означает « Скобки », поэтому мы сначала решаем все, что внутри скобок.

Затем «Извините», что означает « Экспоненты ». Мы решаем это после того, как решим все в скобках.

Умножение , то есть «Мое», и это происходит слева направо.

А потом деление , то есть «Дорогой», что тоже бывает слева направо.

А потом у нас есть сложение и вычитание , что тоже происходит слева направо, а это «тетя» и «Салли».

Порядок операций Примеры

Итак, теперь, когда мы знаем порядок операций, давайте применим его к нашей задаче и решим ее.

\(7\times 4-6=?\)

 

У нас нет круглых скобок и у нас нет показателей степени, но у нас есть умножение, так что мы делаем это до того, как будем делать сложение или вычитание. Давайте продолжим и умножим \(7\х4\). Это дает нам 28.

\(28-6\)

 

Теперь мы вычитаем 6, что дает нам 22.

\(28-6=22\)

 

Теперь давайте рассмотрим другую задачу.

\(7+7\умножить на 3\)

 

Без операций эту задачу можно вычислить как \(7+7=14\умножить на 3=42\).

И это было бы неправильно!

Помните, вы умножаете, прежде чем складывать. Следовательно, уравнение должно выглядеть так:

9{2})\)
 
\(=6\умножить на 9\)
 
\(=54\)

 

Видите? Решение уравнения в правильном порядке дает правильный ответ.

Давайте попробуем еще одну задачу. Этот немного сложнее, но он прекрасно иллюстрирует порядок операций.

\(5\умножить на 10-(8\умножить на 6\)\(-15)+4\умножить на 20\дел 4\)

 

Запомните порядок. Что мы делаем в первую очередь? Цифры в скобках. Итак, \(8\times 6=48\), затем мы вычитаем 15 и получаем 33. Вот как теперь выглядит задача:

\(5\умножить на 10-33+4\умножить на 20\дел 4\)

 

Итак, наш следующий шаг – умножение и деление, поэтому давайте решим все наши задачи на умножение и деление, а затем посмотрим, что у нас получилось оставил.

\(50-33+80\дел 4\)
 
\(50-33+20\)

 

Теперь закончим со сложением и вычитанием, вот что мы имеем:

\(

2 50-33+20\)


 
\(=50-13\)
 
\(=37\)

 

И наш ответ 37!

Есть исключение. Если уравнение имеет только одно выражение, вам не нужно соблюдать порядок операций.

Вот несколько примеров одиночных выражений.

\(10+10\): Ну, других операций нет, так что просто сложите их и получите 20. То же самое с вычитанием, умножением и делением. Все это единичные выражения.

Итак, ребята, это наше видео о порядке действий. Я надеюсь, что это было полезно!

Увидимся в следующий раз!

Часто задаваемые вопросы

Q

Каков порядок операций в математике?

A

Порядок операций — это порядок, в котором вы работаете с математическими выражениями: скобки, показатели степени, умножение, деление, сложение, вычитание. Все выражения должны быть упрощены в этом порядке. Единственным исключением является то, что умножение и деление могут выполняться одновременно, вам разрешено делить до умножения, то же самое касается сложения и вычитания. Однако умножение и деление ДОЛЖНЫ предшествовать сложению и вычитанию. Аббревиатура PEMDAS часто используется для запоминания этого порядка. 2-4+2\).

Скобки: их нет, поэтому пропустите этот шаг.

Показатель степени: \(36-4+2\)

Умножение/Деление: Нет, поэтому пропустите этот шаг.

Сложение/вычитание: \(34\)

Q

Выполняют ли калькуляторы порядок операций?

A

Нет, большинство калькуляторов не следуют порядку операций, поэтому будьте очень осторожны при подстановке чисел! Убедитесь, что вы следуете порядку операций, даже если это означает вставлять числа в порядке, отличном от того, как они выглядят на вашей странице.

Q

Какая математическая операция идет первой?

A

Скобки — это первая операция, которую нужно решить в уравнении. Если круглых скобок нет, то перемещайтесь по порядку операций (PEMDAS), пока не найдете операцию, которая у вас есть, и начните с нее.

Q

Каковы основные операции?

A

Четыре основных операции: сложение (+), вычитание (-), умножение (×) и деление (÷). 93+3×6\)
Далее идут показатели степени.
\(19+7(8)+3×6\)
Затем умножьте слева направо.
\(19+56+3×6\)
\(19+56+18\)
Наконец, складываем слева направо.
\(75+18\)
\(93\)

Скрыть ответ

Вопрос №3:

 
\(11+3-7×2+1×4÷2\)

26

19

4

2

Показать Ответ

Ответ:

Правильный ответ: 2. Порядок операций можно запомнить по аббревиатуре PEMDAS, которая означает: круглые скобки, деление, умножение. слева направо, а сложение и вычитание слева направо. 92+3×11-1\)
Затем возведите в степень.
\(64+3×11-1\)
Далее умножаем.
\(64+33-1\)
Наконец, сложите и вычтите слева направо.
\(97-1\)
\(96\)

Скрыть ответ

Рабочие листы

Используйте наши бесплатные печатные рабочие листы для дополнительной практики!

Рабочий лист порядка действий

Порядок действий (Ключ ответа)

 

Вернуться к видеороликам по основам арифметики

259675275605159288

Полное руководство по словесным задачам SAT по математике

Около 25% вашего общего раздела SAT по математике будут составлять текстовые задачи, а это означает, что вам придется создавать свои собственные изображения и уравнения для решения ваших ответов. Хотя фактические математические темы могут различаться, текстовые задачи SAT имеют несколько общих черт, и мы здесь, чтобы помочь вам решить их наилучшим образом.

Этот пост будет вашим полным руководством по задачам SAT Math. Мы расскажем, как переводить текстовые задачи в уравнения и диаграммы, различные типы математических задач, которые вы увидите на тесте, и как решить ваши текстовые задачи в день экзамена.

 

Характерное изображение: Антонио Литтерио/Викимедиа

 

Что такое SAT Math Word Problems?

Задача со словами — это любая математическая задача, основанная в основном или полностью на письменном описании. Вам не будет предоставлено уравнение, диаграмма или график для задачи со словами, и вместо этого вы должны будете использовать свои навыки чтения, чтобы перевести слова вопроса в выполнимую математическую задачу. Как только вы это сделаете, вы сможете решить эту проблему.

Вам будут давать текстовые задачи в разделе SAT по математике по разным причинам. Во-первых, словесных задач проверяют ваше понимание прочитанного и вашу способность визуализировать информацию.

Во-вторых, эти типы вопросов позволяют разработчикам тестов задавать вопросы, которые невозможно задать, используя только диаграмму или уравнение. Например, если в математическом вопросе вас просят вместить как можно больше маленьких объектов в один больший, будет сложно продемонстрировать и задать это, используя только диаграмму.

 

Преобразование словесных математических задач в уравнения или рисунки

Чтобы преобразовать словесные задачи SAT в действенные математические уравнения, которые вы можете решить, вам необходимо понимать и знать, как использовать некоторые ключевые математические термины. Всякий раз, когда вы видите эти слова, вы можете перевести их в правильное математическое действие.

Например, слово “сумма” означает значение, когда два или более элементов складываются вместе. Итак, если вам нужно найти сумму a и b , вам нужно будет составить уравнение следующим образом: a+b.

Также обратите внимание, что ко многим математическим действиям присоединено более одного термина, которые могут использоваться взаимозаменяемо.

Вот таблица со всеми ключевыми терминами и символами, которые вы должны знать для SAT Math Word Word:

Ключевые термины Математическое действие
Сумма, увеличенная на, добавленная к, более чем, всего +
Разница, уменьшенная на менее чем, вычтенная из —
Продукт, раз, __ раз больше, __ раз больше (число, например, «в три раза больше»)* или х
Делится на, per, __ столько, __ столько (доля, например, «одна треть») / или ÷
Равно, эквивалентно =
Меньше <
Больше >
Меньше или равно ≤
Больше или равно ≥

 

Теперь давайте посмотрим на эти математические термины в действии, используя несколько официальных примеров:

 

Мы можем решить эту задачу, переведя полученную информацию в алгебру. Мы знаем индивидуальную цену каждого салата и напитка, а также общий доход от продажи 209салаты и напитки вместе взятые. Итак, давайте запишем это в алгебраической форме.

 

Будем говорить, что количество проданных салатов = S , а количество проданных напитков = D . Задача говорит нам, что было продано 209 салатов и напитков , что можно представить следующим образом: количество S и D были проданы и принесли общий доход в размере 836 долларов 50 центов. Мы не знаем точного количества S и D , но мы делаем знаем, сколько стоит каждая единица. Таким образом, мы можем написать это уравнение:

6,50 S + 2 D = 836,5

Теперь у нас есть два уравнения с одинаковыми переменными ( D и 90). Поскольку мы хотим узнать, сколько салатов было продано, нам нужно найти D , чтобы мы могли использовать эту информацию для решения S . Первое уравнение говорит нам, чему равны S и D , если их сложить вместе, но мы можем изменить это уравнение, чтобы сказать нам, чему равны только D с точки зрения S :

 

S +

9 +

9 = 209

 

Теперь просто вычтите S с обеих сторон, чтобы получить то, что равно D :

 

D = 209- S

Наконец, подключите это выражение для D в другое уравнение, а затем решайте для S :

6.50 S + 2 (209 – S ) = 8368) = 8368) = 8368).

6.50 S + 418 − 2 S = 836.5

6.50 S − 2 S = 418.5

4.5 S = 418.5

S = 93

 

The correct выбор ответа (В) 93.

 

 

В этой текстовой задаче нам предлагается найти одно возможное решение (запрашивается «возможная сумма»), поэтому мы сразу знаем, что будет несколько правильных ответов.

 

Вятт может очистить от шелухи не менее 12 дюжин початков кукурузы и не более 18 дюжин початков кукурузы в час. Если он очищает 72 дюжины со скоростью 12 дюжин в час, это равно 72/12 = 6 часов. Таким образом, вы можете написать 6 в качестве окончательного ответа.

 

Если Вятт очищает 72 дюжины со скоростью 18 дюжин в час (наивысшая возможная скорость), получается 72/18 = 4 часа. Вы можете написать 4 в качестве окончательного ответа.

 

Поскольку минимальное время, затрачиваемое Уайеттом, составляет 4 часа, а максимальное — 6 часов, любое число от 4 до 6 будет правильным.

 

Хотя сейчас самые сложные словесные задачи SAT могут показаться вам латынью, практика и изучение скоро помогут вам перевести их в рабочие вопросы.

 

Типичные задачи SAT Word

Задания SAT Word можно сгруппировать в три основные категории:

  • Задания Word, для которых нужно просто составить уравнение
  • Задачи Word, которые необходимо решить на определенное значение
  • Задачи Word, для которых необходимо определить значение значения или переменной

Ниже мы рассмотрим каждый тип мировых проблем и приведем примеры.

 

Тип задачи 1: Составление уравнения

Это довольно необычный тип задачи SAT, но вы, как правило, встретите ее хотя бы один раз в математическом разделе. Вы также, скорее всего, увидите его первым в разделе.

Для этих задач вы должны использовать предоставленную вам информацию, а затем составить уравнение. Нет необходимости искать отсутствующую переменную — это все, что вам нужно сделать.

Почти всегда вы будете видеть этот тип вопросов в первых четырех вопросах раздела SAT Math, что означает, что Совет колледжа считает эти вопросы легкими. Это связано с тем, что вам нужно предоставить только настройку, а не выполнение.

Чтобы решить эту задачу, нам нужно знать ситуации как Арманда, так и Тайрона, поэтому давайте рассмотрим их отдельно:

Арманд: Арманд отправил m текстовых сообщений каждый час в течение 5 часов, поэтому мы можем запишите это как 5m — количество отправляемых им сообщений в час, умноженное на общее количество часов, в течение которых он отправлял текстовые сообщения.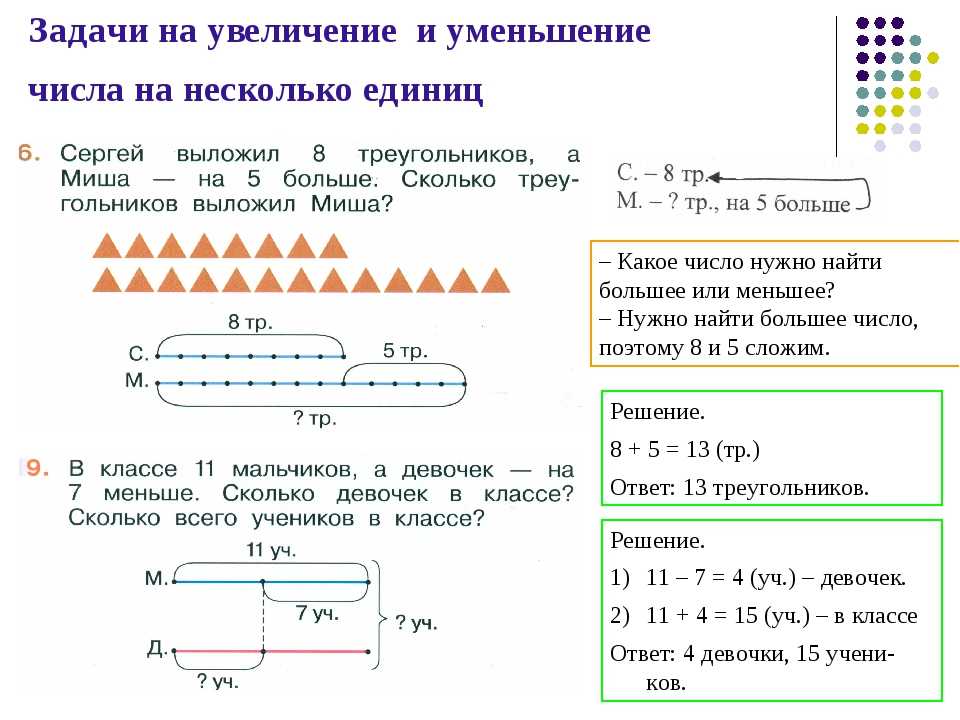

Тайрон: Тайрон отправлял p текстовых сообщений каждый час в течение 4 часов, поэтому мы можем записать это как 4 p — количество сообщений, которые он отправлял в час, умноженное на общее количество часов, в течение которых он отправлял текстовые сообщения.

Теперь мы знаем, что ситуацию Армана можно алгебраически записать как 5m , а ситуацию Тайрона можно записать как 4 p . Поскольку нас просят ввести выражение, представляющее общее количество сообщений, отправленных Арманом и Тайроном, , мы должны сложить два выражения:

5M + 4 P

Правильный ответ – выбор (C) 5M + 4 P

WORD WORD WORD. большинство задач SAT по математике попадают в эту категорию.

Для этих вопросов вы должны настроить уравнение и решить для определенной части информации.

Большинство (хотя и не все) текстовых задач этого типа будут сценариев или историй, охватывающих все виды тем SAT Math, , таких как средние значения, уравнения с одной переменной и отношения. Вы почти всегда должны иметь четкое представление о рассматриваемой математической теме, чтобы решить текстовую задачу по этой теме.

Давайте попробуем подумать об этой проблеме с точки зрения x . Если деревья типа А произвели на 20% больше груш, чем деревья типа Б, мы можем записать это в виде выражения:

x + 0,2 x = 1,2 x = количество груш, произведенных деревьями типа A

В этом уравнении x – это количество груш, произведенных деревьями типа B. Если мы добавим 20% от x (0,2 x ) к x , мы получим количество груш, произведенных деревьями типа А.

Задача говорит нам, что деревья типа А произвели в общей сложности 144 груши. Поскольку мы знаем, что 1,2 x равно количеству груш, произведенных типом A, мы можем написать следующее уравнение:

1,2 x = 144

Теперь все, что нам нужно сделать, это разделить обе части на 1,2, чтобы найти количество груш, произведенных деревьями типа B:

Правильный вариант ответа: (B) 120.

Вы также можете получить задачу по геометрии в виде словесной задачи, , которая может быть поставлена ​​или не поставлена ​​вместе со сценарием. Вопросы по геометрии обычно представляются в виде текстовых задач, потому что составители теста считают, что задачу было бы слишком легко решить, если бы вам дали диаграмму, или потому что задачу было бы невозможно показать с помощью диаграммы. (Обратите внимание, что 9Геометрия 0057 составляет очень небольшой процент от SAT Math. )

Это случай проблемы, которую трудно показать визуально, , поскольку x не заданное значение степени, а скорее значение больше , чем 55; таким образом, это должно быть представлено как словесная проблема.

Поскольку мы знаем, что x должно быть целым числом в градусах больше 55, давайте присвоим ему значение. В этом случае назовем x 56°. (Почему 56? Есть и другие значения x может быть, но 56 гарантированно сработает, так как это наименьшее целое число больше 55. По сути, это беспроигрышный вариант!) — необходимо измерить следующее:

56*2 = 112

Сделаем грубый набросок (не в масштабе) того, что мы знаем на данный момент:

треугольник, , поэтому мы можем найти значение y Говоря об этом:

Y = 180 – 112 – 56

Y = 12

Одним из возможных значений для Y является 12. (другие возможные значения – 3, 6 и 888. )

 

Word Задача типа 3: Объяснение значения переменной или значения

Этот тип задачи появится хотя бы один раз. Он просит вас определить часть уравнения, предоставленного словом задача — обычно значение определенной переменной или числа.

 

 

Сначала этот вопрос может показаться сложным, но на самом деле он довольно прост.

 

Мы знаем, что t P — это количество телефонов, которые Кэти оставила , чтобы починить, а d — это количество дней, которые она проработала в неделю. Если она проработала 0 дней (т. е. если мы подставим 0 в уравнение), вот что мы получим:

 

P = 108 − 23(0)

 

P = 108

 

Это означает, что, не работая ни в какие дни недели, Кэти нужно отремонтировать 108 телефонов. Таким образом, правильный вариант ответа: (B) Кэти начинает каждую неделю со 108 телефонами, которые нужно починить.

 

 

Чтобы помочь справиться со всеми различными задачами SAT, давайте рассмотрим имеющиеся в нашем распоряжении математические стратегии и советы.

 

Готовы не только читать о SAT? Тогда вам понравится бесплатная пятидневная пробная версия нашей программы SAT Complete Prep . Наша программа SAT, разработанная и написанная экспертами PrepScholar SAT , адаптируется к вашему уровню навыков по более чем 40 поднавыкам, чтобы вы могли сосредоточить свое обучение на том, что принесет вам наибольший прирост баллов.

Нажмите на кнопку ниже, чтобы попробовать!

 

Математические стратегии SAT для решения текстовых задач

Несмотря на то, что в разделе SAT Math вы встретите текстовые задачи по различным математическим темам, все же есть несколько методов, которые вы можете применить для решения текстовых задач в целом.

 

#1: Нарисуйте

Независимо от того, является ли ваша проблема геометрической или алгебраической, иногда быстрый набросок сцены может помочь вам понять, с чем именно вы работаете. Например, давайте посмотрим, как картинка может помочь вам решить словесную задачу о круге (в частности, о пицце):

Если у вас часто возникают проблемы с визуализацией подобных задач, нарисуйте ее. Мы знаем, что имеем дело с кругом, поскольку наше внимание сосредоточено на пицце. Мы также знаем, что пицца весит 3 фунта.

Поскольку нам нужно вычислить вес каждого кусочка в унциях, давайте сначала переведем общий вес нашей пиццы из фунтов в унции. Нам дано преобразование (1 фунт = 16 унций), поэтому все, что нам нужно сделать, это умножить нашу 3-фунтовую пиццу на 16, чтобы получить ответ:

3 * 16 = 48 унций (для всей пиццы)

Теперь нарисуем картинку. Сначала пицца делится пополам (не в масштабе):

Теперь у нас есть два куска одинакового размера. Продолжим рисовать. Затем проблема говорит, что мы делим каждую половину на три равные части (опять же, не в масштабе):

Таким образом, мы получаем шесть одинаковых частей. Поскольку мы знаем, что общий вес пиццы составляет 48 унций, все, что нам нужно сделать, это разделить на 6 (количество кусков), чтобы получить вес (в унциях) одного куска пиццы:

48/6 = 8 унций. за штуку

Правильный выбор ответа: (C) 8.

Что касается задач по геометрии, помните, что вы можете получить текстовую задачу по геометрии, написанную как текстовая задача. В этом случае сделайте свой собственный рисунок сцены. Даже грубый набросок поможет вам визуализировать математическую задачу и упорядочить всю информацию.

 

#2: Запомните ключевые термины

Если вы не привыкли переводить английские слова и описания в математические уравнения, то поначалу вам может быть трудно понять текстовые задачи SAT. Посмотрите на диаграмму, которую мы дали вам выше, чтобы вы могли научиться переводить ключевые слова в их математические эквиваленты. Таким образом, вы можете точно понять, что проблема просит вас найти и как вы должны это найти.

В Интернете доступны бесплатные вопросы по математике SAT, поэтому запомните свои термины, а затем потренируйтесь на реалистичных текстовых задачах SAT, чтобы убедиться, что вы записали свои определения и сможете применить их к реальному тесту.

 

#3: Подчеркните и/или запишите важную информацию

Ключом к решению задачи со словами является объединение всех ключевых фрагментов данной информации и размещение их в нужных местах. Убедитесь, что вы записали все эти данные на диаграмме, которую вы нарисовали (если проблема требует диаграммы), чтобы все ваши движущиеся части были в порядке.

Один из лучших способов привести все части в порядок — это подчеркнуть ключевую информацию в задаче, , а затем записать ее самостоятельно, прежде чем составлять уравнение. Поэтому найдите время, чтобы выполнить этот шаг, прежде чем сосредоточиться на решении вопроса.

 

№ 4. Внимательно относитесь к тому, что спрашивают

Если вам приходится искать неправильную переменную или записывать значения в неправильных местах, это может раздражать. И все же это слишком легко сделать при работе с математическими задачами.

Убедитесь, что вы уделяете пристальное внимание именно тому, что вы должны решать, и именно какие части информации куда направляются. Вы ищете площадь или периметр? Значение x, 2x или y?

Всегда лучше перепроверить то, что вы должны найти до того, как вы начнете , чем через две минуты понять, что вам придется начинать решать проблему заново.

 

#5: Освежите в памяти любую конкретную математическую тему, которую вы чувствуете слабой В

Вы, вероятно, увидите как задачу на диаграмму/уравнение, так и задачку со словами почти по каждой теме SAT по математике в тесте. Вот почему существует так много разных типов текстовых задач и почему вам нужно знать все тонкости каждой темы SAT по математике, чтобы иметь возможность решить текстовую задачу по ней.

Например, если вы не знаете, как найти среднее значение по набору чисел, вы, конечно, не будете знать, как решить текстовую задачу, связанную со средними значениями!

Поймите, что решение текстовой задачи SAT по математике представляет собой двухэтапный процесс: требуется, чтобы вы оба понимали, как работают текстовые задачи и , чтобы понимать рассматриваемую математическую тему. Если у вас есть слабые места в математике, самое время освежить их, иначе текстовые задачи SAT могут оказаться сложнее, чем вы ожидали!

 

Все готово? Пойдем!

 

Проверьте свои знания математических словесных задач SAT

Наконец, пришло время проверить ваше слово «ноу-хау» против реальных задач по математике SAT:

Проблемы с словом

1. Нет калькулятор

2. Расчет OK 9000

.

3. Калькулятор OK

4. Калькулятор OK

0057 Ответы: C, B, A, 1160

 

Объяснение ответов

1. В этой задаче мы должны использовать информацию, которую нам дали, чтобы составить уравнение.

Мы знаем, что Кен потратил x долларов, а Пол потратил на 1 доллар больше, чем Кен. Следовательно, мы можем написать следующее уравнение для Пола:

x + 1

Кен и Пол поровну поделили счет. Это означает, что нам нужно найти общую сумму обоих их бутербродов, а затем разделить ее на 2. Так как бутерброд Кена стоил x долларов и стоимость Пола x + 1, вот как выглядит наше уравнение, если мы объединим два выражения:

x + x + 1

0 2 Теперь , мы можем разделить это выражение на 2, чтобы получить цену, которую заплатил каждый человек:

(2 x + 1) / 2

x + 0,5

Но мы еще не закончили. Мы знаем, что и Кен, и Пол также платили 20% чаевых за свои счета. В результате мы должны умножить общую стоимость одного счета на 0,2, а затем добавить эти чаевые к счету. Algebraically, this looks like this:

( x + 0.5) + 0.2( x + 0.5)

x + 0.5 + 0.2 x + 0.1

1.2 x + 0.6

Правильный вариант ответа: (C) 1,2 x + 0,6

 

2. Чтобы понять, о чем этот вопрос, вам необходимо ознакомиться со статистикой.

Поскольку Ник опросил случайную выборку своего класса первокурсников, мы можем сказать, что эта выборка будет точно отражать мнение (и, следовательно, те же проценты), что и весь класс первокурсников.

Из 90 опрошенных первокурсников 25,6% заявили, что хотят, чтобы Праздник Осени прошел в октябре. Все, что нам нужно сделать сейчас, это найти этот процент всего класса первокурсников (который состоит из 225 студентов) , чтобы определить, сколько всего первокурсников предпочли бы октябрьский фестиваль:

225 * 0,256 = 57,6

Поскольку вопрос касается «сколько студентов» — и поскольку у нас, очевидно, не может быть доли человека! — нам придется округлить это число до ближайшего доступного варианта ответа, что 60, или выбор ответа (B).

 

3. Это одна из тех задач, которая требует от вас определить значение в приведенном уравнении. Это может показаться запутанным, но не пугайтесь — на самом деле это не так сложно, как кажется!

Во-первых, мы знаем, что t представляет количество секунд, прошедших после запуска объекта вверх. Но что, если время еще не прошло? Это будет означать, что t = 0. Вот что произойдет с уравнением, если мы подставим 0 вместо t :

h (0) = -16(0)2 + 110(0) + 72

ч (0) = 0 + 0 + 72

ч (0) = 72

Как мы видим, еще до запуска объекта его высота составляет 72 фута. Это означает, что 72 должен представлять начальную высоту объекта в футах или вариант ответа (A).

 

4. У вас может возникнуть соблазн нарисовать диаграмму для этой задачи, поскольку речь идет о бассейне (прямоугольнике), но на самом деле быстрее просто посмотреть на приведенные числа и работать с ними.

Мы знаем, что бассейн в настоящее время вмещает 600 галлонов воды и что вода подавалась в него из шланга со скоростью 8 галлонов в минуту в течение 70 минут.

Чтобы найти количество воды в бассейне сейчас, мы должны сначала найти количество воды, добавленной в бассейн из шланга. Мы знаем, что каждую минуту в течение 70 минут добавлялось 8 галлонов, поэтому все, что нам нужно сделать, это умножить 8 на 70: ​​

8 * 70 = 560 галлонов

Это говорит нам о том, что в наш уже заполненный бассейн на 600 галлонов было добавлено 560 галлонов воды. Чтобы найти общее количество воды, мы просто сложим эти два числа вместе:

560 + 600 = 1160

Правильный ответ: 1160.

 

Основные выводы: понимание словесных задач SAT по математике

Словесные задачи составляют значительную часть раздела SAT по математике, , поэтому было бы неплохо понять, как они работают и как перевести слова на странице в правильное выражение или уравнение. Но это еще только полдела.

Хотя вы не будете знать, как решить текстовую задачу, если не знаете, что такое произведение или как нарисовать прямоугольный треугольник, вы также не будете знать, как решить текстовую задачу о пропорциях, если не знаете не знаю, как работают коэффициенты.

Поэтому не забудьте узнать не только о том, как подходить к математическим задачам в целом, но и о том, как сузить свое внимание к любым темам SAT Math, с которыми вам нужна помощь. Здесь вы можете найти ссылки на все наши руководства по SAT Math, которые помогут вам в учебе.

 

Что дальше?

Хотите освежить знания по темам SAT Math? Ознакомьтесь с нашими отдельными руководствами по математике, чтобы получить обзор каждой темы SAT Math. От полигонов и склонов до вероятностей и последовательностей — мы обеспечим вас!

Не хватает времени на секцию математики SAT? У нас есть ноу-хау, которые помогут вам выиграть время и увеличить свой счет.

Откладывали учебу на SAT? Узнайте, как преодолеть желание откладывать дела на потом и составить сбалансированный план подготовки.

Пытаетесь получить идеальный результат SAT? Взгляните на наше руководство по получению идеальных 800 баллов по математике SAT, написанное отличным бомбардиром.

 

Хотите улучшить свой результат SAT на 160 баллов?

Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к SAT. Мы гарантируем возврат ваших денег , если вы не улучшите свой результат SAT на 160 или более баллов.

Наша программа полностью онлайн, и она настраивает то, что вы изучаете, в соответствии с вашими сильными и слабыми сторонами. Если вам понравилось это руководство по математической стратегии, вам понравится и наша программа. Наряду с более подробными уроками вы получите тысячи практических задач, организованных по отдельным навыкам, чтобы вы могли учиться наиболее эффективно.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *