Разное

Задачи по математике 1 класс с решением и ответами: Логические задачи для 1 класса с ответами и решениями, развивающие задания на логику для детей 7-8 лет

Содержание

100 задач по математике с решениями и ответами. 1 класс (Оксана Рыдзе)

Купить офлайн

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

Пособие предназначено для учащихся общеобразовательных организаций. Оно направлено на поэтапное обучение первоклассников умению решать задачи. .Материал пособия представлен в определённой системе. Ребёнок учится слушать и читать текст, представлять его в заданном виде (“Читаем текст, отвечаем на вопрос, делаем рисунок”), работать со структурой задачи (“Составляем задачу”), находить способ решения и упорядочивать свои действия по поиску ответа (“Планируем решение”), записывать решение (“Записываем решение и ответ”). Предусмотрено решение по образцу и самостоятельно разных видов задач, традиционно изучаемых в первом классе (“Решаем самостоятельно”): на нахождение суммы и остатка, на сравнение и уравнивание, на сложение и вычитание, увеличение и уменьшение на несколько единиц, а также логических задач.

Задания, содержащиеся в пособии, способствуют пониманию цели чтения, формированию умения выделять сущностные отношения и зависимости в задаче, развитию логических и информационных умений. .Работа с пособием позволит ученику в дальнейшем самостоятельно работать с новыми видами задач, “открывать” и конструировать другие способы решения на основе изученных. .

Описание

Характеристики

Пособие предназначено для учащихся общеобразовательных организаций. Оно направлено на поэтапное обучение первоклассников умению решать задачи. .Материал пособия представлен в определённой системе. Ребёнок учится слушать и читать текст, представлять его в заданном виде (“Читаем текст, отвечаем на вопрос, делаем рисунок”), работать со структурой задачи (“Составляем задачу”), находить способ решения и упорядочивать свои действия по поиску ответа (“Планируем решение”), записывать решение (“Записываем решение и ответ”). Предусмотрено решение по образцу и самостоятельно разных видов задач, традиционно изучаемых в первом классе (“Решаем самостоятельно”): на нахождение суммы и остатка, на сравнение и уравнивание, на сложение и вычитание, увеличение и уменьшение на несколько единиц, а также логических задач.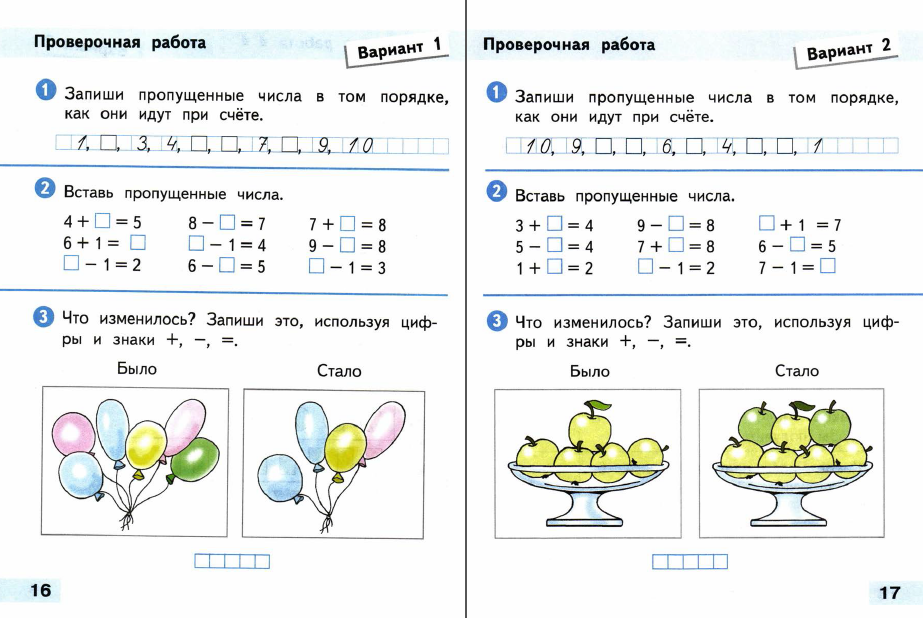

Задания, содержащиеся в пособии, способствуют пониманию цели чтения, формированию умения выделять сущностные отношения и зависимости в задаче, развитию логических и информационных умений. .Работа с пособием позволит ученику в дальнейшем самостоятельно работать с новыми видами задач, “открывать” и конструировать другие способы решения на основе изученных. .

Просвещение

На товар пока нет отзывов

Поделитесь своим мнением раньше всех

Как получить бонусы за отзыв о товаре

1

Сделайте заказ в интернет-магазине

2

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

3

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Книга «100 задач по математике с решениями и ответами. 1 класс» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Оксана Рыдзе «100 задач по математике с решениями и ответами. 1 класс» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

Задания математической олимпиады 1 класс

На данной страницы размещены олимпиадные задания с решением для 1 класса.

Олимпиада по математике прошла 14 января 2018 года

Cкачать задание в формате Pdf
Посмотреть ответы на все задания олимпиады

Вторая Олимпиада, 14.01.2018

 

Задача №1

Какие две снежинки надо поменять местами, чтобы они расположились в порядке убывания размера (от бОльшей к мЕньшей). Обведите их.

Задача №2

Проведите ровно две прямые линии так, чтобы они разрезали ёлку на 8 кусочков.

Задача №3

Разделите фигуру по сторонам клеток на две одинаковые по форме и размеру части.

Задача №4

На Новый Год Лиза получила подарков больше, чем Оксана, но меньше, чем Ника. Ника и Юля получили подарков поровну.  Каждая девочка что-то получила. Всего подарков у них 9. Сколько подарков получила каждая девочка?

Лиза ______ , Оксана ______, Ника _______ , Юля __________.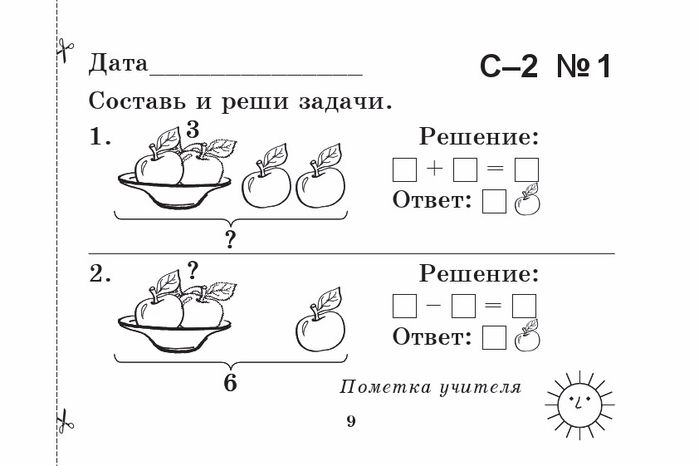

Задача №5

В мешке лежат синие, красные и зеленые фигуры разной формы: круги, квадраты, треугольники. Вероника достала из мешка три фигуры и разложила их на столе. Все фигуры оказались и разной формы, и разного цвета. Треугольник лежит между синей фигурой и квадратом. Какого цвета круг?

 

Задача №6

Мальчики построились на физкультуру.

  • Антон носит шорты в горошек;
  • Боря не с краю;
  • Вася не в очках;
  • Гога носит шорты в горошек;
  • Боря не самый высокий, но выше Гоги.

Подпишите имена мальчиков.

Задача №7

Ореховых конфет больше, чем шоколадных на столько же, на сколько шоколадных и мармеладных вместе больше, чем ореховых. Шоколадных конфет меньше, чем ореховых на 3 штуки. Сколько мармеладных конфет?

 

Задача №8

Соедини все точки 4 прямыми отрезками, не отрывая карандаша от бумаги.

Задания, ответы и разборы, списки победителей

Другие задания олимпиад по математике для 1-х классов

Осень 2017 — Математическая олимпиада, 1 класс

Зима 2018 — Математическая олимпиада, 1 класс
Осень 2018 — Математическая олимпиада, 1 класс
Зима 2019 — Математическая олимпиада, 1 класс
Осень 2019 — Математическая олимпиада, 1 класс
Зима 2020 — Математическая олимпиада, 1 класс

Задачи, ответы и разборы, списки победителей

26 февраля 2023 года завершился 2 тур XII олимпиады по математике
Очередная олимпиада проводится с 15 по 31 мая 2023 года
Для учеников 1-9 классов

Регистрация на олимпиаду по математике 2023

Наши курсы олимпиадной математики

для 2-7 классов

27 февраля – 15 марта

Интенсив по подготовке к конкурсу Кенгуру

27 февраля – 15 марта

2-7 класс

для 5-7 классов

Курс в записи

Курс олимпиадной математики для 5-7 классов

Идёт набор

для 3-4 классов

Курс в записи

Курс олимпиадной математики для 3-4 классов

Идёт набор

для 9 классов

Онлайн занятия

Олимпиадная математика 9 класс

Идёт набор

для 7-8 классов

Онлайн занятия

Олимпиадная математика 7-8 класс

Идёт набор

5-6 класс продолжающие

Онлайн занятия

Олимпиадная математика 5-6 класс продолжающие

Идёт набор

5-6 класс начинающие

Онлайн занятия

Олимпиадная математика 5-6 класс начинающие

Идёт набор

3-4 класс продолжающие

Онлайн занятия

Олимпиадная математика 3-4 класс продолжающие

Идёт набор

3-4 класс начинающие

Онлайн занятия

Олимпиадная математика 3-4 класс начинающие

Идёт набор

для 1 классов

Онлайн занятия

Олимпиадная математика 1 класс

Идёт набор

для 2 классов

Онлайн занятия

Олимпиадная математика 2 класс

Идёт набор

для 2 классов

Курс в записи

Курс олимпиадной математики для 2 классов

Идёт набор

для 1 классов

Курс в записи

Курс олимпиадной математики для 1 классов

Идёт набор

задач по истории.

Рабочие листы и учебные пособия по математике для первого класса.

Числа и операции (NCTM)

Понимать числа, способы представления чисел, отношения между числами и системы счисления.

Развивать чувство целых чисел, представлять и использовать их гибкими способами, включая связывание, составление и разложение чисел.

Соедините числовые слова и цифры с величинами, которые они представляют, используя различные физические модели и представления.

Понимать значения операций и их взаимосвязь.

Понимать различные значения сложения и вычитания целых чисел и связь между этими двумя операциями.

Понимание эффектов сложения и вычитания целых чисел.

Свободно считать и делать разумные оценки.

Разработать и использовать стратегии для вычисления целых чисел, уделяя особое внимание сложению и вычитанию.

Развивайте беглость с основными комбинациями чисел для сложения и вычитания.

Алгебра (NCTM)

Представление и анализ математических ситуаций и структур с использованием алгебраических символов.

Используйте конкретные, изобразительные и словесные представления, чтобы развить понимание изобретенных и общепринятых символических обозначений.

Используйте математические модели для представления и понимания количественных отношений.

Моделируйте ситуации, связанные со сложением и вычитанием целых чисел, используя предметы, изображения и символы.

Координаторы учебной программы 1 класса (NCTM)

Числа и операции и алгебра: развитие понимания сложения и вычитания и стратегии для основных фактов сложения и связанных фактов вычитания

Дети развивают стратегии сложения и вычитания целых чисел на основе их предыдущей работы с маленькими числами. Они используют различные модели, в том числе дискретные объекты, модели на основе длины (например, длины соединяющихся кубов) и числовые линии, для моделирования «часть-целое», «добавление», «отнятие» и «сравнение». ‘ ситуации, чтобы развить понимание значений сложения и вычитания и стратегии решения таких арифметических задач. Дети понимают связь между счетом и операциями сложения и вычитания (например, сложение двух — это то же самое, что «подсчет до двух»). Они используют свойства сложения (коммутативность и ассоциативность) для сложения целых чисел, а также создают и используют все более изощренные стратегии, основанные на этих свойствах (например, «составление десятков») для решения задач на сложение и вычитание, связанных с основными фактами. Сравнивая различные стратегии решения, дети связывают сложение и вычитание как обратные операции.

Связи с Фокусными точками 1-го класса (NCTM)

Число, операции и алгебра: Дети используют математические рассуждения, включая такие идеи, как коммутативность и ассоциативность, а также начальные идеи десятков и единиц, для решения двузначных задач на сложение и вычитание с помощью стратегии, которые они понимают и могут объяснить. Они решают как рутинные, так и нестандартные задачи.

Вопросы и решения по математике для 11 класса

The Smarter Balanced Assessment Consortium (SBAC) — это стандартизированный тест, который включает в себя различные вопросы, основанные на новых технологиях.

Некоторые из них: Множественный выбор – один правильный ответ, Множественный выбор – несколько правильных ответов, Сопоставление таблиц, Перетаскивание, Горячий текст, Заполнение таблицы, Графики, Уравнения / числа, Расширенный построенный ответ, Короткий ответ и многое другое. .

Эта страница содержит несколько примеров вопросов и ссылки на практические тесты по математике для 11 класса, которые помогут вам составить представление о вопросах, которые ваши учащиеся, скорее всего, увидят в тесте. После каждого примерного вопроса следует объяснение ответа. Объяснение включает в себя важные аспекты задачи, которые вам, возможно, потребуется рассмотреть для навыков, процессов и информации, которые должны знать ваши студенты.

Домен: 11 класс >> Число и количество – Система реальных чисел

Пример вопроса:

Умножьте 36/49 и 21/63. Какой тип числа получается в результате

  1. Числа нельзя умножать
  2. 57/112, рациональный
  3. 12/49, рациональный
  4. 12/49,иррациональный

Объяснение ответа: Напомним, что рациональное число — это любое число, которое может быть выражено как отношение или частное двух целых чисел (дробей). Иррациональные числа — это числа, которые нельзя представить в виде дроби. Оба числа дробные. Следовательно, они оба являются рациональными числами. Перемножьте их вместе и упростите ответ:
36/49,21/63=(4/7,9/7).3/9,7/7=12/49. Ответ – дробь. Таким образом, это рациональное число.

Стандарты: HSN.RN.B.3

Нажмите здесь, чтобы потренироваться: Число и количество – Реальная система счисления. Пример вопроса: На приведенном ниже графике показаны колебания одной из струн скрипки при игре на ней. Что верно в отношении масштаба оси Y графика?

  1. Каждая отметка на оси Y, вероятно, может быть равна одному футу.
  2. Каждая отметка на оси Y, вероятно, может быть равна одному сантиметру.
  3. Каждая отметка на оси Y, вероятно, может быть равна одному миллиметру.
  4. Каждая отметка на оси Y, вероятно, может быть равна одному дюйму.

Ответ Объяснение: На графике представлена ​​амплитуда колебаний скрипичной струны. Когда струна скрипки следует этому графику, струна растягивается в одном направлении, а затем в другом. Каждый раз, когда струна пересекает ось x, она находится в исходном положении. Это движение настолько мало, что человеческий глаз почти не замечает его. Поэтому блок должен быть очень маленьким. Наименьший выбор – миллиметр.

. Стандарты: HSN.RN.A.1. Вопрос:

Чему равно комплексное число 7+3i?

  1. -7+3i
  2. -7-3i
  3. 3i
  4. 7-3i

Объяснение ответа:

Стандарты: HSN.RN.A.1

Нажмите здесь, чтобы попрактиковаться: 11 класс. : Вычтите эти два вектора ⟨−12,−23⟩−⟨−8,−14⟩.

  1. ⟨−4,−9⟩
  2. (4,9)
  3. ⟨−9,−4⟩
  4. ⟨−20,−37⟩

Объяснение ответа:
В вопросе нам предлагается вычесть эти два вектора ⟨−12,−23⟩−⟨−8,−14⟩ . Если у нас есть два вектора, v→=(x 1 ,y 1 ) и w→=(x 2 ,y 2 ), то разность двух векторов равна v→−w→=⟨x 1 −x 2 , у 1 − у 2 ⟩ . В этом вопросе мы вычитаем ⟨−12,−23⟩−⟨−8,−14⟩ . Разница ⟨−12−(−8),−23−(−14)⟩=⟨−4,−9⟩

Стандарты: HSN.VM.B.4

Нажмите здесь, чтобы потренироваться: Число и количество – Векторные и матричные количества Вопросы для 11 класса Математика

Предмет: 11 класс >> Алгебра – Арифметика с многочленами и рациональными выражениями

. 3х-14

  • -3x 3 -4x 2 -3x+14
  • 3x 3 +4x 2 +3x
  • 3x 3 +4x 2 +3x-14

    • Объяснение ответа: При комбинировании полиномов объединяйте одинаковые члены, комбинируя коэффициенты.
    Вычесть (x 3 +2x 2 -x+7) из (4x 3 +6x 2 +2x-7)
    (4x 3 }+6x 2 +2x-901) – ( 3 +2x 2 -x+7)
    (4x 3 -x 3 ) +(6x 2 -2x 2 ) +(2x-(-x)) +(-7- 7)
    3x 3 +4x 2 +3x-14

    Стандарты: HSA. APR.A.1

    Щелкните здесь, чтобы попрактиковаться: Алгебра – арифметика с полиномами, вопросы по градации 1 и рациональные выражения

    Предмет: 11 класс >> Алгебра – Видение структуры в выражениях

    Пример вопроса: Чему равен коэффициент третьего члена выражения
    5x 3 y 4 +7x 7 8 18 8908 −6xy 2 −8xy?

    1. 6
    2. 7
    3. -8
    4. -6

    Объяснение ответа: Выражение 5x 3 y 4 +7x 2 y 3 −6xy 2 −8xy представляет собой полиномиальное выражение с четырьмя членами. Коэффициент члена – это число, стоящее перед членом. Если термин начинается с отрицательного, то коэффициент является отрицательным числом, независимо от того, есть ли у термина переменные. Третий член равен −6xy 2 , а число перед членом равно -6.

    Стандарты: HSA.SSE.A.1

    Нажмите здесь, чтобы попрактиковаться: Алгебра – Видение структуры в выражениях Вопросы для 11 класса Математика

    Домен: 11 класс >> Алгебра.

    Создание уравнений

    Пример вопроса: Мэдисон работает продавцом в компании, занимающейся перевозками. Каждый месяц она продает две машины на каждые 10 велосипедов и четыре мотоцикла на каждую машину. Если она совершает 40 продаж в месяц, а переменная x представляет количество автомобилей, которые она продает, какое уравнение вы можете использовать, чтобы найти, сколько автомобилей она продает?

    1. х+5х+4х=40
    2. х+5х+4х=20
    3. 2х+10х+8х=40
    4. 2х+10х+8х=20

    Объяснение ответа: Если мы используем переменную x для количества автомобилей, которые продает Мэдисон, и она продает две машины на каждые 10 велосипедов, то она продает в пять раз больше велосипедов, чем автомобилей. Таким образом, она продает 5x велосипедов. Тогда, если она продает четыре мотоцикла на каждую машину, количество проданных ею мотоциклов в 4 раза больше. В задаче говорится, что она продает 40 товаров в месяц, поэтому сложите автомобили, велосипеды и мотоциклы и сделайте эту сумму равной 40.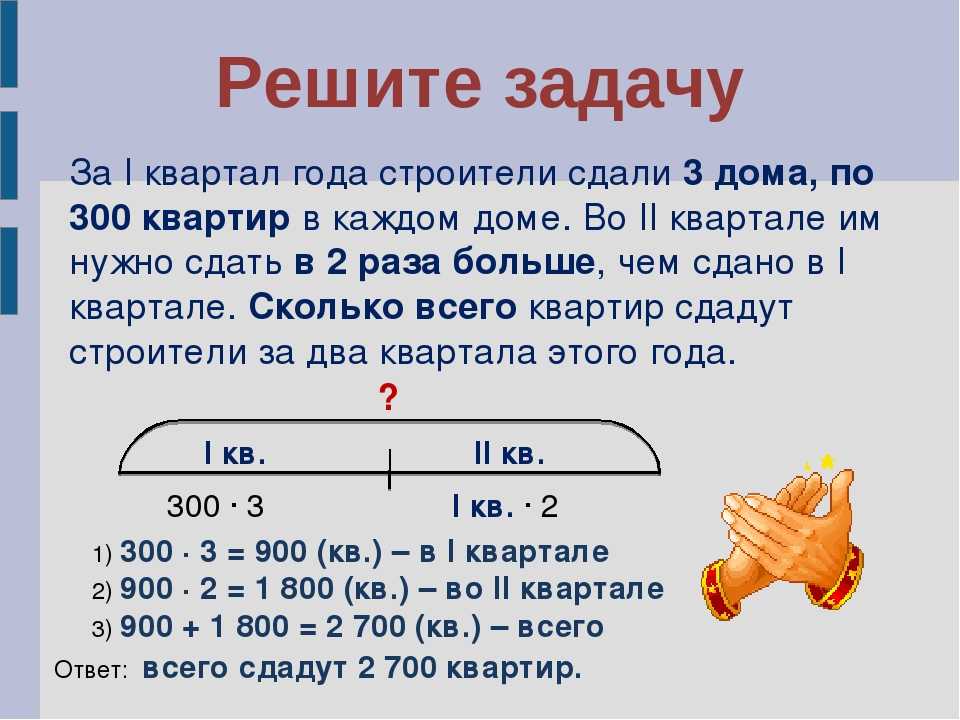

    Уравнение x+5x+4x=40.

    Стандарты: HSA.CED.A.1

    Нажмите здесь, чтобы попрактиковаться: Алгебра – составление уравнений. Вопрос: Как решить 6x+5=101?

    1. 19
    2. 13
    3. 17
    4. 16

    Объяснение ответа: Вопрос просит вас найти решение 6x+5=101. Начните с вычитания 5 из обеих частей уравнения. Это дает вам 6x=96. Затем разделите обе части на 6 и x=16.

    Стандарты: HSA.CED.A.4

    Нажмите здесь, чтобы попрактиковаться: Алгебра – рассуждения с помощью уравнений и неравенств. Вопрос: Функция f(x)=−1/8(x−7/2)2+3/2 — это траектория футбольного мяча в тренировочном матче. Его график показан ниже. Какая часть области этой функции фактически моделирует эту ситуацию?

    1. [7,0]
    2. [−1,7]
    3. (-∞, ∞)
    4. [0,7]

    Ответ Объяснение: Функция является полиномиальной функцией. Область определения всех полиномиальных функций в математическом контексте равна (−∞, ∞). Однако в контексте реального мира домен должен позволять функции подчиняться правилам реального мира. Мяч попадает в момент времени, равный 0 секундам, а мяч приземляется, согласно графику, в момент времени, равный 7 секундам. Следовательно, домен равен [0,7].

    . Стандарты: HSF.IF.B.5. Чем график f(x) = x + 7 отличается от графика g(x) = x + 12?

    1. Если f(x) сдвинуть вверх на 5 единиц, получится g(x)
    2. g(x) получается сдвигом f(x) вниз на 5 единиц
    3. Если g(x) сдвинуть вверх на 5 единиц, f(x) будет получено
    4. f(x) получается сдвигом g(x) вверх на 5 единиц

    Ответ Объяснение: Добавленное к функции значение вызывает вертикальное смещение графика. Поскольку 12 на 5 единиц больше, чем 7, график g(x) получается путем сдвига f(x) на 5 единиц вверх.

    Стандарты: HSF.BF.B.3

    Нажмите здесь, чтобы попрактиковаться: Функции — построение функций Вопросы для 11 класса по математике

    Предмет: 11 класс >> Функции — линейные, квадратичные и экспоненциальные модели

    Пример вопроса: График какой функции изображен ниже?

    1. f(x)=5(0,5) x
    2. f(x)=5(0,4) х
    3. f(x)=4(0,5) х
    4. f(x)=5(1,5) x

    Ответ Объяснение: График показывает, что функция является функцией экспоненциального роста. Формула экспоненциальной функции: f(x)=ab x , где a — точка пересечения с осью y, а b — коэффициент роста. Если экспоненциальная функция является функцией роста, то b>1. Если экспоненциальная функция является функцией затухания, то 0 х.

    Стандарты: HSF.LE.A.2

    Щелкните здесь, чтобы попрактиковаться: Функции — линейные, квадратичные и экспоненциальные модели.

    Пример вопроса: Если cosσ=−1, каково значение sinσ ?

    1. не определено
    2. 1
    3. 0
    4. -1

    Объяснение ответа: Правило :

    В таблице ниже приведены точные значения триггерных функций для особых углов.

    Угол, косинус которого равен -1, равен 180 градусам. Синус 180 градусов равен 0.

    . Стандарты: HSF.TF.C.8. PQRS переводится, как показано на рисунке ниже. Как переводится параллелограмм?

    Ответ Объяснение: На рисунке показано, что перевод осуществляется вправо и вниз. Судя по рисунку, расстояние, на которое параллелограмм переместится вправо, равно длине стороны PQ. Кроме того, судя по рисунку, расстояние, на которое параллелограмм перемещается вниз, составляет примерно половину длины стороны QR.

    Стандарты: HSG.CO.A.4

    Нажмите здесь, чтобы попрактиковаться: Геометрия – вопросы на соответствие для 11 класса Математика

    Предмет: 11 класс >> Геометрия – подобие, прямоугольные треугольники и тригонометрия

    Пример вопроса: Выполнение расширение в точке C с центром в начале координат с масштабным коэффициентом, равным 1/2. Какова координата полученной точки изображения C’?

    1. (2 , -3/2)
    2. (-3/2, 2)
    3. (8 , -6)
    4. (-6 , 8)

    Ответ Объяснение: Когда расширение выполняется относительно начала координат, координаты точки изображения являются произведением коэффициента масштабирования и координат исходной точки. ½*4 = 2. ½* -3 = -3/2.

    Стандарты: HSG.SRT.A.1

    Нажмите здесь, чтобы попрактиковаться: Геометрия – подобие, прямоугольные треугольники и тригонометрия0002 Пример вопроса: Касательная к окружности проведена из точки вне окружности. Радиус проводится от центра окружности до точки касания прямой. Какой угол образует радиус с касательной?

    1. 0 или
    2. 90 или
    3. 180 или
    4. 270 или

    Ответ Объяснение: Радиус окружности, проведенной к точке касания касательной, перпендикулярен касательной.

    Стандарты: HSG.C.A.2

    Нажмите здесь, чтобы попрактиковаться: Геометрия – круги Вопросы для 11 класса по математике

    Предмет: 11 класс >> Геометрия – выражение геометрических свойств с помощью уравнений

    2 : 9005 Вопрос Написав уравнение y=x 2 +6x+7, Анжелика использовала следующие шаги. Если она сделала какие-либо ошибки, объясните их и напишите правильное уравнение.
    у=х 2 +6х+7
    у-7=х 2 +6х
    y−7−9=x 2 +6x+9
    y−16=(x+3) 2
    y=(x+3) 2 +16

    Ответ Пояснение: Поставить уравнение в стандартной форме, мы должны завершить квадрат, чтобы получить квадрат бинома, который необходим для стандартной формы. Чтобы завершить квадрат, мы берем половину коэффициента линейного члена, который будет равен 3, затем возводим его в квадрат и прибавляем к обеим сторонам. Затем разложите совершенный квадратный трехчлен, чтобы получить квадратный бином. Затем решить для y.

    Стандарты: HSG.GPE.A.2

    Нажмите здесь, чтобы попрактиковаться: Геометрия – Выражение геометрических свойств с помощью уравнений Вопрос: Какова плотность кирпича, занимающего 310 см 3 при массе 853 г?

    1. 0,36 см 3 /г
    2. 2,75 г/см 3
    3. 2,64 г/см 3
    4. 0,36 г/см 3

    Объяснение ответа: V = Bh = lwh Объем прямоугольной призмы

    Формула плотности: d = m/V. Объем равен 310 см 3 , а масса 853 г. Подставьте эти значения в формулу, чтобы найти плотность.

    Стандарты: HSG.MG.A.2

    Нажмите здесь, чтобы попрактиковаться: Геометрия – Моделирование с помощью геометрии0051

    Пример вопроса: Полусфера радиусом 3 см находится на вершине конуса одинакового диаметра и высоты 10 см, как показано на диаграмме ниже. Найдите объединенный объем составного объекта.

    1. 24πсм 3
    2. 36πсм 3
    3. 48πсм 3
    4. 60πсм 3

    Ответ Пояснение: Полный объем объекта равен сумме объемов полусферы и конуса.
    В = ½ (4/3) πr 3 +(1/3)πr 2 h
    В = ½ (4/3) π(3m) 3 +(1/3)π(3m) 2 (10 см)V=48πcm 3

    Стандарты: HSG.GMD.A.3

    Нажмите здесь, чтобы попрактиковаться: Геометрия – вопросы по геометрическим измерениям и размерам для 11 класса, математика

    90de 11 >> Статистика и вероятность — интерпретация категорийных и количественных данных

    Пример вопроса: Какое влияние оказывает группа очень больших значений на среднее и медиану набора данных?

    1. Среднее значение и медиана увеличиваются
    2. Среднее значение не изменилось, а медиана увеличилась
    3. Среднее значение и медиана не изменяются
    4. Среднее значение увеличивается, но медиана уменьшается

    Объяснение ответа: На рисунке ниже показано влияние на среднее значение и медиану в результате добавления в набор данных очень больших элементов. Поскольку новые элементы очень большие, они оказывают существенное влияние на среднее значение, поскольку их очень большие значения усредняются с другими значениями в наборе. Медиана также затрагивается и движется в том же направлении, что и среднее.

    Стандарты: HSS.ID.A.3

    Щелкните здесь, чтобы попрактиковаться: Статистика и вероятность – интерпретация вопросов по категориальным и количественным данным для 11 класса по математике

    Область: Статистика и вероятность – 11 класс >> Выводы и обоснование выводов

    Пример вопроса: Есть десять игральных карт, четыре из них красные и шесть черных. Джулиан выбирает карту наугад. Какова вероятность того, что он выберет красную карточку?

    Ответ Пояснение: Вероятность рассчитывается как отношение количества успехов к количеству возможных вариантов.

    Вопрос касается вероятности выбора красной карточки. Из десяти карточек четыре красные.

    Таким образом, вероятность выбора красной карточки составляет четыре из десяти, что сводится к двум из пяти. Это соотношение равно 2/5

    Стандарты: HSS.IC.A.1

    Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность – выводы и обоснование выводов Правила вероятности

    Пример вопроса: На приведенной ниже диаграмме Венна показаны результаты опроса о том, какие виды спорта люди любят смотреть по телевизору. Участники опроса могли выбрать один вид спорта, два вида спорта или все три вида спорта. В каком регионе (регионах) есть ответы, в которых участник опроса указал, что ему нравится смотреть только один вид спорта?

    1. Б, В, Г
    2. Э, Ж, Г
    3. Б, А, Д
    4. А, Б, С

    Объяснение ответа: Каждый кружок содержит ответы, которым нравится определенный цвет. Таким образом, регионы A, B, C, E содержат ответы, которые любят смотреть бейсбол. Области D, A, D, G содержат ответы, которые любят смотреть баскетбол. Регионы A, B, D, F содержат ответы, которые любят смотреть футбол. Если письмо находится в двух кругах, в регионе есть ответы, которые любили смотреть виды спорта, представленные в обоих кругах. Если регион указан во всех трех кругах, этот регион содержит ответы, в которых нравится смотреть все три вида спорта. Если регион находится только в одном круге, этот регион содержит ответы, в которых говорится, что им нравится смотреть только тот вид спорта, который представлен в этом круге. Области, которые находятся только в одном круге, это E, F, G.

    Стандарты: HSS.CP.A.1

    Нажмите здесь, чтобы потренироваться: Статистика и вероятность – Условная вероятность и правила вероятности Вопросы для 11 класса по математике Использование вероятности для принятия решений

    Пример вопроса: Бюро переписи населения предоставило отчет, в котором говорится, что средний уровень дохода жителей Флориды составляет 47 463 человека.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *