Задачи по логике 3 класс: Логические задачи для 3 класса

Урок логики в 3-м классе по теме “Решение логических задач”. Урок-путешествие

Познавательный аспект.

1. Формирование и развитие различных видов памяти, внимания, воображения.
2. Формирование и развитие общеучебных умений и навыков.
3. Формирование общей способности искать и находить новые решения, необычные способы достижения требуемого результата, новые подходы к рассмотрению предлагаемой ситуации.
4. Формирование межпредметной связи.

Развивающий аспект.

1. Развивать речь, мышление в ходе усвоения таких приемов мыслительной деятельности, как умение анализировать, сравнивать, синтезировать, обобщать выделять главное, доказывать и опровергать.
2. Развивать двигательную сферу.
3. Развивать познавательную способность ребенка.
4. Развитие навыков контроля и самоконтроля.

Воспитывающий аспект.

1. Воспитывать у детей чувство дружбы, товарищества.
2. Воспитывать любовь к предмету.
3. Воспитывать систему нравственных межличностных отношений.

Оборудование.

Таблицы и рисунки:

• граф – «Дерево»;
• магические квадраты;
• «Памятка» по решению задач на сравнение;
• задачи, план-путешествие по стране «Логика».

Раздаточный материал для каждого ученика:

• граф– «Дерево»;
• магические квадраты;
• «Памятка» по решению задач на сравнение;
• «мозговая» гимнастика, логические «жучки», «цветы»;
• загадки, логические и нелогические высказывания.

Ход урока

1. Организация класса.

2. Актуализация знаний.

– Какой сейчас урок? Логика. Что такое Логика? Как вы понимаете? Посмотрите на доску и прочитайте предложения. Что вы можете о них сказать? (Логические и нелогические суждения, утверждения.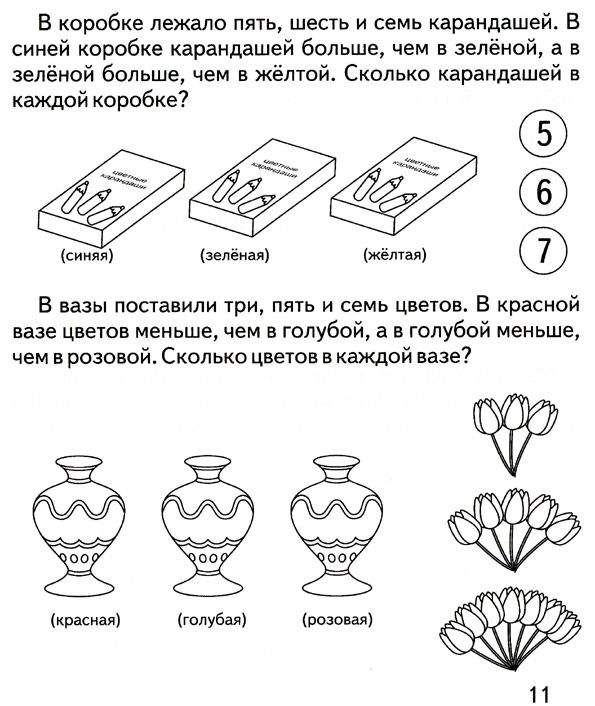

)

– Прочитайте логические предложения (правильные по смыслу).

– Прочитайте логические вопросы. А что такое логические вопросы? (На которые можно утвердительно ответить: Да! или Нет!) (Приложение 1)

– Мы ученики 3 «Б» класса. (Логические.)

– Мы любим учиться? (Логические.)

– Какой сейчас урок? (Нелогические.)

– Мы будем на уроках слушать и слышать, развивать память, внимание, воображение? (Логические.)

– Завтра я был в школе? (Нелогические.)

– Вы хотите узнать новое и интересное на уроке? (Логические.)

– Какой послезавтра был день? (Нелогические.)

– Что значит задать логический вопрос?

– Мы будем на уроках сравнивать, анализировать, обобщать, уважать мнение своих товарищей? (Логические.)

– В конце урока вы хотите оценить свою деятельность? (Логические.)

– Прочитайте логические суждения и утверждения, предложения и определите цели и задачи нашего урока. Чем мы будем заниматься на уроке?

3.

«Школа Сотрудничества». Путешествие по стране «Логика».

– Для этого мы с вами отправимся в путешествие по стране? Какой? – Логика! Что вам говорят наши станции, на которых мы будем останавливаться! (Это цели и задачи нашего урока?) Знакомство со станциями в стране «Логика».

I. Станция «Выполняй-ка». Мозговая гимнастика.

1. Качания головой. (Упражнение стимулирует мыслительные процессы.)
2. «Ленивые восьмерки». (Упражнение активирует структуры мозга, обеспечивающее запоминание, повышает устойчивость внимания.)
3. Моргания. (На вдох-выдох, моргания, при всех нарушениях зрения.)
4. «Стрельба глазами».
5. «Письмо носом». (Снижает напряжение в области глаз. Используя нос, как длинную ручку, пишете или рисуете что-нибудь в воздухе, развиваем воображение.)
6. Веселая переменка:
   1. Координация движений «Нос, ухо». Вначале левой рукой дотроньтесь до правого уха, а потом правой рукой – до кончика носа, затем быстро поменяйте положение рук.
   2. Наложите левую руку на голову и погладьте себя от затылка ко лбу. В это время правой рукой делайте круговые движения по животу. Действия выполняйте одновременно.
   3. Левой рукой как бы забиваете гвоздь молотком, а правой гладьте что-то утюгом.

II. Станция «Разминай-ка» (разминка).

Кто это или что это?

1. Рыбок дома держат в нем, что это за водоем? (Аквариум.)
2. Как зовем мы человека, что зимой ползет он в реку? (Морж.)
3. Ствол дерева покрывает и надежно защищает? (Кора.)
4. Если зрение пропало, время их носить настало? (Очки.)
5. Если месяцев двенадцать, как им вместе называться? (Год.)
6. Служит он на корабле, его узнаешь на земле: на голове фуражка, а на груди – тельняшка. (Моряк.)
7. По реке плывет бревно, ох и злющее оно! Тем кто в речку угодил, нос откусит… (Крокодил.)
8. Он в телевизоре сидит и четко, ясно говорит, все новости он вам расскажет. (Диктор.)
9. Мороженое в шоколаде. (Эскимо.)
10. Страна всех сумчатых. (Австралия.)

III. Следующая станция «Угадай-ка».

– Что нам предстоит делать на этой станции? (Угадывать фигуры.)

На доске:

1. Что вы можете сказать об этих фигурах? (4 формы; 2 размера, 4 цвета.)
2. Сколько вопросов будем задавать, чтобы узнать форму (3), цвет (3), размер (1).

Договоренность, о чем будем спрашивать:

1. Форма.
2. Размер.
3. Цвет.

Станция «Угадай-ка».

1. Угадывание фигуры по графу – «Дерево» (Приложение 4) на доске по памяти (гости загадывают фигуру, дети отгадывают).
2. Угадывание фигуры:
   1. с помощью указки;
   2. с помощью жестов;
   3. с помощью глаз.
3. Работа в парах по графу – «Дерево» (индивидуально у каждого ребенка на парте).

IV. Станция «Размышляй-ка».

1. На доске логические и математические квадраты. О чем будем говорить на этой станции. Давайте поработаем магами, т.е. волшебниками, и определим какие квадраты магические, а какие не магические. Докажите.

1. Закономерность магического квадрата? (Звездочка.)
2. Какой праздник приближается? (Новый Год.)

Сделайте так, чтобы квадрат стал магическим, используя предметы (новогодние: снеговик, игрушка, снежинка). Дети на месте выполняют самостоятельную работу и у доски.

Взаимопроверка. Какой алгоритм мы использовали, чтобы квадраты стали магическими?

– На каких уроках нам помогает эта тема? (Математика.)

V. Станция «Думай-ка» (группы).

– Скажите, Новый Год – чудесный праздник?

– Да? Какие чудеса случаются на Новый Год? А может такое случится, что у нас появятся зимой цветы, насекомые? Давайте с вами поработаем группами у доски и создадим весеннее настроение для всех? Помните о договоренности.

• Если будем создавать логические «цветы» о чем будем спрашивать?
• Если логических «жучки», то

– Какое самое строгое утверждение? Какой ответ будет самый строгий? (Да, да, да.) Нестрогий? (Нет, нет.) (Нет, нет, нет.) Взаимопроверка.

VI. Станция «Сравнивай-ка», «Соображай-ка», «Решай-ка».

1) Сколько задач перед нами стоят на этой станции. Что значит сравнивать? (Значит, определить, одинаковы или нет объекты, при чем не обязательно в целом, а хотя бы в чем-то. Таким образом, чтобы сравнивать, надо выяснить, что мы хотим сравнить: цвет, форму, размер, вкус, силу, то есть мы сравниваем по какому-то признаку.)

Предлагаю учащимся назвать слова, с помощью которых в речи фиксируется сравнение. Каждый признак может характеризоваться двумя словами с противоположным смыслом. Как называются такие слова? (Антонимы.) Где они встречаются? (На уроках русского языка, литература.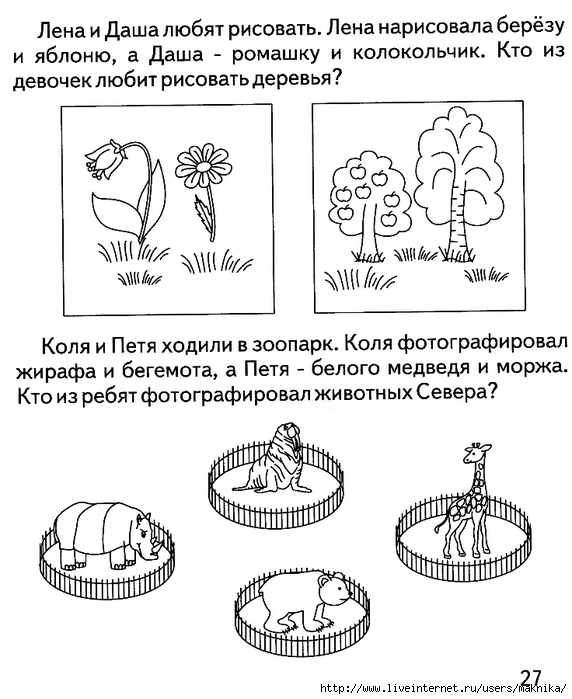

)

2) Игра.

Я называю слово, вы называете противоположное.

• Веселье – грусть, печаль (по состоянию).
• Сильнее – слабее (по силе).
• Тяжелее – легче (по массе, весу).
• Быстрее – медленнее (по скорости).
• Добрее – злее (по качеству).

Придумайте по цвету, вкусу.

3) Я начинаю читать предложения, а вы закончите по смыслу (сравнение).

• Если Света светлее Маши, то Маша …
• Если Костя слабее Миши, то Миша …
• Если Андрей печальнее Вити, то Витя …

Признаки детей.

4) Сегодня мы будем решать задачи по двум и более признакам на сравнение.

У вас есть «Памятка» решения задач на сравнение. (Приложение 3)

1. Выписать участников.
2. Выяснить сколько признаков сравнения в задаче.
3. Выбрать слово для обозначения с помощью стрелки .

4. Переформулируем сравнения с другими словами («сказать наоборот»).
5. Составить схему.
6. Найти начало и конец.
7. Записать ответ.

5) Решим задачу. Таня веселее Риты. Рита легче Нины. Нина сильнее Тани. Таня тяжелее Нины. Нина печальнее Риты. Рита слабее Тани. Назовите признаки каждой девочки. (Каждому выдается индивидуальный листок с текстом задачи и «Памятка» по решению задач на сравнение. Дети находят в задаче сначала отдельно признаки со словами «веселее – грустнее; легче – тяжелее; сильнее – слабее». В связи с этими признаками выписывают участников и составляют схему решения задачи, используя «Памятку».) (Приложение 2)

Ответ: Таня веселее и тяжелее всех. Рита легче и слабее всех. Нина сильнее и печальнее всех.

VII. Станция «Побеждай-ка», «Оценивай-ка».

– Ребята, давайте подведем итог нашего путешествия. Встречались ли у нас на пути трудности? Какие? Давайте оценим свою деятельность на всех станциях или этапах пути. Если вы считаете, что вы хорошо поработали, вы можете взять красный флажок, если не все получалось, то желтый, а если нужно над чем-то работать еще, то зеленый.

Дети выбирают и показывают.

4. Итог.

– Вот мы вернулись в «Школу Сотрудничества». Будем продолжать работать на следующих уроках.

– Поздравление с наступающим Новым Годом!

5. Домашнее задание.

Придумать задачу с 4-мя признаками на сравнение, логические жучки, цветы, квадраты.

§ 4. Примеры задач на использование законов алгебры логики и формализацию высказываний — ЗФТШ, МФТИ

Максимально упростить, это значит довести выражение до такого вида, когда невозможно применить ни один из законов алгебры логики, которые сокращают длину выражения.

Для того, чтобы не запутаться, можно использовать общую стратегию упрощения логических выражений.

1) Избавиться от операций импликации.

2) Продвинуть отрицание вглубь выражения. То есть применять законы де Моргана, и закон двойного отрицания пока знак отрицания не будет стоять только над переменными (но не над операциями).

После пункта 2 наступает относительная свобода действий. Можно использовать тождества поглощения или раскрывать скобки.

В нашей задаче операция импликации отсутствует, поэтому первый пункт мы пропускаем. Переходим к пункту 2. Применяем два раза второй закон де Моргана (для дизъюнкции) и закон двойного отрицания к правой скобке и получаем следующее логическое выражение:

  `bar C vv ` (`A`  &  `C`) `vv` (`bar A` & `bar C` & `B`)

Если теперь внимательно посмотреть на выражение, то очевидно, что к первому и третьему слагаемому  можно применить первый закон поглощения, так как отрицание переменной `C` является первым слагаемым и входит в третье в качестве множителя.

Поскольку дизъюнкцию ещё называют логическим сложением, её операнды называют слагаемыми, аналогично конъюнкция – это логическое умножение, и её операнды называют множителями.

После применения первого закона поглощения получается следующее логическое выражение:

`bar C` `vv` (`A` & `C`)

Применим второй (нестандартный для алгебры) закон дистрибутивности. Получаем: 

(`bar C vv A`) & (`bar C vv C`)

Ко второй скобке применяем закон исключённого третьего, превращаем её в единицу, а затем применяем закон поглощения константы `1` и в итоге получаем выражение: `bar C vv A`, которое упростить уже нельзя.

Для лучшего понимания, рекомендуется выписать исходное логическое выражение, последовательно применить к нему все описанные действия и сравнить свой результат с приведённым в конце решения задачи.

Обратите внимание, что исходное логическое выражение зависело от трёх переменных (`A, B, C`) , в то время как упрощённое в итоге зависит от двух логических переменных (`A` и `C`). При этом выражения всё равно остаются равносильными! Это происходит потому, что в процессе упрощения применялись законы поглощения. Аналогичный результат мог бы получиться, если в процессе упрощения выражения используются законы поглощения переменных константами. Исчезновение переменной при упрощении означает, что в исходном выражении она является несущественной.

Чтобы решить эту задачу, необходимо провести процесс формализации условия, сформировать единое логическое выражение и провести его упрощение. Выделим из условия четыре простых высказывания: «`A` нарушил правила», «`B` нарушил правила», «`C` нарушил правила»,  и «`D` нарушил правила». Обозначим их соответственно буквами `A`, `B`, `C`, `D`. Тогда высказывания из условия формализуются следующим образом (конъюнкция не обозначается никак):

1) `A -> B`;

2) `B -> C` \/ `¬A`;

3) `¬D -> A¬ C`;

4) `D -> A`.

Нам известно, что выполняются все 4 высказывания, следовательно, нужно объединить их знаками конъюнкции и найти наборы, при которых получившееся общее высказывание будет истинным. Эти наборы и покажут нам, какие возможны ситуации (правила обмена нарушил тот, у кого переменная в итоговом наборе имеет значение «1»).

Итак, строим логическое выражение:

      `(A -> B)( B -> C` \/ `¬A)( ¬D -> A¬C)( D -> A)`.

Теперь будем его упрощать. По алгоритму первым делом избавляемся от операции импликации. Получаем следующее выражение:

     `(¬A` \/ `B)( ¬B` \/ `C` \/ `¬A)( D` \/  `A¬C)( ¬D` \/  `A)`.

Раскрываем скобки. Первую перемножаем со второй, а третью с четвёртой.

     `(¬A¬B`  \/ `¬AC` \/ `¬A` \/ `BC` \/ `B¬A) ( DA` \/ `A¬C¬D` \/  `A¬C)`.

Напомним, что слагаемые, равные нулю по причине того, что в них входит сразу и переменная и её отрицание, мы не записываем. В первой скобке теперь можно применить тождество поглощения, и «съесть» все слагаемые, имеющие в своём составе `A` с отрицанием. Во второй скобке можно также применить тождество поглощения, и «съесть» второе слагаемое. В итоге получаем:

     `( ¬A` \/ `BC ) ( DA` \/ `A¬C)`.

При раскрытии оставшихся скобок три из четырёх слагаемых окажутся равными нулю, а последнее будет выглядеть следующим образом: `ABCD`. Из этого следует, что все четверо работников банка нарушили правило обмена валюты. (Только в этой ситуации предположения из условия задачи одновременно выполняются).

Правила обмена валюты нарушили все.

В заключение приведём общую схему решения текстовых логических задач, которую мы уже применяли на практике при разборе примеров.

Среди задач алгебры логики часто встречаются задачи на определение количества решений систем логических уравнений. Рассмотрим примеры некоторых их них.

Заметим, что часто перед решением больших систем логических уравнений сначала удобно упростить исходную систему с помощью законов алгебры логики, а также воспользоваться заменой переменных, если это возможно.

Займитесь решением проблем, логическим мышлением и критическим мышлением с помощью этих увлекательных занятий!

Когда вы думаете о решении задач, логических рассуждениях и критическом мышлении, представляете ли вы скучные рабочие листы, о которых учащиеся стонут и стонут? Что ж, положим этому конец! Логические задачи — это увлекательный и интерактивный способ включить эти важные навыки в математический класс, что приводит к повышению мотивации и интереса.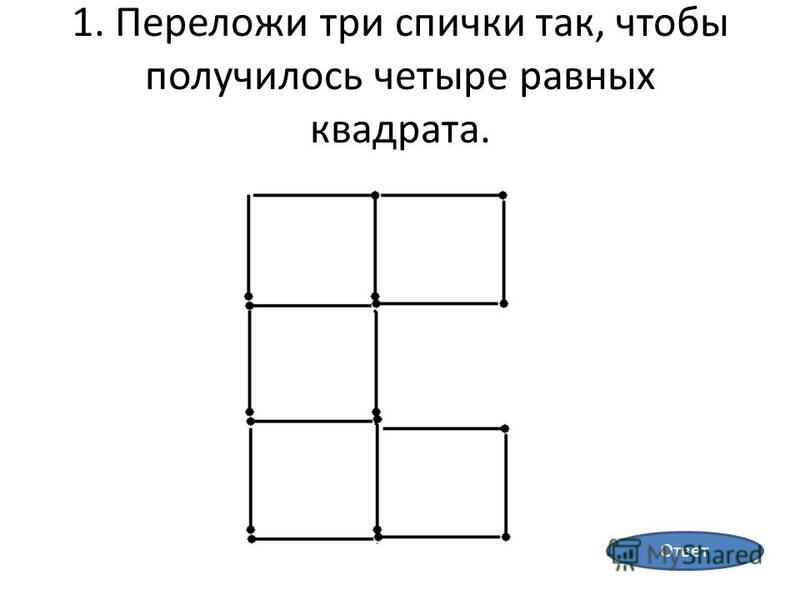 Они также являются эффективным способом познакомить учащихся с алгебраическим мышлением и помочь учащимся развить навыки, необходимые для успешного изучения алгебры в более поздних классах. Слишком часто работа, которую мы даем студентам, состоит из поверхностного мышления, когда они просто повторяют ответы. Но логические задачи могут создать новый тип задач и побудить их мыслить гораздо глубже.

Как решить логическую задачу

Чтобы собрать головоломку, учащиеся быстро поймут, что они должны начать с символов, которые они ЗНАЮТ наверняка. Например, в приведенной ниже головоломке мы начинаем с решения автоматов с жевательной резинкой, поскольку знаем, что 5+5=10. Теперь, когда мы знаем, что автомат с жевательной резинкой равен 5, мы можем решить вторую строку. Сердце равно 10, так как 10+5=15. Наконец, мы можем решить нижнюю строку. Поскольку мы знаем, что сердце равно 10, мы можем заключить, что леденец должен быть 6.

Сложнее, чем кажется

Хотя приведенный выше пример кажется простым, детям не всегда легко думать таким образом, особенно когда головоломки усложняются. Решая, какие головоломки использовать со своими учениками, помните, что если они не привыкли выполнять действия, связанные с логическими рассуждениями, они, скорее всего, сочтут их сложными. Вашим учащимся 3-4 классов может быть достаточно сложно решить головоломки с числами до 20, даже если они работают с числами в тысячах в других математических заданиях.

Я рекомендую сделать несколько уровней головоломок доступными для ваших учеников и позволить им выбирать те, которые «достаточно сложны» для их мозга. Я обычно нахожу, что студенты стремятся работать в полную силу и обычно выбирают те, которые лучше всего соответствуют их способностям.

Идеи для использования

Вы можете хранить и использовать эти головоломки в своем классе разными способами:

• Используйте в одном из своих математических центров. Поместите логические головоломки в центр стола и предложите учащимся выбрать те, которые они хотят решить. Чтобы добавить дифференциации, позвольте своим ученикам выбирать между различными наборами логических головоломок.
• Хранить на кольце или в папке и использовать досрочное завершение.
• Разложите головоломки по комнате и используйте их для прогулки по галерее «Вокруг комнаты». Пусть ученики ходят по комнате, собирая головоломки по ходу дела! *Совет: дайте каждому учащемуся буфер обмена, если он у вас есть.
• Используйте их как партнерскую работу. Вам ПОНРАВИТСЯ удивительная математическая беседа, которая будет происходить, когда ученики будут говорить о том, что представляет каждая картинка.

Лично я предпочитаю распечатывать их в цвете и ламинировать каждую карточку, но вы также можете просто сделать черно-белые буклеты, чтобы ваши ученики хранили их в своих папках по математике.

Бесплатный образец для вашего класса

Если вы хотите попробовать эти головоломки в своем классе, но не уверены, какой набор подойдет лучше всего, я подготовил для вас бесплатный образец. Возьмите их в свой класс и посмотрите, как реагируют учащиеся, прежде чем совершить покупку всего пакета или полного пакета для нескольких классов. В бесплатном образце вы получите по одной головоломке из каждого пакета. Загрузите бесплатный образец ниже!

 

Получите бесплатный образец здесь.

Полная упаковка и комплект

Если вы готовы использовать эти головоломки в своем классе, я добавил ссылки на отдельные пакеты ниже. Каждый пакет логических задач содержит 20 головоломок. Просто заламинируйте, вырежьте и сделайте копии листов для записей, и вы позаботитесь об одном из своих математических центров!

 

Сделайте дифференциацию легкой! См. полный многоуровневый комплект здесь.

Или посмотрите отдельные пакеты логических задач здесь.

Логическая головоломка / Командный побег из комнаты 3 и 4 года [Том 1]

☆ Любите БЕСПЛАТНЫЕ вещи? ☆

Ищете интересный способ поощрить командную работу и сотрудничество в классе?

Решая 4 логические головоломки на критическое мышление, учащиеся не только оттачивают свои логические и логические навыки, но и развивают навыки общения и решения проблем.

 Вашим ученикам понравится работать вместе, чтобы раскрыть 3 секретных послания:

“Командная работа” “Доброта” “Будь тем изменением, которое ты хочешь увидеть в мире”

_________________________________

Что включено?

✏ 4 ​​сложных логических задания, которые развивают навыки решения проблем и требуют совместной работы

✏ Доступ к эксклюзивному и оригинальному видео, которое устанавливает сцену (см. предварительный просмотр видео!)

✏ Доступ к форме Google для самопроверки/оценки — оценка учителя не требуется!

✏ Доступ к цифровой (Google Slide) версии занятий (Примечание: учителям и учащимся потребуется электронная почта Google, чтобы получить доступ к этой версии)

___________________________________

Почему вам это понравится!

☆ Все задания практичные и увлекательные

☆ Все задания сложные, но достижимые

☆ Все задания поощряют командную работу и сотрудничество

☆ Может использоваться в любое время года – нет необходимости предварительно -учить чему угодно!

☆ Часть от распечатки листов и предоставления ссылки на гугл форму НИКАКОЙ подготовки и НИКАКОЙ маркировки!

Откройте для себя учебные ресурсы, соответствующие учебной программе

Все ресурсы, созданные Джесс, учителем из Сиднея, соответствуют результатам австралийской учебной программы.

Откройте для себя учебные ресурсы, соответствующие учебной программе

Все ресурсы, созданные Джесс, учителем из Сиднея, соответствуют результатам австралийской учебной программы.

Цифровые ссылки для загрузки становятся доступными на странице сводки заказа сразу после покупки. Эти ссылки также приходят по электронной почте прямо на ваш почтовый ящик! Просто нажмите на ссылку, чтобы начать процесс загрузки, и файлы будут сохранены на вашем устройстве.

Для вашего удобства все цифровые загрузки также могут быть доступны и повторно загружены неограниченное количество раз через вашу учетную запись клиента. Просто создайте учетную запись  ЗДЕСЬ  с адресом электронной почты, который использовался для совершения покупки, установите пароль, и все предыдущие покупки будут перечислены.

Цифровые ссылки для загрузки становятся доступными на странице сводки заказа сразу после покупки.