Задачи на расстояние скорость и время: Текстовые задачи на движение 5 класс – Всё о детях – беременность, воспитание, уроки для детей

Решение задач на скорость, путь и время движения | 7 класс

Содержание

Скорость, путь и время являются важными характеристиками любого механического движения. Они связаны между собой формулами:

$\upsilon = \frac{S}{t}$
$S = \upsilon t$
$t = \frac{S}{\upsilon}$

Данные формулы описывают равномерное движение. При неравномерном движении мы говорим о средней скорости: $\upsilon_{ср} = \frac{S}{t}$.

Чтобы полноценно научиться использовать вышеупомянутые определения и величины, в данном уроке мы рассмотрим решение разнообразных задач. Вы научитесь вычислять скорость, среднюю скорость, время и путь, переводить единицы измерения скорости из одних в другие, узнаете, как использовать графики этих величин.

Задача №1

Выразите в метрах в секунду ($\frac{м}{с}$) скорости: $60 \frac{км}{ч}$; $90 \frac{км}{ч}$; $300 \frac{км}{ч}$; $120 \frac{м}{мин}$.

Дано:
$\upsilon_1 = 60 \frac{км}{ч}$
$\upsilon_2 = 90 \frac{км}{ч}$
$\upsilon_3 = 300 \frac{км}{ч}$
$\upsilon_4 = 120 \frac{м}{мин}$

Показать решение и ответ

Скрыть

Решение:

Для перевода скорости в метры в секунду нам нужно:

перевести километры в метры ($1 \space км = 1000 \space м$)
выразить часы или минуты в секундах ($1 \space мин = 60 \space с$; $1 \space ч = 60 \space мин = 3600 \space с$)

Тогда,
$\upsilon_1 = 60 \frac{км}{ч} = 60 \frac{1000 \space м}{3600 \space c} = \frac{1000 \space м}{60 \space c} \approx 16.7 \frac{м}{с}$.

При вычислениях старайтесь увидеть величины, которые можно сократить (как 60 и 3600).

Если мы вычислим множитель $\frac{1000 \space м}{3600 \space c}$, то получим, что $1 \frac{км}{ч} = \frac{}{3.6} \frac{м}{с}$.

Вы можете каждый раз последовательно переводить величины (километры в метры и часы в секунды) или просто разделить скорость, выраженную в километрах в час на $3. 6$ и получить скорость в метрах в секунду. Рекомендуется идти первым путем, потому что второй способствует потере точности.

Переведем следующие две скорости в единицы СИ:
$\upsilon_2 = 90 \frac{км}{ч} = 90 \frac{1000 \space м}{3600 \space c} = 1000 \cdot 0.025 \frac{м}{с} = 25 \frac{м}{с}$,
$\upsilon_3 = 300 \frac{км}{ч} = 300 \frac{1000 \space м}{3600 \space c} = \frac{1000 \space м}{12 \space c} \approx 83.3 \frac{м}{с}$.

Теперь переведем скорость, выраженную в метрах в минуту в метры в секунду:
$\upsilon_4 = 120 \frac{м}{мин} = 120 \frac{м}{60 \space c} = 2 \frac{м}{с}$.

Ответ: $\upsilon_1 \approx 16.7 \frac{м}{с}$; $\upsilon_2 = 25 \frac{м}{с}$; $\upsilon_1 \approx 83.3 \frac{м}{с}$; $\upsilon_4 = 2 \frac{м}{с}$.

Задача №2

Пуля, выпущенная из винтовки, долетела до цели, находящейся на расстоянии $1 \space км$, за $2.5 \space с$. Найдите скорость пули.

Дано:
$S = 1 \space км$
$t = 2.5 \space с$

СИ:
$S = 1000 \space м$

$\upsilon — ?$

Показать решение и ответ

Скрыть

Решение:

Формула для расчета скорости:
$\upsilon = \frac{S}{t}$.

Перед вычислениями не забывайте переводить единицы измерения величин в СИ!

Рассчитаем скорость:
$\upsilon = \frac{1000 \space м}{2.5 \space с} = 400 \frac{м}{с}$.

Ответ: $\upsilon = 400 \frac{м}{с}$.

Задача №3

Пароход, двигаясь против течения со скоростью $14 \frac{км}{ч}$, проходит расстояние между двумя пристанями за $4 \space ч$. За какое время он пройдет то же расстояние по течению, если его скорость в этом случае равна $5.6 \frac{м}{с}$?

Дано:
$\upsilon_1 = 14 \frac{км}{ч}$
$t_1 = 4 \space ч$
$\upsilon_2 = 5.6 \frac{м}{с}$

$t_2 — ?$

Показать решение и ответ

Скрыть

Решение:

Найдем расстояние между двумя пристанями:
$S = \upsilon_1 t_1$,
$S = 14 \frac{км}{ч} \cdot 4 \space ч = 56 \space км = 56 \space 000 \space м$.

Обратите внимание, что мы изначально не перевели единицы измерения в СИ (километры в час в метры в секунду и часы в секунды), потому что удобнее это сделать после расчета расстояния $S$. Таким образом мы сохраняем более высокую точность вычислений.

Итак, мы знаем расстояние и скорость движения парохода по течению. Теперь мы можем рассчитать время движения парохода по течению:
$t_2 = \frac{S}{\upsilon_2}$,
$t_2 = \frac{56 \space 000 \space м}{5.6 \frac{м}{с}} = 10 \space 000 \space с$.

Ответ: $t_2 = 10 \space 000 \space с$.

Задача №4

Автомобиль проехал равномерно участок дороги длиной $3.5 \space км$ за $3 \space мин$. Нарушил ли правила дорожного движения водитель, если на обочине расположен дорожный знак “скорость не более $50 \frac{км}{ч}$”?

Дано:
$S = 3.5 \space км$
$t = 3 \space мин$

$\upsilon — ?$

Показать решение и ответ

Скрыть

Решение:

После того, как мы рассчитаем скорость движения автомобиля, нам нужно будет сравнить ее со скоростным ограничением в $50 \frac{км}{ч}$. Для того чтобы это сделать, нужно, чтобы скорость тоже была выражена в километрах в час.

Так как водитель двигался равномерно, рассчитывать скорость его движения мы будем по формуле:
$\upsilon = \frac{S}{t}$.

Путь $S$ у нас и так выражен в километрах, а время — в минутах. Поэтому, перед рассветом скорости переведем время из минут в часы:
$t = 3 \space мин = \frac{3}{60} \cdot ч = 0.05 \space ч$.

Теперь мы можем рассчитать скорость движения автомобиля:
$\upsilon = \frac{3.5 \space км}{0.05 \space ч} = 70 \frac{км}{ч}$.

Получается, что водитель нарушил правила дорожного движения, ведь $70 \frac{км}{ч} > 50 \frac{км}{ч}$.

Ответ: нарушил.

Задача №5

Росток бамбука за сутки вырастает на $86.4 \space см$. На сколько он вырастает за $1 \space мин$?

Дано:
$S = 86.4 \space см$
$t = 1 \space сут$
$t_1 = 1 \space мин$

$S_1 — ?$

Показать решение и ответ

Скрыть

Решение:

Переведем сутки в минуты:
$t = 1 \space сут = 24 \space ч = 24 \cdot 60 \space мин = 1440 \space мин$.

Рассчитаем скорость роста бамбука, выраженную в сантиметрах в минуту:
$\upsilon = \frac{86.4 \space см}{1440 \space мин} = 0.06 \frac{см}{мин}$.

Понятие скорости в физике определяет расстояние, которое тело проходит в единицу времени. В нашем случае полученную скорость роста мы можем описать так:
бамбук вырастает на расстояние, равное $0.06 \space см$, за $1 \space мин$.

Значит,
$S_1 = 0.06 \space см = 0.6 \space мм$.

Ответ: $S_1 = 0.6 \space мм$.

Задача №6

Самолет, летящий со скоростью $300 \frac{км}{ч}$, в безветренную погоду пролетел расстояние между аэродромами A и B за $2.2 \space ч$. Обратный полет из-за встречного ветра он совершил за $2.5 \space ч$. Определите скорость ветра.

Дано:
$\upsilon_1 = 300 \frac{км}{ч}$
$t_1 = 2.2 \space ч$
$t_2 = 2.5 \space ч$

$\upsilon_в — ?$

Показать решение и ответ

Скрыть

Решение:

Сначала вычислим расстояние между аэродромами, которое пролетает самолет:
$S = \upsilon_1 t_1$,
$S = 300 \frac{км}{ч} \cdot 2. 2 \space ч = 660 \space км$.

Теперь рассчитаем скорость, с которой самолет совершил обратный полет:
$\upsilon_2 = \frac{S}{t_2}$,
$\upsilon_2 = \frac{660 \space км}{2.5 \space ч} = 264 \frac{км}{ч}$

Если бы ветра не было, то скорость самолета составила бы $300 \frac{км}{ч}$. Но ветер направлен противоположно движению самолеты, вектор его скорости противоположно направлен вектору скорости самолета. Поэтому мы можем записать, что скорость самолета, летящего при встречном ветре, равна разности скорости самолета в безветренной обстановке и скорости ветра:
$\upsilon_2 = \upsilon_1 — \upsilon_в$.

Рассчитаем скорость ветра:
$\upsilon_в = \upsilon_1 — \upsilon_2$,
$\upsilon_в = 300 \frac{км}{ч} — 264 \frac{км}{ч} = 36 \frac{км}{ч}$,
или в СИ $\upsilon_в = 36 \cdot \frac{1000 \space м}{3600 \space с} = 10 \frac{м}{с}$.

Ответ: $\upsilon_в = 10 \frac{м}{с}$.

Задача №7

Определите по графику равномерного движения, изображенному на рисунке 1:

скорость движения
путь, пройденный телом в течение $4. 5 \space с$
время, в течение которого пройден путь, равный $15 \space м$

Показать решение и ответ

Скрыть

Решение:

Скорость равномерного движения рассчитывается по формуле:
$\upsilon = \frac{S}{t}$.

Выберем на графике такую точку, данные которой мы можем точно определить. Например, в момент времени, равный $4 \space с$, был пройден путь, равный $16 \space м$.

Используя эти данные, рассчитаем скорость:
$\upsilon = \frac{16 \space м}{4 \space с} = 4 \frac{м}{с}$.

Найдем путь, пройденный телом в течение $4.5 \space с$. Если мы взглянем на график, то в этот момент времени тело прошло путь, приблизительно равный $18 \space м$. Давайте проверим точность этих данных с помощью вычислений:
$S = \upsilon t$,
$S = 4 \frac{м}{с} \cdot 4.5 \space с = 18 \space м$.

Используя график, мы не можем точно определить время, в течение которого пройден путь, равный $15 \space м$. Поэтому вычислим его:
$t = \frac{S}{\upsilon}$,
$t = \frac{15 \space м}{4 \frac{м}{с}} = 3.75 \space с$.

Ответ: $4 \frac{м}{с}$, $18 \space м$, $3.75 \space с$.

Задача №8

Средняя скорость велосипедиста на всем пути равна $40 \frac{км}{ч}$. Первую половину пути он ехал со скоростью $60 \frac{км}{ч}$. С какой скоростью велосипедист проехал остаток пути?

Дано:
$\upsilon_{ср} = 40 \frac{км}{ч}$
$\upsilon_1 = 60 \frac{км}{ч}$
$S_1 = S_2 = \frac{1}{2}S$

$\upsilon_2 — ?$

Показать решение и ответ

Скрыть

Решение:

Запишем формулу средней скорости при неравномерном движении:
$\upsilon_{ср} = \frac{S}{t}$.

Общее время движения $t$ мы можем представить в виде суммы $t_1 + t_2$, где $t_1$ — это время движения на первой половине пути, а $t_2$ — время движения на второй половине пути:
$\upsilon_{ср} = \frac{S}{t_1 + t_2}$.

Время мы можем выразить через скорость на данном участке пути и пройденный за это время путь:
$t_1 = \frac{S_1}{\upsilon_1} = \frac{\frac{1}{2}S}{\upsilon_1} = \frac{S}{2 \upsilon_1}$,
$t_2 = \frac{S_2}{\upsilon_2} = \frac{\frac{1}{2}S}{\upsilon_2} = \frac{S}{2 \upsilon_2}$,
$\upsilon_{ср} = \frac{S}{\frac{S}{2 \upsilon_1} + \frac{S}{2 \upsilon_2}} = \frac{S}{\frac{S(\upsilon_1 + \upsilon_2)}{2 \upsilon_1 \upsilon_2}} = \frac{2 \upsilon_1 \upsilon_2}{\upsilon_1 + \upsilon_2}$.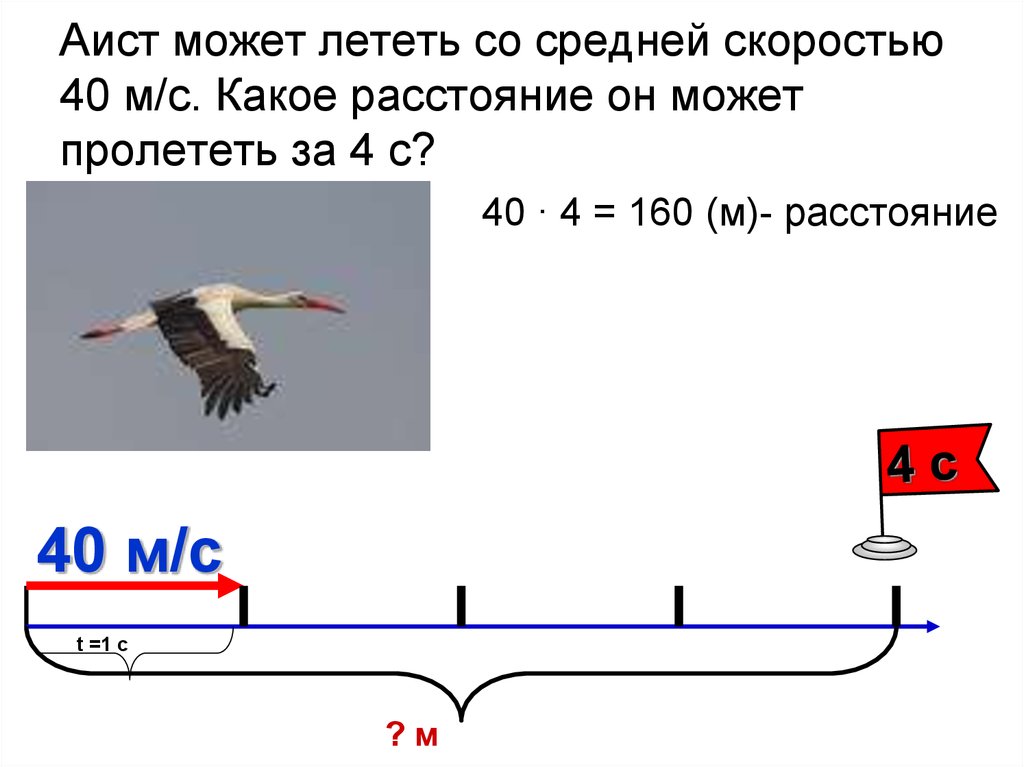

Теперь выразим отсюда скорость $\upsilon_2$, с которой велосипедист двигался вторую половину пути:
$2 \upsilon_1 \upsilon_2 = \upsilon_{ср} \upsilon_1 + \upsilon_{ср} \upsilon_2$,
$2 \upsilon_1 \upsilon_2 — \upsilon_{ср} \upsilon_2 = \upsilon_{ср} \upsilon_1$,
$\upsilon_2 \cdot (2 \upsilon_1 — \upsilon_{ср}) = \upsilon_{ср} \upsilon_1$,
$\upsilon_2 = \frac{\upsilon_{ср} \upsilon_1}{2 \upsilon_1 — \upsilon_{ср}}$.

Рассчитаем эту скорость:
$\upsilon_2 = \frac{40 \frac{км}{ч} \cdot 60 \frac{км}{ч}}{2 \cdot 60 \frac{км}{ч} — 40 \frac{км}{ч}} = \frac{2400 \frac{км}{ч}}{80} = 30 \frac{км}{ч}$.

Ответ: $\upsilon_2 = 30 \frac{км}{ч}$.

Задача №9

На рисунке 2 дан график пути движения поезда. Определите скорости движения на участках, изображенных отрезками графика OA, AB и BC. Какой путь пройден поездом в течении $3 \space ч$ с начала его движения?

Дано:
$t = 3 \space ч$

$\upsilon_1 — ?$, $\upsilon_2 — ?$, $\upsilon_3 — ?$
$S — ?$

Показать решение и ответ

Скрыть

Решение:

Для того чтобы определить скорость на каждом участке пути, мы будем выбирать удобную нам точку на графике и проводить вычисления.

Определим скорость движения поезда на участке OA. В момент времени, равный $1 \space ч$, пройденный поездом путь составил $40 \space км$:
$\upsilon_1 = \frac{S_1}{t_1}$,
$\upsilon_1 = \frac{40 \space км}{1 \space ч} = 40 \frac{км}{ч}$.

Участок графика AB параллелен оси времени, пройденный путь не изменяется. Значит скорость здесь равна нулю: $\upsilon_2 = 0 \frac{км}{ч}$.

Определим скорость движения поезда на участке BC. По наклону прямой графика мы видим, что скорость после остановки изменилась. За время с $2 \space ч$ до $3 \space ч$, пройденный путь изменился с $60 \space км$ до $80 \space км$. Значит, за $1 \space ч$ поезд прошел путь, равный $20 \space км$:
$\upsilon_3 = \frac{S_3}{t_3}$,
$\upsilon_3 = \frac{20 \space км}{1 \space ч} = 20 \frac{км}{ч}$.

Теперь нам нужно найти путь, пройденный поездом за $3 space ч$ с момента начала движения. Этот путь будет складываться из трех составляющих на разных участках:
$S = S_1 + S_2 + S_3$.

Путь $S_2$, соответствующий участку AB будет равен нулю, так как на нем скорость движения равна нулю.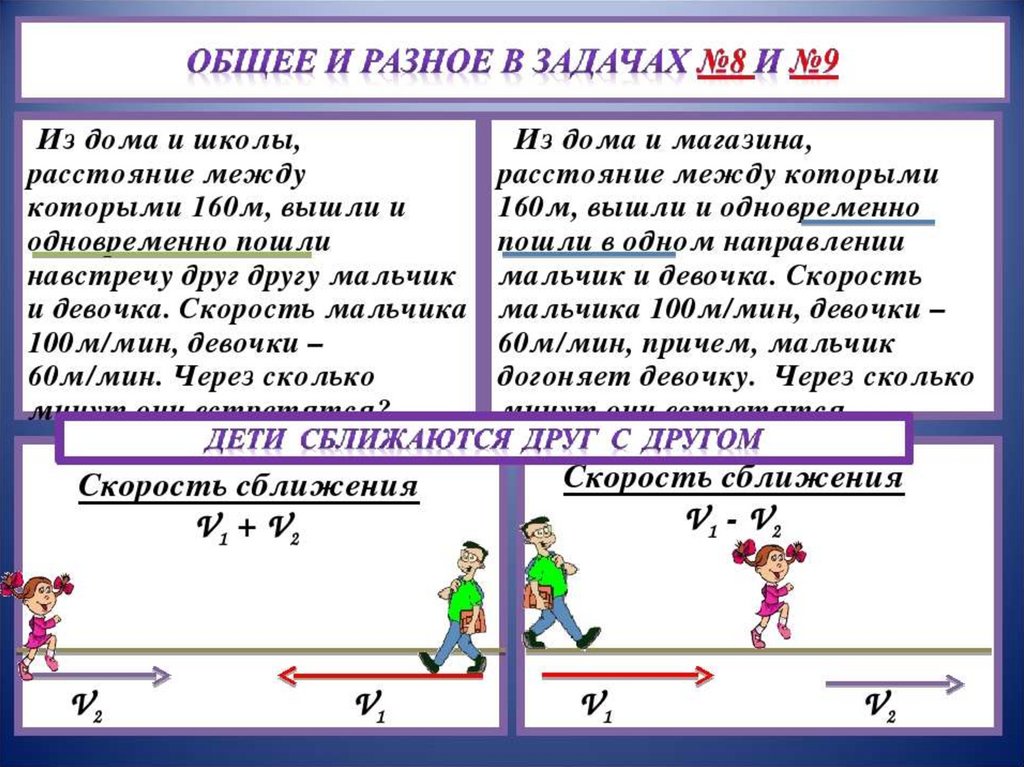

Тогда, используя данные графика и рассчитанные значения скоростей, мы можем записать:
$S = S_1 + S_3 = \upsilon_1 t_1 + \upsilon_3 t_3$,

$S = 40 \frac{км}{ч} \cdot 1.5 \space ч + 20 \frac{км}{ч} \cdot 1 \space ч = 80 \space км$.

Ответ: $\upsilon_1 = 40 \frac{км}{ч}$, $\upsilon_2 = 0 \frac{км}{ч}$, $\upsilon_3 = 20 \frac{км}{ч}$, $S = 80 \space км$.

Задача №10

От одной и той же станции в одном и том же направлении отправляются два поезда. Скорость первого $30 \frac{км}{ч}$, второго $40 \frac{км}{ч}$. Второй поезд отправляется через $10 \space мин$ после первого. После сорокаминутного движения первый поезд делает пятиминутную остановку, потом продолжает двигаться дальше с прежней скоростью.
Определите графически, когда и на каком расстоянии от станции второй поезд догонит первый. Графическое решение проверьте вычислением.

Дано:
$\upsilon_1 = 30 \frac{км}{ч}$
$\upsilon_2 = 40 \frac{км}{ч}$
$t_{01} = 0 \space мин$
$t_{02} = 10 \space мин$
$t_1 = 40 \space мин$
$t_{1о} = 5 \space мин$

$t — ?$
$S — ?$

Показать решение и ответ

Скрыть

Решение:

Сначала займемся построением графика движения поездов.

По оси $x$ мы будем откладывать время, а по оси $y$ — расстояние. Время оставим в $мин$, а расстояние будем отмечать в $км$.

Построим график движения первого поезда (рисунок 3). Он начинает свое движение в момент времени $t_{01} = 0 \space мин$.

Движется он со скоростью $30 \frac{км}{ч}$ в течение $t_1 = 40 \space мин$. Переведем эту скорость в $\frac{км}{мин}$ и вычислим, какое расстояние этот поезд пройдет за указанное время:
$\upsilon_1 = 30 \frac{км}{ч} = 30 \frac{км}{60 \space мин} = 0.5 \frac{км}{мин}$,
$S_1 = \upsilon_1 t_2$,
$S = 0.5 \frac{км}{мин} \cdot 40 \space мин = 20 \space км$.

Поставим эту точку на графике и соединим с началом координат.

Далее поезд сделал остановку. Этот участок графика будет параллелен оси времени — значение пройденного пути остается постоянным, ведь поезд никуда не двигается.

Далее поезд продолжает движение с прежней скоростью. Без вычислений мы можем провести из точки, соответствующей концу остановки, прямую параллельную первой части графика.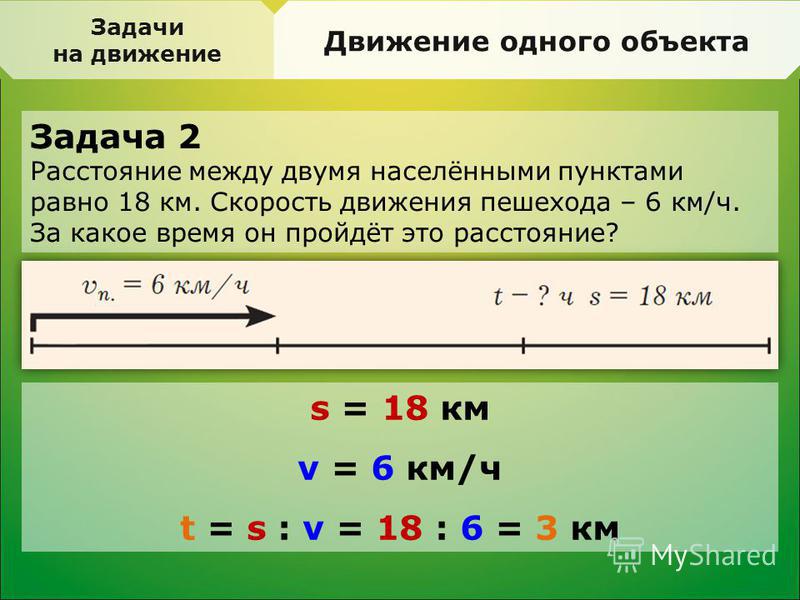

Теперь построим тут же график движения для второго поезда (рисунок 4).

Он начинает свое движение не из начала координат, а из точки, соответствующей времени $t_{02} = 10 \space мин$.

Он движется со скоростью $40 \frac{км}{ч}$. Это означает, что за $1 \space ч = 60 \space мин$ он проходит путь, равный $40 \space км$. Отметим эту точку на координатной плоскости и соединим с точкой начала движения.

Итак, графически мы получили, что

Второй поезд догонит первый в момент времени $t = 40 \space мин$
Поезда встретятся на расстоянии $S = 20 \space км$ от места отправления

Теперь подтвердим полученные данные вычислениями. Поезда встретятся друг с другом, пройдя определенный путь $S$. Это случится через определенное время $t$:
$S = S_1 = S_2$,
$S_1 = \upsilon_1 t$,
$S_2 = \upsilon_2 (t — t_{02})$.

Найдем это время:
$\upsilon_1 t = \upsilon_2 (t — t_{02})$,
$\upsilon_2 t — \upsilon_1 t = \upsilon_2 t_{02}$,
$t (\upsilon_2 — \upsilon_1) = \upsilon_2 t_{02}$,
$t = \frac{\upsilon_2 t_{02}}{\upsilon_2 — \upsilon_1}$.

Перед расчетом переведем $мин$ в $ч$: $t_{02} = 10 \space мин = \frac{10}{60} \space ч = \frac{1}{6} \space ч$.

Теперь рассчитаем время встречи двух поездов:
$t = \frac{40 \frac{км}{ч} \cdot \frac{1}{6} \space ч}{40 \frac{км}{ч} — 30 \frac{км}{ч}} = \frac{4}{6} \space ч = \frac{2}{3} \space ч = 40 \space мин$.

Используя полученное значение времени и скорость движения первого поезда, рассчитаем расстояние, на котором встретятся поезда:
$S = \upsilon_1 t$,
$S = 30 \frac{км}{ч} \cdot \frac{2}{3} \space ч = 20 \space км$.

Ответ: $t = 40 \space мин$, $S = 20 \space км$.

Задача №11

Поезд прошел $25 \space км$ за $35 \space мин$, причем первые $10 \space км$ он прошел в течение $18 \space мин$, вторые $10 \space км$ в течение $12 \space мин$, а последние $5 \space км$ за $5 \space мин$. Определите среднюю скорость поезда на каждом участке и на всем пути.

Дано:
$S = 25 \space км$
$t = 35 \space мин$
$S_1 = 10 \space км$
$t_1 = 18 \space мин$
$S_2 = 10 \space км$
$t_2 = 12 \space мин$
$S_3 = 5 \space км$
$t_3 = 5 \space мин$

$\upsilon_{1ср} — ?$, $\upsilon_{2ср} — ?$, $\upsilon_{3ср} — ?$
$\upsilon_{ср} — ?$

Показать решение и ответ

Скрыть

Решение:

Переведем время из $мин$ в $ч$:

$t = 35 \space мин = \frac{35}{60} \space ч = \frac{7}{12} \space ч$
$t_1 = 18 \space мин = \frac{18}{60} \space ч = \frac{3}{10} \space ч = 0. 3 \space ч$
$t_2 = 12 \space мин = \frac{12}{60} \space ч = \frac{1}{5} \space ч = 0.2 \space ч$
$t_3 = 5 \space мин = \frac{5}{60} \space ч = \frac{1}{12} \space ч$

Теперь рассчитаем среднюю скорость на каждом участке пути:

$\upsilon_{1ср} = \frac{S_1}{t_1}$,
$\upsilon_{1ср} = \frac{10 \space км}{0.3 \space ч} \approx 33.3 \frac{км}{ч}$
$\upsilon_{2ср} = \frac{S_2}{t_2}$,
$\upsilon_{2ср} = \frac{10 \space км}{0.2 \space ч} = 50 \frac{км}{ч}$
$\upsilon_{3ср} = \frac{S_3}{t_3}$,
$\upsilon_{3ср} = \frac{5 \space км}{\frac{1}{12} \space ч} = 60 \frac{км}{ч}$

Рассчитаем среднюю скорость на на всем пути:
$\upsilon_{ср} = \frac{S}{t}$,
$\upsilon_{ср} = \frac{25 \space км}{\frac{7}{12} \space ч} \approx 42.9 \frac{км}{ч}$

Ответ: $\upsilon_{1ср} \approx 33.3 \frac{км}{ч}$, $\upsilon_{2ср} = 50 \frac{км}{ч}$, $\upsilon_{3ср} = 60 \frac{км}{ч}$, $\upsilon_{ср} \approx 42.9 \frac{км}{ч}$.

Как объяснить ребёнку тему «Скорость. Время. Расстояние»

По статистике образовательной платформы iSmart, решение задач на движение входит в топ-10 самых сложных тем по математике для учеников начальной школы. Трудности возникают во взаимосвязях основных понятий и с путаницей в формулах. Давайте разбираться вместе.

С первых шагов человек преодолевает расстояние: от кроватки до игрушки, от дома до школы, от одного города до другого, от Земли до Луны.

Расстояние – это длина от одного пункта до другого, промежуток между чем-либо.

Например: расстояние от Москвы до Сочи 1361 км, от дома до детской площадки – 100 м.

Расстояние измеряется в шагах, в метрах, в километрах и т. д. То есть при измерении расстояния используют меры длины.

Расстояние можно измерить с помощью: линейки, измерительной ленты, рулетки, шагомера и т.п.

Расстояние обозначается латинской буквой S.

Время

Все мы помним, как медленно тянется время урока, когда нам неинтересно. И как быстро оно пролетает, если это любимый урок.
Что же такое время?

Время – это продолжительность каких-то действий, событий.

Например, можно доехать на машине до магазина за 10 минут, а пешком дойти за час.

Измерить время можно минутами, часами, сутками и т. д.
Время измеряют с помощью часов: электронных, механических, песочных, атомных.

Время движения обозначается латинской буквой t.

Скорость

Если ребёнок уже с детства мечтает научиться водить автомобиль, можно рассказать, что в будущем ему точно пригодится знание формулы скорости. Ну и правила дорожного движения не помешают.

Скорость – это расстояние, пройденное за определённое время.

Её можно сравнить и измерить.

В чём же измеряют скорость? В м/сек (метр в секунду), км/ч (километр в час) и т.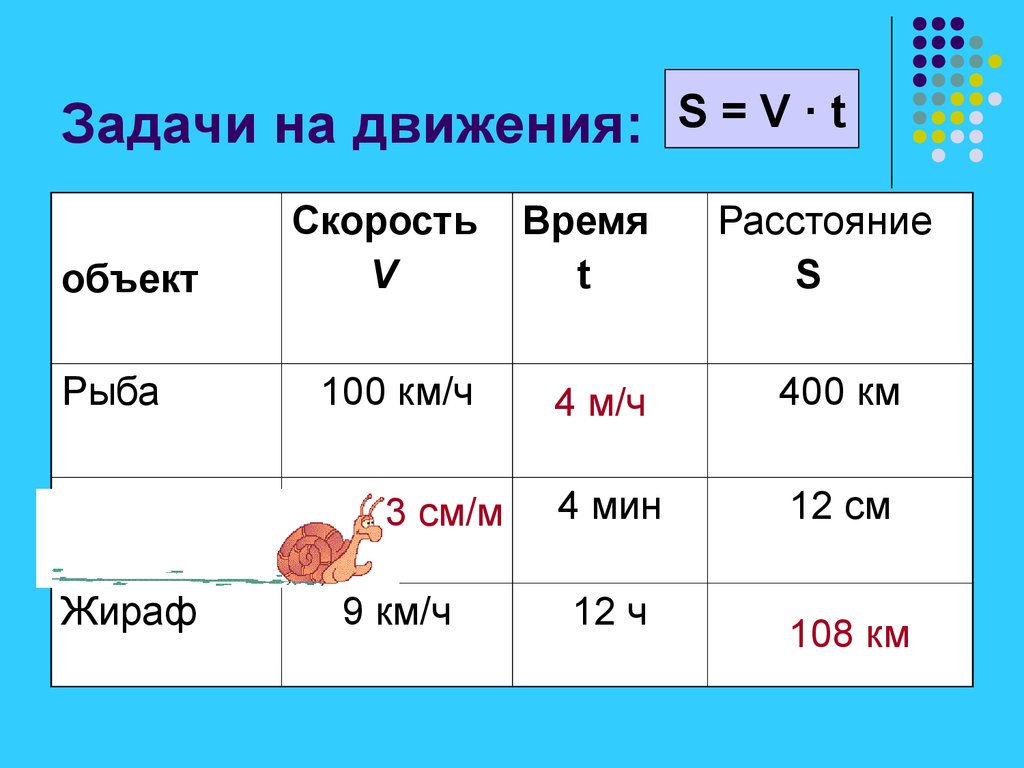

Приборы измерения скорости:

^{Спидометр – прибор, измеряющий скорость движения в автомобиле, мотоцикле, самокате.}
^{Радар – прибор, определяющий превышение скорости движущегося объекта.}

Например:

Опасность! Автомобиль движется с превышением скорости по трассе. На спидометре 200 км/ч. Радар инспектора дорожной полиции зафиксировал превышение скорости.

Скорость обозначают латинской буквой V.

Взаимосвязь расстояния, времени и скорости

Скорость, время и расстояние взаимосвязаны. Как их найти? Существуют формулы определения скорости, времени и расстояния.

А теперь повторим формулы и приступим к работе.

‍

Формула определения расстояния

Чтобы найти расстояние (S), нужно умножить скорость (V) на время движения (t):

S = V × t

‍

Например:

Мотоциклист ехал 4 часа со скоростью 80 км/ч. Какое расстояние он проехал?

Если известны скорость и время, можно найти расстояние. Чтобы найти расстояние нужно:

4 часа – t (время)

80 км/ч – V (скорость)

неизвестно S (расстояние)

S = v (80 км/ч) × t (4 часа) = 320 км

S= 320 км

‍

Формула определения времени

Чтобы найти время (t), нужно разделить расстояние (S) на скорость (V):

t = S : V

‍

Например:

Электросамокат проехал 20 км со скоростью 10 км/ч. Какое время он был в пути? Как найти время, зная скорость и расстояние?

Если известны расстояние и скорость, можно найти время.

20 км – S (расстояние)

10 км/ч – V (скорость)

неизвестно t (время)

t = S (20 км) : 10 (км/ч)= 2 часа

t = 2 часа

Формула определения скорости:

Чтобы найти скорость (V), нужно расстояние (S) разделить на время движения (t):

V = S : t

‍

Например:

Мышка, убегая от кота, пробежала 12 метров до норки за 4 секунды. С какой скоростью она бежала? Как найти скорость?

Если известны расстояние и время, можно найти скорость.

12 м – S (расстояние)

4 сек. – t (время)

неизвестно V (скорость)

Чтобы найти скорость, нужно:

V = S (12м) : t (4 сек.) = 3 м/сек.

V = 3 м/сек.

‍

Чтобы ребёнку легче было запомнить условные обозначения, предложите вариант в стихотворной форме.

Хоть до дома, хоть до небес

Расстояние – это буква S.

И в Париже, и в Москве

Скорость – это буква V.

Точно скажем, без сомнения,

Буква t – это время движения.

‍

5 полезных советов для родителей

А ещё постарайтесь следовать простым советам, которые здорово помогут вам сократить время выполнения домашней работы.

_{1. Не начинайте заниматься с ребёнком, если он голоден, устал, не хочет погружаться в тему или его что-то тревожит. Обязательно настройтесь на позитив.}

_{2. Не ругайте ребёнка, если что-то не получается. Это нормально.}

_{3. Хвалите его и радуйтесь даже незначительным успехам. Это очень важно для ребёнка.}

_{4. Не начинайте новое задание, если не разобрались с предыдущим.}

_{5. Используйте современные онлайн-платформы.}

Если хотите, чтобы ваш ребёнок отточил навык решения задач на движение и добился хороших результатов, предложите ему выполнить задания на о iSmart. Здесь собрано около тысячи примеров на эту тему. Занимаясь 15 минут в день, ваш школьник самостоятельно:

^{устранит пробелы в знаниях;}
^{доведёт до автоматизма вычислительные навыки;}
^{не будет бояться проверочных работ;}
^{повысит успеваемость на 1-2 балла.}

Регистрируйте ребёнка на платформе iSmart и начинайте заниматься.

Лёгких вам совместных решений даже самых сложных задач!

‍

Speed, Distance & Time – Go Teach Maths: Ресурсы ручной работы для учителей математики

Для использования этого ресурса требуется подписка на Go Teach Maths.
Подписка дает доступ к каждому ресурсу на сайте!

Индивидуальная подписка

25 фунтов стерлингов на 1 год

Школьный абонемент

75 фунтов стерлингов на 1 год

Всестороннее освещение темы
Более 6500 учебных ресурсов

Покрытие GCSE и IGCSE

Подписка на Go Teach Maths дает вам доступ к каждому ресурсу на веб-сайте!

Индивидуальная подписка

25 фунтов стерлингов на 1 год

Школьный абонемент

75 фунтов стерлингов на 1 год

Всестороннее освещение темы
Более 6500 учебных ресурсов
Покрытие GCSE и IGCSE

Войдите в свой индивидуально или
школьный аккаунт

Сбросьте свой пароль

Если вы забыли пароль от своей школьной учетной записи, обратитесь к сотруднику, настроившему учетную запись.

Презентации

Демонстрация

Рабочие листы

Цифровая головоломка

2 уровня

Найди ошибку

Лабиринт «Правда или ложь»

Рабочий лист

Представляем «Пер»

Рабочий лист

2 уровня

Рабочий лист

2 уровня

Рабочий лист

С Пифагором

Деятельность

Card Match

Tarsia Jigsaw

Standard

Деятельность под руководством учителя

Бинго

Метод

Крестики-нолики

Перестрелка

Покажи мне

Экзаменационные вопросы

AQA Foundation

Standard

AQA Higher

Standard

Edexcel Foundation

Standard

Edexcel Higher

PPT

Standard

PDF

Small

PDF

9-1 Foundation

Standard

9-1 Higher

Standard

Calculating скорость, расстояние и время

В этом уроке мы научимся вычислять и интерпретировать скорость, расстояние и время.

В этом тесте есть изображения без замещающего текста. Пожалуйста, свяжитесь со своим учителем, который сможет помочь вам с аудиоописанием.

Тест:

Прежде чем мы начнем этот урок, давайте посмотрим, что вы можете запомнить из этой темы. Вот быстрый тест!

расстояние/времяскорость

speedtimevelocitymeters

3 км6,7 км66,7 км60 км

180 км/ч90 км/ч55 км/ч40 км/ч

15 км/ч26 км/ч500 км/ч30 км/ч

В этом тесте есть изображения без замещающего текста.

Тест:

Прежде чем мы начнем этот урок, давайте посмотрим, что вы можете запомнить из этой темы. Вот быстрый тест!

расстояние/времяскорость

speedtimevelocitymeters

3 километра 6,7 километра 66,7 километра 60 километров

180 км/ч90 км/ч55 км/ч40 км/ч

15 км/ч26 км/ч500 км/ч30 км/ч

Эти слайды помогут вам выполнить некоторые задания урока. Если вам нужно повторно воспроизвести видео, нажмите значок «Возобновить видео». Если вас попросят добавить ответы на слайды, сначала загрузите или распечатайте рабочий лист. После того, как вы выполнили все задачи, нажмите «Далее» ниже.

Тест:

Покажите, чему вы научились

расстояние умножить на времярасстояние разделить на времявремя умножить на расстояниевремя разделить на расстояние

3,5 км14 км0,07 км7 км

27 миль в час0,083 мили в час12 миль в час36 миль в час

225 часов20 минут1/3 часа3 часа

61,67 км/ч70 км/ч60 км/ч53,33 км/ч

В этом тесте есть изображения без замещающего текста. Обратитесь к своему учителю, который сможет помочь вам с аудиоописанием.

Тест:

Покажите, чему вы научились

3,5 км14 км0,07 км7 км

27 миль в час0,083 мили в час12 миль в час36 миль в час

225 часов20 минут1/3 часа3 часа

Решение задач на скорость, путь и время движения | 7 класс

Задача №1

Задача №2

Задача №3

Задача №4

Задача №5

Задача №6

Задача №7

Задача №8

Задача №9

Задача №10

Задача №11

Как объяснить ребёнку тему «Скорость. Время. Расстояние»

Speed, Distance & Time – Go Teach Maths: Ресурсы ручной работы для учителей математики

Презентации

Рабочие листы

Деятельность

Деятельность под руководством учителя

Экзаменационные вопросы

Calculating скорость, расстояние и время

Добавить комментарий Отменить ответ