Задачи на множества для дошкольников: Тема: «Множество» | Методическая разработка по математике (подготовительная группа) на тему:
Тема: «Множество» | Методическая разработка по математике (подготовительная группа) на тему:
Муниципальное бюджетное дошкольное образовательное учреждение
детский сад № 57 «Катюша»
Материал подготовила воспитатель:
Говердовская Надежда Алексеевна.
Конспект занятия по математике в подготовительной группе с использованием здоровьесберегающих технологий
Тема: «Множество»
Программное содержание:
Обучающие задачи:
- Познакомить детей с понятием « Множество»
- Учить разбивать множество на подмножества по совместным признакам, дать понятия математического выражения « пересечение множеств»
- Продолжать упражнять детей в составлении задач по картинкам на сложение и вычитание
Развивающие задачи:
- создать условия для развития логического мышления, сообразительности, внимания;
- развивать воображение, умение ориентироваться в пространстве и времени.
- способствовать формированию мыслительных операций
- развитию речи, умению аргументировать свои высказывания.

Воспитательные задачи:
- воспитывать интерес к математическим знаниям;
- воспитывать умение понимать учебную задачу, выполнять ее самостоятельно.
Демонстрационный материал: наглядный материал для решения арифметических задач; карточка со схемой задачи, буквы, таблица-рисунок (с изображением множеств), наборное полотно, цифры и знаки к нему
Раздаточный материал: карточки с числами, конверты с карточками для решения задач, план группы, блоки Дьенеша, круги синего и красного цвета.
.
Предварительная работа:
1. Решение с детьми задач
Методические приемы и методы:
1. Наглядные (использование наглядного материала): использование карточек, таблиц.
2. Словесные (напоминания, указания, беседа, вопросы, индивидуальные ответы детей).
3. Игровые (работа по плану, выкладывание из букв слово « Множество»).
4. Практическая деятельность ( решение задач, выкладывание множеств из геометрических фигур, выкладывание из букв слово « Множество»).
5. Индивидуальный подход.
6. Анализ занятия.
Ход занятия :
Воспитатель: – Ребята, давайте посмотрим, друг на друга, и улыбнемся, настроение у нас хорошее, мы готовы начать занятие.
Ребята, каждое утро мы делаем зарядку. Для чего она нам нужна?
Дети: Чтобы быть здоровыми и крепкими.
Воспитатель: Я с вами согласна. А сейчас я хочу предложить гимнастику для ума. Это вопросы, на которые вы должны ответить :
- Какое сегодня число ?
- Какое число было вчера?
- Прошло 3 дня после воскресения, какой наступил день недели?( четверг)
- Сколько месяцев в году?
- Как называется первый осенний месяц?
- Каким месяцем заканчивается весна?
Умницы, на все вопросы ответили правильно!
Воспитатель: Ребята, хотите узнать тему нашего занятия? Но для этого нужно выполнить задание. Сейчас каждый из вас получит план нашей группы. На нем указано место, где лежит для вас конверт с заданием. Кто найдет свой конверт, садится за стол .
( Дети находят по плану конверт с заданиями)
Воспитатель: Откройте конверты .Что находится в конвертах ?
Дети: Карточки.
Воспитатель : Посмотрите внимательно на карточки. Я предлагаю вам составить по ним каждую свою задачу. Но давайте вспомним из каких частей состоит задача?
Дети: Задача состоит из условия и вопроса.
Воспитатель: Правильно! Решение задачи выложите на листе.
( Дети самостоятельно выполняют задание)
Воспитатель : Я вижу, что вы уже выполнили задание.
( Ребенок выходит к доске , рассказывает составленную задачу, решение задачи показывает на доске)
Воспитатель: Все ли согласны с решением? Да, решение было верным. Молодец!
А теперь посмотрите внимательно на эту схему. У кого из вас условие задачи соответствует этой схеме? Андрюша, выйди, пожалуйста, к доске и расскажи теперь свою задачу.
Воспитатель: А теперь посмотрите на ваши конверты. Что вы видите
на них ? Да на каждом конверте написана буква. Сейчас вы подойдете к доске и поместите такую же букву на то место, которое соответствует ответу вашей задачи. Если вы все правильно выполнили свои задания, то на доске мы сможем прочитать слово.
Сейчас вы подойдете к доске и поместите такую же букву на то место, которое соответствует ответу вашей задачи. Если вы все правильно выполнили свои задания, то на доске мы сможем прочитать слово.
( Дети выкладывают слово « МНОЖЕСТВО» )
Воспитатель: Прочитайте слово. ( Дети читают). Я вижу , что с заданием вы все справились. Молодцы! Ребята, сегодня на занятии мы будим говорить о множестве. Прежде чем приступить к следующему заданию. Я предлагаю сделать небольшую физминутку.
Физминутка. Раз – согнуться, разогнуться.
Два – нагнуться, потянуться.
Три – в ладоши три хлопка
Головою – три кивка;
На четыре – руки шире
Пять, шесть – тихо сесть
Воспитатель: Посмотрите на доску, что на ней находится.
Дети: На ней находятся геометрические фигуры.
Воспитатель: Назовите мне их. ( Дети называют геометрические фигуры)
– Сколько всего кругов?
– Сколько всего треугольников?
– Чего больше треугольников или квадратов?
– Как все эти геометрические фигуры можно назвать одним математическим выражением? ( Ответы детей)
Воспитатель: Я вам подскажу.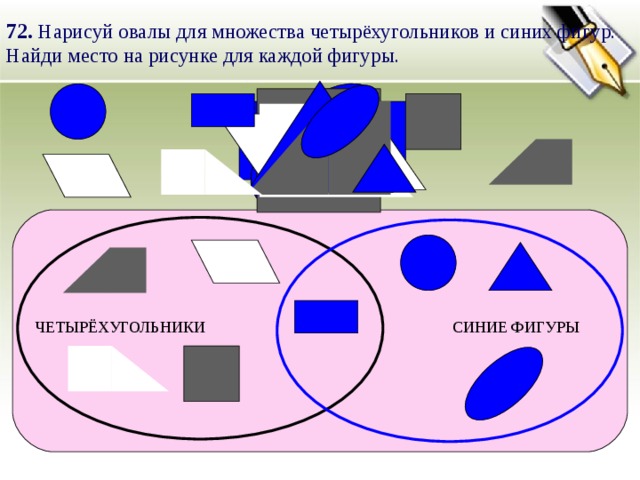 Их можно назвать «множество». Повтори Катя.
Их можно назвать «множество». Повтори Катя.
Посмотрите на это множество и скажите, по каким двум признакам можно разделить его на 2 группы.
Дети: Это множество можно разделить по цвету и форме; по размеру и цвету; по размеру и форме.
Воспитатель: Я с вами согласна. Вы назвали много признаков. Молодцы.
У вас на столе стоят коробки с геометрическими фигурами. Каким математическим выражение мы их можем назвать ? ( Множеством)
Я предлагаю вам выбрать два признака и по ним разделить ваше множество самостоятельно, располагая геометрические фигуры в красные и синие круги. Ярослав разделит мое множество у доски.
( Дети выполняют самостоятельно.)
Воспитатель: Ярослав, положи, пожалуйста, в красный круг все красные фигуры, а в синей- все круги. Сколько множеств стало сейчас? ( Ответы детей)
Воспитатель: По какому признаку объединено первое множество? ( По цвету)
– По какому признаку объединено второе множество?( По форме)
– Сколько множеств получилось у Максима? По какому признаку объединил множества?
Воспитатель:
Итак. Одно множество мы можем разделить на два новых множеств. Каждое новое множество будит иметь один общий признак. В нашем случае первое множество объединено по цвету, а второе множество по форме.
Одно множество мы можем разделить на два новых множеств. Каждое новое множество будит иметь один общий признак. В нашем случае первое множество объединено по цвету, а второе множество по форме.
А теперь встали и сделали гимнастику для глаз
Посмотрите в угол №1. Сколько множеств вы видите?( Одно)
Посмотрите в угол №2 . Сколько множеств вы видите здесь?(Два)
Посмотрите в угол №3. По каким признакам объединены эти множества? ( По цвету и форме)
Посмотрите в угол №4. Сколько здесь множеств? По каким признакам объединены эти множества? А теперь просто посмотрите в угол №1, 2; 3; 4.
Гимнастику для глаз
Глазки вправо, глазки влево,
И по кругу проведем.
Быстро – быстро поморгаем
И немножечко потрем.
Посмотри на кончик носа
И в «межбровье» посмотри.
Круг, квадрат и треугольник
По три раза повтори.
Глазки закрываем,
Медленно вдыхаем.
А на выдохе опять
Глазки заставляй моргать.
А сейчас расслабились
На места отправились.
Воспитатель: Посмотрите на плакат. Сколько множеств на нем изображено?
( Ответы детей)
Воспитатель: А я вижу еще одно подмножество. ( Показать его) Кто догадался, в результате чего оно получилось? ( Ответы детей)
Воспитатель: Я вам подскажу. Оно получилось в результате пересечения первого множества и второго множества, поэтому так и называется
« пересечение множеств». Повтори Андрюша.
Назовите фигуры, которые попали в это пересечение множеств. ( Все круги красного цвета)
Воспитатель: Правильно! Фигуры . которые попадают в пересечение множеств будут иметь признаки, которые возьмут у первого множества и у второго множества.
– Какой признак взяли геометрические фигуры у первого множества?( Из первого множества они взяли цвет)
– Какой признак взяли геометрические фигуры у второго множества?( Из первого множества они взяли форму)
Воспитатель: Молодцы! В пересечении множеств оказались все фигуры круглой формы красного цвета.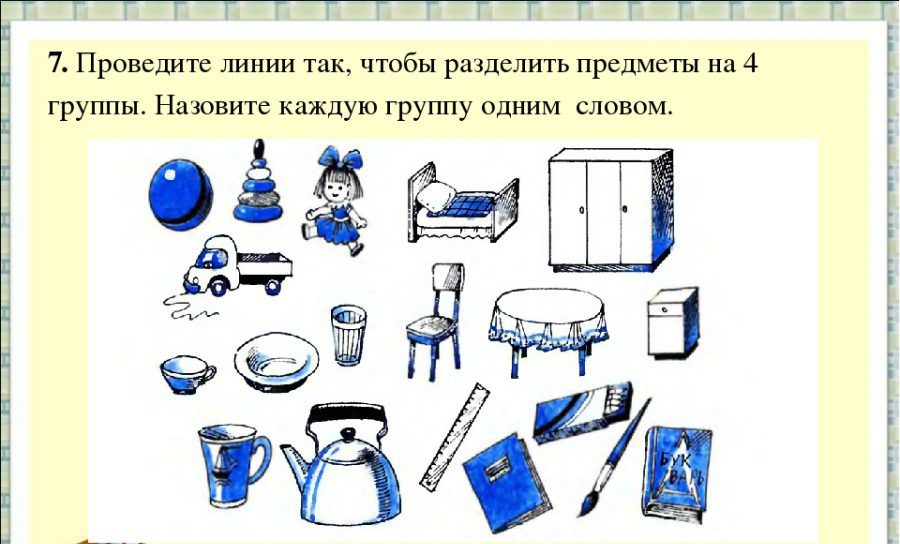 А теперь поработайте самостоятельно. Расположите свои круги так, чтобы они пересеклись, как у меня на плакате. Покажите место их пересечения. В это место положите такие геометрические фигуры, которые имеют признаки первого множества и признаки второго множества.
А теперь поработайте самостоятельно. Расположите свои круги так, чтобы они пересеклись, как у меня на плакате. Покажите место их пересечения. В это место положите такие геометрические фигуры, которые имеют признаки первого множества и признаки второго множества.
( Дети выполняют работу самостоятельно)
Воспитатель: Катя, какие фигуры пополи у тебя в пересечение множеств?
– Юля, покажи где у тебя пересечение множеств? Какие фигуры попали в это пересечение? Молодцы! Все с заданием справились.
Итак, с каким новыми математическими выражениями мы сегодня познакомились?
ГБДОУ детский сад №14 Василеостровского района
КАК РЕШАТЬ МАТЕМАТИЧЕСКИЕ ЗАДАЧИ
К моменту поступления в школу дети должны усвоить относительно широкий круг взаимосвязанных знаний о множестве и числе, форме и величине, научиться ориентироваться в пространстве и во времени.
В процессе математического и общего умственного развития детей дошкольного возраста существенное место занимает обучение их решению и составлению простых математических задач. В детском саду проводится подготовительная работа по формированию у детей уверенных навыков вычислений при сложении и вычитании однозначных чисел и быстрых устных вычислений с двузначными числами с целью подготовки их к обучению в начальной школе. Если в школе обучение вычислениям ведется при решении примеров и арифметических задач, то в практике работы дошкольных учреждений принято знакомить детей с арифметическими действиями и простейшими приемами вычисления на основе простых задач, в условии которых отражаются реальные, в основном игровые и бытовые ситуации. В условии задачи указываются связи между данными числами, а также между данными и искомыми. Эти связи и определяют выбор арифметического действия.
В детском саду проводится подготовительная работа по формированию у детей уверенных навыков вычислений при сложении и вычитании однозначных чисел и быстрых устных вычислений с двузначными числами с целью подготовки их к обучению в начальной школе. Если в школе обучение вычислениям ведется при решении примеров и арифметических задач, то в практике работы дошкольных учреждений принято знакомить детей с арифметическими действиями и простейшими приемами вычисления на основе простых задач, в условии которых отражаются реальные, в основном игровые и бытовые ситуации. В условии задачи указываются связи между данными числами, а также между данными и искомыми. Эти связи и определяют выбор арифметического действия.
Первый этап – подготовительный. Основная цель этого этапа – организовать систему упражнений по выполнению операций над множествами. Так, подготовкой к решению задач на сложение являются упражнения по объединению множеств. Упражнения на выделение части множества проводятся для подготовки детей к решению задач на вычитание. С помощью операций над множествами раскрывается отношение «часть — целое», доводится до понимания смысл выражений «больше на…», «меньше на…» Учитывая наглядно-действенный и наглядно-образный характер мышления детей, следует оперировать такими множествами, элементами которых являются конкретные предметы.
С помощью операций над множествами раскрывается отношение «часть — целое», доводится до понимания смысл выражений «больше на…», «меньше на…» Учитывая наглядно-действенный и наглядно-образный характер мышления детей, следует оперировать такими множествами, элементами которых являются конкретные предметы.
На втором этапе нужно учить детей составлять задачи и подводить к усвоению их структуры. Детей учат устанавливать связи между данными и искомым и на этой основе выбирать для решения необходимое арифметическое действие. Подводить к пониманию структуры задачи лучше всего на задачах-драматизациях. Воспитатель знакомит детей со словом задача и при разборе составленной задачи подчеркивает необходимость числовых данных и вопросов: «Что известно?», «Что нужно узнать?».
На этом этапе обучения составляются такие задачи, в которых вторым слагаемым или вычитаемым является число 1. Это важно учитывать, чтобы не затруднять детей поиском способов решения задачи. Прибавить или вычесть число 1 они могут на основе имеющихся у них знаний об образовании последующего или предыдущего числа.
Прибавить или вычесть число 1 они могут на основе имеющихся у них знаний об образовании последующего или предыдущего числа.
При обучении дошкольников составлению задач важно показать, чем отличается задача от рассказа, загадки, подчеркнуть значение и характер вопроса
Для усвоения значения и характера вопроса в задаче можно применить такой прием; к условию задачи, составленной детьми («С одной стороны стола поставили двух девочек, а с другой стороны одного мальчика»), ставится вопрос не арифметического характера («Как зовут этих детей?»). Дети замечают, что задача не получилась. Далее можно предложить им самим поставить такой вопрос, чтобы было понятно, что это задача.
Чтобы показать отличие задачи от рассказа и подчеркнуть значение чисел и вопроса в задаче, воспитателю следует предложить детям рассказ, похожий на задачу. В рассуждениях по содержанию рассказа отмечается, чем отличается рассказ от задачи.
Чтобы научить детей отличать задачу от загадки, воспитатель подбирает такую загадку, где имеются числовые данные. Например: «Два кольца, два конца, а посередине гвоздик». «Что это?» – спрашивает воспитатель. «Это не задача, а загадка»,- говорят дети. «Но ведь числа указаны»,- возражает воспитатель. Однако ясно, что в этой загадке описываются ножницы и решать ничего не надо.
Например: «Два кольца, два конца, а посередине гвоздик». «Что это?» – спрашивает воспитатель. «Это не задача, а загадка»,- говорят дети. «Но ведь числа указаны»,- возражает воспитатель. Однако ясно, что в этой загадке описываются ножницы и решать ничего не надо.
На конкретных примерах из жизни дети яснее осознают необходимость иметь два числа в условии задачи, лучше усваивают отношения между величинами, начинают различать известные данные в задаче и искомое неизвестное.
После таких упражнений можно подвести детей к обобщенному пониманию составных частей задачи.
Детям надо объяснить, что решать задачу – это значит понять и рассказать, какие действия нужно выполнить над данными в ней числами, чтобы получить ответ. Таким образом, структура задачи включает четыре компонента: условие, вопрос, решение, ответ: Выяснив структуру задачи, дети легко переходят к выделению в ней отдельных частей. Дошкольников следует поупражнять в повторении простейшей задачи в целом и отдельных ее частей.
Далее задача анализируется, выясняется, что известно из задачи (поставили шесть стульев, а затем один убрали) и что неизвестно (сколько стульев осталось у стола). Детям предлагается решить задачу и ответить на ее вопрос.
Обучающее значение приведенных выше задач на сложение и вычитание состоит не столько в том, чтобы получить ответ, а в том, чтобы научить анализировать задачу и в результате этого правильно выбрать нужное арифметическое действие.
Итак, на втором этапе работы над задачами дети должны: а) научиться составлять задачи; б) понимать их отличие от рассказа и загадки; в) понимать структуру задачи; г) уметь анализировать задачи, устанавливая отношения между данными и искомым.
Учить детей формулировать арифметические действия сложения и вычитания – задача третьего этапа.
На предыдущей ступени дошкольники без затруднения находят ответ на вопрос задачи, опираясь на свои знания последовательности чисел, связей и отношений между ними. Теперь же нужно познакомить с арифметическими действиями сложения и вычитания, раскрыть их смысл, научить формулировать их и «записывать» с помощью цифр и знаков в виде числового примера.
Прежде всего, детей надо научить формулировать действие нахождения суммы по двум слагаемым при составлении задачи по конкретным данным (пять рыбок слева и одна справа).
На основе предложенного наглядного материала составляются еще одна-две задачи, с помощью которых дети продолжают учиться формулировать действие сложения и давать ответ на вопрос.
На первых занятиях словесная формулировка арифметического действия подкрепляется практическими действиями: «К трем красным кружкам прибавим один синий кружок и получим четыре кружка». Но постепенно арифметическое действие следует отвлекать от конкретного материала: «Какое число прибавили к какому?» Теперь уже при формулировке арифметического действия числа не именуются. Спешить с переходом к оперированию отвлеченными числами не следует. Такие абстрактные понятия, как «число», «арифметическое действие», становятся доступными лишь на основе длительных упражнений детей с конкретным материалом.
Когда дети усвоят в основном формулировку действия сложения, переходят к обучению формулировке вычитания. Работа проводится аналогично тому, как это описано выше.
При формулировке арифметического действия можно считать правильным, когда дети говорят вычесть, сложить. Слова сложить, вычесть, получится, равняется, являются специальными математическими терминами. Этим терминам соответствуют бытовые слова прибавить, отнято, стало, будет. Разумеется, бытовые слова ближе опыту ребенка и начинать обучение можно с них. Но желательно, чтобы воспитатель в своей речи пользовался математической терминологией, постепенно приучая и детей к употреблению этих слов. Например, ребенок говорит: «Нужно отнять из пяти яблок одно», а воспитатель должен уточнить: «Нужно из пяти яблок вычесть одно яблоко».
Этим терминам соответствуют бытовые слова прибавить, отнято, стало, будет. Разумеется, бытовые слова ближе опыту ребенка и начинать обучение можно с них. Но желательно, чтобы воспитатель в своей речи пользовался математической терминологией, постепенно приучая и детей к употреблению этих слов. Например, ребенок говорит: «Нужно отнять из пяти яблок одно», а воспитатель должен уточнить: «Нужно из пяти яблок вычесть одно яблоко».
Упражняя детей и формулировке арифметического действия, полезно предлагать задачи с одинаковыми числовыми данными на разное действие. Например: «У Саши было три воздушных шара. Один шар улетел. Сколько шаров осталось?» Или: «Коле подарили три книги и одну машину. Сколько подарков получил Коля?» Устанавливается, что это задачи на одно и то же действие. Важно при этом обращать внимание на правильную и полную формулировку ответа на вопрос задачи.
Можно показывать задачи и внешне похожие, но требующие выполнения разных арифметических действий.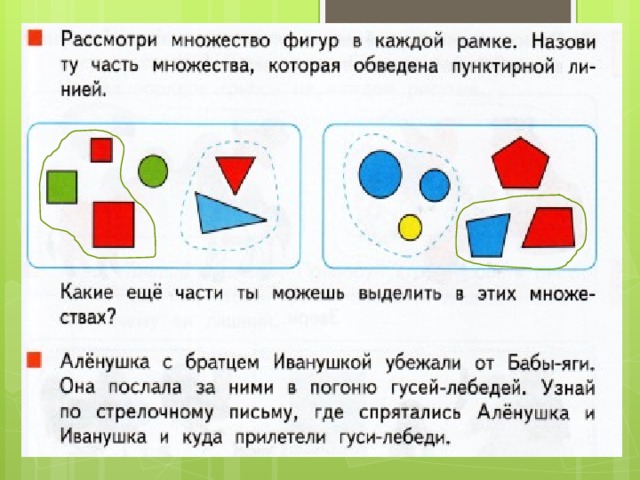 Например: «На дереве сидели четыре птички, одна птичка, улетела. Сколько птичек осталось на дереве?» Или: «На дереве сидели четыре птички. Прилетела еще одна. Сколько птичек сидит на дереве?» Хорошо, когда подобные задачи составляются одновременно и детьми.
Например: «На дереве сидели четыре птички, одна птичка, улетела. Сколько птичек осталось на дереве?» Или: «На дереве сидели четыре птички. Прилетела еще одна. Сколько птичек сидит на дереве?» Хорошо, когда подобные задачи составляются одновременно и детьми.
На основе анализа данных задач дети приходят к выводу, что хотя в обеих задачах речь идет об одинаковом количестве птичек, но они выполняют разные действия.
Такое сопоставление задач, их анализ полезны детям, так как они лучше усваивают как содержание задач, так и смысл арифметического действия, обусловленного содержанием.
Работа над задачами не только обогащает детей новыми знаниями, но и дает богатый материал для умственного развития.
НИИ Эврика. Понятие «множество» для дошкольников
развивающие занятия для детей 3–4 лет, развивающие занятия для детей 5–7 лет 22 марта 2018
Добрый день, уважаемые взрослые! Сегодня мы рассмотрим понятие «множество» для дошкольников — один из важнейших математических терминов. Ваш малыш когда-нибудь спрашивал у вас, кого же на свете больше: птиц или зверей? А арбуз — это растение или фрукт? А лодка — это транспорт или плавательное средство?
Ваш малыш когда-нибудь спрашивал у вас, кого же на свете больше: птиц или зверей? А арбуз — это растение или фрукт? А лодка — это транспорт или плавательное средство?
Умение распределять предметы и живые существа в группы, наделённые определёнными признаками, — это важный этап развития ребёнка. К тому же это благодатная почва для развития:
- логики;
- мышления;
- математических способностей.
Знакомим малыша с понятием «множество»
В возрасте 2–3 лет кроха с удовольствием рассматривает картинки, на которых изображены животные, растения, транспорт и другие группы предметов. Это подходящий момент для того, чтобы научить малыша систематизировать и упорядочивать информацию и производить над множеством различные операции. Как это сделать?
Предложите крохе разложить игрушки по разным ёмкостям: машинки — в одни ящик, животных — в другой ящик, а детали конструктора — в третий ящик. Спросите у крохи:
- «Чем занимаются машинки? Они перевозят людей и грузы».
 Скажите малышу, что этим они отличаются от других предметов и устройств.
Скажите малышу, что этим они отличаются от других предметов и устройств. - «А для чего нужны детали конструктора? Это строительный материал».
- «А много ли у тебя машинок или животных?»
В результате вашей беседы ребёнок поймёт, что разные группы предметов имеют разные свойства и признаки. А также, если элементов много, можно сказать слово «множество» и дать ему название. Делаем вывод: «множество» — от слова «много», а «много» — это больше, чем один.
Развивающие занятия с группами предметов
Продолжайте развивать способность малыша структурировать информацию. Для этого ненавязчиво предложите ему следующие занятия.
«Назови множество»
Покажите ему серию карточек с изображением, например, различных рыб. Попросите назвать эту коллекцию одним словом. Также можно показать ребёнку изображения птиц, одежду, обувь, мебель, растения, животных, музыкальные инструменты. Для детей 5–6 лет предлагайте и более сложные варианты, например геометрические фигуры, природные явления, народные костюмы.
Второй вариант для этого занятия — подобрать название множества для нескольких одинаковых элементов:
- Как называется группа поющих людей? Хор.
- Как называют много пасущихся лошадей? Табун. А овец? Стадо.
- Как называются пчёлы, летящие вместе? Рой.
- Как называют спортсменов, выступающих или играющих вместе? Команда.
- Как называют большое собрание книг? Библиотека. А картин? Галерея или выставка.
«Выдели подмножество»
Поговорите с ребёнком о его группе в детском саду или о детях на площадке во дворе. Например: «Скажи, кто ходит в твою группу?» Дети. «Как их зовут?», «А чем отличается Катя от Пети?» Правильно, Катя — девочка, а Петя — мальчик. Значит, группу детей можно разделить на подмножества «девочки» и «мальчики».
Таким же образом разделите группу «растения» на подмножества «деревья», «кустарники», «трава» и другие. Музыкальные инструменты могут делиться на струнные, духовые, ударные и т. д.
Свой — чужой
Спросите у крохи, принадлежит ли предмет указанному множеству:
- солнце — горячим предметам;
- цветы — украшениям;
- трава — множеству еды;
- скала — множеству всего живого на планете Земля;
- крокодил — рептилиям.

Кто лишний?
Попросите ребёнка найти лишний элемент в группе и объяснить своё решение:
- Карандаш, альбом, краски, кисть, мороженое.
- Красный, синий, зелёный, белый, розовый, пушистый.
- Грусть, злость, тоска, скука, веселье.
- Медведь, заяц, лиса, белка, волк, корова.
Операции с множествами
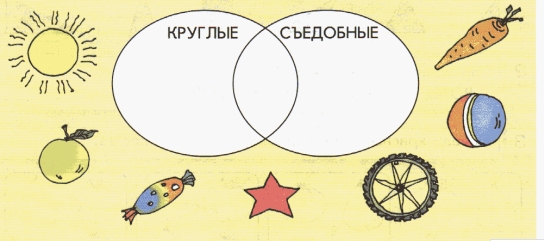
Множества могут пересекаться, не пересекаться или быть вложенными одно в другое. Как рассказать это дошкольнику? На примере обручей или колец.
- Непересекающиеся множества. Положите на пол 2 обруча или обозначьте круги верёвками на небольшом расстоянии друг от друга. Теперь перемешайте, например, кубики и мячики и попросите ребёнка разложить их в 2 разных кольца. Объясните малышу, что эти множества не пересекаются, то есть не имеют общего пространства.
- Пересекающиеся множества. Положите на пол обручи таким образом, чтобы у них было общее пространство, то есть один должен немного накладываться на другой.
 Теперь попросите кроху из кучи игрушек выбрать только машинки и синие предметы, а затем разложить их в круги. Эта задачка посложнее, ведь тут есть варианты:
Теперь попросите кроху из кучи игрушек выбрать только машинки и синие предметы, а затем разложить их в круги. Эта задачка посложнее, ведь тут есть варианты:
- Куда отправится жёлтая машинка? В поле одного кольца.
- Куда положим синий мячик? В поле другого кольца.
- А куда же нужно поместить синюю машинку? Она отвечает сразу двум условиям: и «машинка», и «синего цвета». Значит, её нужно положить на пересечении двух кругов.
- Вложенные множества. Возьмите 2 окружности разного диаметра и поместите меньший круг в больший. Теперь попросите кроху разложить 2 группы предметов: игрушки и куклы. Но вот интересный нюанс: кукла — это тоже игрушка. Поэтому её нужно поместить в поле меньшего круга. А вот остальные игрушки нужно поместить в область большего круга.
Чтобы усложнить задачу, предлагайте ребёнку разложить вещи или картинки с изображениями в 2 и более кольца, но сами не выкладывайте круги в правильное положение. Пусть малыш догадается сам, как это сделать.
Пусть малыш догадается сам, как это сделать.
Или разложите обручи, а ребёнок пусть сам придумает для них правильную задачку. Варианты могут выглядеть так:
1.
Например: машинки, книжки, куклы.
2.
Например: предметы из пластика, вилки (в 2 верхних круга), ложки (нижний круг).
3.
Например: кубики, красные игрушки, жёлтые игрушки.
4.
Например: игрушки (большой круг), мячики (средний круг), зелёные мячики (маленький круг).
Множества для детей: от интересных игр до сложных задач
Вы убедились, уважаемые взрослые, что головоломки с группами предметов отлично развивают логику и смекалку не только у детей? К тому же они позволяют проявить фантазию и учат малышей структурировать и анализировать информацию. Помогите вашему ребёнку разобраться с этим увлекательным понятием математики при помощи:
- занимательных бесед;
- вопросов с подвохом;
- различных предметов, картинок и обручей.
Ну а мы желаем вам учиться вместе с крохой творчески и увлечённо!
Понравился материал?
Расскажите о нем свои знакомым, нажав на одну из кнопок соц. сетей:
сетей:
Учение о числовых множествах Джин Уоррен
Учение о числовых множествах Джин Уоррен
|
| ||||||||||||||||||||||||||||||||
15 лучших заданий по сортировке для дошкольников
С этими заданиями по сортировке для дошкольников научить детей сравнивать и сортировать никогда не будет так просто. Этот пост поможет вашему дошкольнику научиться сравнивать, упорядочивать и сортировать. Вы узнаете, почему эти навыки важны и как их развивать. Помогите своим дошкольникам быстро овладеть навыками наблюдения, сравнения и группировки. .. и все это самостоятельно!
.. и все это самостоятельно!
Это ваше окончательное руководство как стать успешным родителем-учителем в обучении дошкольников сравнению и сортировке.
Что нужно знать об обучении детей сортировке и сравнению
Существует так много практических способов научить сравнивать и сортировать!Хотите верьте, хотите нет, но навыки сортировки начинают развиваться в младенчестве.
Ребенок плачет или смеется, что вызывает реакцию родителей, и он немедленно начинает изучать, какие из них наиболее эффективны для получения желаемого. Она быстро учится организовывать эти ответы и начинает понимать свой мир.
Дети продолжают сортировать и классифицировать, систематизируя свое понимание языка, людей и объектов в своем окружении. Это помогает им построить понимание того, как различные части их окружения связаны с ними самими и друг с другом.
Проще говоря, они определяют сходства и различия. Этот процесс является первым шагом ребенка в математических действиях по сопоставлению, сортировке и классификации.
Что такое сортировка и сравнение для дошкольников?
Сортировка — это способность определять сходства и различия между набором объектов, а также соответствующим образом группировать и называть их. Такая организация характерна для целого ряда дисциплин, включая математику, естествознание и музыку.
Сортировка систематическая. Это заказ. Это сравнение и противопоставление. Сортировка — это сопоставление, а также самая основная форма алгебры.
В дошкольном возрасте навыки сортировки и сравнения включают:
- сортировка по цвету
- сопоставление
- сравнение
- упорядочивание
- классификация
- сортировка по размеру
- сортировка по форме
продвинутые концепции алгебры, которые будут изучены в последующие годы.
Преимущества занятий по сортировке для дошкольников
Сортировка помогает маленьким детям делать наблюдения о сходстве и различии вещей, что является двумя важными навыками ранней грамотности и математики.
Будучи взрослыми, мы каждый день сортируем вещи. Перед стиркой мы сортируем белье по цвету. Мы носим одинаковые туфли, которые, вероятно, парами лежали в шкафу. И разделите наше столовое серебро в специальном органайзере в ящике.
Один из самых важных навыков, которым когда-либо учатся дети, — это обработка информации. Сортировка может помочь им в этой важной способности. Это улучшит успеваемость в школе, но, что более важно, развивает важные исполнительные функции, которые необходимы в жизни после школы!
Этот дошкольник сортирует бусины по цвету.Советы по обучению сортировке
Расширение Мичиганского государственного университета сообщает, что в целом процесс сортировки включает три этапа:
- Дети решают, по какой характеристике сортировать.
- Дети должны физически рассортировать предметы. (Здесь нет рабочих листов!)
- Они смогут объяснить причину сортировки.
Описание их обоснования побуждает детей думать о других характеристиках, по которым следует сортировать.
Процесс обучения сортировке
Естественно, когда дети в раннем детстве исследуют окружающую их среду, они замечают, что вещи похожи и различны. Ваш дошкольник заметит, когда вы купите новые стаканы или когда за ужином вы использовали маленькие тарелки, а не большие.
Дети начинают сортировать по характеристикам, которые имеют для них значение, обычно начиная с таких характеристик, как цвет, размер и форма. В конечном итоге они перейдут к текстуре и звуку.
Большинство детей сначала сопоставляют конкретные объекты, такие как кубики одного цвета или пуговицы одинаковой формы, потому что это проще для развития. Затем они переходят к совпадающим картинкам или кусочкам головоломки. Ребенок развивает навыки естественным образом, постепенно прогрессируя в сложности.
Когда ребенок сопоставляет более двух объектов, они сортируются. Сортировка включает в себя разделение объектов на группы в соответствии с их сходством, что означает, что они также замечают различия. Это также сортировка, когда ваш малыш или дошкольник выстраивает всех своих пони в прямую, чистую линию.
Это также сортировка, когда ваш малыш или дошкольник выстраивает всех своих пони в прямую, чистую линию.
У детей есть свои представления о сортировке
У детей могут быть свои представления о том, как связаны между собой объекты. Это не только нормально, но и поощряется. Дошкольники получают пользу от собственной деятельности по сортировке и определения условий своей сортировки.
Например, когда дошкольника просят рассортировать пуговицы по группам, он может сложить вместе звездочки и сердечки, потому что у них обоих есть точки. Точно так же они могут соединять круги, овалы и сердца вместе, потому что все они имеют «гибкие части». Или они могут сортировать их, сравнивая размеры, объединяя в группы большие и маленькие!
Пока дошкольник может объяснить свой выбор, это абсолютно нормально, потому что происходит серьезное критическое мышление и решение проблем!
Это важные аспекты предварительной сортировки. Используйте эти возможности, чтобы поговорить со своим от дошкольника до малыша, и позвольте им поделиться идеями.
Используйте эти возможности, чтобы поговорить со своим от дошкольника до малыша, и позвольте им поделиться идеями.
Как я могу бросить вызов своему дошкольнику, когда он сортирует и сравнивает?
Начните с обучения детей ясельного и дошкольного возраста цветам, а затем попрактикуйтесь в их сопоставлении и сортировке. На моем сайте есть много учебных пособий по цвету и обучающих мероприятий, в том числе много бесплатных ресурсов — просто воспользуйтесь строкой поиска и найдите «сортировка по цвету».
Можно сортировать по цвету все что угодно!Освоив это, вы можете научить дошкольников сортировать животных (суша или вода), одежду (лето или зима) или игрушки (кубики или лего).
После того, как дошкольники освоят классификацию по одному признаку, они, безусловно, могут начать сортировку по более чем одному признаку, например, вытащить все красные сердечки из корзины для пуговиц, но оставить красные звездочки позади.
Занятия по сортировке и сравнению в школе или дома для дошкольников
Занятия по сортировке наиболее полезны, когда они связаны с повседневной жизнью, чтобы дети могли видеть математику в своем повседневном мире. Дошкольные занятия по сортировке цветов — одни из самых простых!
Дошкольные занятия по сортировке цветов — одни из самых простых!
Для эффективного обучения сортировке не нужны специальные манипуляторы в классе. На самом деле, есть много занятий по сортировке и классификации для дошкольников, которые вы можете выполнять с предметами, которые у вас есть под рукой!
Вот некоторые другие простые задания по сортировке, которые вы можете помочь своему дошкольнику отсортировать и сравнить без какой-либо подготовки! Вы можете добавить их в любой из своих планов уроков для дошкольников.
- Размещение столового серебра
- Сортировка белья
- Размещение собственного белья (распределение по соответствующим ящикам)
- Сортировка продуктов по месту их хранения (холодильник, кладовая или шкаф)
- Размещение игрушек кто сказал, что с едой нельзя играть?)
- Картинки для размещения в фотоальбоме (по событию или теме)
- Сортировка мелков по цвету или длине
сортировка задач. Будь креативным. Вы не ограничены действиями по сортировке цветов!
Вы не ограничены действиями по сортировке цветов!
В следующий раз, когда ваш ребенок будет помогать вам убирать игрушки, попросите все игрушки с определенными характеристиками, такими как размер, цвет или форма. Затем вы можете перейти к объектам определенного типа или с определенной функцией, например к игрушкам, которые издают шум или которые можно прижимать друг к другу, складывать друг на друга или катить. Это также может стать отличным уроком непрямой лексики!
Эта задача сортировки немного сложнее.Используйте книжки с картинками для обучения сортировке!
В дошкольном классе или дома никогда не бывает слишком много книжек с картинками!! Их можно использовать для обучения или закрепления практически любых навыков, включая сортировку и сравнение! Вот некоторые из наших любимых.
Получите ежедневные уроки в разделе «Сравнение и сортировка» для дошкольников
Избавьтесь от ненужной нагрузки при обучении дошкольников сравнению и сортировке, следуя этим простым пошаговым планам уроков по сортировке. Вы получите четыре недели ежедневных уроков сортировки для вашего дошкольника, а также дополнительные занятия, советы для учителей, занятия по интеграции грамотности и даже еженедельные распечатанные дошкольные центры.
Вы получите четыре недели ежедневных уроков сортировки для вашего дошкольника, а также дополнительные занятия, советы для учителей, занятия по интеграции грамотности и даже еженедельные распечатанные дошкольные центры.
Этот модуль является систематическим, что означает, что навыки развиваются таким образом, который подходит для развития дошкольников. А так все по делу и весело! Модуль “Сравнение и сортировка” для дошкольников включает в себя все необходимое, чтобы научить вашего дошкольника навыкам сортировки и дифференцирования.
БЕСПЛАТНЫЕ ЗАНЯТИЯ ДЛЯ ДОШКОЛЬНИКОВ ПО СОРТИРОВКЕ
Сортировка и сравнение расходных материалов
При обучении сравнению и сортировке может быть очень полезно иметь разнообразные материалы для работы! Их можно использовать с матами для сортировки по цвету и многими другими видами сортировки. Вот некоторые из наших любимых.
Секреты обучения математике дошкольников
Обучение математике — это огромная задача, а с новыми изменениями в принятых государственных стандартах планка для учителей поднялась еще выше.
Это потому, что преподавание математики требует многого.
Всеобъемлющий и систематический. И графика — это только одна часть головоломки.
Математики указывают, что существует пять математических дисциплин (как упомянуто выше), которые следует преподавать, а именно:
- чувство чисел и разложить числа и понять их различные отношения
- алгебра – понимание закономерностей и отношений, включая сортировку и классификацию
- геометрия – понимание пространственных отношений, предложных терминов и свойств двух- и трехмерных фигур
- измерение – способность делать сравнения и упорядочивать, понимать измеряемые атрибуты
- анализ данных и вероятность – (вы здесь) понимать данные как средство обмена организованной информацией и понимать, что определенные переменные влияют на данные
Ежедневные уроки математики для дошкольников
Помните, я говорил, что обучение математике дошкольников носит систематический характер? То есть нельзя ставить телегу впереди лошади. Когда дело доходит до обучения математике, навыки должны преподаваться в нужное время и в правильном порядке.
Когда дело доходит до обучения математике, навыки должны преподаваться в нужное время и в правильном порядке.
Упростите обучение математике в дошкольных учреждениях с помощью готовых ежедневных уроков в программе дошкольной математики.
Сара Панкони, MAT
Я Сара, педагог, ставшая домохозяйкой пятерых детей! Я владелец и создатель Stay At Home Educator, веб-сайта о преднамеренном обучении и целенаправленном обучении в раннем детстве. Я преподавал на разных уровнях, от дошкольного до колледжа, и всего понемногу между ними. Сейчас я сосредоточен на обучении своих детей и управлении дошкольным учреждением из моего дома. Полномочия включают: бакалавры в области искусства, магистры в учебной программе и инструкции.
stayathomeeducator.com/
Наборы
Math Strands
AllPrecursor Concepts (13) Наборы (25) Шаблоны (19) Смысл числа (51) Подсчет (50) Операции с числами (42) Измерение (33) Анализ данных (20) ) Пространственные отношения (28) Форма (34)
Типы
AllActivities (71) Видео (188) Статьи (35) Книги (55) Игры (21) Загрузки (10) для
Аудитория
AllAdult Learners (61) Младенцы (35) Малыши (35) Pre-K (303) Детский сад (29)1) 1-й класс (164) 2-й класс (122) 3-й класс (116)
Специальные темы
AllRacial Justice (5) Семейная математика (32) Изучающие английский язык (36)
Наборы являются основой мышления и обучения детей. Они также являются основой нашей системы счисления. Одна из самых важных задач каждого числа — описать, «сколько» их в наборе вещей — будь то один, семь или триста девятнадцать. Прежде чем мы сможем вычислить, сколько яблок, мы должны решить, какие вещи являются яблоками, а какие нет. Как только мы создали множество вещей, которые являются яблоками, возможно, отделив их от апельсинов, мы можем их сосчитать. Для счета требуется набор, и в результате свойства наборов оказывают большое влияние на систему счисления с основанием 10 и на математику.
Они также являются основой нашей системы счисления. Одна из самых важных задач каждого числа — описать, «сколько» их в наборе вещей — будь то один, семь или триста девятнадцать. Прежде чем мы сможем вычислить, сколько яблок, мы должны решить, какие вещи являются яблоками, а какие нет. Как только мы создали множество вещей, которые являются яблоками, возможно, отделив их от апельсинов, мы можем их сосчитать. Для счета требуется набор, и в результате свойства наборов оказывают большое влияние на систему счисления с основанием 10 и на математику.
Авторские права: Сотрудничество ранней математики Эриксоновского института. Перепечатано из книги «Большие идеи ранней математики: что нужно знать учителям маленьких детей» (2014 г.), Pearson Education.
Серия: Идеи в действии
6 июня 2022
Оказывается, математическое мышление развивается в общении с другими; спрашивая учащихся: «Откуда вы это знаете?» раскроет способности ребенка к математическому мышлению. Способность объяснить свои мысли — это когнитивный скачок, который требует защищенного времени для содержательного разговора.
- Тема: Наборы, Чувство чисел
- Возраст/класс Уровень: Pre-K, Детский сад, 1-й класс, 2-й класс, 3-й класс
- Метки Изучающий английский язык, Числовые разговоры
Серия: Ideas at Work
25 мая , 2020Игры, в которые можно играть дома с использованием атрибутов для математического мышления
En Español También. Язык и математика имеют много общего! Например, каждый раз, когда вы описываете что-то — например, как красное, высокое, липкое или громкое — вы помогаете определить и классифицировать вещи. И определение и…
- Тема: Наборы
- Возраст/класс Уровень: Дошкольный, Детский сад, 1-й класс, 2-й класс, 3-й класс
- Теги Игры, Сортировка, Атрибут, Семейная математика, Английский язык
Серия: Ideas at Work
25 апреля 2020 г.
Давайте вымоем эту математику прямо в день стирки
En Español También. Независимо от того, есть ли у вас дома машина или вы посещаете прачечную самообслуживания, в стирке есть все виды математики. И есть много способов, чтобы дети всех…
И есть много способов, чтобы дети всех…
- Тема: Наборы
- Возраст/класс Уровень: Pre-K, Детский сад, 1-й класс, 2-й класс, 3-й класс
- Метки Оценка, Сравнение, Атрибут, Семейная математика, Английский язык
Серия: Book4 March 90 22, 2020
Карточки с домашними занятиями: наборы и сортировка
Эти распечатываемые карточки с заданиями на английском и испанском языках приглашают к домашним исследованиям с наборами и сортировкой с использованием книг и связанных с ними занятий. Книги могут стимулировать разговоры об атрибутах, а также вдохновлять на вопросы…
- Тема: Наборы
- Уровень возраста/класса: Дошкольный, Детский сад
- Теги Тана Хобан, Синтия Вейл, Стюарт Дж. Мерфи, Эмили Дженкинс, Пара носков, Точно противоположность, Opuestos/Противоположности, Пять существ, Красный? Это желтый? Is it Blue?, загрузите
Series: Focus on Play
17 марта 2020 г.Creatures at Home Activity
На английском и испанском языках инструкции описывают, как выполнять домашнее задание, которое может позволить родителям участвовать в обучении, происходящем в классах, и все это связано с книгой…
- Тема: Наборы
- Возраст/класс.
 за способы организовать и осмыслить свой мир через игры в школе и дома, а также во время уборки. Сортировка предметов в группы по определенным признакам дает детям возможность…
за способы организовать и осмыслить свой мир через игры в школе и дома, а также во время уборки. Сортировка предметов в группы по определенным признакам дает детям возможность…- Тема: Наборы
- Возраст/уровень класса: Pre-K, Детский сад
- Теги: Лоис Элерт, Тана Хобан, Семейная математика, Синтия Вейлль, Стюарт Дж. Мерфи, Эмили Дженкинс, Пара носков, Точно противоположное, Opuestos/Противоположности, Пять существ, Is это красный? Это желтый? Синий?
15 июля 2018 г.
Модуль профессионального развития: наборы
Наборы являются основой мышления и обучения детей. Они также являются основой нашей системы счисления. Одна из самых важных задач каждого числа — описать, «сколько» их в наборе…
- Тема: Наборы
- Возраст/класс Уровень: Pre-K, Детский сад
Серия: Книга идей
13 июня 2017 г.Сопоставление и понятия одинакового и разного… с носками!
Подходит ли носок в горошек к носку в полоску? В книге «Пара носков» маленькие дети узнают о важном раннем навыке: сопоставлении.


 Вот несколько простых заданий, которые вы можете выполнять со своими дошкольниками, чтобы познакомить их с наборами.
Вот несколько простых заданий, которые вы можете выполнять со своими дошкольниками, чтобы познакомить их с наборами.
 Скажите своим детям: «В желтом наборе ____ детей» и т. д.
Скажите своим детям: «В желтом наборе ____ детей» и т. д. 