Задачи косвенные по математике 2 класс: Задачи с косвенными вопросами. Объяснение и материал для закрепления . | Учебно-методический материал по математике (2, 3 класс) на тему:

Простые задачи в косвенной форме

Урок 14. Решение текстовых задач по математике 1-4 классы

На уроке мы узнаем, что простые задачи в косвенной форме не такие уж и простые. А всё потому, что над ними потрудился весёлый профессор Хитрюшкин. Его задачи будет учиться решать Петя Всезнайкин. Научится ли Петя решать задачи профессора Хитршкина? Про это узнаете в конце видеоурока.

Конспект урока “Простые задачи в косвенной форме”

Ребята, сегодня мы познакомимся с простыми задачами в косвенной форме.

Ой, посмотрите, откуда-то появилось отрицание «не». Наверное, они не такие уж и простые. И только на первый взгляд кажутся совсем лёгкими. Но дело в том, что над этими задачами потрудился весёлый профессор Хитрюшкин.

Он решил подшутить над нами и предложил решить несколько задач. Вот, например, такую.

Коля Толстиков за час съел 5 бутербродов с колбасой. Это на 2 больше, чем с сыром. Сколько бутербродов с сыром съел Коля?

̶ Ну, подумаешь, трудная задача! – говорит Петя Всезнайкин. – Я такую сразу могу решить. Там сказано – на 2 больше. Поэтому я к 5 прибавлю 2

5 + 2 = 7 (б.)

Ответ готов: 7 бутербродов с сыром. Да уж, любит поесть этот Коля!

̶ Не-е-т, Петя! Ты поспешил! Посмотри внимательно, ведь в задаче сказано: Коля Толстиков за час съел 5 бутербродов с колбасой. Это на 2 больше, чем с сыром. Значит, именно с колбасой больше, чем с сыром. А раз с колбасой больше, то с сыром – меньше, чем с колбасой. Значит, задачу мы должны решать не сложением, а вычитанием. Мы из 5 вычтем 2.

5 – 2 = 3 (б.)

Получается 3 бутерброда с сыром. Не такой уж он и обжора, этот Коля Толстиков.

А вот вторая задача, подготовленная профессором Хитрюшкиным.

Для украшения комнаты к празднику Витя надул 9 жёлтых шариков, что на 6 меньше, чем красных.

Сколько красных шариков надул Витя?

̶ Ну, уж эту-то задачу я точно решу правильно, – говорит Петя.

9 жёлтых шариков. Красных на 6 меньше. Значит, из 9 вычитаем 9.

9 – 6 = 3 (ш.)

Получается 3 красных шарика!

̶ Будь внимательнее, Петя. Ведь в задаче говорится не «красных шариков на 6 меньше». Там говорилось про жёлтые, что их на 6 меньше, чем красных. Значит жёлтых меньше, а красных, наоборот, больше. Поэтому задачу будем решать не вычитанием, а сложением. К 9 прибавить 6, получается 15 красных шариков!

9 + 6 = 15 (ш.)

̶ Ого! Как красиво будет у Вити! Я тоже на свой день рождения украшу комнату шариками. А ещё я обязательно научусь правильно решать такие хитрые задачки.

̶ Конечно, Петя. А я подскажу тебе, на что надо обратить особое внимание, чтобы ты всегда мог распознать задачи, которые придумывает профессор Хитрюшкин.

Посмотри внимательно на условия обеих задач.

В первой задаче про бутерброды с колбасой говорится – «это на 2 больше, чем с сыром». Если больше, чем с сыром, значит, с колбасой больше, а с сыром – меньше. И мы выполняли действие вычитания.

Во второй задаче говорится про жёлтые шарики – «что на 6 меньше, чем красных». Если меньше, чем красных, значит, меньше жёлтых, а красных больше, и мы находили их количество действием сложения.

Понял-понял… В задаче нужно разобраться, что именно больше, а что меньше. В первой задаче подсказкой служили слова ЭТО НА 2 БОЛЬШЕ, ЧЕМ С СЫРОМ. Во второй задаче – ЧТО НА 5 МЕНЬШЕ, ЧЕМ КРАСНЫХ. Теперь я внимательно буду читать условие задачи и разбираться, что больше, а что меньше. Давайте решим ещё одну задачу. Я обещаю быть внимательным!

-Хорошо, Петя. Слушай ещё одну задачу.

Пчёлка собирала нектар на лугу. Она садилась на колокольчики 14 раз. Это на 6 больше, чем на ромашки.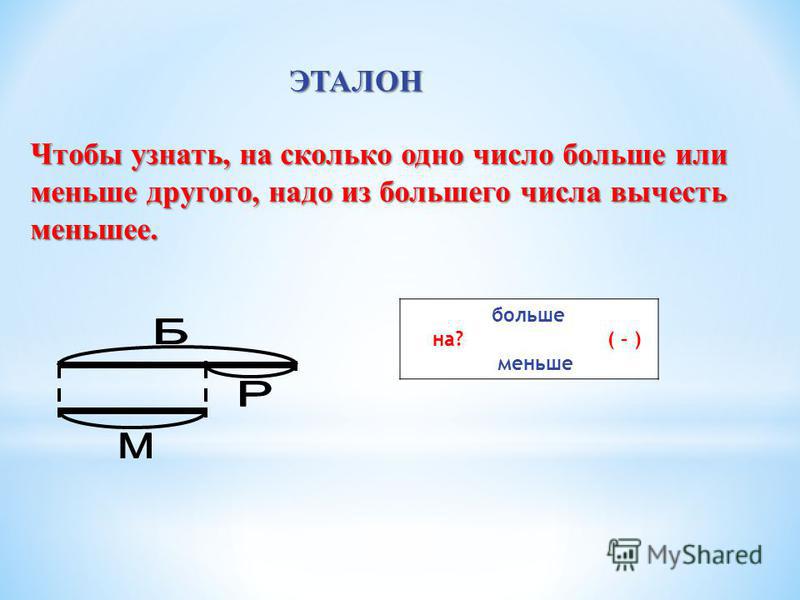 Сколько раз пчёлка садилась на ромашки?

̶ Та-а-ак… Пчёлка на колокольчики садилась 14 раз. Это на 6 больше, чем на ромашки. Ага! Я нашёл важные слова. «ЭТО НА 6 БОЛЬШЕ, ЧЕМ НА РОМАШКИ» говорится про колокольчики. Если на колокольчики больше, то значит на ромашки на 6 меньше. И я буду вычитать. 14 минус 6 равно 8.

14 – 6 = 8 (р.)

На ромашки пчёлка садилась 8 раз.

̶ Молодец, Петя! Ты был внимателен на этот раз и правильно решил задачу. А вы, ребята запомнили, о чем мы говорили?

В задаче нужно разобраться, что именно больше, а что меньше. Подсказкой могут служить слова «ЭТО НА несколько единиц БОЛЬШЕ или МЕНЬШЕ» или «ЧТО НА несколько единиц БОЛЬШЕ или МЕНЬШЕ»

Запомните эти слова – они предупреждают о том, что эта задача – непростая, и надо быть очень внимательными при её решении.

Ну, а Петя Всезнайкин всё понял, и такие задачи будет решать на отлично!

Предыдущий урок 13 Составные задачи на нахождение неизвестных компонентов

Следующий урок 15 Составные задачи в 3 действия на нахождение неизвестного слагаемого

Получите полный комплект видеоуроков, тестов и презентаций Решение текстовых задач по математике 1-4 классы

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Составление косвенных задач | Статья в сборнике международной научной конференции

Библиографическое описание:

Жуйкова, Т. П. Составление косвенных задач / Т. П. Жуйкова. — Текст : непосредственный // Педагогика: традиции и инновации : материалы III Междунар. науч. конф. (г. Челябинск, апрель 2013 г.). — Т. 0. — Челябинск : Два комсомольца, 2013. — С. 46-48. — URL: https://moluch.ru/conf/ped/archive/69/3676/ (дата обращения: 26.04.2023).

В обучении решению арифметических задач условно можно выделить два взаимосвязанных этапа: ознакомление со структурой задачи, способами решения ее, и обучение приемам вычислений [1, с. 201].

Решая задачи, ребенок усваивает: смысл арифметических действий и понятия: прибавить, получится, вычесть, остаток, равно и т. д. Развивается логическое мышление, смекалка, сообразительность, совершенствуются умения проводить анализ и синтез, обобщать, выделять главное в задачи. В дошкольном образовательном учреждении дети решают как простые, так и косвенные задачи.

Исследования и практика показывают, что детям старшего дошкольного возраста доступно решение некоторых видов косвенных задач. Их можно предлагать детям, будучи уверенными, что обязательный программный материал усвоен ими хорошо. И лишь при необходимости усложнить работу можно ввести такие задачи. Поскольку в косвенных задачах логика арифметического действия противоречит действию по содержанию задачи, они дают большой простор для рассуждений, доказательств, приучают детей логически мыслить.

Исходя из этого, для детей высокого уровня интеллектуального развития можно предлагать проблемные (косвенные) задачи. Ознакомление детей седьмого года жизни с задачами такого типа возможно и имеет большое значение для их умственного развития. На этой основе в дальнейшем будут формироваться умения осуществлять анализ более сложных арифметических задач, объяснять ход решения, выбор арифметического действия. Косвенные задачи отличаются тем, что в них оба числа характеризуют один и тот же объект, а вопрос направлен на определение количества другого объекта.

Трудности в решении таких задач определяются самой структурой и содержанием задачи. Как правило, в этих задачах есть слова, которые дезорганизуют ребенка при выборе арифметического действия. Несмотря на то, что в условии задачи есть слова больше, прилетели, старше и др., следует выполнять как бы обратное этому действие — вычитание. Для того чтобы ребенок правильно сориентировался, воспитатель учит его более тщательно анализировать задачу. Чтобы выбрать арифметическое действие, ребенок должен уметь рассуждать, логически мыслить. Пример косвенной задачи: «В корзине лежит пять грибочков, что на два грибочка больше, чем их лежит на столе. Сколько грибочков лежит на столе?» Часто дети, ориентируясь на несущественные признаки, а именно на отдельные слова (в данном случае слово больше), спешат выполнить действие сложения, допуская грубую математическую ошибку.

Воспитатель подчеркивает особенности таких задач, предлагая совместное рассуждение так: в условии задачи оба числа характеризуют один объект — количество грибов в корзине: в ней пять грибочков и в ней же на два больше, чем на столе. Необходимо узнать, сколько грибочков на столе. Если в корзине на два больше, то на столе лежит на два грибочка меньше. Чтобы узнать, сколько их на столе, следует от 5 вычесть 2 (5–2=?).

При составлении задач воспитатель должен помнить о том, что важно разнообразить формулировки в условии и вопросе задачи: насколько выше, тяжелее, дороже и т. д.

Приведем примеры косвенных задач:

1. В большую лодку сели 7 детей, в маленькую 3 ребёнка. Сколько детей разместилось в двух лодках?

а) 10 детей разместились в двух лодках: в большую лодку село 7 детей, а остальные в маленькую. Сколько детей село в маленькую лодку?

б) 10 детей разместилось в двух лодках: несколько детей село в большую лодку, а 3 ребёнка село в маленькую. Сколько детей село в большую лодку?

1. В одной коробке было 5 карандашей, а во второй 3 карандаша. Сколько карандашей было в двух коробках?

а) В двух коробках было 8карандашей: 3 в одной, а остальные во второй коробке.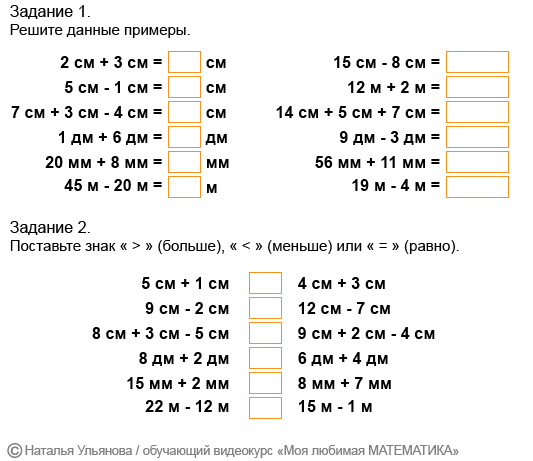

Сколько карандашей было во второй коробке?

б) В двух коробках было 8 карандашей. Во второй коробке было 5 карандашей. Сколько карандашей было в первой коробке?

в) В двух коробках было 8 карандашей. Сколько карандашей было в первой коробке? в одной коробке, если в другой лежало пять карандашей?

1. Школьники сделали 7 флажков. Один флажок был синий, а остальные зелёными. Сколько было зелёных флажков?

2. Мама и дочка собрали 10 стаканов малины. 5 стаканов мама помыла к ужину. Из остальных ягод она сварила варенье. Сколько стаканов малины пошло на варенье?

3. Колхозница купила 10 цыплят. Осенью 8 цыплят превратились в курочек, остальные стали петушками. Сколько было петушков?

4. В 2 солонках было 5 ложек соли. В одной из них было 3 ложки соли. Сколько ложек соли было в другой солонке? [2. с. 195]

Важно, чтобы задачи, которые мы даём ребёнку, были разнообразными, потому что если дошкольник, получат однотипные задачи, начинает решать их по аналогии, не вдумываясь в содержание и не анализируя задачу при решении. Дети очень скоро усваивает, что если что-то дали, кто-то приехал, прилетел и т. д. — надо прибавлять, а если наоборот — отнимать.

Не научившись объяснять, как получен ответ задачи, дошкольник привыкает механически ориентироваться только на слово, побуждающее к действию сложения или вычитания.

Однако очень скоро ребёнок сталкивается с такими задачами, где слово, обозначающее, что надо что-то складывать, не совпадает с тем арифметическим действием, которое надо произвести, чтобы решить задачу. Приведём пример такой задачи.

«На дереве сидели птички. После того, как пролетела ещё одна птичка, их стало шесть. Сколько птичек сидело на дереве»

Нередко такого рода задачи могут поставить дошкольников неподготовленных к решению задач, в тупик. Они дают ответ: «Семь птичек, ориентируясь на слово «прилетела» и прибавляя к шести птичкам ещё одну птичку».

По тому, как умеет ребёнок решать такого рода задачи, можно судить об уровне умственного развития ребёнка: умеет ли логически мыслить, рассуждать, доказывать правильность ответа. Именно при решении таких задач выявляется то, что мы называем нормальным усвоением знаний. Если дети, услышав знакомые слова «прилетели, прибежали, приехали», не давая себе труда вдуматься в смысл задачи, начинают складывать те числовые данные, которые имеются в задачи — значит, они не научены рассуждать при решении задачи, рассказывать, каким образом получился именно такой ответ.

Задачи, о которых идёт речь, нельзя решить без рассуждений. Именно важно предлагать детям подобные задачи уже в дошкольном возрасте.

Предлагая ребёнку задачу, аналогичную, следует его предупредить, что это особенная задача, не такая, как всегда, труднее. Например, «Собираясь идти в школу, девочка купила карандашей, но, выйдя из магазина, она увидела, что их мало. Пошла и купила ещё один карандаш, после чего карандашей стало пять. Сколько карандашей купила девочка в начале?» Задачу надо повторить несколько раз, чтобы ребёнок запомнил её. Потом предложить ему самому пересказать задание.

Теперь давай вместе рассуждать, — предлагает ребёнку взрослый. В задаче сказано, сколько карандашей купила девочка?

• Нет, — отвечает ребёнок.

• Правильно, это надо узнать, это нам не известно, когда девочка вернулась в магазин и купила ещё один карандаш, карандашей у неё стало больше или меньше?

Очевидно, ребёнок правильно ответит, что карандашей стало больше.

• Совершенно верно, после покупки одного карандаша их стало больше: пять. Значит, до покупки этого карандаша их было меньше?

• Меньше, — соглашается ребёнок.

• На сколько меньше?

• На один. Это нам известно из условия задачи.

• Значит, чтобы узнать, сколько карандашей купила девочка в начале, то есть, сколько карандашей было у неё до покупки ещё одного, надо от пяти карандашей отнять один карандаш.

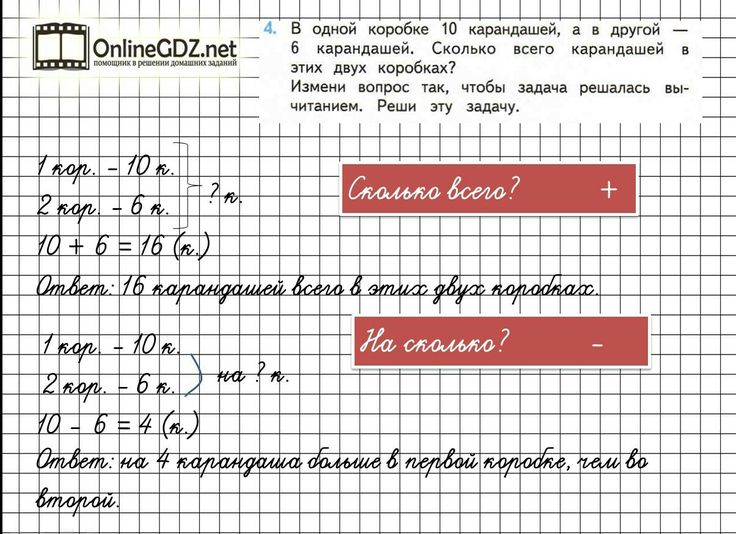
Теперь, предложив ребёнку самому узнать, сколько же карандашей купила девочка вначале, можно узнать, понял ли ребёнок задачу. Если он знает правильный ответ: «4 карандаша», можно ещё раз уточнить, как получен такой ответ. Ребёнок должен сказать, что он от 5 карандашей отнял 1 карандаш, получилось 4 карандаша [3].

Если ребёнок не может сразу усвоить логику рассуждений, можно прибегнуть к знакомому способу — предметной иллюстрации задачи и повторить приведённое выше рассуждение, держа в руке, пять карандашей. Ребёнок пересчитывает карандаши и убеждается, что их пять: «Сколько карандашей стало у девочки, когда она вернулась и купила ещё один карандаш.

Теперь давай посмотрим, сколько было карандашей до покупки вот этого карандаша» (При этом убираем один карандаш). Пересчитав карандаши, ребёнок убеждается, что карандашей было четыре.

Кроме того, путём соответствующего действия с предметами мы иллюстрируем задачу и помогаем представить ту жизненную ситуацию, которая описывается в ней. И хотя в задаче говорится, что девочка купила ещё один карандаш (со словом «купила» связывается действие сложение), ребёнок наглядно видит, что для получения правильного ответа необходимо произвести действие вычитание.

Обучая ребёнка решению обратных арифметических задач, взрослые рассуждают вместе с ребёнком, затем необходимо предложить ребёнку самому попробовать порассуждать. Можно и поиграть с ребёнком, предложив ему самому придумать трудную задачу, для того чтобы её решил взрослый. Ребёнок с удовольствием включается в такую игру, когда он выступает в роли учителя. При этом можно лишний раз убедиться, как ориентируется ребёнок при решении такого рода задачах, и поддержать интерес, необходимый при обучении вычислительной деятельности.

Решите задачи с условием в косвенной форме.

1. Девочки шили куклам платья. Когда они одели их на кукол, то увидели, что одного платья не хватило. 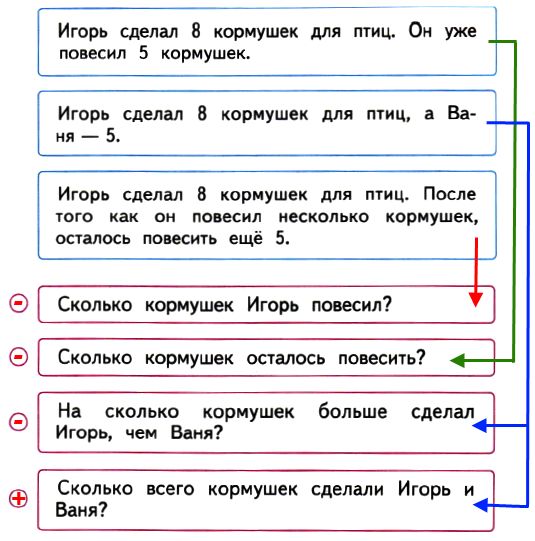Они сшили его. Теперь платьев стало пять. Сколько платьев они сшили в начале?

2. Девочка собирала грибы. В её корзине лежали только белые. Вдруг под ёлкой она увидела три подосиновика. Срезав их, девочка пересчитала все собранные грибы. Их стало 10. Сколько белых грибов было?

3. Кате 5 лет. Она моложе своего брата на 1 год. Сколько лет брату?

4. Юре 9 лет. Он старше своего товарища на 2 года. Сколько лет товарищу?

5. Красных тюльпанов 8, их на 1 больше чем жёлтых. Сколько жёлтых тюльпанов?

6. В парке 9 голубых скамеек. Их на 1 меньше, чем белых. Сколько белых скамеек в парке?

7. Белая курица снесла 2 яйца, это на одно яйцо меньше, чем снесла чёрная курица. Сколько яиц снесла чёрная курица?

8. Бригада строителей строила 9 этажный дом. Через месяц осталось построить три этажа. Сколько этажей построено?

9. На блюде лежали яблоки. 3 из них взяли и съели. Осталось на блюде 4 яблока. Сколько яблок было? [4. с. 196]

Подытоживая анализ проблемного поля, обучение детей старшего дошкольного возраста косвенным задачам, рекомендуем предлагать подобные задачи лучше всего в виде сюрприза: «Кто сообразит, как решать задачу, которую я вам сейчас задам?» Надо отметить, что эти задачи вызывают большой интерес у детей.

Итак, работа над задачами не только обогащает детей новыми знаниями, но и дает богатый материал для умственного развития.

Литература:

1. Щербакова Е. И. Методика обучения математике в детском саду: Учеб пособие для студ. дош. отд-ний и фак. сред. пед. учеб. заведений. — 2-е изд., стереотип. _ М.: Издательский центр «Академия», 2000. — 201 с. 2. Столяр А. А. Формирование элементарных математических представлений у дошкольников: Учеб. пособие для студентов пед. институтов. М.: Просвещение, 1988. — 195 с.

2. Белошистая В. А. Формирование и развитие математических способностей дошкольников: Вопросы теории и практики: Курс лекций для студ. дошк. Факультетов высш. учеб. заведений. — М.: Гуманит, изд. Центр ВЛАДОС, 2003. — 400 с.

3. Столяр А. А. Формирование элементарных математических представлений у дошкольников: Учеб. пособие для студентов пед. институтов. М.: Просвещение, 1988. — 196 с.

Измерение – Группа по изучению уроков

Как правило, обучение и изучение каждого атрибута измерения состоит из четырех этапов: (1) прямое сравнение; (2) косвенное сравнение; (3) измерение в произвольных (нестандартных) единицах; и (4) измерение в стандартных единицах. В CCSS эти этапы четко описаны в преподавании и изучении линейных измерений от детского сада до 2-го класса. Однако учащиеся должны пройти эти этапы со всеми измеримыми атрибутами, даже если они могут тратить меньше времени на некоторые этапы, поскольку они приобретают больше опыта в измерениях. . Например, когда учащиеся узнают об объеме твердых тел в пятом классе, они, скорее всего, потратят гораздо меньше времени на первые три этапа по сравнению с тем, что они сделали, когда узнали о длине. Тем не менее, для студентов по-прежнему важно пройти эти этапы, чтобы они могли понять, что такое объем, процесс его измерения и как использовать инструменты для этого.

Стадия 1: Прямое сравнение

Итак, почему важно следовать этим четырем стадиям, когда мы начинаем наши инструкции по измерению? Основное внимание на первых двух этапах уделяется тому, чтобы помочь учащимся понять измеряемые атрибуты. В конце концов, прежде чем мы сможем что-то измерить, нам действительно нужно понять, что именно мы хотим измерить. Например, прежде чем мы сможем измерить длину, нам нужно понять, что такое длина. Поставив рядом два предмета (прямое сравнение), учащиеся могут определить, какой из них длиннее, а какой короче. Благодаря такому опыту учащиеся понимают, что длина — это расстояние между двумя концами объекта.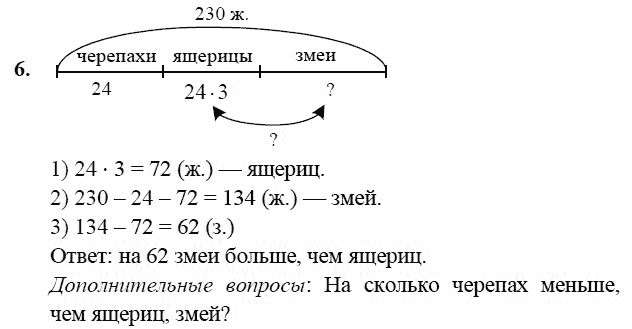 (Хотя мы можем использовать разные слова, «высота» на самом деле не является атрибутом. Ее можно рассматривать как длину в вертикальной ориентации.) Конечно, посредством прямого сравнения учащиеся получают некоторое фундаментальное понимание того, как измерять объект. также. Например, при сравнении длин двух объектов важно, чтобы один конец объектов был выровнен.

Нельзя сказать, что верхний сегмент на рисунке ниже длиннее только потому, что он «выпирает» дальше вправо.

Учащиеся также узнают, что интересующее нас «пространство» находится на прямой траектории. Таким образом, мы не можем просто сравнить положения конечных точек, как показано на рисунке ниже.

Прежде чем мы сможем сравнить эти два объекта, конечные точки второго объекта должны быть расположены по прямой линии. Эти знания имеют основополагающее значение для понимания ребенком измерения.

Стадия

2: Косвенное сравнение

К сожалению, не всегда возможно прямое сравнение двух объектов. В ситуациях, когда это не так, иногда полезно использовать третий объект, который можно сравнивать непосредственно с каждым из двух объектов и действовать как ссылка между ними. Например, если один дверной проем шире размаха ваших рук, а другой уже, чем размах рук, вы знаете, что первый шире второго. Косвенное сравнение обеспечивает большую гибкость при сравнении двух объектов. Это также дает детям возможность испытать важное математическое свойство отношений, называемое транзитивностью. Это свойство утверждает, что если a > b и b > c, то a > c. Конечно, формальное изучение такого свойства произойдет гораздо позже.

Этап 3: Измерение с произвольными (нестандартными) Единицы

Возможно, более важной причиной обучения и изучения непрямого сравнения является то, что оно готовит почву для самой фундаментальной идеи о процессе измерения: использование единицы измерения . При использовании третьего объекта для косвенного сравнения его количество не всегда может быть промежуточным между количеством исходных двух объектов. Например, деревянная палка может быть намного короче обоих дверных проемов. Однако в этих случаях можно определить, что один дверной проем выше трех (одних и тех же) деревянных палочек, поставленных встык, а другой короче трех деревянных палочек. Теперь мы можем сказать, что первый дверной проем выше (длиннее), чем второй.

Нетрудно заметить, что такие переживания становятся основанием для идеи выражения признака через число третьего предмета, единицы, необходимого для его «покрытия». Когда мы переходим на эту стадию, мы теперь действительно «измеряем» в том смысле, что мы присваиваем номер объекту с точки зрения того, сколько атрибутов он имеет. Есть много преимуществ для выражения количества атрибута с помощью чисел. Ясно, что это упрощает процесс сравнения, поскольку нам больше не нужно находить разные объекты для использования в качестве эталона — сравнение нескольких объектов можно легко выполнить, просто сравнив числа одной установленной единицы. Еще одним важным преимуществом присвоения атрибутам чисел является то, что мы можем ответить не только на вопрос «что длиннее?» но и «на сколько?» В общем, как только мы выражаем количество атрибута числами, арифметические операции могут использоваться для ответа на более сложные вопросы. Несмотря на то, что CCSS прямо не заявляет об этих достоинствах, я надеюсь, что учителя помогут учащимся испытать и понять их.

Зачем

учить студентов использовать нестандартные единицы измерения?

Некоторые люди могут возразить, что, как только мы дойдем до этого этапа, мы должны просто использовать стандартные единицы измерения. Этот аргумент, возможно, имеет смысл позже, в начальных классах, когда учащиеся узнают об измерении трех или четырех различных атрибутов.   Однако на уровне начального класса важно помнить, что учащиеся все еще изучают процесс измерения: выберите единицу измерения, затем определите, сколько итераций единицы необходимо, чтобы сравняться с атрибутом объекта, который вы измеряют. Для нас это так очевидно, а с детьми не так. Введение стандартных единиц на этом этапе потребует от детей одновременного изучения двух новых идей — новых единиц и нового процесса.  Есть и другие соображения. Во-первых, некоторые единицы могут быть слишком маленькими или слишком большими, так что размер полученных чисел может не подходить для детей в данное время. Используя нестандартные единицы измерения, учителя могут контролировать диапазон чисел, которые могут получить учащиеся. Кроме того, важно отметить, что измерение в стандартных единицах обычно означает измерение с помощью различных инструментов. Например, если вы измеряете в дюймах, скорее всего, вы будете измерять линейкой. Однако обучение использованию линейки или любого измерительного инструмента также является сложной задачей само по себе — это может быть третьей новой идеей, с которой придется столкнуться учащимся, если мы введем стандартные единицы измерения, не обучая нестандартным единицам .

Этап

Четвертый: измерение в стандартных единицах измерения

Хотя это может показаться несколько парадоксальным, использование нестандартных единиц полезно для детей, чтобы понять необходимость наличия стандартных единиц. Например, если два ученика измерят ширину одного и того же дверного проема карандашами, они могут получить разные результаты. Этот тип опыта позволит им увидеть, что они не могут сравнивать числа, если их единицы измерения не совпадают. Именно тогда мы можем представить идею общих единиц, а затем, наконец, идею стандартных единиц, таких как дюймы, футы, сантиметры и метры.

Образовательный опыт: типы, преимущества, методы

Правильный набор учебного опыта для учащихся может помочь им добиться успеха на протяжении всей жизни. Благодаря хорошему учебному опыту и стратегиям учителя могут радикально изменить то, как ученики взаимодействуют с предметными областями. Они могут вдохновить студентов думать с большей ясностью и любопытством в любой предметной области или области.

Суть увлекательного обучения может вызывать интерес в любом возрасте, поэтому это один из самых эффективных методов, используемых ведущими учителями во всем мире.

Учащиеся могут подходить к предметам с установкой на развитие, предоставляя им правильные инструменты для всестороннего рассмотрения тем. Математика, естествознание, география и ряд других предметов можно преподавать с помощью мультисенсорных средств, чтобы создать ощущение волнения и радости при повседневном обучении.

• Что такое учебный опыт в учебной программе
• Преимущества обучения в классе
• Типы обучения
• Важность обучения, ориентированного на учащихся
• Методы использования учебного опыта в классе
• Отслеживание успеваемости учащихся
• Часто задаваемые вопросы

Что такое учебный опыт в учебной программе? Разве студенты еще не учатся?

Хотя термин «учебный опыт» может означать разные вещи для разных учителей, это масштабируемая стратегия, которую можно использовать для улучшения успеваемости учащихся. Учебный опыт может улучшить успеваемость учащихся, участие в группах и активное взаимодействие в классе.

Итак, что такое опыт обучения?

Опыт обучения — это стратегический подход к обучению, который включает в себя переработку учебного плана, чтобы сосредоточиться на конечных целях и задачах. Он также подчеркивает использование нескольких методологий обучения для привлечения учащихся разных типов. Социальное участие, совместное взаимодействие, мультимедийные игры и другие формы обучения используются для обеспечения более целостного опыта.

Также больше внимания уделяется цели изучения предмета, а также тщательно структурированному пути к достижению конкретных целей. Учителя также устанавливают контекст уроков, которые преподают их ученикам, что помогает создать более прочные отношения с предметом.

SplashLearn пробуждает любознательность на протяжении всей жизни благодаря своей обучающей программе PreK-5, основанной на играх, которую полюбили более 40 миллионов детей. С более чем 4000 веселых игр и занятий, это идеальный баланс между обучением и игрой для вашего малыша.

Попробуйте бесплатно

Понимая текущий уровень знаний учащихся в классе, определяя конечные цели на семестр и используя несколько инструментов взаимодействия для лучшего контекста, учителя могут эффективно внедрять учебный опыт.

Преимущества обучения в классе

Существует несколько неотъемлемых преимуществ обучения, которые могут обеспечить лучшие результаты для учителей, работающих в сложных цифровых и традиционных средах.

1.

Ассимиляция в различных измерениях

Предметные области, такие как десятичные дроби, счет, языковые комплексы и т. д., требуют изучения в различных измерениях. Студенты получают возможность учиться на когнитивном, эмоциональном и поведенческом уровне для всестороннего образовательного опыта. Это способствует более сильной связи памяти, лучшему воспоминанию и большей способности использовать простые темы для сложной обработки.

2.

Применение за пределами классной комнаты

Еще одно преимущество, которое дает учащимся процесс обучения, — это применение в различных предметных областях. Через призму конечной цели каждого плана урока учителя могут представить учебный опыт с упором на применение. Это может помочь связать разные темы вместе, способствуя более сложному мышлению при изучении новых предметов. Учащиеся могут обнаружить, что используют различия, распознавание образов и визуализацию вне традиционной классной обстановки.

3.

Контекстное обучение для учащихся

Благодаря занятиям, играм, интерактивным занятиям и мультимедийным инструментам можно установить более глубокий контекст изучаемого материала. Учителя могут создавать новые разговоры о языке, алгебре, геометрии и истории, что помогает наполнить урок более глубоким смыслом. Установление реальных применений счета, глаголов и множественных чисел также может помочь учащимся относиться к предмету с практической точки зрения.

4.

Усиленное внимание к мастерству

Благодаря учебному опыту учащиеся получают возможность овладеть предметными областями, которые ранее считались сложными. Они могут изменить свой подход к изучению предмета, интерпретируя информацию с помощью различных средств. Отличным примером этого может быть использование игры на основе уровней, ориентированной на фракции, специально разработанной для повышения сложности для повышения мастерства.

5.

Персонализированное обучение для учащихся

Жизненно важным преимуществом обучения в классе является масштабируемость персонализации. Учителя могут исследовать новые методы доставки уникального сообщения в класс и предлагать отдельным учащимся получать информацию так, как они предпочитают. Используя несколько инструментов, фокусируясь на конечных целях и управляя непосредственным контекстом, все учащиеся имеют больше шансов на успешное обучение одновременно.

6.

Развитие социального обучения и сотрудничества

Благодаря близкому пониманию тем и предметных областей учащиеся также более уверенно учатся в группах. Они могут совместно решать задачи, основанные на решении проблем, и учиться у других учащихся в увлекательной среде. Открытые мероприятия, групповые задания и совместные задачи могут помочь учащимся получить новые идеи, которые, возможно, не имели возможности исследовать традиционно.

7.

Помогает быстро выявить пробелы в обучении

Еще одна важная причина, по которой процесс обучения имеет ключевое значение для современных классов, — это простота выявления пробелов. Поскольку существуют различные типы обучения, учителя могут использовать их для оценки уровня понимания определенных тем. Благодаря нетрадиционному тестированию с помощью классных заданий и интерактивных занятий учителя могут находить пробелы в обучении и мгновенно устранять их.

Типы обучения

Важной причиной растущего внедрения методов обучения в академические учебные программы является гибкость, которую они предлагают учителям по предметам и классам. Есть несколько источников опыта обучения, которые учителя могут использовать, чтобы донести информацию до своих учеников. Учащиеся, которые лучше реагируют на совместное обучение, могут усваивать знания так же быстро, как и те, кто предпочитает обучение на основе визуализации.

Давайте рассмотрим различные виды обучения, которые учителя могут адаптировать к своим классам.

Непосредственный опыт обучения полезен для нескольких учащихся, которым нравится учиться с помощью прикосновений, ощущений и других сенсорных средств. Они могут манипулировать карточками со словами, математическими инструментами, мобильными научными играми и другими сенсорными средствами обучения и быстрее получать знания. Учителя также могут внедрять новые инструменты, чтобы использовать их, когда учащиеся адаптируются к существующим для повышения производительности.

На самом деле дети, которые играют в SplashLearn более 4 раз в неделю, демонстрируют улучшение обучения более чем на 77% в течение первых 2 месяцев.

2. Косвенный опыт обучения

Косвенный опыт обучения абстрагируется через учетные записи, без физического опыта. Эти методы легко масштабируются и могут включать в себя мультимедийный контент, графические изображения, обсуждения, дебаты, рабочие тетради и т. д. Они могут помочь стимулировать чувство любопытства и обучения, расширяя возможности творческого мышления учащихся. Такие стратегии, как словесные игры, мысленные эксперименты, ролевые игры и т. д., могут помочь учащимся изучить предметы под другим углом.

3. Индивидуальный опыт обучения

Многие учащиеся также лучше реагируют на учебный опыт при индивидуальном обучении. Эти учащиеся предпочитают рабочие листы, письменные задания, рассказывание историй и ряд стимулирующих упражнений. Этот опыт индивидуального уровня имеет решающее значение для использования, особенно когда у вас есть небольшой класс учеников, которые могут проводить время в интроспективной среде. Они также хорошо реагируют на аудиокниги, видеожурналы, встречи один на один и другие подобные стратегии.

4. Опыт обучения на уровне группы

Некоторые из лучших примеров обучения, ориентированного на студента, вытекают из концепции обучения на уровне группы. Обсуждения, занятия в классе, командные задания и другие совместные инициативы могут вызвать чувство радости в сложных предметных областях. Стратегии геймификации и выразительного обучения являются основной частью обучения на групповом уровне, поэтому они настоятельно рекомендуются учащимся от Pre-K до 2 класса.

5. Гибридное или смешанное обучение

Гибридное обучение является одним из наиболее эффективных видов обучения, поскольку оно фокусируется на сочетании различных стратегий для максимального воздействия. Классы становятся все более разнообразными, оцифрованными и ориентированными на результат. Гибридные методы помогают вовлечь учащихся в различные типы обучения, вовлекая их в различные виды деятельности, которые стимулируют творческое мышление, социальную активность и применение знаний.

Важность учебного опыта для успеха в классе

Учащиеся всех возрастов сталкиваются с проблемами в изучении концепций, которые не являются для них инстинктивными. Внедрение учебного опыта может открыть их когнитивный горизонт для более сложного мышления. Такие мероприятия, как экскурсии, групповые обсуждения, ролевые игры, эксперименты и творческое самовыражение, могут полностью раскрыть потенциал учащегося и повысить его успеваемость в школе.

1.

Влюбить учеников в предмет

Учащимся также нравится изучать предмет, если он преподается нетрадиционным и интерактивным способом. Хотя это может быть обременительно для каждой темы, общий предмет можно преподавать, используя учебный опыт, интегрированный в курс. Например, при обучении словесным задачам 5 ^–-классников учителя могут использовать реквизит, игры, анимацию и вырезки, чтобы помочь разбить задачу на более простые понятия.

2.

Лучший подход к домашнему обучению

Дети, обучающиеся на дому, предпочитают учиться с помощью нескольких средств, которые могут расширить их способ мышления по поводу формулировки проблемы. Благодаря сочетанию технологий и бумажных инструментов учащиеся могут гораздо проще изучать сложные предметы. Отличным примером этого является использование кукол, карт памяти, игр и других интерактивных средств для обучения детей младшего возраста счету и сложению.

3.

Обучение тому, как хочет учиться учащийся

Почему учебный процесс так хорошо объясняет темы? Это потому, что они помогают учить студентов так, как они хотят, чтобы их учили. Некоторые дети предпочитают читать, в то время как другие учатся с помощью головоломок. Включение опыта обучения в учебную программу позволяет всем учащимся учиться так, как они хотят учиться, не чувствуя себя обделенными импульсом занятия. В конечном счете, учащийся получает огромную пользу, поскольку его стимулируют с помощью нескольких средств.

4.

Расширенное внимание в долгосрочной перспективе

Учителя, использующие традиционные методы объяснения и решения вопросов, получат новый опыт обучения. Благодаря различным занятиям, упражнениям и мысленным экспериментам учащиеся гораздо дольше сосредотачиваются на поставленной задаче и получают больше стимулов, чем пассивное чтение. Они активно участвуют в обучающих упражнениях, богатых контекстом, что значительно увеличивает продолжительность их внимания.

Методы внедрения стратегического опыта обучения в классе

Существует множество стратегий, которые учителя могут использовать для внедрения учебного опыта в своих классах.

1.

Начиная с самого ученика

Потребности и интересы учащихся должны быть контекстуализированы, а план обучения с учетом индивидуальных особенностей должен их мгновенно заинтересовать. Хотя каждый класс уникален, учителя должны иметь возможность разрабатывать эффективные планы на семестр, исходя из уровня знаний своих учеников.

Учителя также должны сосредоточиться на том, какой учебный опыт может лучше всего повлиять на их учеников, экспериментируя с различными стратегиями. Имея в виду конкретную цель на день, учителя могут работать в обратном направлении и разрабатывать увлекательный подход, чтобы расширить возможности учащихся и сделать их более любопытными к предмету.

   Прочтите по теме:    Эти математические упражнения для детского сада сделают процесс обучения увлекательным  

2.

Сосредоточение внимания на мультисенсорных стимулирующих стратегиях

Учащиеся, как правило, больше участвуют в мультисенсорных мероприятиях. Инструменты и методы, которые обеспечивают прямое, косвенное и групповое обучение, могут лучше активировать когнитивную, аффективную и психомоторную области знаний.

Результатом этого будет более когнитивная стимуляция ума учащегося с более сильным акцентом на рациональное мышление и логические рассуждения. Эти навыки трудно привить с помощью преподавания, и они требуют опыта обучения и практического взаимодействия со студентами в долгосрочной перспективе.

3.

Поощрение практического обучения в классе

Для учителей важно поощрять практическое обучение при изучении новых предметов и сложных тем. С помощью различных ролевых упражнений, экспериментов и задач учащихся можно попросить продемонстрировать уроки дня в веселой и увлекательной форме.

Это улучшает понимание учащимся и применение предметной области, позволяя учителям анализировать пробелы в знаниях. Студенты также испытывают чувство гордости, когда они выполняют задания самостоятельно, что улучшает запоминание информации.

4.

Устранение препятствий для обучения в классе

Учителя могут устранить препятствия для обучения, обеспечив следующее –

• Сосредоточение внимания на одном виде деятельности или упражнении за раз, чтобы не перегружать учащихся.
• Устранение отвлекающих факторов при обучении онлайн или в классе.
• Внесение ясности в цели, чтобы избежать второстепенных задач. Например, сказать, что это наша задача на сегодня, вместо того, чтобы двусмысленно говорить о том, что студенты узнают.
• Сотрудничество со студентами в процессе обучения.
• Обеспечение самостоятельности в принятии решений на учениях.
• Встраивание нескольких цифровых и бумажных инструментов, карточек, игр и т. д. для обеспечения оптимального обучения.

Отслеживание успеваемости учащихся при реализации учебных программ

Лучший способ вовлечь учащихся в учебный процесс — отслеживать, как они взаимодействуют с различными видами деятельности с течением времени. Учителя могут анализировать успеваемость студенческих групп в классе, выбирая наиболее подходящее для них вмешательство.

Успеваемость учащихся можно отслеживать с помощью различных действий и сравнивать с их общей оценкой. Затем учителя могут менять занятия, вводить новые устройства, добавлять веселые игры и снова проверять успеваемость учащихся.

Готовы начать свое обучение? Зарегистрируйтесь бесплатно по телефону – https://www.splashlearn.com/register

Узнайте больше о том, как SplashLearn может поддержать ваши учебные программы, изучив наше решение Pre-K to Grade 5. Планы начинаются с 5 долларов в месяц с комплексной поддержкой и регулярно обновляемым контентом.

Часто задаваемые вопросы

С какими проблемами я столкнусь при внедрении учебного опыта в классе?

Учителя могут столкнуться со следующими проблемами при первом внедрении учебного опыта –

• Сопротивление изменению стиля преподавания или дополнительной работе.
• Перевозбуждение, вызванное слишком большим количеством упражнений и занятий.
• Отвлечения и посторонние разговоры во время обучения.
• Отсутствие интереса к новой концепции обучения.

В каком возрасте лучше всего знакомить учащихся с опытом обучения?

Учебный процесс можно знакомить с учащимися 1-го класса, поскольку они уже знакомы с большинством инструментов и структур деятельности.

Что делать, если опыт обучения не работает для моих учеников?

Лучше всего попробовать разные методы и наладить отношения с отдельными учащимися, чтобы оценить их стиль обучения. Анкета или простое вводное упражнение могут дать первоначальную информацию для лучшей адаптации.

Каковы будущие тенденции в обучении?

Несколько тенденций будут определять то, как учителя будут внедрять учебный опыт в классе, а именно –

• Более широкое внедрение мобильных приложений, ориентированных на обучение на основе вовлечения.