Задача время скорость расстояние: Скорость время расстояние. Решение задач 4 класс.

Как найти расстояние зная скорость и время. Формула нахождения значений скорости, времени и расстояния

Как решать задачи на движение? Формула зависимости между скоростью, временем и расстоянием. Задачи и решения.

Формула зависимости времени, скорости и расстояния за 4 класс: как обозначается скорость, время, расстояние?

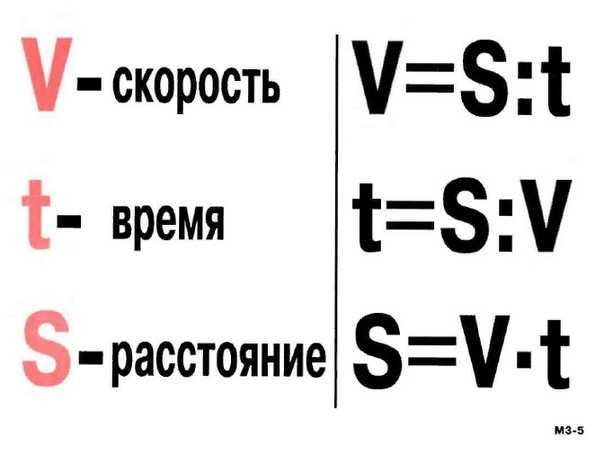
Люди, животные или машины могут двигаться с определенной скоростью. За определенное время они могут пройти определенный путь. Например: сегодня вы можете дойти до своей школы за полчаса. Вы идете с определенной скоростью и преодолеваете 1000 метров за 30 минут. Путь, который преодолевается, в математике обозначают буквой S . Скорость обозначается буквой v . А время, за которое пройден путь, обозначается буквой t .

• Путь – S
• Скорость – v
• Время – t

Если вы опаздываете в школу, вы можете этот же путь пройти за 20 минут, увеличив свою скорость. А значит, один и тот же путь может быть пройден за разное время и с различной скоростью.

Как зависит время прохождения пути от скорости?

Чем больше скорость, тем быстрее будет пройдено расстояние. И чем меньше скорость, тем больше времени понадобится для прохождения пути.

Как найти время, зная скорость и расстояние?

Для того, чтобы найти время, понадобившееся для прохождения пути, нужно знать расстояние и скорость. Если расстояние разделить на скорость — вы узнаете время. Пример такой задачи:

Задача про Зайца. Заяц убегал от Волка со скоростью 1 километр за минуту. Он пробежал до своей норы 3 километра. За какое время Заяц добежал до норы?

Как легко решать задачи на движение, где нужно найти расстояние, время или скорость?

1. Внимательно прочитайте задачу и определите, что известно из условия задачи.
2. Напишите на черновике эти данные.
3. Также напишите, что неизвестно и что нужно найти
4. Воспользуйтесь формулой для задач про расстояние, время и скорость
5. Введите в формулу известные данные и решите задачу

Решение для задачи про Зайца и Волка.

• Из условия задачи определяем, что нам известно скорость и расстояние.
• Также из условия задачи определяем, что нам нужно найти время, которое нужно было зайцу, чтобы добежать до норы.

Пишем в черновик эти данные например так:

Время — неизвестно

Теперь запишем то же самое математическими знаками:

S — 3 километра

V — 1 км/мин

t — ?

Вспоминаем и записываем в тетрадь формулу для нахождения времени:

t = S: v

t = 3: 1 = 3 минуты

Как найти скорость, если известно время и расстояние?

Для то, чтобы найти скорость, если известно время и расстояние, нужно расстояние разделить на время. Пример такой задачи:

Заяц убегал от Волка и пробежал до своей норы 3 километра. Он преодолел это расстояние за 3 минуты. С какой скоростью бежал Заяц?

Решение задачи на движение:

1. В черновик записываем, что нам известно расстояние и время.
2. Из условия задачи определяем, что нужно найти скорость
3. Вспоминаем формулу для нахождения скорости.

Формулы для решения таких задач показаны на картинке ниже.

Формулы для решения задач про расстояние, время и скорость

Подставляем известные данные и решаем задачу:

Расстояние до норы — 3 километра

Время, за которое Заяц добежал до норы — 3 минуты

Скорость — неизвестна

Запишем эти известные данные математическими знаками

S — 3 километра

t — 3 минуты

v — ?

Записываем формулу для нахождения скорости

v = S: t

Теперь запишем решение задачи цифрами:

v = 3: 3 = 1 км/мин

Как найти расстояние, если известно время и скорость?

Чтобы найти расстояние, если известно время и скорость нужно время умножить на скорость. Пример такой задачи:

Заяц убегал от Волка со скоростью 1 километр за 1 минуту. Чтобы добежать до норы ему понадобилось три минуты. Какое расстояние пробежал Заяц?

Решение задачи: Записываем в черновик, что нам известно из условия задачи:

Скорость Зайца — 1 километр за 1 минуту

Время, которое Заяц бежал до норы — 3 минуты

Расстояние — неизвестно

Теперь, то же самое запишем математическими знаками:

v — 1 км/мин

t — 3 минуты

S — ?

Вспоминаем формулу для нахождения расстояния:

S = v ⋅ t

Теперь запишем решение задачи цифрами:

S = 3 ⋅ 1 = 3 км

Как научиться решать более сложные задачи?

Чтобы научиться решать более сложные задачи нужно понять как решаются простые, запомнить какими знаками обозначаются расстояние, скорость и время. Если не получается запомнить математические формулы их нужно выписать на лист бумаги и всегда держать под рукой во время решения задач. Решайте с ребенком несложные задачи, которые можно придумать на ходу, например во время прогулки.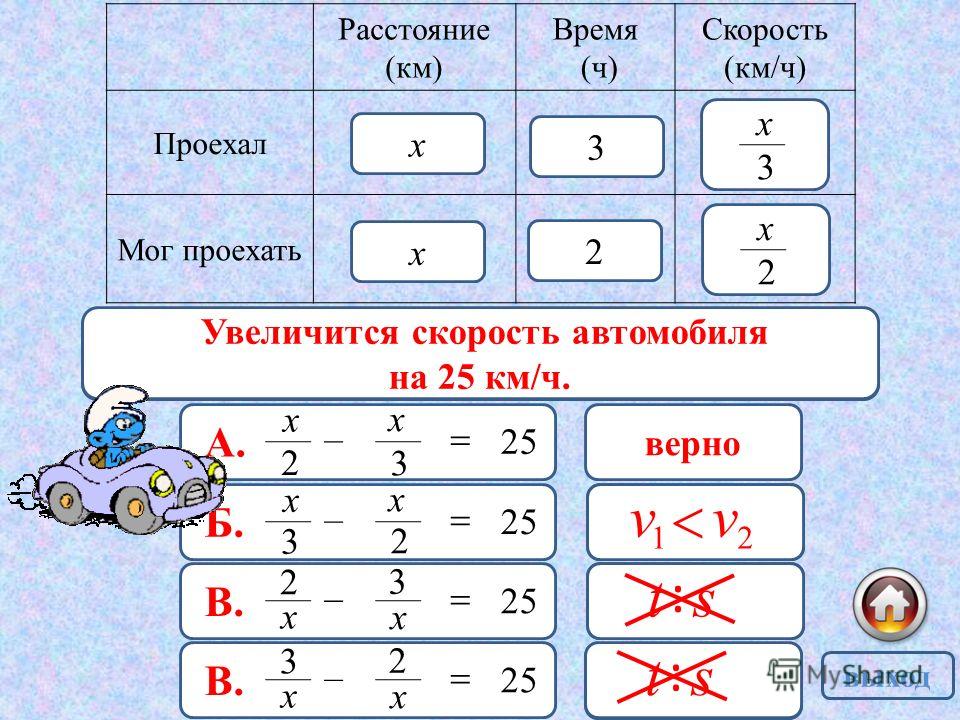

Ребенок, который умеет решать задачи, может гордиться собой

Когда решают задачи про скорость, время и расстояние, очень часто делают ошибку, из-за того, что забыли перевести единицы измерения.

ВАЖНО: Единицы измерения могут быть любыми, но, если в одной задаче есть разные единицы измерения, переведите их одинаковые. Например, если скорость измерена в километрах за минуту, то расстояние обязательно должно быть представлено в километрах, а время в минутах.

Для любознательных : Общепринятая сейчас система мер называется метрической, но так было не всегда, и в старину на Руси использовали другие единицы измерения.

Задача про удава : Слоненок и мартышка мерили длину удава шагами. Они двигались навстречу друг другу. Скорость мартышка была 60 см за одну секунду, а скорость слоненка 20 см за одну секунду. На измерение они потратили 5 секунд. Какова длина удава? (решение под картинкой)

Решение:

Из условия задачи определяем, что нам известно скорость мартышки и слоненка и время, которое им понадобилось для измерения длины удава.

Запишем эти данные:

Скорость мартышки — 60 см/сек

Скорость слоненка — 20 см/сек

Время — 5 секунд

Расстояние неизвестно

Запишем эти данные математическими знаками:

v1 — 60 см/сек

v2 — 20 см/сек

t — 5 секунд

S — ?

Запишем формулу для расстояние, если известна скорость и время:

S = v ⋅ t

Посчитаем, какое расстояние прошла мартышка:

S1 = 60 ⋅ 5 = 300 см

Теперь посчитаем, сколько прошел слоненок:

S2 = 20 ⋅ 5 = 100 см

Суммируем расстояние, которое прошла мартышка и расстояние, которое прошел слоненок:

S = S1 + S2 = 300 + 100 = 400 см

График зависимости скорости тела от времени: фото

Расстояние, преодолеваемое с разной скорость преодолевается за разное время. Чем больше скорость — тем меньше потребуется времени для передвижения.

Таблица 4 класс: скорость, время, расстояние

В таблице ниже приведены данные для которых нужно придумать задачи, а потом их решить.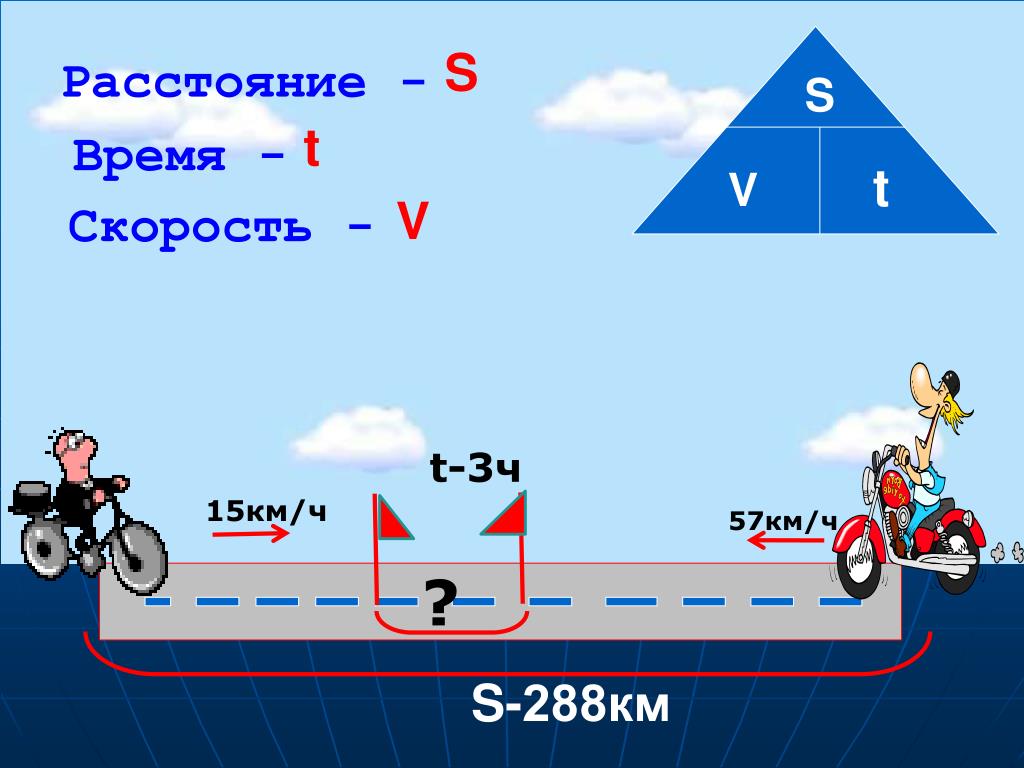

№	Скорость (км/час)	Время (час)	Расстояние (км)
1	5	2	?
2	12	?	12
3	60	4	?
4	?	3	300
5	220	?	440

Вы можете пофантазировать и придумать задачи к таблице сами. Ниже наши варианты условия задач:

1. Мама отправила Красную Шапочку к бабушке. Девочка постоянно отвлекалась и шла по лесу медленно, со скоростью 5 км/час. На путь она потратила 2 часа. Какое расстояние за это время прошла Красная Шапочка?
2. Почтальон Печкин вез на велосипеде посылку со скоростью 12 км/час. Он знает, что расстояние между его домом и домом Дяди Федора 12 км. Помогите Печкину рассчитать, сколько времени понадобится на дорогу?
3. Папа Ксюши купил автомобиль и решил отвезти семью на море. Машина ехала со скоростью 60 км/час и на дорогу было потрачено 4 часа. Какое расстояние между домом Ксюши и морским побережьем?
4. Утки собрались в клин и полетели в теплые края. Птицы махали крыльями без устали 3 часа и преодолели за это время 300 км. Какой была скорость птиц?
5. Самолет АН-2 летит со скоростью 220 км/час. Он вылетел из Москвы и летит в Нижний Новгород, расстояние между этими двумя городами 440 км. Сколько времени самолет будет в пути?

Ответы на приведенные задачи можно найти в таблице ниже:

№	Скорость (км/час)	Время (час)	Расстояние (км)
1	5	2	10
2	12	1	12
3	60	4	240
4	100	3	300
5	220	2	440

Примеры решения задач на скорость, время, расстояние за 4 класс

Если в одной задаче есть несколько объектов движения, нужно научить ребенка рассматривать движение этих объектов отдельно и только потом вместе. Пример такой задачи:

Двое друзей Вадик и Тема решили прогуляться и вышли из своих домов навстречу друг другу. Вадик ехал на велосипеде, а Тема шел пешком. Вадик ехал со скоростью 10 км/час, а Тема шел со скоростью 5 км в час. Через час они встретились. Какое расстояние между домами Вадика и Темы?

Эту задачу можно решить используя формулу зависимости расстояния от скорости и времени.

S = v ⋅ t

Расстояние, которое проехал Вадик на велосипеде будет равно его скорости умноженной на время в пути.

S = 10 ⋅ 1 = 10 километров

Расстояние, которое прошел Тема считают аналогично:

S = v ⋅ t

Подставляем в формулу цифровые значения его скорости и времени

S = 5 ⋅ 1 = 5 километров

Расстояние, которое проехал Вадик нужно прибавить к расстоянию, которое прошел Тема.

10 + 5 = 15 километров

Как научиться решать сложные задачи, для решения которых требуется логически мыслить?

Развивать логическое мышление ребенка, нужно решая с ним простые, а затем и сложные логические задачи. Эти задачи могут состоять из нескольких этапов. Перейти с одного этапа на другой можно только в том случае, если решен предыдущий. Пример такой задачи:

Антон ехал на велосипеде со скоростью 12 км/час, а Лиза ехала на самокате со скоростью в 2 раза меньше, чем у Антона, а Денис шел пешком со скоростью в 2 раза меньше, чем у Лизы. Какова скорость Дениса?

Чтобы решить эту задачу нужно сначала узнать скорость Лизы и только после этого скорость Дениса.

Кто едет быстрее? Задача про друзей

Иногда в учебниках для 4 класса попадаются непростые задачи. Пример такой задачи:

Два велосипедиста выехали из разных городов навстречу друг другу. Один из них спешил и мчался со скоростью 12 км/час, а второй ехал не спеша со скоростью 8 км/час. Расстояние между городами из которых выехали велосипедисты 60 км. Какое расстояние проедет каждый велосипедист, перед тем как они встретятся? (решение под фото)

Решение:

• 12+8 = 20 (км/час) — это общая скорость двух велосипедистов, или скорость с которой они приближались друг к другу
• 60 : 20 = 3 (часа) — это время через которое велосипедисты встретились
• 3 ⋅ 8 = 24 (км) — это расстояние, которое проехал первый велосипедист
• 12 ⋅ 3 = 36 (км) — это расстояние, которое проехал второй велосипедист
• Проверка: 36+24=60 (км) — это расстояние, которое проехали два велосипедиста.
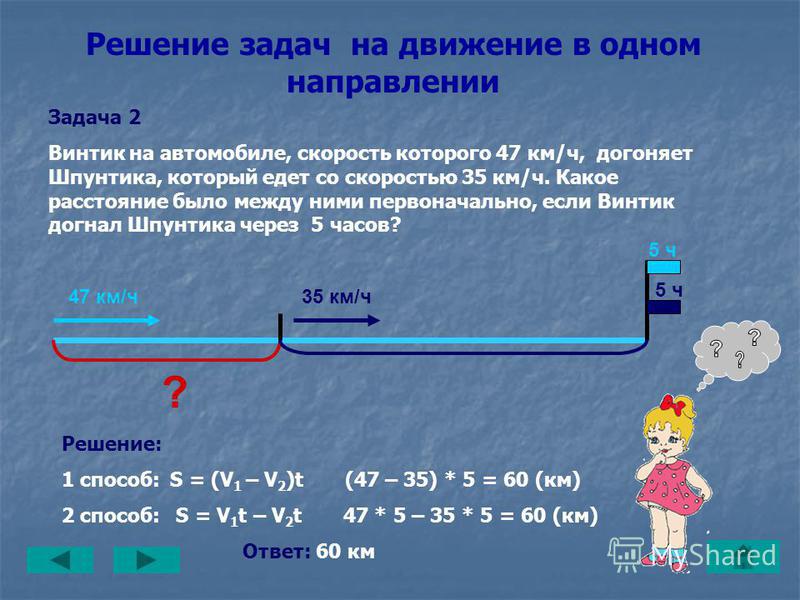
• Ответ: 24 км, 36 км.

Предлагайте детям в форме игры решать такие задачи. Возможно, они сами захотят составить свою задачу про друзей, животных или птиц.

ВИДЕО: Задачи на движение

В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.

Определение средней скорости

Средней скоростью движения тела называется отношение пути , пройденного телом, ко времени , в течение которого двигалось тело:

Научимся ее находить на примере следующей задачи:

Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей и , которое равно:
м/с.

Частные случаи нахождения средней скорости

1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.

2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.

Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.

Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.

Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения.

Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила:
м/с.

Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!

Сергей Валерьевич

Скоростью является тем, насколько быстро движется точка или же тело. Это векторная величина и для того, чтобы задать скорость, необходимо предварительно задать величину скорости, а также непосредственно направление, в сторону которого она измеряется. Рассмотрит то, как рассчитать скорость.

Обычно, скорость рассматривают вдоль траектории движения тела. Тогда, величина будет определяться как путь, который был пройден в единицу времени. Другими словами говоря, для нахождения скорости тела, путь необходимо разделить на время, за которое он был пройден. И в таком случае, формула скорости движения будет выглядеть так: V=S/t.

Как рассчитать среднюю скорость?

В кинематике это понятие является ничем иным, как усредненной характеристикой скорости частиц за время их движения. Есть два основных способа вычисления средней скорости. Средняя скорость пути – это скорость, в которой длина пути, пройденная телом, соотносится со временем, за которое он был пройден. Такая скорость, в отличие от мгновенной скорости, векторной величиной не является. Если тело одинаковые промежутки времени двигалось с одинаковыми скоростями, средняя скорость будет равняться среднему арифметическому от скоростей. Но, если половина пути была с одной скоростью, а вторая половина – с другой, средняя скорость будет равняться среднему гармоническому от всех взятых отдельно скоростей, которые будут равны между собой на разных участках дороги. Формула вычисления следующая:

Как вычислить среднюю скорость по перемещению?

Среднюю скорость можно вывести и по перемещению, она будет векторной, то есть равной по отношению к времени, за которое его совершили.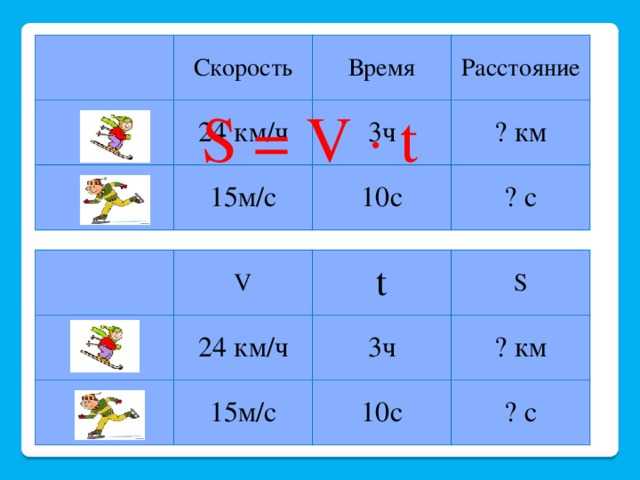 2/2. Из нее следует, что если на торможение дается одинаковое усилие, то тормозной путь будет прямо пропорционален массе тела и квадратно – скорости.

Единицы измерения, естественно, очень важны для всякого рода расчетов, что касается расчетов скорости движения, то тут единицами измерения будут единицы измерения скорости. Но, важно не только знать их, нужно уметь переводить значения в разные величины. Например, скорость измеряется в метрах на секунду (м/с), как перевести такое значение, например, в километры на секунду? Все просто! В одном метре на секунду содержится шесть тысяч сантиметров в минуту и, соответственно, сто сантиметров в секунду. Кроме того, один метр на секунду это три тысячи шестьсот метров в час и шестьдесят метров в минуту. А три и шесть километра в час – это один метр в секунду. Надеемся, что теперь у прочитавших эту статью не будет возникать вопросов о том, как рассчитать скорость движения.

Все задачи, в которых присутствует движение объектов, их перемещение или вращение, так или иначе связаны со скоростью.

Данный термин характеризует перемещение объекта в пространстве за определенный отрезок времени – число единиц расстояния за единицу времени. Он является частым «гостем» как разделов математики, так и физики. Исходное тело может менять свое расположение как равномерно, так и с ускорением. В первом случае величина скорости статична и в ходе движения не меняется, во втором наоборот – увеличивается или уменьшается.

Как найти скорость – равномерное движение

Если скорость движения тела оставалась неизменной от начала перемещения и до окончания пути, то речь идет о перемещении с постоянным ускорением – равномерном движении. Оно может быть прямолинейным или же криволинейным. В первом случае траекторией перемещения тела является прямая.

Тогда V=S/t, где:

• V – искомая скорость,
• S – пройденное расстояние (общий путь),
• t – общее время движения.

Как найти скорость – ускорение постоянно

Если объект двигался с ускорением, то его скорость по мере движения менялась. В таком случае найти искомую величину поможет выражение:

V=V (нач) + at, где:

• V (нач) – первоначальная скорость движения объекта,
• a – ускорение тела,
• t – общее время пути.

Как найти скорость – неравномерное движение

В данном случае имеет место ситуация, когда разные участки пути тело проходило за разное время.
S(1) – за t(1),
S(2) – за t(2) и т.д.

На первом участке движение происходило в “темпе” V(1), на втором – V(2) и т.д.

Чтобы узнать скорость перемещения объекта на всем пути (ее среднее значение) воспользуйтесь выражением:

Как найти скорость – вращение объекта

В случае вращения речь идет об угловой скорости, определяющей угол, на который поворачивается элемент за единицу времени. Обозначается искомая величина символом ω (рад/с).

• ω = Δφ/Δt, где:

Δφ – пройденный угол (приращение угла),
Δt – прошедшее время (время движения – приращение времени).

• В случае, если вращение равномерное, искомая величина (ω) связана с таким понятием как период вращения – за какое время наш объект совершит 1 полный оборот. В таком случае:

ω = 2π/T, где:
π – константа ≈3,14,
T – период.

Или ω = 2πn, где:
π – константа ≈3,14,
n – частота обращения.

• При известной линейной скорости объекта для каждой точки на пути движения и радиусе окружности, по которой она перемещается, для нахождения скорости ω потребуется следующее выражение:

ω = V/R, где:
V – численное значение векторной величины (линейной скорости),
R – радиус траектории следования тела.

Как найти скорость – сближение и отдаление точек

В подобного рода задачах уместным будет использование терминов скорость сближения и скорость отдаления.

Если объекты направляются друг к другу, то скорость сближения (отдаления) будет следующей:
V (сближ) = V(1) + V(2), где V(1) и V(2) – скорости соответствующих объектов.

Если одно из тел догоняет другое, то V (сближ) = V(1) – V(2), V(1) больше V(2).

Как найти скорость – движение по водоему

Если события разворачиваются на воде, то к собственной скорости объекта (движение тела относительно воды) добавляется еще и скорость течения (т.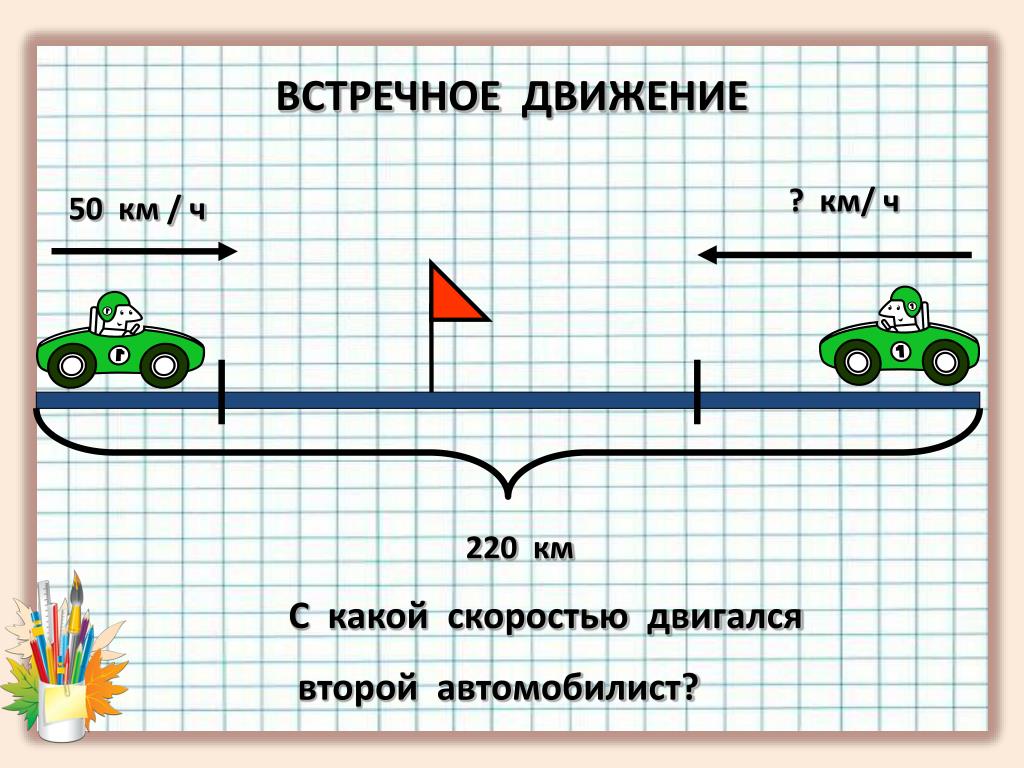 е. движение воды относительно неподвижного берега). Как взаимосвязаны эти понятия?

В случае перемещения по течению V=V(собст) + V(теч).
Если против течения – V=V(собств) – V(теч.).

Скорость – это величина, которая описывает быстроту перемещения объекта из точки А в точку Б. Обозначается латинской буквой V – сокращение от латинского velocitas – скорость. Скорость можно узнать, если известно время (t), в течение которого перемещался объект, и расстояние (S), которое объект преодолел.

Чтобы расчитать скорость, используйте формулу пути: V=S/t. Например, за 12 секунд объект продвинулся на 60 метров, значит его скорость равнялась 5 м/с (V=60/12=5). Используйте одинаковые единицы измерения, если сравниваете скорость двух разных объектов. Основной единицей измерения скорости в международной системе единиц являются метры в секунду или сокращенно м/с. Также распространены километры в часы, километры в секунду, метры в минуту и метры в секунду. В англоязычных странах используются мили в секунду, мили в час, футы в секунду и футы в минуту. Помните, точность определения скорости зависит от характера движения. Точнее всего формула пути помогает найти скорость при равномерном движении – объект преодолевает одинаковое расстояние за равные промежутки времени. Однако равномерное движение очень редко встречается в реальном мире. Это, к примеру, движение секундной стрелки в часах или вращение Земли вокруг Солнца. В случае неравномерного движения, например, прогулка по городу, формула пути помогает найти среднюю скорость.

Скорость, время, расстояние / Задачи / Справочник по математике для начальной школы

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Задачи
5. Скорость, время, расстояние

Скорость движения – это расстояние, пройденное за единицу времени.

Единицей времени является 1 секунда, 1 минута или 1 час.

Чтобы определить скорость движения, нужно использовать величины – расстояние и время.

Чтобы найти скорость, нужно расстояние разделить на время.

---

В качестве единиц измерения скорости мы будем пользоваться единицами длины и единицами времени. Обычно используют такие единицы скорости, как метр в секунду, метр в минуту, километр в час и другие, а записывают так: м/с, м/мин, км/ч. Обратите внимание, что предлог “в” в математике заменили чёрточкой “ / ”.

Например, скорость страуса – 7 км/ч.

---

Скорость черепахи – 5 м/с.

---

Прибор для измерения скорости: спидометр.

---

Чем меньше времени затрачено на дорогу, тем больше скорость движения.

---

Чем меньше скорость движения, тем больше времени требуется на дорогу.

---

Чтобы найти время, нужно расстояние разделить на скорость.

Чтобы найти расстояние, нужно скорость умножить на время.

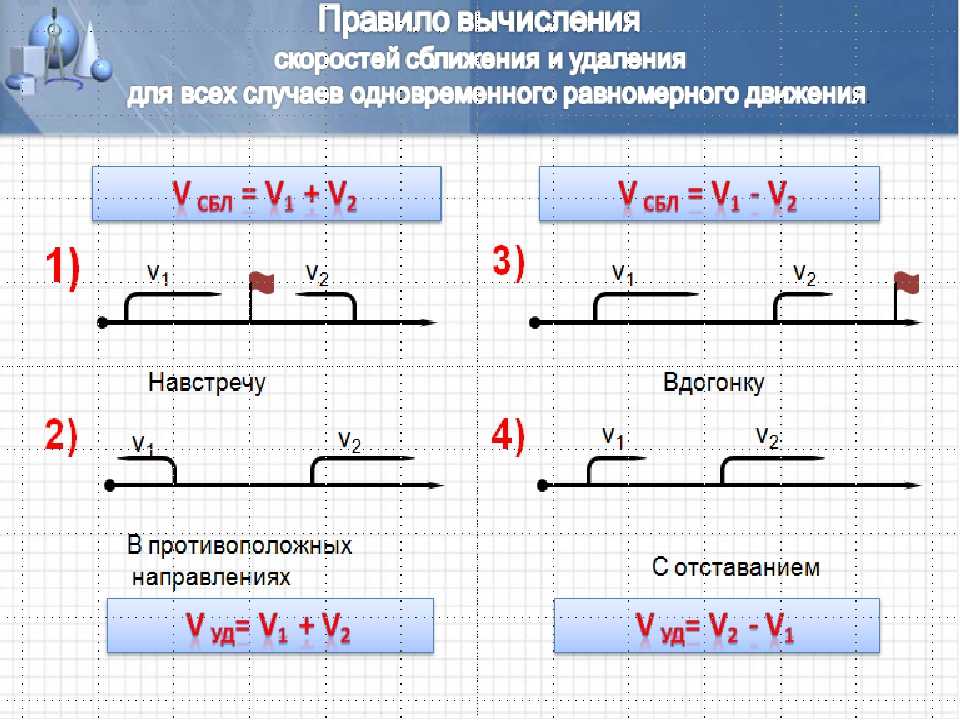
При решении задач на движение стоит помнить, что при движении навстречу друг другу скорости складываются, а при движении друг за другом – вычитается.

---

Складывая две скорости при движении навстречу, мы получаем скорость, с которой пешеходы приближаются друг к другу. Её мы будем называть скоростью сближения.

Складывая две скорость при движении в противоположных направлениях, мы получаем скорость, с которой объекты удаляются друг от друга. Её мы будем называть скоростью удаления.

---

Место встречи всегда ближе к пункту, из которого вышел пешеход, у которого скорость меньше.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Образцы оформления задачи

Обратные задачи

Цена. Количество. Стоимость

Задачи

Правило встречается в следующих упражнениях:

4 класс

Страница 55. Проверочная работа. Вариант 2, Моро, Волкова, Проверочные работы

Страница 70. Вариант 1. Проверочная работа 2, Моро, Волкова, Проверочные работы

Страница 86. Вариант 1. Тест 4, Моро, Волкова, Проверочные работы

Страница 27, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2

Страница 39, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2

Страница 65, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2

Страница 72, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2

Страница 76, Моро, Степанова, Волкова, Бантова, Бельтюкова, Учебник, часть 2

Страница 7, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 71, Моро, Волкова, Рабочая тетрадь, часть 2

5 класс

Задание 457, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 458, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1335, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1427, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1526, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1787, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 9, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2

Номер 4, Мерзляк, Полонский, Якир, Учебник

Номер 839, Мерзляк, Полонский, Якир, Учебник

Номер 951, Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 326, Мерзляк, Полонский, Якир, Учебник

Номер 370, Мерзляк, Полонский, Якир, Учебник

Номер 753, Мерзляк, Полонский, Якир, Учебник

Задание 370, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 450, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 481, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 617, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1168, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1309, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1459, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 15, Мерзляк, Полонский, Якир, Учебник

Номер 107, Мерзляк, Полонский, Якир, Учебник

Номер 109, Мерзляк, Полонский, Якир, Учебник

Номер 111, Мерзляк, Полонский, Якир, Учебник

Номер 525, Мерзляк, Полонский, Якир, Учебник

Номер 559, Мерзляк, Полонский, Якир, Учебник

Номер 767, Мерзляк, Полонский, Якир, Учебник

Номер 980, Мерзляк, Полонский, Якир, Учебник

Номер 1028, Мерзляк, Полонский, Якир, Учебник

Номер 1095, Мерзляк, Полонский, Якир, Учебник

---

Текстовые задачи.

Задачи на движение с решениями

Математика

Задачи на движение с решениями

перейти к содержанию курса текстовых задач

1. Первый турист проехал 2 ч на велосипеде со скоростью 16 км/ч. Отдохнув 2 ч, он отравился дальше с прежней скоростью. Спустя 4 ч после старта велосипедиста ему вдогонку выехал второй турист на мотоцикле со скоростью 56 км/ч. На каком расстоянии от места старта мотоциклист догонит велосипедиста? Решение
2. Из пункта A в пункт B отправились три машины друг за другом с интервалом в 1 ч. Скорость первой машины равна 50 км/ч, а второй — 60 км/ч. Найти скорость третьей машины, если известно, что она догнала первые две машины одновременно. Решение
3. Поезд был задержан в пути на 12 мин, а затем на расстоянии 60 км наверстал потерянное время, увеличив скорость на 15 км/ч. Найти первоначальную скорость поезда. Решение
4. Расстояние между станциями A и B равно 103 км. Из A в B вышел поезд и, пройдя некоторое расстояние, был задержан, а потому оставшийся до B путь проходил со скоростью, на 4 км/ч большей, чем прежняя. Найти первоначальную скорость поезда, если известно, что оставшийся до B путь был на 23 км длиннее пути, пройденного до задержки, и что на прохождение пути после задержки было затрачено на 15 мин больше, чем на прохождение пути до нее. Решение
5. Скорость автомобиля по ровному участку на 5 км/ч меньше, чем скорость под гору, и на 15 км/ч больше, чем скорость в гору. Дорога из A в B идет в гору и равна 100 км. Определить скорость автомобиля по ровному участку, если расстояние от A до B и обратно он проехал за 1 ч 50 мин. Решение
6. Автобус проходит расстояние между пунктами A и B по расписанию за 5 ч. Однажды, выйдя из A, автобус был задержан на 10 мин в 56 км от A и, чтобы прибыть в B по расписанию, он должен был оставшуюся большую часть пути двигаться со скоростью, превышающей первоначальную на 2 км/ч. Найти скорость движения автобуса по расписанию и расстояние между пунктами A и B, если известно, что это расстояние превышает 100 км. Решение
7. Поезд проходит мимо платформы за 32 с. За сколько секунд поезд проедет мимо неподвижного наблюдателя, если длина поезда равна длине платформы? Решение
8. Два поезда отправляются навстречу друг другу с постоянными скоростями, один из А в В, другой из В в А. Они могут встретиться на середине пути, если поезд из А отправится на 1,5 ч раньше. Если бы оба поезда вышли одновременно, то через 6 ч расстояние между ними составило бы десятую часть первоначального. Сколько часов каждый поезд тратит на прохождение пути между А и В? Решение
9. От пристани А одновременно отправились вниз по течению катер и плот. Катер спустился вниз на 96 км, потом повернул обратно и вернулся в А через 14 ч. Найти скорость катера в стоячей воде и скорость течения, если известно, что катер встретил плот на обратном пути расстоянии 24 км от А. Решение
10. Пункт В находится по реке ниже пункта А. В одно и то же время из пункта А отплыли плот и первая моторная лодка, а из пункта В – вторая моторная лодка. Через некоторое время лодки встретились в пункте С, а плот за это время проплыл третью часть пути от А до С. Если бы первая лодка без остановки доплыла до пункта В, то плот за это время прибыл бы в пункт С. Если бы из пункта А в пункт В отплыла вторая лодка, а из пункта В в пункт А – первая лодка, то они встретились бы в 40 км от пункта А. Какова скорость обеих лодок в стоячей воде, а также расстояние между пунктами А и В, если скорость течения реки равна 3 км/ч? Решение
11. Два тела, двигаясь по окружности в одном направлении, встречаются через каждые 112 мин, а двигаясь в противоположных направлениях – через каждые 16 мин. Во втором случае расстояние между телами уменьшилось с 40 м до 26 м за 12 с. Сколько метров в минуту проходит каждое тело и какова длина окружности? Решение
12. Две точки, двигаясь по окружности в одном направлении, встречаются каждые 12 мин, причем первая обходит окружность на 10 с быстрее, чем вторая. Какую часть окружности проходит за 1 с каждая точка? Решение
13. Два тела движутся навстречу друг другу из двух точек, расстояние между которыми 390 м. Первое тело прошло в первую секунду 6 м, а в каждую последующую секунду проходило на 6 м больше, чем в предыдущую. Второе тело двигалось равномерно со скоростью 12 м/c и начало движение спустя 5 с после первого. Через сколько секунд после того, как начало двигаться первое тело, они встретятся? Решение

Задачи для самостоятельного решения

1. Дорога от A до D длиной в 23 км идет сначала в гору, затем — по ровному участку, а потом — под гору. Пешеход, двигаясь из A в D, прошел весь путь за 5 ч 48 мин, а обратно, из D в A, — за 6 ч 12 мин. Скорость его движения в гору равна 3 км/ч, по ровному участку — 4 км/ч, а под гору — 5 км/ч. Определить длину дороги по ровному участку. Ответ:  8 км
2. В 5 ч утра со станции A вышел почтовый поезд по направлению к станции B, отстоящей от A на 1080 км. В 8 ч утра со станции B по направлению к A вышел пассажирский поезд, который проходил в час на 15 км больше, чем почтовый. Когда встретились поезда, если их встреча произошла в середине пути AB? Ответ: в 5 ч дня
3. Из пункта A впунктB отправились три велосипедиста. Первый из них ехал со скоростью 12 км/ч. Второй отправился на 0,5 ч позже первого и ехал со скоростью 10 км/ч. Какова скорость третьего велосипедиста, который отправился на 0,5 ч позже второго, если известно, что он догнал первого через 3 ч после того как догнал второго? Ответ: 15 км/ч
4. Два поезда — товарный длиной в 490 м и пассажирский длиной в 210 м — двигались навстречу друг другу по двум параллельным путям. Машинист пассажирского поезда заметил товарный поезд, когда он находился от него на расстоянии 700 м; через 28 с после этого поезда встретились. Определить скорость каждого поезда, если известно, что товарный поезд проходит мимо светофора на 35 с медленнее пассажирского. Ответ:  36 км/ч; 54 км/ч
5. Турист A и турист B должны были выйти одновременно навстречу друг другу из поселка M ипоселкаN соответственно. Однако турист A задержался и вышел позже на 6 ч. При встрече выяснилось, что A прошел на 12 км меньше, чем B. Отдохнув, туристы одновременно покинули место встречи и продолжили путь с прежней скоростью. В результате A пришел в поселок N через 8 ч, а B пришел в поселок M через 9 ч после встречи. Определить расстояние MN и скорости туристов. Ответ:  84 км; 6 км/ч; 4 км/ч.
6. Пешеход, велосипедист и мотоциклист движутся по шоссе в одну сторону с постоянными скоростями. В тот момент, когда пешеход и велосипедист находились в одной точке, мотоциклист был на расстоянии 6 км позади них, а тот момент, когда мотоциклист догнал велосипедиста, пешеход отстал от них на 3 км. На сколько километров велосипедист обогнал пешехода в тот момент, когда пешехода настиг мотоциклист? Ответ: 2 км
7. Два туриста вышли одновременно из пункта A в пункт B.Первый турист проходил каждый километр на 5 мин быстрее второго. Пройдя 20% расстояния от A до B, первый турист повернул обратно, пришел в A, пробыл там 10 мин, снова пошел в B и оказался там одновремен-
   но со вторым туристом. Определить расстояние от A до B, если второй турист прошел его за 2,5 ч. Ответ: 10 км
8. Рыбак проплыл на лодке от пристани против течения 5 км и возвратился обратно на пристань. Скорость течения реки равна 2,4 км/ч. Если бы рыбак греб с той же силой в неподвижной воде озера на лодке с парусом, увеличивающим скорость на 3 км/ч, то он за то же время проплыл бы 14 км. Найти скорость лодки в неподвижной воде. Ответ:  9,6 км/ч
9. Моторная лодка проплыла по озеру, а потом спустилась вниз по реке, вытекающей из озера. Расстояние, пройденное лодкой по озеру, на 15% меньше расстояния, пройденного по реке. Время движения лодки по озеру на 2% больше, чем по реке. На сколько процентов скорость движения лодки вниз по реке больше скорости движения по озеру? Ответ: на 20%
10. Турист проплыл в лодке по реке из города A в город B и обратно, затратив на это 10 ч. Расстояние между городами равно 20 км. Найти скорость течения реки, зная, что турист проплывал 2 км против течения реки за такое же время, как 3 км по течению. Ответ: 5/6 км/ч
11. По окружности длиной 60 м равномерно в одном направлении движутся две точки. Одна из них совершает полный оборот на 5 с быстрее другой. При этом совпадение точек происходит каждый раз через 1 мин. Определить скорости точек. Ответ:  4 м/с; 3 м/с.
12. Из точек A и B одновременно начали двигаться два тела навстречу друг другу. Первое в первую минуту прошло 1 м, а в каждую последующую проходило на 0,5 м больше, чем в предыдущую. Второе тело проходило каждую минуту по 6 м. Через сколько минут оба тела встретились, если расстояние между A и B равно 117 м? Ответ: через 12 мин.
13. Два приятеля в одной лодке прокатились по реке вдоль берега и вернулись по одной и той же речной трассе через 5 ч с момента отплытия. Протяженность всего рейса составила 10 км. По их подсчетам получилось, что на каждые 2 км против течения в среднем потребовалось столько же времени, сколько на каждые 3 км по течению. Найти скорость течения реки, а также время проезда туда и время проезда обратно. Ответ:  5/12 км/ч; 2 ч и 3 ч.

 

Метки движение, текстовые задачи. Смотреть запись.

Задания на скорость, расстояние, время

Продолжаем изучать элементарные математические задания. Этот урок посвящен подвижным задачам.

Задача на определение расстояния, скорости, времени

Задача 1. Автомобиль движется со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?

Решение

Если автомобиль проедет 80 километров за час, то за три часа он проедет в три раза больше. Чтобы найти расстояние, умножьте скорость автомобиля (80 км/ч) на время в пути (3 часа)

80 × 3 = 240 км

Ответ: автомобиль проедет 240 километров за три часа.

---

Задача 2. Автомобиль проехал 180 км с той же скоростью за 3 часа. Рассчитайте скорость автомобиля.

Решение

Скорость – это расстояние, пройденное телом за единицу времени. Единицей является 1 час, 1 минута или 1 секунда.

Если автомобиль проехал 180 километров за 3 часа с той же скоростью, то разделив 180 километров на 3 часа, мы определим расстояние, пройденное автомобилем за один час. А это скорость передвижения. Для определения скорости нам нужно пройденное расстояние разделить на время в пути:

180 : 3 = 60 км/ч

Ответ: скорость автомобиля 60 км/ч

---

Задача 3. За 2 часа машина проехала 96 км, а велосипедист км за 6 часов. Во сколько раз автомобиль проехал быстрее велосипедиста?

Решение

Определите скорость автомобиля. Для этого разделите пройденное расстояние (96 км) на время его движения (2ч)

96 : 2 = 48 км/ч

Определите скорость велосипедиста. Для этого разделите пройденное расстояние (72 км) на время его движения (6ч).

72 : 6 = 12 км/ч.

Узнайте, во сколько раз автомобиль ехал быстрее велосипедиста. Для этого найдите отношение 48 к 12

Ответ: автомобиль был в 4 раза быстрее велосипедиста.

---

Задание 4. Вертолет пролетел расстояние 600 км со скоростью 120 км/ч. Сколько времени находился в полете?

Решение

Если вертолет может пролететь 120 километров за 1 час, то нам нужно узнать, сколько часов вертолет провел, пролетев эти 600 километров. Чтобы найти время, разделите пройденное расстояние на скорость движения 9.0003

600 : 120 = 5 часов

Ответ: Вертолет летел 5 часов.

---

Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он прошел за это время?

Решение

Если вертолет пролетел 160 км за 1 час, то за 6 часов полета он преодолел в шесть раз больше. Чтобы определить расстояние, умножьте скорость на время

160 × 6 = 960 км

Ответ: вертолет преодолел 960 км за 6 часов.

---

Задача 6. Машина проехала из Перми в Казань (723 км) за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.

Решение

Определите, сколько километров проехал автомобиль за первые 9 часов. Для этого умножим скорость, с которой он ехал в течение первых 9 часов (55 км/ч), на 9.

55 × 9 = 495 км

Определим расстояние, которое осталось проехать. Для этого вычтите из общего расстояния (723 км) расстояние, которое он проехал за первые девять часов

723 – 495 = 228 км

Автомобиль проехал 228 км за оставшиеся 4 часа. Чтобы определить скорость автомобиля за оставшееся время, разделите 228 километров на 4 часа:

228 : 4 = 57 км/ч

Ответ: скорость автомобиля за оставшееся время составила 57 км/ч

---

Две машины (транспортные средства) – математическая задача

Например, если два пешехода начинают идти из двух точек навстречу друг другу, причем скорость первого 100 м/мин, а второго пешехода 105 м/мин, затем оба они покрывают 205 м/мин. Это означает, что каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.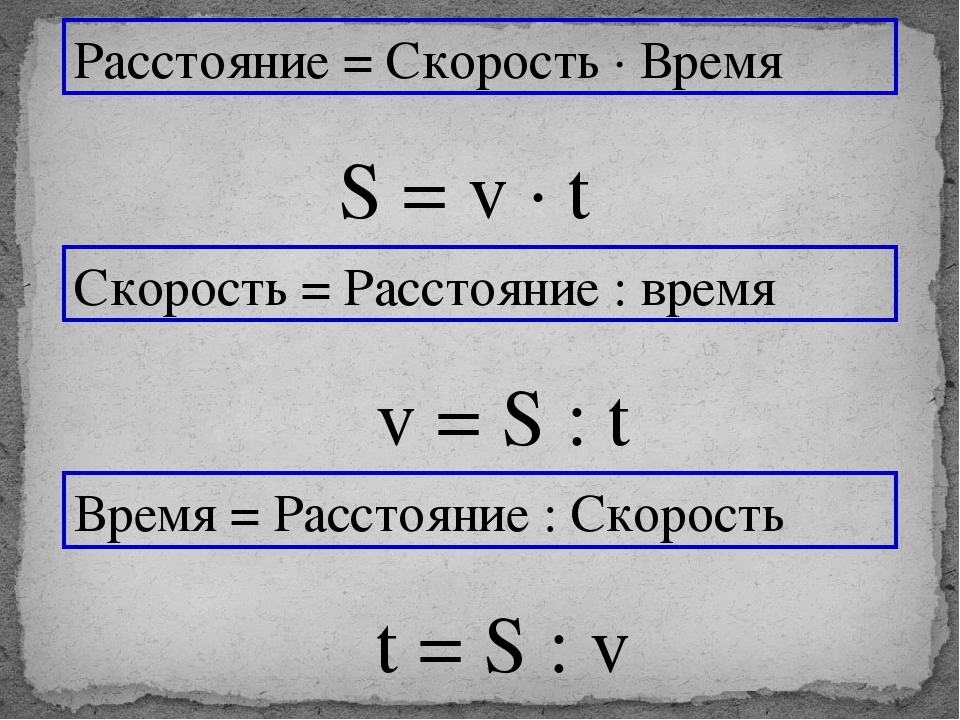

Чтобы найти скорость схождения, сложите скорости объектов.

Предположим, что пешеходы встретились через три минуты после того, как начали идти. Зная, что они встретились через три минуты, мы можем рассчитать расстояние между двумя точками.

Каждую минуту пешеходы преодолевали расстояние, равное двумстам пяти метрам. Через три минуты они встретились. Итак, умножив сумму скоростей на время движения, мы можем определить расстояние между двумя точками:

205 × 3 = 615 метров.

Вы также можете использовать другой способ определения расстояния между точками. Для этого найдите расстояние, которое прошел каждый пешеход до встречи.

Например, первый пешеход шел со скоростью 100 метров в минуту. Встреча произошла через три минуты, значит, за 3 минуты он прошел 100×3 метра

100 × 3 = 300 метров.

А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метра.

105 × 3 = 315 метров.

Теперь можно сложить результаты и определить расстояние между двумя точками:

300 м + 315 м = 615 м

---

Задача 1. Два велосипедиста одновременно выехали из двух населенных пунктов навстречу друг другу. Скорость первого велосипедиста 10 км/ч, скорость второго велосипедиста 12 км/ч. Они встретились через 2 часа езды. Определить расстояние между двумя населенными пунктами.

Решение

Найдем скорость, с которой велосипедисты подъехали к

10 км/ч + 12 км/ч = 22 км/ч.

Определить расстояние между населенными пунктами. Для этого умножаем ближайшую скорость сближения на время в пути.

22 × 2 = 44 км

Решим эту задачу вторым способом. Для этого найдите расстояния, пройденные каждым из них, и сложите результаты.

Найдите расстояние, пройденное первым велосипедистом:

10 × 2 = 20 км

Найдем расстояние, пройденное вторым велосипедистом:

12 × 2 = 24 км

Складываем полученные расстояния:

20 км + 24 км = 44 км

Ответ: расстояние между населенными пунктами 44 км.

---

Задание 2. Два велосипедиста одновременно выехали из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу. Скорость первого велосипедиста 14 км/ч, а скорость второго велосипедиста 16 км/ч. Через сколько часов они встретились?

Решение

Найдем скорость, с которой велосипедисты приблизились друг к другу:

14 км/ч + 16 км/ч = 30 км/ч

За час расстояние между велосипедистами уменьшилось на 30 км. Чтобы определить, через сколько часов они встретятся, разделите расстояние между двумя населенными пунктами на скорость их сближения:

60 : 30 = 2 часа

Итак, велосипедисты встретились через два часа.

Ответ: Велосипедисты встретились через два часа.

---

Задание 3. Два велосипедиста выехали из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу одновременно. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.

Решение

Определите расстояние, пройденное первым велосипедистом. Как и второй велосипедист, он провел в дороге два часа. Умножая скорость первого велосипедиста на 2 часа, мы можем узнать, сколько километров он проехал до встречи

12 × 2 = 24 км

За два часа первый велосипедист проехал 24 км. За час он прошел 24:2, т. е. 12 км. Представим это графически

Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Это определит, сколько километров проехал второй велосипедист:

56 км – 24 км = 32 км

Второй велосипедист, как и первый велосипедист, проехал два часа. Если разделить пройденное им расстояние на 2 часа, то узнаем, с какой скоростью он ехал:

32 : 2 = 16 км/ч.

Значит, скорость второго велосипедиста 16 км/ч.

Ответ: Скорость второго велосипедиста 16 км/ч.

---

Возьмем в качестве примера двух пешеходов, которые начали идти из одной и той же точки в противоположных направлениях, причем первый пешеход двигался со скоростью 4 км/ч, а второй со скоростью 6 км/ч, затем мы прибавляем скорости (потому что они идут в в противоположных направлениях), что составляет 10 км/ч.

Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.

Чтобы найти скорость двух объектов, движущихся в противоположных направлениях, сложите скорости объектов .

Значит в первый час расстояние между пешеходами будет 10 километров. На следующем рисунке вы можете увидеть, как это происходит

Вы можете видеть, что первый пешеход прошел свои 4 километра за первый час. Второй пешеход также прошел 6 километров за первый час. В первый час расстояние между ними было 4+6, т. е. 10 километров.

Через два часа расстояние между пешеходами будет 10×2, то есть 20 километров. На следующем рисунке показано, как это происходит:

---

Задача 1. Товарный поезд и Пассажирский экспресс отправились с одной станции одновременно в противоположных направлениях. Скорость товарного поезда 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?

Раствор

40 + 180 = 220 км/ч.

Эта скорость показывает, что за один час расстояние между поездами увеличится на 220 км. Чтобы узнать, какое расстояние будет между поездами через два часа, нужно умножить 220 на 2.

220 × 2 = 440 км.

Ответ: Через два часа расстояние между поездами составит 440 км.

---

Задача 2. Велосипедист и мотоциклист выехали из точки одновременно в противоположных направлениях. Скорость велосипедиста 16 км/ч, мотоциклиста 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?

Решение

16 км/ч + 40 км/ч = 56 км/ч.

Эта скорость показывает, что за один час расстояние между велосипедистом и мотоциклистом увеличится на 56 км.

Определите расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого умножьте (56 км/ч) на 2 часа

56 × 2 = 112 км

Ответ: Через 2 часа расстояние между велосипедистом и мотоциклистом составит 112 км.

---

Задача 3. Велосипедист и мотоциклист выехали из точки одновременно в противоположных направлениях. Скорость велосипедиста 10 км/ч, мотоциклиста 30 км/ч. Через сколько часов расстояние между ними будет 80 км?

Решение

10 км/ч + 30 км/ч = 40 км/ч.

За один час расстояние между велосипедистом и мотоциклистом увеличивается на 40 км. Чтобы узнать, сколько часов расстояние между ними будет 80 км, надо определить, сколько раз 80 км содержит 40 км

80 : 40 = 2

Ответ: Через 2 часа после начала движения между велосипедистом и мотоциклистом будет 80 километров.

---

Задание 4. Велосипедист и мотоциклист выехали из точки одновременно в противоположных направлениях. Через 2 часа расстояние между ними составило 90 км. Скорость велосипедиста была 15 км/ч. Вычислите скорость мотоциклиста.

Решение

Определите расстояние, пройденное велосипедистом за 2 часа. Для этого умножьте его скорость (15 км/ч) на 2 часа

15 × 2 = 30 км

На рисунке показано, что велосипедист проезжает 15 километров каждый час => 30 километров за два часа.

Вычтем расстояние, пройденное велосипедистом (30 километров), из общего расстояния (90 километров). Это покажет нам, сколько километров проехал велосипедист:

90 км – 30 км = 60 км

Мотоциклист проехал 60 км за два часа. Если разделить пройденное им расстояние на два часа, то узнаем, с какой скоростью он ехал:

60 : 2 = 30 км/ч.

Значит, скорость мотоциклиста была 30 км/ч.

Ответ: скорость мотоциклиста была 30 км/ч.

---

Задание на движение в одну сторону.

В предыдущей задаче мы рассматривали задачи, в которых объекты (люди, автомобили, лодки) двигались либо навстречу друг другу, либо в противоположные стороны. Мы нашли разные расстояния, которые менялись между объектами с течением времени.

В первом случае мы нашли связанные скорости – в ситуации, когда два объекта двигались навстречу друг другу. В единицу времени расстояние между объектами уменьшилось на определенное расстояние

Во втором случае это была ситуация, когда два объекта двигались в противоположных направлениях. В единицу времени расстояние между объектами увеличилось на определенное расстояние

 

Но объекты также могут двигаться в одном направлении и с разной скоростью. Например, велосипедист и мотоциклист могут выехать из одной точки в одно и то же время, причем скорость велосипедиста может быть 20 километров в час, а скорость мотоциклиста – 40 километров в час

 

На рисунке показано, что мотоциклист опережает велосипедиста на двадцать километров. Это потому, что он проезжает на 20 километров в час больше, чем велосипедист. Следовательно, каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров .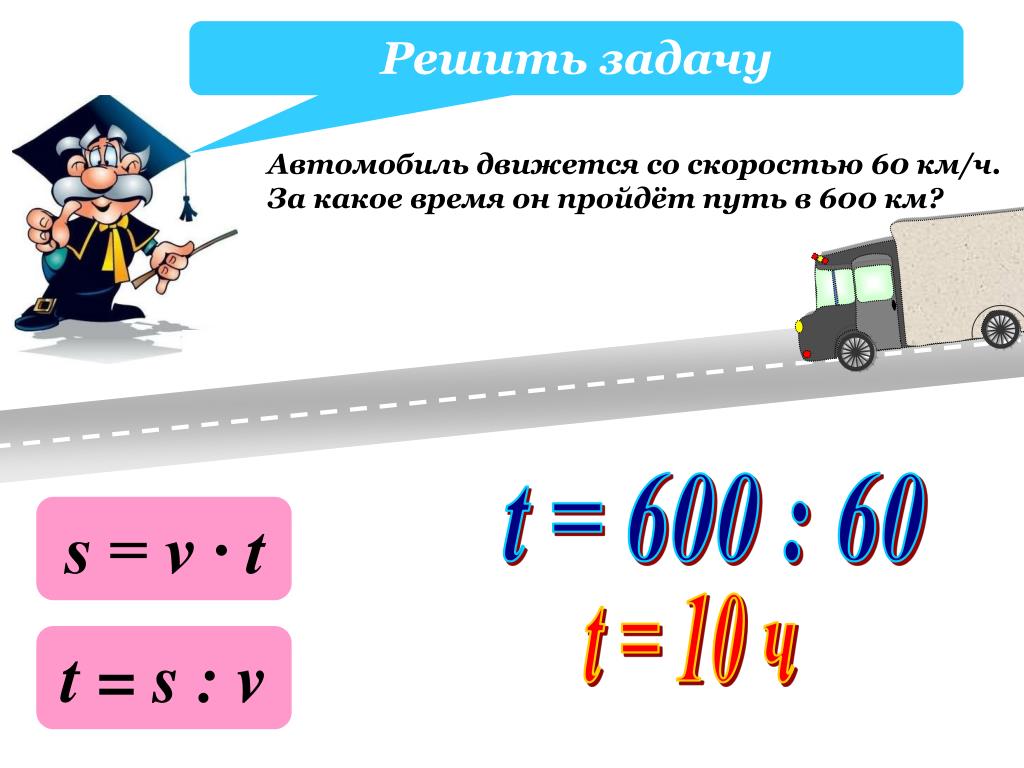

В данном случае 20 км/ч — это разница скоростей между мотоциклистами и велосипедистами.

Через два часа велосипедист проедет 40 км. Мотоциклист преодолеет 80 километров и отодвинется от велосипедиста еще на двадцать километров — общее расстояние между ними составит 40 километров.

Чтобы найти скорость, с которой один объект удаляется от другого при движении в одном направлении, вы должны вычесть меньшую скорость из большей скорости.

В приведенном выше примере скорость погружения одного объекта от другого составляет 20 км/ч. Его можно найти, вычитая скорость велосипедиста из скорости мотоциклиста. Скорость велосипедиста 20 км/ч, мотоциклиста 40 км/ч. Скорость мотоциклиста больше, поэтому из 40 вычитаем 20

40 км/ч – 20 км/ч = 20 км/ч

---

Задача 1. Автомобиль и автобус выехали из города в одном направлении. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? два часа?

Решение

120 км/ч – 80 км/ч = 40 км/ч.

Каждый час легковой автомобиль отъезжает от автобуса на 40 км. За 1 час расстояние между автомобилем и автобусом составит 40 км. Через 2 часа это в два раза больше:

40 × 2 = 80 км

Ответ: через час расстояние между автомобилем и автобусом будет 40 км, через два часа 80 км.

---

Рассмотрим ситуацию, в которой объекты начали свое движение из разных точек, но в одном направлении.

Предположим, есть дом, школа и аттракцион. От дома до школы 700 метров

Задание 6 Два пешехода вышли на прогулку одновременно. Первый пешеход пошел на аттракцион от дома со скоростью 100 метров в минуту, а второй пешеход ехал по маршруту от школы со скоростью 80 метров в минуту. Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после старта первый пешеход догонит второго пешехода?

Ответим на первый вопрос задачи: Каково расстояние между пешеходами через 2 минуты?

Определите расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдет вдвое больше, т. е. 200 метров.

100 × 2 = 200 метров

Определите расстояние, пройденное вторым пешеходом за 2 минуты. Он двигался со скоростью 80 метров в минуту. За две минуты он пройдет в два раза больше, т. е. 160 метров.

80 × 2 = 160 метров

Теперь нам нужно найти расстояние между пешеходами

Чтобы найти расстояние между пешеходами, можно прибавить расстояние, пройденное вторым пешеходом (160м) к расстоянию от дома до школы (700 м) и вычесть из результата расстояние, пройденное первым пешеходом (200 м).

700 м + 160 м = 860 м

860 м – 200 м = 660 м

Вычтите расстояние, пройденное первым пешеходом (200 м), из расстояния от дома до школы (700 м) и прибавьте пройденное расстояние второй пешеход (160м) до результата.

700 м – 200 м = 500 м

500 м + 160 м = 660 м

Таким образом, через две минуты расстояние между пешеходами будет 660 метров

Попробуем ответить на следующий вопрос задачи: Через сколько минут после начала движения первый пешеход догонит второго?

Посмотрим какая ситуация была в начале пути-когда пешеходы еще не начали движение

Как видно на рисунке расстояние между пешеходами в начале пути было 700 метров . Но через минуту после начала движения расстояние между ними будет 680 метров, так как первый пешеход движется на 20 метров быстрее второго пешехода:

100 м × 1 = 100 м

80 м × 1 = 80 м

700 м + 80 м – 100 м = 780 м – 100 м = 680 м

 

Через две минуты после начала движения расстояние уменьшится еще на 20 метров и составит 660 метров. Это был наш ответ на первый вопрос задачи:

100 м × 2 = 200 м

80 м × 2 = 160 м

700 м + 160 м – 200 м = 860 м – 200 м = 660 м

Через три минуты расстояние уменьшится еще на 20 метров и составит уже 640 метров:

100 м × 3 = 300 м

80 м × 3 = 240 м

700 м + 240 м – 300 м = 940 м – 300 м = 640 м подойдет ко второму пешеходу на 20 метров и в итоге догонит его. Можно сказать, что скорость двадцать метров в минуту — это скорость схождения пешеходов. Правила нахождения скорости сближения и удаления в одном направлении идентичны.

Чтобы найти скорость схождения при движении в одном направлении, нужно вычесть меньшую скорость из большей скорости.

А так как 700 метров каждую минуту уменьшается на те же 20 метров, то мы можем узнать сколько раз 700 метров содержат по 20 метров, тем самым определив через сколько минут первый пешеход догонит второго

700 : 20 = 35

Значит через 35 минут после начала движения первый пешеход догонит второго пешехода. Ради интереса узнайте, сколько метров прошел к этому времени каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше

100 × 35 = 3500 м

Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше

80 × 35 = 2800 м

Первый прошел 3500 м, а второй 2800 м. Первый прошел еще 700 метров, потому что шел от дома. Если из 3500 метров вычесть эти 700 метров, то получится 2800 метров.

---

Задача 7 Рассмотрим ситуацию, в которой объекты движутся в одном направлении, но один из объектов начал свое движение раньше другого.

Предположим, есть дом и школа. Первый пешеход шел в школу со скоростью 80 метров в минуту. Через 5 минут второй пешеход последовал за ним в школу со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого пешехода?

Второй пешеход начал идти через 5 минут. К тому времени первый пешеход уже преодолел некоторое расстояние. Найдем это расстояние. Для этого умножьте его скорость (80 м/м) на 5 минут

80 × 5 = 400 метров

Первый пешеход находится в 400 метрах от второго пешехода. Следовательно, в момент начала движения второго пешехода между ними будут эти 400 метров.

Но второй пешеход движется со скоростью 100 метров в минуту. То есть он движется на 20 метров быстрее первого пешехода, а значит, с каждой минутой расстояние между ними будет уменьшаться на 20 метров. Наша задача узнать, через сколько минут это произойдет.

Например, через одну минуту расстояние между пешеходами будет 380 метров. Первый пешеход помимо своих 400 метров пройдет еще 80 метров, а второй пешеход пройдет 100 метров.

Принцип здесь тот же, что и в предыдущей задаче. Расстояние между пешеходами в момент движения второго пешехода необходимо разделить на скорость приближения пешеходов. Скорость сближения в этом случае составляет двадцать метров. Следовательно, чтобы определить, через сколько минут второй пешеход догонит первого пешехода, разделите 400 метров на 20

400 : 20 = 20

Значит, через 20 минут второй пешеход догонит первого пешехода.

---

Задание 2. Автобус и велосипедист выехали из двух сел, расстояние между которыми 40 км, одновременно в одном направлении. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?

Решение

Найти скорость схождения

35 км/ч – 15 км/ч = 20 км/ч.

Через сколько часов автобус догонит велосипедиста?

40 : 20 = 2

Ответ: Автобус догонит велосипедиста через 2 часа.

---

Задача о движении реки, лодки и ручья

Суда движутся по реке с разной скоростью. Они могут двигаться как вниз по течению, так и вверх по течению. В зависимости от того, как они движутся (вверх по течению или вниз по течению), скорость будет меняться.

Предположим, скорость реки 3 км/ч. Если вы бросите лодку в реку, река унесет лодку со скоростью 3 км/ч.

Если спустить лодку в стоячую воду, в которой нет течения, лодка тоже будет стоять. Скорость лодки в этом случае будет равна нулю.

Если лодка плывет в стоячей воде при отсутствии течения, говорят, что лодка плывет со своей собственной скоростью .

Например, если моторная лодка плывет в стоячей воде со скоростью 40 км/ч, то говорят, что собственная скорость моторной лодки равна 40 км/ч.

Как найти скорость корабля?

Если корабль плывет по течению, вы должны добавить скорость течения реки к собственной скорости корабля.

Например, если моторная лодка плывет со скоростью 30 км/ч по реке и скорость течения реки 2 км/ч, то к собственной скорости моторной лодки (30 км/ч) необходимо прибавить скорость речной поток (2 км/ч)

30 км/ч + 2 км/ч = 32 км/ч

Можно сказать, что речной поток помогает моторной лодке с дополнительной скоростью, равной двум километрам в час.

Если корабль плывет против течения реки, из скорости корабля нужно вычесть скорость течения реки.

Например, если моторная лодка плывет со скоростью 30 км/ч против течения реки , а скорость течения реки 2 км/ч, то от скорости моторной лодки (30 км/ч) необходимо вычесть скорость речного течения (2 км/ч)

30 км/ч – 2 км/ч = 28 км/ч

Речное течение в этом случае препятствует свободному движению моторной лодки вперед, уменьшая ее скорость на два километра в час.

---

Задание 1. Скорость лодки 40 км/ч, скорость течения 3 км/ч. С какой скоростью лодка будет двигаться по течению реки? Против течения реки?

Ответ:

Если бы лодка двигалась вниз по течению реки, ее скорость была бы 40 + 3, что равно 43 км/ч.

Если лодка движется против течения реки, то ее скорость будет 40 – 3, т. е. 37 км/ч.

---

Задание 2. Скорость катера в стоячей воде 23 км/ч.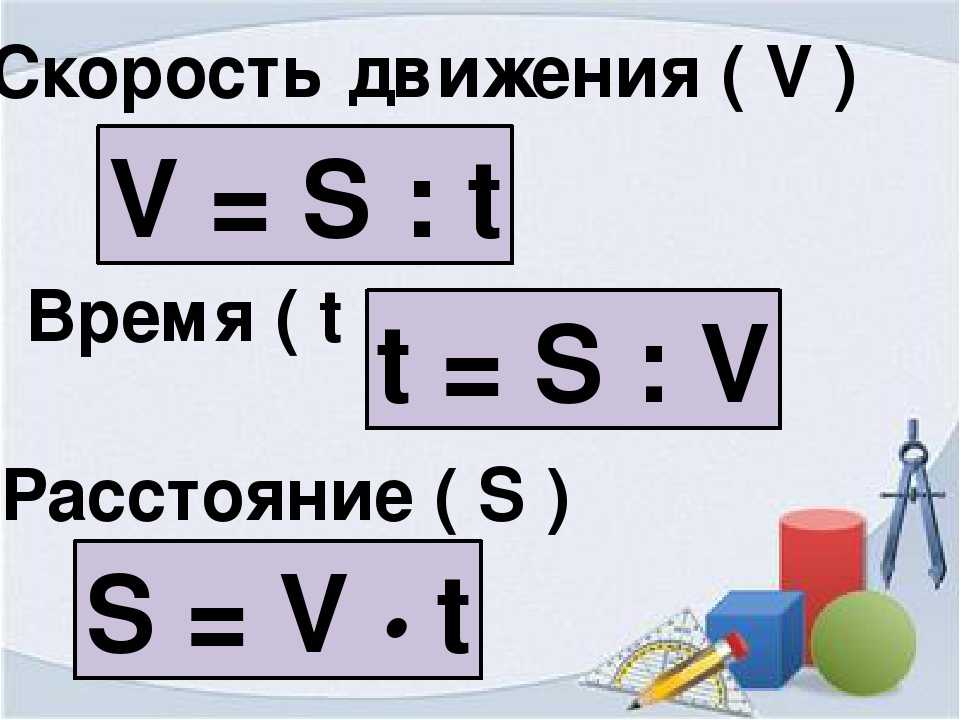 Скорость течения реки 3 км/ч. Какой путь пройдет теплоход за 3 часа вниз по течению реки? Против течения?

Решение

Фактическая скорость корабля 23 км/ч. Если корабль движется по течению, то его скорость будет 23 + 3, т. е. 26 км/ч. За три часа он пройдет в три раза больше

26 × 3 = 78 км

Если корабль будет двигаться против течения реки, его скорость будет 23 – 3, т. е. 20 км/ч. За три часа она проедет в три раза больше

20 × 3 = 60 км

---

Задача 3. Лодка прошла расстояние от точки А до точки В за 3 часа 20 минут, а расстояние от точки В до А за 2 часа 50 минут. В каком направлении течет река: из А в Б или из Б в А, если известно, что скорость лодки за время пути не изменилась?

Решение

Скорость лодки не изменилась. Выясним, какое направление реки занимало больше времени: путь из А в В или путь из В в А. Самый длинный путь — это путь, пройденный течением реки против лодки

3 часа и 20 минут более 2 часа 50 минут.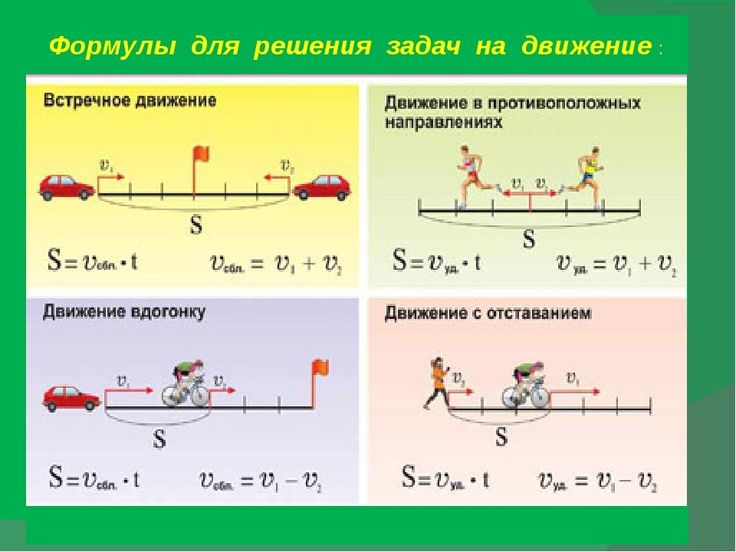 Это означает, что течение реки уменьшило скорость лодки, и это отразилось на времени в пути. 3 часа 20 минут — это время, которое потребовалось, чтобы добраться из точки А в точку Б. Итак, река течет из точки В в точку А

---

Задание 4. За какое время при движении против течения реки корабль пробежит 204 км, если его собственная скорость 15 км/ч, а скорость течения в 5 раз меньше скорости корабля скорость?

Решение

Найдите время, за которое корабль пройдет 204 км против течения реки. Скорость корабля 15 км/ч. Он движется против течения реки, поэтому нам нужно определить его скорость при этом движении.

Чтобы определить скорость против течения реки, вычтите скорость корабля (15 км/ч) из его собственной скорости (15 км/ч). Условие гласит, что скорость течения реки в 5 раз меньше скорости лодки, поэтому сначала определите скорость течения реки. Для этого уменьшите 15 км/ч в пять раз

15 : 5 = 3 км/ч

Скорость течения 3 км/ч. Вычтем эту скорость из скорости лодки

15 км/ч – 3 км/ч = 12 км/ч.

Теперь определите время, необходимое кораблю, чтобы пройти 204 км со скоростью 12 км/ч. Корабль движется со скоростью 12 км в час. Чтобы узнать, за сколько часов пройдет 204 км, определите, сколько раз в 204 км содержится 12 км

204 : 12 = 17 ч

Ответ: корабль пройдет 204 км за 17 часов

---

Задача 5. Двигаясь по течению реки, за 6 часов катер
прошел 102 км. Определить собственную скорость лодки
, если скорость течения 4 км/ч.

Решение

Найдите скорость, с которой лодка двигалась по реке. Разделите пройденное расстояние (102 км) на время в пути (6 ч).

102 : 6 = 17 км/ч.

Определим собственную скорость лодки. Это делается путем вычитания скорости течения (4 км/ч) из скорости, с которой лодка плыла по реке (17 км/ч)

17 – 4 = 13 км/ч

---

Задача 6. Двигаясь против течения, через 5 часов лодка
проехал 110 км. Определить собственную скорость лодки
, если скорость течения 4 км/ч.

Решение

Найдите скорость, с которой лодка двигалась по течению. Это делается путем деления пройденного расстояния (110 км) на время в пути (5 ч).

110 : 5 = 22 км/ч.

Определим собственную скорость лодки. В условии указано, что лодка двигалась против течения реки. Скорость течения реки 4 км/ч. Это означает, что собственная скорость лодки уменьшилась в 4 раза. Наша задача — прибавить 4 км/ч и найти собственную скорость лодки

22 + 4 = 26 км/ч.

Ответ: собственная скорость лодки 26 км/ч

---

Задание 7. За какое время лодка, идущая против течения реки
, пройдет 56 км, если скорость течения 2 км/ч, а собственная скорость лодки была
собственная скорость на 8 км/ч больше текущей скорости?

Решение

Найдите собственную скорость лодки. Условие гласит, что она на 8 км/ч больше скорости потока. Поэтому добавим к скорости течения (2 км/ч) еще 8 км/ч, чтобы найти собственную скорость лодки

2 км/ч + 8 км/ч = 10 км/ч

Лодка идет против течения реки, поэтому вычтем скорость реки (2 км/ч) из собственной скорости лодки (10 км/ч)

10 км/ч – 2 км/ч = 8 км/ч

Узнайте, за какое время лодка проедет 56 км. Для этого разделим расстояние (56 км) на скорость лодки:

56 : 8 = 7 ч

Ответ: Если лодка пойдет против течения, то она пройдет 56 км за 7 часов.

---

Упражнения

Задание 1. За какое время пешеход пройдет 20 км, если его скорость 5 км/ч?

Решение

За один час пешеход проходит 5 километров. Чтобы определить, за какое время он пройдет 20 км, нужно узнать, сколько раз в 20 км содержится 5 км. Или воспользуйтесь правилом нахождения времени: разделите пройденное расстояние на скорость движения

20 : 5 = 4 часа

Показать решение

Задача 2.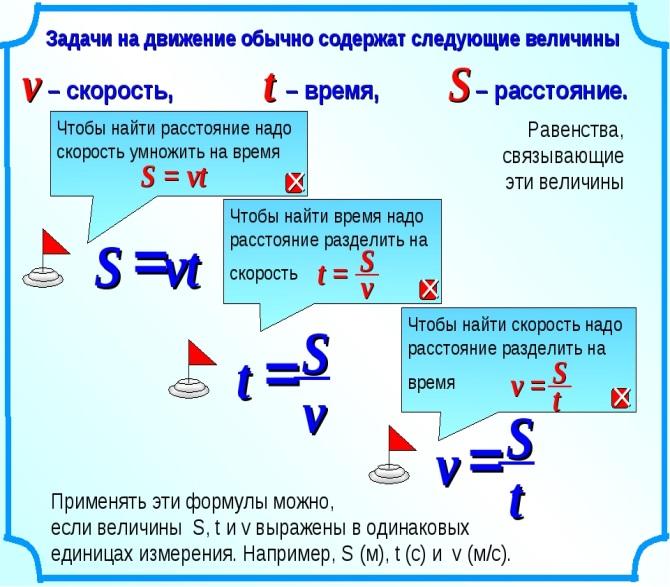 Велосипедист ехал из пункта А в пункт Б 5 часов со скоростью 16 км/ч, а обратно по тому же пути ехал со скоростью 10 км/ч. Сколько времени велосипедист ехал обратно?

Решение

Определить расстояние от точки A до точки B . Для этого умножьте скорость, с которой велосипедист ехал из точки А в точку В (16 км/ч), на время в пути (5 ч)

16 × 5 = 80 км

Найдите, сколько времени велосипедист потратил на обратный путь. Для этого разделите расстояние (80 км) на скорость (10 км/ч)

80 : 10 = 8 ч

Показать решение

Задача 3. Велосипедист ехал 6 ч в скорость. После того, как он проехал еще 11 км с той же скоростью, его путь стал 83 км. С какой скоростью ехал велосипедист?

Решение

Найдите расстояние, пройденное велосипедистом за шесть часов. Вычитаем из 83 км расстояние, пройденное за шесть часов (11 км).

83 – 11 = 72 км

Определите, с какой скоростью велосипедист ехал первые 6 часов. Для этого разделите 72 км на 6 часов

72 : 6 = 12 км/ч

. скорость 12 км/ч – это ответ на задачу.

Ответ: велосипедист ехал со скоростью 12 км/ч.

Показать решение

Задача 4. Двигаясь против течения реки, корабль проходит расстояние 72 км за 4 часа, а плот проходит то же расстояние за 36 часов. За сколько часов лодка преодолеет расстояние 110 км, если будет плыть по течению?

Решение

Найдите скорость течения реки. В условии указано, что плот может пройти 72 километра за 36 часов. Плот не может двигаться против течения реки. Таким образом, скорость, с которой плот проходит 72 километра, является скоростью течения реки. Чтобы найти эту скорость, разделите 72 километра на 36 часов.

72 : 36 = 2 км/ч

Найдем скорость лодки. Сначала найдем ее скорость против течения реки. Для этого делим 72 километра на 4 часа

72 : 4 = 18 км/ч

Если скорость корабля против течения 18 км/ч, то его собственная скорость 18+2, т.е. 20 км /час. А ниже по течению его скорость 20+2, т. е. 22 км/ч

Собственная скорость корабля 20+2, т. е. 22 км/ч.

Разделив расстояние 110 км на скорость корабля в течении реки (22 км/ч), вы узнаете, за сколько часов корабль пройдет расстояние 110 км

110 : 22 = 5 ч

Ответ: по течению реки корабль пройдет 110 километров за 5 часов.

Показать решение

Задание 5. Два велосипедиста одновременно выехали из одной точки в противоположных направлениях. Один из них ехал со скоростью 11 км/ч, а другой ехал со скоростью 13 км/ч. Какое расстояние между ними через 4 часа?

Решение

Найти скорость удаления велосипедистов

11 + 13 = 24 км

Найдите расстояние между ними через 4 часа

24 × 4 = 96 км

Ответ: Через 4 часа расстояние между велосипедистами составит 96 км.

Показать решение

Задание 6. Два теплохода вышли с двух причалов на встречу друг другу одновременно и встретились через 6 часов. Какое расстояние прошло каждое судно до встречи друг с другом и какое расстояние между причалами, если одно судно шло со скоростью 21 км/ч, а другое со скоростью 24 км/ч?

Решение

Найдите расстояние, пройденное первым кораблем. Для этого умножаем его скорость (21 км/ч) на время в пути до встречи (6ч).

21 × 6 = 126 км

Определите расстояние, пройденное вторым кораблем. Для этого умножьте его скорость (24 км/ч) на время в пути до встречи (6 ч)

24 × 6 = 144 км

Определите расстояние между причалами. Для этого суммируем расстояния, пройденные первым и вторым судами

126 км + 144 км = 270 км

Ответ: первый корабль прошел 126 км, второй корабль 144 км. Расстояние между маринами составляет 270 км.

Показать решение

Задача 7. Два поезда вышли из Нью-Йорка и Орландо одновременно. В 16 часов они встретились. Поезд из Нью-Йорка двигался со скоростью 51 км/ч. С какой скоростью шел поезд, отправившийся из Орландо, если расстояние между Нью-Йорком и Орландо было 1520 км? Какое расстояние было между поездами через 5 часов после их встречи?

Решение

Найдите, за сколько километров поезд ушел из Нью-Йорка до встречи. Для этого умножьте его скорость (51 км/ч) на 16 часов

51 × 16 = 816 км

Выясним, сколько километров проехал поезд, отправившийся из Орландо, до встречи. Для этого вычтем расстояние, пройденное поездом, отправившимся из Нью-Йорка, из расстояния между Нью-Йорком и Орландо (1520 км).

1520 – 816 = 704 км

Найдите скорость, с которой поезд покинул Орландо. Для этого разделите расстояние, пройденное им до встречи, на 16 часов

704 : 16 = 44 км/ч

Найдем расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдите скорость поезда и умножьте ее на 5

51 км/ч + 44 км/ч = 95 км/ч

95 × 5 = 475 км.

Ответ: поезд, вышедший из Орландо, двигался со скоростью 44 км/ч. Через пять часов после встречи поездов расстояние между ними составит 475 км.

Показать решение

Задание 8. Два автобуса одновременно выехали из одного пункта в противоположных направлениях. Скорость одного автобуса 48 км/ч, другого на 6 км/ч больше. Через сколько часов расстояние между автобусами составит 510 км?

Решение

Найдите скорость второго автобуса. Это на 6 км/ч больше скорости первого автобуса

48 км/ч + 6 км/ч = 54 км/ч

Найдите скорость удаления автобусов. Для этого складываем их скорости:

48 км/ч + 54 км/ч = 102 км/ч

За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать, через сколько часов расстояние между ними будет 510 км, нам нужно узнать, сколько раз в 510 км содержится 102 км/ч

510 : 102 = 5 ч

Ответ: 510 км между автобусами будет через 5 часов.

Показать решение

 

Задача 9. Расстояние от Чикаго до Нью-Йорка 1230 км. Два поезда отправились из Нью-Йорка и Чикаго навстречу друг другу. Поезд из Нью-Йорка движется со скоростью 63 км/ч, а скорость поезда в Чикаго равна скорости поезда в Нью-Йорке. На каком расстоянии от Чикаго встретятся поезда?

Раствор

Найдем скорость поезда в Чикаго. Она равна

скорости поезда в Нью-Йорке. Значит, чтобы определить скорость чикагского поезда, нужно найти 63 км.

63 : 21 × 20 = 3 × 20 = 60 км/ч

Найдем скорость сближения поездов

63 км/ч + 60 км/ч = 123 км/ч

Определим, через сколько часов поезда встретятся

1230 : 123 = 10 часов

Найдем расстояние, на котором встретятся поезда из Чикаго. Для этого достаточно найти расстояние, пройденное чикагским поездом до встречи

60 × 10 = 600 км.

Ответ: поезда встретятся на расстоянии 600 км от Чикаго.

Показать решение

Задание 10. От двух причалов одновременно отплыли две моторные лодки, расстояние между которыми 75 км, навстречу друг другу. Один двигался со скоростью 16 км/ч, а скорость другого составляла 75% скорости первого катера. Какое расстояние между катерами через 2 ч?

Раствор

Найдите скорость второй лодки. Это 75% скорости первого катера. Следовательно, чтобы найти скорость второй лодки нам нужно 75% от 16 км

16 × 0,75 = 12 км/ч

Найдите скорость сближения лодок

16 км/ч + 12 км/ч = 28 км/ч

Расстояние между лодками будет уменьшаться на 28 км каждый час. Через 2 часа будет 28×2, т.е. 56 км. Для того, чтобы определить расстояние между лодками в это время, из 75 км вычтем

9 56 км.0002 75 км – 56 км = 19 км

Ответ: Через два часа между лодками будет 19 км.

Показать решение

Задание 11. Автомобиль со скоростью 62 км/ч догоняет грузовик со скоростью 47 км/ч. Через какое время и на каком расстоянии от начала движения легковой автомобиль догонит грузовой автомобиль, если начальное расстояние между ними было 60 км?

Решение

Найти скорость приближения

62 км/ч – 47 км/ч = 15 км/ч

Если изначально расстояние между автомобилями было 60 км, то каждый час это расстояние будет уменьшаться на 15 км, и в итоге легковой автомобиль догонит грузовая машина. Чтобы узнать, через сколько часов это произойдет, определим, сколько раз в 60 км содержится 15 км

60 : 15 = 4 ч

Выясним, на каком расстоянии от начала движения легковой автомобиль догнал грузовой автомобиль . Для этого умножаем скорость автомобиля (62 км/ч) на время его движения до встречи (4 ч)

62 × 4 = 248 км

Ответ: легковой автомобиль догонит грузовик через 4 часа. На момент встречи легковой автомобиль будет находиться в 248 км от начала движения.

Показать решение

Задание 12. Два мотоциклиста выехали из одной точки в одно и то же время в одном направлении. Скорость одного была 35 км/ч, а скорость другого 80% от скорости первого мотоциклиста. Какое расстояние будет между ними через 5 часов?

Решение

Найдите скорость второго мотоциклиста. Это 80% скорости первого мотоциклиста. Следовательно, чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч

35 × 0,80 = 28 км/ч

Первый мотоциклист движется со скоростью 35-28 км/ч

35 км /ч – 28 км/ч = 7 км/ч

За 1 час первый мотоциклист проедет еще 7 км. С каждым часом он будет приближаться ко второму мотоциклисту на эти 7 километров.

За 5 часов первый мотоциклист проедет 35х5, т.е. 175 км, а второй мотоциклист проедет 28х5, т.е. 140 км. Определим расстояние, которое находится между ними. Для этого из 175 км вычтем 140 км

175 – 140 = 35 км

Ответ: через 5 часов расстояние между мотоциклистами будет 35 км.

Показать решение

Задание 13. Мотоциклист, скорость которого 43 км/ч, догоняет велосипедиста, скорость которого 13 км/ч. Через сколько часов мотоциклист догонит велосипедиста, если первоначальное расстояние между ними было 120 км?

Решение

Найдите скорость сближения:

43 км/ч – 13 км/ч = 30 км/ч

Если изначально расстояние между мотоциклистом и велосипедистом было 120 км, то каждый час это расстояние уменьшится на 30 км, и в конце концов мотоциклист догонит велосипедиста. Чтобы узнать, через сколько часов это произойдет, определите, сколько раз в 120 км содержится 30 км

120 : 30 = 4 ч

Значит, через 4 часа мотоциклист догонит велосипедиста

На рисунке показано движение мотоциклиста и велосипедиста. Вы можете видеть, что после 4 часов вождения они выровнялись.

Ответ: мотоциклист догонит велосипедиста через 4 часа.

Показать решение

Задача 14. Велосипедист, скорость которого 12 км/ч, догоняет велосипедиста, скорость которого составляет 75% его скорости. Через 6 часов второй велосипедист догнал велосипедиста, ехавшего первым. Каково было начальное расстояние между велосипедистами?

Решение

Найдите скорость велосипедиста, едущего впереди. Для этого найдем 75% скорости велосипедиста, едущего сзади:

12 × 0,75 = 9 км/ч скорость велосипедиста, едущего впереди

Выясним, сколько километров проехал каждый велосипедист раньше второго велосипедиста догнал первого:

12 × 6 = 72 км — ехавший сзади
9 × 6 = 54 км — ехавший впереди

Найдем начальное расстояние между велосипедистами. Для этого вычтем из пути, пройденного первым велосипедистом (догонявшим), расстояние, пройденное вторым велосипедистом (догонявшим)

72 км – 54 км = 18 км

Ответ: между велосипедистами изначально было 18 км.

Показать решение

Задание 15. Автомобиль и автобус выехали из одной точки в одно и то же время в одном направлении. Скорость автомобиля 53 км/ч, скорость автобуса 41 км/ч. Через сколько часов после выезда автомобиль будет впереди автобуса на 48 км?

Решение

Найдите скорость автомобиля на удалении от автобуса

53 км/ч – 41 км/ч = 12 км/ч

Каждый час автомобиль будет удаляться от автобуса на 12 км. На рисунке показано положение автомобилей после первого часа

Видно, что автомобиль опережает автобус на 12 км.

Чтобы узнать, через сколько часов автомобиль будет на 48 км опережать автобус, нужно определить, сколько раз в 48 км содержится 12 км

48 : 12 = 4 часа

Ответ: 4 часа после выезда машина будет на 48 километров впереди автобуса.

Показать решение

---

Как рассчитать скорость, расстояние и время с помощью треугольника

Расчет скорости, расстояния и времени является важной частью многих ролей, в том числе в вооруженных силах или на транспорте.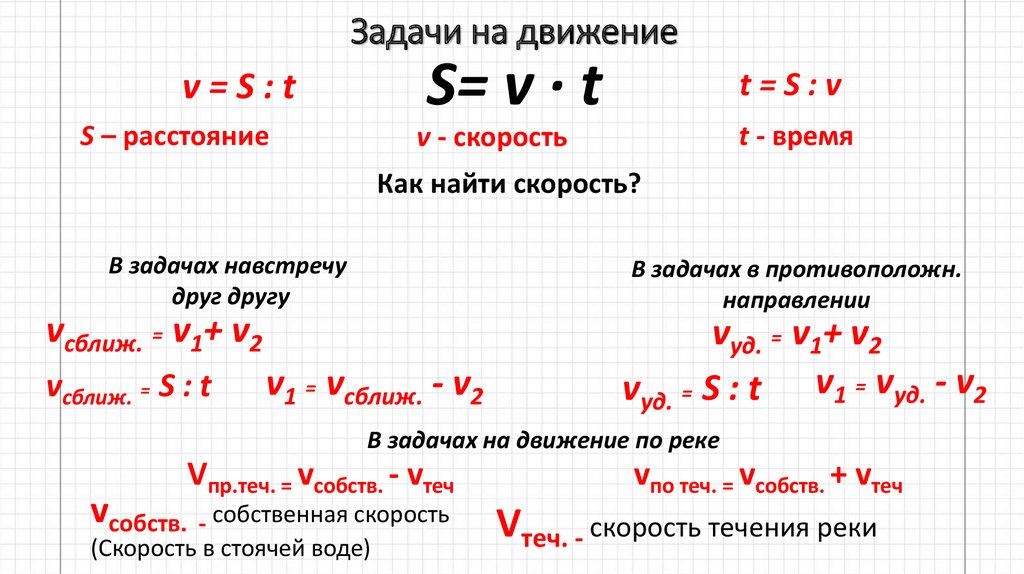

Если вы претендуете на должность в этих отраслях, вы можете пройти тестирование в рамках процесса найма. Вопросы позволят вашему работодателю проверить ваши прикладные математические способности.

Как рассчитать скорость, расстояние и время: формула треугольника вам понадобится?

Чтобы вычислить скорость, разделите расстояние пути на время, затраченное на путешествие, таким образом, скорость = расстояние, деленное на время. Чтобы рассчитать время, разделите расстояние на скорость. Чтобы получить расстояние, умножьте скорость на время.

Вы можете увидеть эти уравнения в упрощенном виде: s=d/t, , где s — скорость, d — расстояние, а t — время.

Эту формулу можно представить в виде треугольника выше. В треугольнике скорость и время образуют основу, так как они перемножаются, чтобы вычислить расстояние.

Треугольник позволяет легко запомнить формулу и сэкономить время при работе над экзаменационными вопросами.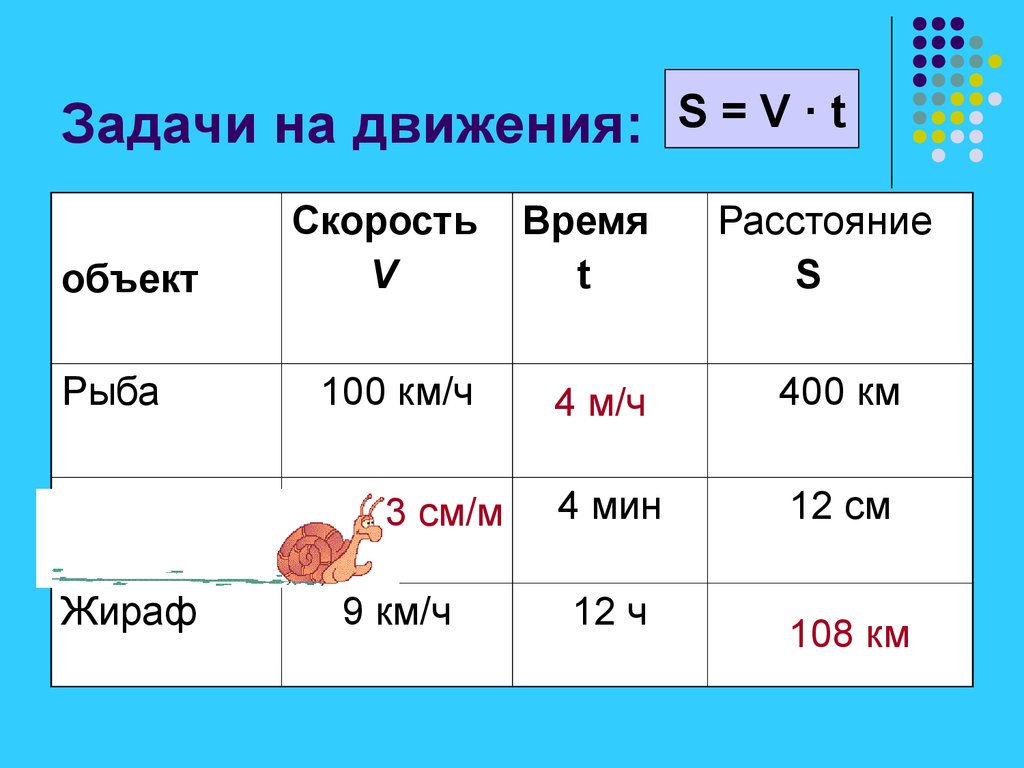 Треугольник поможет вам запомнить три формулы:

• Формула скорости Скорость = Расстояние ÷ Время
• Формула времени: Время = Расстояние ÷ Скорость
• Формула расстояния: Расстояние = Скорость x Время

Треугольник показывает, какой расчет следует использовать. Поскольку расстояние находится в верхней части треугольника, чтобы вычислить его, вам нужно умножить скорость на время.

Поскольку скорость и время находятся в нижней части треугольника, вам нужно разделить это число на цифру расстояния, чтобы получить правильный ответ.

Приступая к подготовке к пробному тесту, обязательно напишите треугольник на бумаге. Это поможет вам запомнить его.

Как рассчитать скорость

Чтобы рассчитать скорость, нужно расстояние разделить на время. Вы можете решить это, используя треугольник. Если вы скроете скорость, со временем у вас останется дистанция.

Вот пример:

Если водитель проехал 180 миль и ему понадобилось 3 часа, чтобы преодолеть это расстояние, то для расчета его скорости вы должны взять:

180 миль / 3 часа -> 180 / 3 = 60

Значит, скорость водителя будет 60 миль в час.

Как рассчитать расстояние

Чтобы вычислить пройденное расстояние, вам нужно будет умножить скорость и время.

Вот пример:

Если водитель ехал со скоростью 100 миль в час в течение 4 часов, то для расчета расстояния вам нужно будет умножить скорость на время.

100 миль в час x 4 часа -> 100 x 4 = 400

Расстояние 400 миль.

Как рассчитать время

Чтобы рассчитать время, которое заняло путешествие, вам нужно знать скорость движения и пройденное расстояние.

Вот пример:

Если водитель проехал 50 миль со скоростью 5 миль в час, то для определения затраченного времени нужно разделить:

50 миль / 5 миль в час -> 50 / 5 = 10

Затраченное время пройти это расстояние составляет 10 миль в час.

Три примера вопросов о скорости/расстоянии/времени

1. Энди проезжает на своем грузовике 400 миль, что занимает у него 8 часов. Гарри проезжает 200 миль, что занимает у него 4,5 часа. Кто едет быстрее?

Ответ: Энди едет со скоростью 50 миль в час, а Гарри едет со скоростью 44,44 мили в час. Итак, Энди едет быстрее.

1. Каждую субботу Тесса участвует в забеге на 5 км со своим беговым клубом. Она проходит это за 40 минут. Если она будет поддерживать ту же скорость, за какое время она пробежит 8 км?

Ответ: Ее скорость 7,5 км/ч. Если она пробежит 10 км со скоростью 7,5 км/ч, чтобы вычислить время, нужно разделить 8 на 7,5, что равно 1,066. Если мы переведем это в часы и минуты, ей потребуется 1 час и 4 минуты, чтобы пробежать 8 км.

1. Ханна отправляется на велосипедную прогулку. В первой половине пути она ехала со скоростью 10 миль в час в течение 2 часов. Во второй половине она едет со скоростью 20 миль в час в течение 90 минут. Сколько всего она проедет?

Ответ: В первой половине своего пути она проходит 20 миль (10 х 2 = 20). Во второй половине она проходит 30 миль (20 х 1,5 = 30). 20+30=50, значит, всего она проехала 50 миль.

Методы улучшения ответов на эти вопросы

Чтобы улучшить свои навыки ответов на вопросы о скорости, расстоянии, времени, вы можете сделать две основные вещи.

Во-первых, убедитесь, что вы знакомы с формулой треугольника. Ключом к ответу на эти вопросы является знание формулы наизнанку, чтобы вы всегда знали, какое уравнение использовать, независимо от того, просит ли вас экзаменационный вопрос вычислить скорость или расстояние.

Убедившись, что вы запомнили формулу во всех ее вариантах, вы сэкономите время при ответах на вопросы.

Во-вторых, вам следует сосредоточиться на улучшении общих математических навыков. Вы можете получить составной вопрос, в котором вас просят использовать формулу в сочетании с другими математическими навыками для решения задачи.

Вы можете пройти несколько тестов по математике, таких как эти, которые помогут вам попрактиковаться в своих основных навыках счета.

Скорость Расстояние Время: практические вопросы и ответы

Обновлено 18 мая 2022 г.

Автор: команда WikiJob

Все представленные продукты и услуги выбираются WikiJob независимо друг от друга. Когда вы регистрируетесь или совершаете покупку по ссылкам на этой странице, мы можем получать комиссию.

Как правило, эти вопросы касаются чего-либо, движущегося с постоянной скоростью. Из трех переменных (скорость, время или расстояние) вам даются две и требуется вычислить третью.

Где чаще всего используются вопросы о скорости, расстоянии, времени?

Эти тесты являются обычными при приеме на работу в авиационную промышленность и вооруженные силы, где эти навыки считаются важными.

Солдаты должны планировать, сколько времени им потребуется, чтобы преодолеть определенное расстояние. Пилоты также нуждаются в хороших навыках скорости, расстояния, времени, чтобы определить, сколько времени потребуется, чтобы пролететь определенное расстояние при движении с определенной скоростью.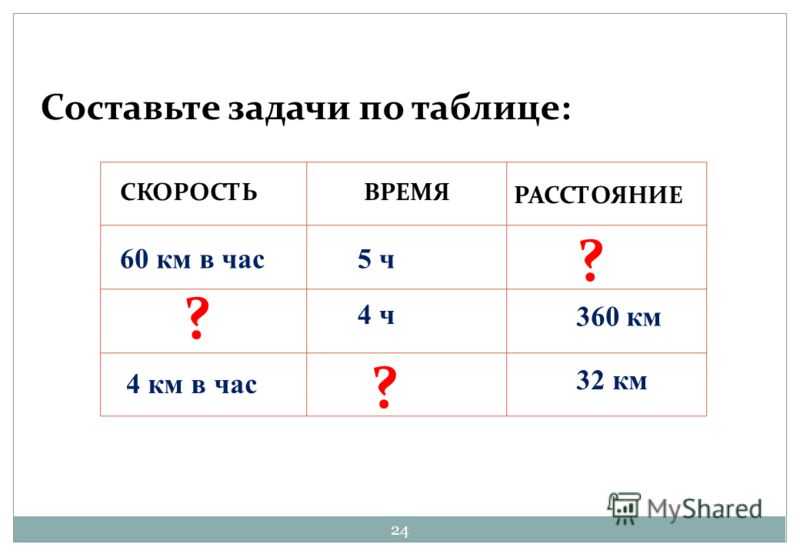

Чтобы стать компетентным в этих вопросах, вам нужно хорошо освоить таблицы умножения до 12, а также ряд различных шаблонов и формул, которые будут объяснены более подробно в этой статье.

Вопросы о скорости, расстоянии и времени всегда основываются на трех ключевых формулах. Тщательно практикуйте каждое из них.

Ключевые формулы, которые вам необходимо знать

Успех в этих тестах зависит от понимания трех различных формул, которые используются:

• Скорость = Расстояние / Время
• Время = Расстояние/Скорость
• Расстояние = скорость x время

Расчет средней скорости: два примера вопросов

Вопрос 1

Если вам потребуется 3 часа, чтобы проехать по автомагистрали расстояние 192 км, какова будет ваша средняя скорость в км/ч?

Скорость = Расстояние/Время

Скорость = 192/3 = 64

Таким образом, средняя скорость составляет 64 км в час.

Вопрос 2

Какова будет ваша средняя скорость в милях в час, если вы проедете 15 миль за 2 часа 30 минут?

Скорость = Расстояние/Время

Первым шагом является преобразование времени в минуты; 2 часа 30 минут это 150 минут.

Скорость = 15/150

Разделите обе стороны на 15

Скорость = 1/10

Другими словами, за десять минут вы проедете 1 милю. Итак, за шестьдесят минут вы проедете 6 миль.

Значит, средняя скорость 6 миль в час.

Пройти тест

Расчет расстояния: два примера вопросов

Вопрос 1

Джон решил доехать до дома своего друга на велосипеде со скоростью 5 км/ч, и дорога заняла 2 часа. Какое расстояние проехал Джон?

После первого часа Джон проехал на велосипеде 5 км

Через два часа Джон проехал на велосипеде 10 км

Используя формулу Расстояние = Скорость x Время, это будет рассчитано как:

Расстояние = 5 х 2 = 10 км.

Вопрос 2

Другой пример: Салли бежит со скоростью 8 км/ч. Если она бежала в течение четырех часов, какое расстояние она пробежала?

Опять же, используя формулу Расстояние = Скорость х Время:

Расстояние = 8 х 4 = 32 км.

Расчет времени: два примера вопросов

Вопрос 1

Если бы вы ехали со скоростью 30 миль в час, сколько времени вам потребуется, чтобы преодолеть расстояние в 70 миль?

Здесь необходима формула Время = Расстояние/Скорость.

Расстояние 70 миль, скорость 30 миль в час

Время = 70/30

Как и при расчете скорости, знаменатель должен укладываться в 60 минут.

Время = 70/30 = 2,33

2,33 х 60 = 140 минут = 2 часа 20 минут.

Вопрос 2

Автобус движется со скоростью 54 км/ч во время движения, но после учета времени остановки, чтобы посадить и высадить пассажиров, его средняя скорость составляет 45 км/ч. Сколько минут автобус останавливается каждый час?

За один час без остановок автобус проехал бы 54 км. С учетом остановок автобус фактически проезжает 45 км. В результате он проезжает на 9 км меньше.

Расстояние/скорость = время

9 км/54 км/ч = 0,16 часа

0,16 x 60 = 10 минут

Таким образом, автобус останавливается в среднем на десять минут каждый час.

Пройдите тест

Хорошие способы тренировки Скорость Расстояние Время Вопросы

Как и в случае с каждым тестом, существуют рекомендуемые стратегии и приемы для ответов на вопросы. Следование перечисленным ниже поможет вам усовершенствовать технику и повысить точность.

• Понять вопрос . Внимательно прочитайте вопрос, чтобы убедиться, что вы полностью понимаете, о чем вас спрашивают. Как и во всех тестах на способности, неудача в понимании может иметь катастрофические последствия.

  Чем больше вы будете практиковаться в этих тестах, тем больше вы поймете, как легко быть пойманным на том, что вы не читаете вопрос так внимательно, как следует. Это может включать в себя ответ на вопрос в часах и минутах, а не только в минутах, или использование неправильной формулы скорости, расстояния, времени.

  Всегда стоит перечитывать вопросы после того, как вы на них ответили. Хотя это займет больше вашего времени, это может предотвратить потерю ценных очков.

• Возьми свой калькулятор . Если разрешено, принесите на тест свой собственный калькулятор, так как вы будете лучше знакомы с ним, что может сэкономить вам жизненно важные секунды. В ходе всего теста эти дополнительные секунды могут иметь решающее значение.

• Остерегайтесь человеческой ошибки . Выполняя расчеты, читайте числа непосредственно с контрольной бумаги или экрана компьютера, а не с любых сделанных вами заметок, так как можно легко неправильно прочитать написанное или посмотреть на другой ответ на другой вопрос.

• Учитывать время . Научитесь отвечать на вопросы в сжатые сроки. 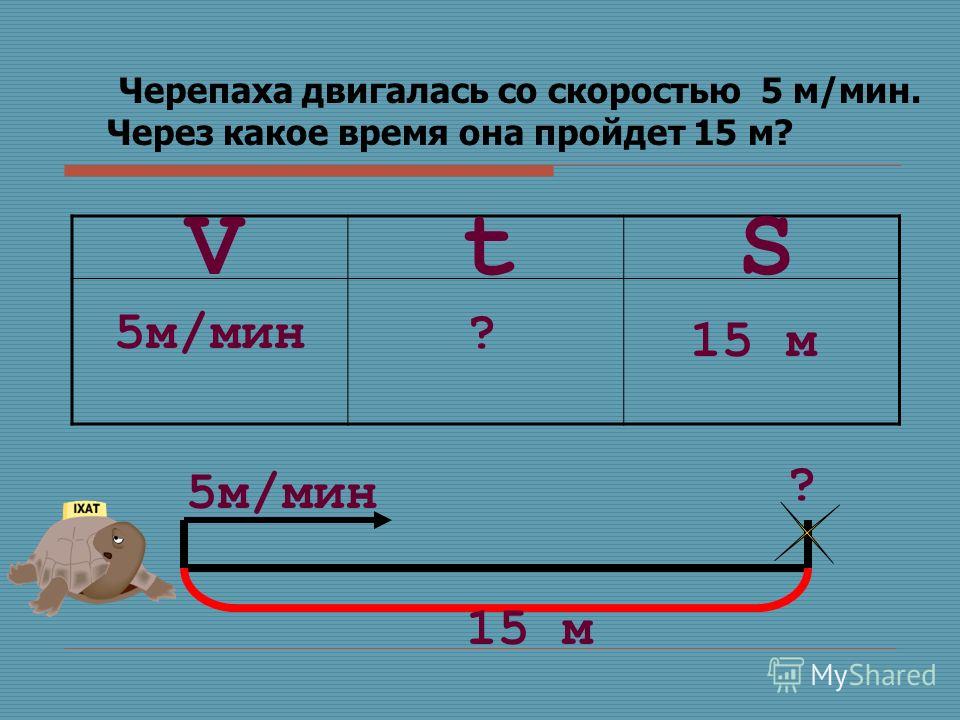Тест на скорость, расстояние и время предполагает, что вы будете работать быстро и точно, чтобы выполнить каждый из вопросов с точностью и умением.

• Выучить формулы . Запомните формулы, необходимые для расчета ответов на каждый из трех типов вопросов.

• Практика . Существует множество веб-сайтов, которые предоставляют симуляционные тесты для отработки различных типов вопросов на скорость, расстояние, время — используйте их как можно чаще. Попробуйте, например, JobTestPrep.

Практика с JobTestPrep

WikiJob также имеет приложение для психометрических тестов , доступный как для Apple, так и для Android, который включает в себя 10 числовых тестов и 8 вербальных тестов. Тесты включают таймер и отработанные решения в конце.

Часто задаваемые вопросы

Вопросы такого рода чаще всего используются в процессе найма в авиационную промышленность и вооруженные силы.

Вопросы скорости, расстояния и времени обычно можно решить, используя одну из трех формул:

Скорость = Расстояние/Время
Время = Расстояние/Скорость
Расстояние = Скорость x Время

Лучшее, что вы можете сделать, это запомнить три формулы, которые используются для расчета таких вопросов.

Как только вы их запомните, вам будет намного легче отвечать на любые вопросы о скорости, расстоянии или времени.

Вам необходимо выучить следующие формулы:

Скорость = Расстояние/Время
Время = Расстояние/Скорость
Расстояние = Скорость x Время

Да. Если вы вычисляете вопрос, который имеет несколько разных переменных или построен таким образом, что учитывает разные типы данных, например, конвертирование километров и миль, то найти правильный ответ может быть непросто.

Вот почему так важна практика. Чем больше вы будете практиковаться, тем больше различных типов вопросов вы столкнетесь.

Чем на больше различных типов вопросов вы ответите на практике, тем выше вероятность того, что вы сможете правильно ответить на экзамен.