Задача по математике 3: Задачи по математике 4 класс
Комментарии к материалу Тест по математике в картинках: попробуйте решить эти 10 задач без калькулятора | 74.ru
Все новости«Оказалось, она встречалась с нами обоими». История парня, чьи первые отношения обернулись адом
«Ушла своими ногами, а теперь заберу два трупа»: в челябинской больнице умерли беременная женщина и ее ребенок
Голову сломаешь: 10 логических задач, с которыми вам не справиться
А по чесноку? Врачи объяснили, что будет, если каждый день есть лимоны и чеснок
Сексуальность или скромность? Как выглядят южноуральские участницы Miss MAXIM в обычной жизни
В Челябинске 15 многоквартирных домов остались без отопления
«Тяжелый люкс — в прошлом»: почему россиянок оставляют без норковых шуб и предлагают носить зеленые из экомеха
Под санкции Евросоюза попали два южноуральских завода и депутат Госдумы
«Ни слова не скажут ни Росгвардия, ни полиция, дон!»: блогер устроил массовый террор заведений Челябинска
Запретят удаленку? Как смогут работать те, кто уехал за границу
«Вы ж потом выкидывать их будете!»: почему елочные базары в Челябинске оскудели, но взвинтили цены
Окно в Европу: как теперь купить новый iPhone и кроссовки Nike по параллельному импорту
Если под ногами лед: как выжить в скользком городе
«Шкодный» дефицит. В России закончились популярные иномарки
В России закончились популярные иномарки
Центробанк рассказал о нехватке рабочей силы в России из-за мобилизации: новости о СВО за 16 декабря
«Все деревья поснесло»: неопознанные летающие объекты рухнули в Волгоградской области
«Звуки были очень страшные»: всё, что известно о падении неопознанных летающих объектов под Волгоградом
В выходные на Южном Урале ожидаются снегопады. Дорожники попросили водителей отказаться от дальних поездок
«Двое детей влетели в фонарный столб»: родители малышей пожаловались на горку возле администрации
Минус 20 см без диет и спорта: модель раскрыла секрет, как быстро избавиться от выпирающего живота
Трехлетний мальчик с лопаткой вышел откапывать увязший в снегу автобус — смотрите самое милое видео этого года
Бастрыкин потребовал доложить ему обстоятельства нападения убийцы на конвой в южноуральском суде
Челябинцев насторожили похожие на взрыв звуки. Их было слышно в разных районах города
В Челябинске ночью несколько машин разрисовали краской из баллончика. Подозреваемый попал на видео
Подозреваемый попал на видео
Мальчик, поющий в парках Магнитогорска, попал на шоу «Голос.Дети»
Центробанк не стал повышать ключевую ставку
Известный отель на северо-западе Челябинска распродают под апартаменты
Кинули людей по всей России больше чем на миллиард. Как администрация Сочи плодит обманутых дольщиков
Мэрии Челябинска предписали расселить раньше срока общежитие с разобранной стеной. Теперь это 2030-й
Напавший на конвойных убийца был участником боевых действий и «героем» сюжета МВД про погоню со стрельбой
Моргенштерн* лишился бизнеса и уехал из страны. Взлеты и падения главного скандалиста российского шоу-бизнеса
Немецкая компания Henkel с заводом на Южном Урале останется в России, но сменит название
Из-за коммунальной аварии в «Академе» без воды остались около 300 квартир
Начальника управления в челябинском Минстрое приговорили за взятку к условному сроку
Убийца напал на конвойных, получив почти 10 лет колонии за расправу над тещей: подробности и видео из суда
12 больных вопросов про грипп и антибиотики — очень полезные карточки (отвечает искусственный интеллект, комментирует врач)
В Челябинской области спасали супругов, заблудившихся на уральском Бали в мороз
Где в Челябинске можно безопасно лечить зубы под наркозом
ЮУрГУ поймал ветер перемен: в университете огласили лауреатов ежегодной премии
Все новости
К постижению (не)эффективности преподавания математики
Сергей Лыткин,
кандидат физико-математических наук
«Троицкий вариант» №17(361), 6 сентября 2022 года
Оригинал статьи на сайте «Троицкого варианта»
The reasonable man adapts himself to the world:
the unreasonable one persists in trying to adapt the world to himself.
Therefore all progress depends on the unreasonable man.
George Bernard Shaw1
Статья Александра Шеня «О непостижимой (не)эффективности преподавания математики» , год назад опубликованная в ТрВ-Наука2 , затрагивала ряд важных проблем в современном математическом образовании. После ее прочтения, однако, оставалось некоторое неудовлетворение: не вполне ясно, кто же виноват в текущем положении дел, и уж совсем непонятно, что делать. Так почему же «математика идет так плохо», и поддается ли это лечению?
Из очевидного: неприятие школьной и вузовской математики есть прямое следствие кричащей бесполезности и архаичности контента. Глядя на варианты ЕГЭ (причем не только по математике), хорошо понимаешь смысл фразы «забудьте всё, чему вас учили в школе». Не связывающие свое будущее с математикой школьники забудут ее на следующий день после сдачи ЕГЭ. И правильно сделают: такая математика во взрослой жизни им не пригодится примерно никогда.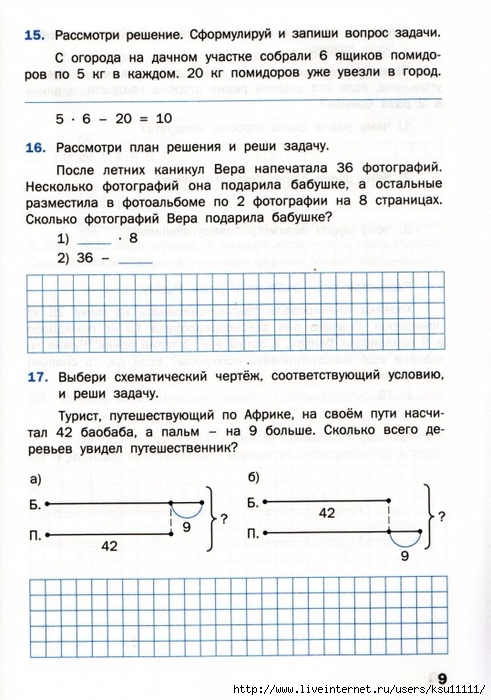 Парадокс в том, что многое из того, что спрашивается на ЕГЭ по математике, не пригодится и тем, кто пойдет в IT, естественные науки или даже в математику!3 Неудивительно, что школьники регулярно задают вопрос «зачем мне учить математику?» и саботируют этот процесс, не получая вразумительного ответа.
Парадокс в том, что многое из того, что спрашивается на ЕГЭ по математике, не пригодится и тем, кто пойдет в IT, естественные науки или даже в математику!3 Неудивительно, что школьники регулярно задают вопрос «зачем мне учить математику?» и саботируют этот процесс, не получая вразумительного ответа.
Не лучше обстоит дело с высшей математикой в вузах. Сопровождение студента со стороны преподавателя уменьшается по сравнению с тем, что было в школе, материал становится сложнее, а его практическая польза еще менее ясна. Устаревшие программы не обновляются должным образом из-за бюрократии и консерватизма, что приводит к хроническому отставанию от потребностей рынка труда. В итоге выпускники математических специальностей зачастую вынуждены много чему доучиваться или даже переучиваться, чтобы устроиться на работу (в которой математики может оказаться очень мало или даже не быть совсем). Спрашивается, зачем тогда надо было тратить столько времени на всякий «хлам» вроде вычисления пределов или неопределенных интегралов? 4 Тем более, что для этих целей давно уже создан Wolfram5.
Тут мне могут возразить, например, в таком духе:
- «математику уже затем учить надо, что она ум в порядок приводит»6;
- нейронные связи, выработанные и натренированные годами изучения математики, в будущем позволят человеку с легкостью освоить что угодно другое;
- экзамены тренируют стрессоустойчивость человека и формируют навык продуктивной работы в условиях жестких дедлайнов;
- штудирование безумно сложно написанных учебников и прорешивание массы задач не очень понятного назначения готовит к аналогичным трудностям на реальной работе («тяжело в учении — легко в бою»).
Всё это может работать только для очень узкого класса так называемых когнитивных атлетов, отличающихся быстротой усвоения материала и большой работоспособностью. На таком уровне дела в целом обстоят неплохо: есть и сильные школы с прекрасными учителями, проводятся олимпиады и специальные мастер-классы от лучших ученых страны, индустрия и бизнес организуют собственные образовательные мероприятия и программы с целью привлечь к себе в будущем лучшие кадры.
Обучение, даже университетское, приводит студентов к состоянию «самораспространяющейся псевдообразованности», при котором никто ничего толком не понимает, а только может успешно сдавать экзамены.
Такое «образование» по сути является вредительством, поскольку затраченное количество времени, денег и человеко-часов всеми участниками процесса совершенно непропорционально полученному на выходе результату. До определенного возраста человеку кажется, что впереди бесконечность, и поэтому у него практически отсутствуют сожаления о времени, потраченном на всякую ерунду. Этим психологическим фактором и злоупотребляют составители различных программ по математике. По сути школьная (да и вузовская) математика в нынешнем виде — это навязанная услуга со стороны государства, оказываемая в принудительном порядке весьма неэффективным способом и поэтому практически не достигающая целей, которые должно ставить перед собой качественное образование.
В современном быстро меняющемся мире основную ценность представляют не знания сами по себе (для этого есть Google, а на случай блокировки — «Яндекс») и не вычислительные навыки (для этого есть компьютеры). На рынке труда больше всего ценятся специалисты, способные быстро и эффективно решать поставленные задачи. Виртуозное умение решать квадратные уравнения или знание наизусть таблицы простых чисел до миллиона тут совершенно бесполезно. Критически важно же обладать ясным пониманием сущностных основ различных математических концепций и способностью распознать, какие из них целесообразнее всего применять при решении реальных практических задач. Вот этому как раз таки особо и не учат.
Также нельзя исключать, что сингулярность8 уже близко, и недалек тот день, когда знания будут по требованию непосредственно перетекать в мозг. Пока же можно констатировать, что объемы и потоки информации сегодня настолько возросли, что можно смело похоронить идею единоразового получения всех необходимых знаний и умений в школе и вузе. Чтобы оставаться успешными и востребованными в будущем, нынешним школьникам и студентам придется периодически усваивать всё новые и новые порции информации, в том числе и порции математики. Нет никаких рациональных причин пичкать среднего школьника десять лет подряд ненужной и непонятной ему математикой, кроме бюрократической необходимости хорошо написать контрольную или набрать некоторое число баллов на ЕГЭ/ОГЭ. Гораздо продуктивнее ограничиться самым базовым набором математических понятий, и обязательно добиться того, чтобы ученик реально их осознал и освоил. Тогда, если в будущем возникнет необходимость расширить и углубить познания в математике, у него не должно возникнуть непреодолимых препятствий к этому.
Чтобы оставаться успешными и востребованными в будущем, нынешним школьникам и студентам придется периодически усваивать всё новые и новые порции информации, в том числе и порции математики. Нет никаких рациональных причин пичкать среднего школьника десять лет подряд ненужной и непонятной ему математикой, кроме бюрократической необходимости хорошо написать контрольную или набрать некоторое число баллов на ЕГЭ/ОГЭ. Гораздо продуктивнее ограничиться самым базовым набором математических понятий, и обязательно добиться того, чтобы ученик реально их осознал и освоил. Тогда, если в будущем возникнет необходимость расширить и углубить познания в математике, у него не должно возникнуть непреодолимых препятствий к этому.
Тут мы вплотную подошли к вопросу о природе математического познания. Объективная сложность изучения математики заключается в том, что она имеет дело исключительно с абстракциями, представления о которых вырабатываются субъектом познания в результате рефлексии после взаимодействия с реальным миром. Есть много разных метафор, характеризующих процесс математического познания. Одна из самых метких трактует изучение математики как движение по спирали познания, поскольку к одному и тому же понятию ученик возвращается неоднократно, каждый раз находясь на более высоком уровне по сравнению с предыдущим обращением9. Переход на следующий уровень возможен только после решения некоторого числа задач, необходимое количество и скорость выполнения которых сугубо индивидуальны. Именно по этой причине лучшие математические школы вынуждены устраивать жесткий конкурс с целью отбора наиболее сильных когнитивных атлетов, способных взбираться по спирали познания с примерно одинаковой и довольно высокой скоростью.
Есть много разных метафор, характеризующих процесс математического познания. Одна из самых метких трактует изучение математики как движение по спирали познания, поскольку к одному и тому же понятию ученик возвращается неоднократно, каждый раз находясь на более высоком уровне по сравнению с предыдущим обращением9. Переход на следующий уровень возможен только после решения некоторого числа задач, необходимое количество и скорость выполнения которых сугубо индивидуальны. Именно по этой причине лучшие математические школы вынуждены устраивать жесткий конкурс с целью отбора наиболее сильных когнитивных атлетов, способных взбираться по спирали познания с примерно одинаковой и довольно высокой скоростью.
В начальной школе витки спирали познания довольно короткие и легкие для освоения, ведь с маленькими детьми по-другому и нельзя. С проникновением в глубь математики соответствующие различным понятиям спирали расширяются и частично переплетаются между собой. Достаточно взглянуть на программу школьной математики, чтобы понять ошибочность утверждения «школьный курс математики, в общем-то, довольно прост».
Неотработанные витки спирали познания ставят под угрозу дальнейшего продвижение ученика. К старшим классам, когда материал усложняется, а лакуны и обрывы у многочисленных спиралей познания достигают критической массы, большинство школьников и их родителей смиряются с неизбежным: надо срочно нанять репетитора, чтобы в спешном порядке залатать дыры и кое-как сдать ЕГЭ. Речи о понимании и познании математики уже не идет.
Тех, кто пережил10 школьный курс математики, может ожидать еще более серьезное испытание в институте. Методическая проработка пособий по высшей математике традиционно слабее, чем школьных; бытует также мнение, что студенты уже не дети и сами разберутся и всё поймут, раз выбрали математическую специальность.
Суммируя всё выше сказанное, можно констатировать, что в математическом образовании прежде всего не хватает тщательной методической проработки различных аспектов обучения. Не претендуя на исчерпывающую полноту, перечислим некоторые из них.
- Инвентаризация. Все элементы математических программ требуют тщательной ревизии, которая должна внятно и аргументированно ответить на вопросы, чему и как учить. Незачем обучать тому, что вряд ли когда-то пригодится. А если элемент признан достойным внимания, надо предусмотреть различные подходы и методики для его изучения. Также вполне может оказаться, что чего-то важного не хватает.
- Адаптивность. Когнитивные возможности у всех разные. Там, где когнитивный атлет быстро проскочит, решив пару задач, ученик средних способностей может застрять надолго.
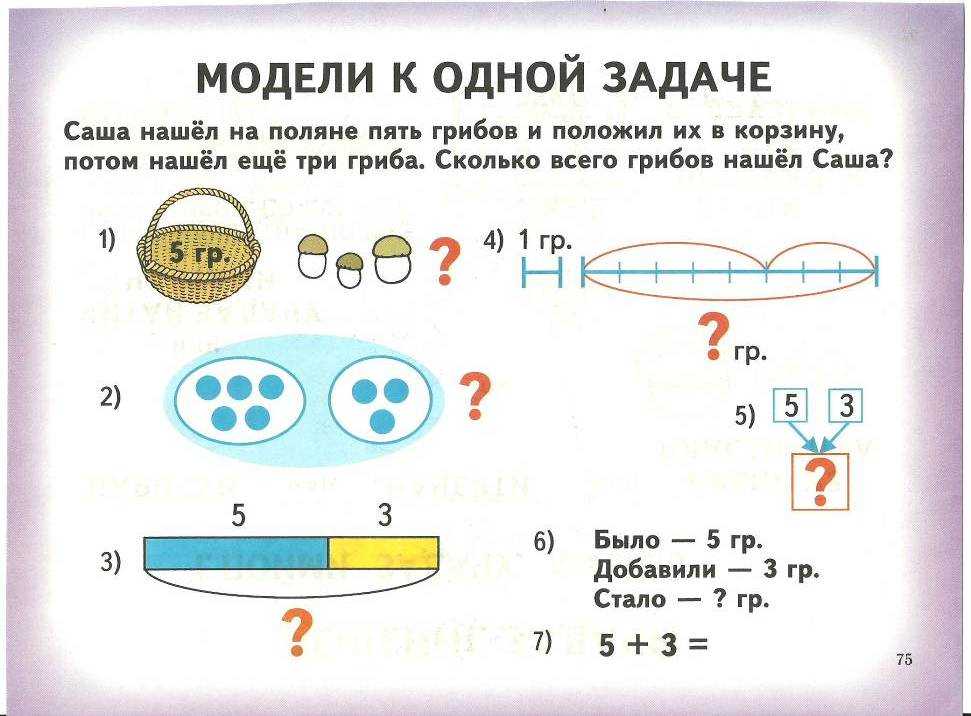 Каждое изучаемое понятие должно быть «разжевано» без существенных потерь в содержании до такого состояния, в котором ученик сможет его переварить. А чтобы когнитивные атлеты тем временем не скучали, для них следует предусмотреть задания более высокого уровня.
Каждое изучаемое понятие должно быть «разжевано» без существенных потерь в содержании до такого состояния, в котором ученик сможет его переварить. А чтобы когнитивные атлеты тем временем не скучали, для них следует предусмотреть задания более высокого уровня. - Адекватный контроль. Оценки, зачеты и экзамены представляют собой довольно посредственные и разреженные прокси-метрики для выявления реальных знаний учащегося. Требуется выработать набор инструментов и критериев, по которым можно непрерывно и с приемлемым уровнем точности судить о текущем прогрессе ученика. Это позволит быстрее и эффективнее достигать образовательного результата, оперативно внося необходимые коррективы при необходимости.
- Интеграция математики в другие области. Физику нужна одна математика, программисту — другая, экономисту — третья. И каждая имеет свои специфические отличия от «чистой математики»! Между тем учебники набиты абстрактными задачами ради задач, а прикладные задачи зачастую выглядят искусственно и откровенно притянутыми за уши.
 Если математика действительно настолько непостижимо эффективна11 в естественных науках, так покажите товар лицом! Обеспечение возможности бесшовного перехода в смежные дисциплины повысит мотивацию и послужит дополнительной иллюстрацией практической полезности математики.
Если математика действительно настолько непостижимо эффективна11 в естественных науках, так покажите товар лицом! Обеспечение возможности бесшовного перехода в смежные дисциплины повысит мотивацию и послужит дополнительной иллюстрацией практической полезности математики. - История математики. Этот компонент практически игнорируется в математическом образовании, которое в значительной степени сводится к предоставлению обучаемому уже готовых истин. Между тем ко многим их них математики шли веками и даже тысячелетиями. Прослеживание (подчас весьма извилистого) пути развития того или иного понятия интересно не только с познавательной точки зрения; оно помогает лучше осознать, почему математика устроена именно так, а не иначе, а также служит источником для методических находок. Ведь прогресс обычно движется от простого к сложному, следовательно, ранее открытые математические истины, как правило, проще и доступнее для понимания, нежели последующие. А вот преподавание, скажем, математического анализа, построено в противоестественном обратном направлении.
 Сначала студентов обучают действительным числам и теории пределов (эти понятия устаканились лишь к середине XIX века), а затем переходят к производным и интегралам12, которые вошли в математику почти на 200 лет раньше благодаря трудам Ньютона и Лейбница. Стоит ли удивляться, что матан традиционно считается самым убойным предметом высшей математики?
Сначала студентов обучают действительным числам и теории пределов (эти понятия устаканились лишь к середине XIX века), а затем переходят к производным и интегралам12, которые вошли в математику почти на 200 лет раньше благодаря трудам Ньютона и Лейбница. Стоит ли удивляться, что матан традиционно считается самым убойным предметом высшей математики? - Метакогнитивные навыки. Студентов не учат, как надо учиться. Например, в книге «Думай как математик» Барбара Оукли13, опираясь на исследования о том, как работает наш мозг, дает ряд ценных советов и приводит несколько полезных практик для повышения эффективности изучения математики и других наук. Много ли внимания уделяется этому важному моменту в школах и вузах?
- Обучение взрослых. Это направление особо не прорабатывалось в прошлом за ненадобностью. Современный тренд на автоматизацию ручного и рутинного труда приводит к тому, что люди вынуждены всё чаще обращаться к более интеллектуальным сферам деятельности.
 К примеру, в последние годы особую популярность набрало такое направление, как машинное обучение и data science, а в Интернете появилось множество коммерческих предложений типа «Обучаем с нуля профессии дата-сатаниста». Желающих перекатиться в новомодную область тоже немало, но многих отпугивает имеющаяся там математика14, которой они не знают. Это в свою очередь привело к появлению некоторого количества курсов а-ля «Изучи математику для ML/DS» 15. Главное тут — не переобучиться16.
К примеру, в последние годы особую популярность набрало такое направление, как машинное обучение и data science, а в Интернете появилось множество коммерческих предложений типа «Обучаем с нуля профессии дата-сатаниста». Желающих перекатиться в новомодную область тоже немало, но многих отпугивает имеющаяся там математика14, которой они не знают. Это в свою очередь привело к появлению некоторого количества курсов а-ля «Изучи математику для ML/DS» 15. Главное тут — не переобучиться16. - Математика и компьютеры. Среди ортодоксальных математиков встречается весьма пренебрежительное отношение к компьютерам. Дескать, настоящему математику нужны только проверенные веками средства: ручка, бумага и голова. А решение математических задач, полученное с помощью навороченных калькуляторов, является неполноценным.
Вряд ли стоит много говорить о близорукости и ущербности подобного взгляда. Уже упоминавшееся машинное обучение представляет собой яркий пример синтеза передовых компьютерных технологий и весьма сложной математики. Общее число программистов в мире удваивается каждые пять лет17. IT-сфера давно стала главной областью приложения математики, и, по-видимому, эта тенденция будет только нарастать, а посему должна обязательно учитываться при разработке методических программ по математике. Конечно, не дело вычислять производную от функции xn с помощью компьютера, но и отработка формулы Тейлора путем ручного разложения функций до десятого порядка — чрезмерный фанатизм, эту задачу лучше предоставить компьютеру.
Общее число программистов в мире удваивается каждые пять лет17. IT-сфера давно стала главной областью приложения математики, и, по-видимому, эта тенденция будет только нарастать, а посему должна обязательно учитываться при разработке методических программ по математике. Конечно, не дело вычислять производную от функции xn с помощью компьютера, но и отработка формулы Тейлора путем ручного разложения функций до десятого порядка — чрезмерный фанатизм, эту задачу лучше предоставить компьютеру.
По этому перечню ясно, что методической (и не только) работы тут непочатый край, причем ее ни в коем случае нельзя поручать «методистам» 18 в привычном смысле этого слова. Я ни в коей мере не призываю ни к перекраиванию всех школьных и вузовских программ, ни к написанию новых учебников по математике, памятуя о предостережении Н. И. Лобачевского: «Новая книга начал математики не должна напрасно умножать число существующих, потому что их и без того уже много»19. Полагаю, что все утвержденные программы и пособия разрабатывались действительно лучшими методистами, и если они (программы и пособия) такие, какие они есть, то это лишь потому, что «других писателей у нас для вас нет» 20. И вряд ли они волшебным образом одномоментно возникнут откуда-либо. К тому же всякая надежда на быстрые изменения в крайне инерционной системе образования выглядит утопично. Государству нынче явно не до образования, оно занято более важными делами, поэтому спасение утопающих — дело рук самих утопающих.
Полагаю, что все утвержденные программы и пособия разрабатывались действительно лучшими методистами, и если они (программы и пособия) такие, какие они есть, то это лишь потому, что «других писателей у нас для вас нет» 20. И вряд ли они волшебным образом одномоментно возникнут откуда-либо. К тому же всякая надежда на быстрые изменения в крайне инерционной системе образования выглядит утопично. Государству нынче явно не до образования, оно занято более важными делами, поэтому спасение утопающих — дело рук самих утопающих.
Об одном пути «спасения» имеет смысл сказать отдельно. Бытует ультраконсервативная точка зрения, согласно которой всё зло — от реформ последних тридцати лет, и поэтому надо срочно вернуться в «золотой век» советского образования, год эдак в 1937-й21. Дескать, лучшие учебники — это те, по которым учились наши дедушки и бабушки, а все дальнейшие реформы образования вели только к его неуклонной деградации. А уж всякие современные электронные прибамбасы надо срочно запретить как средство дебилизации населения. Утверждается, что к имущественному расслоению добавилось интеллектуальное (умные умнеют, глупые глупеют), и всевозможные онлайн-платформы и самоучители предоставляют дешевое и некачественное образование «для бедных». Хорошо научить может только живой учитель, поэтому надо срочно наладить их выпуск, подняв престиж профессии.
Утверждается, что к имущественному расслоению добавилось интеллектуальное (умные умнеют, глупые глупеют), и всевозможные онлайн-платформы и самоучители предоставляют дешевое и некачественное образование «для бедных». Хорошо научить может только живой учитель, поэтому надо срочно наладить их выпуск, подняв престиж профессии.
Еще недавно можно было бы снисходительно посмеяться над очередным стариковским брюзжанием в стиле «раньше было и солнце ярче, и трава зеленее». Казалось очевидным, что нельзя войти дважды в одну и ту же реку, и новые динамично меняющиеся времена ставят перед образованием совсем иные задачи, которые не решить средствами столетней давности. Но теперь подобный ретроградский охранительский стиль мышления идеально попадает в тренд. Верной дорогой идете, товарищи!
Да, искусственный интеллект в области образования еще не созрел; есть много платформ, сочетающих обучающий и развлекательный математический контент22, однако в основном они занимаются тем, что развлекают, но не учат. Но современные технологии развиваются стремительно. Лучшие шахматные программы до конца 1970-х годов не могли составить сколько-нибудь серьезной конкуренции гроссмейстеру, однако, в конце XX века компьютер победил чемпиона мира по шахматам. Еще более сложная игра го, считавшаяся неприступной на десятилетия вперед, пала под натиском нейронных сетей23. В последние годы у искусственного интеллекта появилось множество достижений и в других областях, поэтому есть все основания полагать, что в недалеком будущем цифровой учитель превзойдет белкового. Если не лучших из лучших, но наиболее массовый средний уровень — почти наверняка. Все технологии для этого уже есть, надо лишь соединить их вместе.
Но современные технологии развиваются стремительно. Лучшие шахматные программы до конца 1970-х годов не могли составить сколько-нибудь серьезной конкуренции гроссмейстеру, однако, в конце XX века компьютер победил чемпиона мира по шахматам. Еще более сложная игра го, считавшаяся неприступной на десятилетия вперед, пала под натиском нейронных сетей23. В последние годы у искусственного интеллекта появилось множество достижений и в других областях, поэтому есть все основания полагать, что в недалеком будущем цифровой учитель превзойдет белкового. Если не лучших из лучших, но наиболее массовый средний уровень — почти наверняка. Все технологии для этого уже есть, надо лишь соединить их вместе.
1 «Благоразумный человек приспосабливается к миру, неблагоразумный — упорно пытается приспособить мир к себе. Поэтому прогресс зависит от неблагоразумных людей» (Бернард Шоу).
2 Александр Шень. О непостижимой (не)эффективности преподавания математики. «Троицкий вариант» № 11(330), 1 июня 2021 года.
«Троицкий вариант» № 11(330), 1 июня 2021 года.
3 Я закончил школу до появления ЕГЭ, но содержание математики старших классов тогда не сильно отличалось от теперешнего. И хоть я и стал немного математиком, не могу не признать, что практически весь этот зоопарк уравнений и неравенств, хитрых стереометрических задач и задач с параметром, которые я с успехом нарешивал в 10–11 классах, не имеет применений за пределами школьной математики. Конечно, это помогло мне поступить на мехмат МГУ, а впоследствии проверять олимпиадные работы и заниматься репетиторством школьников. Однако по сути это всего лишь воспроизводство того же самого контента, которым меня питали в школе. Задачи ради задач.
4 Мне неоднократно приходилось слышать весьма нелестные мнения выпускников мехмата МГУ о бессмысленно прожитых там годах. Мол, лучше бы потратили время на изучение чего-нибудь действительно полезного.
5 WolframAlpha.
6 Эти слова приписывают М. В. Ломоносову.
В. Ломоносову.
7 Эта цитата из книги В. И. Арнольда «Математическое понимание природы» перефразирует слова Фейнмана из книги «Вы, конечно, шутите, мистер Фейнман!». Необходимо заметить, что сказаны они были о бразильской системе образования, где Фейнман преподавал в послевоенные годы. Вряд ли можно отрицать, впрочем, что данное утверждение в той или иной степени верно относительно любой образовательной системы.
8 Ray Kurzweil. The Singularity is Near.
9 Возможно, эта метафора была вдохновлена одним из законов диалектики Гегеля.
10 Кого еще не «кокнули», если выражаться языком А. М. Райгородского.
11 Как утверждается в классической статье E. Wigner. The Unreasonable Effectiveness of Mathematics in the Natural Sciences, Comm. Pure and Appl. Math. 131, 1 (1960). Русский перевод можно прочесть здесь.
12 В свое время я был сильно удивлен, обнаружив, что тема первой лекции в MIT по предмету Single Variable Calculus — производная! Как же они ее вычисляют без строго понятия предела? Немного поразмыслив, однако, я пришел к выводу, что ничего страшного в этом нет. Вполне можно сначала позаниматься интегралами и производными без полной математической строгости, а потом вернуться к ним еще раз на следующем уровне после изучения понятия предела. Спираль познания в действии.
Вполне можно сначала позаниматься интегралами и производными без полной математической строгости, а потом вернуться к ним еще раз на следующем уровне после изучения понятия предела. Спираль познания в действии.
13 Oakley B. A Mind For Numbers. По мотивам этой книги запущен один из самых популярных курсов на Coursera.
14 И это при том, что в подобных онлайн-курсах математику стараются по возможности обойти стороной. Доходит до смешного. В каком-то курсе рассказывалось о бизнес-экономике и предлагалась такая задача. У маленького бизнеса есть постоянные издержки, а каждый новый клиент приносит ему одинаковую дополнительную прибыль. Спрашивается: если число клиентов растет, в какой момент бизнес перестанет быть убыточным и выйдет в ноль? Любому мало-мальски сведущему в математике человеку ясно, что тут идет речь о точке пересечения двух прямых (горизонтальной и наклонной), которую легко можно найти, решив линейное уравнение. Однако авторы курса боялись математики как огня и потому предлагали студенту решить задачу перебором (!) с помощью компьютера.
15 ML = Machine Learning, DS = Data Science.
16 «Переобучение» — специальный термин из машинного обучения, обозначающий типичную ситуацию, когда модель очень плохо работает.
17 Такую оценку дает Роберт Мартин
18 Людям, которые «не умеют ни делать, ни учить, как делать, а потому им остается лишь учить, как учить».
19 Если их уже было много в XIX веке, то как же тогда охарактеризовать их количество в веке XXI?
20 Эти слова приписывают И. В. Сталину.
21 См., например, Костенко И. П. Не ошибка, а целенаправленное многолетнее разрушение // Математическое образование, 4 (100), 2021, с. 58–62
22 Для этого даже придумано новое слово: edutainment, от EDUcation и enterTAINMENT.
23 В 2016 году программа AlphaGo победила чемпиона мира по го Ли Седоля.
Три быстрых математических задачи. Можете ли вы решить все три? | Бо Хеллгрен
Мне нравятся эти три математические задачи! Первый требует очень мало математических навыков, но он, пожалуй, самый сложный. Второй требует только базовой геометрии. Для третьего нужно знать элементарную алгебру.
Второй требует только базовой геометрии. Для третьего нужно знать элементарную алгебру.
Проблема 1: Проблема 316
Я называю эту проблему «проблемой 316», потому что 316 не решение, но почти! Проблема:
Проблема 316
Найдите целое число, которое увеличится ровно в два раза, если сначала переместить последнюю цифру.
Возьмем, к примеру, 316: если вы переместите сначала последнюю цифру, вы получите 631. Если вы удвоите ее, вы получите 632. Близко, но не равно. Нам нужно нормальное десятичное число.
Задача 2: 90 градусов равно 100 градусам
Шаг A. Нарисуйте четыре линии, как показано на рисунке ниже. Угол DAB равен 90 градусов. Длина АД 5 см. Угол АВС равен 100 градусов. Длина ВС также равна 5 см.
Слева : Шаг A. Справа : Шаг B. Шаг B: Проведите линию, перпендикулярную AB, точно посередине AB (перпендикуляр биссектрисы).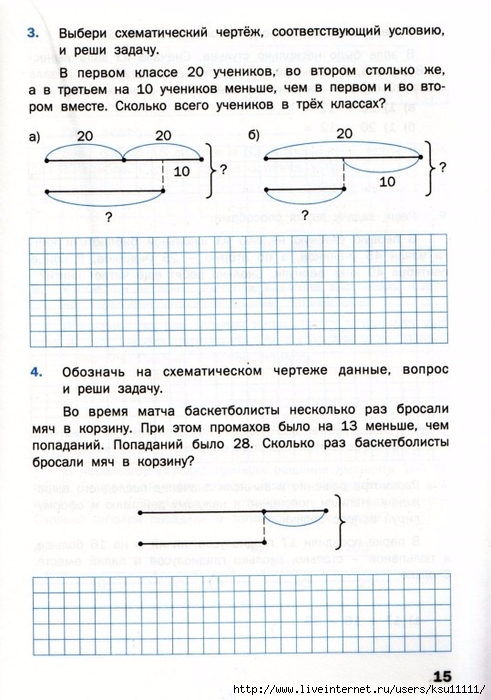 Сделайте то же самое с компакт-диском. Поскольку AB и CD не параллельны, две новые прямые также не будут параллельны. Назовите точку пересечения E.
Сделайте то же самое с компакт-диском. Поскольку AB и CD не параллельны, две новые прямые также не будут параллельны. Назовите точку пересечения E.
Шаг C: Нарисуйте линии от E до всех четырех углов исходной фигуры.
Слева : Шаг C. Справа : Шаг D.Шаг D : Рассмотрим два треугольника △ EAD (красный) и △EBC (зеленый).
- Стороны EA и EB имеют одинаковую длину, так как E лежит на биссектрисе AB.
- Стороны ED и EC имеют одинаковую длину, так как E лежит на биссектрисе DC
- Стороны AD и BC имеют одинаковую длину, так как обе имеют длину 5 см.
Следовательно, два треугольника конгруэнтны и их углы равны.
В частности, угол DAE равен углу EBC. Но углы EAB и EBA также равны, так как E лежит на биссектрисе AB. Теперь вычтите меньшие углы из больших углов. Остаток – это угол DAB, который равен 90 градусов и угол ABC, равный 100 градусам. Что доказывает, что 90 градусов равны 100 градусам.
Что не так с этим геометрическим доказательством того, что 90 градусов равны 100 градусам?
Задача 3: Мнимая мощность
Мнимая единица i определяется своим свойством i² = −1. Большинству людей, включая меня, трудно представить число, которое при умножении само на себя становится -1!
Действительное число, возведенное в само себя, не так сложно понять, как 3³, равное 27. Но i поднял себе? Если и трудно представить, то , и , возведенные в и , должны быть совершенно немыслимы.
Нет, это 0,21! Вы можете это доказать?
Решение 1: Задача 316
Пусть цифры решения представлены буквами a b c … x y z (не подразумевается, что решение обязательно имеет 26 цифр). Тогда мы можем написать следующее дополнение:
Какая последняя цифра, z? Мы можем только догадываться. Есть ли причина, почему это не будет 3? Давайте попробуем:
Теперь мы можем видеть, что если z равно 3, y должно быть 6:
Теперь мы можем видеть, что если y равно 6, x должно быть равно 2!
Тогда w должно быть равно 5. И так далее. Теперь мы просто продолжаем, пока не получим решение:
И так далее. Теперь мы просто продолжаем, пока не получим решение:
Последняя цифра 3 — это просто удачная догадка? Нет, подходит все, кроме 0 и 1. Я сделал небольшой лист Excel, который вычисляет решение, когда вы вводите конечную цифру. Вот решения, заканчивающиеся от 2 до 9:
Решение 2: 90 градусов ≠ 100 градусов
Рисунки на иллюстрациях неверны. Точка пересечения E должна быть гораздо выше . Тогда линия ЕС будет справа от точки В, а не слева. Увеличьте угол ABC со 100 градусов до 135 градусов, и это станет очевидным.
Слева : Рисунок из шага D. Справа : Рисунок из решенияНазовите угол ∠EAB α и угол ∠ABC β. При неправильном рисунке имеем α + 90 = α + β. При β = 100 это приводит к противоречию 90 = 100.
При правильном начертании имеем α + 90 = 360 — α — β. α = (270 – β)/2. При β = 100 мы получаем α = 85, что показывает, что точка E находится намного выше, но противоречия нет.
Решение 3: Мнимая степень
Начните с известного тождества Эйлера:
Перепишите его как:
Извлеките квадратный корень из обеих частей:
Возведите обе части в степень i:
Для a более подробное обсуждение этой проблемы см. , например, в этой ссылке.
, например, в этой ссылке.
3 чтения Стратегия успешного решения задач по математике
Словесные задачи часто являются самой сложной частью нашего обучения математике. Они могут визуально ошеломить студентов. Они часто содержат постороннюю информацию или несколько шагов для завершения. Учащиеся часто пытаются справиться со сложными задачами. Но, в конечном счете, именно через эти сложные задачи мы можем по-настоящему увидеть понимание нашими учениками математических концепций и стандартов. Ожидается, что наши студенты будут настойчиво решать их, демонстрировать понимание и использовать различные стратегии. Я подробно описываю свой опыт с трудностями при решении задач в своей статье «Почему ваши ученики борются со словесными задачами». Я использую модифицированную стратегию «3 чтения» в своем классе, чтобы помочь учащимся разобраться в сложных текстовых задачах во время нашей «Словесной задачи дня». Я связываю это с Закрытым чтением, которое мы проводим во время E/LA.
Мы должны внимательно прочитать задачу , чтобы по-настоящему понять, что требуется от нас как от математиков.
Стратегия 3 чтения представляет собой серию шагов, которые помогают учащимся разобраться в текстовых задачах. Он ориентирован на понимание контекста. Существуют различные интерпретации шагов. Я обнаружил, что мои ученики становятся все более успешными, следуя этому ежедневному протоколу «3 чтения». Мы делаем это во время нашей рутины Word Problem of the Day, поэтому мы тренируемся почти каждый божий день. В начале года я провожу своих учеников через 3 чтения, и мы обсуждаем этапы каждого чтения. С течением недель моя опора уменьшается, поскольку я ожидаю, что студенты будут применять одни и те же шаги независимо друг от друга. Я часто, особенно с более сложными текстовыми задачами, провожу первое чтение устно, чтобы обеспечить доступ для всех учащихся. Вот шаги, которые мы предпринимаем во время нашей программы «3 чтения».
1-е чтение: чтение для сути
Цель первого чтения — понять суть проблемы. Студенты должны быть в состоянии ответить, о чем проблема; контекст .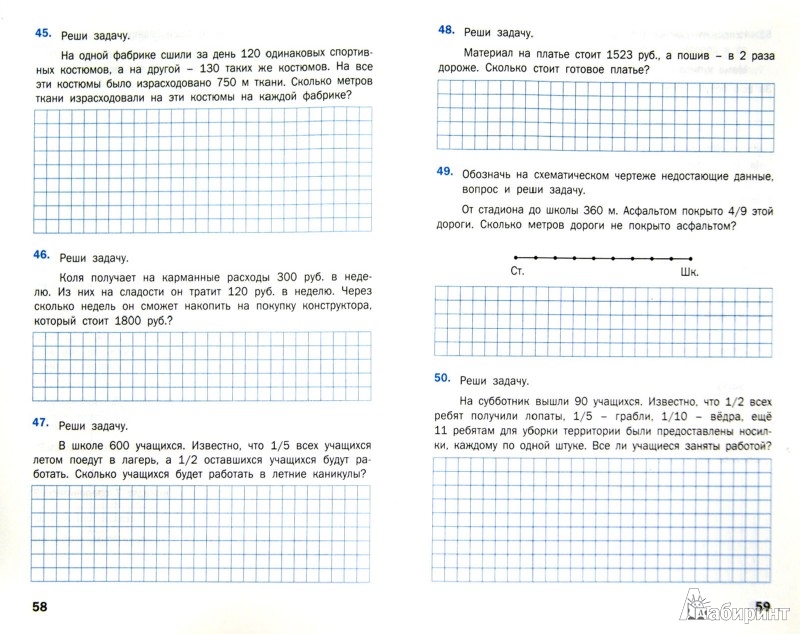 Учащиеся должны уметь пересказывать своими словами, что происходит в словесной задаче.
Учащиеся должны уметь пересказывать своими словами, что происходит в словесной задаче.
2-е чтение: чтение для неизвестного
Второе чтение сосредоточено на неизвестном ; за что решается. Выявление неизвестного помогает учащимся определить важную и необходимую информацию для решения во время третьего чтения. Это помогает им анализировать постороннюю информацию. Это также помогает учащимся убедиться, что они решают то, о чем на самом деле спрашивают. Я прошу своих учеников подчеркнуть важную информацию в вопросе, а также написать рамку предложения для решения.
3-е чтение: чтение количества
В этом чтении учащиеся определяют количества и соответствующие единицы измерения. Во время этого чтения я предлагаю учащимся обвести числа и подчеркнуть ключевые слова (чаще всего единицы) для решения. Важно отметить, что я не имею в виду ключевых слов , которые обычно являются словами, относящимися к операциям, таким как more. В этом чтении мы сосредоточимся на том, что известно ; предоставленная информация. С неизвестным, уже идентифицированным. Затем учащиеся пишут уравнение или выражение для решения. Они также могут нарисовать картинку, если это поможет понять шаги, необходимые для решения.
С неизвестным, уже идентифицированным. Затем учащиеся пишут уравнение или выражение для решения. Они также могут нарисовать картинку, если это поможет понять шаги, необходимые для решения.
Составьте план
Последний шаг — составить план решения. Теперь, когда учащиеся определили, о чем спрашивают, какую информацию им дают и что они решают, последний шаг — это действительное решение. Это может включать в себя моделирование проблемы с десятичными блоками. Это может также включать использование стандартного алгоритма для решения. Какую бы стратегию студенты ни считали необходимой, они делают.
После того, как учащиеся решили задачу, мы делимся решениями и стратегиями. Основное внимание уделяется гораздо большему, чем правильное решение! Я предлагаю ученикам показать свою работу и объяснить свое мышление. Во время нашего разговора мы можем критиковать чужую работу, чтобы выявить их ошибку. Мы можем использовать различные стратегии решения уравнения. Мы можем сравнить уравнения или выражения, написанные для задачи.