Высота в математике: ВЫСОТА (в геометрии) | это… Что такое ВЫСОТА (в геометрии)? – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Материал по математике на тему “Высота треугольника. Задача Фаньяно”

Высота треугольника. Задача Фаньяно

Высота треугольника

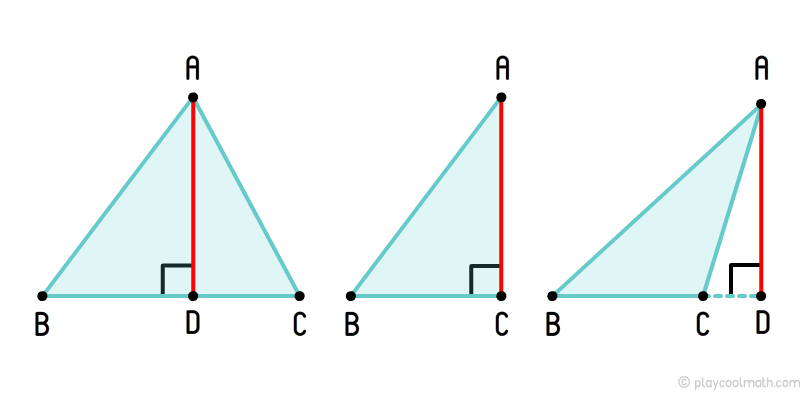
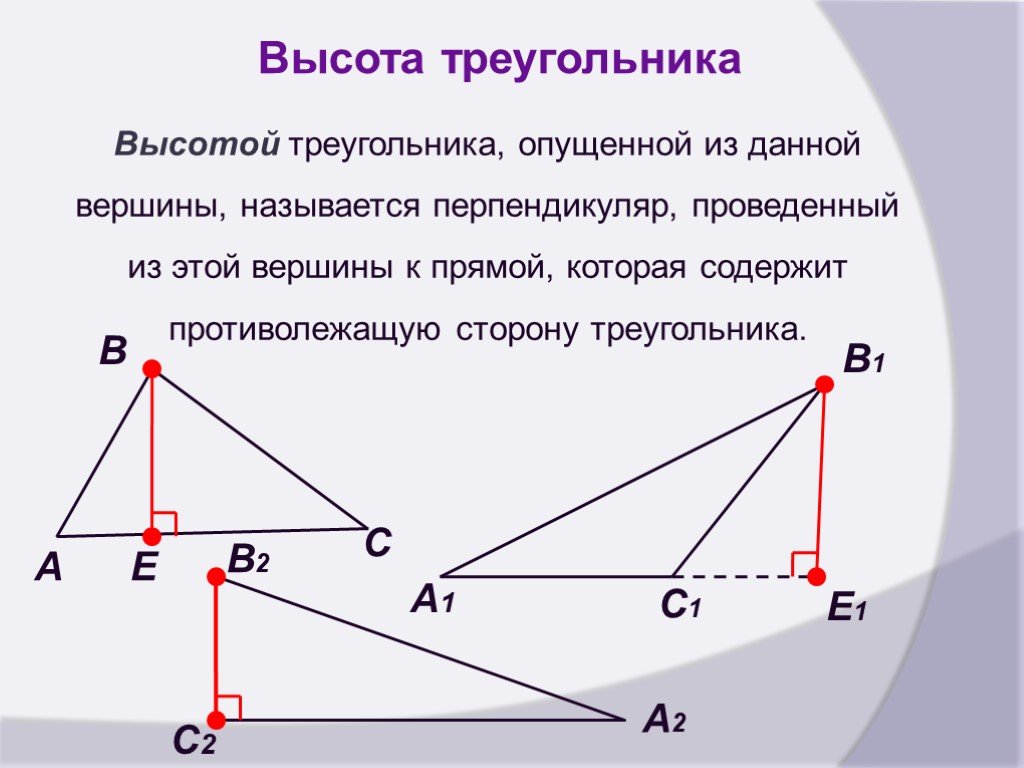
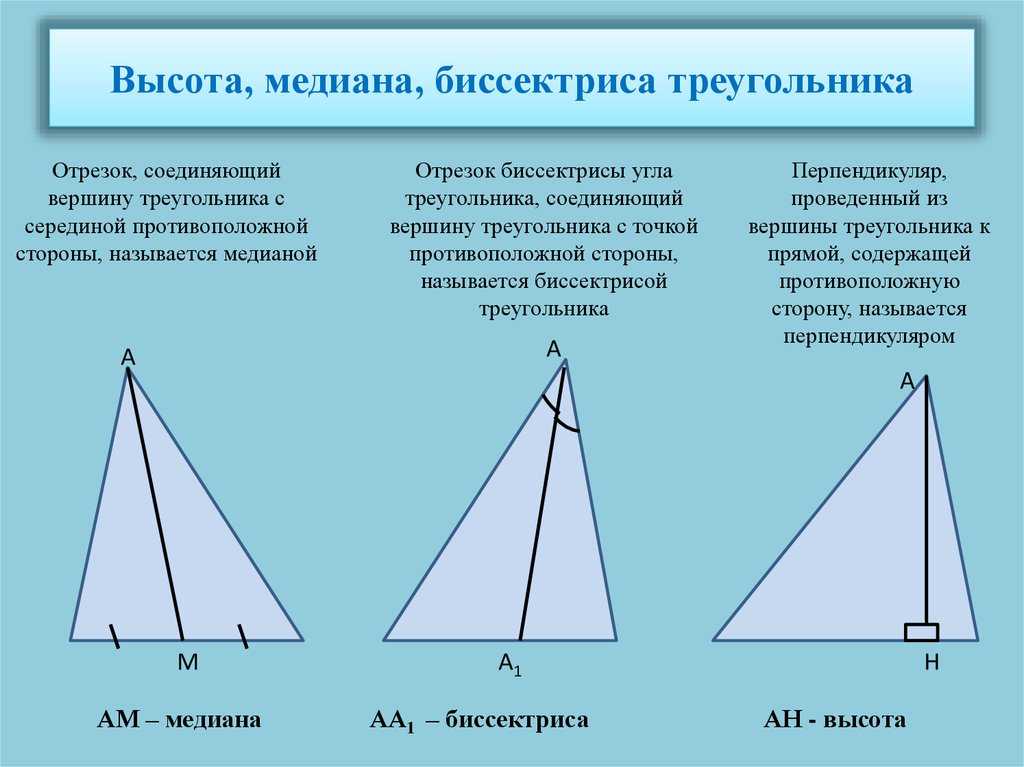
Определение 1. Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника. Основанием высоты называют основание этого перпендикуляра (рис.1).

Рис.1

На рисунке 1 изображена высота BD, проведённая из вершины B треугольника ABC. Точка D – основание высоты.

Для высоты прямоугольного треугольника, проведённой из вершины прямого угла, справедливо следующее утверждение.

Утверждение. Длина высоты прямоугольного треугольника, опущенной на гипотенузу, является средним геометрическим между длинами отрезков, на которые основание высоты делит гипотенузу (рис.2).

Рис.2

Доказательство. Углы треугольников BCD и ACD (рис.2) удовлетворяют соотношениям

В силу признака подобия прямоугольных треугольников треугольники BCD и ACD подобны. Следовательно,

Таким образом, длина отрезка CD является средним геометрическим между длинами отрезков BD и AD, что и требовалось доказать.

Высоты можно провести из каждой вершины треугольника, однако у треугольников различных типов высоты располагаются по-разному, как показано в следующей таблице.

Расположение высот у треугольников различных типов

Фигура	Рисунок	Описание
Остроугольный треугольник		Все высоты остроугольного треугольника лежат внутри треугольника.


Прямоугольный треугольник		Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника


Тупоугольный треугольник		Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника

Ортоцентр треугольника

Теорема 1. Высоты треугольника (или их продолжения) пересекаются в одной точке.

Доказательство. Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, параллельную противолежащей стороне (рис.3).

Рис.3

Обозначим точки пересечения этих прямых символами A₁, B₁ и C₁, как показано на рисунке 3.

В силу параллельности прямых AC и C₁A₁, а также BC и C₁B₁ четырёхугольники AC₁BC и ABA₁C – параллелограммы, откуда вытекают равенства

C₁B = AC = BA₁.

Следовательно, точка B является серединой стороны C₁A₁.

В силу параллельности прямых BC и C₁B₁, а также AB и B₁A₁ четырёхугольники AC₁BC и ABCB₁ – параллелограммы, откуда вытекают равенства

C₁A = BC = A₁B₁.

Следовательно, точка A является серединой стороны C₁B₁.

В силу параллельности прямых AB и B₁A₁, а также AC и C₁A₁ четырёхугольники ABA₁C и ABCB₁ – параллелограммы, откуда вытекают равенства

A₁C = AB = B₁C.

Следовательно, точка C является серединой стороны B₁A₁.

Таким образом, высоты треугольника ABC являются серединными перпендикулярами треугольника A₁B₁C₁ (рис. 4),

Рис.4

и в силу теоремы о серединных перпендикулярах пересекаются в одной точке.

Теорема 1 доказана.

Определение 2. Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.

У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.

Расположение ортоцентров у треугольников различных типов

Фигура	Рисунок	Описание
Остроугольный треугольник		Ортоцентр остроугольного треугольника лежит внутри треугольника.
Прямоугольный треугольник		Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла
Тупоугольный треугольник		Ортоцентр тупоугольного треугольника лежит вне треугольника. В ортоцентре тупоугольного треугольника пересекаются не высоты, а продолжения высот треугольника.

Ортоцентрический треугольник

Решим следующую задачу.

Задача. В остроугольном треугольнике ABC проведены высоты AD и BE (рис.5). Доказать, что треугольник DCE подобен треугольнику ABC.

Рис.5

Решение. Рассмотрим треугольники ADC и BEC. Эти треугольники подобны в силу признака подобия прямоугольных треугольников с равными острыми углами (угол C общий). Следовательно, справедливо равенство

Это равенство, а также наличие общего угла C позволяют на основании признака подобия треугольников заключить, что и треугольники DCE и ABC подобны. Решение задачи завершено.

Из подобия треугольников ABC и EDC (рис.5) вытекает важное следствие.

Следствие 1.

Определение 3.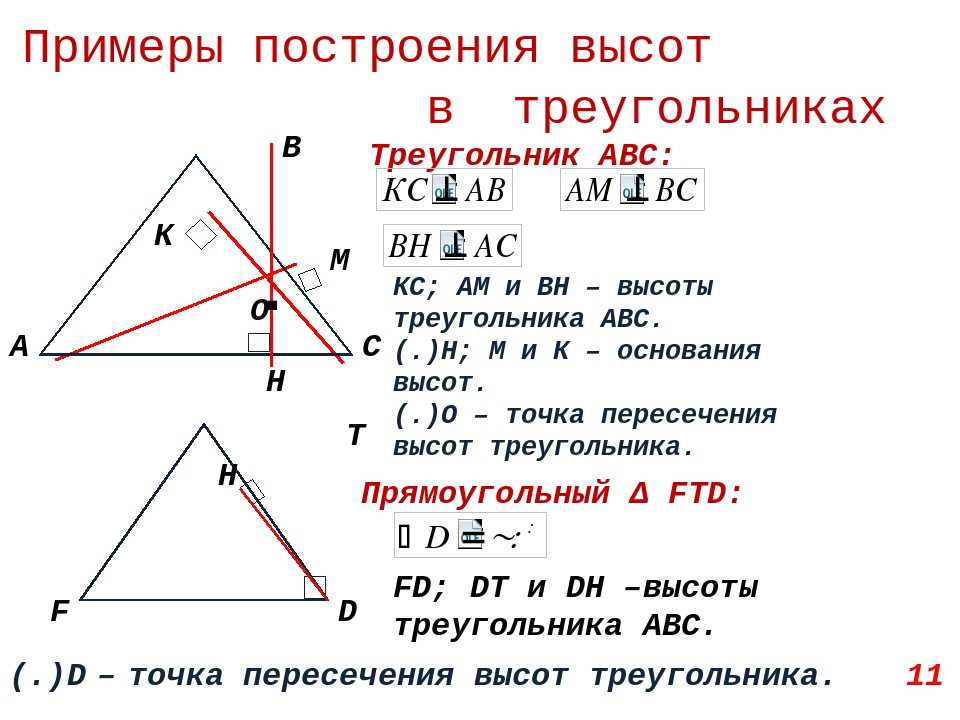 Ортоцентрическим треугольником (ортотреугольником) называют треугольник, вершинами которого служат основания высот исходного треугольника (рис 6).

Рис.6

Из определения 3 и следствия 1 вытекает следствие 2.

Следствие 2. Пусть FDE – ортоцентрический треугольник с вершинами в основаниях высот остроугольного треугольника ABC (рис 7).

Рис.7

Тогда справедливы равенства

Из следствия 2 вытекает теорема 2.

Теорема 2. Высоты остроугольного треугольника являются биссектрисами углов его ортоцентрического треугольника (рис.7).

Доказательство. Воспользовавшись следствием 2, получаем:

что и требовалось доказать.

Задача Фаньяно

Задача Фаньяно. Рассматриваются всевозможные треугольники DEF, вершины D, E и F которых лежат на сторонах BC, AC и AB остроугольного треугольника ABC соответственно.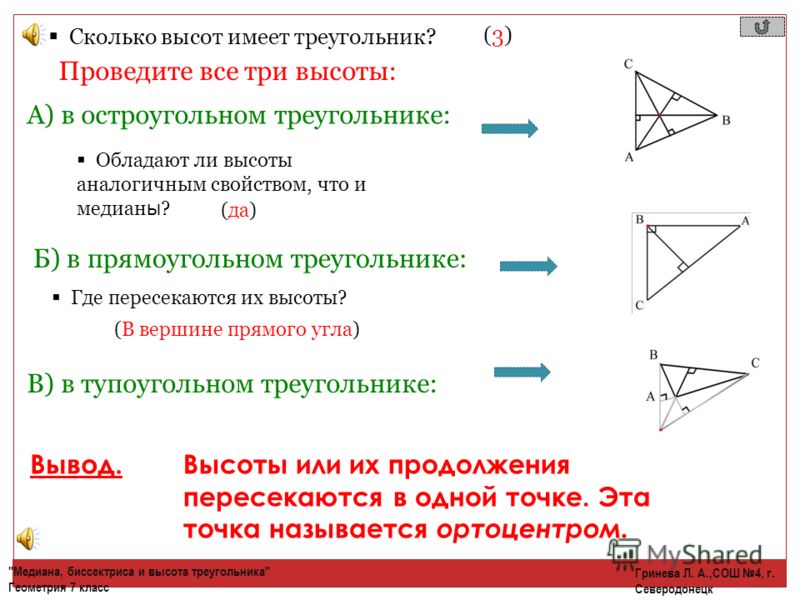 Доказать, что из всех треугольников DEF наименьшим периметром обладает ортоцентрический треугольник треугольника ABC.

Решение. Пусть DEF – один из рассматриваемых треугольников. Обозначим символом D₁ точку, симметричную точке D относительно прямой AC, и обозначим символом D₂ точку, симметричную точке D относительно прямой AB (рис.8).

Рис.8

Поскольку отрезок прямой – кратчайшее расстояние между двумя точками, то периметр треугольника DEF оказывается не меньшим, чем длина отрезка D₁D₂. Отсюда вытекает, что при фиксированной точке D наименьшим периметром обладает такой треугольник DEF, вершины F и E которого являются точками пересечения прямой D₁D₂ с прямыми AB и AC соответственно. Периметр этого треугольника равен длине отрезка D₁D₂ (рис.9).

Рис.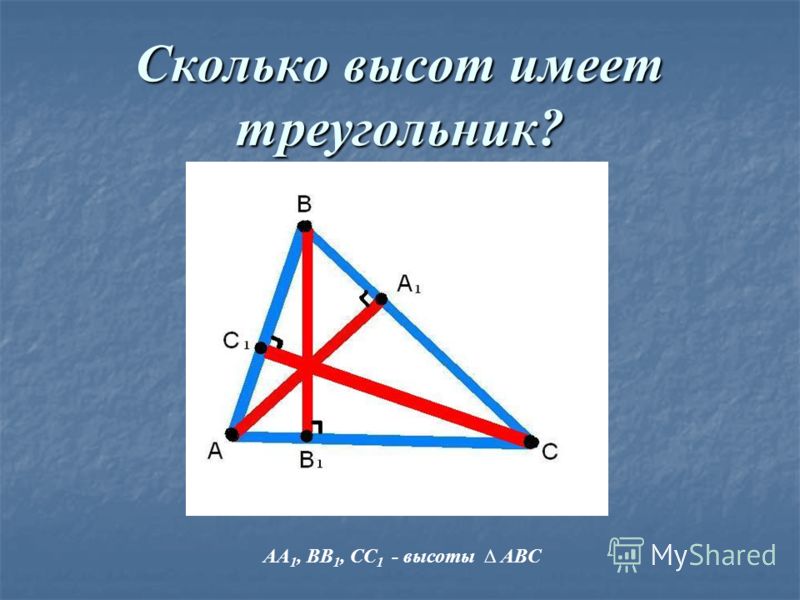 9

Заметим также, что выполнено равенство

AD = AD₁ = AD₂.

Кроме того, выполнено равенство

Поэтому

Отсюда вытекает, что длина отрезка D₁D₂ будет наименьшей тогда, когда длина отрезка AD будет наименьшей, т.е. в том случае, когда отрезок AD является высотой треугольника ABC. Другими словами, наименьшим периметром обладает такой треугольник DEF, у которого вершина D является основанием высоты треугольника ABC, проведённой из вершины A, а вершины E и F построены по описанной выше схеме. Таким образом, среди всевозможных треугольников DEF треугольник с наименьшим периметром является единственным.

Если обозначить длину высоты, проведённой из вершины A, длину стороны AB и радиус описанной около треугольника ABC окружности буквами h, c и R соответственно, то, воспользовавшись теоремой синусов, получим:

Следовательно, наименьший периметр рассматриваемых треугольников DEF равен

Теперь докажем, что ортоцентрический треугольник и является треугольником с наименьшим периметром. Для этого воспользуемся следующей леммой.

Лемма. Пусть DEF – ортоцентрический треугольник треугольника ABC (рис.10).

Рис.10

В этом случае отрезок D₁D₂ проходит через точки F и E.

Доказательство. Заметим, что в силу следствия 2 выполняются равенства:

Кроме того, в силу равенства треугольников DFK и KFD₂, а также в силу равенства треугольников DEL и LED₁ выполняются равенства:

Следовательно,

откуда вытекает, что углы AEF и D₁EL , а также AFE и D₂FK являются вертикальными углами. Это означает, что точки D₁, F, E, D₂ лежат на одной прямой. Лемма доказана.

Доказательство леммы и завершает решение задачи Фаньяно.

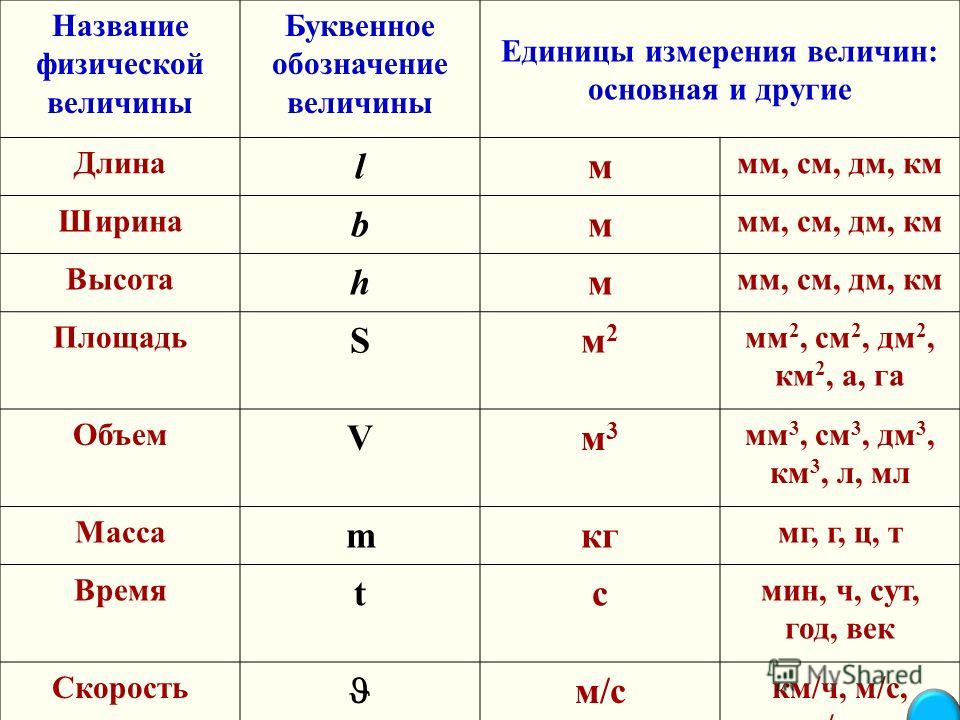
ОБОЗНАЧЕНИЕ: ВЫСОТА, ШИРИНА, ДЛИНА.

ШИРИНА

– От чертежей к реальной жизни.

Длина, ширина, высота, площадь и другие обозначения относятся не только к физическим, но и к математическим показателям. С помощью этих обозначений можно построить чертежи, графики и т. д.

С ними нас знакомят еще в школе, когда мы приходим на урок геометрии, а далее эти обозначения появляются и в алгебре, и на черчении, и на уроке физики.

Если кто забыл, напомню, как обозначаются высота, длина, ширина и площадь, а так же нанесем их на рисунок для наглядности.

Смотрите рисунок.

Вы видите, как построить параллелепипед. На рис. изображено построение параллелепипеда, а так же даны обозначения длины, ширины и высоты. То есть трех (3) измерений.

Где

а – длина;

б – ширина;

h – высота.

В математике и геометрии всегда а, б и h являются неизменными обозначениями сторон любой объемной фигуры. Важно именно наличие объема. Ведь, если речь идет о плоскости, то есть о плоской фигуре, тогда мы видим и рисуем всего 2 измерения: ширину с длиной. Но, если нам задано изобразить геометрическую фигуру с тремя измерениями, обязательно появляется высота, которая всегда обозначается как h.

На рисунке №2 изображен прямоугольный параллелепипед, у которого есть все три обозначения, только вместо привычной h появляется с, обозначающая высоту. И такое обозначение допускается.

Так же, мы можем рассчитать площадь трехмерной фигуры, взяв величины ширины, длины и высоты и умножив их между собой. Получается площадь фигуры.

S= a*b*c, где

S – это площадь фигуры.

На рис. изображен скат, имеющий три величины измерения, как и предыдущие фигуры.

Рассмотрим подробнее каждую из величин и ее обозначение.

Ширина – это линейный размер в поперечном направлении.

Как уже стало известно, ширина обозначается буквой “б”. При чем, по ГОСТу правильно ее обозначать хоть маленькой буквой, хоть заглавной. Ширина является одной из трех пространственных измерений любой фигуры. Однако надо сказать о том, чтобы его замеры снимались в поперечном направлении.

Длина – это линейный размер в продольном направлении.

Измеряется длина как и ширина, в одной и той же единице, например, в метрах, сантиметрах, миллиметрах и т. д. Обозначают длину как “а”, а так же можно встретить и другое обозначение: “L”. Может обозначаться как и ширина, и заглавной буквой, и строчной. Произошло от английского “Lenght”.

Не все фигуры имеют высоту. Если речь идет о двухмерном пространстве, то высоту мы там не найдем, а вот, если дело предстоит с трехмерным пространством, тогда появляется и третье измерение, именуемое высотой. И направление высоты – вертикальное.

В английском языке существует слово, обозначающее высоту, и пишется оно так: “Height”. Поэтому существует международный стандарт, при котором берется первая буква английского слова Height, и обозначается высота как “H”. Как и в предыдущем случае, разрешено использовать и заглавную букву, и строчную.

В некоторых чертежах может встретиться слово “Глубина”. Это то же самое, что и высота.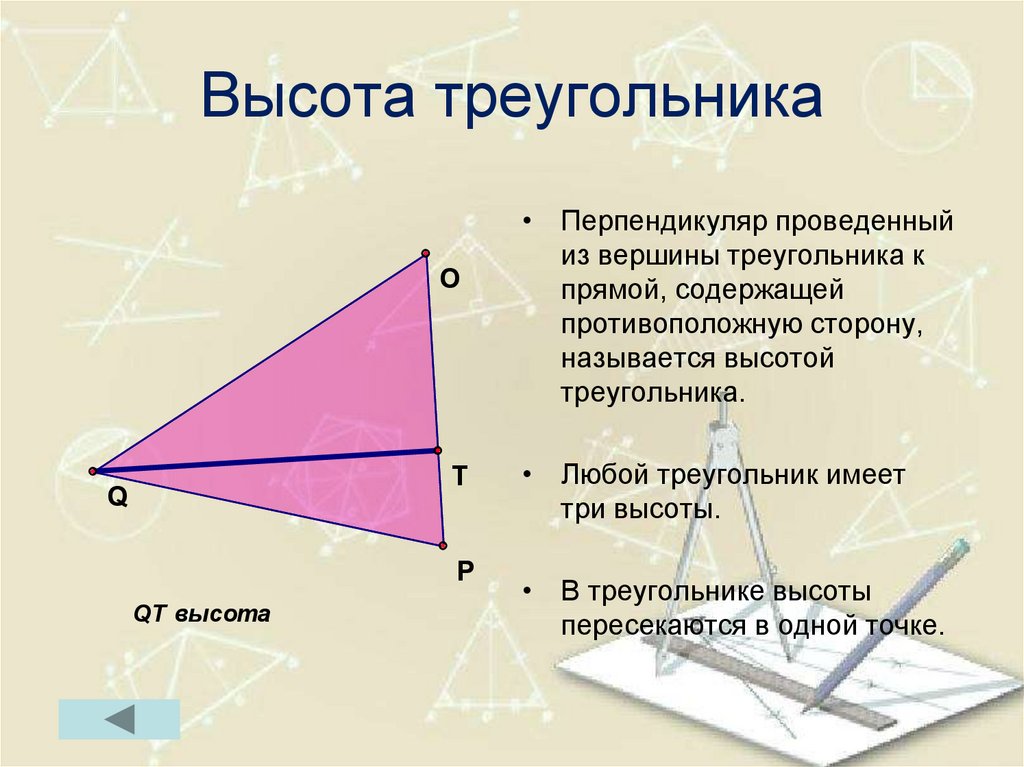 Измеряется высота как и другая фигура, в километрах, сантиметрах, миллиметрах и пр.

Если отстраниться от геометрии, чертежей и математики, то мы легко увидим все то, что только что узнали или вспомнили о трех измерениях, в нашей жизни. Ведь вся наша мебель состоит из длины, ширины и высоты. Взгляните сами.

Вот вам наглядный пример того, что наша мебель имеет все три измерения. Высота обозначается как Н, ширина как В, а длина – L. Известный нам предмет из спальни – кровать, а вместе с ним и матрас. Ведь, когда мы покупаем кровать и другую мебель, мы сталкиваемся с ее размерами, которые должны подходить нам. А матрас подбираем, исходя их размеров кровати.

Видео обзор

Все(5)

Солнечный вегетарий. Проект

Геометрия с нуля 01 – точка, прямая, луч.

Определения, условные обозначения, хитрости.

Урок 1 ) ) ПЕРИМЕТР И ПЛОЩАДЬ КВАДРАТА

Прямоугольный параллелепипед

FIREWATE

Что такое рост в математике? Определение, единицы измерения, примеры, факты

Введение в рост

Рост — это способ измерить кого-то или что-то от основания до макушки или от головы до пят. Другими словами, рост показывает, насколько высок кто-то или что-то. Мы можем сравнить, насколько высокими мы становимся, когда вырастаем. Мы часто сравниваем средний рост мужчин и женщин в разных странах.

В математике высота определяется как расстояние по вертикали от вершины до основания объекта. Иногда его называют «высотой».

Термин “высота” в геометрии относится к измерению объекта вдоль оси Y в координатной геометрии. Некоторые примеры роста в математике показаны ниже.

Высота прямоугольной призмы и треугольника показана на изображении выше.

Как измерить рост?

Мы можем измерить рост объекта или человека с помощью различных измерительных инструментов. Некоторые инструменты для измерения длины по вертикали:

1. Линейка

Линейки имеют прямые края и жесткие. Одна сторона линейки имеет отметки в дюймах, а другая сторона – в сантиметрах. Линейки хорошо использовать для более коротких длин, таких как длина карандаша или блокнота.

2. Рулетка

Рулетка представляет собой гибкие прямые края с градуированной маркировкой. Поскольку большинство рулеток измеряют только одну систему единиц (американскую или метрическую), вам нужно найти ту, которая использует нужную вам систему единиц.

3. Критерий

Резиновые и измерительные линейки аналогичны по структуре. Оба имеют прямые края и жесткие. Метры измеряют все длины до 1 метра, а аршины измеряют все измерения до 3 футов.

Единицы роста

Наш мир состоит из крошечных существ, от божьих коровок в саду до могучих китов в море! Измерение их высоты в одних и тех же единицах может оказаться непростой задачей.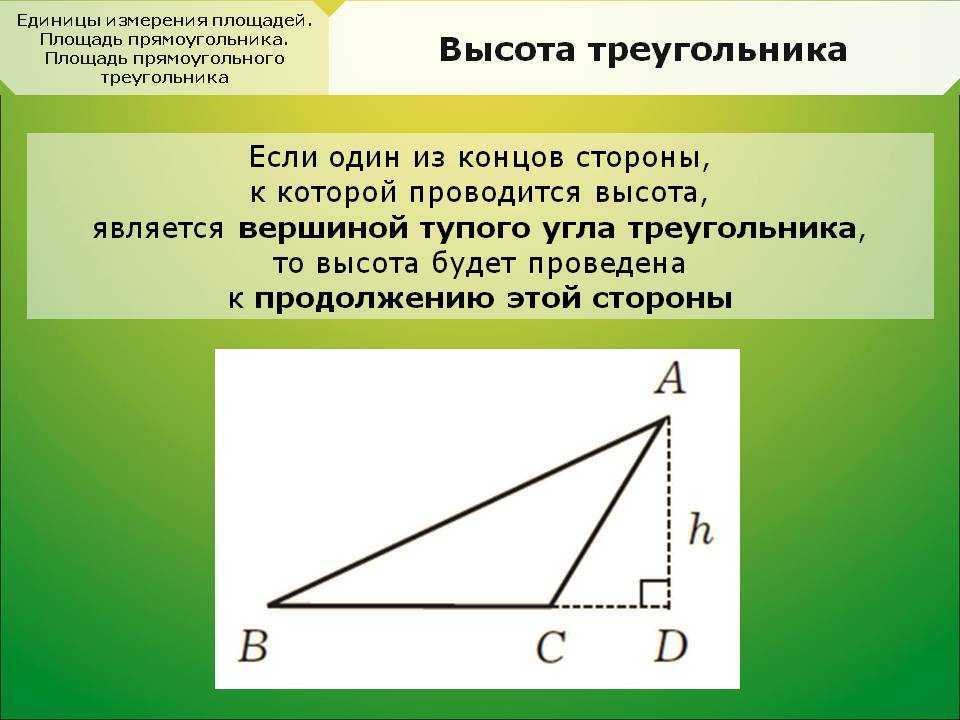 Итак, мы используем разные единицы измерения, чтобы упростить работу. Некоторыми единицами измерения являются метры (м), футы (футы или ‘), дюймы («) и так далее.

При описании вертикальной длины различных объектов лучше всего использовать соответствующие единицы измерения.

Мелкие предметы, такие как ластик или ноготь, можно измерять в миллиметрах или сантиметрах.
Соответствующими единицами измерения роста человека являются футы и дюймы или сантиметры.
Такие единицы, как метры или футы, используются для измерения высоты памятника или здания.

Определение одинаковой высоты

Говорят, что два или более объектов имеют одинаковую высоту, если каждый из них равен другому.

Например, мы обычно живем в прямоугольной комнате. Если мы внимательно посмотрим и сравним стены, то увидим, что высота каждой стены одинакова.

Как узнать, имеют ли два объекта одинаковую высоту

Мы можем использовать различные инструменты измерения, такие как шкала или дюймовая лента, чтобы измерить размер и проверить, имеют ли два объекта одинаковую высоту.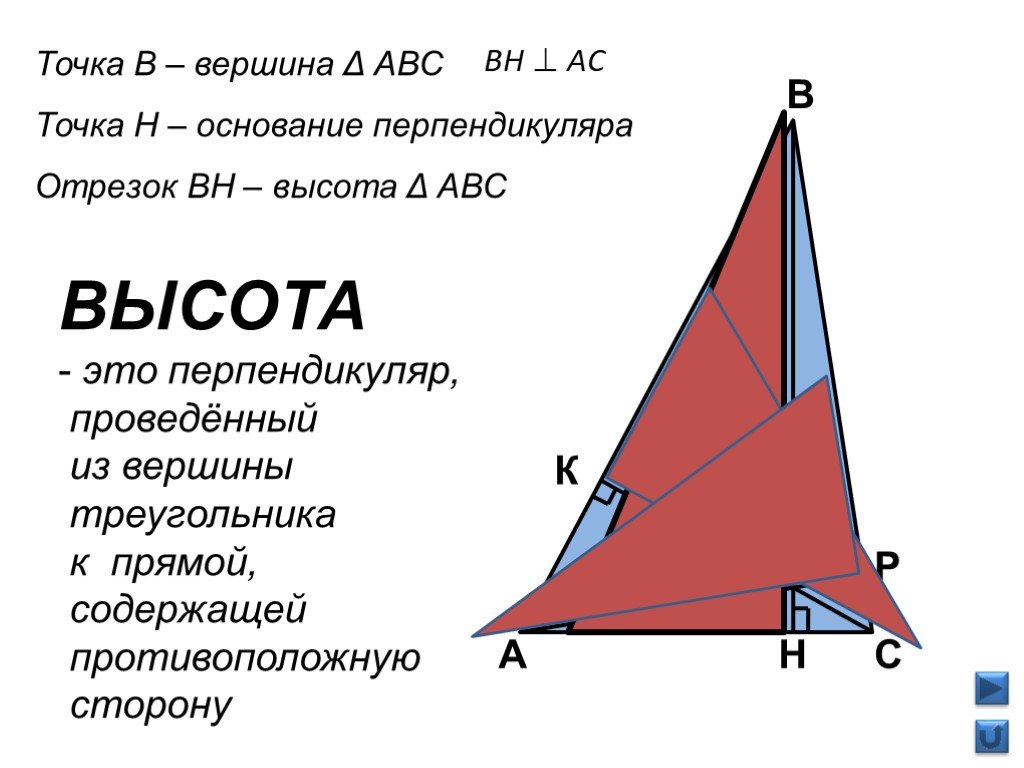 Иногда мы не можем напрямую проверить, имеют ли объекты одинаковый размер, потому что они измеряются в разных единицах. Ниже приведены шаги, с помощью которых мы можем проверить, имеют ли две или более вещи одинаковую высоту или нет —

Шаг 1: Преобразуйте единицы измерения и сделайте их одинаковыми.

Шаг 2: Сравните высоты объектов в одинаковых единицах измерения.

Преобразование единиц измерения

1 километр (км) $= 1000$ метров

1 метр (м) $= 100$ см $= 1000$ мм

1 сантиметр (см) $= 10$ Миллиметры (мм) $= 0,01$ метр

1 миллиметр $= 0,001$ метр

1 ярд $= 3$ фута $= 36$ дюймов

1 фут $= 12$ дюймов

Например:

Рост Чи 5 футов, а рост Хоппи 48 дюймов.

Мы знаем, что 1 фут $ = 12 $ дюймов.

Следовательно, 5 футов $= 5 \x 12$ дюймов $= 60$ дюймов.

60 дюймов $\gt$ 48 дюймов

Следовательно, Чи выше Хоппи. Таким образом, они не имеют одинаковой высоты.

Происхождение термина: Высота

Высота происходит от слова «высокий», происходящего от древнеанглийского héah и происходящего из протоиндоевропейской языковой семьи.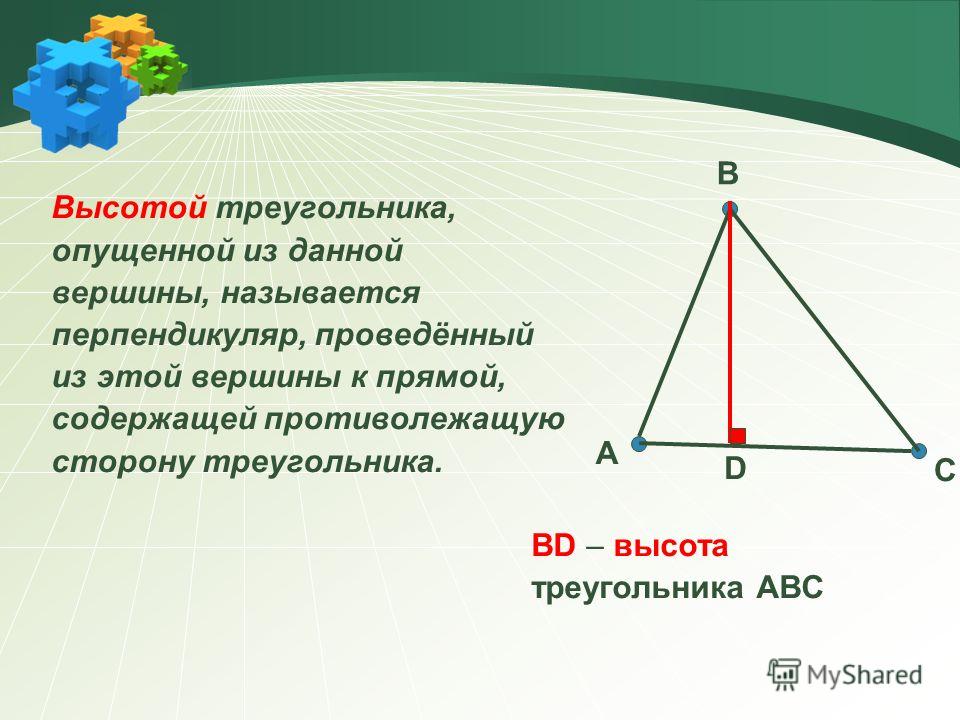

Забавные факты!

Высота измеряется по вертикальной оси на графике.
Высота над уровнем моря называется высотой.

Советы по освоению понятия роста

Если вы хотите, чтобы ваш ребенок выучил понятие роста, вот несколько вещей, которые могут помочь:

Расскажите им о сходствах и различиях между формами и размерами.
Ежедневно используйте такие термины, как «меньше» или «выше», чтобы помочь им понять концепцию легко и быстро.
Сделайте это увлекательным заданием. Попросите ребенка измерить каждую мягкую игрушку и расположить их от самой низкой до самой высокой или наоборот.

Давайте сделаем это!

Вместо того, чтобы раздавать детям листы с заданиями по математике, чтобы научить их понятию «рост», выберите веселые и увлекательные способы понять это понятие. Вы должны пойти на SplashLearn, поскольку они верят в то, что привнесут обучение в мир вашего ребенка! Они легко объясняют каждую концепцию, поэтому вашему ребенку понравится учиться, а самое приятное то, что он может посещать занятия в комфортной обстановке.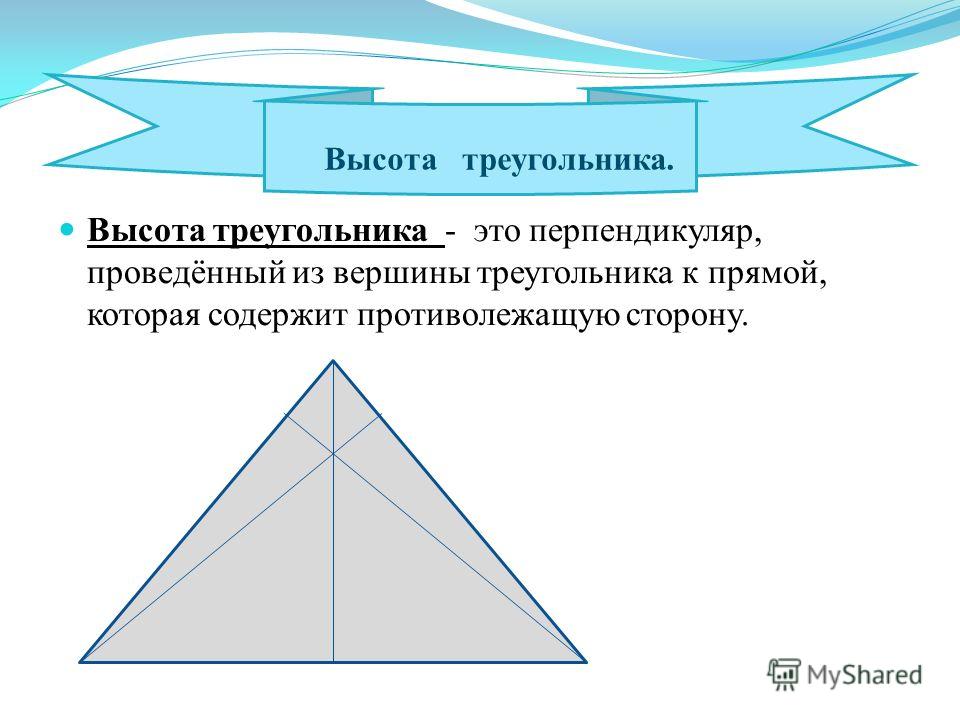

Повеселитесь и попросите ребенка встать перед стеной. Теперь попросите ребенка отметить верхнюю часть головы каждого. Расстояние от ступней до макушки головы будет называться «Высотой».

Длина, Ширина

Решенные примеры

Какое дерево самое короткое?

Решение: Расположив дерево в порядке возрастания, от самого короткого к самому высокому, получим

Дерево B $\lt$ Дерево A $\lt$ Дерево C. Следовательно, дерево B является кратчайшим деревом.

Высота черного стула составляет 26 дюймов, тогда как высота синего стула составляет 66,04 см. Какой стул короче?

Решение: Высота черного стула $= 26$”

1 дюйм $= 2,54$ см

26 дюймов $= 26 2,54$ см $= 66,04$ см (синий стул)

они имеют одинаковую высоту.

Рост Тома 1 м 35 см, его сестра на 40 см ниже Тома. Найдите рост его сестры.

Решение: рост Тома 1 м и 35 см $= 135$ см.

Его сестра на 40 см ниже Тома.

Итак, рост его сестры 135 см $- 40$ см $= 95$ см.

Практические задачи

Найдите высоту лампы на данном рисунке.

150 см

165 см

170 см

175 см

Правильный ответ: 165 см

Рост Джерри 1 м 25 см, его сестра выше Джерри на 50 см. Найдите рост его сестры.

135 см

165 см

175 см

180 см

Правильный ответ: 175 см
Джерри ростом 1 м и 25 см или 125 см. Его сестра на 50 см выше Джерри. Итак, рост его сестры $125\text{см} + 50\text{см} 175$ см.

Сравните высоты и заполните пропуск правильным символом? 29 футов ____ 348 дюймов

$\gt$

$\lt$

Ничего из этого

Правильный ответ: =
Так как 1 фут $= 12$ дюймов 29 футов $= 348$ дюймов

Часто задаваемые вопросы

В чем разница между «одинаковым ростом» и «одинаковым весом»?

Точная высота означает, что длина сверху вниз одинакова для двух или более объектов/людей.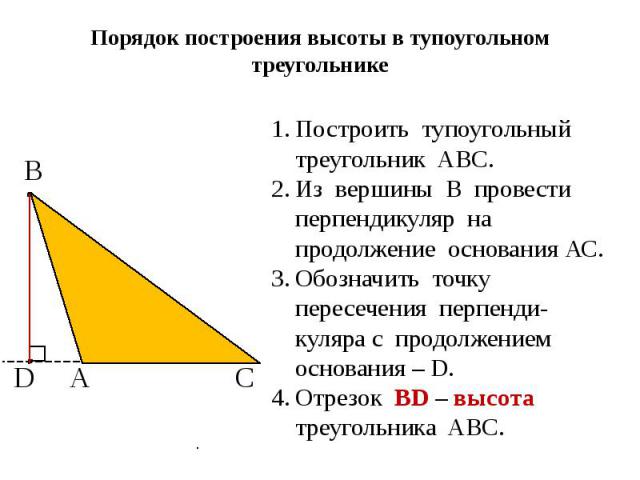 Напротив, одинаковый вес означает, что два объекта/человека весят одинаково.

В чем сходство длины и высоты?

И длина, и высота являются линейными измерениями и выражаются в единицах расстояния. У них одинаковые единицы измерения: футы, дюймы, метры и ярды.

Обязательно ли, чтобы два объекта одинаковой длины имели одинаковую высоту?

Нет. Например, две фоторамки могут иметь одинаковую длину, но различаться по высоте.

Какой рост?

Студенты, вероятно, слышали о некоторых соотношениях, которые, как говорят, существуют в организме. Например, часто говорят, что если вы откроете свой широко раскинув руки и измерьте длину от кончиков пальцев одной руки до кончиками пальцев другого и сравните это со своим ростом, двумя измерения равны. Другим примером является утверждение, что если вы Измерьте свой рост и сравните его с расстоянием от пола до ваш пупок, то результирующее соотношение будет примерно 1,618:1, т.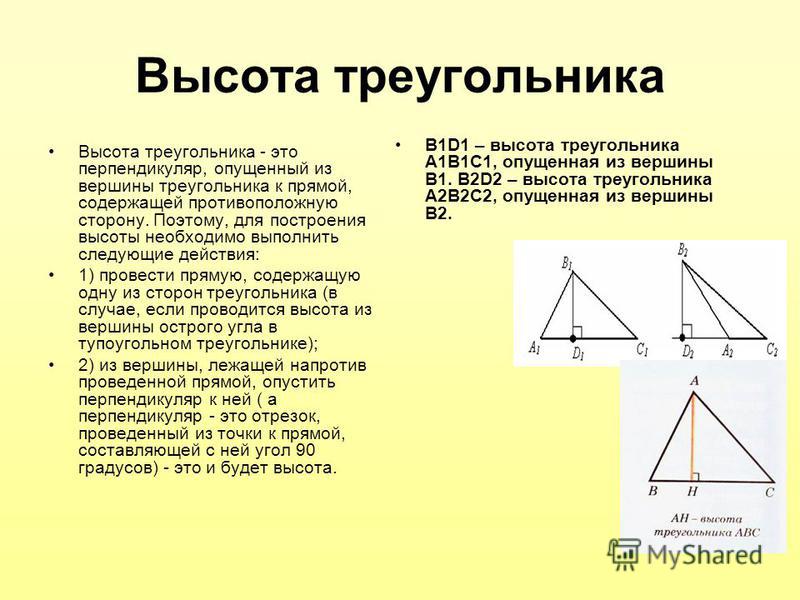 е. также известный как золотое сечение.

Если учащиеся измерят эти соотношения на собственном теле, они могут обратите внимание, что отношения не совсем то, что предсказывают учащиеся, но они, вероятно, довольно близко. Один вопрос, который естественно возникнет Отсюда следует, какое соотношение тел будет ближе всего к тому же самому для каждый человек? Эта деятельность позволяет учащимся найти ответ. Все отношения, которые они будут исследовать, сравнивают размеры тела с ростом. Этот позволит учащимся узнать, какое измерение тела является лучшим предсказатель высоты.

Сбор данных

Во-первых, вам нужно решить, сколько измерений тела будет записывать каждый учащийся. В листе отчета о классе указаны 10 измерений тела, что позволяет вашему классу выбрать до 4 дополнительных измерений тела для работы. Решите как класс, какие другие измерения могут быть хорошими предикторами.

Рабочий лист отчета по классу

Учащиеся должны работать в парах, чтобы снять мерки друг с друга. Прежде чем учащиеся начнут работать, назначьте каждому учащемуся номер строки в таблице. лист активности, в котором записываются их личные данные. Если у вас больше более 20 учащихся, скопируйте лист с заданиями и измените нумерацию на вторая страница.

Создайте надбавку с помощью листа активности по отчетности класса, чтобы учащиеся могли сообщать свои индивидуальные данные. Однажды заполнение заполнено, каждый студент или пара должны скопировать все данные на свой лист активности.

Анализ данных

Разрешить учащимся продолжать работу в тех же парах. Назначьте каждой паре одно измерение тела для исследования. Распространите какой рост? Лист активности для всех учащихся. Назначьте каждой паре измерение тела сравнить с высотой. Если у вас меньше параметров тела, чем у студента пары, назначать конкретное измерение двум или более парам и иметь эти пары сравнивают свои результаты перед докладом классу. если ты имеют больше измерений тела, чем учащиеся, назначьте более одного измерение каждой паре учащихся.

Какой рост? Рабочий лист

Для вычисления коэффициента корреляции r и линейного уравнения y = m x + b учащиеся могут использовать апплет Line of Best Fit или графический калькулятор, в зависимости от технологии, доступной в ваш класс.

Линия апплета наилучшего соответствия

Когда учащиеся начнут вычислять r и y = m x + b , спросите их, какое измерение должно быть независимым ( x ) переменная и которая должна быть зависимой ( y ) переменная. Биологически говоря, ваш рост не определяет длина вашей стопы, а длина вашей стопы не определяет ваш рост — они оба контролируются вашим генетическим составом. Может быть корреляцией между этими величинами, но никто не определяет Другой. Однако в этом упражнении учащиеся прогнозируют рост. цель состоит в том, чтобы определить рост, когда вы уже знаете другое измерение, делая рост зависимым от этого другого измерения. Другой измерение (например, длина стопы) является, таким образом, независимым (

x ) переменная.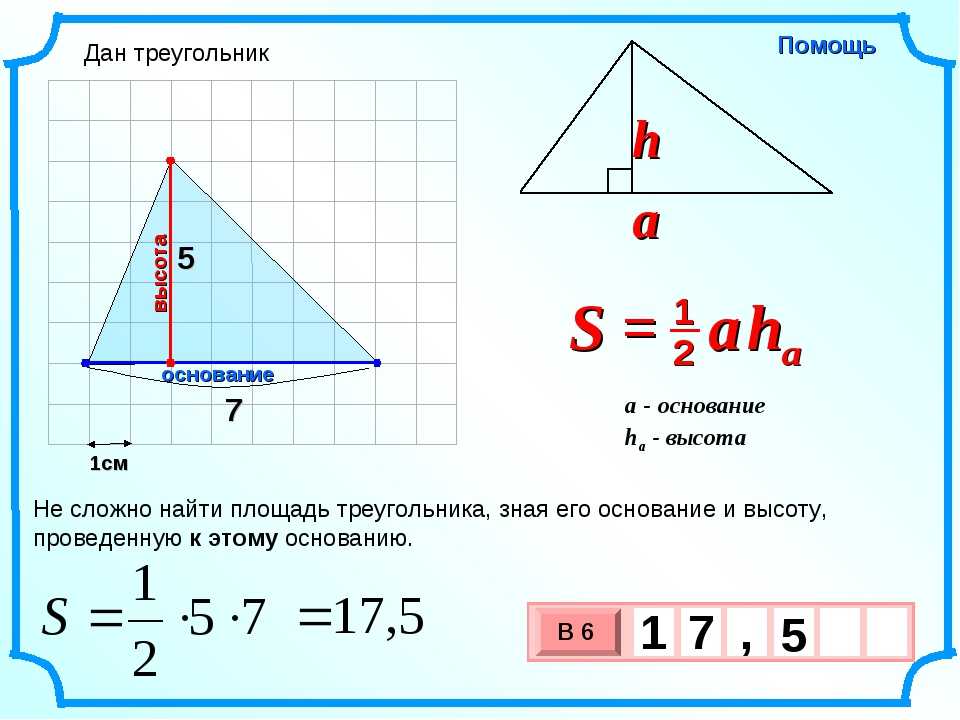

Обсудите с учащимися значение коэффициента корреляции r . Он измеряет, насколько данные близки к формированию идеальной линии. Чем ближе значение r к 1 или –1, тем ближе данные к формированию линии. Если р равен 0, данные не имеют корреляции, что означает, что переменные не связаны друг с другом, и нет единой линии, которую можно провести через все точки данных. График, который производит r – значение, ближайшее к 1, представляет собой лучший показатель роста для вашего класса.

Группы учащихся должны сообщить r -значения и линейные уравнения для их измерений на вопросе “Какой рост?” Накладные расходы. Затем учащийся может скопировать данные в свой «Какой рост?». Листы активности. Если вы хотите собрать эти рабочие листы позже, убедитесь, что учащиеся отмечают, за какие измерения они несут ответственность.

Какой рост? Накладные расходы

Дайте учащимся время на обсуждение вопроса 1 на тему “Какой рост?” Рабочий лист, а затем обсудите этот вопрос в классе.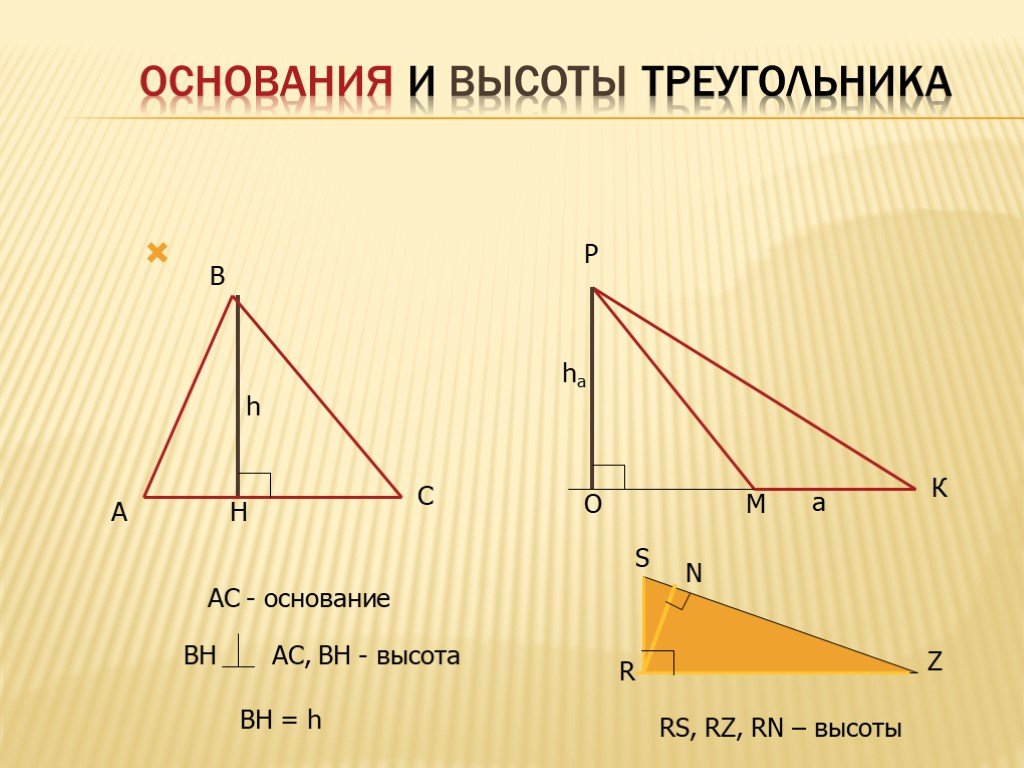 Измерение, которое произвело р значение, ближайшее к 1, является ответом, потому что это измерение и рост имеют наибольшую корреляцию. Вы также можете задать эти вопросы во время обсуждение:

Что произойдет, если есть 2 похожих значения r ?
[Если 2 r -значения точно равны, ваш класс может сделать вывод, что они одинаково хорошо предсказывают рост. Ан интересный дополнительный вопрос в этой ситуации: что коэффициент корреляции между этими двумя измерениями тела?]
Если есть 2 r -значений, которые примерно равны, какая разница потребуется, чтобы определить, какой из 2 измерения на самом деле лучший предсказатель? Тысячная? А сотый? Десятый?
[На этот вопрос очень сложно ответить в абсолютный смысл. Возможно, вы захотите поддержать дискуссию о том, как точные студенты считают, что их измерения были. Могли ли они быть отклонился на сантиметр? миллиметр? Студентам было бы разумно верить, что их измерения точны с точностью до сантиметр. Глядя на их r -значения, то они могли бы сделать вывод, что значения, близкие к ближайшим сотым, можно считать равными.]

Чтобы проверить результаты вашего класса, пригласите учащихся (того же возраста) в из другого класса, и пусть ваши ученики измерят их на конкретных измерение тела, которое было лучшим предиктором роста. Иметь свой затем учащиеся используют линейное уравнение, чтобы предсказать высоту посетители. Затем ваши ученики могут измерить рост посетителей, чтобы посмотрите, насколько точен их предсказатель роста. Предложите учащимся записать свои ценности и ответьте на вопросы 2 и 3 в разделе “Какой рост?” Лист активности. Если трудно привлечь других студентов, учащиеся выполняют эту часть задания с другом или семьей член дома.

Если результаты измерения другого учащегося не соответствуют ожидается, найдите время, чтобы обсудить, почему это может быть. Некоторые возможности находятся:

Люди растут неравномерно — разные части тела растут с разной скоростью. Это называется аллометрическим ростом.
Предсказатель высоты делает прогноз на основе население класса, а не характеристики одного физическое лицо.
При этом гендерные различия не учитывались активность. Может быть другое измерение тела, которое лучше предиктор для одного пола, чем для другого.

Вопросы для студентов

1. Что означает r ?

[Значение r называется коэффициентом корреляции. Он измеряет, насколько данные близки к формированию идеальной линии.]

2. Как узнать, связаны ли 2 измерения друг с другом?

[Чем ближе r к 1 или –1, тем ближе данные к формированию линии и тем больше одна переменная связана с другой. Если r равно 0, данные не имеют корреляции, а это означает, что значения, нанесенные на график, не связаны друг с другом.]

3. Если бы вы построили график зависимости длины волос от роста и обнаружили, что r = 0. 3, что бы это тебе сказало?

[Существует очень небольшая связь между длиной волос человека и его ростом.]

4. Существуют ли в организме коэффициенты, которые можно использовать для точного предсказания размеров тела?

[Ответом является отношение, которое дает r – значение, ближайшее к 1 для вашей группы учеников. Если бы не было отношений, которые давали бы r -значение близко к 1, то учащиеся могли сделать вывод, что соотношение в организме измерения не могут быть использованы для прогнозирования конкретных размеров тела длины.]

Размышления учителя

Увлеклись ли ученики идеей существования в теле пропорций?
Как на вашем уроке учитывались слуховые, тактильные и визуальные стили обучения?
Этот урок имеет много переходов, встроенных в его структуру. Что сработало с управлением поведением в классе? Что не сработало? Как вы бы изменили то, что не сработало?

Учащиеся должны:

Собирать и отображать данные.
Определение коэффициентов корреляции.
Используйте коэффициенты корреляции, чтобы определить, какой набор данных ближе всего к линейному и, следовательно, является лучшим предиктором.

Общие базовые государственные стандарты – математика

С 6 по 8 класс

6 класс

CCSS.Math.Practice.MP1
Разбираться в проблемах и настойчиво решать их.

CCSS.Math.Practice.MP4
Модель с математикой.

CCSS.Math.Practice.MP5
Стратегически используйте соответствующие инструменты.

CCSS.Math.Practice.MP7
Ищите и используйте структуру.

6-8 класс

7 класс

CCSS.Math.Practice.MP1
Разбираться в проблемах и настойчиво решать их.

CCSS.Math.Practice.MP4
Модель с математикой.

CCSS. Math.Practice.MP5
Стратегически используйте соответствующие инструменты.

CCSS.Math.Practice.MP7
Ищите и используйте структуру.